Вектор скорости как найти: Скорость в физике, теория и онлайн калькуляторы

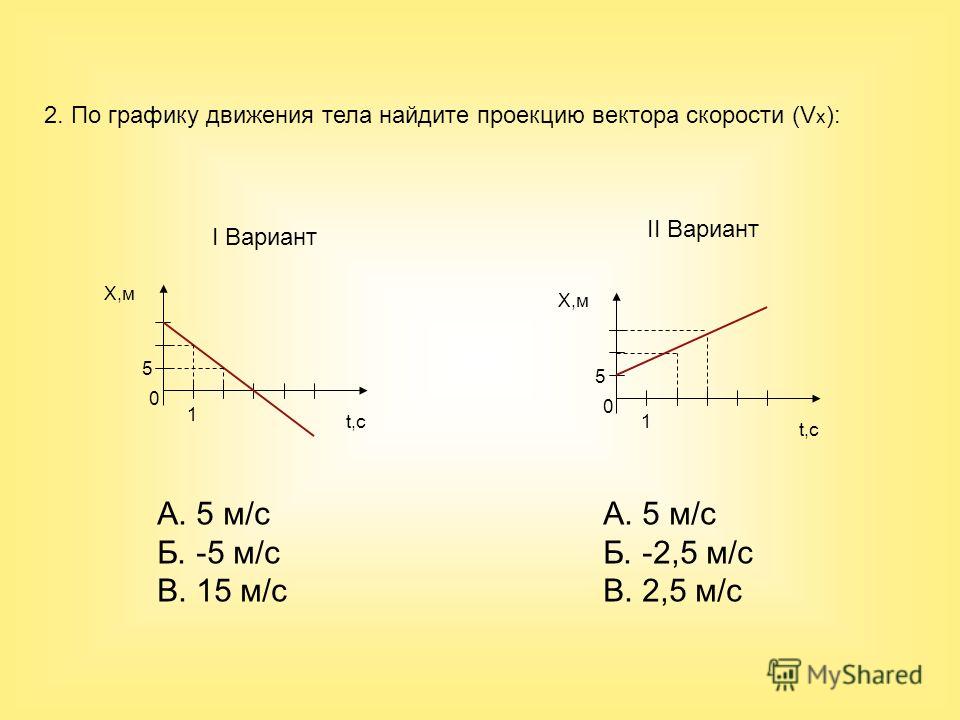
1.2. Кинематика

1.2.1. Кинематика точки
Основные положения. Кинематика – раздел теоретической механики, в котором изучается механическое движение, без учета масс и приложения сил. Всякое движение тел происходит в пространстве и во времени, по отношению к другим телам, с которыми жестко связывают систему координат, называемую системой отсчета. Абсолютно неподвижных тел в окружающем нас мире нет, поэтому движение и покой любого тела являются относительными. При изучении движения самолета по аэродрому или при полетах на небольшие расстояния Землю считают неподвижной и связывают с ней систему отсчета. При скоростных полетах на большие расстояния систему отсчета по-прежнему связывают с Землей, но не считают ее неподвижной, а учитывают суточное, а в некоторых случаях и годовое движение. При расчетах движения космических кораблей систему отсчета связывают с Солнцем и так называемыми “непод-вижными” звездами.

Для измерения расстояний в пространстве используют единицу длины – метр.
Время в механике считают скалярной, непрерывно изменяющейся величиной, одинаковой для всех систем отсчета. За единицу времени принята секунда.
Для характеристики рассматриваемого движения в механике пользуются понятиями “траектория точки”, “скорость точки” и “ускорение точки”.
Траекторией называют множество последовательных положений движущейся точки в рассматриваемой системе отсчета.
Скоростью точки называют пространственно-временную меру, характеризующую быстроту и направление движения точки.

Ускорением точки называют пространственно-временную меру, характеризующую изменение абсолютной величины и направления скорости. Способы задания движения точки. Определение скорости и ускорения точки. Для задания движения точки в пространстве пользуются каким-либо одним из трех основных способов: векторным, координатным, естественным.
Векторный способ. Положение точки в пространстве однозначно определяется заданием радиуса-вектора , проведенного из некоторого неподвижного центра О в данную точку М. Для определения движения точки должна быть задана вектор-функция аргумента t (рис. 1.43):

(1.40)
Траекторией точки является г о д о г р а ф радиуса-вектора.
Вектор скорости точки в данный момент времени t равен первой производной от радиуса-вектора точки по времени и направлен по касательной к траектории точки в сторону движения (рис. 1.44). (1.41)
Размерность [V] = [длина/время] = L/t = м/с.
С к о р о с т ь – это векторная величина, характеризующая быстроту и на-правление движения точки в данной системе отсчета.
У с к о р е н и е м точки называется вектор, характеризующий быстроту изменения вектора скорости (рис. 1.45) (1.42)
Ускорение точки равно первой производной от вектора скорости или вто-рой производной от радиуса-вектора точки по времени. Вектор ускорения точ-ки всегда направлен в сторону вогнутости траекториии и лежит в так называемой соприкасающейся плоскости.

Рис. 

1.43              Рис. 1.44            Рис. 1.45

Рис. 1.46
Координатный способ. Рассмотрим движение точки в прямо угольной системе декартовых координат. Положение точки М в системе отсчета OXYZ определяется тремя декартовыми координатами точки x, y, z.

уравнения движения точки в декартовых коорди-натах. Обозначим орты осей координат . Проведем из начала координат в движущуюся точку М радиус-вектор, где , тогда

где

проекции вектора скорости точки на неподвижные оси декартовых координат. Модуль и направление вектора скорости V = = (1.45)
; ; (1.46)

Ускорение точки определяем, зная, что

где

проекции ускорения на координатные оси.
Модуль и направляющие косинусы вектора ускорения: (1. 48)
(1.49)Естественный способ. Движение точки определено, если зада-ны (рис. 1.47):
– траектория, положение которой относительно выбранной системы от-счета известно;
– начало и направление отсчета дуговой координаты;
– уравнение движения
s = f(t), (1.50)
связывающее расстояние S движущейся точки от начала отсчета со временем. В общем случае расстояние S не равно пройденному точкой М пути, так как точ-ка может начать движение не из начала отсчета О, а из другого положения (М1). Численное значение скорости
(1.51)
т.е. равно первой производной по времени от расстояния. Знак скорости показывает направление движения точки в данный момент. При знаке “плюс” точка движется в сторону положительного отсчета расстоя-ний и наоборот.

При естественном способе задания движения ускорение точки определя-ют его составляющими, направленными по так называемым естественным осям. Траектория точки, как и любая кривая, имеет три естественные оси (рис. 1.48):
– касательную (орт оси- ) направленную в сторону положительно-го отсчета;
– главную нормаль (орт оси- ) – линию пересечения соприкасаю-щейся и нормальной плоскостей, направленную в сторону вогнутости кривой;
– бинормаль (орт оси- ), перпендикулярную касательной и главной нормали.

Кривизной К кривой в данной точке называют предел отноше-ния угла смежноcти (рис. 1.49) к длине дуги

Величина, обратная кривизне K, называется радиусом кривизны:

                   Рис. 1.47               Рис. 1.48                  Рис. 1.49

Ускорение точки лежит в соприкасающейся плоскости и равно производной от вектора скорости по времени (рис. 1.50). Представим вектор скорости как произведение ее численного значения V на орт касательный :

Первое слагаемое есть касательное ускорение точки, характеризующее изменение вектора скорости этой точки только по модулю:
Рассмотрим второе слагаемое. Величину найдем, взяв предел отношения
Получим ,где – единичный вектор, направленный по главной нормали, p- радиус кривизны траектории.
Тогда – составляющая ускорения точки вдоль главной нормали к траектории называется нормальным ускорением точки и характеризует изменение направления вектора скорости:
(1.55)Нормальное ускорение всегда направлено к центру кривизны траектории

Полное ускорение

(1.56)
Модуль ускорения и его направление определяют по формулам:

(1.57)

или (1.58)

(1.59)

                                                 а                  б

                         Рис. 1.50              

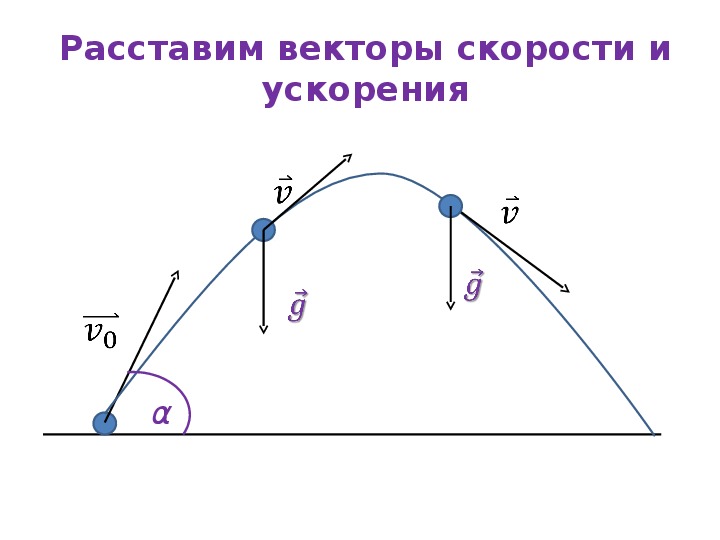
     Рис. 1.51

Движение точки будет ускоренным (рис. 1.51а), если направление векторов скорости и касательного ускорения совпадает, и замедленным (рис. 1.51б), если наоборот.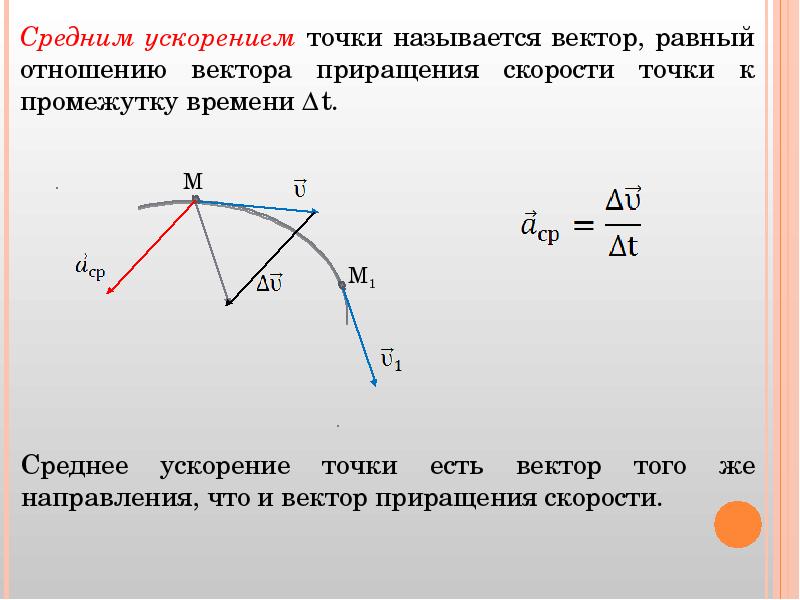

Прямолинейное равномерное движение точки – единственный вид движения, при котором ускорение точки равно нулю

Прямолинейное неравномерное движение точки характеризуется изме-нением скорости по модулю Криволинейное и равномерное движение точки – происходит изменение направления скорости

Криволинейное неравномерное движение точки

Скорость и уравнение равнопеременного движения точки

Уравнение равнопеременного движения точки при

Пример 2.1. Посадочная скорость самолета =140 км/ч, длина пробега после посадки L = 450 м. Найти время t пробега и ускорение

Решение. Для определения ускорения самолета используем уравнение равнопеременного прямолинейного движения точки , т.к. в конце пробега самолет останавливается, то его конечная скорость обращается в нуль

Пример 2.2. Самолет при взлете, разбегаясь по ВПП, движется в соответствии с уравнением , (где S – в м; t – в с) и взлетает через 30 с. Определить ускорения самолета в начальный момент и в момент отрыва , скорость отрыва Vотр и длину разбега L.

Решение. Скорость движения точки равна первой производной от рас-стояния по времени
Ускорение прямолинейного движения (когда отсутствует нормальное ус-корение) равно производной от скорости точки по времени

= dV/dt = 2,2 – 0,006tОтсюда найдем ускорение в начальный момент (t = 0) и в момент от-рыва (tотр = 30c) = 2,2 м/с2 , = 2,2 – 0,006*30 = 2,02 м/с2 .
Скорость отрыва определим, подставляя tотр = 30сДлину разбега найдем
T>

Вектор скорости жидкости – Справочник химика 21

    V = и/и— вектор нормализованной скорости и— вектор локальной скорости и — вектор скорости жидкости в канале. [c.192]

    Линией тока называется линия, касательная к каждой точке которой совпадает с вектором скорости жидкости в этой точке.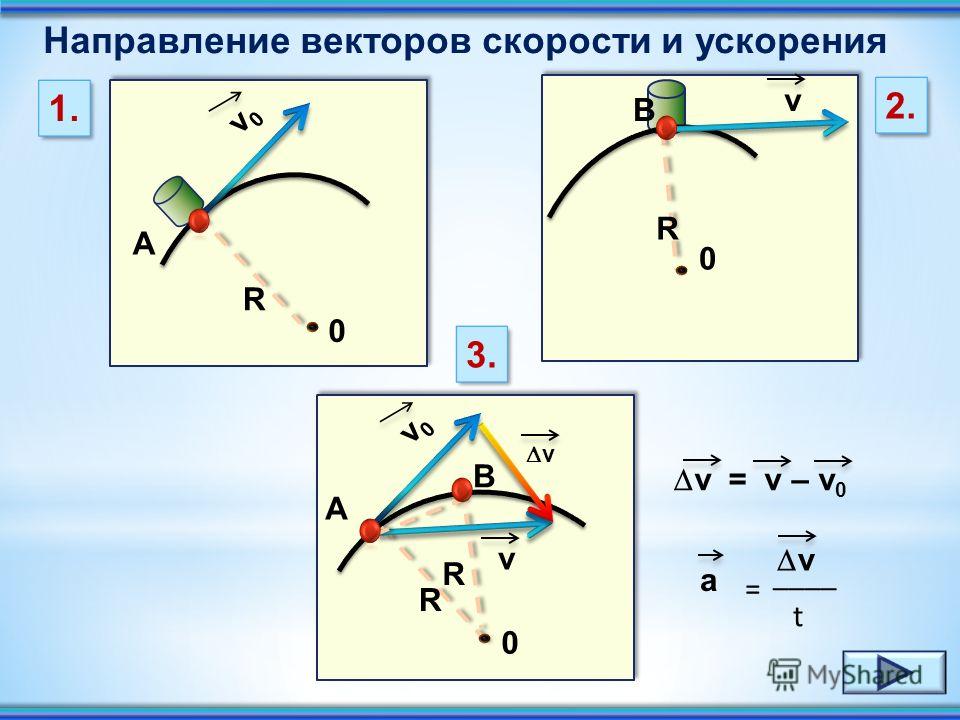 Уравнение линии тока  [c.254]

    Для анализа распределения концентрации в области циркуляции ( )е цилиндрической системы координат г, 0 к новой ортогональной системе координат ф, ф, где координата ф отсчитывается вдоль линии тока. В новой системе координат вектор скорости жидкости будет иметь лишь одну отличную от нуля компоненту V p = Yg

уравнение диффузии (6.1) и граничные условия записываются в виде [c.119]

    Здесь Ух, У у и У 2 — декартовы составляющие вектора скорости жидкости  [c.42]

    Здесь И) (х, у, 2, т) — вектор скорости жидкости, являющейся в общем случае функцией пространственных координат и времени  [c.5]

    Мы начнем с рассмотрения основных уравнений для невязких жидкостей, выведенных Эйлером и Лагранжем. Пусть и = = и(х, t) означает вектор скорости жидкости в точке х в момент времени t. Пусть р(х, t) означает плотность жидкости, g(x, t) — внешнее гравитационное ) поле и р(х, t)—давление в жидкости.  [c.18]

    Из перечисленных типов двухфазных потоков в химической промышленности чаще всего используют газожидкостные системы, которые различают по направлению движения отдельных фаз и по скорости 1) жидкость в целом остается неподвижной (хотя локальные движения жидкости допустимы) 2) жидкость и газ (пар) движутся перекрестным током (перпендикулярно друг к другу) 3) векторы скорости жидкости и газа (пара) направлены одинаково или противоположно (прямоток или противоток). [c.245]

    Если полагать движение стационарным, то решение задачи сводится к интегрированию уравнений движения вязкой жидкости при граничных условиях, предусматривающих равенство нулю всех компонентов вектора скорости жидкости, непосредственно прилегающей к поверхности шара (условие прилипания), а также равенство скорости движения жидкости на бесконечном расстоянии от шара заданной величине скорости стационарного движения шара и. Такие же граничные условия [c.39]

    Вектор скорости жидкости в любой точке винтового канала можно разложить на компоненты Vx, Vy и Vz, которые действуют в направлении, параллельном соответствующим осям.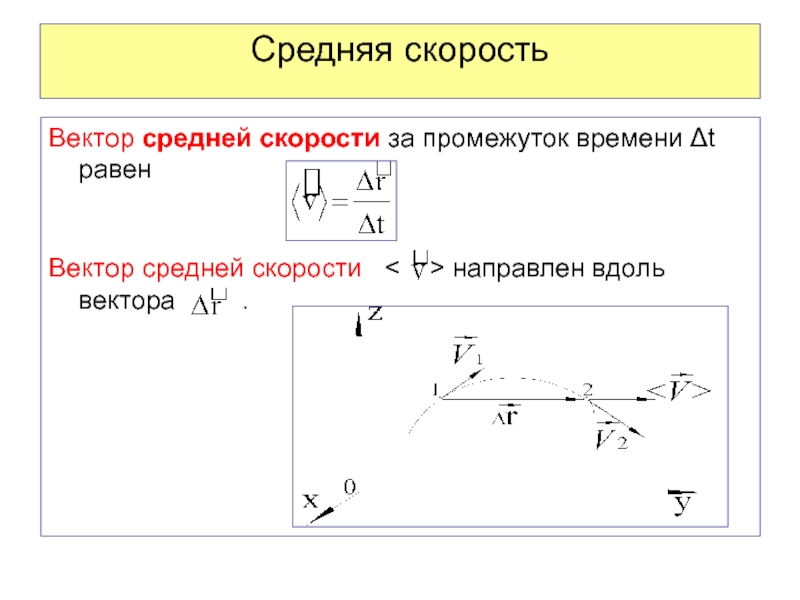 Верхнее основание канала, в котором движется жидкость, представляет собой поверхность цилиндра. Оно движется с постоянной скоростью в плоскости, параллельной плоскости д —z и на расстоянии Я от нее. Его движение описывается вектором скорости V, который направлен перпендикулярно оси A. Величина этого вектора представляет собой скорость на поверхности цилиндра и обозначается через V. Можно записать, Что , [c.249]

    Объемный расход Q можно получить интегрированием компоненты г вектора скорости жидкости по поперечному сечению канала, перпендикулярному оси г. Математически это выразится уравнением [c.253]

    Вектор скорости жидкости [c.259]

    Так как движение частицы жидкости в канале червяка чрезвычайно сложно, то полный анализ этого движения до настоящего времени не проведен. В данном разделе рассматриваются различные компоненты вектора скорости жидкости и на основании этого делаются выводы, касающиеся движения частиц жидкости в канале червяка.  [c.259]

    IO-3. Вектор скорости жидкости 261 [c.261]

    Таким образом, линию тока можно определить как линию, в каждой точке которой в данный момент вектор скорости жидкости к ней касателен. [c.116]

    Таким образом, линию тока можно определить как линию, в каждой точке которой в данный момент вектор скорости жидкости к ней касателен. Дифференциальное уравнение линий тока будет [c.86]

    Возьмем в жидкости точку Л, принадлежащую замкнутому контуру длиной I (рис. 52) вектор скорости жидкости гш в точке А, а касательная к контуру К. Угол, образованный между вектором скорости ы> и касательной к, обозначим через а. Если взять сумму произведений проекций скорости на соответствующую касательную в каждой точке контура на элемент длины линии контура й1, то получим так называемую циркуляцию по контуру  [c.100]

    V — вектор скорости жидкости в рассматриваемой точке пространства (составляющие V . и V,, этого вектора определяются, по предположению, известными формулами Адамара — Рыбчинского [6]) D — коэффициент диффузии к — константа скорости химической реакции. Если направить полярную ось в сторону, противоположную направлению движения капли, и предположить, что число Пекле Ре = и RID (U — скорость движения цеНтра тяжести капли) велико по сравнению с единицей, то в приближении диффузионного пограничного слоя, т. е. с точностью до членов нулевого порядка по параметру е = [(1 -Ь д, )/Ре] ( .i — отношение динамических вязкостей внутренней и внешней фаз), уравнение (1) примет вид  [c.146]

    V — вектор скорости жидкости  [c.311]

    Линия тока. Пусть движение жидкости происходит в канале произвольной формы (рис. 19). В момент времени 1 в точке 1 мгновенная скорость жидкости по величине и направлению равна щ. На векторе скорости п выберем точку 2, в которой мгновенная скорость жидкости по величине и направлению определяется вектором 2- На векторе скорости г выберем точку 3 и осуществим аналогичные построения. Соединим отрезки 1-2, 2-3, 3-4 полученной ломаной линии 1-2-3-4 плавной огибающей кривой. Допустим, что отрезки стремятся к нулю. Очевидно, что мы построили кривую а-Ь, для которой в момент времени 1 векторы скорости жидкости в любой ее точке направлены по касательной. Такая линия называется линией тока. При установившемся движении все частички жидкости движутся вдоль этой линии. [c.33]

    На поверхности твердого тела 5, движущегося в потоке вязкой жидкости, выставляется условие прилипания. Это условие равенства вектора скорости жидкости на поверхности тела У д вектору скорости твердого тела Т . Если твердое тело покоится, то = 0. В проекциях на нормаль п и касательную т к поверхности 5 это дает  [c.11]

    Возьмем в жидкости точку А, принадлежащую замкнутому контуру дли1ЮЙ (рис. 65) вектор скорости жидкости ш в точке А, а касатель-1[ая к контуру К. Угол, образованный между вектором скорости т и [c.106]

    Третий интеграл /3 обращается в нуль ввиду условия непротекания жидкости через поверхность частицы (5. 3). Четвертый интеграл /4 также равен нулю в силу представлений (5.10) и (5.40) для функций 4 и которые справедливы вдали от частицы. Шестой интеграл 1 обращается в нуль ввиду равенства (5.10) с учетом того, что интеграл от нормальной составляющей вектора скорости жидкости (г п) по поверхности сферы равен нулю (это следует из условия непротекания (5.3) и уравнения неразрывности (5.4)). Пятый интеграл вычисляется путем предельного перехода при Л оо с учетом асимптотических свойств функций 4 (5.10), (5.18) и 4 (5.40), [c.261]

    Для интервала чисел Рейнольдса 50 больших числах Пекле широкое распространение получила нестационарная циркуляционная модель Кронига и Бринка [36]. 1Сак было показано в предыдущем разделе, конвективная диффузия в основной массе жидкости при больших числах Пекле описывается уравнением (5.3.2.9), которое, однако, не вьшолняется вблизи межфазных поверхностей. Левая часть уравнения (5.3.2.9) представляет собой записанное в принятой системе координат скалярное произведение двух векторов скорости жидкости и и градиента концентрации V . Равенство нулю этого произведевшя означает, что либо абсолютное значение одного из векторов равно [c.282]

    Вид последнего слагаемого в уравненип (I.I) определяется пропорциональностью напряжения вязкого трения Отр значению поперечного градиента скорости dw/dn согласно закону вязкого трения для ньютоновских жидкостей Отр = (dwjdn), в котором направление я перпендикулярно векторам скорости жидкости и силы трения. Для жидкостей с более сложным законом вязкого трения (неньютоновские жидкости) третье слагаемое в уравнении (1.1) будет иметь более сложную форму. [c.7]

    Составим уравнение движения жидкости п частитл. Обозначил через Р силу, действующую на частицу со стороны жидкости. Частица и жидкость образуют замкнутую систему. Пусть VI —вектор скорости частицы, а Уо — вектор скорости жидкости в том месте, где находится частица. [c.182]

    Для дальнейшего изложения окажется полезным переписать уравнение (1.1) в несколько более полной форме. Касательное напряжение, прилагаемое в направлении х к поверхности слоя жидкости, расположенного на расстоянии у от нижней пластины, обозначим через Хух1 а компонент вектора скорости жидкости но координате X — через Ух- Заметим, что не равно ду дх. В тексте книги для указания дифференцирования компонентов скорости нижни  [c.23]

    Рассмотрим сначала злектроосмос. Сложные распределения электрического поля и скорости жидкости в порах мембран хаотической структуры не могут быть определены теоретически. Однако если жидкость перетекает в порах только под действием приложенного извне электрического напряжения, то для мембран с широкими порами можно найти зависимость вектора скорости жидкости (г) от напряженности электрического поля Е (г) в каждой точке перового пространства мембраны, характеризующейся радиусом-вектором г и лежащей вне двойного электрического слоя. Эта зависимость следует из подобия электрических и гидродинамических полей порового пространства мембраны [78, 79], согласно которому (/) пропорционально Е (г). Для того чтобы найти коэффициент пропорциональности, воспользуемся соотношением (5.129). Учитывая, что это соотношение для Ар=0 и точек, лежащих вне двойного слоя, когда (/ ) =0, преобразуется к виду и = е/Ео ДС//р,/1, получаем  [c.208]

    Как уже упоминалось, непосредственное измерение окружных скоростей в камере закручивания центробежной форсунки представляет большие трудности. Вместе с тем анализ уравнений движения жидкости в форсунке показывает, что при определенных условиях, а именно, когда радиальная и поступательная соста-вляюш,ие вектора скорости жидкости в камере малы по сравнению с окружной составляюш,ей, между давлением и окружной соста-вляюш,ей скорости суш,ествует однозначная связь, подчиняюш,аяся уравнению (1.56). Однозначная зависимость между р и Уф позволяет обойти экспериментальные сложности, связанные с непосредственным измерением Уф, и предложить способ косвенного ее определения измерением распределения давления в камере закручивания с последуюш,им вычислением Уф.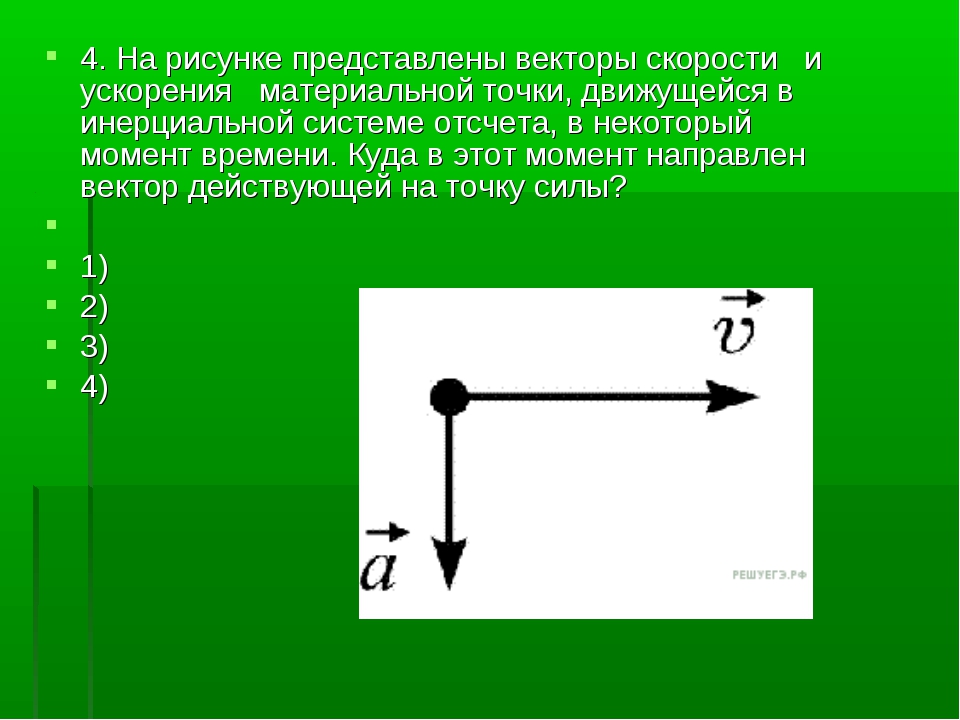  [c.52]

    Во всех методах расчета угод расшишвания а определяется отношением тангенциальной и осевой составляющих скоростей, но в связи с тем, что указанные составляющие вектора скорости жидкости на срезе выходного сопла определяются различно, форп мулы для вычисления а имеют разный вид. [c.105]

    Вводя вектор скорости жидкости У = г Ух + гуУу + г У , где гх, у, % — единичные направляющие векторы декартовой системы координат, и используя символические дифференциальные операторы [c.10]

    Во всех описанных выше трех случаях функция тока зависит только от двух ортогональных координат. Линии тока определяются равенством Ф = onst. Каждой линии тока отвечает постоянное значение функции тока. Вектор скорости жидкости направлен по касательной к линии тока. (Отметим, что с траекториями жидких частиц линии тока совпадают только в стационарном случае.) [c.15]

---

Скорость и ускорение в сферических координатах

Движение в пространстве может быть задано, если известен закон изменения трех декартовых координат x, y, z в качестве функции времени.

Определение 1

Имеются случаи, когда перемещение материальной точки не может быть описано с помощью уравнения движения в декартовых координатах, так как запись становится громоздкой. Тогда следует выбирать три независимые скалярные параметра q1, q2, q3, называемые криволинейными (обобщенными) координатами, которые способны четко определить положение точки в пространстве.

Вектор скорости

Определение точки М во время задания ее движения в криволинейных координатах возможно в виде векторной суммы составляющих скоростей, параллельных координатным осям:

υ=dr→dt=∂r→∂q1q˙1+∂r→∂q2q˙2+∂r→∂q3q˙3=υq1e1¯+υq2e2¯+υq3e3¯.

Запись проекции вектора скорости на соответствующие координаты оси примет вид:

υqi=υ¯·ei¯=Hiqi˙, i=1,3.

Определение 2

Hi=∂r→∂qiM является параметром, называющимся i – м коэффициентом Ламе и равняющимся значению модуля частной производной от радиус-вектора точки по i – ой криволинейной координате, которая была вычислена в данной точке М.

Направление каждого из векторов ei соответствует направлению движения точки конца радиус-вектора ri при возрастании i – й обобщенной координаты.

Определение 3

Расчет модуля скорости в ортогональной криволинейной системе координат рассчитывается по формуле:

υ=υq12+υq22+υq32=h22q˙12+h32q˙22+h42q˙32.

Чтобы вычислить текущее положение точки М, необходимо найти производные и коэффициенты Ламе приведенных формул в пространстве.

В сферической системе координат координатами точки являются скалярные параметры r, φ, θ, отсчитываемые так, как изображено на рисунке 1.

Рисунок 1. Вектор скорости в сферической системе координат

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Ускорение системы

Составленная система уравнений движения точки запишется как:

r=r (t)φ=φ (t)θ=θ (t).

Определение 4

На рисунке 1 показаны радиус-вектор, проведенный из начала координат, углы φ и θ, координатные линии, оси рассматриваемой системы в произвольной точке М траектории.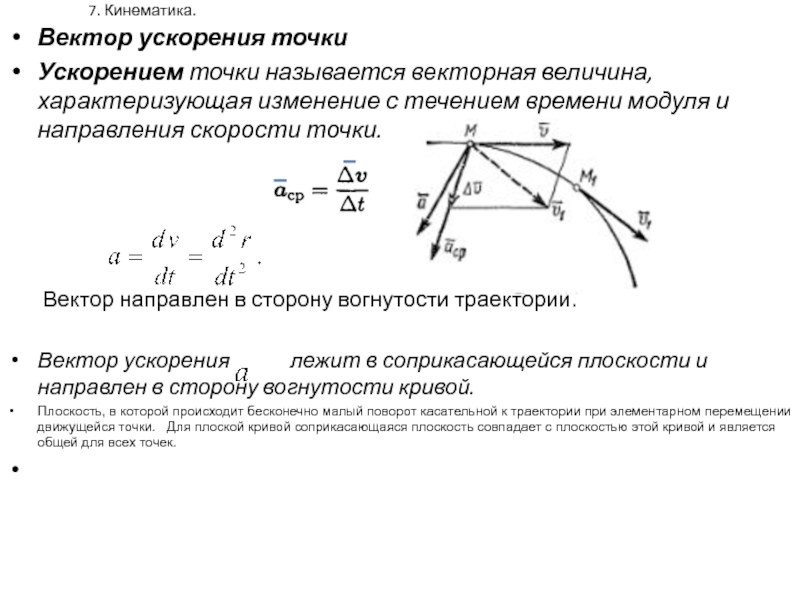

Расположение координатных линий (φ) и (θ) идет на поверхности сферы радиусом r. Данная система получила название ортогональной.

Выражение декартовых координат возможно через сферические:

x=rcosφsinθ; y=rsinφcosθ; z=rcosθ.

Отсюда следует, что коэффициенты Ламе Hr=1; Hφ=rsin φ; H0=r, проекции скорости точки на оси сферической системы координат υr=r˙; υθ=rθ˙; υφ=rφ˙sin θ, а модуль вектора скорости υ=υr2+υφ2+υθ2=r˙2+r2φ˙2+r2θ˙2.

Запись ускорения в сферических координатах примет вид:

a→=arer→+aφeφ→+aθeθ→.

А проекции ускорения точки:

ar=r˙-rθ˙2+φ˙2sin2φ; aφ=rφ¨sin φ+2rφ˙(sin θ+θ˙cos θ);aθ=rθ¨-rφ˙2sinθcosθ+2r˙θ˙.

Изображение модуля ускорения будет равняться a=ar2+aφ2+aθ2.

Пример 1

Задана точка, которая производит движение по линии пересечения сферы и цилиндра по уравнению r=R, φ=kt2, θ=kt2, где r, φ, θ являются сферическими координатами.

Произвести поиск модуля и проекции скорости точки на оси сферической системы координат.

Решение

Необходимо найти проекции вектора скорости на оси сферических координат.

Получим:

υr=r˙=0; υφ=rφ˙sin θ=Rk2sinkt2; υθ=rθ˙=Rk2.

Определяем модуль скорости:

υ=υr2+υφ2+υθ2=Rk2sin2kt2+1.

Пример 2

Применив условие предыдущего задания, определить модуль ускорения точки.

Решение

Произведем нахождение проекции вектора ускорения на оси сферических координат.

Получаем, что:

ar=r˙-rθ˙2+φ˙2sin2φ=Rk241+sin2kt2;aφ=rφ¨sin φ+2rφ˙sin θ+θ˙cos θ=-Rk22sinkt2;aθ=rθ¨-rφ˙sinθcosθ+2r˙θ˙=-Rk24sinθcoskt2.

Далее определим модуль ускорения: a=ar2+aφ2+aθ2=Rk244+sin2kt2.

Ответ: a=Rk244+sin2kt2

Вектор скорости – это… Что такое Вектор скорости?

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь v — модуль скорости,  — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью.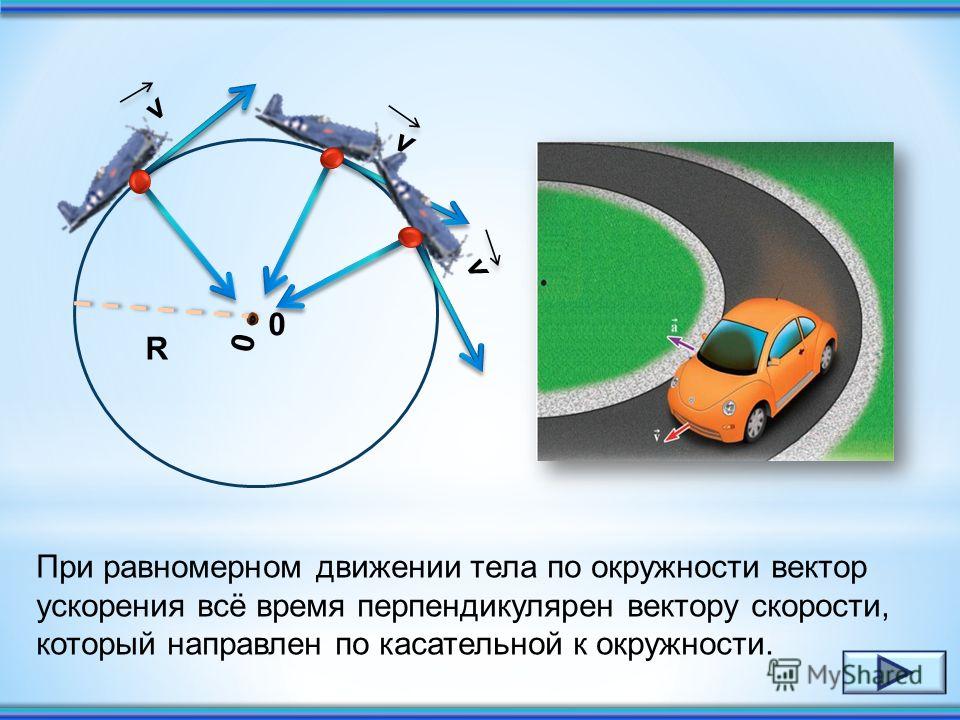 Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела в при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

• 1 м/с = 3,6 км/ч
• 1 узел = 1,852 км/ч = 0,514 м/c
• Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
• c = 299 792 458 м/c

См. также

Wikimedia Foundation. 2010.

Линии и трубки тока

Содержание:

Линии и трубки тока

• Концепция обтекания используется при рассмотрении движения сплошной среды и применении переменных Эйлера. То есть линия, вектор скорости которой параллелен касательной этих линий в каждый момент времени. Если вектор в любой точке линии тока является касательным к этой линии, он должен быть параллелен вектору скорости v в этой точке по определению линии тока.

Найти положение равновесия однородного тяжелого бруска длиной 2А, опирающегося на неподвижную точку О, которая расположена в вертикальной плоскости и может скользить, и поместить конец а на вертикальную стенку. Людмила Фирмаль

Два параллельных вектора отличаются только скалярным коэффициентом k (положительным или отрицательным). так Рисунок болезни др = кв. (15) Если проекция вектора dr на оси координат равна dx, dj, dz, уравнение (15) принимает вид: dx = A «x; dy = kvy; dz = kvt. Отбрасывая любой коэффициент k, эти уравнения можно выразить как: dx _ dj> _ dz v, (X, y, z, (15 ‘) Два уравнения (15 ‘) для координат x, y, z в постоянное время t являются линейными дифференциальными уравнениями группы.

• Когда эти уравнения объединяются, отображается произвольная постоянная. Эти разные значения соответствуют разным линиям тока. Если вектор скорости не зависит от времени, семейство линий тока соответствует семейству орбит. Для нестационарного движения это разные семейства линий. Линия тока — это векторная линия в векторном поле скорости точки на сплошной среде. Аналогичные векторные линии могут быть получены для других векторных полей, таких как вихревое векторное поле вектора скорости.

Например, если рассматривать систему кузова, являющуюся железнодорожным поездом, то внешняя сила — это сила веса вагона и Локомотива, действие рельсов на колеса вагона и Локомотива, сила сопротивления воздуха. Людмила Фирмаль

Выберите замкнутый контур L в пространстве, в котором движется сплошная среда (Рисунок 111), и проведите уникальную линию тока через каждую точку, чтобы получить трубку тока. В точках, состоящих из линий тока, скорость точки непрерывной среды направлена ​​против поверхности текущей трубки, поэтому непрерывная среда не может выходить из текущей трубки через ее сторону. Непрерывная среда может входить и выходить из текущей трубки только через концевую секцию. Токовые трубки используются для формулировки некоторых необходимых форм теоремы для движения сплошных сред.

Смотрите также:

Задачи по теоретической механике

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Результирующая скорость – обзор

II.B.2 Экспериментальные методы

II.B.2.a Ударные волны, возбуждаемые взрывом

Интерес к воздействию взрывчатых веществ на материалы возник из соображений военных по поводу стабильной работы этих устройств и позже связанный с этим вопрос о бронепробиваемости. В последнем случае серьезной проблемой стало выкрашивание. Это разрушение части мишени на противоположной стороне от удара из-за разрыва при растяжении внутри, где встретились две волны высвобождения.Интерес к этой области был заметно увеличен необходимостью предсказуемого, хорошо контролируемого использования взрывчатых веществ в исходной последовательности срабатывания атомной бомбы. Именно этот фактор стимулировал накопление большого количества данных о воздействии ударов на различные материалы и стал основой для многих исследовательских программ, проводимых в настоящее время.

Существует два способа взрывного генерирования ударных волн: один, при котором взрывчатое вещество находится в непосредственном контакте с целью, и другой, при котором взрывчатое вещество запускает летучую пластину, которая затем поражает цель. В первом случае важно, чтобы взрывное воздействие достигло всех точек на передней части цели одновременно. Поскольку детонация обычно начинается в точке или вдоль линии, взрывное горение будет происходить вдоль сферического или цилиндрического фронта соответственно. Некоторые коммерческие поставщики взрывчатых веществ предоставляют генераторы линий треугольной формы, которые перфорированы множеством отверстий, которые служат для разделения криволинейного фронта ударной волны на серию множества меньших фронтов, которые приблизительно образуют линию.

Один из видов генератора плоских волн называется «мышеловка» (см. Рис. 7). Он состоит из листа взрывчатого материала, уложенного на тонкую инертную (стеклянную или металлическую) пластину привода, которая наклонена над основным зарядом под углом θ, так что sin (θ) равен v / d , где d – это скорость детонации по листу над приводной пластиной, а v – результирующая скорость пластины от давления, создаваемого взорвавшимися газами.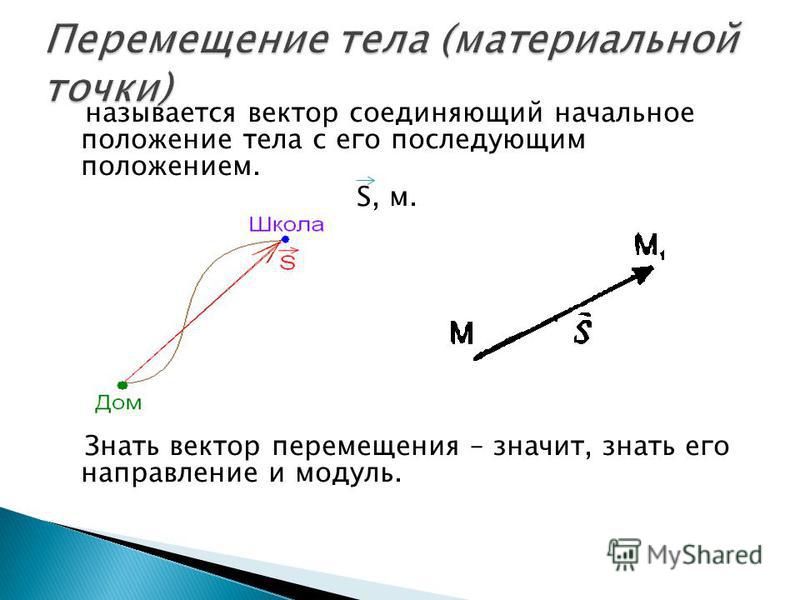 Запущенная на своей верхней кромке, драйверная пластина ударяет по основному заряду одновременно во всех точках и инициирует плоскую детонационную волну, если скорость пластины достаточно велика.Краевые эффекты и вариации конструкции ограничивают плоскостность этого устройства.

РИСУНОК 7. Генератор плоских ударных волн «мышеловка». Взрывчатое вещество A детонирует вдоль его верхнего края и горит в направлении шарнира, генерируя продукты детонации D и движущуюся пластину B к цели C, которая может быть основным зарядом взрывчатого вещества. Угол между ведущей пластиной и мишенью выбирается таким, чтобы его синус был равен v / d , где v – скорость пластины, полученная при детонации A со скоростью d .

Могут быть изготовлены конические линзы взрывчатого вещества, которые будут производить одновременное детонацию на ведущей поверхности с точностью до 0,1 мкс, но результирующий импульс может быть неоднородным. Эти линзы образованы либо конусом взрывчатого вещества над инертным конусом большего угла, либо аналогичным внутренним конусом взрывчатого вещества с меньшей скоростью детонации (см. Рис. 8). В последнем случае базовый угол внутреннего, более медленного взрывчатого вещества α определяется соотношением скоростей детонации (то есть sin α = [ d _из / d _в ]).

РИСУНОК 8. Пластинчатый генератор конической ударной волны. Детонатор A воспламеняет быстро горящее взрывчатое вещество B., которое, в свою очередь, воспламеняет медленно горящее взрывчатое вещество C. Конический угол выбирается таким образом, чтобы его синус был равен отношению скорости C к скорости B, в результате чего в формировании фронта детонации в C параллельно основанию.

Мишень может быть прикреплена непосредственно к поверхности взрывчатого вещества, или она может быть установлена ​​на небольшом расстоянии с помощью летящей пластины, прикрепленной к взрывчатому веществу.Самая простая форма последнего случая – мышеловка, в которой ударная пластина поражает цель, а не основной заряд.

Давление, которое может быть получено с помощью этих методов, составляет до нескольких десятков гаусс-паскалей. Основное преимущество – относительно простая установка и, соответственно, низкая стоимость.

II.B.2.b Guns

Метательные пистолеты, первоначально разработанные для военных целей, представляют собой особый пример летательного аппарата с приводом от взрывчатого вещества. Они также обеспечивают несколько более управляемый механизм, чем описанные выше взрывные методы.Результирующее давление, возникающее при ударе снаряда с плоской головкой о цель, несколько больше, чем давление, достигаемое с помощью летающей пластины.

Легкие газовые пистолеты позволяют лучше контролировать условия удара. В этих устройствах снаряд направляется вниз по откачанному стволу к цели за счет расширения сжатого легкого газа, такого как H ₂ или He. Газ внезапно выходит из резервуара высокого давления в результате разрыва диска за снарядом в казённой части орудия.Эти устройства также могут работать в два этапа, используя снаряд сжимающего газа большего диаметра для второй, меньшей пушки.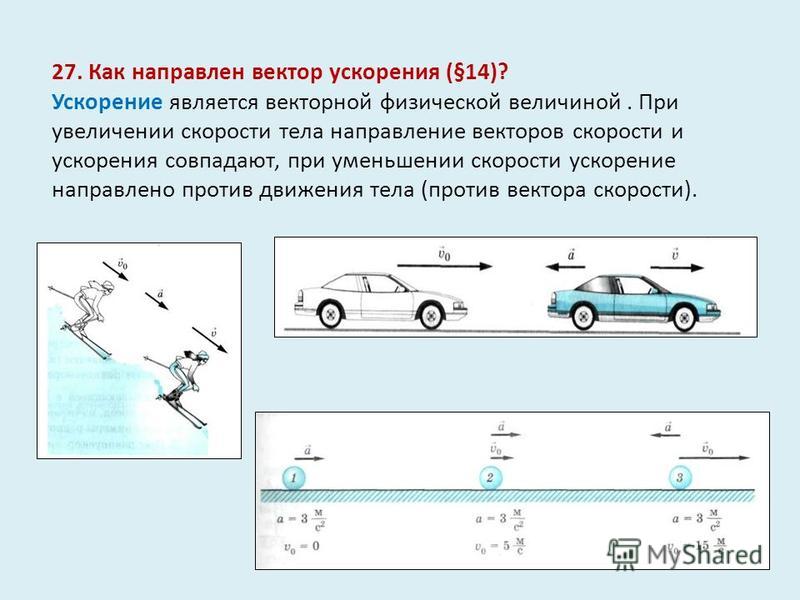 Снаряды этих устройств могут развивать скорость до 7 км / сек, что приводит к целевому давлению более 150 ГПа.

II.B.2.c Взрывающаяся проволока или фольга

Сила в этой системе создается за счет взрыва тонкой металлической фольги при прохождении чрезвычайно высокого электрического тока. Резистивный нагрев металла вызовет испарение фольги; это, в свою очередь, ускоряет прилегающую тонкую диэлектрическую пластину к цели.При выравнивании планарности пластины могут возникнуть серьезные проблемы, поскольку она ударяет по цели с серьезным ухудшением результирующего давления. Соответствующее электрическое оборудование также сильно зависит от электромагнитного шума, создаваемого системой.

Взрывающиеся фольги использовались для заряжания стрелкового оружия со стволами длиной всего несколько миллиметров. Используя листовую пластину, состоящую из пластика и металла, было достигнуто давление, превышающее 1 ТПа, с указанными характеристиками до 5 ТПа.Такие системы просты по концепции и относительно недороги в установке.

II.B.2.d Ударные волны, возбуждаемые лазером

Лазерные лучи высокой энергии, падающие на поверхность цели, вызывают очень быстрый нагрев, вплоть до образования плазмы. Эти очень высокие температуры образуются довольно быстро, и, поскольку материал или тепловой поток относительно медленный, недостаточно времени для рассеивания этой энергии, в результате чего ударные волны запускаются в материал. Хотя для этого процесса также можно использовать пучки частиц, например электронов, внимание будет сосредоточено исключительно на лазерных ударах.

Одним из преимуществ лазерного инициирования является то, что энергия, выделяемая лазерным лучом, приводит к возникновению ударной волны, которая инициируется одновременно по облучаемой области. Обычно лазерный луч фокусируется в размер пятна диаметром до 1 мм. Энергия излучения более 10 ⁸ Вт / см ² требуется для зажигания плазмы и создания ударной волны. Эти небольшие области воздействия приводят к большим потерям энергии из-за двумерного расширения плазмы. Краевые эффекты также будут значительными при оценке шока.Тот факт, что лазерные импульсы обычно длятся не более нескольких сотен наносекунд и плазма очень быстро рассеивается после прекращения подачи энергии, приводит к запуску вышеупомянутой волны высвобождения, которая быстро догоняет и разрушает ударный фронт. В результате этих ограничений эффективная толщина образца была ограничена несколькими десятками микрометров, хотя давление, достигаемое с помощью этих систем, может достигать 10 ТПа. Этот диапазон давлений представляет значительный интерес при разработке уравнений состояния.

Не вся энергия лазера эффективна для генерации ударной волны; часть теряется при образовании плазмы, часть уносится с плазмой, а часть отражается без эффекта. Эффективность поглощения большинства материалов увеличивается с увеличением энергии фотонов, в диапазоне от примерно 30% в ближнем инфракрасном диапазоне до примерно 90% в ближнем ультрафиолете. Короткие волны дают еще одно преимущество, а именно уменьшение образования надтепловых электронов.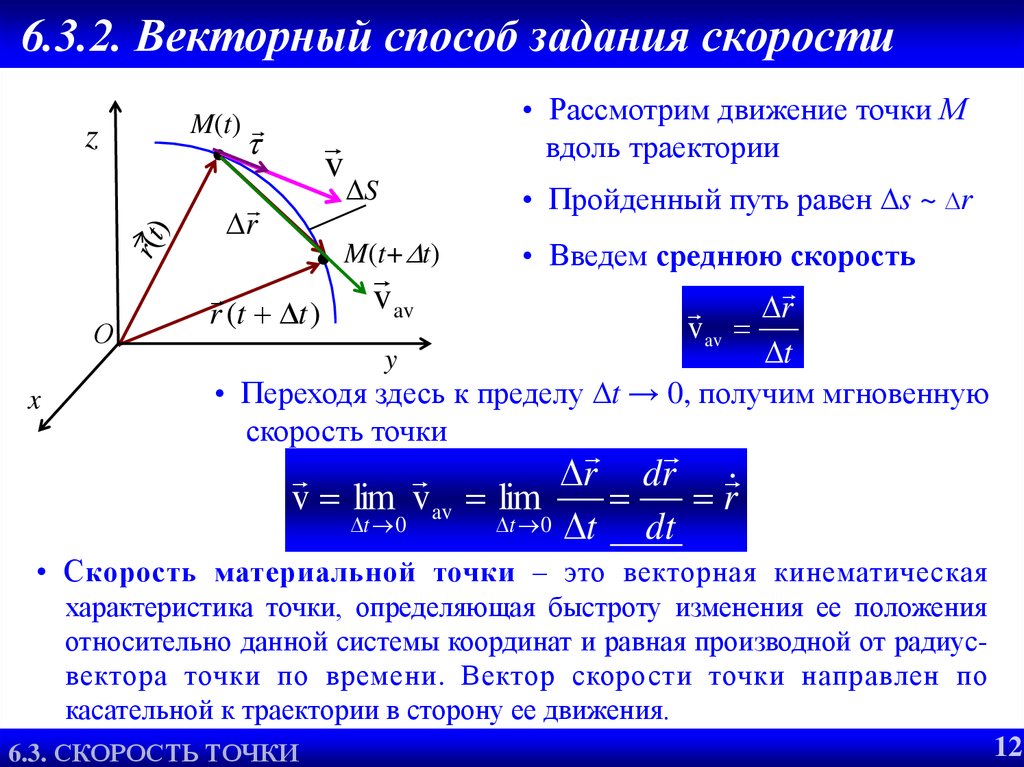 Это, в свою очередь, уменьшает предварительный нагрев мишени электронами перед прохождением ударного фронта.Однако производство рентгеновского излучения увеличивается на более коротких длинах волн и для материалов с более высоким Z, что может вызвать некоторый предварительный нагрев мишени. Лазерные лучи могут иметь локальные флуктуации плотности энергии или «горячие точки», которые могут привести к непланарности фронта ударной волны. Эти эффекты сводятся к минимуму на более длинных волнах за счет теплопроводности, но более выражены на более коротких длинах волн, поскольку энергия выделяется ближе к поверхности абляции.

Концепция листовой пластины также применялась к лазерным ударам.Углеродные диски облучались лазерным импульсом длительностью 3 нсек, создавая ударное давление 0,5 ТПа и разгоняя диск до скорости 100 км / с. Удар этого диска по второму диску передает энергию за гораздо более короткое время, что приводит к возникновению ударного давления 2 ТПа.

Обычный прибор для диагностики удара электрическим током.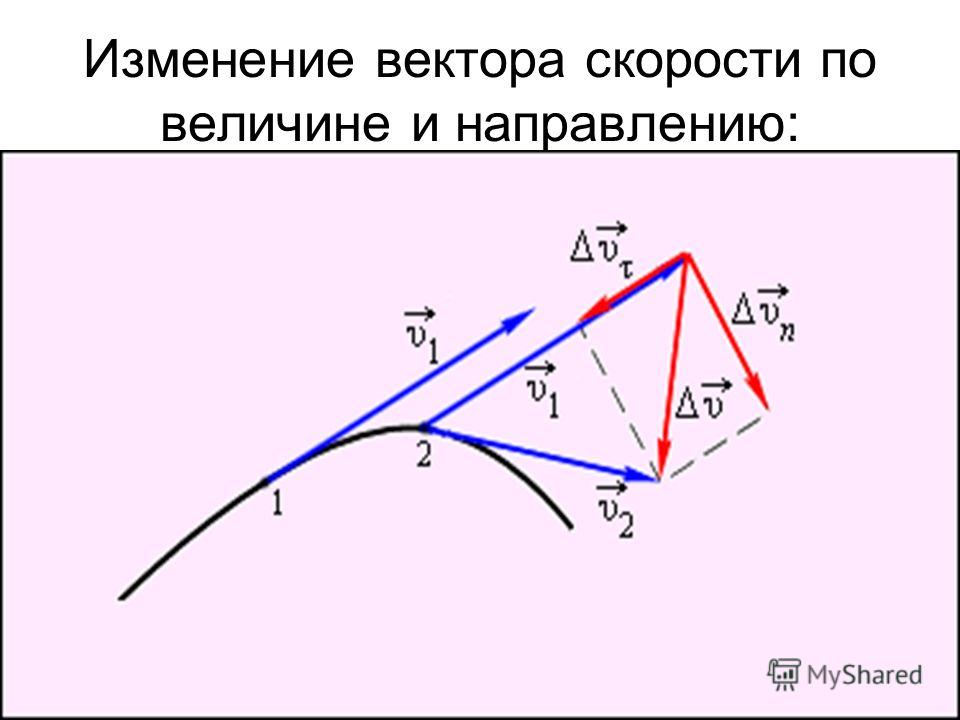 Интенсивная электромагнитная буря, создаваемая лазером и лучами частиц, представляет собой чрезвычайно враждебную среду для этих чувствительных детекторов.Однако лазеры предлагают свое собственное решение. Поскольку синхронизация лазерного импульса может быть точно установлена, входящий лазерный импульс может использоваться для отключения оптической диагностики, или часть самого лазерного луча может использоваться для диагностических целей на цели.

Плазма также генерирует рентгеновское излучение с длиной волны, изменяющейся в зависимости от состава мишени. Это излучение можно использовать либо напрямую, регистрируя удар на рентгеновской камере, либо косвенно, возбуждая рентгеновские лучи от второй мишени, которые затем используются для наблюдения за прохождением ударной волны.Скорость удара может быть определена путем наблюдения за светом, генерируемым, когда удар достигает задней поверхности цели, с помощью полосовой камеры.

II.B.2.e Ядерные ударные волны

Ядерные взрывы использовались для получения данных по уравнениям состояния в течение многих лет. Давление, полученное с помощью этого метода, приблизилось к 7 ТПа, и хотя это кажется меньше, чем достижимое с помощью лазерных лучей, площадь мишени была около 30 см в диаметре, а ядерное устройство взорвалось около 3.5 м от образца.

Оптические методы предпочтительнее для генерации начального сигнала, поскольку электромагнитные помехи очень сильны. Обычно скорость ударной волны измеряется для эталонного материала и нескольких образцов, установленных на пластине-мишени эталонного материала. Согласование импеданса используется для получения скоростей частиц в образцах из известного уравнения состояния эталонного материала.

Доступ к ядерным испытаниям затруднен, и хотя методика кажется сравнительно простой, в процессе теряется не только образец, но и большая часть дорогостоящего оборудования для обработки сигналов; таким образом, эксперименты ограничиваются материалами, представляющими наибольший интерес.

II.B.2.f Электрические рельсовые пушки

Эти устройства представляют собой разновидность газовой пушки; однако здесь сила, используемая для ускорения снаряда, является электрической. «Пушка» состоит из двух параллельных электропроводящих рельсов. Между ними лежит снаряд – проводник, замыкающий рельсы. Система образует линейный двигатель постоянного тока, и ускорение снаряда увеличивается за счет образования плазмы позади него, что способствует его ускорению. Хотя несколько групп экспериментировали с этим методом, трудности помешали его полностью успешному применению.Теоретические оценки показывают, что конечная эффективность ударных элементов достигает 40 км / сек. это привело бы к ударному давлению до 10 ТПа.

Векторные операции

В физическом мире некоторые величины, такие как масса, длина, возраст и стоимость, могут быть представлены только величиной. Другие величины, такие как скорость и сила, также включают направление. Вы можете использовать векторы для представления тех величин, которые включают как величину, так и направление. Одним из распространенных способов использования векторов является определение фактической скорости и направления самолета с учетом его воздушной скорости и направления, а также скорости и направления попутного ветра.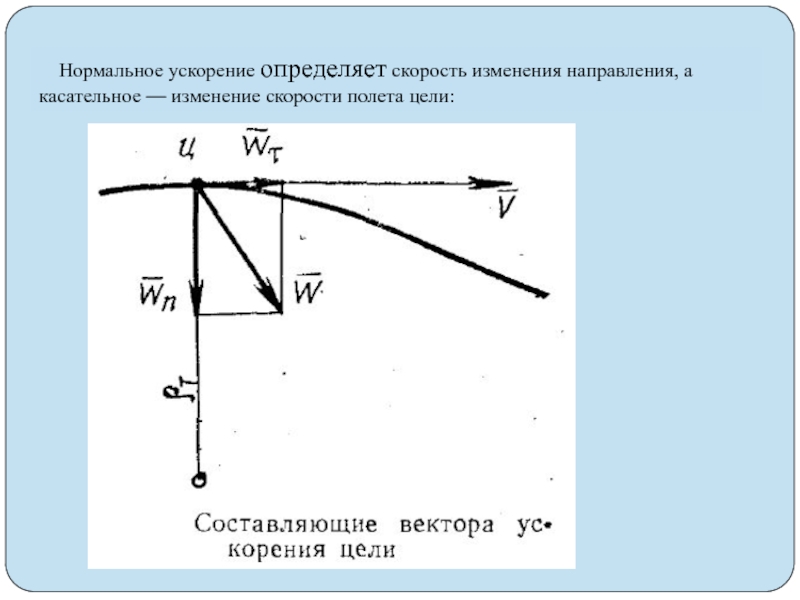 Другое распространенное использование векторов заключается в нахождении результирующей силы на объекте, на которую действуют несколько отдельных сил.

Любая величина, имеющая и размер, и направление, называется векторной величиной . Если A, и B – две точки, расположенные на плоскости, направленный сегмент от точки A, к точке B обозначается значком. Точка A – это начальная точка , а точка B – это конечная точка .

Геометрический вектор – это величина, которая может быть представлена ​​направленным линейным сегментом. С этого момента вектор будет обозначаться жирным шрифтом, например v или u . Величина вектора – это длина направленного отрезка прямой. Величину иногда называют нормой . Два вектора имеют одинаковое направление , если они параллельны и указывают в одном направлении. Два вектора имеют противоположных направлений , если они параллельны и указывают в противоположных направлениях.Вектор, который не имеет величины и указывает в любом направлении, называется нулевым вектором . Два вектора называются эквивалентными векторами , если они имеют одинаковую величину и одинаковое направление.

На рисунке 1 показано сложение векторов с использованием правила хвостового конца . Чтобы сложить векторы v и u , переместите вектор на так, чтобы начальная точка u находилась в конечной точке v . Результирующий вектор от начальной точки v до конечной точки u является вектором v + u и называется результирующим .Векторы v и u называются компонентами вектора v + u . Если два добавляемых вектора не параллельны, то можно также использовать правило параллелограмма . В этом случае начальные точки векторов совпадают, а в результате получается диагональ параллелограмма, образованная двумя векторами в качестве смежных сторон параллелограмма.

Рисунок 1
Пример сложения векторов.

Чтобы умножить вектор u на действительное число q , умножьте длину u на | q | и измените направление на , если q <0. Это называется скалярным умножением . Если вектор u умножается на -1, результирующий вектор обозначается как – u . Он имеет ту же величину, что и и , но в противоположном направлении. На рисунке 2 показано использование скаляров.

Рисунок 2
Примеры векторов.

Пример 1: Самолет летит строго на запад со скоростью 400 миль в час. Попутный ветер дует в юго-западном направлении со скоростью 50 миль в час. Нарисуйте диаграмму, отображающую путевую скорость и направление самолета (Рисунок 3).

Рисунок 3
Рисунок для примера 1 – векторное представление.

Вектор, представленный в предыдущем примере, известен как вектор скорости .Пеленг вектора v – это угол, измеренный по часовой стрелке от северного направления до v . В этом примере пеленг самолета составляет 270 °, а пеленг ветра – 225 °. Нарисовав фигуру в виде треугольника с помощью правила кончика хвоста, можно рассчитать длину (путевую скорость самолета) и азимут полученного результата (Рисунок 4).

Рис. 4
Чертеж для примера 1 – представление угла.

Во-первых, используйте закон косинусов, чтобы найти величину результирующей.

Затем используйте закон синусов, чтобы найти подшипник.

Таким образом, пеленг β составляет 270 ° – 4,64 °, или приблизительно 265,4 °.

Пример 2: Самолет летит со скоростью 300 миль в час. Ветер дует с юго-востока со скоростью 86 миль в час с пеленгом 320 °. На каком пеленге должна стоять плоскость, чтобы иметь истинный пеленг (относительно земли) 14 °? Какая будет путевая скорость самолета (рис. 5)?

Рисунок 5
Рисунок для примера 2.

Используйте закон синусов для расчета пеленга и путевой скорости. Поскольку эти альтернативные внутренние углы совпадают, угол 54 ° является суммой угла 14 ° и угла 40 °.

Следовательно, пеленг плоскости должен быть 14 ° + 13,4 ° = 27,4 °. Базовая скорость самолета составляет 342,3 мили в час.

Любой вектор может быть разбит на два вектора , горизонтальный компонент и вертикальный компонент. Эти составляющие векторы называются проекциями (рисунок 6).

Рисунок 6
Пример проекций.

Пример 3: Сила в 11 фунтов и сила в 6 фунтов действуют на объект под углом 41 ° по отношению друг к другу. Какова величина результирующей силы и какой угол образует результирующая сила с 11-фунтовой силой (рис. 7)?

Рисунок 7
Чертеж для примера 3.

Во-первых, используйте Закон косинусов, чтобы найти величину равнодействующей силы.2 \\ y = 6 \ ln t \ end {case}} {x = t2y = 6lnt

Учитывая указанные выше компоненты положения частицы в пространстве, найдите ее скорость при t = 2.t = 2.t = 2.

Планарное движение

Положение и траектория

Предположим, что частица движется в плоскости. Тогда его положение можно выразить как

.

\ [{\ mathbf {r} = x \ mathbf {i} + y \ mathbf {j}}, \]

, где \ (x, y \) – декартовы координаты, а \ (\ mathbf {i}, \ mathbf {j} \) – единичные векторы вдоль осей координат \ (x- \) и \ (y- \). , соответственно.

Поскольку координаты \ (x, y \) зависят от времени, мы можем записать вектор положения в параметрической форме:

\ [\ mathbf {r} = x \ left (t \ right) \ mathbf {i} + y \ left (t \ right) \ mathbf {j}. \]

Это векторное уравнение определяет траекторию частицы.

Скорость и скорость

Скорость \ (\ mathbf {v} \) частицы определяется как производная по времени вектора положения частицы, то есть

\ [\ mathbf {v} = \ frac {{d \ mathbf {r}}} {{dt}}.2}}. \]

Движение с постоянным ускорением

Предположим, что частица или объект движутся с постоянным ускорением \ (\ mathbf {a}: \)

\ [\ mathbf {a} = \ frac {{d \ mathbf {v}}} {{dt}} = \ text {const}. \]

Тогда скорость в момент времени \ (t \) записывается как

\ [\ mathbf {v} \ left (t \ right) = {\ mathbf {v} _0} + \ mathbf {a} t, \]

, где \ ({\ mathbf {v} _0} \) – вектор начальной скорости в точке \ (t = 0. \)

Рисунок 1.3}, \] где \ (x, y \) измеряются в метрах. Найдите скорость и скорость частицы в \ (t = 1 \, \ text {s}. \)

Пример 2

Предположим, что объект движется по траектории в соответствии с уравнениями \ [x \ left (t \ right) = t + \ cos t, y \ left (t \ right) = t – \ sin t \]. Найдите величину вектора ускорения.

Пример 3

Частица движется по гиперболе \ [y = \ frac {{12}} {x}, \], так что координата \ (x – \) увеличивается с постоянной скоростью \ (3 \) метров в секунду.2} t} = 1. \]

Пример 3.

Частица движется по гиперболе \ [y = \ frac {{12}} {x}, \], так что координата \ (x – \) увеличивается с постоянной скоростью \ (3 \) метров в секунду. Найдите скорость частицы, когда она находится в точке \ (\ left ({3,4} \ right). \)

Решение.

Сначала определим вектор скорости частицы по формуле

\ [\ mathbf {v} = \ frac {{dx}} {{dt}} \ mathbf {i} + \ frac {{dy}} {{dt}} \ mathbf {j}.2}} = 5 \, \ frac {\ text {m}} {\ text {s}}. \]

Пример 4.

Частица движется по кривой, заданной параметрическими уравнениями \ [x = 1 + t, y = 1 – t. \]. Определите уравнение \ (xy – \) траектории и скорости вдоль нее.

Решение.

Мы решаем первое уравнение относительно \ (t \) и подставляем его во второе уравнение:

\ [х = 1 + т, \; \; \ Rightarrow t = x – 1, \; \; \ Rightarrow y = 1 – \ left ({x – 1} \ right), \; \; \ Rightarrow y = 2 – x.\]

Следовательно, траектория частицы – прямая \ (y = 2 – x. \). Найдите вектор скорости:

\ [\ frac {{dx}} {{dt}} = \ frac {d} {{dt}} \ left ({1 + t} \ right) = 1, \]

\ [\ frac {{dy}} {{dt}} = \ frac {d} {{dt}} \ left ({1 – t} \ right) = – 1. \]

Затем

\ [\ mathbf {v} = \ frac {{dx}} {{dt}} \ mathbf {i} + \ frac {{dy}} {{dt}} \ mathbf {j} = 1 \ cdot \ mathbf {i} + \ left ({- 1} \ right) \ cdot \ mathbf {j} = \ mathbf {i} – \ mathbf {j}. \]

Скорость равна

\ [v = \ sqrt {{{\ left ({\ frac {{dx}} {{dt}}} \ right)} ^ 2} + {{\ left ({\ frac {{dy}} {{ dt}}} \ right)} ^ 2}} = \ sqrt {{1 ^ 2} + {{\ left ({- 1} \ right)} ^ 2}} = \ sqrt 2.2} + \ frac {1} {2}} \, \ left (\ text {m} \ right). \]

См. Другие проблемы на странице 2.

Векторов

Векторов

Векторов

---

Вектор – это величина, которая имеет такие свойства, как величина (размер) и направление. Чтобы представить это, мы рисуем векторы в виде стрелок, где величина вектора указывается длиной стрелки, а направление вектора указывается ориентацией стрелки. Общие векторы, которые возникают в двигательной установке, – это силы (например, тяга и сопротивление), скорость и ускорение.

---

Сложение векторов

Часто в проблему вовлечено несколько векторов, и нам нужно найти их «чистый» или «результирующий» эффект. Чтобы найти результирующий вектор, мы должны использовать векторное сложение (суммирование). Сложение векторов отличается от сложения двух чисел, потому что мы должны учитывать как величину, так и направление векторов.

Типичный пример – это суммирование сил, действующих на объект, для определения результирующей или “чистой” силы на объект. Это показано на рисунке ниже, где две силы воздействуют на блок.Одна сила имеет величину 30 Н в направлении x , а другая сила имеет величину 40 Н в направлении y . Поскольку эти силы направлены в разные стороны, мы не можем просто сложить их величины, чтобы получить результирующую силу.

Схема сил на блоке

Вместо этого мы можем сложить эти векторы графически, как показано на рисунке ниже. Сложение графических векторов происходит путем совмещения двух векторов «голова к хвосту». Тогда векторная сумма или результирующий вектор – это вектор, проведенный от хвоста первого вектора к голове последнего вектора.

Общая задача сложения векторов

Математически мы можем использовать теорему Пифагора, чтобы найти величину результирующей силы. Точно так же мы можем использовать тригонометрию, чтобы найти направление результирующей силы, выраженное как угол силы θ относительно горизонтали. Соответствующие расчеты приведены ниже.

Векторные обозначения: Иногда неудобно представлять векторы графически в виде стрелок. Вместо этого мы часто представляем векторы символически, используя векторные обозначения.Один из распространенных методов – представить вектор как комбинацию его компонентов в направлении x или « i » и направлении y или « j ». В приведенном выше случае коэффициент чистой силы выражается как

.

, где символы i и j служат для напоминания нам о направлении, связанном с каждой величиной компонента, а маленькая стрелка над F _net указывает, что это вектор.

В качестве альтернативы мы можем просто указать величину и направление вектора напрямую как

Обратите внимание, что величина вектора может быть представлена ​​либо размещением вертикальных полос вокруг вектора, либо использованием символа вектора курсивом без стрелки над ним.

---

Разложение векторов

Разложение вектора – это деконструкция вектора, который не лежит только в одном направлении, на несколько векторов в разных направлениях. По сути, векторное разложение – это векторное сложение в обратном порядке. Обычно мы разлагаем векторы на составляющие векторы, которые ортогональны. Это должно быть сделано таким образом, чтобы составляющие векторы суммировались с исходным вектором.

Для иллюстрации рассмотрим вектор скорости ниже, который составляет 10 м / с при 53.1 ° относительно горизонтали. Мы хотели бы разложить этот вектор на его горизонтальную и вертикальную составляющие.

Общая задача разложения векторов

Используя базовую тригонометрию, мы можем напрямую вычислить величину составляющих векторов как в горизонтальном ( i ), так и вертикальном ( j ) направлениях. Используя синусоидальную функцию, величина вертикальной составляющей может быть определена как

.

Тогда, используя теорему Пифагора, можно определить оставшийся катет векторного треугольника следующим образом:

В качестве альтернативы можно снова использовать тригонометрию для определения третьего отрезка треугольника, а именно

Часто бывает удобно разложить векторы на их компоненты, когда только один из компонентов важен для задачи.Кроме того, знание горизонтальной и вертикальной составляющих вектора позволяет нам представить вектор в векторной нотации. Используя наши результаты, вектор скорости, рассмотренный выше, можно записать в векторной записи как

---

Относительное движение и векторы

Векторы также полезны для понимания концепции относительного движения. Чтобы проиллюстрировать, как векторы используются при определении относительного движения, мы определим относительную скорость ветра, наблюдаемую с движущегося парусника.

Парусник, показанный ниже, идет на северо-восток со скоростью 20 узлов, а ветер дует с востока со стабильной скоростью 10 узлов. Какое направление и величина скорости ветра ощущают (наблюдают) моряки на борту парусника?

Иллюстрация относительной скорости ветра

Чтобы определить скорость ветра, наблюдаемую моряками, мы должны рассмотреть проблему с их точки зрения. В частности, они видят, как океан движется мимо них со скоростью 20 узлов от носа лодки к корме, а это означает, что они видят, как океан движется в юго-западном направлении со скоростью 20 узлов.Добавление юго-западного движения, наблюдаемого моряками, к западному движению ветра на 10 узлов дает скорость ветра, наблюдаемую моряками. Графическое сложение векторов показано на рисунке ниже.

Поскольку скорость парусника находится под углом 45 °, будет легче найти величину ( W ) и направление относительной скорости ветра, если мы сначала разложим вектор скорости парусника на его горизонтальную и вертикальную составляющие. Компонентные векторы показаны на рисунке выше.Поскольку скорость парусного судна находится под углом 45 °, величины его горизонтальной и вертикальной составляющих равны и легко определяются из теоремы Пифагора как

.

После разложения скорости парусника на составляющие становится очевидным, что горизонтальная составляющая относительной скорости ветра является суммой двух горизонтальных составляющих (10 м / с и 14,1 м / с), а вертикальная составляющая такой же. как вертикальная составляющая скорости парусника. Итак, в векторной нотации имеем

Векторные вычисления

Обратите внимание, что знаки «-» используются для обозначения того, что вертикальный компонент указывает нечетное число, а горизонтальный компонент указывает влево.Аналогично, величина и направление W могут быть определены как

Расчет звездных величин и направлений

---

Часть 4 – Расчет движения станции

Шаг 1 –

Добавьте линейную линию тренда к графикам временных рядов

1. На листе, содержащем каждый график, выберите Диаграмма> Добавить линию тренда …
2. На вкладке Тип в разделе Тип тренда / регрессии выберите Линейный .
3. Щелкните вкладку Параметры .Установите флажок рядом с Отображать уравнение на диаграмме и нажмите ОК.
4. На графике щелкните уравнение, чтобы выбрать его и переместите туда, где оно будет хорошо видно. При желании увеличьте размер шрифта, чтобы уравнение было удобочитаемым.

Шаг 2 –

Расчет вектора скорости для каждого графика временных рядов GPS

1. Уравнение линии тренда, созданной для каждого TSP, имеет вид y = mx + b . В этом уравнении
   • y представляет положение на север (или восток) в миллиметрах,
   • м представляет собой наклон линии,
   • x представляет время в днях, а,
   • b представляет точку пересечения по оси y.Это значение не имеет значения для этих расчетов.
2. Какова средняя годовая скорость станции SEAT в направлении север-юг?
3. Какова средняя годовая скорость станции SEAT в направлении восток-запад?

Шаг 3 –

Определите годовое движение станции GPS.

Фактическое горизонтальное движение GPS-станции в течение года представлено вектором, который получается путем сложения векторов скорости на север и восток.Рассмотрите примеры обоих методов, используемых для определения годовой скорости. В примерах будут использоваться среднегодовые скорости 3 мм / год на севере и 6 мм / год на востоке.

Графический метод “голова к хвосту”

1. Нарисуйте ортогональные оси X и Y на миллиметровой бумаге. Масштабируйте каждую ось от -10 до +10. Обязательно используйте одинаковое расстояние на единицу по обеим осям.
2. Нарисуйте вектор север-юг по оси Y и вектор восток-запад по оси X.
   
3. Сложите векторы вместе, чтобы графически получить результирующий вектор.
4. Чтобы охарактеризовать этот вектор, чтобы вы могли наложить его на карту, измерьте его длину в тех же единицах, которые вы использовали на миллиметровой бумаге. С помощью транспортира измерьте угол от севера.

Математический метод

Количественные значения как скорости движения, так и направления (два компонента скорости) станции GPS могут быть рассчитаны на основе северной и восточной скоростей.

1. Вычислите длину вектора (скорость движения) с помощью теоремы Пифагора.
   a ² + b ² = c ²

   a ² + b ² = c ²
   3 ² + 6 ² = c ²
   45 = c ²
   квадратный корень (45) = c
   6,7 мм / год = с
   

2. Рассчитайте направление движения, используя соотношение, в котором угол a равен обратной тангенсе длины вектора севера, деленной на длину вектора востока.

   a = tan ^-1 (N / E)
   a = tan ^-1 (3/6)
   a = tan ^-1 (.5)
   a = 26,6 градуса

   Решение указывает направление движения в градусах с востока. Как правило, при отображении векторов проще использовать градусы от севера. Вычислите угол от севера, вычтя угол a из 90 градусов.

   Направление с севера = 90 – Направление с севера = 90 – 26,6 Направление с севера – 63.4 градуса

   
   

Векторов

Если наша цель – описать и понять движение, тогда просто движение вверх и вниз по линии не хватит. Движение в реальном мире происходит в трех измерениях. Мы Нужен способ описания движения сложный, как у пчелы или игрушечного вертолета. Мы делаем это с векторами.

Вначале я хочу, чтобы вы подумали о векторах как о геометрических объектах. Модель для все векторы – смещения.Что-то начинается в одном месте и заканчивается в другом. Один можно протянуть эластичный шнур между двумя точками в пространстве и отметить, на каком конце пункт назначения маленькой бумажной стрелкой. Как видите, у этого есть два аспекта. смещение, которое мы называем вектором. Во-первых, у него есть длина или величина. во-вторых у него есть направление: что-то связано с его углом. Первый пункт нашей повестки дня описание векторов состоит в том, чтобы выяснить, когда два вектора равны.

Давайте совершим еще одно небольшое путешествие такой же длины, как и первое, но взлетим в другом. направление.Если вы натянете шнур между начальной и конечной точками, вы можете визуализируйте два вектора. Они равны? Совершите еще одну поездку в том же направлении, что и первый, а теперь идем дальше. Это еще один вектор. Равно ли оно первому?

Когда векторы равны?

В обоих случаях, когда векторы имеют либо разные направления, либо разную длину, они не равны. Точно так же, если направление и длина различны, они не равны. Два вектора равны только тогда, когда оба направления и длины одинаковы.Два вектора могут быть равными, но в разных местах. Векторы, представленные параллельными линиями, которые имеют одинаковые длина и направление равны.

Как складывать векторы

Когда что-то совершает одно смещение, затем другое, общее смещение равно сумма двух отдельных. Пусть a представляет первое отключение, а b – второе отключение. В общее количество поездок определяется путем выстраивания векторов, представляющих поездки от кончика к хвосту. Положите хвост второй поверх хвоста первого.За полное смещение принимается вектор от хвоста первого до кончика второго. Этот способ добавления векторов возникает естественно, когда мы говорим о смещениях. Иногда другой вектор величины, такие как силы, должны быть добавлены. Тогда часто бывает необходимо переместить один вектор так, чтобы его хвост совпадал с хвостом другого, потому что силовые диаграммы обычно показывают силы со всеми своими хвостами вместе на объекте, к которому приложена сила. Когда вектор не забудьте сохранить его длину и направление одинаковыми.

Коммутативность сложения

Сумма векторов может быть записана как c = a + b . Это означает, что хвост b находится на кончик a и хвост c находится на хвосте a , а кончик c находится на кончике b . Это также можно добавить a к b . Результат такой же, как при добавлении b к a ? Если смещение – это наш вектор модели, то результат будет одним и тем же независимо от того, какое путешествие будет выполнено первым.Итак, мы потребует, чтобы векторы давали одинаковую сумму независимо от того, что добавляется первым. a + b = b + a . Это свойство называется коммутативностью.

Не все количества, которым можно назначить размер и направление, обладают этим свойством, и таким образом, эти некоммутативные величины не могут быть векторами. (Это клуб с высокие стандарты!) Например вращения вокруг оси имеют размер, угол поворота, и направление, направление оси вращения.Попробуйте сначала повернуть книгу на 90 ° вокруг вертикальная ось, а затем 90 ° вокруг горизонтальной оси влево-вправо. Обратный порядок эти два поворота, и вы получите книгу в другом положении. На случай, если вращения, a + b не равно b + a .

На бумаге легко нарисовать векторы, чтобы визуализировать процесс сложения векторов. Также следует попытаться представить векторы в трех измерениях. Все, что мы говорим о двумерные векторы, могут быть расширены до трех измерений без особых усилий трудность.Представьте себе вертолет, выходящий из подвески. Он подруливает 100 м N, затем меняет направление, такси 200 м E, затем поднимается на 300 м. Общее смещение Вертолет получается путем сложения всех трех векторов кончик к хвосту, как мы это делаем в двух измерениях.

Отрицательный вектор и вычитание

Всегда есть случай, когда человек начинает с дела, а затем на полпути к цели. пункт назначения передумал и вернулся домой. Два смещения, наружу и назад сложить до нуля.Второе смещение можно записать как отрицательное значение во-первых – он такой же величины, но противоположного направления. Первый этап маршрута – – , второй – . Следовательно, a + (- a ) = 0.

После определения отрицательного значения вектора начинается процесс вычитания. естественно. Чтобы вычесть b из a , просто найдите отрицательное значение b , затем добавьте это к a .

Другой способ найти a b – соединить хвосты a и b вместе и нарисовать вектор от наконечника b до наконечника a .Этот метод означает поиск вектора, который вы добавляете к b , чтобы получить a. (Это a = b + ( a – b ))

Попробуйте оба метода вычитания, и вы увидите, что они дают вектор с одинаковым величина и направление. (Хотя после постройки они будут в разных местах, но это не имеет значения.) Вы можете выбрать любой метод вычитания, который вам кажется чтобы иметь больше смысла для вас.

Умножение на скаляр

Иногда векторы умножаются или делятся на коэффициент масштабирования.Например, если один растягивает эластичный шнур, представляющий вектор, вдвое больше его длины, сохраняя его направление то же самое, то исходный вектор умножается на два. Точно так же, если позволить ему уменьшить до половину своей длины он делится на два или умножается на половину. как вам нравится. Обычные числа называются скалярами, чтобы отличать их от векторов. Ты был используя скаляры, так как вы научились считать.

Есть также операции с двумя векторами, называемые умножением векторов.Эти мы постараюсь избежать в этом курсе, но вам может потребоваться изучить их, если вы пойдете дальше курсы физики или математики.

Такие величины, как смещение, скорость, ускорение и сила, являются векторами. Масса и время являются скалярами, такими как температура, влажность и энергия.

Векторы скорости и ускорения

Смещение – это наш вектор-прототип. Скорость определяется смещением на разделив его на промежуток времени. Результатом деления вектора на скаляр является вектор.Точно так же деление вектора, представляющего разность скоростей, на временной интервал дает вектор – ускорение. Масса, скаляр, умножающее ускорение, вектор, дает силу, другая векторная величина.

Чтобы увидеть, как скорости могут складываться как векторы, я использую игрушечный трактор. Он сидит на длинном куске мясная бумага, покрывающая стол. Допустим, длина стола ориентирована с востока на запад. Ширина стола около 1 м. Если я поставлю его поперек стола на север, он закроет 1 м дистанции за 10 секунд.Это скорость 0,1 м / с на север. Во второй раз я позволил трактор пересекает стол, я тяну бумагу мясника со скоростью около 0,05 м / с, восток, половина скорость трактора и перпендикулярно его курсу. На этот раз трактор пересекает бумага прямо, но, относительно стола, пересекает под углом. Скорость трактора относительно таблицы уже не 0,1 м / с, а векторная сумма 0,1 м / с, север и 0,5 м / с, вост. В сумме, как показано на диаграмме, получается 0.{-1} \ left (\ frac {v _ {\ rm trac}} {v _ {\ rm paper}} \ right) $$

Навигация

Следующая проблема – узнать, как достичь желаемого направления, когда крест дует ветер. Например, мы хотим лететь на самолете прямо на север, но дует поперечный ветер с востока на запад. В каком направлении должен лететь самолет так что в конечном итоге он едет на север? Допустим, дует боковой ветер со скоростью 40 км / ч и что самолет движется со скоростью 100 км / ч по воздуху.Задайте задачу графически как следующим образом:

1. Проведите прямую линию с севера на юг вдоль желаемого направления.
   
2. Нарисуйте вектор в масштабе, представляющий скорость ветра: 40 км / ч в западном направлении кончиком. на линии север-юг.
   
3. Скорость самолета составляет 100 км / ч, но мы не знаем, в каком направлении. Поместите вектор кончиком на хвосте вектора скорости ветра и найдите такой угол, чтобы хвост Вектор скорости самолета находится на линии север-юг.{-1} \ left (\ frac {v _ {\ rm wind}} {v _ {\ rm airplane}} \ right) $$ В этом случае курс, позволяющий самолету идти строго на север, составляет 23,6 ° к востоку от севера. а скорость самолета относительно земли – 92 км / ч.