Ускорение, вектор, производная скорости, теорема Пифагора для модуля полного ускорения
Ускорение, вектор, производная скорости, теорема Пифагора для модуля полного ускорения.
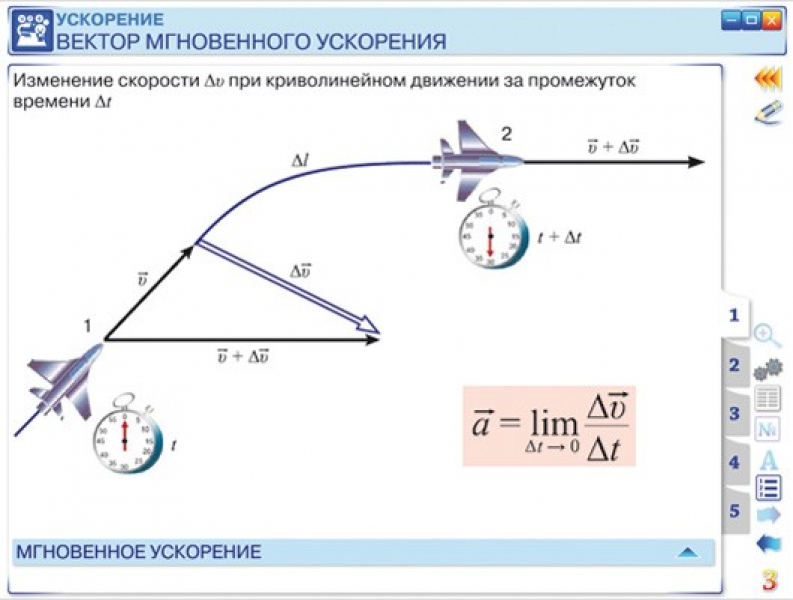
Ускорение. Только при прямолинейном равномерном движении частицы ее скорость остается неизменной. Во всех остальных случаях вектор скорости изменяется. При прямолинейном неравномерном движении изменяется модуль скорости. При криволинейном равномерном движении изменяется направление скорости. В общем случае неравномерного криволинейного движения изменяется и модуль, и направление скорости. Физическая величина, которая характеризует быстроту изменения скорости, называется ускорением. Пусть за промежуток времени вектор скорости изменяется от значения до значения. Отношение изменения скорости к промежутку времени называется средним ускорением за этот промежуток:
Ускорение — вектор. Среднее ускорение представляет собой вектор, направленный вдоль . Он характеризует быстроту изменения скорости за определенный конечный промежуток времени. Неограниченно уменьшая этот промежуток, приходим к физической величине, характеризующей быстроту изменения скорости в данный момент времени. Эта величина называется ускорением:
Он характеризует быстроту изменения скорости за определенный конечный промежуток времени. Неограниченно уменьшая этот промежуток, приходим к физической величине, характеризующей быстроту изменения скорости в данный момент времени. Эта величина называется ускорением:
В отличие от вектора скорости, который всегда направлен по касательной к траектории, вектор ускорения может иметь составляющие, направленные как по касательной, так и по нормали к траектории. Направление ускорения. Вектор ускорения направлен вдоль траектории только тогда, когда эта траектория прямолинейная. Если частица ускоряется, т. е. модуль ее скорости растет, то вектор, направлен вдоль траектории вперед. Такое же направление имеет и вектор ускорения. Если движение частицы замедляется, т. е. модуль ее скорости убывает, то вектор ускорения направлен вдоль траектории назад. Вектор ускорения направлен строго поперек траектории только при равномерном движении по криволинейной траектории, когда модуль скорости неизменен.
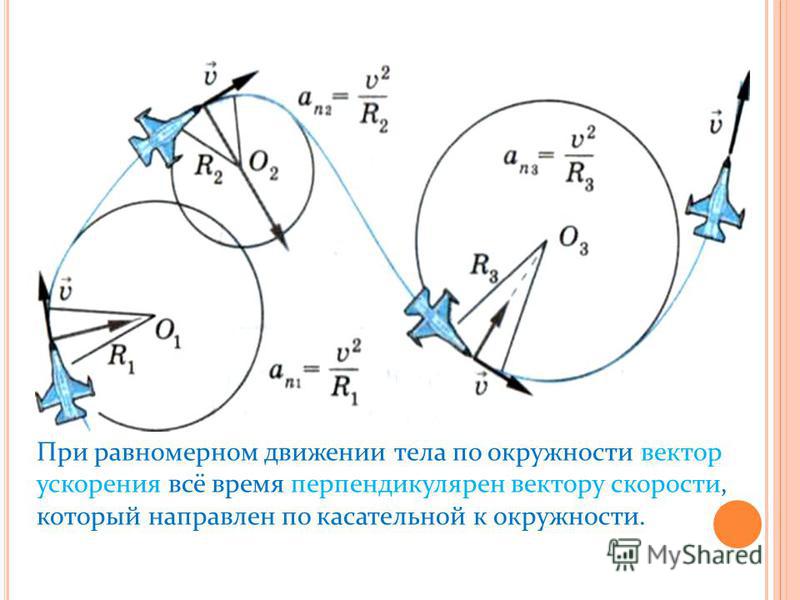
Приращение скорости при равномерном движении по криволинейной траектории. меняется, то все его изменение сводится к повороту. При этом, разумеется, векторы скорости для разных моментов времени изображаются выходящими из одной точки, хотя эти векторы соответствуют разным точкам траектории (рис. 23). Видно, что вектор , а следовательно, и вектор ускорения направлены в сторону вогнутости траектории. Рассмотрим частный случай движения по криволинейной траектории — равномерное движение по окружности радиуса (рис. 24). В этом случае вектор ускорения в любой точке траектории направлен к центру окружности. С этим связано его название — центростремительное ускорение.
Центростремительное ускорение. Модуль центростремительного ускорения зависит от радиуса R окружности и модуля скорости. Для вывода формулы, выражающей эту зависимость, рассмотрим две близкие точки траектории, в которых частица находится через промежуток времени (рис.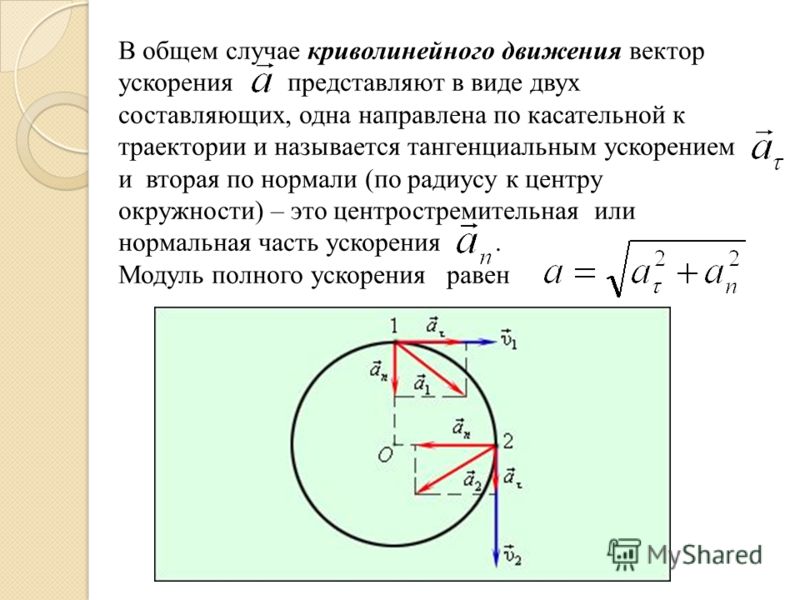
По этой ссылке вы найдёте полный курс лекций по математике:
| Решение задач по математике |
Длина хорды при все меньше и меньше отличается от длины дуги, равной. Поэтому при находим
Полученное выражение (3) для центростремительного ускорения справедливо при равномерном движении по любой криволинейной траектории.
Приближение участков криволинейной траектории дугами окружностей К нахождению центра аппроксимирующей окружности. Дело в том, что достаточно малый участок любой плавной кривой можно приближенно рассматривать как дугу некоторой окружности. Положение центра этой окружности и ее радиус будут своими для каждой точки траектории (рис. 25).
Положение центра этой окружности и ее радиус будут своими для каждой точки траектории (рис. 25).
Для геометрического определения положения центра и радиуса нужно взять две близкие точки криволинейной траектории, провести в них касательные и построить перпендикуляры к этим касательным (рис. 26). Центр окружности, аппроксимирующей криволинейную траекторию в точке, находится как предельное положение точки пересечения этих перпендикуляров при неограниченном уменьшении длины дуги, т. е. при стремлении точки к точке.
Таким образом, любое движение по криволинейной траектории можно представить как движение по дугам окружностей, центры и радиусы которых изменяются от точки к точке траектории. При равномерном движении вектор ускорения в каждой точке траектории направлен к центру соответствующей окружности, т. е. перпендикулярно касательной к траектории, а его модуль дается той же формулой (3).
Поэтому в отличие от равномерного движения по окружности, где вектор ускорения не изменяется по модулю и, поворачиваясь, смотрит все время в одну точку, при равномерном движении по произвольной кривой вектор ускорения уже не сохраняется по модулю и, изменяя свое направление, уже не смотрит в одну точку.
Возможно вам будут полезны данные страницы:
| Заказ №223094 Математическая логика готовое |
| Новое время в Европе как особая фаза всемирно исторического процесса |
| Угловая скорость как вектор. Векторное произведение |
| Подбор стехиометрических коэффициентов ОВР |
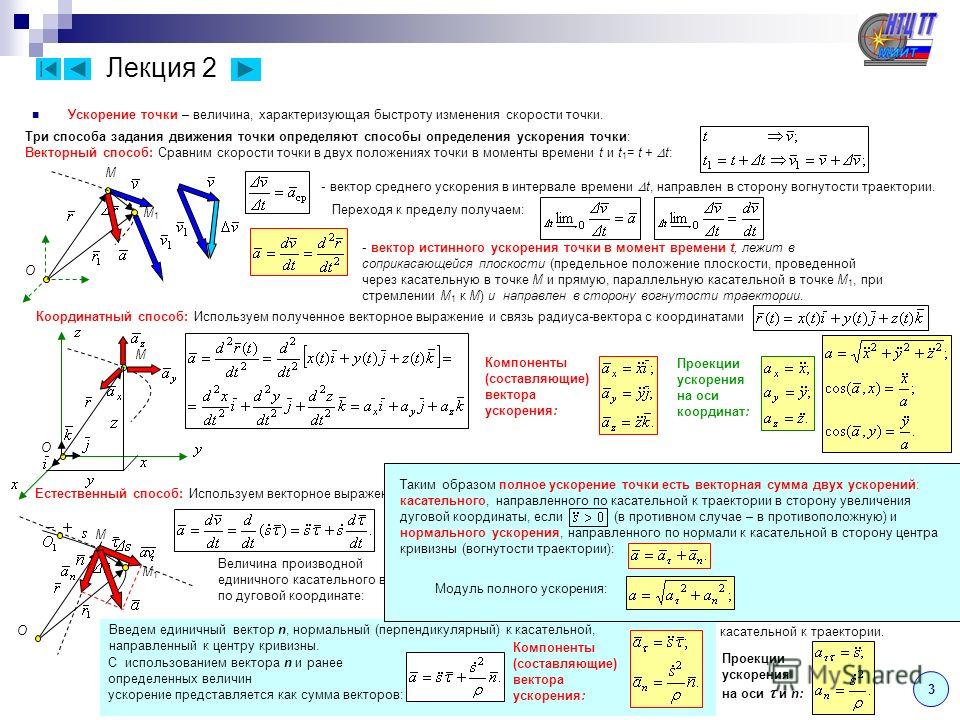
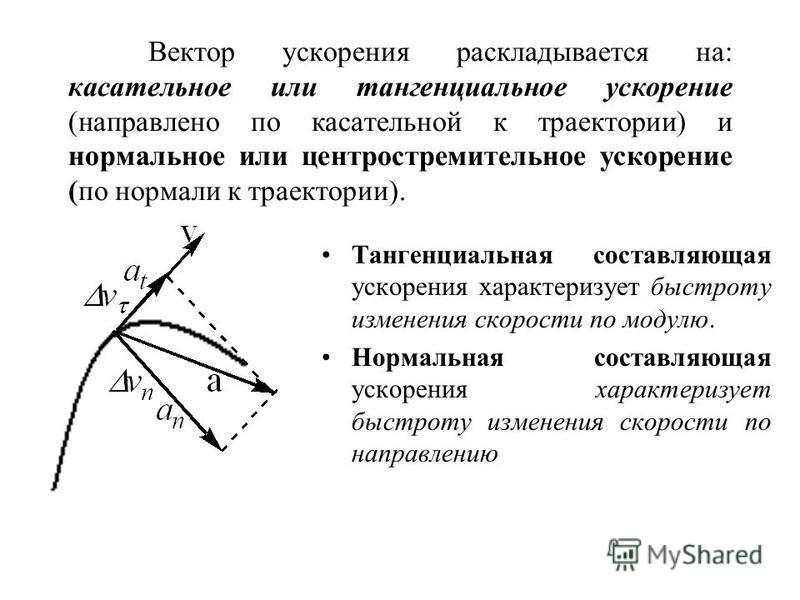
Однако в каждой точке он направлен по нормали к траектории. В общем случае при неравномерном движении по произвольной криволинейной траектории вектор ускорения можно представить в виде суммы двух составляющих: тангенциальной и нормальной. Тангенциальное ускорение направлено по касательной к траектории и характеризует быстроту изменения модуля скорости. Нормальное ускорение направлено в каждой точке к центру окружности, аппроксимирующей траекторию движения в этой точке, и характеризует быстроту изменения направления скорости.
• Объясните, почему при равномерном криволинейном движении вектор ускорения в каждой точке направлен перпендикулярно траектории.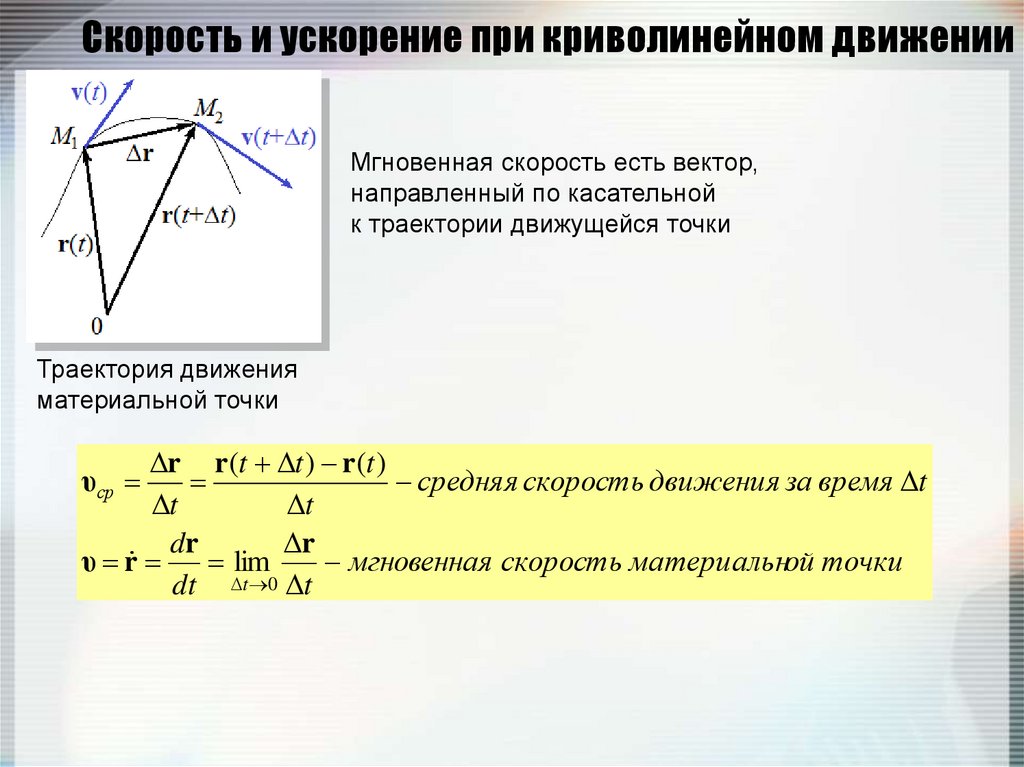
• Опишите способ нахождения центра и радиуса окружности, аппроксимирующей данную траекторию в какой-либо ее точке.
• В какую сторону — вперед или назад — направлен вектор тангенциального ускорения? Другими словами, направлен он вдоль вектора скорости или противоположно ему?
Ускорение — производная скорости. По аналогии с формулой (5) предыдущего параграфа, рассматривая скорость как векторную функцию времени , можно сказать, что определяемое формулой (2) ускорение а представляет собой производную функции по времени 1. Используя для производной же обозначения, что и в формуле (6) предыдущего параграфа, можно написать
Сравнивая эти формулы с соответствующими выражениями (6), можно отметить определенную формальную аналогию между скоростью и ускорением. Пусть конец радиуса-вектора описывает некоторую траекторию, как показано на рис. 27. В каждый момент времени вектор скорости направлен по касательной к траектории.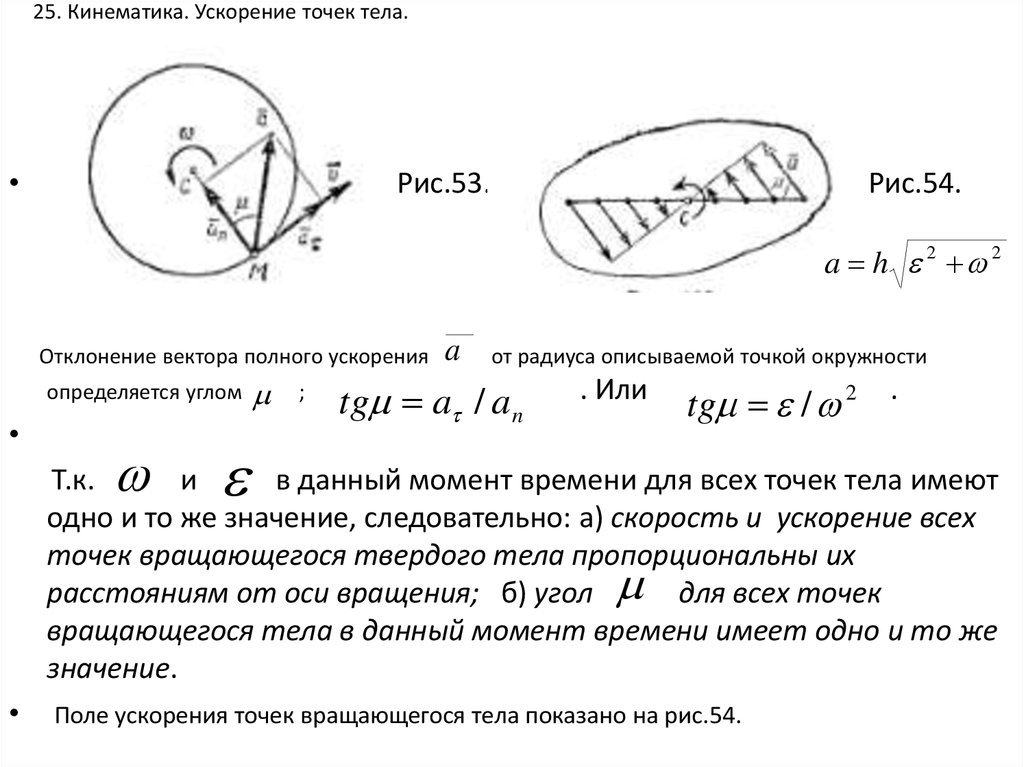 Изобразим все векторы скорости и т.д. для разных моментов времени так, чтобы они начинались из одной точки (рис. 27).
Изобразим все векторы скорости и т.д. для разных моментов времени так, чтобы они начинались из одной точки (рис. 27).
Вектор скорости совершает один оборот по годографу. Модуль скорости частицы равен отношению длины окружности к периоду обращения:
Сравнивая эти формулы, получаем
а сравнивая рис.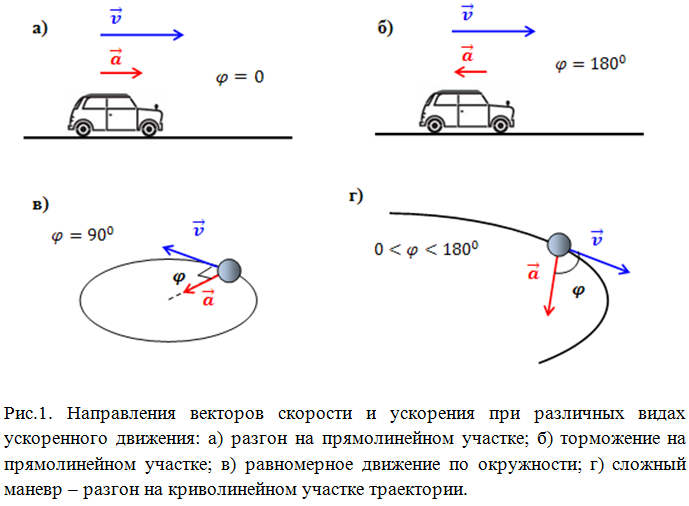 28а, б, убеждаемся, что вектор ускорения а в каждый момент времени направлен противоположно радиусу-вектору частицы для этого же момента времени, проведенному из центра окружности: ускорение а направлено к центру окружности, являющейся траекторией движения. Тангенциальное и нормальное ускорения. Остановимся подробнее на выводе формул для тангенциального и нормального ускорений. Для этого запишем выражение для вектора скорости в определенной точке криволинейной траектории в виде
28а, б, убеждаемся, что вектор ускорения а в каждый момент времени направлен противоположно радиусу-вектору частицы для этого же момента времени, проведенному из центра окружности: ускорение а направлено к центру окружности, являющейся траекторией движения. Тангенциальное и нормальное ускорения. Остановимся подробнее на выводе формул для тангенциального и нормального ускорений. Для этого запишем выражение для вектора скорости в определенной точке криволинейной траектории в виде
модуль скорости, а вектор, равный по модулю единице и направленный вдоль касательной к траектории в ту сторону, куда движется частица. Будем для краткости называть его единичным вектором касательной.
| При движении частицы по криволинейной |
траектории меняется только направление вектора т, а его модуль остается неизменным и равным единице. Так как ускорение в соответствии (2) равно производной скорости по времени, то, применяя к (5) правило дифференцирования произведения двух функций, можно написать
Первое слагаемое в правой части — это тангенциальное ускорение: видно, что оно направлено по касательной к траектории вперед, когда модуль скорости растет , и назад, когда модуль скорости убывает. Второе слагаемое в правой части — это нормальное ускорение, направленное перпендикулярно касательной к траектории. Чтобы убедиться в этом, преобразуем входящую в него производную следующим образом. Направление единичного вектора фактически зависит от положения частицы на траектории, которое можно задавать длиной дуги . Поэтому его зависимость от времени определяется зависимостью от времени длины дуги. Дифференцируя как сложную функцию времени, найдем
Второе слагаемое в правой части — это нормальное ускорение, направленное перпендикулярно касательной к траектории. Чтобы убедиться в этом, преобразуем входящую в него производную следующим образом. Направление единичного вектора фактически зависит от положения частицы на траектории, которое можно задавать длиной дуги . Поэтому его зависимость от времени определяется зависимостью от времени длины дуги. Дифференцируя как сложную функцию времени, найдем
Здесь мы воспользовались тем смыслом производной легко уяснить из рис. 29. Все изменение вектора
при переходе частицы из точки в близкую к ней точку , отстоящую по траектории на длину дуги сводится к повороту на некоторый малый угол . Поэтому для модуля вектора можно написать
Сам вектор можно представить в виде
единичный вектор нормали к траектории, направленный из данной точки траектории к центру аппроксимирующей ее окружности. Из рис. 29 видно, что длину дуги можно выразить через радиус аппроксимирующей окружности:
В результате можно представить следующим образом:
после чего выражение (7) принимает вид
Теперь можно написать окончательное выражение для ускорения, подставляя в (6):
Поскольку единичный вектор нормали п всегда смотрит в сторону вогнутости траектории, вектор полного ускорения а по отношению к траектории может быть направлен только так, как показано на рис.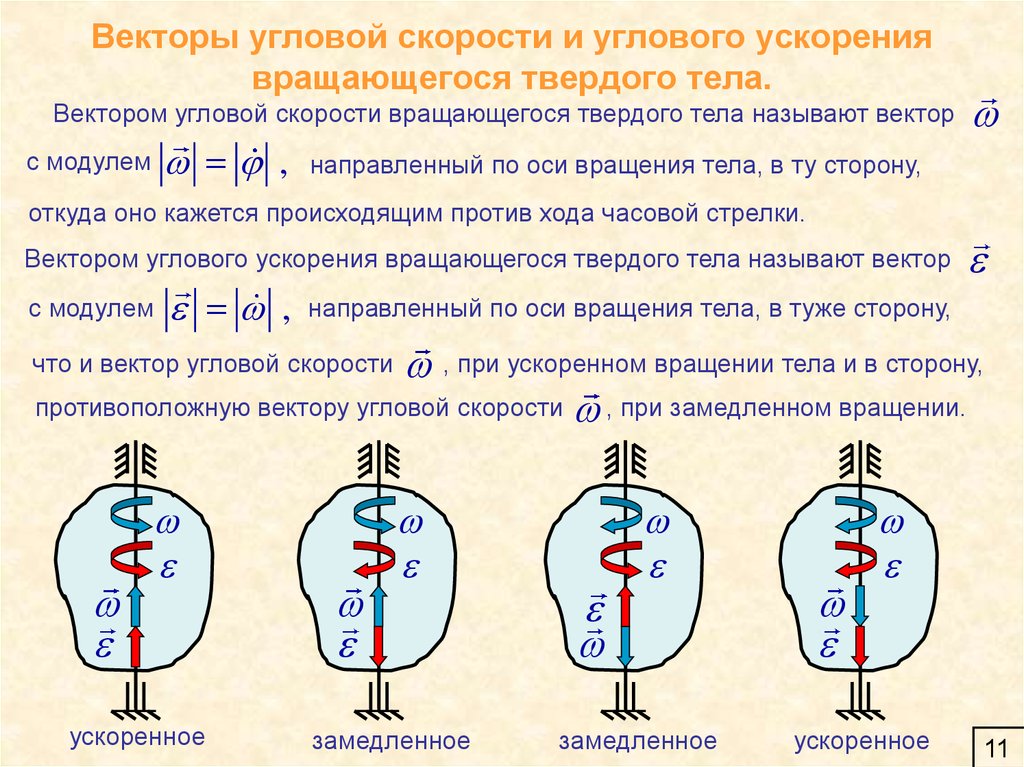 30. Формула (9) фактически представляет собой разложение вектора а на две составляющие. Такое разложение, конечно, может быть выполнено бесконечным числом способов. Данный способ замечателен тем, что две взаимно перпендикулярные составляющие вектора ускорения имеют ясный физический смысл: одна из них характеризует быстроту изменения модуля скорости, а другая — быстроту изменения его направления.
30. Формула (9) фактически представляет собой разложение вектора а на две составляющие. Такое разложение, конечно, может быть выполнено бесконечным числом способов. Данный способ замечателен тем, что две взаимно перпендикулярные составляющие вектора ускорения имеют ясный физический смысл: одна из них характеризует быстроту изменения модуля скорости, а другая — быстроту изменения его направления.
По теореме Пифагора для модуля полного ускорения имеем
• Объясните, почему вектор направлен вдоль вектора п нормали к траектории.
• Почему равны углы, отмеченные дужками на рис. 29?
• От чего зависит угол отклонения вектора а полного ускорения частицы от направления нормали к траектории?
Четырех-ускорения в СТО.
Назад: Виды ускорений в СТО.
Вектора различных 4-ускорений получим взятием производной от V=(v,ic), B=(b,icγ), v=(v/с,i), b=(b/с,iγ) по t и τ:
dV/dt = (dv/dt,
0),
dV/dτ = (γdv/dt,
0),
dB/dt = (db/dt, i(bdb/dt)
/ γc),
dB/dτ = (γdb/dt,
i(bdb/dt) / c),
dv/dt = (dv/(cdt), 0)
dv/dτ = (γdv/(cdt),
0),
db/dt = (db/(cdt), i(bdb/dt)
/ γc2),
db/dτ = (γdb/(cdt),
i(bdb/dt) / c2).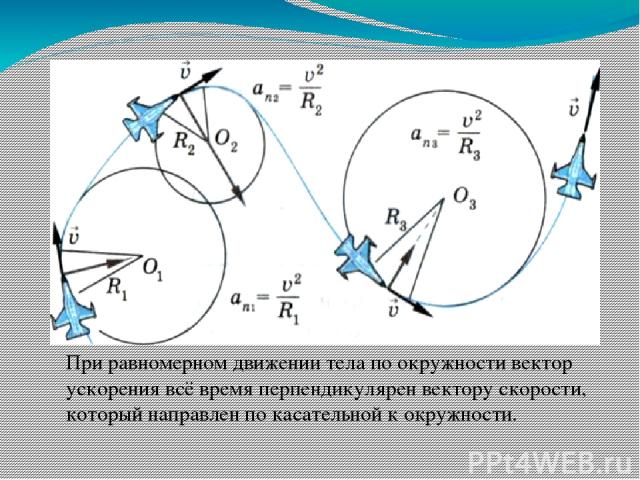
Умножая скалярно 4-вектор собственной скорости B = (b, icγ), или b=(b/с,iγ) на любой из векторов ускорений dB/dt, dB/dτ, db/dt, db/dτ, замечаем, что их скалярные произведения равны нулю, то есть векторы B и b ортогональны векторам dB/dt, dB/dτ, db/dt, db/dτ, а сами параллельны между собой:
(b·db/dt) = 0, (b·db/dτ) = 0, и т.д. для любых комбинаций b и B.
Но 4-вектора v-скоростей и v-ускорений
не являются ортогональными.
4-ускорение у “Ландау и Лифшиц”.
Во 2-ом томе Теоретической Физики (Теория Поля, М. Наука, 1988, стр.41) мы находим параграф о четырехмерной скорости и 4-ускорении. Я переписываю сюда этот параграф красным цветом, добавляя свои комментарии черным цветом.
Из обычного трёхмерного вектора скорости можно образовать и четырехмерный вектор. Такой четырехмерной скоростью (4-скоростью) частицы является вектор
ui = dxi/ds. (7,1)
В (7,1) записан контравариантный вектор, и предполагается, что у ковариантного вектора пространственные компоненты имеют другой знак. Мы пишем то же самое через комплексные вектора, содержащие i=sqr(-1):
b = dR/ds = dR/(cdτ)= dr/dτ = (b/с, iγ).
Для нахождения его компонент замечаем, что согласно (3,1)
ds = c dt sqr(1-v2/c2),
где v – обычная трехмерная скорость частицы. Поэтому
Поэтому
u1 = dx1/ds = dx / (c dt sqr(1-v2/c2)) = vx / (c sqr(1-v2/c2))
и т.п. Таким образом:
ui = (1 / sqr(1-v2/c2), v / (c sqr(1-v2/c2))). (7,3)
Учитывая, что временная компонента здесь идет под индексом “0”, а у нас под номером четыре, замечаем, что это выражение соответствует собственной 4-скорости в наших обозначениях:
b = (b/с, iγ) = (vγ/с, iγ).
Отметим, что 4-скорость есть величина безразмерная.
Компоненты 4-скорости не независимы. Замечая, что dxidxi=ds2, имеем:
uiui = 1. (7,3)
Геометрически ui есть единичный 4-вектор
касательной к мировой линии частицы.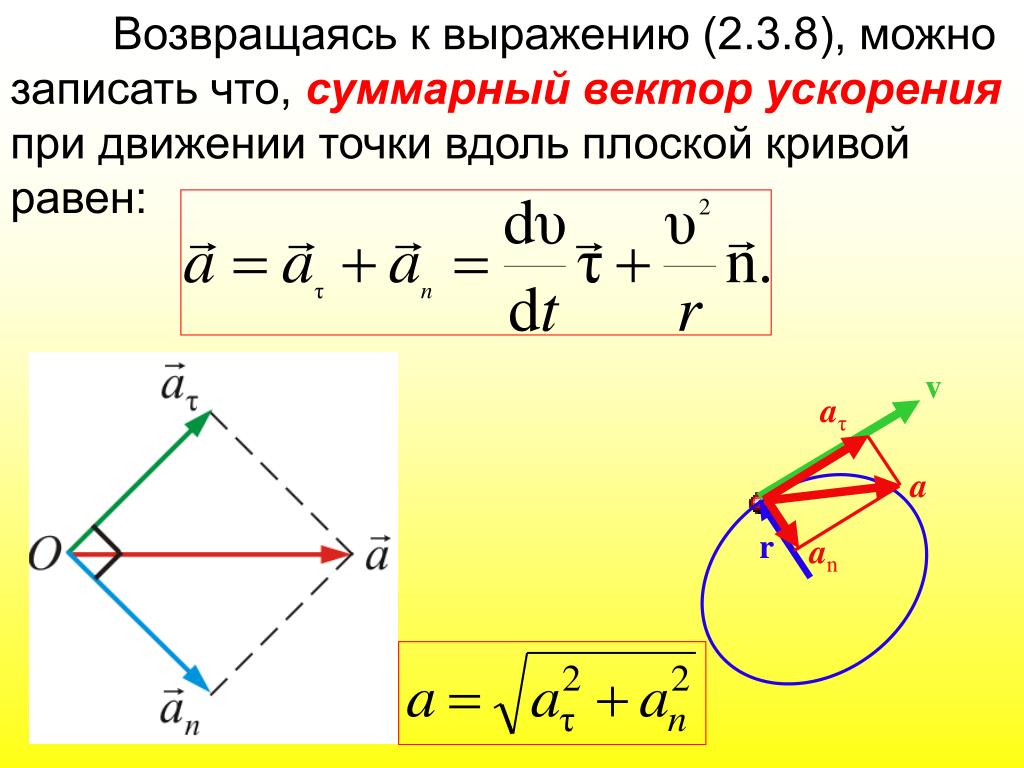
Аналогично определению 4-скорости, вторую производную
wi = d2xi / ds2 = dui / ds = dui / (cdτ)
можно назвать 4-ускорением.
Это действительно 4-ускорение. Это ускорение соответствует второму из наших 4-ускорений, выписанных ниже. Но во второй закон Ньютона входит пространственная компонента первого уравнения
1. dB/dt = (db/dt,
i(bdb/dt) / γc),
2. dB/dτ = (γdb/dt,
i(bdb/dt) / c).
Дифференцируя соотношение (7,3), найдем:
uiwi = 0, (7,4)
т.е. 4-векторы скорости и ускорения взаимно ортогональны.
Да, и полные размерные dB/dt, и dB/dτ,
и единичные безразмерные db/dt и db/dτ
ортогональны собственной 4-скорости, и полной размерной B,
и единичной безразмерной b.
Задача
Определить релятивистское равноускоренное движение, т.е. прямолинейное движение, при котором остается постоянной величина ускорения w в собственной (в каждый данный момент времени) системе отсчета.
Р е ш е н и е. В системе отсчета, в которой скорость частицы v = 0, компоненты 4-ускорения равны wi = (0, w/c2, 0, 0) (w – обычное трехмерное ускорение, направленное вдоль оси x). Релятивистски инвариантное условие равноускоренности должно быть представлено в виде постоянства 4-скаляра, совпадающего с w2 в собственной системе отсчета:
wiwi = const = – w2/c4.
В “неподвижной” системе отсчета, относительно которой рассматривается движение, раскрытие выражения wiwi приводит к уравнению
d(v / sqr(1-v2/c2))
/ dt = w, или v / sqr(1-v2/c2) = wt + const.
Согласно нашим обозначениям этой записи соответствует db/dt = w, или b = wt + const. То есть, поскольку w=const, то и db/dt=const, и dρ/dτ=const, т.к. dρ/dτ=db/dt. Ускорения других типов связаны с этим ускорением через γ в некоторой степени, а γ не является константой, поскольку зависит от скорости, следовательно, другие типы ускорений не являются константами для релятивистски равноускоренного движения.
Полагая v = 0 при t = 0, имеем const = 0, так что
v = wt / sqr(1+w2t2/c2).
Интегрируя еще раз и полагая x = 0 при t = 0, получим:
x = (c2/w) / (sqr(1+w2t2/c2) – 1).
При wt значительно меньше c эти формулы переходят в классические выражения v = wt, x = wt2/2. При wt –> “бесконечность” скорость стремится к постоянному значению c.
Собственное время равноускоренно движущейся частицы дается интегралом
0∫ t sqr(1-v2/c2) dt = (c/w) Arsh
wt/c.
При t → ∞ оно растет по значительно более медленному чем t закону (c/w)ln(2wt/c).
ЛИТЕРАТУРА
Ландау Л.Д., Лифшиц Е.М. Теоретическая Физика, том 2, Теория Поля, М. “Наука”, 1988.
Вперёд: Релятивистская ракета.
Назад: Виды ускорений.
К оглавлению раздела Некоторые вопросы СТО.
К другим разделам Космической Генетики.
Иван Горелик
Моё резюме
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒
Вектор задает направление касательной к траектории в данной точке. Вектор направлен по радиусу кривизны траектории. Компоненты вектора ускорения на эти оси называют тангенциальным и нормальным ускорениями.
Тангенциальное ускорение характеризует быстроту изменения по величине
Нормальное ускорение характеризует быстроту изменения скорости по направлению
Где R – радиус кривизны траектории.
если материальная точка может перемещаться только вдоль одной оси координат, то она обладает одной степенью свободы. Если тело перемещается в пространстве и одновременно вращается вокруг оси, проходящей через тело, то оно обладает четырьмя степенями свободы; если же вращается вокруг двух взаимно-перпендикулярных осей – пятью степенями свободы.
Абсолютно твердым телом называется тело, расстояние между двумя любыми точками которого остается постоянным при любых взаимодействиях.
Любое движение абсолютно твердого тела можно разложить на два простейших вида: поступательное и вращательное.
Поступательным называется движение, при котором прямая, соединяющая две произвольные точки этого тела, перемещается параллельно самой себе. При поступательном движении скорости и ускорения всех точек тела одинаковы. Поэтому для описания поступательного движения абсолютно твердого тела достаточно задать уравнение движения одной его точки.
Вращательным называется движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, а плоскости окружностей перпендикулярны этой прямой, называемой осью вращения.
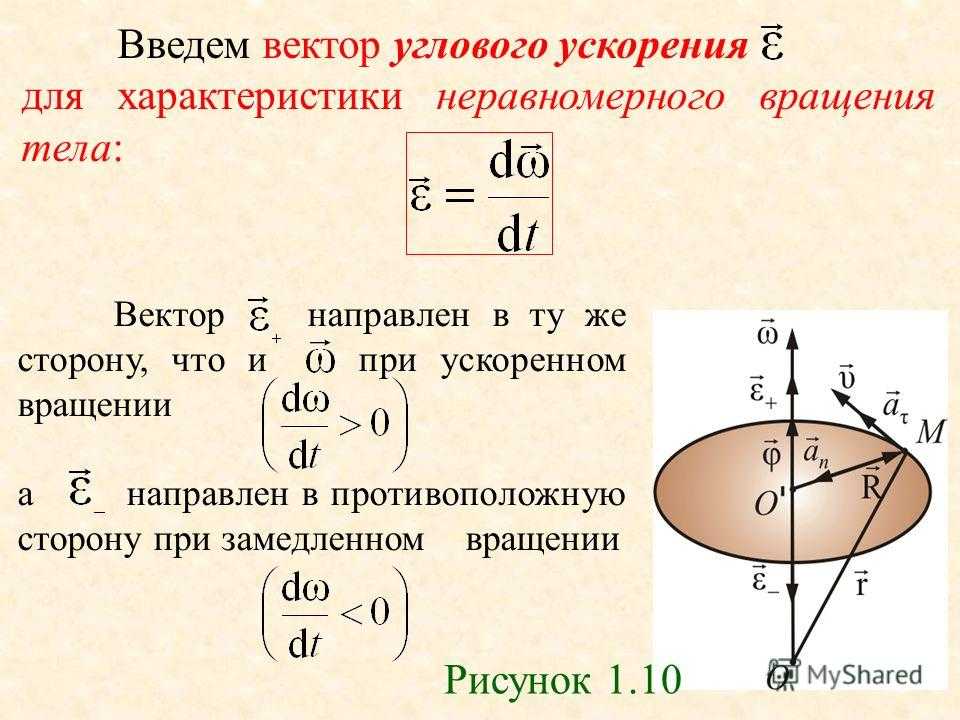
Для описания вращающегося движения вводятся угловые кинематические характеристики: угловой путь, угловое перемещение, угловая скорость и угловое ускорение.
Угловая скорость – вектор, показывающий быстроту изменения угла поворота
.Направление вектора совпадает с направлением вектора углового перемещения dф .
Угловое ускорение Е – вектор, показывающий быстроту изменения угловой скорости:
1) прямолинейного равномерного движения скорость 2) равнопеременного движения скорость путь .
Скорость является первой производной от пути по времени, а ускорение – второй:
; 3) движения по окружности угловая скорость и угловой путь соответственно
Условия равновесия тел. Статикой называется раздел механики, изучающий условия равновесия тел. Из 2 закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. То силы, приложенные к телу, уравновешивают друг друга. Равновесие тел – состояние механической системы, в которой тела остаются неподвижными по отношению к выбранной системе отсчета. Рычаг (Архимед). Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил. F1/F2=L2/L1 Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю.
Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. *В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Безразличное: При малом отклонении тело остается в равновесии. Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие. Центр тяжести. Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. xc = (∑ Gixi) / ∑ Gi; yc = (∑ Giyi) / ∑ Gi; zc = (∑ Gizi) / ∑ Gi. Вес Gi каждого отрезка li можно представить в виде произведения Gi = lid, где d – постоянный для всей фигуры вес единицы длины материала.
*Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты. У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла Колебания точки. Колебания-это повторяющиеся во времени изменения состояния системы. Виды: 1) свободные (гармонические) колебания, происходящие под действием линейной восстанавливающей силы, т. е. силы стремящейся вернутьточку в положение равновесия и пропорциональной её отклонению от этого положения равновесия.(F=-kx) 2) затухающие колебания, происходящие под действием восстанавливающей силы и силы сопротивления среды,(* в случае большого сопротивления движение точки является апериодическим движением.
3) вынужденные колебания, когда кроме восстанавливающей силы и силы сопротивления среды действует сила, периодически зависящая от времени.
⇐ Предыдущая123456Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь – 161. |
4.2 Вектор ускорения – общая физика с использованием исчисления I
4 Движение в двух и трех измерениях
Цели обучения
К концу этого раздела вы сможете:
- Вычислять вектор ускорения по заданной функции скорости в представлении единичного вектора.
- Опишите движение частицы с постоянным ускорением в трех измерениях.
- Используйте уравнения одномерного движения вдоль перпендикулярных осей для решения задачи в двух или трех измерениях с постоянным ускорением.
- Выразите ускорение в виде единичного вектора.
Мгновенное ускорение
Помимо получения векторов смещения и скорости движущегося объекта, мы часто хотим знать его вектор ускорения в любой момент времени на его траектории. Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе. Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени [latex]\mathbf{\overset{\to }{v}}(t),[/latex] находим
Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени [latex]\mathbf{\overset{\to }{v}}(t),[/latex] находим
[латекс] \ mathbf {\ overset {\ to {a}} (t) = \ underset {t \ to 0} {\ text {lim}} \ frac {\ mathbf {\ overset {\ to }{ v}} (t + \ Delta t) – \ mathbf {\ overset {\ to {v}} (t)} {\ Delta t} = \ frac {d \ mathbf {\ overset {\ to {v}} (t)}{dt}.[/latex]
Ускорение по компонентам равно
[латекс]\mathbf{\overset{\to }{a}}(t)=\text{}\frac {d {v} _ {x} (t)} {dt} \ mathbf {\ hat {i}} + \ frac {d {v} _ {y} (t)} {dt} \ mathbf {\ hat { j}}+\frac{d{v}_{z}(t)}{dt}\mathbf{\hat{k}}.[/latex]
Кроме того, поскольку скорость является производной функции положения , мы можем записать ускорение через вторую производную функции положения: 9{2})\mathbf{\шляпа{i}}+5t\mathbf{\шляпа{j}}+5t\text{}\mathbf{\шляпа{k}}\text{m}.[/latex] а) Какова скорость? б) Чему равно ускорение? в) Опишите движение от до = 0 с. {2}.[/latex] Вектор ускорения является константой в отрицательном направлении x.
{2}.[/latex] Вектор ускорения является константой в отрицательном направлении x.
(c)
Показать ОтветТраекторию частицы можно увидеть на рисунке.
Давайте сначала посмотрим в направлениях y и z. Положение частицы неуклонно увеличивается во времени с постоянной скоростью в этих направлениях. Однако в направлении x частица следует по пути с положительным значением x до момента t = 5 с, после чего она меняет направление. Мы знаем это, глядя на функцию скорости, которая в это время становится нулевой, а затем отрицательной. Мы также знаем это, потому что ускорение отрицательное и постоянное, то есть частица замедляется или ускоряется в отрицательном направлении. Положение частицы достигает 25 м, где затем она меняет направление и начинает ускоряться в отрицательном направлении x. Позиция достигает нуля при t = 10 с.
Рисунок 4.9 Частица начинается в точке (x, y, z) = (0, 0, 0) с вектором положения [латекс]\mathbf{\overset{\to }{r}}=0.[/latex] Показана проекция траектории на плоскость xy. Значения y и z увеличиваются линейно как функция времени, тогда как x имеет точку поворота при t = 5 с и 25 м, когда оно меняет направление. В этот момент x-компонента скорости становится отрицательной. В t = 10 с частица возвращается на 0 м в направлении x.
Значения y и z увеличиваются линейно как функция времени, тогда как x имеет точку поворота при t = 5 с и 25 м, когда оно меняет направление. В этот момент x-компонента скорости становится отрицательной. В t = 10 с частица возвращается на 0 м в направлении x.Значение
9{2},[/latex], где a, b, и c — константы. Что можно сказать о функциональном виде функции скорости? Показать решение Вектор ускорения постоянен и не меняется со временем. Если a, b и c не равны нулю, то функция скорости должна быть линейной во времени. У нас есть [латекс] \ mathbf {\ overset {\ to {v}} (t) = \ int \ mathbf {\ overset {\ to {a}} dt = \ int (a \ mathbf {\ hat {i }}+b\mathbf{\шляпа{j}}+c\mathbf{\шляпа{k}})dt=(a\mathbf{\шляпа{i}}+b\mathbf{\шляпа{j}}+ c\mathbf{\hat{k}})t\,\text{м/с},[/latex], поскольку взятие производной функции скорости дает [латекс]\mathbf{\overset{\to} {a} }(t).[/latex] Если какая-либо из составляющих ускорения равна нулю, то эта составляющая скорости будет константой.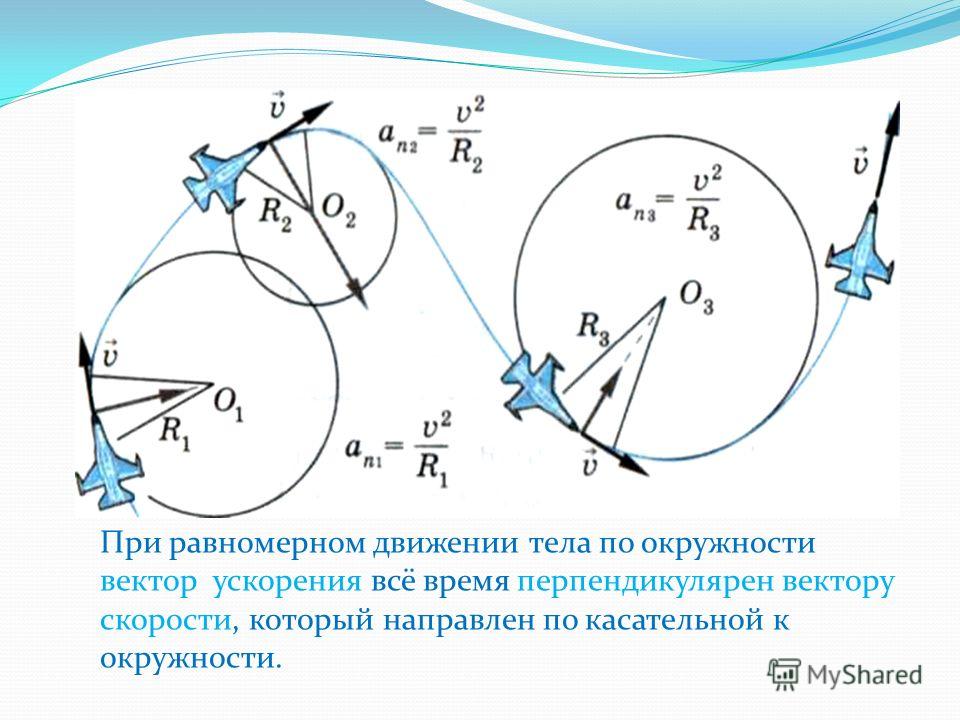
Постоянное ускорение
Многомерное движение с постоянным ускорением можно рассматривать так же, как показано в предыдущей главе для одномерного движения. Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое вдоль оси, перпендикулярной другим. Для построения соответствующих уравнений в каждом направлении рассмотрим двумерную задачу о движении частицы в плоскости xy с постоянным ускорением без учета z -компонент на данный момент. Вектор ускорения равен
[латекс]\mathbf{\overset{\to }{a}}={a}_{0x}\mathbf{\hat{i}}+{a}_{0y}\mathbf{ \hat{j}}.[/latex]
Каждая составляющая движения имеет отдельный набор уравнений, аналогичный рисунку–рисунку из предыдущей главы об одномерном движении. Мы показываем только уравнения для положения и скорости в направлениях x и y . Аналогичная система кинематических уравнений может быть записана для движения в 9{2}+2{a}_{y}(y-{y}_{0}).[/latex]
Здесь нижний индекс 0 обозначает начальное положение или скорость. Figure to Figure можно заменить на Figure и Figure без компонента z , чтобы получить вектор положения и вектор скорости как функцию времени в двух измерениях:
Figure to Figure можно заменить на Figure и Figure без компонента z , чтобы получить вектор положения и вектор скорости как функцию времени в двух измерениях:
[латекс]\mathbf{\overset{\to} }{r }} (t) = x (t) \ mathbf {\ hat {i}} + y (t) \ mathbf {\ hat {j}} \, \ text {and} \, \ mathbf {\ overset {\ to }{v}}(t)={v}_{x}(t)\mathbf{\шляпа{i}}+{v}_{y}(t)\mathbf{\шляпа{j}}.[ /латекс]
9\circ[/latex] at t = 0. С началом системы координат в передней части домика ее начальное положение и скорость равны[латекс]\mathbf{\overset{\to} {r} }(0)=(75,0\mathbf{\шляпа{i}}-50,0\mathbf{\шляпа{j}})\,\текст{м}[/латекс]
и
[латекс]\mathbf{ \overset{\to }{v}}(0)=(4.1\mathbf{\шляпа{i}}-1.1\mathbf{\шляпа{j}})\,\text{м/с}.[/latex ]
(a) Каковы x- и y -компоненты положения и скорости лыжника как функции времени? б) Каковы ее положение и скорость в точке 9?\circ.[/latex] Начало системы координат находится в лыжной базе.
Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам необходимо найти компоненты ускорения и подставить их в кинематические уравнения.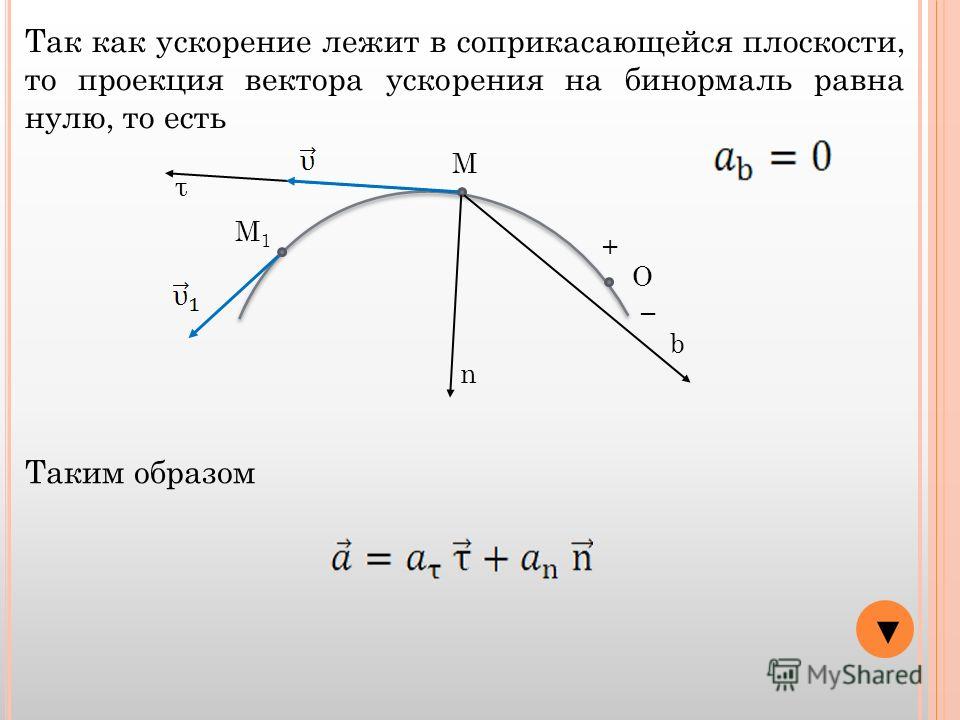 Компоненты ускорения находятся в системе координат на рис. Затем, подставляя компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время 9{2})(10,0\,\текст{с})=-6,5\,\текст{м/с}.[/латекс]
Компоненты ускорения находятся в системе координат на рис. Затем, подставляя компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время 9{2})(10,0\,\текст{с})=-6,5\,\текст{м/с}.[/латекс]
Положение и скорость при t = 10,0 с, наконец,
[латекс]\mathbf{\overset{\to}}{r}}(10,0\,\текст{s})=(216,0\mathbf{\шляпа{i}}-88,0\mathbf{\шляпа{j}} ) \, \ text {m} [/ латекс] [латекс] \ mathbf {\ overset {\ to {v}} (10,0 \, \ text {s}) = (24,1 \ mathbf {\ hat {i}} -6,5\mathbf{\шляпа{j}})\текст{м/с}.[/латекс]
Величина скорости лыжника в 10,0 с равна 25 м/с, что составляет 60 миль/ч.
Значение
Полезно знать, что, зная начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое время позже.
С помощью рисунка через рисунок мы завершили набор выражений для положения, скорости и ускорения объекта, движущегося в двух или трех измерениях.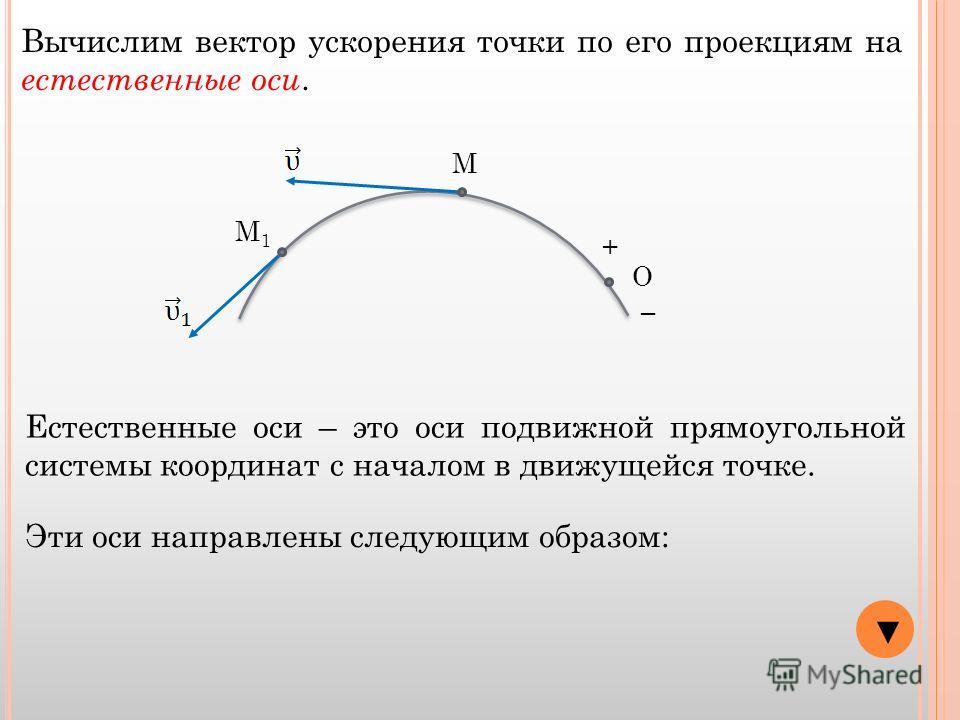 Если траектории объектов выглядят примерно как «красные стрелки» на заставке к главе, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы рассмотрим два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
Если траектории объектов выглядят примерно как «красные стрелки» на заставке к главе, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы рассмотрим два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
На этом веб-сайте Университета Колорадо в Боулдере вы можете изучить позиционную скорость и ускорение божьей коровки с помощью интерактивного моделирования, позволяющего изменять эти параметры.
Резюме
- В двух- и трехмерном пространстве вектор ускорения может иметь произвольное направление и не обязательно указывает на заданную составляющую скорости.
- Мгновенное ускорение создается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение представляет собой вектор в двух или трех измерениях. Его находят, взяв производную функции скорости по времени.
- В трех измерениях ускорение [латекс]\mathbf{\overset{\to }{a}}(t)[/latex] может быть записано как векторная сумма одномерных ускорений [латекс]{a}_{ x}(t),{a}_{y}(t),\text{and}\,{a}_{z}(t)[/latex] по x- , y -, и оси z- .

- Кинематические уравнения для постоянного ускорения могут быть записаны как векторная сумма уравнений постоянного ускорения в направлениях x , y и z .
Концептуальные вопросы
Если функция положения частицы является линейной функцией времени, что можно сказать о ее ускорении?
Если объект имеет постоянную составляющую скорости x и внезапно испытывает ускорение в направлении y , изменится ли составляющая его скорости x – ?
Показать решениеНет, движения в перпендикулярных направлениях независимы.
Если объект имеет константу 9{2}\mathbf{\hat{i}}.[/latex] Сильный ветер толкает лодку, придавая ей дополнительную скорость [latex]2,0\,\text{м/с}\mathbf{\hat{ i}}+1,0\,\text{м/с}\mathbf{\hat{j}}.[/latex] (a) Какова скорость лодки при t = 10 с? б) Каково положение лодки через t = 10 с? Нарисуйте эскиз траектории и положения лодки в момент времени t = 10 с, показав оси x и y . {-2}\mathbf{\шляпа{k}})\,\text{m}. [/latex] (а) Какова скорость как функция времени? б) Чему равно ускорение в зависимости от времени? в) Какова скорость частицы в точке 9?{2}[/латекс],
{-2}\mathbf{\шляпа{k}})\,\text{m}. [/latex] (а) Какова скорость как функция времени? б) Чему равно ускорение в зависимости от времени? в) Какова скорость частицы в точке 9?{2}[/латекс],
в. [латекс] \ mathbf {\ overset {\ to {v}} (2,0 с) = (12,0 \ mathbf {\ hat {i}} -84,0 \ mathbf {\ hat {j}} + 1,25 \ mathbf {\ hat {к}})\текст{м/с}[/латекс],
д. [латекс] \ mathbf {\ overset {\ to {v}} (1,0 \, \ text {s}) = 6,0 \ mathbf {\ hat {i}} -21,0 \ mathbf {\ hat {j}} +10,0 \mathbf{\шляпа{к}}\текст{м/с},\,|\mathbf{\overset{\to}}{v}}(1,0\,\текст{с})|=24,0\,\текст {м/с}[/латекс]
[латекс]\mathbf{\overset{\to}}{v}}(3,0\,\текст{s})=18,0\mathbf{\шляпа{i}}-189,0\mathbf{\шляпа{j}}+ 0,37\mathbf{\шляпа{к}}\текст{м/с},[/латекс] [латекс]|\mathbf{\overset{\to}}{v}}(3,0\,\текст{с})| =19{-2}\mathbf{\шляпа{к}})\текст{см}[/латекс]
[латекс] \ begin {массив} {cc} \ hfill {\ mathbf {\ overset {\ to} {v}}} _ {\ text {avg}} & = 9,0 \ mathbf {\ hat {i}} – 49.0\mathbf{\шляпа{j}}-6.3\mathbf{\шляпа{k}}\текст{м/с}\hfill\end{массив}[/латекс]
Ускорение частицы является постоянной величиной.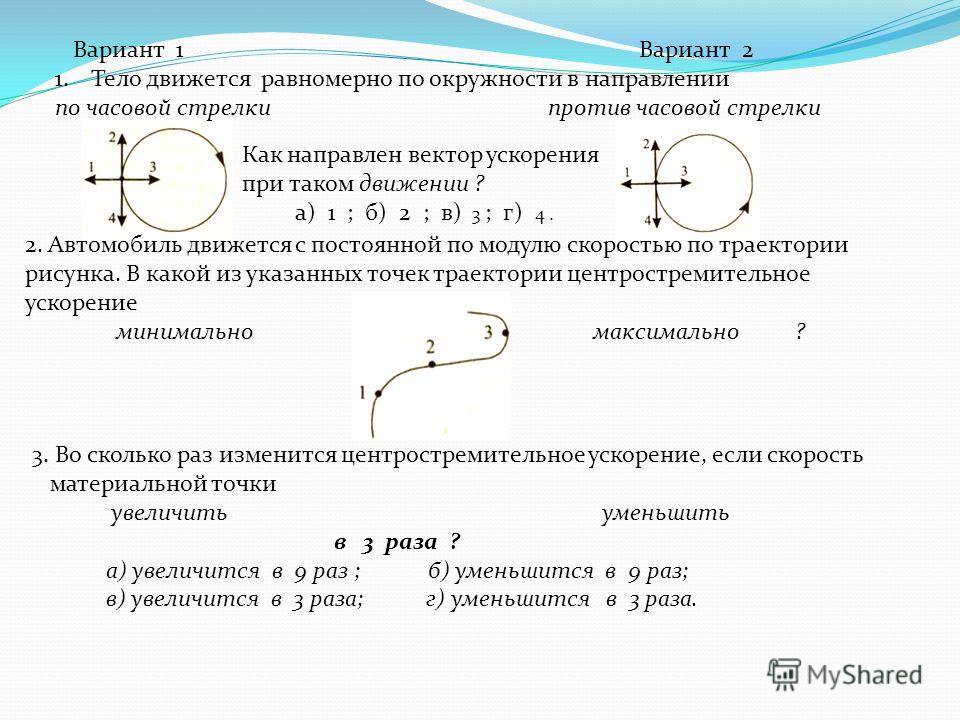 При t = 0 скорость частицы равна [латекс](10\mathbf{\шляпа{i}}+20\mathbf{\шляпа{j}})\текст{м/с}.[/латекс] При t = 4 с скорость равна [латекс]10\mathbf{\шляпа{j}}\текст{м/с}.[/латекс] (а) Чему равно ускорение частицы? б) Как изменяются со временем положение и скорость? Предположим, что частица изначально находится в начале координат.
При t = 0 скорость частицы равна [латекс](10\mathbf{\шляпа{i}}+20\mathbf{\шляпа{j}})\текст{м/с}.[/латекс] При t = 4 с скорость равна [латекс]10\mathbf{\шляпа{j}}\текст{м/с}.[/латекс] (а) Чему равно ускорение частицы? б) Как изменяются со временем положение и скорость? Предположим, что частица изначально находится в начале координат.
Частица имеет функцию положения [латекс]\mathbf{\overset{\to }{r}}(t)=\text{cos}(1.0t)\mathbf{\hat{i}}+\text{ sin}(1.0t)\mathbf{\hat{j}}+t\mathbf{\hat{k}},[/latex], где аргументы функций косинуса и синуса выражены в радианах. а) Чему равен вектор скорости? б) Чему равен вектор ускорения?
Показать раствор а. [латекс] \ mathbf {\ overset {\ to} {v}} (t) = \ text {− sin} (1,0 t) \ mathbf {\ hat {i}} + \ text {cos} (1,0 t) \ mathbf{\шляпа{j}}+\mathbf{\шляпа{k}}[/латекс], b. [латекс] \ mathbf {\ overset {\ to} {a}} (t) = \ text {−cos} (1.0t) \ mathbf {\ hat {i}} – \ text {sin} (1.0t) \ mathbf{\шляпа{j}}[/латекс] 9\circ[/latex] относительно горизонтали.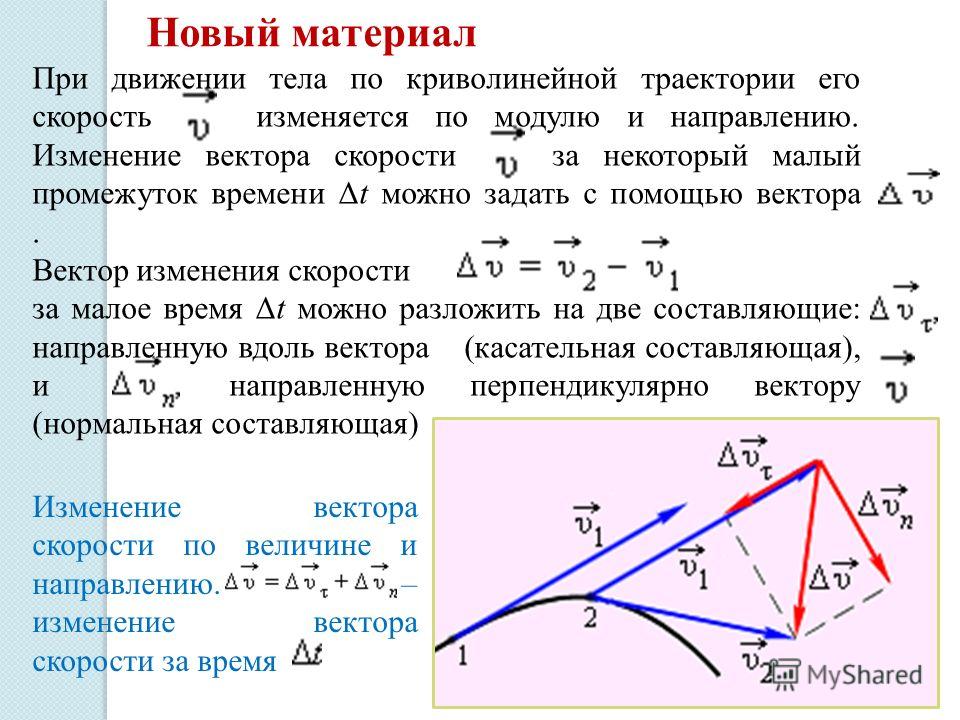 а) Каково начальное ускорение F-35 на палубе авианосца, чтобы он поднялся в воздух? (b) Запишите положение и скорость F-35 в виде единичного вектора от точки, в которой он покидает палубу авианосца. в) На какой высоте находится истребитель через 5,0 с после того, как он покинет палубу авианосца? г) Какова его скорость и скорость в это время? д) Какое расстояние он прошел по горизонтали?
а) Каково начальное ускорение F-35 на палубе авианосца, чтобы он поднялся в воздух? (b) Запишите положение и скорость F-35 в виде единичного вектора от точки, в которой он покидает палубу авианосца. в) На какой высоте находится истребитель через 5,0 с после того, как он покинет палубу авианосца? г) Какова его скорость и скорость в это время? д) Какое расстояние он прошел по горизонтали?
Глоссарий
- вектор ускорения
- мгновенное ускорение, найденное путем взятия производной функции скорости по времени в виде единичного вектора
17Исчисление – Векторные функции – Вектор ускорения
На этой странице мы берем вектор ускорения, который вы научились находить на странице движения снаряда, и выражаем его через единичный тангенс и главный единичный вектор нормали.
Рекомендуемые книги на Amazon (партнерские ссылки) | ||
|---|---|---|
Полный список рекомендуемых книг 17Calculus | ||
Prime Student 6-месячная пробная версия | ||
Объяснение компонентов вектора ускорения
На странице движения снаряда мы показали вам, как найти вектор ускорения по вектору положения или скорости.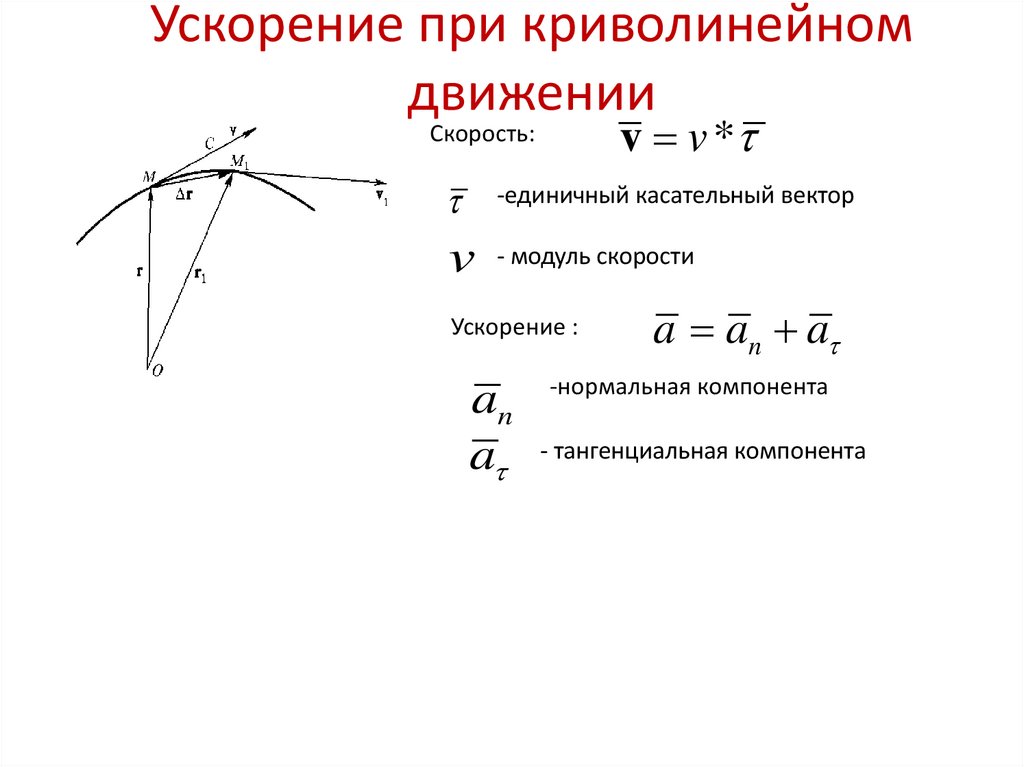 Вектор ускорения можно записать в виде
Вектор ускорения можно записать в виде
\(\vec{a}(t)=a_x(t)\vhat{i}+a_y(t)\vhat{j}+a_z(t)\vhat{k}\) |
Как написано выше, вектор ускорения \(\vec{a}(t)\) выражается с использованием трех стандартных единичных векторов, \(\vhat{i}\), \(\vhat{j}\) и \(\что{к}\). Это только один из бесконечного множества способов записи вектора. Пока единичные векторы покрывают (или охватывают) все трехмерное пространство (концепция из линейной алгебры), мы можем использовать их для записи любого вектора в их терминах. Здесь мы не будем беспокоиться о деталях линейной алгебры, за исключением того, что скажем, что единичный касательный вектор и главный единичный вектор нормали покрывают все пространство, необходимое для описания вектора ускорения. Другими словами, вектор ускорения лежит в плоскости, определяемой \(\vhat{T}\) и \(\vhat{N}\). Таким образом, мы можем записать вектор ускорения через эти два единичных вектора в следующей форме.
\(\vec{a}(t) = a_{\vhat{T}}(t)\vhat{T} + a_{\vhat{N}}(t)\vhat{N}\ ) |
Примечания – –
1. На этой странице мы пишем единичный касательный вектор и главный единичный вектор нормали со знаком “шляпа” (\(\vhat{T}\)) вместо стрелка (\(\vec{T}\)). Знак «шляпа» подчеркивает, что речь идет о векторах длины один (единичных векторах). Ваш учебник и преподаватель могут следовать или не следовать этому соглашению.
На этой странице мы пишем единичный касательный вектор и главный единичный вектор нормали со знаком “шляпа” (\(\vhat{T}\)) вместо стрелка (\(\vec{T}\)). Знак «шляпа» подчеркивает, что речь идет о векторах длины один (единичных векторах). Ваш учебник и преподаватель могут следовать или не следовать этому соглашению.
2. Возможно, на предыдущих уроках математики или физики вы узнали, что ускорение всегда перпендикулярно скорости. Это верно только для постоянной скорости, т. е. \(\|\vec{v}\| = C\), где C — константа.
Как рассчитать компоненты вектора ускорения
Давайте на мгновение задумаемся об этом. У нас есть единичный вектор (давайте будем работать с единичным касательным вектором), и мы хотим найти проекцию вектора ускорения в направлении единичного касательного вектора. Вы уже знаете, как это сделать, верно? На какую операцию это похоже? Скалярный продукт, верно? По сути, скалярное произведение вычисляет проекцию одного вектора на другой.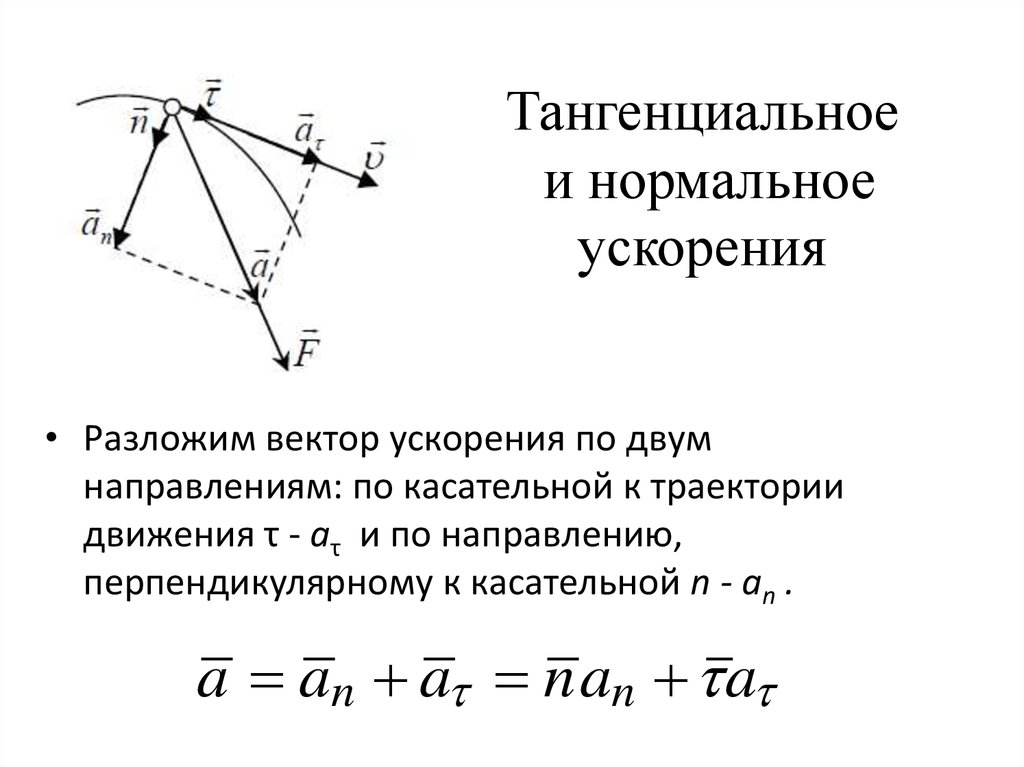 Зная это, наши основные уравнения просты.
Зная это, наши основные уравнения просты.
\(a_{\vhat{T}} = \vec{a} \cdot \vhat{T}\) | \(a_{\vhat{N}} = \vec{a} \cdot \vhat{N}\) |
Мы называем \(a_{\vhat{T}}\) тангенциальной составляющей ускорение и \(a_{\vhat{N}}\) нормальная составляющая ускорения.
Другие уравнения для расчета компонентов вектора ускорения
Существуют другие уравнения, используемые для расчета компонентов вектора ускорения с точки зрения единичного касательного вектора и главного единичного вектора нормали. Какое уравнение вы используете, зависит от постановки задачи и имеющихся у вас данных. Давайте разработаем несколько здесь, начиная с единичного касательного вектора.
Наше основное уравнение для тангенциальной составляющей ускорения: \(a_{\vhat{T}} = \vec{a} \cdot \vhat{T}\). Поскольку \(\vhat{T} = \vec{v}/\|\vec{v}\|\), мы можем написать \(\displaystyle{a_{\vhat{T}} = \frac{\vec{ a} \cdot \vec{v}}{\|\vec{v}\|} }\), который мы также можем использовать для вычисления \(a_{\vhat{T}}\).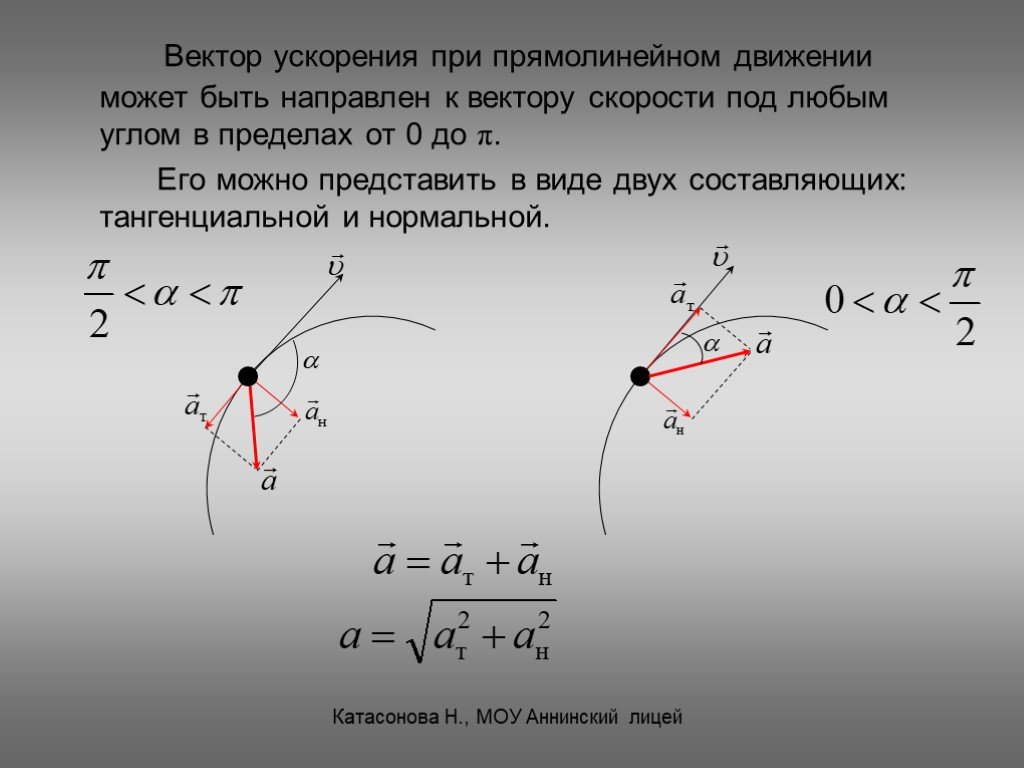
Для следующего уравнения мы собираемся вывести тангенциальную и нормальную составляющие ускорения, что может показаться «заходом через черный ход», то есть косвенно, но уравнения в равной степени действительны и применимы. (Примечание. Большинство преподавателей не ожидают, что вы придумаете эти уравнения таким образом.)
Начнем с \(\vhat{T}=\vec{v}/\|\vec{v}\|\), что является основным определением единичного касательного вектора. Решая для \(\vec{v}\), мы получаем \(\vec{v}=\|\vec{v}\|\vhat{T}\). Теперь возьмем производную от обеих частей. Слева у нас есть вектор ускорения. Справа нам нужно использовать правило произведения, которое дает нам
\(\vec{a} = \vec{v}’ = \|\vec{v}\|\vhat{T}’ + \|\ vec{v}\|’\vhat{T}\)
Далее мы собираемся сделать то, что обычно делается при работе с уравнениями. Это техника, которую вам нужно принять к сведению, если вы еще этого не сделали. Мы собираемся умножить один из множителей на специальную форму константы 1, а именно \(\|\vhat{T}’\|/\|\vhat{T}’\|\), чтобы получить
\(\displaystyle{\vec{a} = \|\vec{v}\|\vhat{T}’ \frac{ \|\vhat{T}’\| }{\|\vhat{T}’ \|} + \|\vec{v}\|’\vhat{T}}\).
Теперь мы знаем, что главный единичный вектор нормали равен \(\displaystyle{ \vhat{N} = \frac{\vhat{T}’}{\|\vhat{T}’\|}}\), поэтому мы используем это в первом члене выше, чтобы получить
\(\displaystyle{\vec{a} = \|\vec{v}\| \|\vhat{T}’\| \vhat{N} + \| \vec{v}\|’\vhat{T} }\).
Итак, если мы внимательно посмотрим на это последнее уравнение, мы сможем выделить тангенциальную составляющую ускорения и нормальную составляющую ускорения. Тангенциальная составляющая ускорения является коэффициентом \(\vhat{T}\), а именно \(\|\vec{v}\|’\). Точно так же нормальный компонент ускорения является коэффициентом \(\vhat{N}\), а именно \(\|\vec{v}\| \|\vhat{T}’\|\). Теперь у нас есть еще два уравнения для составляющих ускорения.
\(a_{\vhat{T}} = \| \vec{v} \|’ \) |
\(a_{\vhat{N}} = \|\vec{ v}\| \|\vhat{T}’\|\) |
Осторожно — Особо внимательно отметьте, где штрих стоит в каждом из этих уравнений. Для \(a_{\vhat{T}}\) вам нужно найти величину скорости, прежде чем брать производную. С \(a_{\vhat{N}}\) вам нужно сначала взять производную от основного единичного вектора нормали, а затем найти величину.
Для \(a_{\vhat{T}}\) вам нужно найти величину скорости, прежде чем брать производную. С \(a_{\vhat{N}}\) вам нужно сначала взять производную от основного единичного вектора нормали, а затем найти величину.
Рисунок 1 |
|---|
Итак, это все уравнения, которые мы собираемся составить для единичного касательного вектора. Получим еще два уравнения для главного единичного вектора нормали. Мы будем использовать рисунок 1, чтобы визуализировать векторные уравнения.
Если обозначить θ как угол между единичным касательным вектором и вектором ускорения, как показано на рис. 1, то нормальная составляющая ускорения может быть записана как \(a_{\vhat{N}} = \|\ vec{a}\|\sin\theta\). Умножая и деля на \(\|\vec{v}\|\), мы получаем \(\displaystyle{a_{\vhat{N}} = \frac{\|\vec{v}\| \|\vec {a}\|\sin\theta}{\|\vec{v}\|} }\). Теперь помните из векторного произведения, что \(\|\vec{v}\| \|\vec{a}\| \sin\theta = \|\vec{v} \times \vec{a}\|\ ).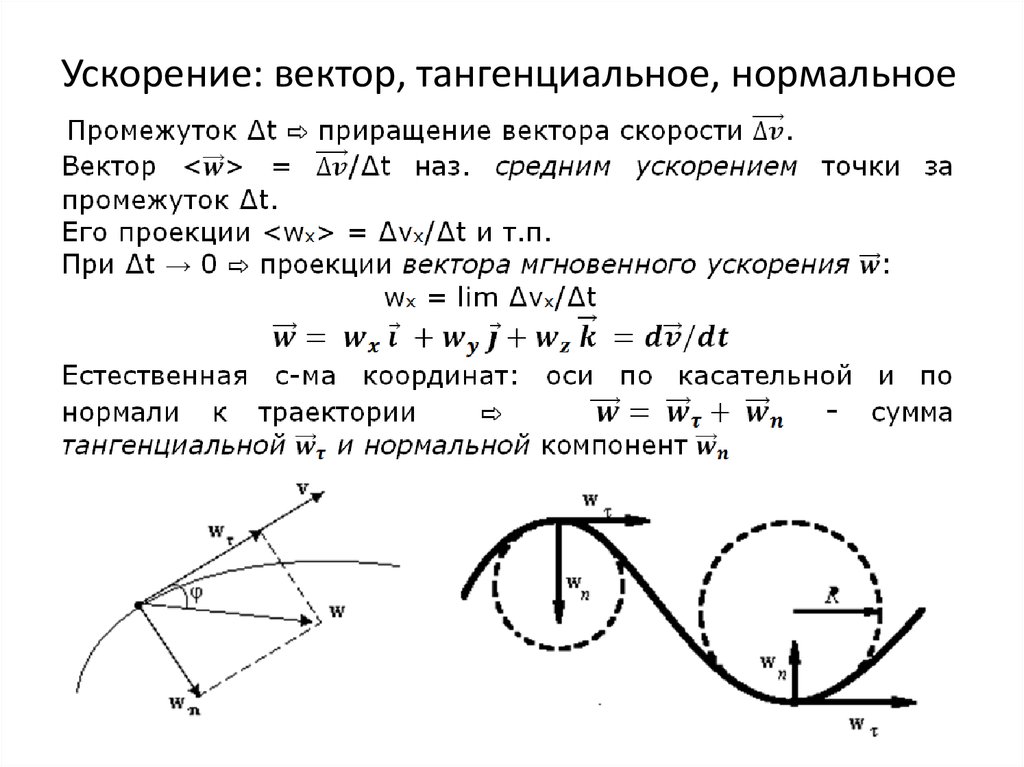 Итак, теперь у нас есть другое уравнение для нормальной составляющей ускорения, \(\displaystyle{a_{\vhat{N}} = \frac{\|\vec{v} \times \vec{a}\|}{\| \vec{v}\|} }\). 92}\).
Итак, теперь у нас есть другое уравнение для нормальной составляющей ускорения, \(\displaystyle{a_{\vhat{N}} = \frac{\|\vec{v} \times \vec{a}\|}{\| \vec{v}\|} }\). 92}\).
Если подумать, мы могли бы вывести и другие уравнения. Тем не менее, это те, которые используются чаще всего, и теперь, когда вы понимаете некоторые из используемых нами методов, вы можете вывести другие, которые могут вам понадобиться в будущем. Вот короткий видеоклип, в котором обсуждаются уравнения на этой странице, но не выводятся их.
MIP4U – Определение тангенциальной и нормальной составляющих ускорения [2мин-9сек]видео MIP4U |
|---|
Итак, время для некоторых практических задач.
У вас может быть потрясающая память: изучите техники и советы, которые изменят вашу жизнь, из памяти Маэстро
Практика
Если не указано иное, рассчитайте тангенциальную и нормальную составляющие вектора ускорения для заданного вектора положения.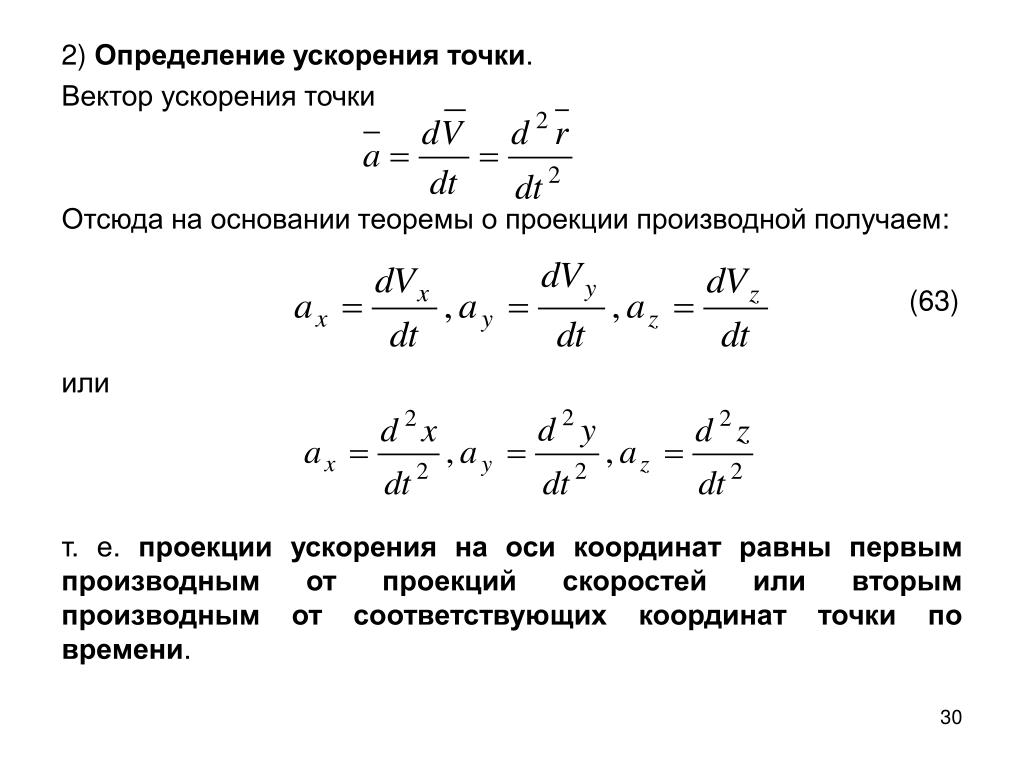 Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме.
Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме.
- 94}} }\), \( a_{\vec{N}}(1) = 6/\sqrt{10} \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
\( \vec{r}(t) = \cos t\vhat{i} + \sin t\vhat{j} + t\vhat{k} \)
Постановка задачи
Вычислить тангенциальную и нормальную составляющие ускорения вектора \( \vec{r}(t) = \cos t\vhat{i} + \sin t\vhat{j} + t\vhat{k} \).
Окончательный ответ
\( a_{\vec{T}}(t) = 0 \), \( a_{\vec{N}}(t) = 1 \)
Задача Заявление
Вычислить тангенциальную и нормальную составляющие вектора ускорения \( \vec{r}(t) = \cos t\vhat{i} + \sin t\vhat{j} + t\vhat{k} \ ).

Решение
Krista King Math – 2071 Видео Решение
367Видео Криста Кинг Математи. , \( a_{\vec{N}}(t) = 1 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
- 92, 2t \угол\).
Решение
В своем ответе на \(a_{\vec{N}}\) ему нужно сократить множитель 2 в дроби, чтобы получить упрощенный ответ.
Стив Батлер – 4330 видео решениевидео Стив Батлер
Войдите, чтобы оценить текущий рейтинг этой практической задачи и посмотреть рейтинг этой проблемы.
Really UNDERSTAND Calculus
Войдите, чтобы оценить эту страницу и увидеть ее текущий рейтинг.
Topics You Need To Understand For This Page
Уравнения на этой страницеvectors
vector functions
projectile motion
unit tangent vector
principal unit normal вектор
Это неполный список уравнений для расчета тангенциальной и нормальной составляющих ускорения.
 Полный список см. на странице уравнений векторных функций.
Полный список см. на странице уравнений векторных функций.\(\vec{a}\)
вектор ускорения
\(\vhat{T} = \vec{T}\)
единичный касательный вектор
\(\vhat{N} = \vec{N}\)
вектор нормали к главной единице
\( \vec{a} = a_{\vhat{T}}\vhat{T} + a_{\vhat{N}}\vhat{N}\)
тангенциальная составляющая ускорения
\(a_{\vhat{T}} = \vec{a} \cdot \vhat{T} \)
style( a_{\vhat{T}} = \frac{\vec{a} \cdot \vec{v}}{\|\vec{v}\|} }\)
\(a_{\ vhat{T}} = \| \vec{v} \|’ \)
нормальная составляющая ускорения
\(a_{\vhat{N}} {а} \cdot \vhat{N} \) 92}\)
Чтобы добавить эту страницу в закладки и попрактиковаться в решении задач, войдите в свою учетную запись или создайте бесплатную учетную запись.

Практические проблемы поиска
У вас есть номер практической задачи, но вы не знаете, на какой странице она находится? Если это так, введите номер ниже и нажмите «страница», чтобы перейти на страницу, на которой он находится, или нажмите «практика», чтобы перейти к практической задаче.
бесплатные идеи, как сэкономить на сумках и расходных материалах
Присоединяйтесь к Amazon Prime Music — единственному сервису потоковой передачи музыки с бесплатной 2-дневной доставкой — 30-дневной бесплатной пробной версией
Как партнер Amazon я зарабатываю на соответствующих покупках.
Недавно я открыл учетную запись Patreon, чтобы покрывать расходы, связанные с этим сайтом. Чтобы этот сайт оставался бесплатным, пожалуйста, поддержите меня.
Поддержите 17Calculus на Patreon Объяснение компонентов вектора ускорения
Как рассчитать компоненты вектора ускорения
Другие уравнения для расчета компонентов вектора ускорения
Практика
Практический поиск
Разделы страниц
Объяснение компонентов вектора ускорения
Как рассчитать компоненты вектора ускорения
Другие уравнения для расчета компонентов вектора ускорения
Практика
Практические инструкции
Если не указано иное, рассчитайте тангенциальную и нормальную составляющие вектора ускорения для заданного вектора положения.
 Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме.
Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме.Разложение ускорения
Разложение ускоренияЧасть 2:
Разложение ускоренияПоскольку скорость кривой можно записать как v = v T где v — скорость, а T — единичный касательный вектор, ускорение для кривой равно
Более того, если мы теперь объединим (3) для д Т / дт с (4), то мы находим, что ускорение кривая, параметризованная параметрами r ( t ), равнаa = д дт ( v T ) = дв дт T + v д Т дт (4)
Количество a T = dv / dt есть скорость изменения скорость и часто называется линейным ускорением для параметризации.а = дв дт T + k v 2 N (5)  Линейный
ускорение также известно как тангенциальная составляющая ускорения потому что он измеряет ускорение в направлении скорости.
Линейный
ускорение также известно как тангенциальная составляющая ускорения потому что он измеряет ускорение в направлении скорости.Величина a N = k v 2 называется нормальной составляющей ускорение , потому что оно измеряет ускорение, приложенное под прямым углом к скорости. В частности, нормальная составляющая ускорения равна мера того, насколько быстро меняется направление вектора скорости.
Более того, поскольку a · T = dv / dt , из разложения (5) следует, что
Таким образом, k 2 v 4 = || и || 2 – ( a · T ) 2 , так что|| и || 2 = a T 2 + a N 2 = ( a · T ) 2 +k 2 v 4
который не требует вычисления перекрестного произведения.к = || и || 2 – ( а · Т ) 2
v0 2 0 (6) 
ПРИМЕР 2 Найти кривизну вектор-функции
г ( т ) = ш( т ), т , ш( т ) – Решение: Скорость равна v ( t ) = акош( т ) ,1,ш( т ) ñ , так что скорость
В результате линейное ускорение равноv = ш 2 ( t ) +1+шв 2 ( t ) = 2кош 2 ( т ) = Е2 кош( т )
Производная v ( t ) затем дает ускорение,дв дт = д дт Ö2cosh( t ) = Ö2sinh( t )
а скалярное произведение a · T определяется выражениема ( т ) = ш( т ),0,ш( т ) –
Таким образом, из (8) следует, что кривизна естьa · T = 1
Ö2кош( т )(2sinh( t ) ch( t ) ) = …2 sh( t )
так как ch 2 ( t ) -sinh 2 ( t ) = 1.к = шв 2 ( т ) +ш 2 ( т )-2 шв 2 ( т ) 2 2 кош 2 ( т ) = ш 2 ( t ) – ш 2 ( t )
2 2 кош 2 ( т )
= 1 4кош 2 ( т ) 
Действительно, если скорость v постоянна, то dv / dt = a · T = 0 и (6) сводится к
357
357к = || и || 2
7357 .  =
= и
v 27 (7) где a — величина ускорения. То есть кривизна объект, движущийся с постоянной скоростью по кривой, пропорционален величина ускорения.ПРИМЕР 3 Найдите линейное ускорение и кривизну спираль
Решение: Скорость и ускорение соответственно равныг ( т ) = á 3cos( t ),3sin( t ),4 t –
Отсюда следует, что скорость задается какv ( т ) = á -3sin( т ),3cos( т ),4 с , а = á -3cos( t ),-3sin( t ),0 –
Таким образом, мы можем использовать (7).v = 9sin 2 ( t ) +9cos 2 ( т ) +16 = 5 


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

 При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.
При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.


 97.168.212 (0.009 с.)
97.168.212 (0.009 с.)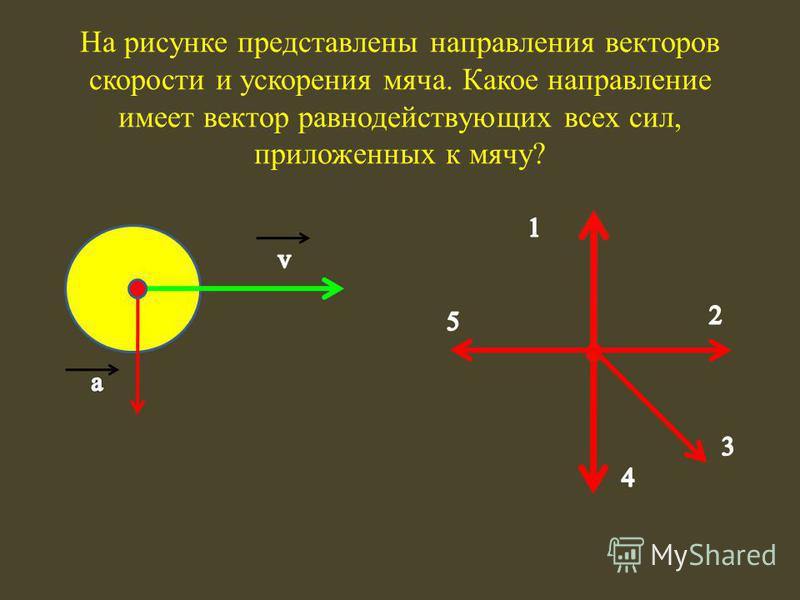

 Полный список см. на странице уравнений векторных функций.
Полный список см. на странице уравнений векторных функций.
 Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме.
Если задано значение \(t\), также найдите значения в это время. Дайте ответы в точной форме. Линейный
ускорение также известно как тангенциальная составляющая ускорения потому что он измеряет ускорение в направлении скорости.
Линейный
ускорение также известно как тангенциальная составляющая ускорения потому что он измеряет ускорение в направлении скорости.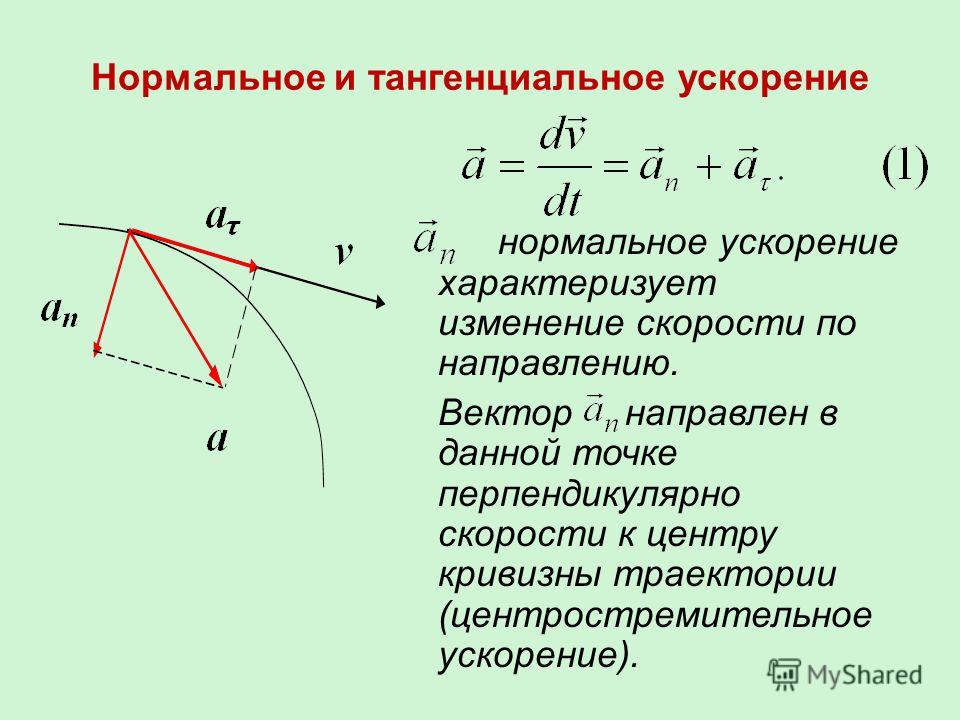

 =
= 