PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5. 3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
2 Термодинамика
3 Фотометрия
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Средняя путевая скорость – формула движения, определение ф физике кратко (7 класс)
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
4.
6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
Из курса физики в 10 классе известно, что быстрота движения характеризуется такой величиной, как скорость. При этом скорость может быть мгновенной, а может быть средней. Средняя скорость, в свою очередь, может рассчитываться по перемещению, а может по пройденному пути. Рассмотрим понятие средней скорости, получим формулу средней путевой скорости.
Мгновенная и средняя скорость
Скорость движения материальной точки — это физическая величина, характеризующая быстроту движения и равная отношению пройденной длины ко времени, за которое эта длина была пройдена:
$$v={Δl \over Δt}$$
Поскольку длина в системе СИ измеряется в метрах, а время — в секундах, то скорость измеряется в метрах в секунду.
Рис. 1. Скорость движения в физикеНаиболее точной является мгновенная скорость, то есть такая скорость, при которой величина $Δt$ стремится к нулю. При этом получающееся значение скорости $v$ может быть постоянным, а может меняться в каждой точке пройденного пути.
Вычисление мгновенной скорости позволяет моделировать движение материальной точки наиболее детально. Однако в реальных условиях настолько большая точность чаще всего не требуется. Как правило, важно, чтобы движение было совершено к определённому моменту времени, а как именно это произошло — не имеет значения.
В этом случае используется понятие средней скорости. Средняя скорость отличается от мгновенной тем, что для вычисления используется сразу весь отрезок времени. Величина $Δt$ в приведённой формуле равна общему времени движения:
$$v_{ср}={l_{общ} \over t_{общ}}$$
Средняя путевая скорость
В приведённой формуле числитель (величина $l_{общ}$) может быть рассчитан по-разному.
Во-первых, эта величина может быть равна разности координат в начале и в конце пути. В этом случае мы получаем вектор перемещения $\overrightarrow {Δx}$, полученное значение средней скорости также будет вектором $\overrightarrow {v_{ср}}$, направленным в ту же сторону.
Во-вторых, эта величина может быть равна длине траектории движения.
В этом случае мы получаем пройденный путь $S$. Это скалярная величина, и значение средней скорости $v_{ср}$ также получается скаляром.
Как правило, в физике, когда говорят о средней скорости, имеют в виду первый случай — среднюю скорость по перемещению. В бытовом же обиходе чаще используется длина пройденного пути, и говорят о средней путевой скорости.
Использование средней путевой скорости удобно потому, что затраты на движение (и материальные, и временные), как правило, зависят именно от длины пройденного пути, а не от перемещения. Расстояние между начальным и конечным пунктом по прямой (это и есть перемещение) может быть значительно меньше пути между этими пунктами. Но если нам задана средняя скорость движения транспортного средства, то для нахождения времени прибытия мы должны исходить именно из путевой средней скорости, поскольку при движении будет пройдена вся траектория пути.
Отсюда можно сделать важный вывод — средняя путевая скорость, как правило, больше средней скорости по перемещению (при одинаковом времени).
Ещё одно важное отличие — скалярный характер средней путевой скорости. Зная координаты начального пункта, время пути и вектор средней скорости по перемещению, мы можем найти координаты конечного пункта. Если же известна средняя путевая скорость, то мы можем указать лишь круг (или сферу в трёхмерном пространстве), в пределах которого находится конечный пункт: точные его координаты по средней путевой скорости установить невозможно.
Рис. 3. Средняя путевая скоростьЧто мы узнали?
Средняя путевая скорость — это величина, равная отношению пути, пройденного материальной точкой, ко время его прохождения. В формуле средней путевой скорости в качестве расстояния используется длина траектории. Средняя путевая скорость удобна для определения затрат, материальных и временных, на движение.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
А какая ваша оценка?
Лицом к пути – TrackMan Golf
Лицом к пути является разница между углом лица и путем клюшки путь и положительная сторона к пути будут представлять угол лица, который «открыт» для пути.
Нулевой путь лицом к лицу представляет угол лица и путь булавы, которые имеют одинаковое значение.
Лицом к траектории является ключевым фактором в определении ожидаемой кривизны (оси вращения) удара в гольфе. Предполагая центральный контакт, мяч должен искривляться в направлении лицевого угла и от траектории клюшки (если отношение лицевой стороны к траектории не равно нулю).
Обратите внимание, что линия “лицом к пути” относится к углу лица и пути булавы. Это не относительно целевой линии. Лицевая сторона пути нуля может быть +5, 0, -5 или любым другим значением относительно целевой линии.
Нулевой путь от лицевой стороны к траектории представляет только разницу между тем, где клюшка движется горизонтально (траектория клюшки), и тем, где лицевая сторона клюшки направлена горизонтально (угол лицевой стороны).
Техническое определение:
Лицом к пути — разница углов между УГЛОМ ЛИЦА и ПУТИ КЛУБЫ, как определено (УГОЛ ЛИЦА минус ПУТЬ КЛУБЫ).
- Положительное положение лицом к пути означает, что лицо направлено вправо от пути булав, независимо от ловкости
- Отрицательное значение лицом к пути означает, что лицо направлено влево от пути булав, независимо от ловкости
Примеры «лицом к пути» (при условии контакта по центру)
Водитель PGA TOUR (перенос на 275 ярдов)
- -2 градуса лицом к пути ≈ 19 ярдов левой кривизны
- 5 градусов лицом к дорожке ≈ 44 ярда вправо по кривизне
PGA TOUR 6-айрон (перенос на 183 ярда)
- 2 градуса лицом к дорожке ≈ 8 ярдов правой кривизны
- -5 градусов лицом к пути ≈ 20 ярдов по кривизне влево
LPGA Tour Driver (218 ярдов)
- 2 градуса лицом к пути ≈ 14 ярдов по правому изгибу
- -5 градусов лицом к пути ≈ 32 ярда по кривизне влево
LPGA Tour 6-айрон (152 ярда)
- -2 градуса лицом к пути ≈ 6 ярдов по кривизне влево
- 5 градусов лицом к пути ≈ 14 ярдов по кривизне вправо
Стандартное предположение о том, что путь лицом к пути равен нулю для всех клюшек.
Это стандартное предположение, что мяч стартует прямо к цели и не имеет кривизны (ось нулевого вращения).
Прочитайте, что говорят мастера нашего университета TrackMan о Face to Path…
Джон Паркинсон
Гольф-клуб Донау, Германия
«Для элитных игроков, которые постоянно водят мяч более чем на 300 ярдов, разница в 1 градус между лицом и траекторией необходима для последовательного и точного вождения, учитывая, что типичная ширина фарватера PGA TOUR составляет всего 30-32 ярда. Разница в один градус от лица до пути на 300 ярдах приведет к выстрелу с кривизной 12 ярдов. Любое отклонение лица от пути более чем на 1,5 градуса заставит игрока целиться в сторону от фервея, чтобы попасть в центр фервея».
Райан Джонсон
Carl’s Golfland, MI, US
«Лицом к траектории — это отличное число, на которое стоит обратить внимание, потому что оно сочетает в себе две ключевые части поворота при ударе, которые могут повлиять на направление запуска и вращение ось.
Мне всегда нравится смотреть лицом к пути, чтобы объяснить клиенту контакт на клубном лице. Можно было увидеть отрицательное отношение лица к пути, но положительную ось вращения. Возможность показать и объяснить причину этого чрезвычайно полезна».
Хью Марр
Premium Golf Consulting, UK
. Я использую это в сочетании с осью вращения, чтобы проверить центральный контакт и определить, где игрок склонен промахиваться».
Определение e/m для электрона
Введение
В этом опыте вы измерите e / m , отношение заряда электрона к массе электрон. В настоящее время принятое значение для e / m составляет 1,758820 × 10 11 Кл/кг. Когда электрон попадает в область с однородным магнитным полем B , перпендикулярную скорость электрона v (Внимание: заглавная буква V будет использоваться ниже для обозначения напряжения.
Не путайте и с и 9.0025 !), на электрон действует сила F , величина которой определяется следующим уравнением.( 1 )
F = evB
Сила перпендикулярна как v , так и B , и ее направление можно найти с помощью правой правило. Сила заставит электрон двигаться по круговой орбите с радиусом r (равномерная круговая движение). Приравнивая эту силу к массе, умноженной на центростремительное ускорение, мы получаем следующее уравнение.( 2 )
evB = m
Решение уравнения. 2evB = m
для e / m мы получаем следующее уравнение.( 3 )
=
Если измерить радиус циклотронной орбиты, мы можем рассчитать e / м из уравнения. 3=
. Все, что нам нужно это скорость электрона. В нашем эксперименте электрон ускоряется набором пластин с разность потенциалов, V , между ними. Таким образом, скорость электрона может быть получена из сохранение энергии.
( 4 )
мв 2 = эВ акк
Решение уравнения. 4mv 2 = eV acc
для скорости мы получаем следующее уравнение.(5)
V =
|
Наконец, заменив скорость из уравнения. 5 v =
в Ур. 3 = и решая для e / m , мы получаем Уравнение. 6=
относительно e / m 9002 5 к разности потенциалов, магнитному полю и радиусу круговой орбиты электрона. орбита. ( 6 ) =
АппаратРисунок 1 Установка оборудования, использованного в этом эксперименте, показана на рис. 1. Основные элементы на e / m – блок трехэлементной электронной лампы и катушки Гельмгольца. Электронная лампа, катушки Гельмгольца и источники питания нити накала лампы и ускоряющего напряжения смонтированы в
единая база называется блоком e / m . Органы управления и разъемы на передней панели данного аппарата расположены (слева направо).
верно):
Электронная лампа«Электронная пушка» установлена внутри электронной трубки так, чтобы ее центральная линия совпадала с вертикальная ось трубы. Электронная пушка состоит из трех элементов:
Рисунок 2 : Электронная пушка (вид в разрезе) Электронный луч проецируется вертикально через маленькое отверстие в центре диска. Диск установлен горизонтально на верхнем конце электронной пушки. На верхней стороне диска нанесены четыре окружности с центрами, совпадающими с отверстием, и радиусами 0,50, 1,0, 1,5 и 2,0 см. Лампочка и Диск покрыт материалом, который флуоресцирует при ударе электронов. Тюбик содержит следы инертный газ, помогающий сфокусировать электронный луч, а также заставляющий луч создавать видимое след.Катушка ГельмгольцаМагнитное поле создается парой одинаковых круглых катушек, расположенных так, что расстояние между витками равно радиусу витков. Такое устройство, называемое катушками Гельмгольца, обеспечивает очень однородное магнитное поле в области в центре и вблизи центра пары катушек. Рисунок 3 : Катушки Гельмогольца Магнитное поле, создаваемое катушками Гельмгольца, пропорционально электрическому току, я , в катушки.( 7 ) В = jI В точном центре катушек Гельмгольца значение j определяется теоретически как:( 8 ) j = мк 0
где:
 Подстановка этих значений в Уравнение 8 j = мк 0
дает: j = 1,6 78 × 10 –3 Т/А, или 1,678 мТ/А. уравнение 7 В = jI , с приведенным выше расчетным значением j , будет использоваться для определения магнитного поля из измеренных значения тока.ПроцедураПодсоедините аппарат в соответствии со схемой, показанной на рис. 1, и начните снимать данные. следуя шагам, описанным ниже:
Рисунок 4 Луч может не достичь линии диаметром 2,0 см.
Убедитесь, что вы и ваш ассистент парафировали свои листы данных и передали копию данные перед тем, как покинуть лабораторию. АнализВажное изменение необходимо внести в Eq. 6=
прежде чем его можно будет использовать для расчета e / м .  необходима модификация, поскольку катод, из которого исходит электронный пучок, расположен на расстоянии a = 3,2 ± 0,5 мм ниже выходного отверстия.Рисунок 5 Как показано на рисунке выше, измеренный диаметр d не является фактическим диаметром d’ , для орбита электрона. Фактический диаметр можно определить, используя приведенное ниже уравнение Пифагора.( 9 ) d’ =
в уравнении. 6 =
, мы получаем следующее уравнение. ( 10 ) В 2 =
Примечание: использование буквы ‘ В ‘ в этом уравнении означает переменную для напряжения. 1 Используя электронную таблицу, вычислите таблицу d , 1/( d 2 + a 2 ), среднее I , u I 902 11 , Б , и Б , Б 2 и у B 2 из данных для более низкого ускоряющего напряжения (≈50В).2 Постройте B 2 против 1/( d 2 + a 2 ) и выполните линейную подгонку методом наименьших квадратов. Определить наклон и пересечение подобранная кривая.3 По наклону определите значение e / m в Кл/кг, используя уравнение. 10 В 2 =
.  Обязательно используйте соответствующие единицы измерения для переменных B и d . Неопределенность в e / m можно рассчитать с помощью метода верхней-нижней границы.4 Повторите шаги 1, 2 и 3 для данных, полученных от более высокого ускоряющего напряжения.5 Возьмите средневзвешенное значение двух значений e / m , полученное по формуле:e/m = w 1 (e/m) 1 + w 2 (e/m) 2 . Гири w 1 и w 2 взяты пропорциональными обратно квадрат неопределенности каждого e / m соответственно. Таким образом, значение e / м с меньшим неопределенности будет придан больший вес. Таким образом,( 11 ) w 1 = k и w 2 = k где константа пропорциональности, k , выбрана для нормализации весов таким образом, что значение k определяется приведенным ниже уравнением. |
Кнопка позволяет кратковременно подать ускоряющее напряжение для наблюдения за электронным лучом.
Если счетчик показывает положительное значение, все в порядке.
хорошо; в противном случае вы подключили счетчик в обратном направлении. Отключите питание и измените показания амперметра.
соединения. Не допускайте, чтобы ток катушки Гельмгольца превышал 5А!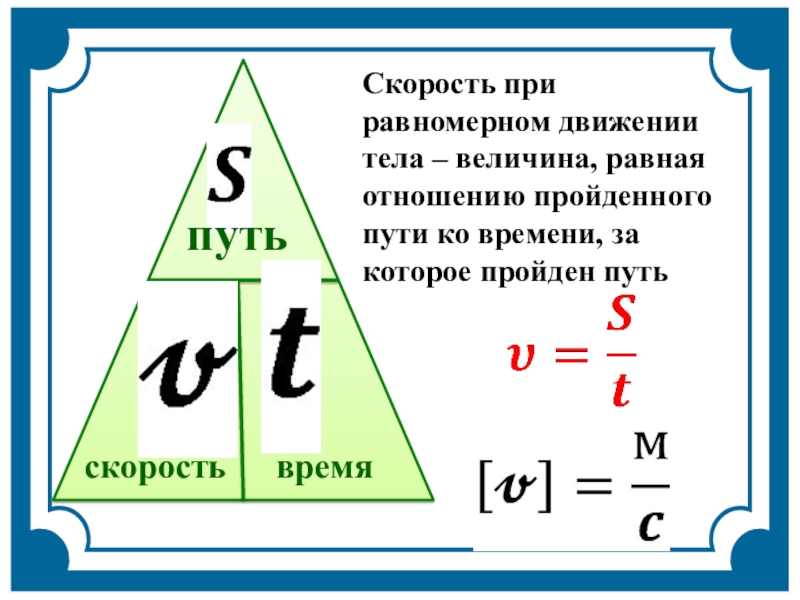 
Выполнение нескольких измерений тока может уменьшить ошибки. Запишите
ускоряющее напряжение, ток катушки Гельмгольца (проведите измерения вверх и вниз по шкале) и
диаметр, d пути электронного луча в вашем техпаспорте.
Что
происходит, когда вы подносите северный конец магнита к лучу? Что происходит, когда вы
поменять направление магнита? Подтвердите свое понимание направления
Сила Лоренца и правило правой руки с помощью компаса определяют направление магнитного поля.
поле, создаваемое катушками Гельмгольца. (Помните, что N — это сокращение от северного полюса
магнит, что означает, что географический северный полюс Земли действует как магнитный южный полюс.) Нарисуйте
эскиз катушек Гельмгольца и отклоненного луча, чтобы показать направление тока в катушках
и результирующее магнитное поле.
Это НЕ
означает, что вы вычисляете B , используя 8 вольт, но используя 8-кратное измеренное напряжение!