Величина ускорение: Единицы измерения ускорения - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Перегрузки и их действие на человека в разных условиях

При взлете обычного авиалайнера пассажиры в салоне испытывают перегрузку в 1,5 g. По международным нормам предельно допустимое значение перегрузок для гражданских самолетов составляет 2,5 g.

В момент раскрытия парашюта человек подвергается действию инерционных сил, вызывающих перегрузку, достигающую 4 g. При этом показатель перегрузки зависит от воздушной скорости. Для военных парашютистов он может составлять от 4,3 g при скорости 195 километров в час до 6,8 g при скорости 275 километров в час.

Реакция на перегрузки зависит от их величины, скорости нарастания и исходного состояния организма. Поэтому могут возникать как незначительные функциональные сдвиги (ощущение тяжести в теле, затруднение движений и т.п.), так и очень тяжелые состояния. К ним относятся полная потеря зрения, расстройство функций сердечно-сосудистой, дыхательной и нервной систем, а также потеря сознания и возникновение выраженных морфологических изменений в тканях.

С целью повышения устойчивости организма летчиков к ускорениям в полете применяют противоперегрузочные и высотно-компенсирующие костюмы, которые при перегрузках создают давление на область брюшной стенки и нижние конечности, что приводит к задержке оттока крови в нижнюю половину тела и улучшает кровоснабжение головного мозга.

Для повышения устойчивости к ускорениям проводятся тренировки на центрифуге, закаливание организма, дыхание кислородом под повышенным давлением.

При катапультировании, грубой посадке самолета или приземлении на парашюте возникают значительные по величине перегрузки, которые могут также вызвать органические изменения во внутренних органах и позвоночнике. Для повышения устойчивости к ним используются специальные кресла, имеющие углубленные заголовники, и фиксирующие тело ремнями, ограничителями смещения конечностей.

Перегрузкой также является проявление силы тяжести на борту космического судна. Если в земных условиях характеристикой силы тяжести является ускорение свободного падения тел, то на борту космического корабля в число характеристик перегрузки также входит ускорение свободного падения, равное по величине реактивному ускорению по противоположному ему направлению.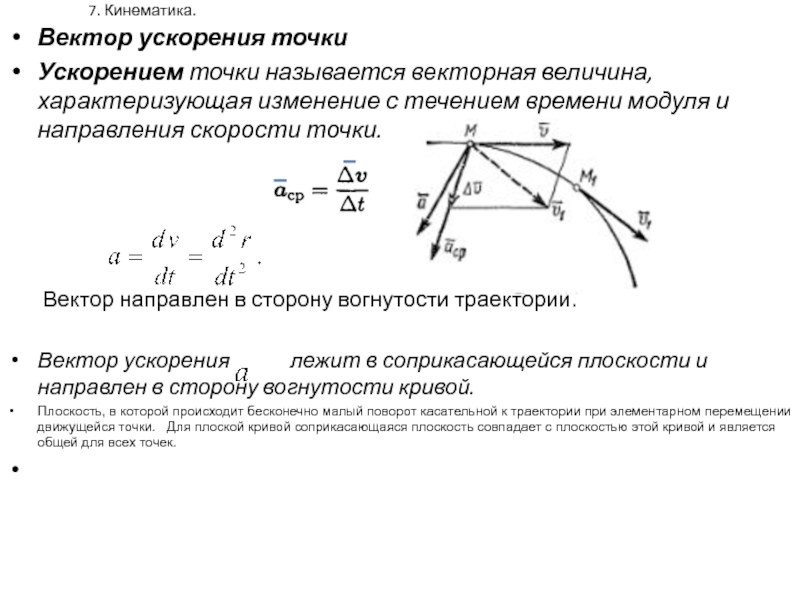 Отношение этой величины к величине называется “коэффициентом перегрузки” или “перегрузкой”.

На участке разгона ракеты-носителя перегрузка определяется равнодействующей негравитационных сил — силы тяги и силы аэродинамического сопротивления, которая состоит из силы лобового сопротивления, направленной противоположно скорости, и перпендикулярной к ней подъемной силы. Эта равнодействующая создает негравитационное ускорение, которое определяет перегрузку.

Ее коэффициент на участке разгона составляет несколько единиц.

Если космическая ракета в условиях Земли будет двигаться с ускорением под действием двигателей или испытывая сопротивление среды, то произойдет увеличение давления на опору из-за чего возникнет перегрузка. Если движение будет происходить с выключенными двигателями в пустоте, то давление на опору исчезнет и наступит состояние невесомости.

При старте космического корабля на космонавта действует ускорение, величина которого изменяется от 1 до 7 g. По статистике, космонавты редко испытывают перегрузки, превышающие 4 g.

Способность переносить перегрузки зависит от температуры окружающей среды, содержания кислорода во вдыхаемом воздухе, длительности пребывания космонавта в условиях невесомости до начала ускорения и т.д. Существуют и другие более сложные или менее уловимые факторы, влияние которых еще не до конца выяснено.

Под действием ускорения, превышающего 1 g, у космонавта могут появиться нарушения зрения. При ускорении 3 g в вертикальном направлении, которое длится более трех секунд, могут возникнуть серьезные нарушения периферического зрения. Поэтому в отсеках космического корабля необходимо увеличивать уровень освещенности.

При продольном ускорении у космонавта возникают зрительные иллюзии. Ему кажется, что предмет, на который он смотрит, смещается в направлении результирующего вектора ускорения и силы тяжести. При угловых ускорениях возникает кажущееся перемещение объекта зрения в плоскости вращения. Эта иллюзия называется окологиральной и является следствием воздействия перегрузок на органы внутреннего уха.

Многочисленные экспериментальные исследования, которые были начаты еще ученым Константином Циолковским, показали, что физиологическое воздействие перегрузки зависит не только от ее продолжительности, но и от положения тела. При вертикальном положении человека значительная часть крови смещается в нижнюю половину тела, что приводит к нарушению кровоснабжения головного мозга. Из-за увеличения своего веса внутренние органы смещаются вниз и вызывают сильное натяжение связок.

Чтобы ослабить действие высоких ускорений, космонавта помещают в космическом корабле таким образом, чтобы перегрузки были направлены по горизонтальной оси, от спины к груди. Такое положение обеспечивает эффективное кровоснабжение головного мозга космонавта при ускорениях до 10 g, а кратковременно даже до 25 g.

При возвращении космического корабля на Землю, когда он входит в плотные слои атмосферы, космонавт испытывает перегрузки торможения, то есть отрицательного ускорения. По интегральной величине торможение соответствует ускорению при старте.

Космический корабль, входящий в плотные слои атмосферы, ориентируют так, чтобы перегрузки торможения имели горизонтальное направление. Таким образом, их воздействие на космонавта сводится к минимуму, как и во время запуска корабля.

Материал подготовлен на основе информации РИА Новости и открытых источников

Ускорение Кориолиса

Ускорение Кориолиса (Кориолисово ускорение) характеризует изменение относительной скорости по направлению за счет переносного вращения и изменение величины переносной скорости за счет относительного движения.

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)

a_a = a_r + a_e + a_C

Рис. 3

Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение

a_r направлено вдоль этой прямой и определяется выражением

Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

a_e = a_e^вр + a_e^цс

где a_e^вр= ε ⋅ OM — вращательное ускорение точки M, направленное перпендикулярно отрезку OM;
a_e^цс= ω²⋅ OM — центростремительное ускорение точки M

, направленное к центру диска.

Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e × ν_r

где ω_e — переносная угловая скорость,
ν_r — относительная скорость точки.

Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского.

Величина ускорения Кориолиса определяется выражением

a_C = 2 ω_e ν_rsinα

где α – угол между векторами ω_e и ν_r.

Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка

M движется относительно диска с постоянной относительной скоростью (рис.4).

Рис. 4

Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_r1. За промежуток времени Δt точка M переместится в положение M₂, при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r. Отношение Δν_r/Δt определяет среднее ускорение точки за промежуток времени

Δt. Предел отношения Δν_r / Δt при Δt→ 0 есть производная dν_r /dt, как производная от вектора постоянного по величине.

Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями ν_e1= ω × OM₁ и ν_e2= ω × OM₂. Тогда приращение вектора ν_e за счет относительного движения будет равно

Δν_e = ω × OM₂ — ω × OM₁

=
= ω ×(OM₂ — OM₁) = ω × ν_r⋅ Δt

Отношение Δν_e/ Δt в пределе при Δt→ 0 дает производную dν_e / dt = ω × ν_r.

Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Рис. 5

Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых

Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

>> Сферическое движение и способы его задания

Ускорение – Класс!ная физика

Ускорение

Подробности: Просмотров: 441

Как изменяются показания спидометра в начале движения и при торможении автомобиля?
Какая физическая величина характеризует изменение скорости?

При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо жеодновременно как по модулю, так и по направлению.

Скорость шайбы, скользящей по льду, уменьшается с течением времени до полной остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает. Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис 1.26). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.

Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении).

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.

Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае её скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость (рис. 1.27). Спустя промежуток времени Δt точка займёт положение М₁ и будет иметь скорость ₁. Изменение скорости за время Δt₁ равно Δ₁ = ₁ – . Вычитание вектора можно произвести путём прибавления к вектору ₁ вектора (-):

Δ₁ = ₁ – = ₁ + (-).

Согласно правилу сложения векторов вектор изменения скорости Δ₁ направлен из начала вектора ₁ в конец вектора (-), как это показано на рисунке 1.28.

Поделив вектор Δ₁ на промежуток времени Δt₁ получим вектор, направленный так же, как и вектор изменения скорости Δ₁. Этот вектор называют средним ускорением точки за промежуток времени Δt₁. Обозначив его через _cр1, запишем:

По аналогии с определением мгновенной скорости определим мгновенное ускорение. Для этого найдём теперь средние ускорения точки за всё меньшие и меньшие промежутки времени:

При уменьшении промежутка времени Δt вектор Δ уменьшается по модулю и меняется по направлению (рис. 1.29). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени Δt к нулю отношение изменения скорости к изменению времени стремится к определённому вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени или просто ускорением и обозначают .

Ускорение точки — это предел отношения изменения скорости Δ к промежутку времени Δt, в течение которого это изменение произошло, при стремлении Δt к нулю.

Ускорение направлено так, как направлен вектор изменения скорости Δ при стремлении промежутка времени Δt к нулю. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения точки при прямолинейном и криволинейном движениях.

В общем случае ускорение направлено под углом к вектору скорости (рис. 1.30). Полное ускорение характеризует изменение скорости и по модулю, и по направлению. Часто полное ускорение считается равным векторной сумме двух ускорений — касательного (_к) и центростремительного (_цс). Касательное ускорение _к характеризует изменение скорости по модулю и направлено по касательной к траектории движения. Центростремительное ускорение _цс характеризует изменение скорости по направлению и перпендикулярно касательной, т. е. направлено к центру кривизны траектории в данной точке. В дальнейшем мы рассмотрим два частных случая: точка движется по прямой и скорость изменяется только по модулю; точка движется равномерно по окружности и скорость изменяется только по направлению.

Единица ускорения.

Движение точки может происходить как с переменным, так и с постоянным ускорением. Если ускорение точки постоянно, то отношение изменения скорости к промежутку времени, за которое это изменение произошло, будет одним и тем же для любого интервала времени. Поэтому, обозначив через Δt некоторый произвольный промежуток времени, а через Δ — изменение скорости за этот промежуток, можно записать:

Так как промежуток времени Δt — величина положительная, то из этой формулы следует, что если ускорение точки с течением времени не изменяется, то оно направлено так же, как и вектор изменения скорости. Таким образом, если ускорение постоянно, то его можно истолковать как изменение скорости в единицу времени. Это позволяет установить единицы модуля ускорения и его проекций.

Запишем выражение для модуля ускорения:

Отсюда следует, что:
модуль ускорения численно равен единице, если за единицу времени модуль вектора изменения скорости изменяется на единицу.
Если время измерено в секундах, а скорость — в метрах в секунду, то единица ускорения — м/с² (метр на секунду в квадрате).

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика – Физика, учебник для 10 класса – Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

Угловое ускорение

Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.

Основные понятия

Определение 1

Угловое ускорение – величина, характеризующая изменение скорости с течением времени.

Пусть рассматриваемый промежуток времени это: Δt=t1-t, а изменение угловой скорости составит Δω=ω1-ω, тогда числовое значение среднего углового ускорения за тот же интервал времени: ε=∆ω∆t=ε. Перейдем к пределу, когда Δt>0, тогда формула углового ускорения будет иметь вид: ε=lim∆t→0∆ω∆t=dωdt=d2φdt=ω˙=φ¨.

Определение 2

Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.

Размерность углового ускорения 1T2 (т.е. 1время2). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается рад/с2 или иначе: 1с2(с-2).

Определение 3

Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.

Определение 4

Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.

В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.

Рисунок 1. Вектор углового ускорения

Если мы представим угловое ускорение как вектор ε→=dω→dt, имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε→ и ω→ совпадут по направлениям (левая часть
рисунка 1) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1).

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Закон равнопеременного вращения

Определение 5

Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным (ε=const).

Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t0 угол вращения равен ϕ=ϕ0; угловая скорость – ω=ω0 (т.е. ω0 является начальной угловой скоростью).

Выражение ε=dωdt=ω˙=φ¨ дает нам возможность сделать запись: dω=εdt. Проинтегрируем левую часть крайней записи в пределах от ω0 до ω, а правую – в пределах от 0 до t, тогда:

ω=ω0+εt, dφ=ω0dt+εtdt.

Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:

Определение 6

Закон равнопеременного вращения: φ=φ0+ωt+εt22.

Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.

Вращение является равнозамедленным, когда ω и ε противоположны по знаку.

Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R, тогда: αr=εR. Нормальное ускорение имеет также связь с угловым: an=ω2R. Учтем это выражение и для полного ускорения получим: a=ar2+an2=Rε2+ω4 Для равнопеременного движения: ω=εt; an=ω2R=ε2t2R и a=Rε2+ε4t4=Rε1+ε2t4.

Практические примеры

Пример 1

На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.

Рисунок 2

Решение

Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2.1. и 2.3. показывают направление псевдовектора вверх, а рисунки 2.2. и 2.4. – вниз.

Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2.1. и 2.4.). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2.2. и 2.3.). Таким образом, все рисунки демонстрируют верное направление углового ускорения.

Пример 2

Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R. При этом выражение ϕ=αt3 отражает зависимость угла поворота от времени.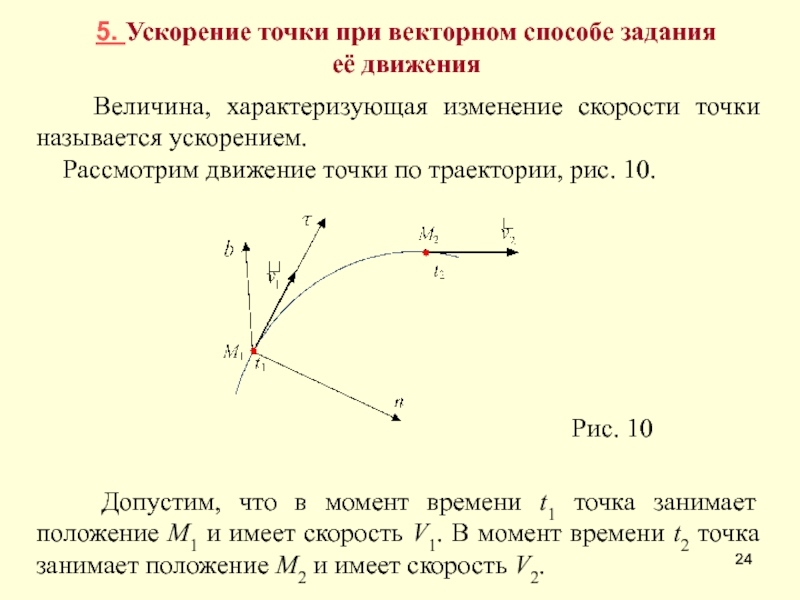 Необходимо найти полное ускорение заданной точки как функцию времени.

Решение

Запишем выражения для угловой скорости и углового ускорения заданной точки:

ω=dφdt=3αt2; ε=6αt.

Полное ускорение запишем как:

a=ar2+an2=Rε2+ω4=R36a2t2+81a4t8=3atR4+9a2t6.

Конвертер ускорения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева

Боинг 737-7h5 N776WN Американской авиакомпании Southwest Airlines, разгоняющийся во время взлета. Аэропорт Форт-Лодердейл/Холливуд (FLL) в штате Флорида, США. 9 августа, 2010.

Общие сведения

Ускорение — это изменение скорости тела за определенный отрезок времени. В системе СИ ускорение измеряется в метрах в секунду за секунду. Также часто используются другие единицы. Ускорение может быть постоянным, например ускорение тела в свободном падении, а может изменяться, например ускорение двигающегося автомобиля.

Инженеры и дизайнеры учитывают ускорение при проектировании и изготовлении автомобилей. Водители используют знания о том как быстро ускоряет или замедляет скорость их автомобиль во время вождения. Также знания об ускорении помогают строителям и инженерам предотвратить или свести к минимуму повреждения, вызванные резким ускорением или замедлением, связанным с ударами или толчками, например, при столкновениях автомобилей или во время землетрясений.

Пирамида «Трансамерика» в Сан-Франциско, США. Это здание устойчиво к силам кручения, которые действуют на него во время сейсмических явлений.

Защита от ускорений с помощью амортизирующих и демпфирующих конструкций

Если строители учитывают возможные ускорения, здание становится более устойчиво к толчкам, что помогает спасти жизнь людей во время землетрясений. В местах с высокой сейсмичностью, например в Японии, здания строят на специальных платформах, которые уменьшают ускорение и смягчают толчки. Конструкция этих платформ похожа на подвеску в автомобилях. Упрощенная подвеска также используется в велосипедах. Ее чаще устанавливают на горных велосипедах, чтобы уменьшить неприятные ощущения, травмы, а также повреждение велосипеда из-за резких ударных ускорений при движении по неровным поверхностям. Мосты также устанавливают на подвесках, чтобы уменьшить ускорение, которое придают мосту движущиеся по нему автомобили. Ускорения, вызванные движением внутри и снаружи зданий, мешают музыкантам в музыкальных студиях. Для его уменьшения всю студию звукозаписи подвешивают на демпфирующих устройствах. Если музыкант устраивает домашнюю студию звукозаписи в помещении без достаточной звукоизоляции, то подвесить ее в уже построенном здании очень сложно и дорого. В домашних условиях устанавливают на подвески только пол. Поскольку влияние ускорения уменьшается с увеличением массы, на которую оно воздействует, вместо использования подвесок иногда утяжеляют стены, пол и потолок. Потолки тоже иногда устраивают подвесными, так как это не так сложно и дорого сделать, но помогает уменьшить проникновение в помещение внешних шумов.

Ускорение в физике

Второй закон Ньютона

Согласно второму закону Ньютона сила, действующая на тело, равна произведению массы тела и ускорения. Силу можно вычислить с помощью формулы F = ma, где F — сила, m — масса, и a — ускорение. Так сила, действующая на тело, изменяет его скорость, то есть придает ему ускорение. Согласно этому закону ускорение зависит не только от величины силы, которая толкает тело, но и пропорционально зависит от массы тела. То есть, если сила действует на два тела, А и B, и B — тяжелее, тогда B будет двигаться с меньшим ускорением. Эта склонность тел противостоять изменению в ускорении называется инерцией.

Мотоцикл, двигающийся с ускорением. Тур де Бос 2010, город Квебек (Канада).

Инерцию легко увидеть в повседневной жизни. Например, автомобилисты не носят шлем, а мотоциклисты обычно путешествуют в шлеме, и часто — в другой защитной одежде, например кожаных куртках с утолщениями. Одна из причин — при столкновении с автомобилем более легкий мотоцикл и мотоциклист быстрее изменят свою скорость, то есть начнут двигаться с большим ускорением, чем автомобиль. Если его не накроет мотоциклом, то мотоциклист, вероятно, вылетит из сидения мотоцикла, так как он еще легче, чем мотоцикл. В любом случае мотоциклист получит серьезные травмы, в то время как водитель — гораздо меньшие, так как автомобиль и водитель получат при столкновении намного меньшее ускорение. В этом примере не учитывается сила всемирного тяготения; предполагается, что она пренебрежимо мала по сравнению с другими силами.

Ускорение и движение по кругу

Велосипедисты испытывают центростремительное ускорение на поворотах. Тур де Бос 2010, город Квебек (Канада).

У тела, которое движется по кругу со скоростью одинаковой величины — переменная векторная скорость, так как его направление постоянно изменяется. То есть, это тело движется с ускорением. Ускорение направлено в сторону оси вращения. В этом случае она в центре окружности, которая является траекторией движения тела. Это ускорение, а также вызывающая его сила, называются центростремительными. Согласно третьему закону Ньютона, у каждой силы есть противодействующая ей сила, действующая в противоположном направлении. В нашем примере эта сила называется центробежной. Именно она удерживает вагонетки на американских горках, даже когда те двигаются в перевернутом состоянии по вертикальным круговым рельсам. Центробежная сила толкает вагонетки от центра окружности, созданной рельсами, так что они прижимаются к рельсам.

Ускорение и сила притяжения

Гравитационное притяжение планет — одна из основных сил, которая действует на тела и придает им ускорение. Например, эта сила притягивает к поверхности Земли тела, находящиеся рядом с Землей. Благодаря этой силе тело, которое отпустили рядом с поверхностью Земли, и на которое не действуют никакие другие силы, находится в свободном падении, пока не столкнется с поверхностью Земли. Ускорение этого тела, называемое ускорением свободного падения, равно 9,80665 метров в секунду за секунду. Эта постоянная величина обозначается g и ее часто используют, чтобы определить вес тела. Так как согласно второму закону Ньютона F = ma, то вес, то есть сила, которая действует на тело — это произведение массы и ускорения свободного падения g. Массу тела легко вычислить, поэтому вес тоже легко найти. Стоит заметить, что слово «вес» в обиходе часто обозначает свойство тела, массу, а не силу.

Ускорение свободного падения — разное для разных планет и астрономических объектов, так как оно зависит от их массы. Ускорение свободного падения вблизи от Солнца в 28 раз больше чем земное, вблизи Юпитера больше в 2,6 раза, а возле Нептуна — в 1,1 раза. Ускорение рядом с другими планетами меньше земного. Например, ускорение у поверхности Луны равно 0,17 ускорения у поверхности Земли.

Ускорение и транспортные средства

Тесты на ускорение для автомобилей

Существует ряд тестов для измерения характеристик автомобилей. Один из них направлен на то, чтобы проверить их ускорение. Для этого измеряют время, за которое автомобиль разгоняется с 0 до 100 километров (62 мили) в час. В странах, где не используют метрическую систему, проверяют разгон с нуля до 60 миль (97 километров) в час. Машины с самым быстрым разгоном доходят до этой скорости примерно за 2,3 секунды, что меньше, чем время, за которое тело достигнет такой скорости в свободном падении. Существуют даже программы для мобильных телефонов, которые помогают вычислить это время разгона, используя встроенные акселерометры телефона. Впрочем, трудно сказать насколько точны такие вычисления.

Влияние ускорения на людей

Ускорение

При движении автомобиля с ускорением пассажиров тянет в сторону, противоположную движению и ускорению. То есть, назад — при ускорении, и вперед — при торможении. При резких остановках, например во время столкновения, пассажиров так резко дергает вперед, что они могут вылететь из сидений и удариться об обшивку автомобиля или окна. Вероятно даже, что они разобьют своим весом стекло и вылетят из машины. Именно из-за этой опасности во многих странах были приняты законы о том, чтобы во всех новых автомобилях должны быть установлены ремни безопасности. Во многих странах также было законодательно закреплено требование о том, что водитель, все дети, и, по крайней мере, пассажир на переднем сидении обязаны пристегиваться ремнями безопасности во время движения.

Космические аппараты во время выхода на орбиту Земли двигаются с большим ускорением. Возвращение на Землю, наоборот, сопровождается резким замедлением. Это не только вызывает у космонавтов дискомфорт, но и опасно, поэтому они проходят интенсивный курс тренировок перед тем, как отправляться в космос. Такие тренировки помогают космонавтам легче переносить перегрузки связанные с высоким ускорением. Пилоты скоростных самолетов также проходят эту тренировку, так как эти самолеты достигают высокого ускорения. Без тренировки резкое ускорение вызывает отток крови от мозга и потерю цветного зрения, потом — бокового, затем — зрения вообще, а дальше — потерю сознания. Это опасно, так как пилоты и космонавты не могут в таком состоянии управлять самолетом или космическим аппаратом. Пока тренировки на перегрузки не стали обязательным требованием в подготовке пилотов и космонавтов, перегрузки с высоким ускорением иногда заканчивались авариями и смертью пилотов. Тренировки помогают предотвратить потерю сознания и позволяют пилотам и космонавтам переносить большое ускорение в течение более продолжительного времени.

Внутри кабины космического аппарата «Аполлон» CM-011A на борту авианосца «Хорнет» (USS Hornet CV-12)

Кроме тренировок в центрифуге, описанных ниже, космонавтов и пилотов обучают специальному приему сокращения мышц живота. При этом кровеносные сосуды сужаются и меньше крови попадает в нижнюю часть тела. Предотвратить отток крови из мозга во время ускорения помогают также противоперегрузочные костюмы, так как встроенные в них специальные подушки наполнены воздухом или водой и давят на живот и ноги. Эти приемы предотвращают отток крови механически, в то время как тренировки в центрифуге помогают человеку повысить выносливость и привыкание к высокому ускорению. Сама центрифуга представляет собой горизонтальную трубу с кабиной на одном конце трубы. Она вращается в горизонтальной плоскости и создает условия с большим ускорением. Кабина снабжена карданным подвесом и может вращаться в разных направлениях, обеспечивая дополнительную нагрузку. Во время тренировок на космонавтах или пилотах надеты датчики и врачи следят за их показателями, например за пульсом. Это необходимо для обеспечения безопасности, а также помогает следить за адаптацией людей. В центрифуге можно имитировать как ускорение в нормальных условиях, так и баллистическое вхождение в атмосферу при авариях. Космонавты, которые проходят подготовку на центрифуге, говорят, что испытывают при этом сильный дискомфорт в груди и в горле.

Литература

Автор статьи: Kateryna Yuri

Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.

Механическая величина, вызывающая ускорение 4 буквы

Ответы на сканворды и кроссворды

Сила

Механическая величина, вызывающая ускорение 4 буквы

НАЙТИ

Как найти величину ускорения для класса 11 по физике CBSE

Подсказка: Скорость изменения скорости называется ускорением. Это векторная величина; это означает, что он имеет как величину, так и ускорение. Величина представлена в единицах. Ускорение зависит от различных параметров, таких как время, скорость, сила и т. Д. Оно может быть поступательным или вращательным.

Полный ответ:
Изменение скорости, которое происходит в единицу времени, называется ускорением.{-2}} $. Он задается как-
$ a = \ dfrac {vu} {t} $
Здесь $ a $ – ускорение
$ v $ – конечная скорость
$ u $ – начальная скорость
$ t $ – время, затраченное
Величина ускорения представлена единицей измерения, а направление – единичным вектором. Для расчета величины мы можем использовать формулы и соотношения. Вышеприведенное уравнение можно использовать для расчета величины ускорения с использованием скорости и времени.
Мы знаем, что произведение массы и ускорения называется силой.{2}} \\
\ end {align} $
Здесь $ v $ и $ u $ – начальная и конечная скорости соответственно.
$ a $ – ускорение
$ s $ – перемещение
$ t $ – затраченное время
Следовательно, величина ускорения – это величина, представленная единицей измерения. Его можно рассчитать, используя различные соотношения между ускорением и другими параметрами, такими как скорость, сила и т. Д.

Примечание:
Согласно второму закону Ньютона, ускорение не равно нулю, если применяется внешняя сила, в противном случае оно равно нулю. .Ускорение может быть переменным или постоянным. Наиболее часто используемой единицей ускорения является ее единица СИ. Ускорение используется для описания движения тела и определения силы.

Магнитуда, интенсивность, энергия и ускорение землетрясения * | Бюллетень сейсмологического общества Америки

В статье исследуются основные физические элементы землетрясений: сила M , энергия E , интенсивность I , ускорение a и их связь с глубиной h и радиус заметности r .( r ² + h ² = R ². Нулевой индекс (₀) относится к эпицентру.) Уравнения

( A = амплитуда земли, T = период, D = гипоцентральное расстояние для данного толчка) установлены эмпирически для калифорнийских толчков. Уравнение (9) справедливо в очень общем случае и предлагает основу для более точного определения I , как это было предложено Канкани.Уравнение (4) здесь используется очень часто на малых расстояниях; но это только приблизительное значение, может отличаться по регионам и перекрывает, вероятно, прерывистый переход максимального ускорения от S̄ к какой-то другой поперечной волне с увеличением расстояния. Однако следствия, вытекающие из (4), нигде не вступают в серьезное противоречие с наблюдениями.

Инструментальная шкала магнитуды землетрясений расширена на короткие расстояния. Результаты входят в эмпирическое соотношение

, из которого и (9) следует

Эти два уравнения установлены и проверены для региона Калифорнии; они также должны сохраняться в других регионах с аналогичной структурой для землетрясений, происходящих примерно на той же глубине (что составляет примерно 18 км.).

Простейшие возможные предположения (постоянная скорость, незначительное поглощение, синусоидальные волны) приводят к общему уравнению

log⁡E = 14.9 + 2log⁡h + log⁡t0 + 2log⁡T0 + 2log⁡a0

( t ₀ = длительность, T ₀ = период последовательности синусоидальных волн в эпицентре).

Уравнения (27), (9) и (4) дают общеприменимые результаты

a _r , минимальное ощутимое ускорение составляет приблизительно 1 галлон.

Для толчков на обычной глубине в Калифорнии

Для других глубин и, вероятно, для других регионов

log⁡E = 9,5 + 3,2log⁡h + 1,1I0

log⁡E = 11,1 + 6,4log⁡R− 3.2log⁡h

Сводка физических элементов для толчков в Калифорнии приведена в таблице 10.

Уравнение (13) используется для расчета кажущейся глубины землетрясений в Соединенных Штатах и Европе. Результаты, как правило, подтверждают относительно неглубокое происхождение толчков на Тихоокеанском побережье по сравнению с теми, которые происходят в других местах, особенно под Канадским щитом, центральной долиной Миссисипи и южными Аппалачами.

Накопление событий ускорения большой величины позволяет прогнозировать изменения цереброваскулярной реактивности у спортсменок-футболистов средней школы

Смягчение последствий повторяющегося воздействия травм головы стало серьезной проблемой для населения в целом, учитывая растущее количество доказательств того, что даже бессимптомное воздействие ускорения головы связано с повышенным риском отрицательных исходов для жизни и что этот риск увеличивается по мере того, как воздействие увеличивается. много лет.Среди женских видов спорта футбол в настоящее время демонстрирует самый высокий рост посещаемости и ежегодно регистрирует самое большое количество легких черепно-мозговых травм, что делает футболисток важной группой для оценки последствий повторяющихся травм головы. Цереброваскулярные биомаркеры могут быть полезны при оценке эффектов повторяющихся травм головы, поскольку считается, что они непосредственно влияют на нейрокогнитивные симптомы, связанные с легкой черепно-мозговой травмой. Здесь мы используем фМРТ в сочетании с задачей гиперкапнической задержки дыхания вместе с мониторингом событий ускорения головы, чтобы оценить взаимосвязь между цереброваскулярными изменениями мозга и подверженностью повторяющимся травмам головы в течение сезона у спортсменок-футболистов женского пола.Мы определили продольные изменения цереброваскулярной реактивности, которые были в значительной степени связаны с длительным накоплением до значительных (> 75-го процентиля) событий ускорения головы. Полученные данные свидетельствуют в пользу активного мониторинга спортсменов в периоды воздействия событий, связанных с ускорением головы, иллюстрируют важность сбора исходных (то есть до воздействия) измерений и предлагают моделирование как средство руководства политикой смягчения последствий повторяющихся травм головы.

Ключевые слова: Цереброваскулярная реактивность; Сотрясение; Функциональная магнитно-резонансная томография; Легкая черепно-мозговая травма; Футбольный; Субконкуссионная травма.

Катящийся объект, ускоряющийся вниз по склону

Это меньшее ускорение, чем у скользящего блока выше – как мы и ожидали.

Катящийся диск с использованием крутящего момента

Можно ли получить ускорение диска, не используя принцип работы-энергии? да. Начнем с диаграммы силы диска, катящегося по склону.

Три силы, это должно быть просто, верно? Диск ускоряется только в направлении оси x (вдоль плоскости), так что это должно быть простой проблемой.Но нет. Это не так просто. Проблема в силе трения. Эта сила трения предотвращает скольжение диска. Поскольку диск катится без проскальзывания, сила трения будет силой трения покоя. Мы можем смоделировать величину этой силы с помощью следующего уравнения.

Здесь μ _s – коэффициент трения покоя. Это зависит от взаимодействия двух типов материалов. Если мне известна нормальная сила, я могу вычислить МАКСИМАЛЬНУЮ силу трения, но не точную силу трения.Я знаю, что это кажется безумным, но представьте себе супершероховатую поверхность для диска и плоскости. В таком случае сила трения может быть довольно большой. Что, если бы сила трения была больше, чем составляющая силы тяжести в направлении плоскости? Это заставило бы диск разогнаться ВВЕРХ самолета. Это было бы безумием. Верно?

Сила статического трения называется сдерживающей силой. Он прилагает любую необходимую силу, так что диск катится, а не скользит – до некоторого максимального значения.Но что это за ценность? Кто знает. Это должно нас остановить? Нет. Вот уравнение для чистых сил в x-направлении (я называю наклон вниз как положительное направление):

Если бы я только мог найти эту силу трения, я бы ответил на ускорение. Давайте посмотрим на другое место, где сила трения имеет значение – на крутящий момент. Принцип углового момента гласит, что чистый крутящий момент (относительно центра) равен моменту инерции, умноженному на угловое ускорение диска (относительно центра).Есть только одна сила, которая создает крутящий момент относительно центра масс диска – это сила трения. И нормальная сила, действующая на диск, и гравитационная сила, действующая на диск, проходят через центр вращения, так что крутящие моменты равны нулю.

Вот уравнение крутящего момента для вращающегося диска.

Поскольку существует только один крутящий момент, я записал это как величину крутящего момента и величину углового ускорения (в этом случае векторы крутящего момента и углового ускорения будут в одном направлении).Также я могу сказать еще кое-что об этом угловом ускорении. Диск катится без проскальзывания. Это означает, что существует следующая взаимосвязь между угловым ускорением и линейным ускорением центра масс:

Подставляя это вместо α и подставляя выражение для момента инерции диска, я получаю:

Теперь я могу поместить это выражение для силы трения в результирующие силы в уравнении x-направления сверху.

СТРЕЛА.Тот же ответ, что и метод Работа-Энергия. Разве не было бы странно, если бы у меня было другое ускорение с помощью этого метода?

Экспериментальный метод

Я не собираюсь делать это. Вы можете сделать это сами. Вот как это сделать:

Получите какой-нибудь пандус.
Угол наклона можно измерить, измерив высоту и длину. Если хотите, вы можете получить одно из этих приложений для измерения уровня для своего смартфона.
Купите автомобиль с низким коэффициентом трения. Да, у них есть колеса, но если масса автомобиля намного больше массы колес, вы можете использовать это как «скользящий объект без трения».
Ускорение можно измерить несколькими способами. Я бы использовал один из датчиков движения Vernier или PASCO. Вы также можете записать видео, на котором объект падает, а затем использовать видеоанализ. Наконец, вы можете просто вывести машину из состояния покоя, а затем измерить расстояние и время.
Теперь найдите диск. Не имеет значения размер или масса, просто то, что он имеет однородную плотность. Попробуйте найти ту, которая будет катиться прямо.
Измерьте ускорение диска при его скатывании по склону.Ради интереса попробуйте и большой, и маленький диск, чтобы увидеть, дают ли они одинаковое (или примерно одинаковое) ускорение.

Вот и все. Весело, правда? Кроме того, вы можете попробовать объекты другой формы, такие как сфера или кольцо.

Хорошо, последнее замечание. Это было немного дольше, чем я ожидал. Тем не менее, я думаю, что это отличный пример, который вводит множество различных понятий из вводной физики. Фактически, я просто собираюсь добавить это в свою электронную книгу по физике – Just Enough Physics (версия для Amazon Kindle).

Это мой план для этой книги. Когда у меня есть что-то, что уместно добавить к нему, я просто так и сделаю. Думайте об этом как о живой и расширяющейся книге. Конечно, вы знаете, что, купив книгу, вы получите обновления бесплатно, верно?

Недавно я обновил эту книгу и решил сделать обложку книги получше. Вот эта обложка.

Помните, это просто электронная книга. Там могут быть какие-то ошибки. Если вы найдете что-то, оставьте комментарий на странице Amazon, и я постараюсь держать его в курсе.

Видео с вопросом: Расчет величины углового ускорения жесткого диска

Стенограмма видео

На жестком диске постоянная крутящий момент 14,0 ньютон-метров прилагается к магнитному диску при запуске привода запись данных. Магнитный диск имеет момент инерция 1,12 килограмм-метра в квадрате. Какова величина угловое ускорение диска?

Мы можем нарисовать диаграмму, которая представляет вращающийся диск с информацией, полученной из задачи.На нашей диаграмме мы пометили величина приложенного крутящего момента составляет 14,0 ньютон-метров, момент инерции размер диска должен составлять 1,12 килограмм-метра в квадрате, и мы решаем для нашего углового ускорение 𝛼.

Для решения поставленной задачи мы требовалось уравнение, которое связывает эти три переменные вместе. Второй закон движения Ньютона, когда применительно к вращательному движению чистый крутящий момент 𝜏 net равен моменту инерция объекта 𝐼, умноженная на угловое ускорение объекта.Проблема просит нас решить для угловое ускорение. Однако прямо сейчас наше уравнение записано в форме решения для крутящего момента. Следовательно, мы должны переставить наши формула для решения относительно 𝛼.

Чтобы изолировать 𝛼, мы должны разделить оба стороны уравнения на 𝐼, вычеркивая из правой части уравнения, Оставляя нас с крутящим моментом, разделенным на момент инерции, получается угловое ускорение. Подставляя наши ценности, мы получаем 14.0 ньютон-метров для нашего крутящего момента и 1,12 килограмм-метров в квадрате на данный момент инерции. Когда мы разделим эти два числа, мы получаем угловое ускорение 12,5 радиан в секунду в квадрате. Величина углового ускорение диска составляет 12,5 радиан в секунду в квадрате.

Ускорение силы тяжести и второй закон Ньютона

Ускорение силы тяжести – одна из наиболее часто используемых физических констант, известная из

Второй закон Ньютона

«Изменение движения пропорционально приложенной силе и происходит вдоль прямой линия действует сила.”

Второй закон Ньютона для силы тяжести – вес – может быть выражен как

W = F _г
= ma _г
= мг (1 )
где
W, F г = вес, сила тяжести (Н, фунт _f)

м = масса (кг, снаряды)

a _g = g = ускорение свободного падения (9.81 м / с ², 32,17405 фут / с ² )

Сила тяжести – a _г – называется весом.

Примечание!

масса – это свойство – величина с величиной
сила – вектор – величина с величиной и направлением

Ускорение свободного падения можно наблюдать, измеряя изменение скорости , связанное с изменением времени для свободно падающего объекта:

a _g = dv / dt (2)
, где
dv = изменение скорости (м / с, фут / с)

dt = изменение во времени (с)

Объект, брошенный на открытом воздухе, разгоняется до скорости 9.81 м / с (32,174 фут / с) дюйм один – 1 – второй .

тяжелое и легкое тела рядом с землей упадут на землю с одинаковым ускорением (если пренебречь сопротивлением воздуха)

Ускорение силы тяжести в единицах СИ

1 a _g = 1 g = 9,81 м / с ² = 35,30394 (км / ч) / с

Ускорение свободного падения в имперских единицах

1 a _g = 1 g = 32.174 фут / с ² = 386,1 дюйм / с ² = 22 миль / с

Скорость и расстояние, пройденное свободно падающим объектом

Скорость свободно падающего объекта через некоторое время можно рассчитать как:

v = a _г t (3)
где
v = скорость (м / с)

Расстояние, пройденное свободно падающий объект через некоторое время может быть выражен как:

s = 1/2 a _g t ² (4)
где
s = расстояние, пройденное объект (м)

Скорость и расстояние, пройденное свободно падающим объектом:

Время (с)	Скорость 90 456				Расстояние
Время (с)	м / с	км / ч	фут / с	миль / ч	м	9045 1 9048 9048 9049 9048 9048 9.8	35,3	32,2	21,9	4,9	16,1
2	19,6	70,6	64,3	43,8	64,3	43,8											96,5	65,8	44,1	144,8
4	39,2	141	128,7	87,7	78.5	257,4
5	49,1	177	160,9	110	122,6	402,2
6	58,9 21492	6	58,9 21492
7	68,7	247	225,2	154	240,3	788,3
8	78.5	283	257,4	176	313,9	1,029,6
9	88,3	318	359,6	198						198		39491	321,7	219	490,5	1,608,7

Примечание! Скорости и расстояния достигаются без аэродинамического сопротивления (в условиях вакуума).Сопротивление воздуха – или сила сопротивления – для объектов, движущихся с более высокой скоростью, может быть значительным – в зависимости от формы и площади поверхности.

Пример – свободно падающий камень

Камень упал с высоты 1470 футов (448 м) – примерно на высоте Эмпайр-стейт-билдинг. Время, необходимое для достижения земли (без сопротивления воздуха), можно рассчитать, переставив (4) :

t = (2 с / год _г) ^1/2

= (2 (1470 футов) / (32.174 фут / с ²)) ^1/2

= 9,6 с

Скорость камня при ударе о землю можно рассчитать с помощью (3) :

v = ( 32,174 фут / с ²) (9,6 с)

= 308 фут / с

= 210 миль / с

= 94 м / с

= 338 км / ч

Пример – Мяч, брошенный прямо вверх

Мяч брошен прямо вверх с начальной скоростью 25 м / с .Время до того, как мяч остановится и начнет падать, можно рассчитать, изменив (3) на

t = v / a _g

= (25 м / с) / (9,81 м / с ²)

= 2,55 с

Расстояние, пройденное мячом до того, как он повернется и начнет падать, можно рассчитать, используя (4) как

с = 1/2 (9,81 м / с ²) ( 2,55 с ) ²

= 31.8 м.

Первый закон Ньютона

«Каждое тело продолжает находиться в состоянии покоя или в равномерном движении по прямой линии, пока его сила не заставит изменить свое состояние покоя или движения».

Третий закон Ньютона

«На каждое действие всегда есть равная реакция – если сила действует, чтобы изменить состояние движения тела, тело оказывает сопротивление, равное силе и прямо противоположное этой силе».

Общие выражения

наложенные нагрузки: кН / м ²
массовые нагрузки: кг / м ² или кг / м ³
напряжение: Н / мм ²
изгибающий момент: кНм
сдвиг: кН

1 Н / мм = 1 кН / м
1 Н / мм ² = 10 ^{3 ³ / м ²}
1 кНм = 10 ⁶ Нмм

Широта и ускорение силы тяжести

Ускорение силы тяжести зависит от широты – примеры:

9049 5049 Вашингтон 38 ° 53 ‘

Местоположение	Местоположение	Сила тяжести (м / с ²)
Северный полюс	90 ° 0 ‘	9.8321
Анкоридж	61 ° 10 ‘	9,8218
Гринвич	51 ° 29′	9,8119
			Париж	9.8011
Панама	8 ° 55′	9.7822
Equator	0 ° 0 ‘	9.7799

Закон Ньютона

3-й закон Ньютона

Рассмотрим следующие ситуации:

Вы с другом сидите на стульях с роликами.У вас обоих есть ваши ноги оторваны от земли и ногами вы отталкиваетесь от друга стул. Ваш друг начинает отходить от вас, а вы начинаете двигаться вдали от друга. Вы оба ускоряетесь. Направление вашего ускорения противоположно направлению вашего друга ускорение.
Вы оба протягиваете руки, хватаете друга и тянете его к вам. Он ускоряется к вам, а вы ускоряетесь к его.Снова вы оба ускоряетесь.

То, что происходит, является следствием третьего закона Ньютона .

Для каждой силы, объект действует на второй объект, существует сила, равная по величине, но противоположно направлению действия второго объекта на первый объект. Силы – это результат взаимодействий.

Ты тянешь за меня, я тяну за тебя. Если нет других сил, я ускорюсь к вам. Мое ускорение величина силы деленная на моей массы .Ты ускоришься ко мне. Ваше ускорение равно силе, деленной на вашей массы .

Вопрос:

Вы толкаете стол, стол толкает вас. Ты ускоряться от стола. Почему стол не ускоряется от вас?

Если стол стоит на роликах, он будет ускоряться от вас. Если таблица очень массивен, величина его ускорения будет намного меньше, чем величина вашего ускорения.Если его нет на роликах, то сила статического трения также действует на него, и векторная сумма двух сил равно нулю.

Стоя на очень скользкой поверхности или на скейтборде, вы бросаете тяжелый объект от вас в северном направлении. Для этого вам нужно приложить сила на объект в северном направлении. Объект оказывает давление на вы, который имеет такую же величину, но указывает на юг. Вы ускоряетесь на юг.

Третий закон Ньютона также называют законом Действие и противодействие . Для каждой силы воздействия существует сила противодействия, равная по величине и противоположное по направлению. Объекты взаимодействуют.

Сила действия и противодействия всегда действует на разные объекты.
Две силы, действующие на один и тот же объект, даже если у них одинаковые величина и направление в противоположном направлении, никогда не образуют пары действие-противодействие.

Проблема:

Яблоко массой 0,2 кг находится на столе в равновесии.
а) Какие силы действуют на него? Укажите их величину и направление.
б) Какова сила противодействия каждой из сил, действующих на яблоко?
(c) Что такое пары действие-противодействие?

Решение:

Рассуждение:
(a) Силы, действующие на яблоко, выражаются в его весе W = mg = 1,96 Н, указывающем вниз и нормальная сила, предусмотренная таблицей F _N = 1.96 с.ш. указывая вверх. Чистая сила, действующая на яблоко, равна нулю.
(b) Сила реакции на W – это сила F _WR = 1,96 Н, направленная вверх, действующая в центре Земли. (Земля тянет за яблоко и яблоко тянет на землю.)
Реакция на F _N – это сила F _NR = 1,96 Н, указывающая вниз действующий на стол. (Стол толкает яблоко, яблоко давит на стол.)
(c) Пары действие-реакция: W – F _WR и N – F _NR.

Модуль 2: Вопрос 2

Устройство, используемое с 1940-х годов для измерения удара или отдачи тела при ударе. к сердцебиению это «баллистокардиограф» Какие физические принципы здесь задействованы для измерения силы сердечного сокращения? Как мог мы построим такое устройство?

Обсудите это со своими однокурсниками на дискуссионном форуме!

Модуль 2: Вопрос 3

Предположим, вы держите в руке чашку кофе.Определить все силы на чашку и реакцию на каждую силу.

Обсудите это со своими однокурсниками на дискуссионном форуме!

Растяжение и сжатие

Предположим, что две противоборствующие команды и противостоящая команда тянут веревку в противоположные направления. Есть ли чистая сила на веревке?

Если веревка ускоряется в сторону одной из команд, то есть – ненулевая чистая сила. F = m a .Чистая сила – это векторная сумма силы тяжести и сил осуществляется двумя командами.
Противоборствующая команда, так как веревка начинает ускоряться в их направление.

Если веревка не ускоряется, даже если каждая команда тянет так сильно, как она Тогда на веревку не действует действующая сила. Однако есть напряжение в веревка. Напряжение возникает из-за различных сил, действующих на разные части тело. Напряжение может сломать вещи.Чистая сила, то есть та же сила действуя на все части тела, не может сломать вещи.
Если вместо потянув за веревку, обе команды толкают тяжелую скалу, но скала не двигаться, то снова результирующая сила на камне равна нулю. Однако теперь рок находится под сжатие .

Напряжение T – скаляр. Он определяется как величина сила, с которой натянутая веревка тянет за все, к чему она прикреплена. Эта сила часто обозначается T .Направление т зависит от того, какой конец веревки рассматривается.

Чистая сила, действующая на объект, всегда является векторной суммой всех сил. воздействуя на объект. Ускорение объекта в направлении эта чистая сила и имеет величину a = (чистая сила / масса объекта).

Проблема:

Блок весом 15 фунтов стоит на полу. (Примечание: фунт – это единицы силы, вес блока 15 фунтов)
(a) Что сила, которую пол оказывает на блок?
(b) Если веревка привязана к блок и проходить вертикально по шкиву, а другой конец прикреплен к свободно висящий 10-фунтовый груз, какова сила, прилагаемая полом к 15-фунтовый блок?
(c) Если мы заменим 10-фунтовый груз в части (b) на 20 фунтов веса, какова сила, прилагаемая полом к 15-фунтовому блоку?

Решение:

Рассуждение:
(a) Блок находится в состоянии покоя, результирующая сила равна нулю.Вес блок на 15 фунтов вниз. Следовательно, пол должен прилагать усилие в 15 фунтов. вверх.
(б) Блок по-прежнему в покое. Вес на 15 фунтов вниз, веревка тянется на 10 фунтов вверх. из-за натяжения веревки. Поэтому пол должен приложите усилие на 5 фунтов вверх.
(c) Вес на 15 фунтов вниз, веревка тянется вверх на 20 фунтов из-за натяжения веревки. Блок будет ускоряться вверх, поскольку чистая сила направлена вверх. Блок не упирается в землю, и земля не отталкиваясь. Земля оказывает на блок нулевую силу.

Проблема:

Два блоки, один из которых стоит на столе, а другой более тяжелый, свисающий с его края, соединены легкой струной, как показано на рисунке. Какая сила заставляет блок на столе ускоряться, натяжение струны или вес подвесной блок? Запишите выражение для ускорения a.

Решение:

Перегрузки и их действие на человека в разных условиях

Ускорение Кориолиса

Ускорение – Класс!ная физика

Ускорение

Угловое ускорение

Основные понятия

Закон равнопеременного вращения

Практические примеры

Конвертер ускорения • Механика • Компактный калькулятор • Онлайн-конвертеры единиц измерения

Общие сведения

Защита от ускорений с помощью амортизирующих и демпфирующих конструкций

Ускорение в физике

Второй закон Ньютона

Ускорение и движение по кругу

Ускорение и сила притяжения

Ускорение и транспортные средства

Тесты на ускорение для автомобилей

Влияние ускорения на людей

Механическая величина, вызывающая ускорение 4 буквы

Ответы на сканворды и кроссворды

Похожие вопросы в сканвордах

Похожие ответы в сканвордах

Как найти величину ускорения для класса 11 по физике CBSE

Магнитуда, интенсивность, энергия и ускорение землетрясения * | Бюллетень сейсмологического общества Америки

Накопление событий ускорения большой величины позволяет прогнозировать изменения цереброваскулярной реактивности у спортсменок-футболистов средней школы

Катящийся объект, ускоряющийся вниз по склону

Катящийся диск с использованием крутящего момента

Экспериментальный метод

Видео с вопросом: Расчет величины углового ускорения жесткого диска

Стенограмма видео

Ускорение силы тяжести и второй закон Ньютона

Второй закон Ньютона

Ускорение силы тяжести в единицах СИ

Ускорение свободного падения в имперских единицах

Скорость и расстояние, пройденное свободно падающим объектом

Пример – свободно падающий камень

Пример – Мяч, брошенный прямо вверх

Первый закон Ньютона

Третий закон Ньютона

Общие выражения

Широта и ускорение силы тяжести

Закон Ньютона

3-й закон Ньютона

Вопрос:

Проблема:

Модуль 2: Вопрос 2

Модуль 2: Вопрос 3

Растяжение и сжатие

Проблема:

Проблема:

Оставить комментарий Отменить ответ