Виды движения формулы в физике: Ошибка: 404 Материал не найден

Урок 03. Лекция 03. Виды механического движения

Виды движения (равномерное, равноускоренное) и их графическое описание

По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).

При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути

Равномерное прямолинейное движение.

Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:

v_х=S/t

Скорость – это физическая величина, показывающая быстроту изменения координаты.

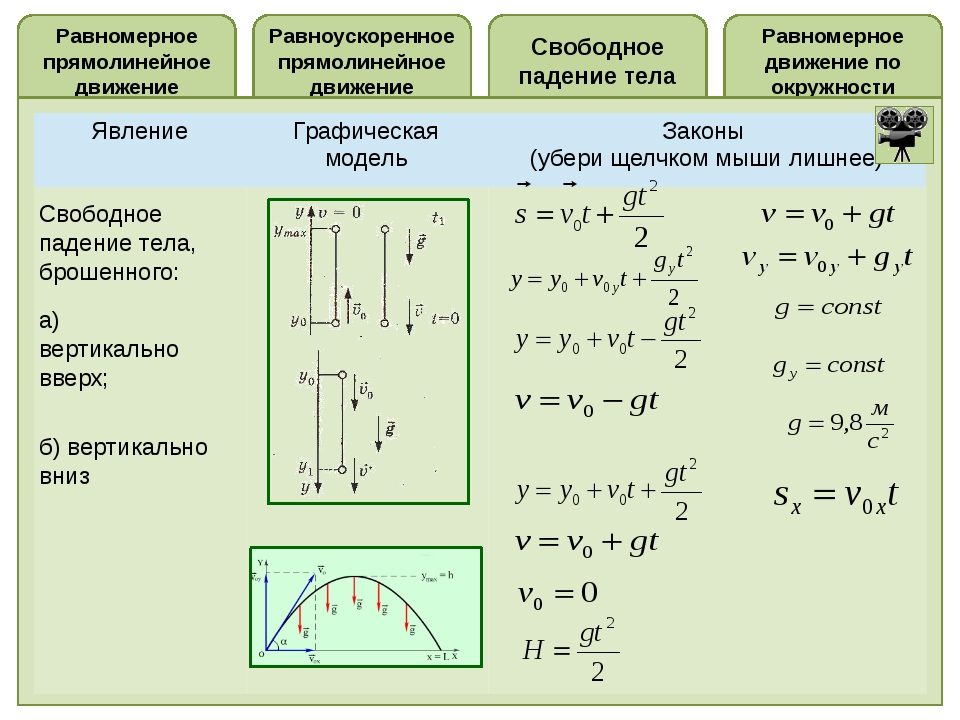
Единицы измерения скорости – метры в секунду [1 м/с]

Уравнение равномерного движения (перемещение тела при равномерном движении):

 S=v_х·t

Уравнение координаты тела:

х=х₀+v_х·t

Обозначения:

х– координата движущегося тела

х₀ – начальная координата движущегося тела

v_ср-Средняя скорость равномерного прямолинейного движения

v_х — Скорость равномерного прямолинейного движения

S — Перемещение тела (расстояние, на которое передвинулось тело)

t — Промежуток времени перемещения (время)

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) – изменение скорости со временем

S(t) – изменение перемещения (пути) со временем

a(t) – изменение ускорения со временем

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно (v=const), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) – прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.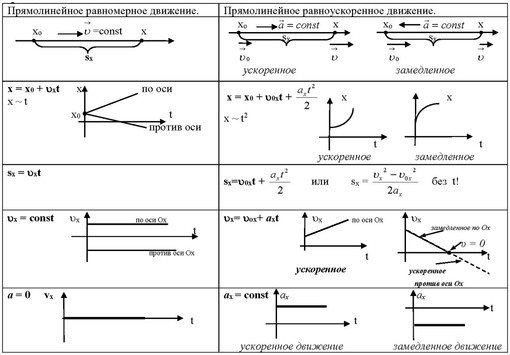

Зависимость перемещения от времени. График s(t) – наклонная линия:

Зависимость координаты от времени. График х(t) – наклонная линия:

Из графика видно, что проекция скорости равна:

v

х=S/t=tga

Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой  к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называютравноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

Обозначения:

v_х— конечная скорость тела при равноускоренном движении по прямой

v_0х— начальная скорость тела

a — ускорение тела

t — время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с²].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения:

 

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

 

Обозначения:

— Перемещение тела при равноускоренном движении по прямой

— Начальная скорость тела

— Скорость тела при равноускоренном движении по прямой

— Ускорение тела

— Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

– если известны начальная, конечная скорости движения и ускорение.

– если известны начальная, конечная скорости движения и время всего движения

Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) – изменение скорости со временем

S(t) – изменение перемещения (пути) со временем

a(t) – изменение ускорения со временем

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости .

Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости

 

В координатах зависимость имеет вид .

Графиком является ветка параболы.

Интерактивный плакат “Механическое движение и его виды” | Электронный образовательный ресурс по физике:

Слайд 1

механическое движение 1 2 3 4 5 и его виды

Слайд 2

механическое движение 1 2 3 4 5 и его виды Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени

Слайд 3

Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, т. е. это движение с постоянной по модулю и направлению скоростью: — кинематическое уравнение равномерного движения (уравнение зависимости координаты от времени). График скорости представлен на рисунке: Площадь заштрихованного прямоугольника численно равна пути s (модулю перемещения), пройденному телом 1 за время . t 1 =t 2 =t 3 ; S 1 =S 2 =S 3 S 3 X S 2 S 1 t 1 =t 2 =t 3 ; S 1 =S 2 =S 3

Слайд 4

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково. Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Слайд 5

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением. Проекция скорости:

Слайд 6

Равнозамедленное движение – движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению. Уравнение координаты: Уравнение скорости : v = v 0 – at Уравнение перемещения:

Слайд 7

Свободное падение — это движение тела под действием только силы тяжести. Ускорение , которое сообщает телу сила тяжести, называют ускорением свободного падения . Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени. Ускорение свободного падения направлено вертикально вниз. В земных условиях g зависит от географической широты местности. Наибольшее значение оно имеет на полюсе (g = 9,81 м/с ), наименьшее — на экваторе (g = 9,75 м/с ). Причины этого: суточное вращение Земли вокруг своей оси; отклонение формы Земли от сферической; неоднородное распределение плотности земных пород. Ускорение свободного падения зависит от высоты h тела над поверхностью планеты. Его, если пренебречь вращением планеты, можно рассчитать по формуле: 2 2 Уравнение скорости: Кинематическое уравнение:

Слайд 8

Прямолинейное движение — механическое движение, происходящее вдоль прямой линии. При прямолинейном движении материальной точки траектория представляет собой прямую линию.

Слайд 9

механическое движение 1 2 3 4 5 и его виды Прямолинейное движение 1. равномерное 2. равнопеременное 3. равноускоренное 4. равнозамедленное 5. свободное падение тел

Кинематика – Формулы по физике

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах

Поступательное и вращательное движения – самые простые виды механического движения.

Относительность механического движения

Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое.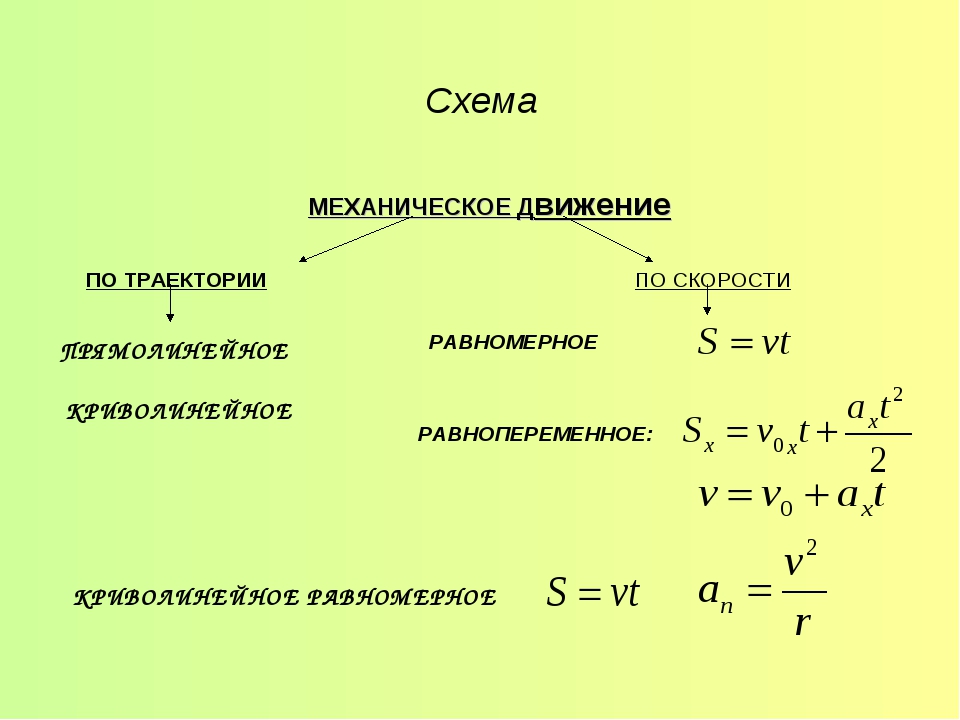 По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.

Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.

Относительность механического движения– это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Материальная точка

Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.

Материальная точка – это тело, размерами которого в данных условиях можно пренебречь.

Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя.

Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.

Система отсчёта

Материальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчёта выбирают произвольно в зависимости от решаемых задач.

С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени.

Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.

Траектория движения также зависит от выбора системы отсчёта.

Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.

.

Прямолинейное движение и движение по окружности | ЕГЭ по физике

Механическое движение.

Относительность механического движения. Система отсчета

Под механическим движением понимают изменение с течением времени взаимного расположения тел или их частей в пространстве: например, движение небесных тел, колебания земной коры, воздушные и морские течения, движение летательных аппаратов и транспортных средств, машин и механизмов, деформации элементов конструкций и сооружений, движение жидкостей и газов и др.

Относительность механического движения

С относительностью механического движения мы знакомы с детства. Так, сидя в поезде и наблюдая за трогающимся с места поездом, стоявшим до этого на параллельном пути, мы часто не можем определить, какой из поездов на самом деле начал двигаться. И здесь сразу следует уточнить: двигаться относительно чего? Относительно Земли, конечно. Потому что относительно соседнего поезда мы начали двигаться независимо от того, какой из поездов начал свое движение относительно Земли.

Относительность механического движения заключается в относительности скоростей перемещения тел: скорости тел относительно разных систем отсчета будут различны (скорость человека, перемещающегося в поезде, пароходе, самолете, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей).

Различными будут и траектории движения тела в разных системах отсчета. Так, например, вертикально падающие на землю капли дождя оставят след в виде косых струй на окне вагона мчащегося поезда. Точно также любая точка на вращающемся пропеллере летящего самолета или спускающегося на землю вертолета описывает окружность относительно самолета и гораздо более сложную кривую — винтовую линию относительно Земли. Таким образом, при механическом движении относительной является также и траектория движения.

Путь, пройденный телом, также зависит от системы отсчета. Возвращаясь все к тому же пассажиру, сидящему в поезде, мы понимаем, что путь, проделанный им относительно поезда за время поездки, равен нулю (если он не передвигался по вагону) или, во всяком случае, намного меньше того пути, который он преодолел вместе с поездом относительно Земли. Таким образом, при механическом движении относительным является также и путь.

Осознание относительности механического движения (т. е. того, что движение тела можно рассматривать в разных системах отсчета) привело к переходу от геоцентрической системы мира Птолемея к гелиоцентрической системе Коперника. Птолемей, следуя наблюдаемому издревле движению Солнца и звезд на небосклоне, в центре Вселенной расположил неподвижную Землю с вращающимися вокруг нее остальными небесными телами. Коперник же считал, что Земля и другие планеты вращаются вокруг Солнца и одновременно вокруг своих осей.

Таким образом, изменение системы отсчета (Земля — в геоцентрической системе мира и Солнце — в гелиоцентрической) привело к гораздо более прогрессивной гелиоцентрической системе, позволяющей решить многие научные и прикладные задачи астрономии и изменить взгляды человечества на Вселенную.

Система координат $X, У, Z$, тело отсчета, с которым она связана, и прибор для измерения времени (часы) образуют систему отсчета, относительно которой рассматривается движение тела.

Телом отсчета называется тело, относительно которого рассматривается изменение положения других тел в пространстве.

Систему отсчета можно выбрать произвольно. При кинематических исследованиях все системы отсчета равноправны. В задачах динамики также можно использовать любые произвольно движущиеся системы отсчета, но удобнее всего инерциальные системы отсчета, так как в них характеристики движения имеют более простой вид.

Материальная точка

Материальная точка — объект пренебрежимо малых размеров, имеющий массу.

Понятие «материальная точка» вводится для описания (с помощью математических формул) механического движения тел. Делается это потому, что описывать движение точки проще, чем реального тела, частицы которого к тому же могут двигаться с разными скоростями (например, при вращении тела или деформациях).

Если реальное тело заменяют материальной точкой, то этой точке приписывают массу этого тела, но пренебрегают его размерами, а заодно пренебрегают различием характеристик движения его точек (скоростей, ускорений и т. д.), если таковое имеется. В каких случаях это можно делать?

Практически любое тело можно рассматривать как материальную точку, если расстояния, проходимые точками тела, очень велики по сравнению с его размерами.

Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении различных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.

Следовательно, если в изучаемом движении тела можно пренебречь его вращением вокруг оси, такое тело можно представить как материальную точку.

Однако при решении задач, связанных с суточным вращением планет (например, при определении восхода Солнца в разных местах поверхности земного шара), считать планету материальной точкой бессмысленно, так как результат задачи зависит от размеров этой планеты и скорости движения точек ее поверхности.

Материальной точкой правомерно считать самолет, если требуется, например, определить среднюю скорость его движения на пути из Москвы в Новосибирск.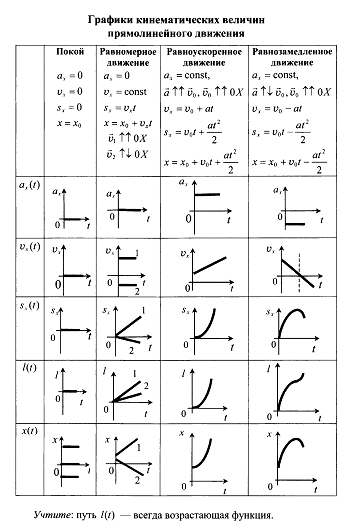 Но при вычислении силы сопротивления воздуха, действующей на летящий самолет, считать его материальной точкой нельзя, поскольку сила сопротивления зависит от размеров и формы самолета.

Если тело движется поступательно, даже если его размеры сопоставимы с расстояниями, которые оно проходит, это тело можно рассматривать как материальную точку (поскольку все точки тела движутся одинаково).

В заключение можно сказать: тело, размерами которого в условиях рассматриваемой задачи можно пренебречь, можно считать материальной точкой.

Траектория

Траектория — это линия (или, как принято говорить, кривая), которую описывает тело при движении относительно выбранного тела отсчета.

Говорить о траектории имеет смысл лишь в том случае, когда тело можно представить в виде материальной точки.

Траектории могут иметь разную форму. О форме траектории иногда удается судить по-видимому следу, который оставляет движущееся тело, например, летящий самолет или проносящийся в ночном небе метеор.

Форма траектории зависит от выбора тела отсчета. Например, относительно Земли траектория движения Луны представляет собой окружность, относительно Солнца — линию более сложной формы.

При изучении механического движения в качестве тела отсчета, как правило, рассматривается Земля.

Способы задания положения точки и описание ее движения

Положение точки в пространстве задается двумя способами: 1) с помощью координат; 2) с помощью радиус-вектора.

Положение точки с помощью координат задается тремя проекциями точки $х, у, z$ на оси декартовой системы координат $ОХ, ОУ, OZ$, связанные с телом отсчета. Для этого из точки А необходимо опустить перпендикуляры на плоскости $YZ$ (координата $х$), $ХZ$ (координата $у$), $ХУ$ (координата $z$) соответственно. Записывается это так: $А(х, у, z)$. Для конкретного случая, $(х=6, у=10.2, z= 4.5$), точка $А$ обозначается $А(6; 10; 4.5)$.

Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси ($х$ на ось $ОХ$ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат $О$ и лежащая на диагонали параллелепипеда, и будет искомой точкой $А$.

Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: $ОХ$ и $ОУ$. Тогда положение точки на плоскости определяют двумя координатами $х$ и $у$.

Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.

Задание положения точки $А$ с помощью радиус-вектора осуществляется соединением точки $А$ с началом координат $О$. Направленный отрезок $ОА = r↖{→}$ называется радиус-вектором.

Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.

Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций $r_x, r_у, r_z$ на оси координат $ОХ, ОY, OZ$, либо углы между радиус-вектором и осями координат.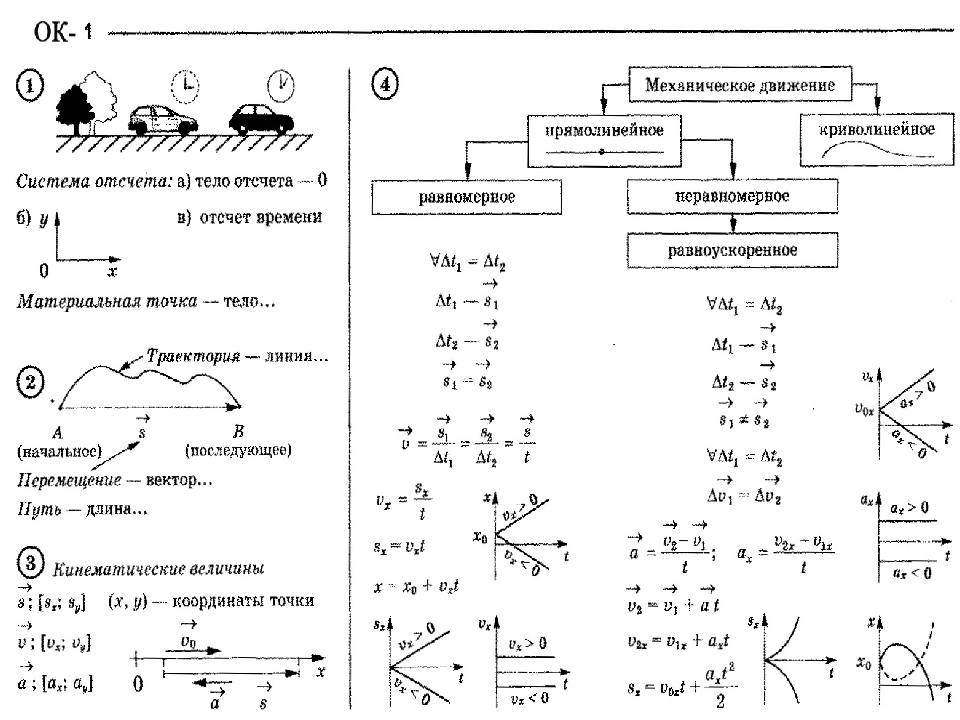 Для случая движения на плоскости имеем:

$x=r_x=rcosα,$

$y=r_y=rsinα.$

Здесь $r=|r↖{→}|$ — модуль радиус-вектора $r↖{→}, r_x$ и $r_y$ — его проекции на оси координат, все три величины — скаляры; хжу — координаты точки А.

Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.

Вектор $r↖{→}$ можно также разложить на составляющие по осям $Х$ и $Y$, т. е. представить в виде суммы двух векторов:

$r↖{→}=r↖{→}_x+r↖{→}_y$

Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус-вектором.

Способы описания движения точки

В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.

При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:

$x = x(t),$

$y = y(t),$

$z = z(t).$

Уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.

При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:

$r↖{→}=r↖{→}(t)$

Уравнение представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений равносильно заданию одного векторного уравнения.

Для каждого случая движения вид уравнений будет вполне определенным. Если траекторией движения точки является прямая линия, движение называется прямолинейным, а если кривая — криволинейным.

Перемещение и путь

Перемещение в механике — это вектор, соединяющий положения движущейся точки в начале и в конце некоторого промежутка времени.

Понятие вектора перемещения вводится для решения задачи кинематики — определить положение тела (точки) в пространстве в данный момент времени, если известно его начальное положение.

На рис. вектор ${М_1М_2}↖{-}$ соединяет два положения движущейся точки — $М_1$ и $М_2$ в моменты времени $t_1$ и $t_2$ соответственно и, согласно определению, является вектором перемещения. Если точка $М_1$ задана радиус-вектором $r↖{→}_1$, а точка $М_2$ — радиус-вектором $r↖{→}_2$, то, как видно из рисунка, вектор перемещения равен разности этих двух векторов, т. е. изменению радиус-вектора за время $∆t=t_2-t_1$:

$∆r↖{→}=r↖{→}_2-r↖{→}_1$.

Сложение перемещений (например, на двух соседних участках траектории) $∆r↖{→}_1$ и $∆r↖{→}_2$ осуществляется по правилу сложения векторов:

$∆r=∆r↖{→}_2+∆r↖{→}_1$

Путь — это длина участка траектории, пройденного материальной точкой за данный промежуток времени. Модуль вектора перемещения в общем случае не равен длине пути, пройденного точкой за время $∆t$ (траектория может быть криволинейной, и, кроме того, точка может менять направление движения).

Модуль вектора перемещения равен пути только при прямолинейном движении в одном направлении. Если направление прямолинейного движения меняется, модуль вектора перемещения меньше пути.

При криволинейном движении модуль вектора перемещения также меньше пути, т. к. хорда всегда меньше длины дуги, которую она стягивает.

Скорость материальной точки

Скорость характеризует быстроту, с которой происходят любые изменения в окружающем нас мире (движение материи в пространстве и времени). Движение пешехода по тротуару, полет птицы, распространение звука, радиоволн или света в воздухе, вытекание воды из трубы, движение облаков, испарение воды, нагрев утюга — все эти явления характеризуются определенной скоростью.

При механическом движении тел скорость характеризует не только быстроту, но и направление движения, т. е. является векторной величиной.

Скоростью $υ↖{→}$ точки называется предел отношения перемещения $∆r↖{→}$ к промежутку времени $∆t$, в течение которого это перемещение произошло, при стремлении $∆t$ к нулю (т. е. производной $∆r↖{→}$ по $t$):

$υ↖{→}={lim}↙{∆t→0}{∆r↖{→}}/{∆t}=r↖{→}_1’$

Составляющие вектора скорости по осям $X, Y, Z$ определяются аналогично:

$υ↖{→}_x={lim}↙{∆t→0}{∆x}/{∆t}=x’; υ_y=y’; υ_z=z’$

Определенное таким образом понятие скорости называют также мгновенной скоростью. Это определение скорости справедливо для любых видов движения — от криволинейного неравномерного до прямолинейного равномерного. Когда говорят о скорости при неравномерном движении, под ней понимают именно мгновенную скорость. Из этого определения непосредственно вытекает векторный характер скорости, поскольку перемещение — векторная величина. Вектор мгновенной скорости $υ↖{→}$ всегда направлен по касательной к траектории движения. Он указывает направление, по которому происходило бы движение тела, если бы с момента времени $t$ на него прекратилось действие любых других тел.

Средняя скорость

Средняя скорость точки вводится для характеристики неравномерного движения (т.е. движения с переменной скоростью) и определяется двояко.

1. Средняя скорость точки $υ_{ср}$ равна отношению всего пройденного телом пути $∆s$ ко всему времени движения $∆t$:

$υ↖{→}_{ср}={∆s}/{∆t}$

При таком определении средняя скорость — скаляр, т. к. пройденный путь (расстояние) и время — величины скалярные.

Такой способ определения дает представление о средней скорости движения на участке траектории (средней путевой скорости).

2. Средняя скорость точки равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло:

$υ↖{→}_{ср}={∆r↖{→}}/{∆t}$

Средняя скорость перемещения — величина векторная.

Для неравномерного криволинейного движения такое определение средней скорости не всегда позволяет определить даже приблизительно реальные скорости на пути движения точки. Например, если точка двигалась по замкнутой траектории в течение некоторого времени, то перемещение ее равно нулю (но скорость явно отличалась от нуля). В этом случае лучше пользоваться первым определением средней скорости.

В любом случае следует различать эти два определения средней скорости и знать, о какой из них идет речь.

Закон сложения скоростей

Закон сложения скоростей устанавливает связь между значениями скорости материальной точки относительно различных систем отсчета, движущихся друг относительно друга. В нерелятивистской (классической) физике, когда рассматриваемые скорости малы по сравнению со скоростью света, справедлив закон сложения скоростей Галилея, который выражается формулой:

$υ↖{→}_2=υ↖{→}_1+υ↖{→}$

где $υ↖{→}_2$ и $υ↖{→}_1$ — скорости тела (точки) относительно двух инерциальных систем отсчета — неподвижной системы отсчета $K_2$ и системы отсчета $K_1$ движущейся со скоростью $υ↖{→}$ относительно $K_2$.

Формула может быть получена путем сложения векторов перемещений.

Для наглядности рассмотрим движение лодки со скоростью $υ↖{→}_1$ относительно реки (система отсчета $K_1$), воды которой движутся со скоростью $υ↖{→}$ относительно берега (система отсчета $K_2$).

Векторы перемещений лодки относительно воды $∆r↖{→}_1$, реки относительно берега $∆r↖{→}$ и суммарный вектор перемещения лодки относительно берега $∆r↖{→}_2$ изображены на рис..

Математически:

$∆r↖{→}_2=∆r↖{→}_1+∆r↖{→}$

Поделив обе части уравнения на интервал времени $∆t$, получим:

${∆r↖{→}_2}/{∆t}={∆r↖{→}_1}/{∆t}+{∆r↖{→}}/{∆t}$

В проекциях вектора скорости на оси координат уравнение имеет вид:

$υ_{2x}=υ_{1x}+υ_x,$

$υ_{2y}=υ_{1y}+υ_y.$

Проекции скоростей складываются алгебраически.

Относительная скорость

Из закона сложения скоростей следует, что если два тела движутся в одной и той же системе отсчета со скоростями $υ↖{→}_1$ и $υ↖{→}_2$, то скорость первого тела относительно второго $υ↖{→}_{12}$ равна разности скоростей этих тел:

$υ↖{→}_{12}=υ↖{→}_1-υ↖{→}_2$

Так, при движении тел в одном направлении (обгон) модуль относительной скорости равен разности скоростей, а при встречном движении — сумме скоростей.

Ускорение материальной точки

Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.

Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖{→}$ по $t$):

$a↖{→}=lim↙{∆t→0}{∆υ↖{→}}/{∆t}=υ↖{→}_t’$

Составляющие $a↖{→} (а_х, а_у, а_z)$ равны соответственно:

$a_x=υ_x’;a_y=υ_y’;a_z=υ_z’$

Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории.2}$

При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.

Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с² и называют «метр на секунду в квадрате».

Равномерное прямолинейное движение

Движение точки называется равномерным, если за любые равные промежутки времени она проходит равные пути.

Например, если автомобиль за каждую четверть часа (15 мин) проходит 20 км, за каждые полчаса (30 мин) – 40 км, за каждый час (60 мин) – 80 км и т. д., то такое движение считается равномерным. При равномерном движении численная величина (модуль) скорости точки $υ$ – величина постоянная:

$υ=|υ↖{→}|=const$

Равномерное движение может происходить как по криволинейной, так и по прямолинейной траектории.

Закон равномерного движения точки описывается уравнением:

$s=s_0+υt$

где $s$ – расстояние, измеренное вдоль дуги траектории, от некоторой точки на траектории, принятой за начало отсчета; $t$ – время точки в пути; $s_0$ – значение $s$ в начальный момент времени $t=0$.

Путь, пройденный точкой за время $t$, определяется слагаемым $υt$.

Равномерное прямолинейное движение – это движение, при котором тело перемещается с постоянной по модулю и направлению скоростью:

$υ↖{→}=const$

Скорость равномерного прямолинейного движения — величина постоянная и может быть определена как отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло:

$υ↖{→}={∆r↖{→}}/{∆t}$

Модуль этой скорости

$υ={|∆r↖{→}|}/{∆t}$

по смыслу есть расстояние $s=|∆r↖{→}|$, пройденное точкой за время $∆t$.

Скорость тела при равномерном прямолинейном движении — это величина, равная отношению пути $s$ ко времени, за которое этот путь пройден:

$υ={s}/{t}$

Перемещение при прямолинейном равномерном движении (по оси X) можно рассчитать по формуле:

$∆x=υ_xt$

где $υ_x$ — проекция скорости на ось X. Отсюда закон прямолинейного равномерного движения имеет вид:

$x=x_0+υ_xt$

Если в начальный момент времени $x_0=0$, то

$x=υ_xt$

График зависимости скорости от времени — прямая, параллельная оси абсцисс, а пройденный путь — это площадь под этой прямой.

График зависимости пути от времени — прямая линия, угол наклона которой к оси времени $Ot$ тем больше, чем больше скорость равномерного движения. Тангенс этого угла равен скорости.

Урок физики по теме “Расчет пути и времени движения”. 7-й класс

Ключевые слова: скорость, время, расстояние, расчет пути, расчет времени движения

(Презентация, слайд 1)

Цели урока: научить учеников вычислять путь, пройденный телом при равномерном движении и время движения; повышать интерес к физике, как науке об окружающем нас мире (слайд 2)

ХОД УРОКА

I. Повторение (слайд 3)

• Что называют движением?
• Какие виды движения вы знаете?
• Что понимают под скоростью?
• Как вычислить скорость?
• В каких величинах измеряется скорость?

Проверка упр.4(2,4).

– Ребята, а какие вы знаете пословицы о скорости?

Ответы учеников:

–  Долго рассуждай, да скоро делай!
–  Семеро одного не ждут.
–  Большой меньшого не дожидается.
–  Под гору вскачь, а на гору хоть плачь.
–  Тише едешь, дальше будешь. 
–  Делу – время, потехе – час.

II. Изучение

1. Прямолинейное равномерное движение (слайд 4). [4]
2. Так как V = S/t, то S = V · t, а также t = S/V   (слайд 5).
3. Схема для запоминания формул расчета скорости, времени, пути:

Рис.1

4. Графики скорости и пути равномерного движения: (слайд 7)

Скорость – величина векторная (слайд 6) [4], поэтому она характеризуется не только модулем, но и направлением. В зависимости от выбранного положительным направления скорость может быть постоянной по величине, но положительной (если движение происходит по выбранному как положительное направлению) или отрицательной по знаку (если движение происходит противоположно выбранному направлению)

А) Графики скорости равномерного движения:

Рис. 2

Б) График пути равномерного движения:

Рис. 3

5. Вычисление пути и времени неравномерного движения: (слайд 8)

Vср = S / t, где S – весь пройденный телом путь, а t – все время движения.

Формулы для вычисления пути и времени будут иметь тот же вид: S = Vср · t, а также t = S / Vср, но в расчет берут среднюю скорость движения.

Если в течение рассматриваемого промежутка времени направление движения не менялось, то средняя скорость перемещения равняется средней скорости в пути, в том случае, когда движение происходило в сторону возрастающих расстояний, или равняется отрицательно взятой средней скорости в пути, если движение совершалось в сторону убывающих расстояний.

III. Закрепление

1. Обсуждение вопросов к п.16.

2. Решение задач: (слайды 9-11)

1)  Упр. 5(2):

На велосипеде без особого напряжения можно ехать со скоростью 3 м/c. На какое расстояние можно уехать за 1,5 часа?

Дано V = 3 м/с t = 1,5 ч Найти: S

СИ 5400с

Решение S = V·t    S = 3м/c· 5400 с = 16200 м = 16,2 км Ответ: 16,2 км

2)  Упр. 5(3):

На рисунке 38 показан график зависимости пути равномерного движения от времени. Оs – ось пройденных путей, Оt – ось времени. По этому графику найдите, чему равен путь, пройденный телом за 2 часа. Затем рассчитайте скорость тела.

Дано t = 2ч S = 200 км Найти: V

Решение V = S/t V = 200 км/2 ч = 100 км/ч Ответ: 100 км/ч

3)  Упр. 5(4):

График зависимости скорости равномерного движения тела от времени представлен на рисунке 39. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за 2ч, 4ч.

Дано V=8 м/с  t1 = 2ч t2 = 4ч Найти: S1 и S2

СИ 7200с 14400с

Решение S = V·t   S1 = 8м/с 7200с = 57500м = 57,6 км. S2 = 8м/с 14400с = 115200м = 115,2 км Ответ: 57,6км и 115,2 км

IV. Самостоятельное решение задач с последующим обсуждением полученных результатов (слайды 12-14).

а) Это интересно:

1. Самый быстрый зверь на Земле = гепард. Эта стройная пятнистая кошка на длиннющих ногах развивает скорость 110 км/ч. Но бежит недалеко. Если сразу не догонит жертву, тут же возвращается в засаду. Какое расстояние пробегает гепард за 5 секунд? (153 м).   [2]

2. Несмотря на маленькие размеры колибри способны пролететь значительные расстояния. Например, рубиноголовая колибри весной и осенью перелетают Мексиканский залив, преодолевая без остановки примерно 900 км со скоростью 40 км/ч. При порхающем полете крылья колибри движутся со скоростью 3000-4800 взмахов в минуту. Определите время перелета колибри через Мексиканский залив.     (81000с = 22ч.30мин).   [2]

3. Самыми быстрокрылыми считаются ласточки и стрижи. Скорость их полета до 150 км/ч. Какое расстояние пролетают эти птицы за минуту? (2500м). [2]

б)   Смешинки (слайды16-17):

1.  Двигаясь равномерно и нигде не задерживаясь, мелкий отличник Олег добрался из дома до школы за 7 мин.  Его соседка крупная троечница Оля тоже двигалась равномерно, также не задерживалась и добралась до школы за 57 мин. Чем отличался стремительный и целеустремленный бег в школу отличника Олега Хлопушина от тихой и печальной поступи троечницы Оли Ромашкиной?    [3]

2.  Печальный дядя Боря несет из магазина домой авоську с мелкими куриными яйцами. Через равные промежутки времени яйца из авоськи выпадают на землю и разбиваются. Можно ли сказать, что печальный дядя Боря движется равномерно, если коты, бегущие за ним, находят яйца на равных расстояниях одно за другим? [3]

V. Подведение итогов урока, выставление оценок

VI. Рефлексия

– Что нового вы сегодня узнали на уроке?
– Что вам больше всего понравилось?

VII. Домашнее задание (слайд 18)

П.16, упр.5(4,5), придумать и решить две задачи на расчет пути и времени равномерного движения. Постарайтесь сделать их оригинальными.

Использованные ресурсы:

1. А.В.Перышкин. Физика – 7ласс «Дрофа», 2006год.
2. А.М.Семке. «Физика. Занимательные материалы к урокам. 7 класс.» Москва, «НЦ ЭРФС» 2006г
3. Г.Остер. Физика задачник, Москва, «Росмэн»,1995г
4. Физика. Библиотека наглядных пособий. 7-11 кл. ООО «1С», 2004-2011, диск.
5. Интернет ресурсы.

Прямолинейное равномерное движение | Объединение учителей Санкт-Петербурга

ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
Прямолинейное движение– траектория представляет собой прямую линию. Прямолинейным равномерным движением называется механическое движение, при котором тело за любые равные промежутки времени t1 = t2 = t3 = … совершает одинаковые перемещения
Следовательно:   – эта величина является характеристикой движения.
– скорость прямолинейного равномерного движения.
Скорость прямолинейного равномерного движения – это векторная физическая величина, численно равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Скорость показывает, какое перемещение совершает тело за единицу времени, двигаясь прямолинейно и равномерно. Например, если модуль скорости равна 5 м/с, это значит, что за каждую секунду своего движения тело, двигаясь  прямолинейно и равномерно, перемещается на 5 м.
Для описания прямолинейного равномерного одного тела достаточно одной оси координат. По правилам действия с векторами  Из чертежа видим:   , где – проекция вектора скорости на координатную ось x.
Решение основной задачи механики для прямолинейного равномерного движения:
Следовательно: Если движение сонаправлено с осью координат, то. Если движение против оси координат, то .
Графическое представление равномерного прямолинейного движения
1.График зависимости проекции скорости от времени   Площадь под графиком скорости численно равна перемещению. (Справедливо для любого движения)
2. График зависимости проекции перемещения от времени    и  – движение сонаправлено с осью,  – движение против оси.
3. График зависимости координаты от времени.   1, 2, 4 – движение сонаправлено с осью, 3, 5 – движение против оси.

Программа вступительных испытаний “Физика” | Приемная комиссия УГНТУ

Кафедра, обеспечивающая подготовку программы: кафедра физики.

1 Особенности проведения вступительного испытания по физике, проводимого УГНТУ самостоятельно.

 

Результат вступительного испытания оценивается по 100-бальной шкале.

Время проведения вступительного испытания – 120 мин.

Количество заданий в билете – 16.

 

2 Перечень вопросов для подготовки поступающих к сдаче вступительного испытания по физике, проводимого УГНТУ самостоятельно.

 

2.1 Раздел 1 «Механика »

2.1.1 Тема 1 « Кинематика »

Перечень вопросов:

1. Механическое движение и его виды.

2. Относительность механического движения.

3. Скорость, ускорение.

4. Равномерное движение. Прямолинейное равноускоренное движение.

5. Свободное падение (ускорение свободного падения).

6. Движение по окружности с постоянной по модулю скоростью. Центростремительное ускорение.

2.1.2 Тема 2 «Динамика»

Перечень вопросов:

1. Инерциальные системы отсчета. Первый закон Ньютона.

2. Принцип относительности Галилея.

3. Масса тела. Плотность вещества.

4. Сила. Принцип суперпозиции сил.

5. Второй закон Ньютона. Третий закон Ньютона.

6. Закон всемирного тяготения. Искусственные спутники Земли.

7. Сила тяжести. Вес и невесомость.

8. Сила упругости. Закон Гука. Сила трения. Давление.

2.1.3 Тема 3 «Статика»

Перечень вопросов:

1. Момент силы. Условия равновесия твердого тела.

2. Давление жидкости. Закон Паскаля.

3. Закон Архимеда. Условия плавания тел.

2.1.4 Тема 4 «Законы сохранения в механике»

Перечень вопросов:

1. Импульс тела. Импульс системы тел. Закон сохранения импульса.

2. Работа силы. Мощность. Работа как мера изменения энергии.

3. Кинетическая энергия. Потенциальная энергия.

4. Закон сохранения механической энергии.

2.1.5 Тема 5 «Механические колебания и волны»

Перечень вопросов:

1. Гармонические колебания.

2. Амплитуда и фаза колебаний. Период и частота колебаний.

3. Свободные колебания (математический и пружинный маятники).

4. Вынужденные колебания. Резонанс.

5. Длина волны. Звук.

2.2 Раздел 2 «Молекулярная физика. Термодинамика»

2.2.1 Тема 1 «Молекулярная физика»

Перечень вопросов:

1. Модели строения газов, жидкостей и твердых тел.

2. Тепловое движение атомов и молекул вещества. Броуновское движение. Диффузия.

3. Экспериментальные доказательства атомистической теории. Взаимодействие частиц вещества.

4. Модель идеального газа. Связь между давлением и средней кинетической энергией теплового движения молекул идеального газа.

5. Абсолютная температура. Связь температуры газа со средней кинетической энергией его частиц.

6. Уравнение состояния идеального газа для давления. Уравнение Клапейрона – Менделеева.

7. Изопроцессы: изотермический, изохорный, изобарный, адиабатный процессы.

8. Насыщенный и ненасыщенный пары. Влажность воздуха.

9. Изменение агрегатных состояний вещества: испарение и конденсация, кипение жидкости.

10. Изменение агрегатных состояний вещества: плавление и кристаллизация.

11. Изменение энергии в фазовых переходах.

2.2.2 Тема 2 «Термодинамика»

Перечень вопросов:

1. Внутренняя энергия.

2. Тепловое равновесие. Теплопередача. Количество теплоты. Удельная теплоемкость вещества, удельная теплота парообразования, удельная теплота плавления, удельная теплота сгорания топлива. Уравнение теплового баланса.

3. Работа в термодинамике.

4. Первый закон термодинамики.

5. Второй закон термодинамики.

6. КПД тепловой машины. Принципы действия тепловых машин. Цикл Карно.

2.3 Раздел 3 «Электродинамика»

2.3.1 Тема 1 «Электрическое поле»

Перечень вопросов:

1. Электризация тел. Взаимодействие зарядов. Два вида заряда. Закон сохранения заряда.

2. Закон Кулона.

3. Действие электрического поля на электрические заряды.

4. Напряженность электрического поля. Принцип суперпозиции электрических полей.

5. Потенциальность электростатического поля. Потенциал электрического поля. Разность потенциалов.

6. Проводники в электростатическом поле.

7. Диэлектрики в электростатическом поле.

8. Электрическая емкость. Конденсатор. Соединение конденсаторов.

9. Энергия заряженного конденсатора.

2.3.2 Тема 2 «Законы постоянного тока»

Перечень вопросов:

1. Постоянный электрический ток. Сила тока. Напряжение.

2. Закон Ома для участка цепи.

3. Электрическое сопротивление. Удельное сопротивление вещества.

4. Электродвижущая сила. Внутреннее сопротивление источника тока.

5. Закон Ома для полной электрической цепи.

6. Параллельное и последовательное соединение проводников. Смешанное соединение проводников.

7. Работа электрического тока. Закон Джоуля-Ленца. Мощность электрического тока.

8. Носители свободных электрических зарядов в металлах, жидкостях и газах.

9. Полупроводники. Собственная и примесная проводимость полупроводников. Полупроводниковый диод.

2.3.3 Тема 3 «Магнитное поле»

Перечень вопросов:

1. Взаимодействие магнитов. Магнитное поле. Вектор магнитной индукции. Принцип суперпозиции магнитных полей.

2. Сила Ампера и сила Лоренца. Движение заряженной частицы в однородном магнитном поле.

2.3.4 Тема 4 «Электромагнитная индукция»

Перечень вопросов:

1. Явление электромагнитной индукции. Магнитный поток.

2. Закон электромагнитной индукции Фарадея. Правило Ленца. ЭДС индукции в проводнике, движущемся в магнитном поле.

3. Самоиндукция. Индуктивность.

4. Энергия магнитного поля катушки с током.

2.3.5 Тема 5 «Электромагнитные колебания и волны»

Перечень вопросов:

1. Свободные электромагнитные колебания. Колебательный контур.

2. Закон сохранения энергии в колебательном контуре.

3. Вынужденные электромагнитные колебания. Резонанс.

4. Переменный ток. Производство, передача и потребление электрической энергии.

5. Электромагнитное поле.

6. Свойства электромагнитных волн.

7. Различные виды электромагнитных излучений и их применение.

2.3.6 Тема 6 «Оптика»

Перечень вопросов:

1. Прямолинейное распространение света.

2. Закон отражения света. Построение изображений в плоском зеркале.

3. Закон преломления света. Полное внутреннее отражение.

4. Линзы. Оптическая сила линзы. Формула тонкой линзы. Построение изображений в линзах.

5. Оптические приборы. Глаз как оптическая система.

6. Интерференция света.

7. Дифракция света. Дифракционная решетка.

8. Дисперсия света.

2.4 Раздел «Основы специальной теории относительности»

Перечень вопросов:

1. Инвариантность скорости света. Принцип относительности Эйнштейна.

2. Энергия покоя. Энергия свободной частицы, связь массы и энергии.

3. Релятивистский импульс.

2.5 Раздел «Квантовая физика »

2.5.1 Тема 1 «Корпускулярно-волновой дуализм»

Перечень вопросов:

1. Гипотеза М.Планка о квантах. Формула Планка.

2. Фотоны. Энергия фотона. Импульс фотона.

3. Фотоэффект. Опыты А.Г.Столетова. Уравнение Эйнштейна для фотоэффекта.

4. Гипотеза де Бройля о волновых свойствах частиц. Корпускулярно-волновой дуализм. Дифракция электронов.

5. Давление света на полностью отражающую и полностью поглощающую поверхность.

2.5.2 Тема 2 «Физика атома»

Перечень вопросов:

1. Планетарная модель атома. Постулаты Бора. Линейчатые спектры.

2. Лазер.

2.5.3 Тема 3 «Физика атомного ядра»

Перечень вопросов:

1. Нуклонная модель ядра. Заряд ядра. Массовое число ядра.

2. Энергия связи нуклонов в ядре. Ядерные силы.

3. Радиоактивность. Альфа-распад. Бета – распад. Гамма-излучение.

4. Закон радиоактивного распада.

5. Ядерные реакции. Деление и синтез ядер.

 

3  Учебно-методическое и информационное обеспечение дисциплин для подготовки абитуриентов

 

Основная литература

1. Физика. 9 класс.: Учебник. Базовый уровень/А.В.Перышкин, Е.М.Гутник. – М.:Дрофа, 2014.- 317 с.: ил.

2. Физика. 10 класс.: Учебник. Базовый уровень/ Г.Я.Мякишев. – М.: Просвещение, 2014.- 416 с.: ил.

3. Физика. 11 класс.: Учебник. Базовый уровень/ Н.С.Пурышева, Н.Е.Важеевская, Д.А.Исаев. – М.: Дрофа, 2014.- 304 с.: ил.

Дополнительная литература

1. Физика. Подготовка к ЕГЭ. Вступительные испытания.: Учебное пособие/ О.Ф.Кабардин, С.И.Кабардина, В.А.Орлов и др.- М.: Дрофа, 2011.- 480 с.: ил.

Интернет-ресурсы

Движение в двух измерениях | Безграничная физика

Постоянная скорость

Объект, движущийся с постоянной скоростью, должен иметь постоянную скорость в постоянном направлении.

Цели обучения

Изучите термины для постоянной скорости и их применимость к ускорению

Основные выводы

Ключевые моменты

• Постоянная скорость означает, что движущийся объект движется по прямой с постоянной скоростью.
• Эта строка может быть представлена ​​алгебраически как: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] представляет положение объекта в [latex] \ text {t} = 0 [/ latex], а наклон линии указывает скорость объекта.
• Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.

Ключевые термины

• постоянная скорость : Движение, которое не меняется ни по скорости, ни по направлению.

Движение с постоянной скоростью – одна из простейших форм движения. Этот тип движения возникает, когда объект движется (или скользит) в присутствии небольшого или незначительного трения, подобно тому, как хоккейная шайба скользит по льду. Чтобы иметь постоянную скорость, объект должен иметь постоянную скорость в постоянном направлении. Постоянное направление заставляет объект двигаться по прямой траектории.

Второй закон Ньютона ([latex] \ text {F} = \ text {ma} [/ latex]) предполагает, что когда к объекту прикладывается сила, объект испытывает ускорение.Если ускорение равно 0, объект не должен подвергаться воздействию внешних сил. Математически это можно представить следующим образом:

[латекс] \ text {a} = \ frac {\ text {dv}} {\ text {dt}} = 0 ~ \ Rightarrow ~ \ text {v} = \ text {const} [/ latex].

Если объект движется с постоянной скоростью, график зависимости расстояния от времени ([latex] \ text {x} [/ latex] vs. [latex] \ text {t} [/ latex]) показывает такое же изменение положение по каждому интервалу времени. Поэтому движение объекта с постоянной скоростью представлено прямой линией: [latex] \ text {x} = \ text {x} _0 + \ text {vt} [/ latex], где [latex] \ text {x} _0 [/ latex] – это смещение, когда [latex] \ text {t} = 0 [/ latex] (или в точке пересечения оси Y).

Движение с постоянной скоростью : Когда объект движется с постоянной скоростью, он не меняет ни направления, ни скорости, и поэтому отображается как прямая линия на графике как расстояние во времени.

Вы также можете получить скорость объекта, если знаете его след во времени. Имея график, как в, мы можем вычислить скорость по изменению расстояния с течением времени. Графически скорость можно интерпретировать как наклон линии.Скорость может быть положительной или отрицательной и указывается знаком нашего наклона. Это говорит нам, в каком направлении движется объект.

Постоянное ускорение

Анализ двумерного движения снаряда выполняется путем разбиения его на два движения: по горизонтальной и вертикальной осям.

Цели обучения

Анализировать двумерное движение снаряда по горизонтальной и вертикальной осям

Основные выводы

Ключевые моменты

• Постоянное ускорение при движении в двух измерениях обычно происходит по образцу снаряда.
• Движение снаряда – это движение объекта, брошенного или выброшенного в воздух, с учетом только (вертикального) ускорения силы тяжести.
• Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.

Ключевые термины

• кинематика : движение или кинематика или относящиеся к ней

Движение снаряда – это движение объекта, брошенного или выброшенного в воздух, подверженное только силе тяжести.Объект называется снарядом, а его путь называется его траекторией. Движение падающих предметов – это простой одномерный тип движения снаряда, при котором нет горизонтального движения. В двумерном движении снаряда, таком как движение футбольного мяча или другого брошенного объекта, есть как вертикальная, так и горизонтальная составляющие движения.

Движение снаряда : Бросок камня или удар ногой по мячу, как правило, создает образец движения снаряда, который имеет как вертикальную, так и горизонтальную составляющую.

Самый важный факт, о котором следует помнить, это то, что движения по перпендикулярным осям независимы и поэтому могут быть проанализированы отдельно. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения, одно по горизонтальной оси, а другое по вертикали. Чтобы описать движение, мы должны иметь дело со скоростью и ускорением, а также со смещением.

Мы будем считать, что все силы, кроме силы тяжести (например, сопротивление воздуха и трение), незначительны.2} [/ latex] (мы предполагаем, что движение происходит на достаточно малых высотах у поверхности земли, чтобы ускорение свободного падения было постоянным). Поскольку ускорение свободного падения происходит в вертикальном направлении только , [latex] \ text {a} _ \ text {x} = 0 [/ latex]. Таким образом, можно использовать кинематические уравнения, описывающие движение по направлениям [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] соответственно:

[латекс] \ text {x} = \ text {x} _0 + \ text {v} _ \ text {x} \ text {t} [/ latex]

[латекс] \ text {v} _ \ text {y} = \ text {v} _ {0 \ text {y}} + \ text {a} _ \ text {y} \ text {t} [/ latex ]

[латекс] \ text {y} = \ text {y} _0 + \ text {v} _ {0 \ text {y}} \ text {t} + \ frac {1} {2} \ text {a} _ \ text {y} \ text {t} ^ 2 [/ latex]

[латекс] \ text {v} _ \ text {y} ^ 2 = \ text {v} _ {0 \ text {y}} ^ 2 + 2 \ text {a} _ \ text {y} (\ text {y} – \ text {y} _0) [/ latex]

Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям.Горизонтальное движение простое, потому что [latex] \ text {a} _ \ text {x} = 0 [/ latex] и [latex] \ text {v} _ \ text {x} [/ latex], таким образом, является постоянным. Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта; в самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. Движения [latex] \ text {x} [/ latex] и [latex] \ text {y} [/ latex] можно рекомбинировать для получения общей скорости в любой заданной точке траектории.

Кинематика в двух измерениях

Представьте себе шар, катящийся по горизонтальной поверхности, освещенный стробоскопическим светом. На рисунке (а) показано положение мяча через равные промежутки времени по пунктирной траектории. Случай 1 проиллюстрирован позициями с 1 по 3; величина и направление скорости не меняются (изображения расположены равномерно и по прямой линии), следовательно, ускорение отсутствует. Случай 2 указан для позиций с 3 по 5; мяч имеет постоянную скорость, но меняет направление, и поэтому существует ускорение.На рисунке (b) показано вычитание v ₃ и v ₄ и результирующее ускорение к центру дуги. Случай 3 встречается с 5 по 7 позиции; направление скорости постоянно, но величина меняется. Ускорение на этом участке пути соответствует направлению движения. Мяч изгибается из положения 7 в положение 9, показывая случай 4; скорость меняет как направление, так и величину. В этом случае ускорение направлено почти вверх между 7 и 8 и имеет компонент к центру дуги из-за изменения направления скорости и компонент вдоль пути из-за изменения величины скорости.

Рисунок 7

(a) Путь шара по столу. (b) Ускорение между точками 3 и 4.

Любой, кто наблюдал подброшенный объект – например, бейсбольный мяч в полете, – заметил движение снаряда . Для анализа этого распространенного типа движения делаются три основных предположения: (1) ускорение свободного падения постоянно и направлено вниз, (2) влияние сопротивления воздуха незначительно, и (3) поверхность земли неподвижна. плоскости (то есть кривизна земной поверхности и вращение земли незначительны).

Чтобы проанализировать движение, разделите двухмерное движение на вертикальные и горизонтальные составляющие. По вертикали объект испытывает постоянное ускорение силы тяжести. По горизонтали объект не испытывает ускорения и, следовательно, поддерживает постоянную скорость. Эта скорость проиллюстрирована на рисунке, где компоненты скорости изменяются в направлении y ; однако все они имеют одинаковую длину в направлении x (постоянное значение). Обратите внимание, что вектор скорости изменяется со временем из-за того, что вертикальная составляющая меняется.

Рисунок 8

Движение снаряда.

В этом примере частица покидает начало координат с начальной скоростью ( v _o ) вверх под углом θ _o . Исходные компоненты скорости x и y задаются формулами v _x0 = v _o и v _y0 = v _o sin θ _o .

Когда движения разделены на компоненты, величины в направлениях x и y могут быть проанализированы с помощью одномерных уравнений движения, обозначенных индексами для каждого направления: для горизонтального направления v _x = v _x0 и x = v _x0 t ; для вертикального направления v _y = v _y0 – gt и y = v _y0 – (1/2) gt ² , где x и y представляют расстояния в горизонтальном и вертикальном направлениях соответственно, а ускорение свободного падения ( g ) равно 9.8 м / с ² . (Отрицательный знак уже включен в уравнения.) Если объект стреляет под углом, составляющая y начальной скорости будет отрицательной. Скорость снаряда в любой момент времени может быть вычислена по компонентам в то время по теореме Пифагора, а направление может быть найдено по обратной тангенсе соотношений компонентов:

Другая информация полезна при решении проблем со снарядами. Рассмотрим пример, показанный на рисунке, где снаряд выстреливается под углом от уровня земли и возвращается на тот же уровень.Время, за которое снаряд достигнет земли из своей наивысшей точки, равно времени падения свободно падающего объекта, который падает прямо с той же высоты. Это равенство времени связано с тем, что горизонтальная составляющая начальной скорости снаряда влияет на то, как далеко снаряд летит по горизонтали, но не на время полета. Пути полета снаряда параболические и, следовательно, симметричные. Также в этом случае объект достигает вершины своего подъема за половину общего времени (T) полета.В верхней части подъема вертикальная скорость равна нулю. (Ускорение всегда составляет g , даже на пике полета.) Эти факты можно использовать для получения дальности снаряда или расстояния, пройденного по горизонтали. На максимальной высоте v _y = 0 и t = T /2; следовательно, уравнение скорости в вертикальном направлении принимает вид 0 = v _o sin θ – g T /2 или решение для T , T = (2 v ₀ sin θ) / г .

Подстановка в уравнение горизонтального расстояния дает R = ( v _o cos θ) T . Подставьте T в уравнение диапазона и используйте тождество тригонометрии sin 2θ = 2 sin θ cos θ, чтобы получить выражение для диапазона в терминах начальной скорости и угла движения, R = ( v _o ² / г ) sin 2θ. Как указано в этом выражении, максимальный диапазон возникает при θ = 45 градусов, потому что при этом значении θ sin 2θ имеет максимальное значение 1.На рисунке показаны траектории снарядов, выпущенных с одинаковой начальной скоростью под разными углами наклона.

Рисунок 9

Дальность выстрела снарядов под разными углами.

Для равномерного движения объекта по горизонтальному кругу радиусом (R) , постоянная скорость определяется как v = 2π R / T , что представляет собой расстояние одного оборота, деленное на время для одна революция.Время на один оборот (T) определяется как период . За один оборот головка вектора скорости за один период очерчивает окружность 2π v ; таким образом, величина ускорения составляет a = 2π v / T . Объедините эти два уравнения, чтобы получить два дополнительных соотношения в других переменных: a = v ² / R и a = (4π ² / T ² ) R .

Вектор смещения направлен из центра круга движения. Вектор скорости касается пути. Вектор ускорения, направленный к центру круга, называется центростремительным ускорением . На рисунке показаны векторы смещения, скорости и ускорения в различных положениях, когда масса движется по кругу в горизонтальной плоскости без трения.

Рисунок 10

Равномерное круговое движение.

Что такое движение и типы движения

Что такое движение

Когда тело не меняет своего положения со временем, мы можем сказать, что тело находится в состоянии покоя, тогда как если тело меняет свое положение со временем, говорят, что оно находится в движении .

Анализ линейного движения

• Линейное движение – это движение по прямой.
• Нелинейное движение – это движение, которое не находится по прямой линии.
• При анализе линейного и нелинейного движения расстояние, смещение, скорость, скорость, ускорение и замедление являются некоторыми часто встречающимися физическими величинами.

Термины, используемые для определения движения

1. Расстояние и перемещение
2. Скорость и скорость
3. Разгон

Объект называется точечным, если он меняет свое положение на расстояния, намного превышающие его размер. Точка или некоторый неподвижный объект, относительно которого тело непрерывно меняет свое положение в состоянии движения, называется исходной или опорной точкой.

Когда мы говорим, что объект движется, это всегда относительно другого объекта. Например, когда мы говорим, что автомобиль движется по дороге, он движется относительно деревьев и столбов на дороге, которые «неподвижны». Когда вы говорите, что отдыхаете или не двигаетесь во время чтения книги, это касается вашего стула или стола. Когда объект перемещается, его положение (относительно другого объекта) изменяется со временем. Возьмем, к примеру, автомобиль, удаляющийся от здания.

Когда автомобиль находится в положении A, расстояние между автомобилем и зданием очень мало.По мере того, как автомобиль удаляется от здания (позиция B), его расстояние от здания увеличивается. Другими словами, когда автомобиль движется, его положение по отношению к зданию меняется со временем. Считается, что объект находится в движении, если его положение (относительно другого объекта) изменяется со временем.

Типы движения

Существуют разные типы движения: поступательное, вращательное, периодическое и непериодическое.

Поступательное движение
Тип движения, при котором все части объекта перемещаются на одинаковое расстояние за заданное время, называется поступательным движением.Примеры: автомобили, движущиеся по дороге, ребенок, сбивающий птицу, летящую в небе. Поступательное движение бывает двух типов: прямолинейное и криволинейное. В таблице показаны различия между прямолинейными и криволинейными движениями.

Прямолинейное движение	Криволинейное движение
1. Когда объект в поступательном движении движется по прямой линии, говорят, что он находится в прямолинейном движении.	1. Когда объект в поступательном движении движется по криволинейной траектории, говорят, что он находится в криволинейном движении.
2. Примерами являются автомобиль, движущийся по прямой дороге, и поезд, движущийся по прямой дороге.	2. Примеры: камень, подброшенный в воздух под углом, и разворачивающаяся машина.

Примеры поступательного движения: ребенок спускается с горки.

Вращательное движение
Когда объект движется вокруг оси и различные его части перемещаются на разные расстояния в заданный интервал времени, говорят, что он находится во вращательном движении.Примерами объектов, совершающих вращательное движение, являются лопасти вращающегося вентилятора, карусели, лопасти ветряной мельницы. Когда объект совершает вращательное движение, все его части не перемещаются на одинаковое расстояние за заданный интервал времени. Например, внешняя часть лопастей ветряной мельницы перемещается намного больше, чем часть, расположенная ближе к центру.

Карусель показывает вращательное движение:

Периодическое движение
Тип движения, который повторяется через равные промежутки времени, называется периодическим движением.Примерами объектов, совершающих периодическое движение, являются движение маятника вперед и назад, Земля (вращающаяся вокруг своей оси), стрелки часов, лопасти вращающегося электрического вентилятора и щипковая струна гитары.

Объекты, совершающие периодическое движение

Непериодическое движение
Движение, которое не повторяется через равные промежутки времени, или движение, которое вообще не повторяется, называется непериодическим движением. Примеры непериодического движения: машина, едущая по дороге, птица, плывущая по небу, и дети, играющие в парке.В повседневной жизни мы наблюдаем более одного типа движения, например

• Птицы, парящие по небу (поступательные и непериодические).
• Вращение Земли вокруг своей оси (вращательное и периодическое).

Согласно Директиве

1. Одномерное движение – это движение частицы, движущейся по прямой линии.
2. Двумерное движение Частица, движущаяся по криволинейной траектории в плоскости, имеет
   двумерное движение.
3. Трехмерное движение Частица, беспорядочно перемещающаяся в пространстве, имеет трехмерное движение.

Согласно State of Motion

1. Равномерное движение: Тело считается находящимся в состоянии равномерного движения, если оно проходит равные расстояния за равные промежутки времени. Если график временных расстояний представляет собой прямую линию, движение называется равномерным.
2. Неравномерное движение: Тело движется неравномерно, если оно преодолевает неравные расстояния за равные промежутки времени.Бывший. свободно падающее тело.
   Время – график расстояний для тела с неравномерным движением представляет собой кривую линию.

Анализ графиков движения

Смещение – Временные графики:

1. На рисунке показана черепаха, движущаяся с медленной и постоянной скоростью, в то время как заяц крепко спал с момента времени t = 0 до 8 с.
2. Мы можем представить ситуацию с помощью графиков смещения-времени.
   (a) График на рисунке (a) показывает смещение черепахи от стартовой линии с момента времени t = 0 до 8 с.
   (b) График на Рисунке (b) показывает, что за время от t = 0 до 8 с заяц смещался на 0,5 м от стартовой линии. В течение 8 секунд он вообще не двигался, так как спал.
3. Градиент s-t графика объекта дает скорость изменения смещения, которая является скоростью объекта.
   
4. Таблица иллюстрирует некоторые графики смещения-времени.
   

Прямая линия, наклоненная к оси времени на графике s-t, представляет постоянную скорость.

На графике s-t прямая линия, наклоненная к оси времени под углом более 90 °, показывает отрицательную скорость

Тело с ускоренным движением

Тело с замедленным движением

График скорости-времени:

1. Градиенты графиков s-t для черепахи и зайца составляют 0,25 м с ^-1 и 0 м с ^-1 соответственно.
2. Графики v-t на рисунке представляют ситуацию.
   
   (a) Градиент графика v-t – это скорость изменения скорости, которая представляет собой ускорение объекта .
   (b) Область под графиком дает смещение объекта.
3. В таблице показаны некоторые графики зависимости скорости от времени.
   

Для тела с постоянной скоростью или нулевым ускорением.

Тело движется с постоянным замедлением и его начальная скорость не равна нулю.

Тело ускоряется, начальная скорость равна нулю.

Кузов замедленный

График времени ускорения:
Ускорение постоянно

Ускорение увеличивается и составляет + ve

Ускорение уменьшается и составляет –ve

Пример 1. Мальчик катался по прямой, проходящей через две точки P и Q. Его время t и смещение s от точки P показаны на рисунке.

Из представленной информации нарисуйте график
(a) s-t
(b) график v-t
Решение:

Пример 2. Азлан ехал на велосипеде по прямой дороге. График на рисунке (b) иллюстрирует его движение.

(a) Рассчитайте скорость Азлана от t = 0 до 10 с.
(b) Опишите, что произошло с Азланом от t = 10 до 20 с.
(c) Рассчитайте смещение Азлана при t = 25 с.
(d) Где был Азлан при t = 35 с?
Решение:
(a) См. Часть AB графика.
Скорость = Градиент графика
= 50/10 = 5 м с ^-1
(b) См. Часть BC графика. Наклон графика равен 0. Это означает, что Азлан находился в состоянии покоя от t = 10 до 20 с.
(c) См. Точку D на графике. При
t = 25 с водоизмещение Азлана s = 14 м.
(d) См. Точку E графика.При
t = 35 с водоизмещение Азлана s = 0 м.
Это означает, что Азлан вернулся на исходную позицию.

Пример 3. На рисунке показан огромный кран, поднимающий стальную балку с земли. График v-t показывает движение балки за первые 9 с.

(a) Кратко опишите движение балки, обозначенного AB, BC, CD и DE.
(b) Рассчитайте начальное и конечное ускорение балки.
(c) Рассчитайте высоту луча от земли через 9 секунд.
Раствор:

Пример 4. График v-t на рисунке показывает движение шахтной тележки по прямой железной дороге.

а) Каково общее расстояние, пройденное минной тележкой?
(b) (i) Где находилась минная тележка при t = 10 с?
(ii) Объясните свой ответ в пункте (b) (i).
Решение:

С t = 0 с до 5 с шахтная тележка переместилась на 15 м вперед (положительная скорость).
С t = 5 до 10 с минная тележка переместилась на 15 м назад (отрицательная скорость).
Таким образом, вагонетка вернулась в исходную точку.

Уравнения движения с постоянной скоростью

Движение с постоянной скоростью , также известное как равномерное прямолинейное движение (urm) , это движение с постоянной скоростью , т. Е. Траектория является прямой, а скорость равна постоянный. В этом разделе мы собираемся объяснить:

Определение движения с постоянной скоростью

Хотя обнаружение прямолинейного равномерного движения или движения с постоянной скоростью в природе встречается довольно редко, его легче всего изучать, и оно будет полезно при изучении других, более сложных движений.Равномерное прямолинейное движение имеет следующие свойства:

• Ускорение равно нулю ( a = 0 ), потому что ни величина, ни направление не меняются
• С другой стороны, начальная, средняя и мгновенная скорости всегда имеют одинаковые значения

Тело имеет движение с постоянной скоростью или равномерное прямолинейное движение , когда его траектория является прямой линией и его скорость постоянна .Это означает, что он преодолевает равные расстояния за равное время .

Уравнения движения с постоянной скоростью

Прямолинейное и равномерное движение

Равное время тратится на путешествие на равные расстояния. Средняя скорость постоянна и равна величине скорости.

Уравнения движения с постоянной скоростью :

Где:

• x , x ₀ : Позиция тела в данный момент времени ( x ) и в начальный момент времени ( x ₀ ).Единицей измерения в Международной системе (S.I.) является метр (м)
.
• v , v ₀ : Скорость тела в данный момент времени ( v ) и в начальный момент времени ( v ₀ ). Его единица измерения в Международной системе (S.I.) – метр в секунду (м / с)
.
• a : Разгон кузова. Его единица измерения в Международной системе (S.I.) – метр на секунду в квадрате (м / с ² )

Вывести уравнений равномерного прямолинейного движения u.среднеквадратичное значение следует учитывать, что:

• Средняя скорость совпадает с мгновенной скоростью
• Нет разгона

С этими ограничениями получаем:

vavg = vvavg = ΔxΔt = x-x0t-t0 = ⏟t0 = 0x-x0t → x-x0 = v⋅t → x = x0 + v⋅t

Пример

Два мраморных игрока смотрят друг на друга со своими шариками в руках. Игра состоит из одновременного бросания шариков по прямой линии так, чтобы они ударялись друг о друга.Игроки расположены в 36 метрах друг от друга, и игрок A запускает шарик со скоростью 2 м / с, а игрок B – со скоростью 4 м / с, в равномерном прямолинейном движении. Вычислите расстояние от игрока B, на котором шарики столкнутся.

Физика: поступательное движение | Медицинская онлайн-библиотека Lecturio

---

Изображение: «Движение подразумевает изменение положения, например, в перспективе быстрого выхода со станции Ёнсан». Машиночитаемый автор не предоставлен.Лицензия: CC BY 2.5

.

---

Определение движения

Равномерное поступательное движение

Равномерное поступательное движение – это движение, которое происходит с постоянной скоростью в одном направлении. Это означает, что объект совершает равные перемещения за равные промежутки времени. В данном случае ускорение равно 0. Этот тип движения можно описать следующими терминами:

v ⇒ скорость (м / с)
с ⇒ перемещение (м)
t ⇒ время (с)

Движение с равномерным ускорением

Этот тип движения можно охарактеризовать изменяющейся скоростью.Объект движется быстрее или медленнее, что означает, что ускорение не равно 0 и остается постоянным. Движение с равномерным ускорением можно описать 3 уравнениями :

Время вытеснения

Скорость-время

с (или с ₀ ) ⇒ смещение (м)

a ⇒ ускорение (м / с ² )

т ⇒ время (с)

v ₀ ⇒ скорость (м / с)

Свободное падение

Свободное падение – это движение объекта, при котором сила тяжести является единственной силой, действующей на него.Сила тяжести – постоянный параметр с ускорением a = g = 9,81 м / с. Таким образом, свободное падение относится к движению с равномерным ускорением. После пренебрежения воздушным трением и подъемной силой остаются следующие уравнения:

г = 9,81 м / с

ч ⇒ высота

Равномерное круговое движение

В этом типе движения объект движется по круговой траектории. Поскольку скорость является вектором, ее постоянно меняющиеся направления уравновешивают друг друга. Таким образом, равномерное круговое движение определяется постоянной суммой скоростей или, проще говоря, если автомобиль движется по кругу со скоростью 50 км / ч, ускорение постоянное, но направление постоянно меняется.

ω ⇒ угловая скорость (1 / с)
α ⇒ угловое ускорение (1 / с ² )
n ⇒ скорость вращения (1 / с)
r ⇒ радиус (м)
π ⇒ Pi (приблизительно 3,14)

Периодическое движение

Периодическое движение относится к изменениям в системе или физической переменной на основе фиксированного положения, которое повторяется прибл. или ровно через равные промежутки времени. Его можно описать следующими переменными:

T ⇒ период, измеренный в секундах (с)
f ⇒ частота, измеренный в герцах (Гц)
ω ⇒ угловая скорость (1 / с)

Графики движения

Типы движения, описанные выше, могут быть представлены на следующих графиках.Равномерное линейное движение отображается красным цветом, а движение с равномерным ускорением – зеленым.

График вытеснения-времени

График скорости-времени

График времени разгона

Визуализация кинематики

Определение

Кинематика связана с геометрией движения и, таким образом, является разделом математики. Он начинается с описания геометрии системы с начальными условиями известных значений.Эти значения отображают положение, скорость и / или ускорение различных точек, которые являются частью системы. Кинематика помогает описывать движение точек, тел и групп тел без учета масс объектов или сил, вызывающих движение.

Аспект визуализации

Кинематика может отображаться в виде двухмерных графиков. Сюжеты помогут понять движение объекта во времени. Обычно используются 3 графика: график положения, график скорости и график ускорения.

График положения отображает местоположение объекта по прошествии времени.
График скорости отображает скорость объекта с течением времени.
График ускорения показывает, насколько быстро объект движется с течением времени.

График двумерный, поэтому он содержит ось x и ось y. Ось x представляет время в секундах. Ось Y может представлять любой из 3 элементов выше –: положение (также называемое смещением), скорость и ускорение.

Векторы

Определение

Вектор – это величина, имеющая как величину, так и направление.Эта величина отличается от скалярной величины, которая имеет величину, но не имеет направления. Например, если проверить температуру, результатом будет скалярная величина, поскольку температура не имеет направления. Однако если измерить ветер, это векторная величина. Ветер имеет как величину, так и направление, так как 30 миль в час с запада означает, что величина составляет 30 миль в час, а направление – с запада.

Движение снаряда

Движение снаряда – это форма движения, при которой объект (называемый снарядом) бросается рядом с земной поверхностью, перемещаясь по кривой траектории только под действием силы тяжести.В этом случае сопротивление воздуха считается незначительным. Путь, по которому движется объект, является параболическим, с единственной силой, действующей на него, – это сила тяжести (ускорение), которая, как было указано ранее, равна 9,8 м / сек ² .

Компоненты движения снаряда

Компоненты по оси x и оси y вычисляются по-разному.

По горизонтальной оси (ось x) ускорение равно 0, поскольку нет ни ветра, ни сопротивления воздуха. Скорость по горизонтальной оси будет равна начальной скорости по горизонтальной оси.Пройденное расстояние по горизонтальной оси (смещение) также можно определить на основе пройденного времени. Можно использовать следующие уравнения:

a _x = 0

( _x = ускорение в направлении оси x)

v _x = v _0x

(v _x = скорость в направлении x, v _0x = исходная скорость в направлении x)

x = x ₀ + v _0x т

(x = смещение в направлении x, x ₀ = исходное положение, t = время)

По вертикальной оси (ось y) ускорение равно силе тяжести.Уравнения скорости и смещения будут другими, поскольку ускорение будет влиять на объект по вертикальной оси.

a _y = -g

(a _y = ускорение в направлении y, g = сила тяжести)

v _y = v _oy – g t

(v _y = скорость в направлении y, v _oy = исходная скорость в направлении y, t = время)

y = y _o + v _oy t – ½ g t ²

(y = смещение в направлении y, y ₀ = исходное положение)

Список параметров

т (или т 0 )	Время (с)
v (или v 0 )	Скорость (м / с)
с (или с 0 )	Водоизмещение (м)
и	Ускорение (м / с 2 )
г = 9.81 м / с 2	Ускорение свободного падения (м / с 2 )
ч	Высота (или высота падения)
α	Угловое ускорение
с	Длина дуги или смещение (м)
р	Радиус (м)
n	Скорость вращения (1 / с)
v	Скорость (м / с)
Т	Период, измеряемый в секундах
из	Частота, измеренная в герцах (Гц)
ω	Угловая скорость (частота кругового движения в секунду) (1 / с)
Φ	Превышен угол
п.	Импульс (кг м / с или Нс)
м	Масса (кг)
Ф.	Сила (Н или кг м / с 2 )
I →	Импульс (кг м / с)
F ср.	Среднее или полезное усилие (Н или кг м / с 2 )
M s	Центр масс, без единицы
M	Крутящий момент (Н · м)
Дж	Момент инерции (кг · м 2 )
р	Ось вращения
ρ	Массовое распределение
л	Угловой момент [(кг · м 2 ) / с]
п.	Угловой момент основной массы [(кг · м) / с]
Вт	Работа (Дж или Н · м)
E	Энергия (Дж или Н · м)
п.	Мощность (Вт или Дж / с)
Δp	Столкновение [(кг · м) / с]
ρ	Давление (Па или Н / м 2 )
А	Площадь поверхности (м 2 )
В	Объем (м 3 или л)

Сила, масса и ускорение: второй закон движения Ньютона

Первый закон движения Исаака Ньютона гласит: «Покоящееся тело будет оставаться в покое, а движущееся тело останется в движении, если на него не действует внешняя сила.«Что же тогда происходит с телом, когда к нему прикладывается внешняя сила? Эта ситуация описывается вторым законом движения Ньютона.

Согласно НАСА, этот закон гласит:« Сила равна изменению количества движения за одно изменение. во время. Для постоянной массы сила равна массе, умноженной на ускорение. ” математика, стоящая за этим, довольно проста.Если вы удвоите силу, вы удвоите ускорение, но если вы удвоите массу, вы уменьшите ускорение вдвое.

Ньютон опубликовал свои законы движения в 1687 году в своей основополагающей работе «Philosophiæ Naturalis Principia Mathematica» («Математические принципы естественной философии»), в которой он формализовал описание того, как массивные тела движутся под влиянием внешних сил.

Ньютон расширил более раннюю работу Галилео Галилея, который разработал первые точные законы движения масс, по словам Грега Ботуна, профессора физики в Университете Орегона.Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью, независимо от размера и массы. Ньютон также раскритиковал и расширил работы Рене Декарта, который также опубликовал свод законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.

Ускорение и скорость

Второй закон Ньютона гласит, что когда на массивное тело действует постоянная сила, она заставляет его ускоряться, то есть изменять его скорость с постоянной скоростью.В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация рассматривается из движущейся инерциальной системы отсчета, это тело может казаться ускоряющимся, замедляющимся или меняющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета движутся относительно друг друга.

Жирные буквы F и a в уравнении указывают, что сила и ускорение являются векторными величинами , что означает, что они имеют как величину, так и направление.Сила может быть одной силой или сочетанием более чем одной силы. В этом случае мы бы записали уравнение как ∑ F = м a

Большой Σ (греческая буква сигма) представляет векторную сумму всех сил, или чистую силу, действующую на тело.

Довольно сложно представить приложение постоянной силы к телу в течение неопределенного промежутка времени. В большинстве случаев силы могут применяться только в течение ограниченного времени, создавая так называемый импульс .Для массивного тела, движущегося в инерциальной системе отсчета без каких-либо других сил, таких как трение, действующих на него, определенный импульс вызовет определенное изменение его скорости. Тело может ускориться, замедлиться или изменить направление, после чего оно продолжит движение с новой постоянной скоростью (если, конечно, импульс не заставит тело остановиться).

Однако есть одна ситуация, в которой мы действительно сталкиваемся с постоянной силой – силой, вызванной гравитационным ускорением, которая заставляет массивные тела оказывать на Землю нисходящую силу.В этом случае постоянное ускорение свободного падения записывается как g , а Второй закон Ньютона становится F = mg . Обратите внимание, что в этом случае F и g обычно не записываются как векторы, потому что они всегда указывают в одном направлении, вниз.

Произведение массы на гравитационное ускорение, мг , известно как вес , что представляет собой просто еще один вид силы. Без гравитации массивное тело не имеет веса, а без массивного тела гравитация не может создавать силу.Чтобы преодолеть гравитацию и поднять массивное тело, вы должны создать направленную вверх силу м a , которая больше, чем сила тяжести, направленная вниз мг .

Второй закон Ньютона в действии

Ракеты, путешествующие в космосе, охватывают все три закона движения Ньютона.

Если ракете необходимо замедлить, ускориться или изменить направление, для ее толчка используется сила, обычно исходящая от двигателя. Величина силы и место, в котором она обеспечивает толчок, могут изменять либо скорость (часть величины ускорения), либо направление, либо и то, и другое.

Теперь, когда мы знаем, как массивное тело в инерциальной системе отсчета ведет себя, когда на него действует внешняя сила, например, как двигатели, создающие толкающий маневр, маневрируют ракетой, что происходит с телом, которое проявляет эту силу? Эта ситуация описывается третьим законом движения Ньютона.

Дополнительный отчет от Рэйчел Росс, автора Live Science.

См. Также:

Дополнительные ресурсы

Основные типы движения в физике с примерами

Типы движения

В основном, существует три типа движения: поступательное движение, вращательное движение и вибрационное движение.Некоторые другие примеры движения: линейное движение, случайное движение, круговое движение, равномерное и неоднородное движение.
Этот пост также включает лоты:

• Определение движения
• Примеры движения в реальной жизни
• Изображения
• Типы
• Видео
• Участки еще

Итак, если вы хотите изучить Motion и Type of Motion , вам понравится этот пост.

Давайте нырнем.

Что такое движение в физике?

Окрестности – это места по соседству с различными предметами.Состояние покоя или движения тела относительное.

Например, пассажир, сидящий в движущемся автобусе, находится в состоянии покоя, потому что он не меняет своего положения по отношению к другим пассажирам или объектам в автобусе. Но для наблюдателя за пределами автобуса пассажиры и предметы внутри автобуса находятся в движении.

Следовательно, мы можем определить покой как «Тело считается покоящимся, если оно не меняет своего положения по отношению к своему окружению.

Мы живем во вселенной непрерывного движения.В каждой части материи атомы находятся в состоянии бесконечного движения. Мы движемся по поверхности Земли, в то время как Земля движется по своей орбите вокруг Солнца. Солнце и звезды тоже находятся в движении.

Все на просторах космоса находится в состоянии вечного движения. Каждый физический процесс включает в себя какое-то движение. Из-за его важности в окружающем нас физическом мире. Логично, что изучению движения следует уделить должное внимание. Движение обычно описывается следующим образом:

• Рабочий объем
• Расстояние
• Время
• Скорость

См. Также: Разница между расстоянием и смещением

Сколько видов движения в физике?

Примеры движения

Если мы внимательно понаблюдаем, мы обнаружим, что все во Вселенной находится в движении.Однако разные объекты двигаются по-разному.

Некоторые объекты движутся по прямой линии, некоторые – по кривой, а некоторые – иным образом. В соответствии с этим можно сказать, что существует три типа движения. Которые даются как:

• • Поступательное движение
  • Вращательное движение
  • Вибрационное движение

Что такое поступательное движение?

«При поступательном движении тело движется по прямой без вращения.Линия может быть прямой или изогнутой ». Наблюдайте, как движутся различные объекты. Они движутся по прямой? Они движутся по кругу? Автомобиль, движущийся по прямой, имеет транснациональное движение. Точно так же самолет, движущийся по прямой, находится в поступательном движении. Поступательное движение далее делится на линейное движение, круговое движение и случайное движение.

Примеры трансляционного движения

• • • Движение поезда
    • движение земли
    • движение птиц
    • движение насекомых
    • движение самолета
    • Движение молекул газа

Подробнее о: Разница между равномерным и неравномерным движением

Что такое линейное движение?

«Прямолинейное движение тела называется его линейным движением.”

linear motion

Мы сталкиваемся с множеством объектов, движущихся по прямой линии. Движение объектов, например автомобилей, движущихся по прямой и ровной дороге, является линейным движением. Самолеты, летящие прямо в воздухе, и объекты, падающие вертикально вниз, также являются примерами линейного движения.

На приведенной выше диаграмме мальчик скользит по прямой линии, что является примером линейного движения.

Примеры линейного движения в повседневной жизни

• • • Движение автомобиля по дороге
    • Движение футбола
    • Направление мальчика по прямой – пример линейного движения

Читайте также: Законы движения

Круговое движение

«Движение объекта по круговой траектории называется круговым движением.«Игрушечный поезд движется по круговой колее. Земля, вращающаяся вокруг Солнца, является примером кругового движения.

Велосипед или автомобиль, движущиеся по круговой колее, обладают круговым движением. Движение Луны вокруг Земли также является примером кругового движения.

Примеры кругового движения в повседневной жизни

• • • Движение электрона вокруг ядра
    • Движение машинки по круговой трассе
    • Движение планет вокруг Солнца

Случайное движение

«Беспорядочное или нерегулярное движение тела называется случайным движением.«Вы заметили тип движения насекомых и птиц? Их движения нерегулярные и беспорядочные. Движение насекомых и птиц является примером случайного движения. Движение частиц пыли или дыма в воздухе также является случайным движением. Броуновское движение молекул газа или жидкости по зигзагу также является примером случайного движения. «Случайное движение молекул газа называется броуновским движением».

Это может вам помочь: Уравнения движения

Что такое вращательное движение?

«Вращательное движение тела вокруг своей оси называется его вращательным движением.
Изучите движение крана. Он вращается вокруг оси. Частицы волчка движутся по кругу, поэтому отдельные частицы совершают круговое движение. Имеет ли волчок круговое движение?

Вершина вращается вокруг своей оси, проходящей через нее, и, таким образом, обладает вращательным движением. Ось – это линия, вокруг которой вращается тело. При круговом движении точка, вокруг которой движется тело, находится вне тела. Во вращательном движении одиночка, вокруг которой движется тело, проходит через само тело.

Примеры вращательного движения

• • • Движение Земли вокруг своей географической оси, вызывающее день и ночь, является вращательным движением.
    • Движение колеса вокруг своей оси и движение рулевого колеса являются примерами вращательного движения.

Что такое вибрационное движение?

«Движение тела относительно его среднего положения известно как колебательное движение».

Представьте ребенка на качелях, как показано на рисунке выше.Когда его толкают, качели перемещаются взад и вперед относительно своего среднего положения. Движение ребенка повторяется от одной крайности до другой с качелями.
Движение маятника часов вокруг своего среднего положения также является примером колебательного движения.

Дети, играющие в морскую пилу, являются примером колебательного движения.
Помимо этих примеров, ребенок в люльке, двигающийся взад и вперед, вперед и назад, движение молотка электрического звонка и движение струны ситара являются некоторыми примерами колебательного движения . Простое гармоническое движение также является примером колебательного движения.

Предлагаемое видео:

Посетите нашу страницу, чтобы узнать больше о связанных темах по механике.
Связанные темы

Физика Ссылки по теме:

.