Википедия момент инерции: HTTP 429 – too many requests, слишком много запросов

ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения » РобоВики

В этой статье

1. История понятия «инерция»
2. Инерция, кинетическая энергия, работа
3. Момент инерции
4. Вопросы

История понятия «инерция»

До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.

Бюст Аристотеля. Римская копия греческого бронзового оригинала

Это утверждение закономерно вытекало из реальных наблюдений.  При этом Аристотель объяснял движение снарядов, выпущенных из орудия, невидимым действием окружающей среды, которая каким-то образом продолжает двигать снаряд. При этом философ пришел к выводу, что такое движение в пустоте невозможно.

Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.

Эта теория движения неоднократно оспаривалась. Например, в 6 веке византийский филолог Иоанн Александрийский (Иоанн Грамматик) раскритиковал тезисы Аристотеля, что среда поддерживает движения тела и что тело остановится в пустоте. В 11 веке персидский исламский врач, астроном, философ и писатель Ибн Сина [Авиценна] (980 – 1037 гг.) сделал вывод, что снаряд при отсутствии действия внешних сил, то есть в пустоте, не остановится.

Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.

Портрет Кеплера в 1610 году

Термин «инерция», от латинского слова «безделье» или «лень» (лат. inertia),  был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг.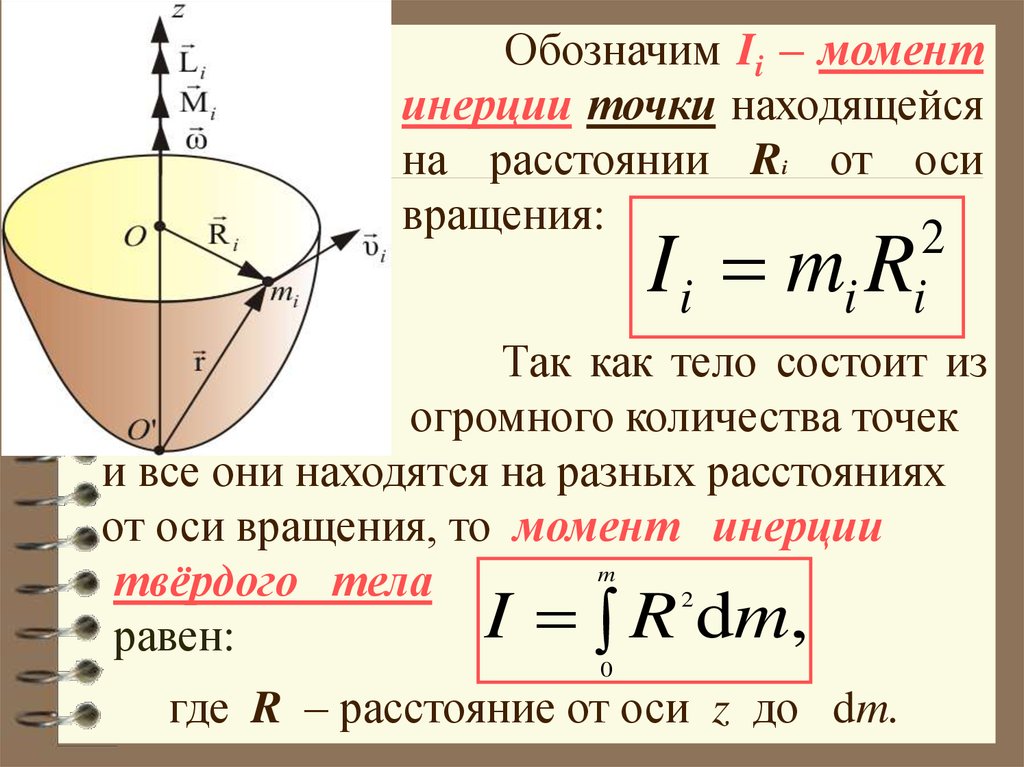 Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.

Юстус Сустерманс. Портрет Галилея Галилея. 1636

Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».

Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов. Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.

Мысленный эксперимент Галилея

Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».

Готфрид Кнеллер. Портрет Исаака Ньютона. 1689

Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.

Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.

Три закона НьютонаИнерция: взгляды от Аристотеля до Ньютона

Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.

Посмотрим на второй закон Ньютона.

Чаще его записывают в виде:

так как в инерциальной системе отсчета сила является причиной ускорения тела.

Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).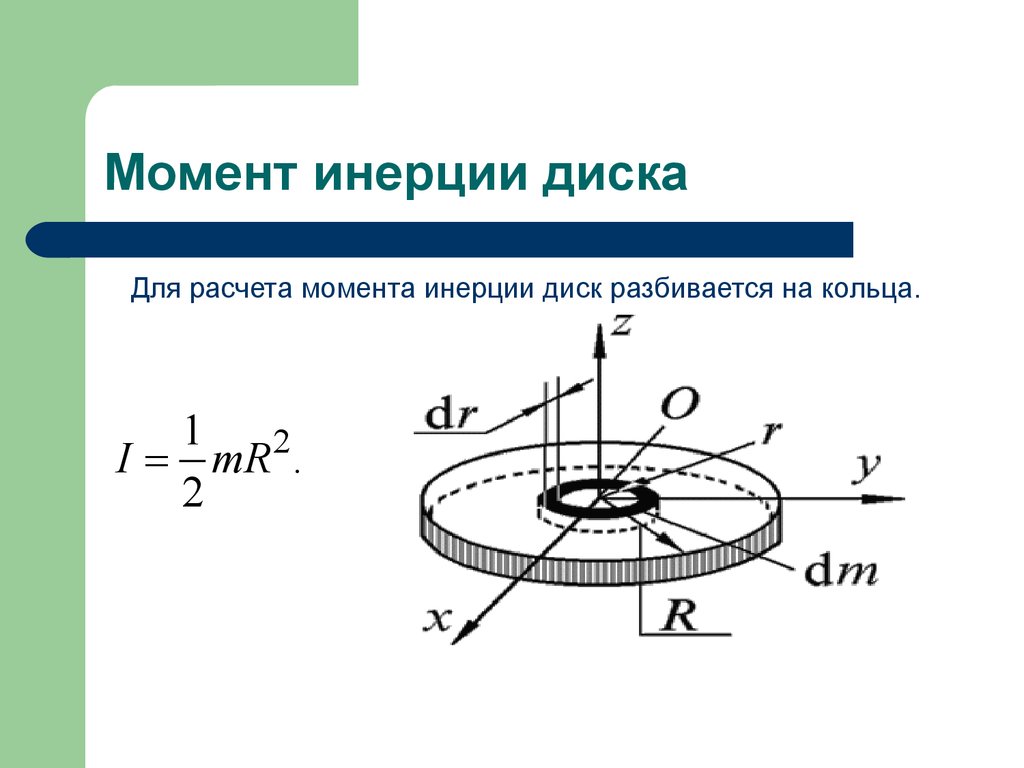

Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).

Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.

Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).

Тормозной путь грузовика и легковушки

Из-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза).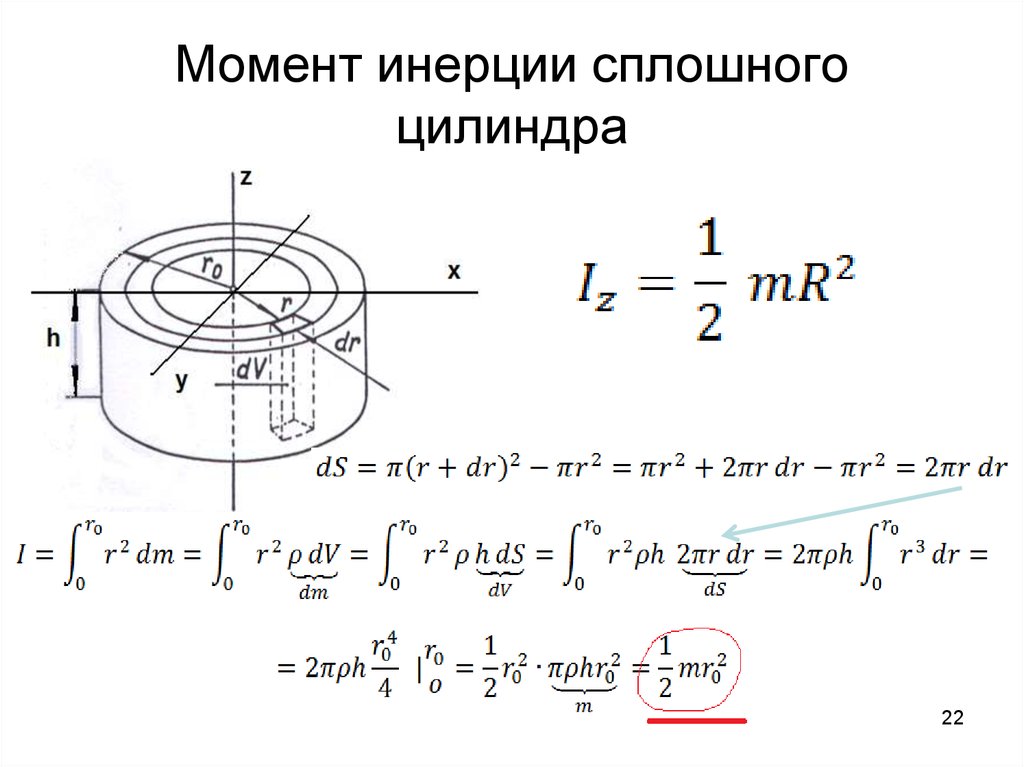 Говорить, что у грузовика больше инерция – некорректно.

Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.

Инерция, кинетическая энергия, работа

Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.

Силачи тянут Ил-76

А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.  

Трюк со скатертью

Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.

Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):

Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).

Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.

Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:

Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.

Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.

При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?

Момент инерции

Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.

Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Вращение на фигурном катании

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.

Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

Скорость вращающегося тела

При этом кинетическая энергия вращающегося тела примет вид:

Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.

Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.

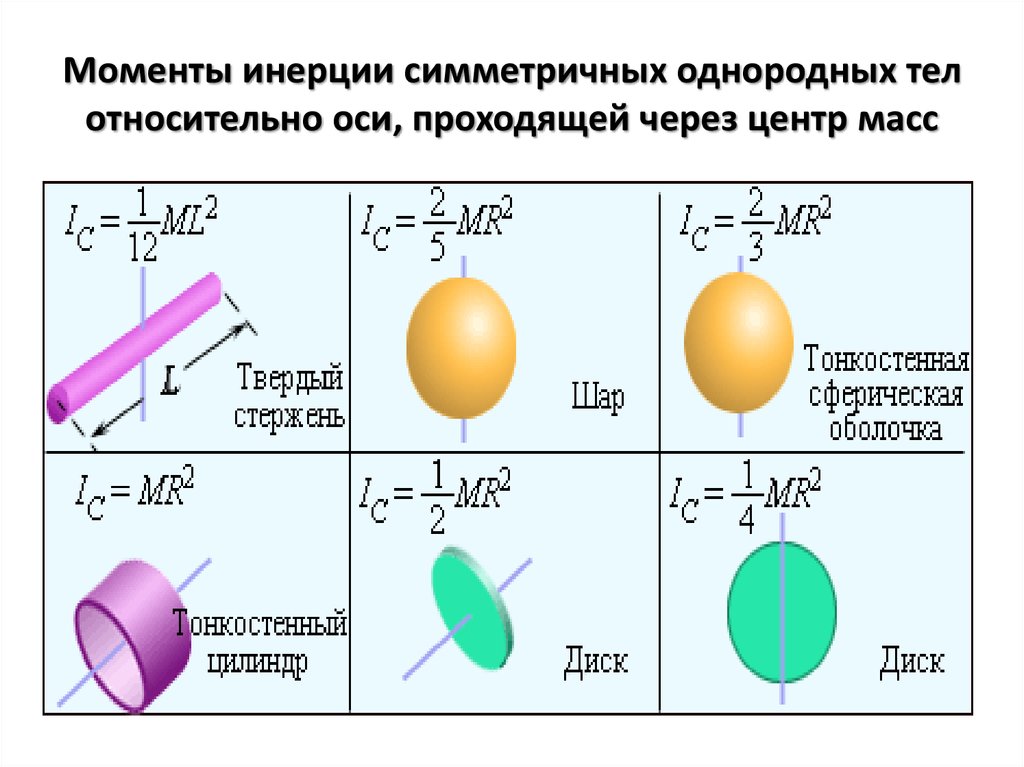
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.

Некоторые формулы для расчета момента инерции для тел разной формы

Пример.

Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r₁ < r₂), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?

Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h

В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.

Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точке

При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.

Кинетическая энергия первого и второго цилиндра в нижней точке

Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

Тогда для кинетической энергии поступательного движения будет справедливо отношение:

Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.

Вопросы

1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i

Маховик автомобиля

2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?

3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?

Видео:

1. Инерция. GetAClass
2. Момент инерции. GetAClass
3. Момент инерции вращающихся тел. Эксперимент. Зависимость момента инерции от распределения массы
4. Момент инерции вращающихся тел. Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
5. Момент инерции вращающихся тел. Фигурное катание. Юлия Липницкая, вращение
6. Момент инерции. Работа двигателя с маховиком и без него

Статьи:

1. Первый закон Ньютона и инерциальные системы отсчёта
2. Второй закон Ньютона
3. Равнодействующая
4. Третий закон Ньютона
5. Неинерциальные системы отсчёта

Момент инерции. Уравнение моментов. (Лекция 7)

1. Механика Лекция 7 Момент Инерции. Уравнение моментов. Лектор профессор А.М.Тишин рекомендованная литература: 1. Д.В.Белов,

Механика, Уч. Пособие, М.:
Физический ф-т, МГУ, НЭВЦ ФИПТ., 1998, 144 с.
2. И.В. Савельев, Курс Физики, том 1.

2. Вес тела и сила тяжести

m
Fцб
Весом тела называется сила, с
которой тело действует на опору
или подвес вследствие
гравитационного притяжения.
Fg
В условиях
Земли – вследствие притяжения к Земле. 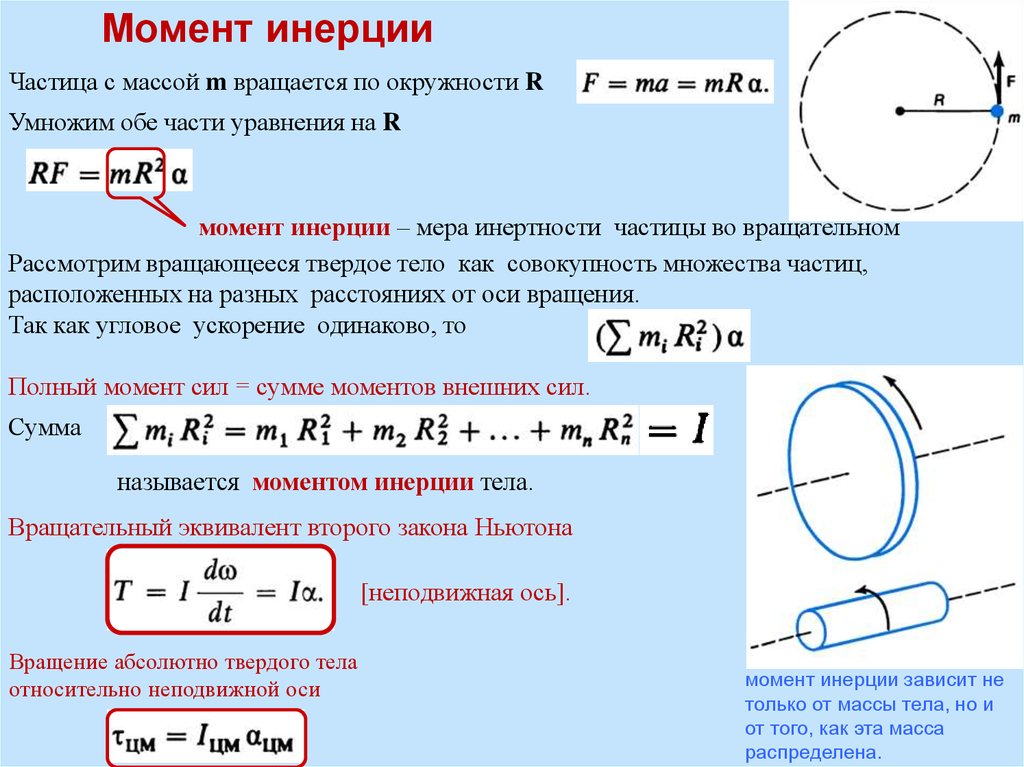Вес
M
тела не надо путать с силой тяжести P = mg, где g одинаковое для всех тел вблизи вращающейся (т.е. во
вращающейся системе отсчета) поверхности Земли
ускорение, называемое ускорением свободного падения.
P хотя и обусловлена притяжением тел к Земле но
результат двух сил и не равна силе гравитационного
притяжения тела Fg из-за действия Fцб .

3. Различие силы тяжести и веса

m
Fцб
На любое тело, находящееся на
поверхности Земли (кроме полюса)
действует центробежная сила инерции
Fцб , что и приводит к некоторому
Fg
различию силы тяжести P и силы гравитационного притяжения
M
Fg как по величине,
так и по направлению. Те во вращающейся
системе отсчета складываем два вектора
P=mg=Fg+Fцб
‫׀‬Fцб‫=׀‬mωЗ2RЗcos
Результирующая сила направлена не к центру Земли.
Максимальное различие получается на экваторе и составляет
0,3% от силы P. На экваторе на тело массой 1 кг действует
Fцб=0.0337Н=1/291 mgh. Т.е. в ряде случаев ей можно пренебречь.
Угол между направлениями векторов P и Fg также очень мал и
его max значение равно 0,0018 рад (на широте 45 градусов).

4. Момент инерции МТ относительно оси вращения

L’
O’
d
ω
Величина угловой скорости
dt
Изменение угловой скорости со временем
определяется вектором углового ускорения
ω
ω
t 0 t
L
β lim
При вращении по окружности момент импульса МТ L
относительно точки О: L r ,mv и направления векторов L и
не совпадают если точка О не в центре окружности. Если
движение идет по окружности и точка О’ в центре окружности, то
направления векторов L’ и совпадают.
L’ Rmvsin 90 Rmv Rm ωR mR ω Iω
0
2
Скалярная величина I mR 2 называется моментом
инерции материальной точки относительно оси вращения.

5. Уравнение моментов для материальной точки

Как уже говорилось момент импульса МТ, двигающейся
по окружности:
L mR ω Iω
2
Производная по времени равна:
dL
dω
I
Iβ
dt
dt
В соответствии с законом изменения момента импульса
для МТ получаем:
Iβ N iвнеш
i

6.

Абсолютно твердое телоПод твердым телом будем подразумевать абсолютно
твердое тело, в котором расстояния между любыми
двумя точками неизменны. Твердое тело можно
представить как совокупность большого количества
очень малых масс m i , которые можно считать МТ.
Теорема о движении центра масс твердого тела:
центр масс твердого тела движется так, как двигалась
бы материальная точка с массой, равной массе тела, и к
которой приложены все внешние силы, действующие на
тело. Т.е. раньше мы говорили о МТ и о системе МТ
и ее центре масс, теперь еще и об абсолютно
твердом теле.

7. Момент инерции твердого тела

Твердое тело можно представить как систему МТ, удерживаемых
внутренними силами на неизменных расстояниях друг от друга и
по аналогии с МТ записать: dL
dt
N внеш
Пусть момент импульса i-й частицы , ri — радиус окружности, по
которой движется МТ m i
относительно оси вращения тела.
Направление Li относительно оси вращения всех точек тела
одинаковое, так как в каждый момент времени направление и
величина угловых скоростей всех точек одинаковы (тело твердое).
L Li ω mi ri Iω
2
I mi ri называется моментом инерции
Величина
твердого тела относительно данной оси. Направление векторов L
и совпадают только в случае симметричного тела.
2

8. Уравнением моментов

Подставим момент импульса тела
L Iω
dL
Iβ N внеш
dt
Это закон изменения момента импульса твердого тела или основной
закон динамики для вращения твердого тела вокруг неподвижной
оси.
Как и в случае с МТ можно сопоставить все величины для
поступательного и вращательного движения.
mv 2
Заменив в выражении для кинетической энергии T
2
массу на момент инерции I, а скорость v на угловую скорость
получим кинетическую энергию вращающегося вокруг
неподвижной оси тела или просто подставив v= R:
1 2
T Iω
2
1. Скамья Жуковского Т=const ? Произведение момента инерции на угловую
скорость в замкнутой системе (N=0) остается постоянным?
2. Видео с вращением штанги.

9. Момент инерции сложных тел

Для полного определения момента инерции более сложных тел
выражение I Δmi ri2 следует уточнить, устремив элемент mi
к нулю и найдя соответствующий предел:
I lim
Δm 0
r Δm
2
i
i
Как известно, такой предел называется интегралом:
I r dm ρ r dV
2
2
Интегрирование производится по всему объему тела V. Если
плотность тела постоянна, то можно вынести из под знака
интегрирования. Но даже для яйца (желток, белок и
скорлупа имеют разную плотность)! Земля?

11. Момент инерции полого цилиндра

Найдем момент инерции полого цилиндра
относительно его оси симметрии ОО.
I Δmi ri2 R 2 Δmi R 2 m mR 2
где m — масса цилиндра.
Итак, момент инерции полого цилиндра прямо не зависит от
высоты этого цилиндра (косвенно естественно зависит так как
чем больше высота тем больше площадь и масса). Точно также
выглядит и выражение для момента инерции обруча.

12. Момент инерции сплошного цилиндра и однородного шара

Момент инерции сплошного однородного цилиндра
относительно оси симметрии ОО можно найти разбив его
на цилиндры радиуса r и толщиной dr. Так как объем
одного слоя равен dV=2πrhdr то
I r 2 dm r 2ρ dV r 2ρ 2π r h dr 2π ρ h r 3dr
4
2
2
R
R
R
mR
2
2π ρ h
ρ (π R h)
ρV
4
4
4
2
2
– плотность, dr и h –толщина и высота цилиндра . А у
полого цилиндра было mR2. Чем дальше удалена масса
от центра тем больше I. При равных m и R у полого
момент инерции I в 2 раза больше
1. Опыт с двумя скатывающимися цилиндрами.
2. Опыт со скатыванием пенопласта не через
главную ось

13. Фигуристка на льду и Торнадо: Что общего?

Сохранение кинетической энергии?
Приблизительно !
Торнадо – увеличивается масса того, что поднято с
Земли – увеличивается момент инерции и
увеличивается кинетическая энергия. Как зависит I от
радиуса торнадо ? Узнаем чуть позже ~ R2
Куда расходуется кинетическая энергия? Вспомним :
машины, цунами, лавины…..

14. Демонстрации на момент инерции

1.
Гироскопы не путать с гороскопами
2.
Волчки
3.
Прошу принести на следующую лекцию два куриных
яйца. Одно сырое, другое сваренное вкрутую. Лучше
кто живет в общежитии
4.
Китайский волчок (момент силы трения)
5.
Кусок пенопласта 3 оси (при вращении выходит на
главную ось)
6.
Палочки кельтов (срезаны наискосок)

15. Условия равновесия твердого тела

В общем случае для равновесия
абсолютно твердого тела
необходимо выполнение двух
условий.
1. Сумма всех внешних сил,
приложенных к телу, должна быть
равна нулю:
F
внеш
0
i
2. Сумма моментов внешних сил
относительно любой точки должна
быть равна нулю:
http://www.youtube.com/watch?v=n_6p-1J551Y
N
i
внеш
0

16. Момент инерции в природе

Самолеты убирают шасси во время
полета, а, например, пчелы,
напротив, вытягивают вперед
задние лапки для того, чтобы
лететь устойчиво с большей
скоростью.
При максимальной скорости в 7.25 м/с пчелы теряют
вращательную устойчивость. Это говорит о том, что скорость
пчелы ограничивает не сила мускулов или амплитуда машущих
крыльев, а наклон тела и умение балансировать в неустойчивом
положении. Т.е. определенной скорости пчелы умеют управлять
своим моментом инерции и изменять момент импульса так, чтобы
обеспечить условия равновесия (нулевую сумму моментов
внешних сил).

17. Факультативно: приливы, отливы и не только?

• Гравитация действует не только на Земле. Земля притягивается
силами гравитации к другим телам, включая Солнце и Луну.
Луна 19 марта 2011 подошла к Земле на самое близкое
расстояние, начиная с 1992 года. Предыдущие фазы
максимального сближения происходили в 1955, 1974, 1992 и
2005 годах.
• 2005 – мощный цунами Индонезии за две недели до перигея.
• 1974 – циклон Трэйси в австралийском городе Дарви.
• Возможное проявление воздействия дополнительных сил
и/или моментов сил, нарушающих равновесное состояние
плит внутри Земли ?

18. Механика поступательного и вращательно движения относительно неподвижной оси

Все выражения для МТ и для твердого тела внешне очень
похожи. 2-го закон Ньютона:
dp
ma Fi
dt
dL
Iβ N iвнеш
dt
i
Аналогами также являются:
координата
х
– угол ,
линейной скорости
v
– угловая скорость ,
линейного ускорения a
– угловое ускорение ,
массы
m
– момент инерции I,
силы
F
– момент силы N,
импульса
р
– момент импульса L,
кинетическая энергия mv2/2 – кинетическая энергия I 2/2,
работа
dA=Fsds – работа dA=N d
мощность
P=Fvv – P=N

19.

Момент инерции сплошного однородного шара. Земля?• 11 марта 2011 года (мистика? нет! а разрушение двух небоскребов в США
11 сентября 2001 года ?) в Японии произошла серия сильнейших за 140 лет
землетрясений, силой до 8,9 по шкале Рихтера, что спровоцировало цунами .
Волна высотой до 10 метров проникла вглубь на несколько километров, и
израсходовали свою кинетическую энергию на уничтожение всего на своем
пути. Ось вращения Земли после японского землетрясения могла
dI
N внеш .
кратковременно сместиться на 10-15 см. Печальное следствие
dt
По сути тот же гироскоп, который мы уже обсуждали. Момент инерции
однородного шара относительно оси, проходящей через его центр:
2
I mR 2
5
• Для оценки если масса Земли приблизительно равна 6×1024 кг и считая Землю
однородным шаром радиусом 6,4х106 м. Можно оценить I=9.8х1037 кг м2.
Близко! Так как общепринятое значение 8х1037 кг м2. На самом деле моменты
инерции внутреннего ядра, внешнего ядра , мантии и коры могут отличаться и
лежать в диапазоне от 5. 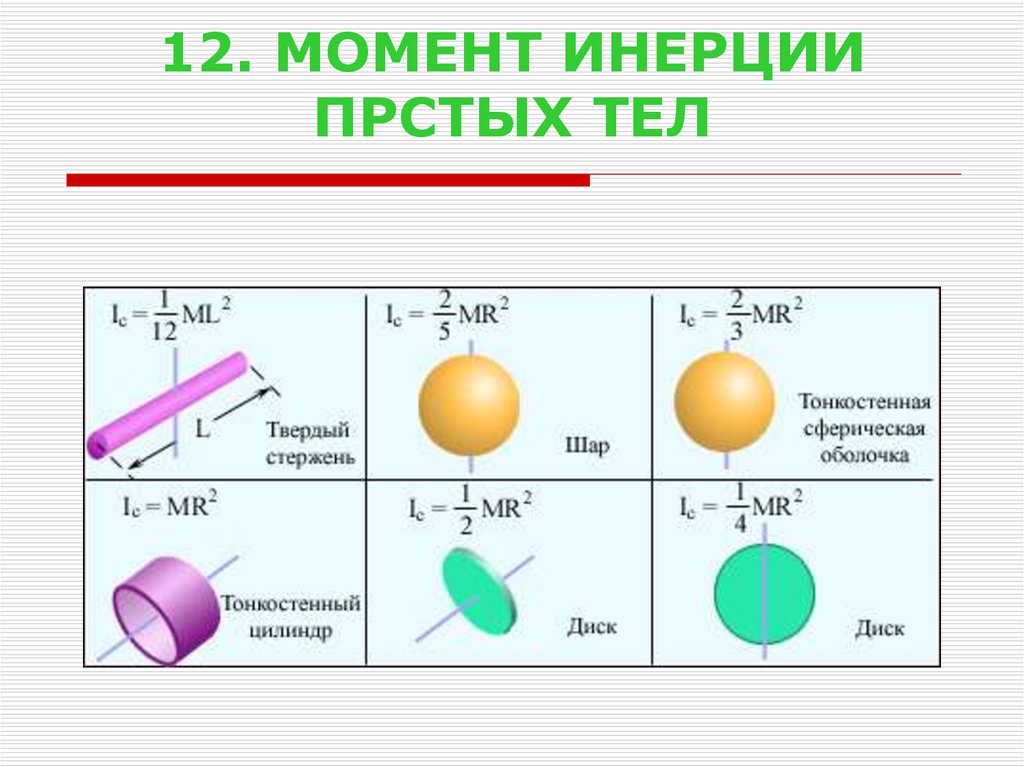8х1034 до 7х1037 кг м2
• http://lnfm1.sai.msu.ru/~chujkova/Trudi/zharov.htm

20. Факультативно: Безразмерный момент инерции

Безразмерный момент инерции твердого тела радиуса R и массы
m равен отношению его момента инерции относительно оси
2
вращения к моменту инерции МТ той же массы I mR
относительно неподвижной оси вращения, расположенной на
расстоянии R. Как мы уже знаем МТ отличается от однородного
шара на 2/5=0.4
Безразмерный момент инерции Земли равен 0,335, что меньше,
чем у шара и что является аргументом в пользу неравномерного
распределения массы (существования плотного ядра).
Факультативно: ядро Земли кристалл?
– проф. Борье Йоханссон (Börje Johansson), Факультет материаловедения и
машиностроения Королевский технологический институт (Швеция),
председатель и член Нобелевского комитета по физике, член Шведской
королевской академии наук, почётный профессор МИСиС.
Профессор Йоханссон является одним из авторов концепции, согласно
которой ядро Земли является кристаллом с кубической решёткой. Твёрдое
железное ядро Земли обладает кристаллической
структурой с объёмноцентрированной кубической
решеткой (в одной ячейке такой решётки атомы расположены по углам
куба и ещё один атом — в центре куба). Данная теория способна
перевернуть существующие представления о природе нашей планеты и о её
магнитном поле. Статья, посвящённая этому исследованию, была
опубликована в авторитетном научном журнале “Science”.

22. Теорема Штейнера

Зная момент инерции тела
относительно оси, проходящей через
центр масс, момент инерции
относительно произвольной оси
вычисляют по теореме Штейнера:
момент инерции относительно произвольной оси I
равен сумме момента инерции Ic относительно оси,
параллельной данной и проходящей через центр масс
тела, и произведения массы тела на квадрат расстояния
между осями d.
I I c md
2
Вспомним опыт с гантелями на скамье Жуковского

23. http://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0%B8

http://ru.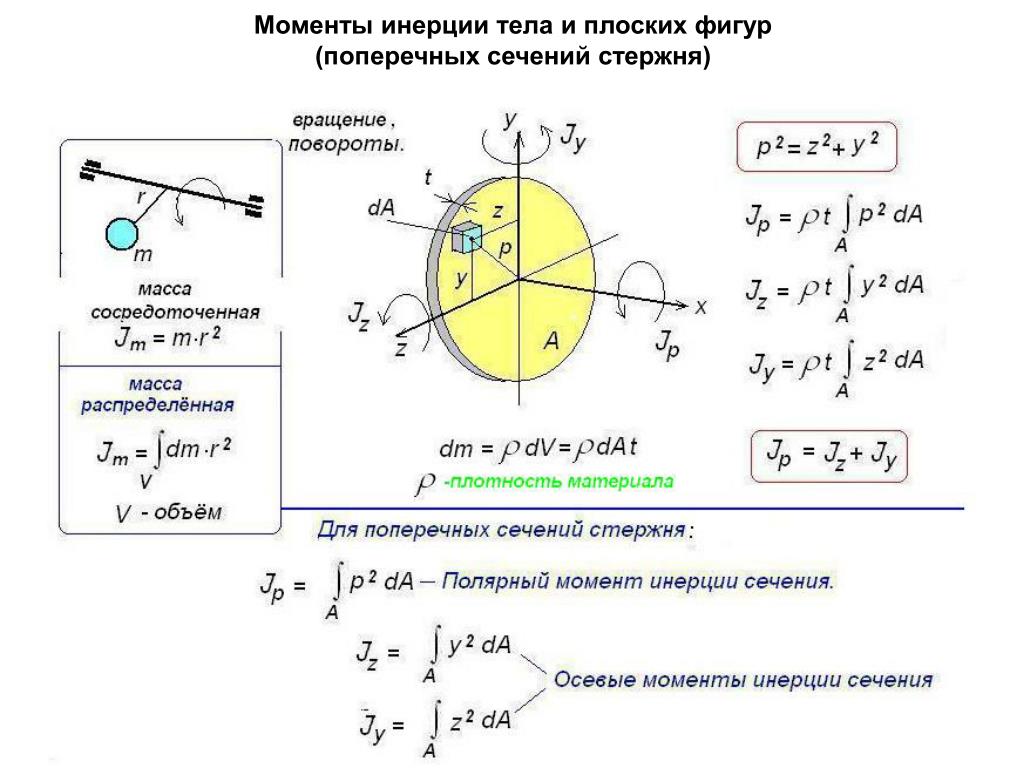 wikipedia.org/wiki/%D0%9C%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D0%B8%D0%BD%D0%B5%D1%80%D1%86%D0%B8%D0
%B8

Момент инерции – Википедия, бесплатная энциклопедия

реферат разработка динамика образование инженерные формулы игры гироскоп изображение инерция информация интертия математика мой момент философии физика исследование моделирование написание диссертации Мои теги:

Из Википедии, бесплатная энциклопедия

Перейти к: навигация, поиск

Эта статья о моменте инерции вращающегося объекта . Чтобы узнать о моменте инерции, связанном с изгибом плоскости, см. второй момент площади .

Момент инерции , также называемый моментом инерции массы или угловой массой , (единицы СИ кг м ² ) является мерой сопротивления объекта изменениям скорости его вращения. Это вращательный аналог массы. То есть это инерция твердого вращающегося тела по отношению к его вращению. Момент инерции играет в динамике вращения ту же роль, что и масса в основной динамике, определяя взаимосвязь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также некоторыми другими величинами. В то время как простой скалярной обработки момента инерции достаточно для многих ситуаций, более продвинутая тензорная обработка позволяет анализировать такие сложные системы, как волчки и гироскопическое движение.

Символ I и иногда J обычно используется для обозначения момента инерции.

Момент инерции был введен Эйлером в его книге a Theoria motus corporum solidorum seurigorum в 1730 году. , связанный с моментом инерции.

Содержимое 1 Обзор 2 Скалярный момент инерции 2.1 Определение 2.1.1 Подробный анализ 2.2 Теорема о параллельных осях 2.3 Композитные корпуса 2.4 Уравнения с моментом инерции 3 Тензор момента инерции 3.1 Определение 3.2 Вывод компонентов тензора 3.3 Приведение к скаляру 3.4 Главные моменты инерции 3. 5 Теорема о параллельных осях 3.6 Вращательная симметрия 3.7 Прочие механические величины 3.8 Сравнение с ковариационной матрицей 4 См. также 5 Примечания 6 Каталожные номера 7 Внешние ссылки

[править] Обзор

Момент инерции объекта относительно заданной оси описывает, насколько трудно изменить его угловое движение относительно этой оси. Например, рассмотрим два диска А и В, сделанных из одного и того же материала и имеющих одинаковую массу. Диск A имеет больший радиус, чем B (поэтому он тоньше). Диск B толще и меньше в диаметре. Требуется больше усилий, чтобы разогнать диск А (изменить его угловую скорость), потому что его масса распределена дальше от его оси вращения: масса, которая находится дальше от этой оси, должна при заданной угловой скорости двигаться быстрее, чем масса ближе к ней. В этом случае диск А имеет больший момент инерции, чем диск В.

Водолазы минимизируют свои моменты инерции, чтобы увеличить скорость вращения.

Момент инерции объекта может измениться при изменении его формы. Ярким примером может служить фигурист, который начинает вращение с вытянутыми руками. Вытягивая руки, она уменьшает свой момент инерции, заставляя ее вращаться быстрее (за счет сохранения углового момента).

Момент инерции имеет две формы: скалярную форму I (используется, когда известна ось вращения) и более общую тензорную форму, не требующую знания оси вращения. Скалярный момент инерции I (часто называемый просто «моментом инерции») позволяет провести краткий анализ многих простых задач динамики вращения, таких как скатывание объектов по склонам и поведение шкивов. Например, в то время как блок любой формы будет скользить по склону без трения с одинаковой скоростью, катящиеся объекты могут опускаться с разной скоростью в зависимости от их моментов инерции. Обруч будет опускаться медленнее, чем твердый диск такой же массы и радиуса, потому что большая часть его массы расположена далеко от оси вращения, и поэтому ему необходимо двигаться быстрее, если обруч катится с той же угловой скоростью.

Однако для (более сложных) задач, в которых ось вращения может измениться, скалярное рассмотрение неадекватно, и необходимо использовать тензорное рассмотрение (хотя в особых случаях возможны сокращения). Примеры, требующие такой обработки, включают гироскопы, волчки и даже спутники — все объекты, ориентация которых может изменяться.

Момент инерции также может называться моментом инерции массы (особенно инженеры-механики), чтобы избежать путаницы со вторым моментом площади, который иногда называют моментом инерции (особенно инженерами-строителями) и обозначают тот же символ I . Самый простой способ дифференцировать эти величины — через их единицы. Кроме того, момент инерции не следует путать с полярным моментом инерции , который является мерой способности объекта сопротивляться кручению (скручиванию).

[править] Скалярный момент инерции

[править] Определение

Простое определение момента инерции любого объекта, будь то точечная масса или трехмерная структура, дается формулой:

где d m — масса бесконечно малой части тела, а r — расстояние по перпендикуляру от точки массы до оси вращения.

[править] Подробный анализ

(Скалярный) момент инерции точечной массы, вращающейся вокруг известной оси, определяется как

Момент инерции аддитивен. Таким образом, для твердого тела, состоящего из N точечных масс

m _i с расстояниями r _i до оси вращения, полный момент инерции равен сумме моментов масс точки инерции:

Для твердого тела, описываемого непрерывной функцией плотности массы ρ( r ), момент инерции относительно известной оси можно вычислить путем интегрирования квадрата расстояния (взвешенного по плотности массы) от точки в тела к оси вращения:

где

В объем, занимаемый объектом.

ρ — функция пространственной плотности объекта, а

— координаты точки внутри тела.

Диаграмма для расчета момента инерции диска. Здесь k — это 1/2, а r — это радиус, используемый при определении момента.

Основываясь только на анализе размеров, момент инерции неточечного объекта должен иметь вид:

где

M масса

R — радиус объекта от центра масс (в некоторых случаях вместо него используется длина объекта).

k — это безразмерная константа, называемая постоянной инерции , которая изменяется в зависимости от рассматриваемого объекта.

Инерционные константы используются для учета различий в расположении массы относительно центра вращения. Примеры включают:

• k = 1, тонкое кольцо или тонкостенный цилиндр вокруг центра,
• k = 2 / 5, сплошная сфера вокруг центра
• k = 1/2, сплошной цилиндр или диск вокруг его центра.

Дополнительные примеры см. в разделе Список моментов инерции.

[править] Теорема о параллельных осях

Основная статья: Теорема о параллельных осях

После расчета момента инерции для вращений вокруг центра масс твердого тела удобно пересчитать момент инерции для всех параллельных вращений оси, не прибегая к формальному определению.

Если ось вращения сместится на расстояние R от оси вращения центра масс (например, при вращении диска вокруг точки на его периферии, а не через его центр) смещенный и центральный момент инерции связаны следующим образом:

Эта теорема также известна как правило параллельных осей и является частным случаем теоремы Штейнера о параллельных осях .

[править] Составные тела

Если тело можно разложить (физически или концептуально) на несколько составных частей, то момент инерции тела относительно данной оси получается суммированием моментов инерции каждой составной части вокруг той же заданной оси. ^[2]

[править] Уравнения с моментом инерции

Кинетическая энергия вращения твердого тела может быть выражена через его момент инерции. Для системы с точечными массами N m _i , движущейся со скоростями v _i , кинетическая энергия вращения 4 90 T3 равна3 3 3

, где ω — обычная угловая скорость (в радианах в секунду). Окончательная формула также верна для непрерывного распределения массы с обобщением приведенного выше вывода от дискретного суммирования до интегрирования.

В частном случае, когда вектор углового момента параллелен вектору угловой скорости, их можно связать уравнением

, где L — угловой момент, а ω — угловая скорость. Однако это уравнение не выполняется во многих интересных случаях, таких как прецессия вращающегося объекта без крутящего момента, хотя его более общая тензорная форма всегда верна.

Когда момент инерции постоянен, можно также связать крутящий момент объекта и его угловое ускорение аналогичным уравнением:

, где τ — крутящий момент, а α — угловое ускорение.

[править] Тензор момента инерции

Для одного и того же объекта разные оси вращения будут иметь разные моменты инерции относительно этих осей. В общем случае моменты инерции не равны, если объект не симметричен относительно всех осей.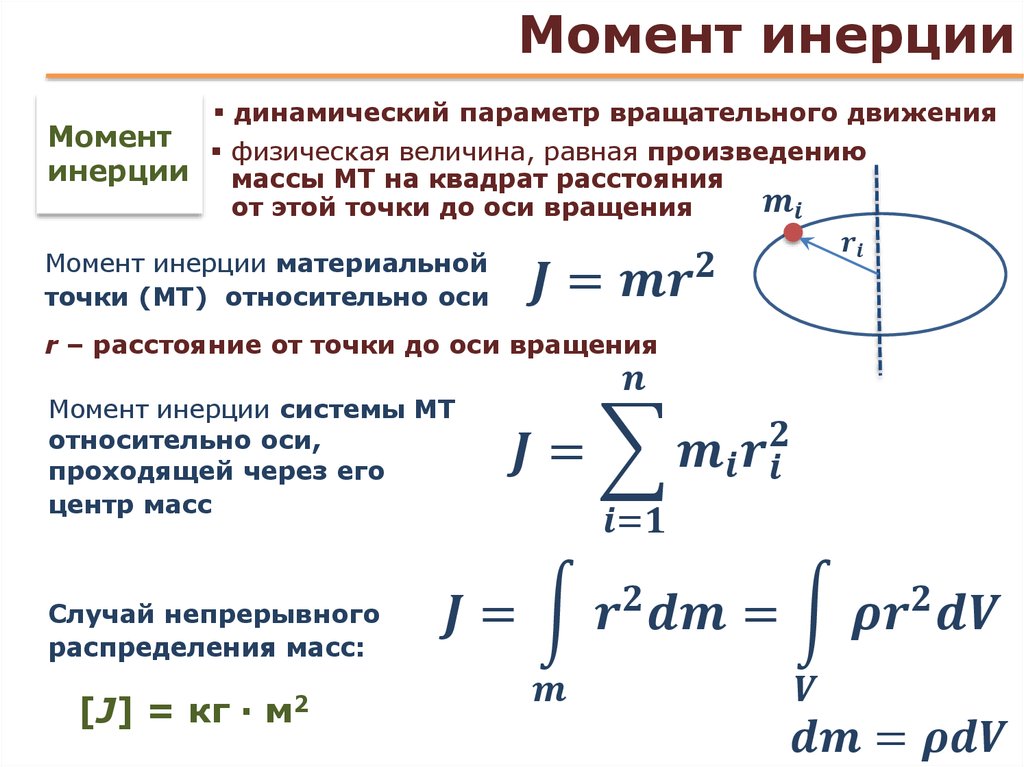 Тензор момента инерции — это удобный способ суммировать все моменты инерции объекта одной величиной. Его можно вычислить относительно любой точки пространства, хотя для практических целей чаще всего используется центр масс.

[править] Определение

Для твердого объекта массой N m _k , тензор момента инерции определяется как

.

Его компоненты определены как

где

i , j равно 1, 2 или 3 для x, y и z соответственно,

r _k = ( r _k1 , r _k2 , r _k3 ) — вектор массы k из точки, относительно которой вычисляется тензор14, а

δ _{i j} – дельта Кронекера.

Диагональные элементы, также называемые главными моментами инерции , более кратко записываются как

, в то время как недиагональные элементы, также называемые произведения инерции ,

и

Here I _{x x} denotes the moment of inertia around the x -axis when the objects are rotated around the x-axis, I _{x y} denotes the момент инерции вокруг оси y при вращении объектов вокруг оси x и так далее.

Эти величины можно обобщить на объект с непрерывной плотностью аналогично скалярному моменту инерции. Тогда у одного

где — их внешнее произведение, E ₃ — единичная матрица 3 × 3, а V — область пространства, полностью содержащая объект.

[править] Вывод компонент тензора

Расстояние r частицы at от оси вращения, проходящей через начало координат в направлении, равно . Используя формулу I = м r ² (и некоторую простую векторную алгебру), можно увидеть, что момент инерции этой частицы (относительно оси вращения, проходящей через начало координат в направлении) is Это квадратичная форма в и, после еще немного алгебры, это приводит к тензорной формуле для момента инерции

.

Это в точности приведенная ниже формула для момента инерции в случае одиночной частицы. Для множества частиц нам нужно только вспомнить, что момент инерции аддитивен, чтобы убедиться, что эта формула верна.

[править] Приведение к скаляру

Для любой оси , представленной в виде вектор-столбца с элементами n _i , скалярная форма I может быть вычислена из тензорной формы I как

Диапазон обеих сумм соответствует трем декартовым координатам.

Следующее эквивалентное выражение позволяет избежать использования транспонированных векторов, которые не поддерживаются математическими библиотеками, поскольку внутренние векторы и их транспонирование хранятся в виде одного и того же линейного массива,

Однако следует отметить, что хотя это уравнение математически эквивалентно приведенному выше уравнению для любой матрицы, тензоры инерции симметричны. Это означает, что его можно упростить до:

[править] Главные моменты инерции

По спектральной теореме, поскольку тензор момента инерции веществен и симметричен, можно найти декартову систему координат, в которой он диагональен, имеющую вид

, где оси координат называются главными осями , а константы I ₁ , I ₂ и I ₃

называются 0011 главные моменты инерции .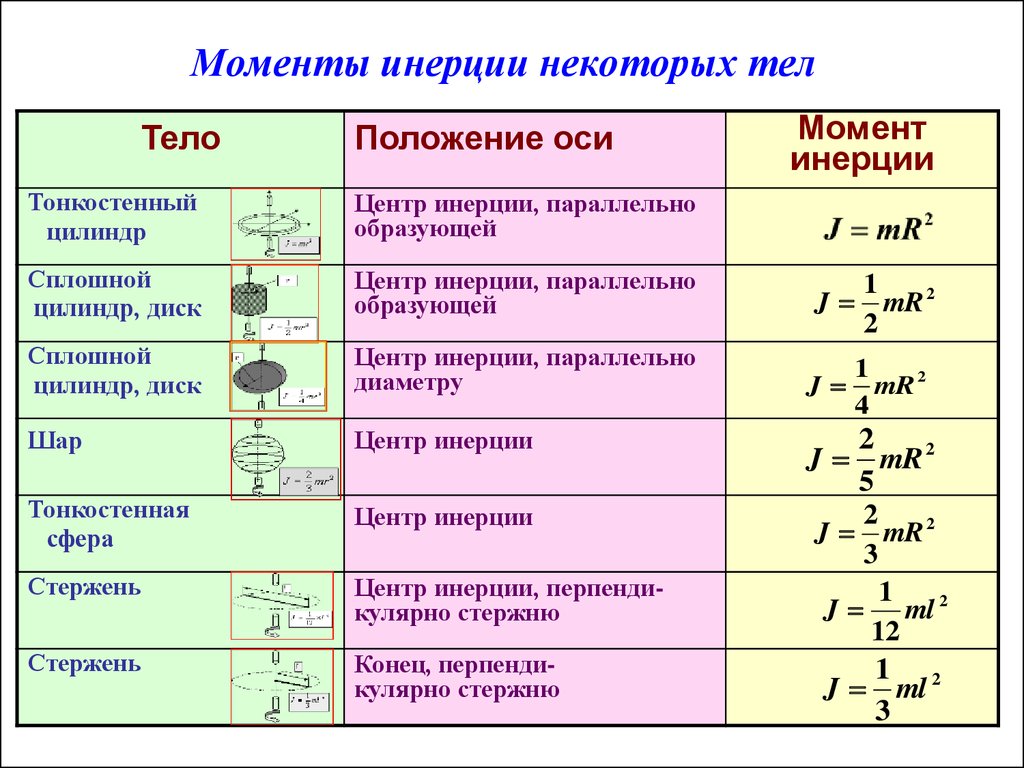 Единичные векторы вдоль главных осей обычно обозначаются как ( e ₁ , e ₂ , e ₃ ).

Когда все главные моменты инерции различны, главные оси задаются однозначно. Если два главных момента одинаковы, твердое тело называется симметричным волчком , и нет однозначного выбора для двух соответствующих главных осей. Если все три главных момента одинаковы, то твердое тело называется сферическая вершина (хотя она не обязательно должна быть сферической), и любая ось может считаться главной осью, а это означает, что момент инерции одинаков относительно любой оси.

Главные оси часто совпадают с осями симметрии объекта. Если твердое тело имеет ось симметрии порядка м , т. е. симметрично относительно поворотов на 360°/ м вокруг данной оси, то ось симметрии является главной осью. При м > 2 твердое тело является симметричным волчком. Если твердое тело имеет хотя бы две оси симметрии, не параллельные и не перпендикулярные друг другу, то оно является сферической вершиной, например, кубом или любым другим платоновым телом. Практическим примером этого математического явления является рутинная автомобильная задача балансировки шины, которая в основном означает регулировку распределения массы автомобильного колеса таким образом, чтобы его главная ось инерции была совмещена с осью, чтобы колесо не качалось.

[править] Теорема о параллельных осях. масса.

Если ось вращения смещена на вектор R от центра масс, новый тензор момента инерции равен

где M – полная масса твердого тела, E ₃ — единичная матрица 3 × 3 и внешнее произведение.

[править] Вращательная симметрия

Для тел с вращательной симметрией вокруг оси моменты инерции для вращения вокруг двух перпендикулярных осей и равны

, где мы определили

Использование приведенного выше уравнения для выражения всех моментов инерции через интегралы переменных вдоль или поперек оси симметрии обычно значительно упрощает вычисление этих моментов.

[править] Другие механические величины

Используя тензор I , кинетическая энергия может быть записана в квадратичной форме

и угловой момент можно записать как произведение

В совокупности можно выразить кинетическую энергию вращения через угловой момент ( L ₁ , L ₂ , L ₃ ) в системе координат главной оси как

Вращательная кинетическая энергия и угловой момент являются константами движения (сохраняющимися величинами) при отсутствии общего крутящего момента. Угловая скорость ω не постоянна ; даже без крутящего момента конец этого вектора может двигаться в плоскости (см. конструкцию Пуансо).

Подробнее о способах выражения кинетической энергии твердого тела см. в статье о жестком роторе.

[править] Сравнение с ковариационной матрицей

Основная статья: Момент (математика)

Тензор момента инерции относительно центра масс трехмерного твердого тела связан с ковариационной матрицей трехмерного случайного вектора, функция плотности вероятности которого пропорциональна поточечной плотности твердое тело по: ^{[ необходима ссылка ]}

, где n — количество точек.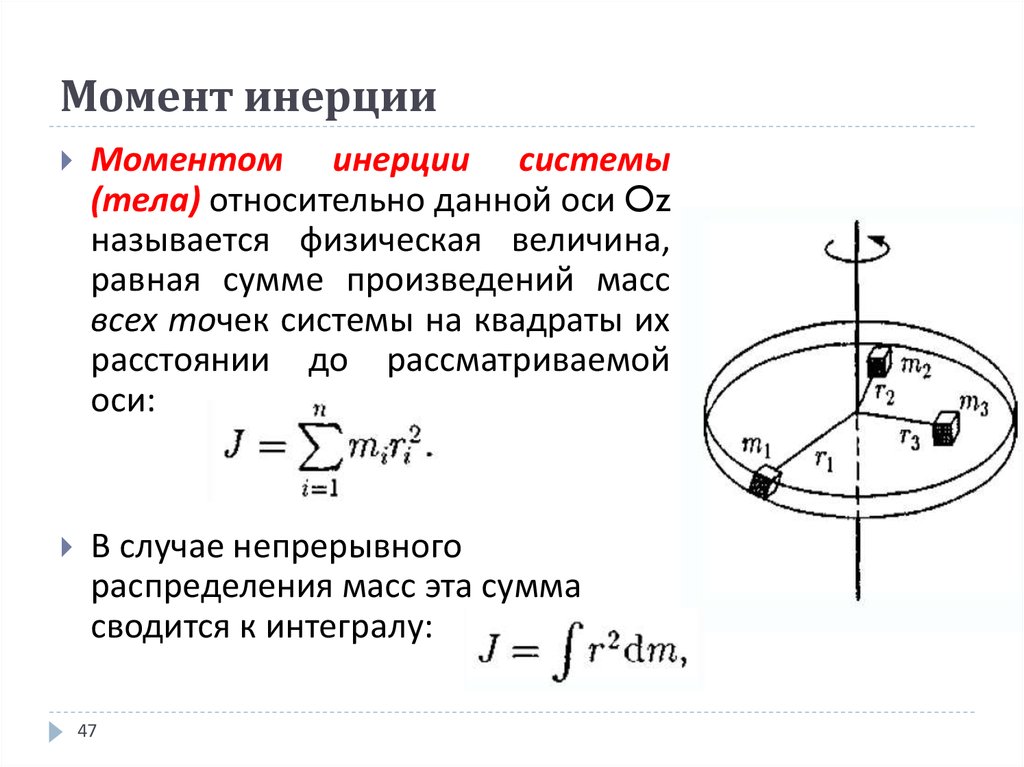

Структура тензора момента инерции исходит из того, что он должен использоваться как билинейная форма на векторах вращения в форме

Каждый элемент массы имеет кинетическую энергию

Скорость каждого элемента массы равна где r — вектор от центра вращения к этому элементу массы. Перекрестное произведение можно преобразовать в матричное умножение, так что

и аналогичные

Так

включение определения термина приводит непосредственно к структуре тензора момента. 9 «Момент инерции массы» Мехрдада Негабана, Университет Небраски

[править] Литература

• Гольдштейн Х. (1980) Классическая механика , 2nd. изд., Аддисон-Уэсли. ISBN 0-201-02918-9
• Ландау Л.Д. и Лифшиц Е.М. (1976) Механика , 3-я. изд., Пергамон Пресс. ISBN 0-08-021022-8 (в твердом переплете) и ISBN 0-08-029141-4 (в мягкой обложке).
• Марион Дж.Б. и Торнтон С.Т. (1995) Классическая динамика систем и частиц , 4-й. изд., Томсон. ISBN 0-03-097302-3
• Саймон КР. (1971) Механика , 3-я. изд., Аддисон-Уэсли. ISBN 0-201-07392-7
• Тененбаум, РА. (2004) Основы прикладной динамики , Springer. ISBN 0-387-00887-X

[править] Внешние ссылки

• Угловой момент и вращение твердого тела в двух и трех измерениях
• Конспект лекций по вращению твердого тела и моментам инерции
• Тензор момента инерции
• Вводный урок по моменту инерции: удерживание вертикальной стойки от падения (симуляция Java)
• Учебное пособие по нахождению моментов инерции с задачами и решениями для различных основных форм

urdf/tutorials/adding%20physical%20and%20collision%20properties%20to%20a%20urdf%20model — ROS Wiki

Пожалуйста, смотрите EditingTheWiki для получения рекомендаций по организации нашей вики и советов по созданию новых страниц.

Пакет ROS или стек

Если вы создаете начальную страницу для стека или пакета, присвойте ей страницу с тем же именем, что и сам стек или пакет, и используйте один из следующих шаблонов:

Если вы создаете дополнительную документацию для пакета или стека, не стесняйтесь структурировать ее по своему усмотрению, но, пожалуйста, держите ее в пределах пространства имен вашего пакета (например, “ros.org/wiki/my_package/more_details”) Создать новую пустую страницу

Учебники

Для систематизации учебных пособий в каждой стопке и пакете есть ссылка на учебные пособия в нижней части страницы. Если вы попали сюда по этой ссылке, начните список руководств с этим шаблоном:

• TutorialIndexTemplate

После сохранения этой страницы на ней будет кнопка «Создать учебное пособие», которую вы можете использовать для создания новых страниц руководств. который будет автоматически проиндексирован и его будет легче найти пользователям.