Идеальный одноатомный газ, теория и примеры
Определение идеального одноатомного газа
Количество атомов в молекуле оказывает влияние на то, как распределяется энергия по степеням свободы. Так для одноатомного газа молекула имеет три степени свободы (). Формулу для расчета внутренней энергии идеального одноатомного газа очень просто получить.
Внутренняя энергия одноатомного идеального газа
Учтем, что молекулы идеального газа представлены как материальные точки, которые не взаимодействуют на расстоянии. Отсутствие сил взаимодействия между молекулами обозначает, что потенциальная энергия взаимодействия молекул постоянна. Суммарная энергия покоя самих молекул также неизменна, так как молекулы при тепловых процессах не изменяются. Следовательно, внутренняя энергия идеального одноатомного газа является суммой кинетических энергий поступательного движения молекул и еще некоторая постоянная.
Обозначим внутреннюю энергию газа как U, тогда сказанное выше запишем как:
где – сумма кинетических энергий поступательного движения молекул; N – число молекул в газе.
По закону о равномерном распределении энергии по степеням свободы имеем:
для одноатомного газа:
– постоянная Больцмана; T – температура по шкале Кельвина.
Внутреннюю энергию одноатомного идеального газа можно записать как:
Обычно постоянную величину в выражении (5) опускают, так как в расчётах она роли не играет.
Выражение (5) говорит о том, что внутренняя энергия идеального газа определена его температурой. Она является функцией состояния и не зависит от процесса который провели для того чтобы газ пришел в состояние с этой температурой. При этом изменение внутренней энергии идеального газа определено только его начальным и конечным состояниями, и не связано с характером процесса.
Выражение (5) часто используют в виде:
где m – масса газа; – молярная масса газа; – универсальная газовая постоянная; – количество вещества.
Теплоемкость одноатомного идеального газа
Для изохорного процесса, проводимого в идеальном газе работа равна нулю (A), поэтому первое начало термодинамики:
запишем как:
где – теплоемкость газа при постоянном объеме. Используя выражения (8) и (6) получим:
Используя формулу (10) можно вычислить молярную теплоемкость любого одноатомного газа при постоянном объеме:
Молярная теплоемкость одноатомного газа при изобарном процессе () связана с соотношением Майера:
Примеры решения задач
Какова внутренняя энергия идеального одноатомного газа
Задача №105Какова внутренняя энергия идеального одноатомного газа 17, занимающего объем V при температуре Т, если концентрация его молекул n?
Обозначим k постоянную Больцмана. Решение. Внутренняя энергия идеального одноатомного газа определяется формулой
Нам не известны ни масса этого газа m, ни его молярная масса M, но зато известен объем газа V и температура Т, поэтому воспользуемся уравнением Менделеева-Клапейрона, в которое тоже входят эти величины: .
Таким образом, вместо мы можем в формулу внутренней энергии подставить pV. Получим
Правда, здесь нам не известно давление газа р, но его можно определить через концентрацию молекул газа и его температуру, воспользовавшись известной формулой молекулярной физики .
Тогда получим окончательно
Задача в общем виде решена.
Ответ: .
Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:
Физика — задачи с решениями и примерами
Возможно вам будут полезны ещё вот эти задачи:
Задача №103 Для охлаждения пулемета во время стрельбы в его кожух наливают V = 5 л воды при — 10°С. За каждую = 1 с пулемет производит N = 10 выстрелов. При этом в патроне сгорает = 3 г пороха. За какое время t выкипит вся вода в кожухе, если КПД процесса теплообмена , а КПД пулемета ? С какой скоростью и вылетает пуля из ствола пулемета, если ее масса г? Удельная теплота сгорания пороха q = Дж/кг, плотность воды , температура кипения воды = 100°С, удельная теплоемкость воды с = 4,2 • 103 Дж/(кг • К), удельная теплота парообразования воды Дж/кг. |
| Задача №104 При уменьшении объема одноатомного газа вдвое его давление увеличилось на 25%. Во сколько раз изменилась внутренняя энергия этого газа? |
| Задача №106 Найти изменение внутренней энергии воды массой , взятой при , при превращении ее в пар с температурой ? Удельная теплоемкость воды Дж/(кг • К), удельная теплота парообразования воды Дж/кг. |
| Задача №100 В сосуд с водой массой = 250 г при температуре = 18°С, опустили медную гирьку массой = 100 г, нагретую до = 90°С. После этого в сосуде установилась температура = 20°С. Удельная теплоемкость воды = 4186 Дж/(кг • К), удельная теплоемкость меди = 380 Дж/(кг • К). Определить теплоемкость сосуда . |
Внутренняя энергия идеального одноатомного газа в физике
Внутренняя энергия идеального одноатомного газа Поскольку молекулы идеального газа не взаимодействуют друг с другом, их потенциальная энергия считается равной нулю. Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул.
Внутренняя энергия идеального газа определяется только кинетической энергией беспорядочного поступательного движения его молекул.
Для её вычисления нужно умножить среднюю кинетическую энергию одного атома на число атомов Учитывая что получим значение внутренней энергии идеального газа:
(2.21) Внутренняя энергия идеального одноатомного газа прямо пропорциональна его температуре.
Следует отметить, что, согласно выражению для средней кинетической энергии одного атома и в силу хаотичности движения, на каждое из трёх возможных направлений движения, или каждую степень свободы, по оси приходится одинаковая энергия
Число степеней свободы — это число возможных независимых направлений движения молекулы.
Газ, каждая молекула которого состоит из двух атомов, называется двухатомным. Каждый атом может двигаться по трём направлениям, поэтому общее число возможных направлений движения — 6.
Средняя кинетическая энергия двухатомной молекулы равна . Соответственно, внутренняя энергия идеального двухатомного газа равна:
Формулы для внутренней энергии идеального газа можно обобщить:
где — число степеней свободы молекул газа ( для одноатомного и для двухатомного газа).
Для идеальных газов внутренняя энергия зависит только от одного макроскопического параметра — температуры и не зависит от объёма, т. к. потенциальная энергия равна нулю (объём определяет среднее расстояние между молекулами).
Эта лекция взята со страницы лекций по всем темам предмета физика:
Предмет физика
Возможно эти страницы вам будут полезны:
Идеальный одноатомный газ.
 Формула внутренней энергии. Решение задач
Формула внутренней энергии. Решение задачИзучение свойств и поведения идеального газа является ключевым моментом для понимания физики этого направления в целом. Рассмотрим в данной статье, что включает в себя концепция идеального одноатомного газа, какими уравнениями описываются его состояние и внутренняя энергия. А также решим пару задач по этой теме.
Общее понятие
Каждый школьник знает, что газ – это одно из трех агрегатных состояний вещества, которое, в отличие от твердого и жидкого, не сохраняет объем. Кроме того, он также не сохраняет свою форму и всегда заполняет полностью предоставленный ему объем. В действительности последнее свойство относится к так называемым идеальным газам.
Концепция идеального газа тесно связана с молекулярно-кинетической теорией (МКТ). В соответствии с ней частицы газовой системы движутся хаотически во всех направлениях. Их скорости подчиняются распределению Максвелла. Частицы не взаимодействуют друг с другом, и расстояния между ними намного превышают их размеры. Если все перечисленные условия соблюдаются с определенной точностью, то газ можно считать идеальным.
Если все перечисленные условия соблюдаются с определенной точностью, то газ можно считать идеальным.
Любые реальные среды близки по своему поведению к идеальным, если они имеют невысокие плотности и высокие абсолютные температуры. Кроме того, они должны состоять из химически неактивных молекул или атомов. Так, водяной пар из-за присутствия между молекулами H2O сильных водородных взаимодействий не считается идеальным газом, а воздух, состоящий из неполярных молекул, является им.
Закон Клапейрона-Менделеева
Во время анализа, с точки зрения МКТ, поведения газа в равновесии можно получить следующее уравнение, которое связывает основные термодинамические параметры системы:
P * V = n * R * T.
Здесь давление, объем и температура обозначены латинскими буквами P, V и T соответственно. Величина n – это количество вещества, которое позволяет определить число частиц в системе, R – газовая постоянная, не зависящая от химической природы газа. Она равна 8,314 Дж/(К*моль), то есть любой идеальный газ в количестве 1 моль при его нагреве на 1 К, расширяясь, совершает работу 8,314 Дж.
Она равна 8,314 Дж/(К*моль), то есть любой идеальный газ в количестве 1 моль при его нагреве на 1 К, расширяясь, совершает работу 8,314 Дж.
Записанное равенство называется универсальным уравнением состояния Клапейрона-Менделеева. Почему? Названо оно так в честь французского физика Эмиля Клапейрона, который в 30-е годы XIX века, изучая установленные до этого экспериментальные газовые законы, записал его в общем виде. Впоследствии Дмитрий Менделеев привел его к современной форме, введя константу R.
Внутренняя энергия одноатомной среды
Одноатомный идеальный газ отличается от многоатомного тем, что его частицы обладают всего тремя степенями свободы (поступательное движение вдоль трех осей пространства). Этот факт приводит к следующей формуле средней кинетической энергии одного атома:
m * v2 / 2 = 3 / 2 * kB * T.
Скорость v называется средней квадратичной. Масса атома и постоянная Больцмана обозначена как m и kB соответственно.
Согласно определению внутренней энергии, она представляет собой сумму кинетической и потенциальной составляющих. Рассмотрим подробнее. Так как потенциальной энергией идеальный газ не обладает, то его внутренняя энергия – это энергия кинетическая. Какова ее формула? Рассчитывая энергию всех частиц N в системе, получим следующее выражение для внутренней энергии U одноатомного газа:
U = 3 / 2 * n * R * T.
Примеры по теме
Задача №1. Идеальный одноатомный газ переходит из состояния 1 в состояние 2. Масса газа при этом остается постоянной (закрытая система). Необходимо определить изменение внутренней энергии среды, если переход является изобарным при давлении, равном одной атмосфере. Дельта объема сосуда с газом составила три литра.
Выпишем формулу для изменения внутренней энергии U:
ΔU = 3 / 2 * n * R * ΔT.
Воспользовавшись уравнением Клапейрона-Менделеева, это выражение можно переписать в виде:
ΔU = 3 / 2 * P * ΔV.
Давление и изменение объема нам известно из условия задачи, поэтому остается перевести их значения в СИ и подставить в формулу:
ΔU = 3 / 2 * 101325 * 0,003 ≈ 456 Дж.
Таким образом, когда одноатомный идеальный газ переходит из состояния 1 в состояние 2, его внутренняя энергия возрастает на 456 Дж.
Задача №2. Идеальный одноатомный газ в количестве 2 моль находился в сосуде. После изохорного нагрева его энергия возросла на 500 Дж. Как изменилась при этом температура системы?
Снова выпишем формулу для изменения величины U:
ΔU = 3 / 2 * n * R * ΔT.
Из нее несложно выразить величину изменения абсолютной температуры ΔT, имеем:
ΔT = 2 * ΔU / ( 3 * n * R ).
Подставляя данные для ΔU и n из условия, получаем ответ: ΔT = +20 К.
Важно понимать, что все приведенные расчеты справедливы только для одноатомного идеального газа. Если система образована многоатомными молекулами, то формула для U уже будет не верна. Закон Клапейрона-Менделеева справедлив для любого идеального газа.
Закон Клапейрона-Менделеева справедлив для любого идеального газа.
Внутренняя энергия идеального одноатомного газа, находящегося при температуре 27 °С, равна 15
Легковая автомашина массой 1540 кг притормаживает на прямолинейном отрезке дороги. Модуль ускорения равен 1,3 мс2, а действующая на машину сила тяги р … авна 250 Н. Чему равна результирующая сила машины? Fрез = Н (округли до единиц). Чему равна сила сопротивления? Fс = Н (округли до единиц).
1. Повец, двигаясь относительно воды перпендикулярно течению со скоростью 5 км/ч, переплывает реку. Скорость течения 3.24 км/ч. Определите: а) скорост … ь пловца относительно берега: Б) под каким углом к берегу плывет ловец?
Три тела с массами m1 = 0,3 кг, m2 = 0,4 кг, т3 = 0,5 кг соединены невесомыми и нерастяжимыми нитями (рис. 117). Коэффициент трения между телами и гор … изонтальной поверхностью равен µ = 0,3. Чему равны силы натяжения каждой нити в случае, если сила F = 6 Н?
Во сколько раз ускорение свободного падения на высоте h = R (R- радиус Земли) меньше ускорения свободного падения на поверхности Земли (g0 = 9,8 м/с2)
… .
что такое фотосинтез?
4.У нерухомому замкнутому дротяному витку виник індукційний струм. Позначте; які з наведених тверджень правильні, а які — неправильні. А. Вільні елект … рони в дроті почали впорядковано рухатися під дією вихрового електричного поля. Б. Вільні електрони в дроті почали впорядковано рухатися під дією сили Лоренца. В. Індукційний струм виник під дією кулонівських сил. Г. Магнітний потік через виток не змінювався.
3.В однорідному магнітному полі, що змінюється, розміщена нерухома замкнута дротяна рамка. Виберіть правильне твердження. А. Якщо вектор індукції магн … ітного поля перпендикулярний до площини рамки, в рамці виникає індукційний струм. Б. Якщо вектор індукції магнітного поля перпендикулярний до площини рамки, магнітний потік через площину рамки весь час дорівнює нулю. В. ЕРС Індукції в рамці залежить тільки від площі рамки. Д. Індукційний струм у рамці виникає за будь-якого положення рамки.
1.У нерухомій дротяній рамці, що розташована в магнітному полі, виникає індукційний струм. Виберіть правильне твердження.А. Сила струму максимальна, к
… оли магнітний потік через рамку не оцінюється.Б. Сила струму прямо пропорційна опору рамки.С. Сила струму тим більша, чим повільніше змінюється магнітний потік через рамку.Д. Якщо площина рамки паралельна лініям індукції магнітного поля, магнітний потік через рамку дорівнює нулю.
Виберіть правильне твердження.А. Сила струму максимальна, к
… оли магнітний потік через рамку не оцінюється.Б. Сила струму прямо пропорційна опору рамки.С. Сила струму тим більша, чим повільніше змінюється магнітний потік через рамку.Д. Якщо площина рамки паралельна лініям індукції магнітного поля, магнітний потік через рамку дорівнює нулю.
як довести що світло відбите від поверхні води є частково поляризованим?
скільки енергії витратили на нагрівання спирту масою 1,33 кг від 25 до 78°С і подальшого утворення пари масою 330 г?
Идеальный газ, внутренняя энергия – Энциклопедия по машиностроению XXL
Действительно, для идеального газа, внутренняя энергия которого является функцией только температуры, частная производная [c.71]Для идеального газа внутренняя энергия не зависит от объема, а в процессе дросселирования газ не совершает работы и не участвует в теплообмене с внешней средой, т. е. внутренняя энергия должна оставаться постоянной.
[c.139]
е. внутренняя энергия должна оставаться постоянной.
[c.139]
Этот факт имеет простое объяснение с позиций кинетической теории идеального газа внутренняя энергия его представляет собой сумму кинетических энергий поступательного движения (для одноатомных молекул) отдельных частиц, равную где [c.23]
Для идеального газа внутренняя энергия не зависит от объёма — закон Джоуля. [c.433]
Для идеального газа внутренняя энергия определяется только его температурой, т. е. [c.55]
Предположим, что рабочим телом цикла является идеальный газ с постоянной теплоемкостью. Поскольку у идеального газа внутренняя энергия и зависит только от температуры, то [c.57]
Напомним, что в этом примере речь идет об источнике работы, обладающем свойствами идеального газа внутренняя энергия идеального газа зависит только от температуры [и не зависит от давления, см. уравнение (2-35)]. Как отмечалось выше, работа в адиабатном процессе производится за счет изменения внутренней энергии.
[c.104]
уравнение (2-35)]. Как отмечалось выше, работа в адиабатном процессе производится за счет изменения внутренней энергии.
[c.104]
Так как для идеального газа внутренняя энергия зависит только от температуры и не зависит от объема, то в соответствии с уравнением (2-37) [c.229]
Оказывается возможным провести аналогию между идеальным газом и парамагнетиком. У идеальных газов внутренняя энергия V зависит только от температуры и не зависит от объема Я= Я(Г). [c.73]
Для случая так называемого соверщенного (идеального) газа внутренняя энергия единицы массы равна [c.90]
В случае идеального газа внутренняя энергия (а также и энтальпия) не за- [c.39]
У идеальных газов внутренняя энергия не зависит от давления и объема, а зависит только от температуры. Поэтому для этих газов [c.25]
Таким образом, непосредственный опыт дает нам возможность утверждать, что изменение объема и давления при неизменной температуре не приводит к изменению внутренней энергии. Следовательно, для идеального газа внутренняя энергия является функцией одной только температуры, т. е.
[c.67]
Следовательно, для идеального газа внутренняя энергия является функцией одной только температуры, т. е.
[c.67]
Выше было установлено ( И), что для идеального газа внутренняя энергия и энтальпия зависят только от температуры. Следовательно, для изотермического процесса получим [c.93]
Идеальный газ, внутренняя энергия [c.300]
Отсюда следует, что энтальпия является величиной, определяемой состоянием тела, и, в свою очередь, она определяет состояние тела, т. е. является параметром состояния. Действительно, для идеального газа внутренняя энергия и, произведение pv, равное КТ, зависят только от температуры, поэтому энтальпия идеального газа зависит только от температуры. [c.31]
Для идеального газа внутренняя энергия не зависит от объёма. [c.511]
АТ — 0, следовательно, и ЛQ = 0. Таким образом, согласно первому закону термодинамики, изменение внутренней энергии газа и = 0.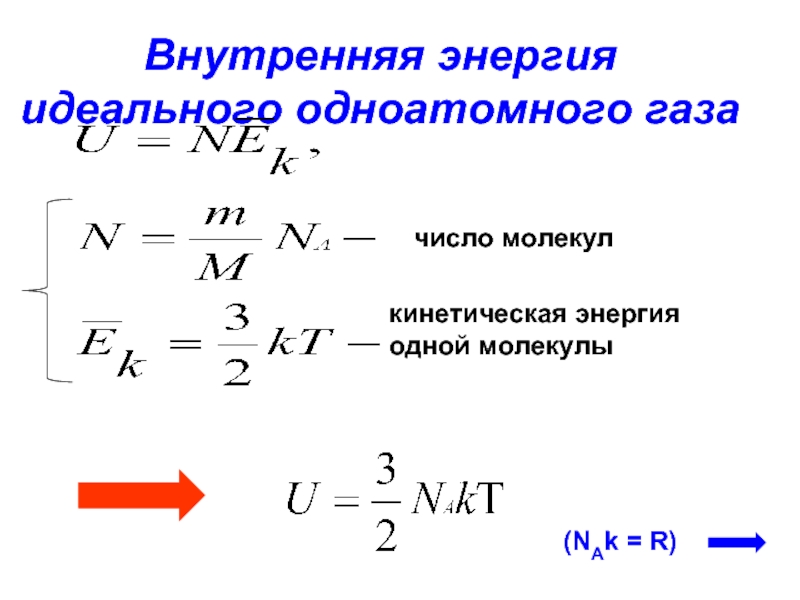 Иными словами, два состояния идеального газа, характеризующиеся одинаковой температурой, но разным объемом, имеют одну и ту же внутреннюю энергию. Поскольку температуру и объем можно выбрать в качестве независимых переменных и поскольку внутренняя энергия и является функцией состояния, мы приходим к выводу, что для идеального газа внутренняя энергия и является функцией только температуры. К этому выводу можно прийти также и теоретически на основе второго закона термодинамики, не обращаясь к специальному эксперименту.
[c.17]
Иными словами, два состояния идеального газа, характеризующиеся одинаковой температурой, но разным объемом, имеют одну и ту же внутреннюю энергию. Поскольку температуру и объем можно выбрать в качестве независимых переменных и поскольку внутренняя энергия и является функцией состояния, мы приходим к выводу, что для идеального газа внутренняя энергия и является функцией только температуры. К этому выводу можно прийти также и теоретически на основе второго закона термодинамики, не обращаясь к специальному эксперименту.
[c.17]
Задача 24. Для идеального парамагнетика, для которого поляризационная внутренняя энергия S m зависит только от температуры и не зависит от М (как для идеального газа внутренняя энергия зависит только от в, но не зависит от V), показать, что уравнение состояния М = М в,Н) и сдвиг энтропии А8 в,Н) = 8 в,Н) – So 0), где So 0) — энтропия системы в случае Af = О, Я = О, имеют вид [c.
 170]
170]В отличие от идеальных газов, внутренняя энергия которых зависит только от температуры или, другими словами, от кинетической энергии молекул, в реальных газах внутренняя энергия слагается из двух составляющих кинетической энергии отдельных молекул или их ассоциаций и потенциальной составляющей. [c.21]
В идеальном газе силы сцепления между молекулами отсутствуют, следовательно, нет и потенциальной энергии, которая обусловлена наличием сил сцепления. Поэтому для идеального газа внутренняя энергия представляет собой функцию, только температуры газа и только ею и определяется. Формулы для определения внутренней энергии даны в 3.1. [c.22]
Поскольку изменение внутренней энергии не зависит от характера процесса и для идеального газа внутренняя энергия является функцией только температуры, то формула (2.5) будет общей для определения изменения внутренней энергии идеального газа во всех термодинамических процессах, в которых температура газа изменяется от до Tg. Очевидно, что при AU > О Т > Ti и при AU С О Т СТ .
[c.26]
Очевидно, что при AU > О Т > Ti и при AU С О Т СТ .
[c.26]
Для идеальных газов внутренняя энергия не зависит ни от объема, ни от давления, следовательно, Аиг,у=Аиг,р-Лиг. Для реальных газов при невысоких давлениях это равенство выполняется приближенно. Комбинируя уравнения (5.37), (5.38) и (5.39), имеем [c.253]
В той мере, в какой воздух, используемый для сгорания, и продукты сгорания можно рассматривать как идеальные газы, теплота сгорания оказывается не зависящей от давления. Это связано с тем, что для идеальных газов внутренняя энергия и энтальпия не зависят от давления и объема и являются функциями только температуры. [c.212]
В технической термодинамике рассматриваются только такие процессы, в которых изменяются кинетическая и потенциальная составляющие внутренней энергии. При этом знания абсолютных значений внутренней энергии не требуется. Поэтому в понятие внутренней энергии будем в дальнейшем включать для идеальных газов кинетическую энергию движения молекул и энергию колебательных движений атомов в молекуле, а для реальных газов еще дополнительно и потенциальную составляющую энергии, связанную с наличием сил взаимодействия между молекулами и зависящую от расстояния между ними. [c.54]
[c.54]
Найдем выражение внутренней энергии U как термодинамического потенциала для идеального (одноатомного) газа. Известно, что для такого газа внутренняя энергия равна [c.110]
Логично принять за условие протекания таких процессов постоянство распределения подводимой теплоты между внутренней энергией газа и работой, которую он совершает. Для получения наиболее ценных обобщений и простых формул изучение уравнений первого закона термодинамики проводится для 1 кг идеального газа, т. е. газа, внутренняя энергия которого является функцией только температуры, а теплоемкость не зависит от температуры и является постоянной. Пусть в изучаемом процессе на изменение внутренней энергии расходуется ф-я часть всей подводимой теплоты [c.50]
Внутренняя энергия тела U представляет собой энергию, обусловленную движением и силами взаимодействия частиц рабочего тела (молекул, атомов, электронов, атомных ядер), и, следовательно, равна сумме кинетической и потенциальной энергий этих частиц. Отсюда следует, что для реальных рабочих тел внутренняя энергия является функцией основных термодинамических параметров состояния т. е. и = f (р, v), и = (р(р, Т) и и = v /(ii, Г). Для идеальных газов потенциальная энергия мельчайших частиц рабочего тела равна нулю и, следовательно, внутренняя энергия их равна кинетической энергии, которая, в свою очередь, является функцией только температуры. Отсюда следует, что внутренняя энергия идеального газа есть функция температуры, т. е. и = j (Т). Молекулярно-кинетическая теория вещества дает для идеального газа следующую конкретную зависимость внутренней энергии одного киломоля от температуры
[c.12]
Отсюда следует, что для реальных рабочих тел внутренняя энергия является функцией основных термодинамических параметров состояния т. е. и = f (р, v), и = (р(р, Т) и и = v /(ii, Г). Для идеальных газов потенциальная энергия мельчайших частиц рабочего тела равна нулю и, следовательно, внутренняя энергия их равна кинетической энергии, которая, в свою очередь, является функцией только температуры. Отсюда следует, что внутренняя энергия идеального газа есть функция температуры, т. е. и = j (Т). Молекулярно-кинетическая теория вещества дает для идеального газа следующую конкретную зависимость внутренней энергии одного киломоля от температуры
[c.12]
Хаотическое движение молекул, являющееся своеобразной особенностью внутренней энергии идеального газа, отличает энергию этого вида движения от энергий направленного движения. В отличие от неорганизованного характера внутренней энергии идеального газа, каждая молекула которого движется в своем направлении и со своей скоростью, в случае энергии направленного характера, свойственного механической, электрической и другим видам энергии, движение тел, молекул или электронов происходит в определенном направлении (вращение вала, движение газа по трубе, движение электрического тока по проводнику).
 Эта характерная особенность тепловой энергии проявляется и в том,
[c.24]
Эта характерная особенность тепловой энергии проявляется и в том,
[c.24]Для идеального газа внутренняя потенциальная энергия, не зависящая от р или V, в расчет не принимается и уравнение (43) превращается в более простое [c.31]
Согласно основному постулату кинетической теории газов внутренняя энергия идеальных газов прямо пропорциональна абсолютной температуре Т, т. е. [c.20]
Важным параметром в термодинамике является внутренняя энергия газа. Внутренняя энергия идеального газа U складывается из кинетической энергии внутримолекулярных колебаний. Удельная внутренняя энергия и представляет собой внутреннюю энергию единицы веса вещества [c.21]
Обстоятельства, определяющие внутреннюю энергию газа— движение молекул и сила взаимодействия между ними, — определяются параметрами состояния газа (например, давлением и темиературой), поэтому внутренняя энергия также может служить параметром состояния газа для идеального таза внутренняя энергия зависит только,от температуры, так как в нем силы взаимодействия между молекулами отсутствуют.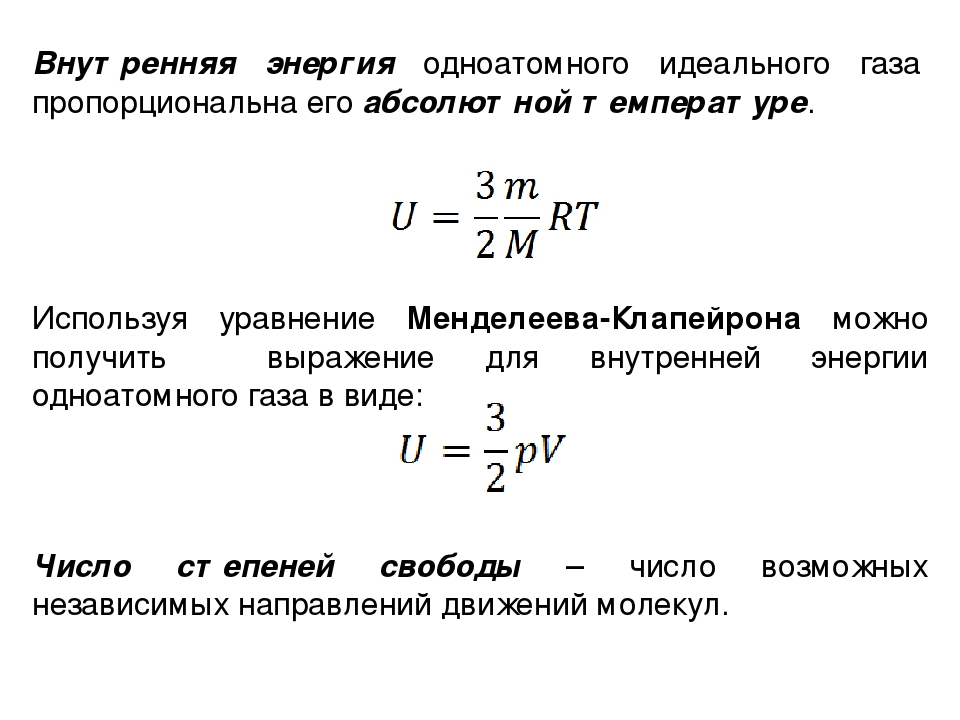 Отсюда следует, что внутренняя энергия идеального газа не зависит от характера процесса, и поэтому количество тепла, затрачиваемое на изменение внутренней энергии, обозначаемое Ли, в любом процессе идеального газа можно подсчитать так, как будто процесс происходит при постоянном объеме, т. е. можно считать, что в любом процессе с идеальным тазом на 1 кг его
[c.23]
Отсюда следует, что внутренняя энергия идеального газа не зависит от характера процесса, и поэтому количество тепла, затрачиваемое на изменение внутренней энергии, обозначаемое Ли, в любом процессе идеального газа можно подсчитать так, как будто процесс происходит при постоянном объеме, т. е. можно считать, что в любом процессе с идеальным тазом на 1 кг его
[c.23]
Найдем выражение для разности между Ср и Су. Рассмотрим сначала Су для многоатомного идеального газа. Его энергия с хорошей точностью равна сумме вкладов от поступательного и внутренних движений последние складываются из колебательного и вращательного движений. Таким образо.м, [c.147]
Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от объема газа или давления [ du/dv)j- = 0, (du/dp)j = 0 a определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная
[c. 12]
12]
Для задач технической термодинамики важно не абсолютное значение внутренней энергии, а ее изменение в различных термодинамических процессах. Поэтому начало отсчета внутренней энергии может быть выбрано произвольно. Например, в соответствии с международным соглашением для воды за нуль принимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при [c.12]
Это уравнение показывает связь между теплоемкостями Ср и v Для идеального газа оно значительно упрощается. Действительно, внутренняя энергия идеального газа определяется только его температурой и не зависит от объема, поэтому ди/ди)т = 0 и, кроме того, из уравнения состояния (1.3) следует р (ди/дТ)р = R, откуда [c.16]
Уравнения (1.3), (1.4) для идеального газа легко получить из молекулярно-кинетических представлений, даже не прибегая к общим статистическим методам. Так, закон (1.4) непосредс]-венно следует из того, что для системы из невзаимодействующих частиц (идеальный газ) внутренняя энергия равна (в среднем) сумме кинетических энергий этих частиц, которая не зависит от объема, занимаемого газом при данной температуре. [c.31]
[c.31]
Любая пара величин (параметров) из приведенных выше шести определяет состояние реального вещества, а состояние идеального газа —кроме пар (Т, и), Т, i), (и, t), так как для идеального газа внутренняя энергия и и энтальпия t являются функциями толйко температуры. [c.40]
При изотермическом изменении состояния идеального газа внутренняя энергия, являющаяся функцией температуры, не меняется и поэтому согласно выражению (1.42) количество полученной теплоты и произведенная работа равны друг другу, т. е. q = I. Если процесс обратим, то dl = р dv = (RT/p) dp и, следовательно, q = I RT- X X in ipilp2)- Это выражение получается из выражений [c.50]
Для одной грамм-молекулы идеального газа внутренняя энергия Ui=dT, где с[c.189]
Значение потенциальной энергии взаимодейстБия всех молекул, содержащихся в 1 кг реального газа, можно получить, разбив все молекулы на пары и сложив потенциальные энергии парных взаимодействий всех возможных пар. Очевидно, что это значение зависит от среднего расстояния между молекулами и, следовательно, от удельного объема газа. Таким образом, в противоположность внутренней энергии идеального газа, которая не зависит от объема, у реального газа внутренняя энергия является функцией удельного объема, а следовательно, Рис. 6-2. и давления.
[c.84]
Очевидно, что это значение зависит от среднего расстояния между молекулами и, следовательно, от удельного объема газа. Таким образом, в противоположность внутренней энергии идеального газа, которая не зависит от объема, у реального газа внутренняя энергия является функцией удельного объема, а следовательно, Рис. 6-2. и давления.
[c.84]
Отсюда вытекает зависимость между тепловыми эффектами изобарной и изохорной реакции. Действительно, для идеального газа внутренняя тепловая энергия зависит лишь от температуры, химическая же внутренняя энергия вообще не зависит от параметров состояния и определяется лишь природой компонентов реакции. Следовательно, если осуществить одну и ту же реакцию при одной и той же температуре один раз при постоянном объеме, а другой раз при постоянном давлении, то в обоих случаях изменение внутренней энергии (представляющей собой сумму внутренней тепловой и внутренней химической энергии) будет одинаковым. Поскольку Qv=lJi—f/г, Qp=Ui—U2—p(l 2—l i), a р Уг—= = AnRT,
[c. 264]
264]
Таким образом, чтобы оценить абсолютное значение внутренней энергии системы, необходимо принять во в1нимание все эти формы движения. Обычно, в соответствии с содержанием исследуемой задачи, рассматриваются весьма упрощенные схемы. Так,, например, рассматривается модель идеального одноатомкого газа, внутренняя энергия которого сводится только к энергии поступательного движения молекул. В случае идеального многоатомного-газа внутреннюю энергию определяют как сумму энергий поступательного и вращательного движений молекул. При высоких температурах к этому добавляют еще энергию колебания атомов, в молекуле. При большем пррцближении к свойствам реальных систем определение величины внутренней энергии весьма затруднительно, так как при этом пришлось бы учитывать также энергию взаимодействия молекул и атомов, энергию электронов, внутриядерную энергию и т. п. [c.25]
Внутренняя энергия
Прежде чем приступить к изучению нового материала, давайте с
вами вспомним, чем мы занимались при изучении молекулярно-кинетической теории. Там наша основная задача заключалась в установлении связи между
макроскопическими параметрами, характеризующими состояние системы, и её микроскопическими
параметрами. Это позволило нам объяснить, почему газ оказывает давление на
стенки сосуда, что такое температура и так далее.
Там наша основная задача заключалась в установлении связи между
макроскопическими параметрами, характеризующими состояние системы, и её микроскопическими
параметрами. Это позволило нам объяснить, почему газ оказывает давление на
стенки сосуда, что такое температура и так далее.
Также мы с вами вывели уравнение состояния идеального газа. Удалось нам это сделать только потому, что мы рассматривали самую простую систему — идеальный газ. Напомним, что в идеальном газе отсутствуют взаимодействия между молекулами, и поэтому нам не нужно было учитывать потенциальную энергию их взаимодействия. Однако, если бы мы попытались построить молекулярно-кинетическую теорию реального газа (не говоря уже о жидкостях и твёрдых телах), то всё было бы гораздо сложнее, а порой и почти невозможно.
Но существует ещё один раздел молекулярной физики, который
пытается установить соответствия между макроскопическими параметрами, абсолютно
не интересуясь, как устроена система (то есть без учёта молекулярного строения
тел). Этот раздел физики называется термодинамикой.
Этот раздел физики называется термодинамикой.
Интересно, что первой научной теорией тепловых процессов была не молекулярная физика, а именно термодинамика. Считается, что она берёт своё начало с работы Сади Карно «О движущей силе огня и о машинах, способных развивать эту силу», опубликованной в 1824 году.
А становление термодинамики как науки началось примерно в 40-х годах XIX века после того, как Юлиус Майер, Герман Гельмгольц и Джеймс Джоуль количественно определили связь между механической работой и теплотой и сформулировали универсальный закон сохранения и превращения энергии.
Выводы термодинамики основаны на фундаментальных законах, называемых началами термодинамики. Это не теоретические законы. Все они были установлены в результате обобщения многочисленных экспериментальных фактов.
Все физические тела и их модели в термодинамике мы будем
называть термодинамическими системами. При этом для каждой
изолированной термодинамической системы существует состояние термодинамического
равновесия, в которое она переходит самопроизвольно. Это утверждение называют нулевым
началом термодинамики.
При этом для каждой
изолированной термодинамической системы существует состояние термодинамического
равновесия, в которое она переходит самопроизвольно. Это утверждение называют нулевым
началом термодинамики.
Основным понятием в термодинамике является понятие внутренней энергии, о которой мы говорили ещё в восьмом классе. Давайте с вами вспомним, что под внутренней энергией тела (или системы тел) понимают сумму кинетической энергии хаотического теплового движения молекул и потенциальной энергии их взаимодействия.
Обозначают внутреннюю энергию большой латинской буквой U. А измеряют её в тех же единицах, что и механическую энергию, то есть в джоулях.
[U] = [Дж].
Теперь давайте с вами вспомним, от каких величин зависит
внутренняя энергия тела или системы тел. Мы уже с вами знаем, что чем выше
температура тела, тем быстрее движутся его молекулы и тем больше их
кинетическая энергия. Значит, внутренняя энергия тела зависит от его
температуры.
Значит, внутренняя энергия тела зависит от его
температуры.
Также нам известно, что для перевода вещества, например, из жидкого состояния в газообразное, нужно к веществу подвести энергию. Следовательно, пар будет обладать большей внутренней энергией, чем жидкость той же массы. Значит, внутренняя энергия тела при неизменной массе зависит от его агрегатного состояния.
Ну а так как масса тела равна сумме масс составляющих его частиц, то внутренняя энергия зависит и от массы тела.
Но внутренняя энергия тела не зависит от его механического движения и от его взаимодействия с другими телами. Так, например, внутренняя энергия мяча, лежащего на полу и поднятого на некоторую высоту от пола, одинакова, так же как и мяча, неподвижного и катящегося по полу (если, конечно, пренебречь силами сопротивления его движению).
Рассчитать внутреннюю энергию можно только для идеального
газа. Давайте с вами определим внутреннюю энергию идеального одноатомного газа,
то есть газа, состоящего из отдельных атомов (к такому газу относятся инертные
газы — гелий, неон, аргон и так далее).
Итак, согласно модели идеального газа, его молекулы не взаимодействуют друг с другом. Поэтому внутренней энергией такого газа является сумма кинетических энергий хаотического движения всех его молекул или атомов. Следовательно, внутренняя энергия идеального одноатомного газа равна произведению средней кинетической энергии теплового движения молекул на их число:
Число молекул в данной порции газа мы можем легко выразить из определения количества вещества:
А значение средней кинетической энергии поступательного движения молекул мы распишем через постоянную Больцмана и абсолютную температуру:
Перепишем формулу для внутренней энергии с учётом последних двух формул:
Теперь давайте с вами вспомним, что произведение постоянной Больцмана и числа Авогадро — это есть универсальная газовая постоянная R. Тогда получаем, что внутренняя энергия идеального одноатомного газа прямо пропорциональна его абсолютной температуре и не зависит от других макроскопических параметров системы:
Для примера давайте с вами определим внутреннюю энергию неона
массой 5 г, находящегося при температуре 27 оС.
Как правило, значение внутренней энергии в большинстве случаев вычислить очень трудно, поскольку каждое тело состоит из огромного числа частиц. Однако нас чаще будет интересовать не само значение внутренней энергии, а её изменение, которое происходит при переходе системы из одного состояния в другое.
Под приращением (или изменением) внутренней энергии понимают разность внутренних энергий системы в конечном и начальном состояниях:
∆U = U2 – U1.
Например, переход некоторой массы идеального газа из состояния один в состояние три можно осуществить или в ходе изохорного нагревания и последующим изобарным расширением, или при изобарном расширении, а затем при изохорном нагревании. Однако изменение внутренней энергии газа и в одном и в другом случае будет одинаковым:
∆U123
= ∆U143 = U3 – U1.
Иными словами, внутренняя энергия является функцией состояния системы. Это означает, что изменение внутренней энергии при переходе термодинамической системы из одного состояния в другое зависит только лишь от значений параметров этих состояний, а не от процесса перехода.
В частности, изменение внутренней энергии данной масса идеального одноатомного газа происходит только при изменении его температуры:
В качестве примера решим такую задачу. На рисунке в координатах (p, V) изображён процесс перехода идеального одноатомного газа определённой массы из состояния 1 в состояние 2. Определите приращение внутренней энергии газа, если его давление в конечном состоянии составляет 2 МПа, а объём в начальном состоянии был равен 3,0 л.
В заключении урока отметим, что при определении внутренней
энергии реальных газов, жидкостей и твёрдых тел необходимо ещё учитывать и потенциальную
энергию взаимодействия частиц, которая зависит от расстояния между ними.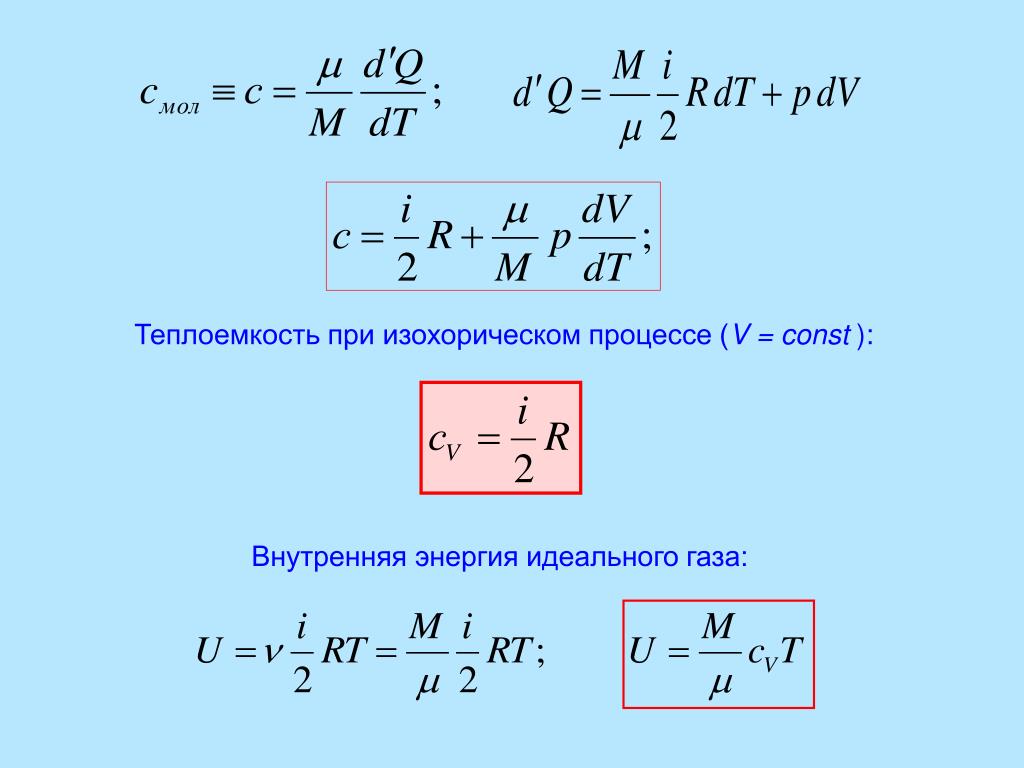 Поэтому в общем случае внутренняя энергия макроскопических тел зависит не
только от абсолютной температуры, но и от объёма.
Поэтому в общем случае внутренняя энергия макроскопических тел зависит не
только от абсолютной температуры, но и от объёма.
При изучении физики в восьмом классе вы узнали, что изменить состояние термодинамической системы можно двумя способами: используя теплопередачу или совершая работу. Процесс теплопередачи и совершение работы характеризуют соответственно физическими величинами — количеством теплоты Q и работой А, которые являются мерами изменения внутренней энергии системы.
Внутренняя энергия – Идеальный газ – Одноатомный, Двухатомный газ
Внутренняя энергия n молей идеального одноатомного (один атом на молекулу) газа равна средней кинетической энергии на молекулу, умноженной на общее количество молекул, N:
E int = 3/2 NkT = 3/2 nRT
Для двухатомного идеального газа:
E int = 5/2 NkT = 5/2 nRT
Внутренняя энергия – это сумма всей энергии, связанной с движением атомов или молекул в системе. Микроскопические формы энергии включают те, которые обусловлены вращением , вибрацией , трансляцией и взаимодействиями между молекулами вещества.
Микроскопические формы энергии включают те, которые обусловлены вращением , вибрацией , трансляцией и взаимодействиями между молекулами вещества.
Одноатомный газ – внутренняя энергия
Для одноатомного идеального газа (такого как гелий, неон или аргон) единственный вклад в энергию дает поступательная кинетическая энергия . Средняя поступательная кинетическая энергия одиночного атома зависит только от от температуры газа и определяется уравнением:
K avg = 3/2 kT.
Внутренняя энергия n молей идеального одноатомного (один атом на молекулу) газа равна средней кинетической энергии на молекулу, умноженной на общее количество молекул, N:
E int = 3/2 NkT = 3/2 nRT
, где n – количество молей, каждое направление (x, y и z) дает вклад (1/2) nRT во внутреннюю энергию . Вот здесь-то и появляется равнораспределение энергетической идеи – любой другой вклад в энергию также должен давать (1/2) nRT .Как видно, внутренняя энергия идеального газа зависит только от температуры и количества молей газа.
Вот здесь-то и появляется равнораспределение энергетической идеи – любой другой вклад в энергию также должен давать (1/2) nRT .Как видно, внутренняя энергия идеального газа зависит только от температуры и количества молей газа.
Двухатомная молекула – внутренняя энергия
Если молекулы газа содержат более одного атома, имеется трех направлений трансляции и кинетическая энергия вращения участвует, но только для вращений вокруг двух из трех перпендикулярных осей. Пять вкладов в энергию (пять степеней свободы) дают:
Двухатомный идеальный газ:
E int = 5/2 NkT = 5/2 nRT
Это только приближение и применяется к промежуточные температуры. Только поступательная кинетическая энергия вносит вклад при низких температурах , а при более высоких температурах два дополнительных вклада (кинетическая и потенциальная энергия) происходят от вибрации. Внутренняя энергия будет больше при данной температуре, чем для одноатомного газа, но она по-прежнему будет работать только как температура для идеального газа.
Внутренняя энергия будет больше при данной температуре, чем для одноатомного газа, но она по-прежнему будет работать только как температура для идеального газа.
Внутренняя энергия реальных газов также зависит, главным образом, от температуры, но, как и в случае с Законом идеального газа , внутренняя энергия реальных газов также в некоторой степени зависит от давления и объема .Все реальные газы приближаются к идеальному состоянию при низких давлениях (плотностях). При низких давлениях молекулы находятся достаточно далеко друг от друга, чтобы не взаимодействовать друг с другом. Внутренняя энергия жидкостей и твердых тел довольно сложна, поскольку включает электрической потенциальной энергии , связанной с силами (или химических связей ) между атомами и молекулами.
Удельная теплоемкость при постоянном объеме и постоянном давлении
Удельная теплоемкость – это свойство, связанное с внутренней энергией , которое очень важно в термодинамике. Интенсивные свойства c v и c p определены для чистых простых сжимаемых веществ как частные производные внутренней энергии u (T, v) и энтальпии ч. (T, p) , соответственно:
Интенсивные свойства c v и c p определены для чистых простых сжимаемых веществ как частные производные внутренней энергии u (T, v) и энтальпии ч. (T, p) , соответственно:
, где индексы v и p обозначают переменные, фиксированные во время дифференцирования. Свойства c v и c p обозначаются как удельная теплоемкость (или теплоемкость ).При определенных условиях они связывают изменение температуры в системе с количеством энергии, добавляемой за счет теплопередачи. Их единицы СИ: Дж / кг K, или Дж / моль K . Для газов определены две удельные теплоты: постоянного объема (c v ), и постоянного давления (c p ) .
Согласно первому закону термодинамики , для процесса постоянного объема с одноатомным идеальным газом молярная удельная теплоемкость будет:
C v = 3 / 2R = 12.5 Дж / моль K
, потому что
U = 3 / 2nRT
Можно вывести, что молярная теплоемкость при постоянном давлении составляет:
C p = C v + R = 5 / 2R = 20,8 Дж / моль K
Это C p больше, чем молярная удельная теплоемкость при постоянном объеме C v , потому что теперь энергия должна быть поставляемый не только с по поднимает температуру газа , но также для газа , чтобы выполнять работу , потому что в этом случае изменяется объем.
Ссылки:
Reactor Physics and Thermal Hydraulics:- Дж.
 Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).
Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983). - Дж. Р. Ламарш, А. Дж. Баратта, Введение в ядерную инженерию, 3-е изд., Прентис-Холл, 2001, ISBN: 0-201-82498-1.
- У. М. Стейси, Физика ядерных реакторов, John Wiley & Sons, 2001, ISBN: 0-471-39127-1.
- Гласстон, Сесонске. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4-е издание, 1994, ISBN: 978-0412985317
- Тодреас Нил Э., Казими Муджид С. Ядерные системы Том I: теплогидравлические основы, второе издание. CRC Press; 2 издание, 2012 г., ISBN: 978-0415802871
- Зохури Б., МакДэниел П. Термодинамика в системах атомных электростанций. Springer; 2015, ISBN: 978-3-319-13419-2
- Моран Михал Дж., Шапиро Ховард Н. Основы инженерной термодинамики, пятое издание, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
- Кляйнштройер К. Современная гидродинамика. Springer, 2010 г., ISBN 978-1-4020-8670-0.
- Министерство энергетики США, ТЕРМОДИНАМИКА, ТЕПЛООБМЕН И ПОТОК ЖИДКОСТИ.
 Справочник Министерства энергетики США по основам, том 1, 2 и 3. Июнь 1992 г.
Справочник Министерства энергетики США по основам, том 1, 2 и 3. Июнь 1992 г.
Процессы идеального газа – Chemistry LibreTexts
В этом разделе мы поговорим о взаимосвязи идеальных газов с точки зрения термодинамики. Мы увидим, как с помощью термодинамики мы сможем лучше понять идеальные газы.
Введение
В области химии мы часто видим много взаимосвязей между первой и ее связью с физикой.Используя как химию, так и физику, мы можем лучше понять оба упомянутых аспекта. Мы будем использовать то, что мы знаем об идеальных газах и термодинамике, чтобы попытаться понять конкретные процессы, происходящие в системе.
Краткий обзор термодинамики Прежде чем мы продолжим обсуждение, давайте сделаем очень краткий обзор важных аспектов термодинамики, которые важно знать для процессов с идеальным газом. Некоторые из них будут кратким обзором, а некоторые будут относительно новыми, если вы не видели их на своем уроке физики.
Итак, прежде всего давайте сформулируем Первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Весь смысл формулировки этого уравнения состоит в том, чтобы напомнить нам, что энергия в любой данной системе сохраняется. Это означает, что энергия НИКОГДА не создается и не уничтожается, а просто преобразуется из одной формы в другую, например, тепло для работы и наоборот.
Если вас могут смутить некоторые из этих символов, вот краткое объяснение в таблице.
| ΔU | Это полное изменение внутренней энергии газа. |
| Q | Это полный тепловой поток газа. • Когда Q отрицательно (-), тепло отводится из системы • Когда Q положительно (+), в систему добавляется тепло |
| Вт | Это общая работа, проделанная на газе или им. • Когда W отрицательно (-), работа выполняется системой • Когда W положительный (+), работа выполняется в системе |
Ниже приведены два уравнения, которые описывают взаимосвязь между внутренней энергией системы одноатомного газа и двухатомного газа. В одноатомном газе ( моно – : один), поскольку он имеет только одну молекулу, способы получения энергии будут меньше, чем у двухатомного газа ( ди – : два), поскольку двухатомный газ имеет больше способов получить энергию. энергия (Следовательно, двухатомный газ имеет фактор 5/2, а одноатомный газ – 3/2).
В одноатомном газе ( моно – : один), поскольку он имеет только одну молекулу, способы получения энергии будут меньше, чем у двухатомного газа ( ди – : два), поскольку двухатомный газ имеет больше способов получить энергию. энергия (Следовательно, двухатомный газ имеет фактор 5/2, а одноатомный газ – 3/2).
Рассматривая эти два уравнения, мы также заключаем, что внутренняя энергия (ΔU) влияет только на кинетическую энергию молекул газа (движение). Нигде в этих двух уравнениях мы не видим влияния на потенциальную энергию.
Одноатомный идеальный газ
Одноатомное уравнение идеального газа:
\ (\ Delta {U} = \ frac {3} {2} nR \ Delta {T} \)
В одноатомном газе у него всего три режима поступательной кинетической энергии (отсюда 3 /2).
Двухатомный идеальный газ
Уравнение двухатомного идеального газа:
\ (\ Delta {U} = \ frac {5} {2} nR \ Delta {T} \)
В двухатомном газе он имеет в общей сложности три режима поступательной кинетической энергии и две моды вращательной энергии (отсюда 5 /2).
Работа в идеальных газах
Что касается первого закона термодинамики, мы можем видеть, что добавлением тепла (Q) или работы (W) внутренняя энергия газовой системы может быть увеличена. Кроме того, во время сжатия системы объем газа будет уменьшаться, а его температура будет увеличиваться, и, таким образом, внутренняя энергия системы также увеличится, поскольку температура связана с энергией. И это верно, за исключением изотермической системы (о которой мы поговорим позже).Поэтому при сжатии газа работа положительная, а при сжатии – отрицательная.
Также может быть полезно знать, что область под кривой – рабочая. Если вы использовали исчисление, вы можете запомнить интеграл, поскольку он используется для определения площади под кривой (или графиком), как показано ниже.
\ [W = – \ displaystyle \ int P dV \]
ИЛИ
W = – (площадь под кривой)
В этом случае можно буквально взять площадь треугольника или работать с интегралами.
Работа = Площадь = (1/2) основание x высота
или
Работа = ∫F (x) dx
Теплоемкость и функции состояния
Когда определенные функции состояния (P, V, T) поддерживаются постоянными, это влияет на удельную теплоемкость газа.
Ниже приведена универсальная формула молекулы газа при постоянном давлении:
\ (c_p = c_v + R \)
Изменив эту формулу, мы получим тепловую мощность газа, когда его объем остается постоянным:
\ (c_v = R – c_p \)
Типы процессов идеального газа
Существует четыре типа термодинамических процессов.В основном это означает, что в системе одна или несколько переменных остаются постоянными. Для простоты ниже приведены примеры того, как может привести к сохранению определенной переменной в системной константе.
Изобарический
• Это процесс, при котором давление в системе поддерживается постоянным.
• P = 0
• Примером может быть вода, кипящая в кастрюле над горелкой. В этом случае между горелкой и кастрюлей происходит обмен теплом, но давление остается постоянным.
В этом случае между горелкой и кастрюлей происходит обмен теплом, но давление остается постоянным.
Чтобы вывести этот процесс, мы начнем с использования того, что мы знаем, и это первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
Далее, поскольку давление равно W ΔV, его можно обозначить как:
\ (Q = \ Delta {U} + p \ Delta {V} \)
Теперь можно применить закон идеального газа (PV = nRΔT), и, поскольку давление постоянно:
\ (Q = ΔU + nR \ Delta {T} \)
Для следующего шага мы предположим, что это количество молей газа остается постоянным на протяжении всего процесса:
\ (Q = n \ c_V \ \ Delta {T} + nR \ Delta {T} \)
Еще больше упростив уравнение, вычеркнув nΔT из обоих уравнений, мы получим:
\ (Q = n \ (c_V + R) \ \ Delta {T} \)
Зная, что c p = c v + R, мы можем заменить cp:
\ (Q = n \ c_P \ \ Delta {T} \)
Теперь мы получили уравнение изобарического процесса!
Рисунок: Изобарический процесс в графической формеИзохорный
• Это процесс, при котором объем системы поддерживается постоянным.
• ΔV = 0
• Примером этого может быть случай, когда газообразный гелий запечатан в контейнере, и объект (например, поршень) толкает контейнер вниз (оказывая давление). Но молекулы газа не входят в систему и не выходят из нее.
Давайте найдем уравнение для этого процесса, как раньше, давайте начнем с первого закона термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
В этом случае, поскольку объем постоянный, ΔV = 0:
\ (Q = \ Delta {U} \)
Поскольку внутренняя энергия системы равна количеству переданного тепла, мы можем заменить ΔU уравнением идеального газа для тепла:
\ (Q = nC_V \ Delta {T} \)
Выше уравнение идеального газа для изохорного процесса!
Рисунок: Изохорный процесс в графической форме
Изотермический
• Это процесс, при котором температура системы поддерживается постоянной.
ΔU = 0, ΔT = 0
• При увеличении объема давление будет уменьшаться, и наоборот.
ΔT = 0, тогда: ΔV ↑ и P ↓ OR ΔV ↓ и P ↑ (обратная зависимость)
• Например, молекулы газа запечатаны в контейнере, но объект наверху контейнера ( например, поршень) давит на контейнер очень медленно, этого недостаточно, чтобы изменить его температуру.
Чтобы вывести уравнение изотермического процесса, мы должны сначала написать первый закон термодинамики:
\ (\ Delta {U} = Q + W \)
Немного изменив это уравнение, получим:
\ (Q = \ Delta {U} + W \)
Так как ΔT = 0.Остается только работа:
\ (Q = W \)
Таким образом получаем:
\ (W = -p \ Delta {V} \)
Превращая это уравнение в уравнение идеального газа, получаем:
\ (W = \ frac {nRt} {V} \)
Чтобы перейти к следующему шагу, нам нужно использовать некоторые вычисления:
\ (Q = nRT ln \ frac {V_f} {V_i} \)
И вот так! Уравнение изотермического процесса.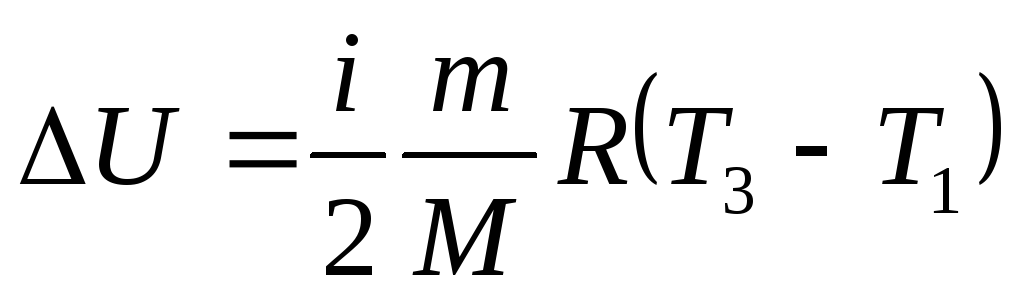
Адиабатический
• Это процесс, при котором система не нагревается и не удаляется.
• Или можно просто сформулировать так: в системе не происходит теплопередачи (или теплового потока).
• На первом курсе химии нужна только основная идея этого процесса, и это когда нет теплопередачи, Q = 0.
Задачи для практики
1
Объем газа в баллоне увеличился с 1 л до 3 л при выпуске поршня вверх.На следующем графике найдите объем работы, связанный с расширением газа.
\ (f (x) = x + 3 \) из [1, 3]
Задача 2
Кальвин наблюдает за неизвестной одноатомной молекулой газа (запечатанной внутри контейнера) в своей химической лаборатории для первокурсников. Инструктор лаборатории сообщил ему, что в контейнере находится четыре моля неопознанного газа. Когда он начал работу в лаборатории, температура в лабораторной комнате была изначально установлена на уровне комнатной, но к тому времени, когда он почти закончил с лабораторией, температура поднялась на 10 ° C.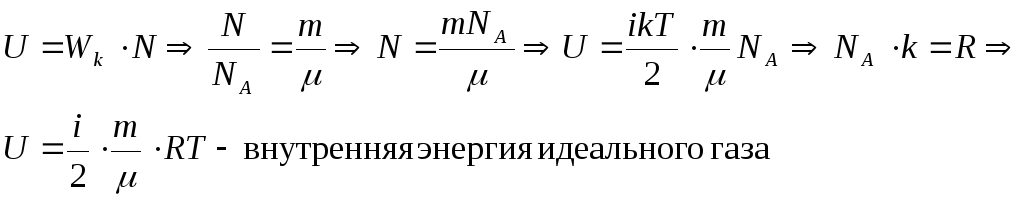 Какова полная внутренняя энергия этого неизвестного газообразного вещества к моменту окончания лабораторного сеанса Кальвина?
Какова полная внутренняя энергия этого неизвестного газообразного вещества к моменту окончания лабораторного сеанса Кальвина?
Задача 3
В изохорной системе три моля газообразного водорода удерживаются внутри закрытого контейнера с поршнем наверху. Общее количество внутренней энергии газовой системы составляет 65 Дж, а температура системы снизилась с 25 ° C до 19 ° C. Какова удельная теплоемкость молекул газа?
Задача 4
Просматривая некоторые из своих лабораторных данных, студентка-химик замечает, что она забыла записать количество молей молекулы газа, на которую она смотрела.Эксперимент, который она провела в тот день, поддерживал постоянное давление, а в процессе эксперимента температура упала на два градуса. Если предположить, что все переменные также идеальны, со сколькими родинками она имела дело?
Задача 5
Студент-химик изучает 5,00 граммов одноатомного гелия, помещенного в контейнер, который расширяется с 10 до 13 литров. Контейнер находится в закрытой системе при постоянной температуре 30 ° C. а) Какова полная энергия системы? (б) Давление в системе увеличивается, уменьшается или не изменяется?
Контейнер находится в закрытой системе при постоянной температуре 30 ° C. а) Какова полная энергия системы? (б) Давление в системе увеличивается, уменьшается или не изменяется?
Решение проблемы 1
Как указано выше, мы знаем, что объем работы равен площади под кривой.В этом случае мы можем искать формы, площадь которых легко найти.
Здесь у нас есть форма, похожая на прямоугольник.
Работа = Площадь = Длина x Ширина
= (3) (3-1)
= (3) (2)
= 6
Работа = 6 Джоулей
Решение проблемы 2
Из задачи мы знаем, что неизвестное газообразное вещество одноатомное, поэтому нам пришлось бы использовать уравнение для одноатомного газа:
\ (\ Delta {U} = \ frac {3} {2} nR \ Delta {T} \)
Также из проблемы мы знаем, что вещество имеет комнатную температуру и 25 ° C, но это была просто дополнительная информация, и нам не нужно было знать это, чтобы решить проблему. Поскольку мы знаем, что изменение температуры от начала до конца было + 10 °.
Поскольку мы знаем, что изменение температуры от начала до конца было + 10 °.
\ (\ Delta {T} = + 10K \)
Задача также дала нам количество родинок в контейнере:
\ (п = 4 моль \)
В качестве значения R мы можем выбрать любую константу R, но, чтобы немного упростить эту задачу, мы выберем константу R, которая компенсирует любые другие единицы, кроме джоулей.
\ (R = 8,3145 \ frac {J} {mol K} \)
Подставляя все эти значения в уравнение, мы получаем:
\ (\ Delta {U} = \ frac {3} {2} (4 моль) (8.3145 \ frac {J} {mol K}) (10K) \)
\ (= 498 Дж \)
Решение проблемы 3
Поскольку система является изохорной системой, изменение объема будет нулевым, следовательно:
\ (\ Delta {V} = 0 \)
И уравнение для изохорной системы будет:
\ (Q = nC_V \ Delta {T} \)
Из уравнения мы знаем следующее:
\ (n = 3 моль \)
\ (Q = \ Delta {T} = (25-19) K = 6K \)
(Поскольку мы только пытаемся найти разницу между начальной и конечной точками, нам не нужно выполнять преобразование в градусы Кельвина)
\ (Q = 65 Дж \)
Перед тем, как подставить значения, давайте изменим изохорическое уравнение и установим для него то, что мы пытаемся найти:
\ (C_V = \ frac {Q} {n \ Delta {T}} \)
Теперь мы можем вставить значения:
\ (C_V = \ frac {65J} {(3 моль) (6K)} \)
\ (= 3. 6 \ frac {J} {mol k} \)
6 \ frac {J} {mol k} \)
Решение проблемы 4
Из задачи нам дается следующее:
\ (\ Delta {T} = + 2K \)
\ (\ Delta {U} = Q = 110 Дж \)
Так как указано, что давление газа поддерживалось постоянным:
\ (C_p = 14 \ frac {J} {K mol} \)
У нас достаточно доказательств, чтобы сделать вывод, что это изобарный процесс:
\ (Q = n \ c_P \ \ Delta {T} \)
Преобразуя уравнение в соответствии с тем, что мы пытаемся найти, мы получаем:
\ (n = \ frac {Q} {\ c_P \ \ Delta {T}} \)
Теперь мы можем ввести наши значения:
\ (n = \ frac {110 Дж} {14 \ frac {J} {K mol} 2K} \)
\ (= 4 моля газа \)
Решение проблемы 5
А)
Сначала перечислим, что дано в задаче:
\ (V_i = 10 л \)
\ (V_f = 13 л \)
Переводя температуру из Цельсия в Кельвин, получаем:
\ (Т = (30 + 273. 15) К = 303,15К \)
15) К = 303,15К \)
А поскольку температура постоянна, это изотермический процесс:
\ (Q = nRT ln \ frac {V_f} {V_i} \)
Чтобы использовать это уравнение, нам нужно преобразовать газообразный гелий в моль:
\ (n = \ frac {grams} {\ frac {grams} {мол}} \)
\ (= \ frac {5,00 г He} {\ frac {4,00 г He} {mol He}} \)
\ (= 1,25 моль He \)
Мы выберем универсальную R-константу, которая легко исключает все единицы, которые помогут нам получить ответ без каких-либо других преобразований:
\ (= 8.31451 \ frac {J} {K mol} \)
Подставляя все эти значения в изотермическое уравнение, получаем:
\ (Q = (1,25 моль) (8,31451 \ frac {J} {K mol}) (303,15 K) ln \ frac {13 L} {10 L} \)
\ (= 827 Дж \)
В)
Как правило, в изотермическом процессе объем и давление имеют обратную зависимость. Это означает, что один идет вверх, а другой должен опускаться. В этом случае объем увеличился, поэтому давление должно было снизиться .
Это означает, что один идет вверх, а другой должен опускаться. В этом случае объем увеличился, поэтому давление должно было снизиться .
Идеальные одноатомные газы
Идеальные одноатомные газыДалее: Парадокс Гибба Up: Приложения статистической термодинамики Предыдущий: Функции разделения
Идеальные одноатомные газы Попрактикуемся теперь в вычислении термодинамических соотношений с использованием разбиения функция, рассмотрев пример, с которым мы уже хорошо знаком: и.е. , г. идеальный одноатомный газ. Рассмотрим газ, состоящий из одинаковых одноатомных молекулы массы заключены в контейнер объема. Обозначим положение и импульс векторов молекулы th по и , соответственно. Поскольку газ идеален, межатомные силы отсутствуют, и полная энергия представляет собой просто сумму отдельных кинетических энергий молекул:
| (427) |
куда .

Давайте подойдем к проблеме классически.В этом подходе мы разделяем фазовое пространство
в ячейки равного объема. Здесь – количество степеней
свободы, и является небольшой постоянной с размерами углового момента, который
параметризует точность, с которой положения и импульсы молекул
определены (см. раздел 3.2).
Каждая ячейка в фазовом пространстве соответствует своему состоянию.
Статистическая сумма представляет собой сумму фактора Больцмана по всем возможным состояниям, где – энергия состояния.
Классически мы можем аппроксимировать суммирование по ячейкам в фазовом пространстве
как интеграция по всему фазовому пространству.Таким образом,
| (428) |
где – число степеней свободы одноатомного газа, содержащего молекулы. Используя уравнение. (427), над выражение сводится к
| (429) |
Обратите внимание, что интеграл по координатам заданного молекула просто дает объем контейнера, так как энергия не зависит от расположение молекул в идеальном газе.
 Такие интегралы есть, поэтому получаем множитель
в приведенном выше выражении. Отметим также, что
каждый из интегралов по импульсам молекул в формуле. (429)
идентичны: они отличаются только нерелевантными фиктивными переменными интегрирования.
Отсюда следует, что статистическая сумма газа складывается из произведения
идентичные коэффициенты: т.е. ,
Такие интегралы есть, поэтому получаем множитель
в приведенном выше выражении. Отметим также, что
каждый из интегралов по импульсам молекул в формуле. (429)
идентичны: они отличаются только нерелевантными фиктивными переменными интегрирования.
Отсюда следует, что статистическая сумма газа складывается из произведения
идентичные коэффициенты: т.е. , | (430) |
куда
| (431) |
– статистическая сумма отдельной молекулы.Конечно, это результат очевиден, поскольку мы уже показали, что статистическая сумма для система, состоящая из ряда слабо взаимодействующих подсистем, – это просто произведение функций распределения подсистем (см. раздел 7.5).
Интеграл в уравнении. (431) легко оценивается:
(431) легко оценивается:
где использовалась формула. (79). Таким образом,
| (433) |
а также
| (434) |
Выражение для среднего давления (414) дает
| (435) |
которое сводится к уравнению состояния идеального газа
| (436) |
где использовались а также .
 Согласно формуле. (399) среднее
энергия газа определяется выражением
Согласно формуле. (399) среднее
энергия газа определяется выражением | (437) |
Обратите внимание, что внутренний энергия зависит только от температуры и не зависит от объем. Молярная теплоемкость при постоянном объеме газа определяется выражением
| (438) |
так что среднюю энергию можно записать
| (439) |
Мы видели все вышеперечисленные результаты
до.Позволь нам
теперь используйте функцию распределения, чтобы вычислить новый результат. Энтропия
газ можно довольно просто рассчитать из выражения
| (440) |
Таким образом,
| (441) |
или
| (442) |
куда
| (443) |
Приведенное выше выражение для энтропии идеального газа, безусловно, ново.
 К сожалению, это также совершенно очевидно неверно!
К сожалению, это также совершенно очевидно неверно! Далее: Парадокс Гибба Up: Приложения статистической термодинамики Предыдущий: Функции разделения Ричард Фицпатрик 2006-02-02
Теплоемкость газа
Теплоемкость чего-либо говорит нам, сколько тепла требуется, чтобы поднять определенное его количество на один градус. Для газа мы можем определить молярную теплоемкость C – тепло, необходимое для повышения температуры 1 моля газа на 1 К.
Q = nCΔT
Значение теплоемкости зависит от того, добавляется ли тепло при постоянном объеме, постоянном давлении и т. Д. Вместо определения всего набора молярных теплоемкостей, давайте сосредоточимся на C V , теплоемкости при постоянном объеме, и C P , теплоемкость при постоянном давлении.
Теплоемкость при постоянном объеме
Q = нКл В ΔT
Для идеального газа применение первого закона термодинамики говорит нам, что тепло также равно:
Q = ΔE int + W, хотя W = 0 при постоянном объеме.
Для одноатомного идеального газа мы показали, что ΔE int = (3/2) nRΔT
Сравнение двух наших уравнений
Q = nC V ΔT и Q = (3/2) nRΔT
мы видим, что для одноатомного идеального газа:
C V = (3/2) R
Для двухатомных и многоатомных идеальных газов получаем:
двухатомный: C V = (5/2) R
многоатомный: C V = 3R
Это дополнительные 2 или 3 вклада во внутреннюю энергию от вращений.
Поскольку Q = ΔE int при постоянном объеме изменение внутренней энергии всегда можно записать:
ΔE внутр = n C V ΔT
Теплоемкость при постоянном давлении
Для идеального газа при постоянном давлении для достижения такого же изменения температуры требуется больше тепла, чем при постоянном объеме. При постоянном объеме все добавленное тепло идет на повышение температуры. При постоянном давлении часть тепла уходит на работу.
Q = нКл P ΔT
Для идеального газа применение первого закона термодинамики говорит нам, что тепло также равно:
Q = ΔE внутр + W
При постоянном давлении W = PΔV = nRΔT
Для одноатомного идеального газа, где ΔE int = (3/2) nRΔT, получаем:
Q = (3/2) nRΔT + nRΔT = (5/2) nRΔT
Итак, для одноатомного идеального газа:
C P = (5/2) R
Для двухатомных и многоатомных идеальных газов получаем:
диатомный: C P = (7/2) R
многоатомный: C P = 4R
Соотношение C
P / C VОказывается, соотношение удельных теплоемкостей является важным числом.Для обозначения отношения используется символ γ. Для одноатомного идеального газа имеем:
γ = C P / C V = [5R / 2] / [3R / 2] = 5/3
Внутренняя энергия идеального газа
В термодинамике внутренняя энергия – это полная энергия, содержащаяся в термодинамической системе. Внутренняя энергия состоит из двух основных компонентов: кинетической энергии и потенциальной энергии. Кинетическая энергия обусловлена движением частиц системы (например, перемещениями, вращениями, колебаниями). В идеальных газах нет межчастичного взаимодействия.Поэтому мы не будем принимать во внимание потенциальную энергию и сосредоточимся только на вкладе кинетической энергии во внутреннюю энергию.
Внутренняя энергия состоит из двух основных компонентов: кинетической энергии и потенциальной энергии. Кинетическая энергия обусловлена движением частиц системы (например, перемещениями, вращениями, колебаниями). В идеальных газах нет межчастичного взаимодействия.Поэтому мы не будем принимать во внимание потенциальную энергию и сосредоточимся только на вкладе кинетической энергии во внутреннюю энергию.
Одноатомные газы
Одноатомный газ – это газ, в котором атомы не связаны друг с другом. Благородные газы (He, Ne и др.) Являются типичными примерами. Гелиевый шар показан на следующем рисунке. В этом случае кинетическая энергия состоит только из поступательной энергии отдельных атомов. Одноатомные частицы не колеблются, и их вращательной энергией можно пренебречь, потому что атомный момент инерции очень мал.Кроме того, они не возбуждаются электронным способом до более высоких энергий, за исключением очень высоких температур. Следовательно, практические изменения внутренней энергии в идеальном газе можно описать исключительно изменениями его поступательной кинетической энергии. 2} = \ frac {3} {2} kT $,
2} = \ frac {3} {2} kT $,
где k – постоянная Больцмана.(См. Атом в разделе «Температура» в кинетической теории.) Для N атомов в газе его полная внутренняя энергия U определяется как:
$ U = \ frac {3} {2} NkT $,
где N равно количество атомов в газе. Обратите внимание, что в одноатомных газах есть три степени свободы: перемещение в направлениях x, y и z.
Поскольку движение атомов является случайным (и, следовательно, изотропным), каждая степень свободы вносит вклад в $ \ frac {1} {2} kT $ на атом во внутреннюю энергию.
Двухатомные газы
Двухатомные молекулы (H 2 , O 2 , N 2 и т. Д.) имеет 5 степеней свободы (3 для перемещения в направлениях x, y и z и 2 для вращения). Следовательно, внутренняя энергия для двухатомных газов равна U = 52NkTU = \ frac {5} {2} NkT.
Теплоемкость и равномерное распределение энергии – Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Решение проблем, связанных с передачей тепла к идеальным одноатомным газам и от них, объемы которых поддерживаются постоянными
- Решить аналогичные задачи для немонатомных идеальных газов на основе числа степеней свободы молекулы
- Оценить теплоемкость металлов с помощью модели, основанной на степенях свободы
В главе о температуре и тепле мы определили удельную теплоемкость с помощью уравнения или.Однако свойства идеального газа напрямую зависят от количества молей в образце, поэтому здесь мы определяем удельную теплоемкость в терминах количества молей, а не массы. Более того, говоря о твердых телах и жидкостях, мы игнорируем любые изменения объема и давления при изменении температуры – хорошее приближение для твердых тел и жидкостей, но для газов мы должны сделать некоторые условия на изменения объема или давления. Здесь мы сосредотачиваемся на теплоемкости при неизменном объеме. Мы можем рассчитать это для идеального газа.
Здесь мы сосредотачиваемся на теплоемкости при неизменном объеме. Мы можем рассчитать это для идеального газа.
Теплоемкость идеального одноатомного газа при постоянном объеме
Мы определяем молярную теплоемкость при постоянном объеме как
Это часто выражается в форме
Если объем не изменяется, общее смещение отсутствует, поэтому работа не выполняется, а единственное изменение внутренней энергии происходит из-за теплового потока (это утверждение обсуждается далее в следующей главе). Мы используем уравнение для напишите и замените Q , чтобы найти, что дает следующий простой результат для идеального одноатомного газа:
Он не зависит от температуры, что оправдывает использование нами конечных разностей вместо производной.Эта формула хорошо согласуется с экспериментальными результатами.
В следующей главе мы обсудим молярную удельную теплоемкость при постоянном давлении, которое всегда больше
.
Расчет температуры Образец 0,125 кг ксенона содержится в жестком металлическом цилиндре, достаточно большом, чтобы ксенон можно было смоделировать как идеальный газ, при температуре. В жаркий летний день баллон выносят на улицу. Когда ксенон приходит в равновесие, достигая температуры окружающей среды, 180 Дж тепла передается ему через стенки цилиндра.Что такое равновесная температура? Не обращайте внимания на расширение металлического цилиндра.
Решение
- Определите известные: мы знаем, что начальная температура равна, тепловыделение Q составляет 180 Дж, а масса м ксенона составляет 0,125 кг.
- Определите неизвестное. Нам нужна конечная температура, значит, нам понадобится.
- Определите, какие уравнения необходимы. Поскольку газ ксенон одноатомный, мы можем использовать Тогда нам нужно количество молей,
- Подставьте известные значения в уравнения и решите для неизвестных.

Молярная масса ксенона составляет 131,3 г, поэтому мы получаем
Следовательно, конечная температура. Проблема также могла быть решена в градусах Кельвина; поскольку градус Кельвина равен градусу Цельсия изменения температуры, вы получите
Значение Нагрев идеального или почти идеального газа при постоянном объеме важен для автомобильных двигателей и многих других практических систем.
Проверьте свое понимание Предположим, 2 моля газообразного гелия при 200 K смешаны с 2 молями газообразного криптона при 400 K в калориметре.Какая конечная температура?
Поскольку количество молей одинаково и мы знаем, что молярные теплоемкости двух газов равны, температура находится на полпути между начальными температурами, 300 К.
Мы хотели бы обобщить наши результаты на идеальные газы с более чем одним атомом на молекулу. В таких системах молекулы могут иметь другие формы энергии помимо поступательной кинетической энергии, такие как кинетическая энергия вращения, кинетическая и потенциальная энергии колебаний. Мы увидим, что простое правило позволяет нам определять средние энергии, присутствующие в этих формах, и решать проблемы во многом так же, как мы это делаем для одноатомных газов.
Мы увидим, что простое правило позволяет нам определять средние энергии, присутствующие в этих формах, и решать проблемы во многом так же, как мы это делаем для одноатомных газов.
степени свободы
В предыдущем разделе мы нашли это и, из чего это следует. То же уравнение справедливо для и для. Таким образом, мы можем рассматривать нашу энергию как сумму вкладов каждого из трех измерений поступательного движения. Переходя к газу в целом, мы видим, что цифра 3 в формуле также отражает эти три измерения.Мы определяем степень свободы как независимое возможное движение молекулы, такое как каждое из трех измерений трансляции. Тогда, если d представляет количество степеней свободы, молярная теплоемкость одноатомного идеального газа при постоянном объеме равна где.
Раздел физики статистическая механика сообщает нам, и эксперимент подтверждает, что любой идеальный газ определяется этим уравнением, независимо от числа степеней свободы. Этот факт следует из более общего результата, теоремы о равнораспределении, которая выполняется в классической (неквантовой) термодинамике для систем, находящихся в тепловом равновесии при технических условиях, которые выходят за рамки наших возможностей.Здесь мы упоминаем только, что в системе энергия распределяется между степенями свободы за счет столкновений.
Теорема о равнораспределении
Энергия равновесной термодинамической системы распределяется поровну между ее степенями свободы. Соответственно, молярная теплоемкость идеального газа пропорциональна его количеству степеней свободы, d :
Этот результат принадлежит шотландскому физику Джеймсу Клерку Максвеллу (1831–1871), имя которого еще несколько раз встречается в этой книге.
Например, рассмотрим двухатомный идеальный газ (хорошая модель для азота и кислорода. Такой газ имеет больше степеней свободы, чем одноатомный газ. В дополнение к трем степеням свободы для трансляции, он имеет две степени свободы для вращение перпендикулярно своей оси.Кроме того, молекула может колебаться вдоль своей оси.Это движение часто моделируется, представляя пружину, соединяющую два атома, и мы знаем из простого гармонического движения, что такое движение имеет как кинетическую, так и потенциальную энергию.Каждой из этих форм энергии соответствует определенная степень свободы, что дает еще две.
Можно ожидать, что для двухатомного газа мы должны использовать 7 как число степеней свободы; классически, если бы молекулы газа обладали только поступательной кинетической энергией, столкновения между молекулами вскоре заставили бы их вращаться и колебаться. Однако, как объяснялось в предыдущем модуле, квантовая механика определяет, какие степени свободы активны. Результат показан на (Рисунок). И вращательная, и колебательная энергии ограничены дискретными значениями.При температурах ниже примерно 60 К энергии молекул водорода слишком низки для того, чтобы столкновение привело к тому, что вращательное или колебательное состояние молекулы перешло от самой низкой энергии ко второй самой низкой, поэтому единственной формой энергии является поступательная кинетическая энергия, и или как в одноатомном газе. Выше этой температуры начинают вносить вклад две вращательные степени свободы, то есть некоторые молекулы переходят во вращательное состояние со второй по величине энергией. (Эта температура намного ниже, чем при вращении одноатомных газов, потому что двухатомные молекулы имеют гораздо более высокую инерцию вращения и, следовательно, гораздо более низкую энергию вращения.) Примерно от комнатной температуры (чуть менее 300 K) до примерно 600 K вращательные степени свободы полностью активны, а колебательные – нет, и. Затем, наконец, выше примерно 3000 K, колебательные степени свободы полностью активны, как и предсказывала классическая теория.
Молярная теплоемкость водорода как функция температуры (в логарифмической шкале). Три «ступеньки» или «плато» показывают разное количество степеней свободы, которых должна достичь типичная энергия молекул для активации.Поступательная кинетическая энергия соответствует трем степеням свободы, вращательная – двум другим, а колебательная – еще двум.
Многоатомные молекулы обычно имеют одну дополнительную степень свободы вращения при комнатной температуре, поскольку они имеют сравнимые моменты инерции вокруг любой оси. Таким образом, при комнатной температуре они имеют, а при высокой температуре. Мы обычно предполагаем, что газы имеют теоретические значения комнатной температуры d .
Как показано на (Рисунок), результаты хорошо согласуются с экспериментами для многих одноатомных и двухатомных газов, но согласие для трехатомных газов только удовлетворительное.Различия возникают из-за взаимодействий, которые мы проигнорировали, между молекулами и внутри них.
А как насчет внутренней энергии двухатомных и многоатомных газов? Для таких газов это функция температуры ((Рисунок)), поэтому у нас нет такого простого результата, как для одноатомных идеальных газов.
Молярная теплоемкость твердых элементов
Идея равнораспределения приводит к оценке молярной теплоемкости твердых элементов при обычных температурах. Мы можем смоделировать атомы твердого тела как прикрепленные к соседним атомам пружинами ((Рисунок)).
Аналогично обсуждению вибрации в предыдущем модуле, каждый атом имеет шесть степеней свободы: по одной кинетической и по одной потенциальной для каждого из направлений x -, y – и z -. Соответственно, молярная теплоемкость металла должна составлять 3 R . Этот результат, известный как закон Дюлонга и Пети, довольно хорошо работает экспериментально при комнатной температуре. (Для каждого элемента он не работает при низких температурах по квантово-механическим причинам. Поскольку квантовые эффекты особенно важны для частиц с малой массой, закон Дюлонга и Пти уже не работает при комнатной температуре для некоторых легких элементов, таких как бериллий и углерод.Он также не работает с некоторыми более тяжелыми элементами по разным причинам, которые мы не можем объяснить.)
Стратегия решения проблем: теплоемкость и равномерное распределение
Стратегия решения этих проблем такая же, как и в случае изменения фазы для эффектов теплопередачи. Единственная новая особенность заключается в том, что вы должны определить, применим ли к проблеме только что представленный случай – идеальные газы при постоянном объеме. (Для твердых элементов определение удельной теплоемкости обычно лучше, чем оценка ее по закону Дюлонга и Пти.) В случае идеального газа определите число d степеней свободы по количеству атомов в молекуле газа и используйте его для вычисления (или используйте его для решения для d ).
Концептуальные вопросы
Экспериментально выясняется, что колебательные степени свободы многих многоатомных молекул могут вносить некоторый вклад в их энергию при комнатной температуре. Ожидаете ли вы, что этот факт увеличит или уменьшит их тепловую мощность со значения R ? Объяснять.
Можно подумать, что внутренняя энергия двухатомных газов определяется выражением. Имеют ли двухатомные газы, близкие к комнатной температуре, большую или меньшую внутреннюю энергию, чем это? Подсказка: Их внутренняя энергия включает общую энергию, добавленную при повышении температуры от точки кипения (очень низкой) до комнатной.
Меньше, так как при более низких температурах их теплоемкость составляла всего 3 RT /2.
Вы смешиваете 5 моль при 300 К с 5 молями Не при 360 К в идеально изолированном калориметре.Конечная температура выше или ниже 330 К?
Проблемы
Чтобы придать атому гелия ненулевой угловой момент, требуется около 21,2 эВ энергии (то есть 21,2 эВ – это разница между энергиями самого низкоэнергетического или основного состояния и самого низкоэнергетического состояния с угловым моментом). Электрон-вольт или эВ определяется как Найти температуру T , где это количество энергии равно. Объясняет ли это, почему мы можем игнорировать энергию вращения гелия для большинства целей? (Результаты для других одноатомных газов и двухатомных газов, вращающихся вокруг оси, соединяющей два атома, имеют сопоставимые порядки величины.)
; Да, это непрактично высокая температура.
(a) Сколько тепла необходимо добавить, чтобы повысить температуру 1,5 моль воздуха с до при постоянном объеме? Предположим, что воздух полностью двухатомный. (b) Повторите задачу для того же количества молей ксенона, Xe.
Герметичный жесткий контейнер с 0,560 моль неизвестного идеального газа при температуре 0 ° C охлаждается до. При этом из газа удаляется 980 Дж тепла. Газ одноатомный, двухатомный или многоатомный?
Проба неонового газа (Ne, молярная масса при температуре 50 ° C) помещается в стальной контейнер массой 47 ° С.2 г, что при температуре. Конечная температура. (Тепло не обменивается с окружающей средой, и вы можете пренебречь любым изменением объема контейнера.) Какова масса образца неона?
Стальной контейнер массой 135 г содержит 24,0 г аммиака с молярной массой 17,0 г / моль. Контейнер и газ находятся в равновесии при. Сколько тепла необходимо отвести, чтобы достичь температуры? Не обращайте внимания на изменение объема стали.
Объем герметичного помещения составляет.Он заполнен воздухом, который можно предположить двухатомным, при температуре и давлении 1.00-килограммовый кусок льда в точке его плавления помещается в комнату. Предположим, что стены комнаты не передают тепло. Что такое равновесная температура?
Гелиокс, смесь гелия и кислорода, иногда назначают больным больным, у которых проблемы с дыханием, потому что малая масса гелия облегчает дыхание, чем воздух. Предположим, что гелий at смешан с кислородом at, чтобы получить смесь, которая является гелием по молям.Какая конечная температура? Не обращайте внимания на любой тепловой поток в окружающую среду или из нее и предполагайте, что конечный объем является суммой начальных объемов.
Глоссарий
- степень свободы
- независимый вид движения, обладающий энергией, такой как кинетическая энергия движения в одном из трех ортогональных пространственных направлений
- теорема о равнораспределении
- Теорема о том, что энергия классической термодинамической системы поровну распределяется между ее степенями свободы
Идеальный одноатомный газ содержится в сосуде постоянного объема 0.3 {/ экв}. Начальная температура и давление газа {eq} 300 \ K {/ eq} и {eq} 5.00 \ атм. {/ eq} соответственно. Цель этой задачи – найти температуру и давление газа после {eq} 18,0 \ кДж. {/ экв} тепловой энергии поступает в газ.?
(a) Использовать закон идеального газа и начальные условия для расчета количества молей газа в сосуде? {экв} \ _ \ _ \ _ \ моль {/ eq}
(б) Найдите удельную теплоемкость газа? {экв} \ _ \ _ \ _ \ Дж / К {/ eq}
(c) Какую работу выполняет газ во время этого процесса? {экв} \ _ \ _ \ _ \ кДж {/ eq}
(d) Использовать первый закон термодинамики, чтобы найти изменение внутренней энергии газа? {экв} \ _ \ _ \ _ \ кДж {/ eq}
(e) Найти изменение температуры газа? {экв} \ _ \ _ \ _ \ K {/ eq}
(f) Рассчитать конечную температуру газа? {экв} \ _ \ _ \ _ \ K {/ eq}
(g) Использовать выражение идеального газа, чтобы найти конечное давление газа? {экв} \ _ \ _ \ _ \ атм {/ eq}
Идеальный газ:
Идеальный газ в гипотетическом газе, в котором молекулы / атомы не взаимодействуют (нет внутренних сил между частицами), а молекулы / атомы имеют точечный размер.У газа есть несколько интересных свойств.
- Закон идеального газа: Температура, давление и объем газа в любой момент времени связаны простым уравнением.
- Внутренняя энергия: Внутренняя энергия идеального газа обусловлена исключительно кинетической энергией отдельных частиц. Сумма кинетических энергий всех частиц равна внутренней энергии газа. Это зависит только от температуры, количества молей и типа газа (одноатомный, двухатомный и т. Д.).3 {/ eq}
- Начальное давление газа: {eq} P_i = 5 \; \ rm atm = 506625 \; \ rm …
См. Полный ответ ниже.
.

 Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).
Р. Ламарш, Введение в теорию ядерных реакторов, 2-е изд., Addison-Wesley, Reading, MA (1983).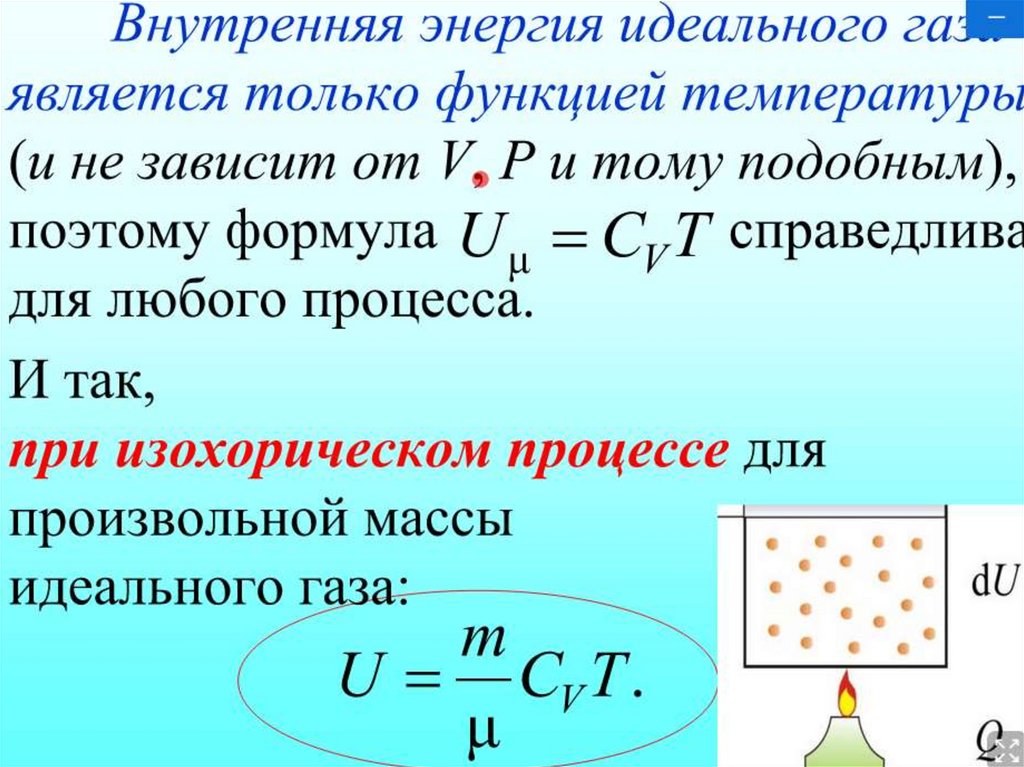 Справочник Министерства энергетики США по основам, том 1, 2 и 3. Июнь 1992 г.
Справочник Министерства энергетики США по основам, том 1, 2 и 3. Июнь 1992 г.