Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы.
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .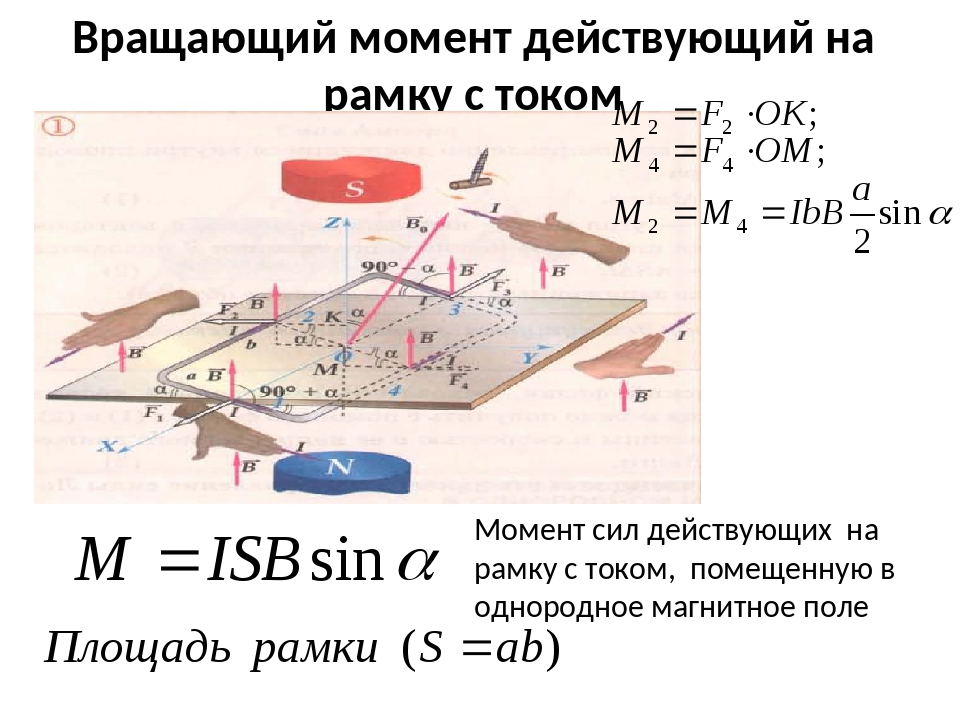
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно.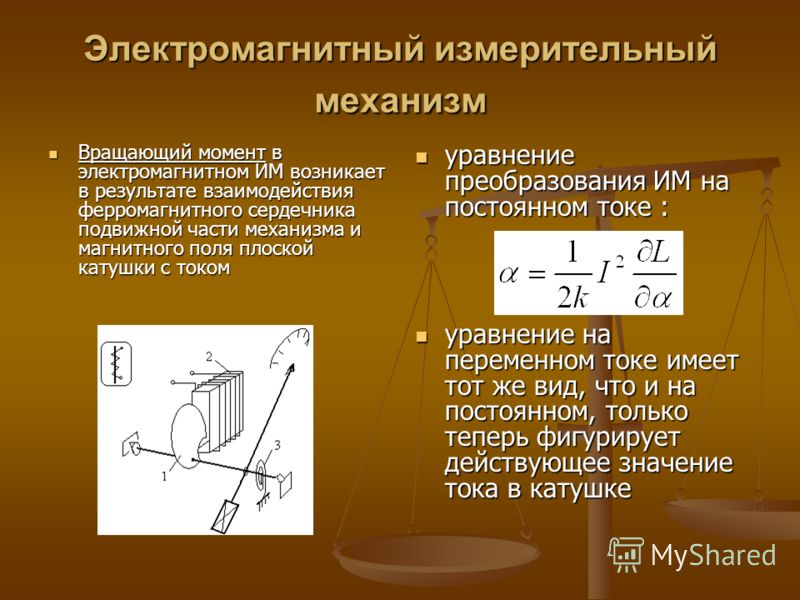 Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в. м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Формула момента силы в физике
Содержание:
Определение и формула момента силы
Определение
Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы,
$l=r \sin \alpha$– плечо силы относительно точки О.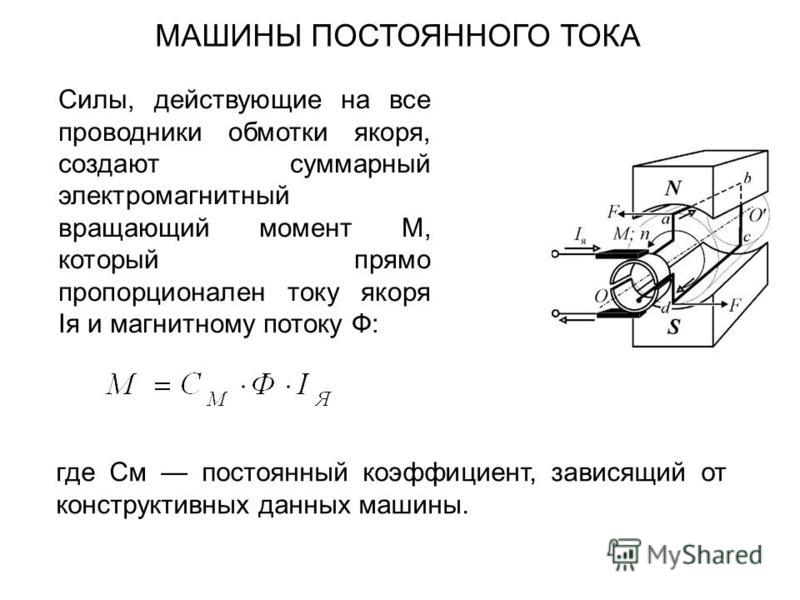 {\prime}}$ – радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
{\prime}}$ – радиус-вектор, который проведен из точки О к точке О’,
$\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO’.
Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.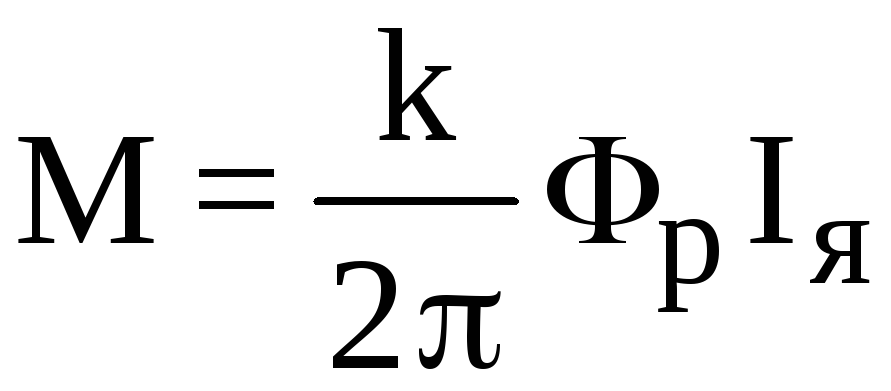 {\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
Слишком сложно?
Формула момента силы не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Формула вращающий момент
Момент силы, формулы 📙 – Физика
1. Основные понятия
2. Формулы для нахождения момента силы
3. Момент нескольких сил
Момент силы – это характеристика вращательного воздействия силы на объект. Момент силы рассчитывают, как векторное произведение вектора силы и радиус-вектора, опущенного от центра вращения до точки, к которой приложена сила.
Определение 1
Момент силы есть вращательным или крутящим моментом, представляющим собой векторную величину.
При этом понятия «крутящий» и «вращающий» нельзя отождествлять, потому что технически вращающим моментом принято считать внешнее усилие, которое прикладывается к телу, а крутящий момент обозначает внутреннее усилие, появляющееся в теле при нагрузке. Данное понятие применимо при расчете сопротивления материалов.
Данное понятие применимо при расчете сопротивления материалов.
Не нашли что искали?
Просто напиши и мы поможем
Момент силы – это вращающая сила. По международной системе СИ единицей измерения момента вращающей силы есть ньютон-метр. Архимед при работе с рычагами отмечал, что моментом силы также считается момент пары сил.
Замечание 1
При перпендикулярном прикладывании силы к рычагу, момент данной силы прямо пропорционален ее величине и расстоянию до оси вращения этого рычага.
Таким образом, сила в \(3 Н\), что действует на рычаг в точке, отдаленной на 2 м от оси вращения, формирует момент, что равняется силе в \(1 Н\), что действует в точке, отдаленной на 6 м. Наиболее точным определением момента силы есть следующее выражение:
\(\vec {M}=\vec{r}\vec{F}\),
где \(\vec {F}\)– сила, что действует на объект;
\(\vec {r}\)– радиус-вектор объекта.
С точки зрения физики момент силы есть псевдо векторной величиной, в отличие от энергии, которая есть величиной скалярной. Но совпадение их размерности не случайно. Момент силы величиной \(1 Н∙м\), что приложена через целый оборот при совершении механической работы, передает энергию в \(2π\) Джоуля:
Но совпадение их размерности не случайно. Момент силы величиной \(1 Н∙м\), что приложена через целый оборот при совершении механической работы, передает энергию в \(2π\) Джоуля:
\(E=Mθ\),
где \(E\) – энергия;
\(θ\) – угол;
\(M\) – вращающий момент.
На сегодняшний день момент силы измеряют при помощи оптических, индуктивных и тензометрических приборов нагрузки.
Момент силы рассчитывают таким образом:
\(\vec{M} = \vec{M_1}\vec{F}\),
где \(\vec{M_1}\) – момент рычага;
\(\vec{F}\)– сила действия.
Данная формула позволяет определить только значение момента силы, но не его направление. Когда сила перпендикулярна вектору \(r ⃗,\) то момент рычага равняется расстоянию от центра вращения до точки действия силы, а момент силы имеет наибольшее значение:
\(\vec{T}=\vec{r}\vec{F}\)
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Если сила воздействует на определённом расстоянии, это значит, что она делает механическую работу. Момент силы тоже делает работу, выполняя действие через угловое расстояние.
Момент силы тоже делает работу, выполняя действие через угловое расстояние.
\(P = \vec {M}\omega\)
где \(P\) – мощность, Ватт;
\(\vec{M}\)– момент силы, ньютон-метр;
\(ω\) – угловая скорость, радиан/секунда.
Замечание 2
Если на тело воздействуют две равных силы, что направлены противоположно и не лежат на одной прямой, тело пребывает в неравновесном состоянии. Это происходит по причине того, что результирующий момент данных сил по отношению к любой оси не равен нулю, поскольку они представлены моментами с одинаковым направлением. То есть, это пара сил.
Если тело закрепить на оси, то под воздействием пары сил оно будет вращаться вокруг этой оси. Если же пару сил приложить к свободному телу, то его вращение будет вокруг оси, проходящей через его центр тяжести.
Момент пары сил одинаков по отношению к любой оси, перпендикулярной плоскости пары. Суммарный момент M пары равняется произведению одной силы \(F\) на отдаленность этих сил \(L\), то есть плечо пары, в независимости от длины отрезков, на которые плечо делит ось.
\(M=FL_1+FL_2=F(L_1+L_2 )=FL\)
Если равнодействующая момента нескольких сил равняется нулю, то он будет одинаковым по отношению ко всем параллельным между собой осям. Поэтому действие на объект данных сил можно заменить воздействием одной пары сил с таким же моментом.
Момент силы. Формула, определение и примеры расчета
Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта (оси, точки).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
Момент определяется как произведение силы F на плечо h:
M(F)=F∙h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
youtube.com/embed/EHkGstkRm7A?rel=0″ frameborder=”0″ allowfullscreen=””/>
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент M=7×0,35=2,45 кНм.
Пример момента силы
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h4>h3).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
Рассмотрим порядок определения плеча h момента:
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку.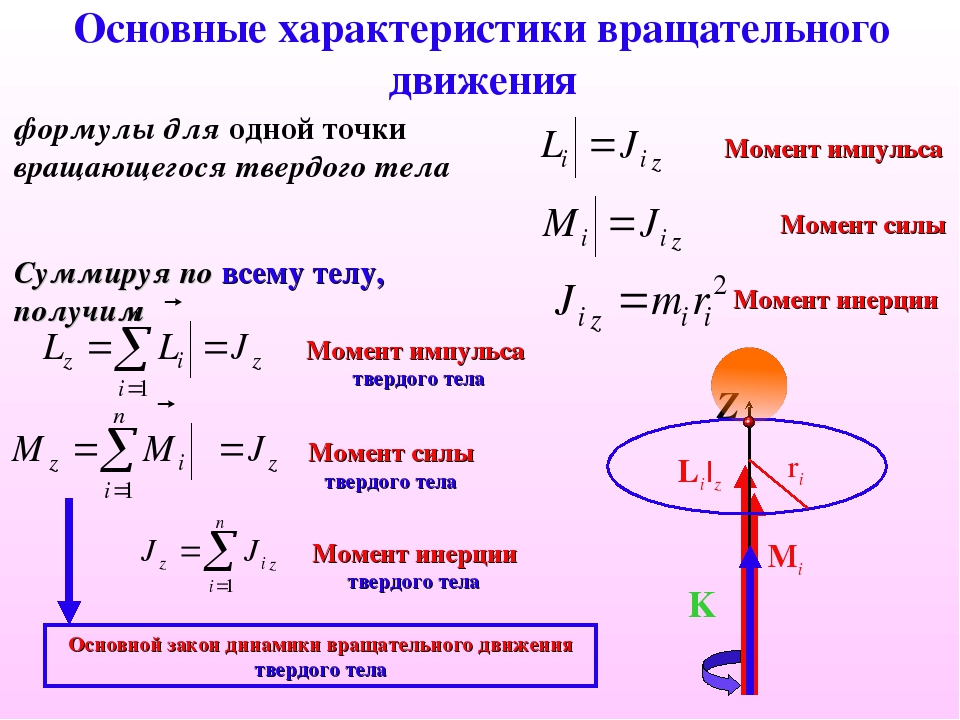 Требуется определить момент силы.
Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МA=F×AB=F×3м
Сила расположена под углом к оси стержня
Момент силы относительно точки B:
MB=F×cos300×AB=F×cos300×3м
Известно расстояние от точки до линии действия силы
Момент силы относительно точки B:
MB=F×3м
См. также:
Формула момента силы в физике
Определение и формула момента силы
ОпределениеВекторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис. 1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы, $l=r \sin \alpha$– плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. {\prime}}$ – радиус-вектор, который проведен из точки О к точке О’, $\bar{F}$ – главный вектор системы сил.
{\prime}}$ – радиус-вектор, который проведен из точки О к точке О’, $\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
ПримерЗадание. На рис.1 показано тело, которое имеет ось вращения OO’. Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка. {\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
ПримерЗадание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.
Вы поняли, как решать? Нет?
Помощь с решением
Мощность и вращающий момент электродвигателя. Что это такое?
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Вращающий момент (T) – это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы – или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила – любая сила – вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т. е. напряжение, коэффициент мощности, потребляемый ток и КПД.
е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.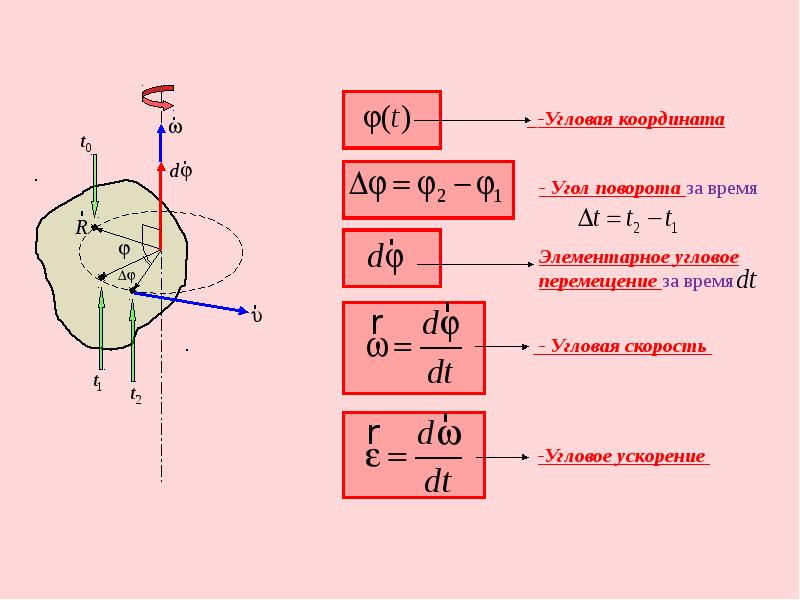
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент – момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот.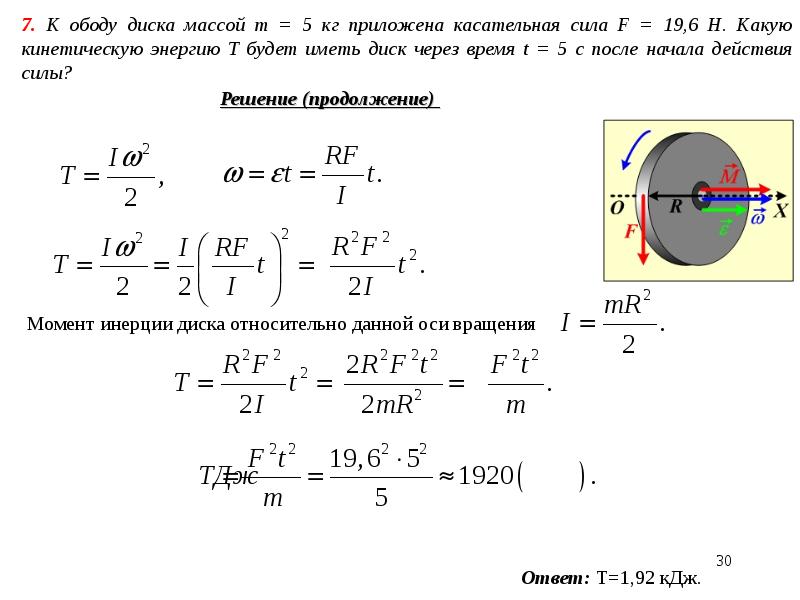 Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Как видно из названия – «постоянный вращающий момент» – подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
Переменный вращающий момент и мощность
«Переменный вращающий момент» – эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения – мал, а потребный вращающий момент при высокой частоте вращения – велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность – кубу скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т. е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
P1 (кВт) Входная электрическая мощность насосов – это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя – это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
что такое, формула и в чем измеряется
Мощность двигателя – важнейший его показатель. Как в плане эксплуатации, так и в плане начисления налогов на авто. Крутящий момент нередко путают с мощностью или упускают его из виду в процессе оценки ходовых качеств авто. Многие упрощают автомобиль, считая, что большое количество лошадиных сил – главное преимущество любого мотора. Однако, вращающий момент – более важный показатель. Особенно, если автомобиль не предполагается использовать в качестве спортивного.
Что такое крутящий момент
Крутящим моментом называют единицу силы, которая необходима для поворота коленчатого вала ДВС. Эта не «лошадиная сила», которой должна обозначаться мощность.
ДВС вырабатывает кинетическую энергию, вращая таким образом коленвал. Показатель мощности двигателя (сила давления) зависит от скорости сгорания топлива. Крутящий момент – результат от действия силы на рычаг. Эта сила в физике считается в ньютонах. Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.
Длина плеча коленвала считается в метрах. Поэтому обозначение крутящего момента – ньютон-метр.
Технически, крутящий момент – это усилие, которое должно осуществляться двигателем для разгона и движения машины. При этом сила, оказывающая действие на поршень, пропорциональна объему двигателя.
Маховик – одна из важнейших деталей, которая должна через редуктор передавать вращательный момент от мотора к коробке передач, от стартера на коленвал, от коленвала на нажимной диск. Собственно, крутящий момент – итог давления на шатун.
Формула расчета крутящего момента
Показатель КМ рассчитывается так: мощность (в л. с.) равно крутящий момент (в Нм) умножить на обороты в минуту и разделить на 5,252. При меньших чем 5,252 значениях крутящий момент будет выше мощности, при больших – ниже.
В пересчете на принятую в России систему (кгм – килограмм на метр) – 1кг = 10Н, 1 см = 0,01м. Таким образом 1 кг х см = 0,1 Н х м. Посчитать вращательный момент в разных системах измерений ньютоны/килограммы и т.д. поможет конвертер – в практически неизменном виде он доступен на множестве сайтов, с его помощью можно определять данные по практически любому мотору.
Таким образом 1 кг х см = 0,1 Н х м. Посчитать вращательный момент в разных системах измерений ньютоны/килограммы и т.д. поможет конвертер – в практически неизменном виде он доступен на множестве сайтов, с его помощью можно определять данные по практически любому мотору.
График:
На графике изображена зависимость крутящего момента двигателя от его оборотов
От чего зависит крутящий момент
На КМ будут влиять:
- Объем двигателя.
- Давление в цилиндрах.
- Площадь поршней.
- Радиус кривошипа коленвала.
Основная механика образования КМ заключается в том, что чем больше двигатель по объему, тем сильней он будет нагружать поршень. То есть – будет выше значение КМ. Аналогична взаимосвязь с радиусом кривошипа коленвала, но это вторично: в современных двигателях этот радиус сильно изменить нельзя.
Давление в камере сгорания – не менее важный фактор. От него напрямую зависит сила, давящая на поршень.
Для снижения потерь крутящего момента при тряске машины во время резкого газа можно использовать компенсатор.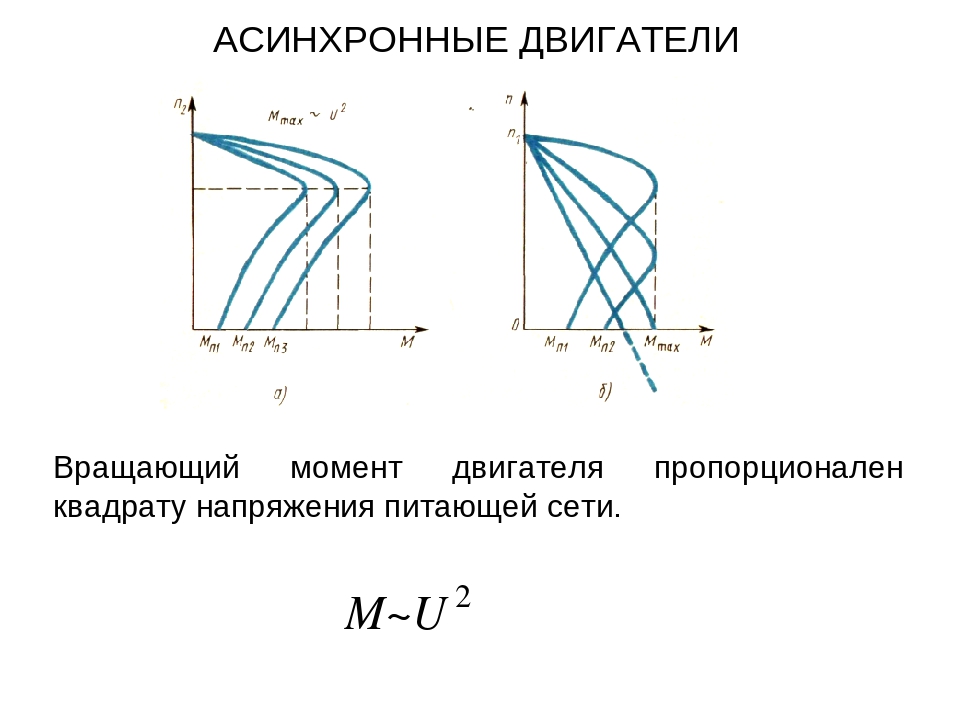 Это специальный (собранный вручную) демпфер, компенсация которого позволит сохранить вращающий момент и повысить срок эксплуатации деталей.
Это специальный (собранный вручную) демпфер, компенсация которого позволит сохранить вращающий момент и повысить срок эксплуатации деталей.
На что влияет крутящий момент
Главная цель КМ – набор мощности. Часто мощные моторы обладают низким показателем КМ, поэтому не способны разогнать машину достаточно быстро. Особенно это касается бензиновых двигателей.
ВАЖНО! При выборе авто стоит рассчитать оптимальное соотношение вращательного момента с количеством оборотов, на которых чаще всего мотор будет работать. Если держать вращательный момент на соответствующем уровне, это позволит оптимально реализовать потенциал двигателя.
Высокий КМ также может влиять на управляемость машины, поэтому при резком увеличении скорости не лишним будет использование системы TSC. Она позволяет точнее направлять авто при резком разгоне.
Широко распространенный 8-клапанный двигатель ВАЗ выдает вращательный момент 120 (при 2500-2700 оборотах).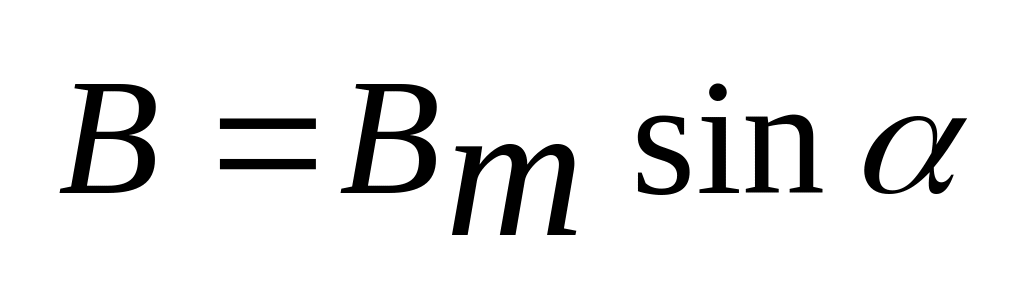 Ручная коробка или АКПП стоит на машине – не принципиально. При использовании КПП немаловажен опыт водителя, на автоматической коробке плавный старт обеспечивает преобразователь.
Ручная коробка или АКПП стоит на машине – не принципиально. При использовании КПП немаловажен опыт водителя, на автоматической коробке плавный старт обеспечивает преобразователь.
Как увеличить крутящий момент
Увеличение рабочего объема. Чтобы повышать КМ используются разные методы: замена установленного коленвала на вал с увеличенным эксцентриситетом (редко встречающаяся запчасть, которую трудно находить) или расточка цилиндров под больший диаметр поршней. Оба способа имеют свои плюсы и минусы. Первый требует много времени на подбор деталей и снижает долговечность двигателя. Второй, увеличение диаметра цилиндров с помощью расточки, более популярен. Это может сделать практически любой автосервис. Там же можно настроить карбюратор для повышения КМ.
Изменение величины наддува. Турбированные двигатели позволяют достичь более высокого показателя КМ благодаря особенностям конструкции – возможности отключить ограничения в блоке управления компрессором, который отвечает за наддув. Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.
Манипуляции с блоком позволят повысить объем давления выше максимума, указанного производителем при сборке автомобиля. Способ можно назвать опасным, поскольку у каждого двигателя есть лимитированный запас нагрузок. Кроме того, часто требуются дополнительные усовершенствования: увеличение камеры сгорания, приведение охлаждения в соответствие повышенной мощности. Иногда требуется отрегулировать впускной клапан, иногда – сменить распредвал. Может потребоваться замена чугунного коленвала на стальной, замена поршней.
Изменение газодинамики. Редко используемый вариант, поскольку двигатель – сложная конструкция, созданием которого занимаются профессионалы. Теоретически можно придумать, как убрать ограничения, заложенные конструкторами для увеличения срока эксплуатации двигателя и его деталей. Но на практике, если убрать ограничитель, результат не гарантирован, поскольку поменяются все характеристики: например, динамика вырастет, но шина не будет цепляться за дорогу. Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.
Чтобы усовершенствовать двигатель такие образом надо быть не просто автомобильным конструктором, но и математиком, физиком и т.д.
ВАЖНО! Простой способ повысить КМ – использовать масляный фильтр. Он снизит засорение двигателя и продлит срок эксплуатации всех деталей.
Определение крутящего момента на валу
Для измерения крутящего момента на валу автомобильного двигателя применяется множество методик. Это может быть показатель подачи топлива, температуры выхлопных газов и т.д. Такие методы не гарантируют высокой точности.
Распространенный метод повышенной точности – применение тензометрического моста. На вал крепятся тензометры, электрически соединенные по мостовой схеме. Сигнал передается на считывающее устройство.
Измеритель крутящего момента
Главная сложность в измерителе крутящего момента, использующего тензометры, является точность передачи данных. Применявшиеся ранее контактные, индукционные и светотехнические устройства не гарантировали необходимой эффективности.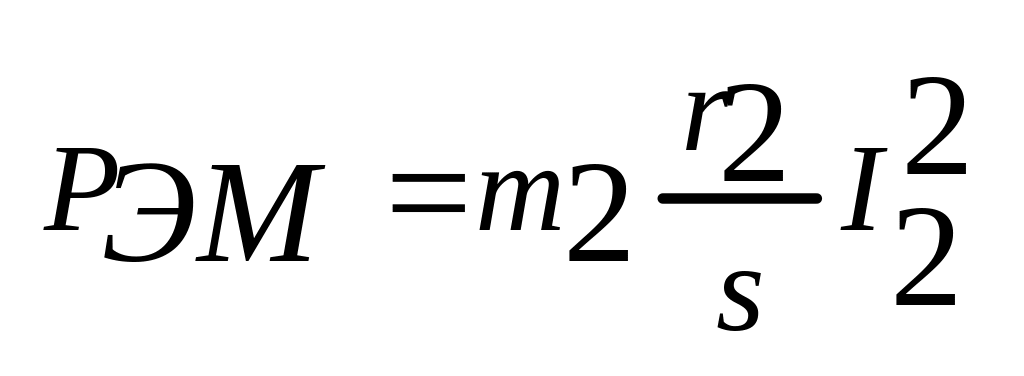 Сейчас данные передаются по цифровым радиоканалам. Измеритель представляет собой компактный радиопередатчик, который крепится на вал и передает данные на приемник.
Сейчас данные передаются по цифровым радиоканалам. Измеритель представляет собой компактный радиопередатчик, который крепится на вал и передает данные на приемник.
Сейчас такие устройства доступны по стоимости и просты в эксплуатации. Применяются в основном в СТО.
Датчик крутящего момента
Аналогичные устройства, измеряющие КМ, в автомобиле могут быть установлены не только на коленвал, но и на рулевое колесо. Он ставится на модели машин с электроусилителем руля и позволяет отслеживать работу системы управление автомобилей. При выходе датчика из строя, усилитель, как правило, отключается.
Максимальный крутящий момент
Максимальным называется крутящий момент, представляющий пик, после которого момент не растет, несмотря на количество оборотов. На малых оборотах в цилиндре скапливается большой объем остаточных газов, в результате чего показатель КМ значительно ниже пикового. На средних оборотах в цилиндры поступает больше воздуха, процент газов снижается, крутящий момент продолжает расти.
При высоких оборотах растут потери эффективности: от трения поршней, инерционных потерь в ГРМ, разогрева масла и т.д. будет зависеть работа мотора. Поэтому рост качества работы двигателя прекращается или само качество начинает снижаться. Максимальный крутящий момент достигнут и начинает снижаться.
В электродвигателях максимальный вращательный момент называется «критический».
Таблица марок автомобилей с указанием крутящего момента:
| Модели автомобиля ВАЗ | Крутящий момент (Нм, разные марки двигателей) | |
| 2107 | 93 – 176 | |
| 2108 | 79-186 | |
| 2109 | 78-118 | |
| 2110 | 104-196 | |
| 2112 | 104-162 | |
| 2114 | 115-145 | |
| 2121 (Нива) | 116-129 | |
| 2115 | 103-132 | |
| 2106 | 92-116 | |
| 2101 | 85-92 | |
| 2105 | 85-186 | |
| Двигатели ЗМЗ | ||
| 406 | 181,5-230 | |
| 409 | 230 | |
| Других популярные в России марки автомобилей | ||
| Ауди А6 | 500-750 | |
| БМВ 5 | 290-760 | |
| Бугатти Вейрон | 1250-1500 | |
| Дэу Нексия | 123-150 | |
| КАМАЗ | ~650-2000+ | |
| Киа Рио | 132-151 | |
| Лада Калина | 127-148 | |
| Мазда 6 | 165-420 | |
| Мицубиси Лансер | 143-343 | |
| УАЗ Патриот | 217-235 | |
| Рено Логан | 112-152 | |
| Рено Дастер | 156-240 | |
| Тойота Королла | 128-173 | |
| Хендай Акцент | 106-235 | |
| Хендай Солярис | 132-151 | |
| Шевроле Каптив | 220-400 | |
| Шевроле Круз | 118-200 | |
Какому двигателю отдать предпочтение
Сегодня множество моделей производители оснащают разными типами моторов: бензиновым или дизельным. Эти модели идентичны только по цене и другим характеристикам.
Эти модели идентичны только по цене и другим характеристикам.
Из-за разных типов мотора одна и та же модель может отличаться по показателям мощности мотора и крутящему моменту, при этом разница может быть значительной.
Бензиновый двигатель
Бензиновый двигатель формирует воздушно-топливную смесь, заполняющую цилиндр. Температура внутри него поднимается до примерно 500 градусов. У таких моторов номинальный коэффициент сжатия составляет порядка 9-10, реже 11 единиц. Поэтому, когда происходит впрыск необходимо использование свечей зажигания.
Дизельный двигатель
В цилиндрах работающего на дизеле движка коэффициент сжатия смеси может достигать показателя в 25 единиц, температура – 900 градусов. Поэтому смесь зажигается без использования свечи.
Электродвигатель
Автомобильный трехфазный асинхронный электродвигатель работает по совершенно другим законам, поэтому его мощность и КМ отличаются от традиционных кардинально. Электромотор состоит из ротора и статора, кратность которых позволяет выдавать пиковый КМ (600 Нм) на любой скорости. При этом мощность электродвигателя, например, у Теслы, составляет 416 л. с.
Электромотор состоит из ротора и статора, кратность которых позволяет выдавать пиковый КМ (600 Нм) на любой скорости. При этом мощность электродвигателя, например, у Теслы, составляет 416 л. с.
Чтобы ответить на вопрос – дизельный, бензиновый или электродвигатель лучше, надо сначала исключить третий вариант, поскольку электродвигатели пока не так распространены, как первые два типа.
ВАЖНО! Что касается выбора между бензиновым и дизельным двигателями, они в первую очередь отличаются мощностью и крутящим моментом. На практике это означает, что при одинаковом объеме двигателя дизельный быстрее разгоняется, а бензиновый позволяет давать более высокую скорость.
Кроме того, благодаря большему крутящему момент автомобиль, использующийся как грузовой, обладает большей грузоподъемностью за счет двигателя. Особенно если двигатель дизель-генераторный.
Улучшение разгона авто за счет изменения момента вращения
Чем выше показатель крутящего момента – тем быстрее двигатель набирает мощность. Таким образом, вырастет скорость движения. На практике это означает, что, например, во время разгона крутящий момент позволит быстрее обогнать едущий впереди автомобиль.
Чтобы улучшить разгон автомобиля за счет изменения момента вращения, достаточно повысить показатели последнего. Как это сделать – описано выше.
Зависимость мощности от крутящего момента
Крутящий момент, как говорилось выше, это показатель того, с какой скоростью двигатель может набирать обороты. По сути, мощность мотора – прямая производная от КМ на коленвале. Чем больше оборотов – тем выше показатель мощности.
Зависимость мощности от вращательного момента выражается формулой: Р = М*n (Р – мощность, М – крутящий момент, n – количество оборотов коленвала/мин).
7.2: Классическая механика
Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.
СКОРОСТЬ – это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.
ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.
УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение – это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью – ускорение отсутствует.
СИЛА – Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.
Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом.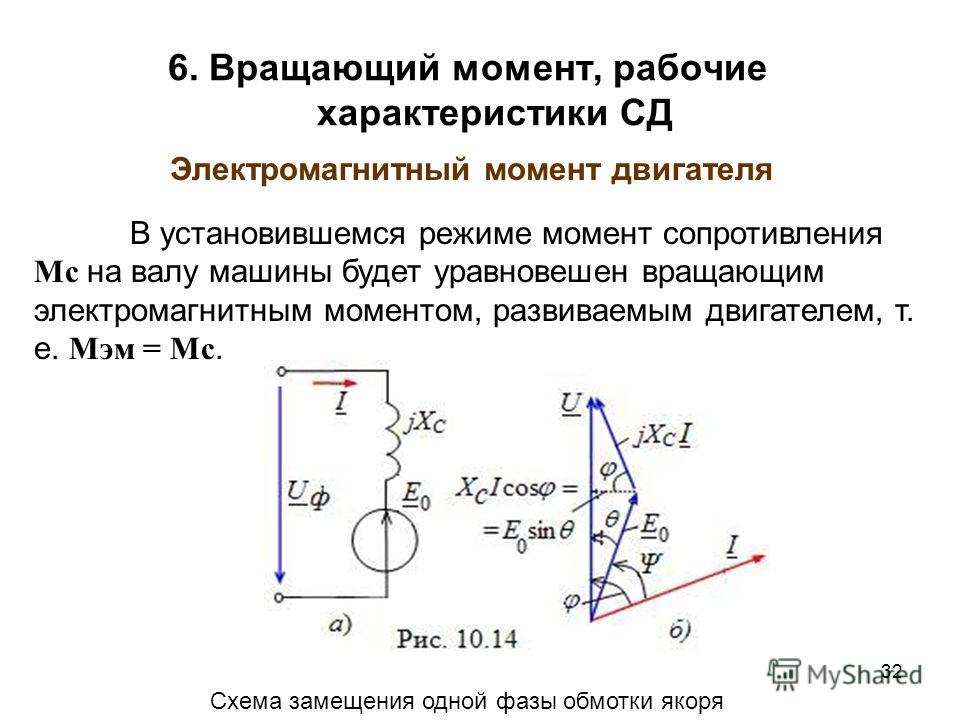 Крутящий момент – это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент – как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.
Крутящий момент – это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент – как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.
В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.
Сила = Крутящий момент/Радиус колеса
В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта.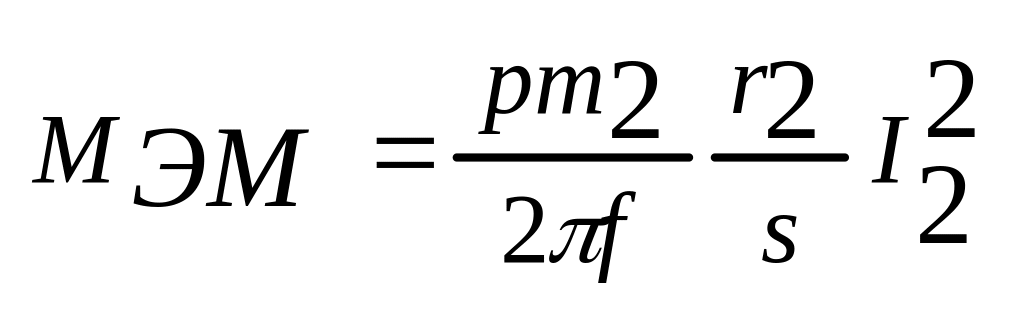 Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда
Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.
Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.
Пример 7.2
Пример 7.3
Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.
Пример 7.2 – Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.
Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.
Пример 7.3 – Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.
Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.
Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.
Пример 7.4
Пример 7.5
Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?
Пример 4 – Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.
Пример 5 – Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.
Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.
Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.
РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.
МОЩНОСТЬ – Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.
Мощность – это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).
Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.
Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]
1 Ватт = 1 (Ньютон х Метр) / Секунда
Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения.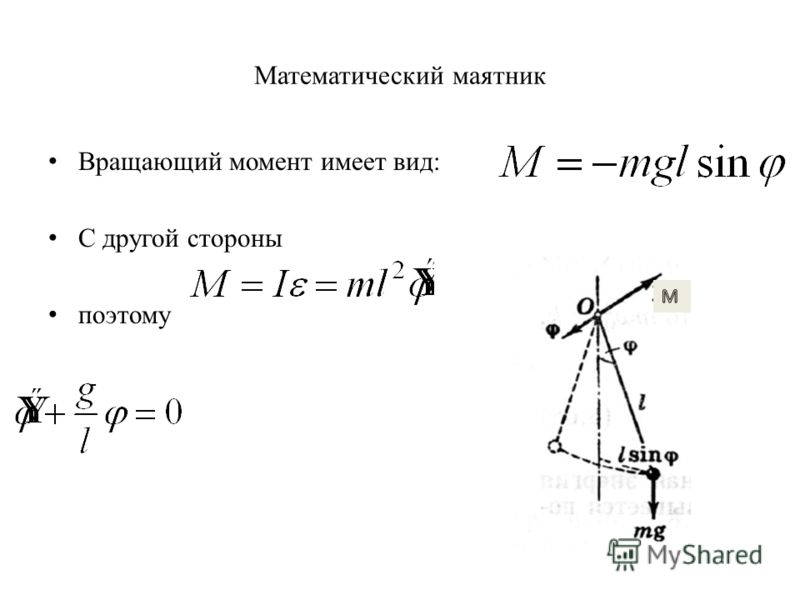 Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.
Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.
Формула крутящего момента (момент инерции и угловое ускорение)
При вращательном движении крутящий момент требуется для создания углового ускорения объекта. Величина крутящего момента, необходимого для создания углового ускорения, зависит от распределения массы объекта. Момент инерции – это величина, описывающая распределение. Его можно найти путем интегрирования по массе всех частей объекта и их расстояниям до центра вращения, но также можно найти моменты инерции для общих форм. Крутящий момент на данной оси является произведением момента инерции и углового ускорения. Единицы крутящего момента – ньютон-метры (Н ∙ м).
Крутящий момент на данной оси является произведением момента инерции и углового ускорения. Единицы крутящего момента – ньютон-метры (Н ∙ м).
крутящий момент = (момент инерции) (угловое ускорение)
τ = Iα
τ = крутящий момент вокруг определенной оси (Н ∙ м)
I = момент инерции (кг ∙ м 2 )
α = угловое ускорение (радиан / с 2 )
Формула крутящего момента Вопросы:
1) Момент инерции твердого диска равен, где M – масса диска, а R – радиус.Каждое колесо игрушечной машинки имеет массу 0,100 кг и радиус 20,0 см. Если угловое ускорение колеса составляет 1,00 радиан / с 2 , каков крутящий момент?
Ответ: Крутящий момент можно найти с помощью формулы крутящего момента и момента инерции твердого диска. Крутящий момент:
τ = Iα
τ = 0,0020 Н ∙ м
Крутящий момент, прилагаемый к одному колесу, составляет 0,0020 Н ∙ м.
2) Момент инерции тонкого стержня, вращающегося на оси, проходящей через его центр, равен, где M – масса, а L – длина стержня.Предположим, что лопасть вертолета представляет собой тонкий стержень массой 150,0 кг и длиной 8,00 м. Какой крутящий момент требуется для достижения углового ускорения 18,00 радиан / с 2 ?
Ответ: Крутящий момент можно найти с помощью формулы крутящего момента и момента инерции тонкого стержня. Крутящий момент:
τ = Iα
τ = 14 400 Н ∙ м
Требуемый крутящий момент составляет 14 400 Н ∙ м.
.Формула крутящего момента (сила на расстоянии)
Формула крутящего момента (сила на расстоянии)Вопросы по формуле крутящего момента:
1) Автомеханик прикладывает усилие 800 Н к гаечному ключу, чтобы ослабить болт. Она прикладывает силу перпендикулярно рычагу гаечного ключа. Расстояние от болта до руки – 0,40 м. Какова величина прилагаемого крутящего момента?
Ответ: Угол между моментным плечом (рычагом гаечного ключа) и силой равен 90 °, а sin 90 ° = 1.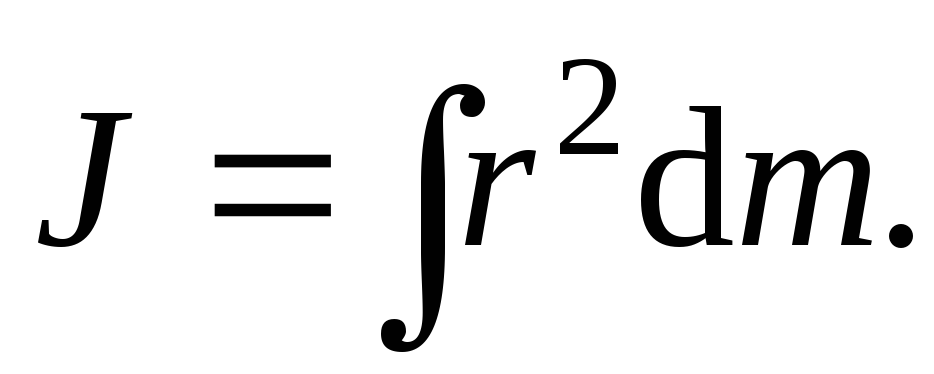 Крутящий момент:
Крутящий момент:
Величина крутящего момента 320 Н ∙ м.
2) Анемометр – это прибор для измерения скорости ветра. Он имеет несколько металлических чашек, установленных на горизонтальных стержнях, которые вращают центральный стержень. Ветер ловит одну из чашек перпендикулярно ее турнику. Ветер оказывает на чашу силу 70,0 Н на расстоянии 0,30 м от центральной оси. Какова величина крутящего момента, создаваемого ветром?
Ответ: Угол между рычагом момента (горизонтальной штангой) и силой равен 90 °, а sin 90 ° = 1.Крутящий момент:
Величина крутящего момента 21,0 Н ∙ м.
Формула крутящего момента (сила на расстоянии)
.Соотношение крутящего момента и мощности
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11 9plar
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Книги NCERT
Какова размерная формула крутящего момента и его вывод?
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11 9plar
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- RD Sharma
- RD Sharma Class 6 Решения
- RD Sharma Class 7 Решения
- Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- PHYSICS
- Механика
- Оптика
- Термодинамика
- Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Статистика
- Числа
- Числа Пифагора Тр Игонометрические функции
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Разделение фракций
- Microology
- Книги NCERT
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 000E
- 000
- 000
- 000 Калькуляторы
- 000 Образцы документов для класса 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 1 1
- Образцы документов CBSE для класса 12
- Вопросники предыдущего года CBSE
- Вопросники предыдущего года CBSE, класс 10
- Вопросники предыдущего года CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- HC Verma Solutions Класс 12 Физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха класса 9
- Решения Лахмира Сингха класса 10
- Решения Лакмира Сингха класса 8
9000 Класс
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке
- CBSE Вопросы
- CBSE Class 10 Дополнительные вопросы по математике
- CBSE Class 10 Science Extra questions
- Class 3
- Class 4
- Class 5
- Class 6
- Class 7
- Class 8 Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия
- Решения NCERT для биологии класса 11
- Решение NCERT s Для класса 11 по математике
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions for Class 12
- Решения NCERT для физики класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- Решения NCERT, класс 12, бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- NCERT Solutions Class 12 Economics
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solut Ионы Для класса 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для класса 6 по социальным наукам
- Решения NCERT для класса 6 Английский язык
- Решения NCERT для класса 7
- Решения NCERT для математики класса 7
- Решения NCERT для науки класса 7
- Решения NCERT для социальных наук класса 7
- Решения NCERT для класса 7 Английский язык
- Решения NCERT для класса 8
- Решения NCERT для математики класса 8
- Решения NCERT для науки 8 класса
- Решения NCERT для социальных наук 8 класса ce
- Решения NCERT для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для класса 9 по социальным наукам
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для математики класса 9, глава 2 Решения NCERT
- для математики класса 9, глава 3
- Решения NCERT для математики класса 9, глава 4
- Решения NCERT для математики класса 9, глава 5 Решения NCERT
- для математики класса 9, глава 6
- Решения NCERT для математики класса 9 Глава 7 Решения NCERT
- для математики класса 9 Глава 8
- Решения NCERT для математики класса 9 Глава 9
- Решения NCERT для математики класса 9 Глава 10 Решения NCERT
- для математики класса 9 Глава 11 Решения
- NCERT для математики класса 9 Глава 12 Решения NCERT
- для математики класса 9 Глава 13
- NCER Решения T для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для науки класса 9 Глава 3
- Решения NCERT для науки класса 9 Глава 4
- Решения NCERT для науки класса 9 Глава 5
- Решения NCERT для науки класса 9 Глава 6
- Решения NCERT для науки класса 9 Глава 7
- Решения NCERT для науки класса 9 Глава 8
- Решения NCERT для науки класса 9 Глава 9
- Решения NCERT для науки класса 9 Глава 10
- Решения NCERT для науки класса 9 Глава 12
- Решения NCERT для науки класса 9 Глава 11
- Решения NCERT для науки класса 9 Глава 13 Решения NCERT
- для науки класса 9 Глава 14
Простая английская Википедия, бесплатная энциклопедия
Взаимосвязь между векторами силы, крутящего момента и импульса во вращающейся системеВ физике крутящий момент – это тенденция силы к повороту или скручиванию. Если сила используется, чтобы начать вращать объект или остановить вращение объекта, создается крутящий момент.
Сила, приложенная к рычагу, умноженная на расстояние от точки опоры рычага, снова умноженная на синус созданного угла, описывается как крутящий момент.Это также известно как «r cross f» или «сила, умноженная на расстояние опоры, умноженное на синус тета».
Точка опоры – это ось вращения или точка опоры, на которой рычаг поворачивается при подъеме или перемещении чего-либо.
Уравнение крутящего момента:
- τ = r × F {\ displaystyle {\ boldsymbol {\ tau}} = \ mathbf {r} \ times \ mathbf {F} \, \!}
, где F – вектор чистой силы, а r – вектор от оси вращения до точки, в которой действует сила.Греческая буква Тау используется для обозначения крутящего момента.
Единицы измерения крутящего момента – это сила, умноженная на расстояние. [1] В системе СИ единицей измерения крутящего момента является ньютон-метр. Самая распространенная английская единица – фут-фунт.
- ↑ Хольцнер, Стивен (2010). Основы физики для чайников . Wiley Publishing. п. 122. ISBN 978-0-470-61841-7 .
Угловое движение – мощность и крутящий момент
Мощность и момент тела при угловом движении
Сила вращающегося тела может быть выражена как
P = T ω
= T 2 π n об / с
= T π n об / мин /30 (1)
где
P = мощность (Вт)
T = крутящий момент или момент (Нм)
= угловая скорость (рад / с)
π = 3.14 …
n об / с = оборотов в секунду (об / с, 1 / с)
n об / мин = оборотов в минуту (об / мин, 1 / мин)
- 1 рад = 360 o /2 π = ~ 57,29578 .. o
Примечание! – объект, такой как электродвигатель, может иметь активный момент без вращения, но без вращения ( ω = 0 ) не вырабатывается энергия.
В имперских единицах
P = T n об / мин /5252 (1b)
где
P = мощность (л.с.)
T = крутящий момент (фут-фунт f )
Пример – момент, создаваемый вращающимся двигателем
Электродвигатель работает со скоростью 3600 об / мин с измеренной потребляемой мощностью 2000 Вт .Момент, создаваемый двигателем (без потерь), можно рассчитать, переставив (1) на
T = 30 P / (π n об / мин )
= 30 (2000 Вт) / (π ( 3600 об / мин))
= 5,3 Нм
Калькулятор моментов
P – мощность (Вт)
n м – обороты (об / мин)
Крутящий момент тела в угловом движении
.T = I α (2)
где
I = момент инерции (кг · м 2 , фунт f фут · с 2 )
α = угловое ускорение (рад / с 2 )
Формула вращающий момент
Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.{\varphi }\left|{\vec {M}}\right|d\varphi }.
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Формула момента рычага[править | править код]
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом[править | править код]
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие[править | править код]
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени[править | править код]
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2).{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}
Вращающий момент – это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
определения, единица измерения, примеры, относительно оси и точки
В статье мы расскажем про момент силы относительно точки и оси, определения, рисунки и графики, какая единица измерения момента силы, работа и сила во вращательном движении, а также примеры и задачи.
Момент силы представляет собой вектор физической величины, равный произведению векторов плеча силы (радиус-вектор частицы) и силы, действующей на точку. Силовой рычаг представляет собой вектор, соединяющий точку, через которую проходит ось вращения твердого тела с точкой, к которой приложена сила.
где: r — плечо силы, F — сила приложенная на тело.
Направление вектора силы момента всегда перпендикулярно плоскости, определяемой векторами r и F.
Главный момент — любая система сил на плоскости относительно принятого полюса называется алгебраическим моментом момента всех сил этой системы относительно этого полюса.
Во вращательных движениях важны не только сами физические величины, но и то, как они расположены относительно оси вращения, то есть их моменты. Мы уже знаем, что во вращательном движении важна не только масса, но и момент инерции. В случае силы, ее эффективность для запуска ускорения определяется способом приложения этой силы к оси вращения.
Взаимосвязь между силой и способом ее применения описывает МОМЕНТ СИЛЫ. Момент силы — это векторное произведение силового плеча R на вектор силы F:
Как в каждом векторном произведении, так и здесь
Следовательно, сила не будет влиять на вращение, когда угол между векторами силы F и рычагом R равен 0o или 180o. Каков эффект применения момента силы М?
Мы используем второй Закон движения Ньютона и связь между канатом и угловой скоростью v = Rω в скалярной форме, действительны, когда векторы R и ω перпендикулярны друг другу
Умножив обе части уравнения на R, получим
Поскольку mR 2 = I, мы заключаем, что
Вышеуказанная зависимость справедлива и для случая материального тела. Обратите внимание, что в то время как внешняя сила дает линейное ускорение a, момент внешней силы дает угловое ускорение ε.
Единица измерения момента силы
Основной мерой измерения момента силы в системной координате СИ является: [M]=Н•м
В СГС: [M]=дин•см
Работа и сила во вращательном движении
Работа в линейном движении определяется общим выражением,
но во вращательном движении,
а следовательно
Исходя из свойств смешанного произведения трех векторов, можно записать
Поэтому мы получили выражение для работы во вращательном движении:
Мощность во вращательном движении:
Момент силы пример и решение задач относительно точки
Найдите момент силы, действующей на тело в ситуациях, показанных на рисунках ниже. Предположим, что r = 1m и F = 2N.
а) поскольку угол между векторами r и F равен 90°, то sin(a)=1:
M = r • F = 1м • 2N = 2Н • м
б) потому что угол между векторами r и F равен 0°, поэтому sin(a)=0:
M = 0
да направленная сила не может дать точке вращательное движение.
c) поскольку угол между векторами r и F равен 30°, то sin(a)=0.5:
M = 0,5 r • F = 1Н • м.
Таким образом, направленная сила вызовет вращение тела, однако ее эффект будет меньше, чем в случае a).
Момент силы относительно оси
Предположим, что данные являются точкой O (полюс) и мощность P. В точке O мы принимаем начало прямоугольной системы координат. Момент силы Р по отношению к полюсным O представляет собой вектор М из (Р), (рисунок ниже).
Любая точка A на линии P имеет координаты (xo , yo , zo ).
Вектор силы P имеет координаты Px , Py, Pz. Комбинируя точку A (xo, yo, zo ) с началом системы, мы получаем вектор p. Координаты вектора силы P относительно полюса O обозначены символами Mx, My, Mz. Эти координаты могут быть вычислены как минимумы данного определителя, где ( i, j, k) — единичные векторы на осях координат (варианты): i, j, k
После решения определителя координаты момента будут равны:
Координаты вектора моментов Mo (P) называются моментами силы относительно соответствующей оси. Например, момент силы P относительно оси Oz окружает шаблон:
Mz = Pyxo — Pxyo
Этот паттерн интерпретируется геометрически так, как показано на рисунке ниже.
На основании этой интерпретации момент силы относительно оси Oz можно определить, как момент проекции силы P на перпендикуляр оси Oz относительно точки проникновения этой плоскости осью. Проекция силы P на перпендикуляр оси обозначена Pxy, а точка проникновения плоскости Oxy — осью Oс символом O.
Из приведенного выше определения момента силы относительно оси следует, что момент силы относительно оси равен нулю, когда сила и ось равны, в одной плоскости (когда сила параллельна оси или когда сила пересекает ось).
Используя формулы на Mx, My, Mz, мы можем рассчитать значение момента силы P относительно точки O и определить углы, содержащиеся между вектором M и осями системы:
Если сила лежит в плоскости Oxy, то zo = 0 и Pz = 0 (см. Рисунок ниже).
Момент силы P по отношению к точке (полюсу) O составляет:
Mx = 0,
My = 0,
Mo (P) = Mz = Pyxo — Pxyo.
Метка крутящего момента:
плюс (+) — вращение силы вокруг оси O по часовой стрелке,
минус (-) — вращение силы вокруг оси O против часовой стрелки.
15.Вращательное движение. Момент силы и момент импульса.
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
Кинетические характеристики:
Вращение твердого тела, как целого характеризуется углом , измеряющегося в угловых градусах или радианах, угловой скоростью (измеряется в рад/с)и угловым ускорением(единица измерения — рад/с²).
При равномерном вращении (T оборотов в секунду):
Частота вращения — число оборотов тела в единицу времени.-
,
Период вращения — время одного полного оборота. Период вращения T и его частота связаны соотношением .
Линейная скорость точки, находящейся на расстоянии R от оси вращения
Угловая скорость вращения тела
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса замкнутой системы сохраняется
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
16.Уравнение динамики вращательного движения. Момент инерции.
Основное уравнение динамики вращательного движения материальной точки – угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.
М = E*J или E = M/J
Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Свойства момента инерции:
1.Момент инерции системы равен сумме момента инерции её частей.
2.Момент инерции тела является величиной, иманентно присущей этому телу.
Момент инерции твердого тела – это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.
Формула момента инерции:
Теорема Штейнера:
Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R – расстояние между осями.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Центральный момент инерции (или момент инерции относительно точки O) — это величина
.
Вращательный момент – это… Что такое Вращательный момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Вращающий момент Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы и вектора этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.{\varphi }\left|{\vec {M}}\right|d\varphi }.
Единицы
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Специальные случаи
Формула момента рычага
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Момент силы относительно точки
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Измерение момента силы
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
См. также
Вращающий магнитный момент — Википедия
Материал из Википедии — свободной энциклопедии
Вращающий магнитный момент — физическая величина численно равная векторному произведению вектора магнитного момента m→{\displaystyle {\vec {m}}} на вектор магнитной индукции B→{\displaystyle {\vec {B}}} :
T=m→×B→{\displaystyle T={\vec {m}}\times {\vec {B}}}
Также вращающий момент можно представить в виде
T=I⋅B→⋅Sc{\displaystyle T=I\cdot {\vec {B}}\cdot {\frac {S}{c}}} , так как магнитный момент m→{\displaystyle {\vec {m}}} равен
m→=Ic⋅S{\displaystyle {\vec {m}}={\frac {I}{c}}\cdot S}
При пропускании через проволочную рамку C{\displaystyle C} тока I{\displaystyle I} на неё действует магнитный момент m→{\displaystyle {\vec {m}}}, величина которого определяется как:
m→=I2⋅∮Cr→×dr→=I⋅∮AdΩ→{\displaystyle {\vec {m}}={\frac {I}{2}}\cdot \oint \limits _{C}{\vec {r}}\times d{\vec {r}}=I\cdot \oint \limits _{A}d{\vec {\Omega }}}A — площадь произвольного контура, ограниченного рамкой C.{2}}
Где A→{\displaystyle {\vec {A}}} — вектор площади кольца. Если в катушках Гельмгольца протекает ток I′{\displaystyle I’}, то из (1):
|T→|=c⋅I⋅n⋅|A→|⋅I′⋅sinα(2){\displaystyle |{\vec {T}}|=c\cdot I\cdot n\cdot |{\vec {A}}|\cdot I’\cdot \sin \alpha (2)}где α{\displaystyle \alpha } — угол между B→{\displaystyle {\vec {B}}} и вектором площади A→{\displaystyle {\vec {A}}}, c{\displaystyle c} — постоянная катушек Гельмгольца.
Результаты экспериментов для различных витков, входящих в экспериментальный набор, доказывают вышеупомянутое уравнение (2).
График зависимости вращающегося момента от количества витковД.В.Сивухин. Электричество. — «МФТИ», 2002. — Т. 3. — 656 с. — ISBN 5-9221-0227-3.
Мощность и вращающий момент электродвигателя. Что это такое?
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Вращающий момент (T) – это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы – или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила – любая сила – вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент – момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Как видно из названия – «постоянный вращающий момент» – подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
Переменный вращающий момент и мощность
«Переменный вращающий момент» – эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения – мал, а потребный вращающий момент при высокой частоте вращения – велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность – кубу скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
P1 (кВт) Входная электрическая мощность насосов – это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя – это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
Механический момент – это… Что такое Механический момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
Момент силы приложенный к гаечному ключу
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .
В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .
И теперь полная работа записывается очень просто или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и OF, на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Формула момента силы в физике
- Главная
- Справочник
- Формулы по физике
Определение и формула момента силы
ОпределениеВекторное произведение радиус – вектора (), который проведен из точки О (рис.1) в точку к которой приложена сила на сам вектор называют моментом силы ( )по отношению к точке O:
На рис.1 точка О и вектор силы ( )и радиус – вектор находятся в плоскости рисунка. В таком случае вектор момента силы () перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора равна:
где – угол между направлениями радиус – вектора и вектора силы, – плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:
При этом точку О называют центром приведения системы сил.
Если имеются два главных моме
Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению вектора силы и радиус-вектора, проведённого от оси вращения к точке приложения этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы.
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=α−π2{\displaystyle \beta =\alpha -{\frac {\pi }{2}}}, а так как cos(α−π2)=sinα{\displaystyle \cos {\left(\alpha -{\frac {\pi }{2}}\right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.{\varphi }\left|{\vec {M}}\right|d\varphi }.
Единицы
Момент силы имеет размерность «сила на расстояние» и единицу измерения ньютон-метр в системе СИ. Энергия и механическая работа также имеют размерность «сила на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина (псевдо) векторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, приложенный через целый оборот, совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоулей. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Специальные случаи
Формула момента рычага
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютон·метр, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Момент силы относительно точки
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Измерение момента силы
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки.
См. также
Крутящий момент: определение, уравнение и формула – видео и стенограмма урока
Physics of Torque
Чтобы найти линейную силу, нам нужно знать массу и ускорение. Однако крутящий момент немного отличается из-за того, что задействовано вращение. Подумайте об открытии двери. Где вы нажимаете на нее, когда хотите, чтобы она открылась? Вы нажимаете на ту сторону двери, где нет петель, потому что нажатие на сторону с петлями затруднит ее открытие. Итак, для крутящего момента нам нужно знать не только массу и ускорение линейной силы, но и то, как далеко эта сила от оси вращения, поскольку мы также можем получить разные результаты в зависимости от этого.Мы можем видеть это на диаграмме и в уравнении для крутящего момента.
T = F * r * sin ( theta )
T = крутящий момент
F = линейное усилие
r = расстояние, измеренное от оси вращения к месту приложения линейной силы
theta = угол между F и r
В нашем уравнении sin ( theta ) не имеет единиц измерения, r имеет единицы измерения (м ), а F имеет единицы измерения в Ньютонах (Н).Объединив их вместе, мы видим, что единицей крутящего момента является Ньютон-метр (Нм).
Наконец, тета необходима для учета направления приложения линейной силы. Силу не всегда толкают прямо, как дверь. Это может происходить с разных сторон.
Равновесие вращения
Итак, мы увидели, как один крутящий момент может воздействовать на объект, но вы можете легко применить более одного крутящего момента одновременно. Вернемся к автомобильному двигателю.В каждом автомобиле имеется более одного поршня, прикладывающего крутящий момент к коленчатому валу. В этом случае есть общий крутящий момент, который является суммой каждого отдельного крутящего момента.
Всего T = T {1} + T {2} + … + T {n}
В этом уравнении n – это общее количество крутящих моментов, прилагаемых к объект. Существует также частный случай этого, называемый вращательным равновесием . Здесь сумма всех крутящих моментов, действующих на объект, равна нулю.Когда это происходит, это может означать, что на объект не действует крутящий момент или все крутящие моменты, действующие на объект, компенсируют друг друга. Чтобы визуализировать взаимно компенсирующиеся крутящие моменты, давайте рассмотрим простой случай с двумя крутящими моментами: качели.
В верхней части изображения двое детей сидят на качелях, которые не двигаются. Они уравновешены на оси вращения, которая в случае качелей является точкой опоры. Оба ребенка своим весом прикладывают силу, также известную как сила тяжести.Ребенок 1 пытается повернуть качели против часовой стрелки, а ребенок 2 пытается повернуть их по часовой стрелке. Пока величины двух крутящих моментов одинаковы, они компенсируют друг друга, поскольку они пытаются перемещать качели в противоположных направлениях.
Проблема тупика с качелями
Давайте посмотрим на пример расчета с использованием как вращательного равновесия, так и уравнения для крутящего момента.
Качели на изображении находятся в состоянии равновесия вращения и не движутся.Мы хотим найти, как далеко ребенок 2 справа от оси вращения в точке опоры. Ребенок 1 слева имеет массу 38 кг и находится на расстоянии 4 м от точки опоры. Ребенок 2 имеет массу 25 кг.
Шаг 1: Учет направления
Чтобы математически показать, что два момента движутся в противоположных направлениях, одному из них присваивается отрицательный знак. Обычно крутящий момент, вращающий объект по часовой стрелке, считается отрицательным, поэтому мы сделаем T {2} отрицательным.Поскольку качели находятся в состоянии вращательного равновесия, мы также знаем, что сумма крутящих моментов должна равняться нулю. Это позволяет нам изменить уравнение, чтобы получить по одному крутящему моменту по обе стороны от знака равенства.
T {1} + (- T {2}) = 0
T {1} – T {2} = 0
T {2} = T { 1}
Шаг 2: Вставьте уравнения крутящего момента и силы
Затем мы подставляем уравнение для крутящего момента с каждой стороны.
F { g 2} * r {2} * sin ( theta {2}) = F { g 1} * r {1} * sin ( theta {1})
F { g 2} и F { g 1} – силы, возникающие под действием силы тяжести.Чтобы получить их, мы умножаем массу каждого ребенка на ускорение свободного падения ( г ).
m {2} * g * r {2} * sin ( theta {2}) = m {1} * g * r {1} * sin ( theta {1})
Шаг 3. Упростите уравнение
Теперь мы можем сделать несколько вещей, чтобы упростить это уравнение. Во-первых, поскольку g одинаково для каждого дочернего элемента, и по обе стороны от знака равенства он отменяется.Во-вторых, если мы посмотрим на изображение, мы увидим, что силы тяжести перпендикулярны качелям. Это означает, что они перпендикулярны r {1} и r {2}. Таким образом, оба тета имеют значение 90 градусов. Помните, sin (90 градусов) = 1. Теперь у нас осталось следующее:
м {2} * r {2} = м {1} * r {1}
Шаг 4. Решите уравнение
Наконец, мы можем подключить наши данные, чтобы найти ответ для r {2}.
25 кг * r {2} = 38 кг * 4 м
25 кг * r {2} = 152 кг м
r {2} = 6 м
Ребенок 2 сидит 6 метрах от точки опоры. Для ротационного равновесия имеет смысл, что более легкий ребенок должен сидеть дальше от точки опоры, чем более тяжелый, чтобы балансировать на качелях.
Краткое содержание урока
Крутящий момент – это скручивающая сила, которая имеет тенденцию вызывать вращение. Точка вращения объекта известна как ось вращения .Математически крутящий момент может быть записан как T = F * r * sin ( theta ), и он имеет единицы измерения в Ньютон-метрах. Когда сумма всех крутящих моментов, действующих на объект, равна нулю, он находится в состоянии равновесия вращения . Крутящие моменты, действующие на один объект, нейтрализуют друг друга, когда они имеют равные величины и противоположные направления. Крутящий момент применяется не только к автомобилям; он также позволяет использовать такие объекты, как замки, дверные ручки, петли и даже качели.
Результаты обучения
Просмотрите урок и практикуйте уравнения, пока не будете готовы:
- Определить крутящий момент, вращательное равновесие и ось вращения
- Напомним уравнение для крутящего момента
- Рассчитать крутящий момент
- Вычислить значение r для объекта, находящегося в состоянии вращательного равновесия
- Перечислите некоторые примеры крутящего момента в повседневной жизни
Крутящий момент (момент)
Силу можно рассматривать как толчок или тянуть в определенном направлении.Когда к объекту прикладывается сила, результирующее движение объекта зависит от того, где сила приложена и как объект удерживается. Если объект не ограничен и сила приложена через центр гравитации, объект движется в чистом виде перевод, как описано Ньютоном законы движения. Если объект ограничен (или закреплен) в каком-то месте, называемом ось , объект вращается насчет стержня, но не переводит.Усилие передается через шарнир а детали вращения зависят от расстояния от приложенное усилие к оси. Если объект не ограничен и сила приложена в некоторой расстояние от центра тяжести, объект как переводит и вращается вокруг центра тяжести. Детали вращения зависят от расстояния до объекта. приложенная сила к центру тяжести. Движение летающих объектов описанный этим третьим типом движения; сочетание перевода и вращения.M называется крутящий момент или момент . Крутящий момент также является векторной величиной и производит вращение. так же, как сила производит перевод. А именно объект на покой или вращение с постоянной угловой скоростью, будет продолжать делать это пока он не подвергнется внешнему крутящему моменту. Крутящий момент вызывает изменение в угловой скорости, которая называется угловым ускорением.
Расстояние L , используемое для определения крутящего момента T , является расстоянием от шарнир p к силе, но измеряется перпендикулярно к направление силы.На рисунке показаны четыре примера крутящих моментов, чтобы проиллюстрировать основные принципы, регулирующие крутящие моменты. В каждом примере синий груз W воздействует на красную полосу, которая называется рука.
В примере 1 сила (вес) приложена перпендикулярно к руке. В этом случае перпендикулярное расстояние – это длина стержня и крутящий момент равен произведению длины и силы.
Т = F * L
В примере 2 к руке прилагается такая же сила, но сила теперь действует прямо через вращаться.В этом случае расстояние от оси перпендикулярно силе равно нулю. Значит, и в этом случае крутящий момент также равен нулю. Представьте себе распашную дверь. Если вы нажмете край двери, в сторону петли, дверь не двигается потому что крутящий момент равен нулю.
Пример 3 представляет собой общий случай, когда сила прилагается. под некоторым углом a к рука. Перпендикулярное расстояние определяется выражением тригонометрия как длина плеча (L), умноженная на косинус (cos) угла.Тогда крутящий момент определяется по формуле:
Т = F * L * cos (а)
Примеры 1 и 2 могут быть получены из этой общей формулы, так как косинус 0 градусов составляет 1,0 (Пример 1), а косинус 90 градусов равен 0,0 (Пример 2).
В примере 4 точка поворота была перемещена с конца стержня на место около середины бара. Вес добавлен с обеих сторон оси. Справа одна гиря W создает силу F1 , действующую на расстоянии L1 от оси.Это создает крутящий момент T1 , равный произведение силы и расстояния.
Т1 = F1 * L1
Слева от Поверните два груза W, , создайте усилие F2 на расстоянии L2 . Это производит крутящий момент T2 в направлении, противоположном T1, потому что расстояние находится в противоположном направлении.
Т2 = F2 * L2
Если бы система находилась в состоянии равновесия , или сбалансирован, крутящие моменты будут равны, и никакой полезный крутящий момент не будет действовать на систему.
T1 = T2 или T1 – T2 = 0
F1 * L1 = F2 * L2
Если система не находится в равновесии или неуравновешена, стержень вращается. вокруг оси в направлении большего крутящего момента. Если F2 = 2 * F1, какова связь между L1 и L2, чтобы сбалансировать систему? Если F2 = 2 * F1, и L1 = L2, в каком направлении будет вращаться система?
Авиационные инженеры используют крутящий момент, создаваемый аэродинамическими поверхностями. для стабилизации и управления самолетом.В самолетах рули производят аэродинамические силы. Эти силы действуют на некотором расстоянии от самолет cg и поэтому заставить летательный аппарат вращаться. В лифты производят момент тангажа, руль направления момент рыскания, и элероны производят момент качения. Возможность варьировать количество сила и момент позволяют пилоту маневрировать или обрезать самолет. На модельных ракетах плавники используются для создания крутящего момента вокруг ракеты центр гравитации предоставлять стабильность во время полета с двигателем.На воздушных змеях аэродинамические и весовые силы произвести крутящий момент вокруг уздечка. Расстояние от точки уздечки и величина сил оказывает сильное влияние на представление воздушного змея.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
10.7. Крутящий момент – Физика LibreTexts
Цели обучения
- Опишите, как величина крутящего момента зависит от величины плеча рычага и угла, который вектор силы образует с плечом рычага
- Определите знак (положительный или отрицательный) крутящего момента, используя правило правой руки
- Рассчитайте отдельные крутящие моменты вокруг общей оси и просуммируйте их, чтобы найти чистый крутящий момент
Важной величиной для описания динамики вращающегося твердого тела является крутящий момент.Мы видим приложение крутящего момента по-разному в нашем мире. У всех нас есть интуитивное представление о крутящем моменте, например, когда мы используем большой гаечный ключ, чтобы открутить прочный болт. Крутящий момент действует невидимым образом, например, когда мы нажимаем на акселератор в автомобиле, заставляя двигатель передавать дополнительный крутящий момент на трансмиссию. Или каждый раз, когда мы перемещаем свое тело из положения стоя, мы прикладываем крутящий момент к нашим конечностям. В этом разделе мы определяем крутящий момент и приводим аргументы в пользу уравнения для расчета крутящего момента для твердого тела с вращением с фиксированной осью.
Определение крутящего момента
До сих пор мы определили множество переменных, которые являются вращательными эквивалентами своих трансляционных аналогов. Давайте посмотрим, какой должна быть противоположность силе. Поскольку силы изменяют поступательное движение объектов, вращательная составляющая должна быть связана с изменением вращательного движения объекта вокруг оси. Мы называем этот вращательный аналог крутящим моментом .
В повседневной жизни мы все время вращаем объекты вокруг оси, поэтому интуитивно мы уже многое знаем о крутящем моменте.Рассмотрим, например, как мы поворачиваем дверь, чтобы открыть ее. Во-первых, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям; открыть дверь эффективнее, если отодвинуть ее далеко от петель. Во-вторых, мы знаем, что нужно толкать перпендикулярно плоскости двери; если мы толкнем параллельно плоскости двери, мы не сможем ее повернуть. В-третьих, чем больше сила, тем эффективнее она открывает дверь; чем сильнее вы толкаете, тем быстрее открывается дверь. Первый пункт подразумевает, что чем дальше сила приложена от оси вращения, тем больше угловое ускорение; второй подразумевает, что эффективность зависит от угла приложения силы; третий подразумевает, что величина силы также должна быть частью уравнения.Обратите внимание, что для вращения в плоскости крутящий момент имеет два возможных направления. Крутящий момент устанавливается по часовой стрелке или против часовой стрелки относительно выбранной точки поворота. На рисунке \ (\ PageIndex {1} \) показано вращение против часовой стрелки.
Рисунок \ (\ PageIndex {1} \): Крутящий момент – это эффективность силы поворота или скручивания, показанная здесь для вращения двери на ее петлях (если смотреть сверху). Крутящий момент имеет как величину, так и направление. (a) Крутящий момент против часовой стрелки создается силой \ (\ vec {F} \), действующей на расстоянии r от шарниров (точки поворота).(b) Меньший крутящий момент против часовой стрелки создается, когда меньшая сила \ (\ vec {F} ′ \) действует на том же расстоянии r от шарниров. (c) Та же сила, что и в (a), создает меньший крутящий момент против часовой стрелки при приложении на меньшем расстоянии от шарниров. (d) Меньший крутящий момент против часовой стрелки создается силой той же величины, что и (a), действующей на том же расстоянии, что и (a), но под углом \ (\ theta \), который меньше 90 °.Теперь давайте рассмотрим, как определять крутящие моменты в общем трехмерном случае.
Момент
Когда сила \ (\ vec {F} \) приложена к точке P, положение которой \ (\ vec {r} \) относительно O (рисунок \ (\ PageIndex {2} \)), крутящий момент \ (\ vec {\ tau} \) около O равно
\ [\ vec {\ tau} = \ vec {r} \ times \ vec {F} \ ldotp \ label {10.22} \]
Рисунок \ (\ PageIndex {2} \): Крутящий момент перпендикулярен плоскости, определяемой \ (\ vec {r} \) и \ (\ vec {F} \), и ее направлению определяется по правилу правой руки.
Согласно определению векторного произведения, крутящий момент \ (\ vec {\ tau} \) перпендикулярен плоскости, содержащей \ (\ vec {r} \) и \ (\ vec {F} \), и имеет величину
.\ [| \ vec {\ tau} | = | \ vec {r} \ times \ vec {F} | = rF \ sin \ theta, \]
, где \ (\ theta \) – угол между векторами \ (\ vec {r} \) и \ (\ vec {F} \). В системе СИ единица измерения крутящего момента – ньютон на метр, обычно записывается как Н • м. Величина r \ (\ perp \) = rsin \ (\ theta \) представляет собой перпендикулярное расстояние от O до линии, определяемой вектором \ (\ vec {F} \), и называется плечом рычага .Учтите, что чем больше плечо рычага, тем больше крутящий момент. По плечу рычага величина крутящего момента
.\ [| \ vec {\ tau} | = r _ {\ perp} F \ ldotp \ label {10.23} \]
Перекрестное произведение \ (\ vec {r} \ times \ vec {F} \) также сообщает нам знак крутящего момента. На рисунке \ (\ PageIndex {2} \) перекрестное произведение \ (\ vec {r} \ times \ vec {F} \) находится вдоль положительной оси z, что по соглашению является положительным крутящим моментом. Если \ (\ vec {r} \ times \ vec {F} \) находится вдоль отрицательной оси z, это создает отрицательный крутящий момент.
Если мы рассмотрим диск, который может свободно вращаться вокруг оси через центр, как показано на рисунке \ (\ PageIndex {3} \), мы можем увидеть, как угол между радиусами \ (\ vec {r} \) а сила \ (\ vec {F} \) влияет на величину крутящего момента. Если угол равен нулю, крутящий момент равен нулю; если угол 90 °, крутящий момент максимальный. Крутящий момент на рисунке \ (\ PageIndex {3} \) положительный, потому что направление крутящего момента по правилу правой руки выходит за пределы страницы вдоль положительной оси z. Диск вращается против часовой стрелки из-за крутящего момента в том же направлении, что и положительное угловое ускорение.
Рисунок \ (\ PageIndex {3} \): Диск может свободно вращаться вокруг своей оси через центр. Величина крутящего момента на диске равна rFsin \ (\ theta \). Когда \ (\ theta \) = 0 °, крутящий момент равен нулю и диск не вращается. Когда \ (\ theta \) = 90 °, крутящий момент максимальный, и диск вращается с максимальным угловым ускорением.Можно рассчитать любое количество крутящих моментов относительно данной оси. Отдельные крутящие моменты складываются, чтобы получить чистый крутящий момент вокруг оси. Когда соответствующий знак (положительный или отрицательный) присваивается величинам отдельных крутящих моментов вокруг указанной оси, чистый крутящий момент вокруг оси является суммой отдельных крутящих моментов:
\ [\ vec {\ tau} _ {net} = \ sum_ {i} | \ vec {\ tau} _ {i} | \ ldotp \ label {10.24} \]
Расчет крутящего момента для твердых тел на фиксированной оси
В следующих примерах мы вычисляем крутящий момент как абстрактно, так и применительно к твердому телу. Сначала мы представляем стратегию решения проблем.
Стратегия решения проблем: определение полезного крутящего момента
- Выберите систему координат с точкой поворота или осью вращения в качестве начала выбранной системы координат.
- Определите угол между плечом рычага \ (\ vec {r} \) и вектором силы.
- Возьмите перекрестное произведение \ (\ vec {r} \) и \ (\ vec {F} \), чтобы определить, является ли крутящий момент положительным или отрицательным относительно точки поворота или оси.
- Оцените величину крутящего момента, используя r \ (\ perp \) F.
- Установите соответствующий знак, положительный или отрицательный, для величины.
- Суммируйте крутящие моменты, чтобы найти чистый крутящий момент.
Пример 10.14: Расчет крутящего момента
Четыре силы показаны на рисунке \ (\ PageIndex {4} \) в определенных местах и ориентациях относительно данной системы координат xy.Найдите крутящий момент, создаваемый каждой силой относительно начала координат, а затем используйте полученные результаты, чтобы найти чистый крутящий момент относительно начала координат.
Рисунок \ (\ PageIndex {4} \): четыре силы, создающие крутящие моменты.Стратегия
Эта задача требует расчета крутящего момента. Все известные величины – силы с направлениями и плечами рычага – приведены на рисунке. Цель состоит в том, чтобы найти каждый отдельный крутящий момент и чистый крутящий момент путем суммирования отдельных крутящих моментов. Будьте осторожны, чтобы назначить правильный знак каждому крутящему моменту, используя перекрестное произведение \ (\ vec {r} \) и вектора силы \ (\ vec {F} \).
Решение
Использование | \ (\ vec {\ tau} \) | = r \ (\ perp \) F = rFsin \ (\ theta \), чтобы найти величину, и \ (\ vec {r} = \ vec {r} \ times \ vec {F} \), чтобы определить знак крутящего момента.
Крутящий момент от силы 40 Н в первом квадранте определяется выражением (4) (40) sin 90 ° = 160 Н • м.
Перекрестное произведение \ (\ vec {r} \) и \ (\ vec {F} \) за пределами страницы, положительное.
Крутящий момент от силы 20 Н в третьем квадранте определяется по формуле – (3) (20) sin 90 ° = – 60 Н • м.
Перекрестное произведение \ (\ vec {r} \) и \ (\ vec {F} \) находится на странице, поэтому оно отрицательное.
Крутящий момент от силы 30 Н в третьем квадранте определяется выражением (5) (30) sin 53 ° = 120 Н • м.
Перекрестное произведение \ (\ vec {r} \) и \ (\ vec {F} \) за пределами страницы, положительное.
Крутящий момент от силы 20 Н во втором квадранте определяется выражением (1) (20) sin 30 ° = 10 Н • м.
Перекрестное произведение \ (\ vec {r} \) и \ (\ vec {F} \) отсутствует на странице.
Таким образом, чистый крутящий момент равен \ (\ tau_ {net} = \ sum_ {i} | \ tau_ {i} | \) = 160 – 60 + 120 + 10 = 230 Н • м.
Значение
Обратите внимание, что каждая сила, действующая в направлении против часовой стрелки, имеет положительный крутящий момент, тогда как каждая сила, действующая в направлении по часовой стрелке, имеет отрицательный крутящий момент. Крутящий момент тем больше, чем больше расстояние, сила или перпендикулярные компоненты.
Пример 10.15: Расчет крутящего момента на твердом теле
На рисунке \ (\ PageIndex {5} \) показано несколько сил, действующих в разных местах и под разными углами на маховик. У нас есть \ (| \ vec {F} _ {1} | \) = 20 N, \ (| \ vec {F} _ {2} | \) = 30 N, \ (| \ vec {F} _ { 3} | \) = 30 Н и r = 0.5 мес. Найдите чистый крутящий момент на маховике вокруг оси, проходящей через центр.
Рисунок \ (\ PageIndex {5} \): Три силы, действующие на маховик.Стратегия
Рассчитываем каждый крутящий момент индивидуально, используя векторное произведение, и определяем знак крутящего момента. Затем суммируем крутящие моменты, чтобы найти чистый крутящий момент. Решение Начнем с \ (\ vec {F} _ {1} \). Если мы посмотрим на рисунок \ (\ PageIndex {5} \), мы увидим, что \ (\ vec {F} _ {1} \) образует угол 90 ° + 60 ° с радиус-вектором \ (\ vec {r } \).{о} = (-0,5 \; м) (30 \; N) = -15,0 \; N \; \ cdotp m \ ldotp \]
Когда мы оцениваем крутящий момент из-за \ (\ vec {F} _ {3} \), мы видим, что угол, который он образует с \ (\ vec {r} \), равен нулю, поэтому \ (\ vec {r} \ раз \ vec {F} _ {3} \) = 0. Следовательно, \ (\ vec {F} _ {3} \) не создает крутящего момента на маховике.
Оцениваем сумму крутящих моментов:
\ [\ tau_ {net} = \ sum_ {i} | \ tau_ {i} | = 5-15 = -10 \; N \; \ cdotp m \ ldotp \]
Значение
Ось вращения находится в центре масс маховика.Поскольку маховик находится на фиксированной оси, его нельзя перемещать. Если бы он был на поверхности без трения и не был зафиксирован на месте, \ (\ vec {F} _ {3} \) заставил бы маховик перемещаться, как и \ (\ vec {F} _ {1} \). Его движение было бы комбинацией перевода и вращения.
Упражнение 10.6
Большое океанское судно садится на мель возле береговой линии, подобно судьбе Costa Concordia , и ложится под углом, как показано ниже. Спасательные бригады должны приложить крутящий момент, чтобы направить судно, чтобы его можно было спустить на плаву для транспортировки.Сила 5,0 x 10 5 Н, действующая в точке A, должна быть приложена справа от судна. Каков крутящий момент в точке контакта корабля с землей (рисунок \ (\ PageIndex {6} \))?
Рисунок \ (\ PageIndex {6} \): Судно садится на мель и наклоняется, требуя приложения крутящего момента, чтобы вернуть судно в вертикальное положение.Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Использование уравнений крутящего момента – AP Physics B
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Формула крутящего момента, калькулятор и ответы на часто задаваемые вопросы
Крутящий момент – это тип измерения, который может применяться для объекта, вращающегося вокруг оси. Все вы знаете, что сила – единственный фактор в линейной кинематике, который вызывает ускорение тела.
Так же, как сила, крутящий момент связан с угловым ускорением тела. Ось вращения – это точка, в которой тело начинает свое вращение. В этой статье мы кратко прочитаем о физике формулы крутящего момента. У физики есть простое объяснение крутящего момента, который представляет собой тенденцию силы, которая способствует скручиванию.
Калькулятор крутящего момента
Физики разработали простой путь, который приводит к формуле расчета крутящего момента.
(Изображение будет добавлено в ближайшее время)
Для этого нам нужно найти плечо рычага.После этого просто умножьте его на приложенную силу. До сих пор вы знаете, что крутящий момент может создаваться двумя факторами, такими как величина силы и нормальное расстояние (перпендикулярное расстояние) между точкой (здесь применяется крутящий момент), относительно которой рассчитывается крутящий момент.
Итак, формула крутящего момента равна τ = F.r. sinθ
Здесь τ = Крутящий момент
F = Сила
θ = Угол между силой и точкой
r = Общая длина плеча рычага
Формула крутящего момента двигателя
Единица измерения, используемая для измерения крутящего момента – Ньютон-метр (Нм).Мы обсудили уравнение, которое помогает нам рассчитать крутящий момент. Что ж, указанное выше соотношение основано на векторном произведении вектора положения и силы.
τ = F x r
Это формула крутящего момента, которую мы используем для расчета двигателя.
Крутящий момент в автомобиле
Как мы знаем, выражение, определяющее крутящую силу или вращающую силу, известно как крутящий момент. Двигатели передают крутящий момент на ось, которая находится внутри автомобиля. Двигатель отвечает за создание силы вращения.Этот крутящий момент считается силой автомобиля.
Если двигатель способен обеспечить максимальный крутящий момент, автомобиль будет обеспечивать максимальную мощность. Все спортивные автомобили используют эти типы двигателей с максимальным крутящим моментом. Двигатель придаст ускорение автомобилю в течение 60 секунд. Кроме того, эти типы двигателей используются в тяжелых транспортных средствах, таких как грузовики, тракторы и другие.
Формула максимального крутящего момента
Это формула, объясняющая максимальный крутящий момент в трехфазном двигателе
Tmax = \ [k.{2}} {2X_ {2}} \]
Заключение
Крутящий момент играет решающую роль в выработке энергии двигателем автомобиля. Крутящий момент – это величина, которая представляет способность двигателя обрабатывать или генерировать максимальную мощность для вращения оси. Выходную мощность двигателя можно измерить с помощью числа оборотов в минуту. Это возможно только при максимальном создаваемом крутящем моменте.
Полный урок для начинающих – получить образование
Крутящий момент – это мера того, насколько сила, действующая на объект, вызывает вращение проблемы.Элемент вращается относительно оси, которую мы назовем точкой поворота и обозначим “O”. Он также обозначает силу буквой «F». Длина от точки поворота до фактора, на который действует сила, называется плечом момента и обозначается буквой «r». Имейте в виду, что этот диапазон, «r», также является вектором и указывает от оси вращения туда, где действует сила. Давайте посмотрим на Формулу крутящего момента.
Проще говоря, крутящий момент – это перекрестный элемент между вектором расстояния (расстояние от оси указывает на коэффициент, на который прикладывается сила), а также вектором силы, «a» – это угол между r и F.
Используя указатель для правого человека, мы можем определить направление вектора крутящего момента. Если мы приложим пальцы к r, а также согнем их в соответствии с инструкциями F, после этого большой палец будет указывать на вектор крутящего момента.
Визуализируйте, как вы нажимаете на дверь, чтобы открыть ее. Сила нажатия (F) заставляет дверь вращаться относительно петель (коэффициент поворота, O). Насколько сильно вам нужно оттолкнуться на расстояние, вы от суставов (r) (и еще несколько вещей, но давайте сейчас ими пренебрегаем).Чем ближе расстояние к петлям (т.е. чем меньше r), тем сложнее нажимать. Вот что происходит, когда вы пытаетесь открыть дверь не с той стороны. Крутящий момент, который вы создали на двери, меньше, чем если бы вы нажали на правую сторону (в сторону от ее стыков).
Немного подробнее о формуле крутящего моментаНа предмет может действовать более одной силы, а также каждое из этих давлений может воздействовать на разные точки предмета.Тогда каждое давление будет создавать крутящий момент. Чистый крутящий момент – это совокупность отдельных крутящих моментов.
Вращательное равновесие аналогично поступательному равновесию, где количество сил равняется нулю. С точки зрения стабильности вращения сумма крутящих моментов абсолютно равна нулю. Проще говоря, на объекте нет интернет-крутящего момента.
∑ τ = 0.
Имейте в виду, что система крутящего момента в системе СИ – это ньютон-метр, который также является средством выражения Джоуля (силового устройства).Тем не менее крутящий момент – это не мощность. Итак, чтобы избежать путаницы, мы будем использовать систему N.m, а не J. Различие возникает потому, что мощность – это скалярная величина, а крутящий момент – вектор.
Формула углового ускорения Крутящий моментПо сравнению со Вторым правилом Ньютона, угловое движение также подчиняется Первому закону Ньютона. Если на объект не действует внешнее давление, движущийся объект остается в движении. Как и оставленный предмет, продолжает оставаться в покое.С вращающимися предметами мы можем сказать это, если не применяется крутящий момент на открытом воздухе. Вращающийся объект, несомненно, останется вращаться, а неподвижный объект определенно не начнет вращаться.
Если бы поворотный стол вращался против часовой стрелки и двигал бы ваши пальцы в противоположные стороны, поворотный стол начал бы замедлять свое вращение. С точки зрения перевода, как минимум, на проигрыватель, несомненно, не было бы никакой силы Интернета. Сила, которая указывает на одну сторону, действительно будет отменена силой, которая указывает на другую.Несомненно, силы обоих пальцев прекратятся. Следовательно, поворотный стол будет в поступательной устойчивости. Несмотря на это, это снизит скорость вращения, а это означает, что скорость больше не будет абсолютной. Мы можем заключить, что только потому, что вращающийся объект находится в поступательном балансе, он не всегда находится в симметрии вращения.
Что такое уравнение крутящего момента?
Фото: geralt через Pixabay, CC0Уравнение для крутящего момента может быть представлено следующим уравнением: τ = F * rsin (θ).
T – вектор крутящего момента, F – заданная сила, r – длина плеча момента, а θ – угол между плечом момента и вектором силы. Это основное уравнение для расчета крутящего момента, но чтобы разобраться в этом уравнении, давайте рассмотрим крутящий момент более подробно, чтобы понять, что он представляет и как измеряется.
Что такое крутящий момент?
Крутящий момент – это сила, которая перемещает объект под углом, или сила, которая заставляет данный объект создавать угловое ускорение.Другими словами, крутящий момент – это сила, которая перемещает объект вокруг оси, и измеряется. Это аналогично тому, как сила является мерой ускорения объекта в линейной кинематике, но вместо этого она измеряет угловое ускорение. Крутящие моменты измеряются в векторах, и направление вектора зависит от направления через ось, по которой распространяется сила.
Фото: susannp4 через Pixabay, CC0Один из самых простых способов проиллюстрировать пример крутящего момента – изучить движение двери, когда вы ее открываете.Когда вы собираетесь открыть дверь, вы кладете руку на ручку и толкаете / тянете ее, это означает, что вы прикладываете силу к двери в точке в пространстве, наиболее удаленной от петли. Если вы хотите попытаться открыть дверь, нажав на сторону двери, ближайшую к петле, вам потребуется гораздо больше силы. Таким образом, хотя дверь по-прежнему будет двигаться на ту же величину, для одного действия потребуется гораздо меньше силы, чем для другого. Сила, которая используется для создания движения открывания двери, и есть крутящий момент.
При измерении крутящего момента он может быть динамическим или статическим.Статический крутящий момент – это крутящий момент, который не приводит к ускорению по оси, сила, которая не может вызвать угловое ускорение. Если бы дверь, которую вы пытались открыть, была закрыта, и вы толкали ее, это был бы статический момент. В то время как сила будет приложена к двери, дверные петли не вращаются, и, следовательно, крутящий момент является статическим. Между тем, примером динамического крутящего момента является запуск вашего автомобиля и его вождение. Когда вы ускоряетесь, это пример динамического крутящего момента, поскольку возникает угловое ускорение, и колеса вашего автомобиля перемещают его из одного положения в другое.
В целях пояснения отметим здесь, что «крутящий момент» – не единственный способ описания силы, вызывающей угловое ускорение. Инженеры могут иногда использовать термин «импульс силы» или просто «импульс» вместо крутящего момента. «Плечо момента» – это радиус, на который действует приложенная сила, от точки вращения до точки приложения силы.
Как вычисляется крутящий момент
Фото: Кришнаведала – собственная работа, CC0, https: //commons.wikimedia.org / w / index.php? curid = 20311913Теперь, когда мы определили крутящий момент, понимание уравнения для расчета крутящего момента стало немного проще. Давайте еще раз посмотрим на уравнение для крутящего момента:
τ = F * rsin (θ)
T представляет вектор крутящего момента, создаваемый определенной силой, которая представлена буквой F. Переменная r представляет длину плеча момента, а Theta это угол между плечом импульса и вектором силы. Для определения направления вектора крутящего момента можно использовать простую эвристику, получившую название «правило правого захвата».Если бы вы согнули правую руку вокруг оси вращения, сомкнув пальцы вокруг вектора, который представляет направление силы, тогда вектор крутящего момента будет указывать в направлении вашего большого пальца.
Крутящий момент определяется количественно с помощью ньютон-метра, измерения крутящего момента, используемого системой единиц СИ. В имперской системе часто используется соотношение фут-фунт, хотя это несколько труднее интерпретировать, чем систему ньютон-метр, потому что термин «фунт» имеет разговорный смысл как единица массы в дополнение к единице силы. .Под фунтом здесь понимается фунт-сила или сила, приложенная к объекту весом 1 фунт под действием силы тяжести Земли. Поскольку 1,7 фут-фунта приблизительно эквивалентны одному Ньютон-метру, измерения величины в основном такие же, если принять это во внимание.
При измерении статического крутящего момента в неподвижной невращающейся среде необходимо учитывать некоторые дополнительные факторы. Этого можно достичь, взяв длину импульсного плеча и напрямую определив крутящий момент, что намного проще, чем измерение крутящего момента во вращающейся системе.Для измерения крутящего момента во вращающейся системе существуют различные методы, но общая система измерения заключается в количественном определении деформации металла в приводном валу, который отвечает за передачу крутящего момента.
Как крутящий момент влияет на кинематику вращения
Как упоминалось ранее, крутящий момент можно рассматривать как эквивалент силы в линейной кинематике. Второй закон движения Ньютона и линейная кинематика представлены уравнением F = ma (Сила = масса x ускорение).
В кинематике вращения есть эквивалентное уравнение: r = Ia.
Переменная «a» здесь представляет угловое ускорение, в то время как инерция вращения системы представлена переменной «I». Инерция вращения зависит от того, как распределяется масса системы, и по мере увеличения значения I объекту становится все труднее набирать угловое ускорение.
Понимание вращательного равновесия
Если вращательное равновесие можно считать эквивалентным уравнению силы в линейной кинематике, тогда оно следует за объектом, который неподвижен и не вращается, останется в этом состоянии, если к нему не приложен внешний крутящий момент.Отсюда также следует, что только внешний крутящий момент может изменить вращение объекта, который вращается с постоянной угловой скоростью. Вращательное равновесие – полезная концепция при попытке определить, как несколько различных крутящих моментов влияют на вращающийся объект. Чтобы вычислить вращение объекта, подверженного воздействию нескольких крутящих моментов, необходимо рассчитать чистый крутящий момент. Объект будет во вращательном равновесии, если чистый крутящий момент равен нулю, и объект не может ускоряться.
Уточнение крутящего момента, мощности и энергии
Людей часто путает соотношение между энергией, мощностью и крутящим моментом.Например, термин «мощность поворота» часто применяется для описания крутящего момента двигателя, но, хотя энергия и крутящий момент могут быть количественно определены с использованием одних и тех же основных единиц, они не описывают одно и то же явление. В то время как мощность может подаваться на невращающиеся системы, крутящий момент применим только к вращающейся системе. Можно рассчитать мощность по значению крутящего момента, если была определена скорость вращения системы. На самом деле мощность в лошадиных силах обычно определяется путем расчета скорости вращения и крутящего момента, а не измеряется напрямую.
Чтобы сделать это более явным, давайте посмотрим на уравнения для мощности:
P = (Сила x Расстояние) / Время = (F x 2πr) / t = 2 ππw (оборотов в секунду)
Макс. крутящий момент часто упоминается как важный статистический показатель при предоставлении технических характеристик транспортного средства, наряду с производной мощностью транспортного средства. Максимальный крутящий момент влияет на ускорение транспортного средства, а также на его тяговую способность. Максимальная скорость транспортного средства, а не ускорение, больше зависит от лошадиных сил, чем от крутящего момента относительно веса транспортного средства.
Общее движение транспортного средства определяется большим количеством факторов, чем просто максимальная мощность и крутящий момент, поэтому, хотя знание максимальной мощности и крутящего момента транспортного средства упростит получение определенных характеристик и расчетов, при определении общей суммы транспортного средства необходимо собрать гораздо больше переменных. маневренность. В действительности и мощность, и крутящий момент могут изменяться в зависимости от скорости вращения, и разные двигатели могут иметь разные отношения между крутящим моментом и скоростью вращения, часто нелинейные отношения.
Изменение уровней крутящего момента
Фото: TheDigitalArtist через Pixabay, CC0Для различных приложений, использующих угловой момент, часто требуются разные уровни крутящего момента, поэтому уровни крутящего момента необходимо увеличивать или уменьшать в соответствии с требованиями проекта. Длина рычага – это то, что уменьшает или увеличивает силу, действующую на объект, в зависимости от расстояния, на которое рычаг перемещается. Если вы заметили сходство между крутящим моментом и силой, вы можете догадаться, что крутящий момент, создаваемый двигателем, можно изменить с помощью аналогичного объекта, чем-то аналогичного рычагу.
Использование зубчатой передачи может уменьшать или увеличивать крутящий момент, который производит двигатель, увеличивая крутящий момент при уменьшении скорости вращения. Две шестерни, сцепляющиеся вместе, действуют как два рычага, толкающих друг друга. Один из наиболее заметных примеров шестерен, влияющих на крутящий момент объекта, – это шестерни велосипеда, позволяющие велосипеду развивать полезную скорость без чрезмерных усилий со стороны водителя.
