Математические обозначения скорость расстояние время. Как обозначается расстояние в физике? Интересные примеры
Тема посвящена тем учащимся, у кого физика только первый год. Здесь мы поговорим не только о том, как обозначается расстояние в физике, но и о других интересных вещах. Пусть этот предмет будет интересным по всем разделам и темам.
Какое же оно – расстояние?
В физике у каждой имеется свой символ (обозначение или на латинице, или греческой буквой). Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Итак, «S» – это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
Поверьте, в решении задач нет ничего сложного. Но при условии, что вы знаете математику и успеваете по ней. Вам понадобятся знания по операциям с дробями, умение считать, раскрывать скобки, решать уравнения. Без таких навыков по физике будет очень сложно.
Примеры из жизни
Что же такое расстояние? Как обозначается расстояние в физике, мы уже уяснили. Теперь разберемся с понятием.
Представьте себе, что вы сейчас стоите возле своего дома. Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?
Почему мы не написали «метров», а ограничились только буквой? Потому что такое вот сокращенное буквенное обозначение. Чуть позже познакомимся и с другими параметрами, которые связаны с расстоянием.
А теперь представьте, что путь от дома до магазина извилистый. Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
С чем связано расстояние?
Понятие “расстояние” не может существовать само по себе, оно должно играть какую-то роль. Например, вы едете на велосипеде в школу, а не идете пешком, потому что опаздываете. Как мы говорили ранее, наш путь до школы прямой. Можно спокойно ехать по тротуару. Естественно, если перемещаться пешком, то получится дольше, чем проделать путь на велосипеде. В чем же здесь дело? Речь, разумеется, идет о скорости, с которой перемещаетесь. Позже мы увидим формулы, которые подскажут, Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Позже мы увидим формулы, которые подскажут, Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Итак, у нас появились еще два параметра:
v – скорость.
Все будет намного интереснее, если научитесь работать с формулами и находить неизвестное с помощью дробей. Напомним лишь только правило из математики: все, что находится рядом с неизвестным, идет в знаменатель (то есть вниз дроби). Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?
В чем измеряются?
Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
S – расстояние – метр, километр [м], [км];
v – скорость – метров в секунду, километров в час [м/с], [км/ч] (в случае может применяться километр в секунду;
t – время – секунда, минута, час [с], [мин],[ч].
Обратите внимание, как обозначается скорость. Правильно, дробью. А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.
Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.
Понятие скорости широко используется в науке: математике, физике, механике. Школьники начинают знакомиться с ним уже в третьем классе. Более подробно это происходит в 7-8 классах. В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
В общепринятом смысле скорость – это величина, которая характеризует, насколько быстро предмет перемещается в пространстве за единицу времени. В зависимости от области применения, скорость обозначается разными символами.
Как обозначается скорость в математике
В учебниках по математике принято использовать строчную прописную латинскую букву v. Скорость взаимосвязана с пройденным путем и временем, за который оно пройдено.
При равномерном движении величина v=S/t, где:
- S – пройденный телом путь,
- t – время движения.
Как обозначается скорость в физике
В разделе физики, именуемом механикой, также изучается скорость. Обозначение скорости зависит от того, векторная это величина или обычная. В первом случае над буквой v ставится стрелочка, направленная вправо →. Если же нет необходимости учитывать направление, то применяют обычный символ v.
Единицы измерения скорости
В международной системе единиц измерения принято оперировать метрами в секунду (м/с).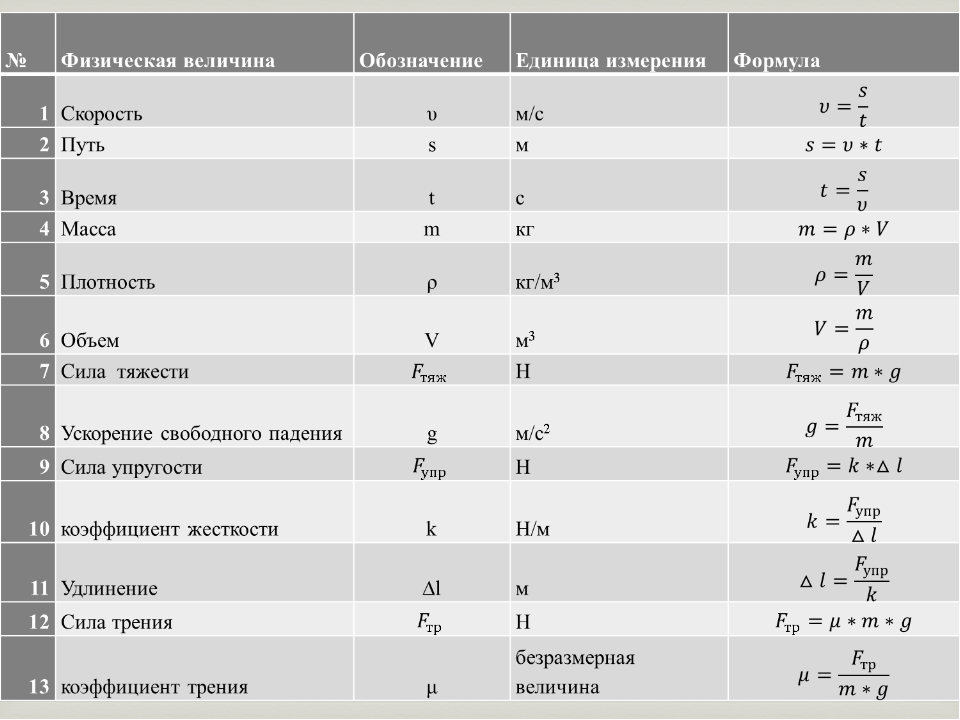
Как обозначается скорость света и звука
Учеными доказано, что скорость света является абсолютной величиной, с которой могут перемещаться информация и энергия. Этот показатель постоянен и равен 299 792 458 ± 1,2 м/с. Его символом выбрали латинскую букву с.
Скорость звука зависит от плотности и упругости среды, в которой распространяются звуковые волны. Ее измеряют в Махах. Например, сверхзвуковая скорость находится в границах от 1,2 до 5 Махов. А все что выше, называют гиперзвуковой скоростью.
Очевидно, что символ, которым обозначается скорость, зависит от математического или физического смысла, которым наполняется данное понятие.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Содержание урокаРасстояние
Расстояние мы уже изучали в уроке . Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра). Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м: 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м: 25с = 4 (м/с)
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м: 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах? Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1000: 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t , пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина.
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s: t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s: t = 900: 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s: v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s: v = 500: 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Цель : продолжить формировать представление о новой величине «скорость, время, расстояние» и единицах ее измерения.
Задачи :
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел – скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
Оборудование : карточки, карточки для работы в парах, интерактивная доска, название единиц времени на карточках, рабочая тетрадь, компьютер, проектор, экран
учебник.
Тип урока: урок закрепления и развития знаний, умений и навыков.
Методы : формы познавательной деятельности учащихся на уроке, индивидуальная работа, работа в парах.
Планируемые достижения учащихся на уроке:
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.

Ход урока
Организационный момент
Психологический настрой
Прозвенел заливистый школьный звонок.
Начинается новый урок.
Мы готовы считать и задачи решать.
Учитель : Я улыбнулась вам, и вы улыбнитесь друг другу, и подумайте, как хорошо, что мы сегодня все вместе. Мы спокойны, добры и приветливы. Глубоко вдохните и выдохните. Выдохните вчерашнюю обиду и злость, беспокойство. Забудьте о них. Я желаю вам хорошего настроения.
Сообщение темы и цели урока
Сегодня на уроке мы с вами вспомним о величинах, с которыми познакомились на предыдущих уроках и решали с ними задачи на движение и ставить свои ответы на листах самооценки.
(Ответы учащихся) Верно, это скорость, время, расстояние. Какими латинскими буквами они обозначаются. (s, v, t).
Слайд № 1
Девиз нашего урока: «Один за всех, все за одного»
Работа в парах
На партах карточки с примерами:
Увеличь произведение чисел 805 и 5 на 1025 (5050)
Из 10000 вычти частное число 40025 и 5 (1995)
Увеличь частное чисел 4025 и 5 в 100 раз (80500)
Прибавь к числу 1207 частное чисел 51300 и 9 (6907)
Из произведения чисел 480 и 7 вычти число 1406 (1954)
Произведение чисел 4070 и 6 уменьши на 4420 (20000)
Записать ответы в порядке возрастания
(ответ записан на интерактивной доске)
Минутка чистописания
Слайд № 2
2 4 6 8 10 (образец в тетради)
Прочитайте числа. Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Какие это числа? В каком порядке они расположены? Как они увеличиваются? Прочитайте число целиком. Сколько цифр использовано? В обратном направлении можем прочитать? Прочитайте. Запишите числа в порядке возрастания, через клеточку в порядке убывания. Прочитайте их, сравните. Запишите еще раз в порядке возрастания, найдите сумму этих четных чисел. Как вы это сделали?
Индивидуальная работа по карточкам
(4 ученика решают № 7)
Устная работа с остальными учениками:
В саду растут груши и ивы. На груше росло 69 груш, а на иве на 100 груш больше. Сколько груш росло на иве?
Мама варила одно яйцо 5 минут. Сколько времени будет варить 3 яйца?
Масса 1 мешка сахара 50 кг. Сколько кг в 4 таких мешках?
За 1 с человек делает 2 шага. Сколько шагов он сделает за 5 с.? За 10 с?
Слайд № 3
Физминутка
Слайд № 4
Качу, лечу во весь опор. (Выполняют ходьбу на месте.)
Я сам – шофер (Имитируют управление автомобильным рулем.)
И сам – мотор. (Круговые движения плечами вперед-назад.)
(Круговые движения плечами вперед-назад.)
Нажимаю на педаль, (Имитируют нажимание на педаль.)
И машина мчится вдаль! (Бег на месте.)
Первичное закрепление
Слайд № 5
Орел летел со скоростью 20 км/ч. За сколько часов он пролетит 80 км?
Cкорость полета космического спутника 8 км/сек. Сколько км он пролетит за 10 сек?
Слайд № 6
Решение задачи № 2
Автобус
S – 90 км 90: 45= 2 часа
T – ?
V – 45 км/ч
Легковая машина
S – 270 км 270: 90 = 3 часа
T – ?
V – 90 км/ч
Самостоятельная работа по учебнику
Итог урока
Давайте подведем итог урока
Чем занимались на уроке?
Что запомнили?
Рефлексия
Окрасьте сегодняшний урок (Дети рисуют сердечко своего настроения от урока) Учитель объясняет значении выбранного цвета.
- Красный – радость
- Жёлтый – приятное
- Зелёный – спокойное
- Синий – грустное
- Фиолетовый – тревожный
- Оранжевый – удовлетворение
- Чёрный – неудовлетворение
И на память об уроке солнышко дарит вам частичку своего тепла и хорошего настроения.
Наш закончен урок –
Спасибо за внимание,
Будем рады новой встрече,
Всем Вам до свидания!
Цели урока:
- ввести понятие скорости как новой единицы измерения; установить зависимости между величинами – скорость, время, расстояние; учить решать задачи на нахождение скорости по известным расстоянию и времени движения используя формулу движения;
- повторить табличные и внетабличные случаи умножения и деления, формировать вычислительные навыки, закрепить знание единиц времени и длины;
- способствовать развитию логического мышления, внимания, речи, самостоятельности;
- прививать интерес к физкультуре и спорту.
Планируемые достижения учащихся на уроке:
- знать понятие скорости как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание
единиц длины и времени.

Оборудование: Петерсон Л.Г. Математика, 3кл., III часть; рабочая тетрадь по математике, сигнальные карты, таблицы с дифференцированными заданиями для самостоятельной работы, название единиц длины и единиц времени на карточках, индивидуальные карточки для учащихся, нарисованные герои “Улицы Сезам” (Зелибоба, Кубик, Бусинка).
ХОД УРОКА
- Самоопределение к деятельности.
Урок я хочу начать словами французского философа Ж.Ж. Руссо (1712-1778гг.): “Вы – талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” Я желаю вам уже сегодня на уроке убедиться в этих словах, ведь вас ждёт открытие новых знаний при решении задач.
- Актуализация знаний.
- Узнав о том, что вы любите смотреть детские телепрограммы, я пригласила
героев одной телепередачи к нам на урок.
 А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать?
А они появятся здесь, как только вы
назовёте эту передачу. Но слова зашифрованы. Что же делать? - Правильно, надо решить примеры и расшифровать слова. Для этого вам необходимо вспомнить табличные и внетабличные случаи умножения и деления.
- Приготовьте сигнальные карты, контролируем правильность решения примеров.
(Два ученика работают индивидуально на карточках.)
Индивидуальные задания на карточках
- Почему некоторые ребята допускали ошибки? Как этого избежать?
- Что мы им посоветуем?
- Прочитайте слова, расставляя ответы в порядке убывания.
I вариант – первое слово (1 столбик)
II вариант – второе слово (2 столбик)
- Кто готов? (Улица, Сезам)
- Молодцы, ваши знания помогли вам расшифровать названия передачи. У нас в гостях “Улица Сезам”.
- Назовите героев этой передачи. (Зелибоба, Бусинка и Кубик)
- Наши друзья ведут здоровый образ жизни, учатся правильно питаться, занимаются
спортом.
 Увлекаясь ходьбой на лыжах, Зелибоба и Кубик решили всерьёз заняться
лыжным спортом и готовиться к Зимним Олимпийским играм, которые пройдут в г.
Сочи в 2014 году.
Увлекаясь ходьбой на лыжах, Зелибоба и Кубик решили всерьёз заняться
лыжным спортом и готовиться к Зимним Олимпийским играм, которые пройдут в г.
Сочи в 2014 году.
Бусинка объявила старт. Соперники преодолели путь 24 метра. Зелибоба пришёл к финишу через 3 минуты, а Кубик через 4 минуты.
Проблемный вопрос: Почему так произошло? (Один быстрее двигался, а другой медленнее)
- Да, они двигались с разной скоростью.
- Где вы встречались с понятием “скорость”? (В машине спидометр измеряет скорость)
- Как измерить скорость движущихся тел, у которых нет спидометра?
- Назовите тему урока.
- Что будем учиться измерять на уроке?
- Постановка темы урока
- Чтобы точнее сформулировать тему и цели урока, найдём опорные слова. Они необходимы для определения скорости. Для этого, работая в парах, расположите данные вас единицы измерения в порядке возрастания.
- Какие единицы измерения у I и III ряда? (Длины)
- У II ряда? (Времени)
Кто готов назвать их в порядке возрастания? (Ученики называют и выкладывают на наборное полотно. )
)
мм, см, дм, м, км
с, мин, ч, сут, мес
Проверьте правильность выполнения, переверните каждую карточку и прочитайте слово. (I и III ряды: расстояние; II ряд: время)
Расстояние – это промежуток между двумя пунктами, точками, между
чем-нибудь. В чём измеряется расстояние? (В единицах длины).
Время – это продолжительность, длительность чего-нибудь. В чём измеряется время? (В единицах времени).
Проблемный вопрос:
- А что называется скоростью?
- В чём измеряется скорость движения?
- Уточните тему нашего урока. (Скорость. Время. Расстояние.)
- Чему будем учиться на уроке? (Ответы детей).
Сегодня нам предстоит узнать как скорость движения связана со временем движения и расстоянием, научиться решать задачи на нахождение скорости движения.
- Открытие новых знаний.
- Что называют скоростью? Где найти ответ на наш вопрос? (В учебнике)
- Откройте учебник с.
 1, найдите выделенное слово “скоростью”. Прочитаем
определение скорости. (Скоростью называют расстояние, пройденное в единицу
времени.)
1, найдите выделенное слово “скоростью”. Прочитаем
определение скорости. (Скоростью называют расстояние, пройденное в единицу
времени.) - Так что же называют скоростью?
- Какими величинами будем пользоваться для определения скорости? (Расстоянием и временем)
- И в качестве единиц измерения скорости мы будем пользоваться и единицами длины и единицами времени.
- Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.
- Прочитайте единицы скорости км/с м/мин км/ч м/с
- Из каких единиц измерения образуются названия единиц скорости? (Из единиц длины и единиц времени).
Физминутка.
Руки ставим все вразлёт,
Появился самолёт.
Мах крылом туда-сюда,
Делай раз и делай два.
Отпустите руки вниз
И на место все садитесь.
Работа с учебником
- Интересно, а какая скорость у самолёта?
- Объясните смысл предложений, записанных в задании № 1, стр.2. (Самолёт летит со скоростью 800 км/ч, т.е. за 1 ч самолёт преодолевает расстояние 800 км)
Молодцы. Откройте тетради, запишите число, классная работа. Следите за осанкой. Мы будем учиться решать задачи на нахождение скорости движения по данному расстоянию и времени. Зелибоба и Кубик очень хотят узнать свою скорость движения. Поможем им. Решим задачу.
Задача 1. Зелибоба прошёл на лыжах расстояние, равное 24 метрам за 3 минуты. С какой скоростью он шёл?
Что нам известно?
- Расстояние – 24 м
- Время – 3 мин.
Что нужно узнать? Скорость Зелибобы, т.е. расстояние, которое проходил Зелибоба за 1 мин.
Сделаем чертёж к задаче
Чертим отрезок. Чему равно расстояние? Обозначим время на отрезке. Весь путь, который прошёл Зелибоба, мы может
разделить на 3 равные части, потому что в каждую минуту Зелибоба проходил
одинаковое расстояние.
- Кто из вас догадался, с какой скоростью двигался Зелибоба?
- Как узнать скорость его движения?
Запись в тетради: 24 ׃ 3 = 8 (м/мин) скорость Зелибобы.
Т.е. за 1 мин Зелибоба проходил 8 м.
Напишем ответ задачи. Ответ: 8 м/мин.
- Первичное закрепление.
Закрепим умение решать задачи на движение, а именно на нахождение скорости.
Задача 2. Кубик прошёл на лыжах расстояние, равное 24 м за 4 минуты. С какой скоростью двигался Кубик?
- Что известно в задаче? (Расстояние – 24 м, время – 4 минуты)
- Что надо узнать? (Скорость Кубика)
На доске чертёж.
Ребята, а всегда ли удобно делать чертёж к задаче? В Математике принято обозначать величины латинскими буквами:
- расстояние – S
- время – t
- скорость – v
Итак, запишем в тетрадь:
- Как найти скорость движения? (Расстояние разделить на время)
- Скажите мне то же самое, только при помощи буквенных обозначений: v = S ׃ t
Вы назвали формулу, по которой находят скорость движения. Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
Этой формулой вы
будете пользоваться и в старших классах. Запишем решение задачи. (Ученик у доски).
v = S ׃ t
24 ׃ 4 = 6 (м/мин) скорость Кубика.
Ответ: 6 м/мин.
Сравните скорость Зелибобы и Кубика. Почему Зелибоба пришёл к финишу раньше?
Вывод: Скорость – это величина, которую можно измерить и сравнить.
Зелибоба и Кубик довольны. Вместе с вами они научились измерять скорость движения.
- Самостоятельная работа.
Давайте потренируемся в решении задач на нахождение скорости, выполняя работу самостоятельно.
Бусинка вам предлагает найти скорость движения своих друзей в других видах спорта. Заполните таблицы, записывая только ответы. (Задание дифференцированные по сложности и обьему.)
Как будете находить скорость движения? Будьте внимательны при обозначении скорости.
1 группа
2 группа
Проверьте свои ответы с ответами Бусинки. Приложение 1
- Кто выполнил работу без ошибок? – Молодцы, поставьте себе 5.

- Кто допустил 1 ошибку? – Поставьте себе 4. – Бусинка вами довольна.
- Кто допусти 2 ошибки? Кто не справился? – Не огорчайтесь, потренируйтесь дома, приложите старание, тогда и у вас всё получится.
А наши друзья вам советуют заниматься спортом. Скажите, зачем нужно заниматься спортом? (Ответ детей). Правильно, спорт – это здоровье, сила, выносливость.
- Повторение с включением новых знаний.
Зелибоба приготовил вам игру. Нужны 3 ученика – это движущиеся модели: самолёт, машина, ракета. Ещё 3 ученика – это скорости движения: 800 км/ч; 90 км/ч; 6 км/с. Найдите пару, соотнесите, у кого из вас какая скорость движения?
(Самолёт – 800 км/ч; ракета – 6 км/с; машина – 90км/ч).
- Кто из них движется быстрее всех?
- У кого самая маленькая скорость движения?
- На каком виде транспорта наши друзья меньше затратят времени на дорогу до Москвы?
А о том, как находить время движения вы узнаете на следующем уроке.
- Итог урока. Рефлексия деятельности.
Наш урок подходит к концу. Чему учились на уроке?
- Назовите формулу, которой будем пользоваться для определения скорости движения?
- Где сможете применить новые знания?
Время передачи “Улицы Сезам” истекает. Давайте “зажжём” фонарики на “Улице Сезам”.
- Кто доволен своей работой на уроке, понял новую тему – “зажгите” красный фонарик.
- Кто не совсем доволен, допускал ошибки – жёлтый.
- Кто не доволен своей работой – “зажжёт” синий.
Ваши фонарики мне говорят о том, что сегодня вы достигли успеха на уроке.
Интересно, а как вашу работу оценят наши друзья? (На “Улице Сезам” “зажигается” красный фонарик.) Как видите, наши друзья из передачи “Улица Сезам” довольны вашей работой на уроке.
- Домашнее задание.
Домашнее задание будет таким: решить задачи, определить скорости движущихся
тел – № 2, стр. 2, или придумать свою задачу, в которой надо найти скорость по
известному расстоянию и времени, и решить её – № 8, стр. 3.
3.
Благодарю за урок.
| Символ | Значение и происхождение |
|---|---|
Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число | |
| Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора | |
| Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы | |
| Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина (нем. Breite) | |
электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), обаяние (англ. charm), коэффициенты Клебша-Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона-Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) | |
| Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоемкость (англ. heat capacity), волшебный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, Вторая радиационная постоянная | |
Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, де-плюс мезон (англ.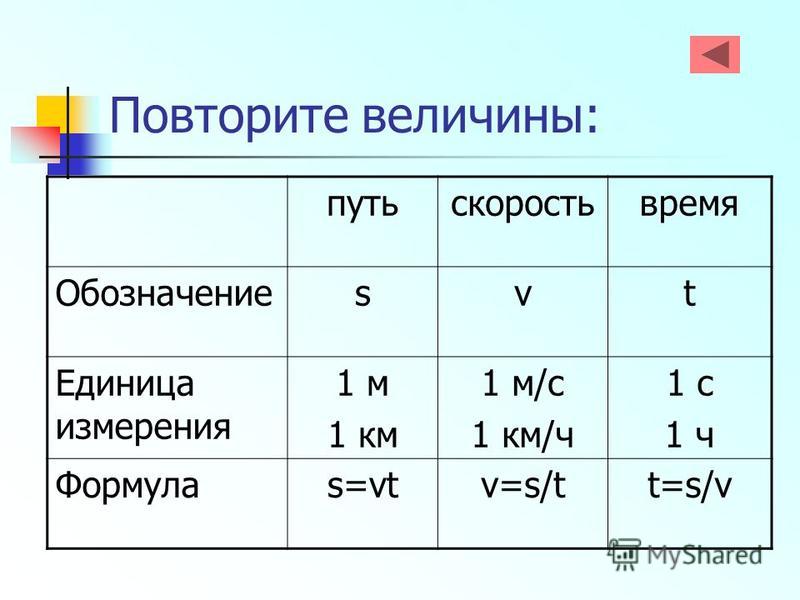 Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) Dmeson), де-ноль мезон (англ. Dmeson), диаметр (лат. diametros, др.-греч. διάμετρος) | |
| Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) | |
| Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга | |
| 2.71828…, электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия | |
Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор напряженности электромагнитного поля, магнитодвижущая сила, модуль сдвига | |
| Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения | |
| Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) | |
Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), константа Калибровочные взаимодействия | |
| Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) | |
| Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) | |
cила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности intēnsiō), cила излучения, сила света, момент инерции, вектор намагниченности | |
| Мнимая единица (лат. imaginarius), единичный вектор | |
| Плотность тока, момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, внутреннее квантовое число, вращательное квантовое число, сила света, J/ψ-мезон | |
| Мнимая единица, плотность тока, единичный вектор, внутреннее квантовое число, 4-вектор плотности тока | |
| Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона | |
| Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор | |
Момент импульса, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) | |
| Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина | |
| Момент силы, вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса | |
| Масса (лат. massa), магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка | |
| Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность | |
Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта | |
| Начало координат (лат. origo) | |
| Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, 4-импульс | |
| Импульс (лат. petere), протон (англ. proton), дипольный момент, волновой параметр | |
| Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), обобщенная сила, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции | |
Электрический заряд, обобщенная координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность quantity of heat), эффективный заряд, добротность | |
| Электрическое сопротивление (англ. resistance), газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние | |
| Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная теплота плавления, удельная рефракция (лат. rēfractiō), расстояние | |
| Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга | |
Перемещение (итал. ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути ь s’postamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути | |
| Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин | |
| Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время | |
| Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение | |
| Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость | |
Объём (фр. volume), напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) Verdet constant) | |
| Скорость (лат. vēlōcitās), фазовая скорость, удельный объём | |
| Механическая работа (англ. work), работа выхода, W бозон, энергия, энергия связи атомного ядра, мощность | |
| Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение | |
| Реактивное сопротивление, продольное увеличение | |
| Переменная, перемещение, декартова координата, молярная концентрация, постоянная ангармоничности, расстояние | |
| Гиперзаряд, силовая функция, линейное увеличение, сферические функции | |
| декартова координата | |
| Импеданс, Z бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление, угловое увеличение, волновое сопротивление вакуума | |
| декартова координата | |
| Символ | Значение |
| Коэффициент теплового расширения, альфа-частицы, угол, постоянная тонкой структуры, угловое ускорение, матрицы Дирака, коэффициент расширения, поляризованность, коэффициент теплоотдачи, коэффициент диссоциации, удельная термоэлектродвижущая сила, угол Маха, коэффициент поглощения, натуральный показатель поглощения света, степень черноты тела, постоянная затухания | |
| Угол, бета-частицы, скорость частицы разделена на скорость света, коэффициент квазиупругой силы, матрицы Дирака, изотермическая сжимаемость, адиабатическая сжимаемость, коэффициент затухания, угловая ширина полос интерференции, угловое ускорение | |
| Гамма-функция, символы Кристофеля, фазовое пространство, величина адсорбции, циркуляция скорости, ширина энергетического уровня | |
| Угол, фактор Лоренца, фотон, гамма-лучи, удельный вес, матрицы Паули, гиромагнитное отношение, термодинамический коэффициент давления, коэффициент поверхностной ионизации, матрицы Дирака, показатель адиабаты | |
Изменение величины (напр. ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект ), оператор Лапласа, дисперсия, флуктуация, степень линейной поляризации, квантовый дефект | |
| Небольшое перемещение, дельта-функция Дирака, дельта Кронекера | |
| Электрическая постоянная, угловое ускорение, единичный антисимметричной тензор, энергия | |
| Дзета-функция Римана | |
| КПД, динамический коэффициент вязкости, метрический тензор Минковского, коэффициент внутреннего трения, вязкость, фаза рассеяния, эта-мезон | |
| Статистическая температура, точка Кюри, термодинамическая температура, момент инерции, функция Хевисайда | |
| Угол к оси X в плоскости XY в сферической и цилиндрической системах координат, потенциальная температура, температура Дебая, угол нутации, нормальная координата, мера смачивания, угол Каббибо, угол Вайнберга | |
| Коэффициент экстинкции, показатель адиабаты, магнитная восприимчивость среды, парамагнитная восприимчивость | |
| Космологическая постоянная, Барион, оператор Лежандра, лямбда-гиперон, лямбда-плюс-гиперон | |
| Длина волны, удельная теплота плавления, линейная плотность, средняя длина свободного пробега, комптоновского длина волны, собственное значение оператора, матрицы Гелл-Мана | |
| Коэффициент трения, динамическая вязкость, магнитная проницаемость, магнитная постоянная, химический потенциал, магнетон Бора, мюон , возведённая масса, молярная масса, коэффициент Пуассона, ядерный магнетон | |
| Частота, нейтрино, кинематический коэффициент вязкости, стехиометрический коэффициент, количество вещества, ларморова частота, колебательное квантовое число | |
| Большой канонический ансамбль, кси-нуль-гиперон, кси-минус-гиперон | |
| Длина когерентности, коэффициент Дарси | |
| Произведение, коэффициент Пельтье, вектор Пойнтинга | |
3. 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон 14159…, пи-связь, пи-плюс мезон, пи-ноль мезон | |
| Удельное сопротивление, плотность, плотность заряда, радиус в полярной системе координат, сферической и цилиндрической системах координат, матрица плотности, плотность вероятности | |
| Оператор суммирование, сигма-плюс-гиперон, сигма-нуль-гиперон, сигма-минус-гиперон | |
| Электропроводность, механическое напряжение (измеряемое в Па), постоянная Стефана-Больцмана, поверхностная плотность, поперечное сечение реакции, сигма-связь, секторная скорость, коэффициент поверхностного натяжения, удельная фотопроводимость, дифференциальное сечение рассеяния, постоянная экранирования, толщина | |
| Время жизни, тау-лептон, интервал времени, время жизни, период, линейная плотность зарядов, коэффициент Томсона, время когерентности, матрица Паули, тангенциальный вектор | |
| Y-бозон | |
| Магнитный поток, поток электрического смещения, работа выхода, язь, диссипативная функция Рэлея, свободная энергия Гиббса, поток энергии волны, оптическая сила линзы, поток излучения, световой поток, квант магнитного потока | |
| Угол, электростатический потенциал, фаза, волновая функция, угол, гравитационный потенциал, функция, Золотое сечение, потенциал поля массовых сил | |
| X-бозон | |
| Частота Раби, температуропроводность, диэлектрическая восприимчивость, спиновая волновая функция | |
| Волновая функция, апертура интерференции | |
| Волновая функция, функция, функция тока | |
| Ом, телесный угол, количество возможных состояний статистической системы, омега-минус-гиперон, угловая скорость прецессии, молекулярная рефракция, циклическая частота | |
| Угловая частота, мезон, вероятность состояния, ларморова частота прецессии, Боровская частота, телесный угол, скорость течения |
что такое n в физике
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь.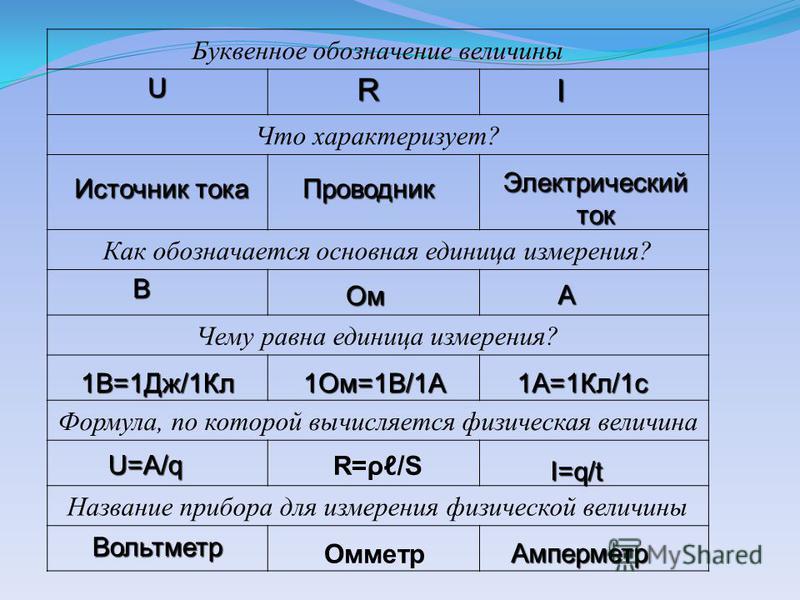 Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной).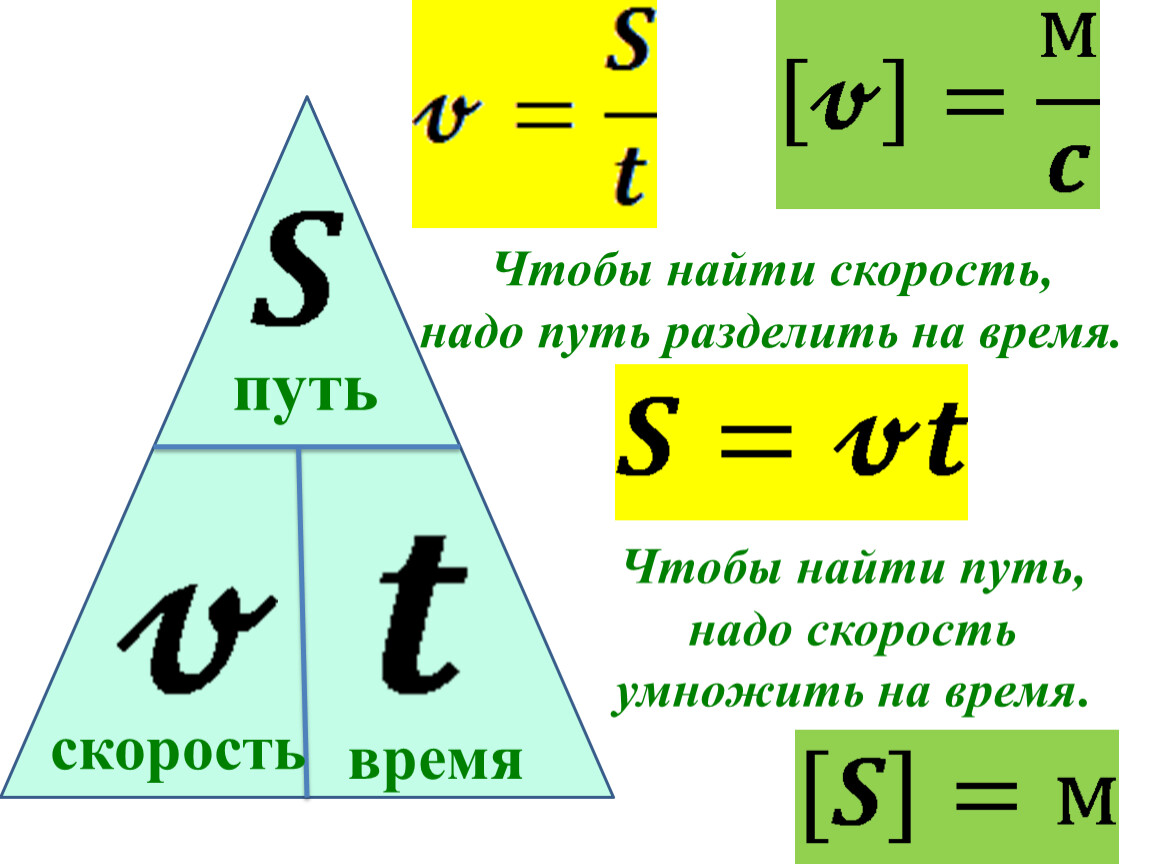 В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:
(читается ¾икс с точкой¿).
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
производная функции x(t) обозначается | ||
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.
Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:
вторая производная функции x(t) обозначаетсяx (t)
(читается ¾икс с двумя точками¿), а вот другое:
вторая производная функции x(t) обозначаетсяdt 2
(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).
Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):
x(t) = 1 + 12t 3t2 )
x(t) = dt d (1 + 12t 3t2 ) = 12 6t:
(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что производная координаты оказалась равна скорости (1.14 ). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.
1.1.7 Предел векторной величины
Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.
Рассмотрим последовательность векторов ~u1 ; ~u2 ; ~u3 ; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис.1.5 ):
Рис. 1.5. lim ~un = ~v | |||||||||
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем: | |||||||||
Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:
lim An = B:
Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un :
~v = lim ~un :
2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.
Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1 ; A2 ; A3 ; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.
Предположим теперь, что концы синих векторов на рис. 1.5 пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un , а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если
при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор
~v = OB является пределом векторной величины ~u(t):
t!t0
1.1.8 Дифференцирование векторов
Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.
Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:
~u = ~u(t + t) ~u(t):
Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).
~u(t) ~u
Рис. 1.6. Изменение вектора
Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:
При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_ не слишком хорошо смотрится) и ограничиваемся обозначением (1.18 ). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.
Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от
предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.
Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.
1. Постоянный скалярный множитель выносится за знак производной: если c = const, то
d(c~u) = c d~u: dt dt
Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона
будет переписан в виде: | ||||
2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt d (x(t)~c) = x(t)~c:
3. Производная суммы векторов равна сумме их производных:
dt d (~u + ~v) =d~u dt +d~v dt :
Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7 ).
Рис. 1.7. Разложение вектора по базису
Как известно, любой вектор ~u единственным образом раскладывается по базису единичных
векторов ~ ,~ ,~ : i j k
~u = ux i + uy j + uz k:
Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.
Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:
~u(t) = ux (t) i | Uy (t) j | Uz (t)k: |
Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:
ux (t)~ i + | uy (t)~ j | uz (t)~ k: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t)i + uy (t)j + uz (t)k: | ||||||||||||||
Таким образом, если вектор ~u имеет координаты (ux ; uy ; uz ), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux ; uy ; uz ).
Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:
~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:
Напишем изменение вектора ~u:
~u = ~u(t + t) ~u(t) =
Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Делим обе части полученного равенства на t: | ||||||||||
T i + | t j + | |||||||||
В пределе при t ! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux , uy , uz , и мы снова получаем соотношение (1.20 ):
Ux i + uy j + uz k.
Почему в физике расстояние обозначается буквой s, а скорость – v?
Автор Вадим Хромов На чтение 3 мин Опубликовано Обновлено
Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?
Как обозначают физические величины и понятия?
В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.
Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.
Впервые термин “физика” фигурирует в сочинениях Аристотеля (IV век до н. э.)Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.
Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.
Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.
Почему в физике расстояние обозначается буквой s?
Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:
- степень удаленности объектов друг от друга;
- длина пути, которую прошел объект.
Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:
- От английского слова «space», которое означает расстояние, пространство, площадь.
- От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.
Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.
Почему в физике скорость обозначается буквой v?
Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.
Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.
Скорость – векторная величинаСлово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».
Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Интервал в физике
Содержание:
Интервал в физике
- Интервал. В будущем часто используют концепцию Существования. Событие определяется тем, где оно произошло. Когда это случилось Следовательно, событие, которое происходит на некоторых материальных частицах, определяется Три координаты этой частицы и когда происходит событие.
Для ясности часто удобно использовать фиктивное четырехмерное пространство на оси с тремя пространственными координатами и временем. В этом пространстве события представлены точками. Эти точки Это называется мировой точкой. Каждая частица соответствует этой 4D конкретной линии (мировой линии). Пространство.
Однородные и линейно движущиеся материальные частицы соответствуют прямым мировым линиям Людмила Фирмаль
Точка этой линии определяет координаты детали Цы во все времена. i) 2] 1/2 (2.3) .
Следовательно, из неизменности скорости света, Когда интервал между двумя событиями равен единице и нулю Для систем отсчета это ноль в других системах. Если два события близки к бесконечности, Расстояние дс между ними cIs2 = c2dt2-dx2-dy2-dz2 (2.4) В зависимости от вида формулы (2.3) или (2.4)
Расстояние с формальной математической точки зрения, расстояние между двумя воображаемыми четырехмерными точками Пространственный (на оси, которая откладывает x, y, z и product ct) Однако существует большое различие в правиле, которое составляет это значение, по сравнению с нормальным правилом Геометрия:
Когда квадрат промежутка сформирован, квадраты различий координат по разным осям не одинаковы, а суммируются с разными знаками1). Как упомянуто выше, если ds = 0 в инерциальной системе отсчета, dsf = 0 в другой системе.
С другой стороны, ds и dsf бесконечно малы одного порядка. от Из этих двух ситуаций ds2 и dsf2 должны быть пропорциональны друг другу. = «Нет». (2-5) Но V \ 2 зависит не только от абсолютного значения вектора V i И от V 2, и от угла между ними.
С другой стороны, последний, как правило, Не вводите левую часть отношения (2.5). Следовательно, ясно, что это соотношение действительно только в том случае, если функция a (y) уменьшается до постоянного значения, равного 1, из того же отношения: Вот так ds1 = ds’2, (2.6) Уравнение с бесконечно малыми интервалами также означает уравнение с конечными интервалами: s = s ‘.
Поэтому самый важный результат достигнут. Интервал между событиями одинаков для всех инерциальных систем отсчета. Другими словами, он инвариантен относительно преобразования из одной инерциальной системы отсчета в любую инерциальную систему отсчета. Еще один.
Эта инвариантность является математическим выражением неизменности скорости света. Опять же, Ж1, 2/1, Z \, t \ и Ж2, У2, Ј2? Координаты -22-2 Вопрос в том, существует ли система отсчета K, где оба эти события происходят в одном и том же месте в пространстве.
Вводя обозначение t2-t i = * 1 2, (x2-2? i) 2 + (g / 2-w) 2 + (2 2-Zi) 2 = l \ 2. Тогда квадрат интервала между событиями в системе K: А в системе К ‘: и * В результате, если s22> 0, то есть интервал между обоими событиями Реальная вещь. Фактический интервал называется временоподобным.
Следовательно, если интервал между двумя событиями подобен времени, существует система отсчета. Оба события произошли в одном и том же месте. Время, которое проходит между этими событиями в этой системе * 12 = \ 1 с H 12 ~ l 12 = S ~ f- (2-7) Когда два события происходят в одном событии В теле расстояние между ними всегда похоже на время.
На самом деле путь, по которому тело движется между обоими событиями, не может быть больше, чем cti2. Скорость тела Возможно больше. Поэтому всегда 1 \ 2 0 во всех точках в этом регионе. Это значит Интервал между событием и событием O в этой области Время как. В этой области t> 0, что означает все эти события В регионе происходит «после» события О.
Однако два события, разделенные временным интервалом, не могут происходить одновременно ни в одной системе отсчета. Поэтому это невозможно Если вы не выбрали опорную рамку, и одно из событий в области aOc происходит «до» события O, то есть t <0. Так что все события в области АО O в будущем и во всех системах отсчета.
Так что эту область можно назвать «абсолютно будущим» в связи с событием О. Точно так же, все события в регионе bOd «Абсолютно в прошлом» относительно O, то есть события в этой области во всех системах отсчета происходят до события Уровень O Наконец, рассмотрим регионы dOa и coB. интервал Что-то вроде события и события O-space в этой области.
В системе отсчета эти события Разные места в космосе. Так что эти области Называется «абсолютно удаленным» по отношению к O Однако «одновременное», «раннее» и «после» этих событий Относительный. Каждое событие в этой области имеет что-то подобное Справочная система.
Событие О, система, О, наконец, где происходит одна система отсчета Местоположение, которое происходит одновременно с O Учитывая все три пробела, Координаты вместо одной на диаграмме, затем координаты вместо двух пересекающихся линий. 2 « коническая » x2 + y2 + z2-c2t2 = 0
Четырехмерная система координат, оси которой совпадают с осями t, x, y, z, Ј (этот конус называется световым конусом). область «Абсолютное будущее» и «Абсолютное прошлое» представлены двумя внутренними полостями в этом конусе. Эти два события могут быть причинно связаны друг с другом.
Только если интервал между ними является временным, это непосредственно следует из того факта, что взаимодействие не может распространяться дальше. Скорость света. Как мы уже видели, понятия «рано» и «поздно» имеют абсолютное значение для таких событий. Смысл понятия причины и следствия.
Смотрите также:
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.
что такое n в физике
Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?
Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.
Что обозначает прописная буква N в физике?
Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.
Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).
Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).
Что такое N в физике, помимо уже указанных величин? Это может быть:
постоянная Авогадро;
увеличение оптического прибора;
концентрация вещества;
число Дебая;
полная мощность излучения.
Что может обозначать строчная буква n в физике?
Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:
показатель преломления, причем он может быть абсолютным или относительным;
нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;
частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).
Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.
Какая физическая величина может быть обозначена n и N?
Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.
Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.
Формулы, в которых фигурирует прописная N
Первая из них определяет мощность, которая равна отношению работы ко времени:
В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро :
Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.
Чтобы определить электрический заряд, потребуется формула:
Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:
Появляется буква «эн» в формуле для периода обращения:
Формулы, в которых встречается строчная n
В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.
Так, для абсолютного показателя преломления формула записывается следующим образом:
Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.
Формула для относительного показателя преломления несколько сложнее:
n 21 = v 1: v 2 = n 2: n 1 ,
где n 1 и n 2 — абсолютные показатели преломления первой и второй среды, v 1 и v 2 — скорости световой волны в указанных веществах.
Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n 21 = sin α: sin γ.
Чему равно n в физике, если это показатель преломления?
Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.
Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.
Задача на мощность
№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.
Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.
Выбор формул. Как уже было сказано выше, N = А: t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.
Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000: 600 = 20 000 Вт.
Ответ. Мощность трактора равна 20 000 Вт.
Задачи на показатель преломления
№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.
В СИ переводить данные не требуется.
При выборе формул остановиться нужно на этой: n = с: v.
Решение. Из указанной формулы видно, что v = с: n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.
Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.
№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.
Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.
Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n 21 = sin α: sin γ. А также: n = с: v.
Решение. В первой формуле n 21 — это отношение двух показателей преломления рассматриваемых веществ, то есть n 2 и n 1 . Если записать вторую указанную формулу для предложенных сред, то получатся такие: n 1 = с: v 1 и n 2 =с: v 2 . Если составить отношение двух последних выражений, получится, что n 21 = v 1: v 2 . Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v 2: v 1).
Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.
Ответ. Значение угла преломления — 26º.
Задачи на период обращения
№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.
Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.
Подбор формул . Период вращения и число оборотов связаны формулой Т = t: N.
Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600: 5 = 720.
Ответ. Число оборотов лопастей мельницы равно 720.
№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?
Все данные приведены с СИ, поэтому переводить ничего не нужно.
Необходимая формула : частота ν = N: t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.
Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.
Ответ. Винт самолета совершает 3000 оборотов за 120 с.
Подведем итоги
Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:
(читается ¾икс с точкой¿).
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
производная функции x(t) обозначается | ||
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (1.16 ). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (1.16 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17 ) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.
Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:
вторая производная функции x(t) обозначаетсяx (t)
(читается ¾икс с двумя точками¿), а вот другое:
вторая производная функции x(t) обозначаетсяdt 2
(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).
Давайте вернёмся к исходному примеру (1.13 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (1.15 ) и (1.16 ):
x(t) = 1 + 12t 3t2 )
x(t) = dt d (1 + 12t 3t2 ) = 12 6t:
(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что производная координаты оказалась равна скорости (1.14 ). Это не случайное совпадение. Связь производной координаты со скоростью тела будет выяснена в следующем разделе ¾Механическое движение¿.
1.1.7 Предел векторной величины
Физические величины бывают не только скалярными, но и векторными. Соответственно, часто нас интересует скорость изменения векторной величины то есть, производная вектора. Однако прежде чем говорить о производной, нужно разобраться с понятием предела векторной величины.
Рассмотрим последовательность векторов ~u1 ; ~u2 ; ~u3 ; : : : Сделав, если необходимо, параллельный перенос, сведём их начала в одну точку O (рис.1.5 ):
Рис. 1.5. lim ~un = ~v | |||||||||
Концы векторов обозначим A1 ; A2 ; A3 ; : : : Таким образом, имеем: | |||||||||
Предположим, что последовательность точек A1 ; A2 ; A3 ; : : : ¾втекает¿2 в точку B:
lim An = B:
Обозначим ~v = OB. Мы скажем тогда, что последовательность синих векторов ~un стремится к красному вектору ~v, или что вектор ~v является пределом последовательности векторов ~un :
~v = lim ~un :
2 Вполне достаточно интуитивного понимания этого ¾втекания¿, но вас, быть может, интересует более строгое объяснение? Тогда вот оно.
Пусть дело происходит на плоскости. ¾Втекание¿ последовательности A1 ; A2 ; A3 ; : : : в точку B означает следующее: сколь бы малый круг с центром в точке B мы ни взяли, все точки последовательности, начиная с некоторой, попадут внутрь этого круга. Иными словами, вне любого круга с центром B имеется лишь конечное число точек нашей последовательности.
А если дело происходит в пространстве? Определение ¾втекания¿ модифицируется незначительно: нужно лишь заменить слово ¾круг¿ на слово ¾шар¿.
Предположим теперь, что концы синих векторов на рис. 1.5 пробегают не дискретный набор значений, а непрерывную кривую (например, указанную пунктирной линией). Таким образом, мы имеем дело не с последовательностью векторов ~un , а с вектором ~u(t), который меняется со временем. Это как раз то, что нам и нужно в физике!
Дальнейшее объяснение почти такое же. Пусть t стремится к некоторому значению t0 . Если
при этом концы векторов ~u(t) ¾втекают¿ в некоторую точку B, то мы говорим, что вектор
~v = OB является пределом векторной величины ~u(t):
t!t0
1.1.8 Дифференцирование векторов
Выяснив, что такое предел векторной величины, мы готовы сделать следующий шаг ввести понятие производной вектора.
Предположим, что имеется некоторый вектор ~u(t), зависящий от времени. Это означает, что длина данного вектора и его направление могут меняться с течением времени.
По аналогии с обычной (скалярной) функцией вводится понятие изменения (или приращения) вектора. Изменение вектора ~u за время t есть векторная величина:
~u = ~u(t + t) ~u(t):
Обратите внимание, что в правой части данного соотношения стоит разность векторов. Изменение вектора ~u показано на рис. 1.6 (напомним, что при вычитании векторов мы сводим их начала в одну точку, соединяем концы и ¾укалываем¿ стрелкой тот вектор, из которого производится вычитание).
~u(t) ~u
Рис. 1.6. Изменение вектора
Если промежуток времени t достаточно мал, то и вектор ~u за это время меняется мало (в физике, по крайней мере, так считается всегда). Соответственно, если при t ! 0 отношение~u= t стремится к некоторому пределу, то этот предел называется производной вектора ~u:
При обозначении производной вектора мы не будем использовать точку сверху (так как символ ~u_ не слишком хорошо смотрится) и ограничиваемся обозначением (1.18 ). Но для производной скаляра мы, разумеется, свободно используем оба обозначения.
Напомним, что d~u=dt это символ производной. Его можно понимать и как дробь, в числителе которой стоит дифференциал вектора ~u, соответствующий промежутку времени dt. Выше мы не стали обсуждать понятие дифференциала, так как в школе его не проходят; не будем обсуждать дифференциал и здесь.
Однако на физическом уровне строгости производную d~u=dt можно считать дробью, в знаменателе которой стоит очень малый интервал времени dt, а в числителе соответствующее малое изменение d~u вектора ~u. При достаточно малом dt величина данной дроби отличается от
предела в правой части (1.18 ) столь мало, что с учётом имеющейся точности измерений этим отличием можно пренебречь.
Этого (не вполне строгого) физического понимания производной нам окажется вполне достаточно.
Правила дифференцирования векторных выражений во многом аналогичны правилам дифференцирования скаляров. Нам понадобятся лишь самые простые правила.
1. Постоянный скалярный множитель выносится за знак производной: если c = const, то
d(c~u) = c d~u: dt dt
Мы используем это правило в разделе ¾Импульс¿, когда второй закон Ньютона
будет переписан в виде: | ||||
2. Постоянный векторный множитель выносится за знак производной: если ~c = const, то dt d (x(t)~c) = x(t)~c:
3. Производная суммы векторов равна сумме их производных:
dt d (~u + ~v) =d~u dt +d~v dt :
Последними двумя правилами мы будем пользоваться неоднократно. Посмотрим, как они работают в важнейшей ситуации дифференцирования вектора при наличии в пространстве прямоугольной системы координат OXY Z (рис. 1.7 ).
Рис. 1.7. Разложение вектора по базису
Как известно, любой вектор ~u единственным образом раскладывается по базису единичных
векторов ~ ,~ ,~ : i j k
~u = ux i + uy j + uz k:
Здесь ux , uy , uz проекции вектора ~u на координатные оси. Они же являются координатами вектора ~u в данном базисе.
Вектор ~u в нашем случае зависит от времени, а это значит, что его координаты ux , uy , uz являются функциями времени:
~u(t) = ux (t) i | Uy (t) j | Uz (t)k: |
Дифференцируем это равенство. Сначала пользуемся правилом дифференцирования суммы:
ux (t)~ i + | uy (t)~ j | uz (t)~ k: | ||||||||||||
Затем выносим постоянные векторы за знак производной: | ||||||||||||||
Ux (t)i + uy (t)j + uz (t)k: | ||||||||||||||
Таким образом, если вектор ~u имеет координаты (ux ; uy ; uz ), то координаты производной d~u=dt являются производными координат вектора ~u, а именно (ux ; uy ; uz ).
Ввиду особой важности формулы (1.20 ) дадим более непосредственный её вывод. В момент времени t + t согласно (1.19 ) имеем:
~u(t + t) = ux (t + t) i + uy (t + t) j + uz (t + t)k:
Напишем изменение вектора ~u:
~u = ~u(t + t) ~u(t) =
Ux (t + t) i + uy (t + t) j + uz (t + t)k ux (t) i + uy (t) j + uz (t)k =
= (ux (t + t) ux (t)) i + (uy (t + t) uy (t)) j + (uz (t + t) uz (t)) k = | ||||||||||
Ux i + uy j + uz k: | ||||||||||
Делим обе части полученного равенства на t: | ||||||||||
T i + | t j + | |||||||||
В пределе при t ! 0 дроби ux = t, uy = t, uz = t переходят соответственно в производные ux , uy , uz , и мы снова получаем соотношение (1.20 ):
Ux i + uy j + uz k.
Ни для кого не секрет, что существуют специальные обозначения для величин в любой науке. Буквенные обозначения в физике доказывают, что данная наука не является исключением в плане идентификации величин при помощи особых символов. Основных величин, а также их производных, достаточно много, каждая из которых имеет свой символ. Итак, буквенные обозначения в физике подробно рассматриваются в данной статье.
Физика и основные физические величины
Благодаря Аристотелю начало употребляться слово физика, так как именно он впервые употребил этот термин, который в ту пору считался синонимом термина философия. Это связано с общностью объекта изучения – законы Вселенной, конкретнее – то, как она функционирует. Как известно, в XVI-XVII веках произошла первая научная революция, именно благодаря ей физика была выделена в самостоятельную науку.
Михаил Васильевич Ломоносов ввел в русский язык слово физика посредством издания учебника в переводе с немецкого – первого в России учебника по физике.
Итак, физика представляет собой раздел естествознания, посвященный изучению общих законов природы, а также материи, ее движение и структуре. Основных физических величин не так много, как может показаться на первый взгляд – их всего 7:
- длина,
- масса,
- время,
- сила тока,
- температура,
- количество вещества,
- сила света.
Конечно, у них есть свои буквенные обозначения в физике. Например, для массы выбран символ m, а для температуры – Т. Также у всех величин есть своя единица измерения: у силы света – кандела (кд), а у количества вещества единицей измерения является моль.
Производные физические величины
Производных физических величин значительно больше, чем основных. Их насчитывается 26, причем часто некоторые из них приписывают к основным.
Итак, площадь является производной от длины, объем – также от длины, скорость – от времени, длины, а ускорение, в свою очередь, характеризует быстроту изменения скорости. Импульс выражается через массу и скорость, сила – произведение массы и ускорения, механическая работа зависит от силы и длины, энергия пропорциональна массе. Мощность, давление, плотность, поверхностная плотность, линейная плотность, количество теплоты, напряжение, электрическое сопротивление, магнитный поток, момент инерции, момент импульса, момент силы – все они зависят от массы. Частота, угловая скорость, угловое ускорение обратно пропорциональны времени, а электрический заряд имеет прямую зависимость от времени. Угол и телесный угол являются производными величинами из длины.
Какой буквой обозначается напряжение в физике? Напряжение, которое является скалярной величиной, обозначается буквой U. Для скорости обозначение имеет вид буквы v, для механической работы – А, а для энергии – Е. Электрический заряд принято обозначать буквой q, а магнитный поток – Ф.
СИ: общие сведения
Международная система единиц (СИ) представляет собой систему физических единиц, которая основана на Международной системе величин, включая наименования и обозначения физических величин. Она принята Генеральной конференцией по мерам и весам. Именно эта система регламентирует буквенные обозначения в физике, а также их размерность и единицы измерения. Для обозначения используются буквы латинского алфавита, в отдельных случаях – греческого. Также возможно в качестве обозначения использование специальных символов.
Заключение
Итак, в любой научной дисциплине есть особые обозначения для различного рода величин. Естественно, физика не является исключением. Буквенных обозначений достаточно много: сила, площадь, масса, ускорение, напряжение и т. д. Они имеют свои обозначения. Существует специальная система, которая называется Международная система единиц. Считается, что основные единицы не могут быть математически выведены из других. Производные же величины получают при помощи умножения и деления из основных.
Построение чертежей – дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения – это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой греческого или английского названия величины. При этом ширина на английском будет выглядеть как “width”.
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина – в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова – «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным – трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как “height”. Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как “radius”. Отсюда и строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: “diameter”. Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как “thickness”, а в латинском варианте – “crassities”. Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от “περιμετρέο” («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык (“perimeter”) и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь – это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
Некоторые по незнанию думают, что это связано с английским написанием слова “square”. Однако в нем математическая площадь – это “area”, а “square” – это площадь в архитектурном понимании. Кстати, стоит вспомнить, что “square” – название геометрической фигуры “квадрат”. Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода “area” в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» (“fortis”).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера – это шаг (винтовых пружин, и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые – «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
границ | Время, стрела времени и квантовая механика
1. Введение; Определение времени
Вселенная, как мы ее знаем, характеризуется структурой, называемой пространство-время , в которой происходят событий . События характеризуются, прежде всего, их местоположениями в пространстве и моментами во времени, все вместе указываются в терминах координат. Количество необходимых координат, обычно действительных чисел, называется измерением пространства-времени.Координата, указывающая время, очень особенная. Это единственная координата, в которой имеет смысл определять порядок в данных значениях, порядок времени. Этот порядок определяет ориентацию, называемую стрелкой времени. Это позволяет нам определять порядок (или, по крайней мере, частичный) всех событий.
Всякий раз, когда мы строим моделей , которые объясняют существование и природу событий, крайне важно иметь такой порядок событий; он позволяет нам объяснять их последовательно: одно событие может быть причиной последующего события, если его временная переменная меньше, или оно может быть следствием события, если его временная координата выше.Трудно, возможно, невозможно разработать модель нашей Вселенной, если для модели не определен порядок описания событий.
Фактически, это приведет нас к тому, чтобы дать определение времени, которое является более первичным, более основным, чем все другие составляющие нашей модели, включая понятие пространства. Известно, что наша Вселенная хранит в себе воспоминания о событиях, которые происходили в прошлом. Всякий раз, когда мы строим модель нашей Вселенной, управляемую «законами физики», она должна иметь совершенно однозначное предписание порядка, в котором законы природы должны накладываться на все события, которые происходят .Рассматривайте законы физики как компьютерную программу для расчета следующей последовательности событий. Данные, которые мы должны ввести в программу, могут быть получены из событий, рассчитанных ранее. Они могут не возникать из событий, которые еще необходимо указать, потому что в этом случае могут возникнуть конфликты: если событие A влияет на характеристики события B , то событие B не должно реагировать на изменение события A , в противном случае правила перестают быть уникальными; они будут буквально круглыми, что сделает их противоречивыми или двусмысленными, и по этой причине они не будут подходить для объяснения наблюдаемых явлений.
Обратите внимание, что это полная противоположность принципу действия Ньютона: если событие A действует на событие B с некоторой силой, событие B должно реагировать , а не , на A . Принцип действия Ньютона, действие = противодействие, отличается, потому что он имеет пространственно-подобные направления и потому, что он часто игнорирует некоторые задействованные минутные задержки: (обратное) действие не может распространяться быстрее скорости света.
Порядок, вызванный правилом « A влияет на B , но B не может повлиять на A », – это то, без чего мы не можем обойтись.Если предположить, что Вселенная допускает существование такого элементарного принципа действия противодействия, мы получаем уникальное определение времени:
Время – это порядок, в котором наши модели природы предсказывают, предписывают или объясняют события .
Обратите внимание, что это определение времени предполагает, что мы конструируем модели для объяснения нашей Вселенной. Если бы один только собирал данные, не пытаясь их объяснить, нам не понадобилось бы никакого понятия времени.Ведь данные могли быть представлены нам в «не хронологическом» порядке. Именно наша модель обязательно требует заказа. Любой параметр, любая координата, которая монотонно увеличивается в этом порядке, будет полезной временной координатой.
Заметьте также, что квантовая механика не является исключением из нашего правила; это также требует определения упорядоченной временной координаты. Мы можем сказать это, потому что уравнение Шредингера включает исключительно производную первого порядка по времени. Следовательно, необходимо только одно граничное условие, принятое за ситуацию в далеком прошлом, чтобы определить ситуацию в будущем.
Первичное определение времени, данное выше, только определяет порядок времени, но не связывает время с действительными числами. Фактически, использование целых чисел для подсчета событий, которые мы вычислили, было бы более подходящим. Учитывая огромные размеры нашей Вселенной и чрезвычайно короткие временные последовательности, которые, как ожидается, будут актуальны в масштабе Планка, можно ожидать, что эти целые числа, если они вообще существуют, будут чрезвычайно большими, больше ~ 10 60 . Уменьшение масштаба этих чисел для практического использования, вероятно, достаточно, чтобы объяснить, почему в настоящее время действительные числа кажутся более полезными, чем целые числа, для обозначения времени.
Согласно специальной теории относительности, можно иметь события, которые пространственно разделены . Это означает, что могут быть события A и B , поэтому наша модель позволяет нам вычислить, что происходит в A и B , без необходимости указывать их порядок. Важность этого состоит в том, что данное выше определение времени не является уникальным; это особенность понятия времени, которую необходимо принимать во внимание при построении более продвинутых моделей, но она, по-видимому, менее проста в том, что касается первых принципов.
Среди заданных автору вопросов был один по специальной теории относительности. Вопросы, касающиеся специальной теории относительности в связи с вопросом о времени и его стрелке, обсуждаются в Приложении B.
2. Квантовая механика
Теория квантовой механики, возможно, является одним из величайших открытий физики; он произвел революцию в нашем понимании молекул, атомов, излучения и мира субатомных частиц. Однако даже сейчас, почти 100 лет спустя, все еще нет полного согласия относительно того, что теория говорит нам о реальности , или даже о том, существует ли «реальность» вообще.Некоторые авторы придерживаются идеи, что все «реальностей» существуют где-то в каких-то альтернативных вселенных, и что эти вселенные вместе эволюционируют как «мультивселенная».
Автор данной статьи не согласен с такими идеями. Квантовая механика – превосходное описание мира крошечных вещей, но на первый взгляд квантовая механика, кажется, просто отражает невежество человечества. Мы не знаем , какую реальность он описывает, и пока это так, мы не должны удивляться тому, что, в определенном смысле, все возможные реальности играют роль всякий раз, когда мы пытаемся сделать наилучшее возможное предсказание исхода событий. эксперимент.Тот факт, что многие из нас испытывают технические трудности с реализацией такой мысли в уравнениях, которые, как известно, работают лучше всего сегодня, вполне может быть вызван недостатком воображения относительно того, как в конечном итоге будет найдено правильное представление.
Автор провел собственный анализ известных фактов и пришел к выводу, что копенгагенская доктрина, то есть консенсус, достигнутый многими мировыми экспертами в начале двадцатого века, частично во время их многочисленных встреч в Датский капитал почти прав: существует волновая функция, или, скорее, то, что мы называем квантовым состоянием, являющееся вектором в гильбертовом пространстве, которое подчиняется уравнению Шредингера.Абсолютные квадраты компонентов вектора могут использоваться для описания вероятностей, когда мы хотим что-то предсказать или объяснить. Были разработаны мощные методы, позволяющие угадать правильное уравнение Шредингера, если кто-то знает, как вещи развиваются классически, то есть в старых теориях, куда квантовая механика еще не была включена. Все это прекрасно работает. Однако, согласно Копенгагену, есть один вопрос, который следует задать , а не : «Как выглядит , реальность из всего, что движется в наших экспериментальных условиях?» или: что на самом деле происходит?
Согласно Копенгагену, такой вопрос никогда не может быть решен с помощью какого-либо эксперимента, поэтому на него нет ответа в рамках набора логических утверждений, которые мы можем сделать о мире.Period, schluss, fini. Эти вопросы бессмысленны.
Мы оспариваем именно этот ответ. Даже если на такие вопросы нельзя ответить с помощью экспериментов , мы все же можем теоретически попытаться построить достоверные модели реальности. Представьте себе известного детектива Шерлока Холмса, входящего в комнату, с мертвым телом, лежащим на полу. Дверь открыта, и окно тоже. Совершено преступление. Преступник прошел через окно или дверь? Или случилось что-то совсем другое? Шерлок Холмс обдумывает все возможности, но он будет , а не сказать: преступник прошел через окно и через дверь, используя волновую функцию и т. Д.и т.д. Ясно, что такие ответы не принимаются в обычном мире. Шерлок Холмс вполне может прийти к выводу, что он не может получить ответ с уверенностью, но он может попытаться выяснить, что могло произойти . Нам промыли мозги, чтобы принять волновые функции в мире атомов? Не следует ли нам здесь также спросить, что это было на самом деле или что могло быть, что происходило?
Возможно, мы говорим не на том языке. Может быть, атомы и молекулы не существуют в том виде, в каком мы их себе представляем.Возможно, истинные степени свободы Природы очень разные, и только когда мы рассматриваем статистику многих атомов, наш язык, который предполагает, что это частицы, подчиняющиеся квантовым уравнениям, может работать правильно.
Когда первые попытки построить такие модели потерпели неудачу, исследователи попробовали другой путь: может быть, можно доказать , что не существует вообще никакой реальности, вероятности которой можно уловить в терминах уравнения Шредингера? Предположим, что мы налагаем условия на такие модели, как , местонахождение и причинно-следственная связь .Можно ли доказать или опровергнуть существование реалистичных моделей?
Что тогда произошло, хорошо известно. Первым такой вариант рассмотрел Эйнштейн и его соавторы Подольский и Розен [1] и Джаммер [2]. Они задумали эксперимент Gedanken , чтобы показать, что квантовая механика не может точно дать локальное описание того, что происходит. Этот вывод на самом деле несколько противоречив, потому что квантовая механика использовалась для как можно более точного описания того, какие прогнозы могут быть сделаны, и этот результат редко кто-либо оспаривал; действительно, позже это было подтверждено реальными экспериментами.
Установка была пересмотрена Беллом в соответствии с несколько более реалистичным сценарием, использующим спины частиц, и он дал очевидное противоречие в более точной формулировке: Теорема Белла:
Никакая физическая теория локальных скрытых переменных никогда не сможет воспроизвести все предсказания квантовой механики;
результат квантово-механических расчетов некоторых нелокальных корреляций противоречит любому приемлемому «классическому» объяснению по крайней мере в два раза. Неравенство, названное неравенством Белла , впоследствии было обобщено и уточнено [3].
3. Причинность, корреляции и квантовая механика
Это открытие не осталось бесспорным. Многие авторы пытались найти изъян в аргументах Эйнштейна и Белла, но с логической точки зрения они казались безупречными. Белл предположил, что детерминизм означает, что можно построить модель, любую модель, в которой классические уравнения управляют поведением динамических переменных, и где в мельчайших масштабах, где эти переменные описывают данные, законы эволюции не оставляют ни малейшей двусмысленности; здесь нет волновых функций, нет статистических соображений, поскольку все, что происходит, контролируется определенностью.Более того, есть некое ощущение локальности: законы управляют всеми процессами, используя только данные, которые расположены в определенных местах, в то время как действия на расстоянии или в обратном направлении запрещены. Классические степени свободы, которые «действительно» существуют, назывались «beables».
Здесь возникает первая тема для обсуждения: что означает «действие назад во времени»? В «Новой кухне» Белл [4, 5] как можно точнее сформулировал, что означает «причинность вперед во времени»:
Теория называется локально причинной, если вероятности, связанные со значениями локальных beables в пространственно-временной области 1, не изменяются посредством спецификации значений локальных beables в пространственно-подобной разделенной области 2, когда то, что происходит в обратном свете конус 1 уже достаточно определен […]
Предполагается, что область 2 полностью находится за пределами светового конуса 1 в прошлом, поэтому то, что там происходит, должно быть несущественным.Звучит нормально, и многие исследователи согласны с этим, но есть проблема:
Область 2 также имеет световой конус прошлого, и если мы рассмотрим некоторые модификации событий в 2, они могут не совпадать с тем, что мы постулировали в области 1, поскольку два световых конуса прошлого перекрываются.
Следовательно, корреляций между данными в области 1 и области 2 не могут быть исключены. На самом деле, известно, что такие корреляции повсеместно встречаются в физическом мире, так что же на самом деле означает «причинность Белла»?
Беллу нужно было сказать, что в любой модели , описывающей законы природы, только данные в прошлом световом конусе 1 должны определять, что происходит в 1, в то время как он не должен был ссылаться на корреляции. Тем не менее, неравенства Белла касаются корреляций , и предполагается, что они отсутствуют за пределами светового конуса.
В том же духе отвергается «обратная причинность»: прошлое не должно зависеть от будущего. Это верно в следующем смысле: наша модель не должна требовать знания данных в будущем, чтобы предписывать данные в настоящее время (она должна требовать только данные в световом конусе прошлого). Корреляции действительно происходят. Фактически, если наша модель отражает обратимость во времени – что делает большинство моделей, – тогда данные внутри светового конуса будущего можно использовать для определения, то есть для восстановления настоящего или прошлого, назад из будущего.
Выше были выделены слова наша модель . Здесь важно то, что причинность не может быть характеристикой или свойством самих физических данных, а скорее свойством уравнений движения, с помощью которых мы пытаемся имитировать эти данные. Если две разные теории можно использовать для описания одного и того же набора данных, тогда одна из этих теорий может иметь причинно-следственную связь, а другая – нет. Это элемент «парадокса» Белла, который, возможно, не был подчеркнут в достаточной степени.
Большинство моделей природы обратимы во времени; мы можем запустить основные уравнения назад во времени так же легко, как и вперед во времени. Это подразумевает, что теории с причинностью, направленной вперед во времени, также должны иметь причинность назад во времени; Белл проигнорировал это.
Тем не менее, есть веская причина, по которой глубокий результат Белла считается неопровержимым большинством современных исследователей. Действия наблюдателей в квантовых экспериментах считаются полностью классическими и отражают свободную волю наблюдателей .Чтобы опровергнуть теорему Белла, свобода воли наблюдателей должна быть соотнесена с квантовыми данными в прошлом. Большинство исследователей считает это «абсурдом». В следующем разделе и в приложениях A и C ответ этого автора относительно того, почему эти корреляции могут быть не столь абсурдными, в конце концов, освещается более подробно.
Теория, использованная автором, была названа «Интерпретация клеточного автомата (CA)» [6], но, возможно, предпочтительным названием является «анализ векторного пространства». Идея заключается в том, что классическая система может быть проанализирована путем связывания любого состояния системы вектором, так что все состояния вместе образуют ортонормированный базис векторного пространства, называемого гильбертовым пространством.«Анализ векторного пространства» состоит из математических процедур, которые стали возможными при выполнении любых преобразований в этом векторном пространстве. В итоге получается уравнение Шредингера точно так же, как в квантовой механике. Таким образом, анализ векторного пространства противоречит теореме Белла. Наша теория состоит из утверждения, что то, что мы сегодня называем квантовой механикой, может быть результатом анализа в векторном пространстве некоторой классической системы. «CA Интерпретация» квантовой механики состоит из предположения, что это правда, в то время как мы воздерживаемся от дальнейших попыток идентифицировать классическую систему, лежащую в основе этого.Однако автор надеется, что поиск подходящих классических моделей будет продолжен и принесет свои плоды.
Мы заканчиваем этот раздел замечанием о существовании ограничения, называемого «причинность», которое может быть наложено на любую модель элементарных частиц. Это не оспаривается, но на самом деле много используется в квантованных теориях поля. Это условие рассматривает операторы ϕ ( x ) в квантовых теориях поля, описывающие (элементарные или составные) поля ϕ в 4-пространственно-временных координатах x .Пусть x 1 и x 2 разделены пробелом. Тогда у нас есть для коммутатора
(x1-x2) 2> 0 → [ϕ (x1), ϕ (x2)] = 0. (3.1)Это говорит о том, что любая операция ϕ ( x 1 ), действующая на любое квантовое состояние в пространственно-временной точке x 1 , не может повлиять на результат какого-либо динамического эффекта ϕ ( x ). 2 ) при x 2 . В Стандартной модели элементарных частиц это условие «нет телефона Белла» выполняется и имеет важные приложения в расчетах.Однако это условие не различает причинно-следственные связи в прямом направлении времени от причинно-следственных связей в обратном направлении, поэтому его нельзя использовать для получения неравенств, таких как неравенство Белла. Условие «без телефона Bell» не зависит от стрелки времени.
4. Неравенства Колокола и ЧШ
Эксперимент Белла Геданкен, по сути, очень похож на установку Эйнштейна Розена Подольского. Создано локальное устройство, которое может испускать две запутанные частицы, α и β , которые покидают машину в противоположных направлениях.Алиса ( A ) и Боб ( B ) оба выбирают, измерять ли свойство X или свойство Y частиц, которые они могут видеть. Алиса выбирает настройку a для измерения α , а Боб устанавливает b для измерения β .
Корреляции, необходимые для объяснения квантово-механического результата, требуют, чтобы настройки a и b , выбранные Алисой и Бобом, коррелировали друг с другом, а также (классические) спины двух запутанных частиц.Автор рассчитал минимальное количество корреляции, необходимое для получения квантового результата. Мы нашли следующее распределение [6]:
W (a, b, λ) = C | sin (2a + 2b-4λ) | , (4.1), где a – угол, выбранный Алисой для ее измерения, b – угол Боба, а λ – параметр, описывающий поляризацию запутанных фотонов, создаваемых источником и обнаруженных Алисой и Бобом. W – это распределение вероятностей, а C – нормировочная константа.Он имеет корреляцию 3 тела : всякий раз, когда мы интегрируем по всем значениям a , или всем значениям b , или всем значениям λ, мы получаем плоское распределение.
Чтобы строго показать, что такие особенности корреляции неприемлемы для любой теории, которая порождает квантовую механику из классических законов механики, Беллу пришлось сформулировать свое определение причинности. Выше мы указали, что его определение не применимо к физическим системам, поэтому можно было бы закончить обсуждение здесь и сейчас, поскольку корреляционные функции не ограничены световыми конусами.Однако большинство исследователей считает корреляционную функцию (4.1) неприемлемой. Как может случиться так, что решения Алисы и Боба, принятые по доброй воле, все же могут быть соотнесены с чем-то, что произошло раньше, – поляризацией, выбранной запутанными фотонами, испускаемыми источником? «Знали» ли эти фотоны, какие настройки Алиса и Боб выберут позже, или это случай «заговора»? Как одиночный фотон может управлять классическими динамическими переменными a и b ?
Чтобы объяснить это, мы теперь резюмируем, как работает анализ векторного пространства.Предположим, у нас есть классическая теория, например, в масштабе Планка 10 – 33 см. Обычно это клеточный автомат. Обычно это может быть 21099 состояний в каждом см 3 . Каждое из этих состояний называется «онтологическим», что означает, что оно реализовано или не реализовано, но суперпозиций не существует. Это именно то, что Эйнштейн, Белл и другие хотели опровергнуть. Просто для того, чтобы заниматься математикой, мы теперь прикрепляем базисный вектор к каждому из этих онтологических состояний.Они настроены так, что образуют ортонормированный базис 21099-мерного векторного пространства, в каждом сантиметре 3 . В такт часам, обычно с частотой Планка около 10 44 Гц, эти состояния переходят в другие состояния. Это мы пишем с использованием матрицы эволюции, которая состоит из единицы в каждой строке и в каждом столбце и нулей во всех остальных местах.
Используемая математика состоит в диагонализации этой матрицы. Это дает нам собственные состояния энергии, то есть гамильтониан.Обнаруживается, что состояния этой модели подчиняются уравнению Шредингера. Теперь все собственные энергетические состояния являются суперпозициями онтологических состояний, и если мы ограничимся состояниями с энергиями ниже 1 ТэВ для каждого возбуждения, то это будет соответствовать очень крошечному подпространству всего гильбертова пространства, в то время как каждое состояние, которое мы можем использовать, является суперпозиция онтологических состояний. Без потери общности, мы можем интерпретировать коэффициенты этих суперпозиций, взяв их абсолютные квадраты для обозначения вероятностей.Это дополнительно поясняется в Приложении A. Здесь важно отметить, что «реальность» всегда описывается как одно из исходных онтологических состояний, а не как суперпозиция, тем не менее мы можем использовать уравнение Шредингера для описания как онтологических состояний, так и суперпозиций. . Элементы онтологического базиса всегда развиваются в другие элементы этого базиса, а суперпозиции – в суперпозиции. Мы называем это законом сохранения онтологии .
Есть веская причина, по которой многие попытки создать реалистичные модели, объясняющие нарушение неравенств Белла, потерпели неудачу, а именно: в этих моделях была предпринята попытка имитировать суперпозицию определенных режимов в терминах других допустимых режимов автомата.Гораздо лучше сохранять суперпозиции такими, какие они есть, суперпозициями действительных автоматных режимов, которые по этой причине не могут сами по себе действовать как онтологические состояния. Вместо этого происходит следующее: если рассматривать некоторую суперпозицию физических состояний, на самом деле рассматривается вероятностная смесь, но то, что именно истинные, несмешанные, физические состояния различаются от одного эксперимента к другому, таким образом, что конечное состояние никогда не может быть в суперпозиции. Поскольку эта функция имеет огромное значение, мы объясняем некоторые технические детали этого момента в Приложении A.
Теперь мы видим, что при выводе своих неравенств Беллу и ЧШШ приходилось делать предположения, с которыми мы не можем согласиться. Их основное предположение состоит в том, что Алиса и Боб могут выбирать, что измерять, и что это не должно коррелировать с онтологическим состоянием запутанных частиц, испускаемых источником. Однако, когда при выборе своих настроек Алиса или Боб хоть немного меняют свое мнение, их классические настройки представляют собой онтологическое состояние, отличное от прежнего. Фотон, на который они сейчас смотрят, будет суперпозицией старых фотонов, которые они хотели обнаружить, но все состояние, фотон плюс настройки, будет ортогональным предыдущему.В частности, из-за онтологического закона сохранения новый фотон, на который они смотрят, должен быть онтологическим. У Алисы и Боба нет свободы воли смотреть на фотоны, которые не являются онтологическими. Итак, передумав, Алиса и / или Боб должны были перевести вселенную в онтологическое состояние, отличное от предыдущего, и эта модификация восходит к миллиардам лет, вплоть до происхождения вселенной. Это можно было бы назвать ретро-причинностью, но это просто связано с тем, что уравнения (как классические, так и квантовые), в принципе, могут быть решены в обратном направлении во времени.
Как следствие, настройки Алисы и Боба могут и будут коррелированы с состоянием частиц, испускаемых источником, просто потому, что эти три переменные действительно имеют общие переменные в своих прошлых световых конусах. Изменение, необходимое для реализации вселенной с новыми настройками, также должно подразумевать изменения в перекрывающихся областях этих трех световых конусов прошлого. Это потому, что вселенная всегда заставляет себя оставаться онтологической.
Ограничение, заключающееся в том, что вселенная всегда должна находиться в онтологическом состоянии, является единственным ограничением.Это означает, что Алиса и Боб все еще имеют свободную волю в классическом смысле; они могут выбрать любое из онтологических состояний вселенной, независимо от того, какой генератор случайных чисел или лотерею они использовали. Но они не могут поместить Вселенную в суперпозицию состояний, а это только то, что мы можем сделать в наших математических моделях при изучении вероятностных распределений, желая привести их в такую форму, чтобы мы могли применять уравнения Шредингера.
Итак, давайте подчеркнем и резюмируем этот важный момент:
Всякий раз, когда кажется, что наблюдатели используют свою «свободную волю» для выбора настроек детекторов, которые они используют, они не могут «изменить свое мнение», если микроскопические данные постоянно не изменяются.Среди прочего, (запутанные) фотоны в эксперименте Белла будут перегруппированы в какое-то другое квантовое состояние таким образом, что фотоны, в конечном итоге измеренные, всегда будут в онтологическом состоянии : они заставляют детектор либо щелкать, либо не щелкать. щелкают, но они никогда не могут заставить детекторы перейти в суперпозицию состояний.
В частности, если мы предположим, что Вселенная началась с данного фиксированного состояния при t = 0 (Большой взрыв), то у любого наблюдателя больше нет возможности изменить свое мнение; его действия фиксированы, даже если он думал, что имеет свободную волю.Настройки a и b коррелируют с поляризациями фотонов λ, которые не следует путать с «причинно-следственной связью назад во времени».
Связанный квантовый парадокс, который был выдвинут как еще одна иллюстрация квантовой странности, – это так называемый парадокс GHZ. Этот парадокс представляет интерес, потому что его разрешение можно описать в терминах чрезмерно упрощенной модели Вселенной, иллюстрирующей важную роль наблюдателя как части системы.В Приложении C мы объясняем, что происходит в теории клеточного автомата, когда проводится этот Gedanken-эксперимент.
5. Потеря информации и стрелка времени
Большинство известных физических теорий, объясняющих очевидное отсутствие симметрии обращения времени, содержат элементы термодинамики и энтропии. На самом деле, в этих описаниях природы можно элегантно объяснить отсутствие этой симметрии, обвиняя ее в асимметрии в граничных условиях . При написании дифференциальных уравнений для законов природы всегда нужно добавлять то, что мы знаем о границах.Что касается границ в космических направлениях, мало что известно, так как Вселенная выглядит очень однородной, и никаких граничных эффектов никогда не было обнаружено. Вселенная либо строго бесконечна в направлениях, подобных пространству, либо мы живем на пространственно компактном многообразии, таком как 3-сфера или тор. Эти граничные условия демонстрируют большую симметрию.
Однако во времениподобном направлении полной симметрии быть не может. Вселенная, кажется, изначально была очень маленькой, возможно, все началось в одной точке.Эта точка, должно быть, была высокоупорядоченной, с очень маленькой или, возможно, нулевой общей энтропией. Это разумное граничное условие в начале времени.
С другой стороны, когда время становится очень большим, мы не видим необходимости в каких-либо граничных условиях; Вселенная может просто продолжать бесконечно расширяться, претерпевая постоянное увеличение энтропии. Таким образом, у нас есть уравнения, симметричные относительно обращения времени, но асимметричные по своим граничным условиям. Этого достаточно, чтобы объяснить наблюдаемую сегодня асимметрию времени.
Однако есть примеры математических систем, в которых существуют особенности, которые могут быть отнесены либо к основной части системы, либо к границе, так что отнесение всех временных эффектов нарушения симметрии к границе может, по-видимому, не всегда работать.
Пока мы придерживаемся квантово-механического описания всех микроскопических динамических законов, мы находим на нашем пути теорему CPT, которая подразумевает, что если мы объединим обращение времени T с обращением четности P и обменом частица-античастица C , то эта симметрия идеальна.Мы вполне могли бы придерживаться нашего вердикта, что граничные условия Природы в направлении времени достаточны, чтобы объяснить стрелу времени.
Однако можно заметить, что можно рассматривать другой источник асимметрии обращения времени. Как объяснялось в предыдущих разделах, этот автор не верит, что «квантовая механика» будет последней и постоянной основой для основных законов природы. Если мы откажемся от него, чтобы заменить его некоторыми классическими идеями, потребность в симметрии обращения времени также исчезнет.Мы могли бы выбрать основную теорию, в которой информация в классическом смысле может исчезнуть. Что касается клеточных автоматов, системы, в которых информация действительно теряется, являются гораздо более общими, чем системы, в которых информация сохраняется, так что переключение направления времени приводит к гораздо более драматическим изменениям.
Как такие модели могут привести к эффективным квантовым теориям? Возникает ли вновь симметрия относительно обращения местного времени? Мы утверждаем, что для автомата возможность генерировать статистические корреляции, основанные исключительно на анализе векторного пространства, то есть вектора, развивающиеся в гильбертовом пространстве, которые приводят к квантовой механике, может быть довольно общей и включать модели с потерей информации.
Способ борьбы с потерей информации в этом контексте очень прост в принципе, но чрезвычайно сложен на практике. Принципиальный способ справиться с этим – введение информационных классов : мы идентифицируем элементы ортонормированного базиса гильбертова пространства не с отдельными состояниями автомата, а с информационными классами. Информационный класс определяется как класс состояний в автомате, обладающих тем свойством, что через конечный промежуток времени все они развиваются, чтобы стать одним и тем же состоянием в автомате.В принципе, такие классы могут стать чрезвычайно большими, но на практике вероятность того, что два состояния, которые похожи друг на друга в один момент времени, превратятся в точно такое же состояние в ближайшем будущем, могут быстро упасть до нуля с течением времени, поэтому что информационные классы могут оставаться управляемыми. Формально они могут стать достаточно большими, чтобы формировать состояния, которые можно различить, только изучая данные, живущие на граничной поверхности, а не уточняя, что происходит в массиве. Это то, что мы видим в физических уравнениях для черных дыр, называемых голографией , так что это можно рассматривать как косвенное свидетельство в пользу основных моделей с потерей информации.
В базовых моделях с потерей информации акт обращения времени принимает очень интересную форму: обратное время онтологических состояний в гильбертовом пространстве (beables) имеет тенденцию формировать квантовые суперпозиции beables в обращенном времени гильбертовом пространстве. Это, возможно, может объяснить, почему суперпозиции следуют тем же законам природы, что и онтологические состояния, но пока мы просто рассматриваем эти общие наблюдения как нечто, о чем нужно помнить, когда, подобно Шерлоку Холмсу, мы пытаемся выяснить это с точки зрения модели, которые могли бы иметь место на самом деле, когда вся информация, которую мы смогли получить, принимает форму квантовых суперпозиций.
Авторские взносы
Автор подтверждает, что является единственным соавтором данной работы, и одобрил ее к публикации.
Заявление о конфликте интересов
Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Автор благодарит Т. Модлина, П. В. Моргана, Т. Майерса, Т. Норсена и многих других за обстоятельное обсуждение этих и связанных с ними вопросов в веб-журналах.Я также благодарен редакторам и рецензентам, которые настаивали на дополнительных пояснениях для улучшения оригинальной рукописи.
Сноски
Список литературы
1. Эйнштейн А., Подольский Б., Розен Н. Можно ли считать квантово-механическое описание физической реальности полным? Phys Rev. (1935) 47 : 777.
Google Scholar
2. Джаммер М. Концептуальное развитие квантовой механики . Нью-Йорк, штат Нью-Йорк: Макгроу-Хилл (1966).
Google Scholar
3. Клаузер Дж. Ф., Хорн М. А., Шимони А., Холт Р. А.. Предлагаемый эксперимент для проверки локальных теорий скрытых переменных. Phys Rev Lett. (1969) 23 : 880–4. DOI: 10.1103 / PhysRevLett.23.880
CrossRef Полный текст | Google Scholar
4. Bell JS. О парадоксе Эйнштейна-Подольского-розена. Физика (1964) 1 : 195.
Google Scholar
5. Bell JS. Новая кухня. В: Белл М., Готфрид К., Вельтман М., редакторы. Об основах квантовой механики. Разговорчивый и непроизносимый в квантовой механике . Анн-Арбор, Мичиган: Мичиганский университет (2001). п. 216–34.
Google Scholar
6. ‘т Хоофт Г. Клеточно-автоматная интерпретация квантовой механики. В: Фундаментальные теории физики , 1-е изд., Т. 185. Чам: Springer International Publishing (2016). п. 298.
Google Scholar
8. Гринбергер Д., Хорн М., Цайлингер А. Выход за рамки теоремы Белла.В: Кафатос М., редактор. Теорема Белла, квантовая теория и концепции Вселенной . Дордрехт: Kluwer Academic (1989), стр. 69–72.
Google Scholar
9. Кауфман Б. Кристаллическая статистика. II. Функция распределения оценена спинорным анализом. Phys Rev. (1949) 76 : 1232.
Google Scholar
Приложение
A. Суперпозиции и вероятности Борна
Всякий раз, когда теории с классической логикой предлагаются для объяснения квантовых явлений, часто возникают следующие вопросы: Вопрос 1: В эксперименте Белла пара частиц – назовем их фотонами – находится в запутанном состоянии.В онтологической теории кажется, что эта пара частиц «заранее знает», какая суперпозиция состояний будет позже выбрана Алисой и Бобом для своих измерений. Почему это не нарушает причинно-следственную связь?
Вопрос 2: Почему квадраты амплитуд точно представляют вероятности результатов измерений? (правило Борна)
И вопрос 3: Что происходит, когда волновая функция схлопывается? А что происходит, когда производится измерение или наблюдение?
Все эти вопросы тесно связаны, и на них можно ответить вместе в том, что было объявлено ранее как «Интерпретация квантовой механики с помощью клеточного автомата» [6].
Основная идея состоит в том, что на крошечной шкале расстояний, имеющей значение в физике, предположительно в масштабе Планка, около 10 – 33 см, существуют законы физики, которые наиболее эффективно формулируются без ссылки на гильбертово пространство, квантовые суперпозиции, кубиты или даже действие на расстоянии. У нас есть клеточный автомат или что-то очень похожее на него. Клеточный автомат лучше всего рассматривать как базовую компьютерную программу, в которой в рамках масштабного предприятия параллельных вычислений цифровые данные, локализованные в какой-то сетке, обновляются в такт чрезвычайно быстрых часов.Скорость часов может в некоторых случаях отличаться, но мы не хотим вдаваться в подробности. Самое главное, информация распространяется с ограниченной скоростью, в основном со скоростью света, и вся эта информация является классической. Временно для простоты мы предполагаем, что система обратима во времени, хотя, как объяснялось ранее, в этом может не быть необходимости.
Это явно та теория, которую Эйнштейн, Белл и многие другие думали, что они могут опровергнуть, но, как мы сейчас объясним более подробно, это еще не конец истории.Существуют различные аспекты системы, которые требуют более тщательного изучения, в частности, повсеместное присутствие очень сильных корреляций на микромасштабе, которое проникает на макроскопические расстояния, и тот факт, что в принципе невозможно сжать («застегнуть») система в более детализированную модель, которая воспроизводит все детали. Как только кто-то пытается что-то сжать, возникают неопределенности, которые проявляются в виде квантовых суперпозиций. Но я забегаю вперед своих аргументов, давайте рассмотрим ситуацию в осмысленном порядке.Более полная история представлена в ‘т Хоофте [6].
В принципе, автомат может находиться в огромном количестве различных состояний, примерно 21099 состояний на каждый кубический сантиметр (число, полученное при допущении одной логической степени свободы в кубической планковской длине). Только если мы рассмотрим все эти состояния, систему можно будет увидеть детерминированной. Каждое из этих состояний важно, но из-за сильной корреляции мы воспринимаем наш мир так, как будто существует гораздо меньше возможных состояний, обычно 21050 в см 3 (одна логическая степень свободы в 1 ТэВ −3 ).Однако сжатие системы не может быть выполнено без потери информации; требуется более мощная техника.
Так получилось, что существует более мощная техника; мы называем это «анализом векторного пространства». В математике это не новость. Например, в теории групп оказалось полезным давать матричные представления элементов группы. Рассмотрим подмножество группы перестановок. Элементы набора, в котором происходят перестановки, представлены как ортонормированные векторы в нашем векторном пространстве.Размерность этого векторного пространства равна размерности (количеству элементов) множества. Он может быть конечным или бесконечным. Это векторное пространство и есть наше гильбертово пространство. Теперь можно использовать все математические приемы, доступные для векторов, для исследования свойств группы. Например, можно диагонализовать матрицы. Это включает в себя ортогональные (унитарные) преобразования всех видов векторов.
Предполагается, что мы можем сделать то же самое в наборе состояний автомата. После ряда преобразований мы получаем матрицы, представляющие эволюцию, диагональные или почти диагональные.Эффективная размерность нашего гильбертова пространства теперь может быть значительно уменьшена за счет факторизации больших его частей. Однако они не разлагаются на исходные разделительные линии нашего ортонормированного множества. Мы получаем разные виды векторов, которые теперь являются суперпозициями векторов исходного набора. Все это просто математическая манипуляция; физика осталась прежней.
В частности, закон эволюции представляет собой онтологическую матрицу в терминах исходных онтологических состояний; онтологическая унитарная матрица – это матрица, содержащая только один, а для остальных нули во всех ее строках и всех ее столбцах (допустимы произвольные фазовые коэффициенты, если каждая строка и каждый столбец содержит только один элемент с абсолютным значением один, а все остальные элементы матрицы обращаются в нуль).После некоторой комбинации обширных линейных суперпозиций наши матрицы будут выглядеть гораздо более общими, чем раньше.
В то время как каждое из наших 21099 состояний эволюционирует в другое состояние за такие малые единицы времени, как планковское время, порядка 10 – 44 секунд, мы обнаружим суперпозиции состояний, которые развиваются намного медленнее. Эффективная единица времени теперь будет обратной энергией наиболее энергичных частиц в наших ускорителях частиц. Эти энергии на много порядков ниже, чем энергия Планка, поэтому действительно, мы имеем гораздо меньшее гильбертово пространство, чем исходное.То, что известно о физике сегодня, – это законы эволюции этого крошечного подпространства гильбертова пространства. Поскольку здесь зависимость от времени намного медленнее, мы можем записать закон эволюции в терминах эрмитовского гамильтониана: уравнения Шредингера. Мы постулируем детерминизм только в исходной модели клеточного автомата с его огромным количеством состояний, а не в эффективной редуцированной модели, которую сегодня называют физикой. Может ли эта система нарушить неравенство Белла / CSHS?
Сначала нам нужно указать, как выполняется наблюдение, в терминах состояний исходного автомата.Предположим, мы хотим установить присутствие планеты. Внутри планеты атомы и молекулы плотно упакованы, так что мир внутри выглядит совсем не так, как в вакууме. Теперь предположим, что состояние вакуума представлено состояниями в автомате, которые показывают разные статистические содержания и корреляции, чем состояния, которые представляют плотно упакованные атомы и молекулы. Локально статистические различия между этими состояниями могут быть незначительными; наша способность отличать состояние вакуума от каменистого материала может быть далека от совершенства; говорят, что внутри небольшого объема 3 мм, данное состояние имеет вероятность (1 – ε) / (1 + ε) быть вакуумом, а не горной породой.Для всей планеты мы должны возвести это число в степень, равную объему планеты, измеренному в мм 3 . Таким образом, можно почти с уверенностью обнаружить, что поблизости есть планета, а не вакуум.
Планета – классический объект. Мы только что обнаружили, что такие классические объекты должны быть достаточно хорошо идентифицированы и охарактеризованы в терминах исходных состояний автомата. Предположим, что это справедливо для всех объектов, которые мы обычно называем «классическими», не обязательно такими большими, как планеты.Когда мы проводим измерения или наблюдаем, мы должны смотреть на большое подмножество классических состояний автомата.
Теперь рассмотрим квантовый эксперимент. Мы не можем использовать все гильбертово пространство, потому что оно содержит слишком много состояний. Поэтому мы используем сильно редуцированное подпространство гильбертова пространства, которое представляет только частицы с низкой энергией. Все эти состояния являются суперпозициями состояний клеточного автомата. Определение нашего начального состояния | ψ 〉 init , как и мы, мы все еще представляем его как суперпозицию онтологических состояний | ont〉 i :
| ψ〉 init = ∑iαi | ont, init〉 i; ∑i | αi | 2 = 1.(A1)На этом этапе нам просто нужно определить , что | αi | 2 представляет вероятность того, что онтологическое состояние | ont〉 i является нашим начальным состоянием. Из математики теории линейного представления было бы трудно вывести какую-либо другую связь между вероятностями и амплитудами, кроме этой. В любом случае, в дальнейшем мы увидим, что то, что справедливо для начального состояния, будет продолжаться для всех состояний, достигнутых в более поздние времена.
Итак, давайте рассмотрим эволюцию этого состояния.Наши математические процедуры разложения наших векторов состояний никогда не влияли на закон физической эволюции онтологических состояний. Это означает, что, , пока мы используем линейные уравнения Шредингера , также и в более поздние времена соотношение (A1) продолжает сохраняться вплоть до конечного состояния:
| ψ〉 final = ∑iαi | ont, final〉 i; ∑i | αi | 2 = 1. (A2)Обратите внимание, что базис состояний изменится, но коэффициенты суперпозиции _ i останутся неизменными, а следовательно, и вероятности останутся прежними.А теперь рассмотрим измерения. Мы сравниваем окончательное наложенное состояние с онтологическими состояниями, в которых должна оказаться система. Это снова онтологические состояния | ont, final〉 i уравнения (A2). Теперь α i наконец распознаются как представляющие вероятности для конечного состояния. Правило вероятности Борна – простое следствие математической теории представлений. Ответ на вопрос, откуда взялось правило вероятности Борна, состоит в том, что если мы поместим его в начальное состояние, правило Борна останется неизменным на протяжении всей эволюции.
Обратите внимание, что если мы начали с одного онтологического состояния | ont, init〉 1 , тогда конечное состояние будет автоматически также будет одним онтологическим состоянием | ont, final〉 1 . Это остается верным, если мы используем уравнение Шредингера для описания эволюции. Следовательно, уравнение Шредингера автоматически вызовет коллапс конечного состояния в одно онтологическое состояние, если исходное состояние было одним онтологическим состоянием.Причина, по которой в обычной квантовой механике этого не происходит, заключается в том, что мы не используем полное уравнение Шредингера для всех состояний, а только для состояний с более низкой энергией, для которых уравнение известно, и мы идеализировали начальное состояние, невольно заменяя онтологическое начальное состояние суперпозицией, отсюда вероятностное распределение начальных онтологических состояний.
Часто утверждают, что квантовые вероятности следует рассматривать как фундаментально отличные от классических неопределенностей, которые возникают из-за незнания начального состояния; Однако в нашем подходе квантовые вероятности существуют по тем же причинам, что и в классических теориях.
Теперь рассмотрим эксперимент ЭПР / Белла. Мы не строим явно микроскопическую классическую модель для всех взаимодействий Стандартной модели. Хотя были предложены общие стратегии для такой конструкции, воспроизвести все симметрии Природы все еще слишком сложно. Однако мы утверждаем, что любое противоречие с неравенствами Белла / CHSH исчезло.
Когда Алиса и Боб проводят свое наблюдение, они не могут выбрать суперпозицию состояний фотона, а только один онтологический фотон.Результатом измерения Алисы всегда является онтологическое состояние формы | a, A 〉 ont , где a – выбранная настройка, заданная углом, а A = ± 1 – ее результат. Вместе с находкой Боба конечным классическим состоянием является | a, A, b, B 〉 по . В нашей модели расчет дает суперпозицию
ψ〉 final = α1 | a, +, b, +〉 ont + 2 | a, +, b, -〉 ont (A3) + Α3 | a, -, b, +〉 ont + α4 | a, -, b, -〉 ont, (A4)Наблюдаемый результат никогда не является конечным состоянием формы (A2) или (A3), но всегда одно конкретное онтологическое состояние, | ont, final〉 1 .Расчет модели дает запутанную суперпозицию онтологического состояния | a, b 〉, объединенные (умноженные) с суперпозицией четырех состояний | +, +〉, | +, -〉, | -, +〉 и | -, -〉.
Если мы изменим начальное состояние, вычисленное конечное состояние будет другой запутанной суперпозицией, но онтологическое состояние будет основано на углах a, b и измерениях A и B . Изменение начального онтологического состояния всегда приводит к единственному конечному онтологическому состоянию, никогда не суперпозиции, поскольку коэффициенты α i никогда не изменяются.
Что вводило в заблуждение в описании эксперимента Беллом, так это то, что он думал, что изменение настроек a и b приведет к другому наложению измерений A = ± и B = ±. В нашем векторном представлении любая модификация a и b , независимо от того, насколько она крошечная, требует модификации начального онтологического состояния. Новое онтологическое состояние будет ортогональным, следовательно, полностью не связанным с предыдущим, так что два фотона, испущенные источником, не могут быть связаны с фотонами, испущенными ранее.Таким образом, идея о том, что можно изменить настройки ( a, b ) без изменения поляризации запутанных фотонов, испускаемых источником, является иллюзией.
Можно также сказать, что настройки a и b оказываются запутанными с поляризованными фотонами. Как только настройки будут зафиксированы, фотоны будут находиться только в одном онтологическом состоянии. Я не буду вдаваться в это описание слишком сильно, потому что в конце у нас должна быть только одна настройка и одно онтологическое состояние фотона.
Наиболее важное различие между нашей презентацией и обычной обработкой наблюдений Белла состоит в том, что наблюдатели Алиса и Боб вместе с выбранными ими настройками a и b , являются частями физической системы . Любое изменение настроек ( a, b ), независимо от того, сделано ли оно «по доброй воле» или иным образом, потребует другого начального онтологического состояния.
Б. Причинность и стрела времени в специальной теории относительности
В рамках CA-интерпретации квантовой механики со специальной теорией относительности трудно справиться в этой процедуре, поскольку группу Лоренца или группу Пуанкаре, как известно, сложно реализовать, поскольку эти группы не компактны.Вполне возможно, что преобразования Пуанкаре связывают онтологические состояния не с другими онтологическими состояниями, а с суперпозициями онтологических состояний. Тем не менее, наличие или отсутствие симметрии не должно вызывать нашего непосредственного беспокойства. Мы можем, например, предположить, что только однородная часть группы Лоренца является подлинной симметрией на онтологическом уровне или, возможно, приблизительной симметрией.
Более важной особенностью специальной теории относительности является тот факт, что она ограничивает скорость распространения сигналов.Теперь это довольно легко наложить на модели или теории CA. Мы просто предполагаем, что в такт часам содержимое данной ячейки нашего автомата может быть передано только в соседнюю ячейку. Таким образом, сигналы никогда не могут распространяться быстрее скорости этого процесса. За пределами соответствующего светового конуса тогда гарантируется выполнение уравнения (3.1) «Телефон без звонка».
Как мы заявили в разделе 3, это единственное приемлемое условие причинности для физических моделей, как классических, так и квантовых.Это подразумевает, что временное упорядочение – это только частичное упорядочение – для пространственно-подобных разделенных событий временное упорядочение не имеет значения. Стрелка времени определяется как порядок, в котором уравнения для наших моделей (классический, квантовый, клеточный автомат теорий континуального поля) должны применяться в наших модельных симуляциях. Таким образом, релятивистские теории будут иметь такую же стрелу времени, как и нерелятивистские. Как мы подчеркивали в разделе 1. фундаментальное определение времени, а также его стрелка, могут быть применены только к нашим моделям Природы, но не к самим физическим данным.Это также относится к концепции причинности.
Трудность наложения симметрии Лоренца и Пуанкаре для моделей CA сохраняется, когда обратимость времени нарушается на онтологическом уровне, но модели, в которых скорость распространения информации ограничена, можно легко расширить до необратимости во времени. Это происходит почти автоматически.
C. Парадокс GHZ и 6-битная Вселенная
Существует много новых версий, обобщений и уточнений оригинальных экспериментов Gedanken, рассмотренных EPR и Bell.Иногда парадоксы связаны не только с вероятностями, но даже с определенностью, когда видны столкновения с «классической» физикой, но все они имеют общее то, что один или несколько наблюдателей выбирают между двумя или более различными настройками, которые измеряют свойства квантовых объектов, чьи операторы не ездят на работу.
Интересным случаем, в котором магическая тайна, кажется, достигает новых высот, является парадокс GHZ. Мы кратко резюмируем установку, которая более подробно описана в литературе [8, 7].
Источник сконструирован так, что он испускает три запутанных частицы, каждая из которых имеет два возможных спиновых состояния, ± 1. Произведенное квантовое состояние –
ψ = 12 (| +, +, +〉 – | -, -, -〉). (C1)Рассматриваются следующие операторы: σx, ya, b, c, где a, b и c относятся к трем частицам a, b и c и
. σxa | ±, ⋯〉 = | ∓, ⋯〉 σya | ±, ⋯〉 = ± i | ∓, ⋯〉 (C2), в то время как σx, yb и σx, yc действуют одинаково на частицу b и c соответственно.Нетрудно вывести, что эти операторы подчиняются
XXX≡ σxaσxbσxc = −1XYY ≡ σxaσybσyc = 1YXY ≡ σyaσxbσyc = 1YYX ≡ σyaσybσxc = 1. (C3)Три матрицы Паули σ i , действующие на одну и ту же частицу, антикоммутируют, σxa, σya = -σyaσxa, в то время как две матрицы Паули, действующие на разные частицы, коммутируют. Таким образом, получается, что если мы переставляем две пары σ-операторов в уравнении (C3), появляются два знака минус, что позволяет нам легко вывести, что все четыре оператора в уравнении (C3) коммутируют друг с другом.Следовательно, все операторы в уравнении (C3) могут быть измерены одновременно, и результат всегда подчиняется (C3).
Теперь три частицы отправляются трем разным наблюдателям, которые находятся в трех разных запечатанных комнатах. Каждый наблюдатель решает «по своему усмотрению» выбрать измерение либо X = σ x , либо Y = σ y . Наблюдатели не могут общаться друг с другом, поэтому они не знают, что выбирают другие.Они просто тщательно записывают, измеряют ли они X или Y , и каков их результат, +1 или -1. После долгой серии измерений они выходят из своих комнат и сравнивают записи.
Все наблюдатели в среднем обнаружили столько же плюсов, сколько минусов, потому что математические ожидания X = σ x и Y = σ y равны нулю. Кроме того, нет парной корреляции, поскольку для каждой пары ожидаемые значения для XX , XY , YX и YY также равны нулю.Но эти три наблюдения коррелированы: трехточечные корреляции, приведенные в уравнении (C3), очень сильны.
Более того, они кажутся противоречащими классической логике. Список наблюдений будет подчиняться (C3). Но при каждом запуске можно было бы спросить: что бы нашел этот наблюдатель, если бы он выбрал другую настройку или, в более общем плане, учитывая, что частица входит в его комнату, и он измеряет либо X , либо Y , каков был бы исход в любом случае? Поэтому мы добавляем в список наблюдений при каждом запуске все возможные ответы: XXX, XXY , ⋯, YYY .Теперь возьмем последние три уравнения (C3). Возьмите их продукт. Поскольку каждые Y встречаются в продукте ровно дважды, Y вместе всегда дают +1 в продукте. Остались три X s. Получаем XXX = +1. Но это неправильно, это нарушает первое уравнение уравнения (C3). Следует сделать вывод, что три запутанные частицы заранее знают, выберут ли их наблюдатели X или Y . По-видимому, наблюдения, которые фактически не проводились, вообще не имеют четко определенных значений для X или Y .Они называются контрфактами . Квантовая механика запрещает контрфактические наблюдения. Как это может произойти в клеточном автомате?
В этом случае анализ векторного пространства предполагает, что простая модель может быть построена для всей Вселенной. В этой вселенной всего 6 двоичных динамических переменных. Априори эта Вселенная могла начать выбирать любое из 2 6 = 64 различных начальных состояния.
Как и наша реальная вселенная, эта модельная вселенная, возможно, началась с Большого взрыва.На тот момент реализованы не все возможные состояния. Были разрешены только 48 из 64 начальных состояний. В период хаоса 48 состояний могли быть взломаны много раз, но есть 16 состояний, которые невозможно реализовать в любой момент. Так запрограммированы законы природы для модельной вселенной.
В начале эксперимента отбираются три частицы. Это три из 6 бит. Все они могут быть +1 или -1. Теперь у нас есть три наблюдателя: A, B и C .Каждый из них должен решить, выбрать ли X или Y . Каждый из них хватается за то, что может найти в своей комнате. Этот бит представляет их свободную волю. Это может быть что угодно, но его свойства определяются законами природы. Каждый наблюдатель знает, что вероятность того, что этот бит будет +1 или -1, будет равна, поэтому наблюдатели будут убеждены, что они действуют по доброй воле. Есть 2 3 = 8 возможных членов в последовательности XXX, YXX , ⋯, YYY .В 4 из них (где число Y s четное) существует ограничение: разрешены только 4 из 2 3 = 8 возможных ответов. Следовательно, 4 × 4 = 16 исходов запрещены. Вот что здесь говорят законы природы: из всех онтологических состояний 16 запрещены.
Таким образом, мы утверждаем, что классические законы природы в 6-битной Вселенной могут прекрасно воспроизводить «чудо» GHZ, но мы должны признать, что свободная воля наблюдателя контролируется законами природы в такой же степени, как и все другие явления.
Конечно, квантовые физики возражают, что это несправедливо: «вы использовали« ретро-причинность », чтобы установить свои законы природы». Что ж, точка зрения, представленная в основной части этой статьи, заключается в том, что законы природы обычно инвариантны относительно обращения времени, и это означает, что если полное состояние Вселенной известно в настоящее время, это также вызывает ограничения для разрешенных состояний. в прошлом, и отсюда наши ограничения. Мы просто не можем ожидать «совершенной» свободы воли в нашей Вселенной.Может быть, вы думаете, что это «заговор». Пусть так, но законы природы в нашем подходе в первую очередь классические.
графиков положения и времени: значение формы
Наше исследование одномерной кинематики было связано с множеством средств, с помощью которых может быть представлено движение объектов. К таким средствам относятся использование слов, использование диаграмм, использование чисел, использование уравнений и использование графиков. Урок 3 посвящен использованию графиков положения и времени для описания движения.Как мы узнаем, особенности движения объектов демонстрируются формой и наклоном линий на графике положения и времени. Первая часть этого урока включает изучение взаимосвязи между формой графика p-t и движением объекта.
Сравнение постоянной и изменяющейся скоростиДля начала представьте, что автомобиль движется с постоянной (+) скоростью вправо – скажем, +10 м / с.
Если бы данные о местоположении и времени для такой машины были нанесены на график, то получившийся график выглядел бы как график справа.Обратите внимание, что движение, описываемое как постоянная положительная скорость, приводит к линии с постоянным и положительным наклоном при построении графика положения-времени.
Теперь рассмотрим автомобиль, движущийся вправо (+) с изменяющейся скоростью, то есть автомобиль, который движется вправо, но ускоряется, или , ускоряясь .
Если бы данные о местоположении и времени для такой машины были нанесены на график, то получившийся график выглядел бы как график справа. Обратите внимание, что движение, описываемое как изменяющаяся, положительная скорость, приводит к линии изменения и положительному наклону, когда строится как график положения-времени.
Графики положения в зависимости от времени для двух типов движения – постоянной скорости и изменяющейся скорости (ускорения) – представлены следующим образом.
| Постоянная скорость Положительная скорость | Положительная скорость Изменение скорости (ускорение) |
|---|---|
Важность уклона
Формы графиков положения в зависимости от времени для этих двух основных типов движения – движения с постоянной скоростью и ускоренного движения (т.е., изменение скорости) – раскрывают важный принцип. Принцип состоит в том, что наклон линии на графике положения и времени раскрывает полезную информацию о скорости объекта. Часто говорят: «Чем больше наклон, тем больше и скорость». Независимо от характеристик скорости, наклон будет одинаковым (и наоборот). Если скорость постоянна, то наклон постоянный (т. Е. Прямая линия). Если скорость меняется, значит, меняется и крутизна (т. Е. Кривая линия). Если скорость положительная, то наклон положительный (т.е.е., двигаясь вверх и вправо). Сам этот принцип может быть распространен на любое мыслимое движение.
Сравнение медленного и быстрого движенияРассмотрим графики ниже как примеры применения этого принципа, касающегося наклона линии на графике положения в зависимости от времени. График слева представляет объект, который движется с положительной скоростью (обозначенной положительным наклоном), постоянной скоростью (обозначенной постоянным наклоном) и небольшой скоростью (обозначенной небольшим наклоном).График справа имеет аналогичные особенности – есть постоянная положительная скорость (обозначенная постоянным положительным наклоном). Однако наклон графика справа больше, чем слева. Этот больший наклон указывает на большую скорость. Объект, представленный графиком справа, движется быстрее, чем объект, представленный графиком слева. Принцип наклона может использоваться для извлечения соответствующих характеристик движения из графика зависимости положения от времени. Чем больше наклон, тем больше и скорость.
| Медленно, вправо (+) Постоянная скорость | Быстро, вправо (+) Постоянная скорость |
|---|---|
Рассмотрим графики ниже как еще одно применение этого принципа наклона. График слева представляет объект, который движется с отрицательной скоростью (обозначенной отрицательным наклоном), постоянной скоростью (обозначенной постоянным наклоном) и небольшой скоростью (обозначенной небольшим наклоном).График справа имеет аналогичные особенности – есть постоянная отрицательная скорость (обозначенная постоянным отрицательным наклоном). Однако наклон графика справа больше, чем слева. Еще раз, этот больший наклон указывает на большую скорость. Объект, представленный графиком справа, движется быстрее, чем объект, представленный графиком слева.
| Медленно, влево (-) Постоянная скорость | Быстро, влево (-) Постоянная скорость |
|---|---|
В качестве последнего применения этого принципа наклона рассмотрим два графика ниже.На обоих графиках нанесены точки, образующие изогнутую линию. Изогнутые линии имеют изменяющийся наклон; они могут начинаться с очень небольшого наклона и начинать резко изгибаться (вверх или вниз) к большому склону. В любом случае изогнутая линия изменения наклона является признаком ускоренного движения (т. Е. Изменения скорости). Применяя принцип наклона к графику слева, можно сделать вывод, что объект, изображенный на графике, движется с отрицательной скоростью (поскольку наклон отрицательный). Кроме того, объект начинает с небольшой скорости (наклон начинается с небольшого наклона) и заканчивается с большой скоростью (наклон становится большим).Это означало бы, что этот объект движется в отрицательном направлении и набирает скорость (малая скорость превращается в большую). Это пример отрицательного ускорения – движение в отрицательном направлении и ускорение. На графике справа также изображен объект с отрицательной скоростью (поскольку имеется отрицательный наклон). Объект начинается с высокой скорости (наклон изначально большой) и заканчивается с небольшой скоростью (поскольку наклон становится меньше). Итак, этот объект движется в отрицательном направлении и замедляется.Это пример положительного ускорения.
| Отрицательная (-) скорость От медленного к быстрому | Скорость влево (-) От быстрого к медленному |
|---|---|
Принцип наклона – невероятно полезный принцип для извлечения релевантной информации о движении объектов, описываемых графиком их положения в зависимости от времени. После того, как вы попрактикуетесь в этом принципе несколько раз, он станет очень естественным средством анализа графиков «позиция-время».
Расследовать! Виджет ниже отображает график положения и времени для объекта с заданными характеристиками. Верхний виджет отображает движение объекта, движущегося с постоянной скоростью. Нижний виджет отображает движение ускоряющегося объекта. Просто введите указанные значения, и виджет затем построит линию с положением на вертикальной оси и временем на горизонтальной оси. Обязательно обратите внимание на разницу между графиком постоянной скорости и графиком ускоренного движения.Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Graph That Motion или наших Graphs and Ramps Interactives. Каждый из них находится в разделе Physics Interactives нашего веб-сайта и позволяет учащемуся применять концепции кинематических графиков (как положение-время, так и скорость-время) для описания движения объектов. Проверьте свое понимание
Используйте принцип наклона для описания движения объектов, изображенных на двух графиках ниже. В описание не забудьте включить такую информацию, как направление вектора скорости (т.е. положительное или отрицательное), постоянная скорость или ускорение, а также то, движется ли объект медленно, быстро, от медленного к быстрому или от быстрого к медленному. Будьте полными в своем описании.
5.3 Замедление времени – Университетская физика, Том 3
Цели обучения
К концу этого раздела вы сможете:
- Объясните, как можно по-разному измерять временные интервалы в разных системах отсчета.
- Опишите, как отличить правильный временной интервал от растянутого временного интервала.
- Опишите значение мюонного эксперимента.
- Объясните, почему парадокс близнецов не противоречит.
- Вычислить замедление времени с учетом скорости объекта в заданном кадре.
Анализ одновременности показывает, что постулаты Эйнштейна подразумевают важный эффект: временные интервалы имеют разные значения при измерении в разных инерциальных системах отсчета. Предположим, например, что космонавт измеряет время, за которое световой импульс проходит расстояние, перпендикулярное направлению движения его корабля (относительно земного наблюдателя), отражается от зеркала и возвращается (рисунок 5.4). Как прошедшее время, которое астронавт измеряет в космическом корабле, сравнивается с прошедшим временем, которое измеряет наземный наблюдатель, наблюдая за тем, что происходит в космическом корабле?
Изучение этого вопроса приводит к глубокому результату. Затраченное время для процесса зависит от того, какой наблюдатель его измеряет. В этом случае время, измеренное космонавтом (в космическом корабле, где космонавт находится в состоянии покоя), меньше времени, измеренного наземным наблюдателем (к которому астронавт движется).Время, прошедшее для одного и того же процесса, для наблюдателей разное, потому что расстояние, которое проходит световой импульс в кадре космонавта, меньше, чем в кадре, привязанном к Земле, как показано на рисунке 5.4. Свет распространяется с одинаковой скоростью в каждом кадре, поэтому требуется больше времени, чтобы пройти большее расстояние в кадре, привязанном к Земле.
Фигура 5,4 (а) Астронавт измеряет время ΔτΔτ, за которое свет проходит расстояние 2 D в кадре космонавта. (b) Ученый НАСА на Земле видит, что свет движется по более длинному пути 2 s и занимает большее время Δt.Δt. (c) Эти треугольники используются для нахождения взаимосвязи между двумя расстояниями D и s .Замедление времени
Замедление времени – это удлинение временного интервала между двумя событиями для наблюдателя в инерциальной системе отсчета, который движется относительно системы покоя событий (в которой события происходят в одном и том же месте).
Чтобы количественно сравнить измерения времени в двух инерциальных системах отсчета, мы можем соотнести расстояния на Рисунке 5.4 друг к другу, затем выразите каждое расстояние через время прохождения (соответственно ΔtΔt или ΔτΔτ) импульса в соответствующей системе отсчета. Полученное уравнение затем может быть решено относительно ΔtΔt через Δτ.Δτ.
Длины D и L на рисунке 5.4 являются сторонами прямоугольного треугольника с гипотенузой s . Из теоремы Пифагора,
Длины 2 s и 2 L представляют собой, соответственно, расстояния, на которые импульс света и космический корабль проходят за время ΔtΔt в системе отсчета земного наблюдателя.Длина D – это расстояние, которое световой импульс проходит за время ΔτΔτ в кадре космонавта. Это дает нам три уравнения:
2s = cΔt; 2L = vΔt; 2D = cΔτ. 2s = cΔt; 2L = vΔt; 2D = cΔτ.Обратите внимание, что мы использовали второй постулат Эйнштейна, приняв скорость света равной c в обеих инерциальных системах отсчета. Подставляем эти результаты в предыдущее выражение из теоремы Пифагора:
s2 = D2 + L2 (cΔt2) 2 = (cΔτ2) 2+ (vΔt2) 2. s2 = D2 + L2 (cΔt2) 2 = (cΔτ2) 2+ (vΔt2) 2.Затем переставляем, чтобы получить
(cΔt) 2− (vΔt) 2 = (cΔτ) 2.(cΔt) 2− (vΔt) 2 = (cΔτ) 2.Наконец, решение для ΔtΔt через ΔτΔτ дает
Δt = Δτ1− (v / c) 2.Δt = Δτ1− (v / c) 2.5.1
Это эквивалент
, где γγ – релятивистский фактор (часто называемый фактором Лоренца), определяемый как
γ = 11 − v2c2γ = 11 − v2c25.2
и v и c – скорости движущегося наблюдателя и света соответственно.
Обратите внимание на асимметрию между двумя измерениями. Только одно из них – измерение временного интервала между двумя событиями – излучением и приходом светового импульса – в одно и то же место.Это измерение временного интервала в кадре покоя отдельных часов. Измерение в наземном кадре включает сравнение временного интервала между двумя событиями, происходящими в разных местах. Временной интервал между событиями, происходящими в одном месте, имеет отдельное название, чтобы отличать его от времени, измеренного наземным наблюдателем, и мы используем отдельный символ ΔτΔτ для его обозначения в этой главе.
Подходящее время
Собственный временной интервал ΔτΔτ между двумя событиями – это временной интервал, измеренный наблюдателем, для которого оба события происходят в одном и том же месте.
Уравнение, связывающее ΔtΔt и ΔτΔτ, составляет поистине замечательно. Во-первых, как указывалось ранее, истекшее время не одинаково для разных наблюдателей, движущихся относительно друг друга, даже если оба находятся в инерциальных системах отсчета. Собственный интервал времени ΔτΔτ для наблюдателя, который, как и космонавт, движется вместе с аппаратом, меньше, чем интервал времени для других наблюдателей. Это наименьшее возможное время между двумя событиями. Приближающийся к Земле наблюдатель видит временные интервалы в движущейся системе как расширенные (т.е., удлинены) относительно того, как движущийся относительно Земли наблюдатель видит их в движущейся системе. В качестве альтернативы, по мнению наземного наблюдателя, меньше времени проходит между событиями в движущейся системе отсчета. Обратите внимание, что самое короткое время между событиями находится в инерциальной системе отсчета, в которой наблюдатель видит, что события (например, испускание и прибытие светового сигнала) происходят в одной и той же точке.
Этот временной эффект реален и не вызван неточными часами или неправильными измерениями.Измерения одного и того же события во временном интервале различаются для наблюдателей, находящихся в относительном движении. Замедление времени – это внутреннее свойство самого времени. Все часы, движущиеся относительно наблюдателя, включая биологические часы, такие как биение сердца человека или старение, наблюдаются медленнее по сравнению с часами, которые неподвижны относительно наблюдателя.
Обратите внимание, что если относительная скорость намного меньше скорости света (v << c), (v << c), то v2 / c2v2 / c2 чрезвычайно мало, а прошедшие времена ΔtΔt и ΔτΔτ почти равны.При низких скоростях физика, основанная на современной теории относительности, приближается к классической физике - повседневный опыт включает очень небольшие релятивистские эффекты. Однако для скоростей, близких к скорости света, v2 / c2v2 / c2 близко к единице, поэтому 1-v2 / c21-v2 / c2 очень мало, и ΔtΔt становится значительно больше, чем Δτ.Δτ.
Период полураспада мюона
Имеется значительное экспериментальное свидетельство того, что уравнение Δt = γΔτΔt = γΔτ является правильным. Один из примеров – частицы космических лучей, которые непрерывно падают на Землю из глубокого космоса.Некоторые столкновения этих частиц с ядрами в верхних слоях атмосферы приводят к образованию короткоживущих частиц, называемых мюонами. Период полураспада (время, в течение которого половина материала распадается) мюона составляет 1,52 мкс, когда он находится в состоянии покоя относительно наблюдателя, который измеряет период полураспада. Это собственный временной интервал Δτ.Δτ. Это короткое время позволяет очень небольшому количеству мюонов достичь поверхности Земли и быть обнаруженным, если ньютоновские предположения о времени и пространстве были правильными. Однако мюоны, производимые частицами космических лучей, имеют диапазон скоростей, причем некоторые из них движутся со скоростью, близкой к скорости света.Было обнаружено, что период полураспада мюона, измеренный наземным наблюдателем (ΔtΔt), изменяется со скоростью точно так, как предсказывается уравнением Δt = γΔτ.Δt = γΔτ. Чем быстрее движется мюон, тем дольше он живет. Мы на Земле видим, что мюон живет намного дольше, чем предсказывает его период полураспада в пределах его собственной системы покоя. Если смотреть с нашего кадра, мюон распадается медленнее, чем в состоянии покоя относительно нас. В результате на землю попадает гораздо большая часть мюонов.
Прежде чем мы представим первый пример решения проблемы относительности, мы сформулируем стратегию, которую вы можете использовать в качестве руководства для этих вычислений.
Стратегия решения проблем
Относительность
- Составьте список того, что дано или может быть выведено из проблемы, как указано (определите известные). В частности, ищите информацию об относительной скорости v .
- Точно определите, что необходимо определить в проблеме (определите неизвестные).
- Убедитесь, что вы понимаете концептуальные аспекты проблемы, прежде чем производить какие-либо вычисления (выразите ответ в виде уравнения).Решите, например, какой наблюдатель видит увеличенное время или сокращенную длину, прежде чем работать с уравнениями или использовать их для выполнения вычислений. Если вы задумались о том, кто что видит, кто движется вместе с наблюдаемым событием, кто видит правильное время и т. Д., Вам будет намного легче определить, обоснован ли ваш расчет.
- Определите основной тип расчета, который необходимо выполнить, чтобы найти неизвестные, указанные выше (выполните расчет). Краткое содержание раздела поможет вам определить, задействовано ли сокращение длины, релятивистская кинетическая энергия или какое-либо другое понятие.
Обратите внимание на , которое не следует округлять при вычислении . Как отмечено в тексте, вам часто приходится выполнять вычисления с использованием многих цифр, чтобы увидеть желаемый эффект. Вы можете округлить решение проблемы в самом конце, но не используйте округленное число в последующих вычислениях. Также проверьте ответ, чтобы увидеть, разумен ли он: имеет ли он смысл? Это может быть труднее для теории относительности, у которой есть несколько повседневных примеров, чтобы дать опыт того, что является разумным.Но вы можете искать скорости выше c или релятивистские эффекты, которые имеют неправильное направление (например, сокращение времени, когда ожидалось замедление).
Пример 5.1
Замедление времени в высокоскоростном транспортном средстве
Hypersonic Technology Vehicle 2 (HTV-2) – экспериментальная ракетная машина, способная двигаться со скоростью 21 000 км / ч (5830 м / с). Если электронные часы в HTV-2 измеряют временной интервал длительностью ровно 1 с, что бы наблюдатели на Земле измерили бы этот временной интервал?Стратегия
Примените формулу замедления времени, чтобы связать собственный временной интервал сигнала в HTV-2 с временным интервалом, измеренным на земле.Решение
- Определите известные: Δτ = 1 с; v = 5830 м / с. Δτ = 1 с; v = 5830 м / с.
- Определите неизвестное: Δt.Δt.
- Выразите ответ в виде уравнения: Δt = γΔτ = Δτ1 − v2c2.Δt = γΔτ = Δτ1 − v2c2.
- Сделайте расчет. Используйте выражение для γγ, чтобы определить ΔtΔt из ΔτΔτ: Δt = 1s1- (5830м / с3.00 × 108м / с) 2 = 1.000000000189s = 1s + 1.89 × 10−10s.Δt = 1s1- (5830m / s3.00 × 108м / с) 2 = 1.000000000189s = 1s + 1,89 × 10–10 с.
Значение
Очень высокая скорость HTV-2 все еще всего в 10 -5 раз больше скорости света.Релятивистские эффекты для HTV-2 пренебрежимо малы почти для всех целей, но не равны нулю.Пример 5.2
Какие скорости релятивистские?
Насколько быстро должно двигаться транспортное средство в течение 1 секунды времени, измеренного на часах пассажира в транспортном средстве, чтобы отличаться на 1% для наблюдателя, измеряющего его с земли снаружи?Стратегия
Используйте формулу замедления времени, чтобы найти v / c для данного отношения времен.Решение
- Определите известные: ΔτΔt = 11.01.ΔτΔt = 11.01.
- Определите неизвестное: v / c .
- Выразите ответ в виде уравнения: Δt = γΔτ = 11 − v2 / c2ΔτΔτΔt = 1 − v2 / c2 (ΔτΔt) 2 = 1 − v2c2vc = 1− (Δτ / Δt) 2.Δt = γΔτ = 11 − v2 / c2ΔτΔτΔt = 1 − v2 / c2 (ΔτΔt ) 2 = 1 − v2c2vc = 1− (Δτ / Δt) 2.
- Сделайте расчет: vc = 1- (1 / 1,01) 2 = 0,14. vc = 1- (1 / 1,01) 2 = 0,14.
Значение
Результат показывает, что объект должен двигаться со скоростью примерно 10% от скорости света, чтобы его движение привело к значительным эффектам релятивистского замедления времени.Пример 5,3
Расчет ΔtΔt для релятивистского события
Предположим, космический луч, сталкиваясь с ядром в верхних слоях атмосферы Земли, производит мюон со скоростью v = 0,950c. V = 0,950c. Затем мюон движется с постоянной скоростью и живет 2,20 мкс, как измерено в системе отсчета мюона. (Вы можете представить это как внутренние часы мюона.) Как долго живет мюон по данным наблюдателя, находящегося на Земле (рис. 5.5)?Фигура 5.5 Мюон в атмосфере Земли живет дольше, если судить по наземным наблюдателям, чем по внутренним часам мюона.
Как мы обсудим позже, в системе отсчета мюон проходит меньшее расстояние, чем измеряется в системе отсчета Земли.
Стратегия
Часы, движущиеся вместе с мюоном, измеряют собственное время процесса его распада, поэтому время, которое нам дано, равно Δτ = 2,20 мкс, Δτ = 2,20 мкс. Приближенный к Земле наблюдатель измеряет ΔtΔt по формуле Δt = γΔτ.Δt = γΔτ. Поскольку скорость задана, мы можем рассчитать время в системе отсчета Земли.Решение
- Определите известные: v = 0.950c, Δτ = 2,20 мкс, v = 0,950c, Δτ = 2,20 мкс.
- Определите неизвестное: Δt.Δt.
- Выразите ответ в виде уравнения. Использовать: с участием γ = 11 − v2c2.γ = 11 − v2c2.
- Сделайте расчет. Используйте выражение для γγ, чтобы определить ΔtΔt из ΔτΔτΔt = γΔτ = 11 − v2c2Δτ = 2,20 мкс1- (0,950) 2 = 7,05 мксек Δt = γΔτ = 11 − v2c2Δτ = 2,20 мкс1- (0,950) 2 = 7,05 мкс. Не забудьте сохранить лишние значащие цифры до окончательного ответа.
Значение
Одним из следствий этого примера является то, что поскольку γ = 3,20, γ = 3,20 при 95.0% скорости света (v = 0,950c), (v = 0,950c), релятивистские эффекты значительны. Эти два временных интервала различаются в 3,20 раза, тогда как классически они были бы одинаковыми. Что-то, движущееся на 0,950 c , считается в высшей степени релятивистским.Пример 5,4
Релятивистское телевидение
Телевизионный дисплей старого образца с неплоским экраном (рис. 5.6) работает, ускоряя электроны на коротком расстоянии до релятивистской скорости, а затем используя электромагнитные поля для управления местом попадания электронного луча на флуоресцентный слой на передней части трубки.Предположим, что электроны движутся со скоростью 6,00 × 107 м / с и 6,00 × 107 м / с на расстоянии 0,200 м 0,200 м от начала луча до экрана. а) Сколько времени проходит электрон в неподвижном кадре телевизора? (б) Каково время путешествия электрона в собственной системе покоя?Фигура 5,6 Электронный луч в телевизионном дисплее с электронно-лучевой трубкой.
Стратегия для (а)
(a) Вычислите время по формуле vt = d.vt = d. Несмотря на то, что скорость является релятивистской, расчет полностью ведется в одной системе отсчета, и поэтому теория относительности не задействована.Решение
- Определите известные: v = 6,00 × 107 м / с; d = 0,200 м. v = 6,00 × 107 м / с; d = 0,200 м.
- Определите неизвестное: время в пути Δt.Δt.
- Выразите ответ в виде уравнения:
- Сделайте расчет: t = 0,200 м 6,00 × 107 м / с = 3,33 × 10–9 с. t = 0,200 м 6,00 × 107 м / с = 3,33 × 10–9 с.
Значение
Как и ожидалось, время в пути очень короткое. Поскольку расчет полностью находится в единой системе отсчета, теория относительности не задействована, хотя скорость электронов близка к c .Стратегия для (b)
(б) В системе отсчета электрона вакуумная трубка движется, а электрон неподвижен. Катод, излучающий электроны, покидает электрон, и передняя часть вакуумной лампы ударяет электрон с электроном в том же месте. Поэтому мы используем формулу замедления времени, чтобы связать собственное время в системе покоя электрона со временем в телевизионном кадре.Решение
- Определите известные (из части а): Δt = 3,33 × 10–9 с; v = 6.00 × 107 м / с; d = 0,200 м. Δt = 3,33 × 10-9 с; v = 6,00 × 107 м / с; d = 0,200 м.
- Опознайте неизвестное: τ.τ.
- Выразите ответ в виде уравнения: Δt = γΔτ = Δτ1 − v2 / c2Δτ = Δt1 − v2 / c2.Δt = γΔτ = Δτ1 − v2 / c2Δτ = Δt1 − v2 / c2.
- Сделайте расчет: Δτ = (3,33 × 10–9 с) 1– (6,00 × 107 м / с3,00 × 108 м / с) 2 = 3,26 × 10–9 с. Δτ = (3,33 × 10–9 с) 1– (6,00 × 107 м / с3. 00 × 108 м / с) 2 = 3,26 × 10–9 с.
Значение
Время путешествия короче в электронной системе отсчета. Поскольку задача требует нахождения временного интервала, измеренного в разных системах отсчета для одного и того же процесса, задействуется теория относительности.Если бы мы попытались вычислить время в системе покоя электрона, просто разделив 0,200 м на скорость, результат был бы немного неверным из-за релятивистской скорости электрона.Проверьте свое понимание 5.2
Что такое γγ, если v = 0,650c? V = 0,650c?
Парадокс близнецов
Интригующее последствие замедления времени состоит в том, что космический путешественник, движущийся с высокой скоростью относительно Земли, стареет меньше, чем привязанный к Земле близнец астронавта.Это часто называют парадоксом близнецов. Представьте космонавта, движущегося с такой скоростью, что γ = 30,0, γ = 30,0, как показано на рисунке 5.7. Путешествие, которое в ее структуре занимает 2,00 года, в ее структуре земного близнеца займет 60,0 лет. Предположим, астронавт путешествует 1,00 год в другую звездную систему, ненадолго исследует местность, а затем возвращается на 1,00 год назад. Астронавту, которому в начале полета было 40 лет, будет 42, когда космический корабль вернется. Однако всему миру было бы 60 лет.0 лет. Прикованному к Земле близнецу, если бы он был жив, было бы 100 лет.
Ситуация может показаться космонавту другой, изображенной на рис. 5.7. Поскольку движение относительное, космический корабль кажется неподвижным, а Земля движется. (Это ощущение, которое вы испытываете при полете на реактивном самолете.) Глядя в окно космического корабля, астронавт увидел бы, что время на Земле замедляется с коэффициентом γ = 30.0.γ = 30.0. Если смотреть с космического корабля, земному брату будет всего 2/30, или 0 лет.07 года, тогда как астронавту было бы 2,00 года.
Фигура 5,7 Парадокс близнецов состоит из противоречивых выводов о том, какой из близнецов стареет больше в результате долгого космического путешествия с релятивистской скоростью.
Парадокс здесь в том, что оба близнеца не могут быть правильными. Как и во всех парадоксах, противоречивые выводы приходят из ложной предпосылки. Фактически, движение космонавта значительно отличается от движения близнеца, привязанного к Земле. Астронавт разгоняется до высокой скорости, а затем ускоряется, противоположно движению, чтобы увидеть звездную систему.Чтобы вернуться на Землю, она снова ускоряется и замедляется. Космический аппарат не находится в единой инерциальной системе отсчета, к которой можно было бы напрямую применить формулу замедления времени. То есть двойник-космонавт меняет инерциальные ориентиры. Связанный с землей близнец не испытывает этих ускорений и остается в той же инерциальной системе отсчета. Таким образом, ситуация не является симметричной, и неверно утверждать, что космонавт наблюдает те же эффекты, что и ее близнец. Отсутствие симметрии между близнецами станет еще более очевидным, когда мы проанализируем путешествие позже в этой главе с точки зрения пути, по которому астронавт следует в четырехмерном пространстве-времени.
В 1971 году американские физики Джозеф Хафеле и Ричард Китинг подтвердили замедление времени при малых относительных скоростях, запустив чрезвычайно точные атомные часы по всему миру на коммерческих самолетах. Они измерили прошедшее время с точностью до нескольких наносекунд и сравнили его со временем, измеренным оставленными часами. Результаты Хафеле и Китинга находились в пределах экспериментальной неопределенности предсказаний теории относительности. Необходимо было принять во внимание как специальную, так и общую теорию относительности, потому что в них участвовали гравитация и ускорения, а также относительное движение.
Проверьте свое понимание 5,3
а. Частица движется со скоростью 1,90 × 108 м / с и 1,90 × 108 м / с и живет 2,10 × 10–8 с2,10 × 10–8 с в состоянии покоя относительно наблюдателя. Как долго живет частица, если смотреть в лаборатории?
г. Космические аппараты A, и B проходят в противоположных направлениях с относительной скоростью 4,00 × 107 м / с. 4,00 × 107 м / с. Внутренние часы в космическом корабле A заставляют его излучать радиосигнал в течение 1,00 с. Компьютер в космическом корабле B корректирует начало и конец сигнала, пройдя разные расстояния, чтобы вычислить временной интервал, в течение которого корабль A излучал сигнал.Какой временной интервал вычисляет компьютер космического корабля B ?
Почему время относительное, объяснение менее чем за 3 минуты
Одна из самых революционных концепций, которые мы усвоили в 20 веке, заключается в том, что время не является универсальным измерением.
Неважно, насколько наша жизнь управляется одними и теми же секундами, минутами, часами, днями и неделями, независимо от того, где мы живем на земном шаре, время никогда не будет абсолютным.Скорость, с которой он проходит, полностью зависит от вашей скорости и ускорения в любой момент.
Но как именно время может быть медленнее и быстрее одновременно?
Как объясняется в последнем выпуске MinutePhysics, скорость, с которой проходит время, фактически замедляется, чем больше вы двигаетесь.
И я не говорю о вашем восприятии времени, которое, как показывают недавние исследования, на самом деле ускоряется благодаря избытку технологий в нашей жизни.Я говорю о скорости реального времени, которая, как показывают многочисленные эксперименты, замедляется, когда частицы, такие как мюоны и фотоны, ускоряются.
В теории относительности Эйнштейна замедление времени описывает разницу в прошедшем времени между двумя событиями, измеренную наблюдателями, которые либо движутся относительно друг друга, либо по-разному, в зависимости от их близости к гравитационной массе. По сути, он гласит, что чем быстрее мы идем, тем больше влияет на время.
Но если время настолько относительное, как это предполагает, оно может показаться немного противоречивым.
Как указывает Генри из MinutePhysics, представьте, что мы вдвоем пробираемся сквозь пустоту космоса в противоположных направлениях, а затем внезапно проходим друг друга.
«С моей точки зрения кажется, что вы двигаетесь, и поэтому время должно идти для вас медленнее, но с вашей точки зрения, похоже, что я двигаюсь, поэтому для меня это должно идти медленнее», – он говорит.
Итак, как мы можем думать, что время для другого человека течет медленнее? У кого-то время должно быть на самом деле медленнее, не так ли?
Ну нет, извините.Хотелось бы, чтобы все было так просто.
Объяснение связано с тем, как вы поворачиваете само направление времени каждый раз, когда меняете скорость. Да, вы меняете время каждый день, как будто это нбд, так что поздравляю.
Посмотрите видео выше, чтобы получить самое быстрое и потрясающее объяснение странностей замедления времени, и оставайтесь до конца, чтобы получить аккуратную маленькую головоломку, которая могла бы связать узлов даже лучших из нас. Наслаждаться.
Развитие знаний внутри и между областями современной физики
Области современной физики
Общее представление об основных областях современной физики можно получить путем базового анализа характеристик наборов данных APS.Рассматриваемые на самом высоком уровне, коды PACS делят современную физику на десять основных областей (см. Таблицу 1). Затем показатель релевантности каждой области может быть получен из объема статей, опубликованных в каждой области. Поскольку каждая статья может быть указана с несколькими кодами PACS, мы назначаем ее нескольким полям. Поэтому мы рассматриваем каждую статью как одну единицу знаний и определяем состав поля статьи как относительную частоту ее кодов PACS. Например, если статья указана с тремя кодами PACS \ ({\ textit {89.75.-k}} \), \ ({\ textit {81.05.-t}} \) и \ ({\ textit {05.45.-a}} \), мы относим две трети этой статьи к междисциплинарной Physics (PACS 80), а оставшаяся треть – General Physics (PACS 00). Общее количество статей \ (N_ {paper} \), связанных с каждым полем за весь период времени в 31 год, указано в таблице 1. Видно, что тремя самыми большими полями являются Condensed Matter (PACS 60 и 70). и General Physics (PACS 00), охватывающая \ (57 \% \) всех публикаций в журналах APS. GPE – самое маленькое поле, всего 8325 листов, что примерно составляет одну пятнадцатую размера самого большого поля CM 2. Для количественной оценки и сравнения темпов роста каждого поля среднее ежегодное изменение количества статей \ (\ Delta N_ {paper} \) также приводится в таблице 1. В соответствии с рейтингом, основанным на размерах полей, GEN и CM 2 также демонстрируют самые высокие темпы роста, более 100 статей в год, в то время как GPE показывает самый медленный рост, в среднем всего 5 статей в год.Напротив, CM 2, третье по величине поле по размеру, занимает четвертое снизу по среднему росту \ (\ Delta N_ {paper} \). Противоположная тенденция наблюдается для Interdisciplinary Physics и Astrophysics , которые соответственно занимают пятое и шестое места по темпам роста, хотя их размеры поля занимают восьмое и девятое место среди этих полей, что отражает их быстрое развитие в течение периода наблюдений.
Мы обнаружили, что \ (91 \% \) статей содержат более одного кода PACS, причем \ (36 \% \) из них сообщают коды PACS, которые взяты как минимум из двух разных полей.Чтобы количественно оценить уровень междисциплинарности данной области, мы собрали все статьи, содержащие хотя бы один код PACS из этого поля, а затем вычислили долю J этих статей, которые также классифицируются по крайней мере одним кодом PACS по сравнению с другими. поля. Результаты в таблице 1 показывают, что Междисциплинарная физика – это область с наибольшим значением Дж. : почти \ (90 \% \) статей по междисциплинарной физике также классифицируются кодами PACS из других областей физики.Этот результат согласуется с ожиданием того, что междисциплинарные исследования объединяют знания из различных дисциплин. Вместо этого в работах по физике Nuclear , Particles и Condensedatter 2 физики с большей вероятностью будут использоваться коды PACS из их собственных областей. Подводя итог, можно сказать, что приведенный выше анализ показывает, что различия между областями физики значительны либо с точки зрения размера и роста полей, либо с точки зрения их взаимодействия с другими полями.
Таблица 1 Десять областей современной физики.Сеть потока знаний
Взаимодействие между научными областями можно лучше охарактеризовать, используя научные цитаты. Опубликованная статья в научной области, цитирующая статьи из другой области, подразумевает, что цитируемая область отражает часть ранее существовавших знаний, на которых строится область цитирования. А это, в свою очередь, указывает на поток знаний из цитируемой области в область цитирования. Следовательно, мы можем построить сеть потока знаний в разных областях, анализируя схему цитирования статей в разных областях.Узлы такой сети представляют десять областей современной физики, как указано кодами PACS, в то время как направленные связи между полями обозначают потоки знаний из одной области физики в другую.
Рисунок 1Сеть потока знаний и ее эволюция во времени. ( a ) Иллюстрация того, как цитирование между двумя статьями преобразуется в вклад в поток знаний между двумя соответствующими областями. ( b ) Построение взвешенной сети потока знаний на основе значимости каждой ссылки.( c ) Сеть потоков знаний между различными областями физики в 1990, 2000 и 2010 годах. Размеры узлов пропорциональны количеству статей, опубликованных в каждой области и заданному году, а ширина линий соответствует весам потоков знаний. между двумя полями. {\ Delta t ‘\ rightarrow t} = \ frac {1} {\ vert \ Delta t’ \ vert} \ sum _ {n \ in \ Delta t ‘} {\ phi (\ alpha _ {tn}, \ beta _ { t})} \ end {align} $$
(2)
где \ (\ vert \ Delta t ‘\ vert \) – длина временного окна.{\ Delta t ‘\ rightarrow t} \ end {align} $$
(3)
Например, пусть \ (\ vert \ Delta t \ vert = 5 \), мы можем разделить весь период времени на пять временных окон наблюдения, а именно [1990, 1994], [1995, 1999], [2000, 2004 ], [2005, 2009] и [2010, 2014]. Вес каждой ссылки в сети отражает, насколько значительны знания между двумя связанными областями. Эта количественная структура позволяет нам исследовать эволюцию потоков знаний в двух временных измерениях: (1) для каждого заданного периода наблюдения \ (\ Delta t \) веса знаний поступают из разных временных интервалов \ (\ Delta t ‘\) можно наблюдать; а также (2) для каждого фиксированного \ (\ Delta t ‘\) можно сравнить веса потоков знаний в течение различных периодов наблюдения \ (\ Delta t \).Хотя в этой статье мы изучали потоки знаний в десяти основных областях физики, мы полагаем, что наша структура также может предоставить важную информацию при применении для исследования передачи знаний между подполями на любом возможном уровне иерархии.
Временной анализ сетей потоков знаний
Сначала мы исследуем, как общие свойства сетей потоков знаний менялись с течением времени. В частности, мы оценивали для каждого года потоки знаний за предыдущие 5 лет, т.е.{\ Delta t ‘\ rightarrow t}> 1 \)) показаны красным цветом.
Рисунок 2Временной анализ сетей потоков знаний. ( a ) Количество важных звеньев в сети потока знаний показано как функция года вместе со средним значением времени, обозначенным пунктирной серой линией. ( b ) Сетевая взаимность, измеряющая долю двунаправленных ссылок, показывает образец с пиком около 1998 года. Верхние \ (50 \% \) двунаправленных ссылок с наибольшей суммой взаимных весов учитывались при вычислении взаимность.( c ) Z-оценка двух типов трехузловых мотивов представлена как функция времени. ( d ) Среднее и стандартное отклонение весов значимых связей со временем постепенно уменьшаются, указывая на то, что потоки знаний между полями больше склоняются к случайным ожиданиям.
Первое, на что следует обратить внимание, это то, что количество значимых звеньев примерно постоянно в течение многих лет, как также показано на рис. 2а. В дополнение к этому, мы наблюдаем, что в 2000 г. наблюдается больше взаимных связей по сравнению с 1990 и 2010 гг., Что говорит о том, что ситуация, в которой пары полей взаимно влияют друг на друга, более распространена в 2000 г.Для дальнейшего изучения этого мы вычислили взаимность сети (см. Раздел «Методы») для каждого года. Результаты, представленные на рис. 2b, показывают, что значение взаимности \ (\ rho \) увеличилось в первые несколько лет, достигло пика примерно в 1998 году, а затем начало снижаться в последующие годы. Это привело нас к выводу, что наивысшие уровни взаимности в передаче знаний между различными областями физики наблюдались между 1995 и 2000 годами.
Затем мы извлекли типичные шаблоны передачи знаний в сети.По этой причине мы сосредоточились на статистически значимых трехузловых мотивах в сетях потока знаний 36 , то есть на направленных связанных подграфах трех узлов, которые появляются в сети чаще, чем случайно. На рисунке 2c показаны Z-баллы (см. Раздел «Методы») двух релевантных трехузловых мотивов за разные годы. Видно, что подграф, представленный двунаправленными путями (ромбовидный символ), является наиболее значимым мотивом на протяжении всего периода времени со средним Z-баллом, равным примерно 6.Кроме того, полные подграфы трех узлов, соответствующие трем взаимосвязанным областям физики, являются статистически значимыми только в период с 1998 по 2000 год, когда появляется полный подграф GEN , EOA и IPR . Обратите внимание, что этот период также соответствует периоду высокой взаимности на рис. 2b.
Кроме того, на рис. 1c показано, что в 2010 г. было меньше связей с большими весами, чем в 1990 и 2000 гг. Для дальнейшего исследования этой тенденции на рис.2d отчеты означают \ (\ overline {w} \) и стандартное отклонение \ (\ sigma _w \) весов значимых связей между 1990 и 2016 годами. Мы обнаружили, что оба значения \ (\ overline {w} \) и \ (\ sigma _ {w} \) постепенно уменьшаются с течением времени и в конечном итоге стабилизируются до значений чуть выше 1 и 0 соответственно. Это указывает на то, что обмен знаниями между областями становится все более однородным по сравнению с началом 1980-х годов, когда каждая область вбирала знания только из горстки близких областей.{\ Delta t ‘\ rightarrow t} \) от поля \ (\ alpha \) к самому себе являются показателем степени самостоятельности области исследования. Чтобы исследовать эволюцию внутренних потоков знаний, мы вычислили для каждой из десяти областей физики веса внутренних потоков в каждый год наблюдений t (между 1990 и 2015 годами) для каждого из предыдущих 5 лет, а именно принятие указанного временного окна \ (\ Delta t ‘= [1,5] \). {\ Delta t ‘\ rightarrow t}> 1 \)) для всех десяти полей за весь 21-летний период времени. , хотя временные тренды могут варьироваться от месторождения к полю.Два поля с наибольшими вариациями: GAA и GPE . Поле GAA демонстрирует заметное снижение степени самореференции после 1993 года, указывая на то, что в этой области внутренняя передача знаний со временем становится все менее и менее значимой. Напротив, поле GPE демонстрирует тенденцию к увеличению и становится наиболее самореференциальным полем после 1995 года. Другие поля демонстрируют убывающие ( EOA и IPR ) или возрастающие ( NUC и ATM ) паттерны, в то время как вклад внутренних потоков относительно низки и остаются почти постоянными для таких полей, как GEN , CM1 и CM2 .
На рис. 3b – e мы фокусируемся на эволюции внутренних потоков четырех месторождений EPF , NUC , IPR и GAA . В частности, мы выполняем двухмерный анализ, в котором мы изменяем положения как временных окон наблюдения \ (\ Delta t \), так и временного окна источника \ (\ Delta t ‘\). {\ Delta t ‘\ rightarrow \ Delta t} \).Глядя на вариации цветов в каждой строке, мы обнаруживаем, что поле NUC показывает все более высокую степень самореферентности с течением времени, в то время как IPR и GAA имеют тенденцию снижать степень своих внутренних потоков, что согласуется с результаты на рис. 3а.
Рассматривая изменение цветов в каждом столбце рис. 3b – e, мы можем вместо этого исследовать влияние возраста референта на внутренние потоки знаний. Можно видеть, что такие поля, как NUC и IPR , демонстрируют тенденцию к снижению от самого недавнего времени к прошлому, что согласуется с предыдущими исследованиями, утверждающими, что вероятность обнаружения бумаги значительно уменьшается с возрастом документов 37 .Напротив, мы наблюдаем неожиданную и очень четкую картину для EPF и GAA , поскольку оба поля показывают максимум значений вдоль антидиагональной линии. Обратите внимание, что каждый квадрат вдоль антидиагональной линии представляет одно и то же указанное временное окно, а именно временное окно за 5 лет до периода [1990, 1994]. Это может быть связано с важными открытиями и публикацией новаторских исследовательских работ в областях EPF и GAA в течение периода [1985, 1990], что явно повысило бы вероятность цитирования исследователями в этой области в последующие годы. , статьи, опубликованные в этот период.Возможным объяснением может быть, например, быстрое развитие в период [1985, 1989] новой области исследований « астрономия частиц », возникшей на стыке физики элементарных частиц, астрономии и астрофизики 38 , и которая в основном объединяет знания из полей EPF и GAA . В качестве доказательства этого быстрого развития обратите внимание на то, что в 1992 году был основан даже новый журнал под названием «Astroparticle Physics». Более того, тот факт, что веса внутренних потоков в GAA почти в три раза больше, чем в EPF , может быть связано с космическим телескопом Хаббла, одним из главных научных достижений в области GAA .Телескоп является одним из крупнейших и наиболее продуктивных инструментов научных исследований в области астрономии, и он действительно был запущен в 1990 году (в период интереса к антидиагональной линии), что значительно способствовало развитию астрономии в GAA . Мы дополнительно изучили эволюцию внутренних потоков для оставшихся шести полей и обнаружили аналогичные закономерности (см. Дополнительную информацию (SI)).
Эволюция знаний в разных областях
Изучение того, как открытия в одной области повлияли на другую область физики, даже более важно, чем изучение потоков знаний в данной области.Чтобы получить общую картину существующих влияний в различных областях современной физики, мы приводим на рис. 4а средние веса потоков знаний между каждой парой областей за весь исследуемый период. Чтобы выделить взаимный обмен потоками, результаты показаны в виде (\ (\ overline {w} _ {\ alpha \ rightarrow \ beta} \)) – (\ (\ overline {w} _ {\ beta \ rightarrow \ альфа} \)) самолет. Каждая точка относится к паре полей, а расстояние от положения точки до биссектрисы (красная линия) измеряет уровень асимметрии в обмене знаниями между двумя полями.Мы замечаем, что большинство точек сосредоточено вокруг биссектрисы, особенно те точки в нижнем левом углу, соответствующие парам полей с небольшими весами значимости. Однако есть также точки, расположенные далеко от линии, например, точка, соответствующая паре GPE и ATM (красный треугольник вверх в правом нижнем углу панели), что указывает на асимметричную передачу знаний между двумя полями.
Рисунок 3Эволюция потоков знаний внутри области.{\ Delta t ‘\ rightarrow t} \) из окна предыдущих 5 лет до t . В ( b ) – ( e ) мы показываем эволюцию внутренних потоков для четырех конкретных полей на двумерных графиках \ (\ Delta t \), \ (\ Delta t ‘\). Сравнивая изменение в каждой строке, мы обнаруживаем, что поле NUC показывает все более высокую степень самореференции с течением времени, в то время как, наоборот, IPR и GAA имеют тенденцию становиться все менее и менее независимыми. Сосредоточив внимание на вариациях в каждом столбце, мы можем изучить влияние эталонного возраста на значимость внутренней передачи знаний.Продолжительность каждого периода цитирования \ (\ Delta t \) и цитируемого периода \ (\ Delta t ‘\) в ( b ) – ( e ) равна 5 годам.
Чтобы исследовать временную эволюцию обмена знаниями между двумя областями на рис. 4b – e, мы рассмотрели одни и те же типы графиков во времени. В таком случае каждая пара полей соответствует траектории, соединяющей точки, соответствующие разным годам с 1990 по 2015 год. Цвета символов от светлого к темному указывают годы от прошлого до самого недавнего.Хотя значимость ссылок в целом со временем снижается, временные шаблоны могут варьироваться от одной пары полей к другой. Четыре панели иллюстрируют четыре основных класса поведения (режимов), которые мы обнаружили, а именно: поглощение, поглощение до взаимного, обратное воспитание и взаимное поведение. Поглощающий режим можно увидеть в поле GPE , которое вобрало больше знаний из полей ATM и EOA на протяжении всего исследуемого периода (рис. 4b). Поля GEN и EPF вначале демонстрируют поведение, аналогичное GPE , вбирая больше знаний из GAA , тогда как в последние несколько лет GEN и EPF , как правило, взаимно обмениваются знаниями с GAA. , хотя веса на звеньях в обоих направлениях становятся менее значимыми (рис.4в). Что еще более интересно, мы также находим режим обратного воспитания, показанный на рис. 4d. Поле GEN сначала поглощает больше знаний из EOA , чем то, что оно предоставляет EOA , но позже ситуация изменилась. Наконец, поля IPR и CM1 показывают другой шаблон, взаимный режим, указывающий, что они обменивались знаниями почти симметричным образом в течение всего периода. Подобные режимы эволюции также наблюдались в оставшихся шести областях (см. SI).Эти различные модели эволюции ясно демонстрируют, что процессы создания и передачи знаний между областями могут быть весьма неоднородными.
Рисунок 4Эволюция знаний в разных областях. ( a ) Для каждой пары полей мы наносим на график средние потоки знаний в любом направлении, усредненные за весь период наблюдения в 26 лет. ( b ) – ( e ) сообщают о некоторых типичных закономерностях временной эволюции, которые мы наблюдали на протяжении многих лет.Цвет символа (от светлого к темному) указывает на годы с 1990 по 2015, а линии соединяют последовательные годы, чтобы помочь проследить траектории. Биссектриса красная линия соответствует случаю совершенно симметричных потоков знаний между двумя полями. ( b ) «Режим поглощения»: поле GPE поглощало знания из полей ATM и EOA на протяжении всего периода времени. ( c ) «От поглощающего к взаимному режиму»: GEN и EPF первоначально вобрали больше знаний из области GAA , а затем склонились к сбалансированному случаю, в котором они поглощают из GAA те же знания, которые они предоставляют к нему.( d ) «Режим обратного воспитания»: хотя в течение первых нескольких лет GEN вобрал в себя больше знаний из области EOA , чем внес свой вклад, на более позднем этапе ситуация изменилась. ( e ) «Взаимный режим»: поля IPR и CM1 имеют тенденцию делиться знаниями симметрично в течение всего периода.
Согласно современной физической теории, может ли человек путешествовать во времени?
Как отметили несколько респондентов, мы постоянно путешествуем по время – просто вперед, и все с одинаковой скоростью.Но серьезно, Путешествие во времени – это больше, чем просто фантазия, как заметил Гэри. Т. Горовиц, профессор физики Университета г. Калифорния в Санта-Барбаре:“Возможно, это удивительно, но это оказался тонкий вопрос. Очевидно, что это не исключается нашими нынешними законами природы. Недавние исследования этого вопроса предоставили некоторые доказательства того, что ответ отрицательный, но это еще не доказано быть невозможным “.
Даже небольшая возможность путешествия во времени оказывает такое увлечение, которое продолжают изучать многие физики, не только возможно ли это, но также как это можно сделать.
Одним из ведущих исследователей в этой области является Уильям А. Хискок, профессор физики из Монтаны. Государственный университет. Вот его мысли по этому поводу:
«Можно ли путешествовать во времени? Чтобы ответить на этот вопрос, мы должны быть более конкретными в том, что мы подразумеваем под путешествием сквозь время. Не принимая во внимание повседневный ход времени, вопрос можно разделить на две части: возможно ли в рамках короткое время (меньше, чем продолжительность человеческой жизни), чтобы отправиться в далекое будущее? А можно ли отправиться в прошлое?
«Наше нынешнее понимание фундаментальной физики говорит нам, что ответ на первый вопрос – однозначно да, а на во-вторых, может быть.
«Механизм путешествия в далекое будущее – использовать эффект замедления времени специальной теории относительности, которая утверждает что движущиеся часы, кажется, тикают тем медленнее, чем ближе они приближается к скорости света. Этот эффект, который был полностью поддерживается экспериментальными испытаниями, применяется ко всем типы часов, в том числе биологическое старение.
“Если бы кто-то покинул Землю на космическом корабле, который мог бы постоянно ускоряться с комфортным значением g (ускорение которая создала бы силу, равную силе тяжести на земном поверхность), можно было бы начать приближаться к скорости света относительно Земли в течение примерно года.Как корабль продолжал чтобы ускориться, он приблизится к скорости света, и его часы, казалось бы, идут все медленнее относительно земли. При таких обстоятельствах поездка туда и обратно центр нашей галактики и обратно к Земле – на расстоянии около 60000 световых лет – можно завершить всего за немного более 40 лет судового времени. По прибытии обратно в Земли, астронавт был бы всего на 40 лет старше, в то время как 60 000 на земле прошли бы годы.(Обратите внимание, что нет «парадокс близнецов», потому что однозначно, что пространство путешественник уже 40 лет ощущает постоянное ускорение, в то время как гипотетический близнец, оставленный на космическом корабле, кружащем земля не имеет.)
“Такая поездка создала бы огромные инженерные проблемы: количество требуемой энергии, даже при условии идеального преобразования масса в энергию больше массы планеты. Но ничего в известных законах физики предотвратит такое путешествие от происходит.
“Путешествие во времени в прошлое, что люди обычно понимают под путешествие во времени – гораздо более неопределенное предложение. Есть многие решения уравнений общей теории относительности Эйнштейна которые позволяют человеку следовать временной шкале, которая приведет к она (или он) встречает себя – или ее бабушку – на более раннее время. Проблема состоит в том, чтобы решить, подходят ли эти решения представляют ситуации, которые могут произойти в реальной вселенной, или являются ли они простыми математическими странностями, несовместимыми с известная физика.Ни один эксперимент или наблюдение никогда не указывало это путешествие во времени происходит в нашей Вселенной. Большая работа было сделано физиками-теоретиками за последнее десятилетие, чтобы попытаться определить, есть ли во вселенной, изначально не имеющей времени путешествия, можно построить машину времени – другими словами, если это можно манипулировать материей и геометрией пространства-времени в таким образом, чтобы создавать новые пути, возвращающиеся в прошлое.
«Как построить машину времени? Самый простой способ сейчас обсуждается – взять червоточину (туннель, соединяющий пространственно разделенные области пространства-времени) и дают один рот червоточина имеет существенную скорость по отношению к другой. -33 сантиметра, или миллиард миллиардов раз меньше электрона.Некоторые физики верю, что можно по-настоящему схватить один из этих микроскопических червоточин и увеличить их до полезных размеров, но при на данный момент все эти идеи очень гипотетичны.
“Даже если бы у нас была червоточина, природа позволила бы нам ее преобразовать в машину времени? Стивен Хокинг сформулировал «гипотезу защиты хронологии»: который гласит, что законы природы предотвращают создание машина времени. Однако на данный момент это всего лишь предположение, не доказано.
«Физики-теоретики изучали различные аспекты физики. чтобы определить, может ли этот закон защитить хронологию и запретить строительство машины времени. Во всех поисках, однако был обнаружен только один кусочек физики, который мог бы запретить путешествовать во времени через червоточину. В 1982 году Дебора А. Конковски из Военно-морской академии США и я показали, что энергия в вакуумном состоянии безмассового квантованного поля (такого как фотон) будет неограниченно расти, как машина времени. включен, эффективно предотвращая его использование.Более поздние исследования Хокинга и Кипа С. Торн из Калифорнийского технологического института показал, что неясно, растущая энергия изменила бы геометрию пространства-времени достаточно быстро, чтобы остановить работу машины времени. Недавний работа Цунэфуми Танака из Университета штата Монтана и меня, наряду с независимым исследованием Дэвида Boulware из Вашингтонского университета показал, что энергия в вакуумном состоянии поля, имеющего массу (например, электрон) не растет до неограниченного уровня; это открытие указывает на то, что может быть способ спроектировать физику элементарных частиц, чтобы позвольте машине времени работать.
«Пожалуй, самым большим сюрпризом из работ последнего десятилетия является что не очевидно, что законы физики запрещают время путешествовать. Становится все более очевидным, что вопрос может быть не в оседает до тех пор, пока ученые не разработают адекватную теорию квантовой сила тяжести.”
Джон Л. Фридман с физического факультета Университета им. Висконсин в Милуоки также много внимания уделяет этой теме. рассмотрения:
“Специальная теория относительности подразумевает, что люди или часы в состоянии покоя (или не ускоряется) стареет быстрее, чем партнеры, путешествующие поездки туда и обратно, в которых человек меняет направление, чтобы вернуться к своему партнер.В мировых ускорителях элементарных частиц это предсказание проверяется ежедневно: частицы движутся по кругу почти на скорость света затухает медленнее, чем в состоянии покоя, и время затухания согласуется с теорией с высокой точностью измерения.
«В рамках специальной теории относительности факт, что частицы не могут двигаться быстрее, чем свет мешает возвращаясь после скоростной поездки во время раньше, чем время отправления.Однако, если учесть гравитацию, пространство-время криволинейна, поэтому существуют решения уравнений общей Относительность, согласно которой частицы могут путешествовать по траекториям, ведущим их назад к прежним временам. Другие особенности геометрии, которая решить уравнения общей теории относительности, включая гравитационные линзы, гравитационные волны и черные дыры; драматический взрыв открытий в радио и рентгеновской астрономии во время последние два десятилетия привели к наблюдению гравитационных линзы и гравитационные волны, а также к неотразимым доказательства существования гигантских черных дыр в центрах галактик и черные дыры звездных размеров, возникающие в результате распада умирающих звезды.Но, похоже, нет областей пространства-времени, которые разрешить путешествие во времени, поднимая фундаментальный вопрос о том, что запрещает их – или если они действительно запрещены.
«Недавняя неожиданность в том, что можно обойти ‘дедушку парадокс ‘, идея о том, что это логически несовместимо для пути частиц, чтобы вернуться к более ранним временам, потому что для Например, внучка могла вернуться в прошлое, чтобы покончить с ее дед. Для нескольких простых физических систем решения к уравнениям физики существуют для любых начальных условий.В в этих модельных системах всегда что-то вмешивается, чтобы предотвратить непоследовательность, аналогичная убийству деда.
«Тогда почему кажется, что машин времени нет? Два разных ответы соответствуют нашим знаниям. Первый просто что классическая теория имеет гораздо более широкий набор решений чем правильная теория квантовой гравитации. Нет невероятно, что причинная структура фундаментально входит в квантовая гравитация и классическое пространство-время с петлями времени являются ложными – другими словами, что они не приближаются ни к какому состояния полной теории.Второй возможный ответ: предоставлено недавними результатами, известными под названием “хронология” защита: предполагается, что квантовая гравитация позволяет микроскопическим структуры, которые нарушают причинно-следственную связь, и один показывает, что характер макроскопической материи запрещает существование областей с макроскопически большими временными петлями. Чтобы создать машину времени потребует отрицательной энергии, и квантовая механика, кажется, допускают только очень маленькие области отрицательной энергии. И силы, необходимые для создания области обычного размера с временными петлями кажутся очень большими.
“Подводя итог: очень вероятно, что законы физики макроскопических машин времени, но возможно, что пространство-время заполнены микроскопическими временными петлями.
Тенденции в физике кандидатов наук | Американский институт физики
В течение 2018–19 учебного года 204 факультета физики в США присудили докторскую степень в общей сложности 1903 докторской степени. Хотя это число относительно не изменилось по сравнению с предыдущим годом, количество присужденных докторов наук по физике выросло на 75% по сравнению с недавним минимумом в 2004 году (см. , рис. 1, ).Даже с резкими колебаниями за последние четыре десятилетия количество ежегодно присуждаемых докторских степеней по физике неизменно составляет около 3% от всех докторских степеней, присуждаемых в Соединенных Штатах.
гражданина США составили большинство докторов наук по физике, присужденных с 2011 года. Период с 2002 по 2010 год был единственным временем, когда учреждения США предоставили больше докторских степеней физики негражданам США, чем гражданам США (см. Рисунок 1 ).
Среднее количество кандидатов наук по физике, присуждаемых факультетами, значительно различается (см. Рисунок 2 ).Половина факультетов физики, присуждающих докторскую степень, присудила в среднем шесть или меньше докторских степеней, а примерно пятая (42 кафедры) присудила в среднем 14 или более, при этом на пяти из этих факультетов в среднем было получено более 30 докторов наук за три академических года.
Подробный список факультетов физики, присуждающих ученую степень, с указанием количества ученых степеней, которые они ежегодно присуждают, можно найти в Реестре физических факультетов.
Из числа кандидатов наук по физике, присужденных в классе 2019 года, 54% были присуждены гражданам США (см. Таблицу 1 ).Средний возраст докторов наук по физике в классах 2017 и 2018 вместе взятых составил 29,5 лет. Средний возраст всех кандидатов наук, присвоенных (независимо от области) в США в 2018 году, составлял 31,4 года. В группе получатели докторской степени в области наук о Земле и физических наук, включая физику, имели самый низкий средний возраст – 29,5 лет [1].
Женщины составляли 19% докторов наук по физике, присужденных в классе 2019 года. Среди респондентов последующего опроса получателей степени AIP, классы 2017 и 2018 вместе взятые, менее 1% сообщили о гендерной идентичности, отличной от мужчины или женщины.Представленность женщин среди новых соискателей докторской степени по физике оставалась довольно стабильной на протяжении более десяти лет и практически не изменилась с 2008 года, когда представительство женщин впервые достигло 19% (см. Рисунок 3 ). Доля неграждан США среди женщин, получивших докторскую степень по физике, больше, чем среди мужчин. В классе 2019 года неграждане США составляли 53% женщин, получивших докторскую степень по физике, и 44% мужчин.
Докторов наук по физике, которые являются афроамериканцами / чернокожими и латиноамериканцами / латиноамериканцами, по-прежнему недопредставлены по сравнению с общим населением 25–34 лет в США, а также среди всех недавних получателей докторской степени (см. таблицу 2 ) [ 2].Идентификация расы и этнической принадлежности разрешена только кандидатам физики, имеющим гражданство США. Из 204 факультетов, на которых в 2018–19 учебном году была получена докторская степень по физике, пять располагались в Исторически черном колледже и университете (HBCU). На этих пяти факультетах афроамериканцам было присуждено около пятой степени доктора философии по физике в классах 2018 и 2019 годов.
Хотя они все еще недостаточно представлены, количество и доля латиноамериканских / латиноамериканских докторов наук по физике в последние годы увеличились.С другой стороны, афроамериканцы / чернокожие доктора философии по физике по-прежнему сильно недопредставлены как по количеству, так и по проценту присужденных докторских степеней по физике. Кроме того, в последние годы эти цифры уменьшались: афроамериканцам / афроамериканцам было присуждено вдвое меньше докторских степеней физики, чем в 2012 году (см. , рис. 4, ).
Как видно из таблицы 1 , граждане, не являющиеся гражданами США, составляли чуть менее половины докторов наук по физике (46%), присвоенных в классе 2019 года. Студенты из стран Азии, особенно Китая, составляют большинство приезжающих иностранных студентов. в США для изучения физики ( Таблица 3 ).
Фон
Доктора физики имеют разное образование, в том числе различные образовательные системы за пределами США. Большинство докторов наук по физике указали, что их степень бакалавра была в области физики или астрономии (см. , Таблица 4, ). Двухгодичная система колледжей стала важной частью образовательной системы США. Если посмотреть только на граждан США, то 16% докторов физики в классах 2017 и 2018 годов вместе взятых указали, что они начали свое высшее образование в двухгодичном или местном колледже.Эти цифры не включают студентов, которые прошли курс обучения в общественном колледже во время учебы в средней школе, а затем поступили сразу в четырехлетнее учебное заведение после окончания учебы.
Некоторые доктора философии начали свое последипломное образование по физике на физическом факультете, отличном от того, на котором они в конечном итоге получили докторскую степень. Это было особенно верно в отношении неграждан США: 40% указали, что они были зачислены в аспирантуру по программе физики до приезда в США на учебу (см. , Таблица 5, ).Перевод с другой программы аспирантуры по физике в США на факультет, на котором они в конечном итоге получили докторскую степень, был еще одним способом получения образования как для граждан США, так и для неграждан. Некоторые из новых докторов наук по физике, которые ранее начинали свое последипломное образование по физике в другом учебном заведении, будь то из-за границы или другого учебного заведения США, возможно, получили степень магистра в результате своей предыдущей учебы в аспирантуре.
Средняя продолжительность получения докторской степени по физике в комбинированных классах в 2017 и 2018 годах составила 6 человек.2 года. В этом отчете количество лет, в течение которых можно получить степень доктора философии, измеряется количеством лет, зарегистрированных на физическом факультете, в эквиваленте полной занятости (ЭПЗ). Данные собираются с интервалом в полгода и округляются до следующего полного года для отображения (см. , рис. 5, ). Хотя средняя продолжительность получения степени составляла 6 лет, 16% новых докторов наук указали, что им потребовалось 8 и более лет.
40% неграждан США, получивших докторскую степень, которые были зачислены в аспирантуру по программе физики за пределами США до того, как приехали изучать физику в Соединенных Штатах, не сообщили о значительно меньшем количестве лет обучения физике в США на ЭПЗ, чем те, кто не получил образования. Граждане США, которые учились только в США.
Физика конденсированного состояния продолжает оставаться наиболее распространенной областью диссертаций для докторов наук по физике, при этом, по оценкам, в среднем 20% докторов физики выбирают это подполе в объединенных классах 2017 и 2018 гг. (См. , рис. 6, ). Большая часть неграждан США (25%) имела подполе конденсированного состояния, чем граждане США (15%).
Было несколько подполей, где гендерная репрезентация различалась статистически значимо. Большая часть мужчин (21%) имела подполе диссертации, посвященной конденсированным веществам, чем женщины (15%).С другой стороны, у женщин больше шансов получить диссертацию по таким направлениям, как астрофизика (22% против 13%) и биофизика (12% против 6%), чем у мужчин.
Более половины (53%) докторов наук в классах 2017 и 2018 годов указали, что их диссертационный метод исследования был экспериментальным. Большинство (37%) оставшихся докторов наук указали, что их метод диссертационного исследования был теоретическим, а оставшийся баланс докторов наук указал либо наблюдательный (7%), либо другой (3%).
Метод исследовательской диссертации, используемый новыми кандидатами физики в классах 2017 и 2018 годов, несколько различается в зависимости от области их диссертации, и различия являются статистически значимыми.Были получены кандидатские диссертации по темам «конденсированное вещество», «ядерная физика», «атомная, молекулярная и оптическая физика», а также в более прикладных областях, таких как «материаловедение», «оптика» и «инженерная физика». склонялся к экспериментаторам. Докторанты, работающие в таких областях, как «частицы и поля», «вычислительная физика», «квантовые основы», «сложные системы» и «теория относительности», как правило, имели большую долю теоретиков. Многие астрофизики указали, что метод их диссертационного исследования был наблюдательным.В целом, граждане США статистически чаще использовали экспериментальный метод исследования основной диссертации, чем не граждане США (59% против 46%). Более половины докторов наук по физике указали, что компьютерное моделирование или моделирование было основным инструментом в связи с их диссертационной работой.
Большинство новых получателей докторской степени по физике в классах 2017 и 2018 гг. Указали, что они все равно получили бы докторскую степень по физике, если бы у них была возможность пережить свои образовательные занятия (см. , таблица 6, ).Существовали значительные различия между гражданами США и неамериканскими гражданами, когда они размышляли о своем образовательном выборе, касающемся получения докторской степени по физике. Большинство (70%) граждан США указали, что они будут повторять свое докторское образование по физике в том же учреждении, в котором они получили свою докторскую степень. Граждане, не являющиеся гражданами США, были менее довольны своим выбором: 53% указали, что они получат докторскую степень по физике в учреждении, присуждающем ученую степень. Однако значительно большая часть неграждан США, чем граждан США, указала, что они по-прежнему будут получать докторскую степень по физике, но в другом учреждении.Достаточное количество граждан США и других стран указали, что они будут учиться на докторскую степень в другой дисциплине или вообще не будут получать докторскую степень, если им будет предоставлена возможность «сделать это заново».
Осенью 2019-20 учебного года 2956 аспирантов-физиков учились на первом году обучения в аспирантуре, на которую они были зачислены. Рост числа студентов-первокурсников, обучающихся по программам аспирантуры по физике на факультетах, присуждающих докторскую степень, замедлился в последние годы, со среднегодовым приростом всего около 1% в год за последнее десятилетие (см. Рисунок 7 ).Ожидается, что в связи с недавним сокращением числа студентов, поступающих в аспирантуру по физическим программам, количество новых кандидатов наук, ежегодно присуждаемых в США, также выровняется.
Список литературы
[1] Национальный научный фонд, Национальный центр науки и инженерной статистики (NCES). Обзор докторских степеней, 2018 г. Таблица 27
[2] Бюро переписи населения США, Текущее обследование населения, Ежегодное социально-экономическое приложение за 2017 год. https: // www.census.gov/data/tables/2017/demo/education-attainment/cps-detailed-tables.html Таблицы 1.1, 1.4, 1.6
Методология
Каждую осень Центр статистических исследований (SRC) проводит обследование набора и ученых степеней. Опрос рассылается на все факультеты физики и астрономии США и Пуэрто-Рико. Департаменты просят предоставить информацию о количестве студентов, которых они в настоящее время зачисляют, и количестве ученых степеней, которые они присвоили в предыдущем учебном году.Мы определяем учебный год с сентября по август.
В 2018/19 учебном году 204 из 753 физических факультетов защитили докторскую диссертацию. Мы получили ответы из 95% этих отделов. Данные в этом разделе о количестве ученых степеней, зачисления, гражданства, пола и расы / этнической принадлежности взяты из этой ежегодной переписи физических лиц. Для отделов, не ответивших на вопросы, мы оценили цифры и включили их в итоговые значения.
В 2018/19 учебном году действовало 45 кафедр, предлагавших кандидатскую диссертацию по астрономии.Тринадцать из этих отделений управлялись как часть объединенного отделения физики и астрономии, а остальные управлялись как отдельные отделения астрономии. Данные о степенях астрономии, присуждаемых как на объединенном, так и на отдельных факультетах, собираются отдельно от ученых степеней по физике и сообщаются отдельно в других тематических обзорах (https://www.aip.org/statistics/astronomy).
Ежегодный опрос Enrollments and Degrees также запрашивает имена и контактную информацию недавних докторов наук.Эта информация о получателе степени используется для проведения нашего последующего опроса зимой после учебного года, в котором респонденты получили свои степени. Мы получили информацию о постдипломном образовании непосредственно от 30% докторов физики в классах 2018 и 2019 годов. Данные в таблицах 1-3 и на рисунках 1-4 и 7 взяты из опроса Enrollments and Degrees. Данные в таблицах 4, 5 и 6, а также на рисунках 5 и 6 получены в результате последующего опроса.
В рамках последующего опроса PhD также собираются данные о результатах после получения степени.Данные, относящиеся к занятости, из Последующего опроса публикуются в отдельных тематических обзорах; см. https://www.aip.org/statistics/employment/phds .
Все различия, обсуждаемые в тексте, были проверены и признаны статистически значимыми.
Этот отчет стал возможным благодаря усилиям заведующих кафедрами, преподавателей и сотрудников, которые год за годом предоставляли данные по своим подразделениям в AIP. Мы также благодарим многих новых докторов наук по физике, которые поделились с нами своим образовательным опытом и опытом работы.
Электронные обновления
Вы можете подписаться на получение предупреждений по электронной почте, которые будут уведомлять вас, когда мы публикуем новый отчет или ресурс. Посетите https://www.aip.org/statistics/stats_subscribe, чтобы зарегистрироваться. Мы отправим вам электронное обновление только тогда, когда опубликуем что-то новое. Вы должны получать не более 20 сообщений в год.
Следуйте за нами в Twitter
Центр статистических исследований – это ваш источник данных об образовании, карьере и разнообразии в физике, астрономии и других физических науках.Следуйте за нами на @AIP_Stats.
Тенденции в физике Кандидатские диссертации
Патрик Дж. Малви, Старр Николсон и Джек Полд
Опубликован: февраль 2021 г.


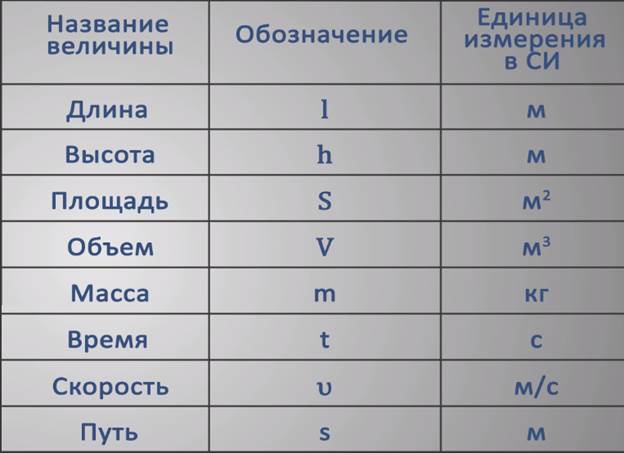 Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами.
Буквы также могут быть записаны различными шрифтами для того, чтобы различать природу величин или математических операций. В частности принято обозначать жирным шрифтом векторные величины, а тензорные величины — рубленым шрифтом. Иногда также для обозначения используется готический шрифт. Интенсивные величины обычно обозначаются строчными, а экстенсивные — заглавными буквами. Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx.
Так, постоянная величина в формуле обозначается часто как const. Дифференциал обозначается малой буквой d перед названием величины, например dx. Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.
Одним примером использования кириллической буквы в современной международной научной литературе есть обозначения инварианта Лагранжа буквой Ж. Гребень Дирака иногда обозначают буквой Ш, так как график функции визуально схож с формой буквы.