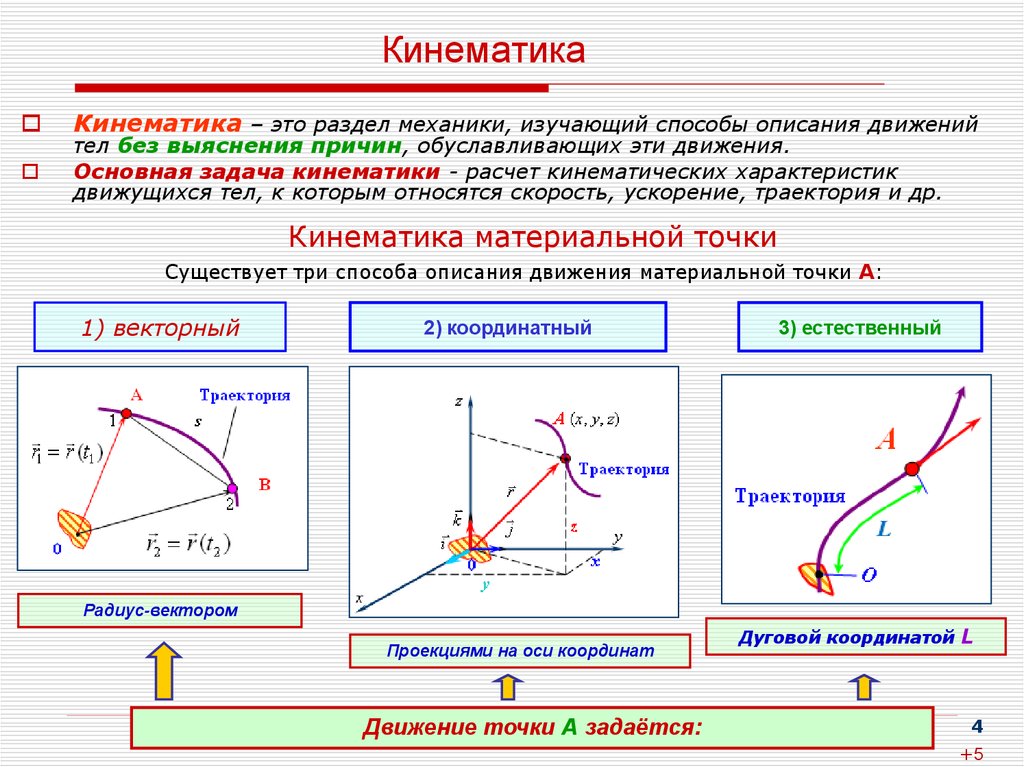
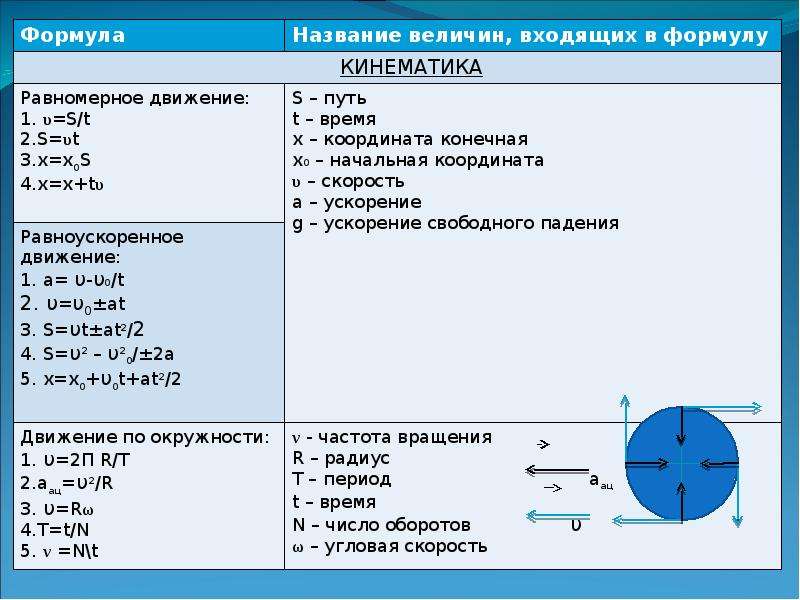
Кинематика
Движение — один из природных феноменов, которые изучает отдельный раздел физики. Название «кинематика» происходит от греческого слова κινειν, которое в переводе означает движение, а звучит это слово как «киней». Основные понятия кинематики — это:
- материальная точка;
- физическое тело;
- пространство;
- время;
- координата;
- ускорение;
- скорость;
- перемещение;
- путь.
Можно увидеть, что здесь нет таких распространенных терминов, как сила, воздействие, взаимодействие. Это предмет изучения другого раздела физики — динамики. А основная задача кинематики — найти положение тела в пространстве в заданный момент времени. Кинематика — это идеализированный раздел физики, который изучает движение в чистом виде, без определения причин, его вызывающих. Используются средства геометрии, алгебры, математического анализа, дифференциального и интегрального исчисления.
В своем большинстве определения и формулы кинематики носят теоретический характер, но создают прочную основу для реального определения характеристик движения конкретного тела. Если искать ответ на вопрос, что изучает кинематика, то наиболее правильным ответом будет — как движутся физические тела. Почему это происходит — предмет других разделов механики.
Если искать ответ на вопрос, что изучает кинематика, то наиболее правильным ответом будет — как движутся физические тела. Почему это происходит — предмет других разделов механики.
Для начала уточним, что в кинематике все измерения и вычисления производятся в пределах системы измерения СИ (SI). При изучении движения нас интересует только несколько величин из довольно широкой таблицы. Это масса, расстояние (длина) и время. Соответственно, единицами измерения становятся килограмм (кг), метр (м) и секунда (с). Угол измеряется не в градусах, а в радианах (рад).
В условиях задачи могут использоваться производные и внесистемные единицы, например, километр, тонна, час. Но при записи условия задачи необходимо перейти к стандартным системным величинам, преобразовав исходные данные. Сделать это несложно, например:
- 1 час — 3600 с;
- 1 тонна — 1000 кг, или 1 ∙103;
- 1 километр — 1000м, или 1 ∙103м;
- 1 сантиметр — 0,01 м, или 1 ∙ 10-2м.

Все ответы в задачах должны быть указаны только в системных единицах и стандартной записи числа (а ∙ 10n, n- целое число).
При вычислениях можно пользоваться только величинами одного размерного ряда, например, умножать, делить, вычитать только километры с километрами, секунды с секундами и т.д. Для упрощения перевода единиц можно воспользоваться таблицей:
Но есть один нюанс, в некоторых задачах ЕГЭ дополнительно указано, в каких единицах представить результат. Всегда дочитывайте задание до конца. Если там указано, что нужно записать ответ в км/час, то м/с могут быть засчитаны как ошибка, даже если все формулы написаны правильно, а вычисления сделаны точно.
Материальная точка — движущееся, или неподвижное тело, размеры которого ничтожно малы по сравнению с расстояниями. Например, исследуя движение самолета из Москвы во Владивосток, или Санкт-Петербург, его можно считать материальной точкой. Длина и размах крыльев намного меньше, чем длина пути. А вот при перемещении того же самолета из ангара на взлетную полосу, размеры и длина пути одного порядка, термин использовать нельзя.
А вот при перемещении того же самолета из ангара на взлетную полосу, размеры и длина пути одного порядка, термин использовать нельзя.
Система отсчета (СО) — координатная сеть, в которой мы изучаем поведение материальной точки. В СО входят тело отсчета, привязанные к нему оси координат, часы и средства измерения длины. Телом отсчета выбирается предмет, или сооружение, которые заведомо неподвижны в данной системе. Например, исследуя движение того же самолета, за тело отсчета можно принять диспетчерскую башню, или вышку наземного флюгера. Координата тела отсчета (0;0). Начальное положение движущегося тела (точка старта) обозначается как А (X0;Y0).
Движение каждой материальной точки можно изобразить линией, которая получила название траектория. Линия может быть прямой, ломаной, дугообразной. Если тело движется по прямой, то движение называют прямолинейным. Каждую ломаную и дугу можно разбить на мелкие участки, которые приближенно считаются прямыми.
В кинематике используются два понятия, которые часто путают — путь и перемещение. Путаницу усугубляет то, что измеряются они в одинаковых единицах, метрах. Но физическая суть их отличается:
- путь — длина траектории;
- перемещение — кратчайшее расстояние между точками начала и конца пути.
Если тело движется по замкнутому кругу, то путь равен периметру получившейся фигуры, а перемещение равно нулю. Формула для определения пути при равномерном движении:
S= v ∙t, где v — скорость движения, а t – время движения. Путь — величина скалярная, то есть, от направления не зависит. Перемещение определяется как вектор, с началом в точке старта и концом в точке финиша. Путь и перемещение совпадают только при прямолинейном движении в одной системе отсчета.
Скорость — векторная величина, показывающая какое расстояние проходит тело за единицу времени. Измеряется в м/с, определяется по формуле:
V=S\t. Это средняя скорость, для определения которой Если тело двигалось с разными скоростями на разных участках, то среднюю скорость нельзя рассчитывать, как среднее арифметическое.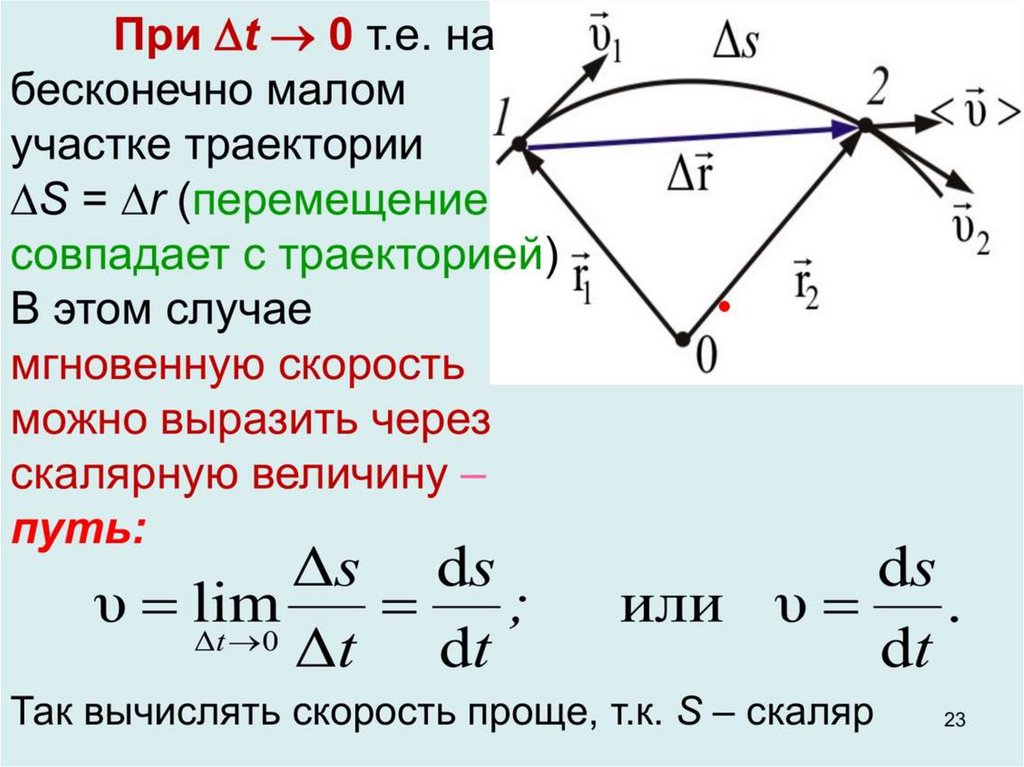 Это ошибка. Нужно длину всего пути разделить на все время движения.
Это ошибка. Нужно длину всего пути разделить на все время движения.
Средняя скорость перемещения — рассчитывается по формуле:
, где Sполн – перемещение, а не путь.
Ускорение — изменение скорости за единицу времени
Единица измерения ускорения — м/с2.
Движение называется равноускоренным, если каждую секунду скорость увеличивается на одну и ту же величину. Перемещение при равноускоренном прямолинейном движении определяется по формуле:
Если тело равномерно замедляется, то формула выглядит так:
Координата (положение) тела в системе отсчета определяется формулой:
Это базовые формулы, из которых легко получить остальные, необходимые для вычисления координаты движущегося тела:
Если отдельно рассматривать движение падающего тела, то формулы отличаются только тем, что ускорение всегда одно и то же — g= 9,8 м/с2.
Рассмотренные формулы применимы в неподвижных системах отсчета, привязанных к одному телу. В движущихся системах координат все происходит значительно сложнее.
В движущихся системах координат все происходит значительно сложнее.
Решу егэ кинематика физика задачи – Справочник
Решу егэ кинематика физика задачи
Задания Д3 № 1118
Пользователь работал с каталогом C:\Физика\Задачи\Кинематика. Сначала он поднялся на один уровень вверх, затем ещё раз поднялся на один уровень вверх и после этого спустился в каталог Экзамен. Укажите полный путь каталога, в котором оказался пользователь.
Поднявшись на два уровня вверх, пользователь оказался в каталоге C:\Физика. Спустившись в каталог Экзамен, пользователь оказался в каталоге С:\Физика\Экзамен.
Задания Д3 № 1118
Укажите полный путь каталога, в котором оказался пользователь.
Inf-oge. sdamgia. ru
24.01.2020 21:54:54
2020-01-24 21:54:54
Источники:
Https://inf-oge. sdamgia. ru/problem? id=1118
Кинематика — Физика — Теория, тесты, формулы и задачи — Обучение Физике, Онлайн подготовка к ЦТ и ЕГЭ.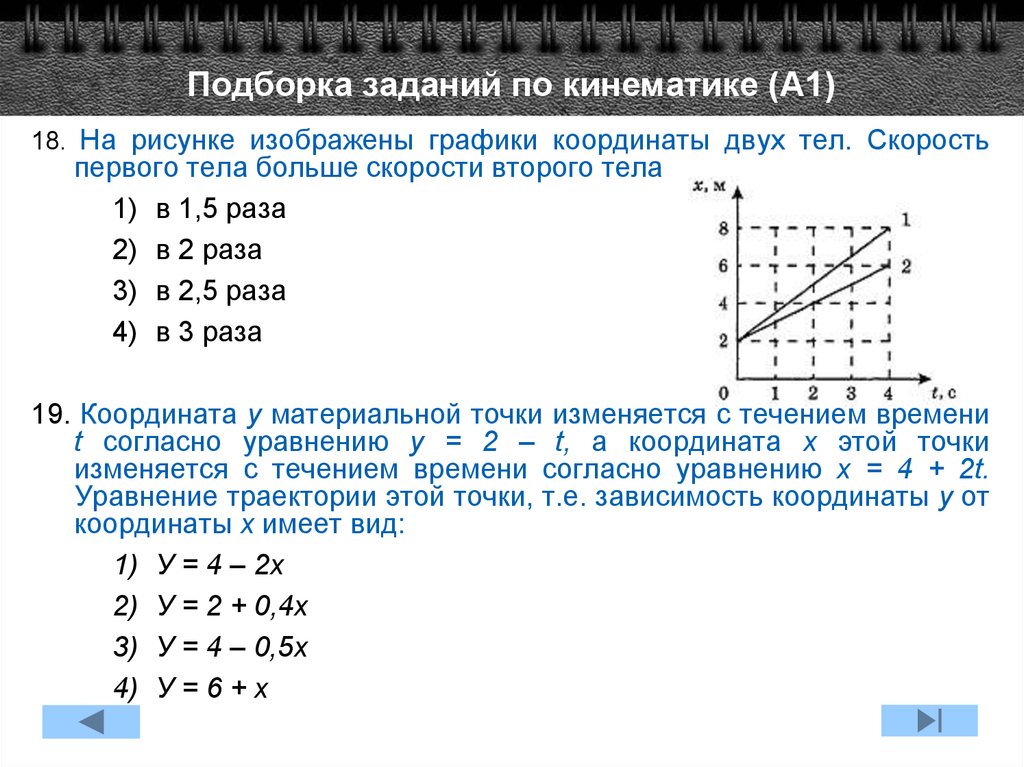 » /> » /> .keyword { color: red; }
» /> » /> .keyword { color: red; }
Решу егэ кинематика физика задачи
Основные единицы измерения величин в системе СИ таковы:
единица измерения длины — метр (1 м), времени — секунда (1 с), массы — килограмм (1 кг), количества вещества — моль (1 моль), температуры — кельвин (1 К), силы электрического тока — ампер (1 А), Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки.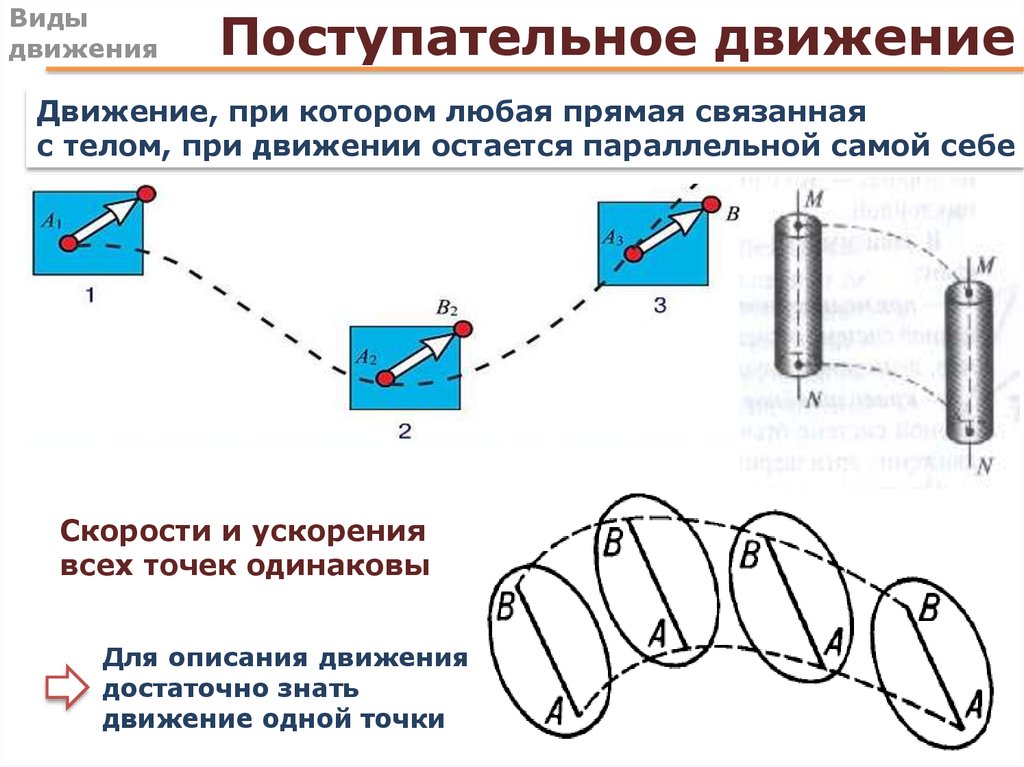 их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать Материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать Материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т. д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют Траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный Путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При Равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
Где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
Где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения.
 Среднее арифметическое получается только в некоторых частных случаях. И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Среднее арифметическое получается только в некоторых частных случаях. И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
Где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется Равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.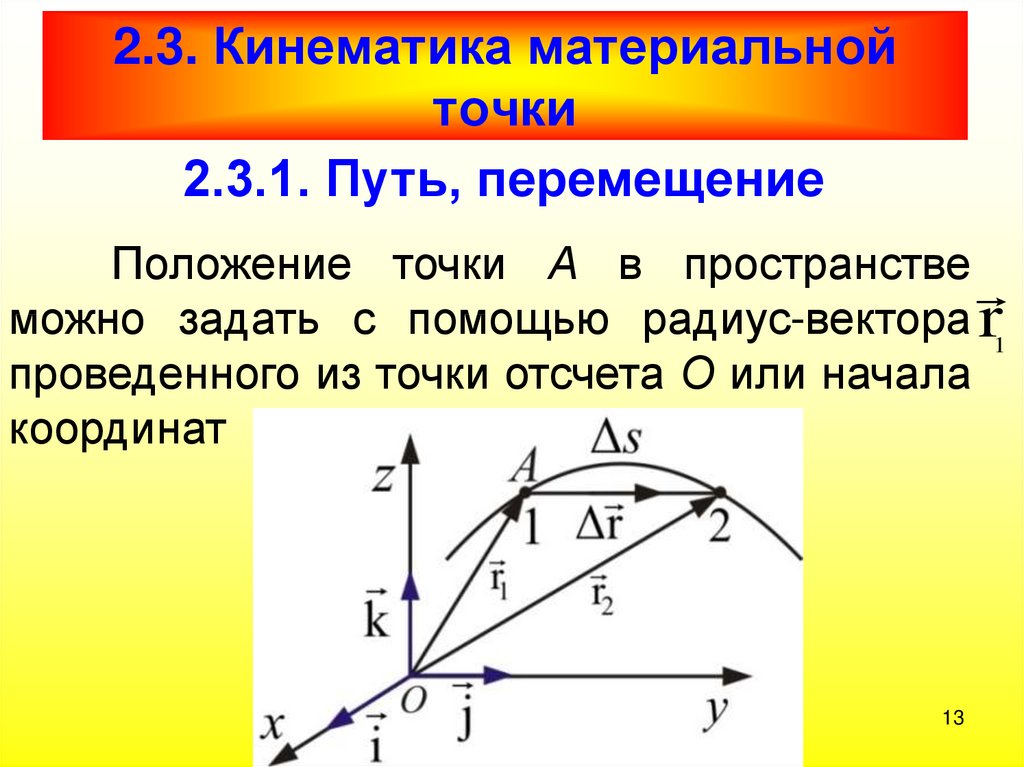
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая Изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли Ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.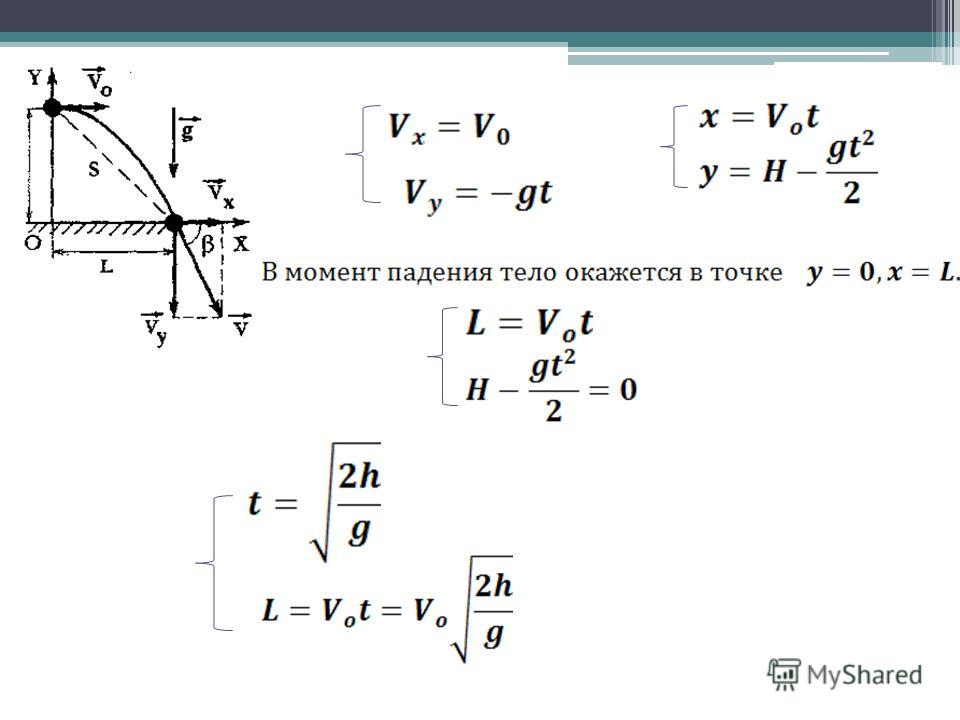
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом Полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, Дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между Горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к Вертикали.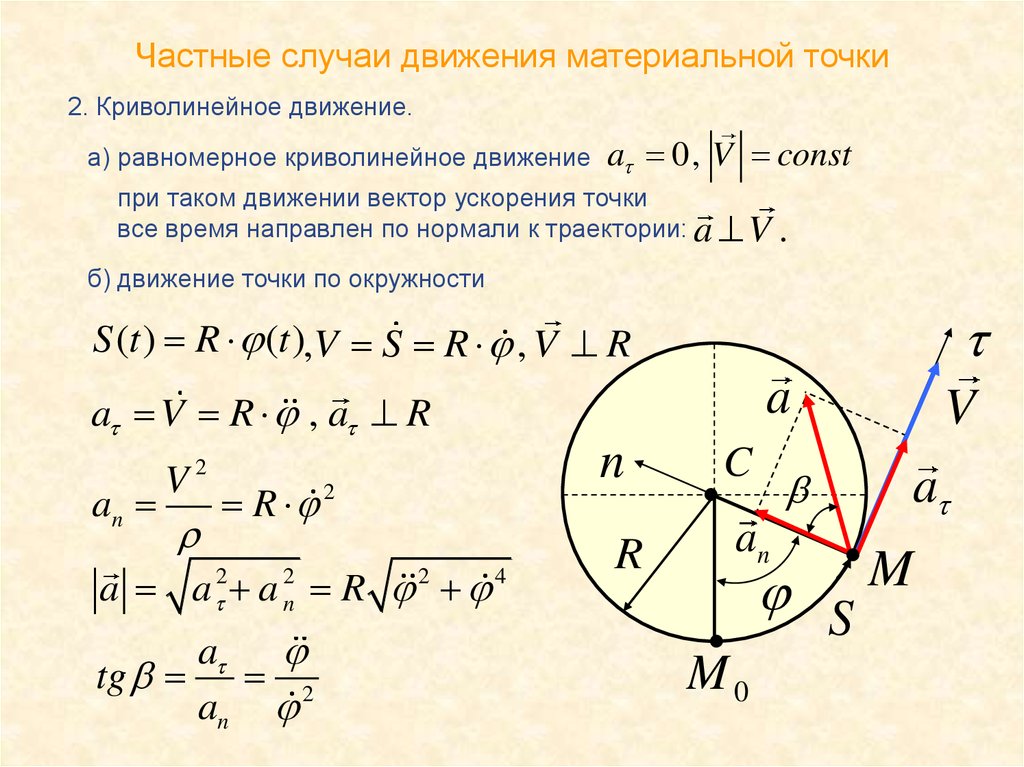 Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При Равномерном вращении скорость тела будет определяется следующим образом:
Где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости.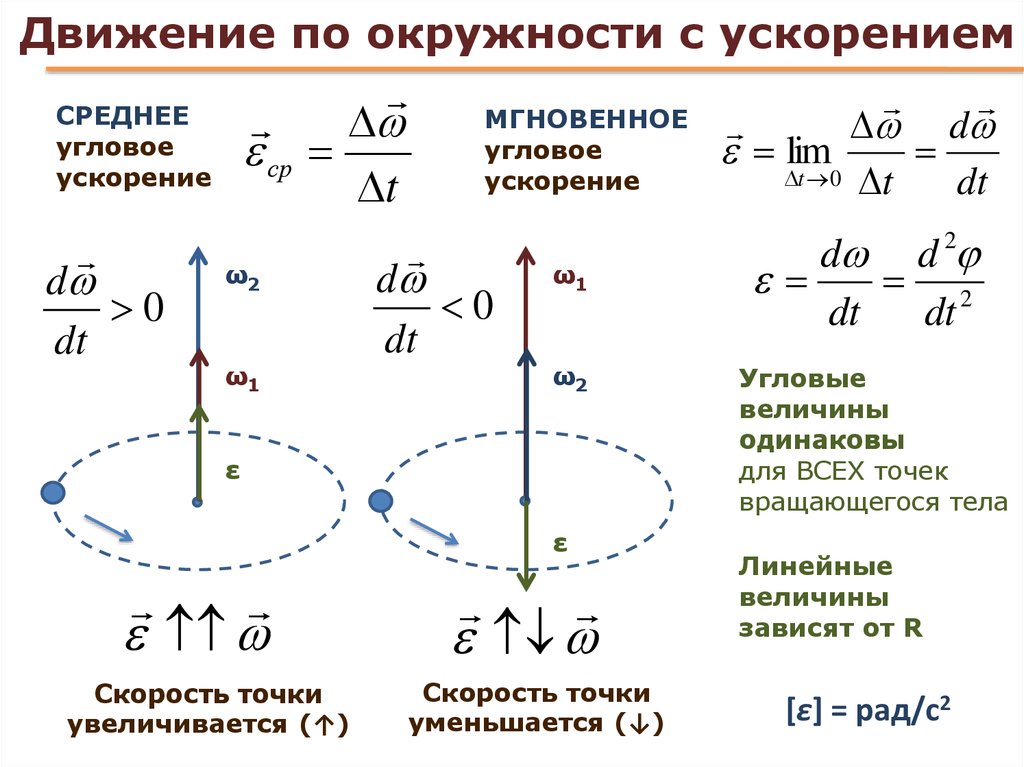 В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или Центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или Центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Нарушение прав правообладателей преследуется по закону. Подробнее.
Свободное падение по вертикали.
Educon. by
25.04.2017 1:49:27
2017-04-25 01:49:27
Источники:
Https://educon. by/index. php/materials/phys/kinematika
Кинематика. Теория и формулы для ЕГЭ шпаргалка » /> » /> .keyword { color: red; }
Решу егэ кинематика физика задачи
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
Типы движений
1. Равномерное движение1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения X = x O + υ Ox T показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
2. Движение с постоянным ускорениемРавноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.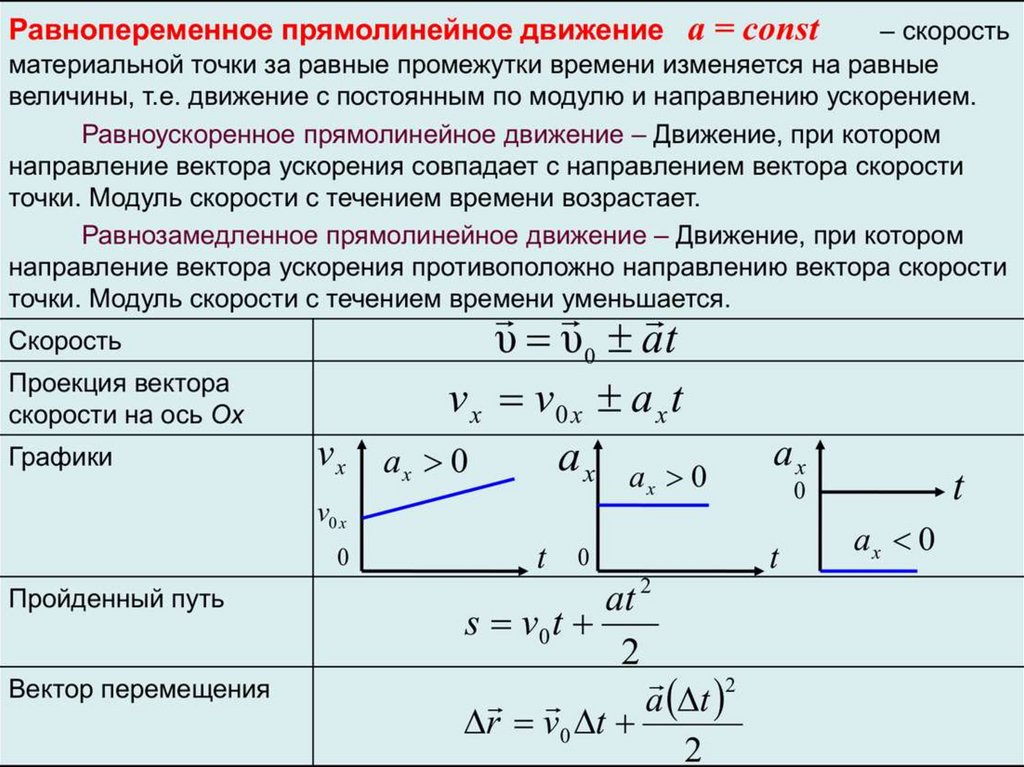
Уравнение равноускоренного движения Y = yO + υOyT + ½aY T² Показывает, что координата квадратично зависит от времени. Уравнение ΥY = υOy + aY T Показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
Типы движений
1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения X = x O + υ Ox T показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Uchitel. pro
08.12.2018 22:41:21
2018-12-08 22:41:21
Источники:
Https://uchitel. pro/%D0%BA%D0%B8%D0%BD%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0/
1.1.Кинематика
ГВУЗ« МАКЕЕВСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
ФИЗИКА.
СБОРНИК ЗАДАЧ
Специальности: 503050901 – бухгалтерский учет.503060101 – организация производства.505010301 – разработка программного обеспечения.505050204 – эксплуатация и ремонт подъемно – транспортных строительных и дорожных машин 506010101 – строительство и эксплуатация зданий и сооружений.507010602 – обслуживание и ремонт автомобилей и двигателей.
2012.
Методическое пособие сборник задач по физике.
Подготовила Шумилина И.А. – преподаватель ГВУЗ « Макеевский политехнический колледж».
2012г.
Пособие предназначено для студентов 1 – го курса, а также может быть полезно студентам старших курсов.
Рецензенты:
Солодовник Ю.В. – преподаватель физики М.П.К
Коваленко Л.Н. – преподаватель электротехники и микроэлектроники МПК.
Рассмотрено и утверждено на заседании цикловой комиссии природных дисциплин
(протокол №1 от 30.08.2011г.)
Содержание.
Предисловие………………………………………………………………….
Общие правила решения задач…………………………………………..
Механика. 1
1.1.Кинематика……………………………………………………………..
1. Путь и перемещение. Равномерное прямолинейное движение. Скорость движения………………………………………………………… ….
2. Ускорение. Равноускоренное прямолинейное движение. Скорость и пройденный путь тела при равноускоренном прямолинейном движении………………………………………………………………………..
3.Свободное падение тел. Ускорение свободного падения……………
4.Равномерное
движение тела по окружности.
Центростремительное
ускорение……………………………………………………………………….
1.2. Динамика…………………………………………………………………..
5.Второй и третий законы Ньютона. Масса. Силы в природе………..
6. Гравитационное взаимодействие . Закон всемирного тяготения.
Деформация тела . Сила упругости………………………………………
7. Сила трения. Сила сопротивления среды. Движения тела под действием нескольких сил……………………………………………………17
8.Равновесие тел. Условие равновесия тел которые имеют ось вращения……………………………………………………………………….
1.3.Законы сохранения……………………………………………………….
9. Импульс тела. Закон сохранения импульса…………………………..
10.Механическая энергия. Кинетическая и потенциальная энергия.
Закон сохранения энергии в механических процессах…………………
Молекулярная физика и термодинамика.2
2.1.Свойства газов жидкостей и твердых тел……………………………
11. Масса молекул. Количество вещества……………………………….
12. Основное уравнение молекулярно – кинетической теории………
13.
Уравнение состояния идеального газа.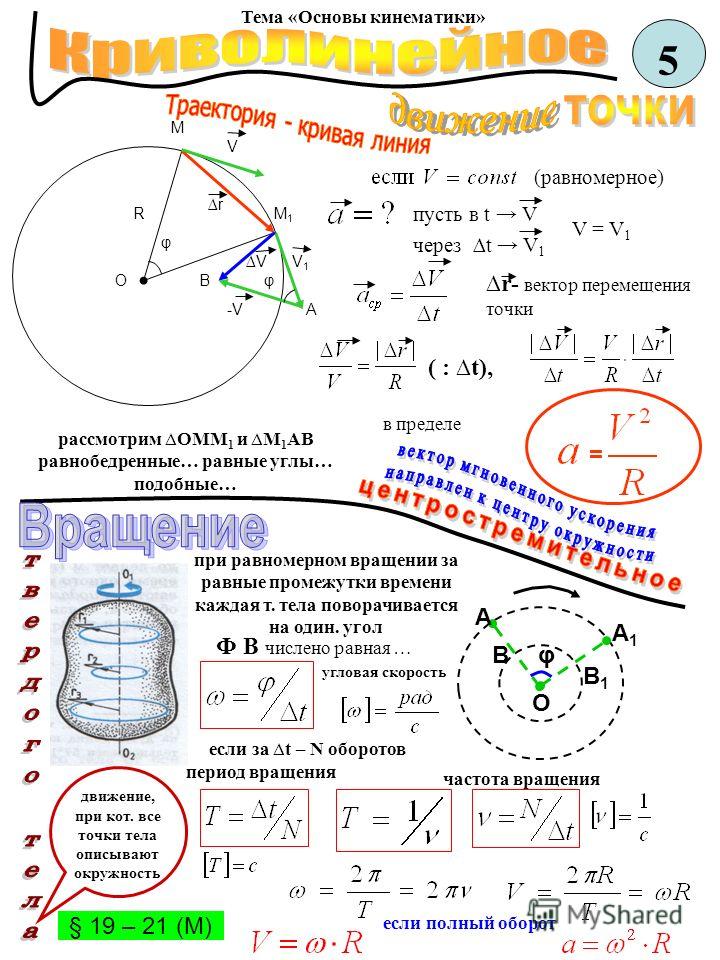 Газовые законы………….
Газовые законы………….
14. Влажность воздуха………………………………………………………
15. Поверхностное натяжение жидкости капиллярные явления……..
2.2. Основы термодинамики………………………………………………
16.Уравнение теплового баланса для тепловых процессов……………
17.Внутреняя энергия одноатомного газа…………………………………
18. Первый закон термодинамики………………………………………….
19. КПД тепловых двигателей………………………………………………
Электродинамика. 3.
3.1.Электрическое поле………………………………………………………
20. 3акон Кулона. Напряженность электрического поля………………..
21.Работа электрического поля при перемещении заряда. Связь между напряжением и напряжённостью…………………………………..
22. Электроёмкость конденсатора. Энергия электрического поля……
3.2. Законы постоянного тока………………………………………………
23. Сила тока. Закон Ома для участка цепи. Сопротивление…………
24. Последовательное и параллельное соединение проводников…..
25.Работа
и мощность тока………………………………………………….
26. Электродвижущая сила. Закон Ома для полной цепи…………….
3.3.Электрический ток в различных средах……………………………….
27. Электрический ток в жидкостях………………………………………
28. Электрический ток в газах и вакууме…………………………………
3.4. Магнитное поле…………………………………………………………
29. Сила Ампера. Сила Лоренца. Магнитный поток……………………
3.5. Электромагнитная индукция……………………………………………
30. ЭДС. индукции. Индукции. Индукционный ток. Закон Ленца………
31.Самоиндукция. Энергия магнитного поля. Напряжённость магнитного поля………………………………………………………………
32.Зависимость ЭДС индукции от времени. Переменный электрический ток. Трансформатор………………………………………
Коливання та хвилі 4
4.1Механічні коливання та хвилі
33.Механические колебания и волны. Звук…………………………………….
4.2 Електромагнітні коливання та хвилі
34.Э.д.с. индукции. Индукционный ток .Закон Ленца………………………
35.Самоидукция.
Энергия магнитного поля. Напряженность
магнитного поля……………………………………………………………………………….
Напряженность
магнитного поля……………………………………………………………………………….
36 .Зависимость э.д.с. индукции от времени. Переменный электрический ток.
Трансформатор…………………………………………………………………
37.Электромагнитные колебания и волны. Формула Томсона……………….
Оптика та основи теорії відносності 5
5.1 Хвильова оптика
38.Скорость света. Природа света. . Отражение и преломление света……….
39.Геометрическая оптика………………………………………………………
40.Явления, объясняемые волновыми свойствами света. Интерференция . Дифракция………………………………………………………………
41.Излучение и спектры. Давление света, фотоэффект……………………….
Елементи квантової фізики та елементи теорії відносності 6
6.1 Основы специальной теории относительности…………………………………………………………………
Атомна та ядерна фізика 7
7.1.Строение атома .Ядерная физика……………………………………………
Приложение…………………………………………………………………..
Предисловие.
Настоящее
пособие составлено с целью помочь
студентам изучить курс физики . Дидактический материал предназначен
для организации дифференцированной
работы студентов на занятиях по физике.
Дидактический материал предназначен
для организации дифференцированной
работы студентов на занятиях по физике.
Данное учебное пособие составлено в полном соответствии с ныне действующей учебной рабочей программой по физике для студентов первого курса.
Задачи расположены в порядке возрастания сложности: задачи 1с. простые, без преобразования формул; 1д. задачи с преобразованием формул изучаемого материала; 1в. задачи на применение ранее изученного материала.
Задачи 1с.- 4с.; 1д. – 4д; 1в – 4в; предназначены для самостоятельных работ на занятии. Задачи 5с; 5д; 5в; предназначены для домашнего выполнения. Задачи 6с; 6д; 6в; решают в аудитории. Задачи предназначаются для индивидуальной работы студентов, как в аудитории, так и дома.
Сборник задач позволяет проводить самостоятельные работы в четырёх вариантах: 1- 1с; 1д; 1в; 2 – 2с; 2д; 2в. и т. д. по всем разделам и темам изучаемыми студентами во втором семестре.
В пособии
содержатся расчетные задачи по всем
разделам курса физики . Расположение
задач соответствует структуре программы
. Задачи отобраны из сборника задач и
вопросов для средних учебных заведений
под общей редакцией Р.А.Гладковой. номера
соответствующих задач по сборнику
указаны в скобках. Поэтому, ознакомившись
с задачами, стоит начинать решения более
простых для Вас задач, постепенно
переходя к более трудным.
Расположение
задач соответствует структуре программы
. Задачи отобраны из сборника задач и
вопросов для средних учебных заведений
под общей редакцией Р.А.Гладковой. номера
соответствующих задач по сборнику
указаны в скобках. Поэтому, ознакомившись
с задачами, стоит начинать решения более
простых для Вас задач, постепенно
переходя к более трудным.
Задача считается правильно решенной в том случае, если приведено полное решение, из которого следует правильный ответ. Решение должно быть завершено числовым ответом. Числовой ответ без решения не засчитывается в качестве правильного решения задачи. Решение задачи только в общем виде при наличии числовых данных также не считается достаточным.
Общие правила решения задач по физике
Для должной подготовки к решению задач на государственной аттестации необходимо знать все формулы и законы, но этого явно мало. Требуется определенный опыт, который может быть накоплен лишь в процессе решения задач.
Решение
задач расчетного характера можно
разделить на несколько этапов.
Внимательно прочитайте условие задачи, определите раздел физики, к которому относится данная задача, попытайтесь оценить её трудность.
Запишите решение задачи в сокращенном виде, используя общепринятые обозначения физических величин. Полное условие задачи переписывать не следует.
Переведите единицы измерения данных физических величин в систему СИ. В редких случаях можно решать задачу, используя внесистемные единицы измерения, а в систему СИ перевести окончательный результат.
Проанализируйте условие задачи и дайте пояснительный рисунок, схему или график зависимости между переменными величинами, если это необходимо. Определите какие соотношения и физические законы необходимо использовать при решении данной задачи, письменно обоснуйте их применение, дайте пояснение к вводимым обозначениям, составьте в соответствии с ними нужное количество уравнений, связывающих физические величины между собой.
 При
этом число уравнений не должно быть
больше числа неизвестных в задаче.
При
этом число уравнений не должно быть
больше числа неизвестных в задаче.При записи уравнений следует обратить особое внимание на характер величин, входящих в это уравнение. Если величины скалярные, то уравнение нужно решать алгебраически. Если величины векторные, то уравнение можно решать алгебраически, предварительно взяв проекции векторов на выбранные оси, или использовать геометрические построения, полученные по законам сложения и вычитания векторов.
Решите задачу в общем виде, используя буквенные обозначения физических величин. Полученная в результате формула должна содержать только физические величины, заданные в условии задачи, необходимые табличные данные и физические постоянные.
Произведите проверку полученной формулы с помощью размерностей величин, входящих в эту формулу. Если размерность правильная, только тогда стоит переходить к производству вычислений. Если полученная размерность не соответствует искомой величине, это значит, что полученная формула неверна и тратить время на вычисления не нужно.
 Следует проверить
составленные уравнения и решения,
полученной системы.
Следует проверить
составленные уравнения и решения,
полученной системы.
Если формула простая, то можно в рабочую формулу подставлять числовые значения величин вместе с их наименованиями.
При решение квадратного уравнения, когда буквенные коэффициенты громоздки, можно использовать их числовые значения, не указывая их наименований, при условии, что все физические величины были выражены в системе СИ.
Подставьте в полученную формулу числовые значения данных в задаче величин и, используя при необходимости значения физических постоянных и табличные величины, определите числовое значение искомой величины.
При
производстве вычислений, когда числовые
значения очень большие или очень
маленькие, удобно записывать числа в
стандартной форме, используя порядок
величин. Например, масса тела равна 150
т. При переводе в систему СИ масса будет
равна 150000 кг. Это значение массы удобно
для дальнейших вычислений записать в
виде 1,5 ∙ 10 5 кг и т.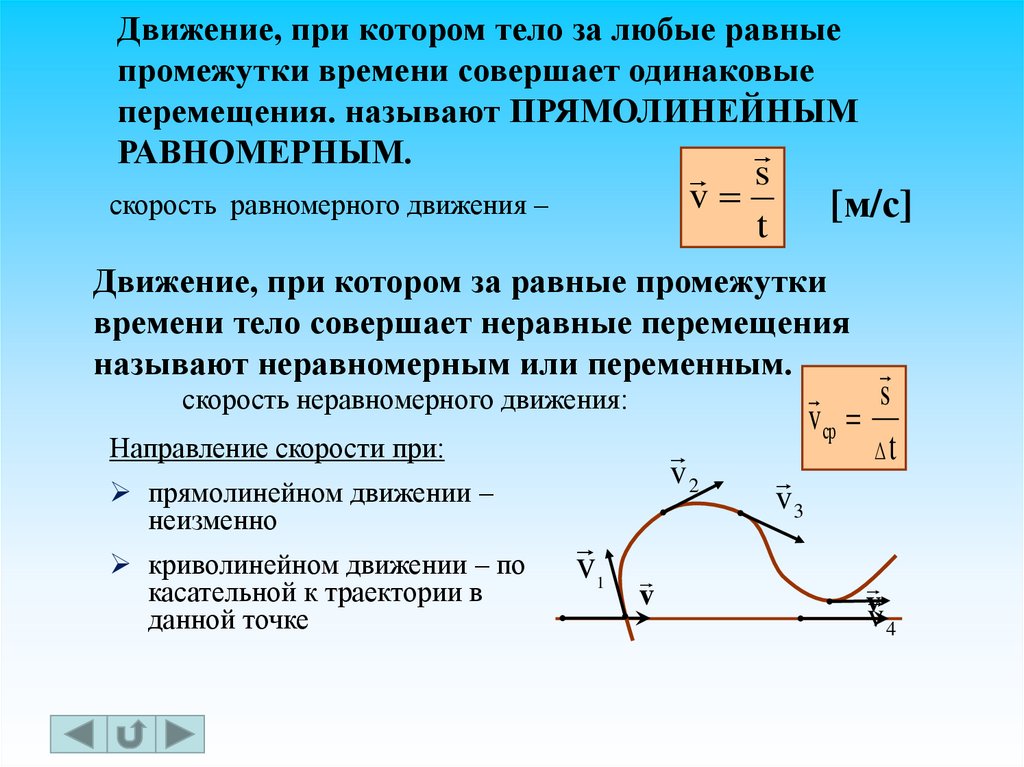 д.
д.
Запишите ответ в соответствии с требованиями, сформулированными в условии задачи, выделив его на отдельной строчке.
Механика. 1
Путь и перемещение. Равномерное прямолинейное движение. Скорость движения.
1с.Скорость зайца 15 м\с, а скорость дельфина 72 км\ч. Кто из них имеет большую скорость?
Ответ: дельфин
2с. За 5ч 30 мин велосипедист проделал путь 99 км. С какой средней скоростью двигался велосипедист?
Ответ: 5 м\с
3с.Вычислите среднюю скорость лыжника, прошедшего путь 20 км за
3 ч.
Ответ:6.66 км\ч.
4с. В течение 30 с поезд двигался равномерно со скоростью 72 км\ч. Какой путь прошел поезд за это время?
Ответ: 600м.
5с.Пассажирский реактивный самолет Ту – 154 пролетел над лесом за 1 мин. Определите протяженность леса в направлении полета самолета, если его скорость 850 км\ч.
Ответ: 14. 2 км.
2 км.
6с. За сколько времени плывущий по течению реки плот пройдет 15 км, если скорость течения 0.5 м\с ?
Ответ: 8 ч 20 мин.
1д. Уравнение движения грузового автомобиля имеет вид
х1 = -270 + 12t, а уравнение движения по обочине того же шоссе пешехода – вид х2=-1,5t. Сделать рисунок и найти положения автомобиля и пешехода в момент начала наблюдения. С какими скоростями и в каком направлении они двигались? Когда и где они встретились?
Ответ: 12 м\с, вправо; 1.5м\с, влево; 20с; -30 м.
2д. Движение двух велосипедистов заданы уравнениями: х1= 5t, х2=150 – 10t. Построить графики зависимости х=х(t). Найти место и время встречи.
Ответ: 50м; 10с.
3д.Написать
уравнения движения тел, изображенных
на рисунке, если автобус движется
равномерно вправо со скоростью 20 м\с,
легковой автомобиль – влево со скоростью
15 м\с, мотоциклист – влево со скоростью
10 м\с, дерево покоится в данной системе
отсчёта. Найти: а) координату автобуса
через 5 с; б) координату легкового
автомобиля и пройденный путь через 10с;
в) через сколько времени координата
мотоциклиста будет равна -600м; г) когда
автобус проходил пост ГАИ; д) где был
легковой автомобиль за 20 с до начала
наблюдения.
Найти: а) координату автобуса
через 5 с; б) координату легкового
автомобиля и пройденный путь через 10с;
в) через сколько времени координата
мотоциклиста будет равна -600м; г) когда
автобус проходил пост ГАИ; д) где был
легковой автомобиль за 20 с до начала
наблюдения.
Ответ: х1=500+20t; х2= 200 – 15t; х3=-300 -10t; х4=0; х5=800; а) 600 м; б)50 м, 150 м; в) 30 с; г) -25 с; д) 500м.
4д.Два поезда идут навстречу друг другу со скоростями 36 км\ч и
54 км\ч . Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 6 с. Какова длинна второго поезда?
Ответ: 150 м.
5д. Вертолёт летел на север со скоростью 20 м\с. С какой скоростью и под каким углом к меридиану будет лететь вертолёт. Если подует западный ветер со скоростью 10 м\с?
Ответ: 22 м\с ,27º
На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути, пройденного телом, от времени?
1в. Вертолёт держит
курс на северо – восток под углом 15º с
направлением на север, но перемещается
точно на север. Найти скорость восточного
ветра, если скорость вертолёта в системе
отсчёта, связанной с движущимся воздухом,
равна 90 км\ч.
Вертолёт держит
курс на северо – восток под углом 15º с
направлением на север, но перемещается
точно на север. Найти скорость восточного
ветра, если скорость вертолёта в системе
отсчёта, связанной с движущимся воздухом,
равна 90 км\ч.
Ответ:23 км\ч.
2в.Скорость продольной подачи резца токарного станка 12 см\мин, а поперечной подачи 5 см\мин. Какова скорость резца в системе отсчёта, связанной с корпусом станка?
Ответ: 13 см\мин.
Основы кинематики (8-й класс)
Цель урока: повторение, обобщение и закрепление знаний и основных понятий по теме “Основы кинематики”; совершенствование навыков постановки опытов, решения экспериментальных задач, развитие навыков расчета скорости, ускорения, перемещения; развитие аналитического мышления, умения анализировать и делать выводы при проведении опытов, развитие устной речи.
Оборудование: штативы, желоба, игрушечный
автомобиль, линейка, проградуированная в
секундах; мяч, секундомер, сантиметровая лента,
плакаты с частями формул кинематики, компьютер,
мультимедийный проектор.
План урока:
- Организационный момент;
- Повторение основных кинематических величин и формул;
- Самостоятельная работа;
- Демонстрация опытов и решение задач по экспериментальным данным;
- Задание на дом;
- Подведение итогов.
Ход урока
Учитель (У): Здравствуйте, ребята. Садитесь, пожалуйста. Сегодня на уроке нам предстоит повторить и систематизировать основные сведения и знания по кинематике.
В руках у меня линейка, которая позволяет определять время реакции человека.
Время реакции – промежуток времени от начала сигнала до реакции организма человека на этот сигнал. Оно зависит от возраста, тренированности, самочувствия человека.
Ребята, как вы думаете, зачем нужно знать время реакции?
Ученики предлагают свои версии ответа на
вопрос.
У: Совершенно верно. А кто из вас знает свое время реакции? Кто хочет его определить?
Выходят 2 ученика.
У: Я отпускаю линейку, а вы должны ее поймать. Время реакции у одного ученика – 0,202 с, у другого – 0,197 с. (линейка проградуирована в секундах). Ребята, как вы думаете, какой принцип лежит в основе создания этого прибора?
Ученик: линейка свободно падает под действием силы тяжести. Ее движение – равноускоренное, с ускорением свободного падения 9,81 м/с2.
У: Правильно! К этому прибору мы еще вернемся. А сейчас повторим основные понятия и формулы кинематики.
Проводится фронтальный опрос.
- Что такое механика? Что она изучает?
- Что называется механическим движением?
- Почему механическое движение относительно?
- Что такое система отсчета и как она выбирается?
- Какие системы координат вы знаете?
- Что такое тело отсчета?
- Какие физические величины характеризуют механическое движение?
- В чем заключается основная задача механики?
- Какова классификация механического движения?
- Что такое равноускоренное движение?
- Что называется ускорением и в каких единицах оно измеряется?
- Что называется свободным падением?
- Чему равно ускорение свободного падения на полюсе и на экваторе и почему эти величины различны?
- Что называется перемещением?
Ученики отвечают на вопросы правильно.
У: Отлично! А теперь вспомним формулы для расчета равноускоренного движения. На доске представлены отдельные части формул. Необходимо правильно их собрать и прокомментировать.
Выходит 1 ученик, собирает правильно формулы на магнитной доске и рассказывает, в каких случаях и для расчета чего служит каждая формула.
; ; S=; ;
; ;
У: Молодцы! Вы показали хорошее знание теории, а сейчас посмотрим, как вы умеете применять эти знания на практике. Приготовили по половинке листочка, подписали свой вариант.
На экране представлены графики зависимости скорости от времени. Написано, что необходимо определить: 5 вопросов – 5 правильных ответов – 5 баллов (рис.1). На выполнение работы отводится 6 мин. Кто выполнит работу раньше, поднимает руку, я подойду и возьму работу.
Вариант 1.
Вариант 2.
Определить:
- Начальную скорость
- Конечную скорость
- Время движения
- Ускорение
- Перемещение
Учащиеся выполняют самостоятельную работу.
У: Отложили, пожалуйста, ручки. Передаем работы по рядам. На экране представлены ответы, вы можете себя проверить и оценить свою работу, а оценки я скажу на следующем уроке. А теперь применим свои знания для решения экспериментальных задач.
Задача № 1 “Движение автомобиля по наклонной плоскости из состояния покоя”.
Вызываются 2 инженера – экспериментатора, а инженерами – теоретиками будет весь класс. Ребята, что мы можем измерить при проведении эксперимента, а какие характеристики можем рассчитать?
Ученики: Измерить можем расстояние S,
пройденное автомобилем, время t, затраченное на
движение, высоту наклонной плоскости h,
рассчитать – ускорение а, конечную скорость ?.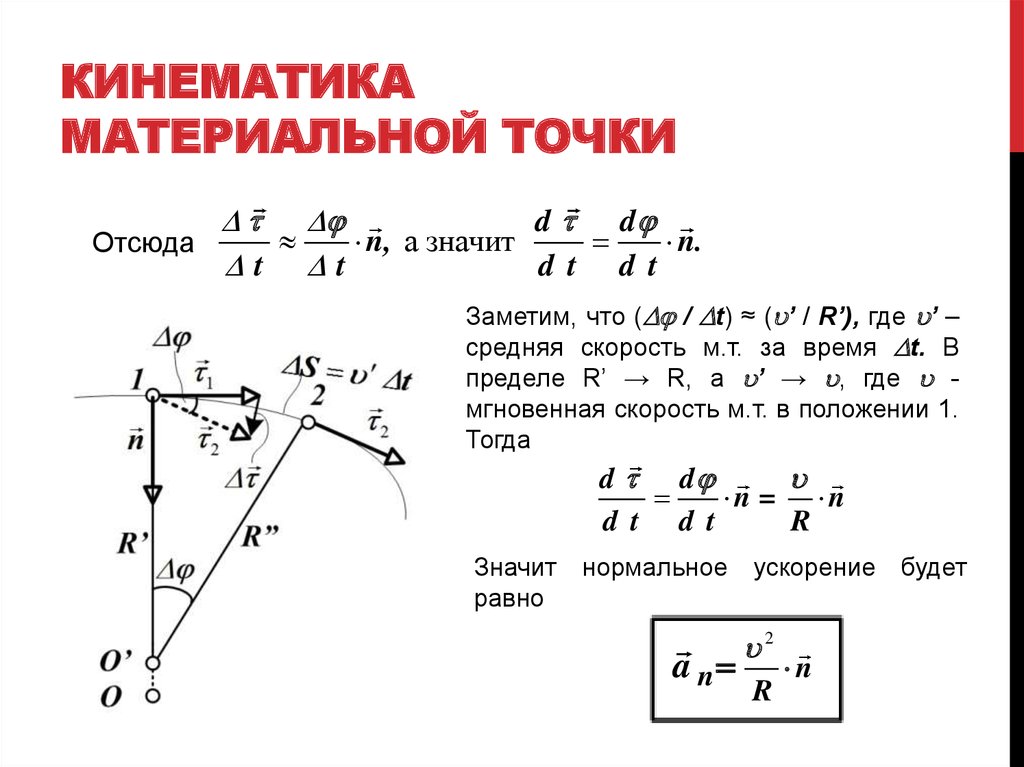
У: Мы будем изменять высоту наклонной плоскости и записывать полученные данные в зависимости от угла наклона.
Инженеры-экспериментаторы запускают автомобиль, измеряя время движения, пройденный путь, высоту наклонной плоскости. Данные заносятся в таблицу 1 на экране.
Таблица 1
| № опыта | 1 | 2 | 3 |
| Перемещение Ѕ, м | |||
| Время t, с | |||
| Высота h, м | |||
| Ускорение a, м/с2 | |||
| Конечная скорость ?, м/с |
Ученики рассчитывают по полученным измерениям
ускорение а, конечную скорость ? и заполняют
таблицу 1.
У: Ребята, какой вывод можно сделать,
анализируя полученные значения?
Ученик: Скорость и ускорение зависят от угла
наклона: чем больше угол наклона, тем больше
скорость и ускорение. Эти знания можно
использовать при катании с горок.
У: Молодец! А при решении задач динамики мы
еще раз подтвердим этот вывод. С первой задачей
мы справились.
Задача № 2 “Движение мяча по вертикали с начальной скоростью под действием силы тяжести”.
У: Какие физические величины мы можем измерить, а какие – рассчитать?
Ученик: Можем измерить время и высоту подъема, а определить начальную скорость.
Вызываются 2 инженера – экспериментатора и 1 теоретик. Они подбрасывают мяч, измеряют высоту подъема мяча, время движения мяча вверх и вниз. Данные заносятся в таблицу 2 на экране.
Таблица 2
| № опыта | 1 | 2 | 3 |
| Высота H ,м | |||
| Время t, с | |||
| Начальная скорость ,м/с |
Ученики рассчитывают по полученным измерениям
начальную скорость .
У: Если мяч брошен с начальной скоростью вверх, то каким будет движение мяча?
Ученик: Мяч будет двигаться под действием силы тяжести равноускоренно. Так движение по вертикали обратимо, то можем для расчета исследовать движение мяча вниз и рассчитать начальную скорость по формуле
Можно проверить свои расчеты, применив формулу
У: Очень хорошо! А теперь вернемся к нашему прибору для определения времени реакции. Кто объяснит принцип его действия?
Ученик: Линейка падает свободно, без начальной скорости. Следовательно, расстояние, пройденное линейкой, определяется по формуле . Зная Н, можно определить t. Это и есть время реакции.
У: Молодец! Ставлю оценку “5”. Ребята, вы
поняли, как сделать такой прибор? Ваше домашнее
задание – изготовить прибор для измерения
времени реакции человека и измерить время
реакции у своих родственников и друзей.
Мы повторили основные понятия по кинематике и решили экспериментальные задачи. У вас есть вопросы? Спасибо за работу на уроке. До свидания.
Литература:
- Громов С.В., Родина Н.А. Физика. 8 класс. – М.: Просвещение, 2006.
- Урок физики в современной школе. Творческий поиск учителей. – М.: Просвещение, 1993.
Основные понятия кинематики | План-конспект урока по физике (9 класс) по теме:
Урок №1 Основные понятия механики
- Что такое механическое движение?
- Механическое движение – это изменение положеия тела в прострастве относительно других тел.
- NB! Всякое движение относительно. Нет абсолютного покоя или абсолютного движения. Обязательно надо указывать относительно ЧЕГО движется тело.
- Тело отсчета (ТО).
За ТО может быть принято любое тело. Мы просто в данной задаче считаем его неподвижным.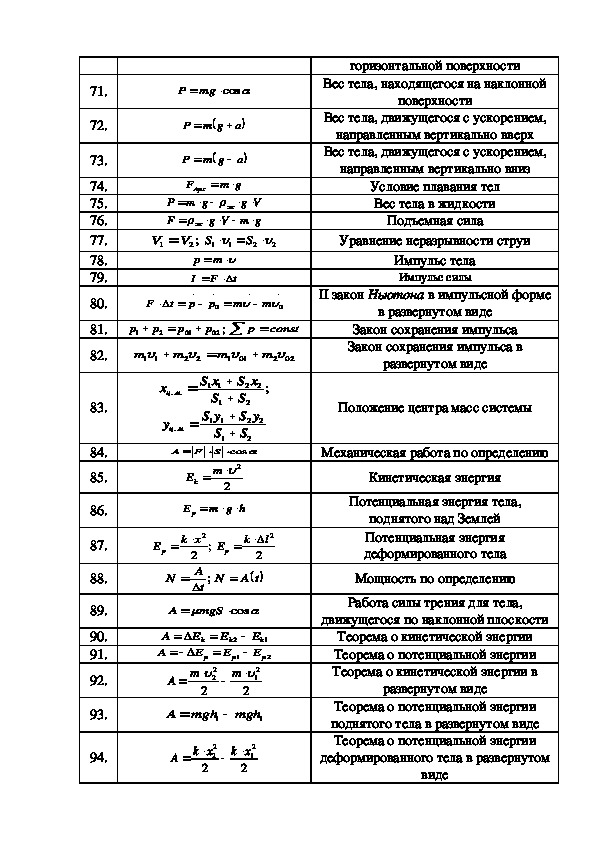
- В чем заключается основная задача механики (ОЗМ)?
Определить положение тела в любой момент времени.
- Большинство материальных тел имеют совершенно определенные размеры. Поэтому возникает вопрос: “положение какой точки тела требуется определить в ОЗМ”?
Проблему можно решить если тело можно будет считать точкой, а это возможно, если выполняются следующие условия:
- размеры тела малы по сравнению с расстояниями, про которые идет речь в задаче,
- все точки тела движутся по одинаковым траекториям – поступательное движение.
Вывод: тело, размерами которого в данной задаче можно пренебречь, называется материальной точкой (МТ).
МТ – это модель реального тела, которую мы будем очень часто использовать.
Но надо учитывать, что корректное использование модели материальной точки требует тщательного анализа условия конкретной задачи.
Например.
Если мы изучаем движение Земли вокруг Солнца, то в этой задаче Землю можно считать материальной точкой, так как размер Земли (d=6400км) гораздо меньше радиуса земной орбиты (R=150 000 000 км).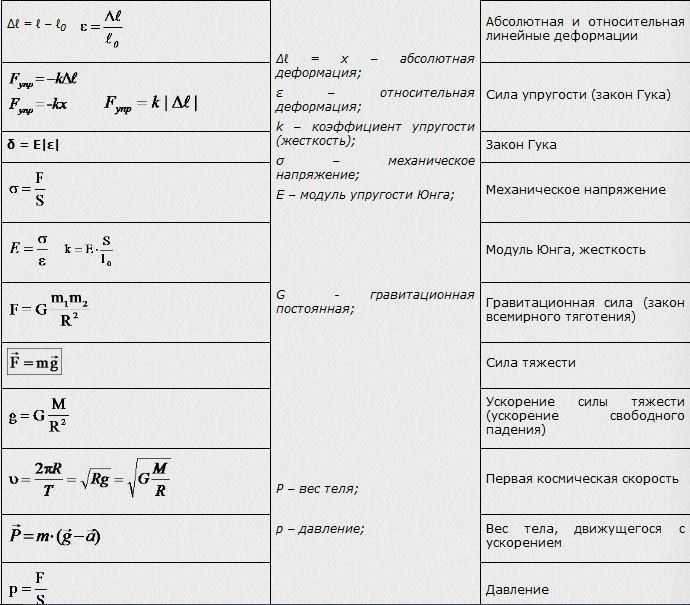
Если мы изучаем движение материков, то Земля уже никак не может считаться материальной точкой.
Мы будем различать два вида движения: поступательное и вращательное.
Поступательное движение – все точки тела движутся по одинаковым траекториям. Например, движение лифта, движение кабины колеса обозрения и др.
Вращательное движение – все точки тела движутся по окружностям, центры которых лежат на прямой, которая называется ось вращения.
Любое движение можно представить, как сумму поступательного и вращательного.
Мы примем это утверждение без доказательства.
Урок №2 Способы описания движения материальной точки. Система отсчета.
- Проблема
Какие числовые данные нужно иметь, чтобы можно было утверждать, что мы решили ОЗМ?
Решим проблему, рассматривая частные случаи движения, и попытаемся сделать правильные выводы.Из геометрии известно, что для того, чтобы определить положение точки, нужно знать ее координаты.
- Способ описания движения с помощь.
 координат, конечно, называется координатный.
координат, конечно, называется координатный.
Рассмотрим самое простое движение: мотоциклист (материальная точка – МТ) движется вдоль прямой. | Для описания положения МТ достаточно одной координатной оси OX. | Для решения ОЗМ надо знать данные таблички (числовые данные в ней это просто пример):
или зависимость координаты от времени (это в математике называется функцией). Записывается это в физике так: X=X(t) (в математике это выглядит так).
Для описания движения вдоль прямой и решения ОЗМ нам потребовалось знать координату x в любой момент времени. Такое движение называется одномерным. | ||||||||||||||||||||||||
Рассмотрим самое более сложное движение:лодка (МТ) плывет по поверхности озера. | Для описания положения МТ необходимо иметь две координатные оси OX и OY. | Для решения ОЗМ нужно знать данные двух табличек, например таких:
или эти таблички можно записать как две функции: x=x(t), y=y(t) Для описания движения на плоскости и решения ОЗМ нам потребовалось знать координаты x и y в любой момент времени. Такое движение называется двумерным | ||||||||||||||||||||||||
И наконец, рассмотрим самый общий случай движения: ракета (МТ) движется в пространстве. |
| Для решения ОЗМ нужно знать теперь данные уже трех табличек, например таких:
или эти таблички можно записать как три функции: x=x(t), y=y(t), z=z(t) движения в пространстве и решения ОЗМ нам потребовалось знать координаты x , y, z в любой момент времени. Такое движение называется трехмерным. |
Вывод: Таким образом, в координатном методе описания движения, для решения ОЗМ необходимо знать три функции зависимости координат от времени:
x=x(t), y=y(t), z=z(t)
Какой способ определения положения точки известен в геометрии?
- Задать положение точки можно еще с помощью вектора. Такой способ описания движения называется векторный
Рассмотрим движение МТ по плоскости. | В механике вектор, задающий положение точки, начинается, например, в 0 системы координат и заканчивается в той точке, в которой находится тело. Этот вектор называется – радиус-вектор. Чтобы решить ОЗМ надо знать
или
или
Связь координатного и векторного способа описания движения.
В прямоугольном треугольнике АВО нам известны два катета. Поэтому по теореме Пифагора мы можем найти гипотенузу ОА или модуль радиус-вектора: r2=x2+y2 Направление вектора мы узнаем, если вычислим угол АОВ. А для этого нам надо знать какую-нибудь его тригонометрическую функцию, например: sin =y/r В дальнейшем нам очень пригодятся подпольные математические правила. | |
Теперь легко можно все понять для движения в трехмерном пространстве. | Как ответить на аналогичные вопросы в трехмерном случае – догадайтесь сами. |
Тело отсчета, система координат и приборы для измерения времени (часы) – называется системой отсчета.
Фактически, система отсчета – это просто лаборатория, в которой есть приборы для измерения положения тел и времени.
Упражнение
Определите координаты точек А, B, C, D, K, M.
Урок №3 Перемещение.
- Что надо знать, чтобы вычислить положение мат. точки в любой момент времени?
Для ответа на этот вопрос воспользуемся векторным способом описания движения.
- Какие у пермещения есть замечательные свойства?
- Так как перемещение – вектор, то если тело совершило подряд два перемещения, то
| |
| |
|
- результирующее перемещение можно найти простым сложением первых двух:
S=S1 + S2
- Если нам каким-нибудь образом удастся его узнать, то мы сможем рещить основную задачу механики!!!! Действительно, из определения и правила сложения вектров следует:
r(t)=ro + S
- Путь и перемещение, конечно, в общем случае не совпадают!
Задания.
- Попробуйте перечислить ??? отличия перемещения и пути.
Решение
|
Урок №4 Средняя скорость. Опрос.
Проблема
Чтобы решить основную задачу механики необходимо знать перемещение S материальной точки. Но как узнать пермещение?
Это в 7 классе и раньше | Так мы это будем понимать теперь в 9 классе |
V=S/t где S – путь пройденный телом за время t
Мы не будем забывать это определение и в 9 классе, но чтобы не путаться будем в дальнейшем называть эту скорость среднепутевой и тогда эта формула может быть использована для любых траекторий.
| Теперь мы рассматриваем не только прямолинейное движение и путь не совпадает с модулем перемещения. Поэтому скорость мы определим так:
|
Опрос “Основные понятия мехнаики”.
- Механическое движение и его относительность.
- Материальная точка.
- Тело отсчета.
- Поступательное и вращательное движение. Примеры.
- Основная задача механики.
- Координатный способ описания движения.
- Векторный способ описания движения.
- Связь векторного и координатного способов.
- Система отсчета.
- Перемещение.
- Путь.
- Траектория.
Урок №5 Правило сложения скоростей
Проблема
Мы знаем, что всякое движение относительно.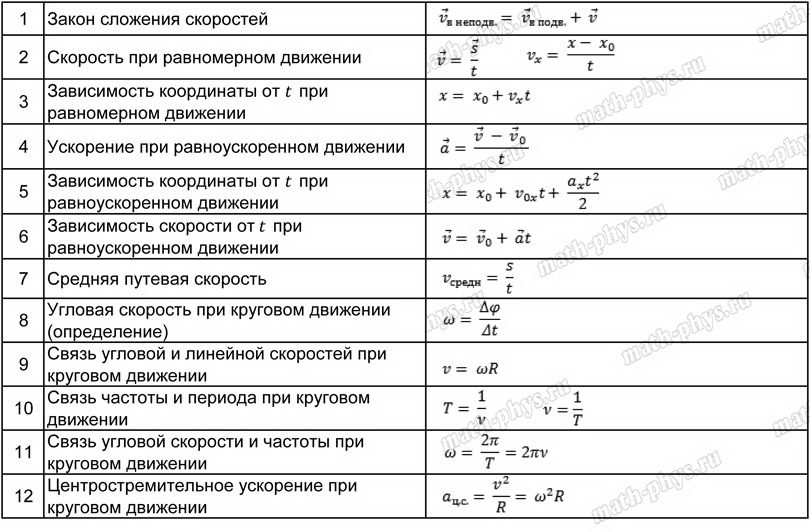 Для описания движения необходимо указать систему отсчета, относительно которой рассмативается движение. Следовательно, физические величины, описывающие движение: радиус-вектор, перемещение, скорость, должны меняться при изменении сситемы отсчета. Например, относительно класса (система отсчета “класс”), парты имеют скорость равную нулю, а относительно Солнца (система отсчета “Солнце”) они движутся со скоростью примерно 30 км/с! Это мы хорошо знали еще в 7 классе.
Для описания движения необходимо указать систему отсчета, относительно которой рассмативается движение. Следовательно, физические величины, описывающие движение: радиус-вектор, перемещение, скорость, должны меняться при изменении сситемы отсчета. Например, относительно класса (система отсчета “класс”), парты имеют скорость равную нулю, а относительно Солнца (система отсчета “Солнце”) они движутся со скоростью примерно 30 км/с! Это мы хорошо знали еще в 7 классе.
На практике очень часто приходится пересчитывать кинематические величины при переходе из одной системы отсчета в другую. Например, в 7 классе, мы умели вычислять скорость лодки относительно берега и относительно воды (в стоячей воде).
Наша задача в 9-м классе найти математические законы, по которым можно пересчитать скорость, перемещение и др. физические величины при переходе из одной системы отсчета в другую.
Решение проблемы
Сделать это очень просто.
Систему К мы будем считать неподвижной, а систему отсчета К1, движущейся со скоростью V относительно системы К | |
Рассмотрим материальную точку А, которая движется относительно обеих систем отсчета. Построим радиус-вектора в начальный момент времени точки А:
Очевидно соотношение между этими векторами: (*) | |
Через некоторое время материальная точка и система отсчета К1 изменят свое положение относительно друг друга. Изменятся, соответственно, и радиус-вектора, но соотношение между ними останется в силе: (**) |
Вычтем из второго уравнения первое и сгруппируем слогаемые:
Заменим разность радиус-векторов на соответствующие перемещения (мы используем уже известную нам формулу для решения основной задачи механики: r(t)=ro + S, из которой следует, что S=r(t) – ro. Получим:
Получим:
(***)
где вектор S – перемещение мат. точки относительно системы отсчета К,
вектор s’ – перемещение мат. точки относительно системы отсчета К1,
вектор S – перемещение системы отсчета К1 относительно К.
Уравнение (***) дает нам возможность считать перемещение в разных ситемах отсчета. Эта математическая запись того факта, что перемещение относительно.
Разделим правую и левую часть уравнения (***) на время, получим:
(****)
где:
вектор v- скорость мат. точки относительно системы К (неподвижной ситемы отсчета),
вектор v’ – скорость материальной точки относительно подвижной системы отсчета (система К1),
вектор V – скорость системы K1 относительно системы К (скорость подвижной системы относительно неподвижной).
- Уравнение (****) называется “Правило сложения скоростей”.
- По этому уравнению можно легко сосчитать скорость в разных системах отсчета.
- Это уравнение годится для любых движений (не слишком быстрых).

- Это математическая запись того факта, что скорость относительна.
Урок №6 Мгновенная скорость. Равномерное движение.
Проблема
Для решения основной задачи механики необходимо знать перемещениеS:
Для вычисления перемещения к моменту времени t мы можем воспользоваться средней скоростью Vср:
Но по этой формуле можно вычислить лишь перемещение к моменту времени t!
Например, пусть шофер перед тем, как отправиться в рейс заехал в кафе пообедать и просидел там 1 час, а потом проехал 100 км за 1 час. Таким образом его средняя скорость составила 100км/2ч=50км/ч. Зная эту скорость мы можем правильно вычислить положение автомобиля через 2 часа, т.е. за тот промежуток времени, за который эта средняя скорость определена. Но диспетчер здорово ошибется, если попробует по этой средней скорости вычислить положение автомобиля через 1 час движения: 50км/ч*1ч=50км (ведь мы же знаем, что в это время шофер только вышел из кафе, которое находилось за углом автобазы!!!)
Получается, что средней скорости недостаточно, чтобы узнать положение мат. точки в любой момент времени: она теряет информацию о движении. Как же поступить???
точки в любой момент времени: она теряет информацию о движении. Как же поступить???
Решение проблемы
Идея!
Ошибка диспетчера была бы невозможна, если бы он имел полную информацию о движении мат. точки, т.е. знал как двигалось тело в каждой точке траектории!
Как осуществить эту идею?
- Разобьем все время движения на очень маленькие отрезки.
- Отрезки должны быть настолько малы, чтобы можно было считать движение на них прямолинейным и равномерным.
- Определим среднюю скорость на каждом маленьком отрезке времени.
Средняя скорость на очень маленьком отрезке времени называется мгновенной скоростью движения мат. точки.
- Зная мгновенную скорость в каждой точке можно вычислить соответствующие перемещения:
Теперь не составляет труда найти полное перемещение за любое конечное время!!!!
и, наконец-то, решить основную задачу механики:
Как пользоваться таким громоздким способом решения основной задачи механики?
Пример: “равномерное движение”.
Пусть все мгновенные скорости равны между собой и равны некоторой постоянной величине V:
Движение, при котором мгновенная скорость не изменяется (по величине и направлению) называется равномерным.(V=const)
Легко вычисляем перемещение:
Получилась очень знакомая формула! Что и следовало ожидать! Теперь решим основную задачу механики для равномерного движения:
Для других движений этот расчет, конечно, труднее… но мы попытаемся этому научиться
Урок №7 Ускорение. Равноускоренное движение.
Как мы уже поняли, для решения основной задачи механики необходимо знать перемещение S:
(1)
А для вычисления перемещения нужно знать мгновенную скорость в каждый момент времени:
(2)
Тогда можно вычислить правую часть уравнения:
(3)
Проблема
Но где взять мгновенную скорость? К сожалению, ее нельзя вычислить из других законов природы!!!
Приходится поступать следующим образом. Для того, чтобы вычислить скорость в момент времени t нужно сложить начальную скорость vo (скорость в момент времени 0, в начале движения) и изменение скорости Δv:
(4)
Но как найти Δv?
Эта задача очень похожа на проблему поиска перемещения.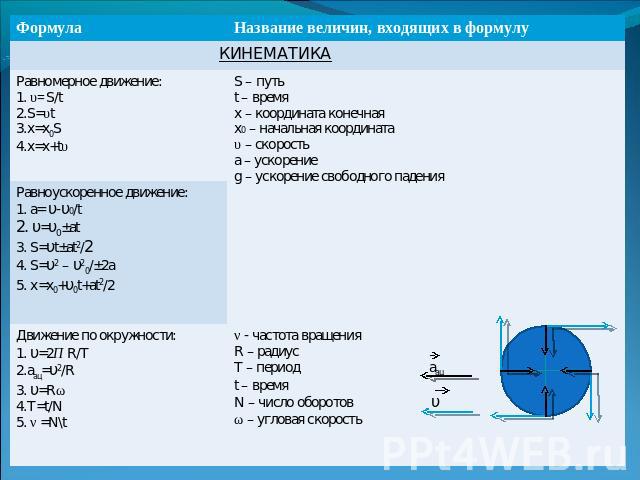 Введем новую для нас физическую величину ускорение (точнее, среднее ускорение) по формуле:
Введем новую для нас физическую величину ускорение (точнее, среднее ускорение) по формуле:
(5)
Здесь мы воспользовались тем обстоятельством, что из формулы (4) следует
(6)
Раз это новая физическая величина, то необходимо указать ед. измерения:
[a]=м/c/c=м/c2
Что показывает нам ускорение?
Пусть t=1, тогдаa= Δv (численно)
Ускорение показывает изменение скорости за единицу времени.
Направление ускорения совпадает с направлением изменения скорости Δv :
Например:
а) “Разгон” (начальная скорость меньше конечной)
б) “Торможение” (конечная скорость меньше начальной)
Теперь можно вычислить мгновенную скорость, т.е. решить нашу проблему:
Эта формула верна для равноускоренного движения.
Равноускоренное движение это такое движение, при котором ускорение мат. точки постоянно. Записывается это так:
Новая проблема.
Но где взять ускорение???
Решение проблемы.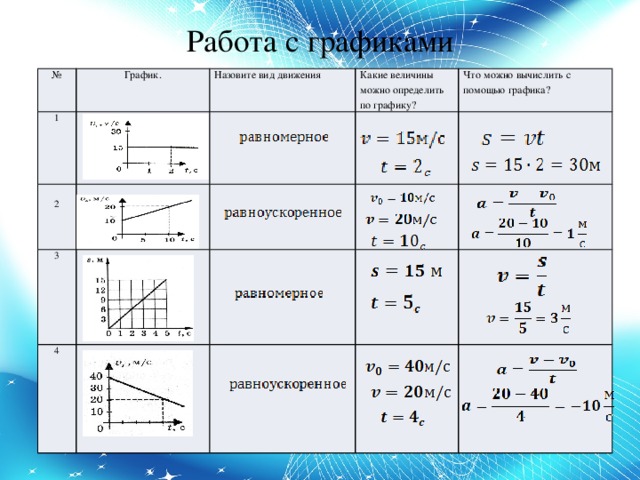
Мир устроен так, что ускорение можно узнать из других законов природы.
Теперь понятно как решать основную задачу механики:
Еще одна проблема.
Как сосчитать что-нибудь по этим формулам? Ведь они векторные!!!
Разберем все на примерах.
Пример №1
“Разгон” вдоль прямой. Все вектора направлены в одну сторону и можно просто написать:
v=vo+at
“Торможение” вдоль прямой.
Вектора скорости направлены против вектора ускорения, поэтому, наверное, надо написать так:
v=vo-at
Но по этой формуле можно получить отрицательный результат. Что это будет означать??? Совершенно очевидно, что это будет означать, что мат. точка движется в сторону противоположную начальной скорости.
Но здесь могут возникнуть проблемы формального характера, которые потом, в более сложных случаях, может привести к ошибкам
Мы уже поняли, что для решения основной задачи механики необходимо знать перемещение , тогда мы сможем узнать положение мат. точки в любой момент времени по формуле:
точки в любой момент времени по формуле:
Чтобы узнать перемещение , надо поступить так: разбить все время движения на очень маленькие интервалы (настолько малые, чтобы можно было считать движения на них равномерным) и вычислить маленькие перемещения за эти промежутки времени, а потом сложить все полученные результаты:
Эту сумму мы уже умеем вычислять для равномерного движения (v=const, ускорение ). Наша задача сегодня научиться вычислять эту сумму для равноускоренного движения, когда ускорение а скорость меняется по закону .
Попробуем это сделать так, рассмотрим самый простой случай равноускоренного движения и для него все посчитаем, а потом попытаемся угадать, что будет в более сложных ситуациях.
Итак, рассмотрим движение вдоль прямой. Причем начальная скорость vo и ускорение a направлены в одну сторону.
Совершенно очевидно, что в этом случае невозможно изменение направление вектора скорости и следовательно можно все вычисления проводить для модулей векторов:
Первый способ (Ну очень простой!!!)
Рассмотрим на графике эту зависимость:
Так как скорость меняется по линейному закону, то легко очевидно, что средняя скорость движения равна средней арифметической в начальный и в конечный момент времени:
Подставим в эту формулу значение скорости в момент времени t и получим:
Теперь, зная среднюю скорость, легко вычислить модуль перемещения:
Ура! Мы получили правильную формулу!
Второй способ (более высоконаучный)
В первом способе мы приняли без доказательства тот факт, что средняя скорость при равноускоренном движении равна среднему арифметическому скоростей в начале и в конце промежутка времени.
Теперь мы попробуем рассуждать немного иначе.
Равномерное движение | Равноускоренное движение |
Рассмотрим график скорости равномерного движения: Перемещение при равномерном движении вычисляется по формуле: S=Vо*t Но если посмотреть на график, то можно легко увидеть, что фигура под графиком скорости – прямоугольник, а площадь прямоугольника равна произведению его сторон, поэтому имеем: площадь прям.=Vо*t=перемещение(S)
| Рассмотрим график скорости равноускоренного движения: Примем (пока без доказательства), что площадь под графиком скорости при равноускоренном движении тоже равна перемещению. Тогда получаем:
S=Vot+at2/2
|
А что делать если ускорение и скорость направлены в противоположные стороны?
График скорости будет убывать и скорость может поменять знак (тело остановилось и поехало в противоположном напрвлении). |
Легко догадаться, что знаки перед начальной скоростью и ускорением будут разными:
S=Vot-at2/2
Но в этом случае перемещение может стать отрицательным. Это надо понимать перемещение в сторону противоположную начальной скорости Vo.
Урок №9 “Ускорение свободного падения”
- Историческая справка
- Эксперимент
- Выводы
- Задачи
Проблема.
Рассмотрим свободное падение тел вблизи поверхности Земли.
Историческая справка
Во времена Аристотеля считалось, что все тела падают на Землю, так стремятся занять на ней свое “естественное положение”, скорость падения зависит от массы тела: чем больше масса тела, тем быстрее падает тело. Действительно, наблюдения показывают, что перышко парит в воздухе гораздо дольше падающего камня. | Аристотель (384 – 322 гг. до н.э.) |
Первым усомнился в правильности взглядов Аристотеля великий Галилео Галилей. Галилею удалось доказать, что
| Галилео Галилей (1564 – 1642). |
Эксперимент
Давайте убедимся в том, что в отсутствии воздуха и легкие и тяжелые тела падают с одинаковой скоростью. Для этого мы воспользуемся трубкой Ньютона. В трубке находится три тела: дробинка, кусочек паралоновой губки и легкая перышко.
Если трубку поставить вертикально, то быстрее всех будет падать дробинка, а последней достигнет дна трубки перышко.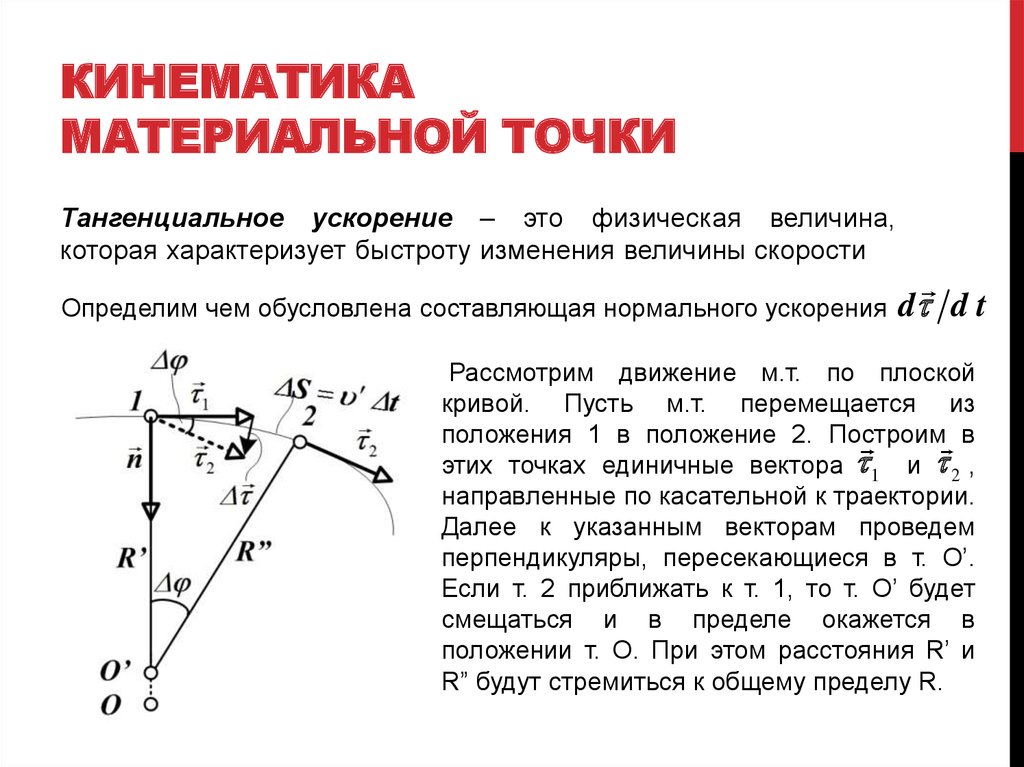
Теперь откачаем насосом воздух из трубки (конечно, откачать весь воздух мы не можем, но сделать его весьма разреженным по нашим силам). Повторим эксперимент – все тела падают с одинаковой скоростью (практически).
Мы можем записать движение свободно падающего тела, например, учебника физики с помощью компьютерной лабортаории. Проанализировав запись, мы приходим к следующим выводам:
- свободное падение является равноускоренным движением (если не учитывать сопротивление воздуха),
- в нашем эксперименте ускорение примерно равно 10м/с2.
Выводы
Все тела, независимо от массы, падают с одинаковым постоянным ускорением, которое называется ускорением свободного падения. и обозначается g.
Ускорение свободного падения равно 9,81м/с2.
Ускорение свободного падения всегда, при любых движениях тела, направлено вертикально вниз.
Все формулы для равноускоренного движения годятся для свободного падения. Надо только в них вместо ускорения а, написать g=9,8м/с2.
Наши любимые формулы получаются такими:
а)тело бросили вниз (начальная скорость и ускорение свободного падения направлены в одну сторону), тело только “разгоняется”:
б)тело бросили вверх (начальная скорость и ускорение свободного падения направлены в разные стороны), тело летит вверх – тормозится, достигает верхней точки, летит вниз – “разгоняется”:
А если не хочется все время мучительно думать о знаках в формулах, то можно написать все в векторном виде:
В таком виде формулы будут правильными для ЛЮБЫХ свободных падений.
Задачи
Камень свободно падает на землю с высоты 80м. Какова скорость камня в момент падения на землю? Сколько времени длилось свободное падение?
Решение
Все очень просто. Свободное падение – это равноускоренное движение с ускорением g=9,8м/с2. Начальная скорость равна 0м/с, так ничего про нее не сказано. Поэтому можно написать:
(1)
(2)
Теперь составим уравнения, подставив конкретные данные в эти функции:
где x – время полета.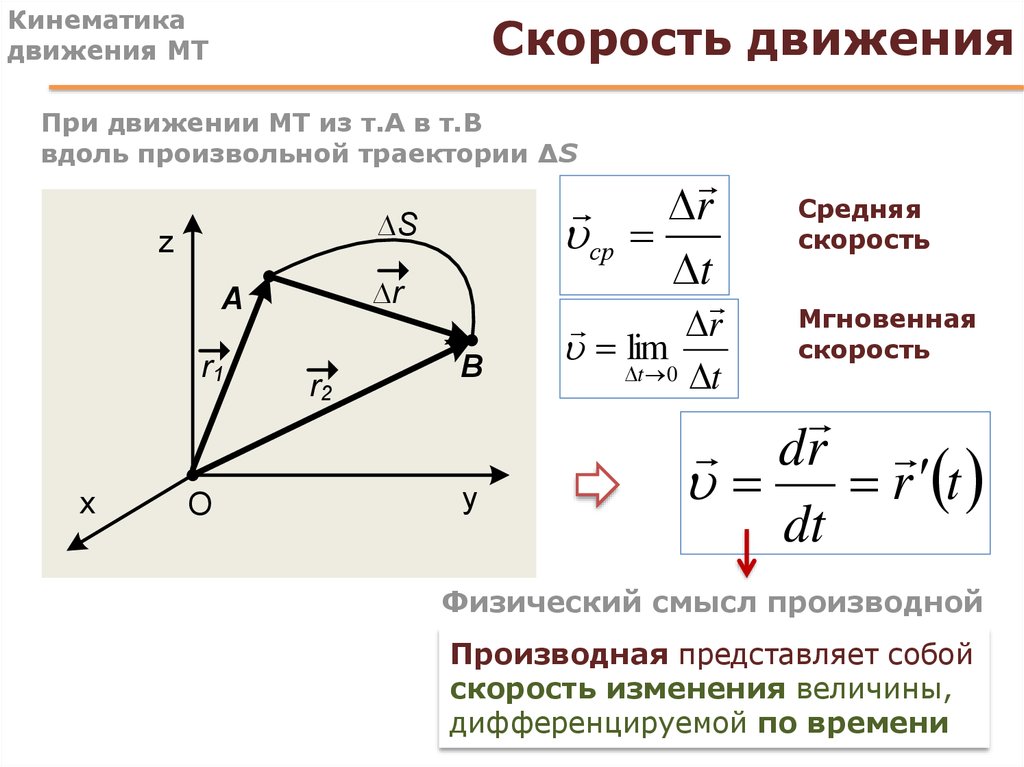
Отсюда получаем: x=4c.
Теперь мы знаем время полета и можем найти скорость. Если подставить данные в формулу (2), то получим:
v(4c)=10м/с2*4с=40м/с
Теперь сами.
Столкните резинку со своего письменного стола. Сколько времени продолжается падение? Какая будет скорость резинки в конце полета?
Урок №10 Скорость и ускорение при движении по окружности
Направление скорости при движении по окружности.
Проблема
Почему искры во время заточки ножа на точильном круге летят по касательной к окружности? |
Решение проблемы.
Направление мгновенной скорости при движении по окружности.
Рассмотрим самой простой случай: пусть материальная точка движется по окружности с постоянной по модулю скоростью. (такая модель для нас удобна, так как нас интересует только то, что происходит с направлением мгновенной скорости).
Как направлен вектор мгновенной скорости при таком движении?
Движение по окружности – это криволинейное движение. | |
Но движение по 4-м хордам совсем не похоже на движение по окружности, поэтому давайте увеличим количество этих хорд и сократим их величину. | |
Теперь, легко догадалась Юлик, чтобы получить “настоящее” движение по окружности надо еще больше сократить размер хорд и еще больше увеличить их число: при этом крошечные хорды практичски станут точками окружности, а направление векторов скорости совпадет с направлением касательной в данной точке к окружности.
|
Выводы.
- Таким образом, мгновенная скорость при движении по окружнсти направлена по касательной, (Поэтому искры точильного летят тоже по касательной).

- Так как мы не использовали в наших рассждениях тот факт, что мат. точка не меняет величину скорости, то можно считать, что наш вывод будет верен и для движения по окружности, когда величина скорости меняется.
Ускорение при движении по окружности с постоянной по модулю скоростью.
Величина ускорения при движении тела по окружности с постоянной скоростью.
Ускорение равно , чтобы найти модуль этого вектора надо вычислить величину
Рассмотрим движение мат. точки на очень маленьком участке траектории АВ. Точки А и В расположены очень близко друг к другу, но мы их на чертеже разнесли подальше, чтобы лучше разобраться в чертеже. Вектора скорости имеют разное направление, но одинаковую величину. | |
Построим вектор изменения скорости . Для этого перенесем вектор V2 в точку А. Построим разность векторов . | |
Рассмотрим треугольники АОВ и ACD.
Следовательно, эти треугольники подобны. Поэтому имеем следующее соотношение: Хорда АВ практически равна дуге АВ, так как точки А и В очень близки друг к другу. Поэтому вместо величины хорды АВ можно подставить величину дуги АВ, которая равна vt. Поэтому имеем: отсюда получаем Теперь получаем то, что хотели: | |
|
|
Направление ускорения при движении по окружности с постоянной по модулю скоростью.
Направлено ускорение к центру окружности, поэтому и называют его центростремительным. |
Инструменты кинематики.
 Прямолинейное движение 9 класс онлайн-подготовка на Ростелеком Лицей
Прямолинейное движение 9 класс онлайн-подготовка на Ростелеком ЛицейВведение
Когда мы рассказываем о чём-то другому человеку, то всегда отбрасываем какую-то информацию, которую считаем неважной. Нас всегда интересует какая-то конкретная задача и информация для её решения. Например, зная рост, обхват груди, талии и т.д., можно купить человеку одежду.
Такая же ситуация и в физике. Мы говорим, что расстояние 360 км машина со средней скоростью 90 км/ч преодолеет за 4 часа. При этом странно спрашивать – насколько раньше передний бампер автомобиля преодолеет это расстояние, чем задний.
Модель
Когда мы говорим слово «модель» в физике, чаще всего имеем в виду уменьшенную копию чего-нибудь, какой-либо образ предмета, его описание, словесное или математическое. Такая копия не является самим «оригиналом», но дает о нем упрощенное представление. Степень упрощения может быть разной в зависимости от того, какой информации нам достаточно. Возьмем модель автомобиля. Некоторые коллекционируют модели, которые выглядят, как настоящие, т.е. дают представление о внешнем виде автомобиля. При этом такая модель не покажет устройство двигателя, но для нашей цели достаточно внешнего вида. Если вы рассказываете другу, как вас обгонял другой автомобиль, вам не обязательно иметь коллекционные модели этих автомобилей, вам не важен внешний вид, вам важно движение и расположение машин. Вам достаточно взять два прямоугольных предмета, например, мобильных телефона и сымитировать на столе обгон.
Возьмем модель автомобиля. Некоторые коллекционируют модели, которые выглядят, как настоящие, т.е. дают представление о внешнем виде автомобиля. При этом такая модель не покажет устройство двигателя, но для нашей цели достаточно внешнего вида. Если вы рассказываете другу, как вас обгонял другой автомобиль, вам не обязательно иметь коллекционные модели этих автомобилей, вам не важен внешний вид, вам важно движение и расположение машин. Вам достаточно взять два прямоугольных предмета, например, мобильных телефона и сымитировать на столе обгон.
Когда происходит упругое столкновение двух шаров, то, кажется, описать их дальнейшее движение несложно – знаем скорости, массы… Но в шарах будут возникать колебания, они будут нагреваться. В некоторых ситуациях и это надо учитывать. Но в рамках модели упругого столкновения мы можем решать конкретные задачи с достаточной точностью.
Основные понятия в кинематике
Если нам необходимо описать движение тела, то мы не будем говорить о его цвете или температуре.
Мы знаем, что от массы зависит изменение скорости тел при взаимодействии. Но в некоторых задачах нас не будут интересовать причины изменения скорости и движения тела. Нужно будет описать движение тела, зная исходные данные: положение, скорость, ускорение и т.д.
Модель, в рамках которой описывается движение, называется кинематика. Важны ли в кинематике размеры и форма тела? Зависит от задачи. В примере с автомобилем, который едет 360 км, размеры автомобиля неважны – на фоне расстояния для нас и легковой, и грузовой автомобиль, и даже самолёт будут одинаково маленькими.
Рис. 1. Пример движения автомобиля
А при решении задачи парковки того же автомобиля его размерами и формой уже пренебречь нельзя.
Для задач, в которых размеры тела не важны придумали модель материальной точки – это обозначение тела, которое рассматривается как точка, имеющая массу. Получается оксюморон (живой труп, горячий снег, мёртвые души) – у точки не может быть массы, но мы всю её туда поместили.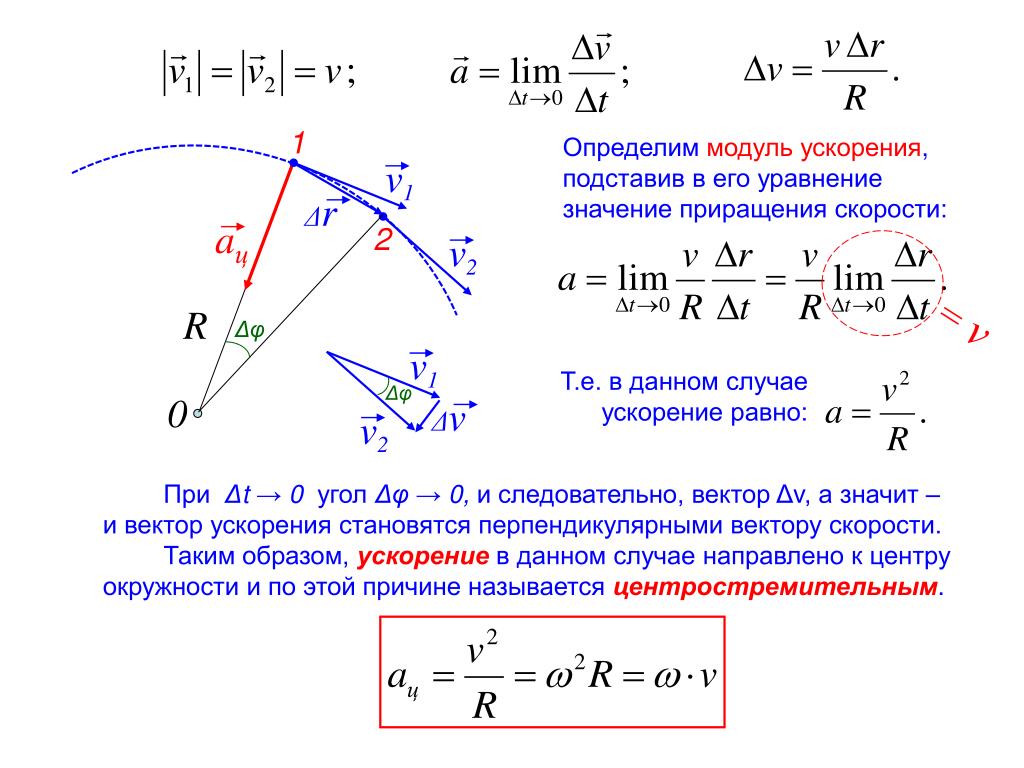
Но такой абстрактный инструмент оказался очень удобным для решения различных кинематических (и не только) задач. Еще одно определение материальной точки – это модель тела, размерами и формой которого в данной задаче можно пренебречь.
Движение – это изменение положения во времени, точка была здесь, а через время оказалась там. В задаче могут быть еще другие тела, могут действовать какие-то силы, и их как-то нужно описывать в единой системе. Введем такую систему.
Выберите на столе какой-нибудь предмет, допустим, компьютерную мышь. А теперь скажите, где она находится, ее положение. Вы скажете что-то вроде «она лежит сразу справа от клавиатуры» или «она в 30 см от экрана». А теперь попробуйте указать ее положение, не упоминая никакие другие предметы. Не получится. Описывая положение тела или точки, нужно выбрать другое тело и относительно него задавать положение, то есть координаты тела.
Рис. 2. Координаты
Координаты – это способ точного указания места, адрес этого места. Этот адрес должен не только идентифицировать место, но и помогать его найти, указывать на его положение в упорядоченном ряду подобных точек (термин «координата» происходит от слова ordinare, которое означает «упорядочивать», с приставкой со-, которая означает «вместе, совместно, согласованно»).
Этот адрес должен не только идентифицировать место, но и помогать его найти, указывать на его положение в упорядоченном ряду подобных точек (термин «координата» происходит от слова ordinare, которое означает «упорядочивать», с приставкой со-, которая означает «вместе, совместно, согласованно»).
Примеры систем координат
Координатой дома на улице является его номер, который отсчитывается с того края улицы, который принят за начало. Номер дома подсказывает, где его можно найти: если мы прошли мимо домов №8 и №10, то дом № 16 должен быть через два дома впереди. Тогда как название улицы зачастую только идентифицирует ее, но не содержит в себе информации о ее положении среди других улиц.
В любом случае, когда мы задаем положение чего-либо, мы в том или ином виде пользуемся его координатами. Например:
— на фото пишут «в первом ряду второй слева Иванов». Координатами являются ряд и место в нем.
— на билетах пишут номер ряда и номер места: координаты ряды и места
— «выйдешь из метро «такого-то», повернешь налево и пройдешь 100м.
— координаты клетки в игре «морской бой»: Б3, Д8…; адреса ячеек в ЭКселе;
Положение тела на поверхности земли можно задать по-разному:
— 30-км на север от Москвы,40км на восток. В данном случае координатами являются пара чисел: расстояние на восток/запад и север/юг – это пример декартовой системы координат;
— 50 км на северо-восток. Здесь координаты угол направления относительно оси восток/запад + длина радиуса-вектора – это пример полярной системы координат.
Выбор системы координат определяется задачей, которую мы в данный момент решаем. В некоторых ситуациях удобно использовать декартову (места в кинотеатре), в некоторых – полярной (в навигации).
В механике мы чаще всего будем использовать прямоугольную (или декартову) систему координат. Есть точка отсчета, то есть начало координат, и есть две взаимно перпендикулярных направленных оси координат. Положение точки задается расстоянием, которое нужно пройти от начала координат вдоль одной и второй оси, чтобы попасть в эту точку.
Рис. 3. Декартова система координат
Вдоль одной оси можно идти в двух противоположных направлениях. Эти направления удобно описать с помощью знака: вдоль оси +, а противоположно оси –.
Рис.4. Направления в декартовой системе координат
Для определения положения точки необходимо:
- Тело отсчета, относительно которого однозначно задавать положение точки в системе координат.
- Прибор измерения времени и момент начала измерения.
Вместе они составляют систему отсчета.
Относительность движения
Все мы знаем, что Земля движется вокруг Солнца, но каждый день мы видим на небе, как Солнце движется вокруг Земли – как с этим быть? Парадокса здесь нет, в системе отсчета, связанной с Землей, Солнце движется вокруг Земли, и некоторые задачи, например, задача о смене дня и ночи, легко решаются в этой системе отсчета. И это не отменяет того, что для задач о движении планет солнечной системы лучше подходит система отсчета, связанная с Солнцем, и в ней планеты движутся вокруг Солнца.
Даже если мы иногда не уточняем систему отсчета, мы ее подразумеваем. Когда мы говорим, что автомобиль движется, мы не имеем в виду, что он движется вместе с планетой вокруг Солнца, мы имеем в виду его движение относительно дороги. А относительно поезда, который едет рядом, автомобиль может быть неподвижен: именно так это увидят пассажиры автомобиля и поезда.
Описание движения зависит от того, относительно чего мы это движение рассматриваем. В физике это называется относительностью движения.
Равномерное и равноускоренное прямолинейное движение
Рассматривать можно много различных параметров движения тела, в зависимости от задачи. Рассмотрим равномерное и равноускоренное прямолинейное движение материальной точки. Здесь главными инструментами будут перемещение, скорость и изменение скорости (с ним связано ускорение).
Движение прямолинейное, значит достаточно рассматривать его вдоль одной оси координат, и положение материальной точки задается координатой .
Перемещение мы задали как вектор , соединяющий начальное и конечное положение движущейся точки.
Рис. 5. Перемещение
Имеется одна ось координат, вдоль которой и направлен вектор перемещения. В такой системе модуль перемещения по-прежнему обозначается длиной вектора, а возможных направлений всего два: в направлении оси или против оси координат. Поэтому, когда ось координат одна, вектор можно задать одним числом, знаком которого обозначим направление вектора. Это число назвали проекцией перемещения на ось и обозначили .
Рис. 6. Проекция перемещения
Итак, в проекции на ось перемещение равно:
Если координата увеличивается, то есть , это значит, что тело движется вдоль оси , и перемещение положительно. Если тело движется против оси , то конечная координата будет меньше начальной , и получится отрицательным. То есть, если вектор перемещения совпадает с направлением оси координат, то знак перемещения – плюс, если противоположен по направлению – минус.
Основная задача механики – определение положения материальной точки в любой момент времени. Выразим из этого уравнения координату :
Теперь, если мы знаем начальное положение тела, поиск координаты тела сводится к поиску перемещения .
Путь и перемещение
Мы много говорили о пути и перемещении, об их различиях, что путь всегда больше или равен модулю перемещения. Мы рассматривали пример с такси, где модуль перемещения один, а путь другой. Если место назначения находится на противоположном берегу реки и по прямой до него 300 метров, нас интересует перемещение, мы указали начальную и конечную точку, и хотим, чтобы нас доставили на эти 300 метров. Но заплатим мы все равно за бензин и время, потраченные на те 5 километров пути, которые мы проехали в объезд по мосту – более короткого пути нет (рис. 7).
Рис. 7. Путь намного больше модуля перемещения при поездке в объезд
Мы также вникали в разницу путевой скорости и скорости по перемещению. Когда хозяин выгуливает собаку, она может всё время бегать около него с путевой скоростью 20 км/ч, не останавливаясь, но за час они так могут перемеситься на 1 км, и модуль их скорости по перемещению будет равен 1 км/ч.
Когда хозяин выгуливает собаку, она может всё время бегать около него с путевой скоростью 20 км/ч, не останавливаясь, но за час они так могут перемеситься на 1 км, и модуль их скорости по перемещению будет равен 1 км/ч.
При прямолинейном движении всё чуть проще. Если тело не меняет направление движения, как при равномерном движении, то путь и модуль перемещения равны, и мы будем говорить только о перемещении – это почти то же самое, только чуть более информативно, так как учитывается еще и направление, кроме модуля. И со скоростью то же: будем рассматривать скорость по перемещению, помня, что она по модулю равна путевой.
При неравномерном прямолинейном движении скорость меняется, и направление движения может измениться на противоположное. Тогда посчитать путь тоже несложно: сложив отрезки до и после изменения направления. Но пути особого внимания не будем уделять, будем так же оперировать перемещением и скоростью по перемещению.
Средняя скорость на участке движения равна перемещению на этом участке, делённому на время, за которое это перемещение было совершено:
Первая модель – равномерное движение. Считаем, что величина скорости не меняется, за любые равные промежутки времени тело совершает одинаковое перемещение. Тогда средняя скорость на любом участке и будет равна той постоянной скорости равномерного движения (запишем сразу в проекции на ось ):
Считаем, что величина скорости не меняется, за любые равные промежутки времени тело совершает одинаковое перемещение. Тогда средняя скорость на любом участке и будет равна той постоянной скорости равномерного движения (запишем сразу в проекции на ось ):
Если выразить отсюда перемещение, то при известной скорости решим главную задачу механики:
Во второй модели, равноускоренного движения, величина скорости меняется. Когда скорость меняется со временем, нам становится важно знать, какое значение она принимает в разные моменты времени. Будем рассматривать скорость на таком небольшом участке, чтобы она не успела заметно измениться. Перемещение на таком участке будет мало, и пройдено оно будет за малое время – мы такое малое время называем мгновением, а среднюю скорость на этом участке – мгновенной скоростью. То есть можно говорить, что это скорость в данной точке в данный момент времени.
Скорость меняется, есть смысл ввести скорость этого изменения, насколько меняется скорость за единицу времени. Скорость изменения скорости мы уже вводили и назвали эту величину ускорением:
Скорость изменения скорости мы уже вводили и назвали эту величину ускорением:
Ускорение – это отношение изменения скорости к промежутку времени , на протяжении которого скорость изменилась на .
Для прямолинейного движения вдоль оси :
При равноускоренном движении считаем, что ускорение постоянно, за любые одинаковые промежутки времени скорость изменяется на одну и ту же величину.
Рис. 8. Равноускоренное движение
Выразим :
Это уравнение при известных начальной скорости и ускорении позволяет нам узнать мгновенную скорость тела в любой момент времени , .
Переход от одной системы отсчета к другой
Как перейти от одной системы отсчета к другой?
Рассмотрим тело, которое в некоторой системе отсчёта движется прямолинейно, а сама система отсчета движется вдоль той же прямой в другой системе отсчета.
Человек идет по вагону поезда по ходу движения или в противоположную сторону. Перейдем к системе отсчета, связанной с Землей. Скорость человека в системе отсчета, связанной с поездом, обозначим . Скорость поезда относительно Земли – это скорость самой системы отсчета относительно Земли, .
Перейдем к системе отсчета, связанной с Землей. Скорость человека в системе отсчета, связанной с поездом, обозначим . Скорость поезда относительно Земли – это скорость самой системы отсчета относительно Земли, .
Для данной модели действует закон сложения скоростей. Запишем в векторном виде, скорость тела относительно Земли равна:
Это уравнение справедливо для скоростей, направленных под разными углами, и мы еще будем им пользоваться. Пока же мы работаем с движением вдоль одной оси координат, давайте перепишем уравнение в проекциях:
Здесь все эти – это проекции, индекс мы не стали писать, чтобы не загромождать формулу.
Рассмотрим другой пример. Мы едем на автомобиле со скоростью 60 км/ч и догоняем автобус, который едет со скоростью 40 км/ч в том же направлении. С какой скоростью движется автобус относительно нас?
В вопросе задачи говорится о скорости автобуса в системе отсчета, связанной с нами и нашим автомобилем, обозначим ее , ее нужно будет найти. Эта система отсчета, наш автомобиль, сама движется относительно Земли со скоростью . А скорость автобуса относительно Земли можно назвать абсолютной скоростью (Землю для задач, которые не затрагивают космос, можно считать абсолютной): . Применим закон сложения скоростей: абсолютная скорость тела равна скорости тела относительно подвижной системы отсчета плюс абсолютной скорости этой подвижной системы отсчета,
Эта система отсчета, наш автомобиль, сама движется относительно Земли со скоростью . А скорость автобуса относительно Земли можно назвать абсолютной скоростью (Землю для задач, которые не затрагивают космос, можно считать абсолютной): . Применим закон сложения скоростей: абсолютная скорость тела равна скорости тела относительно подвижной системы отсчета плюс абсолютной скорости этой подвижной системы отсчета,
Выразим отсюда скорость автобуса относительно нашего автомобиля:
Отрицательное значение скорости означает, что она направлена противоположно направлению дороги, в котором скорости автобуса и автомобиля положительны. Действительно, из автомобиля при обгоне выглядит, как будто автобус движется со скоростью 20 км/ч навстречу.
Чтобы решить главную задачу механики, найти при равноускоренном движении, нам не хватает одного: перемещения при равноускоренном движении.
Для его нахождения удобно использовать графики функции и .
Рис. 9. Графики функции и .
9. Графики функции и .
Рассмотрим график зависимости для равномерного прямолинейного движения:
На нем каждая точка показываем, какая координата у тела в данный момент времени. График такой зависимости – прямая линия, что иллюстрирует определение постоянной скорости: за равные промежутки времени координата изменяется на одну и ту же величину. Легко найти начальную координату – это координата в точке .
Рис. 10. Равномерное прямолинейное движение
График перемещения начинается из начала координат, так как нет нулевого перемещения, в начальный момент времени .
Чем быстрее с течением времени изменяется координата (а это значит, что больше модуль скорости), тем круче график. Если график наклонен вниз, то есть координата убывает, значит, тело движется против оси координат. Оно совершает отрицательное перемещение , и его скорость тоже отрицательна, то есть направлена противоположно оси .
Рис. 11. График равномерного движения (синим – модуль скорости больше, розовым – скорость отрицательна)
Скорость при равномерном движении не меняется, график зависимости скорости от времени – горизонтальная прямая: в любой момент времени скорость одна и та же, положительная или отрицательная.
Рис 12. Скорость прямолинейного равномерного движения
Перемещение при равномерном прямолинейном движении равно . На графике – это определенный отрезок (см. рис. 13) а – это время, которое прошло с момента начала отсчета до интересующего нас момента (рис.13).
Рис. 13. Перемещение при равномерном прямолинейном движении
А их произведение – это площадь прямоугольника, ограниченного графиком . Площадь под графиком может быть и отрицательна – если скорость отрицательна, то площадь получается «над графиком», перемещение получится отрицательным. Формально, площадь прямоугольника не может быть отрицательна, но мы будем считать, что площадь под графиком, который расположен ниже оси, берётся со знаком минус. При этом формула для вычисления не изменится: – знак минус нам обеспечит знак скорости .
Итак, можем сделать вывод: перемещение численно равно площади под графиком функции (с учётом знака).
Расширим этот инструмент определения перемещения для равноускоренного движения и найдём в этом случае.
При равноускоренном движении скорость равномерно изменяется со временем, график – прямая, всё так же, как и для графика для равномерного движения.
Рис. 14. Равноускоренное прямолинейное движение
Теперь найдем перемещение . Разобьем время движения на небольшие интервалы, за которые скорость не успеет сильно измениться. На каждом таком интервале ее можно приближенно считать постоянной.
Рис. 15. Перемещение при равноускоренном прямолинейном движении
Перемещение на каждом промежутке равно площади столбца (рис. 15, обозначены синим и голубым) – фигуры под графиком скорости. А суммарное перемещение за время – это площадь фигуры, состоящей из всех этих столбцов. Чем мельче мы разобьем эти интервалы, тем меньше успевает поменяться скорость за один интервал, тем точнее наше приближение, и тем ближе наша фигура к трапеции под графиком скорости.
Рис. 16. Наиболее точное приближение равноускоренного движения
Вычислим площадь этой трапеции. Здесь высота трапеции равна , а два основания равны начальной скорости и скорости в момент времени t, . Площадь трапеции равна полусумме оснований, умноженной на высоту. Запишем:
Здесь высота трапеции равна , а два основания равны начальной скорости и скорости в момент времени t, . Площадь трапеции равна полусумме оснований, умноженной на высоту. Запишем:
Средняя скорость при равноускоренном движении
Как вычисляется средняя скорость на участке пути?
Нужно всё перемещение на данном участке разделить на всё время движения на этом участке, . Отсюда перемещение на участке пути можно вычислить по формуле: , как бы ни менялась скорость.
А теперь посмотрите на полученное нами из графика уравнение:
Из формулы видно, что множитель перед –это средняя скорость, в нашем случае, для равноускоренного движения, этот множитель равен:
Отметим, что мы обозначали начальную скорость движения, а – это скорость через время , то есть в конце рассматриваемого участка пути. Поэтому средняя скорость равна:
Это не строгий вывод, мы это подметили в уравнении, полученном из графика, но строгий вывод даст такую же формулу, так что можно ею пользоваться.
Получили уравнение, по которому можно найти перемещение в любой момент времени при равноускоренном прямолинейном движении. Подставим его в уравнение для координаты и получим решение основной задачи механики:
Равномерное прямолинейное движение можно считать равноускоренным движением с ускорением ноль. Подставим в эти уравнения и получим знакомые нам:
Если тело начинает двигаться из состояния покоя, в нашей модели будет , и уравнения примут вид:
Можно выбрать систему координат такую, чтобы точка начала движения совпадала в нулем координат, тогда примет вид .
Решение задач
Решим задачу.
Найдите ускорение автомобиля, если он, начиная движение со скоростью 20 м/с, движется до полной остановки 30 с.
По условию задачи автомобиль движется с ускорением. Ускорение по определению равно:
Начальная скорость дана 20 м/с, конечная 0 м/с, можем сразу вычислить ускорение:
Что значит отрицательное значение ускорения? Ускорение – векторная величина. При прямолинейном движении мы рассматриваем движение вдоль одной оси координат и пишем уравнения для проекций перемещения, скорости и ускорения. Раз мы говорим о скорости 20 м/с и она положительна, значит мы подразумеваем ось координат, сонаправленную с начальной скоростью.
При прямолинейном движении мы рассматриваем движение вдоль одной оси координат и пишем уравнения для проекций перемещения, скорости и ускорения. Раз мы говорим о скорости 20 м/с и она положительна, значит мы подразумеваем ось координат, сонаправленную с начальной скоростью.
А ускорение получилось отрицательным – это значит, что оно направлено противоположно этой оси и противоположно скорости. На этом примере мы увидели, что если скорость и ускорение противонаправлены, то есть их проекции имеют противоположные знаки, то скорость по модулю убывает, движение можно назвать замедленным.
Решим еще одну задачу.
Камень с поверхности земли бросают вертикально вверх с начальной скоростью 10 м/с. На какой высоте окажется камень через 0,5 с после броска?
Камень бросили, и он движется свободно, на него ничего не действует, кроме земного притяжения. Такое движение называется свободным полетом или свободным падением. В свободном падении вблизи поверхности Земли все тела, независимо от их массы, движутся с одинаковым ускорением, приблизительно равным . Иногда для упрощения расчетов его округляют до , получая менее точный ответ. Это ускорение направлено вертикально вниз, к центру Земли. Его назвали ускорением свободного падения и обозначили буквой . Свободное падение – это равноускоренное движение с ускорением свободного падения .
Иногда для упрощения расчетов его округляют до , получая менее точный ответ. Это ускорение направлено вертикально вниз, к центру Земли. Его назвали ускорением свободного падения и обозначили буквой . Свободное падение – это равноускоренное движение с ускорением свободного падения .
Выберем систему отсчета. Движение равноускоренное прямолинейное (бросок вертикальный), достаточно одной оси координат. Давайте направим ее в направлении начальной скорости, а начало координат выберем в точке броска. Вопрос, на какой высоте будет камень, сводится к нахождению координаты камня в указанный момент времени. Запишем уравнение для координаты при равноускоренном движении:
Осталось только переписать это уравнение в выбранной системе координат.
В нашей системе координат , начальная скорость положительна, так как сонаправлена с осью . Ускорение – это ускорение свободного падения, оно направлено противоположно оси , поэтому в нашей системе отсчета оно отрицательно.
В момент времени координата камня будет равна искомой высоте . Подставим значения и получим ответ:
Подставим значения и получим ответ:
Задача решена.
Ссылки на литературу:
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е изд, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. — 14-е изд., стереотип. – М.: Дрофа, 2009. – 300.
Ссылки на источники Интернет:
- Интернет-портал «raal100.narod.ru»:
- Материальная точка. Система отсчета
- Прямолинейное равноускоренное движение. Ускорение
- Перемещение
- Интернет-портал «class-fizika.ru» (Источник)
Домашнее задание:
- Поезд прошел по наклонной плоскости 360 метров за 15 секунд, при этом развил скорость 22 м/с. Найдите ускорение поезда.
- Что имеется ввиду под выражением «Человек двигался по эскалатору»? То, что он шел по эскалатору или то, что он был неподвижен во время движения эскалатора? Относительно чего человек покоится и относительно чего движется в данном случае?
- Приведите примеры равномерного и равноускоренного движения в повседневной жизни.
 Может ли один и тот же случай быть примером обоих типов движения?
Может ли один и тот же случай быть примером обоих типов движения?
Что такое кинематика? Простые ответы по физике
Как пользоваться этим руководствомЭтот пост в блоге является первым в серии статей о том, как понимать проблемы кинематики и подходить к ним. Он предназначен для дополнения вашего класса и учебника. Я сосредоточусь на практических применениях, способах решения задач и типичных ошибках, которые допускают учащиеся. Если вы хотите изучить основы кинематики, я рекомендую учебник, но если вы хотите получить более глубокое понимание, избежать путаницы и научиться подходить к проблемам, примите красную таблетку и присоединяйтесь к нам!
Что такое кинематика? Кинематика — это просто изучение движения. Это буквально то, что означает это слово: кинезис (движение) + тики (изучение. Подумайте о математике, политике, пиццатике). На более практическом уровне кинематика, которую вы изучаете на вводном уроке физики, — это изучение положения, скорости и импульса. На самом практическом уровне кинематика — это изучение того, что происходит, когда вы подбрасываете мяч. Это означает, что если вы можете подбрасывать мяч, вы можете изучить кинематику — к вашему сведению, как известно любому, кто когда-либо видел, как я занимаюсь спортом, обратное неверно.
На самом практическом уровне кинематика — это изучение того, что происходит, когда вы подбрасываете мяч. Это означает, что если вы можете подбрасывать мяч, вы можете изучить кинематику — к вашему сведению, как известно любому, кто когда-либо видел, как я занимаюсь спортом, обратное неверно.
Итак, кинематика — это изучение трех вещей, но что это за три вещи?
Позиция :Где находится объект. Его месторасположение. В задачах по физике это будет обозначаться как x, y, z p, r или d. У каждого учителя есть свои предпочтения, поэтому изучите свои, но для этого блога мы будем использовать x и y. Нас также часто интересует изменение положения, известное как смещение, которое обозначается как Δx, Δy, Δp, Δd или иногда просто x, y или d, чтобы все запутать. Положение и смещение обычно измеряются в метрах или метрах.
Скорость : Как быстро объект движется и в каком направлении: то же, как расстояние изменяется во времени. Задачи физики почти всегда относятся к скорости как v. Скорость обычно измеряется в метрах в секунду или м/с. Когда скорость постоянна, ее можно описать уравнением v=Δx/Δt (изменение положения, деленное на изменение во времени).
Задачи физики почти всегда относятся к скорости как v. Скорость обычно измеряется в метрах в секунду или м/с. Когда скорость постоянна, ее можно описать уравнением v=Δx/Δt (изменение положения, деленное на изменение во времени).
Как изменяется скорость объекта. Если Ferrari разгоняется от 0 до 60 миль в час за 2,4 секунды, значит, он ускоряется. Если водитель сходит с ума и врезается в стену, которая останавливает машину, значит, она тоже ускорилась. Ускорение всегда обозначается буквой а и измеряется в метрах в секунду за секунду или м/с 2 .
Когда ускорение постоянно, оно может быть описано уравнением a=Δv/Δt (изменение положения, деленное на изменение во времени). Вы могли заметить, что это уравнение очень похоже на уравнение для скорости. Это не совпадение: оно отражает обширную физику, лежащую в основе всего в мире.
Избегайте распространенных ошибок: положение, расстояние и смещение Положение, смещение и расстояние легко спутать, и учителя физики часто проводят тесты, чтобы убедиться, что вы понимаете разницу. Позиция измеряется от некоторой исходной точки и определяет местоположение объекта — в кинематике мы часто определяем исходную точку как начальное местоположение объекта, чтобы упростить задачу. Расстояние измеряет общее расстояние, пройденное объектом. Смещение измеряет, насколько далеко объект находится от того места, где он начался.
Позиция измеряется от некоторой исходной точки и определяет местоположение объекта — в кинематике мы часто определяем исходную точку как начальное местоположение объекта, чтобы упростить задачу. Расстояние измеряет общее расстояние, пройденное объектом. Смещение измеряет, насколько далеко объект находится от того места, где он начался.
Чтобы понять разницу, представьте себе сценарий, в котором вы начинаете 3 метра вправо от исходной точки и проходите 2 метра влево, затем 4 метра вправо. Ваша позиция в начале 3 метра, а в конце 5 метров. Ваше расстояние составляет 6 метров, потому что именно столько вы прошли. Ваше смещение в конце, однако, составляет 2 метра, потому что вы находитесь всего в 2 метрах от того места, где вы начали.
Избегайте распространенных ошибок: скорость и скорость В обычной жизни мы используем слова скорость и скорость как синонимы, но в физике мы никогда этого не делаем. Скорость — это то, насколько быстро что-то движется, скорость — это то, насколько быстро оно движется И в каком направлении (мы называем эту концепцию величины + направления вектором). Это означает, что объект может изменять скорость без изменения скорости, например, автомобиль, движущийся по круговой дорожке. Это также означает, что скорость может увеличиваться, в то время как скорость уменьшается. Если скорость отрицательна, а ускорение отрицательно, то скорость будет все более и более отрицательной, поэтому скорость будет уменьшаться (от -60 м/с до -120 м/с), но скорость будет увеличиваться (от 60 м/с). до 120 м/с).
Это означает, что объект может изменять скорость без изменения скорости, например, автомобиль, движущийся по круговой дорожке. Это также означает, что скорость может увеличиваться, в то время как скорость уменьшается. Если скорость отрицательна, а ускорение отрицательно, то скорость будет все более и более отрицательной, поэтому скорость будет уменьшаться (от -60 м/с до -120 м/с), но скорость будет увеличиваться (от 60 м/с). до 120 м/с).
Студентов, плохо знакомых с физикой, часто озадачивает мысль о том, что ускорение и скорость могут идти в разных направлениях. Когда объект ускоряется, он должен двигаться быстрее, верно? Не обязательно. Например, если вы подбрасываете объект в воздух, он начинает с положительной скорости вверх, но ускорение отрицательное и направлено вниз. В конце концов, объект перестает подниматься и падает обратно на землю, и в этот момент ускорение и скорость совпадают. Однако в любой момент ускорение может быть в любом направлении — ускорение определяет изменение скорости, а НЕ саму скорость.
Итак, теперь мы понимаем основы кинематики, но как мы их используем? В следующем блоге я расскажу о стандартных уравнениях кинематики и о том, как их использовать для решения одномерных задач.
Что такое кинематика и какие основы необходимо знать?
Перейти к содержимому
Предоставлено: ThisisEngineering RAEngКинематика — одна из старейших областей физики. Точнее, это раздел механики, изучающий движение объектов без учета сил, заставляющих их двигаться. Это очень важная тема в физике, охватывающая широкий круг концепций. В этой статье мы обсудим некоторые из самых основных понятий кинематики. Мы также рассмотрим, как можно использовать кинематику для решения задач.
Кредит: ThisisEngineering RAEngЧто такое кинематика?
Кинематика — это наука о движении без учета вызывающих его сил. Другими словами, это раздел механики, который занимается описанием движения. Самый простой способ описать движение — использовать расстояние и время. Например, если кто-то идет со скоростью 2 м/с в течение 5 минут, мы можем сказать, что он преодолел расстояние в 10 метров. Это пример линейного движения. Однако кинематика также имеет дело с нелинейными движениями, такими как круговое или угловое движение.
Самый простой способ описать движение — использовать расстояние и время. Например, если кто-то идет со скоростью 2 м/с в течение 5 минут, мы можем сказать, что он преодолел расстояние в 10 метров. Это пример линейного движения. Однако кинематика также имеет дело с нелинейными движениями, такими как круговое или угловое движение.
Скорость и ускорение
Кинематика — очень важная тема в физике, имеющая широкий спектр приложений. Он используется для описания движения объектов, независимо от того, движутся ли они по прямой линии или по более сложной траектории. Кинематику также можно использовать для прогнозирования будущего движения объекта на основе его текущего движения и сил, действующих на него. Благодаря кинематике мы теперь лучше понимаем, как устроена Вселенная и как вещи движутся вокруг нас.
Скорость — это векторная величина, описывающая скорость изменения положения. Другими словами, это скорость, с которой объект движется в определенном направлении. Чтобы использовать эти понятия для решения задач, нам нужно уметь вычислять скорость и ускорение. Таким образом, мы должны знать какие кинематические уравнения относятся к этим величинам. Скорость можно представить с помощью следующего уравнения:
Таким образом, мы должны знать какие кинематические уравнения относятся к этим величинам. Скорость можно представить с помощью следующего уравнения:
v=dx/dt, где v — скорость, dx — изменение положения, а dt — изменение во времени.
Ускорение — скорость изменения скорости. Другими словами, это скорость, с которой объект меняет свою скорость. Следовательно, ускорение можно представить с помощью следующего уравнения:
a=dv/dt, где a — ускорение, dv — изменение скорости, а dt — изменение времени.
Кинематические уравнения
Теперь, когда мы знаем, что такое скорость и ускорение, давайте посмотрим, как мы можем использовать их для решения задач. Кинематические уравнения представляют собой набор уравнений, относящихся к переменным, участвующим в движении. Эти уравнения позволяют нам вычислять неизвестные величины, такие как скорость или положение, если мы знаем другие величины. Есть четыре кинематических уравнения, и они следующие:
92/2a где x — смещение, v — конечная скорость, u — начальная скорость, a — ускорение.
С помощью этих уравнений мы можем решать более сложные задачи, поэтому, если вы используете кинематику для решения задачи, убедитесь, что вы с ней знакомы.
Каковы приложения кинематики?
Как мы уже видели, кинематика — очень важная тема в физике. Он имеет широкий спектр применения как в реальном мире, так и в научном сообществе. Чаще всего кинематика используется в области машиностроения и медицины.
В машиностроении кинематика используется для проектирования машин. Он помогает инженерам проектировать и строить машины, которые могут двигаться определенным образом. Например, кинематика используется в конструкции роботов и других автоматизированных систем. Он также используется в области биомеханики, изучающей движения человека, для улучшения конструкции протезов и ортопедических имплантатов.
В медицине кинематика используется для диагностики и лечения пациентов с двигательными нарушениями, а также для диагностики и лечения травм. Это помогает врачам понять, как движется человеческое тело, и выявить проблемы, которые могут вызывать боль или другие симптомы. Кинематика также используется в физиотерапии, чтобы помочь пациентам восстановиться после травм, предоставляя упражнения, которые улучшают диапазон движений и силу. В спортивной медицине кинематика используется для повышения работоспособности спортсменов и предотвращения травм.
Это помогает врачам понять, как движется человеческое тело, и выявить проблемы, которые могут вызывать боль или другие симптомы. Кинематика также используется в физиотерапии, чтобы помочь пациентам восстановиться после травм, предоставляя упражнения, которые улучшают диапазон движений и силу. В спортивной медицине кинематика используется для повышения работоспособности спортсменов и предотвращения травм.
Как видите, кинематика — очень важная тема в физике, имеющая множество приложений в реальном мире. Если вы хотите узнать больше о кинематике или физике в целом, есть много ресурсов, доступных в Интернете и в библиотеках. Вы также можете пройти курс физики в местном колледже или университете. И если вы используете кинематику в своей работе, убедитесь, что вы понимаете все основные понятия, прежде чем начать, чтобы избежать ошибок.
Нравится:
Нравится Загрузка…
2.1: Основы кинематики – Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14438
- Безграничный
- Безграничный
Определение кинематики
Кинематика — это изучение движения точек, объектов и групп объектов без учета причин их движения.
цели обучения
- Определение кинематики
Кинематика — раздел классической механики, описывающий движение точек, объектов и систем групп объектов без ссылки на причины движения (т. е. силы). Изучение кинематики часто называют «геометрией движения».
Объекты движутся вокруг нас. Все, начиная от теннисного матча и заканчивая полетом космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце гонит кровь по венам. Даже в неодушевленных предметах существует непрерывное движение вибраций атомов и молекул. Могут возникнуть интересные вопросы о движении: сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбольный мяч, если его бросить под определенным углом? Однако понимание движения также является ключом к пониманию других концепций физики. Понимание ускорения, например, имеет решающее значение для изучения силы.
Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов, а также их дифференциальные свойства (такие как скорость и ускорение). Кинематика используется в астрофизике для описания движения небесных тел и систем; а в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).
Кинематика используется в астрофизике для описания движения небесных тел и систем; а в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).
Формальное изучение физики начинается с кинематики. Слово «кинематика» происходит от греческого слова «кинезис», означающего движение, и связано с другими английскими словами, такими как «кино» (фильмы) и «кинезиология» (изучение движения человека). Кинематический анализ — это процесс измерения кинематических величин, используемых для описания движения. Изучение кинематики можно свести к чисто математическим выражениям, которые можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, перемещение, время и траектория.
Кинематика траектории частицы : Кинематические уравнения могут использоваться для расчета траектории частиц или объектов. Физические величины, относящиеся к движению частицы, включают: массу m, положение r, скорость v, ускорение a.
Системы отсчета и смещения
Для описания движения объекта необходимо указать его положение относительно удобной системы отсчета.
цели обучения
- Оценить смещение в системе отсчета.
Чтобы описать движение объекта, вы должны сначала описать его положение — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Земле или от нее. Математически положение объекта обычно представляется переменной х .
Системы отсчета
Есть два варианта, которые вы должны сделать, чтобы определить переменную положения x . Вы должны решить, где поставить x = 0 и какое направление будет положительным. Это называется выбором системы координат или выбором системы отсчета. Пока вы последовательны, любой фрейм одинаково действителен. Но вы не хотите менять систему координат в середине расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили движения поезда — всего 9 минут.0199 казалось , будто станция двигалась. Но это показывает, что существует третий произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга. Может показаться странным использовать систему координат, движущуюся относительно земли, но, например, система отсчета, движущаяся вместе с поездом, может быть гораздо удобнее для описания того, что происходит внутри поезда. Системы отсчета особенно важны при описании смещения объекта.
Но вы не хотите менять систему координат в середине расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили движения поезда — всего 9 минут.0199 казалось , будто станция двигалась. Но это показывает, что существует третий произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга. Может показаться странным использовать систему координат, движущуюся относительно земли, но, например, система отсчета, движущаяся вместе с поездом, может быть гораздо удобнее для описания того, что происходит внутри поезда. Системы отсчета особенно важны при описании смещения объекта.
РАМКИ ОТНОШЕНИЯ профессора Хьюма и профессора Дональда Айви из Университета Торонто
В этом классическом фильме профессора Хьюм и Айви искусно иллюстрируют системы отсчета и различают фиксированные и движущиеся системы отсчета.
«Системы отсчета» (1960) Образовательный фильм «: Системы отсчета» — учебный фильм 1960 года, снятый Комитетом по изучению физических наук. Фильм был снят для показа на курсах физики в средней школе. В фильме профессора физики Университета Торонто Паттерсон Хьюм и Дональд Айви объясняют различие между инерциальной и неинтерциальной системами отсчета, демонстрируя эти концепции с помощью юмористических трюков с камерой. Например, фильм начинается с доктора Хьюма, который кажется перевернутым, обвиняя доктора Айви в том, что он перевернут. Только когда пара подбрасывает монетку, становится очевидным, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для поддержания интереса учащихся, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих удивительно непредсказуемые места в зоне просмотра. Прекрасная операторская работа Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая команда режиссеров может весело провести время с предметом, который другим, менее изобретательным типам, может показаться скучным. Продюсер: Ричард Ликок Производство: Educational Development Corp. Спонсор: Эрик Престамон
Прекрасная операторская работа Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая команда режиссеров может весело провести время с предметом, который другим, менее изобретательным типам, может показаться скучным. Продюсер: Ричард Ликок Производство: Educational Development Corp. Спонсор: Эрик Престамон
Смещение
Смещение — это изменение положения объекта относительно его системы отсчета. Например, если автомобиль движется от дома к продуктовому магазину, его перемещение — это относительное расстояние от продуктового магазина до системы отсчета или дома. Слово «смещение» подразумевает, что объект сдвинулся или был смещен. Смещение — это изменение положения объекта, которое может быть представлено математически следующим образом:
\[\mathrm{Δx=x_f−x_0}\]
где \(\Delta x\) — смещение, \(x_f\) — конечное положение, а \(x_0\) — начальное положение.
показывает важность использования системы отсчета при описании перемещения пассажира в самолете.
Перемещение в системе координат : Пассажир перемещается со своего места в заднюю часть самолета. Его положение относительно самолета задается x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой, направленной к задней части самолета. Обратите внимание, что стрелка, обозначающая его смещение, в два раза длиннее стрелки, обозначающей смещение профессора (он перемещается в два раза дальше).
Введение в скаляры и векторы
Вектор — это любая величина, которая имеет как величину, так и направление, тогда как скаляр имеет только величину.
цели обучения
- Отличие скаляров от векторов
В чем разница между расстоянием и перемещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Перемещение является примером векторной величины. Расстояние является примером скалярной величины. Вектор – это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км/ч на восток и силой 500 ньютонов прямо вниз.
Другие примеры векторов включают скорость 90 км/ч на восток и силой 500 ньютонов прямо вниз.
Скаляры и векторы : Г-н Андерсен объясняет разницу между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
В математике, физике и технике вектор — это геометрический объект, который имеет величину (или длину) и направление и может быть добавлен к другим векторам в соответствии с векторной алгеброй. Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Вектор часто изображают отрезком с определенным направлением или графически в виде стрелки, соединяющей начальную точку А с конечной точкой В, как показано на рис. 9.0009
Векторное представление : Вектор часто представляется в виде отрезка с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B.
Некоторые физические величины, такие как расстояние, не имеют направления или не имеют определенного направления. В физике скаляр — это простая физическая величина, которая не изменяется при поворотах или перемещениях системы координат. Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, 9Ограничение скорости 0 км/ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры или величины без указания направления. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура -20ºC. В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на рис. )
Скаляры и векторы : Краткий список величин, которые являются либо скалярами, либо векторами.
Ключевые точки
- Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов.

- Изучение кинематики можно свести к чисто математическим выражениям.
- Кинематические уравнения можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, перемещение и время.
- Для выбора системы отсчета необходимо решить, где находится начальное положение объекта и какое направление будет считаться положительным.
- Действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга.
- Системы отсчета особенно важны при описании смещения объекта.
- Смещение — это изменение положения объекта относительно его системы отсчета.
- Вектор — это любая величина, имеющая величину и направление.
- Скаляром является любая величина, имеющая величину, но не имеющую направления.
- Перемещение и скорость являются векторами, тогда как расстояние и скорость являются скалярами.
Ключевые термины
- кинематика : Раздел механики, изучающий движущиеся объекты, но не действующие силы.

- смещение : Векторная величина, обозначающая расстояние с компонентом направления.
- система отсчета : Система координат или набор осей, в которых измеряется положение, ориентация и другие свойства объектов в ней.
- скаляр : Величина, имеющая величину, но не направление; сравнить вектор.
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
ЛИЦЕНЗИИ И АВТОРСТВО
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, ПРЕДОСТАВЛЯЕМОЕ РАНЕЕ
- Курирование и пересмотр. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
CC ЛИЦЕНЗИОННОЕ СОДЕРЖИМОЕ, КОНКРЕТНОЕ АВТОРСТВО
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.
 org/content/m42122/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
org/content/m42122/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Кинематика. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinematics . Лицензия : CC BY-SA: Attribution-ShareAlike
- кинематика. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/kinematics . Лицензия : CC BY-SA: Attribution-ShareAlike
- Кинематика. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinematics . Лицензия : CC BY: Attribution
- Предоставлено : Свет и Материя.
 Расположен по адресу : http://lightandmatter.com/lmb.pdf . Лицензия : CC BY: Attribution
Расположен по адресу : http://lightandmatter.com/lmb.pdf . Лицензия : CC BY: Attribution - Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42033/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Предоставлено : Свет и Материя. Расположен по адресу : http://lightandmatter.com/lmb.pdf . Лицензия : CC BY: Attribution Объем двигателя
- . Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/displacement . Лицензия : CC BY-SA: Attribution-ShareAlike
- система отсчета.
 Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/frame_of_reference . Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/frame_of_reference . Лицензия : CC BY-SA: Attribution-ShareAlike - Кинематика. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinematics . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики. 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42033/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Системы отсчета (1960) Образовательный фильм. Расположен по адресу : http://www.youtube.
 com/watch?v=aRDOqiqBUQY . Лицензия : Общественное достояние: неизвестно Copyright . Условия лицензии : Стандартная лицензия YouTube
com/watch?v=aRDOqiqBUQY . Лицензия : Общественное достояние: неизвестно Copyright . Условия лицензии : Стандартная лицензия YouTube - Скаляр (физика). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Scalar_(physics) . Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42124/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
- Вектор (физика). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.
 org/wiki/Vector_(physics) . Лицензия : CC BY-SA: Attribution-ShareAlike
org/wiki/Vector_(physics) . Лицензия : CC BY-SA: Attribution-ShareAlike - скаляр. Предоставлено : Викисловарь. Расположен по адресу : en.wiktionary.org/wiki/scalar . Лицензия : CC BY-SA: Attribution-ShareAlike
- вектор. Предоставлено : Викисловарь. Расположен по адресу : http://en.wiktionary.org/wiki/vector . Лицензия : CC BY-SA: Attribution-ShareAlike
- Кинематика. Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinematics . Лицензия : CC BY: Attribution
- Колледж OpenStax, Колледж физики.
 25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42033/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution
25 октября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42033/latest/?collection=col11406/1.7 . Лицензия : CC BY: Attribution - Системы отсчета (1960) Образовательный фильм. Расположен по адресу : http://www.youtube.com/watch?v=aRDOqiqBUQY . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
- Вектор (физика). Предоставлено : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Vector_(physics) . Лицензия : CC BY: Атрибуция
- Скаляры и векторы. Предоставлено : Национальной ассоциацией авиации и космонавтики.
 Расположен по адресу : http://www.grc.nasa.gov/WWW/k-12/airplane/vectors.html . Лицензия : Общественное достояние: Нет данных Авторские права
Расположен по адресу : http://www.grc.nasa.gov/WWW/k-12/airplane/vectors.html . Лицензия : Общественное достояние: Нет данных Авторские права - Скаляры и векторы. Расположен по адресу : http://www.youtube.com/watch?v=EURMI0DIh50 . Лицензия : Общественное достояние: Нет данных Copyright . Условия лицензии : Стандартная лицензия YouTube
Эта страница под названием 2.1: Основы кинематики распространяется по незаявленной лицензии и была создана, изменена и/или курирована Boundless.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Безграничный
- Показать оглавление
- нет
- Метки
- рабочий объем
- система отсчета
- кинематика
- скаляр
- вектор
Определение, примеры, формулы и типы
Планетарные орбиты, езда на велосипеде, бег по треку, летающие пчелы и падающие яблоки — мы всегда в движении, как и мир и вселенная, в которых мы живем. мы познакомимся с одним из основополагающих разделов классической физики: кинематикой. В этой статье мы рассмотрим определение кинематики в физике, некоторые из основных понятий, составляющих эту область, и физические уравнения, которые вам необходимо знать, чтобы начать решать задачи кинематики. Мы также представим несколько основных типов задач кинематики, с которыми вы столкнетесь. Давайте начнем!
мы познакомимся с одним из основополагающих разделов классической физики: кинематикой. В этой статье мы рассмотрим определение кинематики в физике, некоторые из основных понятий, составляющих эту область, и физические уравнения, которые вам необходимо знать, чтобы начать решать задачи кинематики. Мы также представим несколько основных типов задач кинематики, с которыми вы столкнетесь. Давайте начнем!
Определение кинематики в физике
Изучение движения неизбежно: физическое движение является неотъемлемой частью жизни. Мы постоянно наблюдаем, переживаем, вызываем и останавливаем движение. Прежде чем мы рассмотрим источники и движущие силы более сложного движения, мы хотим понять движение, как оно происходит: куда движется объект, как быстро он движется и как долго он длится. Эта упрощенная линза, с которой мы начинаем, представляет собой изучение кинематики в физике.
Кинематика — это изучение движения объектов без учета сил, вызвавших это движение.
Изучение кинематики является важной отправной точкой для понимания движущегося и взаимодействующего мира вокруг нас. Поскольку математика — это язык физики, нам понадобится набор математических инструментов для описания и анализа всевозможных физических явлений в нашей Вселенной. Далее давайте углубимся в некоторые основные концепции кинематики: ключевые переменные кинематического движения и лежащие в их основе уравнения кинематики.
Основные понятия кинематики
Прежде чем мы представим основные уравнения кинематики, давайте кратко рассмотрим справочную информацию и различные параметры, которые вам необходимо знать.
Скаляры и векторы
В кинематике мы можем разделить физические величины на две категории: скаляры и векторы.
Скаляр — это физическая величина, имеющая только величину.
Другими словами, скаляр — это просто числовое измерение с размером. Это может быть простое положительное число или число с единицей измерения, которое не включает направление. Некоторые распространенные примеры скаляров, с которыми вы регулярно взаимодействуете:
Некоторые распространенные примеры скаляров, с которыми вы регулярно взаимодействуете:
Масса (но не вес!) мяча, учебника, себя или другого предмета.
Объем кофе, чая или воды в вашей любимой кружке.
Количество времени, прошедшее между двумя уроками в школе, или как долго вы спали прошлой ночью.
Итак, скалярное значение кажется довольно простым — как насчет вектора?
Вектор — это физическая величина, имеющая как величину, так и направление.
Когда мы говорим, что вектор имеет направление, мы имеем в виду, что направление величины имеет значение . Это означает, что используемая нами система координат важна, потому что направление вектора, включая большинство переменных кинематического движения, меняет знак в зависимости от того, является ли направление движения положительным или отрицательным. Теперь давайте рассмотрим несколько простых примеров векторных величин в повседневной жизни.
Сила, с которой вы толкаете дверь.
Ускорение вниз при падении яблока с ветки дерева под действием силы тяжести.
Насколько быстро вы едете на велосипеде на восток от своего дома.
При изучении физики вы столкнетесь с несколькими соглашениями для обозначения векторных величин. Вектор может быть записан как переменная со стрелкой вправо вверху, например, вектор силы \(\overrightarrow{F}\) или выделенный жирным шрифтом символ, например \(\mathbf{F}\). Убедитесь, что вам удобно работать с несколькими типами символов, в том числе без обозначения векторных величин!
Переменные в кинематике
Математическое решение задач кинематики в физике требует понимания, вычисления и измерения нескольких физических величин. Давайте пройдемся по определению каждой переменной далее.
Положение, смещение и расстояние
Прежде чем мы узнаем, как быстро движется объект, мы должны знать , где что-то находится первым. Мы используем переменную position, чтобы описать, где находится объект в физическом пространстве.
Мы используем переменную position, чтобы описать, где находится объект в физическом пространстве.
позиция объекта — это его физическое положение в пространстве относительно начала координат или другой контрольной точки в определенной системе координат.
Для простого линейного движения мы используем одномерную ось, такую как \(x\), \(y\) или \(z\)-ось. Для движения вдоль горизонтальной оси мы обозначаем измерение положения с помощью символа \(x\), начальное положение с помощью \(x_0\) или \(x_i\), а конечное положение с помощью \(x_1\) или \( х_f\). Мы измеряем положение в единицах длины, причем наиболее часто используемыми единицами измерения являются метры, представленные символом \(\mathrm{m}\).
Если вместо этого мы хотим сравнить, насколько конечное положение объекта отличается от его начального положения в пространстве, мы можем измерить смещение после того, как объект подвергся некоторому линейному движению.
Смещение — это измерение изменения положения или того, насколько далеко объект сместился от контрольной точки, вычисляемое по формуле:
\begin{align*} \Delta x=x_f-x_i \end{align *}
Мы измеряем смещение \(\Delta x\), иногда обозначаемое как \(s\), используя те же единицы измерения, что и положение. Иногда вместо этого мы хотим знать только, сколько земли объект преодолел в целом, например, общее количество миль, пройденных автомобилем во время поездки. Здесь пригодится переменная расстояния.
Иногда вместо этого мы хотим знать только, сколько земли объект преодолел в целом, например, общее количество миль, пройденных автомобилем во время поездки. Здесь пригодится переменная расстояния.
Расстояние — это измерение общего перемещения объекта без привязки к направлению движения.
Другими словами, мы суммируем абсолютное значение длины каждого сегмента пути, чтобы найти общее пройденное расстояние \(d\). И перемещение, и расстояние также измеряются в единицах длины.
Измерения смещения описывают, насколько далеко объект переместился от своего начального положения, а измерения расстояния суммируют общую длину пройденного пути, стандартизировано с помощью Wikimedia Commons CC BY-SA 3.0
Наиболее важное различие между этими величинами заключается в том, что положение и смещение являются векторами, а расстояние — скаляром.
Рассмотрим горизонтальную ось, охватывающую проезжую часть \(\mathrm{10\, m}\), с началом координат, определенным в \(5\,\mathrm{m}\) Вы идете в положительном \(x\) – направление от машины к вашему почтовому ящику в конце подъездной дорожки, где вы затем разворачиваетесь, чтобы пройти к входной двери. Определите свое начальное и конечное положение, перемещение и общее пройденное расстояние.
Определите свое начальное и конечное положение, перемещение и общее пройденное расстояние.
В этом случае ваше начальное положение \(x_i\) совпадает с положением автомобиля в \(x=5\, \mathrm{m}\) в положительном \(x\)-направлении. Путь к почтовому ящику из машины занимает \(5\,\mathrm{m}\), а путь к двери – всю длину подъездной дорожки \(10\,\mathrm{m}\) в обратном направлении. . Ваше смещение:
\begin{align*} \Delta x=\mathrm{5\,m-10\,m=-5\,m} \end{align*}
\(x_f=-5\ ,\mathrm{m}\) также является нашим конечным положением, измеренным вдоль отрицательной оси \(x\) от машины до дома. Наконец, общее пройденное расстояние игнорирует направление движения:
\begin{align*} \Delta x=\mathrm{5\,m+\left |-10\,m \right |=15\,m} \end{align*}
Вы прошли \(15\ ,\mathrm{m}\) всего.
Поскольку при расчете смещения учитывается направление, эти измерения могут быть положительными, отрицательными или нулевыми. Однако расстояние может быть положительным только в том случае, если произошло какое-либо движение.
Время
Важная и обманчиво простая переменная, на которую мы полагаемся как в повседневной жизни, так и во многих физических задачах, — это время, особенно прошедшее время.
Прошедшее время — это измерение того, сколько времени занимает событие, или количество времени, необходимое для того, чтобы произошли наблюдаемые изменения.
Мы измеряем временной интервал \(\Delta t\) как разницу между конечной меткой времени и начальной меткой времени, или:
\begin{align*} \Delta t=t_f-t_i \end{align*}
Мы записываем время обычно в секундах, обозначаемых символом \(\mathrm{s}\) в задачах по физике. На первый взгляд время может показаться очень простым, но когда вы углубитесь в изучение физики, вы обнаружите, что определение этого параметра немного сложнее, чем раньше! Не беспокойтесь — пока все, что вам нужно знать, это как определить и рассчитать, сколько времени прошло в задаче по стандартным часам или секундомеру.
Скорость и скорость
Мы часто говорим о том, насколько «быстро» что-то движется, например, как быстро едет машина или как быстро вы идете. В кинематике понятие скорости движения объекта относится к тому, как его положение меняется во времени, а также направление, в котором он движется.
В кинематике понятие скорости движения объекта относится к тому, как его положение меняется во времени, а также направление, в котором он движется.
Скорость скорость изменения смещения во времени, или:
\begin{align*} \mathrm{Velocity=\frac{Displacement}{\Delta Time}} \end{align*}
In Другими словами, переменная скорости \(v\) описывает, насколько объект меняет свое положение за каждую прошедшую единицу времени. Мы измеряем скорость в единицах длины за время, наиболее распространенной единицей измерения является метр в секунду, обозначаемый символом \(\mathrm{\frac{m}{s}}\). Например, это означает, что объект со скоростью \(10\,\mathrm{\frac{m}{s}}\) перемещается \(\mathrm{10\, m}\) каждую секунду.
Скорость — аналогичная переменная, но вместо этого рассчитывается с использованием общего расстояния, пройденного за некоторый период прошедшего времени.
Скорость скорость, с которой объект проходит расстояние, или:
\begin{align*} \mathrm{Speed=\frac{Distance}{Time}} \end{align*}
Измеряем скорость \ (s\) в тех же единицах, что и скорость. В повседневном разговоре мы часто используем термины «скорость» и «скорость» как синонимы, тогда как в физике различие имеет значение. Как и смещение, скорость — это векторная величина с направлением и величиной, а скорость — это скалярная величина, имеющая только размер. Неосторожная ошибка между ними может привести к неправильному расчету, поэтому обязательно обратите внимание и узнайте разницу между ними!
В повседневном разговоре мы часто используем термины «скорость» и «скорость» как синонимы, тогда как в физике различие имеет значение. Как и смещение, скорость — это векторная величина с направлением и величиной, а скорость — это скалярная величина, имеющая только размер. Неосторожная ошибка между ними может привести к неправильному расчету, поэтому обязательно обратите внимание и узнайте разницу между ними!
Ускорение
При вождении автомобиля, прежде чем мы достигнем постоянной скорости для круиза, мы должны увеличить нашу скорость с нуля. Изменения скорости приводят к ненулевому значению ускорения.
Ускорение — скорость изменения скорости во времени, или:
\begin{align*} \mathrm{Acceleration=\frac{\Delta Velocity}{\Delta Time}} \end{align*}
Другими словами, ускорение описывает, насколько быстро изменяется скорость, включая ее направление, со временем. Например, постоянное положительное ускорение 1 указывает на неуклонное увеличение скорости в каждую единицу прошедшего времени. 2}}\). Подобно смещению и скорости, измерения ускорения могут быть положительными, нулевыми или отрицательными, поскольку ускорение является векторной величиной.
2}}\). Подобно смещению и скорости, измерения ускорения могут быть положительными, нулевыми или отрицательными, поскольку ускорение является векторной величиной.
Силы
Вероятно, у вас уже достаточно физической интуиции, чтобы догадаться, что движение не может просто возникнуть из ничего — вам нужно толкнуть мебель, чтобы изменить ее положение при ремонте, или нажать на тормоз, чтобы остановить машину. Основным компонентом движения является взаимодействие между объектами: силы.
Сила — это взаимодействие, такое как толчок или притяжение между двумя объектами, которое влияет на движение системы. 92}}\end{align*}
Согласно нашему определению кинематики, нам не нужно учитывать какие-либо толкающие или тянущие взаимодействия, которые могли бы запустить движение. На данный момент все, на что нам нужно обращать внимание, — это движение в момент его возникновения: с какой скоростью движется автомобиль, как далеко укатился мяч, с какой скоростью яблоко движется вниз. Однако полезно держать в уме такие силы, как гравитация, когда анализируете проблемы кинематики. Кинематика — это всего лишь ступенька к построению нашего понимания мира, прежде чем мы погрузимся в более сложные концепции и системы!
Однако полезно держать в уме такие силы, как гравитация, когда анализируете проблемы кинематики. Кинематика — это всего лишь ступенька к построению нашего понимания мира, прежде чем мы погрузимся в более сложные концепции и системы!
Уравнения кинематики, также известные как уравнения движения, представляют собой набор из четырех основных формул, которые мы можем использовать для определения положения, скорости, ускорения или времени, затраченного на движение объекта. Давайте рассмотрим каждое из четырех кинематических уравнений и способы их использования.
Первое кинематическое уравнение позволяет нам найти конечную скорость, учитывая начальную скорость, ускорение и период времени:
\begin{align*} v=v_0+a \Delta t \end{align*}
где \(v_0\) — начальная скорость, \(a\) — ускорение и \(\Delta t\) — прошедшее время. Следующее кинематическое уравнение позволяет найти положение объекта по его начальному положению, начальной и конечной скоростям и прошедшему времени:
\begin{align*} x=x_0+(\frac{v+v_0}{2}) \ Delta t,\, \mathrm{or} \\ \Delta x=(\frac{v+v_0}{2}) \Delta t \end{align*}
, где \(x_0\) — начальная позиция в \(x\)-направление. Мы можем заменить \(x\) на \(y\) или \(z\) на движение в любом другом направлении. Обратите внимание, что мы записали это уравнение двумя разными способами — поскольку смещение \(\Delta x\) равно \(x-x_0\), мы можем переместить нашу начальную переменную положения в левую часть уравнения и переписать левая сторона как переменная смещения. Этот удобный трюк также применим к нашему третьему кинематическому уравнению, уравнению для положения, заданного начальным положением, начальной скоростью, ускорением и прошедшим временем: 92+2a\Delta x \end{align*}
Мы можем заменить \(x\) на \(y\) или \(z\) на движение в любом другом направлении. Обратите внимание, что мы записали это уравнение двумя разными способами — поскольку смещение \(\Delta x\) равно \(x-x_0\), мы можем переместить нашу начальную переменную положения в левую часть уравнения и переписать левая сторона как переменная смещения. Этот удобный трюк также применим к нашему третьему кинематическому уравнению, уравнению для положения, заданного начальным положением, начальной скоростью, ускорением и прошедшим временем: 92+2a\Delta x \end{align*}
Все четыре кинематических уравнения предполагают, что значение ускорения является постоянным или неизменным в течение периода времени, в течение которого мы наблюдали движение. Это значение может быть ускорением силы тяжести на поверхности Земли, другой планеты или тела или любым другим значением ускорения в другом направлении.
Поначалу выбор кинематического уравнения может показаться запутанным. Лучший способ определить, какая формула вам нужна, — перечислить информацию, которую вы получили в задаче, по переменной. Иногда в контексте может подразумеваться значение переменной, например нулевая начальная скорость при падении объекта. Если вы считаете, что вам дали недостаточно подробностей для решения проблемы, прочтите ее еще раз и нарисуйте диаграмму!
Иногда в контексте может подразумеваться значение переменной, например нулевая начальная скорость при падении объекта. Если вы считаете, что вам дали недостаточно подробностей для решения проблемы, прочтите ее еще раз и нарисуйте диаграмму!
Типы кинематики
Хотя кинематика в физике в широком смысле включает движение без учета причинных сил, есть несколько типов повторяющихся кинематических проблем, с которыми вы столкнетесь, когда начнете изучать механику. Давайте кратко представим некоторые из этих типов кинематического движения: свободное падение, движение снаряда и вращательную кинематику.
Свободное падение
Свободное падение — это тип одномерного вертикального движения, при котором объекты ускоряются только под действием силы тяжести. На Земле ускорение свободного падения является постоянной величиной, которую мы обозначаем символом \(\mathrm{g}\): 92}} \end{align*}
Движение свободного падения происходит только в вертикальном направлении, начиная с высоты h ноль над землей, MikeRun через Wikimedia Commons CC BY-SA 4. 0
0
В случае свободного падения мы не учитывайте эффекты сопротивления воздуха, трения или каких-либо изначально приложенных сил, которые не вписываются в определение свободно падающего движения. Объект, совершающий свободное падение, опустится на расстояние \(\Delta y\), иногда называемое \(\mathrm{h_0}\), от своего начального положения до земли. Чтобы лучше понять, как работает движение свободного падения, давайте рассмотрим краткий пример.
Ваш калькулятор падает со стола с высоты \(\mathrm{0,7\, м}\) и приземляется этажом ниже. Поскольку вы изучали свободное падение, вы хотите рассчитать среднюю скорость вашего калькулятора во время падения. Выберите одно из четырех кинематических уравнений и найдите среднюю скорость.
Во-первых, давайте систематизируем полученную информацию:
- Смещение — это изменение положения от стола до пола, \(\mathrm{0,7\, м}\). 92}}} \\ v=\mathrm{3.7\, \frac{m}{s}} \end{align*}
Кинематика – это изучение движения объектов без учета действующих причинных сил.

Линейное движение — это движение объекта в одном измерении или в одном направлении в координатном пространстве.
Смещение — это изменение, измеренное между конечным и начальным положением.
Скорость — это изменение положения объекта в единицу времени.
Ускорение — это скорость изменения скорости в единицу времени.
Свободное падение — это тип линейного вертикального движения с постоянным ускорением, возникающим под действием силы тяжести на Земле.
Движение снаряда — это двумерное движение объекта, запущенного под некоторым углом под действием силы тяжести.

Вращательное движение изучает вращательное движение тела или системы и аналогично линейному движению.
Расстояние – это общая пройденная длина независимо от направления движения.
Перемещение — это расстояние, пройденное в определенном направлении.
Скорость – это расстояние, пройденное за единицу времени.
Скорость – скорость изменения смещения.
Ускорение — это скорость изменения скорости.

Перемещение s = f (t) [местоположение относительно начала координат]
Скорость [производная смещения]
Ускорение [производная скорости]
Рассчитайте скорость парома через 12 секунд.
Рассчитайте расстояние, которое проходит паром за эти 12 секунд.
Запишите свой SUVAT, уточните переменные, которые у вас есть, и те, которых у вас нет, и определите, какое уравнение использовать.
Использование
Кто-то бросает мяч.
Пуля в момент выстрела.
Автомобиль съезжает со скалы.
- . Desplerception Ise isfeematics – это изменение. в положении объекта относительно его системы отсчета.
- Ускорение свободного падения равно 9,8 на поверхности земли. Для простоты расчета его можно принять за 10.
- Вы также можете использовать методы исчисления для анализа функций.
- Для решения кинематических задач в двух измерениях необходимо использовать геометрию для определения неизвестных величин и направлений и использовать направления для определения кинематических величин.
- Положение и смещение представлены системой координат x, y , или иногда θ (греческая буква тета, используемая в углах в геометрии движения) и r в полярной координате система. В единицах СИ (международная система) расстояние измеряется в метрах (м).
- Скорость v в метрах в секунду (м/с).
- Ускорение a или
Средняя скорость вычислителя равна \(3. 7\,\mathrm{\frac{m {s}}\).
7\,\mathrm{\frac{m {s}}\).
Хотя большинство проблем свободного падения возникает на Земле, важно отметить, что ускорение силы тяжести на разных планетах или меньших телах в космосе будет иметь разные числовые значения. Например, ускорение силы тяжести значительно меньше на Луне и значительно больше на Юпитере, чем то, к чему мы привыкли на Земле. Итак, это не настоящая константа — она достаточно «постоянна» для упрощения физических задач на нашей родной планете!
Движение снаряда
Движение снаряда — это двумерное, обычно параболическое движение объекта, запущенного в воздух. Для параболического движения положение, скорость и ускорение объекта могут быть разделены на горизонтальную и вертикальную компоненты , используя индексы \(x\) и \(y\) соответственно. Разбив переменную движения на отдельные составляющие, мы можем анализировать, насколько быстро объект движется или ускоряется в каждом направлении, а также предсказывать положение объекта в разные моменты времени.
Объект с движением снаряда, запущенный под углом, будет иметь скорость и ускорение в обоих направлениях x и y, StudySmarter Originals
Все объекты, испытывающие движение снаряда, демонстрируют симметричное движение и имеют максимальную дальность и высоту — как гласит классическая поговорка, “Что идет вверх, должно спуститься вниз”!
Вращательное движение
Вращательное движение, также известное как вращательная кинематика, является расширением изучения линейной кинематики для движения вращающихся по орбите или вращающихся объектов.
Вращательное движение — круговое или вращательное движение тела вокруг фиксированной точки или жесткой оси вращения.
Примеры вращательного движения окружают нас повсюду: возьмем орбиты планет, вращающиеся вокруг Солнца, внутреннее движение шестеренок в часах и вращение велосипедного колеса. Уравнения движения для кинематики вращения аналогичны уравнениям движения для линейного движения. Давайте посмотрим на переменные, которые мы используем для описания вращательного движения.
Давайте посмотрим на переменные, которые мы используем для описания вращательного движения.
Variable | Linear Motion | Rotational Motion |
Position and Displacement | \(x\) | \(\theta\) (Greek theta ) |
Velocity | \(v\) | \(\omega\) (Greek omega ) |
Acceleration | \(a\) | \(\alpha\) (греч. alpha ) |
Кинематика и классическая механика являются обширными разделами физики в целом. Но не волнуйтесь — в следующих нескольких статьях мы подробно расскажем обо всех новых переменных и уравнениях!
Кинематика – основные выводы
Определение, примеры и уравнения, математика |
Кинематика фокусируется на движении объектов. Он имеет дело с силами и геометрическими аспектами движения, связанными со скоростью и ускорением.
Давайте определим некоторые специальные термины, чтобы понять тему кинематики:
Теперь мы можем использовать их для описания движения объекта и геометрии кривой, которую он создает при движении.
Переменное ускорение
При переменном ускорении ускорение меняется со временем. Нам нужно использовать дифференцирование и интегрирование для преобразования между смещением, скоростью и ускорением. Мы используем дифференцирование для преобразования смещения в скорость и из скорости в ускорение. Затем мы используем интегрирование, чтобы вернуться от ускорения к скорости и от скорости к смещению.
Рис. Переменное ускорение
Пример:
Найдите моменты времени, в которые частица находится в состоянии мгновенного покоя, если ее перемещение задано как
Ответ:
Используйте дифференцирование для преобразования смещения в скорость.
Это функция скорости. Мы хотим знать, когда v = 0
(3t -2) (t -4) = 0
Частица находится в момент времени t = 4 с или t = 2/3 с.
Расчет кинематики
Расчет упрощает вывод двух из трех уравнений движения. Поскольку мы знаем, что ускорение — это первая производная скорости по времени, используйте определение, чтобы обратить его вспять. Вместо того, чтобы находить скорость, интегрируйте ее, чтобы найти ускорение.
Различные функции описывают величины ускорения, смещения и скорости. Их также можно преобразовать в функции, описывающие две другие величины. Есть два способа сделать это: дифференцирование (нахождение производной) или интегрирование (нахождение интеграла).
3 Вместе проанализируем эти понятия. Вы можете понять характеристики кинематики на основе вывода нашей функции. Для смещения значение 0 означает, что наша позиция находится в начале координат.
 Если смещение положительное, то оно справа от начала координат, а если отрицательное, то слева от начала координат.
Если смещение положительное, то оно справа от начала координат, а если отрицательное, то слева от начала координат.Скорость имеет аналогичную интерпретацию. Если значение равно 0, это означает, что мы находимся в состоянии покоя. Положительная скорость означает движение вправо, а отрицательная скорость означает движение влево.
Выход 0 для функции ускорения означает, что скорость либо максимальна, либо минимальна, либо постоянна. Положительный результат означает, что скорость увеличивается, а отрицательный результат означает, что скорость уменьшается.
Пример:
Найдите скорость, если перемещение задано как функция времени.
Ответ:
Мы просто продифференцируем это:
Это то же самое, что [Посмотрите на дифференцирование, если вам трудно]
v = 6t
Если вы хотите найти ускорение, это можно записать как вторую производную от перемещение по времени или скорость, дифференцированная по времени.
a = 6
Итак, эта частица имеет постоянное ускорение 6.
Постоянное ускорение
Формально это известно как «одномерные уравнения движения для постоянного ускорения». Кинематические уравнения в этом разделе действительны только тогда, когда ускорение постоянно, а движение ограничено прямой линией.
Как упоминалось ранее, ускорение является постоянным, то есть оно остается неизменным вне зависимости от времени. Здесь мы используем стандартные обозначения, где ускорение представляет собой ускорение, u представляет собой начальную скорость, а t представляет собой время.
Графики движения
Нарисуем графики для всех трех свойств движения: смещения, скорости и ускорения. Определим объекты движения по графикам.
График времени разгона:
Вот сценарий: пуля выпущена вертикально. Единственная сила, действующая на него, — это сила тяжести. Гравитация не меняется; следовательно, ускорение также не меняется. Ниже приведена демонстрация графика времени разгона.
Ускорение
График скорость-время:
Поскольку мы знаем, что ускорение является постоянным и отрицательным, поскольку оно действует в направлении, противоположном скорости, это будет означать, что градиент графика скорость-время должен быть постоянным и отрицательным, что даст нам что-то вроде этого:
Скорость
График времени перемещения:
На приведенном ниже графике показана пуля от ее начальной точки до достижения максимальной высоты, где скорость равна 0, прежде чем она снова начнет снижаться. У вас есть градиент, который является постоянным и отрицательным. Таким образом, график для смещения будет выглядеть следующим образом:
У вас есть градиент, который является постоянным и отрицательным. Таким образом, график для смещения будет выглядеть следующим образом:
Смещение
Обратите внимание, что скорость всегда положительна, но уменьшается до 0. Поэтому градиент графика зависимости смещения от времени всегда должен быть положительным и должен уменьшаться до 0,9.0009
Уравнения SUVAT
Уравнения SUVAT представляют собой набор уравнений, описывающих движение в одном измерении, в каждом из которых опущена одна переменная.
variable | Description | SI unit |
s | Displacement | meters (m) |
u | Initial скорость | m / s (meters per second) |
v | Final velocity | m / s (meters per second) |
a | Acceleration | м / с / с (метры в секунду в секунду) |
T | Время | S (секунды) |
Первое уравнение: V = U + на
6: V = U + на
6: V = U + на
6: V = u + на
6: V = u + на
60009
Второе уравнение:
Третье уравнение:
Четвертое уравнение:
Пример:
Паром перевозит пассажиров между берегами реки, которые находятся на расстоянии 20 м друг от друга. После старта паром разгоняется до 0,2 в течение 12 секунд, затем выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу.
После старта паром разгоняется до 0,2 в течение 12 секунд, затем выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу.
Ответ:
с = х м
u = 0 м/с
v =?
a = 0,2
t = 12 с
Теперь найдем уравнение СУВАТ, которое не включает s.
v = u + at
v = 0 + 0,2 12
v = 2,4 м/с
s = 14,4 м
Снаряды
Снаряды имеют дело с объектами, которые летят по воздуху при броске, ударе, выстреле и т. д. Примеры:
д. Примеры:
Снаряды
Траектория — это путь снаряда. Снаряд всегда имеет некоторую начальную скорость, обычно направленную под углом к горизонтали. Он свободно движется под действием силы тяжести, потому что единственная сила, действующая на него, — это его вес. Чтобы решить проблему со снарядом, вам нужно использовать уравнение SUVAT в двух измерениях, чтобы разделить горизонтальную и вертикальную составляющие каждого значения.
Поскольку тригонометрические функции используются для нахождения неизвестных углов и расстояний, мы будем использовать их для решения компонентов здесь.
Пример:
Частица P брошена из точки O на горизонтальную плоскость со скоростью 28 м/с под углом 30 градусов к горизонту. После выброса частица движется свободно под действием силы тяжести до удара о плоскость в точке А. Найти наибольшую высоту частицы, время полета и расстояние ОА.
Найти наибольшую высоту частицы, время полета и расстояние ОА.
Ответ:
Мы хотим найти вертикальную высоту, поэтому мы будем использовать SUVAT в вертикальном направлении.
с =?
u = 28sin30 = 14 м/с
v = 0
a = -g
t = x
В такой ситуации мы используем уравнение, в котором нет t.
Если мы подставим значения, то получим 0 = 196 – 2gs
И примем g равным 9,8, с = 10м
Второе, что нам нужно найти, это время полета (время, которое требуется P, чтобы добраться от O до A).
с = 0 м
u = 14 м/с
v = x
a = -g
t =?
Итак, t = 0, когда частица P находится в начале координат.
Тогда как решение где находится, когда частица находится в A.
И если мы возьмем g = 9,8, t = 2,9 с.
В заключительной части задачи нам нужно найти расстояние между O и A.
Мы собираемся найти горизонтальное расстояние, поэтому мы будем использовать SUVAT в горизонтальном направлении.
с =?
U = 28COS30 м / с
V = x
A = 0
Расстояние между O и A IS S = 69 M
Кинематика – Ключевые TakeAways
Кинематика: что это такое и почему это важно? (с примерами)
Кинематика — это математическая ветвь физики, которая использует уравнения для описания движения объектов (в частности, траекторий ) без обращения к силам.
Эти уравнения позволяют вам просто подставлять различные числа в одну из четырех основных кинематические уравнения найти неизвестные в этих уравнениях, не применяя никаких знаний физики, лежащих в основе этого движения, или вообще не имея никаких знаний физики. Достаточно хорошо разбираться в алгебре, чтобы пробиться через простые задачи о движении снаряда, не получая реального понимания лежащей в их основе науки.
Достаточно хорошо разбираться в алгебре, чтобы пробиться через простые задачи о движении снаряда, не получая реального понимания лежащей в их основе науки.
Кинематика обычно применяется для решения задач классической механики задач движения в одном измерении (по прямой) или в два измерения (с вертикальными и горизонтальными компонентами, как в движение снаряда ).
В действительности события, описываемые как происходящие в одном или двух измерениях, разворачиваются в обычном трехмерном пространстве, но для целей кинематики х имеет «правое» (положительное) и «левое» (отрицательное) направления, а у — «вверх». (положительное) и «вниз» (отрицательное) направления. Понятие «глубина», то есть направление прямо к вам и от вас, в этой схеме не учитывается, и обычно в этом нет необходимости по причинам, которые будут объяснены позже.
Определения физики, используемые в кинематике
Задачи кинематики связаны с положением, скоростью, ускорением и временем в некоторой комбинации. Скорость — это скорость изменения положения во времени, а ускорение — это скорость изменения скорости во времени; то, как каждый из них получается, является проблемой, с которой вы можете столкнуться в исчислении. В любом случае двумя основными понятиями кинематики являются, следовательно, положение и время.
Скорость — это скорость изменения положения во времени, а ускорение — это скорость изменения скорости во времени; то, как каждый из них получается, является проблемой, с которой вы можете столкнуться в исчислении. В любом случае двумя основными понятиями кинематики являются, следовательно, положение и время.
Подробнее об этих отдельных переменных:
α
(греческая буква альфа), изменение скорости во времени, в м/с/с или м/с 2 . Время t равно в секундах. Если присутствует, начальный и конечный индексы ( i и f , или, альтернативно, 0 и f , где 0 называется “ноль” ) обозначают начальное и конечное значения любого из вышеперечисленных. Это константы в любой задаче, и направление (например, x ) может быть в нижнем индексе для предоставления конкретной информации.
Это константы в любой задаче, и направление (например, x ) может быть в нижнем индексе для предоставления конкретной информации.
Перемещение, скорость и ускорение равны векторные величины . Это означает, что они имеют как величину (число), так и направление, которое в случае ускорения может не совпадать с направлением движения частицы. В кинематических задачах эти векторы, в свою очередь, могут быть разбиты на отдельные векторы x- и y-компонент. С другой стороны, такие единицы, как скорость и расстояние, являются скалярными величинами , поскольку они имеют только величину.
Четыре уравнения кинематики
Математика, необходимая для решения задач кинематики, сама по себе не является сложной. Однако научиться назначать правильные переменные для правильных частей информации, представленной в задаче, поначалу может быть проблемой. Это помогает определить переменную, которую просит вас найти проблема, а затем посмотреть, что вам дано для этой задачи.
Далее следуют четыре формулы кинематики. Хотя «x» используется в демонстрационных целях, уравнения в равной степени действительны для направления «y». Предположим, что в любой задаче постоянное ускорение a (при вертикальном движении это часто g , ускорение свободного падения вблизи поверхности Земли, равное 9,8 м/с 2 ).
x=x_0+/frac{1}{2}(v+v_0)t
Обратите внимание, что (1/2) (v + v 0 ) 92+2a(x-x_0)
Это уравнение полезно, когда вы не знаете (и не должны знать) время.
Другой список уравнений кинематики может иметь немного разные формулы, но все они описывают одни и те же явления. Чем больше вы будете на них смотреть, тем более знакомыми они станут, даже если вы еще относительно новичок в решении задач кинематики.
Подробнее о кинематических моделях
Кинематические кривые — это обычные графики, показывающие положение в зависимости от времени ( x против t , скорость против времени ( против против t ) и ускорение против времени ( a против t ) . В каждом случае время является независимой переменной и лежит на горизонтальной оси. Это делает положение, скорость и ускорение зависимыми переменными , и как таковые они находятся на вертикальной оси. (В математике и физике, когда говорят, что одна переменная «сопоставляется» с другой, первая является зависимой переменной, а вторая — независимой.)
В каждом случае время является независимой переменной и лежит на горизонтальной оси. Это делает положение, скорость и ускорение зависимыми переменными , и как таковые они находятся на вертикальной оси. (В математике и физике, когда говорят, что одна переменная «сопоставляется» с другой, первая является зависимой переменной, а вторая — независимой.)
Эти графики можно использовать для кинематического анализа движения (чтобы увидеть, в какой интервал времени объект был остановлен или ускорялся, например).
Эти графики также связаны тем, что для любого заданного интервала времени, если известен график зависимости положения от времени, два других можно быстро построить, проанализировав его наклон: скорость от времени — это наклон зависимости положения от времени. (поскольку скорость – это скорость изменения положения или, в терминах исчисления, ее производная), а ускорение в зависимости от времени – это наклон скорости в зависимости от времени (ускорение – это скорость изменения скорости).
Заметка о сопротивлении воздуха
На вводных занятиях по механике учащимся обычно предлагается игнорировать влияние сопротивления воздуха в задачах кинематики. В действительности эти эффекты могут быть значительными и могут значительно замедлить частицу, особенно при более высоких скоростях, поскольку сила сопротивления жидкостей (включая атмосферу) пропорциональна не только скорости, но и квадрату скорости. .
Из-за этого каждый раз, когда вы решаете задачу, включающую компоненты скорости или смещения, и вас просят исключить влияние сопротивления воздуха из ваших расчетов, признайте, что реальные значения, вероятно, будут несколько ниже, а значения времени несколько выше, потому что вещи требуется больше времени, чтобы добраться с места на место по воздуху, чем предсказывают основные уравнения.
Примеры одномерных и двумерных задач кинематики
Первое, что нужно сделать, столкнувшись с проблемой кинематики, — определить переменные и записать их. Вы можете, например, составить список всех известных переменных, таких как x 0 = 0, v 0x = 5 м/с и так далее. Это помогает проложить путь к выбору того из кинематических уравнений, которое лучше всего позволит вам перейти к решению.
Вы можете, например, составить список всех известных переменных, таких как x 0 = 0, v 0x = 5 м/с и так далее. Это помогает проложить путь к выбору того из кинематических уравнений, которое лучше всего позволит вам перейти к решению.
Одномерные задачи (линейная кинематика) обычно имеют дело с движением падающих объектов, хотя они могут включать объекты, ограниченные движением по горизонтальной линии, например, автомобиль или поезд на прямой дороге или пути.
Примеры одномерной кинематики:
1. Какова конечная скорость копейки, упавшей с вершины небоскреба высотой 300 м (984 фута)?
Здесь движение происходит только в вертикальном направлении. Начальная скорость v 0y = 0, так как копейка брошена, а не брошена. y – y 0 или общее расстояние равно -300 м. Искомое значение равно v y (или v fy ). Значение ускорения равно –g или –92=(2)(-9,8)(-300) = 5880 \подразумевается v = -76,7\text{ м/с}
Это дает быстрый и фактически смертельный результат (76,7 м/с)(миля /1609,3 м)(3600 с/ч) = 172,5 мили в час. ВАЖНО: возведение в квадрат скорости в задачах этого типа скрывает тот факт, что его значение может быть отрицательным, как в этом случае; вектор скорости частицы направлен вниз по оси ординат. Математически и v = 76,7 м/с, и v = -76,7 м/с являются решениями.
ВАЖНО: возведение в квадрат скорости в задачах этого типа скрывает тот факт, что его значение может быть отрицательным, как в этом случае; вектор скорости частицы направлен вниз по оси ординат. Математически и v = 76,7 м/с, и v = -76,7 м/с являются решениями.
2. Каково перемещение автомобиля, движущегося с постоянной скоростью 50 м/с (около 112 миль в час) по гоночной трассе в течение 30 минут, проехав при этом ровно 30 кругов?
Это своего рода вопрос с подвохом. Пройденное расстояние есть просто произведение скорости на время: (50 м/с)(1800 с) = 90 000 м или 90 км (около 56 миль). Но смещение равно нулю, потому что машина останавливается там же, где и стартовала.
Примеры двумерной кинематики:
3. Игрок в бейсбол бросает мяч горизонтально со скоростью 100 миль в час ( 45 м/с ) с крыши здания в первая проблема. Вычислите, какое расстояние он пройдет по горизонтали, прежде чем упадет на землю.
Сначала нужно определить, как долго мяч находится в воздухе. Обратите внимание, что, несмотря на то, что мяч имеет горизонтальную составляющую скорости, это все еще проблема свободного падения.
Сначала используйте v = v 0 + at и подставьте значения v = –76,7 м/с, v 0 = 0 и a = –9,8 м/с 2 , чтобы найти t, что составляет 7,8 секунды. Затем подставьте это значение в уравнение постоянной скорости (поскольку ускорение в направлении x отсутствует) x = x 0 + vt чтобы найти x, полное горизонтальное перемещение:
x =(45)(7,8) = 351\text{ m}
или 0,22 мили.
Таким образом, теоретически мяч приземлится примерно в четверти мили от основания небоскреба.
Анализ кинематики: скорость и расстояние события в легкой атлетике
Помимо предоставления полезных физических данных об отдельных событиях, данные, относящиеся к кинематике, могут использоваться для установления взаимосвязей между различными параметрами в одном и том же объекте. Если объектом оказывается человек-спортсмен, есть возможность использовать физические данные, чтобы помочь наметить спортивную тренировку и в некоторых случаях определить идеальное место для соревнований на треке.
Если объектом оказывается человек-спортсмен, есть возможность использовать физические данные, чтобы помочь наметить спортивную тренировку и в некоторых случаях определить идеальное место для соревнований на треке.
Например, спринты включают в себя дистанции до 800 метров (чуть меньше полумили), гонки на средние дистанции охватывают от 800 метров до примерно 3000 метров, а настоящие забеги на длинные дистанции составляют 5000 метров (3,107 мили). ) и выше. Если вы изучите мировые рекорды по бегу, вы увидите четкую и предсказуемую обратную зависимость между дистанцией забега (параметр положения, скажем, x ) и скоростью мирового рекорда ( против ) или скалярной составляющей в ).
Если группа спортсменов пробежит серию забегов на разные дистанции и для каждого бегуна будет создана диаграмма зависимости скорости от дистанции, то у тех, кто лучше бегает на более длинные дистанции, кривая будет более плоской, так как их скорость меньше замедляется при увеличение дистанции по сравнению с бегунами, чье естественное «сладкое пятно» – более короткие дистанции.

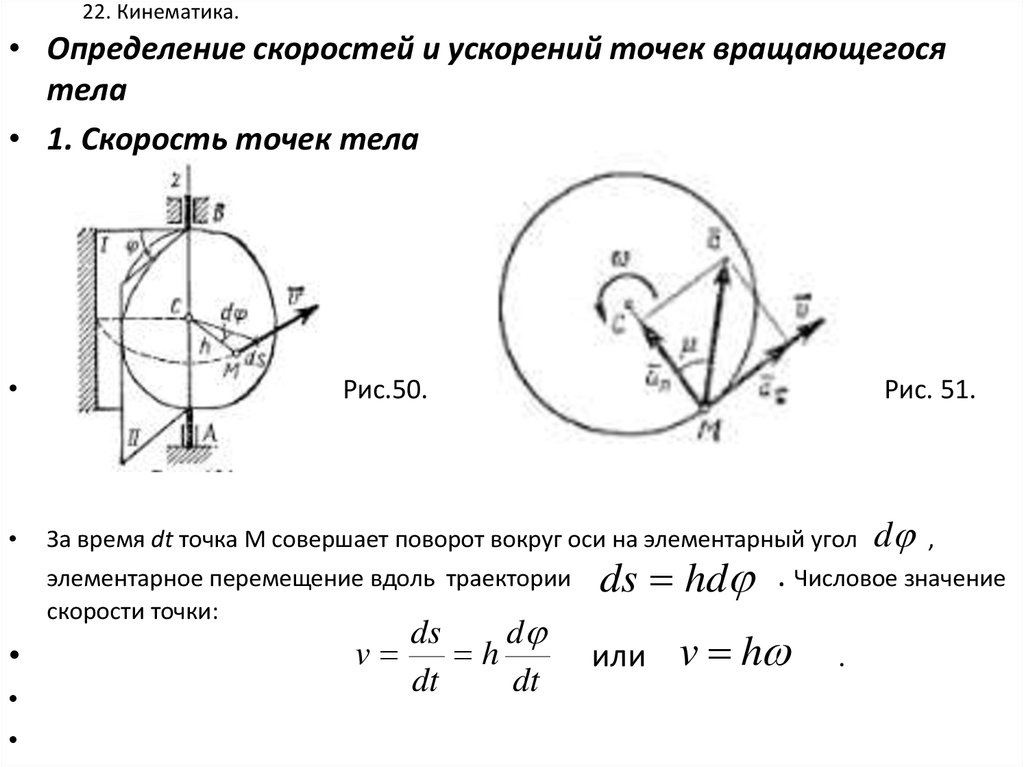
 При
этом число уравнений не должно быть
больше числа неизвестных в задаче.
При
этом число уравнений не должно быть
больше числа неизвестных в задаче. Следует проверить
составленные уравнения и решения,
полученной системы.
Следует проверить
составленные уравнения и решения,
полученной системы.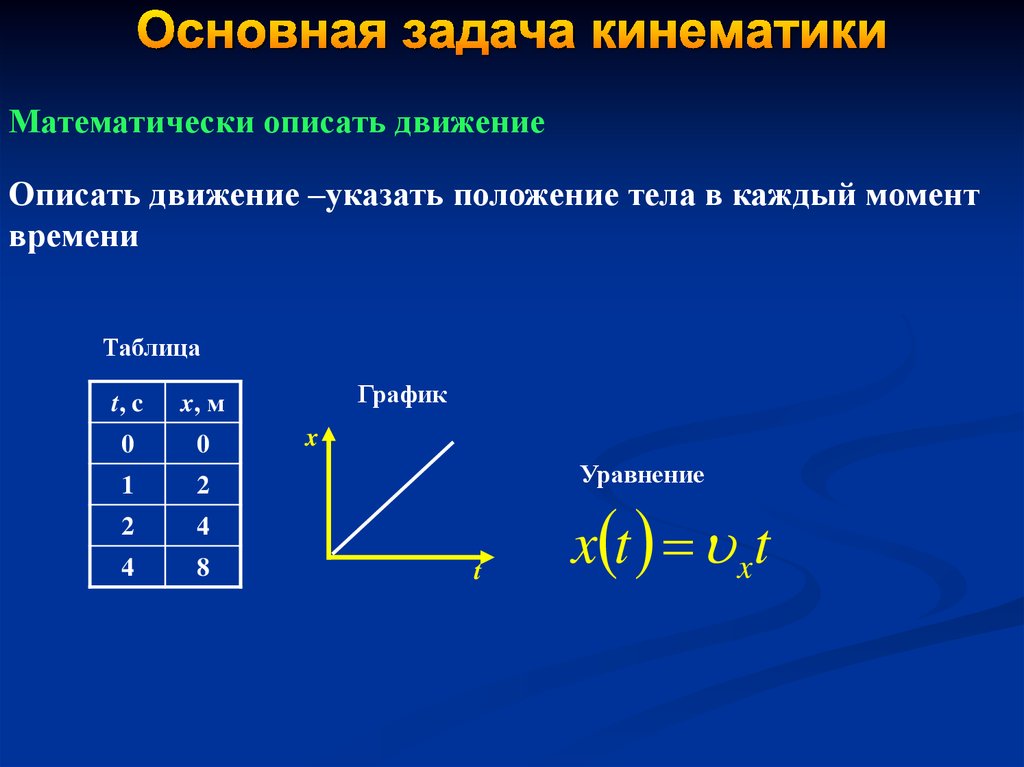 координат, конечно, называется координатный.
координат, конечно, называется координатный.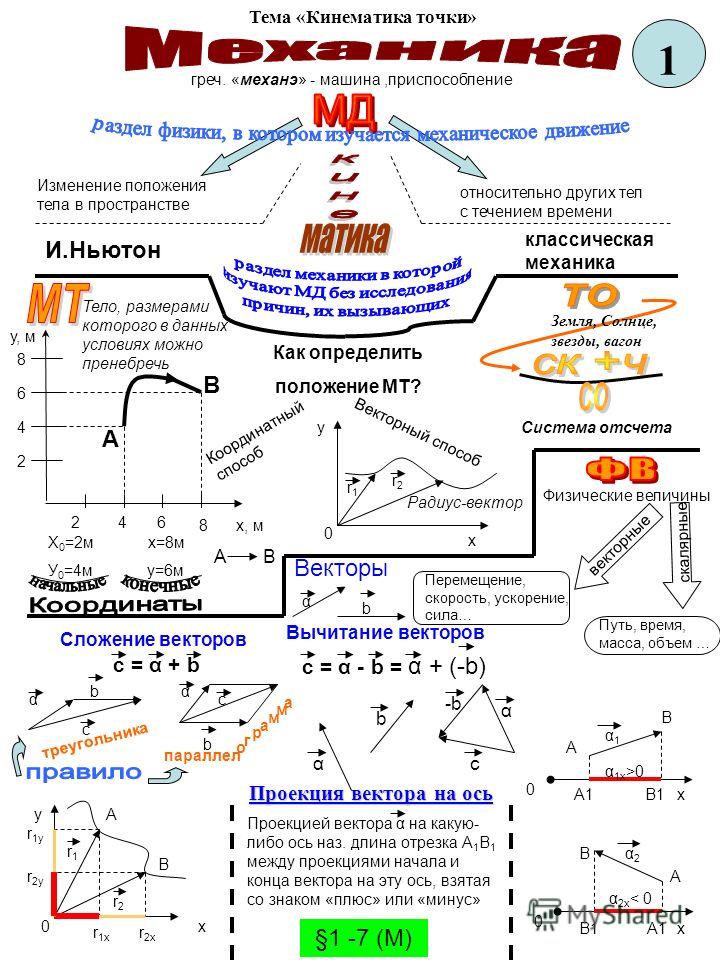
 д.
д. д.
д.


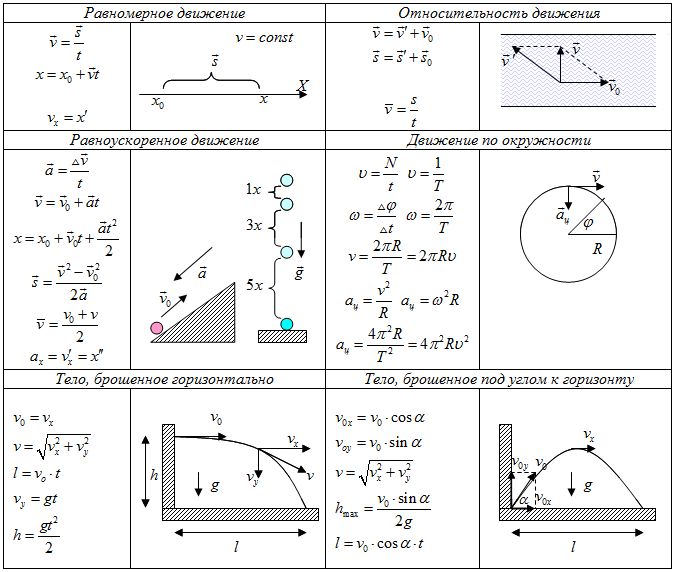 Его величину находим из теоремы Пифагора, построив прямоугольный треугольник. Получаем примерно 15м.
Его величину находим из теоремы Пифагора, построив прямоугольный треугольник. Получаем примерно 15м.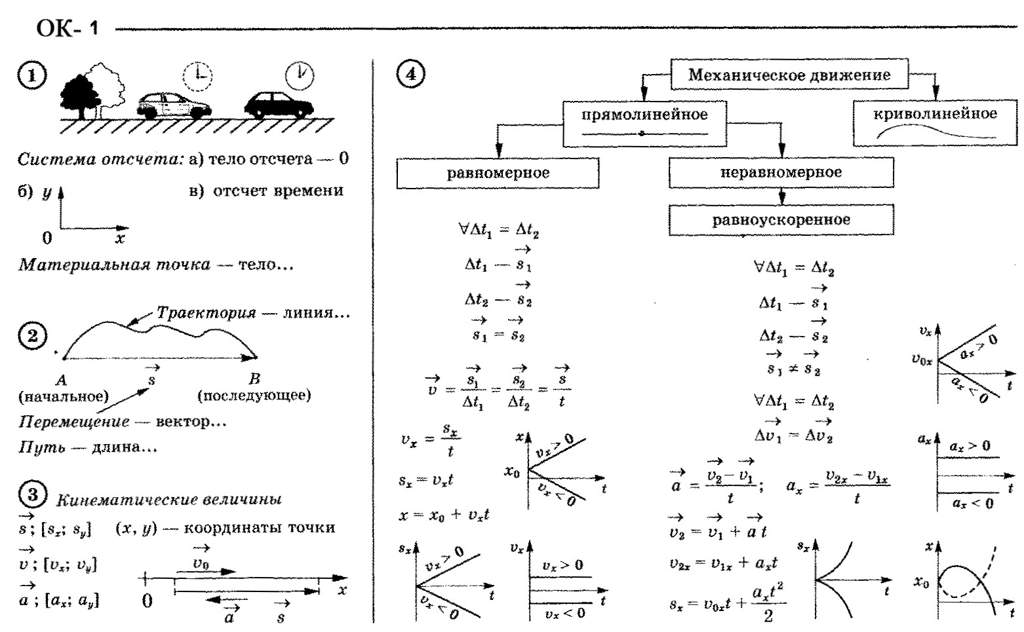



 Как гласит легенда, Галилей сбрасывал с Пизанской башни тела различной массы, а его ассистент фиксировал время их падения. В этоми знаменитом эксперименте, выяснилось, что тела различной массы падают с одинаковой скоростью.
Как гласит легенда, Галилей сбрасывал с Пизанской башни тела различной массы, а его ассистент фиксировал время их падения. В этоми знаменитом эксперименте, выяснилось, что тела различной массы падают с одинаковой скоростью.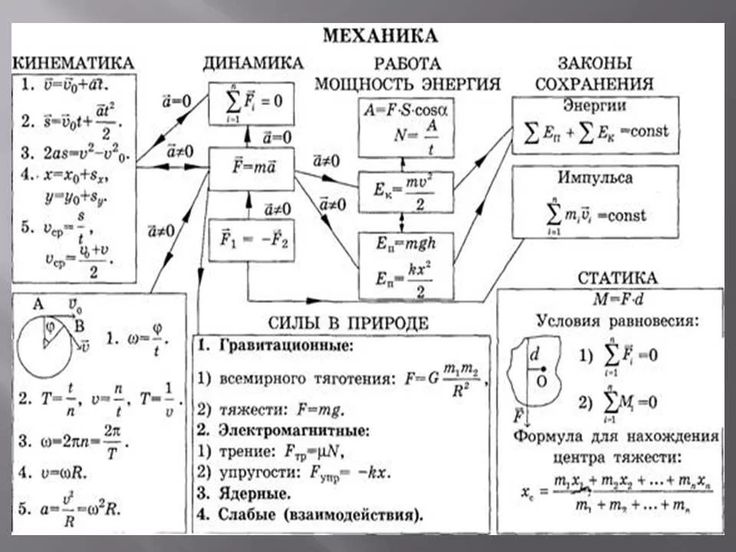 Оно, конечно, гораздо сложнее чем прямолинейное, которым мы занимались все это время. Поэтому Юлик Левкович правильно предложила попробовать рассмотреть движение по хордам окружности. При этом на каждой хорде частица движется с постоянной скоростью и по величине и по напрвлению. Вектор скорости лежит на хорде.
Оно, конечно, гораздо сложнее чем прямолинейное, которым мы занимались все это время. Поэтому Юлик Левкович правильно предложила попробовать рассмотреть движение по хордам окружности. При этом на каждой хорде частица движется с постоянной скоростью и по величине и по напрвлению. Вектор скорости лежит на хорде.