Все что нужно знать о кинематике. Основные понятия кинематики. Свободное падение по вертикали
КИНЕМАТИКА
Основные понятия, законы и формулы.
Кинематика – раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих движение.
Механическим движением называют изменение положения тела в пространстве с течением времени относительно других тел.
Простейшим механическим движением является движение материальной точки – тела, размеры и форму которого можно не учитывать при описании его движения.
Движение материальной точки характеризуют траекторией, длиной пути, перемещением, скоростью и ускорением.
Траекторией называют линию в пространстве, описываемую точкой при своем движении.
Расстояние , пройденное телом вдоль траектории движения, – путь(S).
Перемещение – направленный отрезок, соединяющий начальное и конечное положение тела.
Длина пути – величина скалярная, перемещение – величина векторная.
Средняя скорость – это физическая величена, равная отношению вектора перемещения к промежутку времени, за которое произошло перемещение:
Мгновенная скорость или скорость в данной точке траектории – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Dt:
Величину характеризующую изменение скорости за единицу времени, называют средним ускорением :
.
Аналогично понятию мгновенной скорости вводится понятие мгновенного ускорения:
При равноускоренном движении ускорение постоянно.
Простейший вид механического движения-прямолинейное движение точки с постоянным ускорением.
Движение с постоянным ускорением называется равнопеременным; в этом случае:
; ; https://pandia.ru/text/78/108/images/image014_3.gif”>; ; https://pandia.ru/text/78/108/images/image017_1.gif”>; ;
Связь между линейными и угловыми величинами при вращательном движении :
; ; https://pandia. ru/text/78/108/images/image024_1.gif”>.
ru/text/78/108/images/image024_1.gif”>.
Любое сложное движение можно рассматривать как результат сложения простых движений. Результирующее перемещение равно геометрической сумме и находится по правилу сложения векторов. Скорость тела и скорость системы отсчета так же складывается векторно.
При решении задач на те или иные разделы курса, кроме общих правил решения, приходится учитывать некоторые дополнения к ним, связанные со спецификой самих разделов.
Задачи по кинематике , разбираемые в курсе элементарной физики, включают в себя: задачи о равнопеременном прямолинейном движении одной или нескольких точек, задачи о криволинейном движении точки на плоскости. Мы рассмотрим каждый из этих типов задач отдельно.
Прочитав условие задачи, нужно сделать схематический чертеж, на котором следует изобразить систему отсчета, и указать траекторию движения точки.
После того как выполнен чертеж, с помощью формул:
; ; https://pandia.ru/text/78/108/images/image027_0. gif”>; .
gif”>; .
Подстановкой в них развёрнутых выражений для Sn, S0, vn, v0 и т. д. и заканчивается первая часть решения.
Пример 1 . Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью v1 = 12 км/ч далее половину оставшегося времени он ехал со скоростью v2 = 6 км/ч, а затем до конца пути шел пешком со скоростью v3 = 4 км/ч. Определить среднюю скорость велосипедиста на всем пути.
а) Эта задача на равномерное прямолинейное движение одного тела. Представляем ввиде схемы. При составлении ее изображаем траекторию движения и выбираем на ней начало отсчета (точка 0). Весь путь разбиваем на три отрезка S1,S2, S3, на каждом из них указываем скорости v1, v2, v3 и отмечаем время движения t1, t2, t3.
S = S1 + S2 + S3, t = t1 + t2 + t3.
б) Составляем уравнения движения для каждого отрезка пути:
S1 = v1t1; S2 = v2t2; S3 = v3t3 и записываем дополнительные условия задачи:
S1 = S2 + S3; t2 = t3; .
в) Читаем еще раз условие задачи, выписываем числовые значения известных величин и, определив число неизвестных в полученной системе уравнений (их 7: S1, S2, S3, t1, t2, t3, vср), решаем ее относительно искомой величины vср.
Если при решении задачи полностью учтены все условия, но в составленных уравнениях число неизвестных получается больше числа уравнений, это означает, что при последующих вычислениях одно из неизвестных сократится, такой случай имеет место и в данной задаче.
Решение системы относительно средней скорости дает:
.
г) Подставив числовые значения в расчётную формулу, получим:
; vср 7 км/ч.
Напоминаем, что числовые значения удобнее подставлять в окончательную расчетную формулу, минуя все промежуточные. Это экономит время на решение задачи и предотвращает дополнительные ошибки в расчётах.
Решая задачи на движение тел, брошенных вертикально вверх, нужно обратить особое внимание на следующее. Уравнения скорости и перемещения для тела, брошенного вертикально вверх, дают общую зависимость v и h от t для всего времени движения тела. Они справедливы (со знаком минус) не только для замедленного подъема вверх, но и для дальнейшего равноускоренного падения тела, поскольку движение тела после мгновенной остановки в верхней точке траектории происходит с прежним ускоронием.
Если тело брошено вертикально вверх со скоростью V0, то время tпод и высота hmax его подъема равны:
; .
Кроме того, время падения этого тела в исходную точку равно времени подъема на максимальную высоту (tпад = tпод), а скорость падения равна начальной скорости бросания (vпад = v0).
Пример 2 . Тело брошено вертикально вверх с начальной скоростью v0 = 3,13 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с такой же начальной скоростью бросили второе тело. Определите, на каком расстоянии от точки бросания встретятся тела; сопротивление воздуха не учитывать.
Решение . Делаем чертеж. Отмечаем на нем траекторию движения первого и второго тела. Выбрав начало отсчета в точке, указываем начальную скорость тел v0, высоту h, на которой произошла встреча (координату y=h), и время t1 и t2 движения каждого тела до момента встречи.
Уравнение перемещения тела, брошенного вверх, позволяет найти координату движущегося тела для любого момента времени независимо от того, поднимается ли тело вверх или падает после подъема вниз, поэтому для первого тела
,
а для второго
.
Третье уравнение составляем, исходя из условия, что второе тело бросили позднее первого на время максимального подъема:
Решая систему трех уравнений относительно h, получаем:
; ; https://pandia.ru/text/78/108/images/image017_1.gif”>; ,
где и ; https://pandia.ru/text/78/108/images/image042.gif”>.gif”>
Прямоугольную систему координат выбираем так, чтобы ее начало совпало с точкой бросания, а оси были направлены вдоль поверхности Земли и по нормали к ней в сторону начального смещения снаряда. Изображаем траекторию снаряда, его начальную скорость , угол бросания a, высоту h, горизонтальное перемещение S, скорость в момент падения (она направлена по касательной к траектории в точке падения) и угол падения j (углом падения тела называют угол между касательной к траектории, проведенной в точку падения, и нормалью к поверхности Земли).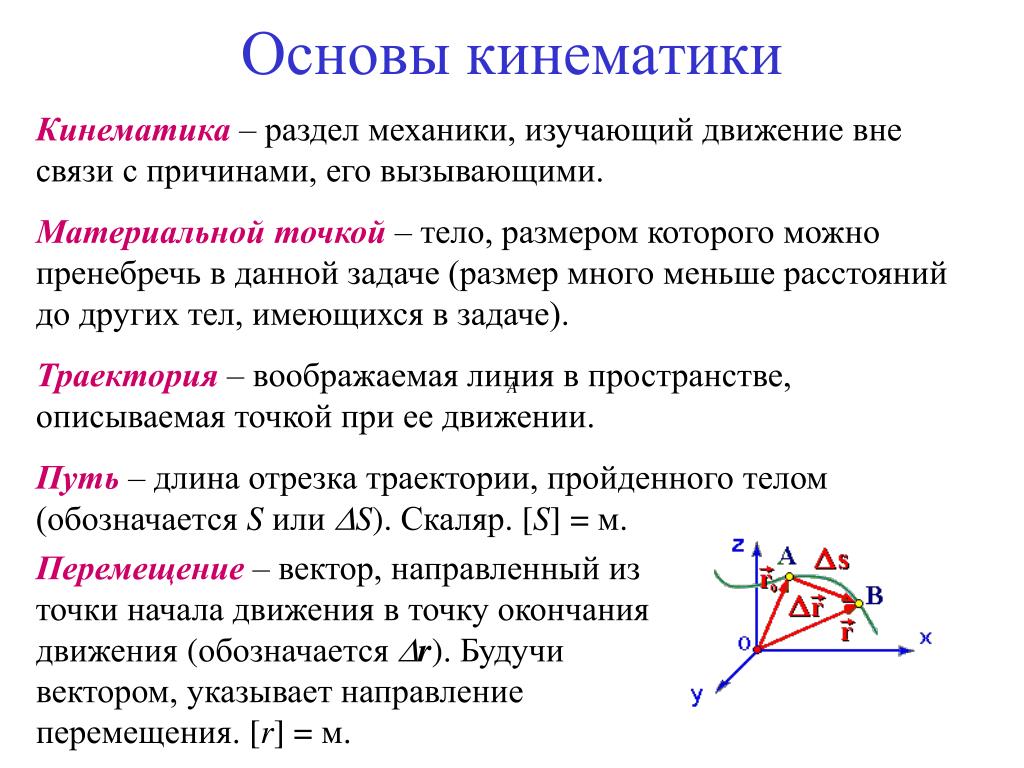
Движение тела, брошенного под углом к горизонту, можно представить как результат сложения двух прямолинейных движений: одного-вдоль поверхности Земли (оно будет равномерным, поскольку сопротивление воздуха не учитывается) и второго-перпендикулярно поверхности Земли (в данном случае это будет движение тела, брошенного вертикально вверх). Для замены сложного движения двумя простыми разложим (по правилу параллелограмма) скорости и https://pandia.ru/text/78/108/images/image047.gif”>и – для скорости и vx и vy – для скорости .
а, б) Составляем уравнение скорости и перемещения для их проекций по каждому направлению. Так как в горизонтальном направлении снаряд летит равномерно, то его скорость и координаты в любой момент времени удовлетворяют уравнениям
и . (2)
Для вертикального направления:
(3)
и . (4)
В момент времени t1, когда снаряд упадет на землю, его координаты равны:
В последнем уравнении перемещение h взято со знаком “минус”, так как за время движения снаряд сместится относительно уровня отсчета 0 высоты в сторону противоположную направлению, принятому за положительное.
Результирующая скорость в момент падения равна:
В составленной системе уравнений пять неизвестных, нам нужно определить S и v.
При отсутствии сопротивления воздуха, скрость падения тел равна начальной скорости бросания независимо от того, под каким углом было брошено тело, лишь бы точки бросания и падения находились на одном уровне. Учитывая, что горизонтальная составляющая скорости с течением времени не изменяется, легко установить, что в момент падения скорость тела образует с горизонтом такой же угол, как и в момент бросания.
д) Решая уровнения (2), (4) и (5) относительно начального угла бросания a получим:
. (10)
Поскольку угол бросания не может быть мнимым, то это выражение имеет физический смысл лишь при условии, что
,
то есть,
откуда следует, что максимальное перемещение снаряда по горизонтальному направлению равно:
.
Подставляя выражение для S = Smax в формулу (10), получим для угла a, при котором дальность полета наибольшая:
Масса.
 Масса m – скалярная физическая величина, характеризующая свойство тел притягиваться к земле и к другим телам.
Масса m – скалярная физическая величина, характеризующая свойство тел притягиваться к земле и к другим телам.Масса тела – постоянная величина.
Единица массы – 1 килограмм (кг).
Плотность.
Плотностью ρ называется отношение массы m тела к занимаемому им объёму V:Единица плотности – 1 кг/м 3 .
Сила.
Сила F – физическая величина, характеризующая действие тел друг на друга и являющаяся мерой их взаимодействия. Сила – векторная величина; вектор силы характеризуется модулем (числовым значением) F, точкой приложения и направлением.Единица силы – 1 ньютон (Н).
Сила тяжести.
Сила тяжести – сила, с которой тела притягиваются к Земле. Она направлена к центру Земли и, следовательно, перпендикулярна к её поверхности:Давление.
Давление p – скалярная физическая величина, равная отношению силы F, действующей перпендикулярно поверхности, к площади этой поверхности S:Единица давления – 1 паскаль (Па) = 1 Н/м 2 .
Работа.
Работа A – скалярная физическая велечина, равная произведению силы F на расстояние S, пройденное телом под действием этой силы:Единица работы – 1 джоуль (Дж) = 1 Н*м.
Энергия.
Энергия E – скалярная физическая величина, характеризующая любое движение и любое взаимодействие и определяющая способность тела совершать работу.Единица энергии, как и работы, – 1 Дж.
Кинематика
Движение.
Механическим движением тела называют изменение с течением времени его положения в пространстве.Система отсчёта.
Связанные с телом отсчёта систему координат и часы называют системой отсчёта.Материальная точка.
Тело, размерами которого можно пренебречь в данной ситуации, называется материальной точкой. Строго говоря, все законы механики справедливы для материальных точек.Траектория.
Линия, вдоль которой перемещается тело, называется траекторией. По виду траектории движения разделяются на два типа – прямолинейное и криволинейное.
Путь и перемещение.
Путь – скальрная величина, равная расстоянию, пройденному телом вдоль траектории движения. Перемещение – вектор, соединяющий начальную и конечную точки пути.Скорость.
Скоростью υ называют векторную физическую величину, характеризующую быстроту и направление перемещения тела. Для равномерного движения скорость равна отношению перемещения ко времени, за которое оно произошло:Единица скорости – 1 м/с, но часто пользуются км/ч (36 км/ч = 10 м/с).
Уравнение движения.
Уравнение движения – зависимость перемещения от времени. Для равномерного прямолинейного движения уравнение движения имеет видМгновенная скорость.
Мгновенная скорость – отношение очень малого перемещения к промежутку времени, за который оно произошло:Средняя скорость:
Ускорение.
Ускорением a называют векторную физическую величину, характеризующую быстроту изменения скорости движения. При равнопеременном движении (т.е при равноускоренном или равнозамедленном) ускорение равно отношению изменения скорости к промежутку времени, за который это изменение произошло:Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия».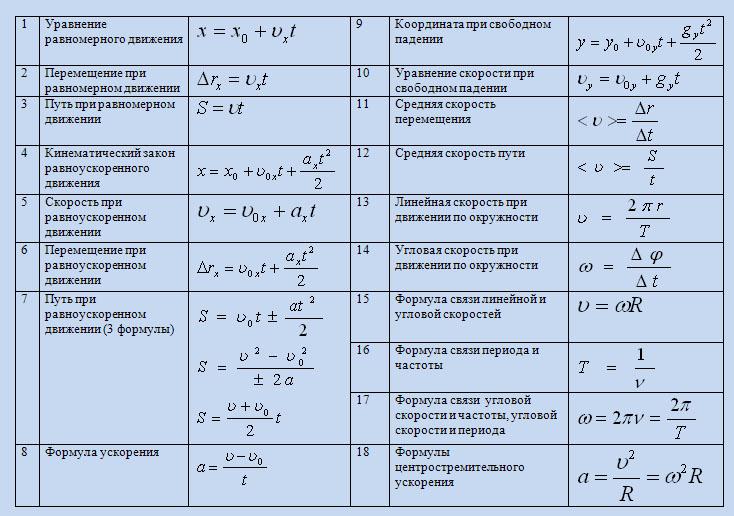 Куда же нам без них!
Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела , объекта или частицы . Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Радиус-вектор точки – это вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой. Радиус-вектор обозначается, как правило, буквой r . К сожалению некоторые авторы обозначают его буквой s . Настоятельно советую не использовать обозначение s для радиус-вектора.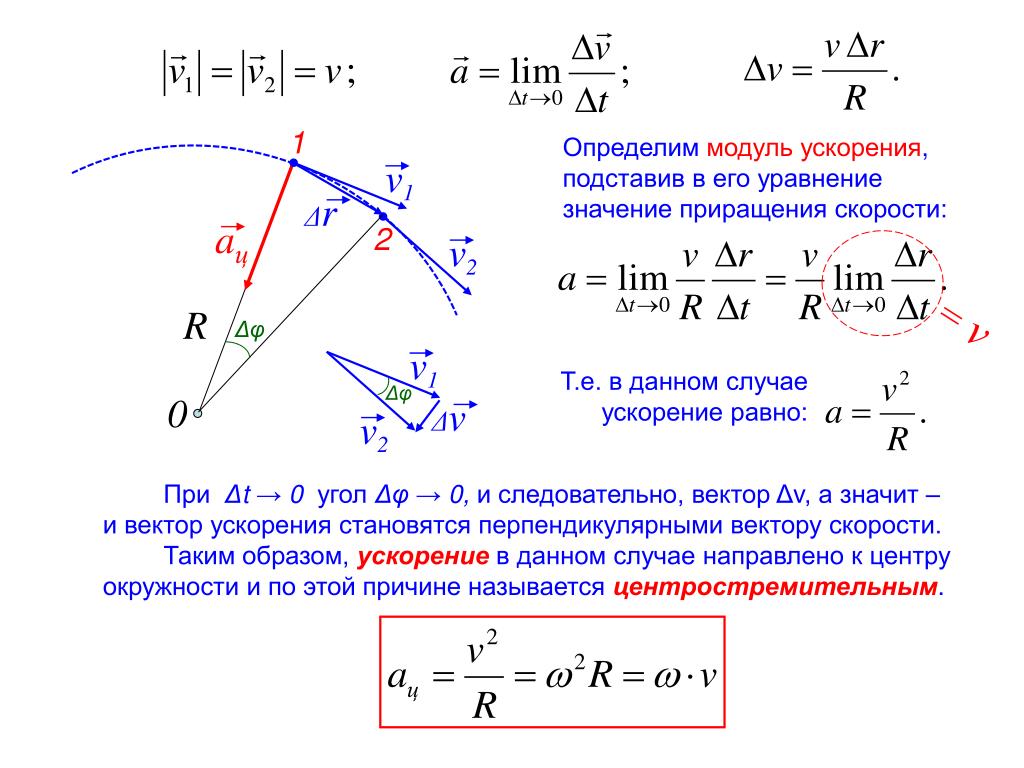 Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r – радиус-вектор точки, s – путь, пройденный точкой.
Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r – радиус-вектор точки, s – путь, пройденный точкой.
Вектор перемещения (часто говорят просто – перемещение ) – это вектор , начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr . Использование символа Δ очевидно: Δr – это разность между радиус-вектором r конечной точки изучаемого отрезка траектории и радиус-вектором r 0 точки начала этого отрезка (рис. 1), то есть Δr = r − r 0 .
Траектория – это линия, вдоль которой движется тело.
Путь – это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r, мы уже об этом говорили). Запомните! Путь – это положительный скаляр ! Путь в процессе движения может только увеличиваться .
Средняя скорость перемещения v ср
v ср = Δr /Δt.
Мгновенная скорость перемещения v – это вектор, определяемый выражением
v = dr /dt.
Средняя скорость пути v ср – это скаляр, определяемый выражением
V ср = Δs/Δt.
Часто встречаются и другие обозначения, например, .
Мгновенная скорость пути v – это скаляр, определяемый выражением
Модуль мгновенной скорости перемещения и мгновенная скорость пути – это одно и то же, поскольку dr = ds.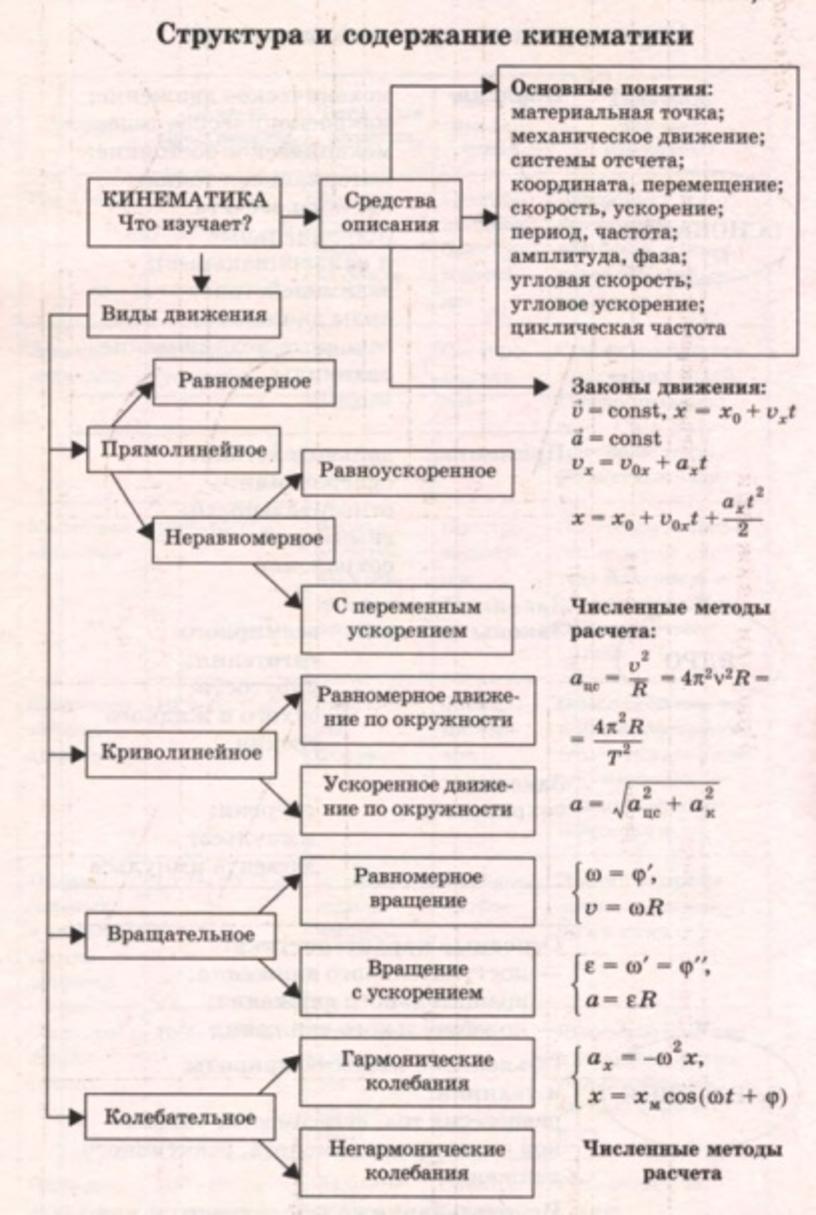
Среднее ускорение a
a ср = Δv /Δt.
Мгновенное ускорение (или просто, ускорение ) a – это вектор, определяемый выражением
a =dv /dt.
Касательное (тангенциальное) ускорение a τ (нижний индекс – это греческая строчная буква тау) – это вектор , являющийся векторной проекцией мгновенного ускорения на касательную ось .
Нормальное (центростремительное) ускорение a n – это вектор , являющийся векторной проекцией мгновенного ускорения на ось нормали .
Модуль касательного ускорения
| a τ | = dv/dt,
То есть это – производная модуля мгновенной скорости по времени.
Модуль нормального ускорения
| a n | = v 2 /r,
Где r – величина радиуса кривизны траектории в точке нахождения тела.
Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.
Запомните!
a τ – это вектор касательного ускорения,
a n – это вектор нормального ускорения.
a τ и a n являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,
A τ – это проекция (скалярная!) касательного ускорения на касательную ось,
A n – это проекция (скалярная!) нормального ускорения на ось нормали,
| a τ |- это модуль вектора касательного ускорения,
| a n | – это модуль вектора нормального ускорения.
Особенно не удивляйтесь, если, читая в литературе о криволинейном (в частности, вращательном) движении, Вы обнаружите, что автор под a τ понимает и вектор, и его проекцию, и его модуль. То же самое относится и к a n . Все, как говорится, «в одном флаконе». И такое, к сожалению, сплошь и рядом. Даже учебники для высшей школы не являются исключением, во многих из них (поверьте – в большинстве!) царит полная неразбериха по этому поводу.
Вот так, не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.
Мгновенная угловая скорость (или просто, угловая скорость ) ω – это вектор, определяемый выражением
ω = dφ /dt,
Где dφ – бесконечно малое изменение угловой координаты (dφ – вектор!).
Мгновенное угловое ускорение (или просто, угловое ускорение ) ε – это вектор, определяемый выражением
ε = dω /dt.
Связь между v , ω и r :
v = ω × r .
Связь между v, ω и r:
Связь между | a τ |, ε и r:
| a τ | = ε · r.
Теперь перейдем к кинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть .
Эти уравнения надо выучить наизусть .
Кинематическое уравнение равномерного и прямолинейного движения имеет вид:
r = r 0 + v t,
Где r – радиус-вектор объекта в момент времени t, r 0 – то же в начальный момент времени t 0 (в момент начала наблюдений).
Кинематическое уравнение движения с постоянным ускорением имеет вид:
r = r 0 + v 0 t + a t 2 /2, где v 0 скорость объекта в момент t 0 .
Уравнение для скорости тела при движении с постоянным ускорением имеет вид:
v = v 0 + a t.
Кинематическое уравнение равномерного движения по окружности в полярных координатах имеет вид:
φ = φ 0 + ω z t,
Где φ – угловая координата тела в данный момент времени, φ 0 – угловая координата тела в момент начала наблюдения (в начальный момент времени), ω z – проекция угловой скорости ω на ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).
Кинематическое уравнение движения по окружности с постоянным ускорением в полярных координатах имеет вид:
φ = φ 0 + ω 0z t + ε z t 2 /2.
Кинематическое уравнение гармонических колебаний вдоль оси X имеет вид:
Х = А Cos (ω t + φ 0),
Где A – амплитуда колебаний, ω – циклическая частота, φ 0 – начальная фаза колебаний.
Проекция скорости точки, колеблющейся вдоль оси X, на эту ось равна:
V x = − ω · A · Sin (ω t + φ 0).
Проекция ускорения точки, колеблющейся вдоль оси X, на эту ось равна:
А x = − ω 2 · A · Cos (ω t + φ 0).
Связь между циклической частотой ω, обычной частотой ƒ и периодом колебаний T:
ω = 2 πƒ = 2 π/T (π = 3,14 – число пи).
Математический маятник имеет период колебаний T, определяемый выражением:
В числителе подкоренного выражения – длина нити маятника, в знаменателе – ускорение свободного падения
Связь между абсолютной v абс, относительной v отн и переносной v пер скоростями:
v абс = v отн + v пер.
Вот, пожалуй, и все определения и формулы, которые могут понадобиться при решении задач на кинематику. Приведенная информация носит только справочный характер и не может заменить электронную книгу, где доступно, подробно и, надеюсь, увлекательно изложена теория этого раздела механики.
Определение 1
Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Определение 2
Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Определение 3
Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета .
Определение 4
Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В С И единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Определение 5
Механическое движение называют поступательным , в случае если все части тела перемещаются одинаково.
Пример 1
Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Определение 6
Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Термин “материальная точка” имеет важное значение в механике.
Определение 7
Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.
Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x = x (t) , y = y (t) , z = z (t) или зависимость от времени радиус-вектора r → = r → (t) , проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке 1 . 1 . 1 .
Рисунок 1 . 1 . 1 . Определение положения точки при помощи координат x = x (t) , y = y (t) и z = z (t) и радиус-вектора r → (t) , r 0 → – радиус-вектор положения точки в начальный момент времени.
Определение 8
Перемещение тела s → = ∆ r → = r → – r 0 → – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.
Перемещение является векторной величиной.
Пройденный путь l равняется длине дуги траектории, преодоленной телом за определенное время t . Путь является скалярной величиной.
Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.
В случае небольшого промежутка времени Δ t преодоленный телом путь Δ l практически совпадает с модулем вектора перемещения ∆ s → . При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок 1 . 1 . 2).
Рисунок 1 . 1 . 2 . Пройденный путь l и вектор перемещения ∆ s → при криволинейном движении тела.
a и b – это начальная и конечная точки пути.
Для описания движения в физике введено понятие средней скорости: υ → = ∆ s → ∆ t = ∆ r → ∆ t .
Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени Δ t , то есть υ → = ∆ s → ∆ t = ∆ r → ∆ t ; ∆ t → 0 .
В математике данный предел называется производная и обозначается d r → d t или r → ˙ .
Мгновенная скорость υ → тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок 1 . 1 . 3 .
Рисунок 1 . 1 . 3 . Средняя и мгновенная скорости. ∆ s 1 → , ∆ s 2 → , ∆ s 3 → – перемещения за время ∆ t 1 соответственно. При t → 0 , υ → с р → υ → .
При перемещении тела по криволинейной траектории скорость υ → меняется по модулю и по направлению. Изменение вектора скорости υ → за какой-то маленький промежуток времени Δ t задается при помощи вектора ∆ υ → (рисунок 1 . 1 . 4).
Вектор изменения скорости ∆ υ → = υ 2 → – υ 1 → за короткий промежуток времени Δ t раскладывается на 2 составляющие: ∆ υ r → , которая направлена вдоль вектора υ → (касательная составляющая) и ∆ υ n → , которая направлена перпендикулярно вектору υ → (нормальная составляющая).
Рисунок 1 . 1 . 4 . Изменение вектора скорости по величине и по направлению. ∆ υ → = ∆ υ → r + ∆ υ → n – изменение вектора скорости за промежуток времени Δ t .
Определение 9
Мгновенное ускорение тела a → – это предел отношения небольшого изменения скорости ∆ υ → к короткому отрезку времени Δ t , в течение которого изменялась скорость: a → = ∆ υ → ∆ t = ∆ υ → τ ∆ t + ∆ υ → n ∆ t ; (∆ t → 0) .
Направление вектора ускорения a → , при криволинейном движении, не совпадает с направлением вектора скорости υ → . Составляющие вектора ускорения a → – это касательные (тангенциальные) a → τ и нормальные a → n ускорения (рисунок 1 . 1 . 5).
Рисунок 1 . 1 . 5 . Касательное и нормальное ускорения.
Касательное ускорение показывает, как быстро меняется скорость тела по модулю: a τ = ∆ υ ∆ t ; ∆ t → 0 .
Вектор a → τ направлен по касательной к траектории.
Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.
Пример 2
Представим криволинейное движение, как движение по дугам окружностей (рисунок 1 . 1 . 6).
Рисунок 1 . 1 . 6 . Движение по дугам окружностей.
Нормальное ускорение находится в зависимости от модуля скорости υ и радиуса R окружности, по дуге которой тело перемещается в определенный момент времени: a n = υ 2 R .
Вектор a n → все время направлен к центру окружности.
По рисунку 1 . 1 . 5 видно, модуль полного ускорения равен a = a τ 2 + a n 2 .
Итак, основные физические величины в кинематике материальной точки – это пройденный путь l , перемещение s → , скорость υ → и ускорение a → .
Путь l – скалярная величина.
Перемещение s → , скорость υ → и ускорение a → – векторные величины.
Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Кинематика материальной точки: основные понятия, элементы
Темой нашей сегодняшней статьи станет кинематика материальной точки. Что это вообще такое? Какие понятия фигурируют в ней и какое определение необходимо дать этому термину? На эти и многие другие вопросы мы сегодня и постараемся ответить.
Определение и понятие
Кинематика материальной точки представляет собой не что иное, как подраздел физики под названием «механика». Она, в свою очередь, изучает закономерности движения тех или иных тел. Кинематика материальной точки занимается также этой задачей, однако делает это не в общем виде. На самом деле этот подраздел изучает методы, которые позволяют описать движение тел. При этом для исследования подходят только так называемые идеализированные тела. К таковым относятся: материальная точка, абсолютно твердое тело и идеальный газ. Рассмотрим понятия подробнее. Все мы со школьной скамьи знаем, что материальной точкой принято называть тело, размерами которого в той или иной ситуации можно пренебречь. К слову, кинематика поступательного движения материальной точки впервые начинает фигурировать в учебниках седьмого класса по физике. Это наиболее простая отрасль, поэтому начинать знакомство с наукой при ее помощи наиболее удобно. Отдельным вопросом является то, какие имеются элементы кинематики материальной точки. Их достаточно много, причем условно их можно разбить на несколько уровней, имеющих различную сложность для понимания. Если говорить, например, о радиус-векторе, то, в принципе, в его определении нет ничего запредельно сложного. Однако согласитесь с тем, что гораздо проще его понять будет студенту, нежели ученику средней или старшей школы. Да и если честно говорить, нет никакой необходимости объяснять особенности этого термина старшеклассникам.
К слову, кинематика поступательного движения материальной точки впервые начинает фигурировать в учебниках седьмого класса по физике. Это наиболее простая отрасль, поэтому начинать знакомство с наукой при ее помощи наиболее удобно. Отдельным вопросом является то, какие имеются элементы кинематики материальной точки. Их достаточно много, причем условно их можно разбить на несколько уровней, имеющих различную сложность для понимания. Если говорить, например, о радиус-векторе, то, в принципе, в его определении нет ничего запредельно сложного. Однако согласитесь с тем, что гораздо проще его понять будет студенту, нежели ученику средней или старшей школы. Да и если честно говорить, нет никакой необходимости объяснять особенности этого термина старшеклассникам.
Краткая история создания кинематики
Еще много-много лет назад великий ученный Аристотель посвятил львиную долю своего свободного времени изучению и описанию физики как отдельной науки. В том числе он работал и над кинематикой, пытаясь представить ее основные тезисы и понятия, так или иначе применяемые при попытках решения практических и даже обыденных задач. Аристотель дал первоначальные представления о том, что представляют собой элементы кинематики материальной точки. Его работы и труды очень ценны для всего человечества. Тем не менее в своих выводах он сделал немалое количество ошибок, и виной тому были определенные заблуждения и просчеты. Работами Аристотеля в свое время заинтересовался другой ученный – Галилео Галилей. Один из основополагающих тезисов, выдвинутых Аристотелем, гласил о том, что движение тела происходит только в том случае, если на него действует какая-то сила, определенная по интенсивности и направлению. Галилей доказал, что это ошибка. Сила будет оказывать влияние на параметр скорости движения, но не более. Итальянец показал, что сила есть причина ускорения, и оно может возникнуть только обоюдно с ней. Также Галилео Галилей уделил немалое внимание изучению процесса свободного падения, выводя соответствующие закономерности. Наверное, все помнят о его знаменитых опытах, которые он проводил на Пизанской башне. В своих работах основы кинематических решений использовал и физик Ампер.
Аристотель дал первоначальные представления о том, что представляют собой элементы кинематики материальной точки. Его работы и труды очень ценны для всего человечества. Тем не менее в своих выводах он сделал немалое количество ошибок, и виной тому были определенные заблуждения и просчеты. Работами Аристотеля в свое время заинтересовался другой ученный – Галилео Галилей. Один из основополагающих тезисов, выдвинутых Аристотелем, гласил о том, что движение тела происходит только в том случае, если на него действует какая-то сила, определенная по интенсивности и направлению. Галилей доказал, что это ошибка. Сила будет оказывать влияние на параметр скорости движения, но не более. Итальянец показал, что сила есть причина ускорения, и оно может возникнуть только обоюдно с ней. Также Галилео Галилей уделил немалое внимание изучению процесса свободного падения, выводя соответствующие закономерности. Наверное, все помнят о его знаменитых опытах, которые он проводил на Пизанской башне. В своих работах основы кинематических решений использовал и физик Ампер.
Исходные понятия
Как говорилось ранее, кинематика изучает способы описания движения идеализированных объектов. При этом на практике могут применяться основы математического анализа, обыкновенной алгебры и геометрии. Но какие же понятия (именно понятия, а не определения и на параметрические величины) лежат в основе этого подраздела физики? Во-первых, все должны четко усвоить, что кинематика поступательного движения материальной точки рассматривает движение без учета силовых показателей. То есть для решения соответствующих задач нам не понадобятся формулы, связанные с силой. Она кинематикой не учитывается, сколько бы их ни было – одна, две, три, хоть несколько сотен тысяч. Тем не менее существование ускорения все же предусматривается. В целом ряде задач кинематика движения материальной точки предписывает определить величину ускорения. Однако причины возникновения этого явления (то есть силы и их природа) не рассматриваются, а опускаются.
Классификация
Мы выяснили, что кинематика исследует и применяет методы описания движения тел без оглядки на воздействующие на них силы. Кстати говоря, такой задачей занимается уже другой подраздел механики, который называют динамикой. Вот уже там применяются законы Ньютона, которые позволяют на практике определить достаточно многие параметры при малом количестве известных первоначальных данных. Основные понятия кинематики материальной точки – это пространство и время. А в связи с развитием науки как в целом, так и в данной области, возник вопрос о целесообразности использования подобной комбинации.
Кстати говоря, такой задачей занимается уже другой подраздел механики, который называют динамикой. Вот уже там применяются законы Ньютона, которые позволяют на практике определить достаточно многие параметры при малом количестве известных первоначальных данных. Основные понятия кинематики материальной точки – это пространство и время. А в связи с развитием науки как в целом, так и в данной области, возник вопрос о целесообразности использования подобной комбинации.
С самого начала существовала классическая кинематика. Можно говорить о том, что ей свойственно не просто наличие как временных, так и пространственных промежутков, но и их независимость от выбора той или иной системы отсчета. Кстати, об этом мы поговорим несколько позже. Сейчас же просто объясним, о чем идет речь. Пространственным промежутком в данном случае будет считаться отрезок, временным – интервал времени. Вроде бы все должно быть понятно. Так вот, эти промежутки будет в классической кинематике считаться абсолютными, инвариантными, иными словами не зависящими от перехода из одной системы отсчета в другую. То ли дело релятивистская кинематика. В ней промежутки при переходе между системами отсчета могут изменяться. Правильнее даже будет сказать, что не могут, а должны, наверное. В силу этого одновременность двух случайных событий также становится относительной и подлежит особому рассмотрению. Именно поэтому в релятивистской кинематике два понятия – пространство и время – объединяются в одно.
То ли дело релятивистская кинематика. В ней промежутки при переходе между системами отсчета могут изменяться. Правильнее даже будет сказать, что не могут, а должны, наверное. В силу этого одновременность двух случайных событий также становится относительной и подлежит особому рассмотрению. Именно поэтому в релятивистской кинематике два понятия – пространство и время – объединяются в одно.
Кинематика материальной точки: скорость, ускорение и другие величины
Чтобы хотя бы немного понимать данный подраздел физики, необходимо ориентироваться в наиболее главных понятиях, знать определения и представлять, что собой представляет в общем плане та или иная величина. Ничего сложно в этом нет на самом деле, все очень легко и просто. Рассмотрим, пожалуй, для начала основные понятия, применяемые в задачах по кинематике.
Движение
Механическим движением мы будем считать процесс, в ходе которого тот или иной идеализированный объект изменяет свое положение в пространстве.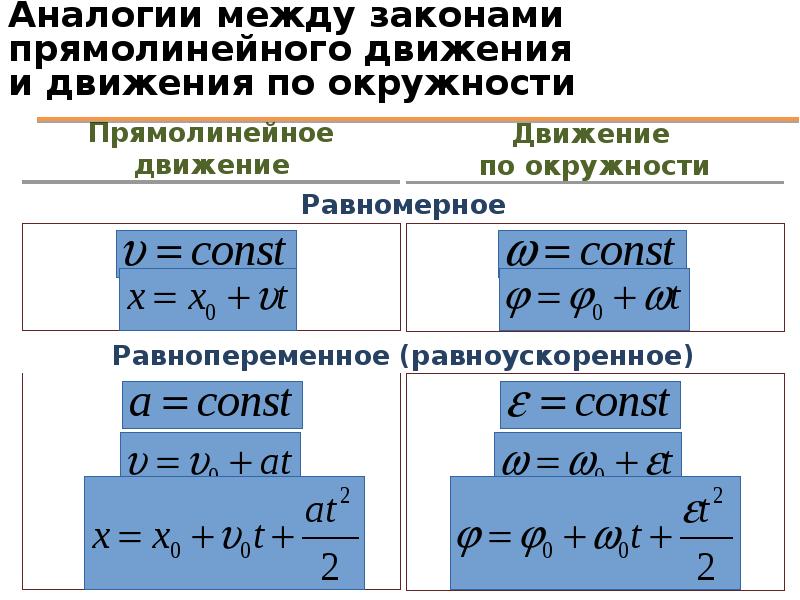 При этом можно говорить о том, что изменение происходит относительно других тел. Необходимо учитывать и тот факт, что одновременно происходит и установление определенного временного промежутка между двумя событиями. Например, можно будет выделить определенный интервал, образовавшийся за время, прошедшее между тем, как тело прибыло из одной позиции в другую. Отметим также, что тела при этом могут и будут взаимодействовать между собой, согласно общим законам механики. Это как раз то, чем чаще всего оперирует кинематика материальной точки. Система отсчета – следующее понятие, которое неразрывно связано с ней.
При этом можно говорить о том, что изменение происходит относительно других тел. Необходимо учитывать и тот факт, что одновременно происходит и установление определенного временного промежутка между двумя событиями. Например, можно будет выделить определенный интервал, образовавшийся за время, прошедшее между тем, как тело прибыло из одной позиции в другую. Отметим также, что тела при этом могут и будут взаимодействовать между собой, согласно общим законам механики. Это как раз то, чем чаще всего оперирует кинематика материальной точки. Система отсчета – следующее понятие, которое неразрывно связано с ней.
Координаты
Их можно назвать обыкновенным данными, которые позволяют определить положение тела в тот или иной момент времени. Координаты неразрывно связаны с понятием системы отсчета, а также координатной сеткой. Чаще всего представляют собой комбинацию букв и цифр.
Радиус-вектор
Из названия уже должно быть понятно, что он представляет собой. Тем не менее все же поговорим об этом подробнее. Если точка движется по некоторой траектории, а мы точно знаем начало той или иной системы отсчета, то можно в любой момент времени провести радиус-вектор. Он будет соединять первоначальное положение точки с мгновенным или конечным.
Если точка движется по некоторой траектории, а мы точно знаем начало той или иной системы отсчета, то можно в любой момент времени провести радиус-вектор. Он будет соединять первоначальное положение точки с мгновенным или конечным.
Траектория
Ею будет называться непрерывная линия, которая прокладывается в результате движения материальной точки в той или иной системе отсчета.
Скорость (как линейная, так и угловая)
Это величина, которая может рассказать о том, как быстро тело проходит тот или иной промежуток дистанции.
Ускорение (и угловое, и линейное)
Показывает, по какому закону и как интенсивно изменяется скоростной параметр тела.
Пожалуй, вот они – основные элементы кинематики материальной точки. Следует отметить, что и скорость, и ускорение являются векторными величинами. А это означает то, что они не просто имеют некоторое показательное значение, но и определенное направление. К слову, они могут быть направлены как в одну сторону, так и в противоположные. В первом случае тело будет ускоряться, во втором – тормозить.
В первом случае тело будет ускоряться, во втором – тормозить.
Простейшие задачи
Кинематика материальной точки (скорость, ускорение и расстояние в которой являются практически фундаментальными понятиями) насчитывает даже не то что огромное количество задач, а много их различных категорий. Давайте попробуем решить достаточно простенькую задачку по определению пройденного телом расстояния.
Предположим, условия, которые мы имеем на руках, следующие. Автомобиль гонщика стоит на стартовой черте. Оператор подает отмашку флагом, и машина резко срывается с места. Определить, сможет ли она поставить новый рекорд в состязании гонщиков, если дистанцию, равную одной сотне метров, очередной лидер прошел за 7,8 секунд. Ускорение автомобиля принять равным 3 метра, деленным на секунду в квадрате.
Итак, как же решить подобную задачу? Она достаточно интересная, поскольку от нас требуется не «сухое» определение тех или иных параметров. Она скрашена оборотами и определенной ситуацией, что разнообразит процесс решения и поиска показателей. 2 + 2VoT – 2S. Это есть не что иное, как квадратное уравнение. Но автомобиль срывается с места, значит, начальная скорость будет равна 0. При решении уравнения дискриминант окажется равным 2400. Для поиска времени необходимо извлечь корень. Сделаем до второго знака после запятой: 48,98. Найдем корень уравнения: 48,98/6 = 8,16 секунд. Получается, что гонщик не сможет побить существующий рекорд.
2 + 2VoT – 2S. Это есть не что иное, как квадратное уравнение. Но автомобиль срывается с места, значит, начальная скорость будет равна 0. При решении уравнения дискриминант окажется равным 2400. Для поиска времени необходимо извлечь корень. Сделаем до второго знака после запятой: 48,98. Найдем корень уравнения: 48,98/6 = 8,16 секунд. Получается, что гонщик не сможет побить существующий рекорд.
Способы описания движения тела
Существует три основных способа описания механического движения: векторный, координатный и естественный. Выбор способа описания зависит от условий конкретной задачи.
Векторный способ описания движения
Рассмотрим движение точки в некоторой системе отсчета (рис.1). Зададим радиус-вектор точки — вектор, соединяющий начало координат с этой точкой.
При движении точки вектор будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость представляет собой закон движения в векторном виде.
В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение точки.
Координатный способ описания движения
При координатном способе положение точки в пространстве задается тремя координатами (рис.2). Выбор системы координат зависит от конкретной задачи. Можно работать в декартовой (прямоугольной) системе, иногда удобнее бывает сферическая или цилиндрическая системы координат.
В декартовой системе координат положение точки определяется тройкой чисел — ее декартовыми координатами.
Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений:
Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки:
Естественный способ описания движения
Пусть точка движется вдоль траектории в системе отсчета (рис. 3). Выберем на траектории какую-нибудь неподвижную точку , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием от точки . При движении точка переместится в точку , соответственно изменится ее расстояние от точки . Таким образом, расстояние зависит от времени, а характер этой зависимости позволит определить положение точки на траектории в любой момент времени. Закон движения в этом случае имеет вид: .
3). Выберем на траектории какую-нибудь неподвижную точку , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием от точки . При движении точка переместится в точку , соответственно изменится ее расстояние от точки . Таким образом, расстояние зависит от времени, а характер этой зависимости позволит определить положение точки на траектории в любой момент времени. Закон движения в этом случае имеет вид: .
Примеры решения задач по теме «Способы описания движения»
Основные понятия кинематики и формулы. Кинематика
Определение 1
Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Определение 2
Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Движение одного и того же тела относительно разных тел может быть разным.
Определение 3
Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета .
Определение 4
Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В С И единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Определение 5
Механическое движение называют поступательным , в случае если все части тела перемещаются одинаково.
Пример 1
Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Определение 6
Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Термин “материальная точка” имеет важное значение в механике.
Определение 7
Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.
Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x = x (t) , y = y (t) , z = z (t) или зависимость от времени радиус-вектора r → = r → (t) , проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке 1 . 1 . 1 .
Рисунок 1 . 1 . 1 . Определение положения точки при помощи координат x = x (t) , y = y (t) и z = z (t) и радиус-вектора r → (t) , r 0 → – радиус-вектор положения точки в начальный момент времени.
Определение 8
Перемещение тела s → = ∆ r → = r → – r 0 → – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.
Пройденный путь l равняется длине дуги траектории, преодоленной телом за определенное время t . Путь является скалярной величиной.
Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.
В случае небольшого промежутка времени Δ t преодоленный телом путь Δ l практически совпадает с модулем вектора перемещения ∆ s → . При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок 1 . 1 . 2).
Рисунок 1 . 1 . 2 . Пройденный путь l и вектор перемещения ∆ s → при криволинейном движении тела.
a и b – это начальная и конечная точки пути.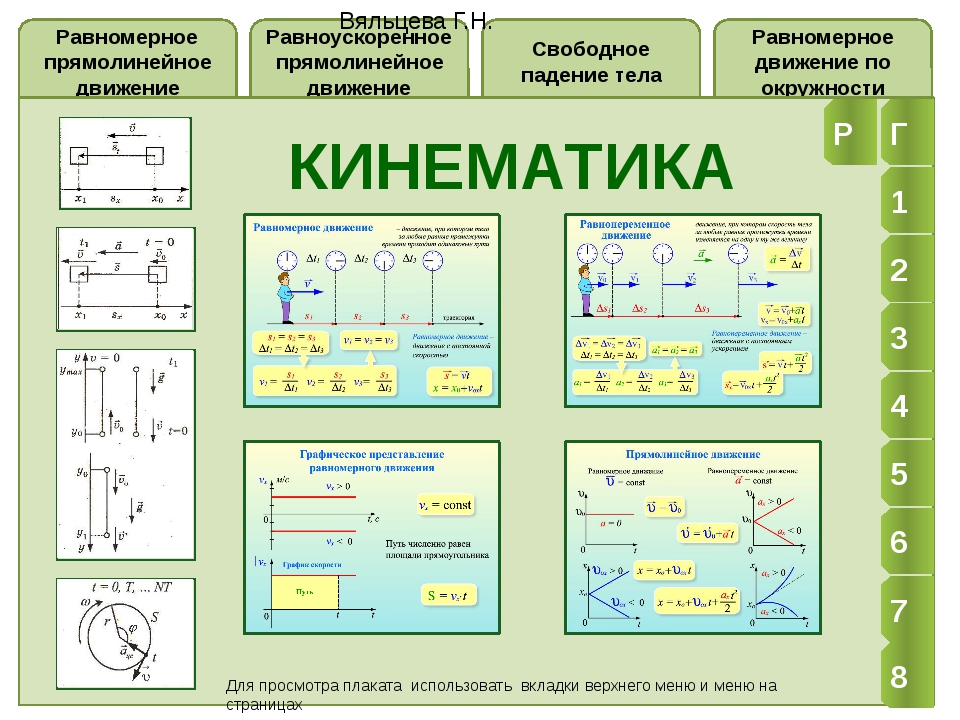
Для описания движения в физике введено понятие средней скорости: υ → = ∆ s → ∆ t = ∆ r → ∆ t .
Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени Δ t , то есть υ → = ∆ s → ∆ t = ∆ r → ∆ t ; ∆ t → 0 .
В математике данный предел называется производная и обозначается d r → d t или r → ˙ .
Мгновенная скорость υ → тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок 1 . 1 . 3 .
Рисунок 1 . 1 . 3 . Средняя и мгновенная скорости. ∆ s 1 → , ∆ s 2 → , ∆ s 3 → – перемещения за время ∆ t 1 соответственно. При t → 0 , υ → с р → υ → .
При перемещении тела по криволинейной траектории скорость υ → меняется по модулю и по направлению. Изменение вектора скорости υ → за какой-то маленький промежуток времени Δ t задается при помощи вектора ∆ υ → (рисунок 1 . 1 . 4).
1 . 4).
Вектор изменения скорости ∆ υ → = υ 2 → – υ 1 → за короткий промежуток времени Δ t раскладывается на 2 составляющие: ∆ υ r → , которая направлена вдоль вектора υ → (касательная составляющая) и ∆ υ n → , которая направлена перпендикулярно вектору υ → (нормальная составляющая).
Рисунок 1 . 1 . 4 . Изменение вектора скорости по величине и по направлению. ∆ υ → = ∆ υ → r + ∆ υ → n – изменение вектора скорости за промежуток времени Δ t .
Определение 9
Мгновенное ускорение тела a → – это предел отношения небольшого изменения скорости ∆ υ → к короткому отрезку времени Δ t , в течение которого изменялась скорость: a → = ∆ υ → ∆ t = ∆ υ → τ ∆ t + ∆ υ → n ∆ t ; (∆ t → 0) .
Направление вектора ускорения a → , при криволинейном движении, не совпадает с направлением вектора скорости υ → . Составляющие вектора ускорения a → – это касательные (тангенциальные) a → τ и нормальные a → n ускорения (рисунок 1 . 1 . 5).
Рисунок 1 . 1 . 5 . Касательное и нормальное ускорения.
1 . 5 . Касательное и нормальное ускорения.
Касательное ускорение показывает, как быстро меняется скорость тела по модулю: a τ = ∆ υ ∆ t ; ∆ t → 0 .
Вектор a → τ направлен по касательной к траектории.
Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.
Пример 2
Представим криволинейное движение, как движение по дугам окружностей (рисунок 1 . 1 . 6).
Рисунок 1 . 1 . 6 . Движение по дугам окружностей.
Нормальное ускорение находится в зависимости от модуля скорости υ и радиуса R окружности, по дуге которой тело перемещается в определенный момент времени: a n = υ 2 R .
Вектор a n → все время направлен к центру окружности.
По рисунку 1 . 1 . 5 видно, модуль полного ускорения равен a = a τ 2 + a n 2 .
Итак, основные физические величины в кинематике материальной точки – это пройденный путь l , перемещение s → , скорость υ → и ускорение a → .
Путь l – скалярная величина.
Перемещение s → , скорость υ → и ускорение a → – векторные величины.
Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Прежде всего, следует заметить, что речь будет идти о геометрической точке, то есть области пространства, не имеющей размеров. Именно для этого абстрактного образа (модели) и справедливы все представленные ниже определения и формулы. Однако для краткости я в дальнейшем буду часто говорить о движении тела , объекта или частицы . Это я делаю только для того, чтобы Вам легче было читать. Но всегда помните, что речь идет о геометрической точке.
Радиус-вектор точки – это вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой. Радиус-вектор обозначается, как правило, буквой r . К сожалению некоторые авторы обозначают его буквой s . Настоятельно советую не использовать обозначение s для радиус-вектора. Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r – радиус-вектор точки, s – путь, пройденный точкой.
К сожалению некоторые авторы обозначают его буквой s . Настоятельно советую не использовать обозначение s для радиус-вектора. Дело в том, что подавляющее большинство авторов (как отечественных, так и зарубежных) используют букву s для обозначения пути, который является скаляром и к радиус-вектору, как правило, отношения не имеет. Если вы будете обозначать радиус-вектор как s , то легко можете запутаться. Еще раз, мы, как и все нормальные люди, будем использовать следующие обозначения: r – радиус-вектор точки, s – путь, пройденный точкой.
Вектор перемещения (часто говорят просто – перемещение ) – это вектор , начало которого совпадает с той точкой траектории, где было тело, когда мы начали изучать данное движение, а конец этого вектора совпадает с той точкой траектории, где мы это изучение закончили. Будем обозначать этот вектор как Δr . Использование символа Δ очевидно: Δr – это разность между радиус-вектором r конечной точки изучаемого отрезка траектории и радиус-вектором r 0 точки начала этого отрезка (рис. 1), то есть Δr = r − r 0 .
1), то есть Δr = r − r 0 .
Траектория – это линия, вдоль которой движется тело.
Путь – это сумма длин всех участков траектории, последовательно проходимых телом при движения. Обозначается либо ΔS, если речь идет об участке траектории, либо S, если речь идет о всей траектории наблюдаемого движения. Иногда (редко) путь обозначают и другой буквой, например, L (только не обозначайте его как r, мы уже об этом говорили). Запомните! Путь – это положительный скаляр ! Путь в процессе движения может только увеличиваться .
Средняя скорость перемещения v ср
v ср = Δr /Δt.
Мгновенная скорость перемещения v – это вектор, определяемый выражением
v = dr /dt.
Средняя скорость пути v ср – это скаляр, определяемый выражением
V ср = Δs/Δt.
Часто встречаются и другие обозначения, например, .
Мгновенная скорость пути v – это скаляр, определяемый выражением
Модуль мгновенной скорости перемещения и мгновенная скорость пути – это одно и то же, поскольку dr = ds.
Среднее ускорение a
a ср = Δv /Δt.
Мгновенное ускорение (или просто, ускорение ) a – это вектор, определяемый выражением
a =dv /dt.
Касательное (тангенциальное) ускорение a τ (нижний индекс – это греческая строчная буква тау) – это вектор , являющийся векторной проекцией мгновенного ускорения на касательную ось .
Нормальное (центростремительное) ускорение a n – это вектор , являющийся векторной проекцией мгновенного ускорения на ось нормали .
Модуль касательного ускорения
| a τ | = dv/dt,
То есть это – производная модуля мгновенной скорости по времени.
Модуль нормального ускорения
| a n | = v 2 /r,
Где r – величина радиуса кривизны траектории в точке нахождения тела.
Важно! Хочу обратить внимание на следующее. Не путайтесь с обозначениями, касающимися касательного и нормального ускорений! Дело в том, что в литературе по этому поводу традиционно наблюдается полная чехарда.
Запомните!
a τ – это вектор касательного ускорения,
a n – это вектор нормального ускорения.
a τ и a n являются векторными проекциями полного ускорения а на касательную ось и ось нормали соответственно,
A τ – это проекция (скалярная!) касательного ускорения на касательную ось,
A n – это проекция (скалярная!) нормального ускорения на ось нормали,
| a τ |- это модуль вектора касательного ускорения,
| a n | – это модуль вектора нормального ускорения.
Особенно не удивляйтесь, если, читая в литературе о криволинейном (в частности, вращательном) движении, Вы обнаружите, что автор под a τ понимает и вектор, и его проекцию, и его модуль. То же самое относится и к a n . Все, как говорится, «в одном флаконе». И такое, к сожалению, сплошь и рядом. Даже учебники для высшей школы не являются исключением, во многих из них (поверьте – в большинстве!) царит полная неразбериха по этому поводу.
Вот так, не зная азов векторной алгебры или пренебрегая ими, очень легко полностью запутаться при изучении и анализе физических процессов. Поэтому знание векторной алгебры является наиглавнейшим условием успеха в изучении механики. И не только механики. В дальнейшем, при изучении других разделов физики, Вы неоднократно в этом убедитесь.
Мгновенная угловая скорость (или просто, угловая скорость ) ω – это вектор, определяемый выражением
ω = dφ /dt,
Где dφ – бесконечно малое изменение угловой координаты (dφ – вектор!).
Мгновенное угловое ускорение (или просто, угловое ускорение ) ε – это вектор, определяемый выражением
ε = dω /dt.
Связь между v , ω и r :
v = ω × r .
Связь между v, ω и r:
Связь между | a τ |, ε и r:
| a τ | = ε · r.
Теперь перейдем к кинематическим уравнениям конкретных видов движения. Эти уравнения надо выучить наизусть .
Эти уравнения надо выучить наизусть .
Кинематическое уравнение равномерного и прямолинейного движения имеет вид:
r = r 0 + v t,
Где r – радиус-вектор объекта в момент времени t, r 0 – то же в начальный момент времени t 0 (в момент начала наблюдений).
Кинематическое уравнение движения с постоянным ускорением имеет вид:
r = r 0 + v 0 t + a t 2 /2, где v 0 скорость объекта в момент t 0 .
Уравнение для скорости тела при движении с постоянным ускорением имеет вид:
v = v 0 + a t.
Кинематическое уравнение равномерного движения по окружности в полярных координатах имеет вид:
φ = φ 0 + ω z t,
Где φ – угловая координата тела в данный момент времени, φ 0 – угловая координата тела в момент начала наблюдения (в начальный момент времени), ω z – проекция угловой скорости ω на ось Z (обычно эта ось выбирается перпендикулярно плоскости вращения).
Кинематическое уравнение движения по окружности с постоянным ускорением в полярных координатах имеет вид:
φ = φ 0 + ω 0z t + ε z t 2 /2.
Кинематическое уравнение гармонических колебаний вдоль оси X имеет вид:
Х = А Cos (ω t + φ 0),
Где A – амплитуда колебаний, ω – циклическая частота, φ 0 – начальная фаза колебаний.
Проекция скорости точки, колеблющейся вдоль оси X, на эту ось равна:
V x = − ω · A · Sin (ω t + φ 0).
Проекция ускорения точки, колеблющейся вдоль оси X, на эту ось равна:
А x = − ω 2 · A · Cos (ω t + φ 0).
Связь между циклической частотой ω, обычной частотой ƒ и периодом колебаний T:
ω = 2 πƒ = 2 π/T (π = 3,14 – число пи).
Математический маятник имеет период колебаний T, определяемый выражением:
В числителе подкоренного выражения – длина нити маятника, в знаменателе – ускорение свободного падения
Связь между абсолютной v абс, относительной v отн и переносной v пер скоростями:
v абс = v отн + v пер.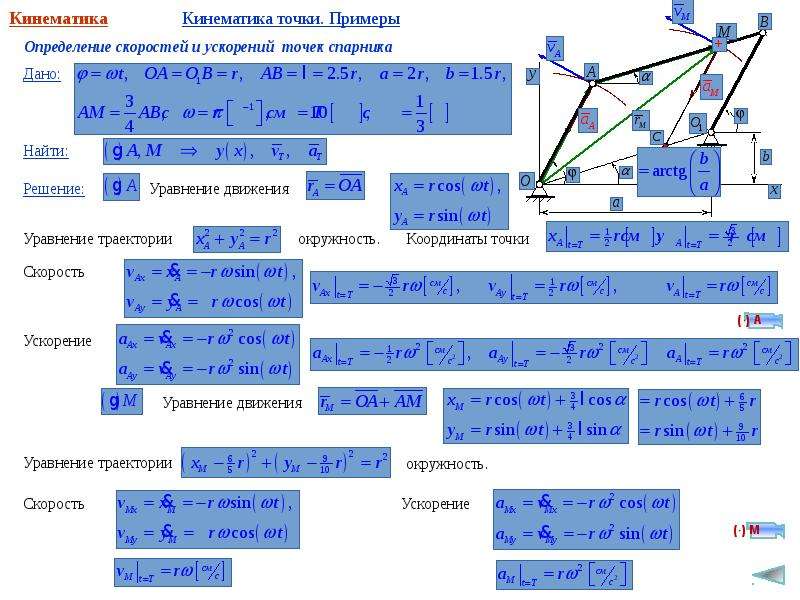
Вот, пожалуй, и все определения и формулы, которые могут понадобиться при решении задач на кинематику. Приведенная информация носит только справочный характер и не может заменить электронную книгу, где доступно, подробно и, надеюсь, увлекательно изложена теория этого раздела механики.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Старое-доброе любимое прямолинейное и равномерное движение.
Формулы кинематики:
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.
После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику
Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!
Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.
Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева – все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .
Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.
И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.
На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины – метр (1 м),
- времени – секунда (1 с),
- массы – килограмм (1 кг),
- количества вещества – моль (1 моль),
- температуры – кельвин (1 К),
- силы электрического тока – ампер (1 А),
- Справочно: силы света – кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой . Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела .
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: L полн – весь путь, который прошло тело, t полн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения.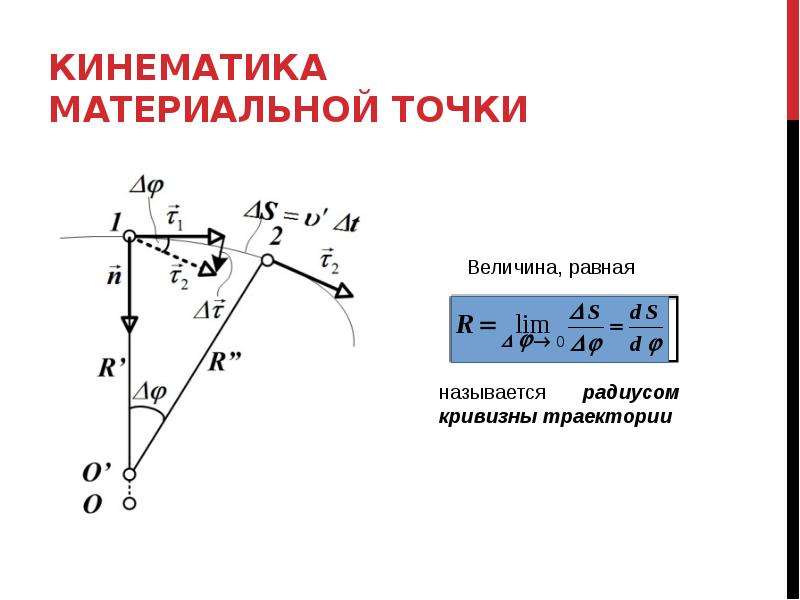 Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v 0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t ).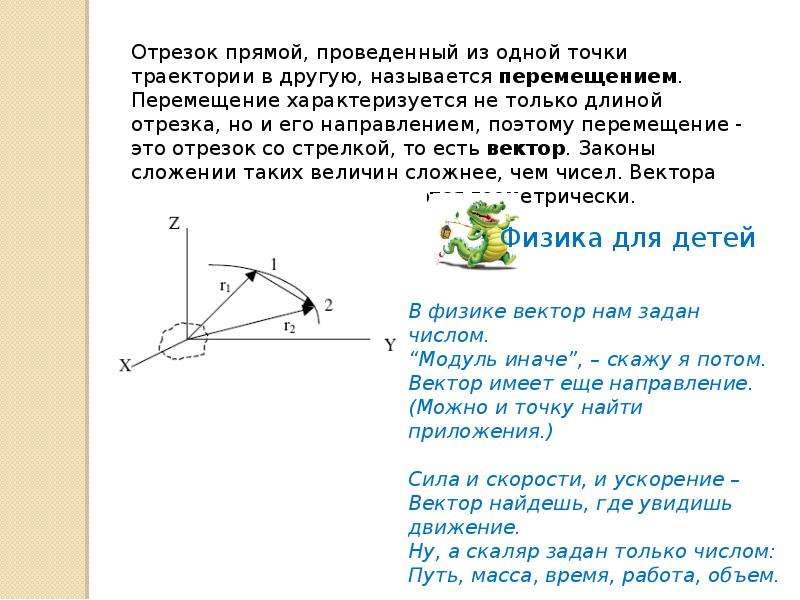
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей.
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения.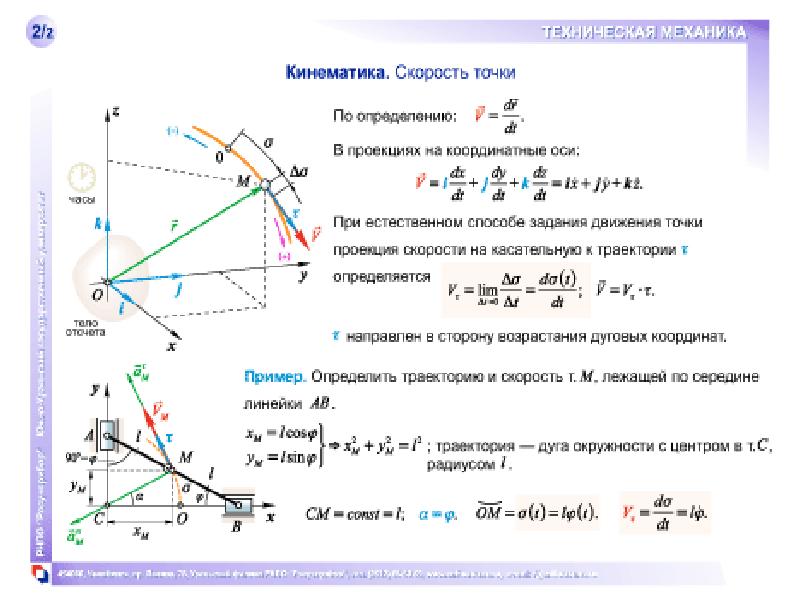 Вблизи поверхности Земли ускорение свободного падения составляет:
Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х » писать «у ». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v 0 , время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v 0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v x = v 0 . А вертикальная возрастает по законам ускоренного движения v y = gt . При этом полная скорость тела может быть найдена по формулам:
При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали . Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной.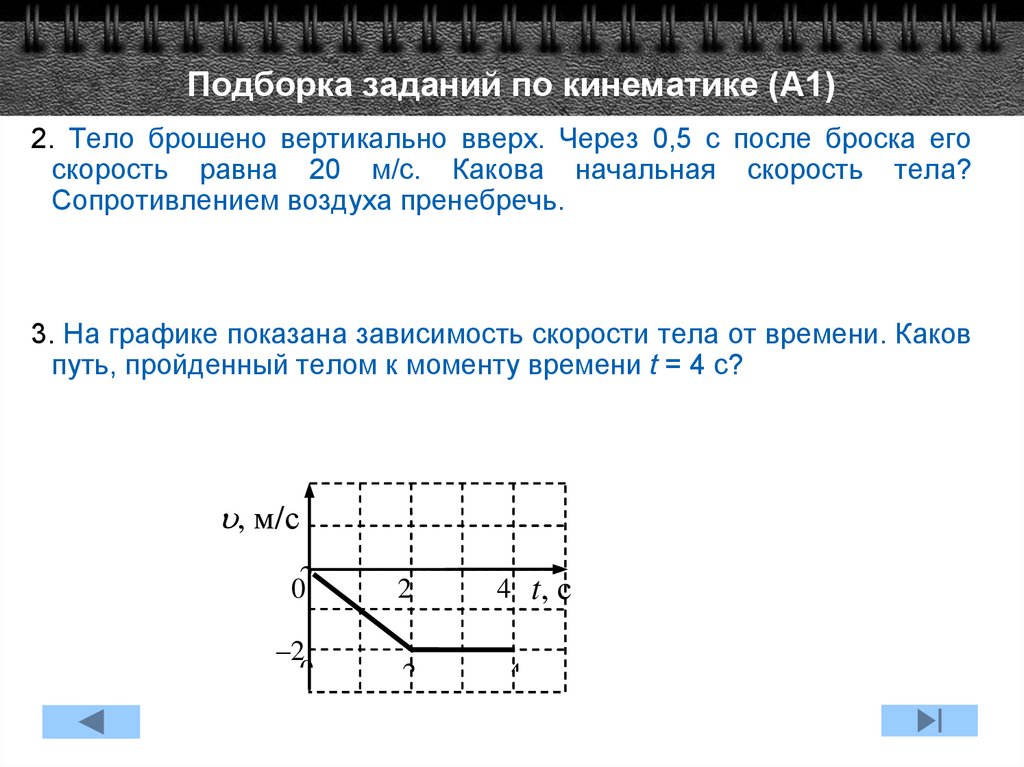 Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны.
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t . Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T . При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt . Очевидно, что за время равное периоду T тело пройдет угол равный 2π , следовательно при равномерном движении по окружности выполняются формулы:
При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt . Очевидно, что за время равное периоду T тело пройдет угол равный 2π , следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω :
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением , так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Его называют нормальным, или центростремительным ускорением , так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v
на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. После этого Вам останется подумать только над самыми сложными задачами.
После этого Вам останется подумать только над самыми сложными задачами.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов , позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Масса.
Масса m – скалярная физическая величина, характеризующая свойство тел притягиваться к земле и к другим телам.Масса тела – постоянная величина.
Единица массы – 1 килограмм (кг).
Плотность.
Плотностью ρ называется отношение массы m тела к занимаемому им объёму V:Единица плотности – 1 кг/м 3 .
Сила.
Сила F – физическая величина, характеризующая действие тел друг на друга и являющаяся мерой их взаимодействия. Сила – векторная величина; вектор силы характеризуется модулем (числовым значением) F, точкой приложения и направлением.Единица силы – 1 ньютон (Н).
Сила тяжести.
Сила тяжести – сила, с которой тела притягиваются к Земле.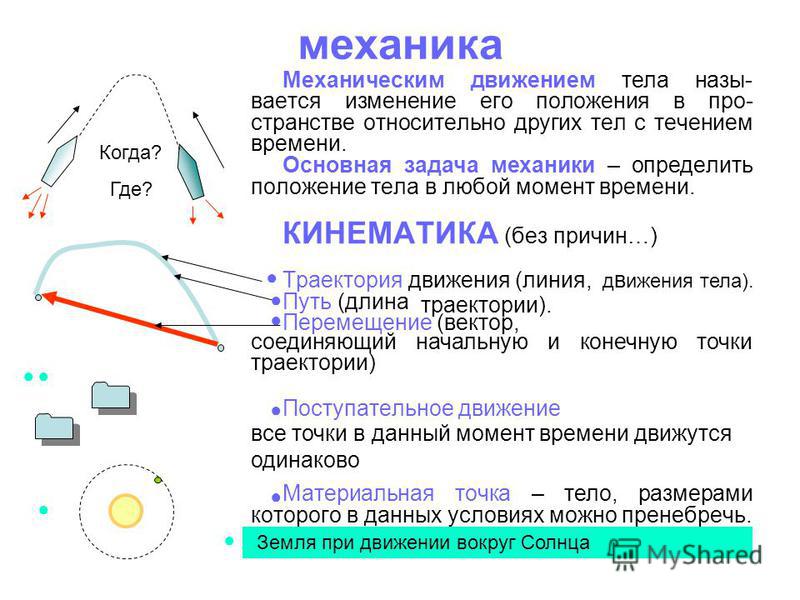 Она направлена к центру Земли и, следовательно, перпендикулярна к её поверхности:
Она направлена к центру Земли и, следовательно, перпендикулярна к её поверхности:Давление.
Давление p – скалярная физическая величина, равная отношению силы F, действующей перпендикулярно поверхности, к площади этой поверхности S:Единица давления – 1 паскаль (Па) = 1 Н/м 2 .
Работа.
Работа A – скалярная физическая велечина, равная произведению силы F на расстояние S, пройденное телом под действием этой силы:Единица работы – 1 джоуль (Дж) = 1 Н*м.
Энергия.
Энергия E – скалярная физическая величина, характеризующая любое движение и любое взаимодействие и определяющая способность тела совершать работу.Единица энергии, как и работы, – 1 Дж.
Кинематика
Движение.
Механическим движением тела называют изменение с течением времени его положения в пространстве.Система отсчёта.
Связанные с телом отсчёта систему координат и часы называют системой отсчёта.Материальная точка.
Тело, размерами которого можно пренебречь в данной ситуации, называется материальной точкой. Строго говоря, все законы механики справедливы для материальных точек.
Строго говоря, все законы механики справедливы для материальных точек.Траектория.
Линия, вдоль которой перемещается тело, называется траекторией. По виду траектории движения разделяются на два типа – прямолинейное и криволинейное.Путь и перемещение.
Путь – скальрная величина, равная расстоянию, пройденному телом вдоль траектории движения. Перемещение – вектор, соединяющий начальную и конечную точки пути.Скорость.
Скоростью υ называют векторную физическую величину, характеризующую быстроту и направление перемещения тела. Для равномерного движения скорость равна отношению перемещения ко времени, за которое оно произошло:Единица скорости – 1 м/с, но часто пользуются км/ч (36 км/ч = 10 м/с).
Уравнение движения.
Уравнение движения – зависимость перемещения от времени. Для равномерного прямолинейного движения уравнение движения имеет видМгновенная скорость.
Мгновенная скорость – отношение очень малого перемещения к промежутку времени, за который оно произошло:Средняя скорость:
Ускорение.
 Ускорением a называют векторную физическую величину, характеризующую быстроту изменения скорости движения. При равнопеременном движении (т.е при равноускоренном или равнозамедленном) ускорение равно отношению изменения скорости к промежутку времени, за который это изменение произошло:
Ускорением a называют векторную физическую величину, характеризующую быстроту изменения скорости движения. При равнопеременном движении (т.е при равноускоренном или равнозамедленном) ускорение равно отношению изменения скорости к промежутку времени, за который это изменение произошло:КИНЕМАТИКА Движение точки – Энциклопедия по машиностроению XXL
Кинематика – это раздел механики, в котором изучают движение материальных тел вне зависимости от причин, вызывающих это движение. Так, например, траектория движения, скорость и ускорение материальной точки есть понятия кинематики движения точки. Все кинематические понятия для материальной точки не зависят от величины массы точки, а определяются [c.86]Кинематика движения точки по окружности [c.23]
В инженерной графике принято рассматривать образование поверхности с точки зрения кинематики — движения, что соответствует технической практике. [c.32]
[c.32]
Секторная скорость. Теорема площадей. Наряду с введенными в кинематике точки скоростью v и ускорением а можно ввести другие характеристики движения точки, например секторные скорость и ускорение. Секторной скоростью точки или do/d/ относительно точки О (рис. 54) называют векторную величину, определяемую по формуле [c.315]
Основная задача кинематики точки и твердого тела- состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение. [c.96]
Как уже указывалось, для решения задач кинематики надо знать закон движения точки. Если движение задано естественным способом (дана траектория н закон движения вдоль траектории), то все характеристики движения (скорость, касательное, нормальное и полное ускорение) определяются по формулам, полученным в 42—44. Этими формулами можно, конечно, пользоваться и когда движение задано другим способом. [c.114]
[c.114]
Уравнения в декартовых координатах. Из кинематики известно, что движение точки в прямоугольных декартовых координатах задается уравнениями (см. 37) [c.186]
Имея уравнения движения точки, можно методами кинематики определить все характеристики данного движения. [c.199]
Уравнение (11.6) является уравнением гармонического колебательного движения точки (см. ч. I, Кинематика , 77). [c.28]
Кинематика изучает движение механической системы, в частности абсолютно твердого тела, независимо от сил, действующих на эту систему. Так как при движении твердого тела различные его точки могут двигаться различно, то в кинематике сначала изучается движение более простого объекта, а именно движение точки, а затем — движение твердого тела. [c.142]
В кинематике применяются три способа, описывающих движение точки векторный, координатный и естественный.
[c.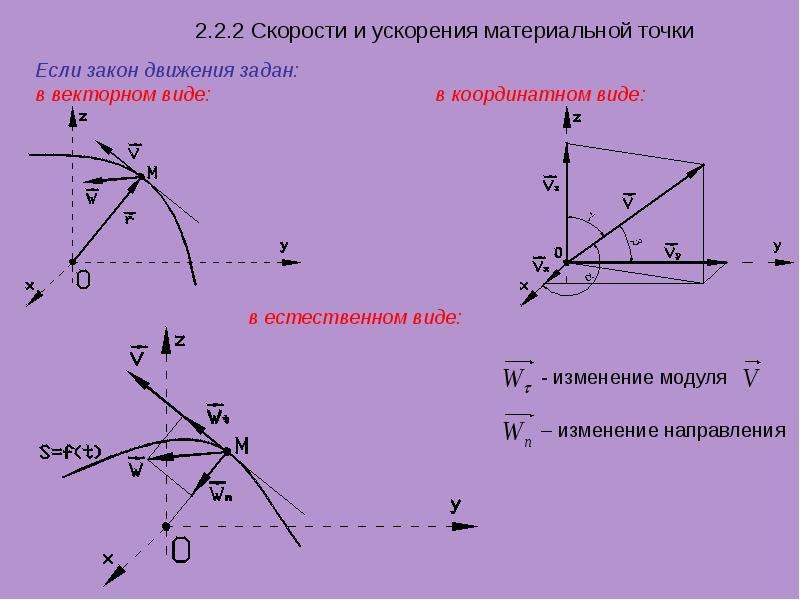 142]
142]
Решение этой задачи сводится к определению ускорения точки, которое в том случае, когда движение точки задано, нетрудно найти по правилам кинематики. [c.237]
Пользуясь определением переносного и относительного движений, а также рассмотренным выше примером, можно указать на следующий метод изучения этих движений. Желая изучить относительное движение точки, следует мысленно остановить переносное движение и изучать движение далее по законам и правилам абсолютного движения точки. Если необходимо изучить переносное движение точки, то следует мысленно остановить относительное движение и рассматривать далее движение точки по формулам кинематики точки в абсолютном движении. Если точка участвует одновременно в относительном и переносном движениях, то ее абсолютное движение называют сложным движением точки, а ее относительное и переносное движения называются составляющими движениями. [c.301]
Для определения относительного ускорения точки следует мысленно отвлечься от переносного движения и вычислить относительное ускорение по правилам кинематики точки.
 Для определения переносного ускорения следует мысленно остановить относительное движение точки и вычислить переносное ускорение по правилам кинематики точки
[c.324]
Для определения переносного ускорения следует мысленно остановить относительное движение точки и вычислить переносное ускорение по правилам кинематики точки
[c.324]Установление тех способов, с помощью которых может быть задано движение точек или тел по отношению к выбранной системе отсчета, является одной из задач кинематики. Основная задача кинематики состоит в том, чтобы по уравнениям, определяющим закон движения данной системы точек (тела), найти все кинематические характеристики этого движения (траектории различных точек, их скорости, ускорения и др.). [c.49]
Сила и масса. В то время как в кинематике движение тел изучают с геометрической точки зрения, рассматривая изменение их положения относительно определенной системы отсчета и принимая во внимание время, в течение которого это изменение происходит, вторая часть механики — кинетика — посвящена изучению движения материальных тел в зависимости от факторов, обусловливающих характер или закон рассматриваемого движения. Эти факторы зависят как от тел, окружающих данное тело, так и от свойств самого тела.
[c.168]
Эти факторы зависят как от тел, окружающих данное тело, так и от свойств самого тела.
[c.168]
При изучении курса физики установлены основные понятия кинематики точки и твердых тел. При движении точки по траектории скорость и ускорение точки рассматриваются как векторные величины. При этом вектор скорости V направлен по касательной к траектории, и его модуль (числовое значение) равен первой производной от пути по времени v = ds вектора скорости по времени а = с1 и/с1/. Он может быть разложен на две составляющие вектор касательного ускорения а , направленный по касательной к траектории и равный по модулю а = dv di и вектор нормального ускорения направленный по главной нормали к траектории в данной точке в сторону вогнутости кривой и имеющий модуль а, == у-/р, где р — радиус кривизны траектории. Модуль вектора ускорения а = ] а + я- [c.28]
В этой главе ознакомимся с некоторыми способами определения движения точки, а также с основными понятиями кинематики (законы движения, перемещение, расстояние, путь, скорость, ускорение), без ясного понимания которых невозможно изучение кинематики. [c.16]
[c.16]
Движение точки можно спи- Дифференциальные у р а в-сать в проекциях на оси Н е Н И Я д В И жения ТОЧКИ естественного трехгранника В форме Эйлера. В кинематике двумя уравнениями изучили три способа определения [c.118]
Этот принцип переводит реакции связей в класс активных сил, благодаря чему они входят в принцип Лагранжа — Даламбера. Принцип освобождаемости связей увеличивает число степеней свободы механической системы, т. е. изменяется ее кинематика, в то время как динамическая картина остается неизменной. Следует заметить, что введение реакций связей в равенство (34.22) приводит к появлению новых неизвестных, в результате чего оно не всегда полностью описывает движение механической системы. [c.54]
При решении задач кинематики приходится определять абсолютное движение точки по переносному ее движению вместе с по- [c.24]
В кинематике, как уже известно, изучается движение точки или тела независимо от причин, вызывающих или изменяющих его, т. е. независимо от сил.
[c.98]
е. независимо от сил.
[c.98]
В кинематике движение задают относительно какой-либо системы отсчета. Задать движение точки или тела относительно какой-либо системы отсчета — значит дать условия, позволяющие найти положение точки или тела в любой момент времени относительно этой системы отсчета. [c.99]
Из кинематики известно, что характер наблюдаемого движения точки или тела зависит от кинематического состояния системы отсчета, ло отношению к которой изучается это движение. Если на материальную точку действуют некоторые силы, то движение точки под их действием представляется различным образом при наблюдении, с неподвижной системы отсчета и с системы отсчета, имеющей некоторое переносное движение относительно неподвижной системы. Все кинематические характеристики точки, в частности и ускорения, различны в этих системах отсчета. В то же время относительные движения имеют большое значение например, в теории космических полетов приходится рассчитывать сложные по виду, большой протяженности, требующие исключительно точных вычислений, траектории космических летательных аппаратов по отношению к подвижным системам координат, связанным с планетами. [c.230]
[c.230]
Наряду с введенными в кинематике точками скоростью V и ускорением а можно ввести другие характеристики движения точки как, например, секторные скорость и ускорение. Секторной скоростью [c.276]
В четвертом издании значительно перестроено изложение разделов Статика (введены элементы дедуктивного изложения материала при рас> смотрении вопросов приведения и равновесия системы сил), Кинематика (в отдельный параграф выделена кинематика сложного движения точки при переносном поступательном движении) и часть Динамики . [c.2]
В курсе теоретической механики обычно изучаются движение точки и твердого тела. Соответственно кинематика делится на кинематику точки и кинематику твердого тела В настоящем курсе дополнительно излагаются также основы кинематики сплошной среды. [c.97]
В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.
[c.98]
Важным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.
[c.98]
ОТНОСЙТЕЛЬНОЕ ДВИЖЕНИЕ. При решении ряда задач кинематики движение точки (или тела) рассматривают одновременно по отношению к двум (или более) системам отсчёта, из к-рых одна, наз. основной, считается условно неподвижной, а другая, определённым образом движущаяся относительно основной,— подвижной системой отсчёта. Движение точки (или тела) по отношению к подвижной системе отсчёта наз. О. д. Скорость точки в О. д. наз. относит, скоростью отн> а ускорение — относит, ускорением лиотд. Движение всех точек подвижной системы относительно основной наз. в ЭТО.М случае переносным движением, а скорость и ускорение той точки подвижной системы, в к-рой в данный момент времени находится движущаяся точка,— переносной скоростью Ювдр и переносным ус кор ением пер Наконец, движение точки (тела) по отношению к оси. системе отсчёта наз. сложным или абсолютным, а скорость и ускорение этого движения — абс. скоростью а и абс. ускорением Шд. Зависимость между названными величина даётся в классич. механике равенствами
[c.493]
системе отсчёта наз. сложным или абсолютным, а скорость и ускорение этого движения — абс. скоростью а и абс. ускорением Шд. Зависимость между названными величина даётся в классич. механике равенствами
[c.493]
Кинематически, задать движение или закон движения тела (точки) — значит задать положение этого тела (точки) относительно данной системы отсчетав любой момент времени. Установление математических способов задания движения точек или тел является одной из важных задач кинематики. Поэтому изучение движения любого объекта будем начинать с установления способов задания. этого движения. [c.96]
Так как в случае прямолпнейного движения точки ускорение ее w = x, то tiu — onst, т. е. движение точки является равнопеременным. Поэтому по формуле кинематики для пройденного пути при равномерно-переменном движении имеем [c.245]
В кинематике изучаются законы движения материальных зо-чек и твердых тел чисто с геометрической стороны. Законом движения точки или тела можно назвать такую совокупность математических образов и уравнений, которая в любой момент времени позволяет установизь, где находится точка или тело, куда и как они движутся. При этом в кинематике не рассматриваются вопросы, почему точка или тело движезся именно так, а не иначе. Эти вопросы изучаются в разделе Динамика .
[c.199]
Законом движения точки или тела можно назвать такую совокупность математических образов и уравнений, которая в любой момент времени позволяет установизь, где находится точка или тело, куда и как они движутся. При этом в кинематике не рассматриваются вопросы, почему точка или тело движезся именно так, а не иначе. Эти вопросы изучаются в разделе Динамика .
[c.199]
В первом томе рассматриваются следующие разделы статики и кинематики система сходяптихся сил, произвольная плоская система сил, равновесие тел при наличии трения скольжения и трения качения, графическая статика, пространственная система сил, центр тяжести движение точки, поступательное движение и вращение твердого тела вокруг неподвижной оси, сложное движение точки, плоское движение твердого тела, вращение твердого тела вокруг неподвижной точки, общий случай движения твердого тела, сложение вращений твердого тела вокруг параллельных и пересекающихся осей, сложение поступательного и вращательного движений твердого тела. [c.2]
[c.2]
Скорость и ускорение точки в полярных, сферических и цилиндрических координатах. Многие задачи кинематики сложного движения точки целесообразно решать в полярных, сферических и цилиндрических координатах. Одним из способов решения задач в криволинейных координатах является разложение абсолютного движения точ1си на переносное и относи-аелыюе движения. [c.341]
Если тот же вал опереть на три подшипника (рис. 2.7. б), то третья опора не изменит кинематики движения вала, так как она является пассивной связью, но существенно изменит условия работы вала. Более высокие требования предъявляются к точности изготовления, так как в этой системе передавае.мые силы зависят от деформации звеньев из-за возможного несовпадения осей вала и подшипников вал вынужден изгибаться в подшипниках появятся дополнительные силы от изгиба вала, трение в них увеличится и снизится кпд механизма. [c.23]
Гаспар Кориолйс исследовал составное движение и доказал (1831 г. ) знаменитую теорему, позднее получившую название теоремы Корио-лиса. Эта теорема является основной в механике относительного движения и имеет огромное значение для различных отраслей науки. Несколько позднее на основе этой теоремы в кинематике составного движения точки стали применять ускорение Кориолиса.
[c.119]
) знаменитую теорему, позднее получившую название теоремы Корио-лиса. Эта теорема является основной в механике относительного движения и имеет огромное значение для различных отраслей науки. Несколько позднее на основе этой теоремы в кинематике составного движения точки стали применять ускорение Кориолиса.
[c.119]
Естественный способ определения движения. Изучение движения точки без учета приложенных к ней сил составляет задачу кинвштики точки. Кинематика точки является основным и вместе с тем наиболее простым отделом кинематики. [c.120]
В динамике изучают зависимость между движением материальных объектов и действующими на них силами, по данному движению точки или тела устанавливают, какие силы его производят, и по действующим силам определяют движение материального объекта. Поэтому динамика не может, подобно кинематике, ограничиться добавлением к понятиям геометрии одного лишь понятия времени.
 Она дополняет понятия кинематики понятием силы, известным нам из статики. Нас не интересует физическая сущность силы, и здесь, как и в статике, мы характеризуем силу величиной, направлением и точкой приложения, разве лишь с тем добавлением, что в динамике чаще, чем в статике, рассматривают силы, переменные по величине и направлению.
[c.246]
Она дополняет понятия кинематики понятием силы, известным нам из статики. Нас не интересует физическая сущность силы, и здесь, как и в статике, мы характеризуем силу величиной, направлением и точкой приложения, разве лишь с тем добавлением, что в динамике чаще, чем в статике, рассматривают силы, переменные по величине и направлению.
[c.246]Дифференциальные уравнения движения Движение точки можно материальной точки в форме Эйлера, описать в проекциях на оси кинематике МЫ изучали три способа естественного трехгранника определения движения точки 1) вектор-двуия уравнениями цый, 2) в прямоугольных координатах, [c.270]
Кинематика точки является нагб лее простым разделом кинематики. Механическое движение точки заключается в изменении с течением времени ее местоположения относительно системы отсчета. Следовательно, чтобы определить движение точки, достаточно дать ее положение в данное мгновение и указать, как оно изменяется с течением времени. [c.16]
[c.16]
Для изучения движения материальной точки в неподвижной системе координат, как уже известно, простым и удобным математическим аппаратом являются методы динамики, созданной на основе законов Ньютона. Эти методы можно перенести и на изучение относительных движений. Различия в относительном и абсолютном движениях точки заключаются в том, что относительное и абсолютное ускорения точки в этих движениях различны и находятся между собой в зависимости, определяемой кинематической теоремой Кориолиса. Как показано в кинематике, различие вызывается фактически переносным движением подвижной системы отсчета, благодаря которому наблюдатель, связанны с этой системой отсчета, изменяет свое ноло- [c.230]
Fla движение отдельной точки тела при поступательном движении никаких ограничений в обнщм случае не накладывается. Следовательно, твердое тело, совершающее поступательное движение, имеет три степени свободы и уравнения (4) считанэтся уравнениями поступательного движения твердого тела. Для изучения поступательного движения твердого тела достаточно использовать кинематику одной точки.
[c.126]
Для изучения поступательного движения твердого тела достаточно использовать кинематику одной точки.
[c.126]
Определение, примеры и уравнения, математика |
Кинематика фокусируется на движении объектов. Он имеет дело с силами и геометрическими аспектами движения, связанными со скоростью и ускорением.
Давайте определим некоторые специальные термины, чтобы понять тему кинематики:
Расстояние – это общая пройденная длина независимо от направления движения.
Перемещение — это расстояние, пройденное в определенном направлении.
Скорость – это расстояние, пройденное за единицу времени.
Скорость – скорость изменения смещения.
Ускорение — это скорость изменения скорости.
Теперь мы можем использовать их для описания движения объекта и геометрии кривой, которую он создает при движении.
Переменное ускорение (ч3)
При переменном ускорении ускорение меняется со временем. Нам нужно использовать дифференцирование и интегрирование для преобразования между смещением, скоростью и ускорением.Мы используем дифференцирование для преобразования смещения в скорость и из скорости в ускорение. Затем мы используем интегрирование, чтобы вернуться от ускорения к скорости и от скорости к смещению.
Рис. Рис. Рис. РИС.
Это функция скорости. Мы хотим знать, когда v = 0
(3t -2) (t -4) = 0
Частица находится в мгновенном состоянии при t = 4 с или t = 2/3 с.
Расчет кинематики (h3)
Расчет упрощает вывод двух из трех уравнений движения. Поскольку мы знаем, что ускорение — это первая производная скорости по времени, используйте определение, чтобы обратить его вспять. Вместо того, чтобы находить скорость, интегрируйте ее, чтобы найти ускорение.
Различные функции описывают величины ускорения, смещения и скорости. Их также можно преобразовать в функции, описывающие две другие величины. Есть два способа сделать это: дифференцирование (нахождение производной) или интегрирование (нахождение интеграла).
Их также можно преобразовать в функции, описывающие две другие величины. Есть два способа сделать это: дифференцирование (нахождение производной) или интегрирование (нахождение интеграла).
Смещение S = F (T) [Расположение в отношении происхождения]
Скорость [производное смещения]
Ускорение [производное скорости]
Давайте проанализируем эти концепции вместе.Вы можете понять характеристики кинематики на основе вывода нашей функции. Для смещения значение 0 означает, что наша позиция находится в начале координат. Если смещение положительное, то оно справа от начала координат, а если отрицательное, то слева от начала координат.
Скорость имеет аналогичную интерпретацию. Если значение равно 0, это означает, что мы находимся в состоянии покоя. Положительная скорость означает движение вправо, а отрицательная скорость означает движение влево.

Выход 0 для функции ускорения означает, что скорость либо максимальна, либо минимальна, либо постоянна.Положительный результат означает, что скорость увеличивается, а отрицательный результат означает, что скорость уменьшается.
Пример:
Найдите скорость, если перемещение задано как функция времени .
Ответ:
Мы просто продифференцируем это:
Это то же самое, что и [Если вам трудно, посмотрите на дифференцирование]
v = 6t
Если вы хотите найти ускорение, это можно записать как вторую производную от перемещение по времени или скорость, дифференцированная по времени.
a = 6
Таким образом, эта частица имеет постоянное ускорение, равное 6.
Постоянное ускорение
Формально это известно как «одномерные уравнения движения для постоянного ускорения». Кинематические уравнения в этом разделе действительны только тогда, когда ускорение постоянно, а движение ограничено прямой линией.

Как упоминалось ранее, ускорение является постоянным, то есть оно остается неизменным вне зависимости от времени. Здесь мы используем стандартные обозначения, где ускорение представляет собой ускорение, u представляет собой начальную скорость, а t представляет собой время.
Графики движения
Нарисуем графики для всех трех свойств движения: перемещения, скорости и ускорения. Определим объекты движения по графикам.
График времени разгона:
Вот сценарий: пуля выпущена вертикально. Единственная сила, действующая на него, — это сила тяжести. Гравитация не меняется; следовательно, ускорение также не меняется. Ниже приведена демонстрация графика времени разгона.
Ускорение
График зависимости скорости от времени:
Поскольку мы знаем, что ускорение является постоянным и отрицательным, поскольку оно действует в направлении, противоположном скорости, это будет означать, что градиент графика зависимости скорости от времени должен быть постоянная и отрицательная, что даст нам что-то вроде этого:
Скорость
График времени перемещения:
На приведенном ниже графике показана пуля от ее начальной точки до достижения максимальной высоты, где скорость равна 0 до он снова начинает снижаться.
 У вас есть градиент, который является постоянным и отрицательным. Таким образом, график смещения будет выглядеть следующим образом:
У вас есть градиент, который является постоянным и отрицательным. Таким образом, график смещения будет выглядеть следующим образом:Смещение
Обратите внимание, что скорость всегда положительна, но уменьшается до 0. Поэтому градиент графика смещения от времени всегда должен быть положительным и должен уменьшаться до 0.
SUVAT уравнения (h4)
Уравнения SUVAT представляют собой набор уравнений, описывающих движение в одном измерении, в каждом из которых опущена одна переменная.
Переменная
Si Unit
S
метра (м)
U
Velocity
м / с (метров в секунду)
V
V
Конечная скорость
м / с (метров в секунду)
A
Ускорение
м / с / с (метры в секунду в секунду)
T
Time
Time
S (секунд)
Первое уравнение: V = U + AT
Второе уравнение:
Третье уравнение:
Четвертое уравнение:
Пример:
Паром перевозит па ssengers между берегами реки, которые находятся на расстоянии 20 м друг от друга.
 После трогания паром разгоняется до 0,2 в течение 12 секунд, после чего выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу.
После трогания паром разгоняется до 0,2 в течение 12 секунд, после чего выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу.Рассчитайте скорость парома через 12 секунд.
Рассчитайте расстояние, которое проходит паром за эти 12 секунд.
Ответ:
Запишите свой SUVAT, уточните переменные, которые у вас есть, и те, которых у вас нет, и определите, какое уравнение использовать.
с = х м
u = 0 м/с
v =?
a = 0,2
t = 12 с
Теперь найдем уравнение СУВАТ, которое не включает s.
v = u + at at
v = 0 + 0,2 12
v = 2,4 м / с
v = 2,4 м / с
с использованием
- Смещение — это изменение положения объекта относительно его системы отсчета.

- Ускорение свободного падения равно 9,8 на поверхности земли. Для простоты расчета его можно принять за 10.
- Вы также можете использовать методы исчисления для анализа функций.
- Для решения кинематических задач в двух измерениях необходимо использовать геометрию для определения неизвестных величин и направлений и использовать направления для определения кинематических величин.
- Первое уравнение
- Второе уравнение
- Третье уравнение
- Четвертое уравнение
- с = водоизмещение
- u = начальная скорость
- v = конечная скорость
- a = ускорение
- t = время.

- Скаляры : Скаляром является любая величина, которая имеет величину (количество или размер), но не имеет направления.
 Для скаляра требуется только число и единицы измерения. Масса и площадь являются примерами скалярных величин, т.е.г. Австралия имеет площадь 7 617 930 км 2 .
Для скаляра требуется только число и единицы измерения. Масса и площадь являются примерами скалярных величин, т.е.г. Австралия имеет площадь 7 617 930 км 2 . - Векторы : Вектор — это любая величина, которая имеет связанную с ней величину и направление. Мы говорим, что город находится в 1000 км к югу или автомобиль движется со скоростью 60 км/ч -1 к востоку.
- Смещение \(\vec s\): изменение положения объекта или разница между его началом и концом.
- Скорость \(\vec v\): насколько быстро или медленно изменяется смещение объекта
\(\vec v=\frac{Δ\vec s}{Δt}\) - Ускорение \(\vec a\): скорость изменения скорости объекта
\(\vec a= \frac{∆\vec v}{∆t}=\frac{\vec v-\vec u }{∆t}\)
, где \(v\) — конечная скорость, а \(u\) — начальная скорость. - Описать вращательные кинематические переменные и уравнения и связать их с их линейными аналогами
- Опишите крутящий момент и плечо рычага
- Решение задач на крутящий момент и кинематику вращения
- (4) Научные концепции.Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и окружностей.
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
- (4) Научные концепции.Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
- (D) рассчитать действие сил на объекты, включая закон инерции, связь между силой и ускорением и природу пар сил между объектами.
- Глаз бури - центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость прямо пропорциональна радиусу кривизны.
- Глаз бури - центр вращения.Ветры слабее в глазу торнадо, потому что тангенциальная скорость обратно пропорциональна радиусу кривизны.
- Глаз бури - центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость прямо пропорциональна квадрату радиуса кривизны.
- Глаз бури - центр вращения. Ветры слабее в глазу торнадо, потому что тангенциальная скорость обратно пропорциональна квадрату радиуса кривизны.
- Линейка находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет равно нулю.
- Линейка не находится в состоянии вращательного равновесия, поэтому она не будет вращаться вокруг своего центра масс.Таким образом, угловое ускорение будет равно нулю.
- Линейка не находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
- Линейка находится в состоянии вращательного равновесия, поэтому она будет вращаться вокруг своего центра масс. Таким образом, угловое ускорение будет ненулевым.
- \frac{1}{144}\,\text{Н-м}
- \frac{1}{12}\,\text{Н-м}
- 12\,\текст{Н-м}
- 144\,\text{Н-м}
- 0,6 рад/с 2
- 1,6 рад/с 2
- 1 рад/с 2
- 5 рад/с 2
- Угловое ускорение — это скорость изменения углового смещения.
- Угловое ускорение — скорость изменения угловой скорости.
- Угловое ускорение — это скорость изменения линейного перемещения.
- Угловое ускорение — это скорость изменения линейной скорости.
- α=ΔωΔtα=ΔωΔt
- α=ΔωΔtα=ΔωΔt
- α=ΔθΔtα=ΔθΔt
- α=ΔθΔtα=ΔθΔt
- Это вращательный эквивалент силы.
- Это сила, влияющая на линейное движение.
- Это вращательный эквивалент ускорения.
- Именно ускорение влияет на линейное движение.
- \тау = {F\,cos\тета}\,{r}
- \тау = \фрак{F\sin\theta}{r}
- \тау = rF\!\cos\тета
- \тау = rF\!\sin\тета
- 5 Решение:
Глава 2 Одномерная кинематика Q.81P
Средство счета от 3,0-м-высокой доски для дайвинга и капель вода внизу. В то же время Тед прыгает вверх со скоростью 4,2 м/с с трамплина высотой 1,0 м. Выбрав начало координат на поверхности воды и вверх в качестве положительного направления x, напишите уравнения движения x-t для Билла и Теда.
Решение:
Глава 2 Одномерная кинематика Q.82P
Повторите предыдущую задачу, на этот раз с исходной точкой. 3,0 м над водой и вниз по положительному направлению x.
Решение:
Глава 2. Одномерная кинематика Q.83P
Жарким летним днем в штате Вашингтон, плавая на байдарках, я увидел, как несколько пловцов прыгнули с железнодорожного моста в реку Снохомиш внизу. пловцы сошли с моста, и я оценил, что они ударились о воду 1.Через 5 с: а) какой высоты был мост? б) С какой скоростью двигались пловцы в момент удара о воду? в) Каково было бы время спуска пловцов, если бы мост был в два раза выше?
Решение:
Глава 2. Одномерная кинематика Q.84P
Самый высокий фонтан Самый высокий фонтан в мире расположен в Фаунтин-Хиллз, штат Аризона. Фонтан поднимается на высоту 560 футов (на 5 футов выше монумента Вашингтона), а) какова начальная скорость воды? б) За какое время вода достигнет верха фонтана?
Решение:
Глава 2 Одномерная кинематика Q.85P
Ошибочно объявленный фол, разгневанный баскетболист бросает мяч прямо на пол. Если мяч отскакивает прямо вверх и возвращается на пол через 2,8 с после первого удара, какова была наибольшая высота мяча над полом?
Решение:
Глава 2 Одномерная кинематика Q.86P
Чтобы отпраздновать победу, питчер бросает перчатку прямо вверх с начальной скоростью 6,0 м/с. а) Через сколько времени перчатка вернется в питчер? б) За какое время перчатка достигнет максимальной высоты?
Решение:
Глава 2 Одномерная кинематика Q.87P
IP Стоя на краю обрыва высотой 32,5 м, вы роняете мяч. Позже вы бросаете вниз второй мяч с начальной скоростью 11,0 м/с. а) Скорость какого мяча увеличивается больше, когда он достигает основания утеса, или скорость обоих мячей увеличивается на одинаковую величину? (б) Подтвердите свой ответ на часть (а) расчетом.
Решение:
Глава 2 Одномерная кинематика Q.88P
Вы выпускаете стрелу в воздух.Через две секунды (2,00 с) стрела поднялась прямо вверх на высоту 30,0 м над точкой запуска, а) какова была начальная скорость стрелы?
(б) Через какое время стрела впервые достигла высоты 15,0 м над точкой запуска?
Решение:
Глава 2 Одномерная кинематика Q.89P
Во время движения на лифте, спускающемся с постоянной скоростью 3,0 м/с, вы случайно уронили книгу из-под руки. а) Сколько времени понадобится книге, чтобы добраться до этажа лифта, 1.на 2 м ниже руки? б) Какова скорость книги относительно вас в момент удара об пол лифта?
Решение:
Глава 2 Одномерная кинематика Q.90P
Воздушный шар снижается со скоростью 2,0 м/с, когда пассажир роняет камеру. Если камера в момент падения находится на высоте 45 м над землей, (а) сколько времени потребуется камере, чтобы достичь земли, и (б) какова ее скорость непосредственно перед тем, как она приземлится? Пусть вверх будет положительное направление для этой задачи.
Решение:
Глава 2 Одномерная кинематика Q.91P
IP Стоя бок о бок, вы и ваш друг в разное время сходите с моста и падаете на 1,6 с в воду внизу. Ваша подруга ходит первой, а вы следуете за ней после того, как она пролетит 2,0 м. (a) Когда ваш друг падает в воду, расстояние между вами составляет 2,0 м, менее 2,0 м или более 2,0 м? (б) Подтвердите свой ответ на часть (а) расчетом.
Решение:
Глава 2 Одномерная кинематика Q.92P
Модель ракеты взлетает и движется вверх с ускорением 12 м/с2, пока не достигнет высоты 26 м, после чего его двигатель выключается, и он продолжает свой полет в свободном падении.
а) Какой максимальной высоты достигает ракета?
(b) Какова скорость ракеты непосредственно перед ударом о землю?
(в) Какова общая продолжительность полета ракеты?
Решение:
Глава 2 Одномерная кинематика Q.93P
Удар по «высокому нападающему» Молодая женщина на карнавале подходит к «высокому нападающему» — популярному испытанию на силу, когда участница ударяет молотком по одному концу рычага, продвигая небольшую металлическую пробку вверх к колокол. Она сильно взмахивает молотком и отправляет заглушку в верхнюю часть бойка, где он звонит в колокол. На рис. 34 показан соответствующий график зависимости положения пробки от времени. Используя информацию, представленную на графике, ответьте на следующие вопросы: а) Какова средняя скорость вилки во время ее движения вверх? б) На сколько уменьшится скорость вилки при движении вверх? в) Какова начальная скорость вилки? (Предположим, что пробка находится в свободном падении во время своего движения вверх без влияния сопротивления воздуха или трения.)
Решение:
Глава 2 Одномерная кинематика Q.94P
Сидя на ветке дерева на высоте 10 м над землей, вы роняете каштан. Когда каштан упал на 2,5 м, вы бросаете второй каштан прямо вниз. Какую начальную скорость вы должны сообщить второму каштану, чтобы оба они одновременно коснулись земли?
Решение:
Глава 2 Одномерная кинематика Q.95GP
В известном романе Жюля Верна Филеас Фогг путешествует вокруг света за 80 дней.Какова примерная средняя скорость мистера Фогга во время его приключения?
Решение:Глава 2 Одномерная кинематика Q.96GP
Астронавт на Луне бросает камень прямо вниз с высоты 1,25 м. Если ускорение свободного падения на Луне равно 1,62 м/с2, какова скорость камня непосредственно перед тем, как он приземлится?
Решение:Глава 2 Одномерная кинематика Q.97GP
Вы прыгаете с вершины валуна на землю 1.5 м ниже. Оцените свое замедление при приземлении.
Решение:Глава 2 Одномерная кинематика Q.98GP
Сверхзвуковой водопад Геологи узнали о периодах в прошлом, когда Гибралтарский пролив перекрывался, а Средиземное море высыхало и превращалось в пустыню. Позже, когда пролив снова открылся, образовался массивный водопад с соленой водой. По словам геологов, вода в этом водопаде была сверхзвуковой; то есть он падал со скоростью, превышающей скорость звука.Игнорируя сопротивление воздуха, какова минимальная высота, необходимая для создания сверхзвукового водопада? (Скорость звука можно принять равной 340 м/с.)
Решение:
Глава 2 Одномерная кинематика Q.99GP
CE На краю крыши вы бросаете мяч A из состояния покоя , а затем бросить мяч B вниз с начальной скоростью v0. Является ли увеличение скорости непосредственно перед тем, как мячи приземлятся, больше для мяча А, больше для мяча В или одинаково для каждого мяча?
Решение:Глава 2 Одномерная кинематика Q.100GP
Предположим, что два шара, описанные в задаче 99, выпущены одновременно, при этом шар A выброшен из состояния покоя, а шар B брошен вниз с начальной скоростью υ0. Определите, какой из пяти графиков, показанных на рис. 2-35, соответствует шару A (a) и шару B (b). начальная скорость υ0. Является ли увеличение скорости непосредственно перед тем, как шары приземлятся, больше для мяча А, больше для дужки В или одинаково для каждого мяча?
Решение:
Поскольку шарики падают с постоянным ускорением, график скорости во времени представляет собой прямую линию с одинаковым наклоном, и начальная точка каждой прямой соответствует их начальной скорости.
(a) Следовательно, для шара A график представлен графиком 3
(b) А для шара B график представлен графиком 2.Глава 2 Одномерная кинематика Q.101GP
Далекая планета бросает камень прямо вверх и записывает его движение на видеокамеру. После оцифровки своего видео они могут построить график зависимости высоты y от времени t, показанный на рис. 2-36. а) Каково ускорение свободного падения на этой планете? б) Какова была начальная скорость камня?
Решение:
Глава 2 Одномерная кинематика Q.102GP
Падающая башня НАСА управляет 2,2-секундной падающей башней в Исследовательском центре Гленна в Гевелэнде, штат Огайо. На этом объекте экспериментальные пакеты сбрасываются с вершины башни, на 8-й этаж здания. В течение 2,2 секунд свободного падения эксперименты находятся в условиях микрогравитации, подобной среде космического корабля на орбите. (a) Каково расстояние падения башни высотой 2,2 с? б) С какой скоростью движутся эксперименты, когда они сталкиваются с подушками безопасности в нижней части башни? (c) Если экспериментальная упаковка остановится на расстоянии 0.75 м после столкновения с подушкой безопасности, каково среднее тормозное ускорение?
Решение:
Глава 2 Одномерная кинематика Q.103GP
Мальчик прыгает прямо вверх и вниз на батуте. Предположим, она удвоила свою начальную скорость с 2,0 м/с до 4,0 м/с. а) Во сколько раз увеличивается время ее пребывания в воздухе? б) Во сколько раз увеличился ее максимальный рост? (c) Подтвердите свои ответы на части (a) и (b) явным вычислением.
Решение:
Глава 2 Одномерная кинематика Q.104GP
На 18-м грине Открытого чемпионата США вам нужно сделать 20,5-футовый удар, чтобы выиграть турнир вничью. Когда вы ударяете по мячу, придав ему начальную скорость 1,57 м/с, он останавливается в 6,00 футах от лунки. (a) Предполагая, что замедление, вызванное травой, является постоянным, какой должна была быть начальная скорость, чтобы просто совершить удар? (b) Какая начальная скорость вам нужна, чтобы сделать оставшийся 6,00-футовый удар?
Решение:
Глава 2 Одномерная кинематика Q.105GP
Популярным развлечением на некоторых карнавалах является бросание одеял (см. фото на стр. 39). (a) Если человека подбросить на максимальную высоту 28,0 футов над одеялом, сколько времени он проведет в воздухе? (b) Является ли количество времени, в течение которого человек находится выше высоты 14,0 футов, больше, меньше или равно количеству времени, в течение которого человек находится ниже высоты 14,0 футов? Объяснять. (c) Подтвердите свой ответ на часть (b) расчетом.
Решение:
Глава 2 Одномерная кинематика Q.106GP
Ссылаясь на концептуальную контрольную точку 2-5, найдите расстояние между камнями при (a) t = 1,0 с, (b) t = 2,0 с и (c) t = 3,0 с, где время отсчитывается от момента второй камень падает. (d) Убедитесь, что расстояние увеличивается линейно со временем.
Решение:
Глава 2 Одномерная кинематика Q.107GP
Бургомистр, поднимаясь прямо вверх со скоростью 5,20 м/с, поднимается над раковиной на высоте 12,5 м.а) Каковы величина и направление ускорения снаряда сразу после его отрыва? б) Найдите максимальную высоту над землей, на которую поднялся снаряд. в) Через какое время снаряд достигнет земли? г) Какова скорость снаряда в этот момент?
Решение:
Глава 2 Одномерная кинематика Q.108GP
Врач, готовясь сделать пациенту инъекцию, впрыскивает небольшое количество жидкости прямо вверх из шприца.Если жидкость вытекает со скоростью 1,5 м/с, а) через какое время она вернется на уровень шприца? б) Какова максимальная высота жидкости над шприцем?
Решение:
Глава 2 Одномерная кинематика Q.109GP
Воздушный шар только что оторвался от земли и поднимается с постоянной скоростью 2,0 м/с. Внезапно одна из пассажиров понимает, что оставила камеру на земле. Друг поднимает его и подбрасывает прямо вверх с начальной скоростью 13 м/с.Если пассажир находится на 2,5 м выше своего друга, когда камера подбрасывается, на какой высоте он находится, когда камера достигает его?
Решение:
Глава 2 Одномерная кинематика Q.110GP
В предыдущей задаче какова минимальная начальная скорость камеры, если она должна просто достичь пассажира? (Подсказка: когда камера брошена с минимальной скоростью, ее скорость при достижении пассажира равна скорости пассажира.)
Решение:
Глава 2 Одномерная кинематика Q.111GP
Old Faithful Наблюдая за извержением Old Faithful, вы замечаете, что требуется время t, чтобы вода вышла из основания гейзера и достигла максимальной высоты. а) какова высота гейзера и б) какова начальная скорость воды? Оцените свои выражения для (c) высоты и (d) начальной скорости для измеренного времени 1,65 с.
Решение:
Глава 2 Одномерная кинематика Q.112GP
Мяч брошен вверх с начальной скоростью υ0.Когда он достигает вершины своего полета, на высоте h вверх брошен второй шар с той же начальной скоростью. (a) Нарисуйте график зависимости x от t для каждого шара. (b) По вашему графику решите, пересекаются ли пути шаров на уровне h/2, выше h/2 или ниже h/2. в) Найдите высоту пересечения путей.
Решение:
Глава 2 Одномерная кинематика Q.113GP
Грузы привязаны к каждому концу 20-сантиметровой нити. Вы держите один груз в руке, а другой позволяете ему висеть вертикально на высоте h над полом.Когда вы отпускаете груз в руке, два груза один за другим ударяются о землю со слышимым глухим стуком. Найдите значение h, при котором время между выстрелом и первым ударом равно времени между первым и вторым ударом.
Решение:
Глава 2 Одномерная кинематика Q.114GP
Мяч, брошенный из состояния покоя, проходит три четверти расстояния до земли в последнюю секунду своего падения. а) С какой высоты упал мяч? б) Каково общее время падения?
Решение:
Глава 2 Одномерная кинематика Q.115GP
Сталактит на крыше пещеры с постоянной скоростью стекает в бассейн на 4,0 м ниже. Когда одна капля воды падает в бассейн, вторая капля находится в воздухе, а третья только что отделилась от сталактита. а) Каковы положение и скорость второй капли, когда первая попадает в бассейн? б) Сколько капель в минуту попадает в бассейн?
Решение:
Глава 2. Одномерная кинематика Q.116GP
Вы бросаете лыжную перчатку с высоты h на свежий снег, и она тонет на глубине d, прежде чем остановиться.а) Какова скорость перчатки, когда она коснется снега, с точки зрения g и h? б) Каковы величина и направление ускорения перчатки при движении по снегу, если предположить, что оно постоянно? Дайте ответ в терминах g, h и d.
Решение:
Глава 2 Одномерная кинематика Q.117GP
Чтобы найти высоту воздушной линии электропередачи, вы бросаете мяч прямо вверх. Мяч пересекает линию по пути вверх после 0.75 с, и снова проходит его по пути вниз через 1,5 с после того, как его подбросили. Каковы высота силовой линии и начальная скорость мяча?
Решение: - 5
- 5 Глава 2 одномерная кинематика Q.118GP
- 5
Глава 2 Одномерная кинематика Q.119GP
Стрелка уволена со скоростью 20,0 м/с у блока пенопласта, лежащего на гладкой поверхности. Стрела проникает в блок на определенное расстояние, прежде чем остановиться относительно него.Во время этого процесса замедление стрелы имеет величину 1550 м/с2, а ускорение блока — 450 м/с2. а) Через какое время стрелка перестанет двигаться с rcspeet к блоку? б) Какова общая скорость стрелы и бруска в этом случае? в) Как далеко в блок проникнет стрела?
Решение:
Глава 2 Одномерная кинематика Q.120GP
Сидя в квартире на втором этаже, физик замечает мяч, движущийся прямо вверх прямо за окном.Мяч виден в течение 0,25 с, поскольку он перемещается на расстояние 1,05 м от низа до верха окна. а) Через какое время мяч снова появится? б) Какова наибольшая высота мяча над верхом окна?
Решение:
- 5 Глава 2 одномерная кинематика Q.121GP
Глава 2 Одномерная кинематика Q.122PP
BAM! -APollo 15 Приземление на Луне
Первое слово, произнесенное на поверхности Луны после приземления Аполлона-15 30 июля 1971 года, было «Бам!» Это была непроизвольная реакция Джеймса Ирвина на их довольно болезненное приземление.«Мы попали сильнее, чем любой другой рейс!» говорит Ирвин. «И я, очевидно, был поражен, когда сказал: «Бам!»
. Причина «твердой посадки» «Аполлона-15», как позже охарактеризовал ее пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочный модуль все еще находился на высоте 4,30 фута над лунной поверхностью и двигался вниз со скоростью 0,500 фута в секунду. С этого момента посадочный модуль спускался в лунном свободном падении с ускорением 1,62 м/с2. В результате посадочная скорость Аполлона-15 была самой большой из всех миссий Аполлона.Для сравнения, посадочная скорость Нила Армстронга на «Аполлоне-11» была самой низкой — 1,7 фута в секунду — он не выключал двигатель, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлились со скоростью от 3,0 до 3,5 фута в секунду.
Чтобы лучше понять спуск Аполлона-15, мы показываем его траекторию на последних этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) показаны различные графики зависимости скорости от времени.
Решение:
Глава 2 Одномерная кинематика Q.123PP
Бам! — Аполлон-15 приземляется на Луну
Первое слово, произнесенное на поверхности Луны после приземления Аполлона-15 30 июля 1971 года, было «Бам!» Это была непроизвольная реакция Джеймса Ирвина на их довольно болезненное приземление. «Мы попали сильнее, чем любой другой рейс!» говорит Ирвин. «И я, очевидно, был поражен, когда сказал: «Бам!»
. Причина «твердой посадки» «Аполлона-15», как позже охарактеризовал ее пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочный модуль был еще 4.На высоте 30 футов над лунной поверхностью и движется вниз со скоростью 0,500 фута в секунду. С этого момента посадочный модуль спускался в лунном свободном падении с ускорением 1,62 м/с2. В результате посадочная скорость Аполлона-15 была самой большой из всех миссий Аполлона. Для сравнения, посадочная скорость Нила Армстронга на «Аполлоне-11» была самой низкой — 1,7 фута в секунду — он не выключал двигатель, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлились со скоростью от 3,0 до 3,5 фута в секунду.
Чтобы лучше понять спуск Аполлона-15, мы показываем его траекторию на последних этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) показаны различные графики зависимости скорости от времени.
Решение:Глава 2 Одномерная кинематика Q.124PP
Бам! — Аполлон-15 приземляется на Луну
Первое слово, произнесенное на поверхности Луны после приземления Аполлона-15 30 июля 197 г. , было «Бам!» Это была непроизвольная реакция Джеймса Ирвина на их довольно болезненное приземление.«Мы попали сильнее, чем любой другой рейс!» говорит Ирвин. «И я, очевидно, был поражен, когда сказал: «Бам!»
. Причина «твердой посадки» «Аполлона-15», как позже охарактеризовал ее пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочный модуль все еще находился на высоте 4,30 фута над лунной поверхностью и двигался вниз со скоростью 0,500 фута в секунду. С этого момента посадочный модуль спускался в лунном свободном падении с ускорением 1,62 м/с2. В результате посадочная скорость Аполлона-15 была самой большой из всех миссий Аполлона.Для сравнения, посадочная скорость Нила Армстронга на «Аполлоне-11» была самой низкой — 1,7 фута в секунду — он не выключал двигатель, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлились со скоростью от 3,0 до 3,5 фута в секунду.
Чтобы лучше понять спуск Аполлона-15, мы показываем его траекторию на последних этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) показаны различные графики зависимости скорости от времени.
РИСУНОК 2-37
Решение:
Поскольку скорость увеличивается линейно со временем, поэтому график B представляет собой график зависимости скорости от времени.Глава 2 Одномерная кинематика Q.125PP
Бам! — Аполлон-15 приземляется на Луну
Первое слово, произнесенное на поверхности Луны после приземления Аполлона-15 30 июля 1971 года, было «Бам!» Это была непроизвольная реакция Джеймса Ирвина на их довольно болезненное приземление. «Мы попали сильнее, чем любой другой рейс!» говорит Ирвин. «И я, очевидно, был поражен, когда сказал: «Бам!»
. Причина «твердой посадки» «Аполлона-15», как позже охарактеризовал ее пилот Дэвид Скотт, заключалась в том, что ракетный двигатель был выключен немного раньше, чем планировалось, когда посадочный модуль был еще 4.На высоте 30 футов над лунной поверхностью и движется вниз со скоростью 0,500 фута в секунду. С этого момента посадочный модуль спускался в лунном свободном падении с ускорением 1,62 м/с2. В результате посадочная скорость Аполлона-15 была самой большой из всех миссий Аполлона. Для сравнения, посадочная скорость Нила Армстронга на «Аполлоне-11» была самой низкой — 1,7 фута в секунду — он не выключал двигатель, пока подножки не оказались на поверхности. Аполлоны 12, 14 и 17 приземлились со скоростью от 3,0 до 3,5 фута в секунду.
Чтобы лучше понять спуск Аполлона-15, мы показываем его траекторию на последних этапах посадки на рис. 2-37 (а). На рис. 2-37 (b) показаны различные графики зависимости скорости от времени.
РИСУНОК 2-37
Решение:
В этом случае ускорение восходящее. Это противоположно направлению его скорости. Поэтому скорость посадочного модуля уменьшается линейно. Следовательно, график C будет описывать ситуацию, описанную в задачеГлава 2 Одномерная кинематика Q.126IP
Обратимся к примеру 2-9 Предположим, что спидер (красная машина) движется с постоянной скоростью 25 м/с, а максимальное ускорение полицейской машины (синяя машина) составляет 3,8 м/с2. Если полицейская машина должна тронуться с места и догнать спидера за 15 с или меньше, какое максимальное расстояние может быть у спидера? Измеряйте время с момента запуска полицейской машины.
Решение:Глава 2 Одномерная кинематика Q.127IP
Ссылаясь на пример 2-9. Спидер проезжает мимо полицейской машины с постоянной скоростью 15 м/с.Полицейская машина сразу трогается с места и преследует спидера с постоянным ускорением. Какое ускорение должна иметь полицейская машина, чтобы догнать спидера за 7,0 с? Измеряйте время с момента запуска полицейской машины.
Решение:Глава 2. Одномерная кинематика Q.128IP
IP. максимальная высота 22 м. Если бы мешок был выпущен в 30. - 5
с использованием
S = 14,4 м
Проектирования (H3)
Проектирование объекты, которые разлетаются по воздуху при броске, ударе, выстреле и т.
 д.Примеры:
д.Примеры:Снаряды
Траектория — это путь снаряда. Снаряд всегда имеет некоторую начальную скорость, обычно направленную под углом к горизонтали. Он свободно движется под действием силы тяжести, потому что единственная сила, действующая на него, — это его вес. Чтобы решить проблему со снарядом, вам нужно использовать уравнение SUVAT в двух измерениях, чтобы разделить горизонтальную и вертикальную составляющие каждого значения.
Поскольку тригонометрические функции используются для нахождения неизвестных углов и расстояний, мы будем использовать их для решения компонентов здесь.
Пример:
Частица P брошена из точки O на горизонтальную плоскость со скоростью 28 м/с под углом 30 градусов к горизонту. После выброса частица движется свободно под действием силы тяжести до удара о плоскость в точке А. Найти наибольшую высоту частицы, время полета и расстояние ОА.
Ответ:
Мы хотим найти вертикальную высоту, поэтому мы будем использовать SUVAT в вертикальном направлении.

с =?
u = 28sin30 = 14 м/с
v = 0
a = -g
t = x
В такой ситуации мы используем уравнение, в котором нет t.
Если мы подставим значения, то получим 0 = 196 – 2gs
И мы примем g равным 9,8, s = 10m
Второе, что нам нужно найти, это второе, что мы должны найти. полета (время, которое требуется P, чтобы добраться из O в A).
с = 0 м
а = -g
t =?
Итак, t = 0, когда частица P находится в начале координат.
В то время как решение где находится, когда частица находится в точке A.
А если взять g = 9,8, t = 2,9с.
В заключительной части задачи нам нужно найти расстояние между O и A.
Мы собираемся найти горизонтальное расстояние, поэтому мы будем использовать SUVAT в горизонтальном направлении.
с =?
U = 28COS30 м / с
a = 0
Расстояние между O A и A IS S = 69 м
Кинематика – Key Takeaways
Часто задаваемые вопросы о кинематике
Кинематика — это область изучения, которая фокусируется на движении объектов.
Кинематика используется в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из частей, соединенных вместе.

Финальная викторина по кинематике
Вопрос
Какие уравнения движения?
Ответить
Вопрос
Что означают буквы в СУВАТ?
Ответить
Ответить
Это когда объект испытывает ускорение под действием силы тяжести.

Вопрос
Приведите два примера снарядов.

Вопрос
Что такое постоянное ускорение?
Ответить
Его также называют одномерным уравнением движения при постоянном ускорении.
 Он имеет дело со всеми кинематическими проблемами, где ускорение является стабильным и постоянным.
Он имеет дело со всеми кинематическими проблемами, где ускорение является стабильным и постоянным.Вопрос
Что такое частица в равновесии?
Ответить
Говорят, что частица находится в равновесии, когда ее результирующая сила равна нулю.

Вопрос
Что такое переменное ускорение?
Ответить
Если ускорение отличается между точками на его пути, это считается переменным ускорением.

Вопрос
Что такое уравнение SUVAT без учета скорости?
Ответить
Вопрос
Есть ли формула времени?
Ответить
Вопрос
Что является примером переменного ускорения?
Ответить
Автомобиль, движущийся в людном месте, будет замедляться до тех пор, пока у него не будет достаточно свободного места для движения вперед.

Ответить
Снаряды поражают объекты, летящие по воздуху, будучи брошенными, пораженными или выпущенными.

Вопрос
Путь снаряда.

Вопрос
Что такое кинематические уравнения?
Ответить
Это уравнения, используемые для описания движения объектов с постоянным ускорением.

кинематических уравнений движения, когда скорость становится серьезным делом.| Адриан Пабло
Для многих термин «кинематические уравнения движения», вероятно, кажется неясным или пережитком старой школы.
Летящая птица — хорошая отправная точка для описания движения, задачи кинематики. Большинство из нас может справиться с базовым и довольно расплывчатым определением скорости, но это не заведет нас слишком далеко, когда возникнет необходимость в решении более сложных ситуаций, связанных со скоростями и ускорениями.
Большинство из нас может справиться с базовым и довольно расплывчатым определением скорости, но это не заведет нас слишком далеко, когда возникнет необходимость в решении более сложных ситуаций, связанных со скоростями и ускорениями. Тот, кто хотя бы раз посещал уроки физики в средней школе, хорошо знает о существовании одного из самых фундаментальных разделов физики.Это кинематика, раздел, посвященный описанию движения тела в пространстве. Это самый базовый подход более широкой ветви, известной как динамика, и его основная цель — описать движение, задача, которая включает в себя использование набора результатов, известных как кинематические уравнения движения.
Наблюдение, как это обычно бывает в науке, является отправной точкой этой задачи кинематики, направленной на описание движения тела. С древних времен многие люди наблюдали за движением тел.Во-первых, они отметили, что все движется относительно чего-то.
 Птица перелетает с одного дерева на другое, и вы интуитивно делаете вывод, что птица движется, потому что дерево остается на месте. Другими словами, дерево служит ориентиром. Позднее эти наблюдения развились и стали основой одного из фундаментальных принципов физики, концепции, известной как «система отсчета».
Птица перелетает с одного дерева на другое, и вы интуитивно делаете вывод, что птица движется, потому что дерево остается на месте. Другими словами, дерево служит ориентиром. Позднее эти наблюдения развились и стали основой одного из фундаментальных принципов физики, концепции, известной как «система отсчета».Было еще кое-что, что заметили еще те первые наблюдатели, лежащие в основе кинематики, не все птицы прилетают одновременно, когда пересаживаются с дерева на дерево.Но сначала они заметили довольно очевидную переменную: расстояние. Теперь, даже если бы они начали летать примерно в одно и то же время, а также учитывая, что они преодолели одинаковое расстояние, было ясно, что только один из них выиграл гонку, тогда было бы второе, третье, четвертое и т. д. место. . Другими словами, птицы летели с разной скоростью, но одна птица была самой быстрой, а это означало, что у каждой из летящих птиц существовала разница в скорости. Это был большой концептуальный скачок, который должен был учитывать новую переменную: время.

Следовательно, если вы хотите говорить о скорости тела (птицы, теленка, бегущих людей и т. д.), вам нужно объединить эти две переменные: расстояние и время. Это основное определение скорости, с которым большинство из нас обращается более или менее интуитивно. Хотя, как некоторые из вас могут помнить из школьных уроков физики, скорость и скорость не совсем одно и то же. Они связаны, но мы все еще не совсем там, и нам все еще нужно определить некоторые другие параметры, чтобы прийти к формулировке уравнений кинематики.
Среди наблюдений, сделанных этими первыми физиками, было еще одно. Вы можете двигаться на север, юг, восток, запад или любую другую комбинацию, которая у вас получится. Это означает, что тело может перемещаться с определенной скоростью (покрывать расстояние за измеренное время), но также тело может перемещаться с заданной ориентацией или, говоря более технически, направлением. Это параметр, который отсутствовал, чтобы дополнить прежнее определение скорости.
 Скорость, направленная вдоль направления, и есть то, что мы должны назвать скоростью.Говоря более формально, это физическая величина, известная как вектор.
Скорость, направленная вдоль направления, и есть то, что мы должны назвать скоростью.Говоря более формально, это физическая величина, известная как вектор.Но есть еще одна переменная, которую нельзя определить, и это тоже вектор, который завершит описание движения. Среди наблюдений, зарегистрированных этими любопытными людьми, был тот факт, что тела часто меняли темп, с которым они двигались по своим траекториям. Вернемся к примеру с летающими птицами. Наблюдатели часто замечали, что, перелетая с дерева на дерево, многие из них внезапно двигались быстрее, направляясь к следующему дереву, а затем, приближаясь, двигались медленнее, пока не останавливались.Это означает, что их скорость не была постоянной величиной, она менялась на их пути, и это была недостающая переменная, оставалось что-то определить, чтобы получить полное описание движения, и это то, что мы называем ускорением. Скорость изменения скорости во времени.
Теперь, когда эти переменные определены, мы можем составить уравнения кинематики, но с одним дополнительным соображением: чтобы уравнения применялись, ускорение должно быть постоянным.
 Затем кинематика основывается на этом наборе уравнений, которые показывают различные отношения, которые могут существовать между смещением, скоростью, ускорением и временем.Остальное простая алгебра. С помощью этой модели теперь вы можете описать полет футбольного мяча, падение камня и ускорение вашего любимого олимпийского спринтера.
Затем кинематика основывается на этом наборе уравнений, которые показывают различные отношения, которые могут существовать между смещением, скоростью, ускорением и временем.Остальное простая алгебра. С помощью этой модели теперь вы можете описать полет футбольного мяча, падение камня и ускорение вашего любимого олимпийского спринтера.Вы можете научиться использовать эти уравнения => Кинематика: иллюстрированная книга по физике
Кинематика, динамика и управление (2-е издание): Джазар, Реза Н.: 9781441
2: Amazon.com: Books профессор машиностроения. Он получил степень магистра машиностроения в Тегеранском политехническом институте (1990 г.) в области робототехники и докторскую степень в Технологическом университете Шарифа (1997 г.) в области нелинейных вибраций и прикладной математики.Он работает в университетах Северной Америки с 1999 года. Работая в нескольких университетах по всему миру, он познакомился со многими различными успешными академическими дисциплинами и методами.
Он имеет многолетний опыт работы в автомобильной промышленности по всему миру. Он работал исследователем или менеджером нескольких проектов для многих известных производителей автомобилей в Японии, Корее, Германии, Framce и США.
Область его научных интересов: нелинейные вибрации и нелинейная динамика, в том числе: транспортные средства; робототехника; МЭМС; Орбитальная механика; Мехатроника.
Он является автором более 200 научных статей и монографий, а также автором нескольких технических книг, в том числе:
«Теория прикладной робототехники: кинематика, динамика и управление», второе издание, Springer, Нью-Йорк, 2010 г.,
«Динамика транспортных средств: теория и приложения», Springer, Нью-Йорк, 2009 г.,
«Вибрации толстых цилиндрических конструкций: теория и приложения», в сотрудничестве с профессором Хамидом Р. Хамидзаде, Springer, Нью-Йорк, 2010 г.,
«Расширенная динамика», Уайли, Нью-Йорк, 2011 г.
«Нелинейные подходы в инженерии», в сотрудничестве с профессором Лиминг Дай, Спрингер, Нью-Йорк, 2012 г.

Основные исследования доктора Джазара включают:
* Ускорение Рази, теорию производной по времени и систему координат.
*Закажите бесплатные преобразования для связанных мультител
*Теория кастера в динамике транспортных средств для повышения устойчивости и маневренности
*Алгоритм автодрайвера в проектировании автономных транспортных средств
*Теория кастера в дизайне интеллектуальных транспортных средств
*Метод плавающего времени в теории оптимального управления
*Метод энергоемкости в устойчивости динамических систем
*Метод оптимизации RMS в оптимизации вибрации
*Математическое моделирование гидроопор в виброизоляции
*Математическое моделирование пленочного и термодемпфирования в МЭМС
*Частотная характеристика кусочно-линейного виброизолятора
Модуль 1: Кинематика | Пособие для начинающих 11 класс Физика
Изо всех сил пытаетесь сдвинуться с мертвой точки со своими отметками по физике? В этом руководстве мы познакомим вас с модулем 1 «Кинематика» для 11-го класса по физике, чтобы ваши оценки получили правильный импульс!
В этой статье мы рассмотрим следующие темы кинематики:
Что такое кинематика?
Прежде чем мы будем изучать физику поведения и взаимодействия объектов, нам нужно установить точную систему языка и математики для описания наших наблюдений.
 В 11-м классе мы будем использовать более технический язык по сравнению с предыдущими годами; некоторые слова, которые имеют широкое значение в повседневной жизни (например, «энергия» и «работа»), имеют особое значение в контексте физики, и поэтому мы должны убедиться, что все согласны с их определениями.
В 11-м классе мы будем использовать более технический язык по сравнению с предыдущими годами; некоторые слова, которые имеют широкое значение в повседневной жизни (например, «энергия» и «работа»), имеют особое значение в контексте физики, и поэтому мы должны убедиться, что все согласны с их определениями.Кинематика — это описание и анализ движения объектов без изучения причины движения.
Мы начнем с введения понятия векторных величин. Оттуда мы применим наши знания к описанию одномерного движения, а затем расширимся до движения на плоскости.
Хотите отлично сдать следующий экзамен по физике?
Тема 1: Векторы
В физике мы имеем дело с различными величинами, такими как масса, расстояние, энергия и т. д.
Физические величины можно разделить на две основные категории:
В кинематике представляющие интерес векторы:
Все эти величины имеют величину и направление, и они математически связаны друг с другом, как мы увидим в этом руководстве.

Перемещение имеет скалярный аналог — расстояние. Расстояние измеряет только общее количество покрытой «земли» без учета направления. Расстояние, пройденное объектом, может сильно отличаться от величины его конечного смещения.
Скалярным аналогом скорости является скорость. У ускорения нет конкретного аналога.
Чтобы работать с векторными величинами, мы должны сначала описать, как их можно интерпретировать и математически обрабатывать (например, сложение и вычитание). Мы можем представить векторы в виде стрелок, где длина линии представляет величину величины, а острие стрелки указывает в нужном направлении.
При добавлении двух векторов, например двух векторов смещения \(\vec s_1+ \vec s_2\), векторы соединяются “голова к хвосту”.
Конец второго вектора соединяется с началом первого вектора.
Результирующий вектор или конечный вектор простирается от конца первого вектора до начала второго вектора.
Например: (10 м вправо) + (20 м вправо) = (30 м вправо)
Вычитание вектора \(\vec s_1- \vec s_2\) эквивалентно векторному сложению \(\vec s_1+ (-\vec s_2)\).

Знак минус меняет направление \(\vec s_2\).Например: (10 м вправо) – (15 м влево) эквивалентно (10 м вправо) + ( -15 м влево ) = (10 м вправо) + ( 15 м вправо ) = (25 м справа)
Векторы также можно складывать и вычитать в двух измерениях.Мы обсудим это в разделе 3.
Вектор можно разделить или умножить на скаляр — например, смещение разделить на время, чтобы получить скорость — и в результате получится другой вектор в том же направлении.
Операции с векторами, помимо описанных здесь, рассматриваются в дополнительных курсах по математике для 12-го класса, и если вы продолжите изучать естественные науки и математику в университете, вы будете часто использовать векторы в качестве инструментов.
Тема 2: Движение по прямой
Если наша задача ограничена движением по прямой линии (которой может быть любая линия: вертикальная, горизонтальная или любая другая, например поверхность наклонной плоскости), векторы могут указывать только в одном из двух направлений (т.
 2+2as\\
2+2as\\
\end {выравнивание*}В этих уравнениях \(u\) представляет собой начальную скорость объекта, а \(v\) – его конечную скорость.
Мы также можем решать задачи, связанные с относительным движением двух объектов или результирующим движением объекта в движущейся среде. Рассмотрим ситуацию, когда самолет летит в ветреный день. Его скорость относительно земли зависит от его воздушной скорости, а также от того, насколько быстро воздух движется относительно земли.
Для объекта A, движущегося через среду B, движущуюся относительно земли G:
\(\vec v_{AG}=\vec v_{AB}+ \vec v_{BG}\)
, где \(v_{AG}\) – скорость A относительно G
\(v_{AB}\) – скорость A относительно B и
\(v_{BG}\) – скорость B относительно Г.В других вопросах вам будет известна скорость обоих объектов относительно земли, и вам нужно рассчитать их скорость относительно друг друга. В этом случае перестройте предыдущее уравнение, чтобы найти, что
\(\vec v_{AB}= \vec v_{AG}- \vec v_{BG}\)
Сложной частью этих вопросов обычно является не вычисление вектора, с которым вам придется много практиковаться.
 Он выясняет, как информация в вопросе преобразуется в векторы.
Он выясняет, как информация в вопросе преобразуется в векторы.Рассмотрим следующий сценарий: автомобиль, едущий на запад со скоростью 100 км/ч -1 , проезжает мимо грузовика, едущего на запад со скоростью 70 км/ч -1 .{-1}\) Запад.
Во всех науках графики используются для обобщения и передачи информации. Физика не исключение. Если у нас есть данные о смещении, скорости или ускорении объекта во времени, мы можем преобразовать их в график.
Что говорит нам этот график? Человек начинает в какой-то исходной точке, затем путешествует \(8 \text{ м}\) на север. Оказавшись там, она остается на месте в течение двух секунд, прежде чем начать возвращаться к исходной точке. В \(t = 10 \text{ с}\) она возвращается в исходное положение.
Мы можем не только строить и читать графики. Дополнительную информацию можно получить, проанализировав их особенности. Например, мы установили, что скорость есть скорость изменения смещения. Следовательно, если мы возьмем градиент графика перемещения-времени, он представляет собой величину \(\frac{Δ\vec s}{Δt}\), которая равна мгновенной скорости.
 Точно так же мы можем взять градиент графика зависимости скорости от времени, чтобы найти мгновенное ускорение.
Точно так же мы можем взять градиент графика зависимости скорости от времени, чтобы найти мгновенное ускорение.Еще одна вещь, которую мы можем сделать с графиком скорость-время, это работать другим способом, чтобы вычислить полное перемещение.Это можно найти, взяв площадь под графиком: любая площадь над осью x добавляется к общему положительному смещению, а любая площадь под осью x добавляется к отрицательному смещению.
Тема 3: Движение на плоскости
В более общем плане мы хотим иметь возможность решать задачи в двух измерениях. К счастью, большинство наших методов остались прежними. Нам просто нужно сначала расширить наше понимание векторных операций.
Добавление векторов по-прежнему работает так же: при добавлении двух векторов векторы соединяются «голова к хвосту».Результирующий вектор простирается от конца первого вектора до конца конечного вектора.
Если задача образует треугольник, вы можете решить для неизвестных длин и углов, используя правила косинуса и/или синуса. В более общем смысле, особенно если вы добавляете три или более векторов, лучшим вариантом является разложение каждого вектора на горизонтальные и вертикальные компоненты с использованием тригонометрии:
После разложения вы можете добавить горизонтальные компоненты отдельно, а также отдельно вертикальные компоненты, чтобы получить горизонтальные и вертикальные компоненты конечного вектора.Добавление этих результатов в прямоугольный треугольник, который вы можете решить, чтобы найти окончательный вектор.
Есть несколько способов выразить ответы при работе в 2D. Наиболее распространенными являются азимуты по компасу (например, N30E) или истинные азимуты (например, 030 T), с которыми вы должны быть знакомы из младшей географии. Предостережение: если вы использовали правила косинуса и синуса для определения свойств неизвестного вектора, углы внутри треугольника, скорее всего, не те углы, которые вам нужны для выражения вашего ответа.
Почти все, что мы могли сделать в 1D, можно расширить, включив в него 2D-движение. Процесс расчета относительной и равнодействующей скоростей такой же — векторные операции просто выполняются в двух измерениях, а не в одном. Уравнения движения с постоянным ускорением нельзя использовать напрямую, но в 12-м классе вы научитесь модифицировать их для решения дальнейших задач движения.
Дополнительное измерение также вводит дополнительный шаг к представлению движения с помощью графиков. Теперь есть две координаты, которые могут меняться со временем, поэтому для полного описания движения мы должны отслеживать обе.Есть две возможности: либо мы следим за движением компонент \(x\) и \(y\) во времени, либо описываем векторы их величиной \(r\) и направлением \(θ\).
Представьте, что автомобиль движется с постоянной скоростью по кольцевой развязке:
Мы могли бы представить его движение так:
или вот так:
Оба набора графиков содержат одинаковую информацию.
Кинематика поначалу может показаться не очень интересной, но она формирует основу нашей способности описывать все, от атомов до Вселенной.После того, как вы освоите этот модуль, вам будет легче усваивать и понимать новую физику, начиная с Модуля 2: Динамика.
© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии полной и четкой ссылки на Matrix Education и www.matrix.edu.au с соответствующим и конкретным указанием на исходный контент.
Основное использование
Параметрическое уравнение движения
Обычный способ описания движения в физике — это приписывание функции времени \(x\) и \(y\). Например, известно, что спираль Архимеда подчиняется следующим уравнениям:
\[ х(т) = т \cdot \cos(t) \\ y(t) = t \cdot \sin(t) \]
Мы можем закодировать его и производить выборку с интервалом в 0,05 единицы времени, используя приведенный ниже фрагмент:
# Сгенерировать время ts <- seq(0, 10, by = 0.05) # Расчет позиций с помощью функции xs <- ts * cos(ts) ys <- ts * sin(ts) # Сохранить как фрейм данных mov <- data.frame(t = ts, х = хс, у = уу)Данные выглядят так:
сюжет(mov$x, mov$y, xlab = "x", ylab = "y", asp = 1)И повторив анализ, показанный в предыдущем примере, мы можем значительно обогатить функции, которые мы видим на данных. Например, снова мы используем цвет для отображения радиусов кривизны и размер для отображения абсолютной скорости.
mov_analyzed <- append_dynamics(mov)ggplot(данные = mov_analyzed, отображение = aes (x = x, y = y, col = curv_radius, size = aspeed)) + geom_point (альфа = 0,5) + координата_фиксированная() + scale_color_gradient (низкий = "синий", высокий = "красный")Выборочная кривая
Гораздо более интересные примеры можно получить из фактических выборочных данных , таких как те, которые были созданы нашим устройством. В этом случае нам придется загрузить данные из любого внешнего источника, который мы использовали, и преобразовать их в формат кадра данных (t, x, y).Иногда нам также нужно немного очистить данные (например, удалить NA, артефакты и т. д.).
В образовательных целях мы включили пример набора данных в этот пакет. Кривая была проведена макробеспозвоночным под названием Asella внутри чашки Петри (ни одно животное не пострадало при изготовлении этой упаковки).
Вот так это выглядит после импорта и очистки:
mov <- кинематика::example_mov сюжет (mov $ x, mov $ y, xlab = "x", ylab = "y", asp = 1)С помощью
append_dynamicsмы можем извлечь много важной информации: И это пример того, как наш анализ обогащает содержащуюся в нем информацию:mov_analyzed <- append_dynamics(mov)И использовать силу R, например, для создания красивых графиков.Например, этот, который сопоставляет ускорение с цветом и скорость с размером маркера.
ggplot(данные = mov_analyzed, отображение = aes(x = x, y = y, col = aaccel, size = aspeed)) + geom_point (альфа = 0,1) + координата_фиксированная() + scale_color_gradient (низкий = "синий", высокий = "красный")Или гистограмма об ускорениях:
история(mov_analyzed$aaccel, перерывы = 500, xlab = 'Ускорения', main = 'Гистограмма ускорения')6.3 Вращательное движение - Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам освоить следующие стандарты:
Кроме того, в Руководстве по физике для старших классов рассматривается содержание этого раздела лабораторной работы под названием «Круговое и вращательное движение», а также следующие стандарты:
Основные термины раздела
угловое ускорение кинематика вращательного движения рычаг тангенциальное ускорение крутящий момент Кинематика вращения
Служба поддержки учителей
Служба поддержки учителей
[BL][OL] Повторить уравнения линейной кинематики.
Предупреждение о неправильном представлении
Учащиеся могут запутаться между замедлением и увеличением ускорения в отрицательном направлении.
В разделе, посвященном равномерному круговому движению, мы обсуждали движение по окружности с постоянной скоростью и, следовательно, с постоянной угловой скоростью. Однако бывают случаи, когда угловая скорость непостоянна — вращательное движение может ускоряться, замедляться или изменять направление. Угловая скорость не является постоянной, когда вращающийся фигурист тянет руки, когда ребенок толкает карусель, чтобы заставить ее вращаться, или когда компакт-диск останавливается при выключении.Во всех этих случаях угловое ускорение возникает из-за изменения угловой скорости ωω. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение αα – скорость изменения угловой скорости. В форме уравнения угловое ускорение равно
.где ΔωΔω — изменение угловой скорости, а ΔtΔt — изменение во времени. Единицы углового ускорения: (рад/с)/с или рад/с 2 . Если ωω увеличивается, то αα положительно. Если ωω уменьшается, то αα отрицательно.Имейте в виду, что по соглашению против часовой стрелки — это положительное направление, а по часовой стрелке — отрицательное направление. Например, фигуристка на рис. 6.9 вращается против часовой стрелки, если смотреть сверху, поэтому ее угловая скорость положительна. Ускорение будет отрицательным, например, когда объект, вращающийся против часовой стрелки, замедляется. Было бы положительно, если бы объект, вращающийся против часовой стрелки, ускорялся.
Рис. 6.9 Фигуристка вращается против часовой стрелки, поэтому ее угловая скорость обычно считается положительной.(Luu, Wikimedia Commons)
Соотношение между величинами тангенциального ускорения a и углового ускорения
α,isa=rαorα=ar.α,isa=rαorα=ar.6.10
Эти уравнения означают, что величины тангенциального ускорения и углового ускорения прямо пропорциональны друг другу. Чем больше угловое ускорение, тем больше изменение тангенциального ускорения, и наоборот. Например, рассмотрим всадников в своих капсулах на колесе обозрения в состоянии покоя.Колесо обозрения с большим угловым ускорением даст гонщикам большее тангенциальное ускорение, потому что, поскольку колесо обозрения увеличивает скорость вращения, оно также увеличивает свою тангенциальную скорость. Обратите внимание, что радиус вращающегося объекта также имеет значение. Например, для данного углового ускорения αα меньшее колесо обозрения приводит к меньшему тангенциальному ускорению для гонщиков.
Советы для достижения успеха
Тангенциальное ускорение иногда обозначается как a t .Это линейное ускорение в направлении, касательном к окружности в интересующей точке при круговом или вращательном движении. Помните, что тангенциальное ускорение параллельно тангенциальной скорости (либо в том же направлении, либо в противоположном направлении). Центростремительное ускорение всегда перпендикулярно тангенциальной скорости.
До сих пор мы определили три вращательные переменные: θθ, ωω и αα. Это угловые версии линейных переменных x , v и a .Таблица 6.2 показывает, как они связаны.
Ротационный Линейный Отношения θθ х θ=xrθ=xr ωω против ω=vrω=vr αα и α=арα=ар Таблица 6.2 Вращательные и линейные переменные
Теперь мы можем начать видеть, как вращательные величины, такие как θθ, ωω и αα, связаны друг с другом. Например, если колесо мотоцикла, находящееся в состоянии покоя, имеет большое угловое ускорение в течение достаточно долгого времени, оно в конечном итоге начинает быстро вращаться и делает много оборотов. Выражая это в терминах переменных, если угловое ускорение колеса αα велико в течение длительного периода времени t , то конечная угловая скорость ωω и угол поворота θθ велики.В случае линейного движения, если объект находится в состоянии покоя и испытывает большое линейное ускорение, то он имеет большую конечную скорость и пройдёт большое расстояние.
Кинематика вращательного движения описывает соотношения между углом поворота, угловой скоростью, угловым ускорением и временем. Только описывает движение — оно не включает никаких сил или масс, которые могут влиять на вращение (это часть динамики). Вспомните уравнение кинематики для линейного движения: v=v0+atv=v0+at (константа a ).
Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение αα также является постоянным, поскольку a=rαa=rα. Уравнение кинематической зависимости между ωω, αα и t равно
ω=ω0+αt(константаα),ω=ω0+αt(константаα),
, где ω0ω0 — начальная угловая скорость. Обратите внимание, что уравнение идентично линейной версии, за исключением угловых аналогов линейных переменных. Фактически все уравнения линейной кинематики имеют вращательные аналоги, которые приведены в таблице 6.3. Эти уравнения можно использовать для решения вращательной или линейной задачи кинематики, в которой a и αα являются постоянными.
Поворотный Линейный θ=ω¯tθ=ω¯t х=v¯tx=v¯t ω=ω0+αtω=ω0+αt v=v0+αtv=v0+αt постоянная αα, a θ=ω0t+12αt2θ=ω0t+12αt2 х=v0t+12αt2x=v0t+12αt2 постоянная αα, a ω2=ω02+2αθω2=ω02+2αθ v2=v02+2αxv2=v02+2αx постоянная αα, a Таблица 6.3 Уравнения вращательной кинематики
В этих уравнениях ω0ω0 и v0v0 — начальные значения, t0t0 равно нулю, а средняя угловая скорость ω¯ω¯ и средняя скорость v¯v¯ равны
ω¯=ω0+ω2иv¯=v0+v2.ω¯=ω0+ω2иv¯=v0+v2.6.11
Fun In Physics
Погоня за штормом
Рис. 6.10. Торнадо опускаются из облаков в виде воронок, которые сильно вращаются. (Дафна Зарас, Национальное управление океанических и атмосферных исследований США)
Охотники за штормами, как правило, попадают в одну из трех групп: любители, гоняющиеся за торнадо в качестве хобби, атмосферные ученые, собирающие данные для исследований, наблюдатели за погодой для средств массовой информации или ученые, развлекающиеся под видом работы.Погоня за штормом — опасное времяпрепровождение, потому что торнадо может быстро изменить курс без малейшего предупреждения. Поскольку за разрушениями, оставленными торнадо, следуют охотники за штормами, замена спущенных шин из-за обломков, оставленных на шоссе, является обычным явлением. Наиболее активная часть мира для торнадо, называемая переулок торнадо , находится в центральной части Соединенных Штатов, между Скалистыми горами и Аппалачами.
Торнадо — прекрасный пример вращательного движения в действии в природе.Они появляются во время сильных гроз, называемых суперячейками, которые имеют столб воздуха, вращающийся вокруг горизонтальной оси, обычно около четырех миль в поперечнике. Разница в скорости ветра между сильными холодными ветрами выше в атмосфере в струйном течении и более слабыми ветрами, движущимися на север от Мексиканского залива, заставляет столб вращающегося воздуха смещаться так, что он вращается вокруг вертикальной оси, создавая торнадо.
Торнадо создают скорость ветра до 500 км/ч (примерно 300 миль/ч), особенно внизу, где воронка самая узкая, потому что скорость вращения увеличивается по мере уменьшения радиуса.Они сдувают дома, как если бы они были сделаны из бумаги, и, как известно, протыкают стволы деревьев кусочками соломы.
Проверка захвата
Какой физический термин обозначает глаз бури? Почему ветры в эпицентре торнадо слабее, чем на его внешнем краю?
Момент затяжки
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила. Чем дальше сила приложена от точки поворота (или точки опоры), тем больше угловое ускорение. Например, дверь открывается медленно, если вы нажимаете слишком близко к петле, но открывается легко, если вы нажимаете далеко от петли. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается; это потому, что угловое ускорение обратно пропорционально массе.Эти отношения очень похожи на отношения между силой, массой и ускорением из второго закона Ньютона. Поскольку мы уже рассмотрели угловые версии расстояния, скорости и времени, вы можете задаться вопросом, что такое угловая версия силы и как она соотносится с линейной силой.
Угловой версией силы является крутящий момент ττ, который представляет собой поворачивающую эффективность силы. См. Рисунок 6.11. Уравнение для величины крутящего момента:
, где r — величина плеча рычага, F — величина линейной силы, а θθ — угол между плечом рычага и силой.Плечо рычага — это вектор от точки вращения (точка вращения или точка опоры) к месту приложения силы. Поскольку величина плеча рычага представляет собой расстояние, его единицы измерения — метры, а крутящий момент — Н⋅м. Крутящий момент является векторной величиной и имеет то же направление, что и создаваемое им угловое ускорение.
Рис. 6.11 Человек толкает карусель за ее край и перпендикулярно плечу рычага для достижения максимального крутящего момента.
Применение большего крутящего момента приведет к большему угловому ускорению.Например, чем сильнее человек толкает карусель на рис. 6.11, тем быстрее она ускоряется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Если человек хочет максимизировать воздействие своей силы на карусель, он должен толкнуть ее как можно дальше от центра, чтобы получить наибольшее плечо рычага и, следовательно, наибольший крутящий момент и угловое ускорение. Крутящий момент также максимизируется, когда сила приложена перпендикулярно плечу рычага.
Поддержка для учителей
Поддержка для учителей
[BL][OL][AL] Продемонстрируйте физические взаимосвязи между крутящим моментом, силой, углом приложения силы и длиной плеча рычага, используя рычаги разной длины. Помогите учащимся установить связь между физическими наблюдениями и математическими соотношениями. Например, крутящий момент максимален, когда сила приложена точно перпендикулярно плечу рычага, потому что sinθ=1sinθ=1 для θ=90θ=90 градусов.
Решение задач кинематики вращения и крутящего момента
Точно так же, как линейные силы могут уравновешиваться, создавая нулевую результирующую силу и линейное ускорение, то же самое верно и для вращательного движения.Когда два крутящих момента одинаковой величины действуют в противоположных направлениях, нет ни чистого крутящего момента, ни углового ускорения, как вы можете видеть в следующем видео. Если нулевой чистый крутящий момент действует на систему, вращающуюся с постоянной угловой скоростью, система будет продолжать вращаться с той же угловой скоростью.
Watch Physics
Введение в крутящий момент
В этом видеоролике крутящий момент определяется с точки зрения плеча момента (которое совпадает с плечом рычага). Он также охватывает проблему с силами, действующими в противоположных направлениях вокруг точки поворота.(На этом этапе вы можете игнорировать упоминания Сала о работе и механических преимуществах.)
Проверка захвата
Если бы чистый крутящий момент, действующий на линейку из примера, был бы положительным, а не нулевым, что бы это сказало об угловом ускорении? Что произойдет с правителем со временем?
Теперь давайте рассмотрим примеры применения вращательной кинематики к рыболовной катушке и концепции крутящего момента к карусели.
Рабочий пример
Расчет времени остановки вращения рыболовной катушки
Глубоководный рыбак использует удочку с катушкой радиусом 4,50 см. Большая рыба берет наживку и уплывает от лодки, вытягивая леску из своей рыболовной катушки. По мере разматывания лески с катушки катушка вращается с угловой скоростью 220 рад/с. Рыбак притормаживает спиннинговую катушку, создавая угловое ускорение −300 рад/с 2 .Сколько времени требуется барабану, чтобы остановиться?
Стратегия
Нас просят найти время t для остановки барабана. Величина начальной угловой скорости ω0=220ω0=220 рад/с, а величина конечной угловой скорости ω=0ω=0 . Величина углового ускорения со знаком равна α=−300α=−300 рад/с 2 , где знак минус указывает на то, что оно действует в направлении, противоположном угловой скорости.Глядя на кинематические уравнения вращения, мы видим, что все величины, кроме t , известны в уравнении ω=ω0+αtω=ω0+αt, что делает его самым простым уравнением для решения этой задачи.
Решение
Используемое уравнение: ω=ω0+αtω=ω0+αt .
Алгебраически решаем уравнение для t , а затем подставляем известные значения.
t=ω-ω0α=0-220рад/с-300рад/с2=0,733st=ω-ω0α=0-220рад/с-300рад/с2=0.733s6.12
Обсуждение
Время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда рвется из-за прилагаемой силы, и рыбаки часто позволяют рыбе немного поплавать, прежде чем затормозить катушку. Усталая рыба будет медленнее, ей потребуется меньшее ускорение и, следовательно, меньшая сила.
Рабочий пример
Расчет крутящего момента карусели
Рассмотрим человека, толкающего игровую карусель на рис. 6.11. Он прикладывает силу 250 Н на краю карусели и перпендикулярно радиусу, который равен 1,50 м. Какой крутящий момент он выдает? Предположим, что трение, действующее на карусель, пренебрежимо мало.
Стратегия
Чтобы найти крутящий момент, обратите внимание, что приложенная сила перпендикулярна радиусу и что трением можно пренебречь.
Решение
τ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅мτ=rFsinθ=(1,50м)(250Н)sin(π2).=375Н⋅м6.13
Обсуждение
Мужчина максимизирует крутящий момент, прикладывая силу перпендикулярно плечу рычага, так что θ=π2θ=π2 и sinθ=1sinθ=1 . Мужчина также максимизирует свой крутящий момент, нажимая на внешний край карусели, так что он получает максимально возможное плечо рычага.
Практические задачи
15.Какой крутящий момент создаст человек, если он приложит силу 12\,\text{N} на расстоянии 1,0\,\text{м} от точки вращения, перпендикулярно плечу рычага?
Угловая скорость объекта изменяется с 3 рад/с по часовой стрелке до 8 рад/с по часовой стрелке за 5 с. Каково его угловое ускорение?
Проверьте свое понимание
17.Что такое угловое ускорение?
Какое уравнение для углового ускорения, α ? Предположим, что θ — угол, ω — угловая скорость, а t — время.
Что из следующего лучше всего описывает крутящий момент?
Какое уравнение для крутящего момента?
Служба поддержки учителей
Служба поддержки учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения в этом разделе.Если учащиеся борются с определенной целью, эти вопросы помогут определить, какая цель вызывает проблему, и направить учащихся к соответствующему содержанию.
Освоение физических решений Глава 2 Одномерная кинематика
Освоение физических решений Глава 2 Одномерная кинематика
Освоение физических решений
Глава 2 Одномерная кинематика Q.1CQ
Вы и ваша собака идете на прогулку рядом парк На подходе.ваша собака совершает много коротких поездок в сторону, чтобы преследовать белок, осматривать пожарные гидранты. и т. д. Когда вы прибываете в парк, имеете ли вы и ваша собака одинаковое перемещение? Вы проехали такое же расстояние? Объяснять.
Решение:
Смещение одинаково для собаки и для нас. в то время как расстояние, пройденное собакой, больше, чем расстояние, пройденное намиГлава 2 Одномерная кинематика Q.1P
Ссылаясь на рисунок, вы идете из дома в библиотеку, затем в парк (a) Что это пройденное расстояние? б) Каково ваше перемещение?
Решение:
Расстояние определяется как скалярная величина, равная тому, сколько земли преодолел объект за время своего полного движения.Смещение — это векторная величина, которая определяется как расстояние, которое объект переместил от своего начального положения.
Расстояние измеряет фактический путь объекта, который движется, а смещение измеряет общее расстояние от начального и конечного положения объекта.Глава 2 Одномерная кинематика Q.2CQ
Измеряет ли одометр в автомобиле расстояние или перемещение? Объяснять.
Решение:
Одометр в автомобиле измеряет расстояние, потому что он не сообщает нам направление, в котором мы движемся.Глава 2 Одномерная кинематика Q.2P
Решение:Глава 2 Одномерная кинематика Q.3CQ
Можете ли вы управлять своим автомобилем в а) больше, (б) равно или (в) меньше величины его смещения? В каждом случае приведите пример, если ваш ответ «да», объясните, почему нет, если ваш ответ «нет».Решение:
(A) Да.
Если мы движемся по полному кругу, пройденное нами расстояние равно длине окружности, а наше перемещение равно нулю.
(Б) Да.
Если мы едем по прямой, наше расстояние и перемещение равны.
(C) №
Любое отклонение от прямой линии приводит к расстоянию, превышающему величину смещения.Глава 2 Одномерная кинематика Q.3P
Решение:Глава 2 Одномерная кинематика Q.4CQ
Земля на орбите астронавта. На одном полном витке величина смещения равна пройденному расстоянию? Объяснять.
Решение:
№
В этой ситуации смещение равно нулю, поскольку начальное и конечное положения совпадают (смещение = конечное положение – начальное положение). Расстояние, пройденное космонавтом, равно 2◊R, где R — радиус орбиты.Глава 2 Одномерная кинематика Q.4P
На рис. 2-20 вы идете из парка к дому вашего друга, а затем обратно к себе домой. Каково ваше (а) пройденное расстояние и (б) перемещение?
Решение:Глава 2 Одномерная кинематика Q.5CQ
После теннисного матча игроки бегут к сетке, чтобы поздравить друг друга. Если они оба бегут со скоростью 3 м/с, равны ли их скорости? Объяснять.
Решение:
№
Их скорости различны, потому что они движутся в разных направлениях.Глава 2 Одномерная кинематика Q.5P
Решение:Глава 2 Одномерная кинематика Q.6CQ
Измеряет ли спидометр скорость Объяснять.
Решение:
Спидометр показывает скорость, с которой мы движемся. Оно не говорит нам, в каком направлении мы движемся. Таким образом, спидометр измеряет, а не скорость.Глава 2 Одномерная кинематика Q.6P
IP Ребенок едет на пони по круговой дорожке радиусом 4,5 м. (а) Найдите пройденное расстояние и перемещение после того, как ребенок прошел половину пути; (б) Увеличивается ли пройденное расстояние, уменьшается или остается неизменным, когда ребенок завершает один круг пути? Объясните, (c) Увеличивается ли перемещение, уменьшается или остается неизменным, когда ребенок завершает один круг дорожки? Объясните, (d) Найдите расстояние и перемещение после полного обхода пути.
Решение:
Глава 2 Одномерная кинематика Q.7CQ
Может ли автомобиль двигаться по гоночной трассе с постоянной скоростью? Можно ли это делать с постоянной скоростью? Объяснять.
Решение:
(i) №
Поскольку автомобиль движется по кругу, его направление движения должно меняться. Следовательно, его скорость изменяется и поэтому не является постоянной.
(ii) Да.
Скорость (модуль скорости) автомобиля постоянна во время гонки.Глава 2 Одномерная кинематика Q.7P
CE Предсказать/объяснить Вы едете на автомобиле по прямой со скоростью 15 м/с на протяжении 10 км, затем со скоростью 25 м/с еще 10 км, (а) Является Ваша средняя скорость за всю поездку больше, меньше или равна 20 м/с? (b) Выберите наилучшее объяснение из следующих:
I. При скорости 15 м/с тратится больше времени, чем при скорости 25 м/с.
II. В среднем 15 м/с и 25 м/с равно 20 м/с.
III. При скорости 15 м/с тратится меньше времени, чем при скорости 25 м/с.
Решение:
Глава 2 Одномерная кинематика Q.8CQ
Друзья говорят вам, что во время недавнего путешествия их средняя скорость была +20 м/с. Возможно ли, чтобы их мгновенная скорость была отрицательной в любой момент пути? Объяснять.
Решение:
Да.
Например, ваши друзья могли выехать задним ходом с парковки в какой-то момент поездки, что на короткое время дало отрицательную скорость.Глава 2 Одномерная кинематика Q.8P
CE Предсказать/Объяснить Вы едете на автомобиле по прямой со скоростью 15 м/с в течение 10 минут, затем со скоростью 25 м/с в течение еще 10 минут, (а) Ваша средняя скорость за всю поездку больше, меньше чем или равна 20 м/с?, (b) Выберите лучшее объяснение из следующих:
I. Для движения со скоростью 15 м/с требуется больше времени, чем со скоростью 25 м/с.
II. При скорости 25 м/с преодолевается меньшее расстояние, чем при скорости 15 м/с.
III. При скорости 15 м/с и 25 м/с затрачивается одинаковое время.
Решение:Глава 2 Одномерная кинематика Q.9CQ
Для какого движения мгновенная и средняя скорости равны?
Решение:
Для движения с постоянной скоростью, т. е. прямолинейного движения с постоянной скоростью, мгновенная и средняя скорости равны.Глава 2 Одномерная кинематика Q.9P
Джозеф ДеЛоач из США установил олимпийский рекорд в 1988 году в беге на 200 метров со временем 19,75 секунды. Какова была его средняя скорость? Дайте ответ в метрах в секунду и милях в час.
Решение:Глава 2 Одномерная кинематика Q.10CQ
Если положение объекта равно нулю, то должна ли быть равна нулю его скорость? Объяснять.
Решение:
№
Если вы, например, подбрасываете мяч вверх, вы можете выбрать точку выброса y = 0.
Это не меняет того факта, что начальная скорость движения вверх не равна нулю.Глава 2 Одномерная кинематика Q.10P
В 1992 году Чжуан Юн из Китая установила олимпийский рекорд среди женщин в плавании на 100 метров вольным стилем со временем 54.64 секунды. Какова была ее средняя скорость в м/с и милях/ч?
Решение:Глава 2 Одномерная кинематика Q.11CQ
Предположим, что тормоза в вашем автомобиле создают постоянное замедление, независимо от того, насколько быстро вы едете. Если вы удвоите скорость движения, как это повлияет на (а) время, необходимое для остановки, и (б) расстояние, необходимое для остановки?
Решение:Глава 2 Одномерная кинематика Q.11P
BIO Кенгуру разгонялись до скорости 65 км/ч.
(a) Какое расстояние может прыгнуть кенгуру за 3,2 минуты с такой скоростью?
(б) За какое время кенгуру прыгнет 0,25 км с такой скоростью?
Решение:Глава 2 Одномерная кинематика Q.12CQ
Скорость объекта равна нулю в данный момент времени, (a) Возможно ли, чтобы ускорение объекта было равно нулю в это время ? Объясните: (b) возможно ли, чтобы ускорение объекта было ненулевым в это время? Объяснять.
Решение:
(A) Да.
Для покоящегося тела мгновенная скорость равна нулю, и мгновенное ускорение также равно нулю.
(Б) Да.
Когда тело брошено вверх, в высшей точке тело имеет нулевую скорость, но ускорение в этой точке равно ускорению свободного падения (g).Глава 2 Одномерная кинематика Q.12
Резиновые уточки Сильный шторм 10 января 1992 года вынудил грузовое судно у Алеутских островов выбросить в океан 29 000 резиновых уточек и другие игрушки для купания.Десять месяцев спустя сотни резиновых уточек начали появляться вдоль береговой линии недалеко от Ситки, Аляска, примерно в 1600 милях от них. Какова примерная средняя скорость океанского течения, которое вынесло уток на берег, выраженная в а) м/с и б) милях в час? (Резиновые уточки из того же разлива начали появляться на побережье штата Мэн в июле 2003 г.)
Решение:
Глава 2 Одномерная кинематика Q.13CQ
Если скорость объекта отлична от нуля, может ли его ускорение быть равным нулю? Приведите пример, если ваш ответ «да», объясните, почему нет, если ваш ответ «нет».
Решение:
Да, если объект движется с постоянной скоростью.Глава 2 Одномерная кинематика Q.13P
Радиоволны распространяются со скоростью света, примерно 186 000 миль в секунду. Сколько времени требуется радиосообщению, чтобы добраться с Земли до Луны и обратно? (Необходимые данные см. на внутренней стороне задней обложки.)
Решение:Глава 2 Одномерная кинематика Q.14CQ
Возможно ли, чтобы объект имел нулевую среднюю скорость за заданный интервал времени, но все еще ускоряться во время интервала? Приведите пример, если ваш ответ «да», объясните, почему нет, если ваш ответ «нет».
Решение:
Да. Мяч, брошенный прямо вверх и пойманный при возвращении в точку выброса, имеет нулевую среднюю скорость, но все время ускоряется.Глава 2 Одномерная кинематика Q.14P
Была темная и ненастная ночь, когда вы вдруг увидели вспышку молнии. Три с половиной секунды спустя вы услышали гром. Учитывая, что скорость звука в воздухе составляет около 340 м/с, на каком расстоянии находилась молния?
Решение:
Скорость звука в воздухе v = 340 м/с
Время, необходимое для того, чтобы услышать гром из-за грозы t = 3.5 с
Расстояние d = vt
= (340 м/с)(3,5 с)
= 1190 мГлава 2 Одномерная кинематика Q.15CQ
Отбивающий попадает в поп-мушку прямо вверх. а) Отличается ли ускорение мяча на пути вверх от его ускорения на пути вниз? б) Отличается ли ускорение мяча в верхней точке полета от его ускорения непосредственно перед приземлением?
Решение:
(A) Нет
(B) НетГлава 2 Одномерная кинематика Q.15P
BIO Нервные импульсы Нервная система человека может распространять нервные импульсы со скоростью около 102 м/с. Оцените время, за которое нервный импульс, возникающий при прикосновении пальца к горячему предмету, доходит до мозга.
Решение:Глава 2 Одномерная кинематика Q.16CQ
Человек на батуте подпрыгивает прямо вверх с начальной скоростью 4,5 м/с. Какова скорость человека, когда он вернется на исходную высоту?
Решение:С помощью кинематических соотношений показано, что скорость человека при возвращении на ту же высоту равна 4.5 м/с.
Глава 2 Одномерная кинематика Q.16P
Оцените скорость роста ваших волос в милях в час.
Решение:Глава 2 Одномерная кинематика Q.17CQ
Выиграв бейсбольный матч, один игрок роняет перчатку, а другой подбрасывает ее в воздух. Как соотносятся ускорения двух перчаток?
Решение:
При отсутствии сопротивления воздуха обе перчатки имеют одинаковое ускорение.Глава 2 Одномерная кинематика Q.17P
Зяблик едет на спине галапагосской черепахи, которая ходит со скоростью 0,060 м/с. Через 1,2 минуты зяблик устает от медленного движения черепахи и летит в том же направлении еще 1,2 минуты со скоростью 12 м/с. Какова была средняя скорость вьюрка за этот 2,4-минутный интервал?
Решение:
Глава 2 Одномерная кинематика Q.18CQ
Вулкан стреляет лавовой бомбой прямо вверх.Зависит ли смещение лавовой бомбы от (а) вашего выбора начала координат или (б) вашего выбора положительного направления? Объясните в каждом случае.
Решение:
(A) Нет, смещение — это изменение положения, поэтому оно не зависит от местоположения, выбранного для начала координат.
(B) Да, чтобы узнать, является ли смещение объекта положительным или отрицательным, нам нужно знать, какое направление было выбрано положительным.Глава 2 Одномерная кинематика Q.18P
Вы бежите 8,0 км со скоростью 9,5 км/ч, затем прыгаете в машину и проезжаете еще 16 км. С какой средней скоростью вы должны ехать на своем автомобиле, если ваша средняя скорость на протяжении всех 24 км должна быть 22 км/ч?
Решение:
Глава 2 Одномерная кинематика Q.19P
Собака бегает туда-сюда между двумя своими владельцами, которые идут навстречу друг другу (рис. 2-24). Собака начинает бежать, когда хозяева находятся на расстоянии 10,0 м друг от друга. Если собака бежит со скоростью 3.0 м/с, а каждый из владельцев идет со скоростью 1,3 м/с, какое расстояние прошла собака, когда хозяева встретились?Решение:
Глава 2 Одномерная кинематика Q.20P
IP Вы едете по прямой со скоростью 20,0 м/с в течение 10,0 минут, затем со скоростью 30,0 м/с в течение еще 10,0 минут, а) Ваша средняя скорость 25,0 м/с, больше 25,0 м/с или меньше 25,0 м/с? Объясните, (б) Проверьте свой ответ на часть (а), рассчитав среднюю скорость.
Решение:Глава 2 Одномерная кинематика Q.21P
В час пик вы едете по прямой со скоростью 12 м/с в течение 1,5 минут, затем вам приходится останавливаться на 3,5 минуты, и, наконец, вы едете со скоростью 15 м/с еще 2,5 минуты, (а) Сюжет график зависимости положения от времени для этого движения. Ваш график должен простираться от t = 0 до t = 7,5 минут. (b) Используйте график из части (a) для расчета средней скорости между t = 0 и t = 7,5 минут.
Решение:
Глава 2 Одномерная кинематика Q.22P
IP Вы едете по прямой со скоростью 20,0 м/с на протяжении 10,0 миль, затем со скоростью 30,0 м/с еще на 10,0 миль, (a) Ваша средняя скорость 25,0 м/с превышает 25,0 м/с, или менее 25,0 м/с? Объясните, (б) Проверьте свой ответ на часть (а), рассчитав среднюю скорость.
Решение:Глава 2 Одномерная кинематика Q.23P
IP Будущий отец расхаживает взад и вперед, создавая график зависимости положения от времени, показанный на рис. 2-25. Не производя вычислений, укажите, является ли скорость отца положительной, отрицательной или равной нулю на каждом из следующих сегментов графика: (а) А, (б) В, (в) С и (г) D.Вычислите численное значение скорости отца для отрезков (e) A, (f) B, (g) C и (h) D и покажите, что ваши результаты подтверждают ваши ответы на вопросы (a)–(d).Решение:
Глава 2 Одномерная кинематика Q.24P
Положение частицы как функция времени определяется выражением x = (-5 м/с)t + (3 м /s2)t2. (a) Постройте график x d в зависимости от t для t = 0 до t = 2 с. б) Найдите среднюю скорость частицы от t = 0 до t = 1 с.в) Найдите среднюю скорость от t = 0 до t = 1 с.
Решение:
Глава 2 Одномерная кинематика Q.25P
Положение частицы как функция времени определяется как x = (6 м/с)t + (-2 м/с) с2)т2. (a) Постройте график x в зависимости от t для времени от t = 0 до t = 2 с. б) Найдите среднюю скорость частицы от t = 0 до t = 1 с. в) Найдите среднюю скорость от t = 0 до t = 1 с.
Решение:
Глава 2 Одномерная кинематика Q.26P
IP Теннисистка двигается вперед и назад вдоль базовой линии, ожидая подачи соперника, создавая график зависимости позиции от времени, показанный на рис. 2-26. а) Не производя вычислений, укажите, на каком из отрезков графика А, В или С игрок имеет наибольшую скорость. Рассчитайте скорость игрока для (b) сегмента A, (c) сегмента B и (d) сегмента C и покажите, что ваши результаты подтверждают ваши ответы на часть (a).Решение:
Глава 2 Одномерная кинематика Q.27P
В день свадьбы вы уходите в церковь за 30 минут до начала церемонии, что должно быть достаточно времени, так как церковь находится всего в 10 милях от вас. Однако по пути вам придется сделать непредвиденную остановку для строительных работ на дороге. В результате ваша средняя скорость за первые 15 минут составляет всего 5,0 миль/ч. Какая средняя скорость вам потребуется на оставшейся части пути, чтобы добраться до церкви вовремя?
Решение:
Глава 2 Одномерная кинематика Q.28P
CE График зависимости положения от времени лодки, находящейся рядом с причалом, показан на рис. 2-27. Расположите шесть точек, указанных на графике, в порядке возрастания значения скорости v, начиная с самой отрицательной. Обозначьте ложь знаком равенства.Решение:
Глава 2 Одномерная кинематика Q.29P
Положение частицы как функция времени определяется выражением x = (2,0 м/с)t + (-3,0 м /s3)t3.(a) Постройте график зависимости x от t для времени от t = 0 до t = 1,0 с. б) Найдите среднюю скорость частицы от t = 0,35 с до t = 0,45 с. в) Найдите среднюю скорость от t = 0,39 с до t = 0,41 с. (d) Ожидаете ли вы, что мгновенная скорость в момент времени t = 0,40 с будет ближе к 0,54 м/с, 0,56 м/с или 0,58 м/с? Объяснять. Глава 2 Одномерная кинематика Q.30P
Положение частицы как функция времени определяется x = (-2.00 м/с)t + (3,00 м/с3)t3. (a) Постройте график зависимости x от t для времени от t = 0 до t = 1,00 с. б) Найдите среднюю скорость частицы от t = 0,150 с до t = 0,250 с. (c) Найдите среднюю скорость от t = 0,190 с до t = 0,210 с. (d) Ожидаете ли вы, что мгновенная скорость в момент t = 0,200 с будет ближе к -1,62 м/с или -1,66 м/с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.31P
CE Предсказать/Объяснить Два лука стреляют одинаковыми стрелами с одинаковой скоростью пуска.Для этого тетива в луке 1 должна оттягиваться назад дальше, чем тетива в луке 2. (a) Является ли ускорение стрелы, выпущенной луком 1, больше, меньше или равно ускорению стрелы, выпущенной из лука 2? (b) Выберите лучшее объяснение из следующих:
I. Стрела в луке 2 ускоряется в течение большего времени.
II. Обе стрелки стартуют из состояния покоя.
III. Стрела в луке 1 ускоряется за большее время.
Решение:
Представьте себе задачу:
Две одинаковые стрелы выпущены из двух луков.Стрела из лука 1 оттягивается дальше, чем из лука 2.
Стратегия:
Для двух луков с одинаковой начальной скоростью после выстрела ускорение стрелы обратно пропорционально времени.
(a) Так как лук 1 оттянут назад дальше, ускорение стрелы из лука 1 меньше, чем ускорение из лука 2.
(b) Поскольку стрела из лука 1 прошла большее расстояние по сравнению со стрелой из лука 2 , чтобы достичь той же скорости, стрела из лука 1 будет ускоряться дольше.Поэтому объяснение III является лучшим.Глава 2 Одномерная кинематика Q.32P
Авиалайнер 747 достигает взлетной скорости 173 миль/ч за 35,2 с. Чему равно его среднее ускорение?
Решение:Глава 2 Одномерная кинематика Q.33P
У скворечника бегун ускоряется со скоростью 1,9 м/с2 за 5,2 с. Ускорение бегуна равно нулю до конца забега. Какова скорость бегуна (а) в момент времени t = 2.0 с, а (б) в конце гонки?
Решение:
Глава 2 Одномерная кинематика Q.34P
Реактивный самолет совершает посадку, летя строго на восток со скоростью 115 м/с. Если струя останавливается через 13,0 с, каковы величина и направление ее среднего ускорения?
Решение:Глава 2 Одномерная кинематика Q.35P
Автомобиль движется строго на север со скоростью 18,1 м/с. Найдите скорость автомобиля через 7 минут.50 с, если его ускорение составляет (a) 1,30 м/с2 на север или (b) 1,15 м/с2 на юг.
Решение:Глава 2 Одномерная кинематика Q.36P
Мотоцикл движется согласно графику зависимости скорости от времени, показанному на рис. 2-28. Найти среднее ускорение мотоцикла на каждом из следующих участков движения: а) А, б) В, в) С
Решение:37P
Человек верхом на лошади движется в соответствии с графиком зависимости скорости от времени, показанным на рис. 2-29. Найдите перемещение человека на каждом из следующих участков движения: (а) А, (б) В и (в) С.
Решение:
Глава 2 Одномерная кинематика Q.38P
Бегущая с начальной скоростью +11 м/с, лошадь имеет среднее ускорение -1,81 м/с2. За какое время лошадь уменьшит свою скорость до +6?5 м/с?
Решение:Глава 2 Одномерная кинематика Q.39P
IP Предположим, что тормоза в вашем автомобиле создают постоянное замедление 4,2 м/с2 независимо от того, насколько быстро вы едете. Если вы удвоите скорость движения с 16 м/с до 32 м/с, (а) увеличится ли время, необходимое для остановки, в два или в четыре раза? Объяснять. Подтвердите свой ответ на вопрос (а), рассчитав время остановки для начальной скорости (б) 16 м/с и (в) 32 м/с.
Решение:
Глава 2 Одномерная кинематика Q.40P
IP В предыдущей задаче (a) увеличивается ли расстояние, необходимое для остановки, в два или четыре раза? Объяснять. Подтвердите свой ответ на часть (а), рассчитав тормозной путь для начальной скорости (б) 16 м/с и (в) 32 м/с.
Решение:Глава 2 Одномерная кинематика Q.41P
По мере того, как поезд ускоряется от станции, он достигает скорости 4.7 м/с за 5,0 с. Если ускорение поезда остается постоянным, какова его скорость по истечении дополнительных 6,0 с?
Решение:Глава 2 Одномерная кинематика Q.42P
Частица имеет ускорение +6,24 м/с2 за 0,300 с. В конце этого времени скорость частицы составляет +9,31 м/с. Какова была начальная скорость частицы?
Решение:Глава 2 Одномерная кинематика Q.43P
Посадка со скоростью 81.9 м/с, двигаясь строго на юг, струя останавливается на высоте 949 м. Считая, что струя замедляется с постоянным ускорением, найти величину и направление ее ускорения.
Решение:Глава 2 Одномерная кинематика Q.44P
Когда вы видите, что сигнал светофора становится красным, вы нажимаете на тормоза, пока не остановитесь. Если ваша начальная скорость была 12 м/с, и вы двигались строго на запад, какова была ваша средняя скорость во время торможения? Предположим постоянное замедление.
Решение:Глава 2 Одномерная кинематика Q.45P
Мяч выпущен в точке x = 2 м на наклонной плоскости с отличной от нуля начальной скоростью. После освобождения мяч движется с постоянным ускорением. Ускорение и начальная скорость мяча описываются одним из следующих четырех случаев: случай 1, а > 0, и0 < 0; случай 2, а > 0, и0<0; случай 3, а<0, и0>0; случай 4, а<0, и0<0. а) В каком из этих случаев мяч через какое-то время обязательно пройдет точку x = 0? (b) В каком из этих случаев требуется больше информации, чтобы определить, пересечет ли мяч точку x = 0? в) В каком из этих случаев мяч остановится на мгновение в какой-то момент своего движения?
Решение:Глава 2 Одномерная кинематика Q.46P
Предположим, что автомобиль в задаче 44 останавливается через 35 м. Сколько времени это занимает?
Решение:
Глава 2 Одномерная кинематика Q.47P
Начиная с состояния покоя, лодка увеличивает свою скорость до 4,12 м/с с постоянным ускорением, (a) Какова средняя скорость лодки? б) Какое расстояние лодка проплыла за 4,77 с, чтобы развить эту скорость?
Решение:Глава 2 Одномерная кинематика Q.48P
IP BIO Гепард может разогнаться из состояния покоя до 25,0 м/с за 6,22 с. Предполагая постоянное ускорение, а) какое расстояние пробежал гепард за это время? (b) После спринта всего за 3,13 с скорость гепарда составляет 12,5 м/с, больше 12,5 м/с или меньше 12,5 м/с? Объясните, (c) Какова средняя скорость гепарда за первые 3,11 с его спринта? За вторые 3,11 с своего спринта? (d) Вычислите расстояние, пройденное гепардом за первые 3,11 с и за вторые 3,11 с.
Решение:
Глава 2 Одномерная кинематика Q.49P
Ребенок скользит с горки на санках с ускорением 1,8 м/с2. Если она начинает движение в состоянии покоя, какое расстояние она прошла за (а) 1,0 с, (б) 2,0 с и (в) 3,0 с?
Решение:Глава 2 Одномерная кинематика Q.50P
Детонатор На аттракционе под названием «Детонатор» в Worlds of Fun в Канзас-Сити пассажиры разгоняются прямо вниз из состояния покоя до 45 миль/ч за 2,2 секунды. . Каково среднее ускорение пассажиров в этой поездке?
Решение:Глава 2 Одномерная кинематика Q.51P
Подушки безопасности Подушки безопасности рассчитаны на срабатывание за 10 мс. Оцените ускорение передней поверхности мешка при его расширении. Выразите ответ через ускорение свободного падения g.
Решение:
Глава 2. Одномерная кинематика Q.52P
Жюль Верн. Колумбияда со скоростью 12000 ярдов/с.«Колумбиада» имеет длину 900 футов, но часть ее заполнена порошком, поэтому космический корабль ускоряется на расстоянии всего 700 футов. Оцените ускорение, испытываемое пассажирами космического корабля во время запуска. Дайте ответ в м/с2. (Верн понял, что «путешественники… столкнутся с сильным отскоком», но он, вероятно, не знал, что люди обычно теряют сознание, если испытывают ускорение более 7 g ~ 70 м/с2.)
Решение:Глава 2 Одномерная кинематика Q.53P
BIO Бактериальное движение Приблизительно 0,1% бактерий в кишечнике взрослого человека составляют Escherichia coli. Было замечено, что эти бактерии двигаются со скоростью до 15 мкм/с и максимальным ускорением 166 мкм/с2. Предположим, бактерия E. coli в вашем кишечнике сначала находится в состоянии покоя, а затем разгоняется до 156 мкм/с2. Сколько (а) времени и (б) расстояния требуется, чтобы бактерия достигла скорости 12 мкм/с?
Решение:Глава 2 Одномерная кинематика Q.54P
Две машины едут по прямому шоссе. В момент времени t = 0 автомобиль 1 проезжает отметку 0 мили, двигаясь строго на восток со скоростью 20,0 м/с. В то же время автомобиль 2 находится в 1,0 км к востоку от отметки мили 0 и движется со скоростью 30,0 м/с строго на запад. Автомобиль 1 ускоряется с ускорением 2,5 м/с2, а автомобиль 2 замедляется с ускорением 3,2 м/с2. положительном направлении, (b) В какое время автомобили проезжают рядом друг с другом?
Решение:
Глава 2 Одномерная кинематика Q.55P
Удар метеорита 9 октября 1992 года 27-фунтовый метеорит ударил в автомобиль в Пикскилле, штат Нью-Йорк, оставив вмятину глубиной 22 см в багажнике. Если метеорит везет автомобиль со скоростью 130 м/с, то какова была величина его замедления, если считать его постоянным?
Решение:Глава 2 Одномерная кинематика Q.56P
Ракета взлетает и движется прямо вверх от стартовой площадки с постоянным ускорением. Через 3,0 с ракета находится на высоте 77 м.а) Каковы величина и направление ускорения ракеты? б) Какова его скорость в это время?
Решение:
Глава 2 Одномерная кинематика Q.57P
IP Вы едете по городу со скоростью 12,0 м/с, когда перед вами внезапно выкатывается мяч. Вы нажимаете на тормоза и начинаете замедляться со скоростью 3,5 м/с2. (a) Какое расстояние вы проедете, прежде чем остановиться? (b) Когда вы преодолели только половину расстояния в части (а), ваша скорость равна 6.0 м/с, больше 6,0 м/с или меньше 6,0 м/с? Подтвердите свой ответ расчетом.
Решение:Глава 2 Одномерная кинематика Q.58P
IP Вы едете по городу со скоростью 16 м/с, когда внезапно перед вами выезжает автомобиль задним ходом. Вы нажимаете на тормоза и начинаете замедляться со скоростью 3,2 м/с2. (а) Сколько времени потребуется, чтобы остановиться? (b) После торможения в половину времени, указанного в части (а), ваша скорость составляет 8,0 м/с, больше 8,0 м/с или меньше 8.0 м/с? Подтвердите свой ответ расчетом: (c) Если машина, двигающаяся задним ходом, изначально находилась в 55 м от вас, каково максимальное время реакции, прежде чем вы нажмете на тормоз и при этом не врежетесь в машину?
Решение:
Глава 2 Одномерная кинематика Q.59P
IP BIO Ускорение языка Когда хамелеон ловит насекомое, его язык может вытянуться на 16 см за 0,10 с. (а) Найдите модуль ускорения языка, считая его постоянным, (б) В первом 0.050 с, выдвигается ли язык на 8,0 см, более 8,0 и менее 8,0 см? Подтвердите свой вывод расчетом
Решение:Глава 2 Одномерная кинематика Q.60P
IP Двигаясь прямо на запад на велосипеде со скоростью 8,4 м/с, вы встречаете песчаный участок дороги шириной 7,2 м. . Когда вы покидаете песчаный участок, ваша скорость снижается на 2,0 м/с до 6,4 м/с. (a) Предполагая, что песок вызывает постоянное ускорение, каково было ускорение велосипеда на песчаном участке? Укажите величину и направление. (b) Сколько времени потребовалось, чтобы пересечь песчаный участок? (c) Предположим, вы входите в песчаный участок со скоростью всего 5.4 м/с. Будет ли ваша конечная скорость в этом случае 3,4 м/с, больше 3,4 м/с или меньше 3,4 м/с? Объяснять.
Решение:Глава 2 Одномерная кинематика Q.61P
БИО Выживание после сильного замедления 13 июля 1977 года во время тест-драйва на британском гоночном треке Сильверстоун дроссельная заслонка автомобиля Дэвида Перли заклинила настежь. . В результате крушения Перли испытал наибольшую перегрузку, когда-либо переживаемую человеком — он разогнался до нуля со 173 км/ч на расстоянии всего около 0.66 м. Вычислите величину ускорения, испытанного Перли (считая его постоянным), и выразите ответ в единицах ускорения свободного падения, g = 9,81 м/с2.
Решение:Глава 2 Одномерная кинематика Q.62P
IP Судно движется прямолинейно с постоянной скоростью 2,6 м/с, когда оно переведено в нейтральное положение. Пройдя 12 м по инерции, двигатель снова включается, и судно продолжает плавание с уменьшенной постоянной скоростью, равной 1.6 м/с. Предполагая постоянное ускорение при движении по инерции, а) сколько времени потребовалось лодке, чтобы пройти 12 м по инерции? б) Каково было ускорение лодки, когда она двигалась по инерции? в) Когда лодка прошла 6,0 м, была ли ее скорость 2,1 м/с, больше 2,1 м/с или меньше 2,1 м/с? Объяснять.
Решение:
Глава 2 Одномерная кинематика Q.63P
Модель ракеты поднимается с постоянным ускорением на высоту 3,2 м, в этой точке ее скорость равна 26.0 м/с. а) За какое время ракета достигнет этой высоты? б) Каково было ускорение ракеты? в) Найдите высоту и скорость ракеты через 0,10 с после старта.
Решение:
Глава 2 Одномерная кинематика Q.64P
Печально известный цыпленок мчится к домашней тарелке со скоростью 5,8 м/с, когда он решает удариться о землю. Цыпленок скользит в течение 1,1 с, едва касаясь тарелки, когда останавливается (безопасно, конечно), а) Каковы величина и направление ускорения цыпленка? б) Как далеко проскользнул цыпленок?
Решение:
Глава 2 Одномерная кинематика Q.65P
Велосипедист заканчивает ремонт проколотой шины, когда друг проезжает мимо с постоянной скоростью 3,5 м/с. Через две секунды велосипедист запрыгивает на свой велосипед и разгоняется до скорости 2,4 м/с2, пока не догонит своего друга. а) Сколько времени потребуется, чтобы догнать своего друга? б) Какое расстояние он проехал за это время? в) Какова его скорость, когда он его догонит?
Решение:
Глава 2 Одномерная кинематика Q.66P
Автомобиль, движущийся с частым движением, начинает движение из состояния покоя, движется вперед 13 м за 8.0 с, затем снова останавливается. График зависимости скорости от времени для этого автомобиля показан на рис. 30. Какое расстояние преодолевает автомобиль за (а) первые 4,0 секунды своего движения и (б) последние 2,0 секунды своего движения? в) Чему равна постоянная скорость V, характеризующая средний участок его движения?
Решение:
Глава 2 Одномерная кинематика Q.67P
Автомобиль и грузовик движутся прямо навстречу друг другу по прямой и узкой улице, но они избегают лобового столкновения, одновременно применяя свои тормоза при t = 0.Полученные графики зависимости скорости от времени показаны на рис. = -35 м? (Обратите внимание, что эта информация определяет, какая линия на графике соответствует какому транспортному средству.)
Решение:
Глава 2 Одномерная кинематика Q.68P
В физической лаборатории студенты измеряют время, необходимое маленькая тележка, которую можно сдвинуть на расстояние 1.00 м по гладкой трассе, наклоненной под углом θ к горизонту. Их результаты приведены в следующей таблице.
θ 10,0° 20,0° 30,0°
время, с 1,08 0,770 0,640
(а) Найдите модуль ускорения тележки для каждого угла.
(b) Покажите, что ваши результаты для части (a) хорошо согласуются с формулой a = g sin θ. (Мы выведем эту формулу в главе 5.)
Решение:
позже вы бросаете мяч 2 вниз с той же начальной скоростью.Шары приземляются одновременно. Какое из следующих утверждений верно для момента непосредственно перед падением мяча на землю? А. Скорость мяча 1 больше скорости мяча 2; B. Скорость мяча 1 равна скорости мяча 2; C. Скорость мяча 1 меньше скорости мяча 2. 70. Легенда гласит, что Исаака Ньютона ударило по голове упавшим яблоком, что вызвало у него мысли о гравитации. Предполагая, что история верна, оцените скорость яблока, когда оно ударило Ньютона.
Решение:
Поскольку перемещение двух шаров одинаково и начальные скорости также одинаковы, поэтому два мяча ударяются о землю с одинаковой скоростью.
Итак, вариант (Б) правильный.
Глава 2 Одномерная кинематика Q.70P
Легенда гласит, что Исаака Ньютона ударило по голове упавшим яблоком, что вызвало его мысли о гравитации. Предполагая, что история верна, оцените скорость яблока, когда оно ударило Ньютона.
Решение:Глава 2 Одномерная кинематика Q.71P
Мультфильм показывает машину в свободном падении. Верно ли утверждение, сделанное в мультфильме? Обосновать ответ.
Решение:
Глава 2 Одномерная кинематика Q.72P
Ссылаясь на карикатуру в задаче 71, сколько времени потребуется, чтобы автомобиль разогнался от 0 до 30 миль/ч?
Решение:Глава 2 Одномерная кинематика Q.73P
Прыжок Джордана Сообщается, что вертикальный прыжок Майкла Джордана составляет 48 дюймов.Какая у него скорость взлета? Дайте ответ m метров в секунду.
Решение:Глава 2 Одномерная кинематика Q.74P
БИОЧасто можно наблюдать, как чайки сбрасывают моллюсков и других моллюсков с высоты на камни внизу, чтобы открыть раковины. Если чайка роняет из состояния покоя раковину с высоты 14 м, с какой скоростью движется раковина, ударяясь о скалы? 75. Вулкан выпускает лавовую бомбу прямо вверх с начальной скоростью 28 м/с.Принимая за положительное направление вверх, найти скорость и направление движения лавовой бомбы (а) через 2,0 с и (б) через 3,0 с после ее запуска.
Решение:Глава 2 Одномерная кинематика Q.75P
Вулкан выпускает лавовую бомбу прямо вверх с начальной скоростью 28 м/с. Принимая за положительное направление вверх, найти скорость и направление движения лавовой бомбы (а) через 2,0 с и (б) через 3,0 с после ее запуска.
Решение:Глава 2 Одномерная кинематика Q.76P
Внеземной вулкан Первый действующий вулкан, наблюдаемый за пределами Земли, был открыт в 1979 году на Ло, одном из спутников Юпитера. Было замечено, что вулкан выбрасывает материал на высоту около 2,00 х 105 м. Учитывая, что ускорение свободного падения на 10 равно 1,80 м/с2, найти начальную скорость выброшенного материала.
Решение:Глава 2 Одномерная кинематика Q.77P
BIO Измерьте время своей реакции Вот что вы можете попробовать дома — эксперимент для измерения времени вашей реакции. Попросите друга держать линейку за один конец, чтобы другой конец свисал вертикально. На нижнем конце держите большой и указательный пальцы по обе стороны от линейки, готовые взять ее. Пусть ваш друг отпустит линейку без предупреждения. Поймай его так быстро, как только сможешь. Если вы поймаете линейку на расстоянии 5,2 см от нижнего края, каково время вашей реакции?
Решение:Глава 2 Одномерная кинематика Q.78P
Плотник на крыше здания случайно уронил молоток. Когда молоток падает, он проходит через два окна одинаковой высоты, как показано на рисунке. (a) Является ли увеличение скорости молотка при его падении за окно больше, меньше или равно увеличению скорости при падении за окно 2? (b) Выберите лучшее объяснение из следующих:
I. Большая скорость в окне 2 приводит к большему увеличению скорости.
II. Постоянное ускорение означает, что молоток ускоряется на одинаковую величину для каждого окна.
III. Молот тратит больше инея на падение мимо окна 1.
Решение:Глава 2 Одномерная кинематика Q.79P
CE Predict/Explain плотник в задаче 78. Обратите внимание, что моменты времени, когда молоток проходит через два окна, обозначены заштрихованными областями, (a) Является ли площадь заштрихованной области, соответствующей окну 1, больше, меньше или равна площади заштрихованная область, соответствующая окну 2? (b) Выберите лучшее объяснение из следующих:
I.Заштрихованная область для окна 2 выше, чем . затемненная зона для окна 1.
II. Окна одинаковой высоты.
III. Заштрихованная область окна 1 шире заштрихованной области окна 2.
Решение:
(a) Площадь заштрихованной области, соответствующей окну 1, равна площади заштрихованной области, соответствующей окну 2.
(b) Поскольку график площади время-скорость показывает расстояние, пройденное объектом, и поскольку два окна имеют одинаковую высоту, то площади равны.
Так что вариант II - лучшее объяснение.Глава 2 одномерная кинематика Q.80P



 У вас есть градиент, который является постоянным и отрицательным. Таким образом, график смещения будет выглядеть следующим образом:
У вас есть градиент, который является постоянным и отрицательным. Таким образом, график смещения будет выглядеть следующим образом: После трогания паром разгоняется до 0,2 в течение 12 секунд, после чего выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу.
После трогания паром разгоняется до 0,2 в течение 12 секунд, после чего выключает двигатель, замедляется с постоянной скоростью и останавливается на противоположном берегу. д.Примеры:
д.Примеры:

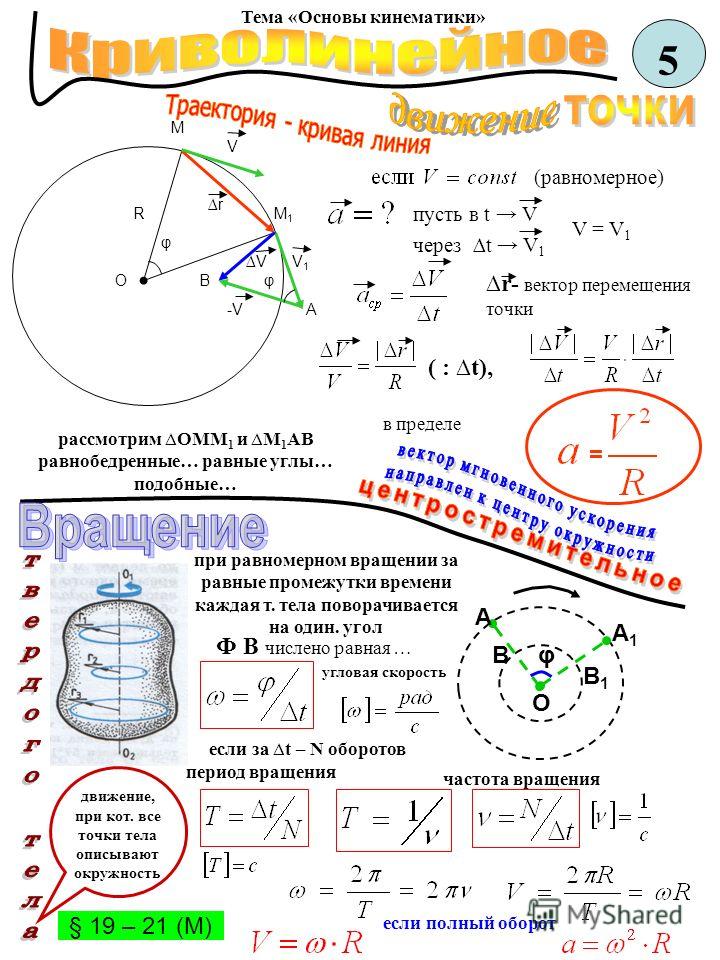

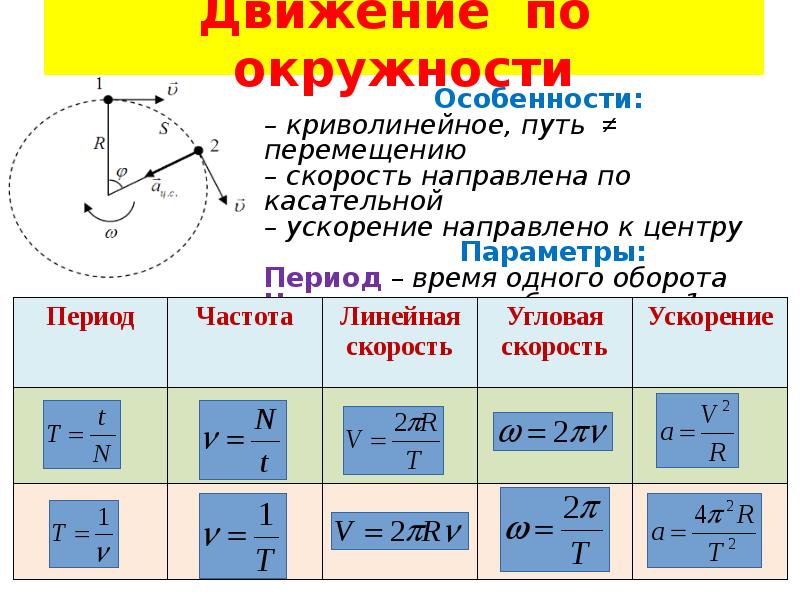

 Он имеет дело со всеми кинематическими проблемами, где ускорение является стабильным и постоянным.
Он имеет дело со всеми кинематическими проблемами, где ускорение является стабильным и постоянным.





 Большинство из нас может справиться с базовым и довольно расплывчатым определением скорости, но это не заведет нас слишком далеко, когда возникнет необходимость в решении более сложных ситуаций, связанных со скоростями и ускорениями.
Большинство из нас может справиться с базовым и довольно расплывчатым определением скорости, но это не заведет нас слишком далеко, когда возникнет необходимость в решении более сложных ситуаций, связанных со скоростями и ускорениями. 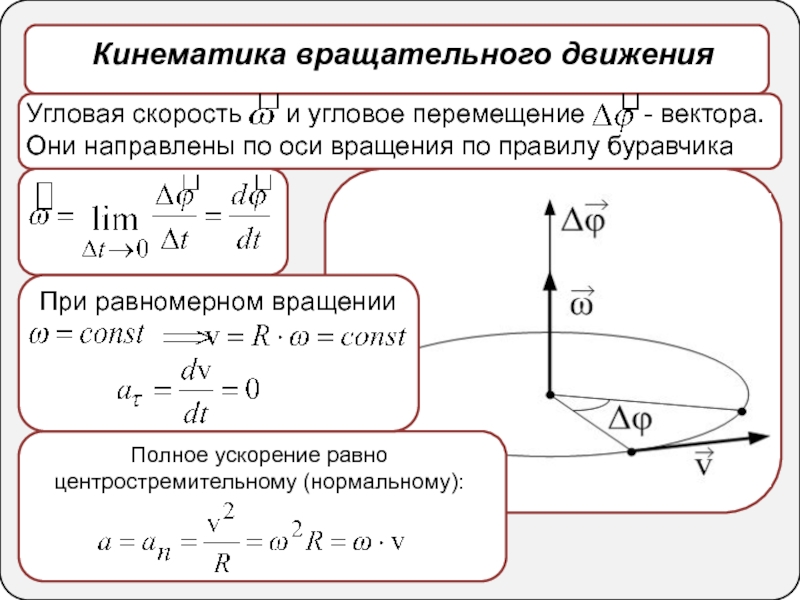 Птица перелетает с одного дерева на другое, и вы интуитивно делаете вывод, что птица движется, потому что дерево остается на месте. Другими словами, дерево служит ориентиром. Позднее эти наблюдения развились и стали основой одного из фундаментальных принципов физики, концепции, известной как «система отсчета».
Птица перелетает с одного дерева на другое, и вы интуитивно делаете вывод, что птица движется, потому что дерево остается на месте. Другими словами, дерево служит ориентиром. Позднее эти наблюдения развились и стали основой одного из фундаментальных принципов физики, концепции, известной как «система отсчета».
 Скорость, направленная вдоль направления, и есть то, что мы должны назвать скоростью.Говоря более формально, это физическая величина, известная как вектор.
Скорость, направленная вдоль направления, и есть то, что мы должны назвать скоростью.Говоря более формально, это физическая величина, известная как вектор. Затем кинематика основывается на этом наборе уравнений, которые показывают различные отношения, которые могут существовать между смещением, скоростью, ускорением и временем.Остальное простая алгебра. С помощью этой модели теперь вы можете описать полет футбольного мяча, падение камня и ускорение вашего любимого олимпийского спринтера.
Затем кинематика основывается на этом наборе уравнений, которые показывают различные отношения, которые могут существовать между смещением, скоростью, ускорением и временем.Остальное простая алгебра. С помощью этой модели теперь вы можете описать полет футбольного мяча, падение камня и ускорение вашего любимого олимпийского спринтера.

 В 11-м классе мы будем использовать более технический язык по сравнению с предыдущими годами; некоторые слова, которые имеют широкое значение в повседневной жизни (например, «энергия» и «работа»), имеют особое значение в контексте физики, и поэтому мы должны убедиться, что все согласны с их определениями.
В 11-м классе мы будем использовать более технический язык по сравнению с предыдущими годами; некоторые слова, которые имеют широкое значение в повседневной жизни (например, «энергия» и «работа»), имеют особое значение в контексте физики, и поэтому мы должны убедиться, что все согласны с их определениями. Для скаляра требуется только число и единицы измерения. Масса и площадь являются примерами скалярных величин, т.е.г. Австралия имеет площадь 7 617 930 км 2 .
Для скаляра требуется только число и единицы измерения. Масса и площадь являются примерами скалярных величин, т.е.г. Австралия имеет площадь 7 617 930 км 2 .
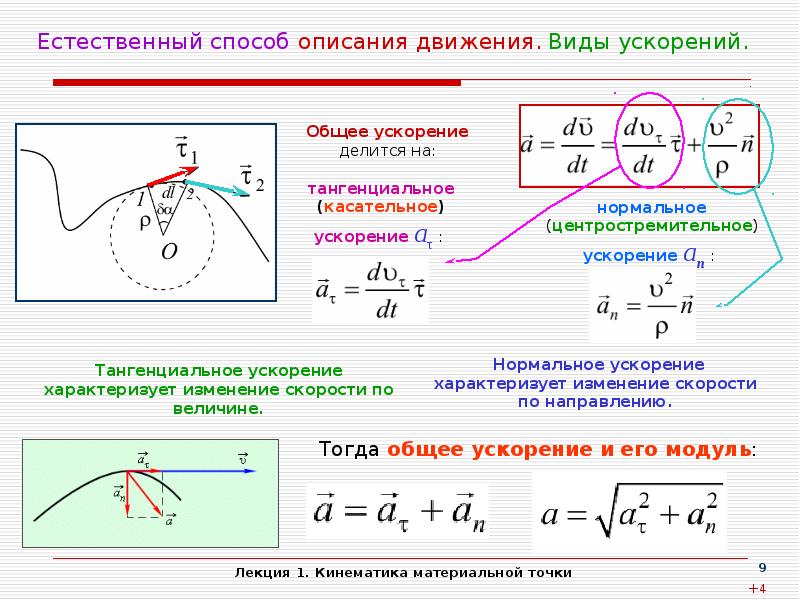
 2+2as\\
2+2as\\  Он выясняет, как информация в вопросе преобразуется в векторы.
Он выясняет, как информация в вопросе преобразуется в векторы. Точно так же мы можем взять градиент графика зависимости скорости от времени, чтобы найти мгновенное ускорение.
Точно так же мы можем взять градиент графика зависимости скорости от времени, чтобы найти мгновенное ускорение.