Динамика – раздел теоретической механики.
Динамика
Основные понятия и аксиомы динамики
Динамика есть часть теоретической механики, изучающая механическое движение тел в зависимости от сил, влияющих на это движение.
Основы динамики заложил итальянский ученый Галилео Галилей (1564-1642), который опроверг существовавшее в науке со времен Аристотеля (IV в. до н.э.) заблуждение о том, что из двух тел, падающих на Землю, более тяжелое движется быстрее. Галилей установил, что причиной изменения скорости тела является сила, т. е. любое ускорение или замедление вызывается силовым воздействием.
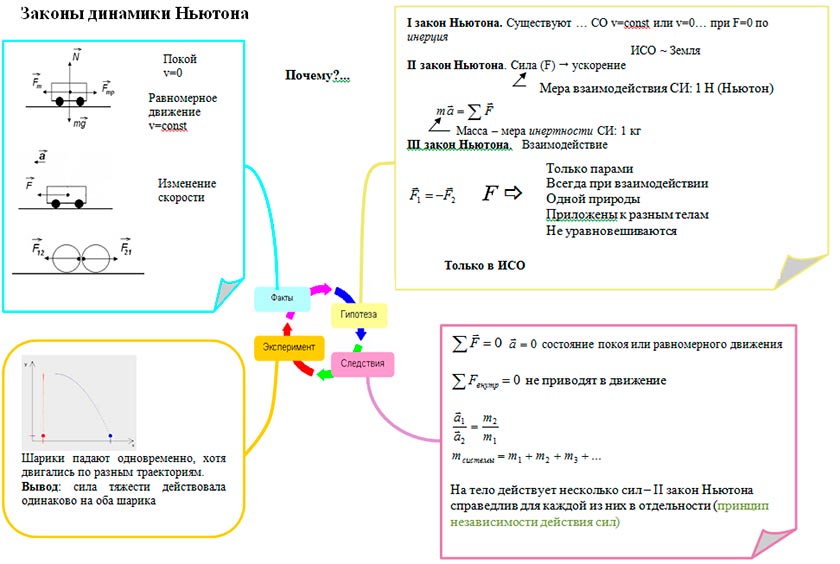
На основе выводов Г. Галилея англичанин И. Ньютон сформулировал основные аксиомы (законы) движения, ставшие фундаментом, на который сотни лет опирается классическая физика, в том числе и современная.
Динамика основывается на ряде положений, которые являются аксиомами и называются законами динамики.
Прежде чем перейти к рассмотрению этих законов, необходимо раскрыть сущность понятий материальной точки и изолированной материальной точки.
Под материальной точкой подразумевают некое тело, имеющее определенную массу (т. е. содержащее некоторое количество материи), но не имеющее линейных размеров (бесконечно малый объем пространства).
Изолированной считается материальная точка, на которую не оказывают действие другие материальные точки.
В реальном мире изолированных материальных точек, как и изолированных тел, не существует, это понятие является условным.
***
Первый закон Ньютона (первый закон динамики)
Первый закон динамики, называемый аксиомой инерции, формулируется в применении к материальной точке так: изолированная материальная точка либо находится в покое, либо движется прямолинейно и равномерно.
В кинематике было установлено, что прямолинейное равномерное движение является единственным видом движения, при котором ускорение равно нулю, поэтому аксиому инерции можно сформулировать следующим образом: ускорение изолированной материальной точки равно нулю.
Итак, изолированная от влияния окружающих тел материальная точка не может сама себе сообщить ускорение. Это свойство тел называют инерцией или инертностью, т. е. инертность (инерция) – свойство тел сохранять скорость по модулю и направлению (в т. ч. и покой – состояние, при котором скорость равна нулю). Изменить скорость, т. е. сообщить материальной точке ускорение способна только приложенная к ней сила.
***
Второй закон Ньютона (второй закон динамики)
Зависимость между силой и сообщаемым ею ускорением устанавливает второй закон Ньютона, который гласит, что ускорение, сообщаемое материальной точке силой, имеет направление силы и пропорционально ее модулю.
Если сила F1 сообщает материальной точке ускорение a1, а сила F2 сообщает этой же точке ускорение a2, то на основании второго закона Ньютона можно записать:

Следовательно, для данной материальной точки отношение любой силы к вызываемому ею ускорению есть величина постоянная. Эту величину (отношение силы к ускорению) называют массой материальной точки, и обозначают ее m:
F/a = m = const.
На основании этого равенства можно сделать выводы:
– две материальные точки, имеющие одинаковые массы, получат от одной и той же силы одинаковые ускорения;
– чем больше масса точки, тем большую силу необходимо приложить, чтобы придать данной точке требуемое ускорение.
***
Что такое масса тела
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства. Ньютон называл массой количество материи, заключенной в теле, считая массу каждого тела величиной постоянной.
Современное представление о мире, после открытий, совершенных А. Эйнштейном, опровергает этот вывод И. Ньютона – масса не является постоянной величиной для тела, она зависит от скорости, с которой это тело движется. Так, например, наблюдения за движением заряженных частиц в ускорителях показали, что инертность частицы (т. е. способность сохранять свою скорость) возрастает с увеличением ее скорости.
Так, например, наблюдения за движением заряженных частиц в ускорителях показали, что инертность частицы (т. е. способность сохранять свою скорость) возрастает с увеличением ее скорости.
Теория относительности устанавливает следующую зависимость между массой тела, находящегося в покое, и массой движущегося тела:
m = m0/√(1 – v2/c2),
где m – масса движущегося тела, m0 – масса покоящегося тела (масса покоя), v = скорость движения тела, c – скорость света.
Из этой формулы видно, что чем больше скорость движения тела, тем больше его масса и, следовательно, тем труднее сообщить ему дальнейшее ускорение. При скоростях близких к скорости света масса тела стремится к бесконечности, и для дальнейшего ускорения такого тела требуется сила бесконечной величины.

На основании теории относительности современная наука дает массе такое определение: масса есть мера инертности тела.
Однако заметное изменение массы (инертности) тела наблюдается лишь при очень больших скоростях, близких к скорости света, поэтому в классической физике массу принимают величиной постоянной, при этом погрешности, возникающие в расчетах, являются ничтожно малыми.
Второй закон Ньютона выражается равенством:
F = ma,
которое называется основным уравнением динамики и читается так: сила есть вектор, равный произведению массы точки на ее ускорение.
Основное уравнение динамики является уравнением движения материальной точки в векторной форме.
Ускорение свободного падения
Опытным путем установлено, что под действием притяжения Земли в вакууме тела падают с одинаковым ускорением, которое называется ускорением свободного падения.
Следует отметить, что это явление будет верным для конкретного географического места на поверхности планеты или над ее поверхностью – ускорение свободного падения не является постоянной величиной и зависит, в частности, от расстояния между центром тяжести тела и центром тяжести нашей планеты, а также от существования центробежной силы инерции, вызываемой вращением Земли.
Так, на полюсах ускорение свободного падения g ≈ 9,83 м/с2, а на экваторе g ≈ 9,78 м/с2. Но в приближенных расчетах принимают среднее значение, равное примерно g ≈ 9,81 м/с2, при этом погрешности результатов незначительны.
Итак, сила тяжести тела равна его массе, умноженной на ускорение свободного падения. Если сила тяжести одного тела G1 = m1/g, а второго тела – G
G1/G2 = (m1g)/(m2g) = m1/m2,
т. е. силы тяжести тел пропорциональны их массам, что позволяет сравнивать массы различных тел путем взвешивания (сравнивания их сил тяжести при помощи весов).
Из второго закона Ньютона следует, что под действием постоянной силы находившаяся в покое свободная материальная точка движется прямолинейно равнопеременно (с постоянным ускорением).
Движение под действием постоянной силы может быть и прямолинейным и криволинейным (в последнем случае материальная точка имеет начальную скорость, вектор которой не совпадает с вектором силы).
***
Третий закон Ньютона
К основным законам динамики относится и рассмотренная в Статике аксиома взаимодействия, или третий закон Ньютона.
Применительно к материальной точке закон формулируется так: силы взаимодействия двух материальных точек по модулю равны между собой и направлены в противоположные стороны (действие равно противодействию).
На основании этого закона можно сделать вывод, что сила, как мера взаимодействия между телами, не может проявляться без пары, т. е. если возникает какое-либо силовое воздействие, то существует и “двойник” этого силового воздействия, равный по модулю и противоположный по вектору.
***
Дифференциальные уравнения движения материальной точки
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Правильные ответы на тестовые вопросы по разделу “Динамика”:
Тест №1 2-3-2-1-1
Тест №2 4-2-4-3-1
Тест №3 3-1-1-2-4
Тест №4 4-2-1-2-3
Тест №5 1-1-4-3-2
Тест №6 1-3-3-2-4
Тест №7 2-2-4-1-3
Эрик Булье: Динамика положительная и постоянная
В дебютном Гран При России гонщики McLaren выступили очень уверенно, заработав 22 очка – это лучший результат команды в сезоне после гонки в Австралии.
Дженсон Баттон (4-й): “Неплохой день, мы добились от машины максимума. На первом круге у меня был опасный момент в третьем повороте, когда мы с Фернандо оказались слишком близко друг к другу, но затем гонка складывалась спокойно. Удивительно, что нам удалось проехать так много кругов на одном комплекте шин – ресурс состава Medium казался вечным, это напомнило мне гонки прошлых лет. В Остине асфальтовое покрытие примерно такое же – посмотрим, какой там будет ситуация с износом.
Этот сезон для нас очень непростой, но за последние несколько этапов мы явно прибавили. Сегодняшний результат – четвертое и пятое места – лучший за долгое время, и двадцать два очка, заработанные мной и Кевином, очень помогут команде в борьбе за позиции в Кубке конструкторов.
Пока вы не поднялись на верхнюю ступеньку подиума, вам всегда хочется большего – таков характер гонщиков Формулы 1. Поверьте мне: сегодня мы выжали из MP4-29 максимум, темп был неплохим, но скоро результаты будут еще лучше”.
Кевин Магнуссен (5-й): “Я решил атаковать с начала гонки, чтобы отыграть как можно больше мест после старта с 11-й позиции, и этот план сработал: мне удался блестящий первый круг, а довольно скоро я оказался пятым. Правда, потом пришлось действовать осмотрительно и экономить топливо, особенно во второй половине гонки, но в целом этап получился не таким уж напряженным. Скорее он напоминал спокойную воскресную поездку, поскольку я отпускал педаль газа за 200 метров до поворота в стремлении сэкономить топливо. Забавно, что никому не удалось подобраться ко мне – очевидно, парни позади испытывали такие же сложности.
Я доволен пятым местом, да и для Дженсона квалифицироваться и финишировать четвертым стало отличным результатом сразу в двух аспектах: во-первых, вместе мы заработали немало очков, а во-вторых, продемонстрировали прогресс машины. Хороший уик-энд, мы оказались чуть быстрее, чем предполагалось, и это здорово! Нужно продолжать работу, чтобы сохранить конкурентоспособность в оставшихся гонках.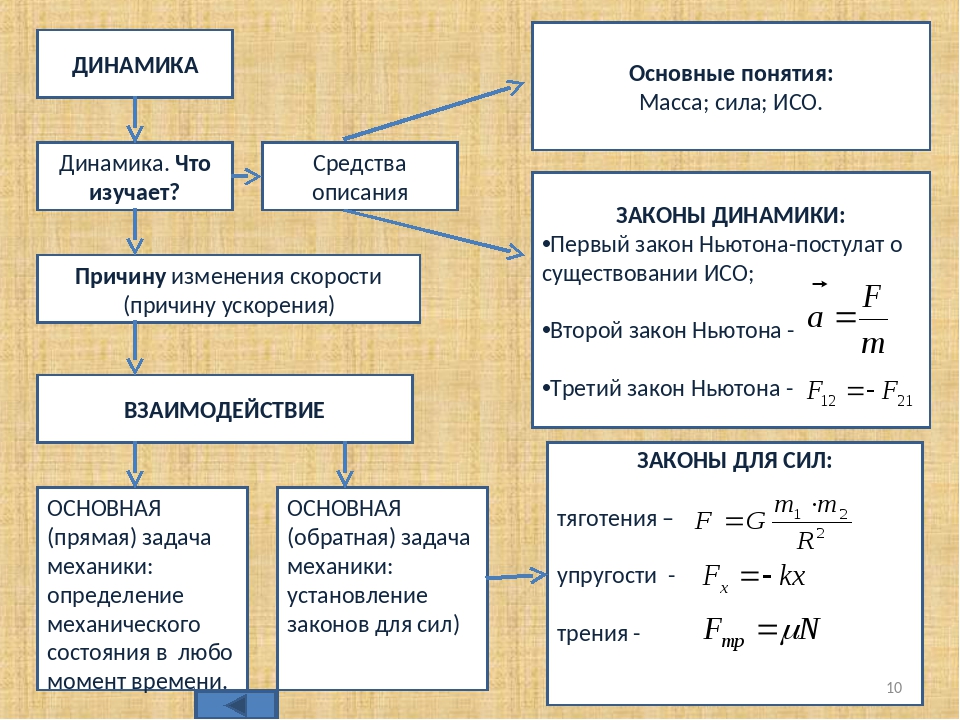 “
“
Эрик Булье, гоночный директор: “После относительно скучного вчерашнего дня для нас стало большим облегчением провести гонку без каких-либо сложностей. Дженсон пилотировал безошибочно, на первых кругах уверенно оборонялся от атак Фернандо Алонсо, а после сохранял четвертое место вплоть до клетчатого флага.
Кевину удался потрясающий старт, к концу первого круга он обогнал не менее пяти машин и в итоге закончил гонку на пятом месте. Как и Дженсон, он пилотировал очень здорово, показал несколько быстрых кругов ближе к концу первого отрезка, желая за счет пит-стопа опередить Алонсо, а на последних кругах экономно расходовал топливо. Раз уж я заговорил о пит-стопах, не могу не похвалить наших механиков, которые снова сработали безупречно – спасибо, парни!
Согласен, финишировав на четвертом и пятом местах, McLaren не добилась своей основной цели, но динамика положительная и постоянная. Заработанные двадцать два очка обеспечили отрыв от Force India в зачете Кубка Конструкторов, и мы намерены закрепить его в оставшихся трех гонках.
Наконец, я хотел бы поздравить наших коллег из Mercedes-Benz с победой в Кубке конструкторов: потрясающая работа и блестящий результат!”
Вычисление значений в сводной таблице
В сводных таблицах можно рассчитывать данные разными способами. Вы узнаете о доступных методах вычислений, о влиянии типа исходных данных на вычисления и о том, как использовать формулы в сводных таблицах и на сводных диаграммах.
Доступные методы вычислений
Для вычисления значений в сводной таблице можно использовать любые из описанных ниже методов.
-
Функции сведения в полях значений. В сводной таблице в области значений отображаются сводные данные, вычисленные на основе исходных данных. Рассмотрим пример с такими исходными данными:
-
Сводная таблица и сводная диаграмма выглядят, как показано на рисунке ниже.
 Если создать сводную диаграмму на основе данных из сводной таблицы, то значения на диаграмме будут соответствовать вычислениям в связанной сводной таблице.
Если создать сводную диаграмму на основе данных из сводной таблицы, то значения на диаграмме будут соответствовать вычислениям в связанной сводной таблице.
-
В сводной таблице поле столбца Месяц содержит элементы Март и Апрель. Поле строки Регион содержит элементы Север, Юг, Восток и Запад.
 Значение на пересечении столбца Апрель и строки Север — это общая выручка от продаж, определенная по исходным данным, для которых столбец Месяц содержит значение Апрель, а столбец Регион — значение Север.
Значение на пересечении столбца Апрель и строки Север — это общая выручка от продаж, определенная по исходным данным, для которых столбец Месяц содержит значение Апрель, а столбец Регион — значение Север. -
В сводной диаграмме поле Регион может представлять собой поле категорий, в котором элементы Север, Юг, Восток и Запад отображаются как категории. Поле Месяц поле может быть полем рядов, в котором элементы Март, Апрель и Май отображаются как ряды, представленные в легенде. Поле значений с именем Сумма продаж может содержать маркеры данных, которые представляют общую выручку в каждом регионе за каждый месяц. Например, один маркер данных может представлять (своим положением на вертикальной оси, т. е. оси значений) сумму продаж за месяц Апрель в регионе Север.
-
Ниже перечислены функции сведения, с помощью которых можно вычислять поля значений.
 Эти функции доступны для всех типов исходных данных, кроме OLAP.
Эти функции доступны для всех типов исходных данных, кроме OLAP.
|
Функция |
Сведение данных |
|---|---|
|
Сумма |
Сумма значений. Функция по умолчанию для числовых данных. |
|
Количество |
Число значений. Действует аналогично функции СЧЁТЗ. Функция по умолчанию для данных, отличных от числовых. |
|
Среднее |
Среднее арифметическое. |
|
Максимум |
Наибольшее значение. |
|
Минимум |
Наименьшее значение. |
|
Произведение |
Произведение значений. |
|
Количество чисел |
Количество числовых значений. Действует аналогично функции СЧЁТ. |
|
Стандартное отклонение |
Оценка стандартного отклонения генеральной совокупности, где выборка является подмножеством всей генеральной совокупности. |
|
Несмещенное отклонение |
Стандартное отклонение генеральной совокупности, которая содержит все сводимые данные. |
|
Дисперсия |
Оценка дисперсии генеральной совокупности, где выборка является подмножеством всей генеральной совокупности. |
|
Несмещенная дисперсия |
Дисперсия генеральной совокупности, которая содержит все сводимые данные. |
-
Настраиваемые вычисления. Служат для отображения значений на основе других элементов или ячеек в области данных.
 Например, можно отобразить значения в поле данных Сумма продаж как процент от продаж за месяц Март или как нарастающий итог по элементам в поле Месяц.
Например, можно отобразить значения в поле данных Сумма продаж как процент от продаж за месяц Март или как нарастающий итог по элементам в поле Месяц.Для настраиваемых вычислений в полях значений доступны перечисленные ниже функции.
|
Функция |
Результат |
|---|---|
|
Без вычислений |
Значение, введенное в данное поле. |
|
% от общей суммы |
Значения в процентах от общей суммы всех значений или точек данных в отчете. |
|
% от суммы по столбцу |
Все значения в каждом столбце или ряду в процентах от итогового значения по этому столбцу или ряду. |
|
% от суммы по строке |
Значение в каждой строке или категории в процентах от итогового значения по этой строке или категории. |
|
Доля |
Значения в процентах от значения базового элемента в соответствующем базовом поле. |
|
% от суммы по родительской строке |
Рассчитывает значения следующим образом: (значение элемента) / (значение родительского элемента по строкам). |
|
% от суммы по родительскому столбцу |
Рассчитывает значения следующим образом: (значение элемента) / (значение родительского элемента по столбцам). |
|
% от родительской суммы |
Рассчитывает значения следующим образом: (значение элемента) / (значение родительского элемента в выбранном базовом поле). |
|
Отличие |
Значения в виде разности по отношению к значению базового элемента в соответствующем базовом поле. |
|
Приведенное отличие |
Значения в виде разности в процентах по отношению к значению базового элемента в соответствующем базовом поле. |
|
С нарастающим итогом в поле |
Значение в виде нарастающего итога для последовательных элементов в базовом поле. |
|
% от суммы с нарастающим итогом в поле |
Значение в виде нарастающего итога в процентах для последовательных элементов в базовом поле. |
|
Сортировка от минимального к максимальному |
Ранг выбранных значений в определенном поле с учетом того, что наименьшему из них присваивается значение 1, а остальным — значения более высокого ранга соответственно. |
|
Сортировка от максимального к минимальному |
Ранг выбранных значений в определенном поле с учетом того, что наибольшему значению в поле присваивается значение 1, а каждому меньшему значению — более высокий ранг. |
|
Индекс |
Рассчитывает значения следующим образом: ((значение в ячейке) x (общий итог)) / ((итог строки) x (итог столбца)). |
-
Формулы. Если функции сведения и настраиваемые вычисления не дают желаемых результатов, вы можете создать собственные формулы в вычисляемых полях и вычисляемых объектах. Например, можно добавить вычисляемый объект с формулой расчета комиссионных за продажу, которые могут быть разными в различных регионах. Эти комиссионные будут автоматически включены в промежуточные и общие итоги в отчете.
Влияние типа источника данных на вычисления
Доступность вычислений и параметров в отчете зависит от того, получены ли исходные данные из базы данных OLAP.
-
Вычисления на основе исходных данных OLAP. При создании сводных таблиц на основе кубов OLAP сводные значения вычисляются на сервере OLAP еще до отображения результатов в Excel. В сводной таблице невозможно изменить способ вычисления этих значений. Например, вы не сможете выбрать другую функцию сведения для вычисления полей данных или промежуточных итогов и добавить вычисляемые поля или вычисляемые объекты.
Кроме того, если сервер OLAP предоставляет вычисляемые поля, называемые “вычисляемыми элементами”, вы увидите их в списке полей сводной таблицы. Вы также увидите все вычисляемые поля и вычисляемые объекты, созданные с помощью макросов, которые написаны на языке Visual Basic для приложений (VBA) и хранятся в книге, но не сможете их изменить. Если вам нужны дополнительные типы вычислений, обратитесь к администратору базы данных OLAP.
Если исходные данные получены из базы данных OLAP, то при вычислении промежуточных и общих итогов можно включить или исключить значения для скрытых элементов.

-
Вычисления на основе исходных данных не из базы данных OLAP. В сводных таблицах, основанных на внешних данных других типов или на данных листа Excel, для вычисления полей значений, содержащих числовые данные, используется функция “Сумма”, а для вычисления полей данных, содержащих текст, — функция “Количество”. Для дальнейшего анализа и обработки своих данных вы можете выбрать другие функции сведения, например “Среднее”, “Максимум” или “Минимум”. Кроме того, можно создавать собственные формулы, в которых используются элементы отчета или другие данные листа. Для этого нужно создать вычисляемое поле или вычисляемый объект в поле.
Использование формул в сводных таблицах
Формулы можно создавать только в отчетах, которые основаны на исходных данных, полученных не из источника данных OLAP. В отчетах, основанных на базе данных OLAP, формулы не поддерживаются. При использовании формул в сводных таблицах нужно учитывать описанные ниже правила синтаксиса и поведения формул.
При использовании формул в сводных таблицах нужно учитывать описанные ниже правила синтаксиса и поведения формул.
-
Элементы формулы сводной таблицы. В формулах, которые создаются для вычисляемых полей и вычисляемых объектов, можно использовать операторы и выражения, как и в других формулах на листе. Также можно использовать константы и ссылаться на данные из отчета, но не допускается использование ссылок на ячейки и определенных имен. Невозможно использовать функции листа, для которых нужны аргументы в виде ссылок на ячейки или определенных имен, а также формулы массива.
-
Имена полей и элементов. В Excel имена полей и элементов используются для идентификации этих элементов отчета в формулах. В приведенном ниже примере для данных в диапазоне C3:C9 используется имя поля Молоко. Для вычисляемого объекта в поле Тип, оценивающего объем продаж нового продукта на основе данных о продажах молочных продуктов, можно использовать формулу =Молоко * 115%.

Примечание: На сводной диаграмме имена полей отображаются в списке полей сводной таблицы, а имена элементов можно просмотреть в каждом раскрывающемся списке полей. Не следует путать эти имена с теми, которые отображаются в подсказках к диаграммам и соответствуют именам рядов и точек данных.
-
Формулы работают с итоговыми суммами, а не с отдельными записями. Формула для вычисляемого поля оперирует суммой исходных данных для каждого используемого поля. Например, формула вычисляемого поля =Продажи * 1,2 умножает сумму продаж для каждого типа и региона на 1,2, а не умножает каждое отдельное значение продаж на 1,2 с последующим суммированием полученных величин.
Формулы для вычисляемых объектов оперируют отдельными записями. Например, формула вычисляемого объекта =Молоко * 115% умножает каждое отдельное значение продаж молочных продуктов на 115 %, после чего полученные величины суммируются в области “Значения”.

-
Пробелы, цифры и символы в именах. В имени, которое содержит два или несколько полей, их порядок не имеет значения. В примере выше ячейки C6:D6 могут называться ‘Апрель Север’ или ‘Север Апрель’. Имена, которые состоят из нескольких слов либо содержат цифры или символы, нужно заключать в одинарные кавычки.
-
Итоги. Формулы не могут ссылаться на итоговые значения (в примере выше — это Сумма за март, Сумма за апрель и Общий итог).
-
Имена полей в ссылках на элементы. Вы можете включить имя поля в ссылку на элемент. Имя элемента должно быть заключено в квадратные скобки, например: Регион[Север]. Используйте этот формат, чтобы избежать ошибок #ИМЯ?, которые возникают, если два элемента в двух разных полях отчета имеют одинаковые имена.
 Например, если в отчете есть два элемента с именем “Мясо” в полях “Тип” и “Категория”, можно избежать появления ошибок #ИМЯ?, ссылаясь на эти элементы следующим образом: Тип[Мясо] и Категория[Мясо].
Например, если в отчете есть два элемента с именем “Мясо” в полях “Тип” и “Категория”, можно избежать появления ошибок #ИМЯ?, ссылаясь на эти элементы следующим образом: Тип[Мясо] и Категория[Мясо]. -
Ссылки на элементы по позиции. Вы можете сослаться на элемент, указав его позицию в отчете (с учетом того, какие элементы фактически отображаются и как они отсортированы в настоящий момент). Тип[1] — это Молоко, а Тип[2] — Морепродукты. Когда позиции элементов изменятся, например, если какие-то из них будут скрыты или снова отображены, такая ссылка, возможно, будет указывать на другой элемент. Скрытые элементы не учитываются в этом индексе.
Для ссылки на элементы можно использовать относительные позиции. Они определяются относительно вычисляемого объекта, содержащего формулу. Если текущим регионом является Юг, то Регион[-1] — это Север.
 Если текущим регионом является Север, то Регион[+1] — это Юг. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Если текущим регионом является Север, то Регион[+1] — это Юг. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Использование формул в сводных диаграммах
Чтобы использовать формулы в сводной диаграмме, их нужно создать в связанной сводной таблице. Там вы увидите отдельные значения, из которых состоят данные, а затем сможете посмотреть на результаты в графическом представлении на сводной диаграмме.
Например, на этой сводной диаграмме представлены данные о продажах для каждого продавца по регионам:
Чтобы посмотреть, как будут выглядеть объемы продаж, если увеличатся на 10 %, можно создать вычисляемое поле в связанной сводной таблице и воспользоваться формулой =Продажи * 110%.
Результат сразу отображается на сводной диаграмме, как показано на этом рисунке:
Чтобы отобразить отдельный маркер данных для продаж в регионе “Север” за вычетом транспортных расходов, которые составляют 8 %, можно создать в поле “Регион” вычисляемый объект с такой формулой: =Север – (Север * 8%).
Диаграмма будет выглядеть следующим образом:
Однако вычисляемый объект, созданный в поле “Продавец”, будет отображаться как ряд, представленный в легенде, и появится на диаграмме в виде точки данных в каждой категории.
Всё, что вы хотели знать о динамическом программировании, но боялись спросить
Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.
Поэтому я постараюсь закрыть этот пробел своей статьёй.
# Весь код в статье написан на языке Python
Основы
Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.
Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.
Порядок пересчёта
Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.
2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.
3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.
Элементарный пример: числа Фибоначчи. Состояние — номер числа.
Прямой порядок:
fib[1] = 1 # Начальные значения
fib[2] = 1 # Начальные значения
for i in range(3, n + 1):
fib[i] = fib[i - 1] + fib[i - 2] # Пересчёт состояния i
Обратный порядок:
fib[1] = 1 # Начальные значения
for i in range(1, n):
fib[i + 1] += fib[i] # Обновление состояния i + 1
fib[i + 2] += fib[i] # Обновление состояния i + 2
Ленивая динамика:
def get_fib(i):
if (i <= 2): # Начальные значения
return 1
if (fib[i] != -1): # Ленивость
return fib[i]
fib[i] = get_fib(i - 1) + get_fib(i - 2) # Пересчёт
return fib[i]
Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.
Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.
Многомерная динамика
Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.
Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:
Пример №1: Количество СМСок
Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:
Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.
1) Состояние динамики:
dp[n][m]— количество различных сообщений длины
n, использующих
m нажатий.
2) Начальное состояние: есть одно сообщение длины ноль, использующее ноль нажатий — пустое.
3) Формулы пересчёта: есть по восемь букв, для написания которых нужно одно, два и три нажатия, а так же две буквы требующие 4 нажатия.
Прямой пересчёт:
dp[n][m] = (dp[n - 1][m - 1] + dp[n - 1][m - 2] + dp[n - 1][m - 3]) * 8 + dp[n - 1][m - 4] * 2
Обратный пересчёт:
dp[n + 1][m + 1] += dp[n][m] * 8
dp[n + 1][m + 2] += dp[n][m] * 8
dp[n + 1][m + 3] += dp[n][m] * 8
dp[n + 1][m + 4] += dp[n][m] * 2
4) Порядок пересчёта:
Если писать прямым методом, то надо отдельно подумать о выходе за границу динамики, к примеру, когда мы обращаемся к
dp[n - 1][m - 4], которого может не существовать при малых
m. Для обхода этого можно или ставить проверки в пересчёте или записать туда нейтральные элементы (не изменяющие ответа).
При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.
5) Ответ — это сумма всех состояний.
UPD:
К сожалению, я допустил ошибку — задачу можно решить и одномерно, просто убрав из состояния длину сообщения n.
1) Состояние: dp[m] — количество различных собщений, которые можно набрать за m нажатий.
2) Начальное состояние: dp[0] = 1.
3) Формула пересчёта:
dp[m] = (dp[m - 1] + dp[m - 2] + dp[m - 3]) * 8 + dp[m - 4] * 2
4) Порядок: все три варианта можно использовать.
5) Ответ — это сумма всех состояний.
Пример №2: Конь
Шахматный конь стоит в клетке
(1, 1)на доске размера
Nx
M. Требуется подсчитать количество способов добраться до клетки
(N, M)передвигаясь четырьмя типами шагов:
Решение1) Состояние динамики:
dp[i][j]— количество способов добраться до
(i, j).
2) Начальное значение: В клетку
(1, 1)можно добраться одним способом — ничего не делать.
3) Формула пересчёта:
Для прямого порядка:
dp[i][j] = dp[i - 2][j - 1] + dp[i - 2][j + 1] + dp[i - 1][j - 2] + dp[i + 1][j - 2]
Для обратного порядка:
dp[i + 1][j + 2] += dp[i][j]
dp[i + 2][j + 1] += dp[i][j]
dp[i - 1][j + 2] += dp[i][j]
dp[i + 2][j - 1] += dp[i][j]
4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.
Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.
Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:
Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.
5) Ответ просто лежит в dp[n][m].
Динамика и матрица переходов
Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы
вики.
Допустим, есть задача, которую мы уже решили динамическим программированием, например, извечные числа Фибоначчи.
Давайте немного переформулируем её. Пусть у нас есть вектор , из которого мы хотим получить вектор . Чуть-чуть раскроем формулы: . Можно заметить, что из вектора можно получить вектор путем умножения на какую-то матрицу, ведь в итоговом векторе фигурируют только сложенные переменные из первого вектора. Эту матрицу легко вывести, вот она: . Назовём её матрицей перехода.
Это значит, что если взять вектор и умножить его на матрицу перехода n - 1 раз, то получим вектор , в котором лежит fib[n] — ответ на задачу.
А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: .
Это свойство даёт нам право сделать так: .
Это хорошо тем, что теперь можно применить метод быстрого возведения в степень, который работает за . Итого мы сумели посчитать N-ое число Фибоначчи за логарифм арифметических операций.
А теперь пример посерьёзнее:
Пример №3: Пилообразная последовательность
Обозначим пилообразную последовательность длины
Nкак последовательность, у которой для каждого не крайнего элемента выполняется условие: он или меньше обоих своих соседей или больше. Требуется посчитать количество пилообразных последовательностей из цифр длины
N. Выглядит это как-то так:
Решение
Для начала решение без матрицы перехода:
1) Состояние динамики: dp[n][last][less] — количество пилообразных последовательностей длины n, заканчивающихся на цифру last. Причём если less == 0, то последняя цифра меньше предпоследней, а если less == 1, значит больше.
2) Начальные значения:
for last in range(10):
dp[2][last][0] = 9 - last
dp[2][last][1] = last
3) Пересчёт динамики:
for prev in range(10):
if prev > last:
dp[n][last][0] += dp[n - 1][prev][1]
if prev < last:
dp[n][last][1] += dp[n - 1][pref][0]
4) Порядок пересчёта: мы всегда обращаемся к предыдущей длине, так что просто пара вложенных
for‘ов.
5) Ответ — это сумма
dp[N][0..9][0..1].
Теперь надо придумать начальный вектор и матрицу перехода к нему. Вектор, кажется, придумывается быстро: все состояния, обозначающие длину последовательности N. Ну а матрица перехода выводится, смотря на формулы пересчёта.
Динамика по подотрезкам
Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.
Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.
Пример №4: Запаковка строки
Вот
Развернутое условие. Я вкратце его перескажу:
Определим сжатую строку:
1) Строка состоящая только из букв — это сжатая строка. Разжимается она в саму себя.
2) Строка, являющаяся конкатенацией двух сжатых строк A и B. Разжимается она в конкатенацию разжатых строк A и B.
3) Строка D(X), где D — целое число, большее 1, а X — сжатая строка. Разжимается она в конкатенацию D строк, разжатых из X.
Пример: “3(2(A)2(B))C” разжимается в “AABBAABBAABBC”.
Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.
Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.
1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.
dp_len = r - l
dp[l][r] = dp_len # Первый вариант сжатия - просто строка.
for i in range(l + 1, r):
dp[l][r] = min(dp[l][r], dp[l][i] + dp[i][r]) # Попробовать разделить на две сжатые подстроки
for cnt in range(2, dp_len):
if (dp_len % cnt == 0): # Если не делится, то нет смысла пытаться разделить
good = True
for j in range(1, (dp_len / cnt) + 1): # Проверка на то, что все cnt подстрок одинаковы
good &= s[l:l + dp_len / cnt] == s[l + (dp_len / cnt) * j:l + (dp_len / cnt) * (j + 1)]
if good: # Попробовать разделить на cnt одинаковых подстрок и сжать
dp[l][r] = min(dp[l][r], len(str(cnt)) + 1 + dp[l][l + dp_len / cnt] + 1)
4) Порядок пересчёта: прямой по возрастанию длины подстроки или ленивая динамика.
5) Ответ лежит в
d[0][len(s)].
Пример №5: Дубы
Динамика по поддеревьям
Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.
Пример №6: Логическое дерево
Дано подвешенное дерево, в листьях которого записаны однобитовые числа —
0или
1. Во всех внутренних вершинах так же записаны числа, но по следующему правилу: для каждой вершины выбрана одна из логических операций: «И» или «ИЛИ». Если это «И», то значение вершины — это логическое «И» от значений всех её детей. Если же «ИЛИ», то значение вершины — это логическое «ИЛИ» от значений всех её детей.
Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.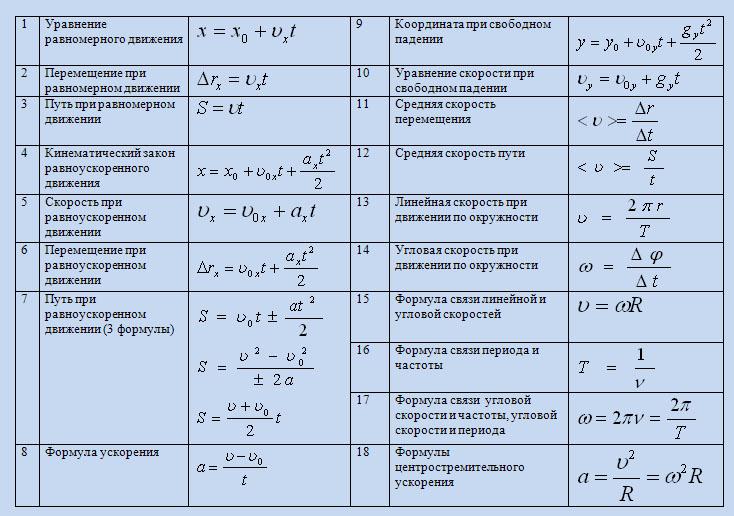
1) Состояние динамики:
d[v][x]— количество операций, требуемых для получения значения
xв вершине
v. Если это невозможно, то значение состояния —
+inf.
2) Начальные значения: для листьев, очевидно, что своё значение можно получить за ноль изменений, изменить же значение невозможно, то есть возможно, но только за
+infопераций.
3) Формула пересчёта:
Если в этой вершине уже значение
x, то ноль. Если нет, то есть два варианта: изменить в текущей вершине операцию или нет. Для обоих нужно найти оптимальный вариант и выбрать наилучший.
Если операция «И» и нужно получить «0», то ответ это минимум из значений d[i][0], где i — сын v.
Если операция «И» и нужно получить «1», то ответ это сумма всех значений d[i][1], где i — сын v.
Если операция «ИЛИ» и нужно получить «0», то ответ это сумма всех значений d[i][0], где i — сын v.
Если операция «ИЛИ» и нужно получить «1», то ответ это минимум из значений d[i][1], где i — сын v.
4) Порядок пересчёта: легче всего реализуется лениво — в виде поиска в глубину из корня.
5) Ответ — d[root][value[root] xor 1].
Динамика по подмножествам
В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.
Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера
Задан взвешенный (веса рёбер неотрицательны) граф
Gразмера
N. Найти
гамильтонов цикл (цикл, проходящий по всем вершинам без самопересечений) минимального веса.
Так как мы ищем цикл, проходящий через все вершины, то можно выбрать за «начальную» вершину любую. Пусть это будет вершина с номером
0.
1) Состояние динамики: dp[mask][v] — путь минимального веса из вершины 0 в вершину v, проходящий по всем вершинам, лежащим в mask и только по ним.
2) Начальные значения: dp[1][0] = 0, все остальные состояния изначально — +inf.
3) Формула пересчёта: Если i-й бит в mask равен 1 и есть ребро из i в v, то:
dp[mask][v] = min(dp[mask][v], dp[mask - (1 << i)][i] + w[i][v])
Где
w[i][v]— вес ребра из
iв
v.
4) Порядок пересчёта: самый простой и удобный способ — это написать ленивую динамику, но можно поизвращаться и написать перебор масок в порядке увеличения количества единичных битов в ней.
5) Ответ лежит в
d[(1 << N) - 1][0].
Динамика по профилю
Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.
Эти задачи можно решить полным перебором за , где a — количество вариантов замощения одной клетки. Динамика по профилю же оптимизирует время по одной из размерностей до линейной, оставив от себя в экспоненте только коэффициент. Получится что-то такое: .
Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.
Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив
Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.
Пример №8: Замощение доминошками
Найти количество способов замостить таблицу
Nx
Mс помощью доминошек размерами
1x
2и
2x
1.
РешениеЗдесь профиль — это один столбец. Хранить его удобно в виде двоичной маски:
0— не замощенная клетка столбца,
1— замощенная. То есть всего профилей
.
0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:
Если в первом профиле на очередном месте стоит 1, значит во втором обязательно должен стоять 0, так как мы не сможем замостить эту клетку никакой фигуркой.
Если в первом профиле на очередном месте стоит 0, то есть два варианта — или во втором 0 или 1.
Если 0, это значит, что мы обязаны положить вертикальную доминошку, а значит следующую клетку можно рассматривать как 1. Если 1, то мы ставим вертикальную доминошку и переходим к следующей клетке.
Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):
После этого сохранить всё в массив can[mask][next_mask] — 1, если можно перейти, 0 — если нельзя.
1) Состояние динамики: dp[pos][mask] — количество полных замощений первых pos - 1 столбцов с профилем mask.
2) Начальное состояние: dp[0][0] = 1 — левая граница поля — прямая стенка.
3) Формула пересчёта:
dp[pos][mask] += dp[pos - 1][next_mask] * can[mask][next_mask]
4) Порядок обхода — в порядке увеличения
pos.
5) Ответ лежит в dp[pos][0].
Полученная асимптотика — .
Динамика по изломанному профилю
Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:
Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с до . Асимптотика улучшилась с до .
Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):
Восстановление ответа
Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.
В таком случае надо восстановить ответ.
В каждой задаче свой способ восстановления ответа, но самые распространенные:
- Рядом со значением состояния динамики хранить полный ответ на подзадачу. Если ответ — это что-то большое, то может понадобиться чересчур много памяти, поэтому если можно воспользоваться другим методом, обычно так и делают.
- Восстанавливать ответ, зная предка(ов) данного состояния. Зачастую можно восстановить ответ, зная только как он был получен. В той самой «Запаковке строки» можно для восстановления ответа хранить только вид последнего действия и то, из каких состояний оно было получено.
- Есть способ, вообще не использующий дополнительную память — после пересчёта динамики пойти с конца по лучшему пути и по дороге составлять ответ.
Небольшие оптимизации
Память
Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.
Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.
Время
Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в
алгоритме Дейкстрыможно воспользоваться
очередью с приоритетамидля изменения асимптотического времени.
Замена состояния
В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.
Пример №9: Разложение числа
Требуется найти количество разложений числа
N на различные слагаемые. Например, если
Например, если
N = 7, то таких разложений
5:
- 7
- 3 + 4
- 2 + 5
- 1 + 7
- 1 + 2 + 4
Два решения с различными состояниями
Решение №1:
1) Состояние динамики:
dp[n][k]— количество разложений числа
nна числа, меньшие или равные
k. Параметр
kнужен, чтобы брать всегда только большие числа, чем уже имеющиеся.
2) Начальные значения:
dp[1][1] = 1,
dp[1][i] = 0.
3) Формула пересчёта:
for last_summand in range(1, k + 1):
dp[n][k] += dp[n - last_summand][last_summand]
4) Порядок: прямой, в порядке увеличения
n.
5) Ответ — сумма
dp[N][1..N].
Состояний: , переходов: . Асимптотика: .
Решение №2:
1) Поменяем состояние. Теперь dp[n][k] — это количество разложений числа
nна
k различных чисел. Казалось бы незачем, но сейчас будет понятно.
Казалось бы незачем, но сейчас будет понятно.
2) Начальные значения:
dp[1][1] = 1,
dp[1][i] = 0.
3) Формула пересчёта:
dp[n][k] = dp[n - k][k] + dp[n - k][k - 1]
Теперь надо пояснить, что значит эта формула. Все состояния можно получить (причём единственным способом) делая поочерёдно два действия:
- Все уже имеющиеся числа увеличить на
1. - Все уже имеющиеся числа увеличить на
1. Добавить число1в разложение.
Чтобы понять, почему это так можно посмотреть на
диаграммы Юнга:
Строки здесь обозначают слагаемые.
Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.
4) Порядок пересчёта: прямой, в порядке увеличения n.
Невооруженным взглядом кажется, что у этого решения асимптотика , ведь есть два измерения в состоянии и переходов. Но это не так, ведь второй параметр — k ограничен сверху не числом N, а формулой (сумма чисел от 1 до k меньше или равна разлагаемого числа). Из этой формулы видно, что количество состояний .
5) Ответ — это сумма dp[N][1..k_max].
Асимптотика: .
Заключение
Основным источником была голова, а туда информация попала с лекций в
Летней Компьютерной Школе(для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (
darnley).
Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.
+Основы динамики СОР
Суммативное оценивание за раздел «Основы динамики»
Цели обучения
9.2.2.2 -формулировать первый закон Ньютона
9. 2.2.4
– формулировать второй закон Ньютона и применять при решении задач
2.2.4
– формулировать второй закон Ньютона и применять при решении задач
9.2.2.5 – формулировать третий закон Ньютона
9.2.2.9 – применять формулу первой космической скорости
9.2.2.10 – определять вес тела, движущегося с ускорением
9.2.2.11 – объяснять состояние невесомости
Критерий оценивания
Обучающийся:
ü Различает законы Ньютона
ü Применяет второй закон Ньютона при решении задач
ü Определяет вес тела, движущегося вертикально с ускорением
ü Применяет формулу первой космической скорости при решении задач
ü Объясняет состояние невесомости
Уровни мыслительных навыков знание, понимание и применение
Время выполнения: 15 – 20 мин
Задание
1. Установите соответствие [3]
ЗАКОНЫ |
| ФОРМУЛИРОВКИ | ||
1 | 1 закон Ньютона |
| А | Модуль ускорения тела прямо пропорционален модулю равнодействующей всех сил и обратно пропорционален массе тела |
|
|
|
|
|
2 | закон Ньютона |
| В | Тело движется равномерно в инерциальной системе, если воздействие других тел скомпенсировано |
|
|
|
|
|
3 | 3 закон Ньютона |
| С | Направление ускорения тела совпадает с направлением равнодействующей всех сил, действующих на тело |
|
|
|
|
|
|
|
| D | Действию всегда есть равное и противоположное противодействие |
|
|
|
|
|
|
|
| E | Ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально его массе |
2. a) Определите cилу,
которая сообщает вагонетке массой 500 кг ускорение 0,25м/с2
[2]
a) Определите cилу,
которая сообщает вагонетке массой 500 кг ускорение 0,25м/с2
[2]
в) Вычислите ускорение трактора, массой 5тонн, который тянет плуг по горизонтали с силой 5 кН. Сопротивление движению 3 кН. [3]
3. Космическая ракета при старте с поверхности Земли движется с ускорением 20 м/с2 Найдите вес лётчика-космонавта в кабине, если его масса 80 кг. [2]
4. Вычислите первую космическую скорость для Солнца. Масса Солнца 2•1030 кг, диаметр Солнца 1,4 • 109 м. [2]
5. Выберите, когда тело брошенное вертикально вверх, находиться в состоянии невесомости и объясните почему?
А) только в верхней точке полёта
В) только при движении вниз
С) только при движении вверх
D) во всё время полёта [2]
Критерий оценивания | № задания | Дескриптор обучающий правильно: | балл |
Различает законы Ньютона. | 1 | Выбирает формулировку первого закона Ньютона | 1 |
Указывает определение, соответствующее второму закону Ньютона | 1 | ||
Выбирает формулировку третьего закона Ньютона | 1 | ||
Применяет второй закон Ньютона при решении задач. | 2 а | Записывает формулу второго закона Ньютона | 1 |
Вычисляет силу | 1 | ||
2 б | Переводит величины в СИ | 1 | |
Рассчитывает равнодействующую силу | 1 | ||
Вычисляет ускорение, применяя второй закон Ньютона | 1 | ||
Определяет вес тела, движущегося вертикально с ускорением. | 3 | Записывает формулу веса тела, движущегося с ускорением направленным вверх | 1 |
Вычисляет вес тела | 1 | ||
Применяет формулу первой космической скорости при решении задач. | 4 | Записывает формулу первой космической скорости | 1 |
Вычисляет первую космическую скорость | 1 | ||
Объясняет состояние невесомости. | 5 | Различает состояние невесомости при свободном падении | 1 |
Объясняет явление невесомости | 1 | ||
Всего баллов | 14 | ||
Рубрика для представления информации
по итогам суммативного оценивания за раздел «Основы динамики»
ФИ учащегося_____________________________________
Критерий оценивания | Уровень учебных достижений | ||
Низкий | Средний | Высокий | |
Различает законы Ньютона. | Затрудняется выбрать правильно формулировки законов Ньютона | Допускает ошибки в правильном выборе одной из формулировок | Выбирает правильно все формулировки законов Ньютона |
Применяет второй закон Ньютона при решении задач. | Затрудняется в применении второго закона Ньютона | Допускает ошибки в формуле второго закона Ньютона или в вычислениях | Правильно записывает формулу и рассчитывает силу и ускорение |
Определяет вес тела, движущегося вертикально с ускорением. | Затрудняется в определении веса тела, движущегося вертикально с ускорением | Допускает ошибки в формуле веса тела движущегося вертикально с ускорением или в вычислениях | Правильно записывает формулу веса тела, движущегося вертикально с ускорением и рассчитывает его |
Применяет формулу первой космической скорости при решении задач. | Затрудняется в применить формулу первой космической скорости | Допускает ошибки в формуле и вычислениях первой космической скорости | Правильно применяет формулу первой космической скорости и вычисляет её |
Объясняет состояние невесомости. | Затрудняется в объяснении состояние невесомости | Допускает ошибки в выборе варианта учитывая состояние невесомости | Правильно объясняет состояние невесомости |
Формулы и версии формул – Управление цепочкой поставок | Динамика 365
- Статья .
- 6 минут на чтение
Оцените свой опыт
да Нет
Любой дополнительный отзыв?
Отзыв будет отправлен в Microsoft: при нажатии кнопки «Отправить» ваш отзыв будет использован для улучшения продуктов и услуг Microsoft. Политика конфиденциальности.
Политика конфиденциальности.
Представлять на рассмотрение
Спасибо.
В этой статье
Формула определяет материалы, ингредиенты и результаты конкретного процесса непрерывного производства. Вместе с соответствующим маршрутом формула определяет весь процесс непрерывного производства. Формулы используются для планирования и производства продуктов в непрерывном производстве.
Формула состоит из ингредиентов и количеств, необходимых для производства определенного количества элемента формулы. В зависимости от выполняемой задачи вы можете получить доступ к функциям формулы из управления запасами и складом или из управления информацией о продукте.
Формулы и строки формул
Формула состоит из одной или нескольких строк формулы, которые определяют ингредиенты или элементы, составляющие формулу. Строка формулы может содержать элементы ведомости материалов (BOM), элементы формулы, элементы промежуточного веса, приобретенные элементы, сопутствующие продукты или побочные продукты. Поскольку многие элементы используются в нескольких продуктах, элемент можно использовать в нескольких формулах.
Поскольку многие элементы используются в нескольких продуктах, элемент можно использовать в нескольких формулах.
Пример формулы – рецепт печенья с шоколадной крошкой. Ингредиенты для этой формулы состоят из нескольких линий, таких как мука, сахар, яйца, масло и шоколадная стружка. Формула печенья с шоколадной крошкой содержит ингредиенты, которые, вероятно, используются в других формулах. Пока вы готовите печенье с шоколадной крошкой, могут остаться остатки, например, крошки, или некоторые из печенья могут быть пережарены или недоварены.Эти элементы могут быть настроены как побочные продукты или побочные продукты, в зависимости от производственных операций.
Когда вы создаете строку формулы, вы используете тип строки, чтобы указать, как система должна обрабатывать строку при выполнении сводного планирования и создании пакетных заказов. Каждый тип линии дает разный результат. В следующей таблице описаны типы линий, которые вы можете выбрать.
| Тип линии | Описание |
|---|---|
Арт. | Выберите Товар , если товар является сырьем или полуфабрикатом, который выбирается из запасов, или когда товар является услугой. |
| Фантом | Выберите Phantom , если нужно расчленить все элементы формулы нижнего уровня, содержащиеся в строках формулы. Когда вы оцениваете пакетный заказ и элементы формулы разнесены, элементы-компоненты перечисляются в виде строк формулы в пакетном заказе. Дополнительно к производственному маршруту добавляются соответствующие маршруты. Элементы формулы разнесены с использованием текущей конфигурации. При использовании линии Phantom вы можете обрабатывать конфигурации производства и измерения, которые возникают на разных уровнях формулы.Если вы выберете Phantom для продукта на экспресс-вкладке Engineer страницы Released product details , а затем используете этот продукт в формуле, тип строки строки формулы изменится на Phantom . Вы не можете выбрать Phantom для позиции с промежуточным весом или для позиций, у которых тип производства – Сопутствующий продукт , Побочный продукт или Элемент планирования . Вы не можете выбрать Phantom для позиции с промежуточным весом или для позиций, у которых тип производства – Сопутствующий продукт , Побочный продукт или Элемент планирования . |
| Привязанный источник питания | Выберите Обособленная поставка , чтобы создать заказ партии, производственный заказ, канбан, заказ на перемещение или заказ на поставку для ингредиента, который содержится в строке формулы.Связанный заказ определяется на основе настроек заказа по умолчанию и типа производства ингредиента и создается при оценке заказа партии. Требуемые количества ингредиентов зарезервированы для заказа партии. |
| Продавец | Выберите Поставщик , если в производственном процессе используется субподрядчик, и вы хотите создать субпроизводство или заказ на поставку для субподрядчика. Услуга или работа, которую выполняет субподрядчик, должны быть созданы с использованием позиции формулы или позиции услуги. Вы можете прикрепить элемент к родительскому элементу в виде строки формулы. Маршрут должен содержать операцию, назначенную операционному ресурсу субподрядчика. Эта операция добавляется к строке формулы с помощью Oper. № поле. Вы можете прикрепить элемент к родительскому элементу в виде строки формулы. Маршрут должен содержать операцию, назначенную операционному ресурсу субподрядчика. Эта операция добавляется к строке формулы с помощью Oper. № поле. |
Формулы версий
При создании новой формулы необходимо сначала создать версию формулы, прежде чем добавлять элементы строк формулы и их конкретные характеристики. У каждой формулы должна быть хотя бы одна версия.Кнопка Утверждено в версии формулы становится доступной только после успешного сохранения записи версии. Каждая запись версии формулы связана с одним или несколькими сопутствующими и побочными продуктами, которые могут быть произведены при производстве готового продукта. Многие продукты можно изготавливать из одних и тех же ингредиентов в партиях разного размера, в нескольких количествах или с разным выходом. Вы можете создать столько версий формулы, сколько вам нужно.
Для управления несколькими активными версиями формулы используйте диапазоны дат действия или поля количества “от”. Несколько активных версий формулы могут существовать только в том случае, если диапазон дат и количество «с» не перекрываются.
Несколько активных версий формулы могут существовать только в том случае, если диапазон дат и количество «с» не перекрываются.
В отличие от спецификаций, где одна спецификация часто связана со многими версиями спецификаций, для каждой формулы обычно существует только одна версия формулы. Помните, что только одна версия формулы может быть активирована для измерений покрытия и количества для данного продукта. Однако многие версии формул могут существовать по другим причинам, и вы можете выбрать их вручную при создании заказа на партию.
Утвердить и активировать формулы и версии формул
Формулы и версии формул должны быть утверждены, прежде чем их можно будет использовать для планирования и производства.Формулы обычно активируются перед использованием. Однако во время производства вы можете выбрать версию формулы, которая утверждена, но не активирована.
Чтобы защитить формулу или версию формулы, вы можете установить Блок редактирования и Блокировать удаление параметров утверждения на странице Параметры управления производством .
Если выбрать Редактирование блока и формула утверждена, никакие поля в строках формулы не могут быть удалены или отредактированы.Однако, если вы удалите утверждение формулы, вы можете удалить и изменить строки формулы. Вы также можете создавать новые формулы и новые версии формул.
При выборе Блокировать удаление утверждения нельзя удалить утверждение утвержденной формулы или версии формулы. Однако вы можете создавать новые формулы и новые версии формул, а также можете удалить активацию версии формулы.
Вы можете добавить больше уровней контроля, используя функцию электронной подписи.Если пользователь настроен так, что во время утверждения формулы требуется электронная подпись, при активации формулы появляется страница Подпись . Пользователь должен быть авторизован для электронной подписи, и сертификат должен быть успешно проверен, прежде чем изменение можно будет зафиксировать. Если подпись не может быть аутентифицирована, утверждение или удаление утверждения отклоняется, а изменение, инициировавшее утверждение или удаление утверждения, возвращается в исходное состояние.
Используйте масштабируемую функцию
Функция масштабирования доступна только в том случае, если для всех компонентов позиции в формуле задано значение Переменное потребление .Эта функция недоступна, если для компонентов элемента задано значение Фиксированное потребление или Шаговое потребление . При использовании функции «Масштабирование» при изменении ингредиента в формуле количество других выбранных ингредиентов корректируется. Размер формулы также корректируется. Аналогичным образом, если вы измените размер формулы, изменится количество всех масштабируемых ингредиентов. Эта функция предназначена специально для создания и обслуживания формул. Он не указывает, будет ли количество ингредиента увеличиваться или уменьшаться в заказе партии.
Использование Шаг потребления
Поэтапное потребление исключает необходимость ввода количества на вкладке Строка формулы для ингредиента. Вместо этого потребление шага настроено так, что оно имеет значение Из серии и значение Количество . Выбирается информация из записи «Шаговое потребление на серию», которая соответствует количеству в заказе партии. Поэтапное потребление полезно, когда скорость потребления не является линейной по отношению к размеру заказа партии и увеличивает требования только при достижении определенного порогового значения количества.Чтобы включить эту функцию для новой формулы, в группе Расчет потребления измените настройку формулы для применимого ингредиента с Стандартный на Шаг . Этот метод потребления указывается на вкладке Настройка страницы Строка формулы .
Выбирается информация из записи «Шаговое потребление на серию», которая соответствует количеству в заказе партии. Поэтапное потребление полезно, когда скорость потребления не является линейной по отношению к размеру заказа партии и увеличивает требования только при достижении определенного порогового значения количества.Чтобы включить эту функцию для новой формулы, в группе Расчет потребления измените настройку формулы для применимого ингредиента с Стандартный на Шаг . Этот метод потребления указывается на вкладке Настройка страницы Строка формулы .
Ch 12,13,14,15 16-Ready-2017 Таблицы формул пружин – ENGR 2302-
Формулы и уравнения
Глава12
Среднее значение
(всегдаположительные номера)
(может быть отрицательным, положительным или нулевым)
Движение снаряда
(X -Направление) (Y-направление)
2
Ch12. КинематикаОтношения: РектилинейноеДвижение
КинематикаОтношения: РектилинейноеДвижение
(УскорениеПостоянное) (УскорениеПостоянное)
Ch12.КинематикаОтношения: ОбщееДвижениевкартезианскихкоординатах
(Скорость) (Ускорение)
=> Найдите Величины из Пифагорейской Теоремы. Например:
Ch12.КинематикаОтношения: ОбщеедвижениевNormal-Tangential (n-t) Coordinates
(Velocity) (Acceleration)
=> Где
/
Радиус кривизны, y (x) ist hetrajectory
Ch12. КинематикаОтношения: ОбщиеДвижениевПолярныхкоординатах (2Dкейс)
КинематикаОтношения: ОбщиеДвижениевПолярныхкоординатах (2Dкейс)
(Скорость) (Ускорение)
(PDF) Классические уравнения динамики
246 4 Классические уравнения динамики
С учетом последних двух уравнений в ( ) получаем
SD1
2mr2R2
1CR2
2C1
5mr2R2
1CR2
2CR2
3
D1
10mr2 7R 2
1CR2
2C2R3:
Поскольку обобщенные силы уравнения вина Аппеля (4.123) равны
нулю, задача сводится к интегрированию трех уравнений
@S
@ Ri
D0; i D1; 2; 3:
Последовательно получаем
@S
@ R1
D7
5mr2R1D0; @S
@ R2
D7
5mr2R2D0; @S
@ R3
D2
5mr2R3D0:
Это означает, что P1D! 1Dconst, P2D! 2Dconst, P3D! 3Dconst, то есть
, что вектор! DE1 ! 1CE2! 2CE3! 3 постоянна при движении мяча
в горизонтальной плоскости. ut
ut
Список литературы
1. A.V. B
acklund, Einiges ¨uber Kurven- and Fl achen-transformationen, vol 10 (Lund
Universitets Arsskrift, 1875) (на немецком языке)
2. P. Appell, Trait´edeM´ecanique Rationnelle, vol 4 (Готье-Виллар, Париж, 1893–1896 гг.)
3. PV Воронец, Об уравнениях движения неголономных систем. Мат. Сб. 22, 659–668
(1901)
4. Гольдштейн Х. Классическая механика. (Аддисон-Уэсли, Кембридж, Массачусетс, 1950)
5.Л.Д. Ландау, Э.М. Лифшиц, Механический курс теоретической физики, том 1. (Книга Франклина
Company, Нью-Йорк, 1972)
6. Э. Богомольный, Сов. J. Nucl. Phys. 24. С. 449–454 (1976)
7. Р.М. Миура, Преобразование Баклунда. (Springer, Берлин, 1976)
8. В.И. Арнольд, Математические методы классической механики. (Springer, Berlin, 1989)
9. Маркеев А.Д. Теоретическая механика. (Наука, М., 1990)
10. Бутенин Н.В., Фуфаев Н.А. Введение в аналитическую механику (Наука, М. , 1991)
, 1991)
11.S.T. Торнтон, Дж. Б. Марион, Классическая динамика частиц и систем (Saunders College
Publishers, Нью-Йорк, 1995)
12. Л.Н. Хэнд, Аналитическая механика (Cambridge University Press, Кембридж, 1998)
13. Дж. Бенуа, Т. Саксена, Т. Лукман, Разложение Богомольного для везикул произвольной гениальности.
J.Phys.AMath.Gen.34, 9417 (2001)
14. A.V. Борисов, И. Мамаев, Динамика твердого тела. (Ижевск, R&C Dynamics, 2001)
15.G.J. Сассман, Структура и интерпретация классической механики (MIT, MA, 2001)
16. Л. Грейнер, Классическая механика: системы частиц и гамильтонова динамика (Springer,
Берлин, 2002)
Динамика поступательного движения
Единицы СИ и физические константы
Поступательная динамика исследует поступательное движение объектов и имеет дело с эффектами, которые силы оказывают на движение
Вот (здесь все единицы):
м – масса объекта
– вектор скорости
– вектор линейного ускорения
– вектор импульса
– вектор силы
Общие формулы и определение Определение массы: Масса, м, вещества или тела – это скалярная величина, которая определяет его инерционные и гравитационные свойства. Единица массы – килограмм, 1 кг , определяется эталоном массы как удельный платино-иридиевый цилиндр
Единица массы – килограмм, 1 кг , определяется эталоном массы как удельный платино-иридиевый цилиндр
Линейный импульс – вектор, определяемый
Сила – это вектор , заданный
Результирующая сила или результирующая сила из н. сил, приложенных к объекту, определяется векторной суммой
Правило многоугольника для чистой силы для случая n = 3
Некоторые силы в механикеСила тяжести
, где g – ускорение свободного падения
Сила трения
где:
коэффициент трения
N – нормальная составляющая полной силы, действующей на объект с поверхности
Усилие пружины
где:
k – жесткость пружины
x o – длина нерастянутой пружины
x Длина пружины, растянутой силой F
Законы движения Ньютона в инерциальной системе отсчетаИнерциальная система отсчета – это система отсчета, которая находится в состоянии покоя или движется с постоянной скоростью, которая подчиняется Первому закону Ньютона
Первый закон Ньютона
Если тогда, то есть объект находится в равномерном движении или в состоянии покоя
Второй закон Ньютона:
– для общего корпуса
– для постоянной массы
Третий закон Ньютона
где: – сила на массу m 1 , приложенная массой m 2 , и – сила на массу m 2 , приложенная массой m 1 , как показано на диаграмме ниже
Закон сохранения количества движенияПолный импульс системы из n частиц определяется векторной суммой
где – импульс и -й частицы с массой и скоростью
Закон сохранения количества движения
Если, то
где – равнодействующая всех внешних сил, приложенных к системе частиц
Полностью неупругое столкновение – это столкновение, после которого объекты движутся вместе как одно тело
Скорость после неупругого столкновения
Полностью упругое столкновение – это столкновение, при котором общая механическая энергия сохраняется при столкновении
Столкновение для однонаправленного движения:
Скорости объектов после столкновения:
где – коэффициент восстановления
Для полностью упругого столкновения
При полностью неупругом ударе
Теорема об импульсе-импульсе
Импульс силы
где – средняя сила, действующая на объект в течение интервала времени, заданного интегралом
.
Теорема об импульсе-импульсе
где и – начальный и конечный импульсы объекта соответственно
Движение центра масс системы частиц
Вектор положения центра масс n частиц:
где:
и – масса и радиус-вектор положения i -й частицы
– полная масса системы частиц
Вектор скорости центра масс
Второй закон Ньютона для движения центра масс
где – равнодействующая всех внешних сил, приложенных к системе частиц
Движение объекта переменной массы
Где:
м – текущая масса объекта
– текущая скорость объекта
– доверие (или реактивная сила)
– скорость выброшенной массы относительно объекта
Сила тяги
где – скорость изменения массы м
Уравнение движения объекта с переменной массой
Текущая скорость объекта массой м из состояния покоя с исходной массой
Сегодня учебная дисциплина механика включает два компонента: кинематику и динамику.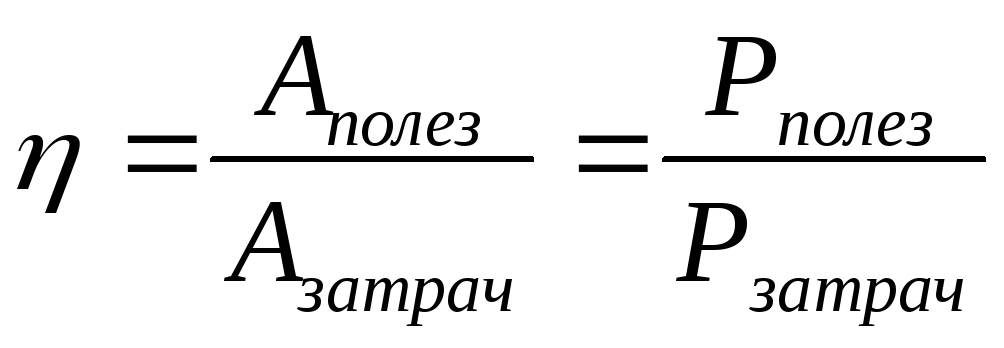 Кинематика – это «геометрия движения», использующая только понятия положения, скорости и ускорения. Динамика вводит понятия массы и силы.
Кинематика – это «геометрия движения», использующая только понятия положения, скорости и ускорения. Динамика вводит понятия массы и силы.
Так называемая «научная революция» 16-17 веков поставила изучение механики на прочную математическую основу с моделями, которые были способны делать предсказания, которые можно было проверить экспериментально.
Коперник и Кеплер моделируют планетную систему.
Гелиоцентрическая модель Солнечной системы Коперника была радикально упрощена (удалены все эпициклы) и поставлена на математически обоснованную основу с тремя законами движения планет Кеплера:
- Каждая планета движется по эллиптической орбите с Солнцем в одном фокусе эллипса.
- Радиус-вектор планеты проходит через равные площади за равное время.
- Квадрат периода обращения планеты равен кубу ее среднего орбитального радиуса.
Галилей находит законы движения Земли.
Галилей изучал земное движение тел с постоянным ускорением, включая падающие тела и снаряды. Он определил понятие ускорения и нашел три закона постоянно ускоряющегося движения:
Он определил понятие ускорения и нашел три закона постоянно ускоряющегося движения:
- d = (т / 2) (v или + v)
- d = v o t + (1/2) a t 2
- v 2 = v o 2 + 2 а • д
Ньютоновская динамика.
Ньютон смотрел на движение в более общем смысле. Его великим достижением было объединить понимание движения, включив в него как земные (земные), так и небесные (небесные) движения. Он ввел (точнее, уточнил и прояснил) два понятия: масса и сила. Мы формулируем его три закона, используя несколько современный язык.
- Покоящееся тело остается неподвижным, если на него не действует сила. Объект в состоянии равномерного движения остается в этом состоянии движения, если на него не действует внешняя сила.
- Когда на тело действует внешняя сила, оно ускоряется. Соотношение между силой и ускорением составляет F = м a .

- Когда тело A воздействует на тело B, тогда B оказывает равное и противоположно направленное усилие на A.
Мы можем изложить содержание этих законов более компактно в виде уравнений:
Сила и ускорение являются векторными величинами, поэтому мы указываем этот факт жирным шрифтом.Масса – это скалярная величина.
Компактная система обозначений – это хорошо, но мы всегда должны делать больше, чем просто запоминать уравнения. Я должен четко понимать (а) значение каждого символа и (б) любые ограничения на уравнения. То есть нам нужно знать контекст, в котором применяются уравнения.
Здесь абсолютно важно, что мы думаем, читая первое уравнение: «Чистая (векторная сумма) всех сил, действующих на массу, равна этой массе, умноженной на ускорение этой массы.«Слишком часто студенты включают силы, действующие на какую-то другую массу, или забывают найти векторную сумму всех сил, действующих на рассматриваемое тело. Обратите внимание, что две силы во втором уравнении действуют на различных тел.
Обратите внимание, что две силы во втором уравнении действуют на различных тел.
Эти законы кажутся достаточно невинными, но содержат огромное количество информации и идей. Философы обсудили значение F = м, – большая длина . Это определение силы? Это определение массы? Это закон природы? Можно возразить, что это все три сразу.Третий закон не менее важен и абсолютно необходим для осмысленного применения первых двух законов. Позже мы увидим, что третий закон играет важную роль в законе сохранения количества движения. Точно так же третье уравнение Галилея приближается к концепциям работы и кинетической энергии, если объединить его с уравнением Ньютона F = м а .
Закон тяготения Ньютона.
Работа Галилея показала, что тела около Земли имеют постоянное ускорение, направленное к Земле.Атмосфера мысли о небесных и земных законах менялась, и теперь люди задавали такие вопросы, как «Что заставляет планеты двигаться?» и «Что удерживает Луну на своей орбите?» Задавая такие вопросы, мы предполагаем, что есть основная причина, аналогичная причинам движения снаряда.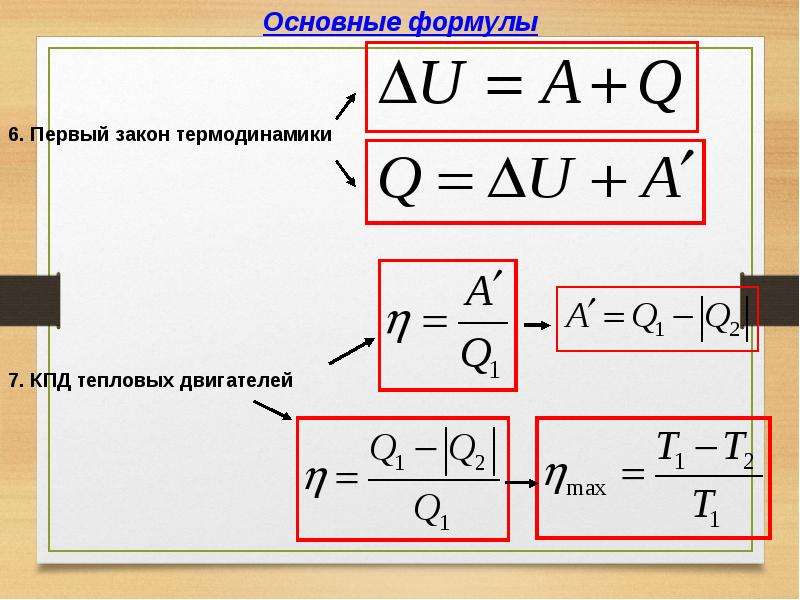 Конечно, ни у кого не было причин для этого, но многие начинали подозревать, что существуют объединяющие принципы и законы, которые могут охватывать как земные, так и небесные явления.
Конечно, ни у кого не было причин для этого, но многие начинали подозревать, что существуют объединяющие принципы и законы, которые могут охватывать как земные, так и небесные явления.
|
Ньютон обдумывал вопрос о том, что удерживает Луну на ее орбите, и ответ не пришел во вспышке озарения, когда он наблюдал, как яблоко упало с дерева. Но в конце концов он пришел к выводу, что Луна движется по круговой орбите, потому что она постоянно падает на Землю. В одной из своих статей он показывает замечательную картинку, иллюстрирующую это и прекрасно связывающую орбиту Луны с траекториями пушечного ядра Галилея.
Представьте себе невероятно высокую гору на земле, как показано на рисунке.Пушечное ядро, выпущенное с вершины горы, упало бы на землю, но если бы оно было выпущено с большей скоростью, у него была бы большая дальность. Если бы можно было как-то увеличить скорость выстрела, он упал бы на круговую орбиту полностью вокруг Земли. Луна падает по такой почти круговой орбите.
Если бы можно было как-то увеличить скорость выстрела, он упал бы на круговую орбиту полностью вокруг Земли. Луна падает по такой почти круговой орбите.
Если скорость выстрела пушечного ядра еще больше, оно могло бы двигаться по эллиптической орбите. Эта диаграмма иллюстрирует идею о том, что все эти движения вызваны одной и той же причиной – ускорением вниз, то есть всегда направленным к центру Земли.
Аристотель считал движение к Земле «естественным», не требующим силы. Для Аристотеля прямолинейное движение было бы «неестественным» и требовало силы. Ньютон переворачивает это с ног на голову, говоря, что прямолинейное движение не требует силы, в то время как все другие пути требуют силы. Далее он говорит, что эта сила всегда направлена в направлении ускорения и связана с ускорением на F = м a . Тела падают на землю, потому что земля оказывает на них силу.Эту силу мы называем силой тяжести . Ньютон разработал закон этой силы, свой закон всемирного тяготения. В нем говорится, что величина гравитационной силы, которую одно тело оказывает на другое тело, пропорциональна произведению масс двух взаимодействующих тел, разделенных на квадрат расстояния между ними.
В нем говорится, что величина гравитационной силы, которую одно тело оказывает на другое тело, пропорциональна произведению масс двух взаимодействующих тел, разделенных на квадрат расстояния между ними.
M и m – массы двух тел, а R – расстояние их разделения. G – это «универсальная гравитационная постоянная». Сила, которую испытывает каждое тело, направлена на другое тело.Его размер F г . Силы, действующие друг на друга, имеют одинаковую величину и противоположно направлены, что удовлетворяет третьему закону Ньютона.
G – универсальная гравитационная постоянная.
- G = 6,67300 10 -11 м 3 кг -1 с -2
Сила, действующая на каждое тело взаимодействующей пары, имеет одинаковый размер, и сила, действующая на каждое тело, направлена в сторону другого тела . Следовательно, они равного размера и противоположного направления, как того требует третий закон Ньютона.
Довольно много людей в то время подозревали, что существует такая гравитационная сила, и даже предполагали, что она может иметь обратную квадратичную зависимость от расстояния (1 / r 2 ).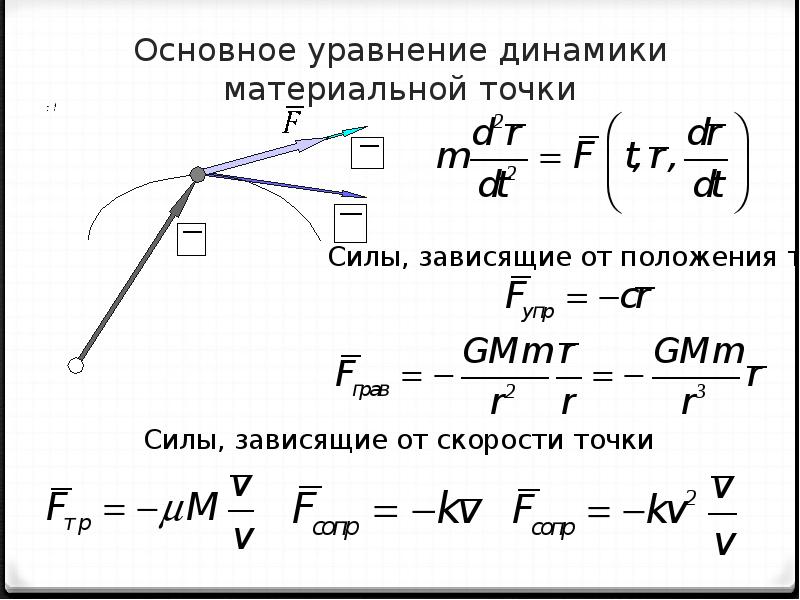 Роберт Гук, Эдмунд Галлей и Кристофер Рен думали в этом направлении. Но именно Ньютон «тщательно продумал детали» и превратил это во всеобъемлющую и объединяющую систему механики, сверяя предсказания с астрономическими данными. Он также изобрел новые математические методы, исчисления, чтобы помочь ему в разработке теории и расчетов.Одна из причин, по которой «Принципы » Ньютона потребовалось так много времени для публикации, заключалась в том, что предсказания для Луны не оправдались. Оказалось, что данные, которые предоставил Ньютон, были не очень точными, и когда он получил более точные данные, предсказания его теории совпали с данными.
Роберт Гук, Эдмунд Галлей и Кристофер Рен думали в этом направлении. Но именно Ньютон «тщательно продумал детали» и превратил это во всеобъемлющую и объединяющую систему механики, сверяя предсказания с астрономическими данными. Он также изобрел новые математические методы, исчисления, чтобы помочь ему в разработке теории и расчетов.Одна из причин, по которой «Принципы » Ньютона потребовалось так много времени для публикации, заключалась в том, что предсказания для Луны не оправдались. Оказалось, что данные, которые предоставил Ньютон, были не очень точными, и когда он получил более точные данные, предсказания его теории совпали с данными.
Тем не менее, многие критики жаловались, что Ньютон до сих пор не объяснил гравитацию, а только дал ей закон. Ответ Ньютона был классическим: «Я не притворяюсь [не изобретаю] никаких гипотез». Он имел в виду, что не собирался строить предположения о причине, изобретая фиктивные «причины», поскольку этого было достаточно, чтобы иметь правильный набор законов. Других критиков беспокоило само представление о том, что тела могут оказывать влияние друг на друга без посредничества между ними. Они назвали эту силу «оккультной силой», поскольку она казалась мистической или магической. Фактически, это было оккультизмом, поскольку «оккультизм» означает «скрытый».
Других критиков беспокоило само представление о том, что тела могут оказывать влияние друг на друга без посредничества между ними. Они назвали эту силу «оккультной силой», поскольку она казалась мистической или магической. Фактически, это было оккультизмом, поскольку «оккультизм» означает «скрытый».
У французского философа Рене Декарта была конкурирующая теория. Он объяснил, что все силы между планетами возникают из-за промежуточной среды, «эфирного» вещества, и он даже постулировал свойства этого эфира, чтобы учесть как гравитационные, так и магнитные силовые взаимодействия.Вы редко встретите упоминание о нем в учебниках, потому что он умер ранней смертью. Это была грандиозная умозрительная теория всего философа, но ей не хватало деталей и дисциплины, чтобы делать какие-либо твердые и проверяемые предсказания. Если бы я подробно описал это здесь, вы бы сочли это довольно сумасшедшей теорией. Даже философ Вольтер, который также был французом, не мог проглотить теорию Декарта, предпочитая ей теорию Ньютона.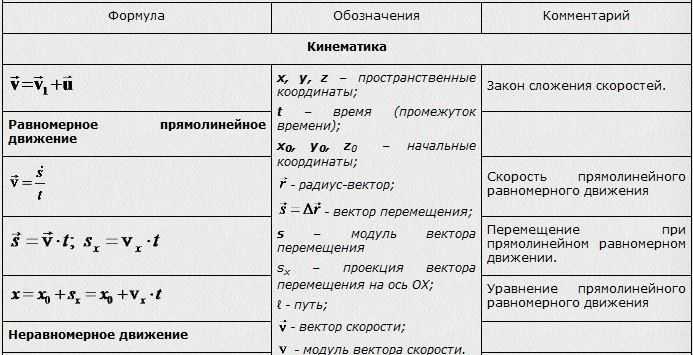 Декарт пытался заниматься физикой так же, как Аристотель, с большим количеством спекуляций и очень слабым контактом с реальным миром точных данных.Но другие натурфилософы продвинулись дальше этого метода, и идеи Декарта не имели никакого влияния. Христиан Гюйгенс упрекнул Декарта, заявив, что если бы Декарт только читал и понимал произведения своих современников, он бы не сделал таких ошибок.
Декарт пытался заниматься физикой так же, как Аристотель, с большим количеством спекуляций и очень слабым контактом с реальным миром точных данных.Но другие натурфилософы продвинулись дальше этого метода, и идеи Декарта не имели никакого влияния. Христиан Гюйгенс упрекнул Декарта, заявив, что если бы Декарт только читал и понимал произведения своих современников, он бы не сделал таких ошибок.
Ньютон также считал, что пространство заполнено “эфирной” субстанцией, но он не разработал детальную теорию этого явления и не использовал эту идею при формулировании своей механики! Мы увидим возрождение идеи эфира в 19 веке до такой степени, что она стала объектом лабораторных экспериментов и многих теоретических рассуждений, только чтобы снова умереть в начале 20 века, когда Альберт Эйнстин разработал теорию относительности, и, как Ньютон, Эйнштейн сделал это. не использовать идею эфира.Это не играло никакой роли в его теории. Этот факт показал, что идея эфира просто не была необходима для понимания физических явлений и никогда не была необходимой. Но об этом позже.
Но об этом позже.
Круговое движение.
В качестве примера силы ньютоновской механики мы рассматриваем проблему кругового движения.
Ускорение тела – это изменение его скорости, деленное на длительность этого изменения, a = ΔV / Δt .Поскольку скорость является вектором, любое изменение ее размера или направления , или обоих, требует ускорения. Тело, движущееся по кривой траектории, ускоряется, даже если его скорость постоянна. Следовательно, из закона Ньютона мы знаем, что результирующая сила, действующая на него, не равна нулю.
На схеме показано тело, движущееся с постоянной скоростью V по криволинейной траектории с радиусом R . Показаны два положения, во время которых тело переместилось на расстояние S по дуге.В начале временного интервала скорость тела равна В 1 . В конце интервала это V 2 .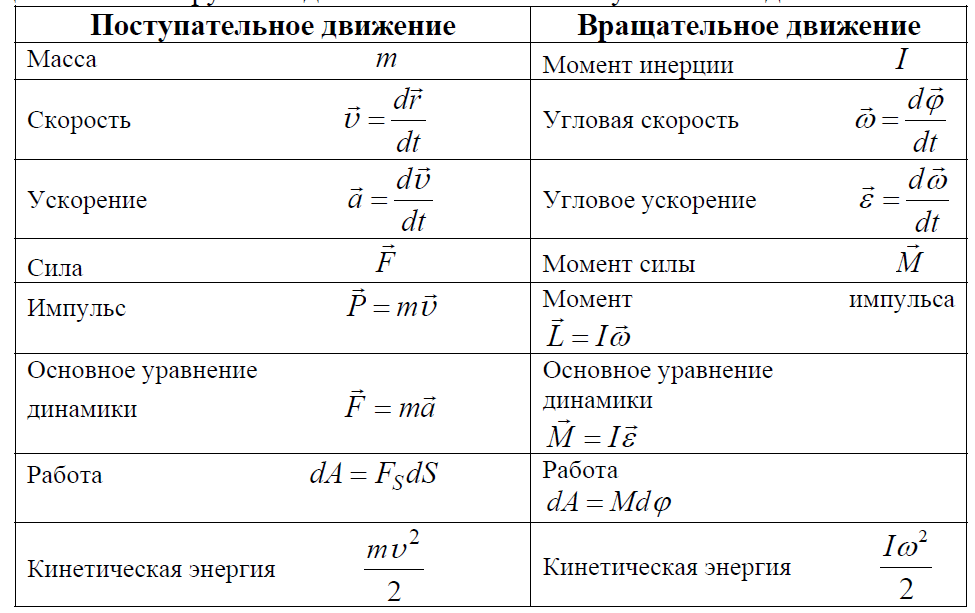 Мы даем им отличительные индексы, потому что они имеют разные направления, даже
хоть они и имеют одинаковый размер.
За это время тело переместилось на угол α . На
справа мы показываем векторную диаграмму отношения между этими скоростями и их векторной разностью, Δ V .
Мы даем им отличительные индексы, потому что они имеют разные направления, даже
хоть они и имеют одинаковый размер.
За это время тело переместилось на угол α . На
справа мы показываем векторную диаграмму отношения между этими скоростями и их векторной разностью, Δ V .
Теперь рассмотрим предельный случай, когда временной интервал становится очень маленьким, приближаясь к нулю. Угол также приближается к нулю. На диаграммах два одинаковых очень тонких треугольника. Мы можем написать:
Итак:
и:
Но
V = Δ S / Δ t , и V = Δ V / Δ t ,
, поэтому мы можем написать:
, которое становится
Это размер вектора ускорения.Направление вектора ускорения в любой момент направлено внутрь к центру дуги и, следовательно, перпендикулярно вектору скорости в этот момент, который всегда касается кривой.
Мы можем связать это ускорение с внутренней (радиальной) составляющей любой результирующей силы. действует на тело (массой м ). Он имеет размер F радиально = m a = mV 2 / R , и представляет собой вектор, направленный радиально внутрь.
действует на тело (массой м ). Он имеет размер F радиально = m a = mV 2 / R , и представляет собой вектор, направленный радиально внутрь.
Таким образом, Ньютон ответил на важный и трудный вопрос: «Как может гравитационная сила Солнца, действующая на планету, быть причиной кругового движения этой планеты с постоянной скоростью?» Общая идея не была новой, но Ньютон поставил ее на прочную математическую основу. Закон тяготения Ньютона выражал величину силы тяжести между любыми двумя телами. Итак, учитывая гравитационную силу Солнца на Земле, заданную законом Ньютона:
, поскольку это единственная сила, действующая на Землю и радиальная (по направлению к Солнцу), мы используем наш ранее полученный результат, приравнивая:
Итак,
Для круговой орбиты ее длина связана с ее радиусом соотношением c = 2 π R
Время одного оборота (период T) круговой орбиты связано с его скоростью соотношением v = c / T
Объединение последних трех уравнений дает:
Обратите внимание на важную идею. Мы использовали законы Ньютона (так же, как это делал Ньютон), чтобы вывести третий закон Кеплера. Но мы сделали больше: мы вычислили выражение для величины константы пропорциональности.
Мы использовали законы Ньютона (так же, как это делал Ньютон), чтобы вывести третий закон Кеплера. Но мы сделали больше: мы вычислили выражение для величины константы пропорциональности.
Работа, кинетическая энергия, импульс, импульс.
Дальнейшее продвижение шло медленно. История формулировки концепций энергии и импульса сложна, и многие люди борются с этой проблемой. Люди признали, что величина mv 2 (называемая «vis viva», что означает «жизненная сила») была ключом к характеристике движения.Лейбницу обычно приписывают использование этого имени с этим определением в терминах массы и скорости. Возникла еще одна полезная величина, действие , действие , эквивалентное тому, что мы теперь выражаем как произведение энергии и времени. Это слово до сих пор встречается в формулировках третьего закона Ньютона с использованием терминов «действие» и «противодействие». Современному студенту лучше всего избегать этого языка.
Чтобы увидеть, как эти концепции возникают из исходных материалов механики Галилея и Ньютона, давайте немного поиграем с уравнениями.
Предположим, что на тело массы m действует сила, за это время масса перемещается на величину d . Далее предположим, что это единственная сила, действующая на тело. Если мы начнем с третьего уравнения Галилея, v 2 = v o 2 + 2 a • d и использовать Ньютона F = m a решено для a , мы можем исключить a получить v 2 – v o 2 = 2 (F / m ) • d .Умножьте обе стороны на m и разделите обе стороны на 2, чтобы получить:
В современных учебниках это называется теоремой «работа – кинетическая энергия», где (m / 2) v 2 – кинетическая энергия, а F • d – работа, совершаемая силой F при перемещении тела на величину d .
Предположим, что на тело массы m в течение времени Δt действует сила. Используя F = Ньютона m a и определение ускорения Галилео, a = (v – v o ) / Δt получаем F = м (в – v o ) / Δt, которое можно преобразовать в:
Величина m v равна импульсу . Величина F Δt называется импульсом , оказываемым силой, действующей на массу в течение времени Δt. Все уравнение фигурирует в современных учебниках как один из примеров «закона сохранения количества движения». Конечно, это последнее математическое упражнение есть не что иное, как перестановка собственной формы второго закона Ньютона:
Величина F Δt называется импульсом , оказываемым силой, действующей на массу в течение времени Δt. Все уравнение фигурирует в современных учебниках как один из примеров «закона сохранения количества движения». Конечно, это последнее математическое упражнение есть не что иное, как перестановка собственной формы второго закона Ньютона:
Или: «Чистая сила, действующая на тело, равна скорости изменения его количества движения». В версии Ньютона использовалось исчисление, и правая часть выражалась как производная от импульса по времени.
Вы можете сказать: «Что такого особенного в импульсе и кинетической энергии? Оба зависят от скорости и массы. Чем они отличаются. Или они?» Они очень разные . Кинетическая энергия – это скаляр, а импульс – это вектор. Импульс пропорционален векторной скорости. Кинетическая энергия пропорциональна квадрату скорости. Очевидно, что они также имеют разные единицы измерения и размеры. Как только у человека есть четкое определение концепции, эта концепция становится важной для четкого обдумывания проблем. Эти два уравнения очень близки к законам сохранения энергии и импульса, которые говорят нам кое-что важное о том, что происходит во Вселенной, как это происходит и почему некоторые вещи не могут произойти .
Эти два уравнения очень близки к законам сохранения энергии и импульса, которые говорят нам кое-что важное о том, что происходит во Вселенной, как это происходит и почему некоторые вещи не могут произойти .
В курсах физики обычно одна глава посвящена энергии, а другая – импульсу. Некоторые проблемы механики поддаются применению той или иной из этих концепций. Но некоторые проблемы, особенно те, в которых два тела взаимодействуют, требуют одновременного применения обеих концепций для получения ответов.
- – Дональд Э. Симанек, февраль 2005 г.
Перейдите к следующей главе, «Ассиметрическая машина Атвуда». Пример линейной и вращательной кинематики.
Вернуться на страницу содержания Краткий курс классической механики .
Вернитесь на главную страницу Дональда Симанека.
Обзор уравнений Эйлера в гидродинамике | Блог системного анализа
Основные выводы
Уравнения Эйлера в гидродинамике описывают течение жидкости без учета вязкости жидкости.

Уравнения Эйлера получены из уравнений Навье-Стокса или из основных уравнений механики сплошных сред.
Хотя уравнения Эйлера рассматривают до некоторой степени невозможную физическую ситуацию нулевой вязкости, они полезны для описания жидкостей с низкой вязкостью, таких как вода или спирты.
Гидродинамика – это математическая дисциплина, требующая особого внимания к физическому значению дифференциальных уравнений.Среди всех уравнений, используемых в гидродинамике, уравнения Эйлера являются одними из самых простых для работы, особенно в тех пределах, где вязкость и сжимаемость жидкости пренебрежимо малы. Большинство занятий по CFD начинаются с уравнений Эйлера гидродинамики, поскольку они могут давать довольно интуитивно понятные результаты и с ними легче работать, чем с полными уравнениями Навье-Стокса для сжимаемых жидкостей.
Хотя к невязким потокам, описываемым уравнениями Эйлера, проще всего подойти с аналитической точки зрения, они все же достаточно эффективны, чтобы описывать явления потока в различных ситуациях.Сжимаемые и несжимаемые потоки можно рассматривать с помощью уравнений Эйлера, но турбулентность – это теоретический случай, который нельзя рассматривать с помощью этих уравнений. В этой статье мы покажем, как используются уравнения Эйлера, их физическая интерпретация и как они дают важные результаты в почти невязких потоках.
Что такое уравнения Эйлера в гидродинамике?
Уравнения Эйлера – это уравнения движения и неразрывности, которые рассматривают чисто теоретическую задачу гидродинамики, в которой жидкость имеет нулевую вязкость, известную как невязкий поток.Реальные жидкости вязкие, хотя некоторые несжимаемые жидкости с очень низкой вязкостью, такие как вода или спирты, можно очень точно обрабатывать в определенных режимах потока с помощью уравнений Эйлера. По этой причине уравнения Эйлера описывают идеальный случай, когда сопротивление жидкости и диссипация энергии незначительны, что является нефизическим и никогда не будет наблюдаться в действительности. Однако мы можем аппроксимировать уравнения Навье-Стокса с очень низкой вязкостью, чтобы получить уравнения Эйлера.
По этой причине уравнения Эйлера описывают идеальный случай, когда сопротивление жидкости и диссипация энергии незначительны, что является нефизическим и никогда не будет наблюдаться в действительности. Однако мы можем аппроксимировать уравнения Навье-Стокса с очень низкой вязкостью, чтобы получить уравнения Эйлера.
Невязкое приближение
Хотя уравнения Эйлера в гидродинамике нефизичны, их можно использовать для описания ситуации, которую можно было бы считать «почти невязкой», в которой силы сопротивления намного меньше любых приложенных извне сил.В этом режиме потока уравнения Эйлера могут быть быстро выведены из уравнений Навье-Стокса. Во-первых, мы можем указать на вязкие члены в уравнении движения Навье-Стокса:
Импульсная часть уравнений Навье-Стокса для вязких сжимаемых течений
В этом уравнении движения второе и третье члены в правой части этого уравнения (пропорциональные μ и λ соответственно) описывают влияние вязкости на сдвиг и диссипацию энергии. Это вязкие термины, которые необходимо удалить, чтобы описать невязкое течение. Это приводит к четырем случаям, когда такое приближение действительно:
Это вязкие термины, которые необходимо удалить, чтобы описать невязкое течение. Это приводит к четырем случаям, когда такое приближение действительно:
- Член градиента давления (1-й член на правой стороне) в системе намного больше, чем вязкие члены.
- Массовые силы или гидростатическая сила (4-й член справа) намного больше, чем вязкие.
- Конструкция системы, которая ограничивает жидкость, ограничивает ее движение вихревым потоком, где вектор скорости подчиняется уравнению Лапласа 𝛻2u = 0 и имитирует невязкий поток.
- Условия 1-3 выполнены.
В любом из этих четырех случаев вязкие члены можно игнорировать в приведенном выше уравнении движения, и мы имеем уравнение движения Эйлера:
Импульсная часть уравнений Эйлера для невязких сжимаемых потоков
В В этом уравнении мы установили μ = 0 и λ = 0, хотя последнее условие иногда вызывает споры для почти невязких потоков. Если бы и μ = 0, и λ = 0 были бы физически осуществимы, мы бы имели случай, когда жидкость, которой был придан некоторый импульс, продолжала бы течь вечно и никогда не рассеивала бы свою энергию и не достигла бы равновесия.В действительности, у нас могут быть очень маленькие значения μ и λ, которые необходимы для описания подхода к равновесию, но они не являются критическими для описания потока при высоких градиентах давления.
Если бы и μ = 0, и λ = 0 были бы физически осуществимы, мы бы имели случай, когда жидкость, которой был придан некоторый импульс, продолжала бы течь вечно и никогда не рассеивала бы свою энергию и не достигла бы равновесия.В действительности, у нас могут быть очень маленькие значения μ и λ, которые необходимы для описания подхода к равновесию, но они не являются критическими для описания потока при высоких градиентах давления.
Непрерывность и эйлерова форма
В дополнение к приведенному выше уравнению движения у нас все еще есть знакомое уравнение неразрывности, описывающее сохранение массы:
Уравнение неразрывности, связывающее плотность жидкости и скорость потока
Наконец, мы имеют дополнительное термодинамическое уравнение, которое связано с параметром рассеяния:
Уравнение энтальпии жидкости
Здесь у нас есть уравнение, описывающее материальную производную термодинамической энтальпии h в терминах теплопроводности жидкости k, материальная производная от давления и диссипации, вызванной вязкостью. В случае, когда μ = 0 и λ = 0, третий член в правой части приведенного выше уравнения исчезает, что означает отсутствие затухания движения в системе.
В случае, когда μ = 0 и λ = 0, третий член в правой части приведенного выше уравнения исчезает, что означает отсутствие затухания движения в системе.
Если мы возьмем все вышеперечисленные уравнения вместе, мы можем записать их в общей форме, известной как форма Эйлера:
Уравнения Эйлера для сжимаемых жидкостей, записанные в форме Эйлера
Здесь e равно внутренняя энергия на единицу массы жидкости. Приведенная выше система уравнений действительна для сжимаемых или несжимаемых невязких потоков.
Вышеупомянутая нефизическая проблема с диссипацией и еще одна проблема означает, что уравнения Эйлера являются только приближением и не могут легко рассматривать конкретный тип потока: турбулентность.
Заметка о турбулентности
Вспоминая на мгновение определение числа Рейнольдса, действительно невязкий поток установил бы число Рейнольдса для жидкости равным бесконечности. Очевидно, что такой случай никогда бы не существовал в действительности, поэтому у нас есть проблема, когда невязкий поток является ламинарным только в том случае, если скорость жидкости равна нулю или его масштаб длины равен нулю, т.е.е., потока не существует!
Очевидно, что такой случай никогда бы не существовал в действительности, поэтому у нас есть проблема, когда невязкий поток является ламинарным только в том случае, если скорость жидкости равна нулю или его масштаб длины равен нулю, т.е.е., потока не существует!
Здесь для описания потока должны использоваться очень слабовязкие приближения, то есть влияние вязкости каким-то образом учитывается путем переноса конкретных значений для μ и λ в некоторых из приведенных выше уравнений. Мы все еще можем получить поле потока, а для ситуаций с низкоскоростным потоком мы сможем определить число Рейнольдса, которое может перевести поток в ламинарный режим. Однако мы можем легко увидеть турбулентность в такой жидкости, поскольку может потребоваться более высокий градиент давления, чтобы гарантировать сохранение невязкого приближения в уравнениях Эйлера.
Пакеты CFD-моделирования для невязких потоков
В то время как предельные случаи вышеуказанных уравнений могут быть решены вручную в простых системах, трехмерные системы со сложной геометрией обычно необходимо обрабатывать с помощью числового решателя. Коммерческие пакеты моделирования CFD предоставляют несколько моделей и алгоритмов для расчета решений этих проблем. Эти приложения могут помочь ускорить проектирование и оценку сложных потоков, включая почти невязкие потоки, которые можно надлежащим образом описать с помощью уравнений Эйлера.
Коммерческие пакеты моделирования CFD предоставляют несколько моделей и алгоритмов для расчета решений этих проблем. Эти приложения могут помочь ускорить проектирование и оценку сложных потоков, включая почти невязкие потоки, которые можно надлежащим образом описать с помощью уравнений Эйлера.
Полный набор инструментов анализа и моделирования в Omnis 3D Solver от Cadence идеально подходит для определения и выполнения моделирования CFD для решения уравнений Эйлера в гидродинамике с использованием современных численных подходов. Система Omnis также может обрабатывать сжимаемые потоки с турбулентностью в сложных системах, обеспечивая более глубокое представление о турбулентности в почти невязких жидкостях. В пакете моделирования Cadence данные физического проектирования используются для построения сетки при моделировании CFD; вам не нужно вручную строить сетки или создавать алгоритмы генерации.
Подпишитесь на нашу рассылку для получения последних обновлений CFD или просмотрите пакет программного обеспечения CFD Cadence, чтобы узнать больше о том, как Cadence предлагает решение для вас.
CFD Software Подпишитесь на нашу рассылку новостей
Particle Dynamic – обзор
1.18.2.1.2 Динамика диссипативных частиц
DPD, впервые представленный Hoogerbrugge and Koelman (1992), как ожидается, будет подходить для промежуточного диапазона масштабов длины. Его связь с МД, а также с методами континуума была исследована (Flekkoy and Coveney 1999, Flekkoy et al. 2000). DPD – это метод мезоскопического моделирования, способный преодолеть разрыв между атомистическим и мезоскопическим моделированием (Groot and Warren 1997).
По сути, DPD – это обработка динамики квазичастиц, представляющих небольшие наборы молекул жидкости, с помощью стохастических дифференциальных уравнений, аналогичных подходу Ланжевена. Он сочетает в себе черты методов МД и решеточного газа. Рисунок 2 представляет собой схематическое представление контекста, в котором DPD должен рассматриваться по сравнению с другими методами моделирования.С момента своего первого внедрения этот метод применялся для моделирования широкого спектра явлений, особенно в материаловедении.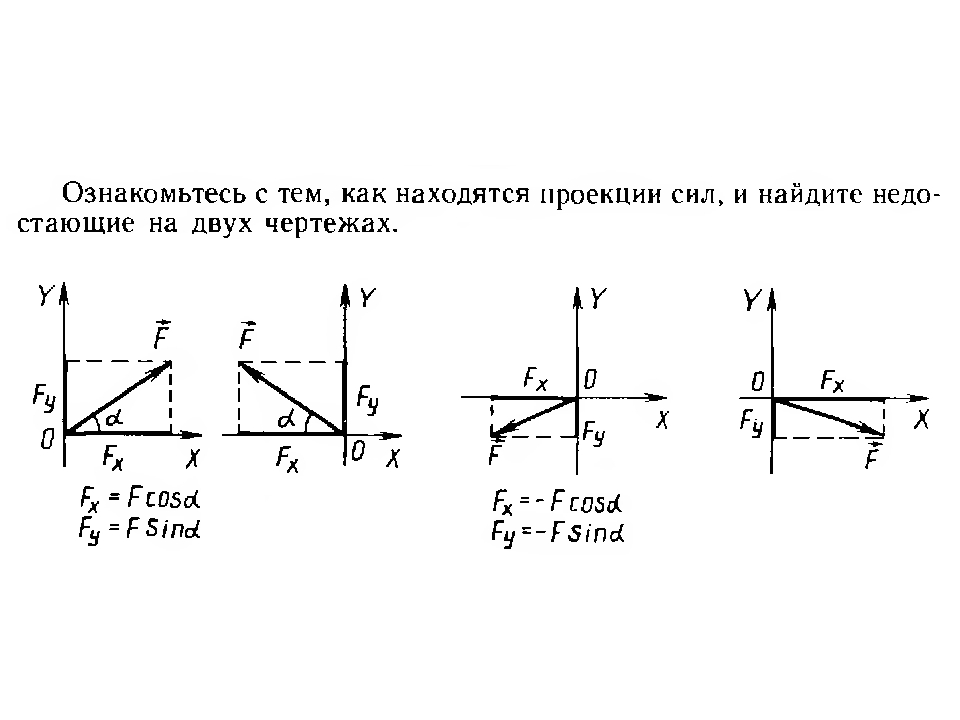 Были проведены тщательные исследования, чтобы понять возможности DPD в применении к вычислительной гидродинамике. В последнее время DPD испытывает растущий интерес различных исследовательских групп к его усовершенствованию в нескольких аспектах. Его алгоритмическая оптимизация была одним из основных направлений, что сделало его подходящим методом для применения в инженерных областях (Kauzlaric et al. 2005). Учет сохранения энергии и импульса во взаимодействии частицы с частицами для набора стохастических дифференциальных уравнений, описывающих модели DPD, является важным расширением для приложений теплового потока. Недавно были включены модели с фазовым переходом, основанные на энергосберегающих моделях DPD (DPDE). Фазовый переход твердое тело – жидкость и сосуществование жидкости – пара можно моделировать с помощью DPD, не отказываясь от всех преимуществ метода, которые возникают из-за использования больших временных шагов, чем в MD.
Были проведены тщательные исследования, чтобы понять возможности DPD в применении к вычислительной гидродинамике. В последнее время DPD испытывает растущий интерес различных исследовательских групп к его усовершенствованию в нескольких аспектах. Его алгоритмическая оптимизация была одним из основных направлений, что сделало его подходящим методом для применения в инженерных областях (Kauzlaric et al. 2005). Учет сохранения энергии и импульса во взаимодействии частицы с частицами для набора стохастических дифференциальных уравнений, описывающих модели DPD, является важным расширением для приложений теплового потока. Недавно были включены модели с фазовым переходом, основанные на энергосберегающих моделях DPD (DPDE). Фазовый переход твердое тело – жидкость и сосуществование жидкости – пара можно моделировать с помощью DPD, не отказываясь от всех преимуществ метода, которые возникают из-за использования больших временных шагов, чем в MD.
Рис. 2. Модель DPD в контексте других методов моделирования. Б.Д., Броуновская динамика; CFD, вычислительная гидродинамика; DPD, диссипативная динамика частиц; SPH, гидродинамика сглаженных частиц. Получение мезоскопической техники из микроскопической или макроскопической техники из мезоскопической обычно включает в себя некую проекцию (усреднение).
Б.Д., Броуновская динамика; CFD, вычислительная гидродинамика; DPD, диссипативная динамика частиц; SPH, гидродинамика сглаженных частиц. Получение мезоскопической техники из микроскопической или макроскопической техники из мезоскопической обычно включает в себя некую проекцию (усреднение).
Кратко опишем основные ингредиенты DPD. Каждая диссипативная частица i с ее положением r i и ее импульсом p i или ее скоростью v i распространяется согласно закону Ньютона с силой F. i , действующий на частицу.Таким образом, уравнения движения задаются следующим образом:
[18] ri = vi
[19] vi = Fi = ∑j ≠ i (FijC + FijD + FijR)
, где сила имеет три основных вклада из-за других частицы в потоке, а именно консервативная часть F C , диссипативный вклад F D и флуктуирующая сила F R . Последние два определены как
Последние два определены как
[20] FijD = −γijw [rij] (eij⋅vij) eij
[21] FijR = σijw1 / 2 [rij] eijξij [t]
, где γ и σ – диссипация сила и амплитуда колебаний соответственно.wrij – это весовая функция расстояния rij между двумя рассеивающими частицами i и j , а e ij – это единичный вектор, указывающий от частицы i к частице j и v ij – относительная скорость двух частиц. ξij [t] описывает гауссовский белый шум согласно следующему уравнению:
[22] 〈ξij [t]〉 = 0
[23] 〈ξiji [t] ξi′j ′ (t ′)〉 = (δii ′ δjj ′ + δij′δji ′) δ [t − t ′]
Моделирование свойств материала выполняется в DPD путем корректировки параметров, вводящих силы, указанные в уравнении [19].Это γ и σ, они образуют консервативный потенциал. Преимущество в вычислительных усилиях достигается только в том случае, если F C является мягким отталкивающим потенциалом.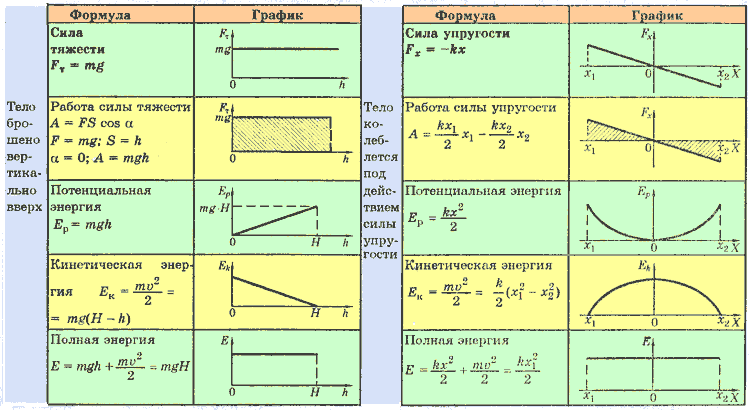 Это позволяет использовать гораздо большие временные шаги, чем в MD. С другой стороны, отсутствие привлекательной детали в F C не допускает свободного поверхностного потока. Следовательно, часть, зависящая от плотности, должна быть добавлена к консервативному потенциалу, учитывающему избыточную поверхностную энергию, для описания границ раздела жидкость-газ.Поскольку это расширение простой модели DPD на поведение многих тел, в литературе она называется MDPD (например, Paganobarraga and Frenkel 2001).
Это позволяет использовать гораздо большие временные шаги, чем в MD. С другой стороны, отсутствие привлекательной детали в F C не допускает свободного поверхностного потока. Следовательно, часть, зависящая от плотности, должна быть добавлена к консервативному потенциалу, учитывающему избыточную поверхностную энергию, для описания границ раздела жидкость-газ.Поскольку это расширение простой модели DPD на поведение многих тел, в литературе она называется MDPD (например, Paganobarraga and Frenkel 2001).
До сих пор мы рассматривали только изотермический DPD даже с его расширением до MDPD. Чтобы включить тепловые свойства материала, необходимо учитывать внутреннюю энергию отдельной диссипативной частицы и ее взаимодействия с поступательными степенями свободы. Внутренняя энергия в качестве примера расширения DPD до DPDE (например, Pastewka et al. 2006) изобретает способ введения различных других степеней свободы. Ясно, что их уравнения движения должны быть связаны с уравнениями существующих степеней свободы, и это задача для моделирования материалов.

 Если создать сводную диаграмму на основе данных из сводной таблицы, то значения на диаграмме будут соответствовать вычислениям в связанной сводной таблице.
Если создать сводную диаграмму на основе данных из сводной таблицы, то значения на диаграмме будут соответствовать вычислениям в связанной сводной таблице. Значение на пересечении столбца Апрель и строки Север — это общая выручка от продаж, определенная по исходным данным, для которых столбец Месяц содержит значение Апрель, а столбец Регион — значение Север.
Значение на пересечении столбца Апрель и строки Север — это общая выручка от продаж, определенная по исходным данным, для которых столбец Месяц содержит значение Апрель, а столбец Регион — значение Север. Эти функции доступны для всех типов исходных данных, кроме OLAP.
Эти функции доступны для всех типов исходных данных, кроме OLAP.
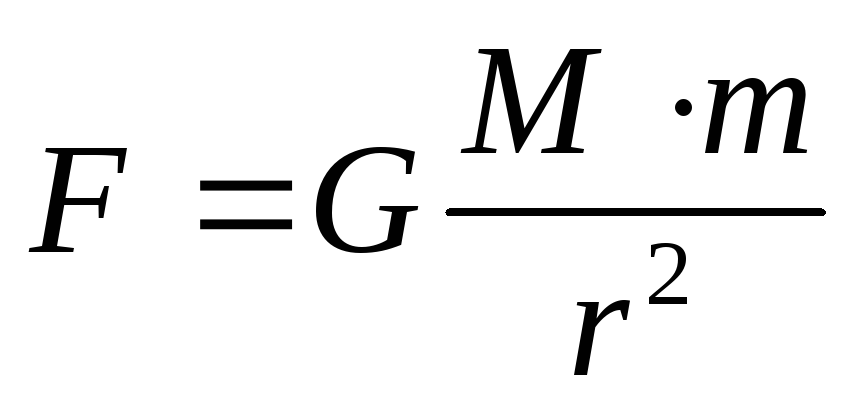
 Например, можно отобразить значения в поле данных Сумма продаж как процент от продаж за месяц Март или как нарастающий итог по элементам в поле Месяц.
Например, можно отобразить значения в поле данных Сумма продаж как процент от продаж за месяц Март или как нарастающий итог по элементам в поле Месяц.





 Например, если в отчете есть два элемента с именем “Мясо” в полях “Тип” и “Категория”, можно избежать появления ошибок #ИМЯ?, ссылаясь на эти элементы следующим образом: Тип[Мясо] и Категория[Мясо].
Например, если в отчете есть два элемента с именем “Мясо” в полях “Тип” и “Категория”, можно избежать появления ошибок #ИМЯ?, ссылаясь на эти элементы следующим образом: Тип[Мясо] и Категория[Мясо]. Если текущим регионом является Север, то Регион[+1] — это Юг. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.
Если текущим регионом является Север, то Регион[+1] — это Юг. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Например, для вычисляемого объекта можно использовать формулу =Регион[-1] * 3%. Если позиция, которую вы указали, находится перед первым или после последнего элемента в поле, формула возвращает ошибку #ССЫЛКА!.