Олимпиада по химии 2019-20 • Формула Единства
В 2019–20 учебном году впервые проводится «Формула Единства» / «Третье тысячелетие» по химии!
К участию в олимпиаде приглашаются российские школьники 8–11 классов. Участие в олимпиаде бесплатное.
Организатор олимпиады — Фонд Эйлера.
Контакты
Ключевые даты
- Отборочный этап: 20 октября — 2 декабря 2019.
- Публикация результатов отборочного этапа: 10 декабря 2019.
- Апелляция отборочного этапа: 11 — 15 декабря 2019.
- Заключительный этап: 16 февраля 2020.
Официальные документы
Окончательные итоги
Апелляция окончена, так что время подвести окончательные итоги первой химической олимпиады «Формула Единства»/«Третье тысячелетие»!
Хронология событий
Все новости олимпиады будут публиковаться ниже от более новых к более старым.
Публикуем предварительные результаты и решения задач заключительного этапа:
Не позднее 23:59 29 марта по московскому времени участники могут запросить работу и/или подать апелляцию (запрос на пересмотр решения определённой задачи). Для этого нужно прислать письмо на адрес жюри (olimp.[email protected]formulo.org), указав в теме письма номер класса. В тексте письма напишите «Запрос работы» или «Апелляция по задаче №…», укажите свои фамилию и имя. Обратите внимание, что в результате апелляции баллы за решение могут как увеличиться, так и снизиться.
Если Вы обнаружили, что результаты участника заключительного этапа отсутствуют или есть ошибка в персональных данных, просим безотлагательно сообщить об этом в жюри.
Решение о присуждении дипломов будет принято при подведении окончательных итогов (31 марта).
Публикуем полный список участников заключительного этапа. Для каждого участника указана площадка, на которую он приглашён. (Указан только город; полный адрес площадки содержится в ранее опубликованной таблице. Внимание! Исправлена ошибка в адресе гимназии №93 Челябинска.)
Для каждого участника указана площадка, на которую он приглашён. (Указан только город; полный адрес площадки содержится в ранее опубликованной таблице. Внимание! Исправлена ошибка в адресе гимназии №93 Челябинска.)
До заключительного этапа олимпиады осталось меньше недели! Публикуем правила участия и проведения:
Публикуем текущий список площадок заключительного этапа, который запланирован на 16 февраля. В него будут вноситься дополнения и уточнения, поэтому предлагаем проверить наличие обновлённой информации на сайте за 1–2 дня до проведения заключительного этапа.
Обратите внимание! Файл был обновлен 14 февраля .
Уважаемые участники заключительного этапа олимпиады!
В связи с многочисленными вопросами спешим сообщить — в данный момент ведутся переговоры с потенциальными площадками для проведения заключительного этапа.
Полный список площадок будет вывешен здесь ориентировочно 30 января. Также информация о заключительном этапе будет выслана по электронной почте.
Уважаемые участники олимпиады!
Апелляция окончена, и жюри спешит опубликовать список участников, приглашенных на заключительный этап:
Спасибо всем за участие и до встречи на заключительном этапе 16 февраля 2020!
Уважаемые участники отборочного этапа!
Жюри завершило проверку поступивших работ. В полночь по МСК вам были высланы набранные Вами баллы по электронной почте.
Если вы не согласны с результатами оценки вашей работы и считаете, что за ваше решение вам полагается больше баллов, то в период до 15 декабря включительно вы можете подать апелляцию. В этом случае Вам необходимо оценить самостоятельно задачу в соответствии с критериями и отправить нам письмо с указанием своих данных, номера задачи и подсчётом баллов по критериям (это и будет вашей аргументацией, дополнительные пояснения не требуются).
Обратите внимание, что при оценке действует система первичных и вторичных баллов. Сначала баллы суммируются в соответствии с критериями (первичный балл), затем умножаются на коэффициент, указанный в условиях и решениях (вторичный). Письма без аргументации рассматриваться не будут.
По окончании апелляции оргкомитет опубликует список прошедших на заключительный этап. Проходные баллы:
| 8 класс | 9 класс | 10 класс | 11 класс |
| 30 баллов | 50 баллов | 40 баллов | 19 баллов |
Отборочный этап первой олимпиады по химии завершен 🙁
В нем приняли участие больше 100 человек из 23 регионов страны, а также из Беларуси, Узбекистана и Турции.
Жюри приступило к проверке работ. Результаты ожидаются 10 декабря несмотря на продление приема.
Отборочный этап продлевается на 5 дней. Отправить свою работу можно до 2 декабря включительно!
Участники, уже отправившие нам свою работу, могут при желании улучшить её и выслать заново.
Дорогие участники олимпиады!
Исключительно для Вас было решено отсрочить повышение базовой стоимости участия в зимних сменах «Формулы Единства» 2020 в д. Гарболово и г. Геленджике до 16 ноября включительно при подаче заявки на химию!
Все подробности смотрите в анонсах смен:
Перед Вами задачи отборочного этапа олимпиады.
Помните, что решение задачи должно включать не только правильный ответ, но и полное обоснование этого ответа. Мы будем рады, если в олимпиаде примут участие Ваши друзья, которым нравится химия. Однако работы с признаками списывания и «коллективного творчества» рассматриваться не будут.
Условия задач в работу переписывать не нужно. Работа должна быть оформлена на русском языке. Использование других языков должно быть заранее согласовано с организаторами.
Работа должна быть оформлена на русском языке. Использование других языков должно быть заранее согласовано с организаторами.
Обратите внимание, что каждая задача сначала оценивается в первичный балл, который затем переводится во вторичный путем умножения на соответствующий коэффициент. Набор максимальных значений первичного, вторичного баллов, а также коэффициентов для каждой задачи указаны в условиях задач. Суммарный балл, по которому составляется рейтинг участников, складывается из вторичных баллов.
Задачи и порядок отправки их решений
Для участия в химической олимпиаде «Формула Единства» / «Третье тысячелетие» 2019/20 необходимо в срок до 27 ноября 2 декабря 2019 г. включительно подготовить файл с решениями задач и отправить его через специальную анкету:
Загрузить можно как текстовые файлы (в форматах TXT, DOC, DOCX или PDF), так и сканы бумажных работ (в форматах JPG, PNG и PDF). Общее количество файлов не должно превышать 10. В файлах с решениями задач не должны указываться фамилия, имя и другие личные данные участника!
Общее количество файлов не должно превышать 10. В файлах с решениями задач не должны указываться фамилия, имя и другие личные данные участника!
Внимание! Не разрешается использовать одни регистрационные данные для отправки работ нескольких участников. Если Вы учитель и хотите отправить работы нескольких учеников, напишите об этом в оргкомитет, мы предложим удобный способ сделать это.
Вопросы?
Все вопросы Оргкомитету по условиям задач и о порядке проведения Олимпиады можно задать по электронной почте olimp.[email protected]formulo.org или по телефону +7 (953) 345–85-17.
В этом году пройдет первая олимпиада «Формула Единства»/«Третье тысячелетие» по химии! К участию приглашаются 8–11 классы. Следуя традиции остальных олимпиад ФЕ/ТТ, она будет проведена в два этапа:
- отборочный (заочный) этап, который пройдет с 20 октября по 20 ноября — от участников потребуется решить 4 задачи;
- заключительный (очный) этап на региональных площадках в первой половине 2020 года.

Предварительная регистрация не требуется. Вся информация об олимпиаде будет публиковаться на этой странице.
Алгоритм решения задачи 35 (С5). Подготовка к ЕГЭ по химии. Задача №35
В настоящее время на Едином госэкзамене по химии во второй (более сложной) части предлагается шесть заданий. Первые четыре не связаны с количественными расчетами, последние два – это достаточно стандартные задачи.
Этот урок целиком посвящен разбору задачи №35 (С5). Кстати, ее полное решение оценивается в три балла (из 60).
Начнем с несложного примера.
Пример 1. 10,5 г некоторого алкена способны присоединить 40 г брома. Определите неизвестный алкен.
Решение. Пусть молекула неизвестного алкена содержит n атомов углерода. Общая формула гомологического ряда CnH2n. Алкены реагируют с бромом в соответствии с уравнением:
CnH2n + Br2 = CnH2nBr2.
Рассчитаем количество брома, вступившего в реакцию: M(Br
Уравнение показывает, что 1 моль алкена присоединяет 1 моль брома, следовательно, n(CnH2n) = n(Br2) = 0,25 моль.
Зная массу вступившего в реакцию алкена и его количество, найдем его молярную массу: М(CnH2n) = m(масса)/n(количество) = 10,5/0,25 = 42 (г/моль).
Теперь уже совсем легко идентифицировать алкен: относительная молекулярная масса (42) складывается из массы n атомов углерода и 2n атомов водорода. Получаем простейшее алгебраическое уравнение:
12n + 2n = 42.
Решением этого уравнения является n = 3. Формула алкена: C3H
Ответ: C3H6.
Приведенная задача – типичный пример задания №35. 90% реальных примеров на ЕГЭ строятся по аналогичной схеме: есть некоторое органическое соединение X, известен класс, к которому оно относится; определенная масса X способна прореагировать с известной массой реагента Y. Другой вариант: известна масса Y и масса продукта реакции Z. Конечная цель: идентифицировать Х.
Другой вариант: известна масса Y и масса продукта реакции Z. Конечная цель: идентифицировать Х.
Алгоритм решения подобных заданий также достаточно очевиден.
- 1) Определяем общую формулу гомологического ряда, к которому относится соединение Х.
- 2) Записываем реакцию исследуемого вещества Х с реагентом Y.
- 3) По массе Y (или конечного вещества Z) находим его количество.
- 4) По количеству Y или Z делаем вывод о количестве Х.
- 5) Зная массу Х и его кол-во, рассчитываем молярную массу исследуемого вещества.
- 6) По молярной массе X и общей формуле гомологического ряда можно определить молекулярную формулу Х.
- 7) Осталось записать ответ.
Рассмотрим этот алгоритм подробнее, по пунктам.
1. Общая формула гомологического ряда
Наиболее часто используемые формулы сведены в таблицу:
| Гомологический ряд | Общая формула |
| Алканы | CnH2n+2 |
| Алкены | CnH2n |
| Алкины | CnH2n-2 |
| Диены | CnH2n-2 |
| Арены | CnH2n-6 |
| Предельные одноатомные спирты | CnH2n+1ОН |
| Предельные альдегиды | CnH2n+1СОН |
| Предельные монокарбоновые кислоты | CnH2n+1СОOН |
Кстати, нет необходимости механически запоминать формулы всевозможных гомологических рядов.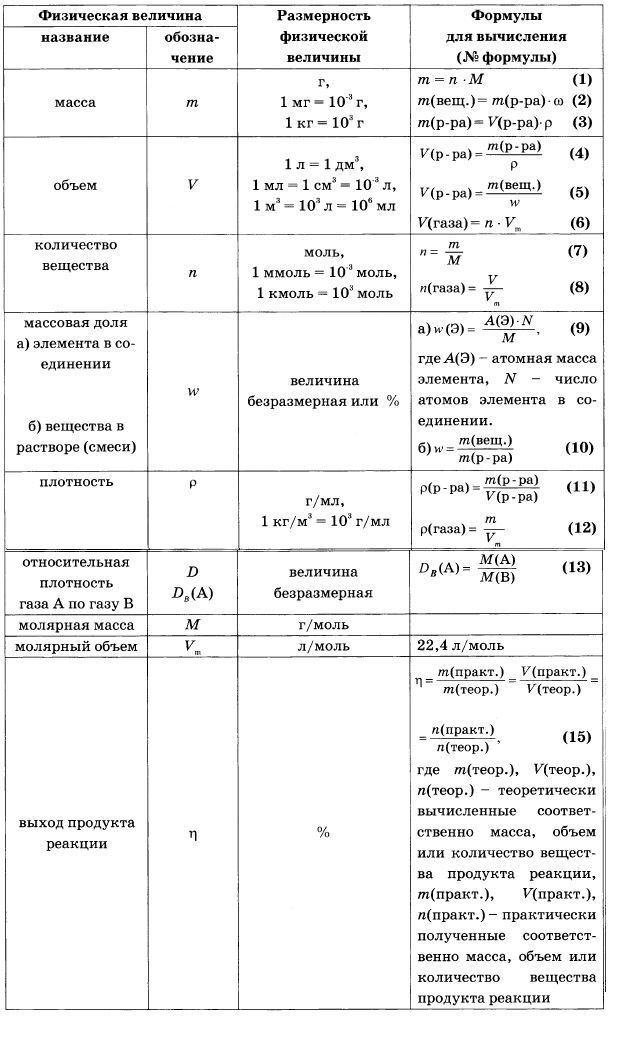
2. Уравнение реакции
Нет надежды, что мне удастся перечислить ВСЕ реакции, которые могут встретиться в задаче 35. Напомню лишь наиболее важные:
1) ВСЕ органические вещества горят в кислороде с образованием углекислого газа, воды, азота (если в соединении присутствует N) и HCl (если есть хлор):
CnHmOqNxCly + O2 = CO2 + H2O + N2
2) Алкены, алкины, диены склонны к реакциям присоединения (р-ции с галогенами, водородом, галогенводородами, водой):
CnH2n + Cl2 = CnH2nCl2
CnH2n + H2 = CnH2n+2
CnH2n + HBr = CnH2n+1Br
CnH2n + H2O = CnH2n+1OH
Алкины и диены, в отличие от алкенов, присоединяют до 2 моль водорода, хлора или галогенводорода на 1 моль углеводорода:
CnH2n-2 + 2Cl2 = CnH2n-2Cl4
C
При присоединении воды к алкинам образуются карбонильные соединения, а не спирты!
3) Для спиртов характерны реакции дегидратации (внутримолекулярной и межмолекулярной), окисления (до карбонильных соединений и, возможно, далее до карбоновых кислот). Спирты (в т.ч., многоатомные) реагируют с щелочными металлами с выделением водорода:
Спирты (в т.ч., многоатомные) реагируют с щелочными металлами с выделением водорода:
CnH2n+1OH = CnH2n + H2O
2CnH2n+1OH = CnH2n+1OCnH2n+1 + H
2CnH2n+1OH + 2Na = 2CnH2n+1ONa + H2
4) Химические свойства альдегидов весьма разнообразны, однако здесь мы вспомним лишь об окислительно – восстановительных реакциях:
CnH2n+1COH + H2 = CnH2n+1CH2OH (восстановление карбонильных соединений в прис. Ni),
CnH2n+1COH + [O] = CnH2n+1COOH
Для последней реакции записана лишь схема, поскольку в качестве окислителей могут выступать разные соединения.
Обращаю внимание на весьма важный момент: окисление формальдегида (НСОН) не останавливается на стадии муравьиной кислоты, НСООН окисляется далее до СО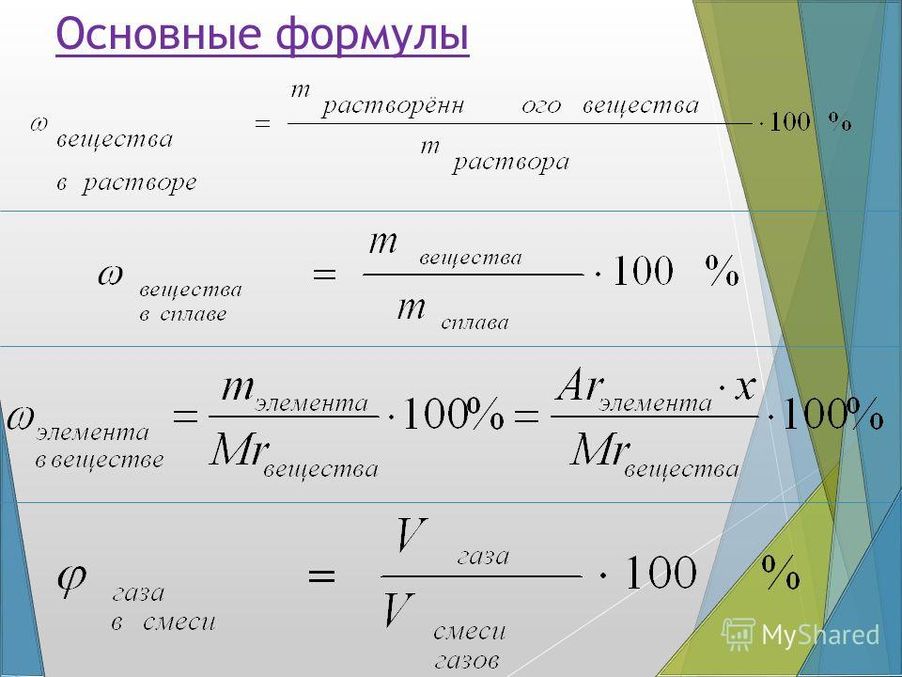
5) Карбоновые кислоты проявляют все свойства “обычных” неорганических кислот: взаимодействуют с основаниями и основными оксидами, реагируют с активными металлами и солями слабых кислот (напр., с карбонатами и гидрокарбонатами). Весьма важной является реакция этерификации – образование сложных эфиров при взаимодействии со спиртами.
CnH2n+1COOH + KOH = CnH2n+1COOK + H2O
2CnH2n+1COOH + CaO = (C
2CnH2n+1COOH + Mg = (CnH2n+1COO)2Mg + H2
CnH2n+1COOH + NaHCO3 = CnH2n+1COONa + H2O + CO2
CnH2n+1COOH + C2H5OH = CnH2n+1COOC2H5 + H2O
Ну, кажется, пора остановиться – я же не собирался писать учебник по органической химии. В заключение этого раздела хотелось бы еще раз напомнить о коэффициентах в уравнениях реакций. Если вы забудете их расставить (а такое, к сожалению, встречается слишком часто!) все дальнейшие количественные расчеты, естественно, становятся бессмысленными!
В заключение этого раздела хотелось бы еще раз напомнить о коэффициентах в уравнениях реакций. Если вы забудете их расставить (а такое, к сожалению, встречается слишком часто!) все дальнейшие количественные расчеты, естественно, становятся бессмысленными!
3. Нахождение количества вещества по его массе (объему)
Здесь все очень просто! Любому школьнику знакома формула, связывающая массу вещества (m), его количество (n) и молярную массу (M):
m = n*M или n = m/M.
Например, 710 г хлора (Cl2) соответствует 710/71 = 10 моль этого вещества, поскольку молярная масса хлора = 71 г/моль.
Для газообразных веществ удобнее работать с объемами, а не с массами. Напомню, что количество вещества и его объем связаны следующей формулой: V = Vm*n, где Vm
4. Расчеты по уравнениям реакций
Это, наверное, главный тип расчетов в химии. Если вы не чувствуете уверенности при решении подобных задач, необходимо тренироваться.
Основная идея заключается в следующем: количества реагирующих веществ и образующихся продуктов относятся так же, как соответствующие коэффициенты в уравнении реакции (вот почему так важно правильно их расставить!)
Рассмотрим, например, следующую реакцию: А + 3B = 2C + 5D. Уравнение показывает, что 1 моль А и 3 моль B при взаимодействии образуют 2 моль C и 5 моль D. Количество В в три раза превосходит количество вещества А, количество D – в 2,5 раза больше количества С и т. д. Если в реакцию вступит не 1 моль А, а, скажем, 10, то и количества всех остальных участников реакции увеличатся ровно в 10 раз: 30 моль В, 20 моль С, 50 моль D. Если нам известно, что образовалось 15 моль D (в три раза больше, чем указано в уравнении), то и количества всех остальных соединений будут в 3 раза больше.
5. Вычисление молярной массы исследуемого вещества
Масса Х обычно дается в условии задачи, количество Х мы нашли в п. 4. Осталось еще раз использовать формулу М = m/n.
6. Определение молекулярной формулы Х.
Финальный этап. Зная молярную массу Х и общую формулу соответствующего гомологического ряда, можно найти молекулярную формулу неизвестного вещества.
Пусть, например, относительная молекулярная масса предельного одноатомного спирта равна 46. Общая формула гомологического ряда: CnH2n+1ОН. Относительная молекулярная масса складывается из массы n атомов углерода, 2n+2 атомов водорода и одного атома кислорода. Получаем уравнение: 12n + 2n + 2 + 16 = 46. Решая уравнение, получаем, что n = 2. Молекулярная формула спирта: C2H5ОН.
Задача решена. Не забудьте записать ответ!
Конечно, не все задачи С 5 полностью соответствуют приведенной схеме. Никто не может дать гарантии, что на реальном ЕГЭ по химии вам попадется что-либо, дословно повторяющее приведенные примеры. Возможны незначительные вариации и даже сильные изменения. Все это, однако, не слишком важно! Не следует механически запоминать приведенный алгоритм, важно понять СМЫСЛ всех пунктов. Если будет понимание смысла, никакие изменения вам не страшны!
Если будет понимание смысла, никакие изменения вам не страшны!
В следующей части мы рассмотрим несколько типичных примеров.
Решение задачи С5 (35) на экзамене по химии. Часть II. →
Дополнительные главы химии. 8 класс: Участники курса
Курс ориентирован на слушателей, владеющих школьной программой 8 класса по химии. Учащиеся познакомятся с основным понятиям и законам химии, начальным сведениям о химии элементов, систематизируют теоретические знания, научатся решать задачи повышенной сложности.
Курс поможет школьникам не только на уроках химии в школе, но и позволит успешнее выступать на олимпиадах, а учителям химии — лучше понять аспекты теории и задачные акценты, примыкающие к школьной программе и характерные для олимпиад по химии, использовать задачную базу курса на занятиях в школе.
Курс состоит из 13 обязательных модулей, 58 видеолекций с конспектами, 232 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
|
– Химическая формула и способы ее определения |
– Смеси веществ |
Внутри каждого модуля есть:
– видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
– упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
– задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт в августе 2021 года.
Создание уравнений и формул
Для набора новой формулы с нуля нажмите Alt += на клавиатуре.
Или
Выберите Вставка > Формула и выберите Вставить новую формулу в нижней части встроенной коллекции формул. Вставится заполнитель, в котором можно ввести формулу.
Вставится заполнитель, в котором можно ввести формулу.
Вставка флажка или другого символа
Добавление формулы в коллекцию
-
Выделите формулу, которую нужно добавить.
-
Щелкните стрелку вниз и выберите Сохранить как новую формулу… .
-
В диалоговом окне Создание нового стандартного блока введите имя формулы.
-
В списке коллекции выберите пункт Формулы.
-
Нажмите кнопку ОК.
Для изменения или правки созданных ранее формул:
-
Выберите формулу для открытия вкладки Работа с формулами в ленте.
-
Выберите Конструктор, чтобы увидеть инструменты для добавления в формулу различных элементов. Можно добавить или изменить следующие элементы формулы.
-
В группе Символы находятся математические символы. Чтобы увидеть все символы, нажмите кнопку Еще. Чтобы увидеть другие наборы символов, щелкните стрелку в правом верхнем углу коллекции.
-
В группе Структуры представлены структуры, которые можно вставить. Просто выберите элемент, а затем замените заполнители в структуре (штрихпунктирные прямоугольники) нужными значениями.
-
Параметр Профессиональный отображает формулу в профессиональном формате, оптимизированном для отображения. Параметр Линейный отображает формулу как исходный текст, который при необходимости можно использовать для внесения изменений в формулу. Параметр «Линейный» отображает формулу в формате UnicodeMath или в формате LaTeX, который можно выбрать в блоке «Преобразования».
-
Преобразовать в формат «Профессиональный» или «Линейный» можно все формулы в документе или только одну, если выбрать математическую зону или навести курсор на формулу.
-
На устройствах с поддержкой сенсорного ввода и пера можно писать формулы пером или пальцем. Для рукописного ввода формулы
-
Выберите Рисование > Преобразовать рукописный фрагмент в математические символы, а затем выберите Рукописное уравнение в нижней части встроенной галереи.
-
С помощью пера или пальца введите математическую формулу от руки. Если у устройства нет сенсорного экрана, напишите уравнение с помощью мыши. Вы можете выделять части формулы и редактировать их по мере ввода, а затем с помощью окна предварительного просмотра проверять, правильно ли Word распознает то, что вы написали.
-
Завершив ввод, щелкните Вставить, чтобы преобразовать текст, который вы только что написали, в формулу.
Глава 15.3: Решение задач равновесия
Пример 15.3.2
1,00 моль NOCl помещали в реактор объемом 2,00 л и нагревали до 227 ° C до тех пор, пока система не достигла равновесия. Затем было проанализировано содержимое реактора, и было обнаружено, что оно содержит 0,056 моль Cl 2 . Вычислите K при этой температуре. Уравнение разложения NOCl на NO и Cl 2 выглядит следующим образом:
\ (2NOCl \ left (g \ right) \ rightleftharpoons 2NO \ left (g \ right) + Cl_ {2} \ left (g \ right) \)
Дано: сбалансированное уравнение равновесия, количество реагента, объем и количество одного продукта в состоянии равновесия
Спрашивали: K
Стратегия:
A Напишите выражение для константы равновесия реакции.Постройте таблицу, показывающую начальные концентрации, изменения концентраций и конечные концентрации (как начальные концентрации плюс изменения в концентрациях). {2}} \)
Для получения концентраций NOCl, NO и Cl 2 в состоянии равновесия мы составляем таблицу, показывающую, что известно и что необходимо рассчитать.Мы начинаем с написания сбалансированного химического уравнения в верхней части таблицы, за которым следуют три строки, соответствующие начальным концентрациям, изменениям концентраций, необходимым для перехода от начального к конечному состоянию, и конечным концентрациям.
| 2NOCl (г) ⇌ 2NO (г) + Cl 2 | |||
|---|---|---|---|
| [NOCl] | [НЕТ] | [Класс 2 ] | |
| начальный | |||
| изменить | |||
| финал | |||
B Изначально система содержит 1.00 моль NOCl в емкости 2,00 л. Таким образом, [NOCl] i = 1,00 моль / 2,00 л = 0,500 М. Начальные концентрации NO и Cl 2 равны 0 М, поскольку изначально продукты отсутствуют. Более того, нам говорят, что в состоянии равновесия система содержит 0,056 моль Cl 2 в емкости 2,00 л, поэтому [Cl 2 ] f = 0,056 моль / 2,00 л = 0,028 М. Мы вставляем эти значения в следующая таблица:
| 2NOCl (г) ⇌ 2NO (г) + Cl 2 | |||
|---|---|---|---|
| [NOCl] | [НЕТ] | [Класс 2 ] | |
| начальный | 0.500 | 0 | 0 |
| изменить | |||
| финал | 0,028 | ||
C Мы используем стехиометрические соотношения, приведенные в сбалансированном химическом уравнении, чтобы найти изменение концентрации Cl 2 , вещества, для которого известны начальная и конечная концентрации:
Δ [Cl 2 ] = [0.028 M (окончание) – 0,00 M (начальное)] = +0,028 M
Согласно коэффициентам в сбалансированном химическом уравнении, на каждый 1 моль Cl 2 образуется 2 моля NO, поэтому изменение концентрации NO выглядит следующим образом:
\ (\ Delta \ left [NO \ right] = \ left (\ dfrac {0.028 \; \ cancel {mol \; Cl_ {2}}} {L} \ right) \ left (\ dfrac {2 \; mol \; NO} {1 \; \ cancel {mol \; Cl_ {2}}} \ right) = 0,056 \; M \)
Аналогичным образом, 2 моль NOCl расходуется на каждый 1 моль произведенного Cl 2 , поэтому изменение концентрации NOCl выглядит следующим образом:
\ (\ Delta \ left [NOCl \ right] = \ left (\ dfrac {0.028 \; \ cancel {mol \; Cl_ {2}}} {L} \ right) \ left (\ dfrac {-2 \; mol \; NO} {1 \; \ cancel {mol \; Cl_ {2}}} \ справа) = – 0,056 \; М \)
Вставляем эти значения в нашу таблицу:
| 2NOCl (г) ⇌ 2NO (г) + Cl 2 | |||
|---|---|---|---|
| [NOCl] | [НЕТ] | [Класс 2 ] | |
| начальный | 0,500 | 0 | 0 |
| изменить | −0.056 | +0,056 | +0,028 |
| финал | 0,028 | ||
D Суммируем числа в столбцах [NOCl] и [NO], чтобы получить конечные концентрации NO и NOCl:
[NO] f = 0,000 M + 0,056 M = 0,056 M [NOCl] f = 0,500 M + (-0,056 M) = 0,444 M
Теперь мы можем заполнить таблицу:
| 2NOCl (г) ⇌ 2NO (г) + Cl 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [NOCl] | [НЕТ] | [Класс 2 ] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| начальный | 0.{-4} \) Упражнение Немецкий химик Фриц Хабер (1868–1934; Нобелевская премия по химии 1918) смог синтезировать аммиак (NH 3 ) путем реакции 0,1248 M H 2 и 0,0416 M N 2 при температуре около 500 ° C. В равновесном состоянии смесь содержала 0,00272 М NH 3 . Что такое K для реакции N 2 + 3 H 2 ⇌ 2NH 3 при этой температуре? Что такое K p ? Ответ: K = 0.105; К p = 2,61 × 10 −5 15.5: Расчет констант равновесия – Chemistry LibreTextsРасчет константы равновесия на основе равновесных концентрацийМы видели в упражнении в примере 6 в разделе 15.2, что константа равновесия для разложения \ (CaCO_ {3 (s)} \) до \ (CaO _ {(s)} \) и \ (CO_ {2 (g )} \) равно \ (K = [CO_2] \). При 800 ° C концентрация \ (CO_2 \) в равновесии с твердым \ (CaCO_3 \) и \ (CaO \) равна \ (2.{-3} \). (Помните, что константы равновесия безразмерны.) Более сложным примером проблемы этого типа является превращение н-бутана, добавки, используемой для повышения летучести бензина, в изобутан (2-метилпропан). Эту реакцию можно записать так: \ [\ ce {н-бутан _ {(g)} \ rightleftharpoons isobutane _ {(g)}} \ label {Eq1} \] и константа равновесия \ (K = [\ text {изобутан}] / [\ text {н-бутан}] \). Было обнаружено, что в состоянии равновесия смесь н-бутана и изобутана при комнатной температуре содержит 0.041 М изобутан и 0,016 М н-бутан. Подставляя эти концентрации в выражение константы равновесия, \ [K = \ dfrac {[\ textit {изобутан}]} {[\ textit {n-бутан}]} = 0,041 \; M = 2,6 \ label {Eq2} \] Таким образом, записанная константа равновесия реакции равна 2,6. Пример \ (\ PageIndex {1} \) Реакция между газообразным диоксидом серы и кислородом является ключевым этапом промышленного синтеза серной кислоты: \ [2SO_ {2 (g)} + O_ {2 (g)} \ rightleftharpoons 2SO_ {3 (g)} \ nonumber \] Смесь \ (SO_2 \) и \ (O_2 \) поддерживалась при 800 К до тех пор, пока система не достигла равновесия. 2 [O_2]} = \ dfrac {(5.{-4} \; М \; И_2 \). Вычислите \ (K \) и \ (K_p \) для этой реакции.
Химики не часто получают концентрации всех веществ, и они вряд ли могут измерить равновесные концентрации всех соответствующих веществ для конкретной системы. В таких случаях мы можем получить равновесные концентрации из начальных концентраций реагентов и сбалансированного химического уравнения реакции, если известна равновесная концентрация одного из веществ.Пример \ (\ PageIndex {2} \) показывает один из способов сделать это. Пример \ (\ PageIndex {2} \) Образец 1,00 моль \ (NOCl \) помещали в реактор объемом 2,00 л и нагревали до 227 ° C до тех пор, пока система не достигла равновесия. Затем было проанализировано содержимое реактора, и было обнаружено, что оно содержит 0,056 моль \ (Cl_2 \). Вычислите \ (K \) при этой температуре. Уравнение разложения \ (NOCl \) в \ (NO \) и \ (Cl_2 \) выглядит следующим образом: \ [2 NOCl _ {(g)} \ rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} \ nonumber \] Дано : сбалансированное уравнение равновесия, количество реагента, объем и количество одного продукта в состоянии равновесия Спросил : \ (K \) Стратегия:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

