Все формулы объемов геометрических тел
1. Расчет объема куба
a – сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):
4.

h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):
5. Как найти объем конуса ?
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8.
 Объем правильного тетраэдра
Объем правильного тетраэдраПравильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h – высота пирамиды
a – сторона основания пирамиды
n
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
12. Расчет объема пирамиды
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
13.
 Расчёт объёма усечённой пирамиды
Расчёт объёма усечённой пирамидыh – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):
14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (
15. Объем шарового сектора
R – радиус шара
h – высота сегмента
π ≈ 3. 14
14
Формула объема шарового сектора, (V):
16. Объем шарового слоя
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
Формулы вычисления объема всех геометрических фигур » Kupuk.net
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a 3
где:
V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
где:
V- объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
где:
V- объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Формула объема пирамиды:
где:
V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем усеченной пирамиды
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
Где:
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формула объема цилиндра:
V= π R2 h
V= Sоh
Где:
V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3. 141592
141592
Объем правильной треугольной пирамиды
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).
Формула объема правильной треугольной пирамиды:
Где:
V — объем пирамиды;
h — высота пирамиды;
a — сторона основания пирамиды.
Объем конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H.
Формула объема конуса:
Где:
V — объем конуса;
R — радиус основания;
H — высота конуса;
I — длина образующей;
S — площадь боковой поверхности конуса.
Объем усеченного конуса
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
Где:
V — объем усеченного конуса;
H — высота усеченного конуса;
R и R2 — радиусы нижнего и верхнего оснований.
Объем тетраэдра
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
Формула тетраэдра:
Где:
V — объем тетраэдра;
a — ребро тетраэдра.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.
Формула объема шара:
Где:
V — объем шара;
R — радиус шара;
S — площадь сферы.
Объем шарового сегмента и сектора
Шаровый сегмент — это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
Формула объема шарового сегмента:
Где:
R — радиус шара
H — высота сегмента
π ≈ 3,14
Формула объема шарового сектора:
Где:
h — высота сегмента
R — радиус шара
π ≈ 3,14
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Где:
V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Формула объема куба
- Главная
- Справочник
- Геометрия
- Формулы объема
- Формула объема куба
- Объем куба
- Формула для расчета объема куба
- Калькулятор объёма куба
Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.
Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных шестиугольников – это сечения через центр куба перпендикулярно 4-м главным диагоналям. В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть, сумма плоских углов у каждой вершины = 270º.
Объем куба
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. 3 $$
3 $$
Уровень5 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема цилиндра
Объем цилиндра равен произведению квадрата радиуса основания, высоты цилиндра и числа пи (3.1415)
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объёма параллелепипеда
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Что такое лошадиная сила
Лошадиная сила — единица мощности.
 Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.Разное Мощность Сила Единицы измерения Деньги Справочник
Сколько должен весить человек?
Чтобы узнать вес человека, достаточно знать его рост в сантиметрах, из этой цифры вычесть 100, а к полученному числу либо прибавить 10, если речь идет о мужчине, либо отнять 10, если вычисляется вес женщины.
Масса и вес Масса Теория Единицы измерения
ЕГЭ: обязательные предметы для сдачи экзамена
ЕГЭ Экзамены
Что такое Вольт
1 Вольт равен электрическому напряжению, вызывающему в электрической цепи постоянный ток силой 1 ампер при мощности 1 ватт.
Электротехника Формулы Физика Теория Электричество
1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?
Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ.
 coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.Разное Единицы измерения Деньги Справочник
Процент / доля от числа
Арифметика Калькулятор Расчёт Проценты
Закон Дальтона
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
Законы Уравнение Формулы Физика Химия Закон Термодинамика
Формула площади треугольника
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h)
Формулы площади Площадь Формулы Геометрия
Формула по физике для объема
- Спросите у экспертов
- Образование
- Помощь с домашним заданием в школе
Вы должны войти в систему, чтобы опубликовать ответ.
Автор: [Аноним]
Можете ли вы дать мне формулу для нахождения объема в физике
Ответы
10 Ответы найдены.
| Точки: |
|---|
93 = атомный вес/плотность x n
| Точки: | 1 |
|---|
Формула, чтобы найти объем
V = м/D
, где можно найти объем
V = M/D
. m — масса, d — плотность.
| Точки: | 2 (₹ 1) |
|---|
HI
не только в физике, в целом
объем = область поперечного сечения * Высота
или
VOLUCT = DISTICE
.3
| Баллы: | 1 (₹ 1) |
|---|
Привет!
В дополнение к приведенным выше формулам формула для газов:
Объем газа V=nRT/P
Где
n=количество молей
R=газовая постоянная
T=температура
P=давление газа
Приведенная выше формула получена путем ретроспективного теоретического объединения законов Бойля (pv = константа и Шарля (V/T = константа). 3
3
| О. О. d = плотность тела Есть некоторые вещи, которые нельзя купить за деньги, такие как манеры, мораль и интеллект.
Volume=m/d
HI Уважаемый MARSE OF BODULE для объема MASS 40014. спасибо аамир хан Никогда не лги тому, кто доверяет тебе. С уважением и благодарностью Войдите, чтобы оставлять комментарии Отправить новую тему Вернуться, чтобы вернуться к разделу “Спросить экспертов” Что такое объем – физика | Определение и расчетОбъем является основной физической величиной . Объем является производной величиной и выражает трехмерную протяженность объекта . Объем часто измеряется численно с использованием производной единицы СИ, кубических метров . Например, объем внутри сфера (то есть объем шара) получается из V = 4/3πr 3 , где r — радиус сферы. Другой пример: объем куба равен произведению стороны на сторону. Если одна сторона квадрата равна 3 метрам, объем будет равен 3 метрам на 3 метра на 3 метра или 27 кубическим метрам. Формулы для расчета различных объемов Формулы объема для некоторых распространенных трехмерных объектов: Что такое удельный объемТипичные плотности различных веществ при атмосферном давлении.Удельный объем является интенсивной переменной , тогда как объем является экстенсивной переменной. Стандартная единица измерения удельного объема в системе СИ — кубический метр на килограмм (м 3 /кг). Стандартной единицей измерения в английской системе является кубический фут на фунт массы (фут 3 /фунт). Плотность (ρ) вещества обратно пропорциональна его удельному объему (ν). ρ = m/V = 1/ρ Плотность определяется как масса на единицу объема . Это также интенсивное свойство , которое математически определяется как масса, деленная на объем: ρ = m/V Материалы с наименьшим удельным объемом — самые плотные материалы на Земле Поскольку нуклонов ( протонов и нейтронов ) составляют большую часть массы обычных атомов, плотность обычной материи имеет тенденцию ограничиваться тем, насколько плотно мы можем упаковать эти нуклоны, и зависит от внутренней атомной структуры вещества. Самый плотный материал , обнаруженный на Земле, — это металлический осмий . Тем не менее, его плотность бледнеет по сравнению с плотностью экзотических астрономических объектов, таких как белые карликовые звезды и нейтронные звезды 9. List of densest materials:
Следует отметить, что плутоний является промышленным изотопом и создается из урана в ядерных реакторах. Если учитывать промышленные элементы, то самым плотным на данный момент является Hassium . Хассий — это химический элемент с символом Hs и атомным номером 108. Это синтетический элемент (впервые синтезированный в Хассе в Германии) и радиоактивный. Самый стабильный известный изотоп, 269 Hs имеет период полураспада примерно 9,7 секунды. Расчетная плотность 40,7 x 10 3 кг/м 3 . Плотность хассия обусловлена его 90 306 высоким атомным весом 90 307 и значительным уменьшением 90 306 ионных радиусов 90 307 элементов в ряду лантанидов, известных как 90 306 лантанидное и актинидное сжатие 90 307 . За плотностью хассия следует мейтнерий (элемент 109, названный в честь физика Лизы Мейтнер), плотность которого оценивается в 9 единиц.0306 37,4 x 10 3 кг/м 3 . Изменения удельного объема В целом, плотность и, следовательно, удельный объем можно изменить путем изменения давления или температуры . Увеличение давления всегда увеличивает плотность материала. Влияние давления на плотность жидкостей и твердых тел очень мало. С другой стороны, плотность газов сильно зависит от давления. Это выражается сжимаемость . Сжимаемость измеряет относительное изменение объема жидкости или твердого вещества в ответ на изменение давления. Влияние температуры на плотность жидкостей и твердых тел также очень важно. Большинство веществ расширяются при нагревании и сжимаются при охлаждении . Однако величина расширения или сжатия варьируется в зависимости от материала. где ∆T — изменение температуры, V — исходный объем, ∆V — изменение объема, а α V — коэффициент объемного расширения . Следует отметить и исключения из этого правила. Например, вода отличается от большинства жидкостей тем, что она становится менее плотной при замерзании . Его максимальная плотность составляет 3,98 °C (1000 кг/м 3 ), тогда как плотность льда составляет 917 кг/м 3 . Он отличается примерно на 9% и поэтому плавает на льду на жидкой воде Объем атома и ядраСтроение материи. Атом состоит из небольшого, но массивного ядра , окруженного облаком быстро движущихся электронов . Ядро состоит из протонов и нейтронов . г = г 0 . A 1/3 где r 0 = 1,2 x 10 -15 m = 1,2 фм Если мы используем это приближение, мы, следовательно, ожидаем, что объем ядра будет порядка 4 /3πr 3 или 7,23 × 10 −45 м 3 для ядер водорода или 1721×10 −45 м 3 для 238 ядер U. Это объемы ядер, а в атомных ядрах (протонов и нейтронов) содержится около 99,95% массы атома. Является ли атом пустым пространством?Образное изображение атома гелия-4 с электронным облаком в оттенках серого. Протоны и нейтроны, скорее всего, находятся в одном пространстве, в центральной точке. Источник wikipedia.org Лицензия CC BY-SA 3.0 Объем атома примерно на на 15 порядков больше , чем объем ядра. Может показаться, что пространство и материя пусты , но это не . Из-за квантовой природы электронов электроны не являются точечными частицами, а размазаны по всему атому. Классическое описание нельзя использовать для описания вещей на атомном уровне. Объем теплоносителя в системе теплоснабжения реактораЯдерный реактор и система теплоснабжения первого контура ВВЭР-1200.Источник: gidropress.podolsk.ru используется с разрешения АО ОКБ «ГИДРОПРЕСС» В типовых современных водо-водяных реакторах (PWR), система охлаждения реактора (RCS), показанная на рисунке, состоит из:
Все компоненты СТР расположены внутри здания защитной оболочки. Внутри корпуса реактора, контуров и парогенераторов при нормальной работе находится сжатая жидкая вода. Давление поддерживается примерно на уровне 16 МПа . При таком давлении вода кипит примерно при 350°C (662°F). Температура воды на входе составляет около 290°C (554°F). Вода (хладагент) нагревается в активной зоне реактора примерно до 325°C (617°F) по мере прохождения воды через активную зону. Как видно, реактор содержит недогретые теплоносители примерно на 25°C (расстояние от точки насыщения). Это высокое давление поддерживается компенсатором давления, отдельным сосудом, подключенным к первому контуру (горячая ветвь) и частично заполненным водой (частично насыщенным паром), которая нагревается до температура насыщения (точка кипения) для желаемого давления с помощью погружных электрических нагревателей . Объемы типичных PWR приведены в следующей таблице. Это иллюстративный пример, и следующие данные не соответствуют какой-либо конструкции реактора. Следует отметить, что объем охлаждающей жидкости значительно изменяется с температурой охлаждающей жидкости. Общая масса хладагента всегда остается неизменной. Изменение объема воды не является изменением запаса воды. Объем теплоносителя реактора изменяется с изменением температуры из-за изменений плотности . Большинство веществ расширяются с при нагревании и сжимаются при охлаждении . где ∆T — изменение температуры, V — первоначальный объем, ∆V — изменение объема и α V – коэффициент объемного расширения . Плотность жидкой (сжатой) воды как функция температуры воды Коэффициент объемного теплового расширения для воды непостоянен в диапазоне температур и увеличивается с температурой ( особенно при 300° С ). Поэтому изменение плотности не является линейным в зависимости от температуры (как показано на рисунке). См. также: Паровые столы. При нормальных условиях общий объем теплоносителя в системе теплоснабжения реактора почти постоянен. Контрольный объем – Анализ контрольного объема Контрольный объем – это фиксированная область в пространстве, выбранная для термодинамического исследования баланса массы и энергии для проточных систем. Граница контрольного объема может быть действительной или воображаемой оболочкой . Поверхность управления является границей контрольного объема. Например, анализ контрольного объема можно использовать для определения скорости изменения количества движения жидкости. В этом анализе будет рассматриваться струйная трубка ( контрольный объем ), как мы это делали для уравнения Бернулли. В этом контрольном объеме любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость внутри объема. См. также: Формула импульса. Как видно из рисунка, метод контрольного объема можно использовать для анализа закона сохранения количества движения в жидкости. Контрольный объем представляет собой воображаемую поверхность , прилагающий интересующий том. Контрольный объем может быть неподвижным или подвижным, жестким или деформируемым. Для определения всех сил, действующих на поверхности контрольного объема, необходимо решить законы сохранения в этом контрольном объеме. Выбор контрольного объема Контрольный объем может быть выбран как любой произвольный объем, через который протекает жидкость. Пример: Струя воды попадает в неподвижную плитуНеподвижная плита (например, лопасть водяной мельницы) отклоняет поток воды со скоростью 1 м/с и углом 90° . Это происходит при атмосферном давлении, а массовый расход равен Q =1 м 3 /с .
Решение
h
Каталожные номера: Реакторная физика и теплогидравлика:
См. выше:Термодинамические свойства сообщить об этом объявлении Что такое формула объема в физикеНе пропуститеФизические формулы для величин в релятивистской динамикеФизика. Что такое плотность? Плотность, масса и объем | Физика плотности Все известные величины в классической механике модифицируются, когда мы переходим к релятивистской механике, основанной на специальной теории относительности. Вот формулы величин в релятивистской динамике. Релятивистский импульс p = m0v, где m0; — масса покоя частицы. Энергия массы покоя E = m0c2 Полная энергия E = ) Является ли атом пустым пространством Объем атома составляет около 15 порядков больше , чем объем ядра. Может показаться, что пространство и на самом деле материя пустая , но это не . Из-за квантовой природы электронов электроны не являются точечными частицами, они размазаны по всему атому. Классическое описание нельзя использовать для описания вещей на атомном уровне. В атомном масштабе физики обнаружили, что квантовая механика очень хорошо описывает вещи в этом масштабе. Калькулятор объема и инструменты, предназначенные для определенных фигурМы решили сделать этот калькулятор объема простым инструментом, который охватывает пять самых популярных трехмерных форм. Однако не каждое уравнение объема и тип формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и неинтуитивным. Поэтому, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных фигур: Не пропустите: как найти биологических бабушек и дедушек, Великобритания Что такое конкретный объем Удельный объем является интенсивной переменной , тогда как объем является экстенсивной переменной. Стандартной единицей удельного объема в системе СИ является кубический метр на килограмм. Плотность вещества обратно пропорциональна его удельному объему . = m/V = 1/ Плотность определяется как масса на единицу объема . It is also an intensive property , which is mathematically defined as mass divided by volume: = m/V nucleons densest material metal osmium dwarf stars neutron stars Список самых плотных материалов:  103 кг/м3 103 кг/м3Следует отметить, что плутоний является искусственным изотопом и создается из урана в ядерных реакторах. Но на самом деле ученые обнаружили следовые количества природного плутония. За хассием следует плотность мейтнерия , расчетная плотность которого составляет 37,4 x 103 кг/м3 . плотность удельный объем измененный давление температура давление всегда увеличивается плотность жидкости твердые тела сжимаемость сжимаемость Как рассчитать объем Формулы объема На этот вопрос нет простого ответа, так как он зависит от формы рассматриваемого объекта. куб = s³, где s длина стороны. Сфера = r³, где r — радиус. Цилиндр = r²h, где r — радиус, а h — высота. Конус = r²h, где r — радиус, а h — высота. Прямоугольное твердое тело = lwh, где l — длина, w — ширина и h — высота. Пирамида = Ah, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием можно использовать и другое уравнение: Пирамида = * h * длина_стороны² * кроватка, где n — количество сторон основания правильного многоугольника. Призма = Ah, где A — площадь основания, а h — высота. Для прямой треугольной призмы уравнение можно легко вывести, как и для правильной прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и коробка.
Не пропустите: что я обозначаю в физике Импульс, сила и импульс произведение массы и скорости тела. Импульс рассчитывается по формуле: P = m x vКак использовать калькулятор объемаДавайте рассмотрим пример использования этого калькулятора объема: Выберите тип 3D-фигуры . Если вы не можете найти фигуру, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы. В этом примере предположим, что вы хотите вычислить объем цилиндра. Выберите нужный раздел калькулятора объема . В нашем случае это деталь под названием Cylinder volume . Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения, просто щелкнув имя единицы измерения. Вот, пожалуйста! Отображается объем выбранной формы . В нашем случае это 9,42478 кубических футов . Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите баррели из выпадающего списка. Наш цилиндр имеет вместимость ~ 2,24 барреля нефти. Что такое трехмерная геометрия? из-за радиоактивных процессов составляет около 19В 0115 миллионов раз в раз больше, чем при любых известных молекулярных изменениях, что ставит вопрос о том, откуда берется энергия. Новозеландский физик Эрнест Резерфорд и британский радиохимик Фредерик Содди в 1903 году предположили существование огромного количества скрытой энергии, хранящейся в материи, после устранения идеи поглощения и испускания каких-то частиц эфира Лесагиана. Физические формулы для класса 9 Список физических формулУравнение непрерывности, объемный расход и массовый расход Задачи по физике
Формула физики том .
См. также: Pre Algebra Order Operations Help Что такое плотность в физикеПлотность в физике Определение: 1. Плотность вещества определяется как отношение его массы к его объему. 2. Плотность – это масса единицы объема любого объекта. Он рассчитывается путем деления массы объекта на его объем. Мы даем подробный и понятный лист по всем заметкам по физике, которые очень полезны для понимания основных концепций физики. Единицы объема и таблица преобразованияПопулярные единицы объема: Если вам нужно перевести единицы объема, вы можете воспользоваться нашим конвертером объема. Еще один полезный инструмент — калькулятор граммов в чашках, который может помочь, если вы хотите использовать рецепт еды из другой страны. Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:
Также проверьте: Что такое молекулярная геометрия Ccl4 Как рассчитать объем, используя плотностьПлотность измеряет количество массы в данном объеме вещества или количество материала в данном пространстве. Плотность вещества постоянна при данной температуре, поскольку увеличение массы образца пропорционально увеличивает объем. Плотность рассчитывается путем деления массы вещества на объем. Если известна плотность вещества, определение массы образца позволит рассчитать объем. Определите плотность вещества. Доступно множество справочных источников, в которых указана плотность различных соединений. Определите массу вещества с помощью весов. Можно использовать либо трехбалочные весы, либо электронные весы. Один из методов измерения массы заключается в обнулении весов контейнером для образца на весах. Затем добавьте образец в контейнер и измерьте массу контейнера и образца. В качестве альтернативы масса может быть определена путем измерения массы контейнера, а затем массы контейнера с веществом. Вычтите массу контейнера из массы вещества и контейнера, чтобы вычислить массу вещества. Статьи по темеПолный список всех физических формулИзучение физики заключается в применении концепций для решения задач. В этой статье представлен исчерпывающий список физических формул, который будет служить готовым справочником при решении физических задач. Вы даже можете использовать этот список для быстрого повторения перед экзаменом. Нравится? Поделись! Изучение физики заключается в применении концепций для решения задач. Физика — самая фундаментальная из всех наук. Это также одна из самых сложных наук для освоения. Изучение физики — это, по сути, изучение фундаментальных законов, управляющих нашей Вселенной. Я бы сказал, что нужно выяснить гораздо больше, чем просто запомнить и разобрать физические формулы. Попытайтесь понять, что формула говорит и означает, и какое физическое отношение она объясняет. Если вы понимаете физические понятия, лежащие в основе этих формул, вывести их или запомнить несложно. В этой статье ScienceStruck перечислены некоторые физические формулы, которые вам понадобятся для решения основных физических задач. Читайте также: Как работают наушники с шумоподавлением Физика Контрольный объем Анализ контрольного объема Контрольный объем представляет собой фиксированную область в пространстве, выбранную для термодинамического исследования баланса массы и энергии для проточных систем. Анализ контрольного объема можно использовать, например, для определения скорости изменения количества движения жидкости. В этом анализе мы будем рассматривать трубку тока так же, как и для уравнения Бернулли. В этом контрольный объем любое изменение импульса жидкости в контрольном объеме происходит из-за действия внешних сил на жидкость в этом объеме. См. также: Формула импульса Как видно из рисунка, метод контрольного объема можно использовать для анализа закона сохранения количества движения в жидкости. Контрольный объем представляет собой воображаемую поверхность , охватывающую интересующий объем. Контрольный объем может быть неподвижным или подвижным, жестким или деформируемым. Для определения всех сил, действующих на поверхности контрольного объема, необходимо решить законы сохранения в этом контрольном объеме. Два способа измерения объемаРазличные способы определения объема
Вам может понравиться: Что означает абиотика в биологии Как найти объемФормула объема зависит от формы объекта . Одной из самых популярных форм является прямоугольная призма, также известная как прямоугольник, где вы можете просто 90 306 умножить длину на ширину и высоту на 90 307, чтобы найти объем. Другой распространенной формой является цилиндр, чтобы найти его объем, умножьте высоту цилиндра на площадь его основания. Для других 3D-форм проверьте калькулятор объема Omni. Объем прямоугольного твердого телаGCSE Physics – Давление и объем – Как использовать уравнение «PV = константа» №30 Прямоугольное твердое тело также называют прямоугольной призмой или параллелепипедом. В прямоугольном твердом теле длина, ширина и высота могут быть разной длины. Объем приведенного выше прямоугольного тела будет произведением длины, ширины и высоты, то есть Объем прямоугольного тела = lwh.0014 Формула объема прямоугольного параллелепипеда: л × ш × ч = лвч , где л — длина, л — ширина и Примеры:
Не пропустите: что такое энергия в квантовой физике Объем атома и ядра Атом состоит из небольшого, но массивного ядра , окруженного облаком быстро движущихся электронов . г = г0 . A1/3 где r0 = 1,2 x 10-15 м = 1,2 фм Если мы используем это приближение, мы ожидаем, что объем ядра будет порядка 4/3r3 или 7,23 × 1045 м3 для ядер водорода или 1721×1045 м3 для ядер 238U. Это объемы ядер, а атомные ядра содержат около 99,95% массы атома. Таблица общих значений удельного объемаИнженеры и ученые обычно обращаются к таблицам значений удельного объема. Эти репрезентативные значения относятся к стандартной температуре и давлению, т.е. температуре 0°C и давлению 1 атм.
Вещества, отмеченные звездочкой, не входят в STP. Поскольку материалы не всегда находятся в стандартных условиях, существуют также таблицы для материалов, в которых указаны конкретные значения объема в диапазоне температур и давлений. Не пропустите: Geometry Dash Practice Song Hack Преобразования импульса и энергии в релятивистской механикеРассмотрим те же два кадра, что и в случае преобразования координат Лоренца выше. S движется со скоростью v вдоль оси x. Здесь снова фактор Лоренца. В кадре S и в кадре S компоненты импульса. Теперь рассмотрим формулы для преобразования импульса и энергии частицы между этими двумя системами отсчета в релятивистском режиме. Объем теплоносителя в системе теплоносителя реактораВ типичных современных водо-водяных реакторах , Система теплоносителя реактора , показанная на рисунке, состоит из:
Все компоненты RCS расположены внутри здания сдерживания. При нормальной эксплуатации внутри корпуса реактора, петель и парогенераторов находится сжатая жидкая вода. ;Давление поддерживается примерно на уровне 16 МПа . При таком давлении вода кипит примерно при 350°C . ;Температура воды на входе составляет около 290°C . Вода нагревается в активной зоне реактора примерно до 325°C по мере того, как вода течет через активную зону. Как видно, в реакторе находится недогретый теплоноситель примерно на 25°C. Это высокое давление поддерживается компенсатором давления, отдельным сосудом, соединенным с первым контуром и частично заполненным водой, нагретой до 9°С.0306 температура насыщения для желаемого давления с помощью погружных электрических нагревателей . Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. При нормальных условиях около 60% объема компенсатора давления занимает сжатая вода и около 40% объема занимает насыщенный пар . |
|---|

 Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
 Поскольку каждая сторона квадрата одинакова, это может быть просто длина одной стороны в кубе .
Поскольку каждая сторона квадрата одинакова, это может быть просто длина одной стороны в кубе .
 0307 .
0307 .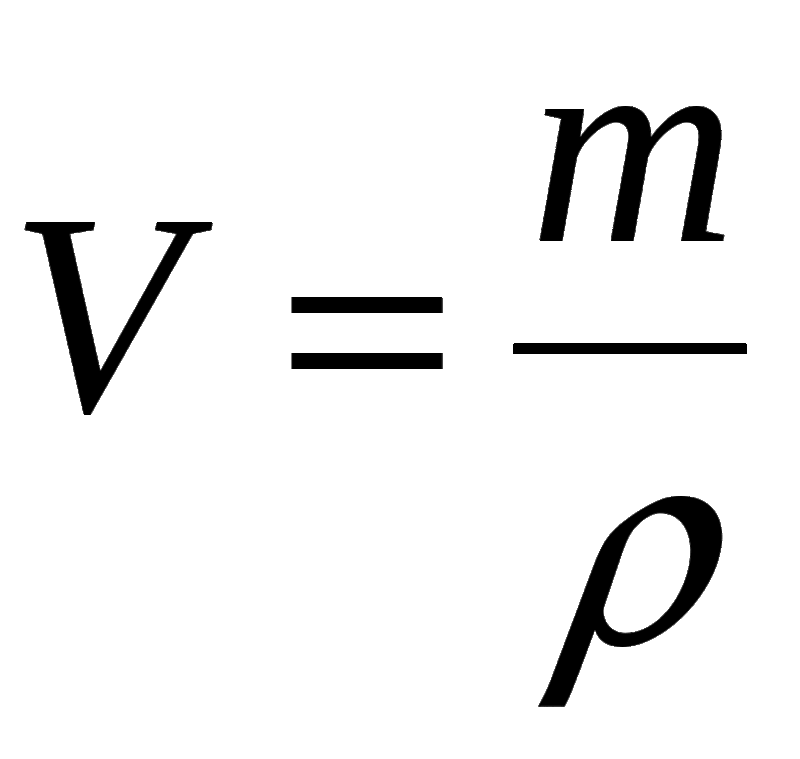 Но ученые обнаружили следовые количества встречающегося в природе плутония.
Но ученые обнаружили следовые количества встречающегося в природе плутония.
 Это явление известно как тепловое расширение . Изменение объема материала при изменении температуры определяется следующим соотношением:
Это явление известно как тепловое расширение . Изменение объема материала при изменении температуры определяется следующим соотношением: Типичные радиусы ядер имеют порядок 10 −14 м. Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму:
Типичные радиусы ядер имеют порядок 10 −14 м. Радиусы ядер можно рассчитать по следующей формуле, предполагая сферическую форму: Для атома урана ван-дер-ваальсов радиус составляет около 186 пм = 1,86 × 10 −10 м . Радиус Ван-дер-Ваальса, r w , атома – это радиус воображаемой твердой сферы, представляющий расстояние наибольшего приближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает всего около 1721×10 −45 м 3 пространства. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома.
Для атома урана ван-дер-ваальсов радиус составляет около 186 пм = 1,86 × 10 −10 м . Радиус Ван-дер-Ваальса, r w , атома – это радиус воображаемой твердой сферы, представляющий расстояние наибольшего приближения для другого атома. Атом урана имеет объем около 26,9 × 10 −30 м 3 , принимая сферическую форму. Но это «огромное» пространство занято в основном электронами, потому что ядро занимает всего около 1721×10 −45 м 3 пространства. Эти электроны вместе весят лишь часть (скажем, 0,05%) всего атома. В атомном масштабе физики обнаружили, что квантовая механика очень хорошо описывает вещи в этом масштабе. Расположение частиц в квантовой механике не находится в точном положении, и они описываются функция плотности вероятности . Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).
В атомном масштабе физики обнаружили, что квантовая механика очень хорошо описывает вещи в этом масштабе. Расположение частиц в квантовой механике не находится в точном положении, и они описываются функция плотности вероятности . Поэтому пространство в атоме (между электронами и атомным ядром) не пусто. Тем не менее, он заполнен функцией плотности вероятности электронов (обычно известной как «электронное облако »).
 Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар .
Температуру в компенсаторе давления можно поддерживать на уровне 350 °C. Около 60% объема компенсатора давления занимает сжатая вода при нормальных условиях, а около 40% объема занимает насыщенный пар . Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением:
Однако величина расширения или сжатия варьируется в зависимости от материала. Это явление известно как тепловое расширение . Изменение объема материала, подвергающегося изменению температуры, определяется следующим соотношением: С другой стороны, в условиях переходной нагрузки, объем может значительно измениться . Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
С другой стороны, в условиях переходной нагрузки, объем может значительно измениться . Эти изменения естественным образом отражаются в изменении уровня воды в компенсаторе давления. При постепенном снижении средней температуры теплоносителя реактора общий объем воды также уменьшается, что снижает уровень компенсатора давления. При постепенном наборе нагрузки увеличение средней температуры теплоносителя реактора вызывает расширение общего объема воды, повышая уровень компенсатора давления. Эти эффекты должны контролироваться системой контроля уровня компенсатора давления.
 Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.
Этот объем может быть статичным, подвижным и даже деформироваться во время течения. Чтобы решить любую задачу, мы должны решить основные законы сохранения в этом томе. Очень важно знать все относительные скорости потока к поверхности управления. Поэтому очень важно точно определить границы контрольного объема при анализе.

 , ISBN: 978-0-470-03037-0
, ISBN: 978-0-470-03037-0 Для атома урана ван-дер-ваальсов радиус составляет около 186 пм = 1,86 × 1010 м . Радиус Ван-дер-Ваальса, rw, атома – это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения с другим атомом. ;Принимая сферическую форму, атом урана имеет объем около ; 26,9 ×1030 м3 . Но это огромное пространство занято в основном электронами, потому что ядро занимает всего около 1721×1045 м3 ;помещения. Эти электроны вместе весят лишь часть всего атома.
Для атома урана ван-дер-ваальсов радиус составляет около 186 пм = 1,86 × 1010 м . Радиус Ван-дер-Ваальса, rw, атома – это радиус воображаемой твердой сферы, представляющий расстояние наибольшего сближения с другим атомом. ;Принимая сферическую форму, атом урана имеет объем около ; 26,9 ×1030 м3 . Но это огромное пространство занято в основном электронами, потому что ядро занимает всего около 1721×1045 м3 ;помещения. Эти электроны вместе весят лишь часть всего атома. Расположение частиц в квантовой механике не находится в точном положении, они описываются функция плотности вероятности . Поэтому пространство в атоме не пусто, а заполнено функцией плотности вероятности электронов.
Расположение частиц в квантовой механике не находится в точном положении, они описываются функция плотности вероятности . Поэтому пространство в атоме не пусто, а заполнено функцией плотности вероятности электронов. Стандартной единицей измерения в английской системе является кубический фут на фунт массы.
Стандартной единицей измерения в английской системе является кубический фут на фунт массы. Вот формулы для некоторых наиболее распространенных форм:
Вот формулы для некоторых наиболее распространенных форм:

 Резерфорд также предположил, что эта внутренняя энергия хранится и в обычной материи. Он продолжал размышлять в 1904: «Если бы когда-либо была найдена возможность по желанию контролировать скорость распада радиоэлементов, огромное количество энергии можно было бы получить из небольшого количества материи».
Резерфорд также предположил, что эта внутренняя энергия хранится и в обычной материи. Он продолжал размышлять в 1904: «Если бы когда-либо была найдена возможность по желанию контролировать скорость распада радиоэлементов, огромное количество энергии можно было бы получить из небольшого количества материи».

 Обратите внимание, что это не простое преобразование, а переход от единицы веса к единице объема, поэтому вам необходимо знать тип ингредиента.
Обратите внимание, что это не простое преобразование, а переход от единицы веса к единице объема, поэтому вам необходимо знать тип ингредиента. Обычно используемые ссылки включают индекс Merck и справочник CRC по химии и физике.
Обычно используемые ссылки включают индекс Merck и справочник CRC по химии и физике. В этой статье представлен исчерпывающий список физических формул, который будет служить готовым справочником при решении физических задач. Вы даже можете использовать этот список для быстрого повторения перед экзаменом.
В этой статье представлен исчерпывающий список физических формул, который будет служить готовым справочником при решении физических задач. Вы даже можете использовать этот список для быстрого повторения перед экзаменом. Граница контрольного объема может быть действительной или воображаемой оболочкой . Поверхность управления является границей контрольного объема.
Граница контрольного объема может быть действительной или воображаемой оболочкой . Поверхность управления является границей контрольного объема.

 Ядро состоит из протонов и нейтронов . Типичные радиусы ядер порядка 1014 м. Принимая сферическую форму, радиусы ядер можно рассчитать по следующей формуле:
Ядро состоит из протонов и нейтронов . Типичные радиусы ядер порядка 1014 м. Принимая сферическую форму, радиусы ядер можно рассчитать по следующей формуле: Вы можете найти подробные таблицы для воздуха и пара.
Вы можете найти подробные таблицы для воздуха и пара.
