Все формулы по электромагнитной индукции: Основные формулы и методические рекомендации по решению задач на электромагнитную индукцию - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

§16. Электромагнитная индукция. Энергия магнитного поля Основные формулы

Магнитный поток Ф через плоский контур площадью S равен:

а) в случае однородного поля

где – угол между вектором нормали к плоскости контура и вектором магнитной индукции ;

б) в случае неоднородного поля

где интегрирование ведется по всей поверхности S.

Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками контура, равно

где N – число витков контура, Ф – магнитный поток сквозь один виток.

Работа по перемещению замкнутого контура с током в постоянном магнитном поле равна

где I – сила тока в контуре; – изменение магнитного потока, пронизывающего поверхность, ограничивающую контур.

Основной закон электромагнитной индукции имеет вид

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью V в однородном магнитном поле с индукцией B, равна

где α – угол между направлениями векторов скорости и индукции магнитного поля;

б) электродвижущая сила индукции, возникающая в рамке, равномерно вращающейся в однородном магнитном поле, равна

где N – число витков в рамке; В – индукция поля; S – площадь одного витка; – угловая скорость вращения рамки; t – время.

Заряд, протекающий по замкнутому контуру при изменении потокосцепления , равен

где R – сопротивление контура.

Индуктивность контура равна

где I – сила тока в контуре ; Ψ– потокосцепление самоиндукции.

Электродвижущая сила самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем, определяется по формуле

Индуктивность соленоида равна

где n – число витков соленоида на единице его длины;

V – объём соленоида; – магнитная проницаемость среды внутри соленоида, которую можно определить из соотношения .

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L, равно:

а) после замыкания цепи

где – электродвижущая сила источника;

б) после размыкания цепи

где – начальное значение силы тока в цепи.

Энергия магнитного поля, создаваемого током I в замкнутом контуре с индуктивностью L , определяется по формуле

Объёмная плотность энергии магнитного поля равна

Задачи

16.1. Найти магнитный поток Ф, создаваемый соленоидом сечением S = 10 см², если он имеет n = 10 витков на каждый сантиметр его длины при силе тока I = 20 А.

16.2. Плоский контур, площадь S которого равна 25 см², находится в однородном магнитном поле с индукцией

B = 0,04 Тл. Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол β = 30° с линиями индукции.

16.3. Соленоид длиной l = 1 м и сечением S = 16 см² содержит N = 2000 витков. Вычислить потокосцепление Ψ при силе тока I в обмотке 10 А.

16.4. Плоская квадратная рамка со стороной а = 20 см лежит в одной плоскости с бесконечно длинным прямым проводом, по которому течет ток I = 100 А. Рамка расположена так, что ближайшая к проводу сторона параллельна ему и находится на расстоянии

l = 10 см от провода. Определить магнитный поток Ф, пронизывающий рамку.

16.5. В однородном магнитном поле с индукцией B = 0,01 Тл находится прямой провод длиной l = 8 см, расположенный перпендикулярно линиям индукции. По проводу течет ток I = 2 А. Под действием сил поля провод переместился на расстояние S = 5 см. Найти работу А сил поля.

16.6. Плоский контур, площадь S которого равна 300 см², находится в однородном магнитном поле с индукцией В = 0,01 Тл. Плоскость контура перпендикулярна линиям индукции.

В контуре поддерживается неизменный ток I = 10 А, Определить работу A внешних сил по перемещению контура с током в область пространства, магнитное поле в которой отсутствует.

16.7. По проводу, согнутому в виде квадрата со стороной длиной a = 10 см, течет ток I = 20 А, сила которого поддерживается неизменной. Плоскость квадрата составляет угол α = 20⁰ с линиями индукции однородного магнитного поля (B = 0,1 Тл). Вычислить работу А, которую необходимо совершить для того, чтобы удалить провод за пределы поля.

16.8. По кольцу, сделанному из тонкого гибкого провода, радиусом R = 10 см, течет ток I = 100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией B = 0,1 Тл по направлению, совпадающему с индукцией В₁ собственного магнитного поля кольца. Определить работу А внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упругих сил пренебречь.

16.9. Виток, по которому течет ток I = 20 А, свободно установился в однородном магнитном поле с индукцией B = 0,016 Тл. Диаметр d витка равен 10 см. Определить работу A, которую нужно совершить, чтобы повернуть виток на угол α= π/2 относительно оси, совпадающей с диаметром.

16.10. Квадратная рамка со стороной a = 10 см, по которой течет ток I = 200 А, свободно установилась в однородном магнитном поле (B = 0,2 Тл). Определить работу, которую необходимо совершить при повороте рамки вокруг оси, лежащей в плоскости рамки и перпендикулярной линиям магнитной индукции, на угол α = 2π/3.

16.11. Магнитный поток

Ф = 40 мВб пронизывает замкнутый контур. Определить среднее значение электродвижущей силы индукции , возникающей в контуре, если магнитный поток изменится до нуля за время Δt = 2 мс.

16.12. Прямой провод длиной l = 40 см движется в однородном магнитном поле со скоростью v = 5 м/с перпендикулярно линиям индукции. Разность потенциалов U между концами провода равна 0,6 В. Вычислить индукцию В магнитного поля.

16.13. В однородном магнитном поле с индукцией B = 1 Тл находится прямой провод длиной l = 20 см, концы которого замкнуты вне поля. Сопротивление

R всей цепи равно 0,1 Ом. Найти силу F, которую нужно приложить к проводу, чтобы перемещать его перпендикулярно линиям индукции со скоростью V = 2,5 м/с.

16.14. Прямой провод длиной l = 10 см помещен в однородное магнитное поле с индукцией B = 1 Тл. Концы его замкнуты гибким проводом, находящимся вне поля. Сопротивление R всей цепи равно 0,4 Ом. Какая мощность Р потребуется для того, чтобы двигать провод перпендикулярно линиям индукции со скоростью v = 20 м/с?

16.

15. По П-образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка 12 (рис. 16.1). Она имеет длину l, массу m и сопротивление R. Вся система находится в вертикальном однородном магнитном поле с индукцией В. В момент t = 0 на перемычку стали действовать постоянной горизонтальной силой F, и перемычка начала перемещаться вправо. Найти скорость перемычки как функцию времени. Магнитное поле индукционного тока и сопротивление П-образного проводника пренебрежимо малы.

16.16. К источнику тока с электродвижущей силой = 0,5 В и ничтожно малым внутренним сопротивлением присоединены два металлических стержня, расположенные горизонтально и параллельно друг другу. Расстояние l между стержнями равно 20 см. Стержни находятся в однородном магнитном поле, направленном вертикально. Магнитная индукция B = 1,5 Тл. По стержням под действием сил поля скользит со скоростью V = 1 м/с прямолинейный провод сопротивлением R = 0,02 Ом. Сопротивление стержней пренебрежимо мало. Определить: 1) электродвижущую силу индукции ε_i; 2) силу F, действующую на провод со стороны поля; 3) силу тока I в цепи; 4) мощность Р₁, расходуемую на движение провода; 5) мощность Р₂, расходуемую на нагревание провода; 6) мощность Р₃, отдаваемую в цепь источника тока.

16.17. В однородном магнитном поле с индукцией B = 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной l = 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения n = 16 с^-1.

16.18. По двум гладким вертикальным проводам, отстоящим друг от друга на расстояние l, скользит под действием силы тяжести проводник-перемычка массы m. Вверху провода замкнуты на сопротивление R (рис. 16.2). Система находится в однородном магнитном поле с индукцией В, перпендикулярном плоскости, в которой перемещается перемычка. Пренебрегая сопротивлением проводов, перемычки и скользящих контактов, а также магнитным полем индукционного тока, найти установившуюся скорость перемычки.

16.19. Система отличается от рассмотренной в предыдущей задаче (см. рис. 16.2) лишь тем, что вместо сопротивления R к концам вертикальных проводов подключен конденсатор емкости С. Найти ускорение перемычки.

16.20. Металлический диск радиуса R = 25 см вращают с постоянной угловой скоростью ω = 130 рад/с вокруг его оси. Найти разность потенциалов между центром и ободом диска, если: а) внешнего магнитного поля нет; б) имеется перпендикулярное диску внешнее однородное магнитное поле с индукцией В = 5,0 мТл.

16.21. Непроводящее тонкое кольцо массы m, имеющее заряд q, может свободно вращаться вокруг своей оси. В момент t = 0 включили однородное магнитное поле, перпендикулярное плоскости кольца. Индукция поля начала нарастать по некоторому закону В(t). Найти угловую скорость ω кольца как функцию В.

16.22. Рамка площадью S = 200 см² равномерно вращается с частотой n = 10 с^-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (B = 0,2 Тл). Каково среднее значение электродвижущей силы индукции за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения?

16.23. В однородном магнитном поле с индукцией В = 0,35 Тл равномерно с частотой n = 480 c^-1 вращается рамка, содержащая N = 500 витков площадью S = 50 см². Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную электродвижущую силу индукции , возникающую в рамке.

16.24. Рамка площадью S = 100 см² содержит N = 10³ витков провода сопротивлением R₁ = 12 Ом. К концам обмотки подключено внешнее сопротивление R₂ = 20 Ом. Рамка равномерно вращается в однородном магнитном поле (B = 0,1 Тл) с частотой n = 8 с^-1. Определить максимальную мощность P_max переменного тока в цепи.

16.25. Магнитная индукция B поля между полюсами двухполюсного генератора равна 0,8 Тл. Ротор имеет N = 100 витков площадью S = 400 см². Определить частоту n вращения якоря, если максимальное значение электродвижущей силы индукции = 200 В.

16.26. Проволочный виток радиусом r = 4 см, имеющий сопротивление R = 0,01 Ом, находится в однородном магнитном поле с индукцией B = 0,04 Тл. Плоскость витка составляет угол α = 30⁰ с линиями индукции поля. Какое количество электричества q протечет по витку, если магнитное поле исчезнет?

16.27. Проволочное кольцо радиусом r = 10 см лежит на столе. Какое количество электричества q протечет по кольцу, если его повернуть с одной стороны на другую? Сопротивление R кольца равно 1 Ом. Вертикальная составляющая индукции B магнитного поля Земли равна 50 мкТл.

16.28. В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. По цепи протекло количество электричества q = 10 мкКл. Определить магнитный поток Ф, пересеченный кольцом, если сопротивление R цепи гальванометра равно 30 Ом.

16.29. Между полюсами электромагнита помещена катушка, соединенная с баллистическим гальванометром. Ось катушки параллельна линиям индукции. Катушка сопротивлением R₁ = 4 Ом имеет N = 15 витков площадью S = 2 см³. Сопротивление R₂ гальванометра равно 46 Ом. Когда ток в обмотке электромагнита выключили, по цепи гальванометра протекло количество электричества q = 90 мкКл. Вычислить магнитную индукцию В поля электромагнита.

16.30. Рамка из провода сопротивлением R = 0,01 Ом равномерно вращается в однородном магнитном поле с индукцией B = 0,05 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь S рамки равна 100 см². Найти, какое количество электричества q протечет через рамку за время поворота ее на угол α = 30° в следующих трех случаях:1) от = 0 до = 30°; 2) от до = 60°; 3) от = 90°.

16.31. Тонкий медный провод массой m = 1 г согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В = 0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определить количество электричества q, которое протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.

16.32. По длинному прямому проводу течет ток. Вблизи провода расположена квадратная рамка из тонкого провода сопротивлением R = 0,02 Ом. Провод лежит в плоскости рамки и параллелен двум ее сторонам, расстояния до которых от провода соответственно равны a₁ = 10 см, a₂ = 20 см. Найти силу тока I в проводе, если при его включении через рамку протекло количество электричества q = 693 мкКл.

16.33. По катушке индуктивностью L = 0,03 мГн течет ток I = 0,6 А. При размыкании цепи сила тока изменяется практически до нуля за время = 120 мкс. Определить среднюю электродвижущую силу самоиндукции , возникающую в контуре.

16.34. С помощью реостата равномерно увеличивают силу тока в катушке на = 0,1 А в 1 с. Индуктивность L катушки равна 0,01 Гн. Найти среднее значение электродвижущей силы самоиндукции .

16. 35. Индуктивность L катушки равна 2 мГн. Ток частотой ν= 50 Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю электродвижущую силу самоиндукции , возникающую за интервал времени Δt, в течение которого ток в катушке изменяется от минимального до максимального значения. Амплитудное значение силы тока I₀ = 10 А.

16.36. Катушка, намотанная на немагнитный цилиндрический каркас, имеет N₁ = 750 витков и индуктивность L₁ = 25 мГн. Чтобы увеличить индуктивность катушки до L₂ = 36 мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить число N₂ витков катушки после перемотки.

16.37. Соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Определить магнитный поток Ф, если сила тока I, протекающего по обмотке, равна 12 А.

16.38. Индуктивность L катушки без сердечника равна 0,02 Гн. Какое потокосцепление Ψ создается, когда по обмотке течет ток I = 5 А?

16.39. Длинный прямой соленоид, намотанный на немагнитный каркас, имеет N = 1000 витков и индуктивность L = 3 мГн. Какой магнитный поток Ф и какое потокосцепление создает соленоид при силе тока I = 1 А?

16.40. В цепи шел ток I₀ = 50 А. Источник тока можно отключить от цепи, не разрывая ее. Определить силу тока в этой цепи через t = 0,01 с после отключения ее от источника тока. Сопротивление R цепи равно 20 Ом, ее индуктивность L = 0,1 Гн.

16.41. Источник тока замкнули на катушку с сопротивлением R = 10 Ом и индуктивностью L = 1 Гн. Через сколько времени сила тока в цепи достигнет 0,9 предельного значения?

16.42. В схеме (рис. 2.104) известны ЭДС ε источника, сопротивление R и индуктивности катушек L₂ и L₂. Внутреннее сопротивление источника и сопротивления катушек пренебрежимо малы. Найти установившиеся токи в катушках после замыкания ключа К.

краткое описание, определение и формулы, закон Ленца и сферы применения

Физика

12.11.21

15 мин.

Электродвижущая сила образуется в том случае, если поместить проводник в радиус действия магнитного поля и перемещать его так, чтобы он пересекал линии напряжения. Речь касается ЭДС индукции. Таких результатов можно добиться даже с учётом того, что проводник останется на прежнем месте, а магнитное поле будет перемещаться, пересекая его линиями напряжения. Индуктированным принято называть явление электромагнитной индукции.

Оглавление:

Краткое описание

Основные параметры ЭДС

Свойства индукции

Борьба с вихревыми токами

Массивные проводники

Законы физики

Сферы применения

Краткое описание

Неподвижными зарядами создаётся статическое электрическое поле. Стабильное во времени магнитное поле возникает благодаря непрерывной подаче тока. Но на этот процесс могут влиять сопутствующие факторы. Магнитные и электрические поля существуют независимо друг от друга. Лучше всего взаимодействие этих полей демонстрирует электромагнитная индукция. Переменное электрическое поле позволяет создать специфическую среду, которая действует на доступные свободные заряды и создаёт ток. В итоге можно будет сформировать электрическое поле в том же проводнике.

Электромагнитным полем принято называть совокупность переменных и электрических магнитных зон, которые в определённых условиях порождают друг друга. Это правило актуально даже по отношению к той среде, которая не имеет свободных зарядов. Распространение в пространстве происходит по принципу электромагнитной волны.

Настоящим достижением человечества является электродинамика. Именно это изобретение оказало колоссальное воздействие на дальнейшее развитие цивилизации. В результате многочисленных экспериментов было доказано, что в природе существуют электромагнитные волны. Благодаря этому появилось радио, телекоммуникационные системы, телевидение, компьютеры, спутниковые средства навигации, а также другие атрибуты современной жизни, к которым человечество так привыкло.

В своей теории Максвелл кратко описал, что основным источником магнитных лучей может являться переменная электрическая зона. Наличие проводника не считается обязательным. Электрическое поле возникает и в пустом пространстве. Все силовые линии замкнуты. А также было установлено, что магнитные и электрические поля электромагнитной волны являются равноправными.

Основные параметры ЭДС

От общего количества задействованных силовых линий (СЛ) зависит величина ЭДС. Итоговые показатели индуктированной электродвижущей силы напрямую зависят от скорости движения объекта в магнитном поле. Большое значение также имеет длина проводника, который пересекается линиями напряжения. ЭДС будет больше индуцироваться в том случае, если основная часть проводника подвержена воздействию СЛ. Показатели электродвижущей силы напрямую зависят от того, какая индукция используется. Именно это правило изучается на уроках физики.

При движении проводника показатели ЭДС будут прямо пропорциональны длине и скорости перемещения объекта, а также индукции магнитного поля. На этот случай предусмотрена следующая формула: W = JOS. Расшифровка выглядит следующим образом:

ЭДС индукции — W.
Магнитная индукция — J.
Длина — O.
Скорость движения — S.

Для решения задач по физике нужно понимать, что ЭДС индукции может возникнуть в проводнике, который не покидает границ магнитного поля, только в том случае, если присутствуют пересекающие линии напряжения. Исключений не предусмотрено. Если траектория движения проводника будет проложена только вдоль этих линий, то никакая электродвижущая сила не будет индуцироваться. Описываемая формула может использоваться не во всех случаях. Её применение уместно только тогда, когда проводник перемещается перпендикулярно магнитным силовым линиям поля.

Направление индуктированной ЭДС не является самопроизвольным. Всё зависит от того, в какую именно сторону будет двигаться проводник. Для правильного определения направления в физике существует правило правой руки. Если человек будет держать ладонь таким образом, чтобы в неё входили магнитные линии, тогда большой палец укажет движение проводника. Остальные 4 пальца покажут направление ЭДС и тока.

Свойства индукции

Во всех научных сферах активно используется индукция, так как она имеет большое значение, когда нужно перейти от эмпирических знаний к теоретическим. Часто проводятся различные эксперименты. Благодаря этому удаётся собрать отдельные факты, которые тщательно анализируются. На этой основе строится индуктивное заключение. Необходимость таких выводов заключается в том, что они гарантируют переход от редких фактов к общим, но максимально развёрнутым положениям. Можно проследить некую связь между стремлением создать точное описание гипотезы и перейти к обобщениям.

В физике отдельное внимание уделяют индукции научного типа, так как она отличается поиском причинных связей между явлением и стремлением выявить существующие признаки объектов, объединённых в класс. Научная индукция делится на 3 категории:

Поиск и изучение причинных связей. Учитывается совокупность обстоятельств, которые предшествуют наблюдаемому явлению.
Фильтрация случаев. В отличие от базовой индукции, когда учитывается только количество исследуемых ситуаций, тщательный отбор случаев подразумевает то, что будут учтены особенности каждой из анализируемых групп. Такой подход позволяет лучше разобраться во всех параметрах ЭДС.
Научная индукция может быть построена не только на основании анализа ряда явлений и объектов. Для достижения желаемого результата должен быть изучен единственный представитель группы. Не учитываются индивидуальные свойства, благодаря которым объект выделяется среди других представителей той же категории.

Эти виды индукции имеют большое значение в научной среде. При правильном подходе можно существенно ускорить поиск правильного ответа, узнать базовые значения и открыть для себя закономерности. Такой подход позволяет не ждать, пока будут подробно исследованы все явления анализируемого класса.

Борьба с вихревыми токами

Если большой проводник находится в пределах переменного магнитного поля, то благодаря явлению электромагнитной индукции будут образованы своеобразные вихревые индукционные токи. Речь касается токов Фуко. Такого результата можно добиться даже в том случае, если проводник будет двигаться в постоянном, но неоднородном пространстве магнитного поля. Токи Фуко отличаются тем, что воздействующая на них сила приостанавливает движение проводника.

Если из немагнитного материала изготовить маятник в виде сплошной пластины, чтобы он совершал колебания между полюсами электромагнита, то при включении магнитного поля он резко остановится. Токи Фуко могут нагревать поверхности, что является крайне опасным. Именно поэтому с такими последствиями приходится бороться.

Роторы электродвигателей, а также сердечники трансформаторов изготавливаются из отдельных железных пластин, которые отделены друг от друга слоями изолятора. Благодаря этому удаётся минимизировать вероятность возникновения больших индукционных токов. Положительный эффект обусловлен тем, что пластины изготовлены из сплавов, которые обладают высоким удельным сопротивлением.

Массивные проводники

Магнитные потоки могут легко индуцировать ЭДС в пределах витков катушки. Аналогичное утверждение касается и проводников. Если магнитный поток пронизывает задействованный массивный проводник и индуцирует ЭДС, то в итоге образуются специфические индукционные токи.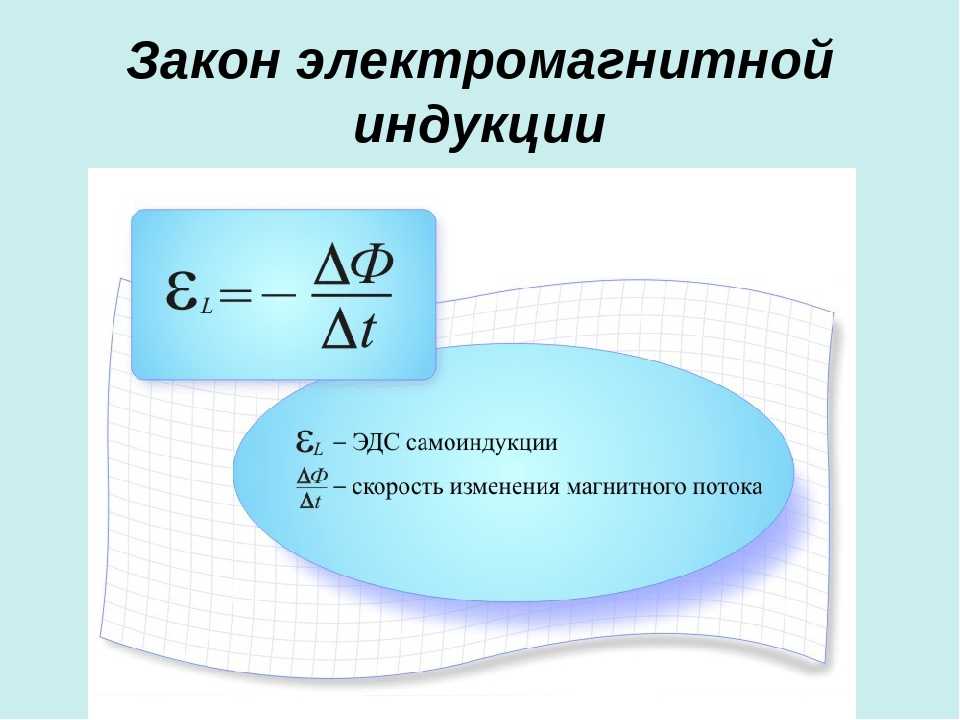 Это физическое явление нашло применение в различных отраслях. Магнитопроводы сложных механизмов, сердечники трансформаторов относятся к разряду массивных проводников, которые под воздействием индукционных токов постепенно нагреваются, что влечёт за собой негативные последствия.

Благодаря многочисленным экспериментам люди поняли, как именно взаимодействуют между собой разные материалы. Из этого становится понятно, что за счёт снижения индукционных токов сердечники и магнитопроводы для электрических установок перестали быть такими массивными. Они состоят из тонких металлических листов, которые изолированы бумагой либо покрыты слоем специального изоляционного лака. Такой подход помог прекратить распространение вихревых токов в проводнике.

Законы физики

Любое изменение магнитного поля внутри катушки обязательно влечёт за собой образование электродвижущей силы индукции. Объясняется это достаточно просто. Если попробовать замкнуть катушку на внешнюю цепь, то в итоге витки будут принимать только индукционный ток. Вокруг проводника сформируется магнитное поле. В результате воздействия всех этих процессов катушка превратится в соленоид. Это явление тщательно изучал Э. Ленц. Учёный смог вывести закон, благодаря которому можно определить, в каком именно направлении движется ток в пределах катушки. Открытие Ленца активно используется в физике.

При изменении магнитного потока электростатическая индукция создаёт в катушке ток, при котором исключено изменение ранее построенного магнитного потока. Закон Ленца актуален по отношению ко всем случаям, когда подразумевается использование индуктированного тока в проводниках. Значения не имеет форма используемого проводника и способ достижения изменения внешнего магнитного поля.

Сферы применения

К изучению электромагнитной индукции нужно отнестись ответственно, так как понимание всех секретов и правил поможет открыть дверь в мир науки. Благодаря этому можно будет создавать новые виды техники и оборудования. Электромагнитная индукция применяется в следующих случаях:

Создание индукционных печей.
Изготовление трансформаторов, различных двигателей. Именно электромагнитная индукция используется при создании асинхронных двигателей с короткозамкнутым или фазным ротором. Производство синхронных и асинхронных генераторов.
Контакторы, магнитные пускатели, датчики движения и различные типы реле не могут работать без ЭДС.
ЭДС индукции применяется в беспроводных зарядных устройствах для смартфонов, а также в микроволновых печах.

Помимо широкого спектра применения и всех преимуществ электромагнитной индукции, есть и негативные моменты. Из-за ЭДС индукции в электроэнергетике существуют большие потери на вихревые токи, присутствующие практически во всех случаях. С ними стараются бороться различными способами, но полностью ликвидировать эту проблему пока не удалось.

Лист формул электромагнитной индукции

1. Магнитный поток

Φ = ∫$\overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}$
Если поверхность замкнута, то
Φ = $\oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{A}}$
, так как магнитные силовые линии являются замкнутыми линиями и свободных магнитных полюсов не существует.
B = $\frac{\phi}{A}$

2. Электромагнитная индукция: законы Фарадея

(a) Первый закон:
Всякий раз, когда происходит изменение магнитного потока, связанного с цепью во времени, в цепи возникает ЭДС индукции, которая существует до тех пор, пока продолжается изменение магнитного потока.

(b) Второй закон:
e ∝ $\left(\frac{d \phi}{d t}\right)$

3. Закон Ленца

Направление ЭДС индукции или тока в цепь такова, что она противостоит причине, из-за которой она создана, так что
e = – N $\left(\frac{d \phi}{d t}\right)$
N → Количество витков в катушке.
Закон Ленца, основанный на сохранении энергии.

4. ЭДС тока и заряда, индуцируемые в цепи

(а) ЭДС индукции e = – N $\frac{d \phi}{d t}$ = – $\frac{\mathrm{N }\left(\phi_{2}-\phi_{1}\right)}{\mathrm{t}}$

(b) Наведенный ток I = $\frac{\mathrm{e}}{\ mathrm {R}} = – \ frac {\ mathrm {N}} {\ mathrm {R}} \ left (\ frac {\ mathrm {d} \ phi} {\ mathrm {dt}} \ right) = – \ frac{\ mathrm {N}} {\ mathrm {R}} \ frac {\ left (\ phi_ {2} – \ phi_ {1} \ right)} {\ mathrm {t}} $

(c) Наведенный заряд q = – $\frac{\mathrm{N}\left(\phi_{2}-\phi_{1}\right)}{\mathrm{R}}=\frac{\ mathrm{N}\left(\phi_{1}-\phi_{2}\right)}{\mathrm{R}}$
Индуцированный заряд зависит только от чистого изменения потока не зависит от скорости изменения потока .

5. ЭДС, вызванная линейным движением проводящего стержня в однородном магнитном поле

e = –$\vec{\ell} \cdot(\overrightarrow{\mathrm{v}} \times \overrightarrow {\mathrm{B}})$
перпендикулярны друг другу, то
e = Bvl вольт

6. ЭДС индукции при вращении проводящего стержня в однородном магнитном поле
e = $\frac{1}{2}$ Bwl ² = Bπnl ² = BAn
, где n — частота вращения.

7. ЭДС индукции при вращении металлического диска в однородном магнитном поле BAn
здесь O имеет более высокий потенциал, чем A (см. рис.)

8. ЭДС индукции, ток и энергия

Сохранение в прямоугольной петле, движущейся в неоднородном магнитном поле с постоянной скоростью:

(i) Чистое увеличение потока, проходящего через катушку во времени Δt
ΔΦ = (B ₂ – B ₁ ) lvΔt

(ii) ЭДС в катушке
e = (B ₁ – B ₂ )l v

R, то ток, индуцируемый в катушке
I = $\frac{\mathrm{e}}{\mathrm{R}}=\frac{\left(\mathrm{B}_{1}-\mathrm{ B}_{2}\right)}{\mathrm{R}} \ell \mathrm{v}$ 9{2}}{\mathrm{R}}\) Δt джоулей
или H = W

9. Вращение прямоугольной катушки в однородном магнитном поле

(a) Магнитный поток, связанный с катушкой
Φ = BAN cos θ
= BAN cos ωt

(b) ЭДС, наведенная в катушке
e = – $\frac{d \phi}{d t}$ = BA Nω sin ωt = e ₀ sin ωt

(c ) Ток, индуцируемый в катушке.
I = $\frac{\mathrm{e}}{\mathrm{R}}=\frac{\mathrm{BAN} \omega}{\mathrm{R}}$ = sin ωt
= $\ frac{\ mathrm {e} _ {0}} {\ mathrm {R}} $ sin ωt

(d) ЭДС и ток, индуцируемые в катушке, являются ЭДС переменного тока и переменного тока.

10. Самоиндукция и собственная индуктивность (L)

При изменении тока в катушке возникает ЭДС индукции. I ПРИМЕЧАНИЯ, то явление называется самоиндукцией j
(i) Φ ∝ I или Φ = LI
или L = $\frac{\phi}{\mathrm{I}}$

( ii) e = – L$\frac{\mathrm{d} \mathrm{I}}{\mathrm{dt}}$
, где L – постоянная, называемая собственной индуктивностью или коэффициентом самоиндукции. 9{2} A}{\ell}\)

(v) Две катушки собственной индуктивности L ₁ и L ₂, расположенные далеко друг от друга (т. е. без соединения j)

(a) Для последовательного соединения : j
L = L ₁ + L ₂ …. L _n

(b) Для параллельной комбинации:
$\frac{1}{L}=\frac{1}{L_{1}}+\frac{1}{L_{2}} \ldots \ldots . \frac{1}{L_{n}}$

11. Взаимная индукция и взаимная индуктивность

(а) Об изменении тока в одной катушке, если магнитный поток связан с § второй катушкой изменения и э.д.с. производится в этой катушке, то это явление называется взаимной индукцией.

(б) Φ ₂ ∝ I ₁ или Φ ₂ = MI ₁
или M = $\frac{\phi_{2}}{I_{1}}$

( c) e ₂ = –$\frac{\mathrm{d} \phi_{2}}{\mathrm{dt}}$ = -M $\frac{\mathrm{dI}_{1} }{\mathrm{dt}}$ или M = $\frac{\mathrm{e}_{2}}{-\left(\mathrm{dI}_{1} / \mathrm{dt}\right )}$

(г) M ₁₂ = M ₂₁ = M

(д) Взаимная индуктивность двух коаксиальных соленоидов
M = $\frac{\mu_{0} N_{1} N_{ 2} А}{\ell}$

(f) Если две катушки собственной индуктивности L ₁ и L ₂ намотаны друг на друга, взаимная индуктивность будет равна
M = K $\ sqrt{\mathrm{L}_{1} \mathrm{L}_{2}}$
, где K называется константой связи.

(g) Для двух катушек, намотанных в одном направлении и соединенных последовательно
L = L ₁ + L ₂ + 2M
Для двух катушек, намотанных в противоположном направлении и соединенных последовательно
L = L ₁ + L ₂ – 2M
Для двух катушек, соединенных параллельно 9{2}}{2 \mu_{0}}\)

13. В цепи L-R

Устройство, преобразующее электрическую энергию в механическую.
Обратная ЭДС e ∝ ω
Ток, протекающий в катушке \)
или e = e _b + i _a R
, где R — сопротивление катушки.
Выходная мощность = i _a e _b
Эффективность η = $\frac{e_{b}}{e}$ × 100 % и очистите все свои запросы и улучшите свои навыки.

Хотя этот закон полностью верен, с современной точки зрения есть два различных явления, количество которых описывается этой формулой: петля, которая меняет свою площадь $A(t)$ в постоянном магнитном поле $\vec{B}$, и петля постоянной площади в переменном магнитном поле $\vec{B}(t)$. Объяснение в каждом случае разное – в первом случае происхождение ЭДС состоит в том, что из-за изменения площади петли возникает асимметричная сила Лоренца (сила внешнего магнитного поля на (связанные или свободные) заряды в петле материал) генерируется в контуре, и это, в свою очередь, вызывает ненулевую ЭДС.

Фундаментальное объяснение второго случая, однако, гораздо менее тривиально и сопряжено с некоторыми трудностями. В курсе по электромагнетизму, который я недавно изучал, лектор привел релятивистский аргумент в пользу правильности правила $ \vec{\nabla} \times \vec{E} = – \frac{ \partial\vec{B}}{\partial t}$, которое основано на фундаментальном наблюдении, что это уравнение является результатом требования, чтобы закон магнетизма Гаусса (который утверждает, что $\nabla \cdot \vec{B} =0$) был инвариантен относительно изменения системы отсчета ссылки.

То есть это наблюдение использует формулы релятивистского преобразования для электромагнитного поля (как электрического $\vec{E}$, так и магнитного $\vec{B}$) и преобразования Лоренца временных и пространственных координат для вывода Фарадея закона в случае изменения магнитного поля.