Практикум по решению задач по «Кинематике». 9, 10 класс
Задачи по кинематике
Задача 1. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличивается со 144 до 216 км/ч?
Задача 2 За какое время ракета приобретает первую космическую скорость 7,9 км/с, если она будет двигаться с ускорением 50 м/с 2 ?
Задача 3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч, а время разгона 40 с.
Задача 4 Скорость гоночного автомобиля в момент начала разгона 10 м/с, ускорение 5 м/с 2. Определите путь, пройденный автомобилем за 10 с после начала движения. Какова скорость автомобиля в конце десятой секунды разгона?
Задача 5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен 10 м. Чему равен тормозной путь этого же автомобиля при скорости 100 км/ч?
Задача 6 Какова длинна пробега самолета при посадке, если его посадочная скорость 140 км/ч, а ускорение при торможении 2 м/с 2 ?
Задача 7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по сухой дороге проходит 30 м, а по мокрой – 90 м. Определите для каждого случая ускорение и время торможения.
Определите для каждого случая ускорение и время торможения.
Задача 8 При равноускоренном движении с начальной скоростью 5 м/с тело за 3 с прошло 20 м. С каким ускорением двигалось тело? Какова его скорость в конце третьей секунды?
Задача 9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную скорость 9 км/ч, спускается с горы с ускорением 0,4 м/с 2. Второй поднимается в гору с начальной скоростью 18 км/ч и ускорением 0,2 м/с 2. Через какое время встретятся велосипедисты, если начальное расстояние между ними 200 м?
Задача 10 Уравнение координаты имеет вид Х = 4 + 1,5t + t 2. Какое это движение? Напишите формулу зависимости скорости тела от времени. Чему равны скорость и координата тела через 6 с?
Задачи по кинематике
Задача 1. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличивается со 144 до 216 км/ч?
Задача 2 За какое время ракета приобретает первую космическую скорость 7,9 км/с, если она будет двигаться с ускорением 50 м/с 2 ?
Задача 3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч, а время разгона 40 с.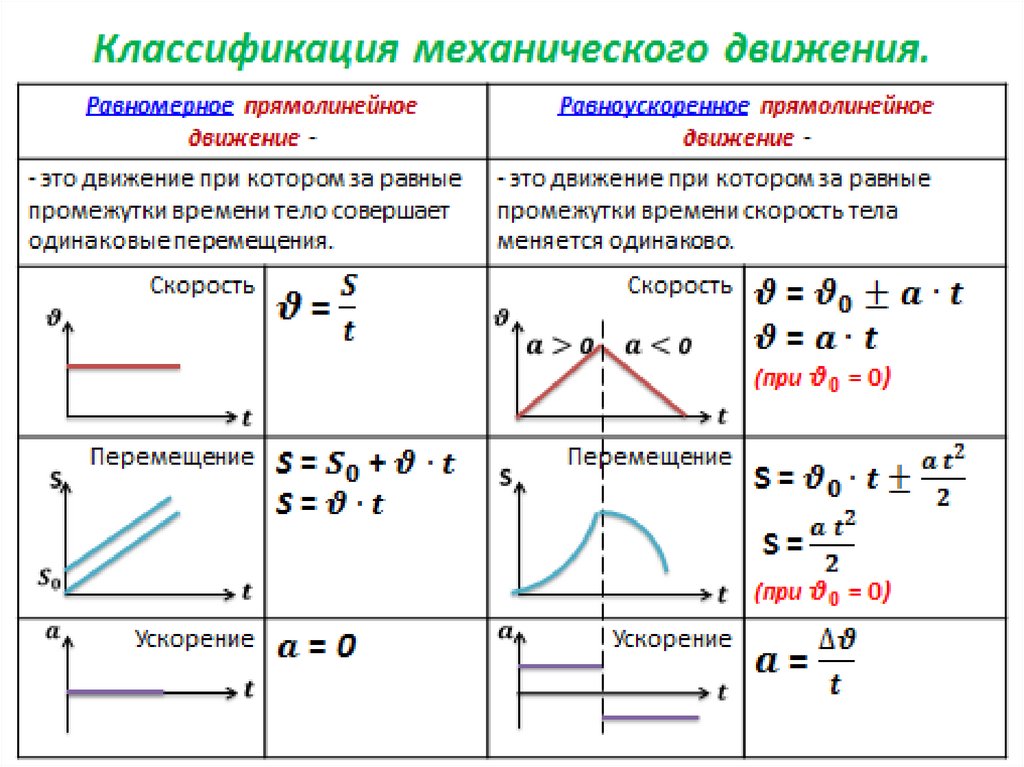
Задача 4 Скорость гоночного автомобиля в момент начала разгона 10 м/с, ускорение 5 м/с 2. Определите путь, пройденный автомобилем за 10 с после начала движения. Какова скорость автомобиля в конце десятой секунды разгона?
Задача 5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен 10 м. Чему равен тормозной путь этого же автомобиля при скорости 100 км/ч?
Задача 6 Какова длинна пробега самолета при посадке, если его посадочная скорость 140 км/ч, а ускорение при торможении 2 м/с 2 ?
Задача 7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по сухой дороге проходит 30 м, а по мокрой – 90 м. Определите для каждого случая ускорение и время торможения.
Задача 8 При равноускоренном движении с начальной скоростью 5 м/с тело за 3 с прошло 20 м. С каким ускорением двигалось тело? Какова его скорость в конце третьей секунды?
Задача 9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную скорость 9 км/ч, спускается с горы с ускорением 0,4 м/с 2. Второй поднимается в гору с начальной скоростью 18 км/ч и ускорением 0,2 м/с 2. Через какое время встретятся велосипедисты, если начальное расстояние между ними 200 м?
Второй поднимается в гору с начальной скоростью 18 км/ч и ускорением 0,2 м/с 2. Через какое время встретятся велосипедисты, если начальное расстояние между ними 200 м?
Задача 10 Уравнение координаты имеет вид Х = 4 + 1,5t + t 2. Какое это движение? Напишите формулу зависимости скорости тела от времени. Чему равны скорость и координата тела через 6 с?
25) A = (VF-VI)/T
Примечания к лекции:
Уравнения кинематики
будут протестированы на эти производные; просто информация для тех, кто заинтересован)
Документы, которые могут вам понадобиться:
Опасности отвлеченного вождения (pdf или google doc)
Distracted Driving Lab (pdf или google doc)
Вопросы по статьям об отвлеченном вождении (pdf)
Лаборатория подбрасывания мяча на детекторе движения (pdf или google doc)
3 октября 2016 г. : Учебные пособия по уравнениям кинематики
: Учебные пособия по уравнениям кинематики
Загрузить полный лист задач EXTRA по уравнениям EXTRA или гугл документ). Сначала попробуйте их, прежде чем загружать ответы (pdf или google doc)! В документе Google , а не есть ответы, только подсказки.
Говорящие уроки! Версия 1 — это полная тренировка брошенного предмета, а версия 2 — предмет, брошенный прямо вверх. Не забудьте скачать его, чтобы он говорил с вами!
Справка по домашнему заданию: Они расположены в хронологическом порядке, самые последние внизу
21 сентября 2015 г. стр. 65 #18, 19, 20, 21 и стр. 69 #26
18. (a) Используйте уравнение оранжевого цвета для определения конечной скорости. Не забудьте использовать + для перехода вперед и – для возврата назад! (<2)
(b) Используйте уравнение оранжевого цвета для определения конечной скорости. Не забудьте использовать + для перехода вперед и – для возврата назад! (<2)
Не забудьте использовать + для перехода вперед и – для возврата назад! (<2)
19. Не забудьте перевести в м/с! В противном случае ваши юниты не будут совпадать. Используйте уравнение оранжевого цвета, чтобы найти конечную скорость. (>30)
20. Используйте уравнение оранжевого цвета, чтобы найти время. (>5)
21. Используйте уравнение оранжевого цвета, чтобы найти время. (<10)
26. Вам даны начальная скорость и конечная скорость, а также ускорение. Поскольку вы ищете время, используйте уравнение Оранжа. (<10)
23 сентября 2015 г. Стр. 69 № 27-29 и стр. 71 #34, 36, 37, 39
27. Вам даны начальная и конечная скорости, а также расстояние. Поскольку вы решаете на время, используйте красное уравнение. (>300)
28. Вам даны начальная и конечная скорости, а также время. Поскольку вы решаете расстояние, используйте красное уравнение. (<10)
(<10)
29. Вам даны конечная скорость, время и расстояние. Используйте красное уравнение для определения начальной скорости. (<1)
34. Вам даны начальная и конечная скорости, а также расстояние. Используйте зеленое уравнение, чтобы найти ускорение. (<2)
36. Вам даны начальная и конечная скорости, а также время. Используйте красное уравнение, чтобы найти расстояние при ускорении. ТОГДА используйте синее уравнение, чтобы найти, как далеко она проехала с этой постоянной скоростью. Сложите два вместе, чтобы получить общее расстояние (> 30).
37.Вам даны начальная скорость, перемещение и ускорение. Используйте зеленое уравнение, чтобы найти конечную скорость. (>70)
39. а. Вам даны начальная скорость, время и ускорение самолета. Используйте фиолетовое уравнение, чтобы найти пройденное расстояние. (>1250) б. Теперь у вас есть гораздо больше информации (вы можете использовать уравнения зеленого, красного или оранжевого цветов), но чтобы быть уверенным, что вы все сделали правильно, используйте только ту информацию, которую вы получили изначально, и игнорируйте тот факт, что вы знаете расстояние, поэтому попробуйте оранжевое уравнение. уравнение. (<100)
уравнение. (<100)
24 сентября 2015 г. с. 74 #42, 44, 45, стр. 80 #63, 75, 76
42. а. Используйте оранжевое уравнение, чтобы найти конечную скорость. Помните, что он должен быть отрицательным, потому что он идет вниз! (<40) б. Теперь у вас есть больше информации (вы можете использовать уравнения зеленого, красного или фиолетового цвета), но чтобы быть уверенным, что вы все сделали правильно, используйте только информацию, которую вы получили изначально, и игнорируйте тот факт, что вы знаете расстояние, поэтому попробуйте уравнение фиолетового цвета. (<80)
44. Вы знаете, что поскольку он упал из состояния покоя, начальная скорость равна нулю. Вы также знаете, как на него действует гравитация и как далеко он падает. Используйте зеленое уравнение, чтобы найти конечную скорость. Но будьте осторожны с квадратным корнем! (<10)
45.а. Поскольку мяч подбрасывается вверх, вы знаете, что гравитация тянет его вниз. В высшей точке конечная скорость равна нулю. Зная конечную скорость, ускорение и начальную скорость, используйте уравнение Грина для определения расстояния. (<30) б. Теперь, когда у вас есть больше информации, вы можете использовать красное, оранжевое или фиолетовое уравнения для решения времени. Вы можете быть осторожны и использовать только то, что было дано в исходной задаче и уравнении апельсина для решения на время. (<5)
В высшей точке конечная скорость равна нулю. Зная конечную скорость, ускорение и начальную скорость, используйте уравнение Грина для определения расстояния. (<30) б. Теперь, когда у вас есть больше информации, вы можете использовать красное, оранжевое или фиолетовое уравнения для решения времени. Вы можете быть осторожны и использовать только то, что было дано в исходной задаче и уравнении апельсина для решения на время. (<5)
#63, 75, 76 – концептуальные вопросы.
28 сентября 2015 г. с. 75 #49, 50, 51 стр. 81 #78, 81, с. 89, 91, с. 85 #1-6
49. Вам известно отрицательное смещение, вызванное падением ключей, а также тот факт, что они падали из состояния покоя и ускорялись под действием силы тяжести. Используйте зеленое уравнение, чтобы найти конечную скорость. (>9)
50. Помните, что подъем и спуск занял 3 секунды! Вы знаете, что конечная скорость на максимальной высоте равна нулю, что на нее действует гравитация и время, которое на это ушло. Используйте оранжевое уравнение для определения начальной скорости. (<15)
Используйте оранжевое уравнение для определения начальной скорости. (<15)
51. Теперь, когда вы знаете начальную скорость, вы можете использовать уравнения зеленого, фиолетового или красного цвета для определения расстояния.
78. Вам не нужно ничего вычислять, но может помочь перечисление ваших переменных.
89. а. Зная начальную скорость, ускорение и время, найдите перемещение, используя фиолетовое уравнение. (>40) б. То же, что и (а), но с другим временем. (>40)
91. Эта проблема состоит из двух частей. Используйте синее уравнение, чтобы найти расстояние, которое она проходит, реагируя на это. (<20) Затем вы должны использовать зеленое уравнение, чтобы найти расстояние, пока она замедляется (отрицательно ускоряется), чтобы остановиться. Вы знаете, каковы ее начальная и конечная скорости и задано ускорение. (<30) Общее расстояние, которое она проходит, равно сумме двух расстояний.
#1-6 являются отличной практикой для части множественного выбора ваших тестов!
1. Попробуйте фиолетовое уравнение.
Попробуйте фиолетовое уравнение.
2. Попробуйте уравнение апельсина.
3. Попробуйте уравнение зеленого цвета.
4. Попробуйте фиолетовое уравнение.
5. Попробуйте фиолетовое уравнение.
6. Попробуйте уравнение зеленого цвета.
Вот решения следующих проблем: стр. 75 #49, 50, 51 стр. 81 #78, 81, с. 89, 91, с. 85 #1-6
29 сентября 2015 г. с. 71 #30; стр. 81 #86, 97, с. 82-83 #106, 107, 113
30. Это двухшаговая задача! Человек движется с постоянной скоростью и затем ускоряется. Найдите d1, когда он движется с постоянной скоростью, а затем d2, когда он ускоряется. (>4000)
86. а. Попробуйте уравнение апельсина. (>600) б. Сравните со скоростью звука 331 м/с.
97. Попробуйте фиолетовое уравнение. (>1)
106. а. Учитывая начальную и конечную скорости и тот факт, что он притягивается вниз под действием силы тяжести, вы можете использовать уравнение Грина для расчета расстояния, на которое он падает. (<300) б. Теперь у вас есть много информации, кроме времени, и вы можете использовать красное, фиолетовое или оранжевое уравнение для определения времени (<8). 92, и вы знаете начальную скорость, вы можете найти расстояние с помощью фиолетового уравнения. Не забудьте перевести скорость в м/с!! (<2)
(<300) б. Теперь у вас есть много информации, кроме времени, и вы можете использовать красное, фиолетовое или оранжевое уравнение для определения времени (<8). 92, и вы знаете начальную скорость, вы можете найти расстояние с помощью фиолетового уравнения. Не забудьте перевести скорость в м/с!! (<2)
Рекомендуется показывать все свои работы; полный расчет GUESS.
Стр. 80 #53, 54, 59, 66, 67, 69
Стр. 65 № 18-21; стр. 69 #26
Стр. 69 № 27-29; стр. 71 #34, 36, 37, 39
Стр. 74 № 42, 44, 45; стр. 80 #63, 75, 76
Стр. 75 № 49, 50, 51; стр. 81 #78, 81; стр. 82 #89, 91; стр. 85 #1-6
стр. 71 #30; стр. 81 #86, 97; стр. 82 #106, 107, 113
Вопросы для ежедневной разминки (7)
1 октября 2014 г. Рабочий лист вождения с отвлечением внимания
Рабочий лист вождения с отвлечением внимания
. (<10)
Сценарий 1:
2. Прежде чем начать торможение, помните, что вы движетесь с постоянной скоростью. (<10)
3. В этой задаче вы замедляетесь до 0 м/с с 11,2 м/с. (<10)
Сценарий 2:
6. Прежде чем начать торможение, помните, что вы движетесь с постоянной скоростью. (>10)
Сценарий 3:
движутся с постоянной скоростью.(>10)
10. В этой задаче вы замедляетесь до 0 м/с с 26,8 м/с. (>40)
Сценарий 4:
13. Прежде чем начать торможение, помните, что вы движетесь с постоянной скоростью. (>40)
21.7 Уравнения движения | Движение в одном измерении
21.7 Уравнения движения (ESAHG)
В этом разделе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения в терминах
слова и графики. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.
Мы рассмотрели описание движения в терминах
слова и графики. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.
Этот раздел посвящен решению задач, связанных с равноускоренным движением. Другими словами, движение в постоянное ускорение.
9{-1}$} \text{ во время } t \\ \vec{s} & = \text{смещение} \text{(м)} \end{align*}Галилео Галилей из Пизы, Италия, первым определил правильный математический закон ускорения: общее пройденное расстояние, начиная с состояния покоя, пропорционально квадрату времени. Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила — часто трение, принял аристотелевскую гипотезу о том, что объекты «естественно» замедляются и останавливаются, если не действует сила на них. Этот принцип был включен в законы движения Ньютона (1-й закон). 9{2} + 2\vec{a}\Delta \vec{x} \qquad (4) \конец{выравнивание*}
 Используйте это, когда
пытаясь ответить на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины
(\({\vec{v}}_{i}\), \({\vec{v}}_{f}\), \(\Delta \vec{x}\), \(t\) или \(\vec{a}\)) чтобы вычислить
четвертый.
Используйте это, когда
пытаясь ответить на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины
(\({\vec{v}}_{i}\), \({\vec{v}}_{f}\), \(\Delta \vec{x}\), \(t\) или \(\vec{a}\)) чтобы вычислить
четвертый.Стратегия решения проблем:
Внимательно прочитайте вопрос, чтобы определить приведенные количества. Запишите их.
Определите используемое уравнение. Запишите!!!
Убедитесь, что все значения указаны в правильных единицах, и заполните их в уравнении.
Подсчитайте ответ и проверьте единицы измерения.
Рабочий пример 7: Уравнения движения 9{-1}$} \\ \Дельта\vec{x} & = \text{725}\text{м} \\ т & = \текст{10}\текст{с} \\ \vec{a} & = ? \конец{выравнивание*}
Найдите уравнение движения, связывающее заданную информацию с ускорением
Если вам трудно найти правильное уравнение, найдите неданную величину, а затем найдите
уравнение, в котором есть эта величина.
Все величины указаны в единицах СИ.
Мы можем использовать уравнение 1 – помните, что теперь мы также знаем ускорение объекта.
\[{\vec{v}}_{f}={\vec{v}}_{i}+\vec{a}t\]
Подставьте значения и рассчитайте конечную скорость
\начать{выравнивать*} {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + at \\ {\vec{v}}_{f} & = \text{0}\text{м·с$^{-1}$} + \left(\text{8}\text{ m·s$^{-2}$}\right)\left(\text{4}\text{s}\right) \\ & = \text{32}\text{ м·с$^{-1}$} \text{ Восток} \end{выравнивание*} 9{-1}$}\) в \(\text{8}\) \(\text{s}\).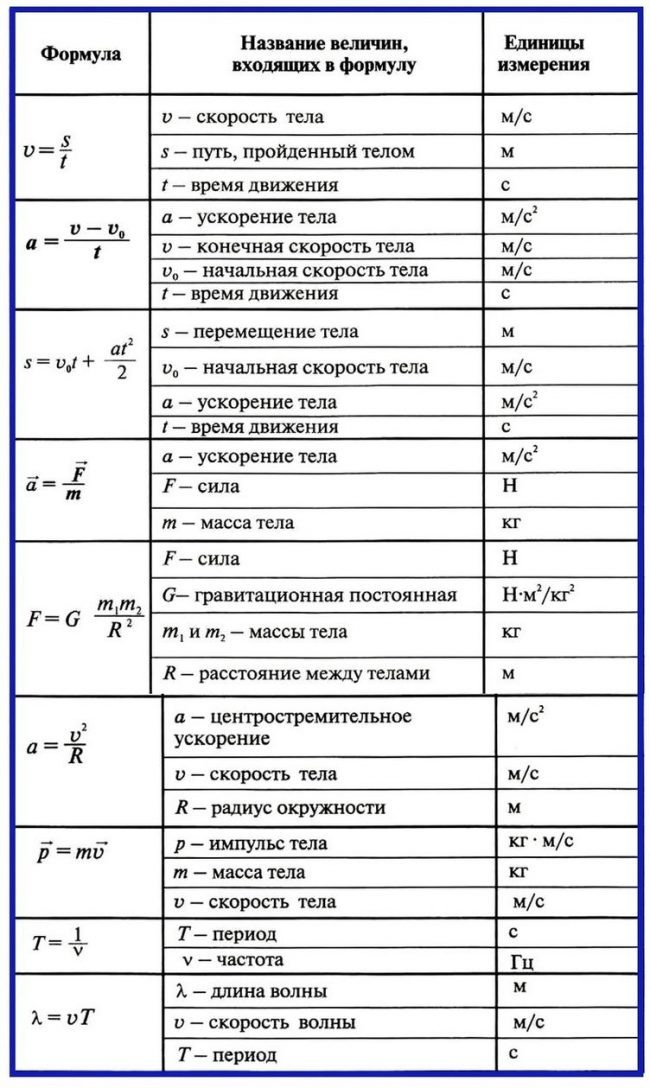 Рассчитайте требуемое ускорение и
общее расстояние, пройденное за это время.
Рассчитайте требуемое ускорение и
общее расстояние, пройденное за это время.Решение пока недоступно
Расширение: Нахождение уравнений движения (ESAHH)
Следующая информация не является частью учебного плана и может рассматриваться как дополнительная информация.
Вывод уравнения 1
По определению ускорения:
\[\vec{a}=\frac{\Delta \vec{v}}{t}\], где \(\Delta \vec{v}\) – изменение скорости, т.е. \(\Delta v={\vec{v}}_{f} – {\vec{v}}_{i}\ ). Таким образом, мы есть
\начать{выравнивать*} \vec{a} & = \frac{{\vec{v}}_{f} – {\vec{v}}_{i}}{t} \\ {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + \ vec {a} t \конец{выравнивание*}Вывод уравнения 2
Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени. Для равноускоренное движение самая сложная диаграмма зависимости скорости от времени, которую мы можем иметь, это прямая
линия.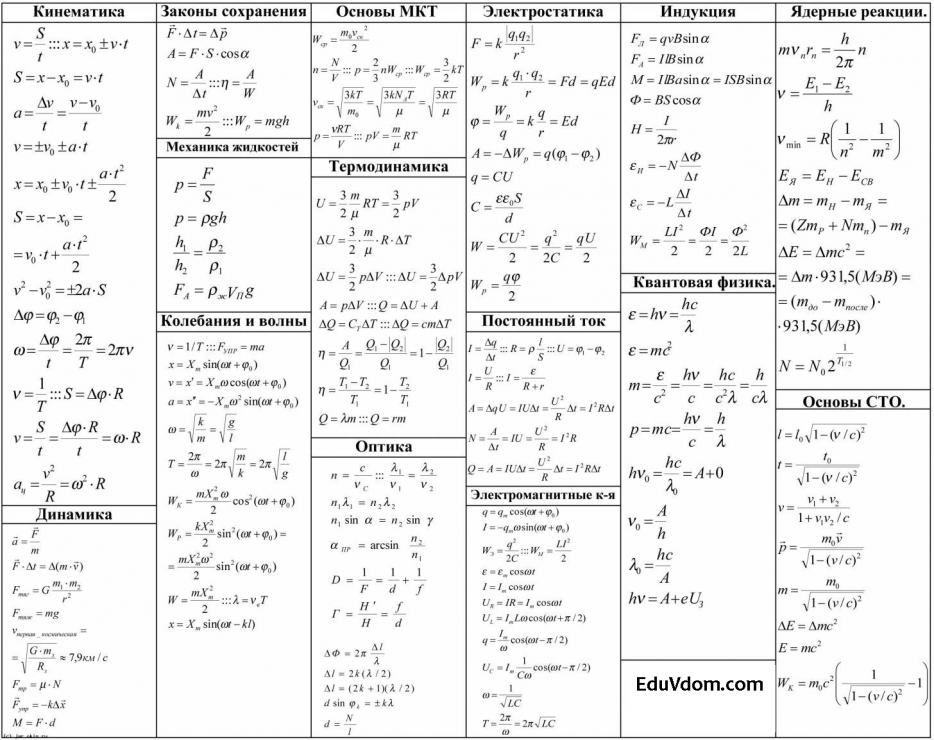 Посмотрите на график ниже — он представляет собой объект с начальной скоростью \({\vec{v}}_{i}\) , разогнавшись до конечной скорости \({\vec{v}}_{f}\) за общее время т .
Посмотрите на график ниже — он представляет собой объект с начальной скоростью \({\vec{v}}_{i}\) , разогнавшись до конечной скорости \({\vec{v}}_{f}\) за общее время т .
Чтобы рассчитать окончательное смещение, мы должны вычислить площадь под графиком — это как раз площадь прямоугольник, добавленный к площади треугольника. Эта часть графика заштрихована для ясности.
\начать{выравнивать*} {\ text {Площадь}} _ {△} & = \ frac {1} {2} b \ times h \\ & = \frac{1}{2} t \times \left({v}_{f} – {v}_{i}\right) \\ & = \frac{1}{2}{v}_{f}t – \frac{1}{2}{v}_{i}t \end{выравнивание*}\begin{выравнивание*} {\ text {Площадь}} _ {\ квадрат} & = l \ раз b \\ & = t\times {v}_{i} \\ & = {v}_{i}t \end{выравнивание*}\begin{выравнивание*} \text{Перемещение} & = {\text{Площадь}}_{\квадрат} + {\text{Площадь}}_{△} \\ \Delta \vec{x} & = {v}_{i}t + \frac{1}{2}{v}_{f}t – \frac{1}{2}{v}_{i} т\\ \ Delta \ vec {x} & = \ frac {\ left ({v} _ {i} + {v} _ {f} \ right)} {2} t \конец{выравнивание*} 9{2} \конец{выравнивание*}Вывод уравнения 4
Это уравнение получено путем исключения переменной времени в приведенном выше уравнении.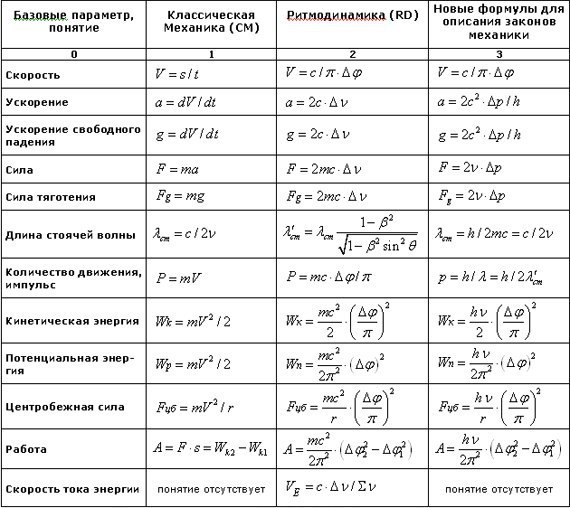 {2} + 2 \ vec {a} \ Delta \ vec {x}
\конец{выравнивание*}
{2} + 2 \ vec {a} \ Delta \ vec {x}
\конец{выравнивание*}
Это дает нам конечную скорость с точки зрения начальной скорости, ускорения и смещения и составляет не зависит от переменной времени.
Реальные приложения (ESAHI)
То, что мы узнали в этой главе, можно непосредственно применить к безопасности дорожного движения. Мы можем проанализировать отношения между скоростью и тормозным путем. Следующий рабочий пример иллюстрирует это приложение.
Рабочий пример 9: Тормозной путь 9{-2}$}\). Время его реакции на удар тормоза составляет \(\text{0,5}\) секунд. Врежется ли грузовик в ребенка?
Проанализируйте проблему и определите, какая информация предоставляется
Полезно нарисовать временную шкалу, подобную этой:
Нам нужно знать следующее:
Какое расстояние преодолевает водитель, прежде чем нажать на тормоз.
Через сколько времени грузовик остановится после нажатия на тормоз.

