Физические величины в 8 классе | Материал для подготовки к ЕГЭ (ГИА) по физике (8 класс) на тему:
Опубликовано 24.01.2017 – 22:07 – Бекетова Татьяна Григорьевна
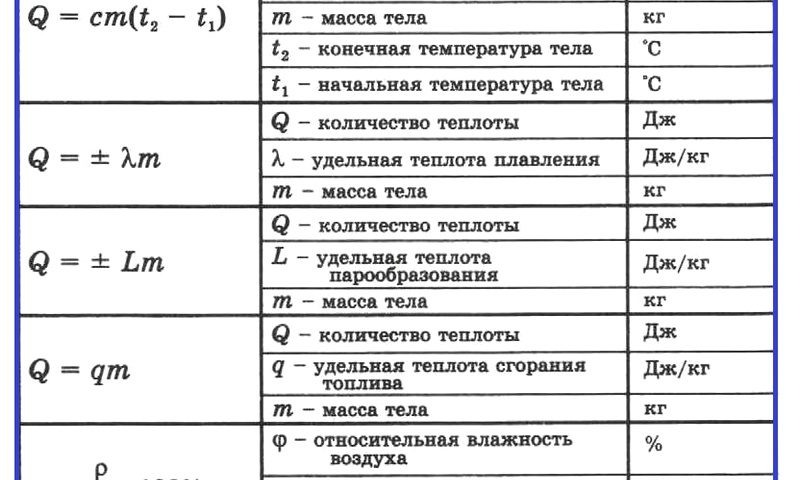
Таблица физических величин, изучаемых в 8 классе (физическая величина, буквенное обозначение, формула для вычисления величины, единицы измерения)
Скачать:
Предварительный просмотр:
Физические величины 8 класс.
№ | Физическая величина | Обозн | Формулы | Единицы измерения | Прибор (способ определения) |
Количество теплоты | Q (ку) | Q = С m ( t 2-t 1 ) | Джоуль (Дж. | ||
Удельная теплоемкость | С (це) | С = Q / m (t 2-t 1) | Дж/кг 0С | по таблице | |
Удельная теплота сгорания | q (ку) | q = Q/m | Дж / кг. | по таблице | |
Удельная теплота плавления | λ(лямбда) | λ= Q/m | Дж / кг. | по таблице | |
Уд. | L (эль) | L = Q/m | Дж / кг. | по таблице | |
КПД двигателя | η (эта) | η =Аполезн/Азатр .100 % | % | ||
Сила тока (Закон Ома) | I (и) | I=U/R I =q/t | Ампер (А) | амперметр | |
Электрический заряд | q (ку) | q=It | Кулон (Кл) | ||
Работа тока | А (а) | A=Uq = UIt=Pt | Джоуль (Дж) | ||
Напряжение | U (у) | U=IR=A/q | Вольт (В) | вольтметр | |
Сопротивление | R (эр) | R = U/I R= ρ l/S | Ом (Ом) | омметр | |
Удельное сопротивление | ρ(ро) | ρ = RS/l | Ом мм2/м | по таблице | |
Длина проводника | l (эль) | l = RS/ ρ | м | линейка | |
Площадь поперечного сечения | S (эс) | S = l ρ / R | мм2 | микрометр | |
Мощность тока | Р(пэ) | P = A / t = UI | Ватт (Вт) | ваттметр | |
Закон Джоуля Ленца | Q = I 2 R t | Дж | |||
Оптическая сила линзы | D(дэ) | D=1/F | диоптрия (дптр) | ||
Фокусное расстояние линзы | F(эф) | F =1/D | м |
По теме: методические разработки, презентации и конспекты
Материалы к уроку “Физические величины” 7 класс
Урок входит в систему вводных уроков по физике 7 класса. ..
..
Урок по физике для 7 класса Тема: Физические величины. Измерение физических величин. Точность и погрешность измерений.
Тема: Измерение физических величин. Точность и погрешность и измерений….
Тест “Основные единицы физических величин” 7 класс
Проверочный тест на знание единиц физических величин. Три варианта заданий и один упрощенный вариант. Проверочная работа проводится в конце учебного года….
“Физические величины. Измерение физических величин” 7 класс
Презентация по теме “Физические величины. Измерение физических величин” 7 класс…
Презентация “Измерение физических величин”, 7 класс
Презентация к уроку “Физические величины “, 7 класс…
Презентация по физике “Физические величины.Измерение физических величин” 7 класс
Презентация по физике “Физические величины.Измерение физических величин” 7 класс…
Конспект урока по теме «Наблюдения и опыты. Физические величины. Измерение физических величин» 7 класс
Конспект урока по теме «Наблюдения и опыты. Физические величины. Измерение физических величин» 7 класс по УМК “Сфера” В.В. Белага…
Физические величины. Измерение физических величин» 7 класс по УМК “Сфера” В.В. Белага…
Поделиться:
Формулы по физике 8 класс
In естественные наукиТэги 8 класс, закон, наука, обучение, физика, формулыПросмотров: 26.3K
Каждый следующий год обучения в школе усложняет список используемых понятий, а также рассматривает явления, которые становятся все более развернутыми. В формулы по физике 8 класса входят криволинейное движение, давление, ускорение, импульс и различные виды энергии тела. Рассмотрим некоторые базовые формулы, которые относятся к механике и термодинамике.
Механика
Одними из важнейших понятий, которыми оперируют формулы по физике в 8 классе, являются давление и плотность. Они участвуют в расчетах многих процессов, которые относятся к области механики.
Давление может быть вычислено как отношение силы на площадь, где она действует.
P = F / S
Здесь
P — величина давления. В базовой системе измерения оно обозначается в Паскалях, единица названа по имени ученого физика, который впервые обосновал введение подобной оценки. В непереведенных единицах давление обозначается как «Ньютон / квадратный метр», что следует из формулы. Сила, деленная на площадь, обе величины — в стандарте СИ;
F — действующая сила;
S — площадь, на которую распространяется действие. Чтобы понять важность этого показателя, стоит вспомнить иголку и молоток. Если положить молоток на руку, человек ничего не почувствует, кроме тяжести и давления на кожу. Если же молоток при этом будет опираться на иглу, у которой площадь острия ничтожная — руку проткнет насквозь. Это следует из формулы давления — большая площадь молотка подразумевает низкое давление, тонкая игла — высочайший показатель.
Обратные формулы позволяют найти любую величину по двум известным другим.
- Действующая сила по известному давлению и площади: F = S * P
- Искомая площадь по силе и величине давления: S = F / P
Участвующие величины в системе измерения СИ
- Давление P — Паскаль, Па, Н/м.
- Сила — Ньютон, Н.
- Площадь — квадратные метры, м2.
Плотность вещества
Численный показатель плотности позволяет производить оценку массы, которую будет иметь тот или иной объем вещества. Базовой плотностью можно считать показатель воды. Один кубический метр имеет массу в 1 тонну. Это очень удобно, можно приводить такую величину в систему СИ без малейших усилий. 1 кубический метр = 1000 кг, 1000 литров = 1000 кг, 1 кубический дециметр — 1 кг и так далее.
В виде формулы плотность записывается так:
p=m/v
Здесь
— показатель плотности вещества, обычно берется из справочных таблиц;
m — масса исследуемого образца;
V — объем физического тела.
Аналогично, можно найти любую из участвующих в расчете величин.
- Масса объекта: m= p*V
- Объем тела по известной плотности и массе: V=m/p
Участвующие величины в системе измерения СИ
- Плотность — килограмм / кубический метр, кг/м3.

- Масса m — килограмм, кг.
- Объем V — кубические метры, м3.
Формула давления жидкости
Одна из первых точек, где проявляется сложность формул по физике в 8 классе, проявляется именно здесь. Вводится понятие базовой механики жидкости и газа. Давление этих веществ распределяется равномерно, во всех направлениях, независимо от площади стенок сосуда или занимаемого объема. По большому счету, влияет только высота «столба» вещества в направлении действия силы притяжения Земли. Формула давления жидкости или газа выглядит следующим образом:
P=p*g*h
Здесь
— плотность исследуемого вещества;
g — табличная величина ускорения свободного падения;
h — величина вертикального столба.

Аналогично всем формулам, можно найти неизвестные величины через другие.
- Плотность исследуемой жидкости или газа по известному давлению и высоте столба: p=P/(g*h)
- Толщина слоя вещества по показателям плотности и давления: h=P/(g*p)
Участвующие величины в системе измерения СИ
- Плотность — килограмм / кубический метр, кг/м3.
- Ускорение свободного падения g — метров за секунду в квадрате, м/с2.
- Высота столба вещества или толщина слоя h — метров, м.
Термодинамика
Основные формулы по физике 8 класса, характеризующие поведение газов, относятся к так называемым изохорным процессам и описывают поведение вещества при условии стабильности одного параметра. Рассмотрим кратко все три закона.
Применяемые величины в системе измерения СИ выглядят так:
- Давление Р — Паскаль, Па.
- Объем V — кубические метры, м3.
Температура Т — градусов Кельвина, К. Используется именно абсолютный показатель, при применении формул следует переводить градусы Цельсия в шкалу Кельвина по простому правилу.
Закон Гей-Люссака
Описывает поведение газа при условии стабильного давления. Он гласит, что соотношение объема и температуры газа постоянно, если его давление не изменялось. В виде формулы записывается так:
V/T=const, при P=const
Из формулы легко найти любую из величин, поскольку давление не изменяется.
- Объем, величина V=P*T
- Показатель абсолютной температуры T=P/V
Закон Шарля
Когда соблюдается условие постоянства занятого объема, давление находится в прямой зависимости от абсолютного показателя температуры. В формульном написании это выглядит так:
P/T=const, при V=const
Используемые величины аналогичны формулам по физике 8 класса для изохорных законов, как приведено в пояснении к единицам измерения формул Гей-Люссака.
Нахождение величин
- Давление газа, известны объем и температура: P = V*T;
- Температура: N = P/V
Закон Бойля-Мариотта
Соблюдение постоянного показателя температуры и неизменной массе газа вызывает явление, когда произведение двух величин, объема и давления вещества – также не изменяется.
PV=const, при T=const
Используемые характеристики и их обозначения в системе СИ приведены выше.
Все изохорные законы в рамках формул по физике 8 класса описывают поведение идеальной газовой среды. Однако, для описания очень многих физических ситуаций, все три закона вполне применимы. Они позволяют успешно решать задачи, которые отвечают на вопросы, как изменится состояние системы при нагревании и охлаждении, а также изменении объема.
Таблица формул для 7 класса
Формулы за 7 класса по физике
Копирование и распространение материалов сайта разрешается и очень приветствуется при наличии ссылки на сайт и автора.
Контакт
«Если у тебя есть яблоко, и у меня есть яблоко, и мы обменяемся этими яблоками, то у каждого из
нас так и будет одно яблоко. Если у тебя есть идея, и у меня есть идея, и мы обменяемся этими идеями,
то у каждого из нас будет по две идеи! «
Если у тебя есть яблоко, и у меня есть яблоко, и мы обменяемся этими яблоками, то у каждого из.
Pta-fiz. jimdofree. com
23.09.2019 16:13:53
2019-09-23 16:13:53
Источники:
Https://pta-fiz. jimdofree. com/%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F-%D0%BA%D0%BE%D0%BF%D0%B8%D0%BB%D0%BA%D0%B0/%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B-%D0%B8-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B/%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D1%8B-%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB-7-%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B0/
Основные формулы по Физике 7 класс для подготовки к ВПР » /> » /> .keyword { color: red; }
Формулы за 7 класса по физике
Найти разницу между значениями двух соседних числовых меток (А и Б) шкалы (из большего вычесть меньшее значение) и разде-лить на количество делений между ними (n).
ЦД = (Б — А) / n
Ед-ца измер. вел-ны/ дел.
2. Механическое движение
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.
S = ʋ*t
4. Время движения
Время движения (t) равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.
5. Средняя скорость
Средняя скорость (ʋСр) равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (T1 + T2+ t3+ …), за который этот путь пройден.
3. Сила тяжести, вес, масса, плотность
6. Сила тяжести
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (G) — постоянную величину для Земли. (G = 9,8 H/кг)
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (G).
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).
9. Плотность
Плотность (Ρ) — масса единицы объёма вещества, численно равная отношению массы
Ρ = m / V
Кг/м 3
4. Механический рычаг, момент силы
10. Момент силы
Момент силы (М) равен произведению силы (F) на её плечо (L)
11. Условие равновесия рычага
Рычаг находится в равновесии, если плечи (L1, L2) действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.
A) F1 / F2 = l1 / l2
Б) F1*l1 = F2*l
5. Давление, сила давления
12. Давление
Давление
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности
(1Па= 1Н/м 2 )
13. Сила давления
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)
6. Давление газов и жидкостей
14. Давление однородной жидкости
Давление жидкости (р) на дно сосуда зависит только от её плотности (Ρ) и высоты столба жидкости (H).
P = g Ρ H
15.Закон Архимеда
На тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.
FВ = Ρ*g*VТ
16. Условие плавания тел
Если архимедова сила (FВ) больше силы тяжести (FТ) тела, то тело всплывает.
17. Закон гидравлической машины
Силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропор-циональны площадям (S1, S2) этих поршней.
F1 / F2= S1 / S2
18. Закон сообщающихся сосудов
1. Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне (H).
2. При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба с меньшей плотностью.
H = const для Однородной жидкости
7. Работа, энергия, мощность
19. Механическая работа
Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.
А = F*S
20.Коэффициент полезного действия механизма КПД
Коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).
21. Потенциальная энергия
Потенциальная энергия (ЕП) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (H) над Землей.
22. Кинетическая энергия
Кинетическая энергия (ЕК) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ 2 ).
ЕК = m*ʋ 2 / 2
23. Сохранение и превращение мех. энергии
Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается пост.
EП + EК = Const
24. Мощность
Мощность (N) — величина, показывающая скорость выполнения работы и равная:
А) отношению работы (А) ко времени (t), за которое она выполнена;
Б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.
1.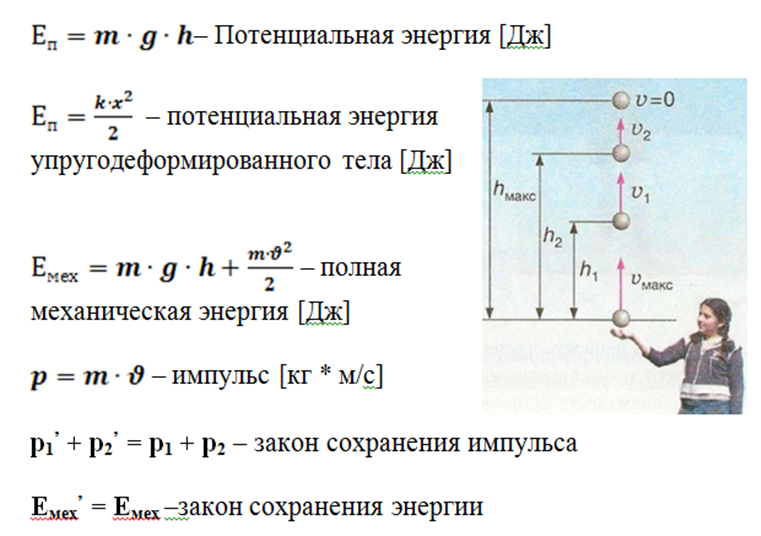 Расчет пути, скорости и времени движения.
Расчет пути, скорости и времени движения.
2. Расчет плотности, массы и объема тела.
3. Сила тяжести, вес тела, сила упругости.
.
6. Расчет давления жидкости на дно и стенки сосуда.
7. Архимедова сила
.
.
Вес Р сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы т тела на коэффициент g.
Multiurok. ru
19.12.2017 12:42:33
2017-12-19 12:42:33
Источники:
Https://multiurok. ru/files/osnovnye-formuly-po-fizike-7-klass. html
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки » /> » /> .keyword { color: red; }
Формулы за 7 класса по физике
Готовясь к экзаменам, удобно иметь под рукой шпаргалку, где будет кратко изложено самое важное. В этом материале мы объединили все основные формулы по физике за 7 класс с пояснениями и терминами. Их можно скачать на свой компьютер, чтобы всегда иметь под рукой.
Их можно скачать на свой компьютер, чтобы всегда иметь под рукой.
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины.
Результат измерения сравнивают с неким эталоном, принятым за единицу.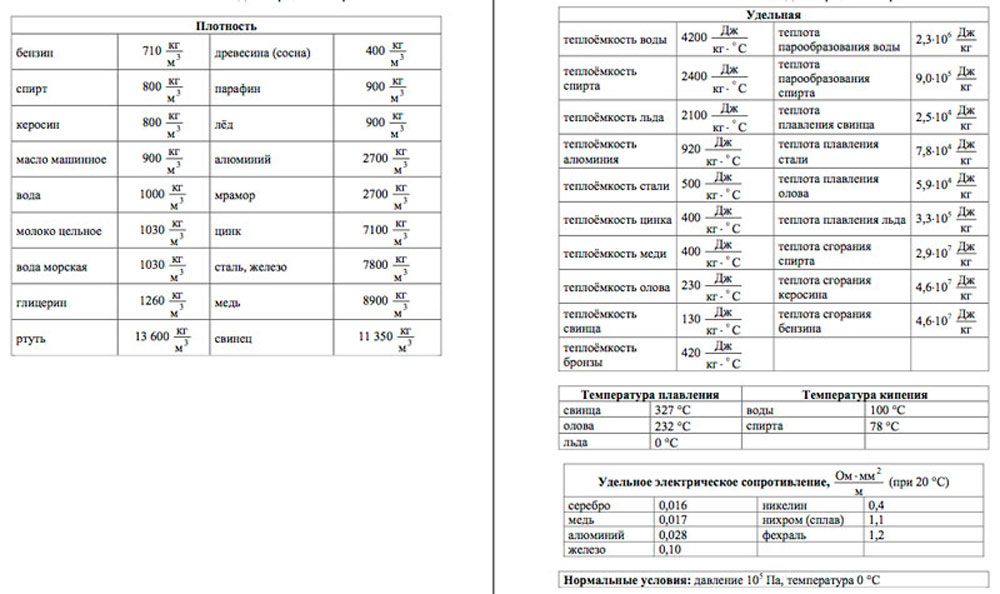 В итоге Значением физической величины считается полученное число с указанием единиц измерения.
В итоге Значением физической величины считается полученное число с указанием единиц измерения.
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
При прямом измерении результат можно увидеть непосредственно на шкале инструмента;
При косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.
Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.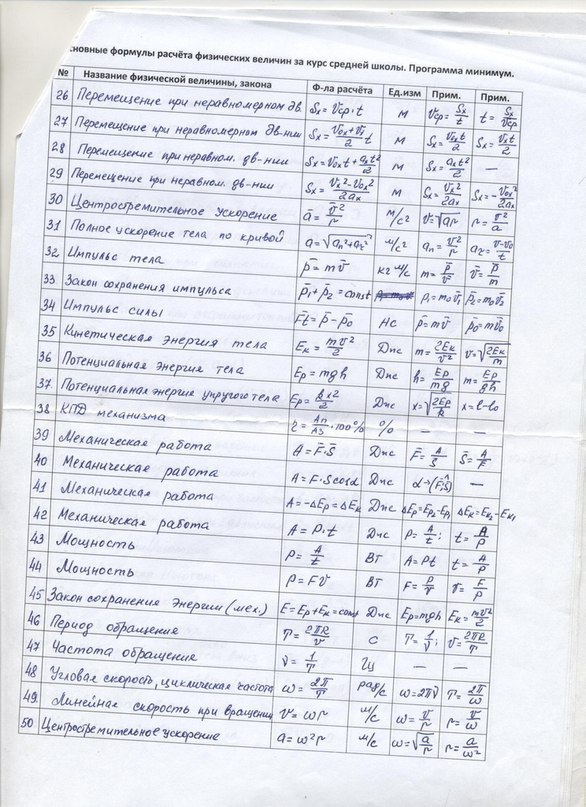
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние.
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
Где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с 2 .
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
G = 9,806 65 м/с 2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Формула плотности:
Ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м 3 .
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз.
Перпендикуляр, проведенный от точки опоры до линии действия силы, называется Плечом силы.
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.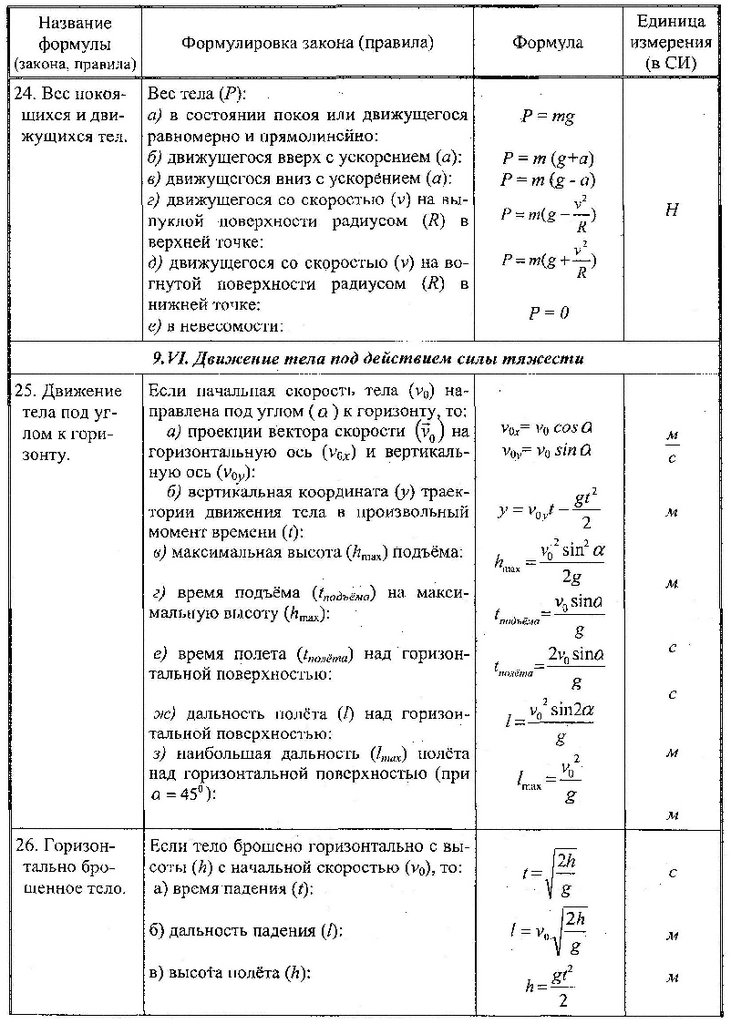
Уравнение равновесия рычага:
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l.
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.
Сила давления направлена перпендикулярно поверхности.
Формула давления:
P = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
Р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
P = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются Сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
P — плотность жидкости,
H — высота столба жидкости,
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.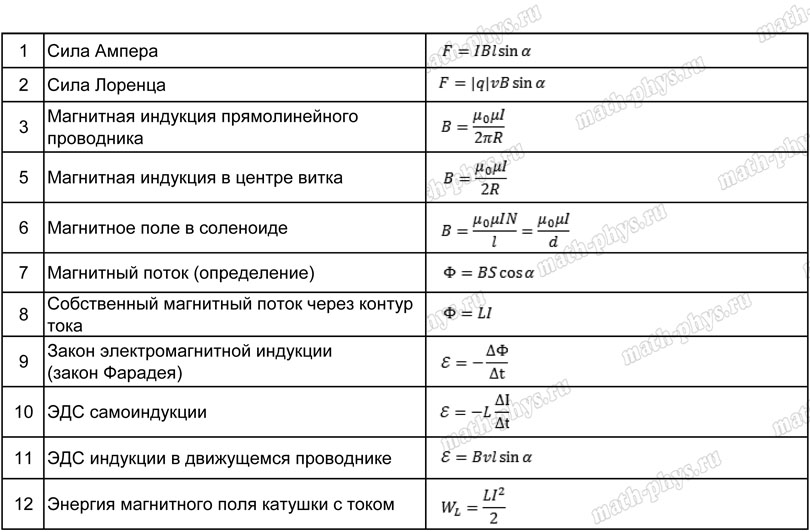
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с 2 .
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
Если плотность тела выше плотности среды, оно уйдет на дно;
Если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение.
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия
Пропорциональна массе тела и квадрату его скорости.
Потенциальная энергия
Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания.
Полная механическая энергия
Складывается из кинетической и потенциальной энергии.
Сохранение и превращение энергии
Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу.
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.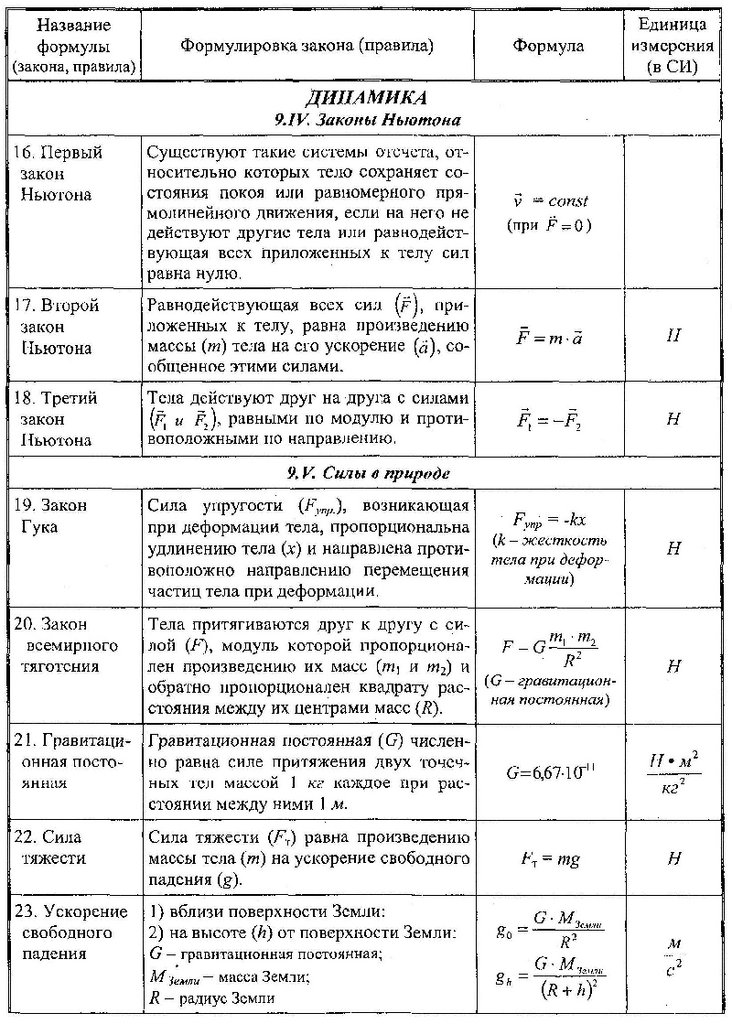
Формула для расчета КПД:
Где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
P F S, где F модуль силы, S площадь поверхности.
Skysmart. ru
01.03.2019 16:37:06
2019-03-01 16:37:06
Источники:
Https://skysmart. ru/articles/physics/vse-formuly-za-7-klass-po-fizike
логарифм | Правила, примеры и формулы
- Ключевые люди:
- Джон Напье Генри Бриггс Йоост Бюрги
- Похожие темы:
- натуральный логарифм сила десятичный логарифм мантисса
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
логарифм , показатель или степень, в которую нужно возвести основание, чтобы получить данное число.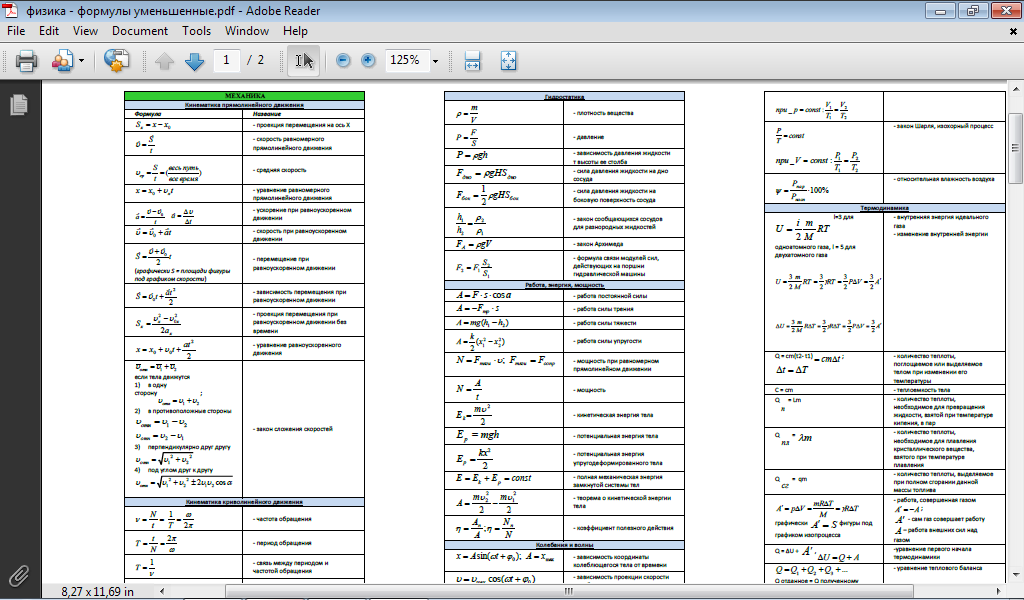 Выражаясь математически, x – это логарифм N до базы B , если B x = N , в этом случае один из них пишет x = log B . Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, то 2 = log 10 100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Выражаясь математически, x – это логарифм N до базы B , если B x = N , в этом случае один из них пишет x = log B . Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, то 2 = log 10 100. Логарифмы последнего вида (что логарифмы с основанием 10) называются обычными или бриггсовскими логарифмами и записываются просто log п .
Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в численной работе более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Натуральный логарифм (с основанием e ≅ 2,71828 и записанный как ln n ), однако, продолжает оставаться одной из самых полезных функций в математике, с приложениями к математическим моделям во всех физических и биологических науках.
Свойства логарифмов
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упрощали долгие и утомительные вычисления. В частности, ученые могли найти произведение двух чисел m и n , просматривая логарифм каждого числа в специальной таблице, складывая логарифмы вместе, а затем снова обращаясь к таблице, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в виде десятичных логарифмов, эта связь определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы (5), а затем найдя антилогарифм (100 000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m − log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также можно преобразовывать между любыми положительными основаниями (за исключением того, что 1 нельзя использовать в качестве основания, поскольку все его степени равны 1), как показано в Щелкните здесь, чтобы увидеть полноразмерную таблицу логарифмических законов.
Обычно в таблицы логарифмов включались только логарифмы чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в научной записи как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 2 , а 0,0046 будет можно записать как 4,6 × 10 −3 . Затем в таблице можно было найти логарифм значащих цифр — десятичную дробь от 0 до 1, известную как мантисса. Например, чтобы найти логарифм числа 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, log 358 = log 3,58 + log 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательным показателем степени, например 0,0046, можно найти log 4,6 ≅ 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 – 3 = -2,33724.
История логарифмов
Изобретение логарифмов было предвосхищено сравнением арифметических и геометрических последовательностей. В геометрической последовательности каждый член образует постоянное отношение со своим последующим; Например,
…1/1000, 1/100, 1/10, 1, 10, 100, 1000…
имеет обыкновенное отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; Например,
…−3, −2, −1, 0, 1, 2, 3…
имеет общую разность, равную 1. Обратите внимание, что геометрическую последовательность можно записать в терминах ее общего отношения; для приведенного выше примера геометрической последовательности:
…10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 … .
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.
В арифметической последовательности каждый последующий член отличается на константу, известную как общая разность; Например,
…−3, −2, −1, 0, 1, 2, 3…
имеет общую разность, равную 1. Обратите внимание, что геометрическую последовательность можно записать в терминах ее общего отношения; для приведенного выше примера геометрической последовательности:
…10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 … .
Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равносильно сложению соответствующих показателей степени обыкновенного отношения, -1 и 2, чтобы получить 10 1 = 10. Таким образом, умножение превращается в сложение. Однако первоначальное сравнение двух серий не было основано на каком-либо явном использовании экспоненциальной записи; это была более поздняя разработка. В 1620 г. швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции соотношения геометрических и арифметических последовательностей.
Шотландский математик Джон Нейпир опубликовал свое открытие логарифмов в 1614 году. Его цель состояла в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Весь синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Непера была 10 7 .) Его определение было дано в терминах относительных скоростей.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Таким образом, логарифм любого синуса представляет собой число, очень точно выражающее линию, которая одинаково увеличивалась в течение определенного времени, в то время как линия всего синуса пропорционально уменьшалась в этом синусе, причем оба движения были равновременны и начало смещалось одинаково.
В сотрудничестве с английским математиком Генри Бриггсом Нейпир привел свой логарифм в его современную форму. Для логарифма Напера сравнение будет между точками, движущимися по градуированной прямой линии, L точка (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, X точка (для синуса) движется от нуля до бесконечности со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
Кроме того, L равно нулю, когда X равно единице, и их скорости в этой точке равны. Суть открытия Непера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; т. е. умножение и возведение в степень значений 9Точка 0023 X соответствует сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бриггсовскому или десятичному логарифму.
Нейпир умер в 1617 году, и Бриггс продолжил работу в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 знаков после запятой для чисел от 1 до 20 000 и от 9.от 0 000 до 100 000. В 1628 году голландский издатель Адриан Влак опубликовал 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влак занимались созданием логарифмических тригонометрических таблиц. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
Такие ранние таблицы были либо с точностью до одной сотой градуса, либо с точностью до одной угловой минуты. В 18 веке таблицы были опубликованы для 10-секундных интервалов, которые были удобны для таблиц с семью десятичными знаками. В общем случае требуются более тонкие интервалы для вычисления логарифмических функций меньших чисел, например, при вычислении функций log sin x и логарифмический тангенс x .
Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для получения формул, в которых операции, зависящие от логарифмов, выполняются одновременно. Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Фрэнсис Дж. Мюррей6.5: Формулы площади, площади поверхности и объема
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 51016
- Эми Лагускер
- Каньонский колледж
Формулы площади
Пусть \(b\) = основание
Пусть \(h\) = высота
Пусть \(s\) = сторона
Пусть \(r\) = радиус
Имя формы | Форма | Формула площади |
|---|---|---|
Прямоугольник 9{2}\конец{массив}\) | ||
Параллелограмм | \(А=ч\) | |
Треугольник | \(A=\dfrac{1}{2} б ч\) | |
Круг 9{2}\) | ||
Трапеция | \(A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)\) |
Формулы площади поверхности
Переменные :
\(SA\) = площадь поверхности
\(B\) = площадь основания фигуры
\(P\) = периметр основания фигуры
\(h\) = высота
\(s\) = наклонная высота
\(r\) = радиус
Геометрическая фигура | Формула площади поверхности | Площадь поверхности Значение |
|---|---|---|
| \(S A=2 B+P h\) | Найдите площадь каждой грани. |
“> | \(S A=B+\dfrac{1}{2} s P\) | Найдите площадь каждой грани. Сложите все области. |
| 9{2}\) | Найдите площадь большого круга и умножьте ее на 4. | |
\(S A=B+\pi r S\) | Найдите площадь основания и прибавьте произведение радиуса, умноженное на наклонную высоту, на число PI. |
Формулы объема
Переменные :
\(SA\) = площадь поверхности
\(B\) = площадь основания фигуры
\(P\) = периметр основания фигуры
\(h\) = высота
\(s\) = наклонная высота
\(r\) = радиус
Геометрическая фигура | Том Формула | Том Значение |
|---|---|---|
\(V=B ч\) | Найдите площадь основания и умножьте ее на высоту | |
\(V=\dfrac{1}{3} B h\) | Найдите площадь основания и умножьте ее на 1/3 высоты. | |
| \(V=B ч\) | Найдите площадь основания и умножьте ее на высоту. |
| 9{3}\) | Найдите площадь большого круга и умножьте ее на радиус, а затем умножьте на 4/3. | |
| \( V=\dfrac{1}{3} B h\) | Найдите площадь основания и умножьте ее на 1/3 высоты. | 9{2}

 )
)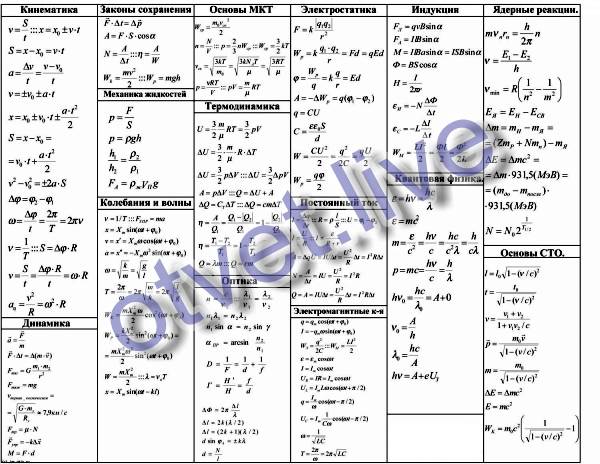 теплота парообразования
теплота парообразования 5.1: Формулы площади
5.1: Формулы площади 5.2: Формулы площади поверхности
5.2: Формулы площади поверхности Сложите все области.
Сложите все области.







 2 + qx + r) / (x – a) (x – b) (x – c) = A / (x – a) + B / (x – b) + C / (x – c)
2 + qx + r) / (x – a) (x – b) (x – c) = A / (x – a) + B / (x – b) + C / (x – c)
 В частности, ∫a→a f(x)dx = 0
В частности, ∫a→a f(x)dx = 0