Все формулы пути в физике: Формула пути

Пути и способы эффективного запоминания физических величин и формул

Библиографическое описание:

Игитханян, Л. Э. Пути и способы эффективного запоминания физических величин и формул / Л. Э. Игитханян, Т. Н. Сазонова. — Текст : непосредственный // Юный ученый. — 2018. — № 4 (18). — С. 82-84. — URL: https://moluch.ru/young/archive/18/1260/ (дата обращения: 15.12.2022).



 

Самарская область один из регионов в стране, где в рамках ОГЭ и ЕГЭ физику сдавать просто необходимо. Связано это с тем, что большинство учебных заведений — технические.

Физика — очень интересный и занимательный предмет, который с удовольствием изучают многие школьники. Каждый учащийся с 7 по 11 класс понимает необходимость хорошо учиться по физике, но не у каждого это получается. В чем причина этого парадокса? Причина тому — индивидуальные особенности памяти. У многих учеников память развита слабо и запоминание формул и законов им дается с трудом. Память нужно постоянно развивать. Если вовремя не помочь этим ребятам, то интерес к предмету быстро пропадает.

Возникает противоречие между необходимостью изучения физики и плохо развитой памятью учащихся. Отсюда вытекает проблема — многим учащимся трудно запоминать физические величины и формулы.

Для её решения мы предлагаем разработку системы запоминания физических величин и формул, используя мнемотехнику.

Изучив литературу по использованию приемов мнемотехники, мы создали копилку эффективных мнемонических приемов и апробировали разработанный нами материал и приемы мнемотехники на уроках физики в 9 классах.

Практическая значимость нашей работы заключается в том, что использование мнемотехники при изучении физических величин и формул поможет отстающим ученикам эффективней их запомнить.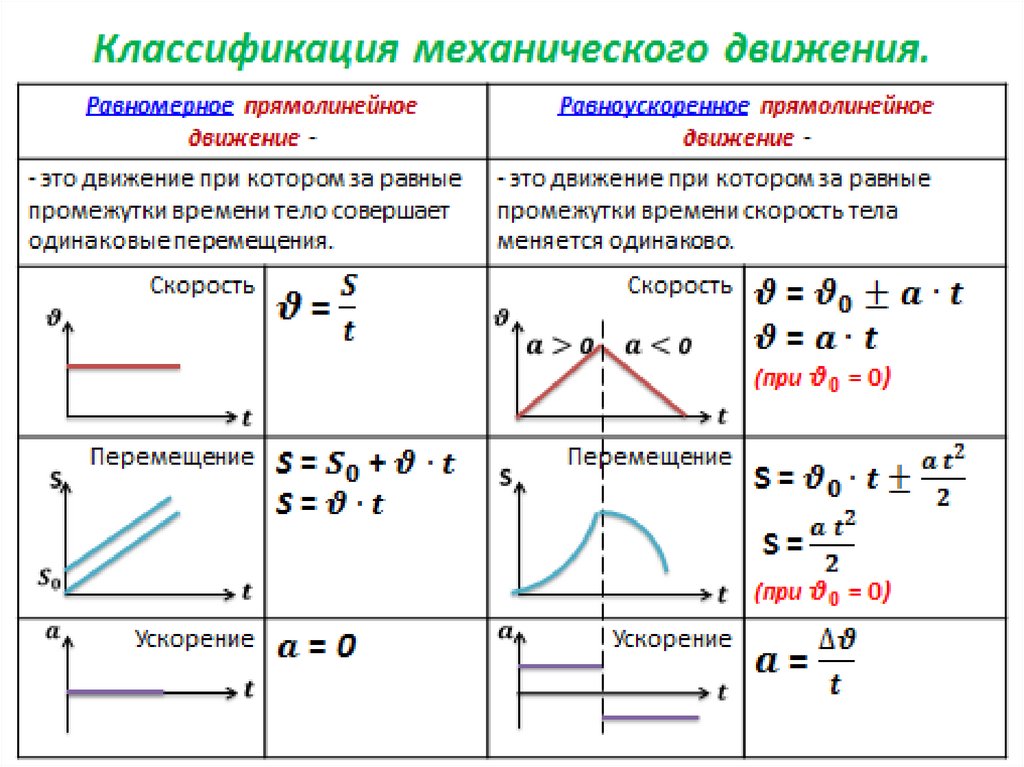

В начале нашего исследования было проведено анкетирование среди 50 учащихся 9 «а», 9 «б» класс и пришли к следующим выводам.

Ребята отвечали на такие вопросы:

1.                «Хорошо ли ты знаешь формулы по физике?»

знаю все — 22 %, знаю, но не все — 76 %, вообще не знаю — 2 %.

2.                «Легко ли ты запоминаешь формулы?» да — 30 %, нет — 30 %, не всегда — 40 %,
3.                «Как ты запоминаешь физические величины и формулы?»

а) Просто зубрю, проговаривая вслух и прошу проверить — 45 %; б) записываю несколько раз — 18 %; в) просматриваю несколько раз в учебнике — 20 %; г) учу правила и сопоставляю с формулой или с чем-то ассоциирую — 5 %; д) составляю таблицы, схемы, алгоритмы — 10 %; е) никак не запоминаю — 2 %.

Как мы видим большинство учащихся просто зубрят, не осмысливая информацию и не придают ей эмоциональную окраску, а значит это запоминание не надолго.

Как же помочь ребятам эффективно запомнить физические величины и формулы. И вот здесь на помощь приходит мнемотехника. Мнемотехника — это и есть возможность понять непонятное, сделать учение интересным.

Следующий шаг нашего исследования — эксперимент.

1 этап — проведение физического диктанта по всем изученным формулам 7–9 класса.

2 этап — выявление типичных ошибок, допущенных в формулах.

3 этап — работа по формированию мнемонических навыков, т. е. объяснение ребятам построения ассоциативных связей, приёмы запоминания. Вместе попробовали себя в роли мнемонистов. Таким образом, у каждого появился свой способ запоминания.

4 этап — проверка этих же формул после нашей работы.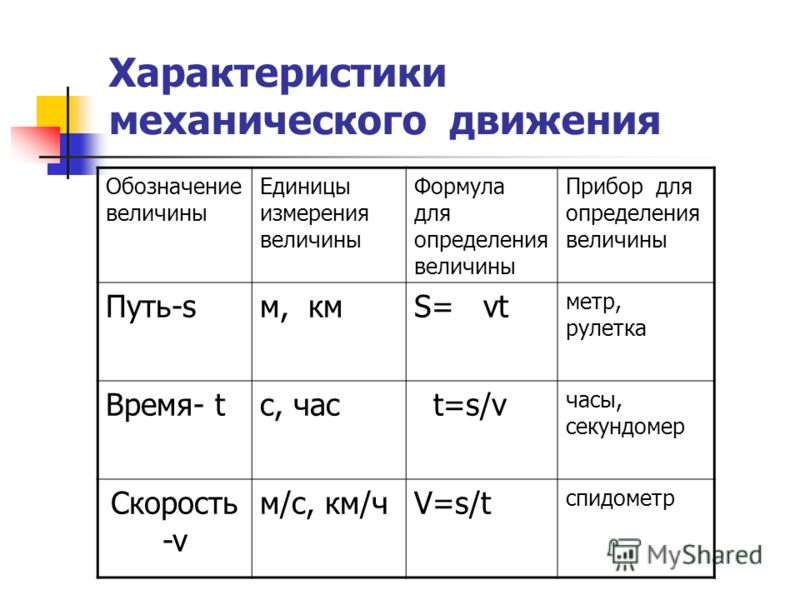 Оказалось, что теперь ошибки допущены не были.

Некоторые приёмы мнемотехники

1.                Треугольник формул
2.                Мнемофразы — фразы которые позволяют запомнить формулы

Учащиеся путают две созвучные формулы и . Мы предложили запомнить закон Архимеда фразой «У Архимеда РоЖа — Во!». Или формула для расчета силы Ампера  — Ампер Б-И-Л синус мы добавили еще сюда, что бил одной левой, т. к. для определения F_A н_. о_. использовать правило левой руки.

3.                Мнемостих (рифмовки) — перевод информации в стихи, песенки, в строки, связанные определенным ритмом или рифмой. Плотность тела мы найдем, разделив массу на объем. Силу тока чтоб найти U на R ты раздели.
4.                Запоминание физических величин с помощью созвучных слов.

Некоторые ребята путают обозначение силы тока, напряжения и сопротивления. Поэтому придумали выделять ударением букву данной величины.

(сИИИИла тока, отчетливо слышится И — значит пишем I, сопР- Р- Р –Р-отивлен, слышится Р, значит записываем R).

5.                Метод историй — нужно находить яркие, необычные образы, картинки, которые по «методу связки» соединяют с информацией, которую надо запомнить. Мама силу приложила, чтоб я быстрей второй з. Ньютона учила . Или для определения проекций векторов силы необходимо помнить определение Sin и Cоs в  прямоугольном треугольнике ребята путаю, когда использовать прилежащий, а когда противолежащий катет к гипотенузе мы придумали свою запоминалку: Соs — буквы округлые, мягкие, как подушка, на которую хочется прилечь => прилегли на подушку — прилежащий катет к гипотенузе. Sin — буквы острые, как иголки. Не хочу лежать на иголках, поэтому постою напротив. Значит противоположный катет к  гипотенузе.

Например, были ошибки в самой простой формуле , хорошо запомнить это формулу можно если вспомнить, что скорость показывают все спидометры автомобилей (), значит в числителе то, что измеряется в км (м) — это путь S, а в знаменателе стоят часы, значит там должно стоять время ч (с). Эта информация легко запоминается и ошибки не будет. Если ребята путаются в обозначениях физической величины, то можно применить методику учителя физики Винокуровой, которая предлагает любую величину нарисовать, например скорость, время, расстояние.

Для учащихся, которым очень тяжело запоминать формулы предложили использовать метод Цицерона, мнемокарточки.

6.                Метод Цицерона — расклеить по всем комнатам стикеры с формулами. Например, массу на стул, силу тяжести и вес на люстру, силу тока или напряжения на розетку. Мощность на — лампочку, Момент силы — на дверь, энергию на холодильник, скорость на мяч, швабру, веник. Количество теплоты на духовку или утюг и т. п.
7.                Мнемокарточки — карточки физических величин и формул. На одной стороне карточки записывается физическая величина, а на другой ее формула или придумайте физическое лото и играйте вместе с родителями и друзьями.
8.                Мнемостикер краткая запись параграфа на стикеры.
9.                Пассивное восприятие слов. Запишите на диктофон телефона формулировки определений и формул. В любое свободное время прослушивайте запись и повторяйте в слух.
10.            Свести все формулы в таблицу в специальную тетрадь физических терминов и формул.

Результаты апробации эффективности использования приёмов мнемотехники на уроках физики

 

Из диаграммы видно, что после ознакомления с приёмами мнемотехники результат запоминания формул стал лучше. Ошибок в разобранных формулах почти не было. Значит можно говорить об эффективности приемов мнемотехники. Однако всегда стоит помнить о том, что приёмы мнемотехники — это не подмена собственно запоминания, а лишь средство для сокращения времени на запоминание. Природная память, данная нам с рождения, всегда участвует в работе. Приёмы — это помощь ей, их нельзя переоценивать и нужно подстраивать под природную память.

Мы пришли к выводу, что мнемотехника позволяет:

1)                 накапливать в памяти большое количество точной информации;

2)                 экономить время при запоминании;

3)                 тренирует внимание и мышление;

4)                 быстро освоить несколько новых формул;

5)                 хорошая зарядка для мозга — мозг нужно тренировать, чтобы он не атрофировался.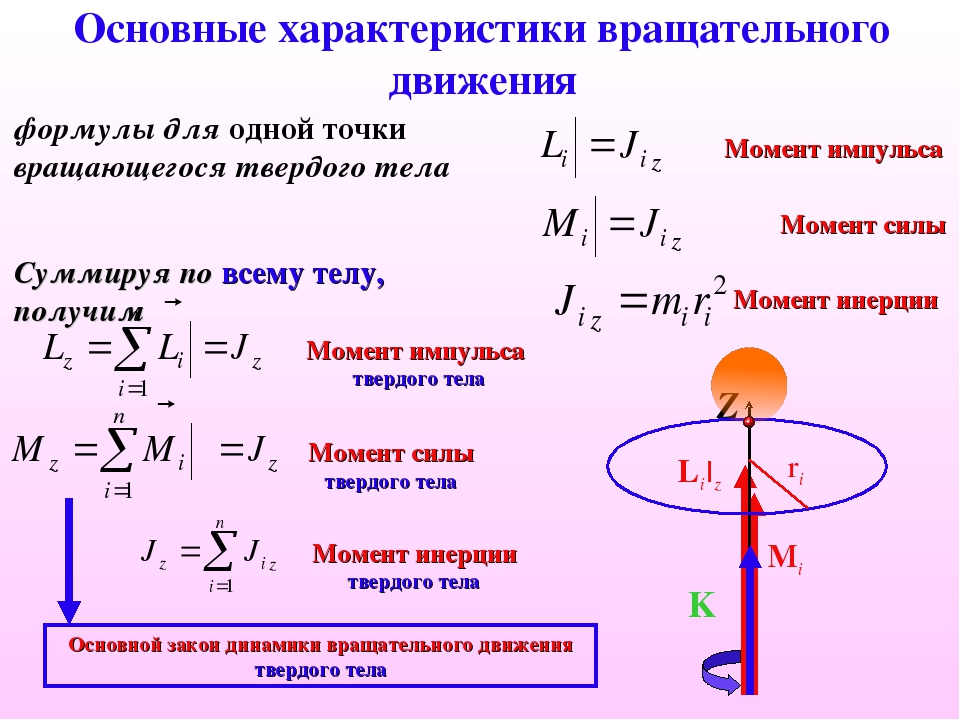

Мы убеждены, что использование мнемотехники на уроках физики повысит эффективность запоминания физических величин и формул.

 

Литература:

 

1.                Бондаренко, С. М. Обучение. Здоровье [Текст]: / С. М. Бондаренко, С. М., Ротенберг А.Н, — М.: Просвещение, 1989.
2.                Зиганов, М. А., Козаренко Запоминание на основе визуального мышленияhttp [Электронный ресурс] — Режим доступа:://school4you.ru/download/memory.pdf.
3.                Козаренко, учебник мнемотехники [Электронный ресурс] — Режим доступа: https://www.e-reading.club/book.php?book=131402.
4.                Маклаков А. Г. М15 Общая психология — СПб: Питер, 2001–592 с: ил — (Серия «Учебник нового века»).
5.                Мнемотехника. Запоминание на основе визуального мышления [Электронный ресурс] — Режим доступа: https://www.e-reading.club/book.php?book=131416.
6.                Мурашов, грамотность: риторические стратегии достижения / // Русский язык в школе№ 3.- С. 3–12.
7.                Никитина, развить суперпамять, или Запоминаем быстро и легко /. — М.: АСТ-ПРЕСС КНИГА, 2006. — 291 с.

Основные термины (генерируются автоматически): формула, прием мнемотехники, урок физики, величина, природная память, физическая величина, использование мнемотехники, сила тока, запоминание, ошибка.

Характеристика

мнемотехники как метода развития мышления…

Мнемотехника — (от греч. mnemonikon- искусство запоминания) — «совокупность специальных приёмов и способов

В современной психологии широко разрабатывается положение мнемотехники, что успешность работы памяти зависит от применяемых способов. ..

Секреты

мнемотехники: метод сжатия информации | Юный ученый

Процессом запоминания и развития речи можно управлять сознательно. Запись образов в память реализуется простой мыслительной операцией «Соединение образов». Мнемотехника предназначена для запоминания точной информации, экономии времени при запоминании…

Использование методов мнемотехники в обучении детей…

Использование методов мнемотехники в развитии дошкольников становится все более актуальным. Актуальность мнемотехники для дошкольников обусловлена тем, что в этом возрасте у детей преобладает образная память, запоминание зачастую происходит…

Эффективность

использования мнемонических приёмов

Проблема улучшения памяти была актуальна во все времена.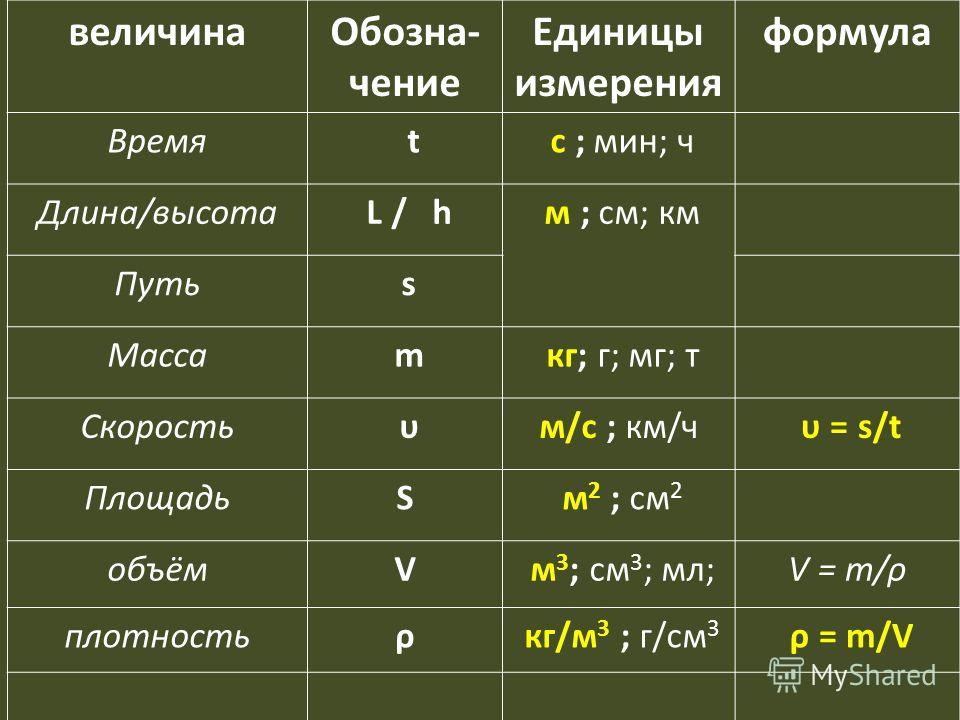 И в современном мире необходимость запоминания больших объёмов информации очень велика. Соответственно появилось много предложений обучить лучшему методу запоминания…

Использование мнемотехники в формате ИКТ для развития речи…

Мнемотехника — это система методов и приемов, обеспечивающих развитие речи, успешное запоминание, сохранение и воспроизведение информации, знаний об особенностях объектов природы и окружающем мире. Использование приемов мнемотехники особенно важно для…

Использование мнемотехники в развитии речи дошкольников

Приёмы мнемотехники облегчают запоминание у детей и увеличивают объём памяти путём образования дополнительных ассоциаций. Мнемотехника — это совокупность правил и приемов, облегчающих процесс запоминания информации.

Формирование мнемических

приемов запоминания у учащихся…

Мнемотехника — искусство запоминания, совокупность приемов и способов, облегчающих запоминание и увеличивающих. Это возможность накапливать в памяти большое количество точной информации экономя время, т. е. процесс запоминания полностью контролируемый.

Пути,

приемы и средства улучшения памяти | Статья в журнале…

Мнемотехника — искусство запоминания, совокупность приемов и способов, облегчающих запоминание и увеличивающих объем

Ночная работа и хроническое недосыпание могут серьезно расстроить здоровье. Необходима физическая активность для улучшения памяти.

Использование мнемотехники в развитии речи

Мнемотехника – это система методов и приёмов эффективного запоминания, сохранения и воспроизведения информации. С её использованием происходит развитие разных видов памяти: слуховой, зрительной, двигательной.

Что такое путь в физике и как его обозначают? Формулы и пример задачи

Кинематика является одним из важных разделов механики, который рассматривает законы перемещения тел в пространстве (причины возникновения движения изучает динамика). В данной статье рассмотрим одну из основных величин кинематики, ответим на вопрос: “Что такое путь в физике?”

Понятие о пути

Что такое путь в физике? Это величина, равная длине отрезка в пространстве, который преодолело в ходе своего движения изучаемое тело. Чтобы вычислить путь, необходимо знать не только начальное и конечное положения тела, но и траекторию его перемещения. На вопрос о том, что такое путь в физике, можно ответить иначе. Под этой величиной понимают длину траектории, то есть воображаемой линии, по которой тело перемещалось.

Для обозначения пути используют разные символы. Так, если речь идет об одномерном перемещении, то могут использовать символ Δx, где Δ означает изменение координаты x. Кроме этого символа, часто для обозначения рассматриваемой величины пользуются буквами s, l и h, причем две последние означают длину и высоту соответственно. Таким образом, в кинематике чаще всего для обозначения пути можно встретить букву s.

Если известно, что тело перемещается по прямой в трехмерном пространстве, а также известны координаты его положения начального (x₀; y₀; z₀) и конечного (x₁; y₁; z₁), тогда путь можно определить по формуле:

s = √((x₁ – x₀)² + (y₁ – y₀)² + (z₁ – z₀)²)

Формулы кинематики

Рассмотрев, как обозначается путь в физике и что собой эта величина представляет, приведем пару формул кинематики, которые применяются для вычисления изучаемой характеристики движения. Это следующие формулы:

s = v × t;

s = v₀ × t ± a × t² / 2

Здесь первое выражение соответствует ситуации, когда тело равномерно прямолинейно перемещается со скоростью v в течение времени t. Второе выражение справедливо для равноускоренного перемещения, где символами v₀ и a обозначены начальная скорость и ускорение соответственно. Знак “плюс” следует использовать, если тело ускоряется, а знак “минус” – если оно замедляет свою скорость.

Пример задачи

Разобрав, что такое путь в физике, решим следующую задачу. Катер со скоростью 13 км/ч движется против течения реки в течение 1,5 часов из одного пункта в другой. Какой путь проходит катер, если скорость течения реки составляет 3 км/ч?

Это классическая задача на применение формулы для равномерного движения тела. Сложность задачи состоит только в том, чтобы определить реальную скорость перемещения катера. Поскольку его движение происходит против течения, то она будет равна разности: 13 – 3 = 10 км/ч. Теперь остается подставить известные величины в формулу для s и получить ответ:

s = v × t = 10 [км/ч] × 1,5 [ч] = 15 км

В задачах на вычисление пути необходимо следить за размерностями используемых значений скорости, времени и ускорения, чтобы не допустить ошибки.

Что такое формула траектории? -Примеры

 Формула траектории используется для определения траектории или траектории полета движущегося объекта, движущегося под действием силы тяжести. Термин траектория используется для снарядов или небесных объектов. Когда камень брошен в воздух, парабола является правильным приближением к траектории снаряда.
Давайте разберемся с формулой траектории на решенных примерах.

Что такое формула траектории?

92 \theta}\)

Где

• θ угол проекции от горизонтали,
• v — абсолютная начальная скорость,
• g — ускорение свободного падения.
• y — горизонтальная составляющая,
• x – вертикальная составляющая
.

Давайте посмотрим на несколько решенных примеров, чтобы лучше понять формулу траектории.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Примеры использования формулы траектории

Пример 1:  Если начальная скорость камня, брошенного мальчиком, равна 6 м/с, а угол, под которым брошен камень, равен 60 ^∘ . Найдите уравнение траектории снаряда. Используйте g = 9,8 м/с ² . Решите это, используя формулу траектории. 92 \тета}\)
y = x tan 60 – (9,8)(x ² )/(2)(6 ² )(cos ² 60)
y = x√3 – 0,544x ²

Ответ: Отсюда уравнение траектории снаряда: y = x√3 – 0,544x ² .

Пример 2: Если Тревор ударит битой по мячу с начальной скоростью 45 м/с в воздухе. По направлению движения мяча конец поля находится на расстоянии 140,0 м. Если начальный угол, под которым брошен мяч, равен 66,4°. Вычислите высоту по вертикали, когда мяч достигнет конца поля. Решите это, используя формулу траектории.

Решение:

Дано, θ = 66,4°
v = 45 м/с
x = 140,0 м

Использование формула траектории,

y = (140)(tan 66,4°) – [ (9,8)(140)(140)/(2)(45) ² (0,4) ² ]

y = 320,6 – 192080 /648

y = 320,6 – 296,4 = 24,2 

Ответ: Высота по вертикали, когда мяч достигает конца поля, составляет 24,4 м.

Рабочие листы по математике и
наглядная программа

Формула линейной скорости Физика | Решенные и практические вопросы

Линейная скорость — это тема, в которой большое значение придается формулам. Вам нужно запомнить несколько формул именно в этой субъединице. Если вы не можете вспомнить формулы, не волнуйтесь, мы здесь, чтобы помочь! Линейная скорость – это расстояние, пройденное движущимся объектом. Скорость, с которой объект движется по линейной траектории, называется линейной скоростью. Простыми словами, мы можем понять, что линейная скорость – это расстояние, пройденное телом за данный интервал времени. Давайте лучше поймем, что такое линейная скорость, а также решим несколько задач!

Определение линейной скорости

Изменение расстояния во времени называется линейной скоростью. Это изменение может быть мгновенным или может происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью. Однако, когда линейная скорость измеряется в течение короткого интервала времени, она является более точной.

Формула линейной скорости

V(линейная скорость) =  \[\frac {\Delta S}{\Delta T}\]

 

Выше приведена формула средней линейной скорости. Это мера изменения линейной скорости по отношению ко времени в течение заданного периода времени.

 

∆S представляет собой изменение расстояния

 

А ∆T представляет собой время, за которое тело проходит заданное расстояние.

 

V(Линейная скорость) = \[\frac {ds}{dT}\]

 

Выше приведена формула мгновенного измерения линейной скорости. Это измеряет изменение расстояния в течение доли секунды движения.

 

Здесь dS представляет мгновенное изменение расстояния, а dT представляет долю секунды, затраченную на изменение. Мгновенная скорость является более точной, так как период, учитываемый при нахождении мгновенной линейной скорости, намного меньше.

Формула линейной скорости при круговом движении

Когда тело совершает круговое движение, оно имеет два разных вида скоростей.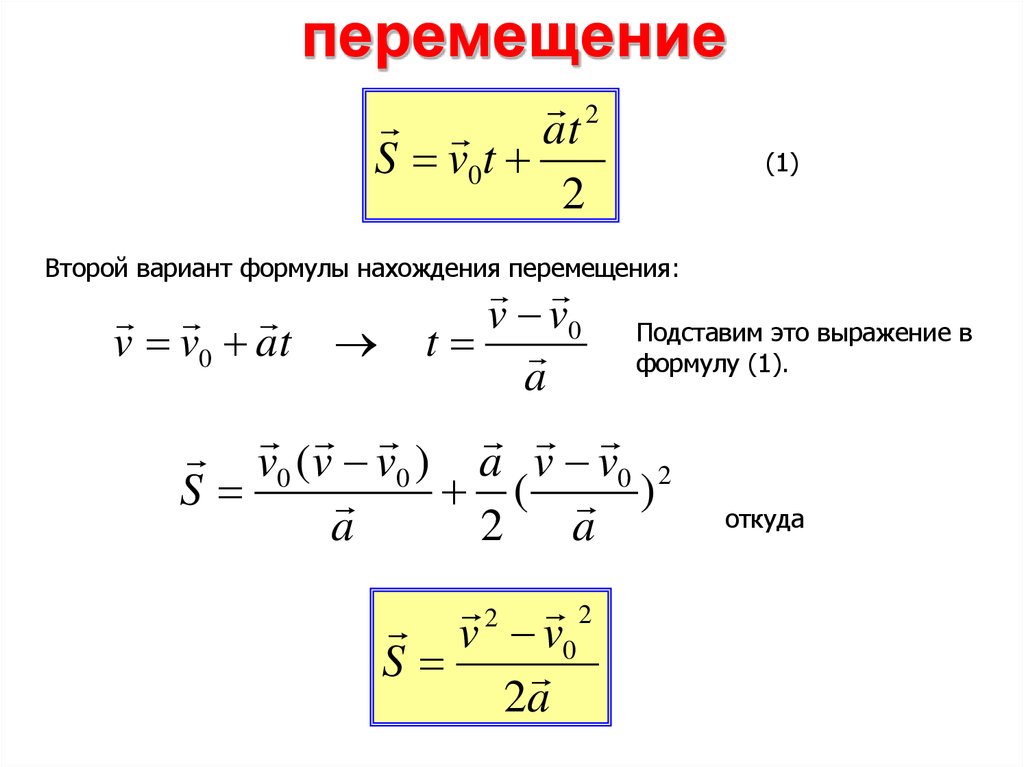

1. Угловая скорость

2. Линейная скорость

Линейная скорость и угловая скорость вместе составляют скорость тела при движении по окружности. Линейная скорость при круговом движении толкает тело двигаться вперед, тогда как угловая скорость возникает из-за центростремительной силы, которая заставляет тело продолжать движение по круговой траектории. Центростремительная сила создает внутреннюю тягу и, следовательно, ограничивает движение по круговой траектории. Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение было бы нарушено и движение продолжилось бы в тангенциальном направлении. Следовательно, оба компонента одинаково важны для ограничения движения тела по круговой траектории.

Угловая линейная скорость

Как мы видели ранее, вращательное движение имеет два вида скоростей. Угловая скорость тела при вращательном движении обусловлена ​​ускорением, которое толкает тело вперед и заставляет его двигаться по круговой траектории. Формула для угловой линейной скорости приведена ниже:

V=rw

Где v — линейная скорость тела, r — радиус кругового пути, а w — омега, угловая скорость тела, движущегося по окружности.

Решенные вопросы

1. Тело выходит из состояния покоя и движется с ускорением 10 рад с ^-2 по окружности радиусом 5м. Найдите линейную скорость тела через 6 с.

ANS:

Ускорение A = 10 RAD S ^-2

RADIUS R = 5 M

Время t = 6 S

Агловичная скорость приводится

ω0 +

=

=

= =

07 = =

07 =

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

. 0 + 10(6)

= 60 рад ^-1

Линейная скорость равна

v = r ω

= 5 м × 60 рад с ^-1

v= 300 м/с.

Следовательно, линейная скорость данного тела равна 300 м/с. Это означает, что если центростремительная сила, действующая на тело, будет устранена, тело продолжит двигаться по касательной.

2. Найдите линейную скорость тела, движущегося со скоростью 30 об/мин по окружности радиусом 5 м?

Ответ:

Дано

 

Угловая скорость  = 30 об/мин

= 30 \ [\ frac {\ pi} {30} \]

= 1 рад/с

Радиус R = 2 M

v = r ω

 

v = 2 м × 1 рад/с

 

v = 2 м/с

 

3. Если линейная или тангенциальная скорость йо-йо равна 6 м/с, найдите угловую скорость йо-йо.

Ans:

Given 

 

R= 5m

 

V=6m/s

 

The formula for Linear Speed ​​

 

v = r ω

 

ω=  \[\frac {v}{r}\]

 

ω= \[\frac {6}{5}\]

 

ω= 1,2

Советы по изучению формулы линейной скорости

Понимание формулы линейной скорости стало проще благодаря вышеуказанному учебному содержанию. Студенты должны были привить уверенность в этой теме.

Подготовка к таким темам для многих может оказаться сложной задачей. Однако тот, кто открывает правильный способ понять, применить и подготовиться к этому, может творить чудеса. На пути вы всегда будете сталкиваться с трудностями. Некоторые люди склонны сдаваться в таких ситуациях, но вам не обязательно быть одним из них. Вы должны вкладывать свою энергию в поиск наилучшего решения каждой проблемы, потому что по мере продвижения вперед эти препятствия будут становиться намного легче. Экзаменационного стресса и беспокойства невозможно избежать, но, безусловно, можно изучить вещи, которые помогут вам успокоиться. При этом вы также сможете делать вещи, которые помогут вам обрести больше уверенности.

Давайте познакомимся с некоторыми приемами яркого пересмотра темы.

Эта техника поможет вам оставаться сосредоточенным и достигать поставленных целей. У вас может быть много способов облегчить себе подготовку, например, составлять списки или следовать контрольному списку и т. д. Как только это войдет в привычку, вы можете предпринять следующие шаги по планированию на неделю и даже на месяц вперед. Убедитесь, что вы можете выделить нужное время для каждой из тем.

Способность анализировать и оценивать последствия, прежде чем планировать свой день или готовиться к какому-либо заданию, является важным навыком, которым должны обладать студенты. Ответы на такие вопросы, как результат или окончательные результаты, помогут вам сделать ваш учебный график более эффективным и действенным.

Две основные области, над которыми вам следует работать, если вы хотите добиться хороших результатов, — это работа над темами, которые оказывают большее влияние, и работа над своими слабостями. Обе области требуют одинакового времени, усилий и внимания. Учащиеся должны следить за тем, чтобы их внимание было сосредоточено, чтобы иметь возможность достичь того, о чем они мечтали.

Подготовиться перед началом — самая большая задача, но она также обязательна. Вы можете очистить свое окружение и оптимизировать свое учебное пространство. Кроме того, не забудьте избавиться от всех отвлекающих факторов вокруг вас. Сделайте свое окружение позитивным и продуктивным. Избавьтесь от всех негативных мыслей и дайте ему толчок. Учащиеся должны понимать, что не только важно поставить себя на работу, но и подготовиться и повысить свою умственную энергию.