Все формулы: Все Формулы по Физике купить в интернет-магазине OZON - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Читать онлайн «Формулы на все случаи жизни. Как математика помогает выходить из сложных ситуаций», Крис Уоринг – Литрес

Переводчик Анна Туровская

Научный редактор Владислав Турченко

Редактор Любовь Макарина

Главный редактор С. Турко

Руководитель проекта О. Равданис

Арт-директор Ю. Буга

Адаптация оригинальной обложки Д. Изотов

Корректор А. Кондратова

Компьютерная верстка М. Поташкин

Все права защищены. Данная электронная книга предназначена исключительно для частного использования в личных (некоммерческих) целях. Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.

Копирование, воспроизведение и иное использование электронной книги, ее частей, фрагментов и элементов, выходящее за пределы частного использования в личных (некоммерческих) целях, без согласия правообладателя является незаконным и влечет уголовную, административную и гражданскую ответственность.

* * *

Уравнения и формулы. Большинству из нас они знакомы по школьным урокам математики, физики и химии. Но, вероятнее всего, даже те из них, что были некогда вызубрены для экзаменов, теперь пылятся где-то на задворках нашего взрослого разума – позабытые и, казалось бы, совершенно ненужные. В конце концов, нам действительно чаще всего требуются простейшие арифметические действия, а в самом крайнем случае (скажем, за неделю до зарплаты) – умение пользоваться калькулятором на смартфоне. Так зачем возвращаться к этим никчемным, бесполезным, никому не нужным штукам, если для задачи, которая внезапно потребовала решения, уже наверняка придумали приложение, электронную таблицу или программу?

Насколько мы можем судить, наша Вселенная подчиняется неким законам. Мы называем эти законы наукой и записываем математическим языком – при помощи уравнений. Абсолютно все – от образования галактик до расположения веснушек на носу ребенка – есть результат решения уравнений. Нравится вам это или нет, предпочитаете ли вы «метод научного тыка» или упорядоченные действия – уравнения сопровождают каждый аспект вашей жизни. Совершенно неважно, насколько решение уравнений доступно вашему пониманию – они управляют всем, что происходит вокруг. Так может быть, пора поближе познакомиться с миром математики?

Безусловно, уравнения помогут вычислить, какой дистанции следует придерживаться, чтобы избежать столкновения машин в час пик. Но они могут оказаться полезными и в чрезвычайных обстоятельствах – когда на кону стоит больше, чем выплата по страховке. Что, если вместо того, чтобы поутру тащиться на скучную работу в офис мистера Претенциозность, вы перехватываете сообщение от обитателей другой галактики? Или, останавливая чудовищный разлив нефти в Тихом океане, предупреждаете международный конфликт? В старом добром уравнении нуждаются даже важные для всех и шаткие с точки зрения международной дипломатии ситуации. Математика – то, что движет миром, а совершенствование математических знаний – то, что поможет развитию технологий и, возможно, спасет планету от экологической катастрофы!

Однако прежде, чем приняться за спасение жизней, давайте вспомним основы математики. Они понадобятся, если вы хотите читать эту книгу хоть сколько-нибудь осознанно.

Любому из нас, бывает, требуется помощь с математикой. Даже такие гении, как Исаак Ньютон и Альберт Эйнштейн, время от времени затруднялись записывать свои теории математическим языком и обращались за помощью к экспертам. Я не смогу быть рядом и помогать, пока вы читаете. Но я написал несколько пояснений: они облегчат понимание тех вещей, которые вы, возможно, успели подзабыть со школьных времен. Уверены в собственных знаниях – пропускайте этот раздел. К нему можно будет вернуться, если вдруг поймете, что переоценили свои способности.

Порядок действий

Всякий раз, когда вы видите выражение, требующее вычислений – или операций, как это называют математики, – вам нужно определить последовательность шагов. В отличие от письма или чтения, где мы движемся слева направо, в математике необходимо следовать определенному порядку.

Вычисления следует производить согласно аббревиатуре BIDMAS^[1]:

Скобки
Возведение в степень
Деление
Умножение
Сложение
Вычитание

Например, выражение 5 – 3 + (2 × 8) ÷ 4² содержит все шесть действий. Итак, начнем со скобок. Мы видим, что 2 × 8 = 16, и наш пример становится таким:

5 – 3 + 16 ÷ 4².

Далее по плану возведение в степень («в степени n» означает «в n раз больше»). Такую степень мы видим над числом 4. 4² – это число 4, умноженное само на себя. Поскольку 4 × 4 = 16, мы получаем:

5 – 3 + 16 ÷ 16.

Затем идет деление: 16 ÷ 16 = 1. Теперь наше выражение принимает вид:

5 – 3 + 1.

Сложение –3 и 1 дает нам –2:

5 – 2.

У нас на руках остается простое вычитание:

5 – 2 = 3.

Сокращение дробей

Эквивалентность дробей – важное понятие: это означает, что дроби, пусть и записанные по-разному, могут соответствовать одному и тому же числу. Например, как мы знаем, одна вторая – то же самое, что и две четверти:

Дроби принято оставлять в несократимом виде, то есть использовать наименьший возможный знаменатель (число под чертой) при целом числителе (число над чертой). Будь нам неизвестно, что две четверти эквивалентны половине, мы могли бы сократить дробь, найдя число, которому кратны и числитель, и знаменатель. Для двух четвертей оно будет равно двум, так как на него делятся и 2, и 4. Поделив оба числа на 2, мы сократим дробь, но ее значение останется таким же.

Если бы у нас было восемь двенадцатых, мы могли бы разделить числитель и знаменатель на 2 или на 4. Чтобы полностью сократить дробь, используем наибольший общий делитель:

Нет такого числа, которому были бы кратны 2 и 3, значит, наша работа завершена.

Степени и корни

Пример возведения в степень мы видели в подразделе «Порядок действий». Степень показывает, сколько раз число следует умножить само на себя. Так, вместо 3⁵ мы могли бы написать 3 × 3 × 3 × 3 × 3. Истинное значение 3⁵ составляет 243 – а это, согласитесь, совсем не то же самое, что 3 × 5 = 15 (при возведении в степень такую ошибку допускают очень часто).

Извлечение корня – операция, обратная возведению в степень. Лучше всего мы знакомы с квадратными корнями, обозначающими действие, противоположное – или обратное, как выражаются математики, – возведению в квадрат (однократное умножение числа на себя). Например:

Возведя 8 в квадрат, мы извлекаем из полученного числа квадратный корень и возвращаемся к тому, с чего начали. А дальше мы можем возводить число в любую степень, которая будет отлична от второй, и точно так же извлекать любой корень, отличный от квадратного: например, вычислить значение третьей степени числа 8 и извлечь из полученного кубический корень:

Решение уравнений

Строго говоря, уравнение – это задача с неизвестным. Сумеете ли вы найти неизвестное, если я скажу, что, умножив его на 4 и прибавив 3, мы получим 13? Алгебра позволяет записать задачу в кратком виде. Заменим загаданное число буквой y – переменной, и мой вопрос станет выглядеть так:

4 × y + 3 = 13.

Чтобы еще больше упростить запись и заодно избежать путаницы между знаком умножения и буквой x, сократим 4 × y до 4y:

4y + 3 = 13.

Чтобы определить неизвестное число, то есть найти решение, или корень уравнения, начинаем с правой части выражения (суммы) и производим действия в обратном порядке. Из числа 13 вычитаем 3, а полученную разность делим на 4:

y = (13 – 3) ÷ 4.

Обратите внимание: наша первая операция – вычитание – заключена в скобки. Не будь их, нам пришлось бы, согласно установленному порядку действий, начинать с деления. Итак:

y = (13 – 3) ÷ 4;
y = 10 ÷ 4;

y = 2,5.

Уравнение решено! Имейте в виду, что есть и альтернатива: разбивать обратные операции на несколько этапов.

Такой подход пригодится, если неизвестное встречается несколько раз:

3a + 6 = 7а – 2.

Например, если мы увеличим обе части уравнения на 2, то в правой избавимся от –2. Задача примет следующий вид:

3а + 8 = 7а,

затем из обеих частей вычтем 3a:

8 = 4а,

и, наконец, разделив и левую, и правую части на 4, получим ответ:

а = 2.

Этот метод прекрасно работает в приведенных выше линейных уравнениях – задачах с неизвестным без степени. Квадратные уравнения, то есть те, где подлежащее определению число возведено в квадрат, сложнее, поскольку у них может быть два, один или даже ни одного корня. И, хотя есть различные методы решения подобных задач, я, опустив подробности, просто предложу использовать для вычисления формулу ax

2 + bx + c = 0. Итак, никакого волшебства:

Оставлю ее как вызов самому добросовестному из читателей. Пусть проверит!

Формулы

Формула – это способ показать математическую связь между величинами. Например, фут равен 30,48 см. Мы можем представить это следующей формулой:

c = 30,48f.

Буква f обозначает количество футов, c – количество сантиметров. Будь мы в США, где фут все еще остается стандартной единицей измерения длины, отношение помогло бы нам вычислить, сколько сантиметров в 6 футах. Нужно только заменить f на 6:

c = 30,48 × 6;
с = 182,88.

Итак, 6 футов – это 182,88 см.

В приведенном примере с – преобразуемое выражение. Если известна длина в сантиметрах, но ее следует перевести в дюймы, f нужно перенести в левую часть формулы, то есть должно получиться «f =». Действия будут напоминать решение уравнения. Чтобы вычислить c, мы умножали f на 30,48. Значит, разделив c на 30,48, получим:

f = с ÷ 30,48.

Другими словами, если бы мы захотели узнать, сколько футов в 182,88 см, то разделили бы это число на 30,48, получив 6 футов.

Неравенства

Часто цель математических действий – удостовериться и показать, что x равно определенному числу. Но иногда подобная конкретика нежелательна или невозможна, поскольку есть необходимость рассмотреть диапазон значений. Именно для этого мы и прибегаем к неравенствам. Допустим, по опыту мне известно, что каждое воскресенье за обедом моя семья съедает больше 7, но до 12 картофелин. Если представить количество картофеля в виде p, то «больше 7» будет выглядеть как p > 7. Предлагаю рассматривать символ неравенства как пасть прожорливого крокодила, который всегда норовит выбрать из двух объектов тот, который больше (в нашем случае это p), и съесть его. Поскольку «7 меньше p» означает то же, что и «p больше 7», выражение можно записать и наоборот: 7 < p. «До 12» означает, что p может быть как меньше, так и равно 12. Неравенство будет выглядеть следующим образом: p ≤ 12. У символа появилась дополнительная палочка, которая означает, что p способно быть не только меньше, но и равняться 12. Записав рядом оба выражения, мы охватим весь диапазон возможных значений p:

7 < p и p ≤ 12, или
7 < p ≤ 12.

Это все, что нам следует знать, чтобы вычислить, сколько картофелин понадобится для воскресного обеда.

Все формулы: математика, физика, химия. Экспресс-справочник для подготовки к ЕГЭ (К. Вилейкин, Н. Любашевская)

199 ₽

150 ₽

+ до 29 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии больше 30 шт.

В наличии в 662 магазинах. Смотреть на карте

234

“Все формулы: математика, физика, химия. Экспресс-справочник для подготовки к ЕГЭ” —учебное пособие удобного карманного формата. Содержит формулы, необходимые для сдачи ЕГЭ. Пособие рассчитано на самостоятельную подго-товку к ЕГЭ.Для старшего школьного возраста.

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Все формулы: математика, физика, химия. Экспресс-справочник для подготовки к ЕГЭ» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу К. Вилейкин, Н. Любашевская «Все формулы: математика, физика, химия. Экспресс-справочник для подготовки к ЕГЭ» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой.

Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Математические формулы — примеры, вывод

Математические формулы — это выражения, созданные после нескольких десятилетий исследований и помогающие быстро решать вопросы. Легко выполнять простые арифметические вычисления, такие как сложение, вычитание и так далее. Однако, когда дело доходит до алгебраических выражений, геометрии и других тем, вам нужны математические формулы, чтобы упростить процесс достижения ответа и сэкономить время в этом процессе. В Cuemath вы не только найдете формулы для каждой темы, но также получите представление о том, как было разработано это уравнение. Таким образом, вам не придется запоминать формулы, так как вы понимаете лежащую в их основе концепцию.

Используйте эти формулы для творческого решения задач, и вы автоматически заметите улучшение своих математических навыков. Ниже приведен список формул, расположенных в алфавитном порядке для вашего удобства.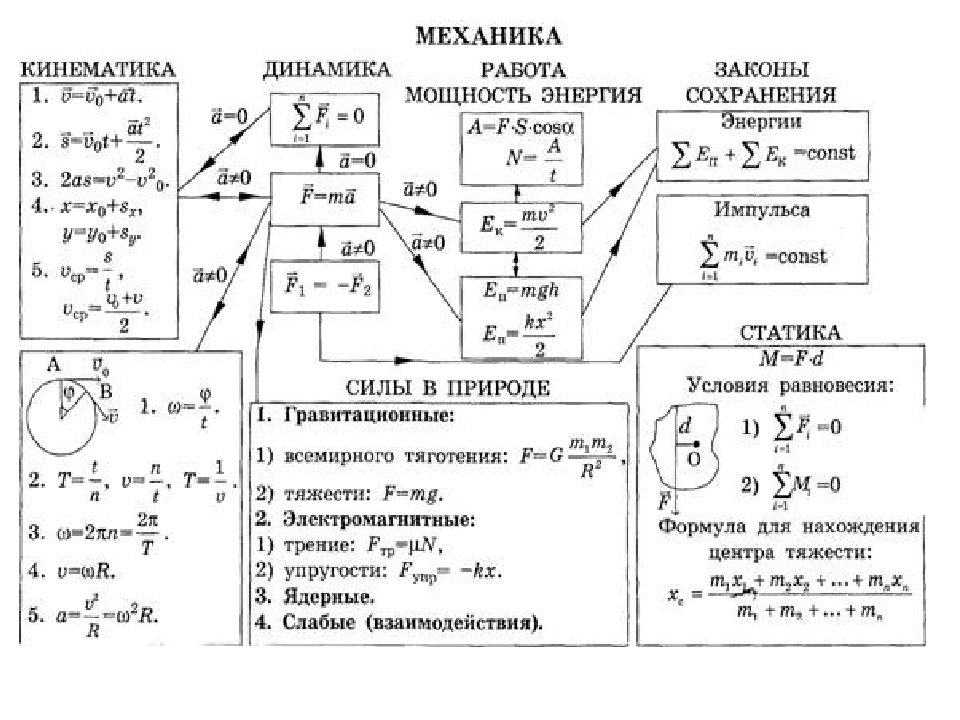 Следовательно, вы можете легко найти формулы, которые необходимо пересмотреть или на которые нужно сослаться.

Для вашего удобства ссылки на список математических формул, доступных по разным темам, расположены в алфавитном порядке. Так что выбирайте тему и приступайте к обучению!

#	А	Б	С	Д	Е	Ф	Г	Х
я	Дж	К	л	М	Н	О	Р	В
Р	С	Т	У	В	Вт	х	Д	З

Список всех математических формул

В зависимости от того, к какому классу вы принадлежите и какую тему изучаете, вы можете найти все возможные математические формулы. Все доступные варианты математических формул с их доказательствами и выводами приведены ниже. И так, чего же ты ждешь? Начните свое обучение уже сегодня!

Важность математических формул для учащихся

Математические формулы были созданы одними из самых умных людей не просто так. Они помогают детям решать вопросы быстро и точно. Это также помогает значительно упростить процесс достижения решения суммы, а не пытаться с нуля. Преимущества математических формул приведены ниже:

Ребенок должен следовать учебной программе, установленной школой, которая зависит от времени. Через определенные промежутки времени дети проверяются на свои знания с помощью различных экзаменов, таких как разделы, полугодия и выпускные экзамены. Таким образом, чтобы гарантировать, что студенты подготовили предмет вовремя с буфером для повторения, им нужны математические формулы.
Ребёнок при повторении вряд ли решит несколько вопросов с ручкой и бумагой. Таким образом, чтобы иметь быстрый взгляд на суммы и способы их решения, детям необходимо знать формулы, поскольку они являются ключом к получению правильных ответов.
Во время экзаменов дети не могут позволить себе роскошь выводить всю формулу для решения вопроса, что означает, что они не могут начать с шага 1. Они должны знать и помнить формулы, чтобы выполнить свой вопросник за заданное количество времени, таким образом, помогая их в планировании и организации своего времени.
Студентам, которые пытаются сдать конкурсные экзамены, необходимо знать не только формулы, но и различные советы и рекомендации, связанные с ними. Поскольку эти экзамены обычно проводятся в форме MCQ, дети должны очень хорошо разбираться в математических формулах.

Важные математические формулы

Прежде чем мы увидим список наиболее важных математических формул, очень важно иметь в виду, что каждая тема в математике взаимосвязана. Если вас не устраивают некоторые формулы, независимо от того, чаще ли они встречаются на экзаменах, вы должны поработать над своими навыками и добиться их четкого понимания. Таким образом, знание всех формул является обязательным; однако данный список дает вам представление о том, какие математические формулы обычно используются для решения экзаменационных вопросов.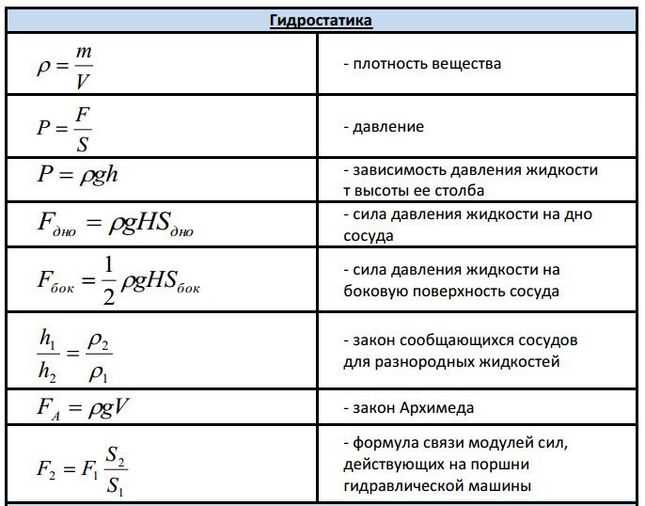

1. Алгебра

Среднее арифметическое или среднее = сумма всех значений/количество значений
Квадратичная формула: x = [-b ± (√b ² – 4ac)]/2a

2. Координатная геометрия

Формула расстояния: d=√[(x₁ – x₂) ² + (y₁ – y₂ ² ]
Пересечение наклона: y = mx + b
Формула средней точки: [(x₁ + x₂)/2, (y₁ + y₂)/2]

3. Плоская геометрия

Теорема Пифагора: а ² + b ² = с ²
Площадь треугольника = (1/2) × основание × высота
Площадь прямоугольника = длина × ширина

4. Тригонометрия

Синус = перпендикуляр/гипотенуза
Косинус = основание/гипотенуза

Советы по запоминанию математических формул

Существуют сотни математических формул, которые дети должны выучить на протяжении всей школьной жизни. Таким образом, учащимся важно иметь несколько советов, которые помогут им точно запомнить математические формулы. Несколько трюков приведены ниже:

Понимание: Очень важно, чтобы ребенок понял концепцию математической формулы. Если он знает вывод и имеет четкое представление о цели, стоящей за математической формулой, то, скорее всего, ребенку даже не придется ее запоминать. Он автоматически узнает, как и когда применить правильную математическую формулу.
Практика: Пока вы не решите вопрос, который требует использования определенной формулы, вам будет очень трудно оценить ее использование. Решая многочисленные вопросы, вы начинаете запоминать формулу за счет мышечной памяти. Следовательно, вам не нужно прилагать активные усилия для изучения формул, поскольку вы уже знаете их применение.
Сделайте контрольные листы: Как только вы ознакомитесь с темой и начнете задавать вопросы по ней, сделайте лист со всеми математическими формулами, которые вы используете. Продолжайте обновлять его по мере продолжения цикла обучения. Когда вам придет время быстро взглянуть на эти формулы или если вы захотите их запомнить, вы можете обратиться к этому листу. Кроме того, вы также можете воспользоваться помощью Cuemath с математическими формулами, перечисленными выше
Мнемотехника и методы запоминания: Существует множество мнемонических устройств, которые могут помочь вам в изучении математических формул. Например, если вы хотите выучить основные тригонометрические формулы, доступная мнемоника: « S ome P eople H ave, C urly B rown H air, T 90 верёвщик B торопится. Таким образом, выделенные буквы помогают запомнить формулы синус = перпендикуляр/гипотенуза и так далее. Если вы воспользуетесь этими техниками запоминания или придумаете свою собственную инновационную мнемонику, вам будет очень легко выучить математические формулы.

Применение математических формул в реальной жизни

При изучении темы учащимся полезно узнать о практическом применении соответствующих математических формул, поскольку это делает предмет более понятным. Ниже перечислены некоторые области, в которых используются математические формулы:

Алгебра:

Алгебраические формулы широко используются в области информатики для выполнения различных аналитических функций. Они также используются в криптографии для защиты финансовой информации. Кроме того, вы используете алгебру ежедневно, сознательно или неосознанно, чтобы планировать свое расписание и выполнять свои задачи.

Исчисление:

Формулы интегрирования и дифференцирования в исчислении широко используются в технике. Он также используется для анализа траектории ракеты, материаловедения, разработки кода физики ударных волн, моделирования воздушного потока над аэродинамическими телами, теплопередачи, распространения сейсмических волн для анализа землетрясений, обработки сигналов и т. д.

Геометрия:

Формулы геометрии широко используются в строительстве и архитектуре для построения различных типов конструкций. Они также используются в моделировании местности, проектировании механических частей, криптологии и схемах воздушного потока.

Вероятность и статистика:

Формулы вероятности и статистики, а также приемы, изученные в школе, можно применять к примерам из реальной жизни. Они используются в таких областях, как моделирование Монте-Карло, обработка сигналов, анализ надежности, анализ рисков, модели прогнозирования фондового рынка, проектирование компьютерных сетей, ценообразование в страховании, оценка океанских течений в геостатистике и т. д.

Часто задаваемые вопросы по математическим формулам

Что математическая формула?

Математические формулы можно рассматривать как выражение, которое используется как ключ к быстрому и эффективному решению задач. Они также включают тождества, которые являются утверждениями, которые верны для всех значений конкретной переменной. Таким образом, математические формулы очень важны для изучения и понимания детьми.

Вам нужно запомнить все математические формулы?

Для детей крайне важно понимать концепцию математической формулы. Как только ребенок овладеет глубокими знаниями, он может переходить к изучению и запоминанию формул, так как ему придется быстро их вспоминать во время экзаменов. Однако, если он знает, как была получена математическая формула и что за ней стоит, ребенок автоматически запомнит формулу.

Какие математические формулы самые важные?

Важные математические формулы относятся к тем формулам, которые часто встречаются на большинстве школьных или конкурсных экзаменов. Однако следует придавать равное значение всем формулам, чтобы получить целостную математическую разработку. Список важных математических формул приведен ниже.

Среднее = сумма всех значений/общее количество значений
Площадь треугольника = (1/2)*(основание)*(высота)
Периметр квадрата = 4 * сторона
Определитель квадратного уравнения = b ² – 4ac

Что такое основные математические формулы?

Основные математические формулы могут использоваться для решения простых вопросов или необходимы для построения более сложных формул. Вот список некоторых основных математических формул.

Алгебраические тождества: (a + b) ² = a ² + b ² + 2ab, (a – b) ² = a ² + b 909156 2 2 – б ² = (а + б) (а – б)
Теорема Пифагора: перпендикуляр ² + основание ² = гипотенуза ²
Формула расстояния: d=√(x₁ – x₂) ² + (y₁ – y₂) ²
Наклон линии: m = y2 – y1 / x2 – x1

Почему математические формулы так важны?

Математические формулы позволяют детям легко и быстро решать сложные задачи. Все, что нужно сделать детям, это найти правильную формулу для решения вопросов, и они смогут продолжить работу без проблем. Особенно, когда мы рассматриваем сценарий экзамена, рассчитанного по времени, становится необходимым использовать эти математические формулы, чтобы работа могла быть завершена хорошо в заданных пределах.

Нужно ли знать, как работает математическая формула?

Для учащихся очень важно знать, как работают математические формулы. Дети должны начать с развития понимания концепции, лежащей в основе формулы, и построения четкой основы вывода. Если у детей есть эти знания, им не придется запоминать формулы. Даже если они забудут, какую математическую формулу применить к конкретному вопросу во время контрольной работы, они будут знать метод и не застрянут.

Как вы учите математические формулы?

Первым шагом в обучении математическим формулам является объяснение учащимся значения формулы. Следующий шаг – познакомить детей с выводом формулы. Наконец, вам нужно показать детям, как применять математическую формулу к вопросам, как простым, так и сложным.

Как мы можем применять математические формулы в повседневной жизни?

Когда мы говорим о такой теме, как дроби или десятичные дроби, мы применяем формулы к таким действиям, как перекрестная проверка правильности квитанции, которую мы получаем от покупки, когда нам нужно разделить объект, такой как пицца, между люди и так далее. Таким образом, сознательно или неосознанно мы используем математические формулы, чтобы эффективно вести свою повседневную жизнь.