Все виды дифференциальных уравнений и методы их решения: Виды дифференциальных уравнений, методы решения. Примеры решений дифференциальных уравнений второго порядка методом лагранжа - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Система дифференциальных уравнений метод методы решения

Для решения системы дифференциальных уравнений методом Рунге — Кутта необходимо выполнить вычисления в следующем порядке [c.124]
Нами выполнены расчеты результатов про-цесса по математическому описанию при тех же входных величинах, что и в промышленном аппарате с использованием стандартной программы решения системы дифференциальных уравнений методом Рунге—Кутта для ЭВМ М-20. Результаты расчетов при нескольких величинах ко показаны в табл. 8.2, где для удобства сравнения приведены и выходные опытные данные. При подборе ко в качестве исходного значения принята величина, рассчитанная на основании работы [147]. [c.181]

Оценим вреия решения задач математического моделирования целиком на ЦВМ с таким быстродействием. Ддя решения системы дифференциальных уравнений, например, методом Рунге-Кутта с заданной точностью обычно требуется [c.

504]

Для решения небольшой системы дифференциальных уравнений (2.159), описывающих с принятыми допущениями переходные процессы в приводах с дроссельным управлением, нет необходимости использовать названные сложные методы расчета. Приемлемые результаты можно достигнуть более простым при малом числе уравнений методом припасовывания. Такой метод успешно применяют для решения некоторых задач механики [4, 20]. Состоит оп в следующем. Полное время переходного процесса разделяют на малые временные интервалы (шаги). В пределах достаточно малого шага коэффициенты дифференциальных уравнений принимают постоянными. Получаемую при этом систему линейных дифференциальных уравнений решают совместно в каждом временном интервале методом преобразования по Лапласу. Формулы для вычисления конечных значений переменных содержат их начальные значения. Процесс припасовывания состоит в том, что значения переменных, полученные в конце предыдущего шага, принимают начальными дли последующего. Совместное решение системы уравнений в пределах каждого шага исключает возникновение численной неустойчивости решения и этим устраняет искажение переходного процесса.

[c.150]

До сих пор мы не останавливались на вопросе вычисления производных 5//39, полагая, что они могут быть вычислены точно. Однако при приближенном (численном) интегрировании исходной системы дифференциальных уравнений (3.141) вычисление производных — наиболее тонкое место во всей обратной задаче. Методы вы числения производных можно разделить на две группы. Первая группа — методы универсальные, не связанные со схемой интегрирования. Сюда относится метод конечных разностей (см. разд. 3.5), точность которого не всегда достаточна для успешного проведения минимизации. В работе [108] предлагается для оценки производных использовать план первого порядка в пространстве параметров около точки 0 . Применение этого метода требует, так же как и метод конечных разностей, (р—1) вычисления функции по крайне мере. Пауэлл [118, 119] предложил численный метод оценки градиента, в котором при каждой итерации переоцениваются компоненты лишь в направлении, задаваемом уравнением.

(3.171) или G GS = —G h. Здесь 0 — решение уравнения, фиксирующее стационарную точку системы (3.171) h — вектор [t —/ (0 )], i = 1,…. .., N G — вектор 5/(0 )/39 , j = i,. . R. Симплекс-метод [12, 92, 115] не обладает быстрой сходимостью [117, 124], тем не менее он с успехом используется для оценки производных. [c.224]

Все проблемы, рассмотренные в этой главе, сводятся к решению обыкновенных дифференциальных уравнений. Мы уже замечали, что в некоторых случаях аналитическое решение невозможно, н решать задачу приходится численными методами. Существуют стандартные программы решения уравнений такого типа на вычислительных машинах. Тем не менее, знакомство с численными методами интегрирования уравнений полезно химику-технологу по двум важным причинам. Во-первых, вопреки распространенному мнению, вычислительная машина не умеет думать , и потому небезопасно давать ей задание, не имея понятия о том, как она его будет выполнять.

Во-вторых, иногда возможно и даже желательно проводить вычисления вручную. Метод, который мы сейчас рассмотрим, применим к решению любой системы обыкновенных дифференциальных уравнений, включая уравнения, описывающие неизотермические процессы. Проиллюстрируем этот метод на примере одного уравнения и системы двух уравнений. [c.114]

Математическое описание моделей для нестационарных условий движения потоков дано в табл. 2.1. Приравнивая нулю производную по времени, можно получить модели для стационарных условий. При этом существенно упрощается и соответствующее математическое описание. Так, для ячеечных моделей вместо системы дифференциальных уравнений описанием будет служить система нелинейных алгебраических уравнений. В общем случае весьма трудно получить аналитическое решение системы уравнений модели. Поэтому при разработке алгоритмов решения используются аппарат передаточных функций и методы вычислительной математики. Эти методы по классам уравнений (дифференциальные в частных производных, обыкновен-

[c. 84]

Этот пример иллюстрирует возможности решения основного кинетического уравнения при наличии моделей с относительно узкими ядрами, которые приводят к ленточной структуре матриц в системе дифференциальных уравнений. При расчете моделей с широкими ядрами, возможно, понадобятся более сложные методы аппроксимации интегралов. Однако при использовании более сложных кубатурных формул на процесс дискретизации уравнения должны быть наложены такие ограничения, чтобы дискретное уравнение сохраняло основные физические свойства непрерывного уравнения.

[c.200]

Решение системы дифференциальных уравнений скоростей реакции в форме квадратур не всегда бывает возможным, поэтому для расчета констант скоростей часто приходится прибегать к числовым методам, используя экспериментальные данные и применяя цифровые вычислительные машины. Во многих случаях уравнения являются нелинейными, и для их решения требуются специальные методы. [c.42]

Нами была сделана попытка учета продольной диффузии и продольного перемешивания, которая сразу же привела к серьезному осложнению” системы дифференциальных уравнений, описывающих динамику рассмат-.

риваемого процесса. В частности, порядок уравнений повысился, что практически не дает возможности получить решение в аналитическом виде. Проведение же глубокого математического анализа такой усложненной системы дифференциальных уравнений асимптотическими методами или методами вычислительной математики с использованием быстродействующих электронных вычислительных машин мы сочли нецелесообразным, поскольку численно сформулировать такую задачу на основе имеющихся экспериментальных данных по динамике поглощения окислителей редокситами к настоящему времени не представляется возможным. [c.62]

Строгое аналитическое решение системы дифференциальных уравнений (2-86) и (2-87) не всегда возможно. Однако наличие дифференциальных уравнений совместно с условиями однозначности позволяет воспользоваться методами теории подобия, которая представляет собой метод обобщения эксперимента. Современная наука широко использует этот метод исследований при анализе процессов горения, сушки и т. д. [c.69]

Нетрудно убедиться, что к такому же решению можно прийти, применив с самого начала для решения системы дифференциальных уравнений метод стационарных концентраций, т. е., полагая, что л/Л Действительно, в этом приближении

[c.331]

В связи с тем, что при расчете стационарных режимов работы технологических схем точное решение динамической модели не является необходимым, целесообразно при интегрировании системы дифференциальных уравнений использовать различные временные шаги интегрирования для каждой перемены, что в случае применения метода Эйлера запишется как [c.404]

Теорема Тихонова является строгой математической формулировкой метода квазистационарных приближений, рассмотренного в ферментативной кинетике (см. гл. 2). Данная теорема позволяет выявить в системе дифференциальных уравнений так называемые быстрые – уравнения, т.е. те уравнения, которые описывают поведение переменных, быстро достигающих стационарного состояния.

Теорема Тихонова позволяет заменить эти дифференциальные уравнения алгебраическими, что существенным образом упрощает решение систем дифференциальных уравнений. [c.707]

Следовательно, расчет реактора сводится к решению системы двух уравнений с двумя неизвестными а и Т. Для проточного реактора полного перемешивания это будет система алгебраических уравнений. В остальных случаях получается система дифференциальных уравнений. Как правило, для решения необходимо использовать численные или графические методы. Ниже будет рассмотрено несколько примеров расчета неизотермических реакторов. [c.332]

Среди научных работников бытует шутка Химик это тот, кто умеет составить дифференциальное уравнение, а физик — тот, кто может его решить . Зачастую, однако, способ решения системы уравнений выходит за рамки методов, известных и физикам. ( Многие вещи кажутся нам непонятными не потому, что наши понятия слабы, а потому, что эти вещи ие входят в круг наших понятий — Козьма Прутков. ) В таких случаях необходима консультация специалиста-математика. В большинстве случаев математик, посмотрев условия, сообщит, что такая задача уже решена, и расскажет метод решения нлн подскажет, где его можно посмотреть. [c.137]

Для решения системы дифференциальных уравнений используются конечно-разностные подходы, причем эти уравнения предварительно модифицируются с помощью специальной процедуры, что обеспечивает более тесную их связь и повышенную устойчивость численных схем. При решении конечно-разностных матричных уравнений может использоваться либо метод прямого исключения диагональных членов, либо итерационный метод Гаусса-Зейделя с верхней релаксацией. [c.570]

Ранее обсуждалось решение системы дифференциальных уравнений (10-34). В дальнейшем будет показано, что этот метод изложения вследствие фундаментального характера обобщенных уравнений Дамкелера ведет непосредственно к таким понятиям, как рабочая линия и единица переноса. [c.161]

Для плохо обусловленной матрицы 5 1 величина е близка к единице и сходимость может быть чрезвычайно плохой. Однако если не очень велико, то подход к методу минимизации с точки зрения решения градиентных систем оказывается более эффективным, так как позволяет перейти от довольно неясной проблемы выбора шага А к более ясной проблеме выбора границы точности решения системы дифференциальных уравнений [27]. [c.215]

Мембраны в общем случае следует рассматривать как распределенные системы, кинетическая модель которых описывается дифференциальными уравнениями (1.26) или (1.27). В таких системах вдали от равновесия возмущения, являясь функцией времени и координаты, могут развиваться, конкурируя со стабилизирующими их диссипативными эффектами, обусловленными нелинейностью химических реакций. Анализ устойчивости подобных систем методом линеаризации достаточно сложен. В частности, для однородных в пространстве, но периодических во времени распределений концентраций в одномерной системе с одной переменной х получено следующее решение [4] для возмущения [c. 37]

В случае нелинейной системы дифференциальных уравнений для решения уравнения (7.9) можно воспользоваться методом Ньютона—Рафсона, (см. формулу (7.7)). Для этого найдем матрицу частных производных дО (Х”)/ЗХ [c.272]

Идеальное перемешивание в дренажном канале. В напорном канале — идеальное вытеснение. Такая организация потоков возможна в аппаратах плоскокамерного типа с отводом пермеата из центра плоскопараллельного двойного мембранного элемента, особенно при работе по вакуумной схеме Рг ниже атмосферного). В этом случае yiA = yip, и расчет модуля при заданных 0 и yif заключается в решении системы дифференциальных уравнений (5.103) с граничными условиями (5.104). Значения yir определяют любым из итерационных методов, а yip — из балансового соотношения (5.107). [c.185]

Рассматриваемая задача представляет собой двухточечную краевую задачу для системы дифференциальных уравнений первого порядка. Используем для решения метод Ньютона, а в качестве промежуточных звеньев в программе — модифицированный метод Эйлера для решения систем обыкновенных дифференциальных уравнений и метод Гаусса для решения систем алгебраических уравнений. [c.309]

Целью кинетического исследования в рассматриваемых системах является определение кинетических констант и возможных выходов изомеров. Традиционным методом использования кинетической модели для этого случая является решение системы дифференциальных уравнений (2.25). Общий способ такого решения методами матричной алгебры заключается в следующем. Будем искать ненулевое частное решение в виде [c.30]

Теория подобия используется для обобщения данных о каком-либо физическом процессе при осуществлении его в аппаратах различного размера. Методы теории подобия применяют для определения физических характеристик процесса в большом аппарате на основе изучения этого процесса в малом аппарате. При этом принимается, что процесс описывается одной и той же системой дифференциальных уравнений, т. е. что структура математического описания неизменна. Предполагается, что аналитическое пли численное решение этого описания вызывает затруднения. [c. 20]

Моделирование процесса эмульсионной полимеризации на ЦВМ. Для численного решения задачи (3.47)—(3.63) с начальными, граничными условиями и условиями сопряжения (3.64) — (3.68) система дифференциальных уравнений приводилась к безразмерному виду и решалась методом прямых с применениеи процедуры Рунге—Кутта—Мерсона на ЦВМ Минск-32 . [c.156]

Существенным моментом при выборе метода является размерность задачи. Некоторые методы эффективны при решении небольших задач, однако с увеличением числа переменных объем вычислений настолько возрастает, что приходится от них отказываться. Такого класса задачи обычно имеют место при решении систем уравнений, поиске оптимальных значений параметров многомерных функций. Соответствующим выбором метода можно уменьшить время решения задачи и объем занимаемой памяти. Так, при решении систем линейных алгебраических уравнений объем вычислений для точных методов (типа метода Гаусса) пропорционален а для итерационных (типа простой итерации) — Л , где N — число неизвестных. При решении дифференциальных уравнений разностными методами матрица коэффициентов системы при числе узловых точек N содержит N элементов (при N = 100 для исходной информации необходимо отвести свыше 10 ООО слов оперативной памяти). Однако при [c.24]

В гл. 1 было показано, что математическое описание типовых процессов обычно выражается определенным классом уравнений (конечные системы уравнений, системы дифференциальных уравнений и т. д.), решение которых возможно с единых методологических позиций. Примерами такого подхода являются методо-ориентированные пакеты прикладных программ, в основе которых используется определенный метод, обладающий достаточным быстродействием и уверенной сходимостью. В примерах 1—4 (см. гл. 1) показано, что центральным звеном пакета, позволяющего решать системы дифференциальных и конечных уравнений, является метод решения системы линейных алгебраических уравнений. При этом нелинейные уравнения некоторым образом приводятся к ли-нейному виду и решаются с использованием итеративных схем. [c.301]

Таким образом, интегрирование системы дифференциальных уравнений в соответствии с формулой (5-48) сводится к решению линейных алгебраических уравнений. Для решения систем алгебраических уравнений используется итерационный метод, описание которого приведено на с. 301. Заметим, что метод позволяет решать как линейные, так и нелинейные системы. Поэтому для решения систем линейных дифференциальных уравнений можно применить формулу (5-45) без линеаризации (5-42). [c.336]

Прежде всего представим нелинейную систему дифференциальных уравнений (8.42) в форме системы линейных и квазилинейных интегральных Зфавнений. Как уже отмечалось, это можно сделать либо путем разложения в степенной ряд решения нелинейного дифференциального уравнения по специальным образом введенному параметру [8 ] (этот метод подробно изложен также в работе [15]), либо с помощью специальной замены переменных [15]. В данном случае к цели быстрее приводит второй метод. Последовательно преобразуем каждое из уравнений системы (8.42) к интегральному виду. [c.485]

Существует два способа расчета параметров жидкости в пограничном слое. Первый способ заключается в численном решении системы дифференциальных уравнений пограничного слоя, впервые полученных Прандтлем, и основывается на использева-пии вычислительных машин. В настоящее время разработаны различные математические методы, позволяющие создавать рациональные алгоритмы для решения уравнений параболического типа, к которому относится уравнение пограничного слоя. Такой подход широко используется для определения характеристик ламинарного пограничного слоя. Развиваются приближенные модели турбулентности, применение которых делает возможным проведение расчета конечно-разностными численными методами и для турбулентного потока. Второй способ состоит в нахождении методов приближенного расчета, которые позволяли бы получить необходимую информацию более простым путем. Такие методы можно получпть, если отказаться от нахождения решений, удовлетворяющих дифференциальным уравнениям для каждой частицы, и вместо этого ограничиться отысканием решений, удовлетворяющих некоторым основным уравнениям для всего пограничного слоя и некоторым наиболее важным граничным условиям на стенке и на внешней границе пограничного слоя. Основными уравнениями, которые обычно используются в этих методах, являются уравнения количества движения и энерпш для всего пограничного слоя. При этом, однако, необходимо задавать профили скорости и температуры. От того, насколько удачно выбрана форма этих профилей, в значительной степени зависит точность получаемых результатов. Поэтому получили распространение методы расчета параметров пограничного слоя, в которых для нахождения формы профилей скорости и температуры используются дифференциальные уравнения Прандтля или их частные решения. Далее расчет производится с помощью интегрального уравнения количества движения. [c.283]

Теория подобия используется для обобщения данных о каком-либо физическол процессе при осуществлении его в аппаратах различного размера. Методы теории подобия применяют для определения физических характеристик процесса в большом аппарате на основе изучения этого процесса в малом аппарате. При этом принимается, что процесс описывается одной и той же системой дифференциальных уравнений, т. е. что структура математического описания неизменна. Предполагается, что аналитическое или численное решение этого описания вызывает затруднения применение же теории подобия позволяет выполнить исследование процесса, не прибегая к решению системы дифференциальных уравнений. [c.134]

Модели табл. 4.4 записаны для нестационарных условий движения потоков. Приравнивая нулю производную по времени, можно получить модели для стационарных условий. При этом существенно упрощается и соответствующее математическое описание. Так, для ячеечных моделей вместо системы дифференциальных уравнений описанием будет система нелинейных алгебраических уравнений. В общем случае весьма трудно получить аналитическое решение системы уравнений модели. Поэтому основными подходами к разработке алгоритмов решения являются аппарат передаточных функций и методы вычислительной математики. Эти методы по классам уравнений (дифференциальным в частных производных, обыкновенным дифференциальным, системам алгебраических уравнений) достаточно разработаны и обычно составляют эиблиотеку стандартных программ для решения задач вычислительной математики. [c.121]

Как указывалось выше, большинство уравнений математического описания представляют собой дифференциальные уравнения с краевыми условиями, заданными на разных границах слоя катализатора. Вообш,е говоря, решать такие уравнения можно как начальные задачи, подбирая ряд условий на одной границе, чтобы в результате расчета выполнить их на другой. Однако подбор краевых условий ( пристрелка ) связан с значительным числом решений одной задачи и поэтому не всегда целесообразен. Кроме того, описанный метод из-за возможной неустойчивости не всегда позволяет получить решение. Более эффективным методом решения стационарной краевой задачи является переход к сложной нестационарной. Оказывается, что при усложнении исходной системы уравнений нахождение решения в стационарном режиме значительно упрощается. В этом случае трудности, связанные с заданием краевых условий, отпадают, поскольку анализируется переходный процесс одновременно во всем слое катализатора из начального состояния в конечное стационарное, определяемое заданной исходной системой уравнений. При помощи рассмотренного метода удается создать общий подход к использованию численных методов, применение которых не зависит от числа уравнений, входящих в математическое описание встречающихся видов граничных условий, кинетических закономерностей процесса и знания приближенного решения. Помимо этого достигаются простота осуществления алгоритма на вычислительной машине, ограничение объема перерабатываемой информации, быстрая сходимость расчетов и т. п. Решение нестационарных задач дает также возможность рассчитывать переходные режимы и влияние различных возмущений на течение процессов. [c.486]

На первом этапе решения, когда величина концентраций существенно зависит от выбранных начальных условий, осуществляется численное интегрирювание полной системы дифференциальных уравнений химической кинетики одним из разностных методов с заданной относительной погрешностью интегр>ирования. Этот этап решения заканчивается, когда наиболее реакционноспособные компоненты выходят на квазистационарный режим (эти условия проверяются на каждом шаге интегрирования). На втором этапе решения часть дифференциальных уравнений для наиболее реакционноспособных компонент заменяются алгебраическими и на каждом шаге интегрирования укороченной системы обыкновенных дифференциальных уравнений решается дополнительно система нелинейных алгебраических уравнений. При этом, если условия квазистационарности нарушаются для некоторых компонент, то соответствующие алгебраические уравнения опять заменяются исходными дифференциальными.Действительно, пусть система уравнений химической кинетики представлена в виде [c.133]

При составлении программы для второго этапа решения задачи обратить внимание на возможность использования программы для первого этапа с незначительной переделкой в первую очередь з астка программы, ответственного за решение системы дифференциальных уравнений методом Эйлера, [c.131]

Кинетика реакции с учетом выгорания. Макрокинетический закон реакции. До сих пор мы считали частоты элементарных процессов VI постоянными, вследствие чего математическая задача кинетики сводилась к решению системы дифференциальных уравнений с постоянными коэффициентами. Такое упрощение задачи возможно, пока мы ограничиваем рассмотрение реакции начальной ее стадией, когда концентрации исходных веществ еще не претерпели сколько-нибудь существенного изменения. При значительной глубине реакции, очевидно, необходимо учитывать изменения концентраций всех присутствующих в зоне реакции веществ вследствие этого возникает задача решения дифференциальных уравнений с переменными коэффициентами, которая в общем виде неразрешима. Однако, пользуясь методом квазистациоиарных концентраций, часто удается свести задачу к решению системы двух уравнений, которая в отдельных простейших случаях может быть решена сравнительно просто. В результате этого решения получаются определенные соотношения между концентрациями активных центров и исходных веществ, позволяющие [c.525]

Вначале рассмотрим течение неограниченного объема жидкости вблизи стенки, внезапно приведенной в движение. В этой задаче показывается применение метода замены переменныл, который позволяет свести уравнение в частных производных к одному обыкновенному дифференциальному уравнению. Данный метод решения возможен только в том случае, когда два граничных условия могут быть объединены в одно. Нужно отметить, что такая гидродинамическая система никогда не достигает предельного стационарного состояния. [c.119]

В предыдущих разделах настоящей главы рассматривались вопросы применения метода динамического программирования для оптимизации д и с к р е т н ы х многостадийных процессов. Именно при анализе таких процессов, которые допускают четкое разбиение на стадии, наиболее наглядно проявляются основные достоинства эгого метода как способа решения оптимальных задач для процессов с произвольным числом управляемых стадий. Однако метод дииами ческого программирования можно использовать также и для оптимизации ироцессов с распределенными параметрами и нестационарных процессов с сосредоточенными параметрами, которые изменяются непрерывно. При этом закон их изменения описывается системами дифференциальных уравнений [c.307]

Рассмотренный вывод кинетики процесса является приближенным не только потому, что мы упростили схему процесса, но и потому, что пользовались методом квазистационарных концентраций, который для данного случая недостаточно обоснован. Более строгое решение задачи можно получить, рассматривая решение системы дифференциальных уравнений (VIII, 36), (VIII, 37) и (VIII, 38) в общем виде. Такое решение возможно, но расчет получается очень громоздким. [c.220]

Методы Уравнения дифференциальные – Энциклопедия по машиностроению XXL

Классификация методов численного интегрирования систем обыкновенных дифференциальных уравнений (ОДУ). Методы численного интегрирования ОДУ являются методами преобразования дифференциальных уравнений в алгебраические. После дискретизации независимой переменной t система ОДУ [c.235]

Дифференциальное уравнение вращательного движения твердого пела в общем случае позволяет решать две основные задачи гю заданному вращению тела определять вращающий момент внешних сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота как функции времени приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным выше методам интегрирования дифференциального уравнения прямолинейного движения точки. [c.315]

Задача 175. Составить, пользуясь методом Лагранжа, дифференциальное уравнение колебаний физического маятника (см, 129). [c.380]

Такие решения с применением систем уравнений Лагранжа второго рода являются приближенными не только из-за численных методов решения дифференциальных уравнений, но и потому, что трение в кинематических парах здесь можно оценить лишь весьма приближенно, а упругость звеньев и зазоры в кинематических парах не учитываются вообще. Поэтому при разработке опытных образцов ПР применяют экспериментальные методы динамического исследования ПР, позволяющие с помощью соответствующих датчиков и аппаратуры записать осциллограммы перемещений, скоростей и ускорений звеньев и опытным путем учесть как неточности теоретического расчета, так и влияние ранее неучтенных факторов. [c.338]

Исходная информация для моделирования формируется из двух частей информации, задаваемой пользователем, и информации, хранящейся в элементной базе данных. Информация, задаваемая пользователем, может включать структуру моделируемой ЭЭС, параметры функциональных элементов, метод интегрирования дифференциальных уравнений, последовательность моделируемых режимов ЭЭС, форму вывода результатов моделирования. Исходная информация, формируемая с помощью базы данных, ограничивается, в основном, параметрами и характеристиками функциональных элементов. [c.229]

Из общего уравнения динамики вытекают дифференциальные уравнения движения системы материальных точек, в которые не входят силы реакций идеальных связей. Возможно решение как прямых (определение сил по заданному движению), так и обратных задач (определение движения по заданным силам) динамики. При решении обратных задач приходится интегрировать составленную систему дифференциальных уравнений движения. Заметим, что использование общего уравнения динамики является формальным методом составления дифференциальных уравнений движения системы. Этот метод является менее удобным и менее эффективным по сравнению с применением уравнений Лагранжа второго рода (читатель сможет в этом убедиться, ознакомившись с содержанием следующего параграфа). [c.414]

При решении задач на устойчивость движения в этом пункте будет применен прямой метод интегрирования дифференциальных уравнений возмущенного движения. Этот метод наиболее эффективен по своим результатам, однако его применение ограничено небольшим числом возможных приложений ввиду математических трудностей, связанных с получением решения в замкнутом виде. [c.646]

Метод Бубнова—Галеркина. И. Г. Бубнов предложил приближенный метод интегрирования дифференциальных уравнений [c.127]

Понятие о циклических координатах имеет существенное значение в теории интегрирования уравнений динамики. Мы возвратимся к этому понятию в главе, содержащей методы интегрирования дифференциальных уравнений движения материальных систем. [c.149]

Необходимо все же отметить, что предварительные соображения, приводящие к упрощению выражений кинетической и потенциальной энергий, нельзя полагать достаточно обоснованными. Действительно, напомним замечания А. Н. Крылова по поводу приближенного метода интегрирования дифференциального уравнения движения сферического маятника ( 229 первого тома). [c.230]

Уравнения (11.327) А. М. Ляпунов называет уравнениями возмущенного движения ). А. М. Ляпунов не останавливается на вопросе о методах составления дифференциальных уравнений возмущенного движения для конкретных случаев задания функций Qh, но замечает, что в уравнениях (11.327) можно заменить независимую переменную t—время — другой переменной, являющейся монотонно возрастающей функцией времени. [c.330]

Дифференциальные уравнения относительного движения маятника можно получить как методом уравнений Лагранжа, так и методом сил инерции. Покажем для сравнения и тот и другой методы. [c.426]

Теория возмущений занимает центральное место среди приближенных методов интегрирования дифференциальных уравнений. Однако в задачах с малым параметром е при старшей производной сколь угодно малые изменения параметра приводят к конечным приращениям решения. При в=0 понижается порядок уравнения. Различие фазовых траекторий исходной и вырожденной систем существенно усложняет получение приближенных решений. Сингулярные уравнения встречаются в механике, релятивистской теории поля и в основном теориях движения плазмы, жидкости и газа. [c.331]

Большой вклад в разработку новых методов интегрирования дифференциальных уравнений динамики внесли Гамильтон и немецкий ученый Якоби (1804—1851). [c.16]

Принцип Гамильтона (4), содержащий в себе геометрическую конструкцию траектории по волновому принципу Гюйгенса, как никакой другой принцип динамики позволяет с общей точки зрения осветить методы интегрирования дифференциальных уравнений движения. [c.278]

Большое внимание уделено численным методам решения линейных и нелинейных задач механики деформирования упругих, упругопластических и вязкоупругих тел, численным методам решения дифференциальных и интегральных уравнений, а также прямым вариационным методам. В учебнике изложены основные положения метода конечных элементов, что обеспечит лучшую подготовленность студентов к изучению курса строительной механики. Даются понятия о методе граничных элементов. [c.3]

После установления Навье в 1821 г. основных уравнений и создания Коши теории напряжений и деформаций важнейшее значение для развития теории упругости имели исследования Сен-Венана. В его классических работах по теории кручения и изгиба на основе общих уравнений теории упругости дано решение задач кручения и изгиба призматических брусьев. В этих исследованиях Сен-Венан создал полуобратный метод решения задач теории упругости, сформулировал знаменитый принцип Сен-Венана , дающий возможность получить решение задач теории упругости. С тех пор было затрачено много усилий на развитие теории упругости и ее приложений, доказан ряд общих теорем, предложены общие методы интегрирования дифференциальных уравнений равновесия и движения, решено много частных задач, представляющих принципиальный интерес. Развитие новых областей техники требует более глубокого и широкого изучения теории упругости. Большие скорости вызывают необходимость постановки и решения сложных вибрационных проблем. Легкие металлические конструкции привлекают серьезное внимание к вопросу упругой устойчивости. Концентрация напряжений вызывает опасные последствия, поэтому пренебрегать ею рискованно. [c.5]

Универсальным численным методом решения дифференциальных уравнений и их систем является разностный метод, называемый еще методом конечных разностей или методом сеток. Сущность этого метода заключается в том, что в области изменения переменных величин вводят некоторую сетку, а все производные, входящие в дифференциальные уравнения и краевые условия, заменяют алгебраическими комбинациями от значений функции в узлах сетки.

Рещая полученную в результате такой замены систему [c.58]

Заметим, что при достаточно малых значениях Дх решение уравнения (3.11) устойчиво и сходится к точному решению исходного уравнения (3 9). Численный метод решения дифференциальных уравнений с использованием разностной схемы вида (3.11) носит название метода Эйлера. [c.59]

И. Г. Бубнов (1872—1919) впервые в 1913 г. изложил новый приближенный метод интегрирования дифференциальных уравнений теории упругости, который широко применялся затем Б. Г. Галеркиным (1871—1945) для решения ряда задач теории упругости. Метод Бубнова—Галеркина, как общий приближенный метод интегрирования дифференциальных уравнений, не связан, вообще говоря, с каким-либо вариационным принципом. [c.109]

Задачи 386—387. В задаче 386 определить прогибы / и углы поворота 0 сечений балок методом интегрирования дифференциальных уравнений упругой линии [c.146]

Одним из эффективных методов решения дифференциальных и интегральных уравнений является метод интегральных преобразований. Применение этого метода к дифференциальным уравнениям позволяет на единицу снизить размерность уравнения, [c.63]

Одним из универсальных методов решения дифференциальных уравнений является метод конечных разностей (см., например, [6]). Он заключается в следующем. Область непрерывного изменения аргумента заменяется конечной совокупностью точек (узлов), называемых сеткой, сами же функции, рассматриваемые в этих точках, называются сеточными функциями. Производные, входящие в дифференциальные уравнения и краевые условия (если они дифференциальные), заменяются теми или иными разностными соотношениями. Тогда для значений функций в узловых точках получается система алгебраических уравнений. [c.172]

Реальные объекты химической технологии, как правило, не обладают свойством линейности, и поэтому для их описания приходится применять нелинейные операторы. Нелинейность функциональных операторов значительно усложняет теоретическое исследование динамики объектов. Это связано прежде всего с необходимостью рассматривать нелинейные дифференциальные уравнения, для которых нет универсальных методов решения (таких, например, как метод сведения дифференциальных уравнений к алгебраическим с помощью преобразования Лапласа) и которые в большинстве случаев вообще не могут быть решены в квадратурах. [c.77]

Формула (3.9.6) представляет общий интеграл линейного дифференциального уравнения с правой частью в форме, наиболее удобной для приложений. Постоянные интегрирования имеют здесь простой смысл это начальные (при 2 = 0) значения искомой функции и ее производных. Поэтому метод интегрирования дифференциальных уравнений, основанный на> формуле (3.9.6) и широко применяемый в строительной механике, называется методом начальных параметров, он разрабатывался рядом советских авторов не только в применении к балкам, но также к пластинкам и оболочкам. [c.105]

И. Г. Бубнов (1872—1919) разработал новый приближенный метод интегрирования дифференциальных уравнений, блестяще развитый Б. Г. Галеркиным (1871—1945). Вариационный метод Бубнова — Галеркина в настоящее время получил широкое распространение. Большое значение имеют труды И. Г. Бубнова и Б. Г. Галеркина в теории изгиба пластинок. Новые важные результаты, продолжая исследования Галеркина, получил П. Ф. Папкович (1887—1946). [c.6]

Из вариационных методов приведения дифференциальных уравнений в частных производных к обыкновенным дифференциальным уравнениям остановимся на методе В. 3. Власова. [c.162]

Для решения нестационарных задач численным методом из дифференциального уравнения теплопроводности (2.54) [c.94]

Метод упрощения дифференциальных уравнений Навье —Стокса для второго предельного случая был разработан Прандтлем. В 1904 г. он представил доклад на эту тему Международному конгрессу математиков, собравшемуся в Гейдельберге. [c.103]

В связи с широким использованием вычислительных машин по-новому оцениваются возможности численных методов решения дифференциальных уравнений, таких, как конечно-разностный метод (метод сеток). [c.189]

Общие замечания о существующих методах решения дифференциальных уравнений (I) и (II). Полученные выше уравнение баланса расхода (I) и уравнение динамического равновесия (II) представляют собой систему двух дифференциальных уравнений, которые принято называть уравнениями Сен-Венана. [c.372]

НИИ дискретизации по направлению распространения и замене интегралов от интенсивности по угловой координате соответствующими квадратурными формулами. В многомерном случае наиболее часто используется численное решение уравнений дифференциального приближения и метод Монте-Карло. Применение последнего наиболее эффективно при необходимости учета переменных радиационных свойств и рассеяния. [c.203]

Наиболее существенные успехи в развитии механики неголономных систем связаны с именами С. А. Чаплыгина, В. Вольтерра, П. В. Воронца и П. Аппеля. В этой главе будут рассмотрены лишь некоторые методы составления дифференциальных уравнений движения неголономных систем. Достаточно полное изложение механики неголономных систем содержится в монографиях А. И. Лурье ) и Ю. И. Ненмарка и Н. А. Фуфаева ). [c.177]

Предполагается, что метод решения дифференциальных уравнений движения должен быть тесно связан с физическими особенностями движения, поэтому в восьмой главе исследуется физическая ка]ртина движения в диффузорах. Рассматривается как движение в диффузоре в целом, так и движение в турбулентном пограничном слое. Показывается, что для внутренней области – вследствие ее консервативности по отношению ко внешним возмущениям – удобно использовать метод последовательных приближений, а для менее устойчивой внешней области – методы типа Бубнова-Галеркина. В последующих главах метод по-зонного решения уравнений пограничного слоя подробно обосновывается. [c.8]

Уравнения Лагранжа второго рода дают общий метод составления дифференциальных уравнений движения механической системы с голономными идеальными удерживающими связями в обобщенных координатах. Строгий вывод этих уравнений выходит за рамки данного курса, поэтому проиллюстрируем их справедливость на очень частном случае механической системы с одной степенью свободы, когда наложенхсые на нее связи являются не только голономными идеальными удерживающими, но и стационарными. [c.300]

Сущность вариацмонных методов решення дифференциальных уравнений [c.153]

Основные понятия теории численных методов решения дифференциальных уравнений будут достаточно подробно рассмотрены в главе 3 на примере дифференциального уравнения теплопроводности. Сейчас лишь кратко сформулируем ряд понятий, которые понадо- [c.27]

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т. д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

называется нормальной.

Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а < t < b, обращающая уравнения системы (3) в тождества по t на интервале (а, b).

Задача Коши для системы (3) формулируется так: найти решение (4) системы, удовлетворяющее при начальным условиям

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

зависящих от t и n произвольных постоянных называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.

Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат Решение

системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Проинтегрировать систему

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

Сумма

двух решений однородной линейной системы уравнений является решением той же системы.

Следствие:

Линейная комбинация

с произвольными постоянными коэффициентами сi решений линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора получаем

Это означает, что сумма есть решение неоднородной системы уравнений

Определение:

Векторы

называются линейно зависимыми на интервале a < t < b, если существуют постоянные числа , такие, что

при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

Определитель

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а < t < Ь, называется фундаментальной.

Теорема:

Определитель Вронского W(t) фундаментальной на интервале а < t < b системы решений линейной однородной системы (6) с непрерывными на отрезке коэффициентами отличен от нуля во всех точках интервала (а, Ь)

Теорема:

О структуре общего решения линейной однородной системы. Общим решением в области линейной однородной системы

с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а < t < b решений системы (6) :

() — произвольные постоянные числа).

Пример:

Система

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

откуда

следовательно,

Матрица называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

Пусть

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя в (2), получаем

Так как

то для определения получаем систему

или, в развернутом виде,

Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a < t < Ь, так что система (10) имеет единственное решение

где — известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения в (9), находим частное решение системы (2)

(здесь под символом понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты — постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Решить систему

Ищем решение в виде

Характеристическое уравнение

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) получаем

откуда а21 = а11. Следовательно,

Полагая в находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

Напомним некоторые понятия из линейной алгебры. Вектор называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как есть нуль-матрица.

Теорема:

Если собственные значения матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь — произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Решить систему

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

и мнимая часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

где сi — произвольные постоянные.

Пример:

Решить систему

Матрица системы

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

где с1, с2 — произвольные действительные числа.

Понятие о системах дифференциальных уравнений

Смотрите также:

Предмет высшая математика

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Извлечение квадратного корня
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Точные уравнения и интегрирующие множители

Привет! Возможно, вам сначала захочется узнать о дифференциальных уравнениях и частных производных!

Точное уравнение

«Точное» уравнение – это дифференциальное уравнение первого порядка, подобное этому:

M (x, y) dx + N (x, y) dy = 0

имеет некоторую специальную функцию I (x, y), частные производные которой могут быть заменены M и N следующим образом:

∂I ∂x dx + ∂I ∂y dy = 0

, и наша задача – найти эту магическую функцию I (x, y), если она существует.

Мы можем знать с самого начала, точное это уравнение или нет!

Представьте, что мы делаем следующие частные производные:

∂M ∂y = ∂ ² I ∂y ∂x

∂N ∂x = ∂ ² I ∂y ∂x

они в итоге те же ! Так и будет:

∂M ∂y = ∂N ∂x

Когда это правда, у нас есть «точное уравнение», и мы можем продолжить.

И чтобы открыть I (x, y) , мы делаем ЛИБО :

I (x, y) = ∫M (x, y) dx (с x в качестве независимой переменной), OR
I (x, y) = ∫N (x, y) dy (с y в качестве независимой переменной)

И затем есть некоторая дополнительная работа (мы покажем вам), чтобы прийти к общему решению

Я (х, у) = С

Давайте посмотрим на это в действии.

Пример 1: Решить

(3x ² y ³ – 5x ⁴) dx + (y + 3x ³ y ²) dy = 0

В данном случае имеем:

M (x, y) = 3x ² y ³ – 5x ⁴
N (x, y) = y + 3x ³ y ²

Мы оцениваем частные производные для проверки их точности.

∂M ∂y = 9x ² y ²
∂N ∂x = 9x ² y ²

Они такие же! Итак, наше уравнение точное.

Мы можем продолжить.

Теперь мы хотим открыть I (x, y)

Сделаем интеграцию с x в качестве независимой переменной:

I (x, y) = ∫M (x, y) dx

= ∫ (3x ² y ³ – 5x ⁴) dx

= x ³ y ³ – x ⁵ + f (y)

Примечание. f (y) – это наша версия постоянной интегрирования «C», потому что (из-за частной производной) у нас было y в качестве фиксированного параметра, который, как мы знаем, действительно является переменной.

Итак, теперь нам нужно найти f (y)

В самом начале этой страницы мы сказали, что N (x, y) можно заменить на ∂I ∂y , поэтому:

∂I ∂y = N (x, y)

Что нас подводит:

3x ³ y ² + df dy = y + 3x ³ y ²

Условия отмены:

df dy = y

Объединение обеих сторон:

f (y) = y ² 2 + C

У нас есть f (y). А теперь просто положи на место:

I (x, y) = x ³ y ³ – x ⁵ + y ² 2 + C

и общее решение (как упоминалось перед этим примером):

Я (х, у) = С

Ой! Эта буква «C» может иметь другое значение, чем буква «C» перед этим. Но оба они означают «любая константа», поэтому назовем их C ₁ и C ₂, а затем превратим их в новый C ниже, сказав C = C ₁ + C ₂

Получаем:

x ³ y ³ – x ⁵ + y ² 2 = C

И вот как работает этот метод!

Поскольку это был наш первый пример, давайте продолжим и убедимся, что наше решение верное.

Выведем I (x, y) относительно к x, то есть:

Начать с:

I (x, y) = x ³ y ³ – x ⁵ + y ² 2

Использование неявного дифференциация получаем

∂I ∂x = x ³ 3y ² y ‘ + 3x ² y ³ – 5x ⁴ + yy ‘

Упростить

∂I ∂x = 3x ² y ³ – 5x ⁴ + y ‘(y + 3x ³ y ²)

Мы используем факты, что y ‘= dy dx и ∂I ∂x = 0, затем умножаем все на dx, чтобы окончательно получить:

(y + 3x ³ y ²) dy + (3x ² y ³ – 5x ⁴) dx = 0

, которое является нашим исходным дифференциальным уравнением.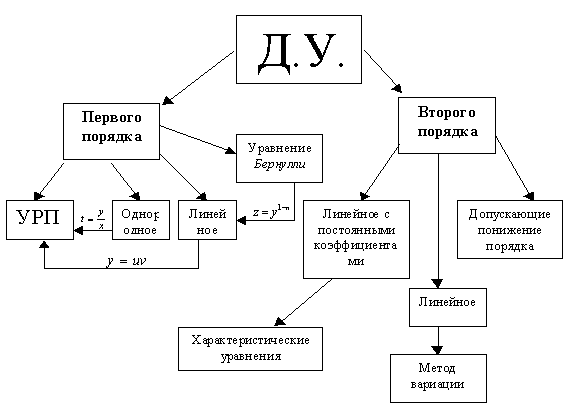

Итак, мы знаем, что наше решение правильное.

Пример 2: Решить

(3x ² – 2xy + 2) dx + (6y ² – x ² + 3) dy = 0

M = 3x ² – 2xy + 2
N = 6 лет ² – x ² + 3

Итак:

∂M ∂y = −2x
∂N ∂x = −2x

Уравнение точное!

Теперь найдем функцию I (x, y)

На этот раз попробуем I (x, y) = ∫N (x, y) dy

Итак, I (x, y) = ∫ (6y ² – x ² + 3) dy

I (x, y) = 2y ³ – x ² y + 3y + g (x) (уравнение 1)

Теперь мы продифференцируем I (x, y) по x и установим его равным M:

∂I ∂x = M (x, y)

0 – 2xy + 0 + g ‘(x) = 3x ² – 2xy + 2

−2xy + g ‘(x) = 3x ² – 2xy + 2

г ‘(x) = 3x ² + 2

А интеграция дает:

г (х) = х ³ + 2x + C (уравнение 2)

Теперь мы можем заменить g (x) в уравнении 2 в уравнении 1:

I (x, y) = 2y ³ – x ² y + 3y + x ³ + 2x + C

И общее решение имеет вид

Я (х, у) = С

и так (помня, что предыдущие две “C” – это разные константы, которые можно объединить в одну, используя C = C ₁ + C ₂), мы получаем:

2 года ³ – x ² y + 3y + x ³ + 2x = C

Решено!

Пример 3: Решить

(xcos (y) – y) dx + (xsin (y) + x) dy = 0

У нас:

M = (xcos (y) – y) dx

∂M ∂y = −xsin (y) – 1

N = (xsin (y) + x) dy

∂N ∂x = sin (y) +1

Таким образом

∂M ∂y ≠ ∂N ∂x

Итак, это уравнение не совсем!

Пример 4: Решить

[y ² – x ² sin (xy)] dy + [cos (xy) – xy sin (xy) + e ^2x] dx = 0

M = cos (xy) – xy sin (xy) + e ^2x

∂M ∂y = −x ² y cos (xy) – 2x sin (xy)

N = y ² – x ² sin (xy)

∂N ∂x = −x ² y cos (xy) – 2x sin (xy)

Они такие же! Итак, наше уравнение точное.

На этот раз мы оценим I (x, y) = ∫M (x, y) dx

I (x, y) = ∫ (cos (xy) – xy sin (xy) + e ^2x) dx

Используя интеграцию по частям, получаем:

I (x, y) = 1 y sin (xy) + x cos (xy) – 1 y sin (xy) + 1 2 e ^2x + f (y)

I (x, y) = x cos (xy) + 1 2 e ^2x + f (y)

Теперь оценим производную по y

∂I ∂y = −x ² sin (xy) + f ‘(y)

И это равно N, что равно M:

∂I ∂y = N (x, y)

−x ² sin (xy) + f ‘(y) = y ² – x ² sin (xy)

f ‘(y) = y ² – x ² sin (xy) + x ² sin (xy)

f ‘(y) = y ²

f (y) = 1 3 y ³

Итак, наше общее решение I (x, y) = C становится:

xcos (xy) + 1 2 e ^2x + 1 3 y ³ = C

Готово!

Интегрирующие факторы

Некоторые неточные уравнения можно умножить на некоторый коэффициент, a функция u (x, y) , чтобы сделать их точными.

Если эта функция u (x, y) существует, она называется интегрирующим коэффициентом . Это сделает действительным следующее выражение:

∂ (u · N (x, y)) ∂x = ∂ (u · M (x, y)) ∂y

Есть несколько особых случаев:

u (x, y) = x ^m y ⁿ
u (x, y) = u (x) (то есть u является функцией только от x)
u (x, y) = u (y) (что есть, u является функцией только y)

Давайте посмотрим на те случаи…

Коэффициенты интегрирования с использованием u (x, y) = x

^m y ⁿ

Пример 5: (y ² + 3xy ³) dx + (1 – ху) dy = 0

M = y ² + 3xy ³

∂M ∂y = 2y + 9xy ²

N = 1 – ху

∂N ∂x = −y

Итак, ясно, что ∂M ∂y ≠ ∂N ∂x

Но мы можем попытаться сделать точным , умножив каждую часть уравнение по x ^m y ⁿ :

(x ^m y ⁿ y ² + x ^m y ⁿ 3xy ³) dx + (x ^m y ⁿ – x ^m y ⁿ xy) dy = 0

Что “упрощает” до:

(x ^м y ^{n + 2} + 3x ^{m + 1} y ^{n + 3}) dx + (x ^m y ⁿ – x ^{m + 1} y ^{n + 1}) dy = 0

А теперь у нас:

M = x ^м y ^{n + 2} + 3x ^{m + 1} y ^{n + 3}

∂M ∂y = (n + 2) x ^m y ^{n + 1} + 3 (n + 3) x ^{m + 1} y ^{n + 2}

N = x ^м y ⁿ – x ^{м + 1} y ^{n + 1}

∂N ∂x = mx ^{m − 1} y ⁿ – (m + 1) x ^m y ^{n + 1}

И мы хотим ∂M ∂y = ∂N ∂x

Итак, давайте выберем правильные значения m и n , чтобы уравнение было точным.

Уравнять:

(n + 2) x ^m y ^{n + 1} + 3 (n + 3) x ^{m + 1} y ^{n + 2} = mx ^{m − 1} y ⁿ – (m + 1) x ^м y ^{n + 1}

Заказать и упростить:

[(m + 1) + (n + 2)] x ^m y ^{n + 1} + 3 (n + 3) x ^{m + 1} y ^{n + 2} – mx ^{m − 1} y ⁿ = 0

Чтобы он был равен нулю, каждый коэффициент должен быть равен нулю, поэтому:

(m + 1) + (n + 2) = 0
3 (п + 3) = 0
м = 0

Последний, m = 0 , очень помогает! При m = 0 можно рассчитать, что n = −3

И результат:

x ^м y ⁿ = г ⁻³

Теперь мы знаем, как умножить наше исходное дифференциальное уравнение на y ⁻³ :

(y ⁻³ y ² + y ⁻³ 3xy ³) dx + (y ⁻³ – y ⁻³ xy) dy

Что становится:

(y ⁻¹ + 3x) dx + (y ⁻³ – xy ⁻²) dy = 0

И это новое уравнение должно быть точным, но давайте еще раз проверим:

M = y ^-1 + 3х

∂M ∂y = −y ⁻²

N = y ⁻³ – xy ⁻²

∂N ∂x = −y ⁻²

∂M ∂y = ∂N ∂x

Они такие же! Наше уравнение теперь точное !

Итак, продолжим:

I (x, y) = ∫N (x, y) dy

I (x, y) = ∫ (y ⁻³ – xy ⁻²) dy

I (x, y) = −1 2 y ⁻² + xy ⁻¹ + g (x)

Теперь, чтобы определить функцию g (x), мы оцениваем

∂I ∂x = y ⁻¹ + g ‘(x)

И это равняется M = y ⁻¹ + 3x, поэтому:

y ⁻¹ + g ‘(x) = y ⁻¹ + 3x

А так:

г ‘(x) = 3x

г (x) = 3 2 x ²

Итак, наше общее решение I (x, y) = C:

−1 2 y ⁻² + xy ⁻¹ + 3 2 x ² = C

Интегрирующие множители с использованием u (x, y) = u (x)

Для u (x, y) = u (x) мы должны проверить это важное условие:

Выражение:

Z (x) = 1 N [ ∂M ∂y – ∂N ∂x ]

должен иметь , а не , член y , так что интегрирующий коэффициент является функцией только x

Если вышеупомянутое условие верно, то наш интегрирующий коэффициент:

u (x) = e ^{∫Z (x) dx}

Давайте попробуем пример:

Пример 6: (3xy – y ²) dx + x (x – y) dy = 0

M = 3xy – y ²

∂M ∂y = 3x – 2y

N = х (х – у)

∂N ∂x = 2x – y

∂M ∂y ≠ ∂N ∂x

Итак, наше уравнение – , а не точное .

Вычислим Z (x):

Z (x) = 1 N [ ∂M ∂y – ∂N ∂x ]

= 1 N [3x − 2y – (2x − y)]

= х-у х (х-у)

= 1 x

Итак, Z (x) является функцией только x, yay!

Итак, наш интегрирующий коэффициент равен

u (x) = e ^{∫Z (x) dx}

= e ^{∫ (1 / x) dx}

= e ^{ln (x)}

= х

Теперь, когда мы нашли интегрирующий коэффициент, давайте умножим дифференциальное уравнение по нему.

x [(3xy – y ²) dx + x (x – y) dy = 0]

и получаем

(3x ² y – xy ²) dx + (x ³ – x ² y) dy = 0

Теперь должно быть точно. Проверим:

M = 3x ² y – xy ²

∂M ∂y = 3x ² – 2xy

N = x ³ – x ² y

∂N ∂x = 3x ² – 2xy

∂M ∂y = ∂N ∂x

Итак, наше уравнение точное!

Теперь решаем так же, как и в предыдущих примерах.

I (x, y) = ∫M (x, y) dx

= ∫ (3x ² y – xy ²) dx

= x ³ y – 1 2 x ² y ² + c ₁

И мы получаем общее решение I (x, y) = c:

x ³ y – 1 2 x ² y ² + c ₁ = c

Объедините константы:

x ³ y – 1 2 x ² y ² = c

Решено!

Коэффициенты интегрирования с использованием u (x, y) = u (y)

u (x, y) = u (y) очень аналогично предыдущему случаю u (x, y) = и (х)

Итак, аналогично имеем:

Выражение

1 M [ ∂N ∂x – ∂M ∂y ]

должен иметь , а не , иметь член x , чтобы интегрирующий коэффициент должен быть функцией всего лишь от до .

И если это условие выполняется, мы называем это выражение Z (y) и наш интегрирующий коэффициент равен

u (y) = e ^{∫Z (y) dy}

И мы можем продолжить, как в предыдущем примере

И вот оно!

дифференциальное уравнение | Britannica

дифференциальное уравнение , математическое утверждение, содержащее одну или несколько производных, то есть членов, представляющих скорости изменения непрерывно изменяющихся величин.Дифференциальные уравнения очень распространены в науке и технике, а также во многих других областях количественного исследования, потому что то, что можно непосредственно наблюдать и измерять для систем, претерпевающих изменения, – это скорость их изменения. Решение дифференциального уравнения, как правило, представляет собой уравнение, выражающее функциональную зависимость одной переменной от одной или нескольких других; обычно он содержит постоянные члены, которых нет в исходном дифференциальном уравнении. Другими словами, решение дифференциального уравнения дает функцию, которую можно использовать для прогнозирования поведения исходной системы, по крайней мере, в пределах определенных ограничений.

Дифференциальные уравнения подразделяются на несколько широких категорий, которые, в свою очередь, делятся на множество подкатегорий. Наиболее важными категориями являются обыкновенные дифференциальные уравнения и уравнения в частных производных. Когда функция, входящая в уравнение, зависит только от одной переменной, ее производные являются обыкновенными производными, а дифференциальное уравнение классифицируется как обыкновенное дифференциальное уравнение. С другой стороны, если функция зависит от нескольких независимых переменных, так что ее производные являются частными производными, дифференциальное уравнение классифицируется как уравнение в частных производных.Ниже приведены примеры обыкновенных дифференциальных уравнений:

Подробнее по этой теме

Анализ

: Ньютон и дифференциальные уравнения

… применение анализа – это дифференциальное уравнение с, которое связывает скорости изменения различных величин с их . ..

В них y обозначает функцию, а t или x являются независимой переменной.Символы k и m используются здесь для обозначения определенных констант.

Независимо от типа, дифференциальное уравнение считается имеющим порядок n , если оно включает производную порядка n , но не имеет производной более высокого порядка. Уравнение является примером уравнения в частных производных второго порядка. Теории обыкновенных дифференциальных уравнений и уравнений в частных производных заметно различаются, и по этой причине эти две категории рассматриваются отдельно.

Вместо одного дифференциального уравнения объектом исследования может быть одновременная система таких уравнений. Формулировка законов динамики часто приводит к таким системам. Во многих случаях одно дифференциальное уравнение n -го порядка предпочтительно можно заменить системой одновременных уравнений n , каждое из которых относится к первому порядку, так что можно применять методы линейной алгебры.

Обыкновенное дифференциальное уравнение, в котором, например, функция и независимая переменная обозначены как y и x , по сути, является неявным обобщением основных характеристик y как функции x .Эти характеристики, по-видимому, были бы более доступны для анализа, если бы могла быть получена явная формула для y . Такая формула или, по крайней мере, уравнение в x и y (не содержащее производных), которое выводится из дифференциального уравнения, называется решением дифференциального уравнения. Процесс вывода решения из уравнения с помощью приложений алгебры и исчисления называется решением или интегрированием уравнения. Следует, однако, отметить, что дифференциальные уравнения, которые могут быть решены в явном виде, составляют незначительное меньшинство.Таким образом, большинство функций необходимо изучать косвенными методами. Даже его существование должно быть доказано, когда нет возможности предъявить его для проверки. На практике методы численного анализа с использованием компьютеров используются для получения полезных приближенных решений.

Операционный метод решения дифференциальных уравнений типа Риккати с функциональными аргументами

1. Введение

Обыкновенные и дифференциальные уравнения в частных производных имеют большое значение в прикладных науках, таких как физика, химия, биология [1–7].Кроме того, дифференциальные уравнения Риккати [8] и их обобщения описывают множество различных явлений в прикладной науке, от финансовой математики до квантовой механики [9–12]. Нахождению точных решений при некоторых предположениях посвящено много работ. Например, Мак и Харко [13] дали условия интегрируемости для обобщенного уравнения Риккати. Однако в общем случае ввиду нелинейности уравнений маловероятно, что такие точные решения будут найдены.Поэтому многие исследователи разработали различные численные методы для этих уравнений, и исследователи продолжают находить новые и эффективные методы. В последние годы большое внимание было уделено изучению численных аспектов различных типов дифференциальных уравнений Риккати [14–25]. При решении уравнения Шредингера, которое является важным уравнением математической физики, возникают дифференциальные уравнения Риккати. Один класс нелинейных уравнений Шредингера изучен в [26].Метод (G ‘/ G) -расширения с помощью уравнения Риккати применялся при решении специального нелинейного уравнения в частных производных [27]. Дифференциальное уравнение Риккати с функциональными аргументами было решено численно с использованием метода кривых Безье [28].

Наша цель в этой статье – представить численный метод, основанный на операционных матрицах, для решения дифференциальных уравнений типа Риккати с функциональными аргументами следующим образом [28] (1) pxu′α1x + β1 + qxu2α2x + β2 + rxuα3x + β3 = gx, 0≤x≤1, (1) с начальным условием (2) u0 = λ.(2) Здесь p , q , r и g – известные непрерывные функции, αi, βi (i = 1,2,3) и λ – константы. Задача (1) – (2) имеет единственное решение. Это наглядно видно из [29].

В 1973 году Коррингтон [30] показал, что линейные дифференциальные и интегральные уравнения могут быть преобразованы в систему алгебраических линейных уравнений с приближением в смысле наименьших квадратов и повторным интегрированием функций Уолша.Это исследование стало источником различных исследователей с функциями Уолша. Метод, основанный на операционных матрицах для функций Уолша, был введен в 1975 г. Ченом и Сяо [31]. Существуют различные работы, касающиеся методов, основанных на различных полиномах и функциях, таких как функции Бесселя [32], полиномы Бернштейна [33], полиномы Лежандра [34], функции Хаара [35], полиномы Чебышева [36], и др. Кроме того, метод операции мартикс [37, 38] для полиномов Тейлора был использован Юзбаси и Нурболом для решения интегро-дифференциальных уравнений и уравнений пантографа.

Операционные матрицы интегрирования P и произведения C в размерности (N + 1) × (N + 1) определяются следующим образом: (3) ∫0xXtdt≃PXx, XxDXx≃CXx, (3) где X (x) = [1 x x2… xN] T и D – известные векторы. В следующем разделе мы дадим схему получения этих матриц.

Остальная часть статьи организована следующим образом. В разделе 2 выводятся операционные матрицы. Раздел 3 содержит использование операционных матриц в методе решения. В разделе 4 дается анализ ошибок. В разделе 5 мы применим этот метод к некоторым примерам и сообщим численные результаты.В последнем разделе приведены выводы.

2. Операционные матрицы

В этом разделе вводится метод наименьших квадратов для нахождения полиномиального приближения любой функции. Это составит основную идею метода. После этого он используется для вывода операционных матриц, которые будут использоваться в методе решения.

2.1. Аппроксимация наименьших квадратов

Пусть Y = Span {1, x, x2,…, xN}. Поскольку Y является конечномерным подпространством L2 [0,1], существует наилучшее приближение из y0∈Y.Ввиду того, что Y содержит все многочлены степени не выше N , многочлен y0 может быть выражен как y0 = ∑k = 0Nakxk = AXx, где ak – неизвестные коэффициенты, которые будут определены. Предположим, что f (x) ∈L2 [0,1], тогда функция f (x) −y0 ортогональна Y , т.е. для всех y∈Y выполняется (4) f − y0, y⟩ = 0 , (4) где скалярное произведение задается как ⟨f, g⟩ = ∫10fxgxdx. Теперь мы подставляем функции 1, x, x2,…, xN в уравнение (4) и, таким образом, получаем систему алгебраических уравнений с неизвестными ak, (k = 0,1,…, N,) (5) ∫ 01fx − y0xidx = 0, i = 0,1,…, N.(5) Решая систему (5), мы получаем наилучшее приближение f (x) из Y . Другими словами, известная функция f (x) приближенно представляется полиномом как (6) fx≃AXx. (6) [37]

2.2. Операционная матрица для интеграции

В этом подразделе мы выводим операционную матрицу для интеграции. Для этого рассмотрим выражение ∫0xXtdt = ∫0x1dt∫0xtdt∫0xt2dt ⋯ ∫0xtNdtT = xx22x33 ⋯ xN + 1N + 1T = ΛX1x, где матрица Λ в размерности (N + 1) × (N + 1) имеет компоненты 1,12,13, ⋯ 1 / (N + 1) на главной диагонали и нули в других элементах и X1 (x) = [x x2 x3 ⋯ xN + 1] T.Используя уравнение (6) для f (x) = xN + 1, мы получаем xN + 1≃AN + 1Xx, где компоненты AN + 1 определены в соответствии с предыдущим подразделом. Функции xj − 1, (j = 1,2,…, N + 1) могут быть записаны как xj − 1 = IjXx, где Ij – это j -я строка единичной матрицы в размерном (N + 1) × (N + 1). В результате интеграл ∫0xX (t) dt можно записать как ∫0xXtdt = Λ X1x≃10… 0012… 0 ⋮⋮ ⋱ ⋮ 00… 1N + 1 × I2I3 ⋮ AN + 11x ⋮ xN. Таким образом, получается операционная матрица для интегрирования в виде (7) P = 10… 0012… 0 ⋮⋮ ⋱ ⋮ 00… 1N + 1I2I3 ⋮ AN + 1.(7) [37, 38]

3. Метод решения

В этом разделе операционные матрицы используются для построения численных решений задачи (1) – (2). Во-первых, мы можем аппроксимировать производную функцию согласно (6) следующим образом (8) u′x≃uN′x = AXx. (8) Здесь компоненты A являются неизвестными коэффициентами ak, (k = 0,1,…, N,). Уравнение (8) интегрируется для аппроксимации неизвестной функции u , и, таким образом, мы получаем ∫0xu′tdt = ux − u0≃A∫0xXtdt. Используя операционную матрицу для интегрирования P, мы получаем следующее приближение (9) ux≃uNx = λ + APXx, (9) где λ – константа в условии (2). Здесь заметим, что многочлен uN ′ (x) не является производным от многочлена uN (x). Однако они используются для приближения к функциям u ′ (x) и u (x) соответственно.

Положив x → αix + βi, (i = 1,2,3) в X (x), получим матричное соотношение (10) Xαix + βi = QiXx, (10) где Qi = 100… 0βiαi0… 0βi22βiαiαi2 … 0 ⋮⋮⋮ ⋱ ⋮ CNNβiNCNN − 1βiN − 1αiCNN − 2βiN − 2αi2… CN0αiN, CNk, (k = 0,1,…, N) – биномиальные коэффициенты.

Теперь, используя уравнения (8) – (10), члены u ′ (α1x + β1) и u (α3x + β3) в уравнении (1) могут быть аппроксимированы следующими полиномами, соответственно, (11) uN ′ Α1x + β1 = AQ1XxuNα3x + β3 = λ + APQ3Xx.(11) Следующий шаг состоит в нахождении полиномиальной аппроксимации нелинейного члена u2 (α2x + β2). Для этого члена мы используем операционную матрицу продукта C следующим образом (12) u2α2x + β2≃uN2α2x + β2 = λ + APQ2Xx2 = λ2 + 2λAPQ2Xx + APQ2XxAPQ2Xx≃λ2 + 2λAPQ2Xx + APQ2CXx. (12) Подставляя приближенные выражения (11) – (12) в уравнение (1) имеем (13) AQ1pxXx + 2λAPQ2qxXx + APQ2CqxXx + APQ3rxXx = gx − λ2qx − λrx. (13) Для каждой компоненты матриц столбцов p (x) X (x), q (x ) X (x), r (x) X (x) и для функции g (x) −λ2q (x) −λr (x) применяем схему аппроксимации методом наименьших квадратов, которая приведена в разделе 2.В результате мы получаем следующие приближения, соответственно, pxXx≃L1Xx, qxXx≃L2Xx, rxXx≃L3Xx, gx − λ2qx − λrx≃GXx. Здесь Li, (i = 1,2,3) – матрицы размерности (N + 1) × (N + 1), а G – вектор.

Подставляем их в уравнение (13), а затем упрощаем X (x). Следовательно, мы получаем систему нелинейных алгебраических уравнений (14) AQ1L1 + 2λAPQ2L2 + APQ2CL2 + APQ3L3 = G. (14) Чтобы построить приближенные функции для неизвестной функции и производной функции, мы решаем систему (14) и используем уравнения (8) – (9).В результате получается приближенное решение функционального дифференциального уравнения Риккати.

4. Анализ ошибок

В этом разделе мы сначала представляем метод оценки, основанный на функциях невязки для функции ошибок eN (x) = u (x) −uN (x). Во-вторых, мы рассматриваем проверку точности приближенных решений. Наконец, дается верхняя граница ошибки.

4.3. Верхняя граница погрешности

В этом разделе мы даем оценку погрешности приближенного решения uN (x).

Теорема 4.1

Пусть uN (x) и u (x) представляют наше приближенное решение и точное решение задачи (1) соответственно. Если u (x) ∈Ck [0,1], k = 0,1,…, N + 1, то | u (x) −uN (x) | ≤ | RNT (x, q) | + | uNT ( x) −uN (x) | где uNT (x) демонстрирует полином Тейлора N -й степени u вокруг точки x = q , а RNT (x, q) представляет его напоминание.

Доказательство.

Поскольку u является N + 1-кратно дифференцируемым, u может быть представлен рядом Тейлора как u (x) = ∑n = 0N (x − q) nn! Un (q) + RNT (x , q), где RNT (x, q) = (x − q) N + 1 (N + 1)! u (N + 1) (cx), 0≤cx≤x≤1.является напоминанием о разложении Тейлора и . Обозначим полином Тейлора N -й степени от u вокруг точки x = q через uNT (x). Таким образом, u (x) −uNT (x) = RNT (x, q). Используя его и неравенство треугольника, получаем | u (x) −uN (x) | = | u (x) −uN (x) + uNT (x) −uNT (x) | ≤ | u (x) −uNT (x) | + | uNT (x) −uN (x) | = | RNT (x, q) | + | uNT (x) −uN (x) |. В результате находится верхняя граница абсолютных ошибок приближенных решений нашего метода.

5.Численные примеры

В этом разделе мы применим предложенный метод к нескольким примерам. Кроме того, для оценки ошибки мы используем метод оценки невязки согласно разделу 4.

Пример 5.1

Наше первое уравнение (16) u′x − xu0,5x + u2x = cos⁡x − xsin⁡ (0,5x) + sin2⁡x, (16) с начальным условием u (0) = 0.

Задача имеет точное решение u (x) = sin⁡x. Для N = 3 применяется настоящий метод. Мы можем записать следующее выражение согласно разделу 3: u′x≃u3′x = AXxu3x = APXxxu30.5x = APL3Q1Xxu32x = APXxAPXx≃APCXx, где X (x) = [1 x x2 x3] T, A = [a1 a2 a3 a4], C – операционная матрица интегрирования, P = 010000−3.571428E − 37.142857E − 2000.5000 .3333333−0.32142850.4999999, Q1 = 100000. 500000.2500000.125.L3 = 010000100001−1 / 702 / 7−9 / 72, F = [1.002042−4.432472E − 20.2233704−0.4109088]. Подставляя указанные выше матричные формы в (16), получаем систему A-APL3Q1 + APC = F. Последняя система решена, и поэтому численное решение будет u3x = −0,143827×3−0,019802×2 + 1,005096x − 0,000287. На рисунке 1 сравнение между методом коллокации Бесселя [25] и настоящим методом выполнено с помощью функции абсолютной ошибки | e3 (x) |.Также на рисунке 2 сравнивается точность приближенных решений этих методов.

Рисунок 1. Сравнение ошибок | e3 (x) |.

Операционный метод решения дифференциальных уравнений типа Риккати с функциональными аргументами https://doi.org/10.1080/16583655.2020.1761661

Опубликовано онлайн:

13 мая 2020 г.

Рисунок 2. Точность приближенных решений | R5 (x) |.

Пример 5.2

Мы рассматриваем дифференциальное уравнение Риккати с функциональными аргументами u′x + 2 − x2u2x − 3 − u2x − 1 = gx с начальным условием u (0) = – 2.

Здесь g (x) = 3 + 2x − 19×2 + 20×3−5×4 и точное решение u (x) = x2 − x − 2. Предлагаемый метод применяется для N = 2, и, таким образом, получаем u2 (x) = 0,082772×2−1,330725x − 1,980444.

Пример 5.3

Теперь решим дифференциальное уравнение Риккати u′x + u2x = 1 с начальным условием u (0) = 0.

Точное решение задачи u (x) = (e2x − 1) / (e2x + 1).Настоящий метод применяется для N = 5, и поэтому мы вычисляем приближенное решение

u5x = −0,01561477×5 + 0,18737947×4−0,43144236×3 + 0,02351138×2 + 0,99776043x + 0,00005064.

Для N = 5, M = 6, мы применяем метод остаточной ошибки и получаем функцию ошибки оценки

e5,6 (x) = – 0,0458177892192055629761837481×6 + 0,13587872934

411134360203203329325 0,03203329325 0,03 .01960633929792095

74570594457×2 + 0.00180125420472189839982135595x − 0.00004431714026062992331997.

В таблице 1 приведены численные результаты. А именно, абсолютные ошибки метода Тейлора [20], метода коллокации Бесселя [25] и настоящего метода для N = 5, 7, 8, 9. Фактическая функция ошибок e ₅ ( x ) и функция ошибки оценки e _5,6 ( x ) приведены на рисунке 3.

Опубликовано на сайте:

13 мая 2020 г.

Таблица 1. Сравнение абсолютных погрешностей.

Пример 5.4

Наконец, решим дифференциальное уравнение Риккати u′x − 2u + u2x = 1 с начальным условием u (0) = 0.

Применяя настоящий метод для N = 6, мы получаем приближенное решение

u6 (x) = 0,3976697967610276496230881093652×6−0,55995447628188066424570479284739×5−0.6573605560148856113642687

41696806392×3 + 0,942898799495859313992696116×2 + 1,005280244228598851563560856448x − 0,00011285708278009885005121332168798.

График функции абсолютной ошибки для N = 7 показан на рисунке 4. На рисунке 5 показано сравнение ошибок. На рисунке 6 мы даем сравнение функций невязки RN (x) и EN (x) для N = 6.

Рисунок 4. График | e7 (x) |.

Опубликовано на сайте:

13 мая 2020 г.

Рисунок 5. Функции абсолютной погрешности, полученные разными методами.

6. Выводы

В этой статье представлен численный метод решения дифференциальных уравнений типа Риккати с функциональными аргументами, основанный на операционных матрицах интегрирования и произведении для стандартных базисных многочленов.Действительно, этот метод также основан на приближении наименьших квадратов. Есть некоторые особенности метода. Например, для метода не требуются точки коллокации. Более того, операционная матрица интегрирования состоит из нулей, что влечет за собой удобство вычислительных работ. Также получены полиномы степени N , которые аппроксимируют неизвестную функцию и ее производную. Из численных примеров видно, что погрешности приближенных решений меньше, чем погрешности других методов.Кроме того, видно, что ошибки оценки в примерах закрыты для фактических ошибок. Следовательно, следует отметить, что метод оценки ошибки является эффективным. Его можно использовать для измерения ошибок, когда точное решение проблемы неизвестно.

Рисунок 2. Точность приближенных решений | R5 (x) |,

Рисунок 5. Функции абсолютных ошибок, полученные разными методами.

Таблица 1. Сравнение абсолютных погрешностей.

9165 955 9165 N = 8 0,1827781660 E-25862586224 0,62 E − 9

	Метод Тейлора [20]	Метод коллокации Бесселя [25]
x	N 5
0. 2	0,679776E − 6	0,517341E − 4	0,194715E − 6
0,4	0,830377E − 4	0,259692E − 4	0,1827781660	0,406570E-4	0,159478E-6
0,8	0,898722E-2	0,123901E-4	0,131850E-6
1,0
1,0	1,0	0,751414E − 3	0,899933E − 6
		Настоящий метод
x	N = 5		N = 5		9
0. 2	0,111371E − 6	0,672756E − 9	0,130042E − 11
0,4	0,761541E − 7	0,3E − 9	0,271098E − 10
0,146507E − 8	0,152924E − 10
0,8	0,500046E − 7	0,224639E − 8	0,1E − 10
−10
0,50	0,697202E − 8	0,310221E − 10

Уравнение в частных производных – обзор

7.6 Формализм специальной системы многокомпонентных дифференциальных уравнений

Аналогично случаю DTSS мы формулируем спецификацию системы многокомпонентных дифференциальных уравнений multiDESS с немодульной связью. Напомним, что основной формализм DESS не определяет функцию следующего состояния напрямую, а только через функции скорости изменения для отдельных переменных непрерывного состояния. В многокомпонентном случае отдельные компоненты определяют скорость изменения своих собственных переменных состояния на основе значений состояния их факторов влияния.Давайте сначала определим общий формализм, а затем обсудим подход к моделированию, рассматривая уравнения в частных производных – особый тип модели, показывающий большое сходство с клеточными автоматами в дискретной временной области.

Спецификация системы многокомпонентных дифференциальных уравнений представляет собой структуру

multiDESS = 〈X, D, {Md}〉

, где X – это набор входных данных, вещественное векторное пространство Rm и D – это индексный набор. Для каждого d∈D компонент Md определяется как

Md = 〈Qd, Yd, Id, fd, λd〉

, где Qd – это набор состояний d , вещественного векторного пространства Rn, Yd – набор выходов d , вещественное векторное пространство Rp, Id⊆D – это набор факторов влияния d , fd: × i∈IdQi × X → Qd – функция скорости изменения для переменных состояния d , λd: × i∈IdQe × X → Yd – функция локального выхода d . Набор влияний Ed d снова определяется как набор {d}. Мы требуем, чтобы каждый fd удовлетворял условию Липшица:

|| fd (q, x) −fd (q ′, x) || ⩽kd || q − q ′ ||

В multiDESS функция производной каждого компонента определяет скорость изменения его локальных переменных состояния. Формально multiDESS = 〈XN, D, {Md}〉 определяет DESS = 〈X, Y, Q, f, λ〉 на уровне системы ввода-вывода следующим образом: Q = × d∈DQd, Y = × d∈DYd, f (q, x) определяется как

f (q, x). d = fd ((…, qi, …), x),

и λ (q) определяется на

λ (q).d = λd ((…, qi, …)),

с i∈Id.

Теперь мы должны показать, что полученная производная функция удовлетворяет условию Липшица:

|| f (q, x) −f (q ′, x) || ⩽k || q − q ′ ||

Это будет следовать из того факта, что каждая из ее координатных функций удовлетворяет такому условию посредством ограничения, наложенного на эти функции, данного ранее. Мы продемонстрируем, как это работает, используя только две координаты:

|| f (q1, q2, x) −f (q1 ′, q2 ′, x) || = || (f1 (q1, q2, x) −f1 ( q1 ′, q2 ′, x), f2 (q1, q2, x) −f2 (q1 ′, q2 ′, x)) || ⩽ || f1 (q1, q2, x) −f1 (q1 ′, q2 ′ , x) || + || f2 (q1, q2, x) −f2 (q1 ′, q2 ′, x) || ⩽k1 || (q − q ′ || + k2 || (q − q ′ | | ⩽ (k1 + k2) || q − q ′ ||

7.

6.1 Пространственная DESS: модели дифференциальных уравнений в частных производных

Модели дифференциальных уравнений в частных производных возникают из расширения дифференциального уравнения, в котором пространственные координаты, помимо времени, вводятся как независимые переменные. Таким образом, заданная система дифференциального уравнения в частных производных показывает изменения как во времени, так и в пространстве.

Системы дифференциальных уравнений в частных производных требуют отдельной науки, и целая дисциплина занимается решением таких систем дифференциальных уравнений.Мы дадим им лишь краткий обзор здесь, чтобы поместить их в нашу структуру формализмов имитационного моделирования.

Для нашего изложения рассмотрим простой пример общего уравнения, консервативного по потоку, от одной переменной u. Уравнение

∂u∂t = −v∂u∂x

выражает, что изменение переменной u во времени равно отрицательной скорости, – v , умноженной на изменение переменной u в пространственном измерении x . Результатом этого уравнения является волна, которая распространяется со скоростью v вдоль размера x .

Подход к решению таких задач, который является представителем так называемого гиперболического уравнения в частных производных , приводит к дискретизации пространственных и временных измерений. Сначала введем дискретизацию пространства. Весь интервал наблюдения [x0, xl] длиной l разделен на k равных частей, каждый шириной Δx = l / k.Затем мы получаем k узлов сети , для которых мы составляем уравнения, чтобы выразить изменения во времени. В так называемом подходе Forward Time Centtered Space (FCTS) это делается для каждой точки сетки j путем замены пространственной производной ∂uj∂x от и в точке j на разность соседних деление состояний на длину пространственного интервала

uj − 1 − uj + 12Δx

(обратите внимание на сходство с методом интегрирования Эйлера), дающее уравнение для производной по времени переменной u в точке j

∂ uj∂t = −vuj − 1 − uj + 12Δx

для каждой точки сетки j . Очевидно, у нас есть multiDESS с k компонентами и набором факторов влияния Ij = {j − 1, j + 1} для каждого компонента j , а также производными функциями, как указано выше.

Обычно при решении уравнений в частных производных модель строится путем дискретизации также измерения времени. Когда мы применяем тот же метод разности для дискретизации измерения времени, а именно деление временного интервала на интервалы равной длины Δ t , мы можем заменить производную по времени u в пространственной точке j и временной точке n + 1. на разность значения в момент времени n + 1 минус значение в момент времени n , деленное на Δt (интегрирование Эйлера)

ujn + 1 − ujnΔt

Таким образом, мы наконец получаем уравнение для состояния в точке сетки j для времени n + 1:

ujn + 1 = uj − 1n − vujn − 1 − ujn + 12ΔxΔt.

Чего мы наконец достигли? Начиная с уравнения в частных производных с производными по времени и пространственному измерению, мы дискретизируем пространство и время. С помощью дискретизации пространства мы получили непрерывную многокомпонентную модель в клеточной форме с равными производными функциями для ячеек. С дискретизацией пространства мы наконец получили клеточный автомат с окрестностью {j − 1, j + 1}, временным шагом Δt и такой же следующей функцией состояния для ячейки j , как указано выше.

Пример дифференциального уравнения

Чтобы увидеть это сначала, мы перегруппируем все y в одну сторону: y (y ′ + 1) = x – 3. Вернемся к упражнению 1 Toc JJ II J I Обратное решение дифференциальных уравнений с использованием преобразования Лапласа. Найдите константу при начальном условии. Дифференциальные уравнения УРАВНЕНИЯ БЕРНУЛЛИ [1] dx dt = x x + 1 Решение: Мы можем легко разделить и интегрировать следующим образом. Решите ODE x. К линейным дифференциальным уравнениям относятся уравнения, которые можно привести к виду L y = f, где L – некоторый линейный оператор.Примеры • Решения линейных дифференциальных уравнений создают векторное пространство, и дифференциальный оператор также является линейным оператором в векторном пространстве. Дифференциальное уравнение типа. Поскольку My = Nx, дифференциальное уравнение не является точным. Это происходит, когда уравнение содержит переменные коэффициенты и не является уравнением Эйлера-Коши, или когда уравнение является нелинейным, за исключением… Пример 6: Дифференциальное уравнение Например, dy / dx = 9x. . Последний пример – дифференциал Эйри… 800a + 40b = ln (56.8) – ln (47,1) = 0,18726. Итак, предположим, что у меня было дифференциальное уравнение DY, DX, производная Y по X, равна E до X, по Y. Неопределенные коэффициенты – первый метод решения неоднородных дифференциальных уравнений, который мы будем искать в этом разделе. (Математическая функция NDSolve, с другой стороны, является средством решения общих численных дифференциальных уравнений.) Из предыдущего раздела мы имеем = G Где, G – постоянная роста. Решение. В физике простое гармоническое движение – это тип периодического движения, в котором возвращающая сила прямо пропорциональна смещению.Это разделимое дифференциальное уравнение. Вариация параметров – еще один метод решения неоднородных однородных дифференциальных уравнений Введение. Пример. . сторона уравнения, в то время как все члены, содержащие t и его дифференциал, помещаются справа, а затем формально интегрируют обе части, что приводит к той же формуле неявного решения: G (u) = Z du F (u) = Z dt = t + k. (2.7) Прежде чем завершить анализ этого метода решения, рассмотрим пару элементарных примеров. . Как мы увидим, этот тип уравнения часто встречается в различных науках.Расшифрованный текст изображения: I. Уравнения Эйлера-Коши 2.5. Любое дифференциальное уравнение, содержащее упомянутые выше члены, является нелинейным дифференциальным уравнением. Автономные уравнения разделимы, но уродливые интегралы и выражения, которые не могут быть… Но тогда хищникам будет меньше еды и они начнут вымирать, что позволит выжить большему количеству добычи. Предположим, что к пружине прикреплена масса, которая оказывает на массу силу притяжения, пропорциональную растяжению / сжатию пружины. Ваш первый случай действительно линейный, поскольку его можно записать как: (d 2 d x 2 – 2) y = ln.Общее решение точного уравнения дается выражением. Теперь, используя второй закон Ньютона, мы можем написать (используя удобные единицы измерения): Мы можем определить 4 новые переменные, от q1 до q4. Линейные неоднородные дифференциальные уравнения второго порядка; Метод неопределенных коэффициентов. Обратимся теперь к неоднородным линейным уравнениям второго порядка, уравнениям стандартной формы y ″ + p (t) y ′ + q (t) y = g (t), g (t) ≠ 0. Общее уравнение первого порядка является слишком общим, то есть мы не можем описать методы, которые будут работать со всеми ними или даже с большой их частью.То есть, если правая часть не зависит от x, уравнение автономно. . Материал главы 7 адаптирован из учебника Стивена «Нелинейная динамика и хаос». Это уравнение Бернулли с n = 4 3. Мы видели следующий пример во введении к этой главе. (2.2.4) d 2 y d x 2 + d y d x = 3 x sin y. является дифференциальным уравнением второго порядка, поскольку в уравнении появляется вторая производная. Эта проблема в некотором роде обратная. . Узнаем решение, определение, примеры однородного дифференциального уравнения.Пример. Например, поскольку скорость является производной от смещения, а ускорение является производной от скорости, a… Уравнение – это утверждение, которое выражает равенство двух математических выражений. У уравнения есть знак равенства, выражение с правой и с левой стороны. Примеры уравнений. 3x + 3 = 2x + 4: левая часть уравнения представляет собой выражение 3x + 3, а правая часть – 2x + 4. 2. Ниже приведены два примера, один для механической системы, а другой – для электрической системы.Взаимодействия между двумя популяциями связаны дифференциальными уравнениями. Это будет общее решение (включающее K, постоянную интегрирования). Решение. Если мы разделим приведенное выше уравнение на x, мы получим: dy dx + 6 x y = 3y43. Однородное уравнение: y 2y y 0 Характеристическое уравнение: r2 2r 1 0 1, 1 (1) 2 0 rrrtt yh C 1e C 2te y et 1 и y tet 2 y et ‘1 и y tet et 2 2. Решение – Если мы разделив приведенное выше уравнение на x, мы получим: dy dx + 6 xy = 3y43. Примеры дифференциальных уравнений первого порядка: Функция σ (x) = напряжение в одноосном растянутом металлическом стержне с коническим поперечным сечением (рис.Вы заметите, что это похоже на нахождение частного решения дифференциального уравнения. Порядок дифференциального уравнения – это порядок производной высшего порядка, присутствующей в уравнении. Обыкновенные дифференциальные уравнения второго порядка (ОДУ) 2.1. Примеры 2.2. … Это функция или набор функций. . Это уравнение Бернулли с n = 4 3. Пример 2. Решите следующие дифференциальные уравнения Бернулли: Дифференциальные уравнения – логистическое уравнение При изучении роста населения можно сначала подумать о модели экспоненциального роста, в которой скорость роста прямо пропорциональна численности населения в настоящее время.a), или Функция v (x) = скорость жидкости, текущей в прямом канале с переменным поперечным сечением (рис. Решение начальной задачи – это решение f (t) дифференциального уравнения, которое также удовлетворяет начальному условие f (t 0) = y 0. Приведены примеры использования преобразования Лапласа для решения обыкновенных дифференциальных уравнений (ОДУ). Убедитесь, что указанная функция {eq} y = \ phi (x) {/ eq} является явное решение данного дифференциального уравнения первого порядка Неоднородные дифференциальные уравнения – Краткий обзор того, как решать неоднородные дифференциальные уравнения в целом.f ‘(x) = dy / dx; х ≠ 0. Мы должны уметь составить дифференциальное уравнение из данной информации. . Например, скорость – это скорость изменения расстояния во времени в определенном направлении. Итак, если мы сделаем замену v = y − 1 3, уравнение преобразуется в: dv dx – 1 3 6 x v = – 1 3 3. Дифференциальное уравнение вида y0 = F (y) автономно. Найдите точное решение дифференциального уравнения. Уравнение можно переписать как: ′ = – 1 3 sin +3 Интегрируя обе части по x, получаем ln = – 1 3 sin + 3 = cos 3 – + 1 ∴ = cos 3 – = Пример 5: Найдите дифференциальное уравнение для семейства кривых x 2 + y 2 = c 2 (в плоскости xy), где c – произвольная постоянная. Следующие примеры демонстрируют, как решить эти уравнения с помощью TI-Nspire CAS, когда x> 0. Еще примеры ODE. Например, обыкновенное дифференциальное уравнение в x (t) может включать x, t, dx / dt, d2x / dt2 и, возможно, другие производные. Итак, поступаем следующим образом: и это… Дифференциальные уравнения имеют в себе производную. φ = C0, C0 = постоянная и u = y x + C0. Примеры: Линейные ОДУ 2-й степени с постоянными коэффициентами: Также известные как уравнения Лотки-Вольтерра, уравнения хищник-жертва представляют собой пару нелинейных обыкновенных дифференциальных уравнений первого порядка.Они представляют собой упрощенную модель изменения популяций двух видов, которые взаимодействуют посредством хищничества. Уравнения в примерах (c) и (d) называются уравнениями в частных производных (PDE), поскольку неизвестная функция зависит от двух или более независимых переменных, t, x, y и z в этих примерах, а их частные производные появляются в уравнения. Покажите, что преобразование к новой зависимой переменной z = y1 − n сводит уравнение к тому, которое линейно по z (и, следовательно, разрешимо с использованием метода интегрирующих множителей). 8.2 Типичная форма однородных дифференциальных уравнений второго порядка (стр. 243) () 0 2 2 bu x dx du xadux (8.1) где a и b – константы Решение уравнения (8.1) u (x) может быть получено путем ПРИНЯТИЯ : u (x) = emx (8.2) в котором m – константа, которую нужно определить с помощью следующей процедуры: Если предполагаемое решение u (x) в уравнении (8.2) является допустимым решением, оно должно УДОВЛЕТВОРЕНИТЬ Закон охлаждения Ньютона. называется точным дифференциальным уравнением, если существует функция двух переменных с непрерывными частными производными такая, что.. Умножая на это, получаем y0ex2 + 2xex2y = xex2 (ex2y) 0 = xex2 ex2y = R xex2dx = 1 2 ex2 + C y = 1 2 + Ce − x2. [1] dx dt =… Одним из основных преимуществ использования преобразования Лапласа для решения дифференциальных уравнений является то, что преобразование Лапласа преобразует дифференциальное уравнение в алгебраическое уравнение. Это разделимое дифференциальное уравнение. Дифференциальные уравнения – это уравнения, включающие функцию и одну или несколько ее производных. Например, приведенное ниже дифференциальное уравнение включает функцию \ (y \) и ее первую производную \ (\ dfrac {dy} {dx} \).На данный момент мы можем игнорировать любые другие силы (гравитацию, трение и т. Д.). m = ± 0,0014142 Следовательно, x x y h K e 0. + 32x = e t с использованием метода интегрирования множителей. Порядок дифференциального уравнения определяется наивысшим порядком производной уравнения. Путь к общему решению включает в себя поиск решения однородного уравнения (т. Е. Отбрасывание константы c), и … Мы рассмотрим два простых примера обыкновенных дифференциальных уравнений ниже, решим их двумя разными способами и покажем, что в них нет ничего пугающего – ну… Решение дифференциальных уравнений означает нахождение связи между y и x только посредством интегрирования.. . Например, dy / dx = 5x + 8, порядок равен 1. y + 2 (dy / dx) + d 2 y / dx 2 = 0. Общая форма уравнения Бернулли – dy dx + P (x) y. = Q (x) yn, где P и Q – функции от x, а n – постоянная. Пример 1 Решите следующее дифференциальное уравнение. Но нам также нужно решить это, чтобы узнать, как, например, th… Точное решение обыкновенного дифференциального уравнения выводится следующим образом. Начальные и краевые задачи 2.2. . 0014142 2 0,0014142 1 = + – Конкретная часть решения дается выражением.Шаг 1. Приведите пример дифференциального уравнения и классифицируйте его по порядку, степени, линейности и типу. Зная эти константы, мы получим: T o = 22,2e-0,02907t +15,6. Уравнение, включающее только частные производные одной или нескольких функций двух или более независимых переменных, называется уравнением в частных производных, также известным как PDE. Пример 5: Функция f (x, y) = x 3 sin (y / x) однородна степени 3, поскольку. Пример 1.9.6. Найдите общее решение 2xey dx + (x2ey + cosy) dy = 0.Суммарное дифференциальное уравнение – любое уравнение, включающее производную или более высокую производную. du = 0 влечет u = C, C = constant ∴ y x = A, A = C −C0 = constant. Автономные дифференциальные уравнения 1. m2 −2 × 10 −6 = 0. 2. Учебное пособие по MATLAB по решению обыкновенных дифференциальных уравнений (Пример 12-1) Решите следующее дифференциальное уравнение для случая прямоточного теплообмена и нанесите X, Xe, T, Ta и -rA по длине реактора (см. LEP 12 -1, Элементы инженерии химических реакций, 5-е издание) использовал учебник «Элементарные дифференциальные уравнения и краевые задачи» Бойса и ДиПримы (John Wiley & Sons, Inc., Седьмое издание, с 2001 г.). Мы запишем растяжение пружины в момент времени t как x (t). Итак, если мы сделаем замену v = y − 1 3, уравнение преобразуется в: dv dx – 1 3 6 x v = – 1 3 3. Теперь мы можем переписать дифференциальное уравнение 4-го порядка как… Примечание. Картинка выше взята из онлайн-симулятора хищник-жертва. Кроме того, левая часть уравнения – производная от \ (y \). Порядок дифференциального уравнения определяется наивысшим порядком производной уравнения.Определите также его зависимые и независимые переменные. Используются другие обозначения :! В некоторых справочниках можно найти ее решение, используя разделение переменных; в противном случае вы также можете использовать уравнение Бернулли, поскольку оно следует форме. ОДУ второго порядка. Линейные однородные ОДУ второго порядка 2.3. Примером линейного уравнения является… Из этого дифференциального уравнения мы можем найти общее решение, которое приведет нас к логистической функции. . Мы используем метод разделения переменных для решения линейных дифференциальных уравнений.В качестве примера мы будем использовать Simulink для решения первого порядка. Итак, чтобы это удовлетворяло этому дифференциальному уравнению, оно должно быть истинным для всех этих x здесь. Напишите свои ответы в поле для ответа ниже в указанном ниже формате. Рассмотрим систему 4-го порядка, представленную одним дифференциальным уравнением 4-го порядка со входом x и выходом z. Решение этого дифференциального уравнения: 0 2t 2 0 1t 2t 1 2 1 1 2N e (6.18) 80. Это линейное уравнение. Например, лисы (хищники) и кролики (добыча).ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ: РОСТ И РАСПАД Чтобы решить более общий тип дифференциального уравнения, мы рассмотрим метод, известный как разделение переменных. Пример: ty ″ + 4 y ′ = t 2 Стандартная форма – ytt Пример Однородные уравнения Вспомогательный многочлен Пример Уравнение y00 + 0 6 = 0 имеет вспомогательный многочлен P (r) = r2 + r 6: Примеры Приведите вспомогательные многочлены для следующие уравнения. Он включает производную, dydx \ displaystyle \ frac {{\ left. {D} {y} \ right.}} {{\ Left. {D} {x} \ right.То есть, если правая часть не зависит от x, уравнение автономно. Линейные однородные ОДУ второго порядка с постоянными коэффициентами 2.4. Пример. Рассмотрим однородное уравнение 3 ′ + sin +3 = 0, где a – постоянная. Пример. Найдите общее решение дифференциального уравнения xy ′ + 6y = 3xy4 / 3. }} dxdy: Как и раньше, мы интегрируем его. В этой таблице показаны примеры дифференциальных уравнений и их синтаксис Symbolic Math Toolbox ™. это так же сложно, как и решить исходное уравнение (1).В элементарной алгебре вы обычно находите одно число как решение уравнения, например x = 12. Найдите решение y0 + 2xy = x, где y (0) = −2. Примечание! где – произвольная постоянная. Линейные неоднородные ОДУ второго порядка. Итак, в общем, идея сделать уравнение (1) точным не дает эффективного метода его решения. . Следующий урок. (D2 7D +24) y = 0 3. y000 2y00 4y0 + 8y = 0 r2 + 2r 3 r2 7r +24 r3 2r2 4r +8 Корни вспомогательного многочлена будут определять Пример: Следующее дифференциальное уравнение разделимо. Это последнее уравнение и есть формула (5), которую мы хотим доказать. В этом примере мы решим неявное уравнение ОДУ. Дифференциальные уравнения могут использоваться в приложениях и компонентах системы и реализовываться в них. Приложения: они часто являются частью решения моделирования запасов и потоков. Модель может быть изменена для включения различных факторов производства, включая рост рабочей силы и технологические усовершенствования. Примером этого является груз на пружине. Мы знаем, что дифференциальное уравнение первого порядка и первой степени может быть выражено в виде Mdx + Ndy = 0, где M и N являются функциями x и y или констант.но . 1.1 Решение ODE Simulink – это графическая среда для моделирования систем. Это текущий выбранный элемент. Чтобы написать указательное уравнение, используйте оператор ограничения TI-Nspire CAS, чтобы подставить значения констант в Содержание 1 Введение 1 1.1 Предварительные сведения. Дифференциальные уравнения часто возникают в физике. . Пока вы не будете уверены, что можете повторно вывести (5) в каждом случае, стоит практиковать метод интегрирования множителей в данном дифференциальном уравнении. Неоднородное дифференциальное уравнение первого порядка. . Это становится проблемой решения двух линейных уравнений с двумя известными a и b. В стороне: Происхождение дифференциального уравнения первого порядка. Посмотрите, сможете ли вы найти общее решение этого дифференциального уравнения. Дифференциальное уравнение является уравнением второго порядка, поскольку оно включает вторую производную y y y. Оно однородно, потому что правая часть равна 0 0 0. Общая стратегия состоит в том, чтобы переписать уравнение так, чтобы каждая переменная появлялась только на одной стороне уравнения.ПРОБЛЕМЫ ПРАКТИКИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ: ОТВЕТЫ 1. Затем мы рассмотрим примеры более сложных систем. Переписанный текст изображения: I. В частности, если M и N являются однородными функциями одной степени по x и y, то уравнение называется однородным уравнением. Теория дифференциальных уравнений, которые широко используются в современном экономическом анализе и предоставляют множество простых, а также всеобъемлющих . .. Другой пример – уравнения Лоренца. Введение в решение дифференциальных уравнений с помощью DSolve Функция DSolve в системе Mathematica находит символьные решения дифференциальных уравнений.И это должно быть верно для всех x, чтобы это было решением этого дифференциального уравнения. Решение: у нас есть M (x, y) = 2xey, N (x, y) = x2ey + cosy, так что My = 2xey = Nx. Вот несколько примеров: 1.. Уравнения непостоянных коэффициентов с отсутствующим y-членом Если y-член (то есть член зависимой переменной) отсутствует в линейном уравнении второго порядка, то уравнение можно легко преобразовать в линейное уравнение первого порядка и решить с помощью интегрирования факторный метод. . . 3. Дифференциальные уравнения.f (…. Порядок дифференциального уравнения – это наивысшая производная, которая появляется в приведенном выше уравнении. Пример – я даю вам огромную подсказку. Обычно вам дают дифференциальное уравнение и просят найти его семейство решений. . Дифференциальное уравнение на рисунке выше является линейным дифференциальным уравнением первого порядка с P (x) = 1 и Q (x) = 6 x 2. Однородное дифференциальное уравнение – это дифференциальное уравнение вида dy / dx = f (x , y), такая что функция f (x, y) является однородной функцией вида f (λx, λy) = λnf (x, y) для любой ненулевой постоянной λ.”! # =” (= “̇ Не все дифференциальные уравнения могут быть решены одним и тем же методом, поэтому MATLAB предлагает множество различных решателей ODE для решения дифференциальных уравнений, таких как ode45, ode23, ode113 и т. Д. 4 Примеры 4.1 Пример 1 Решение дифференциальное уравнение 3x2y00 + xy0 8y = 0. Рабочий пример: экспоненциальное решение дифференциального уравнения. Приведите пример дифференциального уравнения и классифицируйте его по порядку, степени, линейности и типу. Логистические модели. Линейными дифференциальными уравнениями можно манипулировать чтобы выглядеть так: dydx + P (x) y = Q (x) для некоторых функций P (x) и Q (x).2, \), которое является примером дифференциального уравнения, поскольку оно включает производную. Существует связь между переменными \ (x \) и \ (y: y \) – неизвестная функция от \ (x \). Они обладают следующими свойствами: 1. функция y и ее https://www.mathsisfun.com/calculus/differential-equations-solution-guide.html Дифференциальное уравнение – это уравнение, которое содержит один или несколько членов и производные одной переменной (т.е. зависимой переменной) по отношению к другой переменной (т.е.е., независимая переменная) Пример – Найдите общее решение дифференциального уравнения xy ′ + 6y = 3xy4 / 3. • Решения линейных дифференциальных уравнений относительно проще, и существуют общие решения. двойные, корни. Определите также его зависимые и независимые переменные. Дифференциальное уравнение со входом f (t) и выходом y (t) может представлять множество различных систем. Автономные уравнения отделимы, но уродливые интегралы и выражения, которые не могут быть… Порядок равен 2. Для этого уравнения a = 3, b = 1 и c = 8.Повторяющиеся корни – в этом разделе мы обсуждаем решение однородных линейных дифференциальных уравнений второго порядка ay ′ ′ + by ′ + cy = 0 ay ″ + by ′ + cy = 0, в котором корни характеристического многочлена ar2 + br + c = 0 ar 2 + br + c = 0, повторяются, т.