Второе кинематическое уравнение: Какие существуют кинематические формулы? (статья)

2.1.2. Кинематические уравнения движения. Длина пути и вектор перемещения.

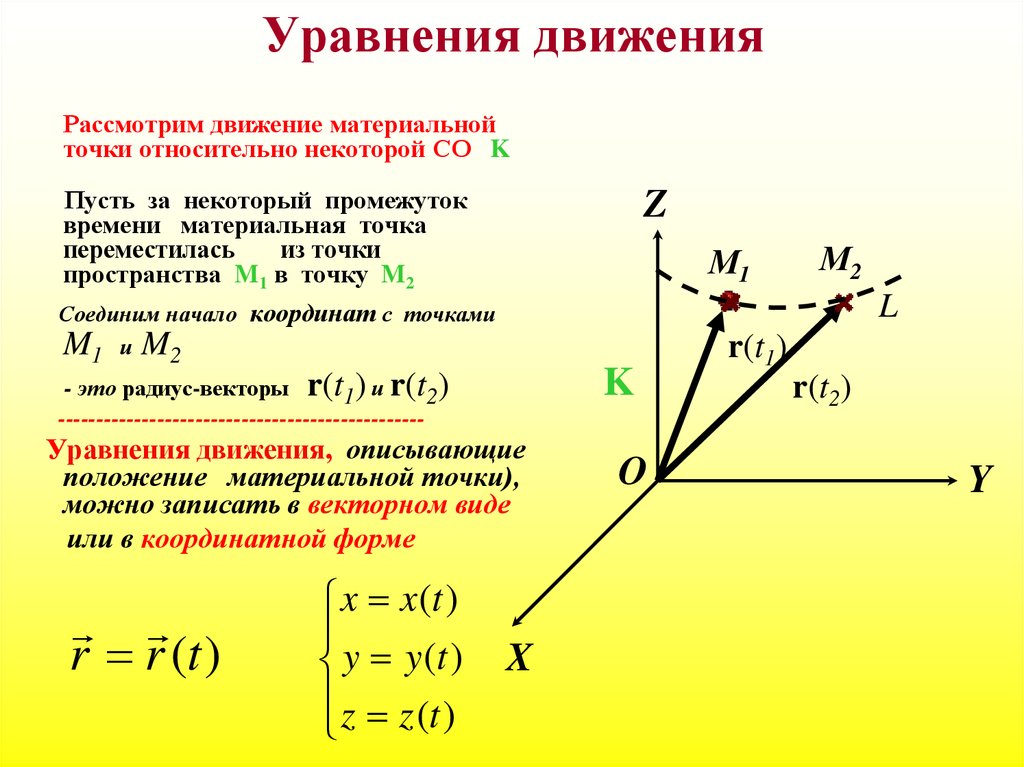
1. При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции времени t:

x = x(t), y = y(t), z = z(t).

Эти уравнения описывают изменение координат точки от времени и называются кинематическими уравнениями движения.

2. Путь – часть траектории, пройденной телом за определенный промежуток времени. Момент времени t₀, от которого начинается его отсчет, называется начальным моментом времени, обычно t₀=0 в силу произвольного выбора начала отсчета времени.

Длиной пути называется сумма длин всех участков траектории. Длина пути не может быть величиной отрицательной, она всегда положительна. Например, материальная точка переместилась из точки траектории С сначала в точку А, а затем в точку В (Рисунок 1). Длина ее пути равна сумме длин

дуги СА и дуги АВ.

2.1.3. Кинематические характеристики. Скорость.

1. Для характеристики быстроты движения тел в физике вводится понятие скорости. Скорость – вектор, а значит, характеризуется величиной, направлением, точкой приложения.

Рассмотрим движение вдоль оси Х. Положение точки будет определяться изменением со временем координаты Х.

Если за время ∆t произошло перемещение точки на ∆r, то величина является средней скоростью движения: .

Средней скоростью движущегося тела называется вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Модуль средней скорости есть физическая величина, численно равная изменению пути за единицу времени.

2. Для определения скорости в данный момент времени, мгновенной скорости, нужно рассмотреть интервал времени ∆t→0, тогда

.

Используя понятие производной, можно записать для скорости

Скорость тела в данный момент времени называется мгновенной скоростью (или просто скоростью).

Вектор V мгновенной скорости направлен по касательной к траектории в сторону движения тела.

2.1.4. Кинематические характеристики. Ускорение.

1. Быстрота изменения вектора скорости характеризуется величиной, называемой ускорением. Ускорение может возникнуть как за счет изменения величины скорости, так и за счет изменения направления скорости.

Пусть в момент времени t скорость тела равна v₁, а через промежуток времени ∆t в момент времени t + ∆t равна v₂, приращение вектора скорости за ∆t равно ∆v.

Средним ускорением тела в интервале времени от t до t + ∆t называется вектор а_ср, равный отношению приращения вектора скорости ∆v к промежутку времени ∆t:

Cреднее ускорение есть физическая величина, численно равная изменению скорости за единицу времени.

2.Для определения ускорения в данный момент времени, т. е. мгновенного ускорения, нужно рассмотреть малый интервал времени ∆t→0. Тогда вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени ∆t к нулю:

Используя понятие производной, можно дать для ускорения следующее определение:

Ускорением (или мгновенным ускорением) тела называется векторная величина а, равная первой производной по времени от скорости тела v или второй производной по времени от пути.

3. При вращении точки по окружности ее скорость может изменяться по величине и по направлению (рисунок 2)

Рисунок 2.- Изменение скорости точки при вращении по

окружности

На рисунке 2 в положении 1 скорость точки v_1, в положении 2 скорость точки v₂. Модуль скорости v₂ больше модуля скорости v₁, ∆v– вектор изменения скорости ∆v= v₂ –v₁

Вращающаяся точка имеет тангенциальное ускорение, равное а_τ=dv/dt, оно изменяет скорость по величине и направлено по касательной к траектории; и

нормальное ускорение, равное а_n= v²/R, оно меняет направление скорости и направлено по радиусу окружности (R) (см. Pисунок 3)

Рисунок 3.- Полное, тангенциальное и нормальное ускорения вращающейся точки

Вектор полного ускорения равен , т.е. он может быть представлен как сумма векторов тангенциального a_τи нормального a_n ускорений. Модуль полного ускорения равен:

.

Угловое уравнение движения: 3 важных понятия –

Угловое уравнение движения, система уравнений, иллюстрирующая поведение вращающейся системы с точки зрения ее движений как функции времени. В статье подробно рассматриваются угловые уравнения движения вращающейся системы.

Система из трех угловых уравнений движения объясняет вращающуюся систему как набор ее математических функций от динамических переменных. 

Как видите, переменными во всех трех уравнениях обычно являются пространственные координаты и время; но также включать компоненты импульса. Если вы идентифицируете динамику системы, вы можете найти эти три набора уравнений, которые являются решениями дифференциальных уравнений, характеризующих движение системы.

Такое описание движения подразделяется на две формы: динамика и кинематика. В динамике движения в картину входят сила, импульсы, энергия объектов. Для сравнения, кинематическое движение касается только переменных, полученных из положений объектов и времени.

В этой статье мы сначала определим набор уравнений, которые показывают связи между переменными; а затем использовать эти соединения для анализа углового движения вращающегося тела. Аналитические отчеты, полученные нами из угловых уравнений движения, являются основой кинематики вращения.

Угловое уравнение движения
вращающегося тела

Угловые уравнения обычно считаются физическими законами, а затем применяют определения этих кинематических физических величин. Следовательно, мы можем получить решения этих уравнений, оценивая начальные значения, которые определяют значения констант.

Подробнее о нашей предыдущей статье на Угловая скорость вращающегося тела.

Аналогия углового движения

Существуют аналоги всех величин линейного движения, таких как расстояние, скорость и ускорение при угловом движении, что делает угловое движение более удобным для работы после изучения линейного движения. 

Запишем уравнение линейной скорости как,

Угловое движение – это движение вращающегося тела вокруг фиксированной оси, равное углу, перемещаемому на оси линией, проведенной к телу. 

Это означает, что угловая скорость тела – это угол, на который вращающееся тело проносится за единицу времени. Аналогия углового движения
с поступательное движение
(источник: наука abc)

Посмотрите на график круговые полярные координаты, которые определяют вектор от оси к ее положению, мы можем представить смещение вращающегося тела. Подобно уравнению угловой скорости, мы можем определить положение, используя такой другой набор координат. Вместо использования координат x, y угловое смещение можно записать в терминах радиус r, что является его расстоянием от начала координат.Аналогия углового движения

«Тета» — это угол между вектором смещения и осью, проходящей через начало координат, обычно измеряемый против часовой стрелки от оси x и обычно выражаемый в радианах, что упрощает преобразование линейного движения в угловое движение.

Мы можем упростить определение более угловых уравнений движения, подобных линейным уравнениям движения, – для описания различных приложений в физике и технике, где система имеет постоянное угловое ускорение.

Первое кинематическое уравнение углового движения.

Первое кинематическое уравнение вращающегося тела иллюстрирует корреляция между его угловой скоростью и угловым ускорением и временем. Проще говоря, он показывает, как вращающееся тело ускоряется, когда его угловая скорость изменяется со временем.  

Угловая скорость постоянна в равномерное круговое движение (UCM), но не во вращательном движении. Следовательно, угловое ускорение возникает из-за изменения его угловой скорости во времени. 

Мы вспоминаем общие кинематическое уравнение для линейного движения как:Связь между
Линейная и угловая скорость

Подставляя значения v и a в уравнение (4), получаем

Сокращая радиус r, мы получаем

Обратите внимание, что приведенное выше уравнение похоже на его линейную версию, за исключением угловых аналогов. Мы можем определить больше других ситуаций с однородным набором угловые уравнения движения после постоянного углового ускорения.

Второе кинематическое уравнение углового движения.

Второе уравнение кинематики вращающегося тела иллюстрирует связь между его угловым перемещением, угловым ускорением и временем. Простыми словами, он показывает, как вращающееся тело ускоряется, когда его угловой перемещение меняется со временем.  

Мы получили первое угловое уравнение движения (A), которое мы будем использовать для решения других задач кинематики вращения.

Выведем второе угловое уравнение движения, преобразовав уравнение (2) к

Поскольку постоянная углового ускорения, интегрируя обе стороны от начальных до конечных значений, получаем

Уравнение (B) дает нам угловое положение вращающегося тела для заданных начальных форм и углового ускорения тела в данный момент времени.

Третье кинематическое уравнение углового движения.

Второе кинематическое уравнение вращающегося тела иллюстрирует связь между его угловой скоростью и угловым перемещением и временем. Проще говоря, он показывает, как вращающееся тело меняет свою скорость вместе со своим перемещением в единицу времени. 

Давайте найдем третье угловое уравнение движения, которое не зависит от времени t, решив уравнение (A) относительно t,

Подставляя значение t в уравнение (B), получаем

Уравнение (2) – уравнение (C) иллюстрирует вращение с фиксированной осью для постоянного ускорения.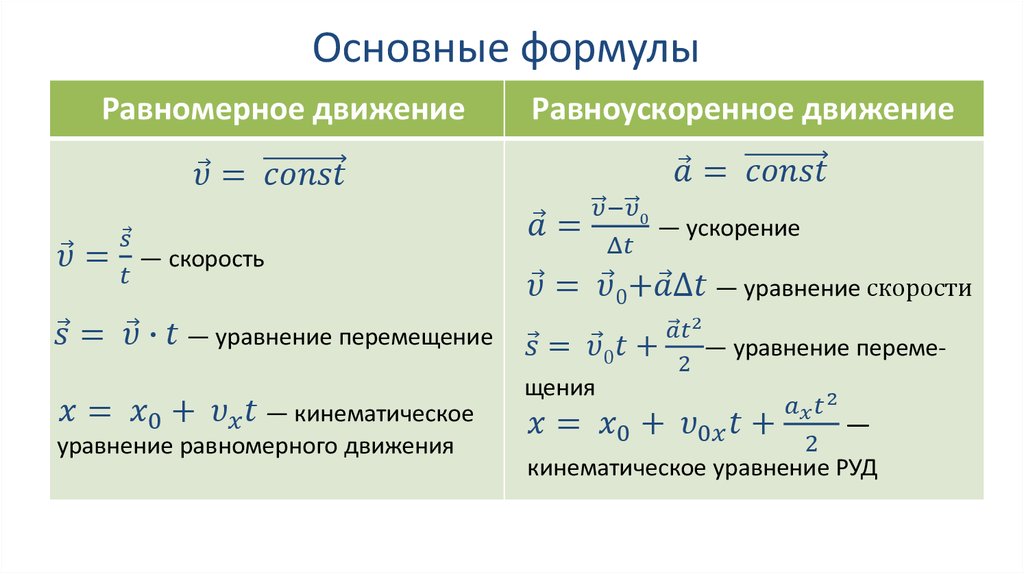 Кинематические уравнения движения

---

Кинематические уравнения: значение и вывод

Когда вы роняете ключи, через сколько времени они упадут на землю? Когда вы бросаете мяч, куда он приземлится? Как быстро вы должны бросить мяч, чтобы он попал туда? Ответы на все эти вопросы требуют изучения кинематических уравнений.

Значение кинематических уравнений

Кинематические уравнения представляют собой набор из трех уравнений, описывающих движение объектов без учета сил, заставляющих их двигаться. Мы можем вывести их из второго закона Ньютона, рассматривая движение снарядов в присутствии постоянного гравитационного поля. Этот набор уравнений может ответить на все вышеперечисленные вопросы и многое другое. Три кинематических уравнения представляют собой линейное кинематическое уравнение 92 + 2a_x(x-x_0).\]

В этих уравнениях \(t\) — время, \(x\) — положение, \(v_x\) — скорость, а \(a_x\) — ускорение. Мы используем нижний индекс \(_0\) для обозначения начального значения величины. Обратите внимание, что условно кинематические уравнения представляют движение в направлении \(x\). Однако они применимы к любому пространственному направлению.

Кинематические уравнения при постоянном ускорении

Эти уравнения применимы только к ситуациям, когда мы имеем постоянное ускорение. Это требование означает, что скорость изменения скорости постоянна. Таким образом, скорость выглядит как прямая линия, когда мы смотрим на график зависимости скорости от времени. Обратите внимание, что это не обязательно означает, что наклон равен 0. Действительно, на диаграмме ниже показана ситуация с постоянным ненулевым ускорением: 92\). Знак минус исходит из выбора системы отсчета, в которой ускорение направлено вниз . Другое предположение, которое мы делаем, состоит в том, что сопротивлением воздуха можно пренебречь.

Применение кинематических уравнений

Приложения могут быть разнообразными и сложными, используя одно, два или три измерения, описывающие некоторую форму движения снаряда. Примеры включают игру в мяч, стрельбу из лука или сброс мяча с Эмпайр-стейт-билдинг. Здесь мы рассмотрим самый простой одномерный случай и более сложный двумерный случай.

Движение снаряда в одном измерении

Вспомните наш предыдущий вопрос, в котором мы уронили ключи. Игнорируйте сопротивление воздуха и примите высоту \(135\;\text{см}\) . Ваши ключи выпадают из рук. Через какое время ключи упадут на землю?

Первым шагом в решении любой физической задачи является рисование диаграммы, содержащей всю необходимую информацию. В этом случае у нас есть довольно простая диаграмма. У нас есть высота \(135\;\text{см}\), начальная скорость \(0 \;\text{м}/\text{с}\) 92}\\ &= \pm 0,52 \;\text{s}.\end{align}\]

Обратите внимание, что у нас есть два решения: \(t_1 = -0,52 \;\text{s}\) и \(t_2 = 0,52 \;\text{s}\). Однако только один из них имеет физический смысл, поэтому мы отбрасываем отрицательное время и остаемся с нашим ответом.

\[\boxed{t = 0,52 \; \text{s}. }\]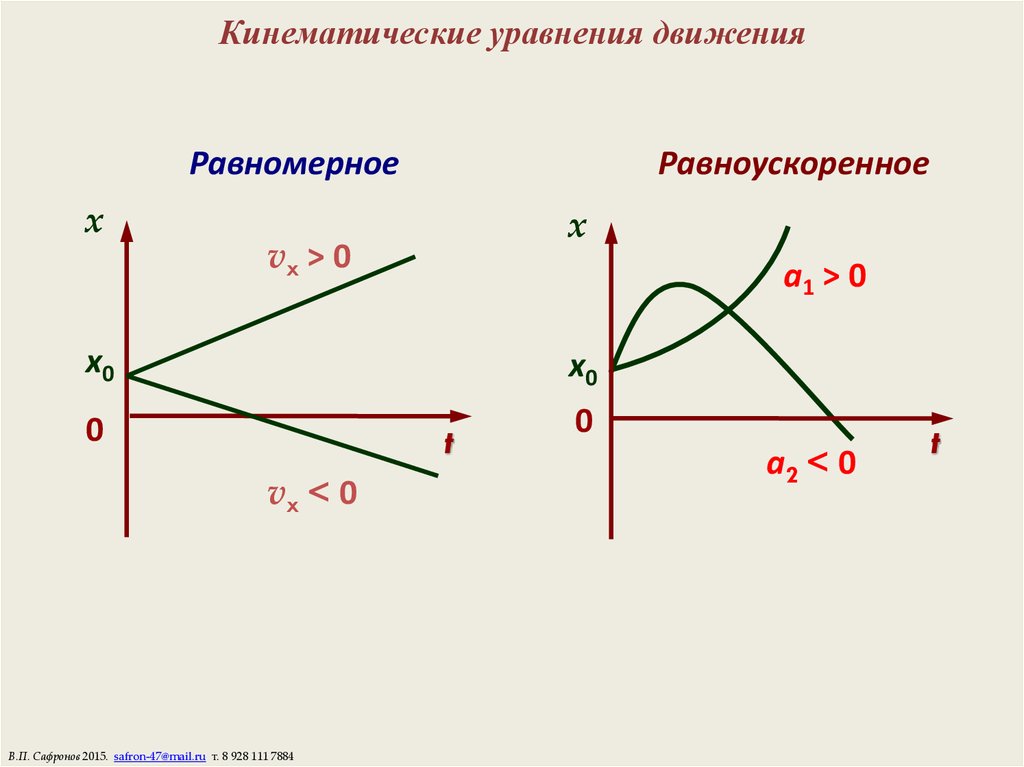

Нашим ключам требуется \(0,52\) секунды, чтобы коснуться земли. В качестве последней проверки всегда проверяйте, что ответ имеет физический смысл. Если бы мы получили решение за час, мы бы знали, что что-то не так. Однако полсекунды имеют физический смысл. Итак, сразу же мы знаем, что не сделали ничего радикально неправильного. 9{\circ}\) угол. Как быстро ты должен бросать ключи, чтобы они дошли до твоего друга?

Как всегда, первым шагом является рисование диаграммы со всей необходимой информацией.

Схема для двумерной задачи о движении снаряда, StudySmarter Originals

Это более сложная задача, поэтому давайте разобьем ее на более простые задачи. Во-первых, нужно понять, что у нас есть и \(x\), и \(y\)-направление, с которыми мы имеем дело, и эти два направления независимы друг от друга, так что мы можем иметь дело с ними по отдельности.

Сначала рассмотрим \(y\)-направление. Обратите внимание, что нам придется разбить нашу начальную скорость на составляющие. Для \(y\)-компонента мы используем тригонометрию, чтобы получить

\[v_{y0} = v_y\sin(\theta).\]

Теперь давайте рассмотрим восходящие ключи. На своем пике они меняют направление, так что мы имеем конечную скорость

\[v_{y} = 0 \;\text{m}/\text{s}.\]

Теперь мы применим эту информацию к кинематические уравнения.

\[\begin{align}v_y &= v_{y0} + a_yt_r \\0 &= v_0\sin(\theta) + a_yt_r \\v_0 &= \frac{-a_yt_r}{\sin(\theta) }. \конец{выравнивание}\]

Мы подписали \(t\) с помощью \(r\), поэтому мы помним, что это только время, необходимое для того, чтобы добраться до вершины во время подъема. Чтобы найти общее время в воздухе, мы должны удвоить это значение, поэтому

\[\begin{align}t &= 2t_r \\ t_r &= \frac{1}{2}t. \end{align}\]

Подставив это, мы получим уравнение для нашей начальной скорости в терминах \(t\):

\[v_0 = \frac{-a_yt}{2\sin(\theta )}.\]

Посмотрим, сможем ли мы найти \(t\), используя \(x\)-направление. 2\). Таким образом 92 \\ &= 0 + v_xt + 0 \\ &= v_xt.\end{aligned}\]

Снова используя тригонометрию, мы получаем, что \(x\)-компонента нашей скорости равна

\[v_x = v_0\cos(\theta),\]

что позволяет нам решить для\(t\) с точки зрения \(v_0\):

\[\begin{aligned}x &= v_xt \\ &= v_0 \cos(\theta)t \\ t &= \frac{x}{v_0\cos(\theta)}.\end{aligned}\]

Затем мы вернемся назад и подставим это в наше уравнение скорости:

\[\begin{aligned} v_0 &= \frac{-a_yt}{2\sin(\theta)}\\ &= \frac{-a_y}{2\sin(\theta)}\cdot \frac{ x}{v_0\cos(\theta)}.\end{выровнено}\] 92 &= \frac{-a_yx}{2\sin(\theta)\cos(\theta)}\\ v_0 &= \pm \sqrt{\frac{-a_yx}{2\sin(\theta)\cos (\theta)}}.\end{aligned}\]

Это наше уравнение в терминах известных переменных для начальной скорости, с которой нам нужно бросать наши ключи, чтобы они достигли нашего друга. Обратите внимание, что ускорение силы тяжести отрицательно в зависимости от нашего выбора координат, поэтому значение под квадратным корнем не вызовет никаких проблем. 2\). Если ваша конечная скорость \(9\circ) \\ h &= 40.5\;\text{m}\end{aligned}$$

Таким образом, наша окончательная высота холма равна

$$\boxed{h=40.5\;\text{м }}$$

Вывод кинематических уравнений

Ниже мы кратко расскажем, как вывести каждое из трех кинематических уравнений.

Вывод линейного кинематического уравнения

Мы можем вывести кинематические уравнения из второго закона Ньютона. Однако для этого необходимо решить дифференциальные уравнения. Другой метод состоит в том, чтобы вывести их алгебраически, используя наши знания об окружающем мире, чтобы разработать отправную точку. Для этого заметим, что ускорение — это изменение скорости по сравнению с изменением времени, поэтому

\[a = \frac{\Delta v}{\Delta t}\]

где \(\Delta v = v – v_0\), и мы обозначаем наш временной интервал через \(t\). Таким образом, мы имеем:

\[a = \frac{v – v_0}{t}.\]

Теперь, чтобы закончить вывод нашего первого кинематического уравнения, мы рассмотрим направление \(x\) и перестроим нашу термины:

\[\begin{align}a_x &= \frac{v_x – v_{x0}}{t} \\ a_xt &= v_x – v_{x0}. \end{align}\]

Таким образом, мы приходим к линейному кинематическому уравнению.

\[\boxed{v_x = v_{x0} + a_xt.}\]

Получение квадратного кинематического уравнения

Обратите внимание, что аналогичным образом мы имеем, что средняя скорость представляет собой изменение положения в зависимости от изменения времени.

\[v = \frac{\Delta x}{\Delta t}\]

где \(\Delta x = x – x_0\). Мы также можем выразить среднюю скорость как среднее значение начальной и конечной скорости. Мы вставляем это в наше уравнение и находим \(v_x\):

\[\begin{align} v_{\text{avg}} &= \frac{x – x_0}{t} \\ \frac{v_x + v_{x0}}{2} &= \frac{x – x_0}{t} \\ v_x &= \frac{2(x – x_0)}{t} – v_{x0}. \конец{выравнивание}\] 92.\end{aligned}\]

Следующим шагом будет выделение общего множителя из выражения и упрощение дробей:

\[\begin{align} x – x_0 &= \left(\frac{v_x – v_{x0}}{a_x}\right)\left(v_{x0} + \frac{1}{2}a_x\left(\frac{v_x – v_{x0}}{a_x}\right)\right ) \\ &= \left(\frac{v_x – v_{x0}}{a_x}\right)\left(\frac{2v_{x0}}{2} + \frac{v_x – v_{x0}}{ 2}\right) \\ &= \left(\frac{v_x – v_{x0}}{a_x}\right)\left(\frac{2v_{x0} + v_x – v_{x0}}{2}\ справа) \\ &= \left(\frac{v_x – v_{x0}}{a_x}\right)\left(\frac{v_{x0} + v_x}{2}\right). \end{выровнено} \] 92 + 2a_x(x-x_0).}\]

Это завершает вывод кинематических уравнений.

Угловые кинематические уравнения

В кинематике вращения есть аналог рассмотренным нами кинематическим уравнениям. Эти уравнения выглядят одинаково по форме, за исключением того, что смещение \(x\) заменено углом \(\theta\), скорость \(v\) , заменена угловой скоростью \ (\omega\), а ускорение \(a\) заменяется угловым ускорением \(\alpha\). Таким образом, уравнение линейной угловой кинематики имеет вид 92 + 2\альфа (\тета – \тета_0).\]

Кинематические уравнения – Основные выводы

• Есть три кинематических уравнения.
• Кинематические уравнения могут быть применены к движению в одномерных и двумерных или трехмерных задачах.
• Кинематические уравнения используются для описания движения объекта с постоянным ускорением.
• Кинематические уравнения выведены из второго закона Ньютона, однако их можно вывести и экспериментально.
• Существует набор уравнений кинематики вращения, аналогичный уравнениям линейной кинематики.

Как использовать кинематические уравнения (с производными)

Уравнения кинематики описывают движение объекта, испытывающего постоянное ускорение. Эти уравнения связывают переменные времени, положения, скорости и ускорения движущегося объекта, позволяя решать любую из этих переменных, если другие известны.

Ниже показано изображение объекта, совершающего движение с постоянным ускорением в одном измерении. Переменная ‌ t ‌ для времени, положение ‌ x, ‌ скорость ‌ v ‌ и ускорение ‌ a ‌. Нижние индексы ‌ i ‌ и ‌ f ‌ означают «начальный» и «конечный» соответственно.

Кинематические уравнения

Ниже перечислены три основных кинематических уравнения движения, которые применяются при работе в одном измерении с постоянным ускорением. Вот эти уравнения:

v_f = v_i + a\Delta t \\ \text{} \\ \Delta x = v_i\Delta t \ + \frac{1}{2}a\Delta t^2 \\ \text {} \\ v_f^2= v_i^2+2a\Delta x

где ‌ a ‌ — ускорение, ‌ v_i ‌ — начальная скорость, ‌ v_f ‌ — конечная скорость объекта через интервал времени ‌ Δt ‌ 9030 ‌ и ‌ является пройденное расстояние. Выше видно, что эта система уравнений позволяет исключить из расчетов одну величину. Первое кинематическое уравнение вообще не использует положение (‌ Δx) ‌, второе уравнение не имеет конечной скорости, а третье уравнение вне времени, поэтому оно не использует ‌ Δт. ‌ Вы можете решить для каждого из этих уравнений и других эквивалентных соотношений, подставив их друг в друга и упростив; они действуют как система уравнений.

Примечания к кинематическим уравнениям

• Эти кинематические формулы работают только с постоянным ускорением (которое может быть равно нулю в случае постоянной скорости).
• В зависимости от того, какой источник вы читаете, окончательные количества могут не иметь нижнего индекса ‌ f ‌ и/или могут быть представлены в функциональном обозначении как ‌ x (t) ‌ – читать «‌ x ‌ как функцию времени» или «‌ x ‌ во времени ‌ t ‌» – и ‌ v (t) ‌. Обратите внимание, что ‌ x (t) ‌ НЕ ​​означает ‌ x ‌, умноженное на ‌ t ‌
• Иногда количество ‌ x _f – x _{i ‌ Δx ‌ , что означает «изменение ‌ x ‌», или даже просто как ‌ d ‌, что означает смещение. Все эквивалентны.}
• Положение, скорость и ускорение являются векторными величинами, т. е. с ними связано направление. В одном измерении направление обычно обозначается знаками — положительные величины указывают положительное направление, а отрицательные величины — отрицательное.
• Нижние индексы: «0» может использоваться для начального положения и скорости вместо ‌ i ‌. Этот «0» означает «при ‌ t ‌ = 0», а ‌ x _o ‌ и ‌ v _o ‌ обычно произносятся как «х-ноль» и «v-ноль».
• Только одно из уравнений не включает время. Когда вы записываете данные и определяете, какое уравнение использовать, это является ключевым моментом!
• Пройденное расстояние — это общее расстояние, пройденное до конечного положения, а не перемещение (т. е. это не обязательно прямая линия от начального положения до конечного положения).

Особый случай: свободное падение

Движение в свободном падении — это движение объекта, ускоряющегося только под действием силы тяжести в отсутствие сопротивления воздуха. Применяются те же кинематические уравнения; однако известно значение ускорения у поверхности Земли. Величину этого ускорения часто представляют как ‌ g ‌, где g = 9,8 м/с ² . Направление этого ускорения – вниз, к поверхности Земли. (Обратите внимание, что некоторые источники могут приближаться к ‌ г ‌ как 10 м/с ² , а другие могут использовать значение с точностью более двух знаков после запятой.)

Стратегия решения задач для задач кинематики в одном измерении:

Нарисуйте диаграмму ситуации и выбрать подходящую систему координат. (Напомним, что ‌ x ‌, ‌ v ‌ и ‌ a ‌ — все это векторные величины, поэтому, задав четкое положительное направление, будет легче отслеживать знаки.)

Напишите список известных величин. (Остерегайтесь, что иногда известные значения не всегда очевидны. Ищите такие фразы, как «начинается из состояния покоя», что означает, что ‌ v _i ‌ = 0, или «ударяется о землю», что означает, что ‌ x _f ‌ = 0 и т. д.)

Определите, какое количество нужно найти в соответствии с вопросом. Какое неизвестное вы будете решать?

Выберите подходящее уравнение кинематики. Это будет уравнение, которое содержит вашу неизвестную величину вместе с известными величинами.

Решите уравнение для неизвестной величины, затем подставьте известные значения и вычислите окончательный ответ. (Будьте осторожны с единицами измерения! Иногда вам потребуется преобразовать единицы перед вычислениями.)

Примеры одномерной кинематики

‌ Пример 1: ‌ В рекламе утверждается, что спортивный автомобиль может развивать скорость от 0 до 60 миль в час. за 2,7 секунды. Каково ускорение этого автомобиля в м/с ² ? Какое расстояние он проходит за эти 2,7 секунды?

‌ Решение: ‌

Известные и неизвестные величины:

v_i=0\text{ mph}\\ v_f=60\text{ mph}\\ t=2.7\text{ s}\\ x_i=0 \\ a=\text{?}\\ x_f=\text{?}

Первая часть вопроса требует решения для неизвестного ускорения. Здесь мы можем использовать уравнение № 1:

v_f=v_i+at\implies a =\frac{(v_f-v_i)}{t}

Прежде чем мы подставим числа, нам нужно преобразовать 60 миль в час в м/ s:

60\cancel{\text{миль в час}}\Bigg(\frac {0,477\text{м/с}} {\cancel{\text{миль в час}}}\Bigg)=26,8\text{м/ с} 92+2(-9,8)(0-1,5)}=\pm\sqrt{254,4}\приблизительно\pm16\text{ м/с}

Здесь есть два решения. Какой из них правильный? Из нашей диаграммы видно, что конечная скорость должна быть отрицательной. Таким образом, ответ:

v_f={\bold{-16}\text{ м/с}}

Чтобы определить время, мы можем использовать либо уравнение №1, либо уравнение №2. Поскольку с уравнением №1 работать проще, мы будем использовать его:

v_f=v_i+at\implies t=\frac {(v_f-v_i)} {a}=\frac {(-16-15)} {-9,8}\приблизительно {\жирный{3,2}\текст{с}}

‌ Обратите внимание, что ответ на первую часть этого вопроса не был 0 м/с. ‌ Хотя это правда, что после приземления мяч будет иметь нулевую скорость, этот вопрос хочет знать, как быстро он движется за эту долю секунды до удара. ‌ Когда мяч коснется земли, наши кинематические уравнения перестанут применяться, поскольку ускорение не будет постоянным. ‌

Кинематические уравнения движения снаряда (два измерения)

Снаряд — это объект, движущийся в двух измерениях под действием силы тяжести Земли. Его траектория представляет собой параболу, потому что единственное ускорение связано с гравитацией. Кинематические уравнения движения снаряда имеют несколько иной вид, чем кинематические уравнения, перечисленные выше. Мы используем тот факт, что компоненты движения, перпендикулярные друг другу, такие как горизонтальные ‌ x ‌ направление и вертикальное ‌ y ‌ направление – независимы.

Стратегия решения задач по кинематике движения снаряда Задачи:

Примеры кинематики движения снаряда

‌ Пример 1: ‌ Снаряд стартовал горизонтально с обрыва высотой 20 м/ 5 м со скоростью 20 м. с. Сколько времени нужно, чтобы удариться о землю? На каком расстоянии от основания скалы он приземлится?

Известные и неизвестные количества: 92 \ подразумевает t = \ sqrt {\ frac {(2 \ times 20)} g} = { \ полужирный {2.02} \ text {s}}

Затем, чтобы найти, где он приземляется, ‌ x _f ‌ , мы можем использовать уравнение горизонтального движения:

x_f=x_i+v_xt=50\times2. 02={\bold{101}\text{s}}

‌ Пример 2: ‌ Мяч запущен на 100 м/с от уровня земли под углом 30 градусов к горизонту. Где он приземляется? Когда его скорость наименьшая? Каково его местонахождение в это время?

Известные и неизвестные количества:

v_x=v_i\cos(\theta)=100\cos(30)\приблизительно 86,6 \text{ м/с}\\ v_{yi}=v_i\sin(\theta)=100\sin(30)= 50 \text{ м/с}\\ x_i = 0\\ y_i = 0

Сначала нужно разбить вектор скорости на составляющие:

v_x=v_i\cos(\theta)=100\cos(30)\ приблизительно 86,6 \text{ м/с}\\ v_{yi}=v_i\sin(\theta)=100\sin(30)=50 \text{ м/с}

Сначала нам нужно найти время мяча находится в полете. Мы можем сделать это со вторым вертикальным уравнением‌ . ‌ Обратите внимание, что мы используем симметрию параболы, чтобы определить, что окончательная ‌ y ‌ скорость отрицательна от начальной:

Затем мы определяем, как далеко он продвинется в направлении ‌ x ‌ за это время:

x_f=x_i+v_xt=86,6\times 10,2\приблизительно{\bold {883}\text m}

Используя симметрию параболического пути, мы можем определить, что скорость наименьшая при ‌ 5,1 с ‌, когда снаряд находится в пике своего движения и вертикальная составляющая скорости равна 0. Компоненты x и y его движения в это время равны:

92\приблизительно {\bold{128}\text{м}}

Вывод кинематических уравнений

‌ Уравнение №1: ‌ Если ускорение постоянно, то:

a=\frac{(v_f- v_i)}{t}

Решая скорость, мы имеем:

v_f=v_i+at

‌ Уравнение № 2: ‌ Средняя скорость может быть записана двумя способами:

v_{avg}= \frac{(x_f-x_i)}{t}=\frac{(v_f+v_i)}{2}

Если мы заменим ‌ v _f ‌на выражение из уравнения № 1, мы получим: 92+2a(x_f – x_i)

Нарисуйте схему ситуации. Как и в случае с одномерным движением, полезно набросать сценарий и указать систему координат. Вместо использования меток ‌ x ‌, ‌ v ‌ и ‌ a ‌ для положения, скорости и ускорения, нам нужен способ маркировать движение в каждом измерении отдельно.

Для горизонтального направления чаще всего используется ‌ x ‌ для положения и ‌ v _x ‌ для x-компонента скорости (обратите внимание, что ускорение равно 0 в этом направлении, поэтому нам не нужна для него переменная). В направлении ‌ y ‌ чаще всего используется ‌ y ‌ для положения и ‌ v _y ‌ для y-составляющей скорости. Ускорение можно обозначить как ‌ a _y ‌, или мы можем использовать тот факт, что мы знаем, что ускорение свободного падения составляет ‌ g ‌ в отрицательном направлении y, и просто использовать его вместо этого.

Напишите список известных и неизвестных величин, разделив задачу на две части: вертикальное и горизонтальное движение. Используйте тригонометрию, чтобы найти x- и y-компоненты любых векторных величин, которые не лежат вдоль оси. Может быть полезно перечислить это в двух столбцах:

Примечание. Если скорость дана как величина вместе с углом, ‌ Ѳ ‌, над горизонталью, тогда используйте векторное разложение:

v_x = v\cos (\тета) \текст{ и } v_y = v\sin(\тета) 92-2g(y_f – y_i)

‌ Обратите внимание, что ускорение в направлении ‌ y ‌ равно -g, если предположить, что вверх положительно.