Определение координаты движущегося тела (9 класс)
Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движенииГде:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.

Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускоренияСледовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
Рис. 3. Прямолинейное равноускоренное движениеПройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение..jpg)
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
Задание 4 из ЕГЭ по физике
Русский язык Математика (профильная) Обществознание Физика История Биология Химия Английский язык Информатика Литература
Задания Варианты Теория
Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27 Задание 28 Задание 29 Задание 30
Бесплатный интенсив по физике
3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 23 января.
Подробнее об интенсиве
За это задание вы можете получить 1 балл на ЕГЭ в 2023 году
Разбор сложных заданий в тг-канале:
Посмотреть
Задача 1
Координата колеблющегося тела меняется так, как показано на графике. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укаж…
Задача 2
Координата колеблющегося тела меняется так, как показано на графике. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика. Укажи…
Задача 3
Тело массой 30 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. 3}$) опускаются три одинаковых груза, вес которых в жидкости измер…
3}$) опускаются три одинаковых груза, вес которых в жидкости измер…
Задача 6
В таблице приведены результаты опытов по изучению движения без начальной скорости металлического шарика по гладкой наклонной плоскости. С помощью таблицы результатов измерений из п…
Задача 7
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения и укажите их номера.
- Ускорение движущегося тел…
Задача 8
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании…
Задача 9
Экспериментатор исследовал зависимость силы трения от величины внешней силы, график которой изображён на рисунке. На основании анализа данного графика выберите два верных утвержден…
Задача 10
На рисунке представлена зависимость кинетической и потенциальной энергий от времени для тела, брошенного вертикально вверх.
Используя графические данные, выберите из предложенного …
Задача 11
На рисунке представлена зависимость скорости движения материальной точки от времени.
Используя графические данные, выберите из предложенного перечня два верных утверждения. Укажите…
Задача 12
Материальная точка движется вдоль оси Ox. На рисунке представлен график зависимости координаты x этой точки от времени t. Из предложенного перечня выберите все правильные утвержден…
Задача 13
На рисунке представлена зависимость пути, пройденного телом массой 1 кг, от времени.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их …
Задача 14
Проанализировав график зависимости координаты колеблющегося тела от времени, выберите из предложенного перечня все верные утверждения и внесите их ответов.
- Период колебаний тела р…
Задача 15
Ученик исследовал прямолинейное движение бруска.
Задача 16
В таблице приведены результаты измерения силы сопротивления движению тела в жидкости в зависимости от скорости тела. Как зависит сила сопротивления от скорости?
Выберите два верных…
Задача 17
Мальчик исследовал, как меняется сила трения при движении санок в зависимости от их скорости. Результаты измерений он нанёс на координатную плоскость, как показано на рисунке. Погр…
При проведении измерения силы гравитационного взаимодействия между двумя близко расположенными вагонами по 20 тонн каждый оказалось, что она меняется с изменением расстоянии между …
Задача 19
Два тела движутся вдоль оси Ox. Графики зависимости проекции скорости движения этих тел от времени представлены на рис.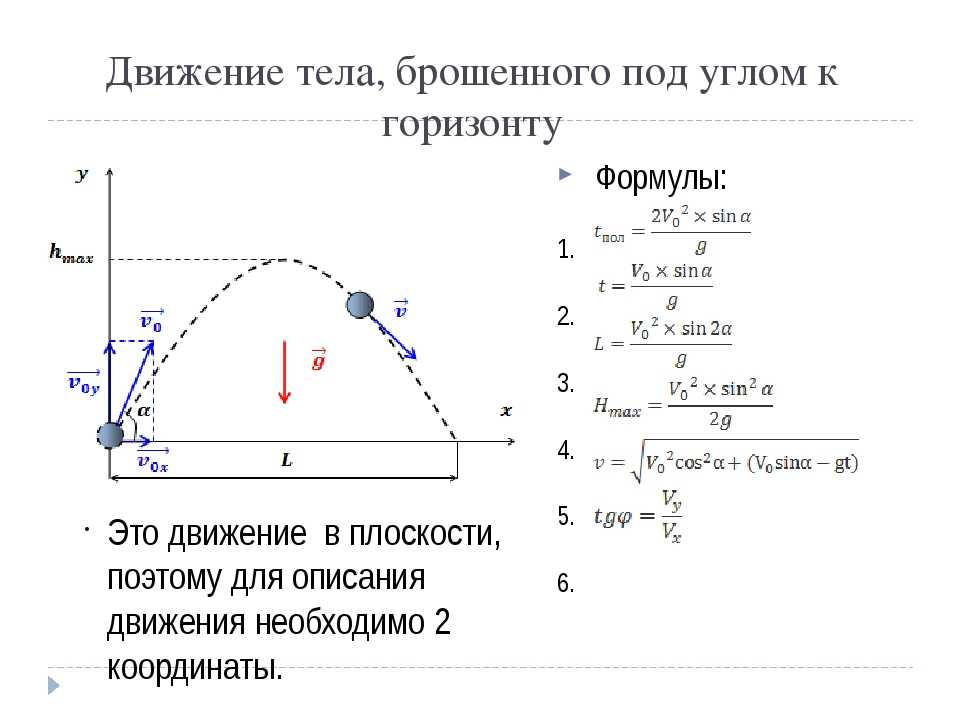
Выберите два верных утверждения на основании анализа предста…
Задача 20
Два тела движутся вдоль оси Ox. Графики зависимости координаты этих тел от времени представлены на рис.
Выберите два верных утверждения на основании анализа представленных графиков…
1 2
В четвертом задании в госэкзамене по физике ученику необходимо продемонстрировать свои знания механического равновесия, колебаний и волн. Для корректного ответа важно повторить материалы учеников, касающиеся закона Архимеда, пружинного и математического маятников, а также волн и колебаний, имеющих механическое происхождение.
Некоторые версии четвертого номера в ЕГЭ по физике создатели кимов посвятили законам Паскаля и Архимеда. Такие упражнения наиболее сложно даются учащимся, поскольку эти темы рассматриваются в средней школе. Для грамотного ответа на вопрос важно прочитать учебник по физике за седьмой и восьмой классы, использовать методички или же пройти тесты в онлайн-формате.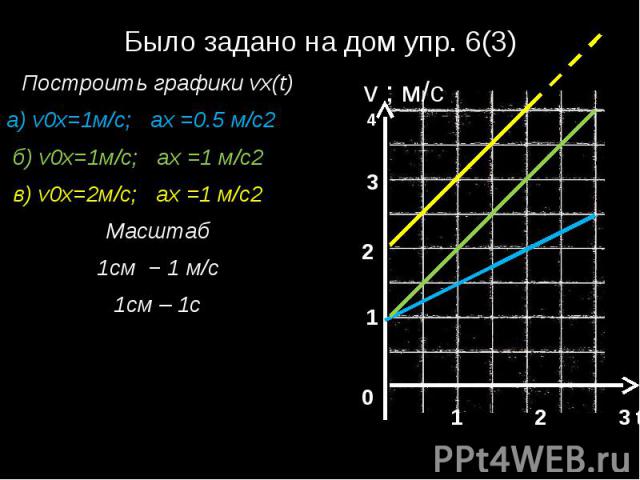
Четвертый номер, посвященный волнам, включает различные задачи по определению их длин, частоты, времени движения звука в разных ситуациях. Часть упражнений проверяет школьника на знание работы маятников и механического равновесия.
Во всех вопросах необходимо дать короткий ответ. Если он представляет собой десятичную дробь, то ее требуется округлить до сотых или десятых по условию задачи.
Теория к заданию 4 по физике: Импульс, энергия, законы сохранения
<< Задание 3
Задание 5 >>
Популярные материалы
Калькулятор горизонтального движения снаряда
Этот калькулятор горизонтального движения снаряда является инструментом для решения частного случая движения снаряда, когда объект запускается горизонтально с приподнятой плоскости . Введите любые два значения, а остальные будут рассчитаны в мгновение ока! Кроме того, траектория будет отображаться под результатами.
Продолжайте прокручивать, чтобы узнать уравнения горизонтального движения снаряда и простой пример расчета — у вас не должно возникнуть проблем с упражнениями после прочтения нашего объяснения!
Уравнения горизонтального движения снаряда
Как мы уже говорили, уравнения горизонтального движения снаряда являются частным случаем общих формул. Нам не нужно указывать угол запуска, так как он параллелен земле (поэтому угол равен 0°). В результате имеем только одну составляющую начальной скорости – Vx=VV_x = VVx=V, тогда как Vy=0V_y = 0Vy=0.
Нам не нужно указывать угол запуска, так как он параллелен земле (поэтому угол равен 0°). В результате имеем только одну составляющую начальной скорости – Vx=VV_x = VVx=V, тогда как Vy=0V_y = 0Vy=0.
Мы возьмем начальную точку в начале координат. Тогда уравнения движения можно записать так:
Расстояние 92y=–21gt2, где ggg — ускорение свободного падения, а hhh — высота над уровнем моря. Скорость Ускорение Уравнения горизонтального движения снаряда 92 = h31gt2=h. Из этого уравнения можно найти, что время полета равно: t=2hgt = \sqrt{\frac{2h}{g}}t=g2h Дальность полета снаряда дальность полета снаряда – полное горизонтальное расстояние, пройденное за время полета. r=Vt=v2hgr = Vt = v\sqrt{\frac{2h}{g}}r=Vt=vg2h Опять же, эта формула будет сложнее, если угол не был установлен на 0 °. Если вам интересно это увидеть, проверьте калькулятор дальности полета снаряда. Мы не будем вычислять здесь максимальную высоту (вместо этого см. калькулятор максимальной высоты), так как у нас нет начальной составляющей вертикальной скорости, а это значит, что максимальная высота та, с которой мы начинаем. Во всех расчетах мы пренебрегали сопротивлением воздуха, действующим на снаряд. Таким образом, сохраняется сумма кинетической и потенциальной энергий. Подробнее о последнем вы можете прочитать в нашем калькуляторе потенциальной энергии. Предположим, мы хотим рассчитать время полета и расстояние, пройденное мячом ⚽, брошенным с Эйфелевой башни только с горизонтальной скоростью, например, 7 м/с. Введите скорость . В нашем случае это 7 м/с. При необходимости измените единицы измерения. Введите начальную высоту, с которой начинается движение . Эйфелева башня имеет высоту 324 метра (1063 фута), но верхняя платформа находится на высоте 276 м (906 футов) над землей. Итак, вводим 276 м в нужное поле. Наш калькулятор горизонтального движения снаряда показывает время полета, расстояние и траекторию! Мы выяснили, что мяч достигает земли за 7,5 секунды, а его горизонтальное перемещение составляет ~52,52 м. Потрясающий! Помните, что наши инструменты очень гибкие: просто введите любые два значения, и калькулятор горизонтального движения снаряда сделает свою работу. Вы можете, например, проверить, какая скорость необходима, чтобы бросить мяч на расстояние 100 м от основания башни. Чтобы рассчитать горизонтальное расстояние при движении снаряда, выполните указанные шаги: Умножить вертикальную высоту Возьмите квадратный корень из результата шага 1 и умножьте на начальную скорость проекции Вы также можете умножить на начальную скорость Для расчета времени полета снаряда при горизонтальном движении выполните следующие действия: Узнать высоту по вертикали Умножить Возьмите квадратный корень из результата шаг 2 , и вы получите время полета при горизонтальном движении снаряда. Нет , отсутствует горизонтальное ускорение при движении снаряда. Скорость снаряда постоянна в горизонтальном направлении . Следовательно, ускорение также равно нулю в горизонтальном направлении. 9,8 м/с² . Снаряд, брошенный горизонтально, движется под действием силы тяжести. Следовательно, его вертикальное ускорение в направлении вниз равно Обновлено 13 декабря 2020 г. Автор: A.J. Hawkins В физике, когда вы работаете над проблемами скорости, вы разбиваете движение на две составляющие: вертикальную и горизонтальную. Вы используете вертикальную скорость для задач, которые включают угол траектории. Горизонтальная скорость становится важной для объектов, движущихся в горизонтальном направлении. В физических задачах, связанных с движением, вы рассматриваете горизонтальную и вертикальную скорости как две отдельные, независимые величины. Горизонтальная скорость в задаче о движении имеет дело с движением в направлении x; то есть из стороны в сторону, а не вверх и вниз. Гравитация, например, действует только в вертикальном направлении и не влияет напрямую на горизонтальное движение. Горизонтальная скорость исходит от сил, действующих по оси x. Чтобы научиться распознавать горизонтальную составляющую скорости в задаче на движение, нужно попрактиковаться. Для общей задачи скорости вы можете просто написать уравнение, используя «V» для скорости, например: V=a\times t горизонтальной и вертикальной скорости отдельно, вы должны различать их, используя V x и V y для горизонтальной и вертикальной скорости соответственно.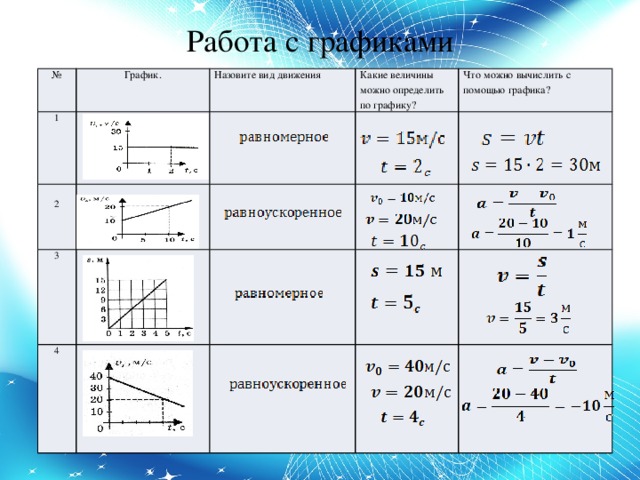 Тогда мы можем записать уравнение как:
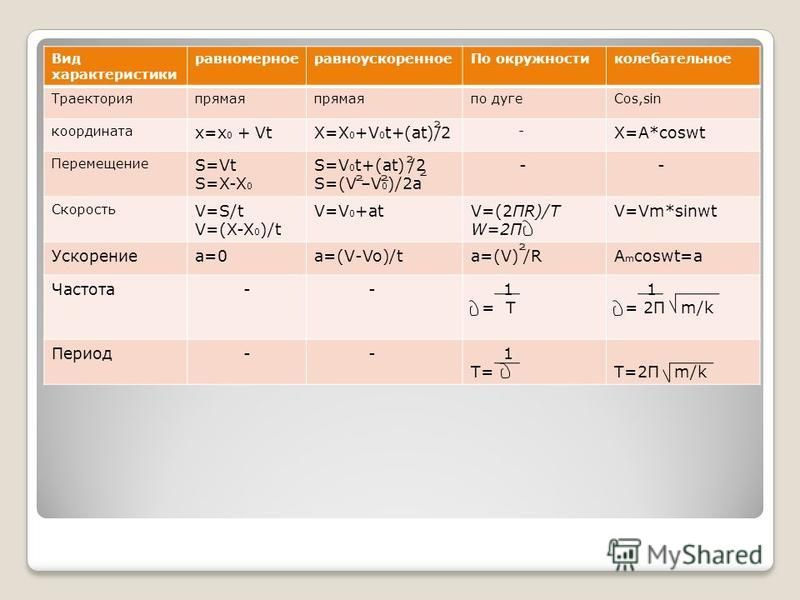
Тогда мы можем записать уравнение как: Пример расчета горизонтального движения снаряда
Часто задаваемые вопросы
Как рассчитать горизонтальное расстояние при движении снаряда?
h на 2 и разделить на ускорение свободного падения g .
u , чтобы получить горизонтальное расстояние. u на время, необходимое снаряду для достижения земли t , чтобы получить расстояние по горизонтали. Как рассчитать время полета снаряда при горизонтальном движении?
ч откуда брошен снаряд. ч на 2 и разделить результат на g , ускорение свободного падения.
Есть ли горизонтальное ускорение при движении снаряда?
Каково вертикальное ускорение снаряда, когда он летит горизонтально?
+ g , где g — ускорение свободного падения. Как рассчитать горизонтальную скорость
 Горизонтальные и вертикальные компоненты не зависят друг от друга, поэтому любое математическое решение будет рассматривать их отдельно. Как правило, горизонтальная скорость представляет собой горизонтальное смещение, деленное на время, например мили в час или метры в секунду. Смещение — это просто расстояние, которое объект прошел от начальной точки.
Горизонтальные и вертикальные компоненты не зависят друг от друга, поэтому любое математическое решение будет рассматривать их отдельно. Как правило, горизонтальная скорость представляет собой горизонтальное смещение, деленное на время, например мили в час или метры в секунду. Смещение — это просто расстояние, которое объект прошел от начальной точки. TL;DR (слишком длинно, не читал)
Определение горизонтальной скорости
Советы по распознаванию горизонтальной скорости
 Ситуации, которые имеют горизонтальную скорость, включают мяч, брошенный вперед, пушку, стреляющую пушечным ядром, или автомобиль, ускоряющийся на шоссе. С другой стороны, камень, брошенный прямо в колодец, не имеет горизонтальной скорости, а имеет только вертикальную скорость. В некоторых случаях объект будет иметь комбинацию горизонтальной и вертикальной скорости, например, пушечное ядро, выпущенное под углом; пушечное ядро движется как по горизонтали, так и по вертикали. Хотя гравитация действует только в вертикальном направлении, у вас может быть непрямая горизонтальная составляющая скорости, например, когда объект катится по пандусу.
Ситуации, которые имеют горизонтальную скорость, включают мяч, брошенный вперед, пушку, стреляющую пушечным ядром, или автомобиль, ускоряющийся на шоссе. С другой стороны, камень, брошенный прямо в колодец, не имеет горизонтальной скорости, а имеет только вертикальную скорость. В некоторых случаях объект будет иметь комбинацию горизонтальной и вертикальной скорости, например, пушечное ядро, выпущенное под углом; пушечное ядро движется как по горизонтали, так и по вертикали. Хотя гравитация действует только в вертикальном направлении, у вас может быть непрямая горизонтальная составляющая скорости, например, когда объект катится по пандусу. Запись горизонтальной составляющей


