Вычисление функции производной онлайн: Калькулятор онлайн - Найти (с решением) производную функции - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Калькулятор онлайн – Найти (с решением) производную функции

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.

Примеры подробного решения >>

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.

В этом случае отключите его и обновите страницу.

Определение производной

Определение. Пусть функция $ y = f(x) $ определена в некотором интервале, содержащем внутри себя точку $ x_0 $. Дадим аргументу приращение $ \Delta x $ такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции $ \Delta y $ (при переходе от точки $ x_0 $ к точке $ x_0 + \Delta x $ ) и составим отношение $ \frac{\Delta y}{\Delta x} $. Если существует предел этого отношения при $ \Delta x \rightarrow 0 $, то указанный предел называют производной функции $ y=f(x) $ в точке $ x_0 $ и обозначают $ f'(x_0) $.

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$

Для обозначения производной часто используют символ $ y’ $. Отметим, что $ y’ = f(x) $ – это новая функция, но, естественно, связанная с функцией $ y = f(x) $, определенная во всех точках $x$, в которых существует указанный выше предел. Эту функцию называют так: производная функции $ y = f(x) $.

Геометрический смысл производной состоит в следующем. Если к графику функции $ y = f(x) $ в точке с абсциссой $ x=a $ можно провести касательную, непараллельную оси $y$, то $ f(a) $ выражает угловой коэффициент касательной:

$ k = f'(a) $

Поскольку $ k = tg(a) $, то верно равенство $ f'(a) = tg(a) $ .

А теперь истолкуем определение производной с точки зрения приближенных равенств. 2 \) справедливо приближенное равенство $ \Delta y \approx 2x \cdot \Delta x $. Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение $ x $, найти $ f(x) $
2. Дать аргументу $ x $ приращение $ \Delta x $, перейти в новую точку $ x+ \Delta x $, найти $ f(x+ \Delta x) $

3. Найти приращение функции: $ \Delta y = f(x + \Delta x) – f(x) $
4. Составить отношение $ \frac{\Delta y}{\Delta x} $
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке $x$.

Если функция $y=f(x)$ имеет производную в точке $x$, то ее называют дифференцируемой в точке $x$. Процедуру нахождения производной функции $y=f(x)$ называют дифференцированием функции $y=f(x)$.

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция $y=f(x)$ дифференцируема в точке $x$. Тогда к графику функции в точке $ M(x; \; f(x)) $ можно провести касательную, причем, напомним, угловой коэффициент касательной равен $ f'(x) $. Такой график не может «разрываться» в точке $M$, т. е. функция обязана быть непрерывной в точке $x$.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция $y=f(x)$ дифференцируема в точке $x$, то выполняется приближенное равенство $ \Delta y \approx f'(x) \cdot \Delta x $. Если в этом равенстве $ \Delta x $ устремить к нулю, то и $ \Delta y $ будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция $ y=|x|$ непрерывна везде, в частности в точке $x=0$, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция $ y=\sqrt[3]{x} $ непрерывна на всей числовой прямой, в том числе в точке $x=0$. И касательная к графику функции существует в любой точке, в том числе в точке $x=0$. Но в этой точке касательная совпадает с осью $y$, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид $x=0$. Углового коэффициента у такой прямой нет, значит, не существует и $ f'(0) $

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

2} $$

вторая производная онлайн

Вы искали вторая производная онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление производной онлайн с подробным решением, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вторая производная онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вторая производная онлайн,вычисление производной онлайн с подробным решением,вычислить производную онлайн с подробным решением,вычислить производную функции онлайн с решением,двойная производная онлайн,дифференцирование онлайн с подробным решением,как найти производную функции y x 2 7x,как обозначается производная в калькуляторе,калькулятор онлайн для функций,калькулятор функций онлайн с решением,найти вторую производную функции онлайн,найти производную второго порядка онлайн,найти производную функции онлайн с подробным решением,найти производные функций онлайн с подробным решением бесплатно,онлайн решение производных с подробным решением бесплатно,производная второго порядка онлайн,производная второго порядка онлайн калькулятор,производная первого порядка онлайн,производные высших порядков онлайн калькулятор.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вторая производная онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить производную онлайн с подробным решением).

Где можно решить любую задачу по математике, а так же вторая производная онлайн Онлайн?

Решить задачу вторая производная онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Kалькулятор производных – найти производную функции онлайн

калькулятор производных онлайн помогает найти производную функции онлайн по заданной переменной и показывает пошаговое дифференцирование. Для лучшего понимания вы можете взглянуть на приведенные примеры, чтобы различать функцию. Вы можете использовать этот калькулятор производной для упрощения первой, второй, третьей или до 5 производных.

Без сомнения, онлайн калькулятор производных – лучший способ получить производные в любой момент и даже поможет вам решить частные производные. Что ж, этот контекст предоставляет вам правила производной, как найти производную онлайн (шаг за шагом) и с онлайн калькулятор.

В математике «производная» измеряет чувствительность к изменению выходного значения по отношению к изменению входного значения, но в расчетах производные являются центральными инструментами.

В случае движущегося объекта по времени производной является изменение скорости за определенное время. Проще говоря, он измеряет, насколько быстро движущийся объект меняет свое положение с течением времени. Следовательно, производная – это «мгновенная скорость изменения» зависимой переменной по отношению к независимой переменной.

Процесс поиска производной известен как дифференциация. Следовательно, калькулятор производных будет большим подспорьем для быстрой идентификации производных.

Многие статистики определяют производные просто по следующей формуле:

производная калькулятор функции f представлена как d / dx * f. «D» обозначает оператор производной, а x – переменную. Калькулятор деривативов позволяет вам находить деривативы без каких-либо затрат и ручных усилий. Однако производная от «производной функции» известна как вторая производная и может быть вычислена с помощью калькулятор производной второй производной. всякий раз, когда вам нужно обрабатывать до 5 деривативов вместе с последствиями правил дифференциации, просто попробуйте поискать деривативы, чтобы избежать риска ошибок.

Есть определенные правила, по которым можно узнать производные. Эти полезные правила помогут вам вычислить деривативы. Следуя им, вы можете добавить вычитание и понять, как брать производную. Посмотрите ниже, чтобы узнать о них:

Правила	Функция	Производная
Умножение на константу	cf	cf’
Правило власти	xⁿ	nxⁿ⁻¹
Правило суммы	f + g	f’ + g’
Правило различия	f – g	f’ − g’
Правило продукта	fg	f g’ + f’ g
Правило частного	f/g	(f’ g − g’ f )/g²
Взаимное правило	1/f	−f’/f²

Правило цепи (как «Состав функций»)	f º g	(f’ º g) × g’
Правило цепи (с помощью ‘ )	f(g(x))	f’(g(x))g’(x)
Правило цепи (используя \ (\ frac {dy} {dx} \))	$ \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}$

Как найти производную (решенные примеры)?

Здесь мы поможем вам решить производные задачи в соответствии с вышеупомянутыми правилами дифференциации. 3) $$

Как работает онлайн-калькулятор производных финансовых инструментов?

Чтобы вычислить производную, вам необходимо выполнить простую пошаговую процедуру:

Вход:

Прежде всего, вы введете уравнение с помощью вспомогательных функций, таких как sqrt, log, sin, cos, tan и т. Д. Вы можете получить помощь при загрузке уравнения, загрузив примеры в раскрывающемся меню. Он также будет предварительно
просматривать ваше уравнение.
Теперь выберите производную по \ (a, b, c, x, y, z или n \).
Выберите количество раз, чтобы различать. Вы можете выбрать до 5 раз
Нажмите кнопку “Рассчитать”

Выход:

Прежде всего, он покажет ваш ввод
Во-вторых, он найдет производную функции
В-третьих, это упростит ваш ответ
Он также покажет вам все расчеты вместе с применяемыми правилами дифференциации.
Калькулятор дифференцирования поможет дифференцировать функцию по первой, второй, третьей, четвертой и пятой производной.

Часто задаваемые вопросы:

Как отличить функцию от двух переменных?

Прежде всего, вы должны взять частную производную z по x. Однако вскоре вы должны снова принять производную по y. x должен оставаться постоянным. Теперь обратите внимание на феномен перекрестного партиала как меры того, каким образом изменяется наклон при изменении переменной y. Для пояснения вы можете воспользоваться помощью калькулятора первой производной, решив задачу о производной.

Что вам говорит вторая производная?

Вторая производная калькулятор измеряет скорость изменения первой производной. Вторая производная покажет увеличение или уменьшение наклона касательной. Следовательно, с помощью калькулятор производных онлайн двойной производной можно отслеживать скорость изменения исходной функции.

Имеет ли значение порядок деривативов?

Порядок дифференцирования или производной совершенно не имеет значения. Вы можете сначала дифференцировать по второй производной, а затем по первой производной или наоборот.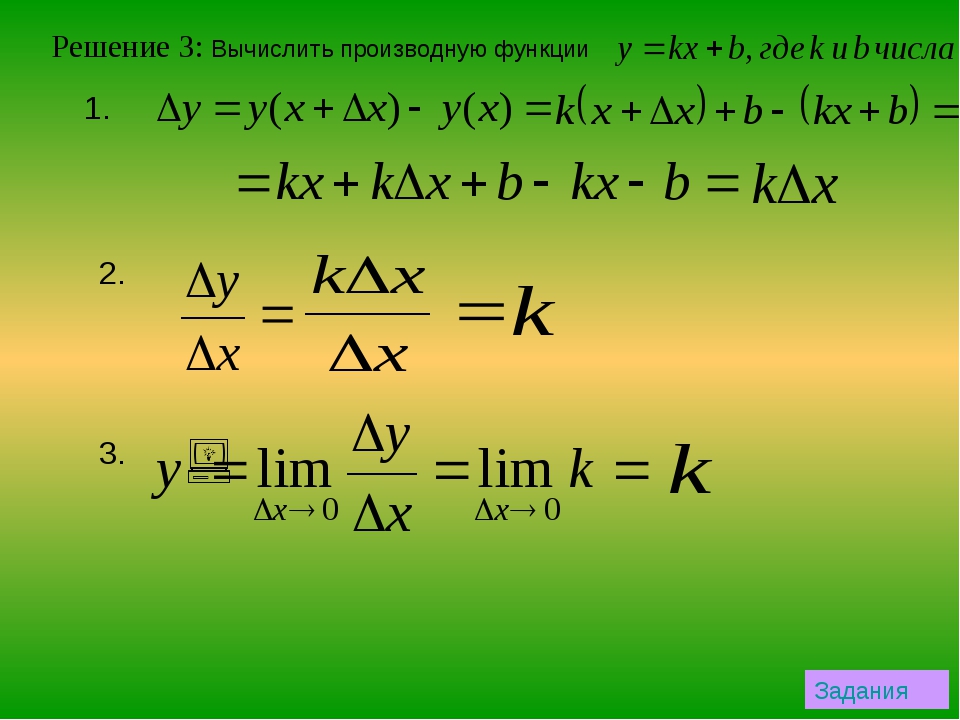 Для удобства вы можете использовать бесплатный калькулятор производной второй, который шаг за шагом вычисляет первое, второе или до 5 дифференциалов.

Как узнать, когда использовать логарифмическое дифференцирование?

Логарифмическое дифференцирование может использоваться для выражения формы \ (y = f (x) g (x) \), переменной в степени переменной. В такой ситуации вы не можете применить правило мощности и правило экспоненты. Вы можете попробовать калькулятор логарифмического дифференцирования, который поможет поэтапно решать ваши задачи логарифмического дифференцирования.

Что происходит, когда вы берете производную функции?

Всякий раз, когда будет производная функции, вы получите другую функцию, которая предоставит наклон исходной функции. Для производной функции должен быть такой же предел слева направо, чтобы она могла быть дифференцируемой в этой точке.

Подведение итогов:

Этот калькулятор производных онлайн демонстрирует пошаговую помощь по нахождению производных и производной функции. Он следует различным правилам дифференцирования, и любой может выполнять простые и сложные вычисления производных с помощью этого средства поиска производных. Это отличный помощник в академических и учебных целях и в равной степени поддерживает как студентов, так и профессионалов. Кроме того, этот производная калькулятор может при необходимости оценивать производные в заданной точке.

Other Languages: Derivative Calculator, Türev Hesaplama, Kalkulator Pochodnych, Kalkulator Turunan Online, 微分計算方法, 미분계산기, Derivace Kalkulačka, Calculadora De Derivada, Calculateur De Dérivée, Calculadora De Derivadas, Calcolatore Derivate.

Решение высшей математики онлайн

‹– Назад

При численном решении задач, связанных с математическими моделями, в которых используются производные (а к таким моделям приводят почти все физические и технические задачи, описывающие процессы, разворачивающиеся во времени), эти производные часто приходится вычислять приближённо, исходя только из того, что имеется некоторая процедура, вычисляющая значения функции , поскольку аналитические формулы, задающие , неизвестны. Обсудим некоторые методы, позволяющие вычислить производные приближённо по значениям функции .

Для приближённого нахождения в заданной точке часто поступают следующим образом. Исходя из того, что при достаточно малых приращениях разностное отношение мало отличается от своего предельного значения, равного производной ,¹⁵ мы можем приближённо заменить этим разностным отношением с малым , полагая , например, равным или . Таким образом, получаем приближённую формулу

Правая часть этой формулы при называется разностной производной вправо (или вперёд) с шагом .

Если же взять отрицательное приращение , , то аналогично получаем, что

Правая часть этой формулы при называется разностной производной влево (или назад) с шагом .

Согласно геометрическому смыслу производной, при замене производной разностной производной вправо или разностной производной влево, мы заменяем угол наклона касательной к графику углом наклона секущей , равным , или углом наклона секущей , равным , соответственно (см. следующий чертёж).

Рис.4.11.Касательная и три секущих к графику функции

Однако из того же чертежа видно, что угол наклона секущей , равный , гораздо лучше приближает угол , чем углы или . Поэтому приближённое равенство гораздо точнее, чем или . Осталось заметить, что , что приводит нас к следующей формуле для приближённого вычисления производной:

Правая часть полученной формулы называется центральной разностной производной с шагом . Эта формула применяется чаще других для практического нахождения .

Имеются и ещё более точные формулы для нахождения первой производной; приведём, например, гораздо более точную, чем (4.18), формулу

которая, правда, требует для своего применения не двух, а четырёх вычислений значения функции .

Однако выигрыш в точности с лихвой перекрывает увеличение количества вычислений. По поводу методов получения приближённых формул вычисления производной см. [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М., Численные методы. — М.: Наука, 1987. — Гл. II] или [Амосов А. А., Дубинский Ю. А., Копченова Н. В., Вычислительные методы для инженеров. — М.: Высш. шк., 1994. — Гл. 12].

Для нахождения способа приближённого вычисления второй производной введём такие обозначения. Разностную производную вперёд с шагом в точке обозначим как

разностную производную назад — как а центральную разностную производную с шагом — как Поскольку вторая производная — это производная от первой производной , то естественно для получения приближённой формулы для заменить первую производную на какое-нибудь её приближение, а затем применить тот же способ приближённого вычисления производной.

Например, если применять оба раза разностную производную вперёд, получим:
Точно так же, применяя два раза разностную производную назад, получим формулу а применяя два раза центральную разностную производную с шагом — формулу Последняя из трёх полученных формул предпочтительнее, поскольку основывается на более точной из трёх приближённых формул для первой производной.

Применяя тот же приём ещё раз, мы можем получить приближённые формулы для третьей производной. Например, основываясь на формуле разностной производной вправо, получим

а основываясь на центральной разностной производной —

Имеются и формулы для старших производных, дающие большую точность, чем приведённые выше. Например, для второй производной приведём формулу

О методах получения таких формул можно прочитать в книгах [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М., Численные методы. — М.: Наука, 1987. — Гл. II] и [Амосов А. А., Дубинский Ю. А., Копченова Н. В., Вычислительные методы для инженеров. — М.: Высш. шк., 1994. — Гл. 12]. Замечание 4.11 Значение шага , которое по своему смыслу должно быть достаточно мало в формулах приближённого вычисления производных, на практике уже для второй разностной производной нельзя брать чересчур малым. Слишком малые значения из-за того, что значения функции вычисляются с некоторой погрешностью, приводят к тому, что в приближённой формуле погрешность числителя становится величиной того же порядка, что сами числитель или знаменатель, и поэтому результат вычисления может быть весьма далёк от искомого точного результата. Вычисляя с очень малым значения при разных и наблюдая за поведением этих значений, мы можем получить “биения” графика функции , даже если эта функция заведомо должна быть монотонной и гладкой.

Для устранения этого недостатка приходится делать выбоp: либо увеличивать точность вычисления функции (что, как пpавило, сделать весьма тpудно), либо довольствоваться большими, скажем, вместо (но не слишком уж большими), значениями шага .

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Производная дроби – доказательство – примеры

Формула производной дроби

Пусть функции и определены в некоторой окрестности точки и имеют в точке производные. И пусть . Тогда их частное имеет в точке производную, которая определяется по формуле:
(1) .

Доказательство

Введем обозначения:
;
.
Здесь и являются функциями от переменных и . Но для простоты записи мы будем опускать обозначения их аргументов.

Далее замечаем, что
;
.
По условию функции и имеют производные в точке , которые являются следующими пределами:
;
.
Из существования производных следует, что функции и непрерывны в точке . Поэтому
;
.

Рассмотрим функцию y от переменной x, которая является дробью из функций и :
.
Рассмотрим приращение этой функции в точке :
.
Умножим на :

.
Отсюда
.

Теперь находим производную:

.

Итак,
.
Формула доказана.

Вместо переменной можно использовать любую другую переменную. Обозначим ее как x. Тогда если существуют производные и , причем , то производная дроби, составленной двух функций, определяется по формуле:
.
Или в более короткой записи
(1) .

Доказательство вторым способом

Примеры

Здесь мы рассмотрим простые примеры вычисления производной дроби, применяя формулу производной частного (1). Заметим, что в более сложных случаях, находить производную дроби проще с помощью логарифмической производной.

Пример 1

Найдите производную дроби
,
где , , , – постоянные.

Решение

Применим правило дифференцирования суммы функций:
.
Производная постоянной
.
Из таблицы производных находим:
.
Тогда
;
.

Заменим на и на :
.

Теперь находим производную дроби по формуле
.

.

Ответ

Пример 2

Найти производную функции от переменной x
.

Решение

Применяем правила дифференцирования, как в предыдущем примере.
;
.

Применяем правило дифференцирования дроби
.

.

Раскрываем скобки.

.

Ответ

Пример 3

Найти производную дроби
.

Решение

Из таблицы производных находим:
.
Применяем правила дифференцирования суммы и постоянной.
;
.

Применяем формулу для производной дроби:
;

.

Ответ

Автор: Олег Одинцов. Опубликовано: 30-10-2016 Изменено: 02-12-2016

Калькулятор онлайн. Найти (с решением) производную функции

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.

Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Определение. Пусть функция $y = f(x) $ определена в некотором интервале, содержащем внутри себя точку $x_0 $. Дадим аргументу приращение $\Delta x $ такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции $\Delta y $ (при переходе от точки $x_0 $ к точке $x_0 + \Delta x $) и составим отношение $\frac{\Delta y}{\Delta x} $. Если существует предел этого отношения при $\Delta x \rightarrow 0 $, то указанный предел называют производной функции $y=f(x) $ в точке $x_0 $ и обозначают $f”(x_0) $.

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$

Для обозначения производной часто используют символ y”. Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
$k = f”(a) $

Поскольку $k = tg(a) $, то верно равенство $f”(a) = tg(a) $ .

А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция $y = f(x) $ имеет производную в конкретной точке $x $:
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x) $$
Это означает, что около точки х выполняется приближенное равенство $\frac{\Delta y}{\Delta x} \approx f”(x) $, т.е. $\Delta y \approx f”(x) \cdot \Delta x $. Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. 2 \) справедливо приближенное равенство $\Delta y \approx 2x \cdot \Delta x $. Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение $x $, найти $f(x) $
2. Дать аргументу $x $ приращение $\Delta x $, перейти в новую точку $x+ \Delta x $, найти $f(x+ \Delta x) $
3. Найти приращение функции: $\Delta y = f(x + \Delta x) – f(x) $
4. Составить отношение $\frac{\Delta y}{\Delta x} $
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство $\Delta y \approx f”(x) \cdot \Delta x $. Если в этом равенстве $\Delta x $ устремить к нулю, то и $\Delta y $ будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция $y=\sqrt{x} $ непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и $f”(0) $

Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями.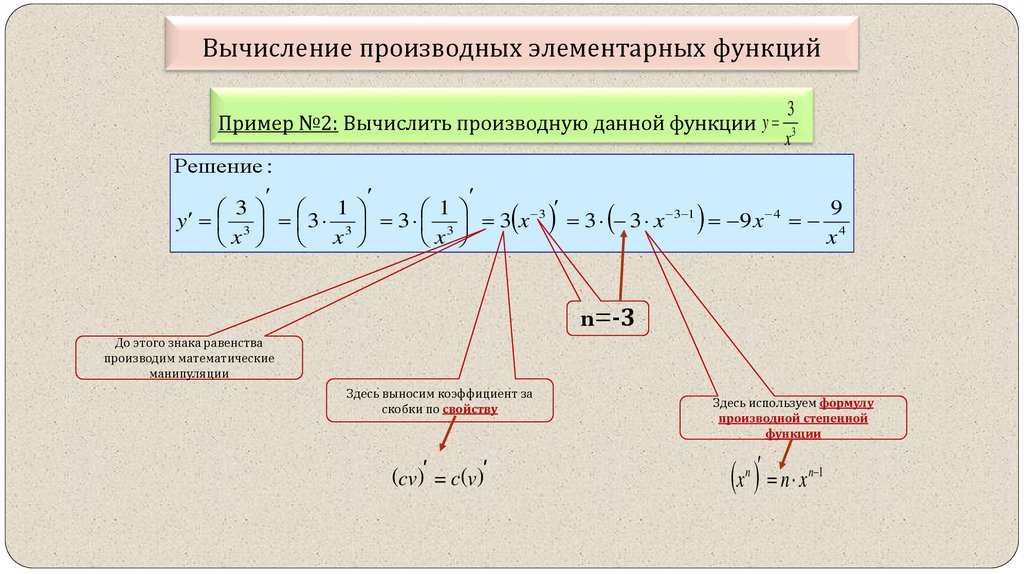 2} $$

Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции.

Вывод формул производных натурального логарифма и логарифма по основанию a

Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln x)′ = .

Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a :
(2) (log a x)′ = .

Доказательство

Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x , которая является логарифмом по основанию :
.
Эта функция определена при . Найдем ее производную по переменной x . По определению, производная является следующим пределом:
(3) .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .

Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).

Воспользуемся свойством (7) и вторым замечательным пределом (8):
.

И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом . Он обозначается так:
.
Тогда ;
.

Тем самым мы получили формулу (2) производной логарифма.

Производная натурального логарифма

Еще раз выпишем формулу производной логарифма по основанию a :
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого , . Тогда
(1) .

Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.

Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.

Другие способы доказательство производной логарифма

Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.

Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае . Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку , то
.
Тогда
.
Формула доказана.

Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x :
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции :
.
Здесь . Подставим в (10):
.
Отсюда
.

Пример

Найти производные от ln 2x, ln 3x и ln nx .

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx . Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от ln 2x и ln 3x .

Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция составлена из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции .
.
Здесь мы подставили .

Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n . Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
– это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.

Ответ

; ; .

Производная логарифма модуля x

Найдем производную от еще одной очень важной функции – натурального логарифма от модуля x :
(12) .

Рассмотрим случай . Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.

Теперь рассмотрим случай . Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n и равна
.
Тогда
.

Объединяем эти два случая в одну формулу:
.

Соответственно, для логарифма по основанию a , имеем:
.

Производные высших порядков натурального логарифма

Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .

Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.

Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.

Доказательство

Подставим в формулу (14) значение n = 1:
.
Поскольку , то при n = 1 , формула (14) справедлива.

Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .

Действительно, при n = k имеем:
.
Дифференцируем по переменной x :

.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1 . Таким образом, из предположения, что формула (14) справедлива при n = k следует, что формула (14) справедлива при n = k + 1 .

Поэтому формула (14), для производной n-го порядка, справедлива для любых n .

Производные высших порядков логарифма по основанию a

Чтобы найти производную n-го порядка от логарифма по основанию a , нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.

Производная калькулятора функции

Поиск инструмента

Производная

Инструмент для вычисления производных. Дифференциация – это фундаментальный инструмент при анализе функции, он позволяет измерить чувствительность к изменению функции.

Результаты

Производная – dCode

Тег (и): Функции

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Рекламные объявления

Ответы на вопросы (FAQ)

Что такое производная? (Определение)

Математики определили производных по формуле $$ \ frac {d} {dx} f = f ‘(x) = \ lim_ {h \ to 0} \ frac {f (x + h) -f (x) } {h} $$

Производная функции $ f $ обозначается $ f ‘$ (с апострофом, называемым простым числом) или $ \ frac {d} {dx} f $, где $ d $ – оператор производной и $ x $ переменная, от которой требуется производная.

Вычисление производной – это операция, обратная примитивному вычислению (неопределенный интеграл).

Как рассчитать производную?

Расчет деривации (дериватив первого порядка ) основан в основном на списке обычных деривативов , уже вычисленных и известных (см. Ниже).

На dCode калькулятор производной знает все производные , указывает функцию и переменные, по которым производится производная, чтобы получить результат вычисления производной .2+ \ sin (x) \ Rightarrow f ‘(x) = 2 x + \ cos (x) $$

Производное исчисление часто используется в физике для вычисления скорости.

Каков список распространенных производных финансовых инструментов?

Более полезные производные :

Имя	Функция	Производная
константа / число	$$ k \ in \ mathbb {R} $$	$$ 0 $ $
переменная	$$ x $$	$$ 1 $$
степень n (показатель степени)	$$ x ^ n $$	$$ nx ^ {n-1} $ $
отрицательная мощность	$$ x ^ {- n} $$	$$ -nx ^ {- n-1} $$
обратная	$$ \ frac {1} {x } $$	$$ – \ frac {1} {x ^ 2} $$
обратная степень	$$ \ frac {1} {x ^ n} $$	$$ – \ frac { n} {x ^ {n + 1}} $$
корень	$$ \ sqrt {x} $$	$$ \ frac {1} {2 \ sqrt {x}} $$
корень n-й степени	$$ \ sqrt [n] x $$	$$ \ frac {1} {n \ sqrt [n] {x ^ {n-1}}} $$
дробная степень 9008 6	$$ x ^ {1 / n} $$	$$ (1 / n) x ^ {(1 / n) -1} $$
натуральный логарифм	$$ \ ln \| x \| $$	$$ \ frac {1} {x} $$
основание логарифма a	$$ \ log_a \| x \| $$	$$ \ frac {1} {x \ ln a} $$
экспонента	$$ e ^ x $$	$$ e ^ x $$
экспонента x	$$ a ^ x $$	$$ a ^ x \ ln a $$
синус	$$ \ sin (x) $$	$$ \ cos (x) $$
косинус	$$ \ cos (x) $$	$$ – \ sin (x) $$
тангенс	$$ \ tan (x) $$	$$ \ frac {1} { \ cos ^ 2 (x)} \\ = \ sec ^ 2 (x) \\ = 1+ \ tan ^ 2 (x) \\ = \ frac {2} {1+ \ cos (2x)} $$
секущая	$$ \ sec (x) = \ frac {1} {\ cos (x)} $$	$$ \ frac {\ tan (x)} {\ cos (x)} \\ = \ sec (x) \ tan (x) \\ = \ frac {2 \ sin (x)} {1+ \ cos (2x)} $$
косеканс	$$ \ csc (x) = \ frac {1} {\ sin (x)} $$	$$ – \ frac {\ cos (x)} {\ sin ^ 2 (x)} \\ = – \ cot (x) \ csc (x ) \\ = \ frac {2 \ cos (x)} {- 1+ \ cos (2x)} $$
котангенс	$$ \ cot (x) = \ frac {1} {\ tan ( x)} $$	$$ – \ frac {1} {\ sin ^ 2 (x)} \\ = -1- \ cot ^ 2 (x) \\ = – \ csc ^ 2 (x) \\ = \ frac {2} {-1+ \ cos (2x)} $$
arcsine	$$ \ arcsin (x) $$	$$ \ frac {1} {\ sqrt {1-x ^ 2}} $$
arccosine	$$ \ arccos (x) $$	$$ – \ frac {1} {\ sqrt {1-x ^ 2}} $$
арктангенс	$$ \ arctan (x) $$	$$ \ frac {1} {1 + x ^ 2} $$
синус-гиперболический	$$ \ sinh (x) $$	$$ \ cosh (x) $ $
Косинус гиперболический	$$ \ cosh (x) $$	$$ \ sinh (x) $$
касательный гиперболический	$$ \ tanh (x) $$	$$ \ frac {1} {\ cosh ^ 2 (x)} \\ = 1 – \ tanh ^ 2 (x) $$
котангенс гиперболический	$$ \ coth (x) $$	$$ \ frac {-1} {\ sinh ^ 2 (x)} \\ = 1 – \ coth ^ 2 (x) $$
arcsinus hyperbolic	$$ \ operatorname {arcsinh} x $$	$$ \ гидроразрыв {1} {\ sqrt {1 + x ^ 2}} $$
arccosinus hyperbolic	$$ \ operatorname {arccosh} x $$	$$ \ frac {1} {\ sqrt {x ^ 2 -1}} $$
арктангенс гиперболический	$$ \ operatorname {arctanh} x $$	$$ \ frac {1} {1-x ^ 2} $$

Что такое список производных сложных функций?

Общие производные составных функций, которые необходимо знать:

Имя	Составная функция	Производная
Составная функция	$$ g \ circ f $$	$$ (g ‘ \ circ f) \ times f ‘$$
функция power n (возведение в степень)	$$ f ^ n $$	$$ nf ^ {n – 1} f’ $$
синус функция	$$ \ sin (f) $$	$$ f ‘\ cos (f) $$
Косинус функции	$$ \ cos (f) $$	$$ – f’ \ sin (f) $$
экспонента функции	$$ \ exp (f) $$	$$ f ‘\ exp (f) $$
квадратный корень из функции (положительная функция )	$$ \ sqrt {f} $$	$$ \ frac {f ‘} {2 \ sqrt {f}} $$
логарифм функции (положительная функция)	$$ \ ln (f) $$	$$ \ frac { f ‘} {f} $$

Как рассчитать вторую производную?

Как рассчитать частную производную?

Частичная производная – это производная , которая применяется только к одной переменной, остальные остаются нетронутыми.

В dCode укажите одну переменную, если функция имеет несколько, чтобы получить частную производную .

Как посчитать примитив?

Используйте простой калькулятор, доступный на dCode.

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код производного онлайн-инструмента. За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого «производного» алгоритма, апплета или фрагмента (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «производной» функции (вычислять, преобразовывать, решать, расшифровывать / шифровать, расшифровывать / шифровать, декодировать / кодировать, переводить), написанные на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Производного» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

производная, функция, дифференцирование, вычислитель, интеграл, скорость, ускорение

Ссылки

Источник: https: // www.dcode.fr/derivative

Упражнение может быть интересным только в одном случае – когда вы знаете все правила и умеете их соблюдать. Если вы хотите проверить свой ответ, этот калькулятор – правильный выбор. Чтобы найти производную от выражения, нужно аккуратно ввести ее и нажать синюю стрелку. После того, как вы увидите список опций, вам нужно выбрать «Найти производную».Правильный ответ волшебным образом появится на вашем экране.

Вычисление производных первого и второго порядка используется во многих прикладных задачах. Рассмотрим самые распространенные из них.

Экстремум функции одной переменной находится приравниванием производной нулю: f ‘(x) = 0. Это основной этап построения графика функции методом дифференциального исчисления.
Значение производной в точке x0 позволяет найти уравнение касательной к графику функции.
Отношение производных позволяет нам вычислять пределы по правилу Л’Оспиталя.
В математической статистике плотность распределения f (x) определяется как производная функции распределения F (x).
При поиске частного решения линейного дифференциального уравнения требуется вычислить производную в точке.
В методе Ньютона с помощью производной разделяются корни нелинейных уравнений.
Производная функции – одно из основных понятий математики.А нахождение производной получило название дифференцирования, которое характеризует скорость изменения функции (на данный момент).

Онлайн-калькулятор производных финансовых инструментов

При решении высшей математики часто бывает необходимо вычислить производную математической функции. Для простых математических функций это больше не проблема, поскольку таблицы разработаны и доступны для производных. Однако если вы хотите найти производную сложной математической функции, вам придется потратить много времени и усилий.Как раз в этом случае наш онлайн-калькулятор, который умеет вычислять производные функций любой сложности, станет отличным выходом.

Наш калькулятор производных финансовых инструментов поможет вам в решении ваших вопросов.

Последнее обновление: четверг, 25 июня 2020 г. – 16:51

Derivative Plotter

Удачи с производными!
Введите функцию и посмотрите ее наклон ниже (рассчитанный программой).
Тогда посмотрите, сможете ли вы вычислить производную самостоятельно.

Он отображает вашу функцию синим цветом, а наклон функции на графике ниже – красным ( вычисляет разность между каждой точкой в исходной функции, поэтому не знает формулы для производной).

У вас также есть возможность построить другую функцию в зеленом под рассчитанным наклоном … если линии совпадают, велика вероятность, что вы нашли производную!

Что стоит попробовать!

Введите функцию вверху, затем посмотрите, сможете ли вы найти производную, пробуя различные функции внизу.

«Силы»:

функция:

х ²

х ³

х ⁴

х ⁵

производная:

? Х ²

? . 3 и т. Д.)

Функции тригонометрии:

функция:	грех (х)	cos (x)	загар (x)
производная:	cos (x)	?	?

Экспоненциальных функций:

функция:	e ^x	лин (х)
производная:	?	?

Предупреждения:

Это всего лишь числовая оценка, не знает, формула для производной… это зависит от вас!

Кроме того, поскольку он просто выполняет простые вычисления, он не будет обрабатывать особые условия, такие как отверстия, прыжки и т. Д. См. «Непрерывность».

Но это забавный и обучающий инструмент, так что наслаждайтесь!

Найти область определения производной функции

Поиск инструмента

Область производной функции

Инструмент для вычисления области определения функции f (x), т.е.набор значений x, существующий через производную f ‘(x).

Результаты

Область производной функции – dCode

Тег (и): Функции

dCode и другие

Рекламные объявления

Калькулятор производных доменов

Ответы на вопросы (FAQ)

Как вычислить область определения производной функции?

Расчет области производной функции, отмеченной $ D_ {f ‘} $, заключается в вычислении набора определений ее производной функции. {* +} =] 0; + \ infty [$, его производная равна $ f ‘(x) = \ frac {1} {x} $.* =] – \ infty; 0 [\ чашка] 0; + \ infty [$

Какова область выводимости рациональной функции?

Какая связь между областью выводимости и областью определения?

Функция дифференцируема только на множестве значений, где она непрерывна, и, следовательно, она непрерывна только на тех значениях, где она определена.

Таким образом, область выводимости функции является подмножеством области ее определения.

Задайте новый вопрос

Исходный код

dCode сохраняет право собственности на исходный код онлайн-инструмента «Домен производной функции».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «Домена производной функции» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция «Домен производной функции» (вычисление, преобразование, решение, расшифровка / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.) .), и никакая загрузка данных, скрипт, копирование и доступ к API для «Домена производной функции» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

область, производная, определение, функция

Ссылки

Источник: https://www.dcode.fr/domain-derivative-function

с шагами – Open Omnia

Войдите в функцию. Используйте x в качестве переменной.
См. Примеры

ПОМОЩЬ

Используйте предоставленную клавиатуру для ввода функций. Используйте x в качестве переменной. Нажмите «РЕШИТЬ», чтобы обработать введенную вами функцию.

Вот несколько примеров того, что вы можете ввести.

Вот как вы используете кнопки

долл. США

РЕШЕНИЕ	Обрабатывает введенную функцию.
ПРОЗРАЧНЫЙ	Удаляет весь текст в текстовом поле.
DEL	Удаляет последний элемент перед курсором.
а-я	Показывает алфавит.
триг	Показывает тригонометрические функции.
◀	Переместите курсор влево.{□} {□}	N-й корень.
(□)	Круглая скобка.
журнал	База 10.
пер.	Натуральное бревно (цоколь е).
\| $ □ $ \|	Абсолютное значение.

Калькулятор неявной дифференциации – Найдите неявную производную

Онлайн-калькулятор неявного дифференцирования помогает определить неявную производную заданных функций по переменной.2 \). Дифференциация – это процесс нахождения производной функции. Другими словами, процесс определения производной зависимой переменной в неявной функции путем дифференцирования каждого элемента отдельно, выражения производной зависимой переменной в виде символа и решения полученного выражения.

Найти dy / dx неявным дифференцированием:

Это метод нахождения неявного дифференцирования функции. 2 – 2 (2) $$

$$ = 6–12 / 27–4 $$

Следовательно, результат неявной задачи дифференцирования:

$$ = – 6/23 $$

Как работает калькулятор неявной дифференциации ?

Онлайн-калькулятор неявной производной вычисляет неявное дифференцирование для введенной функции, выполнив следующие действия:

Ввод:

Сначала введите значение функции f (x, y) = g (x, y).
Теперь выберите переменную из раскрывающегося списка, чтобы различать по этой конкретной переменной.
Если вы хотите оценить производную в определенных точках, замените значения точек x и y. (необязательно)
Нажмите кнопку «Рассчитать» для неявного решения.

Выход:

Решатель неявного дифференцирования быстро предоставляет неявную производную заданной функции.
Этот калькулятор также находит производную для определенных точек.

FAQ:

Почему мы используем неявное дифференцирование?

Неявное дифференцирование используется для определения производной переменной y по x без вычисления заданных уравнений для y.

Что такое явная и неявная функция?

Явная функция – это функция, которая выражается в терминах независимой переменной. В то время как неявная функция – это функция, которую можно записать в терминах как независимых, так и зависимых переменных.

Что такое неявное дифференцирование ab?

Неявная производная от ab равна

dy / dx (ab) = ab ’+ a’b

= ab ’+ b

Заключение:

Используйте этот онлайн-калькулятор неявного дифференцирования для вычисления производной, когда зависимая переменная не изолирована на одной стороне уравнения. Он также может найти неявный вывод в заданных точках.

Артикул:

Из источника в Википедии: Неявная функция, неявное уравнение, индикаторная функция, Алгебраические функции, Неявное дифференцирование, Общая формула для производной неявной функции.

Из источника Cliffs Notes: неявное дифференцирование, теорема о неявной функции, дифференциальные уравнения.

Из источника LibreText: Дифференциация для нахождения касательной линии, Поиск наклонов касательных линий к окружности, Правило степени для дифференцирования.

Калькулятор производных производных

– Как это работает – Получить образование

Калькулятор частной производной на этой веб-странице вычисляет частную производную введенной вами функции символически с помощью компьютерной системы алгебры, и все это за кулисами.Система компьютерной алгебры – это интересное программное приложение, которое может практически усваивать формулы, а также по порядку использовать все существующие производные правила. Он следует тем же шагам, что и человек при определении производной.

О дифференциации и производных финансовых инструментах

Дифференцирование и производные – чисто математические понятия. Тем не менее, важность этих инструментов применима и в повседневной жизни. Эти влиятельные устройства широко используются в биологии, медицине, физике, экономике, финансах, химии, космических технологиях, а также в различных других областях науки.Человек может усомниться в ценности этих математических приемов в повседневной жизни. Вы можете быстро понять эту простую идею. Ваш регулярный ежемесячный или двухмесячный расчет соответствует правилу дифференциации. Как именно? Эта пропорция дает вам размер оплаты труда, который является просто правилом дифференциации.

Читайте также: Калькулятор двойного интеграла – полный обзор

Дифференциация – это процедура оценки количества побочных продуктов.Эти суммы различаются. Связь зависимости или независимости помогает установить производные величин. Примечательно, что побочные продукты используются по-разному в различных разделах математики с небольшими вариациями в количествах, сохраняя при этом определение дифференциации одним и тем же. Например, в исчислении производная определяет изменение входных данных функции.

Читайте также: Калькулятор расчетов – подробное руководство

Что касается зависимых, а также независимых переменных, это скорость изменения зависимой переменной «y» относительно независимой переменной «x».«В дифференциальной геометрии принцип дифференциации несколько искажен. Производная – это наклон кривой на множитель на кривой. Другими словами, это наклон касательной с тем же коэффициентом на кривой. Следует иметь в виду, что побочный продукт линии является постоянным, поскольку для любой прямой линии нет цены корректировки.

Калькулятор производных – понимание на примере

Найти частную производную признака вручную чрезвычайно просто.Если вы в настоящее время понимаете, как делать типичную производную. При определении частичного побочного продукта мы управляем функцией 2 или более независимых переменных. Например, значение признака f (x, y) = x + y зависит от независимых переменных x. Так же, как и y, и, как следствие, это функция с двумя переменными.

Частная производная этого признака относительно x обозначается как ∂ f ⁄ ∂ xf (x, y), где ∂ – частная производная. Тогда как f – это функция, а x – переменная, к которой она относится.Также целесообразно опустить f и записать обозначение как ∂ ⁄ ∂ x.

При определении частной производной по переменной. Просто отдельные относительно этой переменной, обрабатывая другие независимые переменные как константы. Например, при вычислении ∂ f ⁄ ∂ x (yx2). Мы отделены друг от друга относительно x и работаем с y, как если бы он был непротиворечивым. Это приводит к тому, что ∂ f ⁄ ∂ x (yx2) = 2yx.

Заключительные слова

Нахождение или вычисление производных элементарных функций – не сложная работа.Тем не менее, вычисление побочных продуктов более высокого порядка оказывается затруднительным. При решении математических задач оказывается необходимым не терять время. Тем не менее, расчет деривативов занимает много времени. Математики с помощью инженеров нашли прибыльный способ решить этот очень сложный калькулятор. Эти калькуляторы широко используются в настоящее время. Вам нужно указать ценность или переменную, а ваше решение, несомненно, будет придерживаться. Несколько таких калькуляторов.Большинство из них предназначены для решения математических задач на элементарных уровнях. Тем не менее, несколько калькуляторов производных используют уникальные алгоритмы и настройки для устранения производных более высокой степени и проблем. Также доступны специальные программы, которые могут помочь вам решить математические задачи.

Читайте также: Калькулятор определителей – легкий способ выучить

Mathematica, а также Matlab – это два программных устройства для математики. Эти устройства могут быстро упростить математическую задачу.Вы также можете строить графики и диаграммы, используя эти программные инструменты для математики. С помощью этого ценного программного обеспечения можно также спланировать трехмерное изображение фигуры. Основным принципом этих калькуляторов и программных приложений является экономия усилий и времени учащихся или специалистов.

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.