Главная
Вычисление интеграла: Вычисление криволинейных интегралов: теория и примеры

Вычисление интеграла: Вычисление криволинейных интегралов: теория и примеры

Содержание

Вычисление криволинейных интегралов: теория и примеры

Криволинейные интегралы – обобщение понятия определённого интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:

где f(x, y) – функция двух переменных, а L – кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB.

Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?

Пусть на плоскости расположен отрезок AB некоторой кривой L, а функция двух переменных

f(x, y) определена в точках кривой L. Пусть мы выполняем с этим отрезком кривой следующий алгоритм.

  1. Разделить кривую AB на части точками (рисунки ниже).
  2. В каждой части свободно выбрать точку M.
  3. Найти значение функции в выбранных точках.
  4. Значения функции умножить на
    • длины частей в случае криволинейного интеграла первого рода;
    • проекции частей на ось координат в случае криволинейного интеграла второго рода
      .
  5. Найти сумму всех произведений.
  6. Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.

Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f(x, y) по кривой AB.

Случай криволинейного интеграла
первого рода

Случай криволинейного интеграла
второго рода

Введём следующие ообозначения.

Mi(ζi; ηi) – выбранная на каждом участке точка с координатами.

fi(ζi; ηi) – значение функции f(x, y) в выбранной точке.

Δsi – длина части отрезка кривой (в случае криволинейного интеграла первого рода).

Δxi – проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).

d = maxΔsi – длина самой длинной части отрезка кривой.

Криволинейные интегралы первого рода

Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:

.

Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл. Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:

.

В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой

AB (A или B) считать началом отрезка, а какую концом, то есть

.

Криволинейные интегралы второго рода

Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:

.

В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:

.

При составлении интегральной суммы криволинейного интеграла второго рода значения функции fi(ζi; ηi) можно умножать также на проекции частей отрезка кривой на ось Oy. Тогда получим интеграл

.

На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P(x, y) и f = Q(x, y) и интегралы

,

а сумма этих интегралов

называется общим криволинейным интегралом второго рода.

Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.

Кривая дана в декартовых прямоугольных координатах

Пусть на плоскости задана кривая y = y(x) и отрезку кривой AB соответствует изменение переменной x от a до b. Тогда в точках кривой подынтегральная функция f(x, y) = f(x, y(x)) (“игрек” должен быть выражен через “икс”), а дифференциал дуги и криволинейный интеграл можно вычислить по формуле

.

Если интеграл проще интегрировать по y, то из уравнения кривой нужно выразить

x = x(y) (“икс” через “игрек”), где и интеграл вычисляем по формуле

.

Пример 1. Вычислить криволинейный интеграл

,

где AB – отрезок прямой между точками A(1; −1) и B(2; 1).

Решение. Составим уравнение прямой AB, используя формулу (уравнение прямой, проходящей через две данные точки A(x1; y1) и B(x2; y2)):

.

Из уравнения прямой выразим y через x

:

.

Тогда и теперь можем вычислять интеграл, так как у нас остались одни “иксы”:

Кривая дана в параметрической форме

Пусть в пространстве задана кривая

Тогда в точках кривой функцию нужно выразить через параметр t () а дифференциал дуги , поэтому криволинейный интеграл можно вычислить по формуле

Аналогично, если на плоскости задана кривая

,

то криволинейный интеграл вычисляется по формуле

.

Пример 2. Вычислить криволинейный интеграл

,

где L – часть линии окружности

,

находящаяся в первом октанте.

Решение. Данная кривая – четверть линии окружности, расположенная в плоскости z = 3. Она соответствует значениям параметра . Так как

,

то дифференциал дуги

Подынтегральную функцию выразим через параметр t:

.

Теперь, когда у нас всё выражено через параметр

t, можем свести вычисление данного криволинейного интеграла к определённому интегралу:

Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.

Кривая дана в декартовых прямоугольных координатах

Пусть дана кривая на плоскости уравнением функции “игрек”, выраженной через “икс”: y = y(x) и дуге кривой AB соответствует изменение x от a до b. Тогда в подынтегральную функцию подставим выражение “игрека” через “икс” и определим дифференциал этого выражения “игрека” по “иксу”: . Теперь, когда всё выражено через “икс”, криволинейный интеграл второго рода вычисляется как определённый интеграл:

Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции “икс”, выраженной через “игрек”: x = x(y), . В этом случае формула для вычисления интеграла следующая:

Пример 3. Вычислить криволинейный интеграл

, если

а) L – отрезок прямой

OA, где О(0; 0), A(1; −1);

б) L – дуга параболы y = x² от О(0; 0) до A(1; −1).

Решение.

а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке – синяя). Напишем уравнение прямой и выразим “игрек” через “икс”:

.

Получаем dy = dx. Решаем данный криволинейный интеграл:

б) если L – дуга параболы y = x², получим dy = 2xdx. Вычисляем интеграл:

В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.

Теорема. Если функции P(x,y), Q(x,y) и их частные производные , – непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L, находящейся в области D.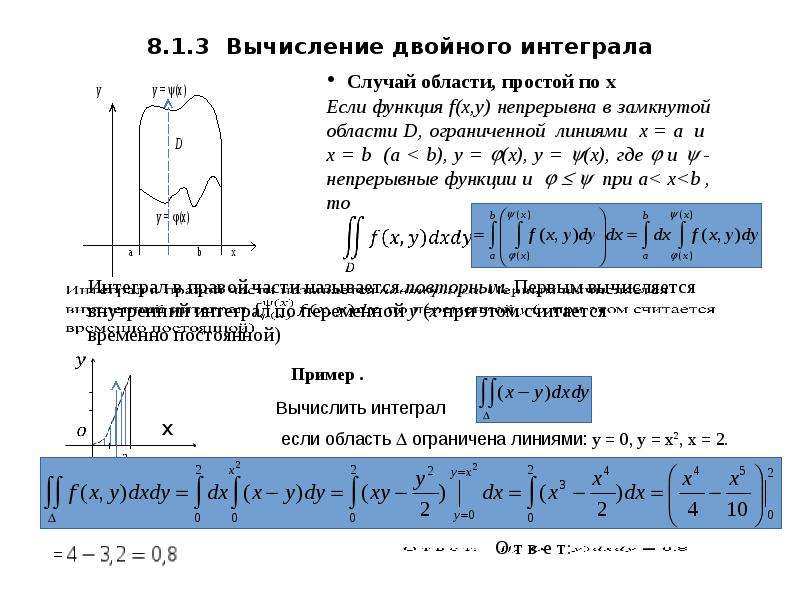

Кривая дана в параметрической форме

Пусть в пространстве дана кривая

.

Тогда

,

а в подынтегральные функции подставим

–

выражения этих функций через параметр t. Получаем формулу для вычисления криволинейного интеграла:

Пример 4. Вычислить криволинейный интеграл

,

если L – часть эллипса

отвечающая условию y ≥ 0.

Решение. Данная кривая – часть эллипса, находящаяся в плоскости z = 2. Она соответствует значению параметра .

Так как

,

можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L – замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина.

Пример 6. Вычислить криволинейный интеграл

,

где L – дуга параболы между точками О(0; 0) и B(2; 2).

Решение. Так как , то .

Теперь можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Пример 7. Вычислить криволинейный интеграл

,

где L – дуга астроиды

в первом квадранте.

Решение. В первом квадранте . Определим дифференциал дуги:

Представляем криволинейный интеграл в виде определённого интеграла и вычисляем его:

Пример 8. Вычислить криволинейный интеграл

,

где L – первая арка циклоиды

Решение. Циклоида образует первую арку при изменении параметра t от 0 до 2π. Определим дифференциал дуги:

Таким образом,

.

Подставим в криволинейный интеграл dl и y, выраженные через параметр t и получаем:

Пример 9. Вычислить криволинейный интеграл

,

где L – отрезок прямой от точки A(1; 1) до точки B(3; 5).

Решение. Составим уравнение прямой AB:

.

Из полученного уравнения прямой выразим “игрек”:

Поэтому и теперь можем вычислить данный криволинейный интеграл:

Пример 10. Вычислить криволинейный интеграл

,

где L – первая арка циклоиды

Решение. Из уравнений кривой следует

.

Так как циклоида образует первую арку при изменении параметра t от 0 до 2π, то получаем соответствующие пределы интегрирования. Решаем данный криволинейный интеграл:

Кратные и криволинейные интегралы

Поделиться с друзьями

Белла Левикова ВЫЧИСЛЕНИЕ ИНТЕГРАЛА

VLADEY в рамках программы «Художник Недели» представляет персональную выставку «Вычисление интеграла» Беллы Левиковой.

Белла Левикова относится к художникам-нонконформистам, которые берут начало в 1960-х годах. В 1965 она нашла своё «творческое видение» и занялась живописной абстракцией. Левикова участвовала в ключевых событиях московского андеграунда 1960-1970-х годов, её работы были отобраны для знаменитого аукциона Sotheby`s в 1988 году в Москве и там успешно проданы. Произведения Левиковой вошли в коллекции Третьяковской галереи и Русского музея.

Белла Левикова в своих картинах суммирует, соединяет, сплавляет тысячи потоков, проходящих через её сознание, одновременно выискивая форму, формулу, лежащую в основе мироздания, и поэтому часто говорит, что у неё «интегральное видение». Мы же предлагаем развязать для себя клубок смыслов, зашифрованный в каждой её новой картине, осуществить попытку вычисления одного из интегралов этого мира.

В основе представления о мироздании Беллы Левиковой лежит сакральная геометрия. На выставке представлены несколько работ, непосредственно отражающих её размышления эту тему – «Активация системы Б», «Глобальный объект» и другие.

Белла Левикова верит, что человеческие возможности огромны, но не раскрыты. В определенный период творчества она почувствовала, что может считывать информацию как бы из пространства, предчувствовать глобальные события, происходящие на планете. Серия «Комиксы», представленная на выставке, относится к такому «сверхчувственному восприятию». Белла Левикова уловила настроение, витающее сегодня, и появилась серия не совсем характерная её живописной манере, но именно так отразилась грань современности. В этих картинах открывается большое количество ассоциативных связей, как в комиксах в этих ярких формах можно увидеть и персонажей, и бесконечную разворачивающуюся связь между ними – это достигается за счёт единства внутри серии и композиционного единства внутри каждого пространства холста.

Выставка «Вычисление интеграла» Белла Левикова в Центре современного искусства ВИНЗАВОД

VLADEY в рамках программы «Художник Недели» представляет персональную выставку «Вычисление интеграла» Беллы Левиковой.

Белла Левикова относится к художникам-нонконформистам, которые берут начало в 1960-х годах.  В 1965 году она нашла своё «неожиданное и спонтанное творческое начало, которое открыло дверь в новую систему координат» и занялась живописной абстракцией. Левикова участвовала в ключевых событиях московского андеграунда 1960-1970-х годов, стала одним из 34 авторов, чьи работы были отобраны для знаменитого аукциона Sotheby`s в 1988 году в Москве, и там успешно проданы. Произведения Левиковой вошли в коллекции Третьяковской галереи и Русского музея.

С самого начала своего творческого пути Белла Левикова шла независимо, часто вдали от бурного художественного сообщества, углубляясь в свои собственные поиски и размышления, которые, по её словам, практически никто не разделял. Творчество Левиковой выходит далеко за пределы искусства: она постоянно расширяет своё сознание, развиваясь во множестве сфер одновременно – квантовая физика, астрофизика, биоэнергетика, философия, психология. Вся эта совокупность знаний, помноженная на собственную «прозрачность» и восприимчивость к окружающим потокам жизни, отразилась в 4-м и 5-м измерениях пространств её картин. В её работах смешивается живописная интуиция и осмысленное содержание, она отображает подвижные, меняющиеся информационно-энергетические потоки космоса, планеты и её населения.

Белла Левикова верит, что человеческие возможности огромны, но не раскрыты. В определенный период творчества она почувствовала, что может считывать информацию как бы из пространства, предчувствовать глобальные события, происходящие на планете. Серия «Комиксы» относится к такому «сверхчувственному восприятию». Белла Левикова уловила настроение, витающее сегодня, и появилась серия не совсем характерная её живописной манере, но именно так отразилась грань современности – в ней много весёлого, ироничного, но есть место и печали. В этих картинах открывается большое количество ассоциативных связей, как в комиксах в этих ярких формах можно увидеть и персонажей, и бесконечную разворачивающуюся связь между ними – это достигается за счёт единства внутри серии и композиционного единства внутри каждого пространства холста.

В основе представления о мироздании Беллы Левиковой лежит сакральная геометрия. На выставке представлены несколько работ, непосредственно отражающих её размышления эту тему – «Активация системы Б», «Глобальный объект» и другие. «Человеческое сознание связано в единое, и далее – с Разумом более высокого порядка. Человек – это не только Земля, но и Космос. Мы все связаны с Целым» – говорит Левикова.

Белла Левикова в своих картинах суммирует, соединяет, сплавляет тысячи потоков, проходящих через её сознание, одновременно выискивая форму, формулу, лежащую в основе мироздания, и поэтому часто говорит, что у неё «интегральное видение». Мы же предлагаем развязать для себя клубок смыслов, зашифрованный в каждой её новой картине, осуществить попытку вычисления одного из интегралов этого мира.  

О художнике

Левикова Белла родилась в 1939 году в Московской области в Кратово. В 1964-1970 годах обучалась на отделении теории и истории искусства МГУ. Картины Левиковой участвовали в знаменательных для неофициального искусства событиях: «Бульдозерной» выставке (1974), выставке в павильоне «Пчеловодство» на ВДНХ (1975), в первом аукционе Sotheby’s 1988-го года в Москве. В 2016 году Левикова получила Диплом почётного члена Российской Академии художеств. Произведения в коллекциях Третьяковской галереи (Москва, Россия), Русского музея (Санкт-Петербург, Россия), Нового Музея (Санкт-Петербург, Россия), Zimmerli Art Museum at Rutgers University (Нью-Джерси, США), в частных коллекциях во Франции, США, России и др.

Приближенное вычисление определенного интеграла

Пусть требуется найти определенный интеграл , причем функция считается непрерывной на отрезке . Если от подынтегральной функции первообразная находится легко, то значение рассматриваемого интеграла находится по формуле Ньютона-Лейбница:

   

Но не в каждом случае отыскание первообразной для подынтегральной функции является достаточно простым, а также не для всякой непрерывной функции существует первообразная, выражающаяся через элементарные функции. В подобных случаях применяют приближенные формулы, которые позволяют вычислить определенный интеграл с любой степенью точности.

Наиболее часто используются три формулы приближенного вычисления определенного интеграла – формула прямоугольников, формула трапеций и формулу парабол или формула Симпсона, основанные на геометрическом смысле определенного интеграла: если функция непрерывна и положительна на отрезке , то определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями , , и (рис. 1).

1. Формула прямоугольников

Пусть на отрезке задана непрерывная функция . Вычислим численно определенный интеграл , который равен площади криволинейной трапеции.

Разобьем основание этой трапеции (отрезок ) на равных частей-отрезков длины

   

Величину будем называть шагом разбиения. В результате получим точки

   

Можно записать, что

   

В середине каждого такого элементарного отрезка отметим точку . Приняв ординату этой точки за высоту, построим прямоугольник с площадью (рис. 2).

Тогда сумма площадей всех прямоугольников равна площади ступенчатой фигуры, которая представляет собой приближенное значение искомого определенного интеграла :

   

Полученная формула называется формулой прямоугольников.

Абсолютная погрешность последнего приближенного равенства удовлетворяет следующей оценке:

   

где – наибольшее значение на рассматриваемом отрезке .

2. Формула трапеций

Эту формулу получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Пусть необходимо вычислить определенный интеграл . Разобьем отрезок интегрирования на равных частей длины . В результате получим точки (рис. 3). Пусть – соответствующие им ординаты функции. Тогда можно записать, что

   

Заменим кривую ломаной линией, звенья которой соединяют концы ординат и . Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями , и высотой , то есть

   

   

Записанная формула называется формулой трапеций.

Абсолютная погрешность

   

где .

3. Формула парабол (Симпсона)

Если заменить график функции на каждом отрезке , которые получены после разбиения отрезка интегрирования на равных частей, не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления определенного интеграла .

Как было сказано выше, разобьем отрезок на равных частей (отрезков) длиной точками

   

причем , . В точках разбиения находим значения подынтегральной функции

   

то есть (рис. 4).

Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями одной элементарной параболической трапецией с основанием . Тогда, например, на частичном отрезке парабола проходит через три точки , , и так далее.

Расчетная формула парабол (или Симпсона) для этого метода имеет вид:

   

   

Абсолютная погрешность вычисления по этой формуле оценивается соотношением

   

где .

Иллюстрированный самоучитель по Mathematica 3/4 › Операции математического анализа › Вычисление интегралов. Вычисление интегралов в символьном виде. [страница – 117] | Самоучители по математическим пакетам

Вычисление интегралов. Вычисление интегралов в символьном виде.

Одна из важнейших операций – вычисление первообразных и определенных интегралов в символьном виде. Первообразная – это функция F(x), удовлетворяющая уравнению:

f(x)dx = F(x) + C.

Где С – постоянная интегрирования. А вычисление определенного интеграла с пределами – верхним b и нижним а – производится по формуле:

f(X)dX = F(b)-F(a).

Заметим, что определенный интеграл может быть представлен как аналитическим, так ” численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов – от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).

Для интегрирования в системе Mathematica используются следующие функции:

  • Integrate [f, x] – возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
  • Integrate [f, {x, xmin, xmax}] – возвращает значение определенного интеграла с пределами от x min до x max ;
  • Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},…] – возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).

Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:

Options[Integrate]

  

{Assumptions > {}, GenerateConditions > Automatic, PrincipalValue > False)

Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком “минус”. Пределы могут задаваться как константами, так и функциями.

Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.


Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)

Вычисление интеграла с помощью метода трапеций на компьютере курсовая по информатике

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ КУРСОВАЯ РАБОТА тема: «Вычисление определённого интеграла с помощью метода трапеций на компьютере» Выполнил: студент ф-та ЭОУС-1-12 Зыков И. Принял: Зоткин С. П. Москва 2001 1. Введение: Определенный интеграл от функции, имеющей неэлементарную первообразную, можно вычислить с помощью той или иной приближенной формулы. Для решения этой задачи на компьютере, можно воспользоваться формулами прямоугольников, трапеций или формулой Симпсона. В данной работе рассматривается формула трапеций. Пусть I= F 0F 2 f(x)dx, где f(x) – непрерывная функция, которую мы для наглядности будем предполагать положительной. Тогда I представит собой площадь криволинейной трапеции, ограниченной линиями x=a, x=b, y=0, y=f(x). Выберем какое- нибудь натуральное число n и разложим отрезок [a,b] на n равных отрезков при помощи точек x0=a<x1<…<xn=b. Прямые x=xi разбивают интересующую нас криволинейную трапецию на n полосок. Примем каждую из этих полосок за обыкновенную прямолинейную трапецию (рис. 1, где n=4). рис. 1 Тогда площадь первой слева полоски будет приближенно выражаться числом ((f(x0)+f(x1))/2)*(x1-x0)=((y0+y1)/2)*((b-a)/n), ибо основания трапеции, за которую мы принимаем полоску, равны f(x0)=y0 и f(x1)=y1, а высота её x1-x0=(b-a)/n. Аналогично площади дальнейших полосок выразятся числами (y1+y2)*((b-a)/2*n), (y2+y3)*((b-a)/2*n), … , (yn-1+yn)*((b-a)/2*n). 3)/12. Задача. Пусть нужно проинтегрировать функцию f(x) = x³ +2x²-3x-8 на отрезке [0, 6]. На этом отрезке функция непрерывна. Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью метода трапеций. Программа состоит из трех функций main, f и trap. Функция main позволяет ввести интервалы интегрирования и задать точность вычисления интеграла, а также вызывает функцию trap для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение интегрируемой функции в этой точке. Trap – основная функция программы: она выполняет все вычисления, связанные с нахождением определенного интеграла. Trap принимает четыре параметра: пределы интегрирования типа float (a и b), допустимую относительную ошибку типа float и указатель на интегрируемую функцию. Вычисления выполняются до тех пор, пока относительная ошибка, вычисляемая по формуле | S-Sn |, не будет меньше или равна требуемой. Функция реализована с экономией вычислений, т. е. учитывается, что S0 постоянная и S1=S1+f(a+(2*i+1)*h), поэтому эти значения вычисляются единожды. Метод трапеций обладает высокой скоростью вычисления, но меньшей точностью, чем метод Симпсона, поэтому его применение удобно там, где не требуется очень высокая точность. Ниже предлагается блок-схема, листинг, спецификации, ручной счет и результат работы программы на примере поставленной выше задачи. Блок-схема позволяет отследить и понять особенности алгоритма программы, спецификации дают представление о назначении каждой переменной в основной функции trap, листинг – исходный код работающей программы с комментариями, а ручной счет предоставляет возможность проанализировать результаты выполнения программы. a double Нижний предел интегрирования b double Верхний предел интегрирования h double шаг разбиения отрезка ep s double допустимая относительная ошибка f double(*) указатель на интегрируемую фун – цию x double аргумент ф-ии f s double текущий результат интегрирования s0 double половина суммы значений функции в точках a и b s1 double сумма значений функции в промежуточных точках sn double предыдущий результат интегрирования 5. Ручной счет: Xi Yi 0 -8 0,7 5 -8,703 125 1,5 -4,625 2,2 5 6,765 625 3 28 3,7 5 61,60 9375 4,5 110,1 25 5,2 5 176,0 78125 6 262 6. Результат работы программы: при eps = 0.1 при eps = 0.001 Введите a, b, eps: Введите a, b, eps: 0 0 6 6 .1 .001 Интеграл= 366.024170 Интеграл= 366.000094 т.е с помощью этой программы можно вычислить интеграл от функции с точностью до 1/10000.

Урок по алгебре “Приближенное вычисление интеграла”

Тема урока: Приближенное вычисление определенного интеграла

Цель урока:

1) Познакомить учащихся с методом приближённого вычисления определённого интеграл;.

2) способствовать развитию логического мышления, грамотной математической речи;

3) воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.

Основные знания и умения. Иметь понятие о приближённых методах вычисления определённого интеграла по формулам прямоугольников

Обеспечение урока:тестовые задания, раноуровневые карточки,лекционный материал

Вид урока: Комбинированный

План урока:

– частично-поисковый;

– практический метод.

10 мин

III. Формирование новых знаний и способов действий

– продуктивный метод;

– практический метод.

30 мин

IV. Применение знаний, формирование умений

– практический метод

40 мин

V. Подведение итогов урока

5 мин

VI. Постановка домашнего задания

3 мин

Ход урока:

I.Самоопределение к деятельности (оргмомент)

Мотивация познавательной деятельности учащихся.

Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.

Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально.

II.Актуализация опорных знаний учащихся

  1. Дайте определение первообразной.

  2. Сформулируйте основное свойство первообразных.

  3. В чем заключается геометрический смысл основного свойства первообразной?

  4. Какую фигуру называют криволинейной трапецией?

  5. Запишите формулу для вычисления площади криволинейной трапеции.

  6. Объясните, что такое интеграл?

  7. В чем заключается геометрический смысл интеграла?

  8. Запишите формулу Ньютона- Лейбница.

  9. Какая связь существует между операциями дифференцирования и интегрирования?

Выполнение диагностического теста:

Вычислить интеграл:

1.)

А) 2 Б) 3 С) 0 Д) 1,5 Е) -2

2.)

А) Б) 0 С ) -1 Д)0,5 Е) -2

3.)

А) 4 Б) 6 С) 0 Д) 3 Е) 2

4. )

А) 10 Б) 0 С) 3 Д) 12 Е) -4

5.)

А) 2 Б) 1 С) – 2 Д)4 Е)0

III. Формирование новых знаний и способов действий

Простейшим приближённым методом является метод прямоугольников. Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой площадей прямоугольников, одна сторона которых равна , а другая – .

Если суммировать площади прямоугольников, которые показывают площадь криволинейной трапеции [Рисунок1], то получим формулу:

Значения у0, у1,…, уn находят из равенств , к = 0, 1…, n .Эти формулы называются формулами прямоугольников и дают приближённый результат. С увеличением n результат становится более точным.

Итак, чтобы найти приближённое значение интеграла , нужно:

1)разделить отрезок интегрирования [a, b] на n равных частей точками х0= а, х1, х2,…, х n -1, х n = b 2)вычислить значения подынтегральной функции в точках деления, т. е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ;

3)воспользоваться одной из приближённых формул.

Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:

Пример 1. Вычислить по формуле прямоугольников . Найти абсолютную и относительную погрешности вычислений.

Решение:

Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,

х k = a + k х

х0 = 2 + 0* = 2 х1 = 2 + 1* = 2,5 х2 = 2 + 2* =3

х3 = 2 + 3 * = 3,5 х4 = 2 + 4* = 4 х5 = 2 + 5 * = 4,5

f (x0) = 22 = 4

f (x 1 ) = 2 ,52 = 6,25

f (x 2 ) = 32 = 9

f (x 3 ) = 3,52 = 12,25

f (x 4 ) = 42 = 16

f (x 5 ) = 4,52 = 20,25

х 2 2,5 3 3,5 4 4,5

у 4 6,25 9 12,25 16 20,25

По формуле (1):

Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:

IV. Применение знаний, формирование умений

  1. Вычислить приближенное значение интеграла:

=12

Разобьем отрезок [a, b] на 8 равных частей

х=

Х0=1+0*1/2=1 х4=1+4*1/2=3

Х1=1+1*1/2=1,5 х5=1+5*1/2=3,5

Х2=1+2*1/2=2 х6=1+6*1/2=4

Х3=1+3*1/2=2,5 х7=1+7*1/2=4,5

῁ ½(1+1,5+2+2,5+3+3,5+4+4,5)=11

=12-11=1

2.Работа по индивидуальным карточкам:

1 уровень 2 уровень

1.Вычислить интеграл:

а)dx a)

b) b)

c) c)

  1. d) e)

V. Подведение итогов урока

VI. Постановка домашнего задания:

№ 362(а,б),№ 363(б),№ 364(а)

Калькулятор интегралов

– первообразные, определенные, неопределенные интегралы

Онлайн-калькулятор интегралов поможет вам оценить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-калькулятора интеграции:

  • Определенные интегралы
  • Неопределенные интегралы (первообразные)

Вычисление интеграла довольно сложно решить вручную, так как оно включает в себя различные сложные формулы интегрирования.Итак, рассмотрим онлайн-программу интегралов, которая решает простые и сложные функции интегралов и показывает вам пошаговые вычисления.

Итак, пришло время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:

Читайте дальше!

Что такое интегральный?

В математике интеграл функций описывает площадь, смещение, объем и другие понятия, возникающие при объединении бесконечных данных. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.

Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.

  • Процесс нахождения интегралов, называемый интегрированием
  • Интегрируемая функция называется подынтегральным выражением
    • .
  • В интегральном представлении ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x

Где f (x) – функция, а A – площадь под кривой.Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Ну а теперь поговорим о типах интегралов:

Типы интегралов:

В принципе, есть два типа интегралов:

  • Неопределенные интегралы
  • Определенные интегралы
Неопределенные интегралы:

Неопределенный интеграл функции принимает первообразную другой функции. Взятие первообразной функции – самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.

Определенные интегралы:

Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], называемый пределами, границами или границами.Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш онлайн-калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:

Основные формулы для интеграции:

Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:

  • ∫1 dx = x + c
  • ∫x n ​​ dx = x n ​​+ 1 / n + 1 + c
  • ∫a dx = ax + c
  • ∫ (1 / x) dx = lnx + c
  • ∫ a x dx = a x / lna + c
  • ∫ e x dx = e x + c
  • ∫ sinx dx = -cosx + c
  • ∫ cosx dx = sinx + c
  • ∫ tanx dx = – ln | cos x | + c
  • ∫ cosec 2 x dx = -cot x + c
  • ∫ сек 2 x dx = tan x + c
  • ∫ cotx dx = ln | sinx | + c
  • ∫ (secx) (tanx) dx = secx + c
  • ∫ (cosecx) (cotx) dx = -cosecx + c

Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:

  • ∫ 1 / (1-x 2 ) 1/2 dx = sin -1 x + c
  • ∫ 1 / (1 + x 2 ) 1/2 dx = cos -1 x + c
  • ∫ 1 / (1 + x 2 ) dx = tan -1 x + c
  • ∫ 1 / | x | (x 2 – 1) 1/2 dx = cos -1 x + c

Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача. Просто введите функцию в специальное поле онлайн-калькулятора интегралов, который использует эти стандартизированные формулы для точных вычислений.

Как решить интегралы вручную (шаг за шагом):

Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, по которым нужно вычислять интегралы:

  • Определить функцию f (x)
  • Возьмем первообразную функции
  • Вычислить верхний и нижний предел функции
  • Определите разницу между обоими пределами

Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решает первообразную данной функции.

Смотрит на примеры:

Пример 1:

Решить интегралы от ∫ x 3 + 5x + 6 dx?

Решение:

Шаг 1:

Применяя правило функциональной мощности для интегрирования:

∫x n ​​ dx = x n ​​+ 1 / n + 1 + c

∫ x 3 + 5x + 6 dx = x 3 + 1 /3 + 1 + 5 x 1 + 1 /1 + 1 + 6x + c

Шаг 2:

∫ x 3 + 5x + 6 dx = x 4 /4 + 5 x 2 /2 + 6x + c

Шаг 3:

∫ x 3 + 5x + 6 dx = x 4 + 10x 2 + 24x / 4 + c

Этот калькулятор неопределенного интеграла помогает интегрировать интегральные функции шаг за шагом, используя формулу интегрирования. 1_5 x * lnx dx = –14

Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интеграции по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.

Пример 3 (Интеграл тригонометрической функции):

Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?

Решение:

Шаг 1:

Используйте формулу для тригонометрической функции:

∫ sinx dx = -cosx + c

Шаг 2:

Рассчитайте верхний и нижний предел для функций f (a) и f (b) соответственно:

Поскольку a = 0 и b = π / 2

Итак, f (a) = f (0) = cos (0) = 1

f (b) = f (π / 2) = cos (π / 2) = 0

Шаг 3:

Рассчитайте разницу между верхним и нижним пределами:

f (а) – f (б) = 1 – 0

f (а) – f (б) = 1

Теперь вы можете использовать бесплатный калькулятор частичного интеграла для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.

Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:

Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:

Проведите по!

Вводы:

  • Сначала введите уравнение, которое вы хотите интегрировать
  • Затем выберите зависимую переменную, участвующую в уравнении
  • Выберите определенный или неопределенный интеграл на вкладке
  • Если вы выбрали конкретную опцию, то вы должны ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
  • Когда закончите, пора нажать на кнопку расчета

Выходы:

Интегральный вычислитель показывает:

  • Определенный интеграл
  • Неопределенный интеграл
  • Полные пошаговые вычисления

Часто задаваемые вопросы (FAQ):

Какое целое значение?

В математике интеграл – это числовое значение, равное площади под графиком некоторой функции для некоторого интервала. Это может быть график новой функции, производная которой является исходной функцией (неопределенный интеграл). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный онлайн-калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.

Как вы оцениваете интеграл, используя основную теорему исчисления?

Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя основную теорему. Затем используйте основную теорему исчисления для вычисления интегралов.Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и получите мгновенные результаты.

Что такое двойной интеграл?

Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.

Заключительные слова:

Интегралы широко используются для улучшения архитектуры зданий, а также мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко вычисляет интеграл любой заданной функции шаг за шагом.

Артикул:

Из авторизованного источника Википедии: Общее представление об интегралах и их типах

С сайта mathisfun: График интегрирования и подынтегрального выражения, интегральная запись

Из истоков математики.com: Формулы от базового до продвинутого уровня для интеграции

С сайта toppr.com: повседневное использование интеграции в исчислении

Другие языки: Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 計算, 적분 계산기, Integrály Kalkulačka, Calculadora De Integral, Calculate Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integretralov,. Lommeregner, Integral Kalkulator, Integralni Kalkulator, คำนวณ อิน ทิ ก รั, Integrale Rekenmachine. 3 + c $$

, где «c» – постоянная.3)} {3} $$

  1. Скорость движущегося объекта :

Вы можете определить скорость объекта, найдя определенный интеграл от ускорения объекта по времени, потому что ускорение просто определяется как скорость изменения скорости во времени.

$$ ∆Vel = ∫Acc \; dt $$

Методы вычисления интегралов

Вы можете вычислить интегралы численно, используя такие методы, как:

  1. Квадратура Симпсона
  2. Квадратурная лобатто
  3. Квадратура Гаусса-Кронрода

Для получения дополнительной информации о числовых и символьных вычислениях интегралов см. MATLAB ® и Symbolic Math Toolbox ™.

Интегральный калькулятор

со ступенями – Open Omnia

Войдите в функцию. Используйте x в качестве переменной.
См. Примеры

ПОМОЩЬ

Используйте клавиатуру для ввода функций. Используйте x в качестве переменной. Нажмите «РЕШИТЬ», чтобы обработать введенную вами функцию.

Вот несколько примеров того, что вы можете ввести.

Вот как вы используете кнопки

долл. США
РЕШЕНИЕ Обрабатывает введенную функцию.
ПРОЗРАЧНЫЙ Удаляет весь текст в текстовом поле.
DEL Удаляет последний элемент перед курсором.
а-я Показывает алфавит.
триг Показывает тригонометрические функции.
◀ Переместите курсор влево.{□} {□} N-й корень.
(□) Скобка.
журнал База журнала 10.
пер. Натуральное бревно (база е).
| $ □ $ | Абсолютное значение.

Вычисление интеграла уравнения в Excel с помощью VBA

Если функция, которую вы хотите интегрировать, известна в терминах переменной, вы можете выполнить интеграцию с использованием VBA вместо табличного метода в последнем разделе.

Допустим, у нас есть функция скорости:

Хотя вы можете интегрировать это уравнение, используя таблицу на рабочем листе, VBA позволит вам получить более точную оценку, используя меньший временной шаг (меньшие срезы).

Откройте редактор VBA ( Alt-F11 ) и вставьте новый модуль в рабочий лист, щелкнув правой кнопкой мыши в окне проекта и выбрав Insert > Module .

Этот модуль будет содержать две функции. 2

Конечная функция

Вторая функция вычислит положение путем интегрирования скорости. У этой функции будет три аргумента: начальная позиция ( x0 ), время начала ( t1 ) и время окончания ( t2 ). Для таких сложных функций, как эта, полезно создать основу того, что функция будет делать, используя комментарии. Создайте функцию положения и каркас:

Функция Position (x0, t1, t2)

‘определите диапазон интеграла

‘ дискретизируйте интеграл на n секторов, dt шириной

‘инициализируйте переменные

‘вычислить площади с использованием правила трапеции

‘ суммировать площадь под кривой для каждого среза

Конечная функция

Последние два шага, вычисление площадей и их суммирование, будут выполняться одновременно с использованием цикла FOR.

После завершения скелета вы можете закодировать каждый шаг. На первом этапе, определяя диапазон интеграла, мы создадим переменную int_range, которая представляет собой разницу между временем t2 и временем t1:

‘определим диапазон интеграла

int_range = t2 – t1

В На втором этапе вы разделите этот диапазон на определенное количество фрагментов. Количество слайсов будет определено как n . Значение 1000 должно дать хорошую точность. Временной шаг dt – это ширина одного из этих срезов, поэтому он будет равен целому диапазону, деленному на количество срезов.

‘дискретизируйте интеграл на «n» срезов, шириной «dt»

n = 1000

dt = int_range / n

Перед оценкой площади среза с помощью правила трапеции вам необходимо установить некоторые начальные условия.

Если вы помните, уравнение трапеции вычисляется от a до b. Поскольку в этом примере время по оси x, мы назовем время в начале среза «ta» и установим его равным нашему начальному времени начала (t1). Мы назовем время в конце среза tb и установим его равным ta + dt.

‘инициализировать переменные

ta = t1

tb = ta + dt

Пока t1 является фиксированным моментом времени, ta и tb будут изменяться при переходе функции от одного среза к следующему.

Остается инициализировать еще одну переменную – позицию. Инициализируйте позицию, установив ее в аргумент x0, который передается в функцию:

Position = x0

После завершения инициализации вы можете настроить цикл FOR, который будет проходить через срезы и вычислять площадь каждого из них.Он также суммирует общую площадь всех срезов по мере продвижения.

Цикл FOR будет запускаться один раз для каждого среза, а количество срезов n, поэтому мы установим это значение Для j = 1 – n . Затем позиция будет рассчитана по правилу трапеции с использованием функции vel, которую мы определили выше для расчета высоты в начале и в конце среза:

‘вычислить площади с использованием правила трапеции

‘ суммировать площадь под кривой для каждого slice

Для j = 1 To n

Position = Position + (tb – ta) * (vel (ta) + vel (tb)) / 2

Чтобы перейти к следующему слою, мы изменим значения ta и tb.2

Конечная функция

__________________________________________________________________________

Позиция функции (x0, t1, t2)

‘определяет диапазон интеграла

int_range = t2 – t1

‘ дискретизирует интеграл на «n» срезов, «dt» широкий

n = 1000

dt = int_range / n

‘инициализировать переменные

ta = t1

tb = ta + dt

Position = x0

‘ вычислить площади с использованием правила трапеций

‘суммировать площадь под кривой для каждого среза

Для j = 1 До n

Позиция = Позиция + (tb – ta) * (vel (ta) + vel (tb)) / 2

ta = tb

tb = ta + dt

Next

End Function

Теперь, когда функция Position завершена, вы можете использовать ее в электронной таблице для выполнения расчетов. Во-первых, используйте его для расчета позиции через 20 секунд. Помните, что этой функции нужно передать три аргумента: x0, t1 и t2. Введите имя функции, затем используйте Ctrl-Shift-A для автоматического заполнения имен аргументов. Первый аргумент x0 – это начальная позиция в ячейке C5; t1 – это нижняя граница в ячейке C6, а t2 – это верхняя граница в ячейке C7.

= Позиция (C5, C6, C7)

Функция Position даст результат 1600 футов через 20 секунд.

Конечно, эту функцию также можно использовать для вычисления позиции в разное время. Рабочий лист уже содержит данные о времени и скорости. Для столбца позиции аргументы будут вводиться несколько иначе. Начальное положение и начальное время такие же, как указано выше. Вы можете начать функцию:

= Position (C5, C6,

) Оба этих аргумента должны быть абсолютными ссылками с использованием F4 , потому что они будут одинаковыми для каждой временной точки в таблице. Однако аргумент t2 будет меняться по мере того, как вы спускаетесь по таблице, поэтому вы можете просто щелкнуть внутри ячейки B17 и оставить это как относительную ссылку.

= Позиция ($ C $ 5, $ C $ 6, B17)

Выберите эту ячейку и дважды щелкните маркер заполнения, чтобы заполнить формулу вниз по столбцу. Это даст вам такое же конечное положение в 1600 футов, но также все точки данных положения и скорости между ними. Вы можете построить их вместе. Выберите все три столбца и вставьте точечную диаграмму .Данные скорости представляют собой гораздо меньшие числа, чем позиция, поэтому нанесите их на вторичную ось. Щелкните правой кнопкой мыши данные скорости и выберите Формат данных серии . Выберите Серия графиков на вторичной оси .

Вы можете видеть, что, когда скорость близка к нулю, наклон кривой положения плоский. Положение увеличивается быстрее по мере увеличения скорости и в конечном итоге увеличивается медленнее, когда скорость снова начинает падать. Наконец, когда скорость снова равна нулю, положение перестает увеличиваться.

Почему вычисление интеграла намного сложнее, чем вычисление производной? : askscience

На самом деле нет, интегралы «проще» производных. И они тоже не противоположны друг другу.

Условием того, что функция f (x) имеет производную в точке x = A, является то, что должен существовать предел (f (A + h) -f (A)) / h при h-> 0. Теперь, если этот предел существует, то эта формула дает нам способ фактически вычислить значение, все, что вам нужно сделать, это вставить достаточно маленькое значение для h, и вы гарантированно приблизите значение производной к любому точность, которая вам нужна.Вы также можете использовать его для получения решения в закрытой форме без ограничений, например, производная sin (x) – это cos (x), но это скорее частный случай, а определенно не норма, нет причин ожидать, что у вас будет возможность сделать это для всех функций.

Итак, узким местом для возможности иметь производную является то, что этот предел существует, и это довольно сильное узкое место. Есть даже точки на относительно простых функциях, таких как f (x) = | x | или f (x) = sin (1 / x), где этот предел не выполняется. Но в общей схеме всех функций относительно немногие функции имеют производные.Быть непрерывным, что само по себе является важным условием с множеством хороших гарантий, недостаточно для обеспечения существования производной, есть функции, которые непрерывны везде, но не имеют производных нигде. Функция, имеющая производную, – это очень хорошее свойство для нее, и вам должно повезти, когда это произойдет. И это становится еще более жестким свойством, когда вы переходите к комплексным числам, где оно становится очень редким, особенным и приятным свойством. Итак, если вы знаете, что функция имеет производную, то значения легко вычислить, но на самом деле функции трудно удовлетворить условиям наличия производной.Так что деривативы – это сложно.

Интегралы – это площадь под графиком функции на определенном отрезке времени, заданная пределом сумм Римана. Условием существования интеграла функции является то, что должен существовать связанный предел сумм Римана, и если он существует, то этот предел дает нам очень хороший способ аппроксимировать фактическое значение интеграла с любой степенью точности, которую мы могли бы хотеть. На самом деле, эти пределы и, следовательно, интегралы могут существовать относительно легко.Фактически, все непрерывные функции имеют интегралы, а это гораздо больше функций, чем производных. Например, функция, которая была непрерывной, но не имела производной, имеет интеграл. Но даже функции с разрывами можно интегрировать, если разрывов не слишком много. Даже в этом случае вы можете использовать альтернативные определения интеграла, такие как интеграция Лебега, чтобы включить еще больше функций. Идея интеграции очень проста и гибка, настолько, что ее можно использовать для работы в странных пространствах, где такие вещи, как производные, сразу не имеют особого смысла.В высшей математике вы увидите, что интегралы все время используются для самых разных удивительных вещей, но аналоги для производной гораздо более тонкие и требуют более строгих условий для работы.

В целом, интегралы = легко, производные = сложно.

Итак, почему люди обычно думают, что интегралы сложны, а производные – просты? Это потому, что часто люди путают интегралы с первообразными, и это происходит из-за ужасно ошибочного названия «неопределенный интеграл», который не имеет абсолютно ничего общего с интегралами. Если f (x) – функция, а F (x) – другая функция, так что F ‘(x) = f (x), то F (x) является первообразной f (x). Если C – любое действительное число, то если F (x) – первообразная f (x), то F (x) + C – тоже. Неопределенный интеграл функции – это совокупность всех первообразных функции. Обратите внимание, что не использовалось ничего о площадях или суммах Римана, поэтому неопределенные интегралы не имеют ничего общего с интегралами.

Итак, когда вы находите интеграл в классе исчисления, вы обычно не находите интеграл, вы обнаруживаете первообразную, замаскированную под интеграл.И действительно может быть очень сложно найти первообразную для функции. Это потому, что вам нужно взять функцию и преобразовать ее в форму f (x) = F ‘(x), используя ваши производные правила, и этот процесс не всегда очевиден и не всегда возможен, особенно когда вы только используя элементарные функции, которые представляют собой очень и очень небольшую часть функций. Существует не так много производных правил вида F ‘(x) = f (x), они у вас есть, когда f (x) – многочлен, триггерная функция, экспоненциальная функция, логарифм, может быть, другие, но это практически ничего . Затем вам нужно взять функцию и попытаться записать ее как производную от одной из этих очень немногих функций, используя в основном только цепное правило (то есть u-подстановку), правило продукта (то есть интеграцию по частям) и линейность, но зная точно какой путь выбрать непросто. С другой стороны, если у вас есть некоторая комбинация элементарных функций, объединенных с использованием сложения / умножения / деления / композиции, тогда вы можете использовать правила в прямом направлении, и это действительно легко сделать. Более того, тот факт, что все эти производные правила переделаны и замаскированы под новые правила / методы, включающие интегралы, разделяет концепции, что затрудняет их использование / изучение.

TL; DR Интегралы на самом деле проще производных, и только в Calc 1 и 2 интегралы кажутся сложнее производных, и это потому, что интегралы не являются интегралами, а являются первообразными. А найти первообразные сложно, потому что вы работаете с очень небольшим банком функций, чьи производные вы действительно знаете, и вам нужно использовать производные правила, чтобы работать в обратном направлении к производным, и все производные правила – это правила, которые говорят нам, как возьмем производные от комбинаций функций, и движение в обратном направлении не так очевидно. {2}} \ Gamma \ left (\ frac {2} {3} \ right)} \) и \ (\ left. \ Frac {dw} {dz} \ right | _ {z = 0} = – \ frac {1} {\ sqrt [3] {3} \ Gamma \ left (\ frac {1} {3} \ right)}. \) Известно, что решение этого дифференциального уравнения с этими граничными условиями является функция Эйри

Сначала преобразуйте это ОДУ в стандартную форму, задав \ (\ mathbf {y} = \ left [\ frac {dw} {dz}, w \ right] \) и \ (t = z \). Таким образом, дифференциальное уравнение принимает вид

\ [\ begin {split} \ frac {d \ mathbf {y}} {dt} = \ left [\ begin {array} {c} ty_ {1} \\ y_ {0} \ end {array} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ left [\ begin {array} {c} y_ {0} \\ y_ {1} \ конец {массив} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ mathbf {y}.{t} \ mathbf {A} \ left (\ tau \ right) d \ tau \ right) \ mathbf {y} \ left (0 \ right), \]

Однако в этом случае \ (\ mathbf { A} \ left (t \ right) \) и его интеграл не коммутируют.

Это дифференциальное уравнение можно решить с помощью функции resolve_ivp . Требуется производная, fprime , временной интервал [t_start, t_end] и вектор начальных условий, y0 , в качестве входных аргументов и возвращает объект, чье поле y представляет собой массив с последовательными значениями решения как столбцы.Поэтому начальные условия приведены в первом выходном столбце.

Как видно, resolve_ivp определяет свои временные шаги автоматически, если нет указано иное. Чтобы сравнить решение solution_ivp с решением airy вектор времени, созданный функцией resolve_ivp , передается функции airy .

Решение resolve_ivp со стандартными параметрами показывает большое отклонение к воздушной функции.Чтобы минимизировать это отклонение, относительные и абсолютные допуски могут быть использованы.

Чтобы указать определенные пользователем моменты времени для решения resolve_ivp , resolve_ivp предлагает две возможности, которые также можно использовать дополнительно. Проходя t_eval опция вызова функции resolve_ivp возвращает решения этих временных точек из t_eval на выходе.

Если матрица якобиана функции известна, ее можно передать в функцию resolve_ivp для достижения лучших результатов.Однако имейте в виду, что метод интеграции по умолчанию RK45 не поддерживает матрицы Якоби, поэтому другой метод интегрирования имеет быть выбранным. Одним из методов интегрирования, поддерживающих матрицу Якоби, является метод для пример метода Radau из следующего примера.

Решение системы с ленточной матрицей Якоби

odeint можно сказать, что якобиан – это с полосами . Для большого система дифференциальных уравнений, которые, как известно, являются жесткими, это может значительно улучшить производительность.2 – (f + k) v \\ \ end {split} \ end {split} \]

где \ (D_u \) и \ (D_v \) – коэффициенты диффузии компоненты \ (u \) и \ (v \), соответственно, и \ (f \) и \ (k \) являются константами. (Для получения дополнительной информации о системе см. http://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/)

Предположим, что граничные условия Неймана (т. Е. «Отсутствие потока»):

\ [\ frac {\ partial u} {\ partial x} (0, t) = 0, \ quad \ frac {\ partial v} {\ partial x} (0, t) = 0, \ quad \ frac {\ partial u} {\ partial x} (L, t) = 0, \ quad \ frac {\ partial v} {\ partial x} (L, t) = 0 \]

Чтобы применить метод линий, мы дискретизируем переменную \ (x \), определяя равномерно распределенная сетка \ (N \) точек \ (\ left \ {x_0, x_1, \ ldots, x_ {N-1} \ right \} \), с \ (x_0 = 0 \) и \ (x_ {N-1} = L \).2 – (f + k) v_ {N-1} \ end {split} \ end {split} \]

Наша полная система обыкновенных дифференциальных уравнений \ (2N \) имеет вид (1) для \ (k = 1, 2, \ ldots, N-2 \) вместе с (2) и (3).

Теперь мы можем приступить к реализации этой системы в коде. Мы должны объединить \ (\ {u_k \} \) и \ (\ {v_k \} \) в один вектор длины \ (2N \). Два очевидных варианта: \ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \) а также \ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \). Математически это не имеет значения, но выбор влияет на то, как эффективно odeint может решить систему.Причина в том, как порядок влияет на структуру ненулевых элементов матрицы Якоби.

Когда переменные заказаны как \ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \), образец ненулевых элементов матрицы Якоби

\ [\ begin {split} \ begin {smallmatrix} * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 \\ 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 \\ 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 \\ 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 \\ 0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 & 0 & * \\ * & 0 & 0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 \\ 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 \\ 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 \\ 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 \\ 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 \\ 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * \\ 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 &) & * & * \\ \ end {smallmatrix} \ end {split} \]

Якобианский паттерн с перемежающимися переменными поскольку \ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \) равно

\ [\ begin {split} \ begin {smallmatrix} * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * \\ \ end {smallmatrix} \ end {split} \]

В обоих случаях нетривиальных диагоналей всего пять, но когда переменные чередуются, пропускная способность намного меньше. То есть главная диагональ и сразу две диагонали вверху и два сразу под главной диагональю – ненулевые диагонали. Это важно, т.к. входы mu и ml of odeint – это верхняя и нижняя полосы пропускания Матрица Якоби. Когда переменные чередуются, mu и ml равны 2. Когда переменные сложены с \ (\ {v_k \} \) после \ (\ {u_k \} \), верхний а нижняя полоса пропускания равна \ (N \).

Приняв это решение, мы можем написать функцию, которая реализует систему дифференциальных уравнений.

Сначала мы определяем функции для источника и реакции условия системы:

 def G (u, v, f, k):
    вернуть f * (1 - u) - u * v ** 2

def H (u, v, f, k):
    возврат - (f + k) * v + u * v ** 2

Затем мы определяем функцию, которая вычисляет правую часть системы дифференциальных уравнений:

 def grayscott1d (y, t, f, k, Du, Dv, dx):
    "" "
    Дифференциальные уравнения для одномерных уравнений Грея-Скотта. 

    ОДУ выводятся методом линий."" "
    # Векторы u и v чередуются по y. Мы определяем
    # видов u и v при разрезании y.
    u = y [:: 2]
    v = y [1 :: 2]

    # dydt - возвращаемое значение этой функции.
    dydt = np.empty_like (y)

    # Так же, как u и v - это виды чередующихся векторов
    # в y, dudt и dvdt - это представления чередующегося вывода
    # векторов в dydt.
    dudt = dydt [:: 2]
    dvdt = dydt [1 :: 2]

    # Вычислить du / dt и dv / dt. Конечные и внутренние точки
    # обрабатываются отдельно.dudt [0] = G (u [0], v [0], f, k) + Du * (-2,0 * u [0] + 2,0 * u [1]) / dx ** 2
    dudt [1: -1] = G (u [1: -1], v [1: -1], f, k) + Du * np.diff (u, 2) / dx ** 2
    dudt [-1] = G (u [-1], v [-1], f, k) + Du * (- 2,0 * u [-1] + 2,0 * u [-2]) / dx ** 2
    dvdt [0] = H (u [0], v [0], f, k) + Dv * (-2,0 * v [0] + 2,0 * v [1]) / dx ** 2
    dvdt [1: -1] = H (u [1: -1], v [1: -1], f, k) + Dv * np.diff (v, 2) / dx ** 2
    dvdt [-1] = H (u [-1], v [-1], f, k) + Dv * (-2,0 * v [-1] + 2,0 * v [-2]) / dx ** 2

    вернуть дыдт

Мы не будем реализовывать функцию для вычисления якобиана, но расскажем означает , что матрица Якоби полосатая. Это позволяет основному решатель (LSODA), чтобы избежать вычисления значений, которые, как ему известно, равны нулю. Для большого системы, это значительно улучшает производительность, как показано на после сеанса ipython.

Сначала мы определяем необходимые входы:

 В [30]: rng = np.random.default_rng ()

В [31]: y0 = rng.standard_normal (5000)

В [32]: t = np.linspace (0, 50, 11)

В [33]: f = 0,024

В [34]: k = 0,055

В [35]: Du = 0,01

В [36]: Dv = 0,005

В [37]: dx = 0,025

Время вычисления без использования полосовой структуры матрицы Якоби:

 В [38]:% timeit sola = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx))
1 петля, лучше 3:25.2 с на петлю

Теперь установите ml = 2 и mu = 2 , так что odeint знает, что матрица Якоби полосатая:

 В [39]:% timeit solb = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx), ml = 2, mu = 2)
10 циклов, лучшее из 3: 191 мс на цикл

Это намного быстрее!

Давайте убедимся, что они вычислили один и тот же результат:

 В [41]: np. allclose (sola, solb)
Out [41]: Верно

8.1: Длина дуги – математика LibreTexts

В этом разделе мы используем определенные интегралы, чтобы найти длину дуги кривой.Мы можем думать о длине дуги как о расстоянии, которое вы бы прошли, если бы шли по кривой. Во многих реальных приложениях используется длина дуги. Если ракета запускается по параболическому пути, мы можем захотеть узнать, как далеко улетит ракета. Или, если кривая на карте представляет дорогу, мы можем захотеть узнать, как далеко нам нужно проехать, чтобы добраться до места назначения.

Мы начинаем с вычисления длины дуги кривых, определенных как функции от \ (x \), затем исследуем тот же процесс для кривых, определенных как функции от \ (y \).(Процесс идентичен, с обратными ролями \ (x \) и \ (y \).) Методы, которые мы используем для определения длины дуги, могут быть расширены, чтобы найти площадь поверхности поверхности вращения, и мы закрываем раздел с рассмотрением этой концепции.

Длина дуги кривой y = f (x)

В предыдущих приложениях интегрирования мы требовали, чтобы функция \ (f (x) \) была интегрируемой или не более непрерывной. Однако для расчета длины дуги у нас есть более жесткие требования к \ (f (x) \).Здесь мы требуем, чтобы \ (f (x) \) была дифференцируемой, и, кроме того, мы требуем, чтобы ее производная \ (f ′ (x), \) была непрерывной. Такие функции, которые имеют непрерывные производные, называются гладкими . (Это свойство снова появится в следующих главах.)

Пусть \ (f (x) \) – гладкая функция, определенная над \ ([a, b] \). Мы хотим вычислить длину кривой от точки \ ((a, f (a)) \) до точки \ ((b, f (b)) \). Начнем с использования отрезков линии, чтобы приблизительно определить длину кривой.Для \ (i = 0,1,2,…, n \) пусть \ (P = {x_i} \) – регулярное разбиение \ ([a, b] \). Затем для \ (i = 1,2,…, n \) постройте отрезок прямой от точки \ ((x_ {i − 1}, f (x_ {i − 1})) \) до точки \ ((x_i, f (x_i)) \). Хотя может показаться логичным использовать либо горизонтальные, либо вертикальные линейные сегменты, мы хотим, чтобы наши линейные сегменты максимально приближались к кривой. Рисунок \ (\ PageIndex {1} \) изображает эту конструкцию для \ (n = 5 \).

Рисунок \ (\ PageIndex {1} \): мы можем приблизительно определить длину кривой, добавив отрезки линии.

Чтобы помочь нам найти длину каждого сегмента линии, мы смотрим на изменение расстояния по вертикали, а также на изменение расстояния по горизонтали на каждом интервале. Поскольку мы использовали регулярное разбиение, изменение горизонтального расстояния на каждом интервале определяется выражением \ (Δx \). Однако изменение вертикального расстояния варьируется от интервала к интервалу, поэтому мы используем \ (Δy_i = f (x_i) −f (x_ {i − 1}) \), чтобы представить изменение вертикального расстояния в интервале \ ([x_ {i − 1}, x_i] \), как показано на рисунке \ (\ PageIndex {2} \).{3/2} \). Вычислите длину дуги графика \ (f (x) \) на интервале \ ([0,1] \). Ответ округлите до трех знаков после запятой.

Подсказка

Используйте процесс из предыдущего примера. Не забывайте менять границы интеграции.

Ответ

\ [\ dfrac {1} {6} (5 \ sqrt {5} −1) ≈1.697 \ nonumber \]

Хотя хорошо иметь формулу для вычисления длины дуги, эта конкретная теорема может генерировать выражения, которые трудно интегрировать.2} \, dx ≈ 8,26815. \ nonumber \]

Упражнение \ (\ PageIndex {2} \)

Пусть \ (f (x) = \ sin x \). Вычислите длину дуги графика \ (f (x) \) на интервале \ ([0, π] \). Используйте компьютер или калькулятор, чтобы приблизительно определить значение интеграла.

Подсказка

Используйте процесс из предыдущего примера.

Ответ

\ [\ text {Длина дуги} ≈ 3.8202 \]

Длина дуги кривой \ (x = g (y) \)

Мы только что видели, как аппроксимировать длину кривой с помощью отрезков прямых.4} dy≈21,0277. \ Nonumber \]

Упражнение \ (\ PageIndex {3} \)

Пусть \ (g (y) = 1 / y \). Вычислите длину дуги графика \ (g (y) \) на интервале \ ([1,4] \). Используйте компьютер или калькулятор, чтобы приблизительно определить значение интеграла.

Подсказка

Используйте процесс из предыдущего примера.

Ответ

\ [\ text {Длина дуги} = 3.15018 \ nonumber \]

Площадь поверхности вращения

Концепции, которые мы использовали для определения длины дуги кривой, могут быть расширены, чтобы найти площадь поверхности вращения. Площадь поверхности – это общая площадь внешнего слоя объекта. Для таких объектов, как кубы или кирпичи, площадь поверхности объекта представляет собой сумму площадей всех его граней. Для криволинейных поверхностей ситуация немного сложнее. Пусть \ (f (x) \) – неотрицательная гладкая функция на интервале \ ([a, b] \). Мы хотим найти площадь поверхности вращения, созданную вращением графика \ (y = f (x) \) вокруг оси \ (x \), как показано на следующем рисунке.

Рисунок \ (\ PageIndex {4} \): (a) Кривая, представляющая функцию \ (f (x) \).(b) Поверхность вращения, образованная вращением графика \ (f (x) \) вокруг \ (оси x \).

Как мы уже делали много раз раньше, мы собираемся разделить интервал \ ([a, b] \) и аппроксимировать площадь поверхности, вычислив площадь поверхности более простых форм. Начнем с использования отрезков линий для аппроксимации кривой, как мы это делали ранее в этом разделе. Для \ (i = 0,1,2,…, n \) пусть \ (P = {x_i} \) – регулярное разбиение \ ([a, b] \). Затем для \ (i = 1,2,…, n, \) построить отрезок прямой от точки \ ((x_ {i − 1}, f (x_ {i − 1})) \) до точки \ ((x_i, f (x_i)) \).Теперь поверните эти линейные сегменты вокруг оси \ (x \), чтобы создать приближение поверхности вращения, как показано на следующем рисунке.

Рисунок \ (\ PageIndex {5} \): (a) Аппроксимация \ (f (x) \) отрезками прямой. (b) Поверхность вращения, образованная вращением отрезков прямой вокруг \ (оси x \).

Обратите внимание, что когда каждый линейный сегмент вращается вокруг оси, образуется полоса. Эти полосы на самом деле представляют собой кусочки рожков (представьте себе рожок мороженого с отрезанным заостренным концом).Такой кусок конуса называется усеченным конусом и конуса.

Чтобы найти площадь поверхности полосы, нам нужно найти площадь боковой поверхности \ (S \) усеченного конуса (площадь только наклонной внешней поверхности усеченного конуса, не включая площади верхней или нижней лица). Пусть \ (r_1 \) и \ (r_2 \) – радиусы широкого конца и узкого конца усеченного конуса, соответственно, и пусть \ (l \) – наклонная высота усеченного конуса, как показано на следующем рисунке.

Рисунок \ (\ PageIndex {6} \): усеченная часть конуса может приблизительно соответствовать небольшой части площади поверхности.

Мы знаем, что площадь боковой поверхности конуса равна

.

\ [\ text {Площадь боковой поверхности} = πrs, \]

, где \ (r \) – радиус основания конуса, а \ (s \) – наклонная высота (рисунок \ (\ PageIndex {7} \)).

Рисунок \ (\ PageIndex {7} \): Площадь боковой поверхности конуса равна \ (πrs \).

Так как усеченную вершину можно рассматривать как часть конуса, площадь боковой поверхности усеченного конуса определяется площадью боковой поверхности всего конуса за вычетом площади боковой поверхности меньшего конуса (заостренный кончик), который был разрезан. выкл. (Рисунок \ (\ PageIndex {8} \)).

Рисунок \ (\ PageIndex {8} \): Расчет площади боковой поверхности усеченного конуса.

Поперечные сечения малого и большого конуса похожи на треугольники, поэтому мы видим, что

\ [\ dfrac {r_2} {r_1} = \ dfrac {s − l} {s} \]

Решая относительно \ (s \), получаем = s − ls

\ [\ begin {align *} \ dfrac {r_2} {r_1} & = \ dfrac {s − l} {s} \\ r_2s & = r_1 (s − l) \\ r_2s & = r_1s − r_1l \\ r_1l & = r_1s − r_2s \\ r_1l & = (r_1 − r_2) s \\ \ dfrac {r_1l} {r_1 − r_2} = s \ end {align *} \]

Тогда площадь боковой поверхности (SA) усеченного конуса равна

. 2}) dx \]

Аналогично, пусть \ (g (y) \) – неотрицательная гладкая функция на интервале \ ([c, d] \).2} dy \]

Пример \ (\ PageIndex {4} \): Расчет площади поверхности вращения 1.

Пусть \ (f (x) = \ sqrt {x} \) на интервале \ ([1,4] \). Найдите площадь поверхности, образованную вращением графика \ (f (x) \) вокруг оси \ (x \) -. Ответ округлите до трех знаков после запятой.

Решение

График \ (f (x) \) и поверхность вращения показаны на рисунке \ (\ PageIndex {10} \).

Рисунок \ (\ PageIndex {10} \): (a) График \ (f (x) \).{17/4} _ {5/4} \\ [4pt] & = \ dfrac {π} {6} [17 \ sqrt {17} −5 \ sqrt {5}] ≈30.846 \ end {align *} \ ]

Упражнение \ (\ PageIndex {4} \)

Пусть \ (f (x) = \ sqrt {1 − x} \) на интервале \ ([0,1 / 2] \). Найдите площадь поверхности, образованную вращением графика \ (f (x) \) вокруг оси \ (x \) -. Ответ округлите до трех знаков после запятой.

Подсказка

Используйте процесс из предыдущего примера.

Ответ

\ [\ dfrac {π} {6} (5 \ sqrt {5} −3 \ sqrt {3}) ≈3.133 \]

Пример \ (\ PageIndex {5} \): Расчет площади поверхности вращения 2

Пусть \ (f (x) = y = \ dfrac [3] {3x} \). Рассмотрим участок кривой, на котором \ (0≤y≤2 \). Найдите площадь поверхности, образованную вращением графика \ (f (x) \) вокруг оси \ (y \) -.

Решение

Обратите внимание, что мы вращаем кривую вокруг оси \ (y \), а интервал выражается в терминах \ (y \), поэтому мы хотим переписать функцию как функцию от \ (y \).2} \) на интервале \ (y∈ [0,2] \). Найдите площадь поверхности, образованную вращением графика \ (g (y) \) вокруг оси \ (y \) -.

Подсказка

Используйте процесс из предыдущего примера.

Ответ

\ (12π \)

.

Оставить комментарий