1 dx интеграл
1 dx интегралВы искали 1 dx интеграл? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 x 2 интеграл, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «1 dx интеграл».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 dx интеграл,1 x 2 интеграл,1 x 3 интеграл,1 х интеграл,2 x интеграл,4 x 2 первообразная,dx x,dx x 2 интеграл,dx x интеграл,dx интеграл,x 1 интеграл,x 2 интеграл,x dx,x dx интеграл,x exp x интеграл,xdx,xdx интеграл,вычисление интеграла онлайн,вычисление интеграла онлайн с подробным решением,вычисление интегралов калькулятор онлайн,вычисление интегралов онлайн,вычисление неопределенных интегралов онлайн,вычисление неопределенных интегралов онлайн с подробным решением,вычисление первообразной онлайн,вычислите интеграл,вычислите интеграл онлайн,вычислите интегралы,вычислите интегралы онлайн,вычислить интеграл x 2 x,вычислить интеграл калькулятор онлайн,вычислить интеграл онлайн,вычислить интеграл онлайн бесплатно с подробным решением,вычислить интеграл онлайн калькулятор,вычислить интегралы,вычислить интегралы онлайн,вычислить интегралы онлайн с решением,вычислить неопределенные интегралы,вычислить неопределенный интеграл,вычислить неопределенный интеграл онлайн,вычислить первообразную онлайн,интеграл 1 dx,интеграл 1 x,интеграл 1 x 1 3,интеграл 1 x 2,интеграл 1 x 2 dx,интеграл 1 x 3,интеграл 1 x dx,интеграл 1 х 2,интеграл 2 x,интеграл 2 x 3 dx,интеграл 2 x 3 x dx,интеграл 2 x 5 x,интеграл 2 x dx,интеграл 2x,интеграл 3 x dx,интеграл dx,интеграл dx 1,интеграл dx 1 x,интеграл dx 1 x 2,интеграл dx x,интеграл dx x 1,интеграл dx x 1 2,интеграл dx x 2,интеграл dx x 2 1,интеграл dx x 2 x 1,интеграл dx x 5,интеграл dx по dx,интеграл x,интеграл x 1,интеграл x 1 2,интеграл x 1 dx,интеграл x 1 x 2,интеграл x 2,интеграл x 2 1,интеграл x 2 1 dx,интеграл x 2 3 x,интеграл x 2 dx,интеграл x 2 x dx,интеграл x 3 1,интеграл x 3 dx,интеграл x 3 x 2,интеграл x 3 x dx,интеграл x 5 dx,интеграл x dx,интеграл x exp x,интеграл x в степени x,интеграл x корень x dx,интеграл x корень из x dx,интеграл x по x,интеграл xdx,интеграл xdx равен,интеграл y dy,интеграл икс от икс,интеграл калькулятор,интеграл калькулятор онлайн,интеграл неопределенный онлайн с решением,интеграл онлайн,интеграл онлайн калькулятор,интеграл онлайн калькулятор с подробным решением,интеграл онлайн калькулятор с подробным решением неопределенный,интеграл онлайн решение,интеграл онлайн с подробным,интеграл онлайн с решением,интеграл от,интеграл от 0,интеграл от 1,интеграл от 1 x,интеграл от 1 x 2,интеграл от 1 до 1,интеграл от 1 до 2 x 2 dx,интеграл от 2 x,интеграл от 2 x dx,интеграл от dx,интеграл от dx x,интеграл от dx x 2,интеграл от x,интеграл от x 1,интеграл от x 1 2,интеграл от x 2,интеграл от x 2 1,интеграл от x 2 dx,интеграл от x 2 x dx,интеграл от x 3 x,интеграл от x dx,интеграл от х,интеграл от х 1,интеграл от х dx,интеграл от х в х,интеграл посчитать,интеграл рассчитать,интеграл решение онлайн,интеграл формула,интеграл х,интеграл х 1,интеграл х 1 2,интеграл х по dx,интеграла онлайн,интегралов онлайн,интегралы калькулятор,интегралы калькулятор онлайн с решением,интегралы неопределенные онлайн,интегралы неопределенные онлайн с подробным решением,интегралы онлайн,интегралы онлайн калькулятор,интегралы онлайн калькулятор с подробным решением,интегралы онлайн калькулятор с решением,интегралы онлайн решение,интегралы онлайн решить,интегралы решать онлайн,интегралы решение онлайн,интегралы решить,интегралы решить онлайн,интегралы с решением онлайн,интегралы формула,интегрирование калькулятор онлайн,интегрирование онлайн,интегрирование онлайн калькулятор,интегрирование онлайн с решением,интегрирование тригонометрических функций онлайн калькулятор,інтеграли онлайн калькулятор,как найти первообразную функции онлайн,калькулятор для интегралов,калькулятор интегралов и производных,калькулятор интегралов неопределенных,калькулятор интегралов неопределенных онлайн,калькулятор интегралов онлайн с подробным решением,калькулятор интегралов с решением,калькулятор интегралов с решением онлайн,калькулятор інтегралів,калькулятор неопределенного интеграла,калькулятор неопределенный интеграл,калькулятор неопределенных интегралов,калькулятор неопределенных интегралов онлайн,калькулятор неопределенных интегралов онлайн с подробным решением,калькулятор неопределенных интегралов онлайн с решением,калькулятор неопределенных интегралов с подробным решением онлайн,калькулятор неопределенных интегралов с решением онлайн,калькулятор онлайн вычислить интеграл,калькулятор онлайн интеграла,калькулятор онлайн интегралы,калькулятор онлайн неопределенный интеграл,калькулятор онлайн неопределенный интеграл с подробным решением,калькулятор онлайн неопределенных интегралов,калькулятор онлайн первообразной,калькулятор онлайн первообразных,калькулятор первообразная,калькулятор первообразной,калькулятор первообразных,калькулятор первообразных онлайн,калькулятор производных и интегралов,калькулятор решение интегралов,найдите интегралы,найдите неопределенный интеграл,найдите неопределенный интеграл онлайн,найдите первообразную для функции f x онлайн,найти интеграл,найти интеграл онлайн,найти интеграл онлайн калькулятор с подробным решением,найти интеграл онлайн с подробным решением,найти интегралы,найти интегралы онлайн,найти неопределенный интеграл,найти неопределенный интеграл калькулятор онлайн,найти неопределенный интеграл онлайн,найти неопределенный интеграл онлайн калькулятор,найти общий вид первообразной для функции f x онлайн калькулятор,найти общий вид первообразной для функции онлайн,найти онлайн первообразную с подробным решением,найти первообразную онлайн с подробным решением,найти первообразную функции онлайн,найти первообразную функции онлайн калькулятор,найти первообразную функции онлайн с решением,нахождение интеграла онлайн,нахождение интеграла онлайн с подробным решением,нахождение интегралов онлайн,нахождение неопределенного интеграла онлайн,нахождение первообразной онлайн калькулятор,неопределенные интегралы онлайн,неопределенные интегралы онлайн с подробным решением,неопределенный интеграл калькулятор,неопределенный интеграл калькулятор онлайн,неопределенный интеграл онлайн,неопределенный интеграл онлайн калькулятор,неопределенный интеграл онлайн с подробным решением,неопределенный интеграл онлайн с решением,неопределенный интеграл решение,неопределенный интеграл решить,неопределенный интеграл решить онлайн,неопределенный интеграл с решением онлайн,онлайн взятие интеграла,онлайн вычисление интеграла,онлайн вычисление интегралов,онлайн вычисление интегралов калькулятор,онлайн вычисление первообразной,онлайн интеграл решение,онлайн интегралы с решением,онлайн интегрирование,онлайн интегрирование с решением,онлайн калькулятор интегралов,онлайн калькулятор интегралов неопределенных,онлайн калькулятор интегралов неопределенных с решением,онлайн калькулятор интегралов с подробным решением,онлайн калькулятор интегралов с подробным решением неопределенных,онлайн калькулятор интегралов с решением,онлайн калькулятор найти первообразную,онлайн калькулятор нахождение первообразной,онлайн калькулятор неопределенных интегралов,онлайн калькулятор неопределенных интегралов с подробным решением,онлайн калькулятор неопределенных интегралов с решением,онлайн калькулятор первообразной,онлайн калькулятор первообразных,онлайн калькулятор первообразных с решением,онлайн калькулятор решение интегралов,онлайн найдите неопределенный интеграл,онлайн нахождение интеграла,онлайн нахождение интегралов,онлайн нахождение неопределенного интеграла,онлайн неопределенный интеграл с решением,онлайн расчет интегралов,онлайн решение интеграл,онлайн решение интеграла,онлайн решение интегралов,онлайн решение интегралов с решением,онлайн решение интегральных уравнений,онлайн решение неопределенного интеграла,онлайн решение неопределенных интегралов,онлайн решение первообразных,первообразная онлайн,первообразная онлайн с решением,первообразная функции онлайн,первообразная функции онлайн калькулятор,первообразные онлайн,посчитать интеграл онлайн,рассчитать интеграл,рассчитать интеграл онлайн,расчет интеграла онлайн,решать интегралы онлайн,решать онлайн интегралы,решение интеграл онлайн,решение интеграла онлайн,решение интегралов калькулятор,решение интегралов онлайн,решение интегралов онлайн калькулятор,решение интегралов онлайн с подробным,решение интегралов с решением онлайн,решение интегралы онлайн,решение интегральных уравнений онлайн,решение неопределенного интеграла онлайн,решение неопределенных интегралов онлайн,решение онлайн интеграл,решение онлайн интегралов с решением,решение первообразных онлайн,решить интеграл,решить интеграл неопределенный,решить интеграл онлайн,решить интеграл с решением онлайн,решить интегралы,решить интегралы онлайн,решить неопределенный интеграл,решить онлайн интегралы,решить онлайн неопределенный интеграл,с решением неопределенный интеграл онлайн,считать интегралы онлайн.
Решить задачу 1 dx интеграл вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Интеграл
Решение интегралов
Наш калькулятор интегралов онлайн с подробным решением поможет
вычислить интегралы и
первообразные функции онлайн
— бесплатно! Пользоваться калькулятором просто.
Чтобы ввести определенный интеграл или неопределенный интеграл, нажмите «+условие» и введите интеграл
Например:
Нажав кнопку Решить вы получите подробное решение интеграла онлайн.
Калькулятором интегралов поддерживается вычисление определенных и неопределенных интегралов (первообразных функций), включая интегрирование функций с несколькими переменными.
Как решить интеграл онлайн с решением?
Введите неопределенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего нажмите на кнопку d и введите переменную, по которой нужно провести интегрирование. Оставьте незаполненными серые квадратики.
Введите определенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего
нажмите на кнопку d. Это можно сделать как на своей клавиатуре, так и на клавиатуре сайта.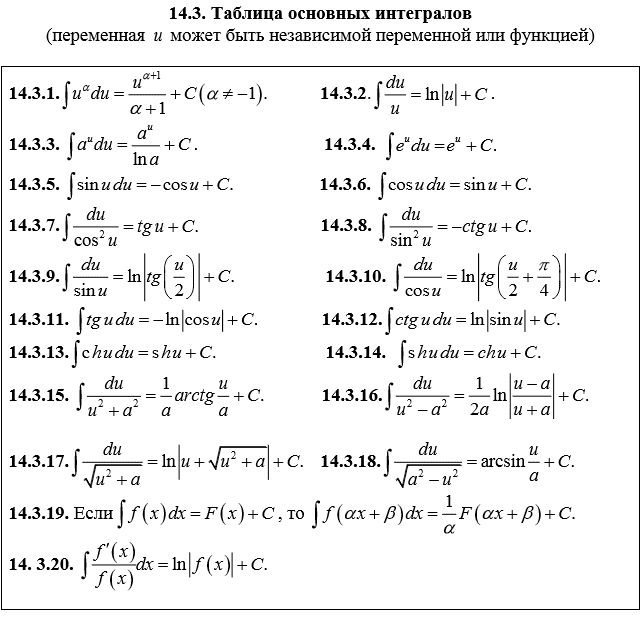
Введите
переменную, по которой нужно провести интегрирование. Далее кликните на нижний серый квадратик и введите
нижний предел, кликните на верхний серый квадратик и введите верхний предел.
На серые квадратики можно перейти либо кликнув на них, либо используя кнопки влево, вправо.
В определённых интегральных уравнениях применяется такое понятие как “предел”. Предел обозначает отрезок функции, в которой происходит вычисление интеграла и результатом такого действия будет число. Физический смысл такого числа – это размер площади под графиком соответствующей функции интеграла, эта операция часто применяется в науке, в частности в физике.
Операция интегрирования является своего рода обратной операции вычисления производной. Если мы будем вычислять неопределённый интеграл, то в результате получим функцию с приплюсованной константой с .
Таблица интегралов
Чтобы найти интеграл, нужно знать таблицу ниже:
Мы живем в удивительное время.
Сегодня вы можете получить онлайн решение интегралов с подробным
решением.
Подробное решение интегралов онлайн стало доступным благодаря современным разработкам в области искусственного интеллекта.
Где можно решить онлайн интеграл? Интеграл калькулятор онлайн Pocket Teacher!
Онлайн интегралы – это просто!
Решить онлайн интегралы вы можете на нашем сайте. Бесплатный
онлайн
решатель
позволит решить интегралы любой сложности за считанные секунды. Вы получите решение интеграла онлайн с подробными шагами. Все, что вам
необходимо сделать – это
просто ввести свои данные в решателе. Так же вы можете посмотреть
видео
инструкцию
и узнать, как получить решение интегралов онлайн с решением на нашем сайте. А если у вас остались
вопросы, то вы можете задать их в
нашей
групе Вконтакте http://vk.
com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Так же читайте нашу статью “Решить систему уравнений методом сложения онлайн решателем”
Калькулятор неопределенных интегралов+ онлайн-решатель с бесплатными шагами
Калькулятор неопределенных интегралов — это онлайн-калькулятор, который используется для вычисления неопределенных интегралов различных функций f(x) по отношению к различным переменным. Калькулятор неопределенных интегралов обеспечивает быстрое и точное решение.
Калькулятор неопределенных интегралов — самый эффективный онлайн-калькулятор, потому что он мгновенно выдает результаты, не занимая много времени на обработку. Он также предоставляет подробное решение, чтобы пользователь мог сразу понять концепцию.
Калькулятор неопределенных интегралов также очень прост в использовании, поскольку он позволяет пользователю удобно перемещаться по интерфейсу.
Он также обслуживает одну из самых фундаментальных концепций исчисления.
Что такое калькулятор неопределенных интегралов?
Калькулятор неопределенных интегралов — это бесплатный онлайн-калькулятор, который используется для решения неопределенных интегралов относительно определенной переменной. Этот калькулятор может иметь дело со всеми видами функций и обеспечивает быстрые результаты.
Калькулятор неопределенных интегралов используется только для вычисления неопределенных интегралов. Неопределенные интегралы являются ключевым понятием в исчислении, поскольку это интегралы, которые не ограничены какими-либо указанными пределами.
Решение этих неопределенных интегралов всегда дает функцию f(x) вместе с константой c. Общая формула, которую использует калькулятор неопределенных интегралов , приведена ниже:
\[ \int f(x) dx = F(x) + c \]
Где $c$ — константа, полученная после вычисления неопределенного интеграла.
Вручную неопределенные интегралы решаются с помощью различных методов, таких как метод подстановки, интегрирование по частям и т.
д., но калькулятор неопределенных интегралов упрощает эту работу, представляя решение за несколько секунд.
Лучшая особенность Калькулятора неопределенных интегралов заключается в том, что он позволяет пользователям вводить любые функции, будь то сложный полином или тригонометрическая функция.
Как пользоваться калькулятором неопределенных интегралов?
Вы можете использовать калькулятор неопределенных интегралов , непосредственно введя функцию, которую нужно интегрировать. Он довольно прост в использовании благодаря простому интерфейсу, который также довольно удобен для пользователя. Интерфейс Калькулятора неопределенных интегралов состоит из 2 простых полей ввода, которые предлагают пользователю ввести входные значения.
Первое поле ввода Калькулятора неопределенных интегралов помечено цифрой 9.0003 «Интегрировать» , который предлагает пользователю ввести функцию, которую он хочет интегрировать. Другими словами, функция f(x) входит в это первое поле ввода.
Второе поле ввода Калькулятора неопределенных интегралов имеет заголовок «относительно» , что позволяет пользователю вводить переменную. Эта переменная является переменной, с которой интегрируется функция.
После двух полей ввода последняя заметная метка Indefinite Integral Calculator — это кнопка с надписью Calculate . После того, как пользователь добавил входные данные, все, что ему нужно сделать, это нажать на эту кнопку, чтобы получить желаемое решение.
Для подробного понимания работы Калькулятора неопределенных интегралов ознакомьтесь с пошаговым руководством, приведенным ниже:
Шаг 1
интегралов, первым шагом является анализ данной функции и переменной. Нет ограничений на тип функции или переменной. Вы можете выбрать любую функцию f(x) для вычисления неопределенного интеграла.
Шаг 2
После того, как вы проанализировали свою функцию f(x), следующим шагом будет ввод входных данных.
Во-первых, перейдите к первому полю ввода с заголовком «Интеграция» и введите свою функцию f(x) в это поле ввода.
Шаг 3
После заполнения первого поля ввода перейдите ко второму полю ввода. Этот ввод имеет заголовок «Относительно» , и введите свою переменную в это поле ввода. Именно по этой переменной интегрируется функция f(x).
Шаг 4
Теперь, когда оба поля ввода заполнены, последний шаг — нажать кнопку с надписью Calculate. При этом Калькулятор неопределенных интегралов начнет обработку и представит решение через несколько секунд.
Вывод калькулятора неопределенных интегралов
После того, как калькулятор закончил свою обработку, он представляет результат. Результат, представленный Калькулятором неопределенных интегралов состоит из решения неопределенного интеграла вместе с входной интерпретацией неопределенного интеграла с функцией f(x) и переменной.
Как работает калькулятор неопределенных интегралов?
Калькулятор неопределенных интегралов работает путем вычисления неопределенных интегралов для функций f(x).
Работа этого калькулятора основана на одной из самых важных концепций исчисления, которая решает неопределенные интегралы.
Чтобы получить четкое представление о работе Калькулятора неопределенных интегралов, давайте кратко повторим предыдущие темы, чтобы укрепить наше понимание работы.
Что такое неопределенные интегралы?
Неопределенные интегралы — это интегралы, вычисляемые без указания пределов. Другими словами, эти интегралы не ограничены ни верхними, ни нижними пределами.
Так как интегрирование является процессом, обратным дифференцированию, то интегрируемая функция является производной, и ее интегрирование даст исходную функцию f(x).
Решение неопределенных интегралов, помимо получения исходной функции f(x), также дает постоянное значение, называемое c. Этот постоянный член с служит основным дифференцирующим фактором между определенными и неопределенными интегралами.
Это потому, что определенные интегралы всегда дают определенный ответ, поскольку эти интегралы ограничены пределами.
Тогда как неопределенные интегралы не заключены в пределы, поэтому они дают неопределенный ответ, который представляется как константа интегрирования c.
Примеры решенных задач
Для лучшего понимания работы Калькулятора неопределенных интегралов ниже приведены несколько примеров.
Пример 1
Для следующей функции вычислите неопределенный интеграл: 9{\frac{2}{3}} \]
При анализе функция f(x) оказывается простой полиномиальной функцией. Так как функция выражается через переменную x, значит, мы будем интегрировать эту функцию f(x) по x.
Следующим шагом является заполнение полей ввода. У нас уже есть функция f(x), поэтому просто вставьте эту функцию f(x) в первое поле ввода. Затем введите переменную во второе поле ввода. Переменная также указана, и это x.
После ввода двух входных значений просто перейдите к кнопке с надписью «Рассчитать» и нажмите на нее. Калькулятор неопределенных интегралов начнет обработку решения. 9{x} \]
Поскольку нет ограничений на тип функции, используемой в качестве входных данных для калькулятора неопределенных интегралов, следовательно, эта функция f(x) идеально подходит.
Эта функция f(x) будет нашим первым входом и войдет в первое поле ввода с заголовком «Интегрировать».
Следующим шагом является заполнение второго поля ввода, которое необходимо заполнить переменной. При анализе функции становится очевидным, что единственная правдоподобная переменная, которую можно использовать для интеграции этой функции, — это x, поэтому вставьте x во второе поле ввода с меткой «В отношении». 9{х}$.
Пример 3
Вычислите неопределенный интеграл для следующей тригонометрической функции:
f(x) = sin(2x)
Решение
Сначала давайте проанализируем нашу функцию f(x). Очевидно, что функция f(x) является тригонометрической функцией. Функция приведена ниже:
f(x) = sin(2x)
Далее, для переменной для интегрирования. При анализе функции f(x), поскольку функция выражается через x, пусть переменная интегрирования будет x.
Теперь, когда у нас есть и функция, и переменная, введите их в первый и второй ввод соответственно.
“> а б
удалить
Этот калькулятор для решения неопределенных интегралов взят от ООО «Вольфрам Альфа». Все права принадлежат владельцу!
Неопределенный интеграл
Нахождение неопределенного интеграла — очень распространенная задача в математике и других технических науках.
На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Поэтому со школьного возраста нас обучают приемам и методам решения интегралов , приводятся многочисленные таблицы интегралов простых функций. Но со временем все благополучно забывается или у нас нет времени на расчеты или нужно найти неопределенный интеграл от очень сложной функции. Наш сервис идеально подойдет для решения этих проблем. Он позволяет точно находить неопределенные интегралы онлайн.
Решить неопределенный интеграл
Онлайн-сервис OnSolver.com позволяет быстро и бесплатно решить интеграл онлайн. Вы можете заменить наш сервис на поиск нужного интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличном виде, просто набрав нужную функцию. Не все математические сайты могут быстро и качественно вычислить неопределенные интегралы от функций онлайн, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не входят в общий курс высшей математики.