“Вычисление определенного интеграла”
Лекция №15
Тема: Вычисление определенного интеграла.
План.
Определение определенного интеграла.
Геометрический смысл определенного интеграла
Примеры определенного интеграла.
Определенный интеграл – Это число, значение которого вычисляется по формуле Ньютона – Лейбница:
– это значение первообразной функции в точке , и, соответственно, – это значение первообразной функции в точке .
Геометрический смысл определенного интеграла:
Определенный интеграл – это число, равное площади криволинейной трапеции – фигуры, ограниченной сверху графиком положительной на отрезке функции , слева прямой , справа прямой , и снизу осью ОХ.
Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как .
Пример 1. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 2. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 3. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 4 Вычислить интеграл
Решение.
На основании формулы произведения синусов, таблицы основных интегралов и формулы (1) имеем:
Пример 5. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем замену ex + 4 = t2, тогда ex= t2– 4, ex dx = 2t dt,
Если x= ln5, то t = 3; если x= ln12, то t = 4.
Тогда
Пример 6. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Пример 7. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем подстановку t = cosx
Если x = 0, то t = cos 0 = 1, если
Следовательно
Пример 8. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Найдем пределы по t:
Находим
Следовательно,
Пример 9. Вычислить интеграл
Решение.
Хороший метод решения интегралов, это метод занесения под дифференциал, его плюс состоит в том, что не требуется менять пределы интегрирования
Пример 10.
Вычислить интеграл
Решение. На основании таблицы основных интегралов и формулы (3) имеем (интегрируем по частям)
Самостоятельная работа по теме «Интеграл»
Уровень | 1 – Вариант | 2 – Вариант |
1 – 2 | 1. Что такое интеграл ? 2. Верно ли, что | 1. Напишите формулу Ньютона – Лейбница. 2. Верно ли, что |
3 – 6 | Вычислите интегралы | Вычислите интегралы |
7 – 10 | Вычислите интегралы | Вычислите интегралы |
Условия оценки
Выполнение заданий каждого уровня оценивается соответствующей оценкой.
Можно выполнять задания из разных уровней. При этом будет учитываться сложность примеров и количество верно решённых заданий.
Оценка повышается в случае выполнения заданий более высокого уровня.
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Оснащения врачебно-сестринской бригады. Интересное: Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 5 из 6Следующая ⇒ Цель:Формирование навыков вычисления определенного интеграла при помощи формулы Ньютона – Лейбница На выполнение работы отводится 2 часа Требования к выполнению практической работы: 1. 2.Оформить задания в тетради для практических работ. Теоретический материал Функция, интегрируемая на промежутке , если при любых разбиениях промежутка , таких, что при произвольном выборе точек (где ), сумма при стремится к пределу . Предел называют определенным интегралом от функции на промежутке и обозначают , то есть . (15.1) Число называется нижним пределом интеграла, – верхним. Промежуток называется промежутком интегрирования, – переменной интегрирования. Для вычисления определенного интеграла от функции в том случае, когда можно найти соответствующий неопределенный интеграл , служит Примеры Вычислить следующие определенные интегралы: 1) ; 2) ; 3) . Решение: 1) ; 2) ; 3) Задания для практической работы Вычислите определенные интегралы: 1) ; 2) ; 3) ; 4) ; 5) 6) 7) ; 8) ; 9) ; 10) ; 11) ; 12) ; 13) . Контрольные вопросы: 1. Что называется интегральной суммой для функции на отрезке? 2. Дайте определение определенного интеграла. 3. Сформулируйте основные свойства определенного интеграла. 4. В чем заключается суть формулы Ньютона – Лейбница? 5. Сформулируйте теорему о среднем. 6. Перечислите основные методы интегрирования для определенного интеграла. 7. Запишите формулы, которые соответствуют вышеперечисленным методам интегрирования. Рекомендуемая литература: 11.1[с. 271-282], 1.2[с. 205-212], 1.3[с. 374-396],2.2[с. 247-250]. Практическая работа №16 Тема: Вычисление площадей фигур с помощью определенных интегралов Цель: Формирование навыков вычисления площадей фигур с помощью определенных интегралов Время выполнения: 2 часа Требования к выполнению практической работы: 1. 2.Оформить задания в тетради для практических работ. Теоретический материал Определенный интеграл широко применяется при вычислениях различных геометрических фигур и физических величин. Найдем площадь криволинейной трапеции, ограниченной кривой , осью и двумя прямыми и , где , (рис.2). Рисунок 2 – Трапеция, ограниченная кривой , осью и двумя прямыми и , где . Так как дифференциал переменной площади есть площадь прямоугольника с основанием и высотой , то есть , то, интегрируя это равенство в пределах от до , получим . основанием и высотой , то есть , то, интегрируя это равенство в пределах от до , получим . Если криволинейная трапеция прилегает к оси так, что , (рис.3), то дифференциал переменной площади равен , откуда .
Рисунок 5 – Трапеция, ограниченная кривой , осью и прямыми и , расположена по обе стороны от оси .
В том случае, когда криволинейная трапеция, ограниченная кривой , осью и прямыми и , лежит под осью (рис.4), площадь находится по формуле . Если фигура, ограниченная кривой , осью и прямыми и , расположена по обе стороны от оси (рис. 5), то . Рисунок 6 – Трапеция, двумя пересекающимися кривыми и , прямыми и .
Пусть фигура ограничена двумя пересекающимися кривыми и , и прямыми и , где и (рис. 6) Тогда ее площадь находится по формуле . Примеры Задание: Вычислить площади фигур, ограниченных указанными линиями , , и (рис. 7). Рисунок 7 – Фигура, ограниченная указанными линиями , , и . Решение: квадратичная функция; ; график – парабола, ветви направлены вверх. Найдемкоординаты вершины параболы: , отсюда следует, что . Таким образом, вершина параболы имеет координаты: . Найдем площадь полученной фигуры: . Ответ: Задания для практической работы 1. Найдите площадь фигуры, ограниченной прямыми , , и осью абсцисс. 2. Найдите площадь фигуры, заключенной между осями координат и прямыми и . 3. Найдите площадь фигуры, ограниченной ветвью гиперболы и прямыми , . 4. Вычислите площадь фигуры, ограниченной параболой , прямыми , и осью абсцисс. 5. Найдите площадь фигуры, ограниченной параболой , осями координат и прямой . 6. Найдите площадь фигуры, заключенной между прямыми , , и . 7. Найдите площадь фигуры, ограниченной указанными линиями и . 8. Найдите площадь фигуры, ограниченной указанными линиями и . 9. Найдите площадь фигуры, ограниченной указанными линиями и . 10. Найдите площадь фигуры, ограниченной указанными линиями и . Контрольные вопросы: 1. По какой формуле вычисляется площадь фигуры, находящейся над осью ? 2. По какой формуле вычисляется площадь фигуры прилегающей к оси ? 3. 4. По какой формуле вычисляется площадь фигуры расположенной по обе стороны оси ? 5. По какой формуле вычисляется площадь фигуры, ограниченной двумя пересекающимися кривыми? Рекомендуемая литература: 1.1[с. 271-281], 1.2[с. 205-212], 1.3[с.395-395],2.2[с. 247-250]. Практическая работа №17 Тема: Нахождение области определения и вычисление частных значений для функции нескольких переменных Цель: Формирование навыков нахождения области определения и вычисления частных значений для функции нескольких переменных Время выполнения: 2 часа Требования к выполнению практической работы: 1.Ответить на теоретические вопросы. 2.Оформить задания в тетради для практических работ. Теоретический материал Уравнение (неявная форма) (17. или (явная форма) (17.2) определяет переменную как функцию независимых переменных . Областью определения функции переменных является множество точек -мерного пространства, в которых функция принимает определенное действительное значение. При уравнение (17.1) определяет функцию трех переменных или , (17.3) Областью определения, которой является множество точек трехмерного пространства . При уравнение (17.1) определяет функцию двух переменных или . (17.4) Частным значением функции называется такое ее значение, которое соответствует системе значений . (17.5) Примеры Задание 1: Найти области определения функций: 1) ; 2) . Решение: 1) Область определения функции состоит из всех точек плоскости, для которых , то есть . Таким образом, искомая область есть круг с центром в начале координат и радиусом 1. она является замкнутой, так как включает свою границу – окружность . 2) Так как логарифм определен только при положительных значениях аргумента, то , откуда . Следовательно, областью определения данной функции служит внутренняя часть круга с центром в начале координат и радиусом 3. эта область открытая, поскольку она не включает свою границу – окружность . Задание 2: Найти частное значение функции в точке . Решение: Подставляя в выражение функции значения и , получим . Задания для практической работы 1. На плоскости постройте область изменения переменных и , заданные нижеследующими неравенствами. Укажите тип области. 1) ; 2) ; 3) ; 4) . 2. Найдите области определения функций и укажите, что будет являться областью определения: 1) ; 2) ; 3) ; 4) ; 5) ; 6) . 3. Вычислите частные значения функций: 1) при и ; 2) в точке ; 3) при и . 4. Дана функция . Вычислите , , , , , , . Контрольные вопросы: 1. Что называется функцией нескольких переменных? 2. Что называется областью определения функции переменных? 3. Что называется частным значением функции двух переменных? 4. Что называется границей области? 5. Какая область называется замкнутой, а какая открытой? Рекомендуемая литература: 1.2[с. 438-439], 2.1[с. 192-204], 2.2[с. 151-166]. Практическая работа №18 ⇐ Предыдущая123456Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций. |
Ответить на теоретические вопросы.
Ответить на теоретические вопросы.
По какой формуле вычисляется площадь фигуры, находящейся под осью ?
1)
..- интеграция
$\endgroup$
1 9a\operatorname{четный}(x)dx$$
$\endgroup$
5
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
О вычислении определенных интегралов с помощью вычисления неопределенных интегралов
Введение
Как известно, с помощью определенных интегралов ученые исследовали многие практические задачи, такие как вычисление площади, ограниченной некоторыми функциями или прямыми линиями , объемы некоторых различных фигур, объемы тел вращения, расстояния между объектами, энергия сигналов, землетрясений и др. (см., например, [1, с. 169–222, 2, 3]). Исследование определенных интегралов тесно связано с нахождением решения начальной задачи для ОДУ. Поэтому для построения методов вычисления определенных интегралов были привлечены такие известные ученые, как Ньютон, Коттес, Гаусс, Чебышев, Симпсон, Адамс и др. (см., например, [4, 5]). Учеными построены различные формулы для вычисления определенных интегралов, имеющие различную точность.
А также известно, что для получения более точных результатов при вычислении определенных интегралов применялось уменьшение размера шага, что приводит к увеличению объема расчетных работ.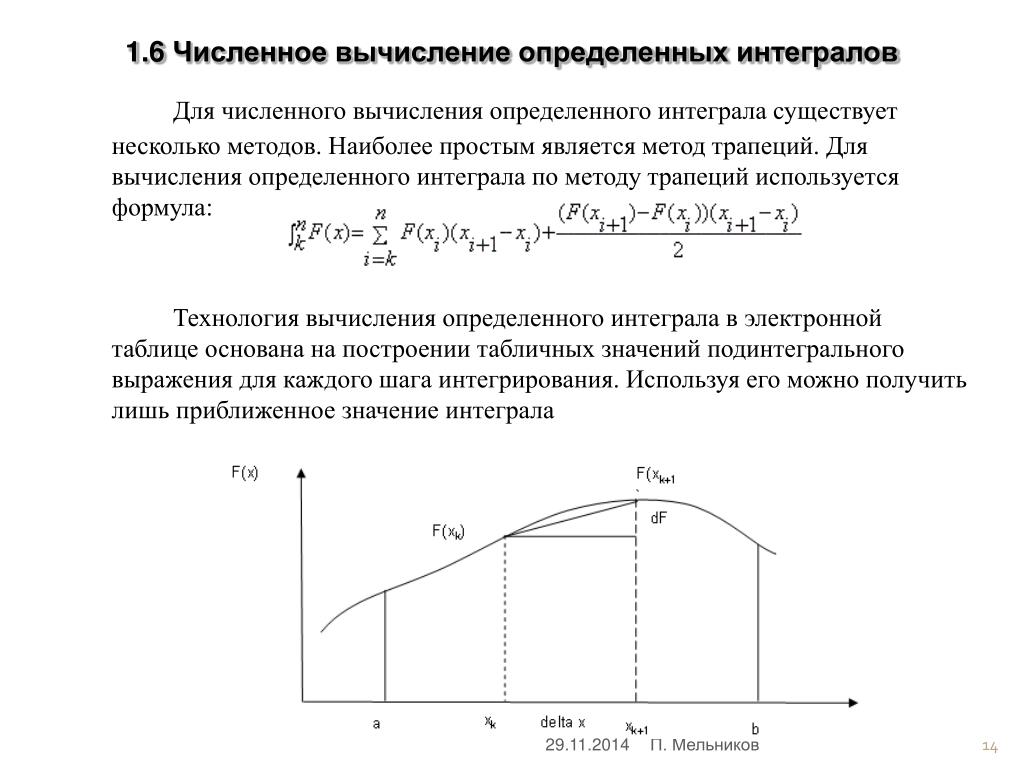
А известно, что первый прямой метод решения начальной задачи для ОДУ был построен Эйлером с использованием простейшей формы квадратурной формулы. Принимая во внимание, что порядок точности метода Эйлера равен 1 (единице), поэтому для построения более точных методов, чем метод Эйлера, специалисты предложили использовать интерполяционные полиномы с высокой точностью при построении методов вычисления определенные интегралы (см., например, [6, 7]). Но вот для построения более точных методов предложили использовать метод неизвестных коэффициентов. А для исследования определенных интегралов методом подынтервалов с помощью этого сравнивали полученные здесь результаты с известными. 9b {f(x)dx},$$
(1)
здесь достаточно гладкая функция f ( x ) определена в интервале \([x_0,b]\). Для построения методов вычисления определенного интеграла (1) обозначим через \(f_i\) значения функции f ( x ) в узловых точках \(x_{i}=x_{ 0}+ih\) \((i=0,1,\ldots ,N)\).
{x_{i+1}} {f(s)ds}, (i=0,1,\ldots ,N- 1).$$
(4)
Используя это равенство, ученые построили методы решения задачи (3) с разными порядками точности. Здесь мы предложили использовать конечно-разностные методы и применили их для решения задач (3) и (4), а также построили методы прямого (расширенного) и гибридного типов для вычисления определенного интеграла (1).
Построение конечно-разностных методов
Как известно, одним из популярных методов решения задачи (3) является конечно-разностный или многошаговый метод, который можно представить в следующем виде: 9k {\beta _{i}f_{n+i}}$$
(5)
$$(n=0,1,\ldots ,N-l; l=\max (s,k)).$ $
Этот метод исследовался некоторыми авторами (см., например, [8,9,10,11,12,13,14]). Отметим, что метод (5) в случае \(s=k\) принципиально исследован Далквистом [8] и показал, что если метод (5) устойчив в случае \(s=k\) и имеет степень p тогда \(p\le 2[k/2]+2\) и для всех значений порядка k существуют устойчивые методы с максимальными степенями.
Здесь мы используем известное определение степени зачатия и устойчивости, предложенное Далквистом [8]. 9{p+1}),\quad h\rightarrow 0.$$
Здесь p — целое число.
Следует отметить, что все известные методы типа (5) подчиняются закону Дальквиста. Но в работе [13] доказано существование устойчивых методов типа (5) со степенью \(p=k+m+1\) (для значений \(k\ge {3m}, m=k-s \)). Методы с таким же свойством были построены и другими авторами (см., например, [14,15,16]). Принимая во внимание это свойство методов прямого скачка, рассмотрим здесь применение методов прямого скачка к решению задачи (3). Поэтому предположим, что \(s
Но для вычисления \(y(x_{N})\) методами прямого перехода нам необходимо использовать некоторые значения функции f ( x ) за пределами рассматриваемого сегмента.
Используя границы \(p\le {k+m+1}\) \((m\le {[k/3]})\), получаем, что для построения более точных устойчивых методов значение k нужно выбрать больше. Например, если \(k\ge 9\), то можно построить устойчивый метод типа (5) со степенью \(p\le {k+4}\) . Как известно, для повышения точности метода (5) необходимо повышение точности начальных значений \(y_{j}\) \((j=0,1,\ldots ,k-1)\) . Поэтому ученые обсудили использование другой схемы для построения устойчивых методов с высокими степенями. Для этой цели предлагается использовать интерполяционные полиномы Гаусса, Чебышева, Лабботто и др. В результате чего появились новые методы. Эти методы остались от гибридных методов и в простом виде могут быть записаны следующим образом (см., например, [17,18,19{l+1}}{(l+1)!}\alpha _{i}}\nonumber \\&l=1,2,\ldots ,p-1.
\end{aligned}$$
(9)
Используя решение нелинейной системы (9), можно построить устойчивые методы типа (8). Заметим, что в системе (9) есть \(p+1\) уравнений и \(4k+3-m\) неизвестных. Если система (9) имеет решение в случае \(p+1=4k+3-m\), то получаем, что существуют методы типа (8) со степенью \(p=4k+2-m \). Обычно методы со степенью \(p=4k+2-m\) непригодны. Докажите, что существуют устойчивые методы для \(k>2\) со степенью \(p\le {3k+2+m}\). Но отсюда не следует, что \(P_{\max }=3k+2+m\)\((k\ge{3m})\). Система (8) является нелинейной, поэтому найти некоторые условия существования единственного решения непросто.
Следовательно, существование устойчивых методов типа (9) с максимальными степенями нам неизвестно. Эти свойства нелинейной системы алгебраических уравнений были встречены при исследовании методов Гаусса и Чебышева. Поэтому для нахождения узловых точек Гаусса авторы использовали известные многочлены (см., например, [4, с. 189–199, 25, с. 463–469]). Но здесь мы для нахождения решения системы (9) воспользовались программой Mathcad и в ряде случаев получили существование решения системы (9) в случае \(p>3k+2+m\).
k {\ gamma _ {i} y”_ {n + i}}, $ $ 9l {\gamma _{i}f’_{n+i}}.$$
(13)
Принимая во внимание, что функция f ( x ) известна, получаем это, используя методом (13) можно вычислить значение определенного интеграла (1). Метод (13) основательно исследовался некоторыми авторами (см., например, [28,29,30,31]). Если метод (13) устойчив и имеет степень p , то существуют методы со степенью \(p\le {2k+2}\) (в случае \(s=k=l\) ) и существуют методы со степенью \(p>2k+2\) в остальных случаях.
Следует отметить, что понятие устойчивости для метода (13) зависит от значений коэффициентов \(\beta _{i}\) \((i=0,1,\ldots ,k)\) . Если выполняются условия \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|\ne 0\), то понятие устойчивости метода ( 13) определяется как устойчивость метода (5). Но в случае \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|=0\) метод (13) называется устойчивым , если корни многочлена \(\rho (\lambda )\) лежат в единичной окружности, на границе которой нет кратных корней без двукратного корня \(\lambda =1\).
Очевидно, что в этом случае степень метода (13) будет такой же, как и степень метода (5). Для простоты положим в равенстве (13) \(s=k=l\). Как отмечалось выше, в этом случае существуют устойчивые методы со степенью \(p=2k+2\), если \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|\ne 0\) выполняется. Нетрудно понять, что с помощью метода (13) можно определить значение \(y_{n+k}\), если значения \(y_{j}\) \((j=0, 1,\ldots ,k-1)\) известны. Для решения этой проблемы предлагается использовать следующий метод: 9{(j)}}.$$
(14)
Из этой формулы можно получить разложение Тейлора для значения \(k=1\). В этом случае получают одношаговый метод, который всегда можно применить к вычислению определенного интеграла (1), так что \(y_{0}=0\). Таким образом, используя описанный способ, мы можем построить методы предиктора-корректора с различными степенями для вычисления значений \(y_{j}\) \((j=0,1,\ldots ,k-1)\) и значения \(y_{n+k}\) \((n=0,1,\ldots ,N-k;x_{N}=x_{0}+Nh)\).
Для построения устойчивых методов типа (13) (в случае \(s=k=l\)) будем считать определяемыми значения коэффициентов метода (13).
Как было отмечено выше, для определения значений коэффициентов метода (13) можно использовать метод неизвестных коэффициентов. И в этом случае получить систему алгебраических уравнений, аналогичную системе (9). Но здесь мы хотим представить способ нахождения значений коэффициентов для метода (13), при использовании которого объем вычислительной работы меньше вычислительной работы, получаемой при решении системы, аналогичной системе (9{(3)} =С. \end{aligned}$$
Здесь константа C есть коэффициент при главной части в разложении остаточного члена построенных методов. Эквиваленты системы (9) и (16) можно найти в работе [25].
Заметим, что в случае \(k=2\) линейную часть метода (13) можно представить в виде: \(y_{n+2}-y_{n}\). В этом случае путем замены ч на ч / 2 из указанной линейной части получим: \(y_{n+1}-y_{n}\). Таким образом, таким образом построили одношаговый метод, аналогичный гибридным методам. Эту схему можно обобщить следующим образом: 9l {\gamma _{i}f’_{n+i}}.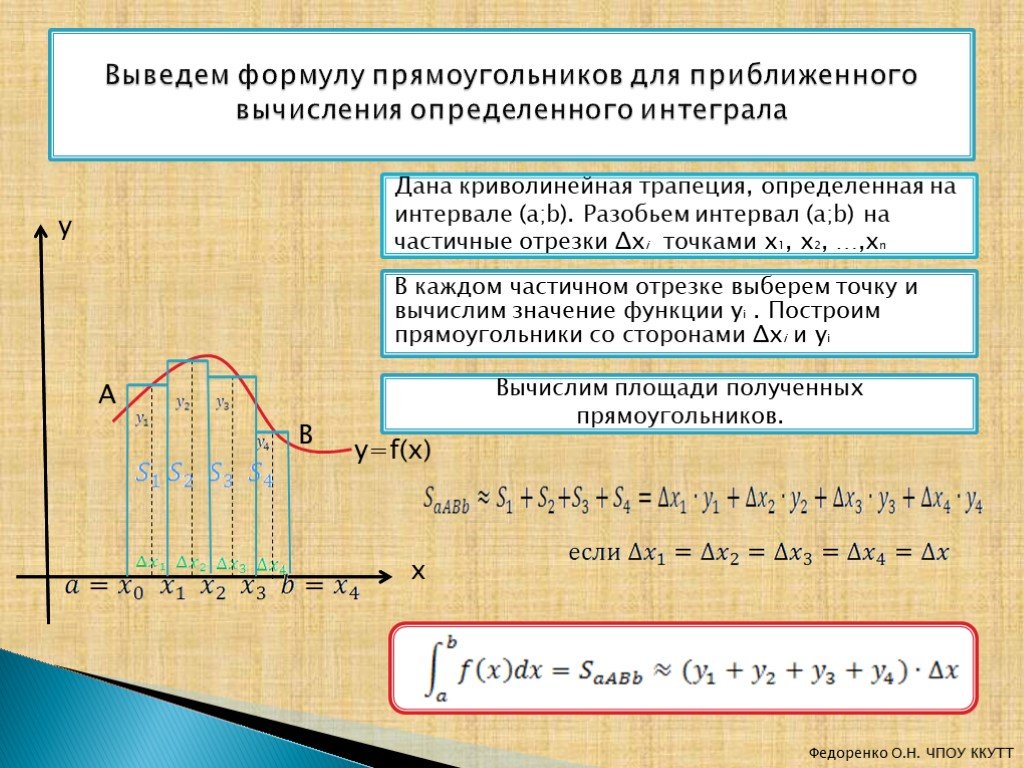
$$
(17)
Для получения одношагового метода из метода (17) достаточно выбрать размер шага h в форме h / k . Следует отметить, что метод (17) может быть неустойчивым при значениях \(k>2\). Но получение одноступенчатой формы, которая будет стабильной.
Построение некоторых простых методов и их применение к вычислению определенных интегралов
Сначала рассмотрим построение устойчивых методов типа (5). Как известно, для случая \(s=k\) можно построить устойчивые методы со степенью \(p\le 8\), имеющей явный и неявный тип для \(k\le 6\). Поэтому рассмотрим случай, когда \(s
$$y_{n+ 1}=y_{n}+h(5f_{n}+8f_{n+1}-f_{n+2})/12.$$
(18)
А теперь положим \(k= 3\) и \(m=2\), то получим:
$$y_{n+1}=y_{n}+h(9f_{n}+19f_{n+1}-5f_{n+2} +f_{n+3})/24.
$$
(19)
Но для случая \(k=4\) и \(m=3\) устойчивый метод можно записать так:
$ $y_{n+1}=y_{n}+h(251f_{n}+646f_{n+1}-264f_{n+2}+106f_{n+3}-19f_{n+4})/720.$$
(20)
Метод (19) имеет степень \(p=4\), а метод (20) имеет степень \(p=5\) . В [11] доказано, что для коэффициентов \(|\beta _{k-m+i}|>|\beta _{k-m+i+1}|\) и \(\beta _{k-m} >0\) (для \(\alpha _{km}>0\) ), \(\beta _{km+i}\beta _{km+i+1}<0\) если коэффициенты удовлетворяют условию: \(\beta _{k-m+i}\ne 0\), \(\beta _{k-m+i+1}\ne 0\). Описанные выше методы удовлетворяют этим условиям.
Применение методов (18) и (20) к вычислению интеграла (1) очень просто, поскольку известно \(y_{0}\). Теперь рассмотрим случай \(k=3\) и \(m=1\). В этом случае метод с максимальной степенью можно записать в виде:
$$y_{n+2}=(8y_{n+1}+11y_{n})/19+h(10f_{n}+57f_{n+1}+24f_{n+2}-f_{ n+3})/57.$$
(21)
Этот метод устойчив и имеет степень \(p=5\). Если в этом методе размер шага ч заменить на ч / 2, то получим:
$$y_{n+2}=(8y_{n+1}+11y_{n})/19+h (10f_{n}+57f_{n+1/2}+24f_{n+1}-f_{n+3/2})/114.
$$
(22)
Метод (22) сложнее метода (20), так что в методе (22) участвует член \(y_{n 1/2}\). Чтобы найти это значение, можно использовать метод (19) или метод (20). Но если рассмотреть случай \(m=0\) и \(k=2\), то получим следующий устойчивый метод со степенью \(p=4\):
$$y_{n+2}=y_{ n}+h(f_{n+2}+4f_{n+1}+f_{n})/3,$$
и в этом методе после замены h на h / 2 получаем:
$$y_{n+1}=y_{n}+h(f_{n+1}+4f_{n+1/2}+f_{n})/6,$$
(23)
, который можно применить для вычисления интеграла (1) в отдельной форме. Теперь рассмотрим построение устойчивого метода типа (8) и положим \(k=1\). В этом случае из метода (8) можно получить устойчивые методы разного порядка точности. Например, метод со степенью \(p=6\) можно записать так:
$$y_{n+1}=y_{n}+h(f_{n}+f_{n+1})/12+5h(f_{n+\alpha }+f_{n+1-\alpha })/12,\,\,\,\,\, \alpha =1/2-\sqrt{5}/10.$$
(24)
Этот метод является неявным. В этом случае явный метод со степенью \(p=5\) можно записать так:
$$\begin{aligned}&y_{n+1}=y_{n}+hf_{n}/9+ h((16+\sqrt{6})f_{n+3/5-\alpha}+(16-\sqrt{6})f_{n+3/5+\alpha})/36,\nonumber \ \&\quad \alpha =\sqrt{6}/10.
\end{aligned}$$
(25)
Если предположить, что \(\beta _{i}=0\) \((i=0,1,\ldots ,k)\), то можно доказать что существуют устойчивые методы со степенью \(p=2k+2\). В случае \(k=1\) метод со степенью \(p=4\) имеет следующий вид:
$$\begin{aligned}&y_{n+1}=y_{n}+h(f_{n+l}+f_{n+1-l})/2,\nonumber \\&\quad l =1/2-\sqrt{3}/6. \end{aligned}$$
(26)
А теперь рассмотрим построение многошаговых методов второй производной. Как отмечалось выше, если эти методы устойчивы, то степень этих методов удовлетворяет условию \(p\le {2k+2}\). Сначала поставим \(s=k=l\) и \(k=1\). Тогда из метода (18) можно получить следующие методы (см., например, [27,28,29,30]): 9{3}f”_{(\xi )}/6. \end{aligned}$$
(29)
Обратите внимание, что метод (27) является неявным, метод (29) явным, но метод (28) в зависимости от его применения может быть явным или неявным. В нашем случае метод (28) является явным, поскольку функция f ( x ) не зависит от функции y ( x ).
{2}(-3f’_{n+2 }-40f’_{n+1}+3f’_{n})/240. \end{выровнено}$$ 9{1} {exp{(\lambda {s}})ds}.$$
(37)
Эта задача была сведена к решению задачи: \(y'(x)=exp{(\lambda { x})}\) \(y(0)=0\), точное решение которого можно записать в виде: \(y(x)=exp{(\lambda {x})}-1\). Эта задача была решена с помощью методов прямого скачка (17)–(20), гибридных методов (24)–(26) и многошаговых методов с множественными производными (27), (35) и (36). Для сравнения полученных результатов была решена рассматриваемая задача для различных значений \(\lambda\) и \(h=0,1\).
Результаты вычисления данного определенного интеграла сведены в таблицы 1 и 2.
Таблица 1 Результаты решения примера в случае \(\lambda =\pm 1\)Полная таблица
Таблица 2 Результаты решения примера в случае \(\lambda =\pm 5\)Полная таблица
Для построения устойчивых методов с высокими степенями здесь предложены три пути. И дали некоторые из конкретных методов прямого скачка, гибридного и многошагового типов вторых производных, которые были сравнены путем их применения для решения примера (37).
9{y} {f(x,t)dt}.$$
Заключение
Как было отмечено выше, здесь описаны некоторые способы вычисления определенного интеграла и их применение к вычислению двойных интегралов. Дано некоторое сравнение методов, рекомендованных для вычисления определенных интегралов. Показали, что поведение ошибок при использовании методов зависит от их типа. Для этого воспользовались результатами, полученными для шага \(h=0,1\), которые сведены в таблицы 1 и 2. А также показали, что ошибки в основном зависят от свойств решения рассматриваемых задач. . Как видно из таблицы 2, результаты, полученные методами прямого скачка для \(h=0,1\) и \(m=5\), не являются удовлетворительными и не могут считаться нормальными. Но результаты, полученные для шага \(h=0,1\) и \(m=1\), можно считать нормальными. Надеемся, что описанный выше метод найдет свое широкое применение при решении научных и технических задач. Чтобы показать преимущества описанного здесь метода, было рассмотрено применение вышеупомянутого метода для вычисления двукратно определенных интегралов.