Вычисление предела: Предел функции, вычисление пределов.

Предел последовательности. Вычисление пределов

Число a называется пределом числовой последовательности {x

_n}, если для любого как угодно малого положительного числа ε>0 найдется натуральное число N=N(ε), такое что при всех n>N выполняется неравенство |x_n-a|<ε.

Если a является пределом последовательности то этому соответствует запись

Вычисление предела числовой последовательности

Пример 1 Легкое задание, которое учит выносить доминантные множители в дробях, которые дают наибольший вклад при номере, стремлящемся к бесконечности, и упрощать на них

В этом вся сложность алгоритма вычисления предела последовательности при переменной стремящейся к бесконечности, но бывают исключения, о которых поговорим делее.
Если последовательность сходится, то она имеет конечный лимит. Если предел равен бесконечности, то говорят, что такая последовательность расходится.
Для установления сходимости последовательностей нужно хорошо уметь находить пределі, что мы с Вами постоянно совершенствуем.

Пример 2 Имеем неопределенность вида бесконечность минус бесконечность (∞-∞), поэтому теорему о разнице пределов здесь применять нельзя. Преобразуем выражение, умножением и делением на сопряженное выражение. Для вычисления значения предела упрощаем дробь на выражение, что вносит наибольший вклад при аргументе стемящемся к бесконечности. Как выносить множители из под корня Вы должны научиться самостоятельно, без этого трудно будет раскрывать пределы с корнями.

 

Пример 3 Разницу корней в знаменателе дроби не уножаєм на сопряженное выражение, а просто номер n выносим из под корня (внимательно посмотрите как это делать), а дальше упрощаем с n выделенным в числителе

 

Пример 4 Последовательность из частки иррациональных выражений имеет конечную границу, если степень номера n в знаменателе равен степени в числителе (или больше). Его выделяем по указанной в методике формуле, и упрощаем

Пример 5 Найти предел последовательности
Вычисления: Проанализировав, как меняются слагаемые для всех номеров k=2,3,4 можем записать формулу

Таким образом исходную сумму сводим к виду

Единого устоявшегося алгоритма, как раскрывать такие суммы нет. Порой можно увидеть простые схемы чередования слагаемых, в других заданиях бывает нужно вычислить суммы арифметических или геометрических прогрессий. Лишь бы оценить сверху, что последовательность ограничена, и к какому значению стремится.

Пример 6 Лимит последовательности из частки показательных выражений вычисляют путем выделения и упрощения доминантных множителей в числителе и знаменателе дроби. В заданном лимите основания равны 2 и 4, их можно свести к общему 4 в (высшем) степени ровному n. Все остальное и даст значение к которому стремится дробь.

Пример 7 Предел последовательности из разности бесконечно больших дробей раскрываем методом сведения их к общему знаменателю и упрощения в числителе и знаменателе множителя, что вносит главный вклад

 

Пример 8 Найти лимит последовательности

Вычисления: Представим общий член последовательности {x_n} в виде

По теореме о границе показательной функции, она равна показателю от границы основы, если степень конечна. 5.

Пример 9 В такого сорта заданиях вынесения n в главной степени за скобки в числителе и знаменателе дроби к упрощению не приведет. Попробуйте проверить самостоятельно, остается взглянуть в формулы сокращенного умножения и расписать разницы и суммы в кубе и в четвертой степени по следующим формулам

Таким образом, получим слагаемые с противоположными знаками, которые в сумме дадут 0, остальные слагаемые в предельном переходе упростятся по приведенной выше методике.
И напоследок, еще несколько решений на предел последовательности, которые предлагаем разобрать самостоятельно.

10

11

12

13

Вычисление пределов функции с примером по высшей математике

Предел элементарной функции при , стремящемся к значению (), которое входит в область ее определения, равен частному значению функции при , т.е. .

Если аргумент стремится к бесконечности или к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.

Рассмотрим основные свойства пределов:

1) Если существуют пределы функций и при , то

2) Если существуют пределы функций и при , то

3) Постоянный множитель можно выносить за знак предела, т.е.

4) Если существует предел функции при , то

, где — натуральное число.

5) Если существуют пределы функций и при , причем предел функции отличен от нуля, то

При вычислении пределов часто используют два замечательных предела:

1. или

2. или

и их следствия:

Второй замечательный предел используют для раскрытия неопределенностей вида , а остальные — для неопределенности вида .

Вычисление пределов значительно упрощается при использовании эквивалентности бесконечно малых.

Функция называется бесконечно малой при , если .

Функция называется бесконечно большой при , если .

Свойства бесконечно малых и бесконечно больших:

1) Если и при , то при .

2) Если при , то при .

3) Если — бесконечно малая при , a — ограниченная в некоторой окрестности точки , то — бесконечно малая функция при .

Две бесконечно малые функции называются эквивалентными (~), если предел их отношения равен 1. С помощью замечательных пределов можно доказать справедливость цепочки эквивалентных бесконечно малых при .

При раскрытии неопределенностей вида или рекомендуется пользоваться указанными замечательными пределами либо пытаться сократить числитель и знаменатель на общие (критические) множители.

При вычислении пределов нередко пользуются правилом Лопиталя:

Пусть при вычислении предела возникает неопределенность вида или , но при этом существует . Тогда .

Использование правила Лопиталя

в большинстве случаев значительно упрощает вычисление пределов, поэтому, прежде чем приступать к вычислению пределов, необходимо повторить правила вычисления производных.

Пример:

Найти пределы функций:

а) б)

в) г)

Решение:

а) Разделив числитель и знаменатель на большую степень получим

б) Умножив числитель и знаменатель на и используя первый замечательный предел, получим

в) Логарифмируя и используя правило Лопиталя, получим

г) Сделав замену переменных и используя второй замечательный предел, получим

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Высшая математика краткий курс лекций для заочников

Возможно вам будут полезны эти страницы:

Вычисление пределов функции. Предел функции на бесконечности. Два замечательных предела. Вычисление числа «е»

1. Вычисление пределов функции. Предел функции на бесконечности. Два замечательных предела. Вычисление числа «е».

(практическое занятие)
Автор: преподаватель
ГПОУ ТО «НПК»
Гусева Л. Г.

2. Цель занятия:

Повторить, обобщить и
систематизировать знания
по теме «Вычисление
пределов функции» и
отработать их применение
на практике

3. Задачи:

Обучающие:
Развивающие:
-ознакомление студентов
с общей схемой
вычисления пределов
функции на основе
обобщения ранее
изученного материала;
– формирование
самостоятельности
мышления,
мыслительных
операций: сравнение,
анализ, обобщение;
– разобрать различные
примеры задач на
определение пределов
функции, охватывающие
все подтемы данной
темы;
– формирование
навыков
самостоятельной
работы;
– закрепление навыков
нахождения пределов
функций при решении
задач
– умение обобщать,
абстрагировать и
конкретизировать
знания при
определении предела
функции.
Воспитательные:
воспитание умения
контролировать
свою деятельность
и оценивать её;
воспитание
познавательной
активности,
культуры общения.

4. Ход урока:

1. Организационный момент
2. Проверка домашнего задания
3. Повторение опорных знаний
4. Изучение нового материала
5. Актуализация знаний
6. Домашнее задание
7. Итоги урока. Рефлексия

5. Проверка домашнего задания

Вычислите пределы:
1 вариант
5
lim
1) x 2 2 x 8
2
3x 2 x
2) lim
x 0 2 x 2 5 x
x
3) lim
x 0 5 x 5 x
2 вариант
1) lim x x 5
x 3
3
x 2 2 x 15
2) lim
2
x 3
x 9
2 x 2 x
3) lim

x 0
5x

6. Проверка домашнего задания

Ответы:
1) -1,2; 0,4; -√5
2) 25, 4/3, 1/5√2

7. Повторение опорных знаний

Что называют пределом функции в
точке?
Записать определение непрерывности
функции.
Сформулируйте основные теоремы о
пределах.
Какие способы вычисления пределов
вы знаете?

8. Повторение опорных знаний

Определение предела. Число b – предел
функции f(x) при x стремящемся к a, если для
каждого положительного числа e можно
указать такое положительной число d, что
для всех x, отличных от a и
удовлетворяющих неравенству |x-a|
имеет место неравенство |f(x)-b|
Если b есть предел
функции f(x) при x стремящемся к a, то
записывают это так:
Функция f(x) непрерывна в точке a, если

9. Повторение опорных знаний

Основные теоремы о пределах:
ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен
сумме пределов этих функций , то есть
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся
к a равен произведению пределов этих функций, то есть
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен
частному пределов, если предел знаменателя отличен от нуля, то есть
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел
числителя конечен и отличен от нуля.

10. Повторение опорных знаний

Способы вычисления пределов:
1) Непосредственной подстановкой
2) Разложение числителя и
знаменателя на множители и
сокращение дроби
3) Домножение на сопряженные с
целью избавления от
иррациональности

11. Изучение нового материала

Предел на бесконечности:
Число А называется пределом функции
y=f(x) на бесконечности (или при х,
стремящимся к бесконечности), если для
всех достаточно больших по модулю
значений аргумента х соответствующие
значения функции f(x) сколь угодно мало
отличаются от числа А.

12. Изучение нового материала

1)
lim
x
2)
3
3
0
x 5
lim ( x
3
6 x 2 5 x 1)
x
3x 2 5 x 4
3) lim 2
x
2
x
3
x
Разделим числитель и знаменатель дроби н старшую степень
переменной:
3x 2 5 x
4
5
3
2
2
2
х
х
х lim
x
2
lim
x
2
x
2x
3
x
1
2 2
2
x
х
х
х
3 0 0
3
1 0 0
4
5
4
3
х2
3
2
3
1
х2

13.

Изучение нового материала Первый замечательный предел
Второй замечательный предел равен

14. Изучение нового материала

Использование замечательных пределов
Первый замечательный предел:
Второй замечательный предел:

15. Изучение нового материала

sin Rx
sin Rx
1. lim
R lim
R
x 0
x 0
x
Rx
x
2
2 3x
2 6
2. lim (1 ) lim ((1 ) ) e 6
x
x
x
x

16. Актуализация знаний

5
1. lim
x 4 x 1
2.
lim
x
3.
7.
x 4 2x 2 3
3x 3 5
lim x
3
3x 2
x
2 3
5
2
lim
x x
x
3x
5. lim
x x 2
8.
9.
4.
6.
lim
x
x5 x6
x3 x4
10.
11.
3tgx
lim
x 0
x
sin 6 x
lim
x 0 sin 2 x
sin 17 x
lim
x 0
8x
5 x
lim (1 )
x
x
2 x
lim (1 )
x
3x
3 x
12.

lim (
)
x 0
3
1
x

17. Задание на дом

Вычислите пределы:
1.
lim
x3 1
x 1
sin 3x
4. lim
x 0 sin 5 x
2
lim
x 7 x 10
x 2 9 x 20
tg 2 x
5. lim
x 0
x
lim
x 1 1
x
x 2 2x
6. lim (
)
x
x
x 1
2.
x 5
3.
x 0
Рефлексия
Сегодня я узнал …
Было трудно …
Было интересно …
Я понял, что…
Теперь я могу …
Я попробую …
Я научился …
Меня заинтересовало …
Меня удивило …

Конспект урока по математике на тему “Вычисление пределов функции”

Тема: «Вычисление пределов функции»

Цель: закрепить и усовершенствовать практические приемы вычисления предела функции.

Задачи:

образовательные:

1. формировать умения и навыки вычисления пределов;

2. познакомить обучающихся со способами раскрытия неопределенностей и других;

3. сформировать у обучающихся навыки вычисления предела многочлена и отношения многочленов;

4. сформировать у обучающихся навыки применения первого и второго замечательных пределов для раскрытия неопределенностей.

развивающие:

5. развивать мышление обучающихся при выполнении упражнений;

6. создать условия для развития у студентов умений формулировать промежуточные проблемы, предлагать пути их решения;

7. создать условия для развития у студентов монологической и диалогической математической речи;

8. формировать умения и навыки самостоятельно умственного труда.

воспитательные:

9. способствовать воспитанию дисциплинированности, усидчивости, навыков самостоятельности и умения работать индивидуально.

Тип урока: практическая работа.

Формы и методы: словесный, наглядный, исследовательский, фронтальная работа, самостоятельная работа.

Оборудование: карточки для обучающихся, опорные конспекты, решение типовых примеров, компьютер, презентация по теме «Предел функции».

Структура занятия:

1. Организационный момент (1 минута)

2. Сообщение темы занятия. Постановка цели и задач занятия. Мотивация. (3 минуты)

3. Актуализация прежних знаний (сопровождается демонстрацией слайдов). (7 минут)

а) фронтальный опрос;

б) устный счет.

4. Воспроизведение изученного и его применение в стандартных условиях. (5 минут)

5. Перенос приобретенных знаний и их применение в новых или измененных условиях с целью формирования умений.(50 мин.)

а) решение примеров у доски с комментированием;

б) самостоятельное выполнение обучающимися заданий под контролем преподавателя;

в) исследование.

6. Проверка умений обучающихся самостоятельно применять полученные знания. (15 мин.)

7. Повторение основных понятий. Разгадывание кроссворда.(5 мин.)

8. Подведение итогов занятия, рефлексия. (3 минуты)

9. Домашнее задание. (1 минута)

Ход занятия

1. Организационный момент.

Перед началом занятия преподаватель проводит проверку подготовленности кабинета к занятию.

Приветствие обучающихся, определение отсутствующих, заполнение группового журнала.

2. Сообщение темы занятия. Постановка цели и задач занятия. Мотивация.

Сообщается тема занятия: «Вычисление пределов функции». Вместе с обучающимися преподаватель формулирует цель и задачи занятия.

Значение теории пределов для математики трудно переоценить – это центральное понятие математического анализа, на основе которого формируются понятия производной, дифференциала и интеграла.

Понятие предела функции имеет большое значение для построения графиков функций. Кроме того, в дальнейшем мы будем изучать понятие производной и без знания предела функции рассмотрение этого понятия невозможно.

Понятие непрерывности играет важную роль, т.к. многие физические процессы характеризуются тем, что плавное изменение физических величин сменяется скачкообразно. То есть количественные изменения переходят в качественные. Это один из основных законов диалектики.

Но предел нашел применение не только в математике. Предельный анализ в экономике исследует изменяющиеся величины затрат или результатов при изменении объемов производства или потребления на основе анализа их предельных значений. Задачи на темы: рост вклада, рост населения страны, распад радиоактивного вещества, размножение бактерий решаются с помощью второго замечательного предела.

Но такое признание теория пределов имела не всегда. В 17 веке известный математик Мишель Ролль писал, что эта наука есть коллекция гениальных ошибок. А великий французский мыслитель – Вольтер заметил, что исчисление пределов представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Начальный период развития новых ветвей математики, связанных с понятиями функции, бесконечно малых величин, пределов и производных, был охарактеризован Марксом как «мистический».

Многие десятилетия величайшие математики, в том числе Ньютон и Лейбниц, предпринимали попытки дать строгое определение предела. Но лишь в 19 веке великому французскому математику Огюстену Луи Коши удалась это сделать.

3. Актуализация прежних знаний (сопровождается демонстрацией слайдов).

а) Фронтальный опрос.

Ответы на вопросы теоретической части темы:

• предел функции в точке;

• односторонние пределы;

• предел функции при x стремящемся к бесконечности;

• основные теоремы о пределах;

• правила вычисления пределов;

• раскрытие неопределенностей;

• первый замечательный предел;

• второй замечательный предел.

б) Устный счет.

Для нахождения предела данных функций заменим аргумент x его предельным значением.

4. Воспроизведение изученного и его применение в стандартных условиях.

Задание 1

На рис. изображены графики функций. Установите для каждой из функции имеет ли она предел в точке х=2. если имеет, то чему он равен?

Ответы:

;;;не существует.

Задание 2.

Общее правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Найти предел функции в точке:

Решение. Функция  определена в точке х = π/6. Получим: 

5. Перенос приобретенных знаний и их применение в новых или измененных условиях с целью формирования умений.

Решение примеров у доски с комментированием.

Рассмотрим теперь такие примеры, когда применение свойств предела становится возможным лишь после некоторых предварительных преобразований.

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.

Задание 3.

а) Найти

Решение. Здесь имеем неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель х-2. В результате получим

Итак, чтобы найти предел частного двух функций, где пределы делимого и делителя равны 0, нужно преобразовать функцию таким образом, чтобы выделить в делимом и делителе сомножитель, предел которого равен 0, и, сократив дробь на этом сомножитель, найти предел частного.

  Самостоятельное выполнение обучающимися заданий под контролем преподавателя.

Один обучающийся решает пример 2б) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.

б)

в) Найти
Сначала попробуем подставить -1 в дробь:
 

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

Далее находим корни:

Таким образом:

Знаменатель. Знаменатель  уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

  Самостоятельное выполнение обучающимися заданий под контролем преподавателя.

Один обучающийся решает пример 2г) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.

г) Найти

Решение. Здесь имеем неопределенность 0/0. Для того чтобы раскрыть эту неопределенность, разложим числитель на множители и до перехода к пределу сократим дробь на множитель х+2.

Здесь предел делителя равен 0. Таким образом, знаменатель дроби неограниченно убывает и стремиться к 0, а числитель приближается к -1. Ясно, что вся дробь неограниченно растет, что условно записывается так: .

Задание 4.

Рассмотрим метод умножения числителя и знаменателя на сопряженное выражение.

Общее правило: Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности  используют метод умножения числителя и знаменателя на сопряженное выражение.

а) Найти предел

 

Получена неопределенность вида , которую нужно устранять.

В числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. По формуле разности квадратов:

Умножаем числитель на сопряженное выражение:

Число лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:

  Самостоятельное выполнение обучающимися заданий под контролем преподавателя.

Один обучающийся решает пример 2б) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.

б) Найти предел

Разложим числитель на множители:

Умножим числитель и знаменатель на сопряженное выражение

Перейдем к примерам нахождения предела функции на бесконечности.

Общее правило: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Задание 5.

а) Найти предел
Снова в числителе и знаменателе находим  в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности  делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на

Исследование.

Группа делится на 2 группы. Каждая группа получает задание и выполняет его общими усилиями.

б) Найти

Решение. При x->∞ имеем неопределенность вида ∞/∞. Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на x³.Тогда получим

в) Найти

Решение. Разделив числитель и знаменатель на x³ и перейдя к пределу, получим

поскольку числитель последней дроби стремиться к пределу, отличному от нуля, а знаменатель – к нулю.

После решения примера в группах. Представитель каждой группы поясняет решение своего примера.

Все три примера на доске. Ответьте на вопросы:

Что общего в этих трех примерах?

Какие отличия?

Какие можно сделать выводы?

1.все пределы на бесконечности

2.пределы от дробно-рациональных функций

3.ответы в каждом примере не случайные

показатели степеней равны

в 1 примере

показатели степеней разные

во 2 и в 3 примерах:

Во 2 примере – у числителя показатель больше, чем у знаменателя;

В 3 примере – у числителя показатель меньше, чем у знаменателя;

1.если показатели степеней числителя и знаменателя равны, то предел равен отношению коэффициентов при этих степенях

2.если показатель степени числителя больше показателя степени знаменателя,

то предел равен бесконечности

3. если показатель степени числителя меньше показателя степени знаменателя, то предел равен 0.

На основании открытого правила вычислить значение пределов устно:

г) Найти

Решение. При стремлении аргумента x к бесконечности имеем неопределенность вида ∞/∞. Чтобы раскрыть ее, разделим числитель и знаменатель дроби на x. Тогда получим

Задание 6.

Рассмотрим примеры, в которых используются замечательные пределы.

а) Найти предел

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:

Обведенное выражение у нас превратилось в единицу и исчезло в произведении:

Теперь только осталось избавиться от трехэтажности дроби:

б) Найти

Решение. Произведем подстановку kx=y. Отсюда следует, что при , а x=y/k. Тогда получим

Так как

в). Найти

Решение. Имеем

Здесь мы разделили числитель и знаменатель дроби на x (это можно сделать, так как но x<>0), а затем воспользовались результатом предыдущего примера.

г) Найти

Решение. Преобразуем числитель к виду 1-cos8x=2sin²4x. Далее находим

  Самостоятельное выполнение обучающимися заданий под контролем преподавателя.

Один обучающийся решает примеры 2д) и 2е) на вращающейся доске. Остальные решают самостоятельно. Затем обсуждается решение.

д) Найти

Решение. 1 способ. Здесь имеет место неопределенность вида 0/0. Применяя известную тригонометрическую формулу и выполняя элементарные преобразования, получим

2 способ. Преобразуем числитель следующим образом:

Следовательно,

е) Найти

Решение. Заменив tg x на sin x/cos x, получим

Задание 7.

а). Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение  .

Нетрудно заметить, что при  основание степени , а показатель – , то есть имеется, неопределенность вида :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать  . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель:

б) Найти

Решение. Запишем основание степени в виде , а показатель степени – в виде . Следовательно,

в). Найти

Решение. Имеем

=

6. Проверка умений обучающихся самостоятельно применять полученные знания.

Самостоятельная работа (4 варианта).

Вариант – 1

Вариант – 2

Вариант – 3

Вариант – 4

1. 7. Повторение основных понятий.

Разгадывание кроссворда.

ПО ГОРИЗОНТАЛИ:

1. Выражение, значение которого не определено, – это неопределенность;

2. Если f(x) не определена в точке х₀ или не является непрерывной в этой точке, то точка х₀ называется точкой разрыва функции f(x).

3. Французский математик, который ввел строгое определение предела. – Коши.

ПО ВЕРТИКАЛИ:

1. Пределы функции в точке слева и справа называются односторонними пределами функции в этой точке.

2. Если для любого найдется такое число, что для всех х, удовлетворяющих условию , будет выполнятся неравенство , то число А – предел функции при х, стремящемся к а.

3. Сколь угодно большое(малое), безграничное число – это бесконечность.

4. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке.

5. Разность односторонних пределов функции f(х) в точке разрыва , если они различны – это скачок функции.

8.Подведение итогов занятия, рефлексия.

Студенты под руководством преподавателя подводят итоги занятия. Преподаватель называет оценки.

В качестве рефлексии обучающимся предлагается ответить на вопросы и высказать свои мнения.

Цель: осознание обучающимися своей учебной деятельности, самооценка результатов своей деятельности.

Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха.

• Что нового узнали на занятии?

• Какую цель мы ставили в начале урока?

• Наша цель достигнута?

• Что нам помогло справиться с затруднением?

• Какие знания нам пригодились при выполнении заданий на уроке?

• Как вы можете оценить свою работу?

• На следующем занятии мне бы хотелось…

9.Домашнее задание.

Вычислить пределы

1. а) б)

2. а) б)

3. а) б)

4. а) б)

Электронный учебник по математическому анализу

3.

n$ не имеет предела.

Определение. Говорят, что последовательность $a_n$ имеет пределом $+\infty$, если для любого $A>0$ существует такое $N$, что при всех $n>N$ выполняется неравенство $a_n>A$.

Обозначение. Этот факт обозначают \[ \lim _{n\rightarrow +\infty}a_n=+\infty, \]

или

\[ a_n \xrightarrow[n\to +\infty]{} +\infty. \]

Аналогично определяется ситуация, когда $ \lim _{n\rightarrow +\infty}a_n=-\infty$.

Определение. Если предел последовательности равен $0$, последовательность называют бесконечно малой. Если предел последовательности равен $\infty$, последовательность называют бесконечно большой.

Теорема. Пусть последовательность $a_n$ имеет конечный предел. Тогда $a_n$ – ограниченная последовательность.

Доказательство.

Возьмем какое-нибудь $\varepsilon >0$. Согласно определению предела, существует такое $N$, что при всех $n>N$ выполняется $|a_n-A|

Теорема. Пусть последовательность $a_n$ имеет конечный предел $A$, \[ a_n \xrightarrow[n\to +\infty]{} A. \]

Тогда последовательность $b_n=(a_n-A)$ является бесконечно малой.

Теорема. Последовательность может иметь только один предел.

Доказательство.

Предположим, что последовательность имеет два предела, \[ a_n \xrightarrow[n\to +\infty]{} A, \] \[ a_n \xrightarrow[n\to +\infty]{} B, \]

$A \neq B$. Будем для определенности считать, что числа $A$ и $B$ конечные. Возьмем $\varepsilon = |A-B|/3$.

Согласно определению предела, найдется такое $N_1$, что при $n >N_1$ выполняется $A-\varepsilon

По тем же причинам найдется $N_2$ такое, что при $n>N_2$ выполняется $B-\varepsilon

Тогда при $n>max(N_1,N_2)$ выполняются оба набора неравенств, что невозможно – отрезки $(A-\varepsilon,A+\varepsilon)$, $(B-\varepsilon,B+\varepsilon)$ не пересекаются. ч.т.д.

3.1.2 Арифметика пределов

Здесь приведена серия теорем, описывающая предел суммы, произведения и частного последовательностей, имеющих конечный предел.

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ – конечные числа. Тогда последовательность $(a_n+b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n+b_n)=A+B. \]

Доказательство.

Возьмем произвольное число $\varepsilon >0 $. Согласно определению предела, существует такое $N_1$, что при всех $n>N_1$ выполняется: \begin{equation} |a_n-A|

По тем же причинам существует такое $N_2$, что при всех $n>N_2$ выполняется: \begin{equation} |b_n-B|

Пусть $N=max(N_1,N_2)$. Тогда при всех $n>N$ выполняются неравенства (1) и (2). Используя неравенство треугольника, получаем: при всех $n>N$ выполняется \begin{equation} |(a_n+b_n)-(A+B)| \[ \varepsilon /2+\varepsilon /2=\varepsilon.(3)\]

ч.т.д.

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ – конечные числа. Тогда последовательность $(a_n\cdot b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n\cdot b_n)=A\cdot B. \]

Теорема. Пусть \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}b_n=B, \]

причем $A$ и $B$ – конечные числа, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ имеет конечный предел, причем

\[ \lim _{n\rightarrow +\infty}(a_n / b_n)=A / B. \]

Теорема. Пусть при всех $n$ выполняется $a_n

Тогда $A \leq M$ (переход в неравенствах к пределу).

Замечание. Разумеется, существуют аналоги этих теорем и в том случае, когда один из пределов (или оба предела) бесконечен.

Контрольный вопрос.

Сформулируйте теорему о пределе суммы, если одна из последовательностей имеет конечный предел, вторая – бесконечный.

3.1.3 Арифметика бесконечно малых

Теорема. Пусть $a_n$, $b_n$ – бесконечно малые при $n \rightarrow +\infty$. Тогда $(a_n+b_n)$ – бесконечно малая при $n \rightarrow +\infty$.

Теорема. Пусть $a_n$ – бесконечно малая при $n \rightarrow +\infty$, $b_n$ – ограниченная последовательность. Тогда $a_n\cdot b_n$ – бесконечно малая при $n \rightarrow +\infty$.

Теорема. Пусть $a_n$ – бесконечно малая при $n \rightarrow +\infty$, \[ \lim _{n\rightarrow +\infty}b_n=B, \] причем $B$ – конечное число, $B \neq 0$. Тогда последовательность $(a_n / b_n)$ бесконечно малая при $n \rightarrow +\infty$.

Определение. Бесконечно малые $a_n$, $b_n$ называются эквивалентными, если существует предел \[ \lim _{n\rightarrow +\infty}a_n/b_n=\theta, \] причем $\theta \neq 0$, $\theta \neq \pm \infty$. Этот факт обозначают следующим образом: $a_n \sim b_n$ при $n \rightarrow +\infty$.

3.1.4 Признаки существования пределов

Следующие теоремы указывают условия, при которых последовательность имеет предел.

Теорема. Пусть $a_n$ – монотонно возрастающая последовательность, ограниченная сверху. Тогда она имеет конечный предел.

Следствие. Если $a_n$ – монотонно возрастающая последовательность, она имеет пределом либо $=+\infty$, либо конечное число. Соответственно, для монотонно убывающей последовательности.

Теорема. Пусть $a_n$ – монотонно убывающая последовательность, ограниченная снизу. Тогда она имеет конечный предел.

Теорема. Пусть для всех $n$ выполняются неравенства $a_n\leq b_n \leq c_n$, и \[ \lim _{n\rightarrow +\infty}a_n=A, \, \lim _{n\rightarrow +\infty}c_n=A. \] Тогда $b_n$ также имеет предел, причем \[ \lim _{n\rightarrow +\infty}b_n=A. \]

Критерий Коши. Для того, чтобы последовательность $a_n$ имела конечный предел, необходимо и достаточно, чтобы для любого $ \varepsilon >0$ существовало такое $N$, что при всех $m,n>N$ выполнялось $|a_n-a_m|

3.1.5 Вычисление пределов

Здесь мы приведем несколько примеров вычисления пределов последовательностей. При этом мы используем приведенные выше теоремы об арифметике пределов. {-1}$. ч.т.д.

2.3: Предельные законы и методы вычисления пределов

1. Последнее обновление

2. Сохранить как PDF

1. Оценка пределов с помощью предельных законов
2. Пределы полиномиальных и рациональных функций
3. Дополнительные методы оценки пределов
   1. Пример \ (\ PageIndex {4} \): оценка предела путем разложения и отмены
   2. Пример \ (\ PageIndex {5} \): Оценка предела путем умножения на конъюгат
   3. Пример \ (\ PageIndex {6} \): Оценка предела путем упрощения комплексной дроби
4. Теорема сжатия
   1. \ [\ lim_ {θ → 0} \ dfrac {\ sin θ} {θ} \]
   2. \ [\ displaystyle \ lim_ {θ → 0} \ dfrac {1- \ cos θ} {θ} \]
5. Ключевые понятия
6. Ключевые уравнения
7. Глоссарий
   1. Участники

В предыдущем разделе мы оценили пределы, глядя на графики или создавая таблицу значений. В этом разделе мы устанавливаем законы для расчета пределов и узнаем, как применять эти законы. В Студенческом проекте в конце этого раздела у вас есть возможность применить эти предельные законы, чтобы вывести формулу для площади круга, адаптировав метод, разработанный греческим математиком Архимедом. Начнем с повторения двух полезных результатов о пределе из предыдущего раздела. Эти два результата вместе с предельными законами служат основой для расчета многих пределов.

Оценка пределов с помощью законов о предельных значениях

Первые два предельных закона были изложены ранее, и мы повторяем их здесь.Эти основные результаты вместе с другими предельными законами позволяют нам оценить пределы многих алгебраических функций.

Результаты базового предела

Для любого действительного числа \ (a \) и любой константы \ (c \),

1. \ (\ Displaystyle \ lim_ {х → а} х = а \)
2. \ (\ Displaystyle \ lim_ {х → а} с = с \)

Пример \ (\ PageIndex {1} \): оценка базового предела

Оцените каждый из следующих пределов, используя Примечание.

1. \ (\ Displaystyle \ lim_ {х → 2} х \)
2. \ (\ Displaystyle \ lim_ {х → 2} 5 \)

Решение:

1. Предел x при приближении x к a равен a: \ (\ displaystyle \ lim_ {x → 2} x = 2 \).
2. Предел константы – это константа: \ (\ displaystyle \ lim_ {x → 2} 5 = 5 \).

Теперь посмотрим на законы пределов , отдельные свойства пределов. Доказательства справедливости этих законов здесь не приводятся.

Предельные законы

Пусть \ (f (x) \) и \ (g (x) \) определены для всех \ (x ≠ a \) на некотором открытом интервале, содержащем \ (a \). Предположим, что \ (L \) и \ (M \) – действительные числа, такие что \ (\ displaystyle \ lim_ {x → a} f (x) = L \) и \ (\ displaystyle \ lim_ {x → a} g (х) = М \).Пусть \ (c \) – постоянная. Тогда выполняется каждое из следующих утверждений:

\ [\ Displaystyle \ lim_ {x → a} (е (x) + g (x)) = \ lim_ {x → a} f (x) + \ lim_ {x → a} g (x) = L + M \]

• Закон разницы для пределов :

\ [\ Displaystyle \ lim_ {x → a} (f (x) −g (x)) = \ lim_ {x → a} f (x) – \ lim_ {x → a} g (x) = L −M \]

• Постоянный множественный закон для пределов :

\ [\ Displaystyle \ lim_ {x → a} cf (x) = c⋅ \ lim_ {x → a} f (x) = cL \]

\ [\ Displaystyle \ lim_ {x → a} (е (x) ⋅g (x)) = \ lim_ {x → a} f (x) ⋅ \ lim_ {x → a} g (x) = L⋅ M \]

\ [\ displaystyle \ lim_ {x → a} \ frac {f (x)} {g (x)} = \ frac {\ displaystyle \ lim_ {x → a} f (x)} {\ displaystyle \ lim_ { x → a} g (x)} = \ frac {L} {M} \]

для \ (M ≠ 0 \). n \]

для каждого положительного целого числа \ (n \).

\ [\ displaystyle \ lim_ {x → a} \ sqrt [n] {f (x)} = \ sqrt [n] {\ lim_ {x → a} f (x)} = \ sqrt [n] {L } \]

для всех \ (L \), если \ (n \) нечетно, и для \ (L≥0 \), если \ (n \) четно.

Сейчас мы практикуем применение этих законов о лимитах для оценки лимита.

Пример \ (\ PageIndex {2A} \): оценка лимита с использованием законов о лимитах

Используйте предельные законы для вычисления \ [\ lim_ {x → −3} (4x + 2). \ nonumber \]

Решение

Давайте применим законы предельных значений пошагово, чтобы убедиться, что мы понимаем, как они работают.Нам необходимо иметь в виду требование, согласно которому при каждом применении предельного закона должны существовать новые пределы для применения предельного закона.

\ (\ displaystyle \ lim_ {x → −3} (4x + 2) \) = \ (\ displaystyle \ lim_ {x → −3} 4x + \ lim_ {x → −3} 2 \) Примените закон суммы .

= \ (\ displaystyle 4⋅ \ lim_ {x → −3} x + \ lim_ {x → −3} 2 \) Примените постоянный кратный закон.

= \ (4⋅ (−3) + 2 = −10. \) Примените основные предельные результаты и упростите.

Обратите внимание, что это эквивалентно замене \ (- 3 \) на \ (x \) в исходной функции.3 + 4} = \ frac {1} {4} \). Применяйте основные предельные законы и упрощайте.

Обратите внимание, что это эквивалентно замене \ (2 \) на \ (x \) в исходной функции. Просто нужно быть осторожным, чтобы предел существовал на данный момент.

Упражнение \ (\ PageIndex {2} \)

Используйте предельные законы для вычисления \ (\ displaystyle \ lim_ {x → 6} (2x − 1) \ sqrt {x + 4} \). На каждом этапе указывайте применяемый предельный закон.

Подсказка

Начните с применения закона о продуктах.

Или просто замените \ (6 \) на \ (x \) в исходной функции. Просто нужно быть осторожным, чтобы предел существовал на данный момент.

Ответ

\ (11 \ sqrt {10} \)

Фундаментальные физические пределы вычислений

Примечание редактора (01.06.2011): мы делаем текст этой статьи от июля 1985 года бесплатно доступным в течение 30 дней, чтобы совпасть с публикацией статьи Влатко об энтропии и квантовых системах. Ведрал.Он является автором нашей обложки и блогов о своей последней работе за июнь 2011 года, в которых обсуждаются исследования, представленные в этой статье 1985 года.

Вычисление, выполняется ли оно электронным оборудованием, на счетах или в биологической системе, такой как мозг, является физическим процессом. Здесь возникают те же вопросы, которые применимы к другим физическим процессам: сколько энергии должно быть затрачено на выполнение конкретного вычисления? Как долго это должно продолжаться? Насколько большим должно быть вычислительное устройство? Другими словами, каковы физические ограничения процесса вычислений?

До сих пор было легче задать эти вопросы, чем ответить на них. В той мере, в какой мы нашли пределы, они ужасно далеки от реальных ограничений современных технологий. Следовательно, мы не можем претендовать на то, чтобы руководить технологом или инженером. То, что мы делаем, действительно более фундаментально. Мы ищем общие законы, которые должны регулировать всю обработку информации, независимо от того, как она осуществляется. Любые ограничения, которые мы обнаруживаем, должны основываться исключительно на фундаментальных физических принципах, а не на какой-либо технологии, которую мы можем использовать в настоящее время.

Существуют прецеденты такого рода фундаментальной экспертизы.В 1940-х годах Клод Э. Шеннон из Bell Telephone Laboratories обнаружил, что существуют ограничения на количество информации, которая может быть передана через шумный канал; эти ограничения применяются независимо от того, как сообщение закодировано в сигнал. Работа Шеннона представляет собой рождение современной информатики. Ранее, в середине и конце 19 века, физики, пытающиеся определить фундаментальные пределы эффективности паровых двигателей, создали науку термодинамику. Примерно в 1960 году один из нас (Ландауэр) и Джон Свансон из IBM начали попытки применить тот же тип анализа к процессу вычислений.С середины 1970-х годов в эту сферу начали приходить все больше других сотрудников других учреждений.

В нашем анализе физических ограничений вычислений мы используем термин «информация» в техническом смысле теории информации. В этом смысле информация уничтожается всякий раз, когда две ранее различные ситуации становятся неразличимыми. В физических системах без трения информация никогда не может быть уничтожена; всякий раз, когда информация уничтожается, некоторое количество энергии должно рассеиваться (превращаться в тепло).В качестве примера представьте две легко различимые физические ситуации, например, резиновый мяч, который удерживается на высоте одного или двух метров от земли. Если мяч упал, он отскочит. Если нет трения и мяч идеально эластичен, наблюдатель всегда сможет сказать, в каком состоянии мяч начинал (то есть, какова была его начальная высота), потому что мяч, упавший с двух метров, будет подпрыгивать выше, чем мяч. упал с одного метра.

Однако, если есть трение, мяч будет рассеивать небольшое количество энергии при каждом отскоке, пока, в конце концов, он не перестанет подпрыгивать и не остановится на земле.Тогда будет невозможно определить, каково было исходное состояние шара; мяч, брошенный с двух метров, будет идентичен мячу, брошенному с одного метра. Информация будет потеряна в результате рассеивания энергии.

Вот еще один пример уничтожения информации: выражение 2 + 2 содержит больше информации, чем выражение = 4. Если все, что мы знаем, это то, что мы сложили два числа, чтобы получить 4, то мы не знаем, сложили ли мы 1 + 3. , 2 + 2, 0 + 4 или другую пару чисел.Поскольку выходные данные неявны во входных данных, никакие вычисления никогда не генерируют информацию

Фактически, вычисления в том виде, в каком они выполняются в настоящее время, зависят от многих операций, уничтожающих информацию. Так называемые вентили и – это устройство с двумя входными линиями, каждая из которых может быть установлена ​​на 1 или 0, и одним выходом, значение которого зависит от значения входов. Если оба входа равны 1, выход будет 1. Если один из входов равен 0 или если оба равны 0, выход также будет 0. Каждый раз, когда выходом логического элемента является 0, мы теряем информацию, потому что мы не знаем, какой из трех возможных состояний, в которых были входные линии (0 и 1, 1 и 0 или 0 и 0).Фактически, любой логический вентиль, у которого больше входных линий, чем выходных линий, неизбежно отбрасывает информацию, потому что мы не можем вывести входные данные из выходных. Когда мы используем такие «логически необратимые» ворота, мы рассеиваем энергию в окружающей среде. Стирание небольшого количества памяти – еще одна операция, которая часто используется в вычислениях, – также фундаментально диссипативна; когда мы стираем бит, мы теряем всю информацию о предыдущем состоянии этого бита.

Важны ли для вычислений необратимые логические вентили и стирания? Если да, то любое вычисление, которое мы выполняем, должно рассеивать некоторое минимальное количество энергии.

Однако, как показал один из нас (Беннетт) в 1973 году, они не являются существенными. Этот вывод с тех пор был продемонстрирован на нескольких моделях; самые простые из них для описания основаны на так называемых обратимых логических элементах, таких как вентиль Фредкина, названный в честь Эдварда Фредкина из Массачусетского технологического института. Вентиль Фредкина имеет три входных линии и три выхода. Вход в одну линию, которая называется каналом управления, проходит через затвор без изменений. Если канал управления установлен на 0, вход на двух других линиях также проходит без изменений.Однако, если линия управления равна 1, выходы двух других линий переключаются: вход одной линии становится выходом другой и наоборот. Ворота Фредкина не сбрасывают никакой информации; входные данные всегда можно вывести из выходных.

Фредкин показал, что любое логическое устройство, необходимое в компьютере, может быть реализовано соответствующей схемой вентилей Фредкина. Чтобы вычисления работали, определенные входные линии некоторых вентилей Фредкина должны быть предварительно установлены на определенные значения.

У ворот Фредкина больше выходных линий, чем у ворот, которые они созданы для имитации. Поэтому в процессе вычислений генерируются то, что кажется «мусорными битами», битами информации, которые не имеют очевидного использования. Эти биты должны быть каким-то образом очищены от компьютера, если мы собираемся использовать его снова, но если мы удалим их, это будет стоить нам всей потери энергии, которую мы пытались избежать.

На самом деле эти биты имеют самое важное применение. После того, как мы скопировали результат наших вычислений, который будет находиться в обычных выходных битах, мы просто запускаем компьютер в обратном порядке.То есть мы вводим «мусорные биты» и выходные биты, которые были произведены при нормальной работе компьютера, как «входные данные» в «бэкэнд» компьютера. Это возможно, потому что каждый из логических вентилей в компьютере сам по себе обратим. Работа компьютера в обратном направлении не отбрасывает никакой информации, поэтому нет необходимости рассеивать энергию. В конце концов компьютер останется таким, каким он был до начала вычислений. Следовательно, можно завершить «вычислительный цикл», чтобы запустить компьютер, а затем вернуть его в исходное состояние без потери энергии.

До сих пор мы обсуждали набор логических операций, а не физическое устройство. Однако нетрудно представить себе физическое устройство, работающее как ворота Фредкина. В этом устройстве информационные каналы представлены трубами. Немного информации представлено наличием или отсутствием шара в определенном участке трубы; наличие шара означает 1, а отсутствие шара означает 0.

Контрольная линия представлена ​​узким сегментом трубы, разделенной по длине посередине.Когда шар входит в разделенный сегмент трубы, он раздвигает две половины трубы, приводя в действие переключающее устройство. Коммутационное устройство направляет любые входные шары, которые могут быть в двух других трубопроводах: когда мяч присутствует в линии управления, любой шар, который входит во входную трубу, автоматически перенаправляется на другую трубу. Чтобы гарантировать закрытие переключателя при отсутствии управляющего шара, имеются пружины, удерживающие вместе две половинки разъемной трубы. Шар, попадающий в разъемную трубу, должен расходовать энергию при сжатии пружин, но эта энергия не теряется; его можно восстановить, когда регулирующий шар покидает разрезную трубу и пружины растягиваются.

Все шары связаны друг с другом и толкаются вперед одним механизмом, так что они движутся синхронно; в противном случае мы не могли бы гарантировать, что различные входные и управляющие шары вместе попадут в логический вентиль. В некотором смысле поступательный прогресс вычислений на самом деле является движением по одной степени свободы, как движение двух колес, жестко прикрепленных к одной оси. После завершения вычислений мы толкаем все шары назад, отменяя все операции и возвращая компьютер в исходное состояние.

Если весь узел погружен в идеальную вязкую жидкость, тогда силы трения, действующие на шарики, будут пропорциональны их скорости; статического трения не будет. Следовательно, сила трения будет очень слабой, если мы будем довольствоваться медленным перемещением шариков. В любой механической системе энергия, которая должна быть затрачена на борьбу с трением, равна произведению силы трения и расстояния, которое проходит система. (Следовательно, чем быстрее пловец перемещается между двумя точками, тем больше энергии он или она потратит, хотя пройденное расстояние одинаково, независимо от того, является ли пловец быстрым или медленным.) Если мы перемещаем шары через ворота Фредкина с небольшой скоростью, то затрачиваемая энергия (произведение силы и расстояния) будет очень мала, потому что сила трения напрямую зависит от скорости шаров. Фактически, мы можем потратить столько энергии, сколько захотим, просто потратив много времени на выполнение операции. Таким образом, не существует минимального количества энергии, которое должно быть затрачено для выполнения любого заданного вычисления.

Энергия, теряемая на трение в этой модели, будет очень небольшой, если машина будет работать очень медленно. Можно ли сконструировать более идеализированную машину, которая могла бы выполнять вычисления без какого-либо трения? Или трение важно для вычислительного процесса? Фредкин вместе с Томмазо Тоффоли и другими из Массачусетского технологического института показал, что это не так.

Они продемонстрировали, что можно проводить вычисления, стреляя друг в друга идеальными бильярдными шарами без трения. В модели бильярдного шара идеально отражающие «зеркала» поверхности, которые перенаправляют движение шаров, расположены таким образом, что движение шаров по столу имитирует движение битов информации через логические элементы.Как и раньше, наличие шара в определенной части компьютера означает 1, а отсутствие шара означает 0. Если два шара одновременно прибывают к логическому элементу, они столкнутся, и их траектория изменится; их новые пути представляют собой выход ворот. Фредкин, Тоффоли и другие описали расположение зеркал, которые соответствуют различным типам логических элементов, и показали, что модели бильярдных шаров могут быть построены для имитации любого логического элемента, необходимого для вычислений.

Чтобы начать вычисление, мы запускаем бильярдный шар в компьютер, куда мы хотим ввести 1. Шары должны входить в машину одновременно. Поскольку они идеально эластичны, они не теряют энергию при столкновении; они выйдут из компьютера с тем же количеством кинетической энергии, которое мы дали им в начале.

При работе бильярдный компьютер производит «мусорные биты», как и компьютер, построенный из ворот Фредкина. После того, как компьютер получил ответ, мы отражаем бильярдные шары обратно в него, отменяя вычисление.Они выйдут из машины именно там, где мы их отправили, и с той же скоростью. Затем механизм, запустивший их в компьютер, можно использовать для поглощения их кинетической энергии. Мы снова выполнили вычисление и вернули компьютер в исходное состояние без потери энергии.

Компьютер для игры в бильярдный шар имеет один серьезный недостаток: он чрезвычайно чувствителен к незначительным ошибкам. Если мяч наведен немного неправильно или если зеркало наклонено под немного неправильным углом, траектории мяча будут сбиваться. Один или несколько шаров отклонятся от намеченных траекторий, и со временем ошибки объединятся, чтобы сделать все вычисления недействительными. Даже если бы можно было изготавливать совершенно упругие бильярдные шары без трения, небольшого количества случайного теплового движения в молекулах, из которых они состоят, было бы достаточно, чтобы вызвать ошибки после нескольких десятков столкновений.

Конечно, мы могли бы установить какое-то корректирующее устройство, которое вернет бильярдный шар, который заблудился, на его желаемую траекторию, но тогда мы уничтожим информацию о более ранней истории шара.Например, мы можем отбрасывать информацию о том, насколько неправильно наклонено зеркало. Отбросить информацию, даже чтобы исправить ошибку, можно только в системе, в которой есть трение и потеря энергии. Поэтому любое исправительное устройство должно рассеивать некоторую энергию.

Многие трудности, присущие компьютеру с бильярдным шаром, можно уменьшить, если вместо бильярдных шаров использовать микроскопические или субмикроскопические частицы, такие как электроны. Как отмечал Войцех Х.Зурек, который сейчас работает в Лос-Аламосской национальной лаборатории, указал, что квантовые законы, которые могут ограничивать частицы несколькими состояниями движения, могут исключить возможность того, что частица может отклониться на небольшое расстояние.

Хотя обсуждение до сих пор было основано в основном на классической динамике, несколько исследователей предложили другие обратимые компьютеры, основанные на квантово-механических принципах. Такие компьютеры, впервые предложенные Полом Бениоффом из Аргоннской национальной лаборатории и усовершенствованные другими, в частности Ричардом П.Фейнмана из Калифорнийского технологического института, до сих пор были описаны только в самых абстрактных терминах. По сути, частицы в этих компьютерах должны быть устроены так, чтобы квантово-механические правила, управляющие их взаимодействием, были бы в точности аналогичны правилам, описывающим предсказанные выходы различных обратимых логических вентилей. Например, предположим, что спин частицы может иметь только два возможных значения: вверх (соответствует двоичной 1) и вниз (соответствует 0). Взаимодействия между спинами частиц могут быть заданы таким образом, что значение спина одной частицы изменяется в зависимости от спина соседних частиц; спин частицы будет соответствовать одному из выходов логического элемента.

Пока что это обсуждение было сосредоточено на обработке информации. Компьютер должен не только обрабатывать информацию, но и хранить ее. Взаимодействие между хранением и обработкой данных лучше всего описать в терминах устройства, называемого машиной Тьюринга, для Алана М. Тьюринга, который впервые предложил такую ​​машину в 1936 году. Машина Тьюринга может выполнять любые вычисления, которые могут быть выполнены на современном компьютере. Один из нас (Беннетт) показал, что можно построить обратимую машину Тьюринга: машину Тьюринга, которая не отбрасывает информацию и, следовательно, может работать с минимальными затратами энергии по желанию пользователя.

Машина Тьюринга состоит из нескольких компонентов. Есть лента, разделенная на отдельные кадры или сегменты, каждый из которых отмечен цифрой 0 или 1; эти биты представляют вход. «Головка чтения / записи» перемещается по ленте. Голова выполняет несколько функций. Он может читать один бит ленты за раз, он может печатать один бит на ленте и может сдвигать свое положение на один сегмент влево или вправо. Чтобы от одного цикла к другому запоминать, что он делает, головной механизм имеет несколько различных «состояний»; каждый штат составляет

В каждом цикле головка считывает бит в сегменте, который она в данный момент занимает; затем он печатает новый бит на ленте, изменяет свое внутреннее состояние и перемещает один сегмент влево или вправо.Бит, который он печатает, состояние, в которое он переходит, и направление, в котором он движется, определяются фиксированным набором правил перехода. Каждое правило определяет определенный набор действий. Какому правилу следует машина, определяется состоянием головки и значением бита, который она считывает с ленты. Например, одно правило может быть таким: «Если головка находится в состоянии A и сидит на сегменте ленты, на котором напечатано 0, она должна изменить этот бит на 1, изменить свое состояние на состояние B . и переместите один сегмент вправо.«Может случиться так, что правило перехода предписывает машине не изменять свое внутреннее состояние, не печатать новый бит на ленте или не останавливать свою работу. Не все машины Тьюринга обратимы, но обратимая машина Тьюринга может быть построена для выполнения любые возможные вычисления.

Обратимые модели машины Тьюринга имеют преимущество перед такими машинами, как компьютер с бильярдным шаром без трения. В бильярдном компьютере случайное тепловое движение вызывает неизбежные ошибки. В моделях обратимой машины Тьюринга на самом деле используется случайное тепловое движение: они построены таким образом, что само тепловое движение с помощью очень слабой движущей силы переводит машину из одного состояния в другое.Ход вычислений напоминает движение иона (заряженной частицы), взвешенного в растворе, находящемся в слабом электрическом поле. Движение иона за короткий промежуток времени кажется случайным; вероятность его движения в одном направлении почти такая же, как и в другом. Однако приложенная сила электрического поля придает чистому движению предпочтительное направление: ион с меньшей вероятностью движется в одном направлении, чем в другом.

На первый взгляд может показаться невероятным, чтобы целенаправленная последовательность операций, такая как вычисление, могла быть достигнута в устройстве, направление движения которого в любой момент времени является почти случайным.Однако этот стиль работы довольно распространен в микроскопическом мире химических реакций. Там действия методом проб и ошибок броуновского движения или случайного теплового движения достаточно, чтобы привести молекулы реагента в контакт, ориентировать и изогнуть их в определенной конформации, необходимой для их реакции, и разделить молекулы продуктов после реакции. Все химические реакции в принципе обратимы: одно и то же броуновское движение, которое завершает прямую реакцию, иногда объединяет молекулы продуктов и толкает их назад через переход.В состоянии равновесия обратная реакция так же вероятна, как и прямая.

Для того, чтобы реакция продолжалась в прямом направлении, мы должны подавать молекулы реагентов и удалять молекулы продуктов; по сути, мы должны обеспечить небольшую движущую силу. Когда движущая сила очень мала, реакция будет делать почти столько же шагов назад, сколько и вперед, но в среднем она будет двигаться вперед. Чтобы обеспечить движущую силу, мы должны расходовать энергию, но, как и в нашей простой реализации ворот Фредкина, общее количество энергии может быть сколь угодно малым; если мы готовы выделить на операцию долгое время, не существует минимального количества энергии, которое необходимо затратить.Причина в том, что общая рассеиваемая энергия зависит от количества шагов вперед, деленного на количество шагов назад. (На самом деле оно пропорционально логарифму этого отношения, но по мере того, как это отношение увеличивается или уменьшается, то же самое происходит и с его логарифмом. Чем медленнее реакция продвигается вперед, тем меньше будет соотношение. (Аналогия с более быстрыми и медленными пловцами снова верна: требуется меньше общей энергии, чтобы продвинуться вперед на такое же чистое количество шагов реакции, если реакция движется медленно. )

Мы можем увидеть, как может работать броуновская машина Тьюринга, исследуя броуновскую машину для копирования ленты, которая уже существует в природе: РНК-полимеразу, фермент, который помогает создавать копии РНК ДНК, составляющей ген. Одна нить ДНК очень похожа на ленту машины Тьюринга. В каждой позиции цепи есть одно из четырех «оснований»: аденин, гуанин, цитозин или тимин (сокращенно A, G, C и I) . РНК представляет собой подобную цепочку молекулу, у которой четыре основания, аденин, гуанин, цитозин и урацил (A.G. C и U) связываются с «комплементарными» основаниями ДНК.

РНК-полимераза катализирует эту реакцию спаривания. Спираль ДНК обычно окружена раствором, содержащим большое количество молекул нуклеозидтрифосфата, каждая из которых состоит из основания РНК, связанного с сахаром, и хвоста из трех фосфатных групп. Фермент РНК-полимераза выбирает из раствора одно основание РНК, которое комплементарно основанию, которое должно быть скопировано на нити ДНК.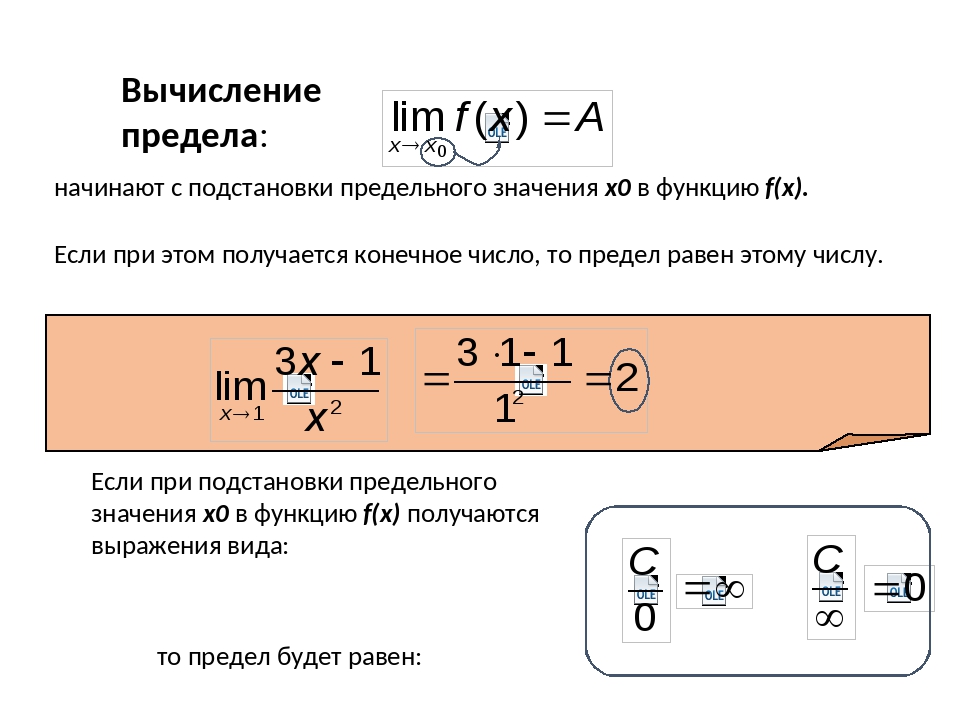 Затем он прикрепляет новое основание к концу растущей цепи РНК и высвобождает два фосфата в окружающий раствор в виде свободного пирофосфат-иона.Затем фермент сдвигается вперед на одну метку вдоль цепи ДНК, готовясь к присоединению следующего основания РНК. В результате получается цепь РНК, которая комплементарна цепи матрицы ДНК. Без РНК-полимеразы этот набор реакций происходил бы очень медленно, и было бы мало гарантии, что молекулы РНК и ДНК будут комплементарными.

Реакции обратимы: иногда фермент захватывает свободный пирофосфат-ион, объединяет его с последним основанием на цепи РНК и возвращает образовавшуюся молекулу нуклеозидтрифосфата в окружающий раствор, при этом делая резервную копию на одну ступеньку вдоль цепи ДНК.В состоянии равновесия шаги вперед и назад будут происходить с одинаковой частотой; обычно другие метаболические процессы ускоряют реакцию, удаляя пирофосфат и поставляя четыре вида нуклеозидтрифосфата.

В лаборатории скорость, с которой действует РНК-полимераза, может быть изменена путем регулирования концентраций реагентов (как показали Джудит Левин и Майкл Дж. Чемберлин из Калифорнийского университета в Беркли). По мере приближения концентраций к равновесию фермент работает медленнее и рассеивает меньше энергии, чтобы скопировать данный участок ДНК, потому что соотношение шагов вперед и назад меньше.

Хотя РНК-полимераза просто копирует информацию, не обрабатывая ее, относительно легко представить, как могла бы работать гипотетическая химическая машина Тьюринга. Лента представляет собой одну молекулу с длинным скелетом, к которой в периодических сайтах прикрепляются два типа оснований, представляющие двоичные 0 и 1. Небольшая дополнительная молекула присоединяется к группе 0 или 1 в одном месте цепи. Положение этой дополнительной молекулы соответствует положению головы машины Тьюринга. Существует несколько различных типов «молекулы головы», каждый из которых представляет свое состояние машины.

Правила перехода машины представлены ферментами. Каждый фермент способен катализировать одну конкретную реакцию. Как работают эти ферменты, лучше всего продемонстрировать на примере.

Предположим, что молекула головы имеет тип A (что указывает на то, что машина находится в состоянии A ) и прикреплена к основанию 0. Также предположим, что применяется следующее правило перехода: «Когда головка находится в состоянии A и читает 0, измените 0 на 1, измените состояние на B и переместитесь вправо.«Молекула фермента, представляющая это правило, имеет сайт, который соответствует головной молекуле типа A , присоединенной к основанию 1. У нее также есть один сайт, который соответствует основанию 0, и один сайт, который соответствует головке B [см. рисунок на противоположной странице).

Для достижения перехода молекула фермента сначала приближается к молекуле ленты в месте «справа от основания, на котором расположена головка A ». Затем он отделяет от ленты и молекулу головы, и основание 0, к которому была прикреплена голова, помещая на их место основание 1.Затем он прикрепляет головку B к основанию, которое находится справа от 1 основы, которую он только что добавил к ленте. На этом переход завершен. Исходный участок головы изменен с 0 на 1, молекула головы теперь имеет тип B , и она прикреплена к основанию, которое находится на одну метку правее предыдущего положения головы.

Во время работы броуновской машины Тьюринга лента должна быть погружена в раствор, содержащий множество молекул фермента, а также лишние O, единицы, A и B .Чтобы продвинуть реакцию вперед, должна быть какая-то другая реакция, которая очистит молекулы фермента от отделившихся головок и оснований. Концентрации реагентов, очищающих молекулы фермента, представляют собой силу, которая движет машину Тьюринга вперед. Опять же, мы можем расходовать столько энергии, сколько захотим, просто очень медленно двигая машину вперед.

Ферментативная машина Тьюринга не безошибочна. Иногда может произойти реакция, которая не катализируется каким-либо ферментом; например, основание 0 может самопроизвольно отщепляться от молекулы скелета, а основание 1 может быть присоединено на его месте. Подобные ошибки действительно происходят при синтезе РНК.

В принципе, можно было бы устранить ошибки, построив броуновскую машину Тьюринга из жесткого часового механизма без трения. Заводная машина Тьюринга предполагает меньшую идеализацию, чем компьютер с бильярдным шаром, но больше, чем ферментативная машина Тьюринга. С одной стороны, его части не нужно изготавливать с идеальными допусками, как это должны были бы быть бильярдные шары; детали плохо прилегают друг к другу, и машина может работать даже при наличии большого количества теплового шума.Тем не менее, его части должны быть абсолютно жесткими и не иметь статического трения – свойств, которых нет ни в одном макроскопическом теле.

Поскольку части машины плохо прилегают друг к другу, они удерживаются на месте не за счет трения, а за счет канавок или выемок в соседних деталях. Хотя каждая часть машины может немного покачиваться, как части изношенной деревянной головоломки, машина в целом может следовать только по одному «вычислительному пути». То есть части машины сцепляются таким образом, что в любой момент машина может совершать только два вида крупномасштабных движений: движение, соответствующее шагу вычисления вперед, и движение, соответствующее шагу назад.

Компьютер совершает такие переходы только как случайный результат случайного теплового движения его частей, смещенных слабой внешней силой. Вероятность продолжения назад по вычислительному пути с отменой самого последнего перехода почти такая же, как и для продолжения вперед. Небольшая сила, приложенная извне, продвигает вычисления вперед. Эта сила может быть сколь угодно малой, поэтому не существует минимального количества энергии, которое необходимо затратить для работы броуновской часовой машины Тьюринга.

Согласно классической термодинамике, нет минимального количества энергии, необходимого для выполнения вычислений. Противоречит ли классический термодинамический анализ квантовой теории? В конце концов, квантово-механический принцип неопределенности гласит, что должна существовать обратная зависимость между нашей неуверенностью в том, сколько времени занимает процесс, и нашей неуверенностью в том, сколько энергии в этот процесс вовлечено. Некоторые исследователи предположили, что любой процесс переключения, происходящий за короткий период времени, должен включать минимальные затраты энергии.

Фактически принцип неопределенности не требует минимальных затрат энергии на быстрое переключение. Принцип неопределенности будет применим только в том случае, если мы попытаемся измерить точное время, в которое произошло событие. Даже в квантовой механике чрезвычайно быстрые события могут происходить без потери энергии. Наша уверенность в том, что квантовая механика позволяет выполнять вычисления без каких-либо минимальных затрат, укрепляется, если мы вспомним, что Бениофф и другие разработали модели обратимых квантово-механических компьютеров, которые не рассеивают энергию и подчиняются законам квантовой механики.

Таким образом, принцип неопределенности, похоже, не налагает фундаментальных ограничений на процесс вычислений; классическая термодинамика тоже. Означает ли это, что у вычислений нет физических ограничений? Отнюдь не. Настоящие ограничения связаны с вопросами, на которые гораздо труднее ответить, чем на те, которые мы задали в этой статье.

Например, требуют ли элементарные логические операции некоторого минимального количества времени? Какое минимально возможное устройство могло бы выполнять такие операции? Поскольку масштабы размера и времени связаны скоростью света, вполне вероятно, что на эти два вопроса есть связанные ответы.Однако мы не сможем найти эти ответы до тех пор, пока не будет определено, существует ли некоторая предельная зернистость в универсальных шкалах времени и длины.

С другой стороны, насколько большой мы можем сделать память компьютера? Сколько частиц во Вселенной мы можем собрать и удержать вместе для этой цели? Максимально возможный размер компьютерной памяти ограничивает точность, с которой мы можем производить вычисления. Это ограничит, например, количество десятичных знаков, до которых мы можем вычислить число пи.Неизбежные процессы ухудшения, которые происходят в реальных компьютерах, ставят другой, возможно связанный, вопрос: может ли износ, по крайней мере в принципе, быть уменьшен до любой желаемой степени, или это налагает ограничение на максимальный промежуток времени, который мы можем посвятить к какому-то одному расчету? То есть, существуют ли определенные вычисления, которые нельзя завершить до тех пор, пока аппаратное обеспечение компьютера не придет в негодность?

Такие вопросы действительно касаются ограничений на физическое выполнение математических операций. Физические законы, на которых в конечном итоге должны основываться ответы, сами выражаются в терминах таких математических операций. Таким образом, мы спрашиваем о конечной форме, в которой могут быть применены законы физики, учитывая ограничения, налагаемые вселенной, которые сами законы описывают.

Пределы вычислений | SpringerLink

Абрамский С. (1991) Теория предметной области в логической форме. Ann Pure Appl Logic 51 (1–77)

Ackermann W (1928) Zum hilbertschen aufbau der reellen zahlen.Math Ann 99: 118–133

Статья Google Scholar

Aczel, P. (1977) Введение в индуктивные определения. В: Barwise J (ed) «Handbook of Mathematical Logic», North-Holland, chapter C.7, pp. 739–780

Aczel P (1978) Теоретико-типовая интерпретация конструктивной теории множеств. В: MacIntyre A (ed) Logic colloquium ’77. Северная Голландия, Амстердам, стр. 55–66

Глава Google Scholar

Авигад Дж. , Феферман С. (1998) Функциональная (диалектическая) интерпретация Гёделя.В: Buss S (ed) Справочник по теории доказательств. Elsevier, pp 337–405

Awodey S (2012) Теория типов и гомотопия, в «Эпистемология против онтологии». Springer 183–201

Awodey S (2013) Теория гомотопического типа: однолистные основы математики. Принстонский университет, Институт перспективных исследований

Google Scholar

Awodey S, Warren M (2009) Теоретико-гомотопические модели типов идентичности.Math Proc Cambridge Philos Soc 146 (1): 145–144

Статья Google Scholar

Barendregt H (1991) Введение в системы обобщенных типов. J Funct Prog 1 (2): 125–154

Статья Google Scholar

Белл Дж., Мачовер М. (1977) Курс математической логики, Северная Голландия

Берарди С. (1988) К математическому анализу исчисления конструкций Кокана – Хуэ и других систем в кубе Барендрегта, Технический отчет CMU-CS-88-131, Universita di Torino

Cardelli L (1988) Структурные подтипы и понятие типа мощности, в ‘POPL ’88: Материалы 15-го симпозиума ACM SIGPLAN-SIGACT по принципам программирования languages ​​’, Ассоциация вычислительной техники, стр.70–79

Чёрч А. (1950) Формулировка простой теории типов. J Symb Logic 5 (2): 56–68

Артикул Google Scholar

Coquand T, Huet G (1988) Расчет конструкций. Inf Comput 76: 95–120

Статья Google Scholar

Карри Х (1934) Функциональность в комбинаторной логике. Proc Nat Acad Sci USA 20 (11): 584–90

Статья Google Scholar

Fairtlough M, Wainer S (1992) Порядковая сложность рекурсивных определений. Inf Comput 99: 123–152

Статья Google Scholar

Фармер В. (2007) Семь достоинств теории простых типов. J Appl Logic 6: 267–286

Статья Google Scholar

Феферман С. (1985) Интенциональность в математике. J Philosop Logic 14 (1): 41–55

Google Scholar

Феферман С. (1988) Вейль подтвердил: Das Kontinuum 70 лет спустя, In C.Целлуччи и Дж. Самбин, ред., «Теми и проспеттив делла логика и делла наука современности», 1: 59–93

Генцен Г. (1969a) Исследования в области логической дедукции. Пер. М. Э. Сабо из «Untersuchungen über das logische Schließen. Я”. Mathematische Zeitschrift. 39 (2): 176–210. 1935 г. и «Untersuchungen über das logische Schließen. II ». Mathematische Zeitschrift. 39 (3): 405–431. 1935., В М. Э. Сабо, изд., «Собрание статей Герхарда Гентцена», Vol. 55 исследований по логике и основам математики, Северная Голландия, стр. 68–131

Генцен Г. (1969b), Новая версия доказательства непротиворечивости элементарной теории чисел. Пер. М. Э. Сабо из «Neue Fassung des Widerspruchsfreiheitsbeweises für die reine Zahlentheorie», Forschungen zur Logik und zur Grundlegung der Exakten Wissenschaften, 4: 19–44, In M. Szabo, ed., «Collected Papers of Volhard. 55 исследований по логике и основам математики, Северная Голландия, стр. 252–286

Гёверс Х., Недерпельт Р.(2014) Теория типов и формальное доказательство, Cambridge University Press

Girard, J.-Y. (1972) Функция интерпретации и определение превосходной арифметики, докторская диссертация, Парижский университет VII

Жирар, JY (1973) Quelques résultats sur les интерпретация fonctionnelles, В А. Р. Д. Матиас и Х. Роджерс, ред., «Кембриджская летняя школа по математической логике, 1971», Vol. 337 Lecture Notes in Mathematics, Springer, pp. 232–252

Girard J-Y (1986) Система F типов переменных, пятнадцать лет спустя. Theoret Comput Sci 45: 159–192

Статья Google Scholar

Girard J-Y (1989) Образцы и образцы. Cambridge University Press

Gödel K (1931) Über form unentscheidbare Sätze der Principia Mathematica und Verwandter Systeme. I. Monatshefte für Mathematik und Physik 38 (1): 173–198

Статья Google Scholar

Gödel, K. (1958) Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes, Dialectica pp.280–287

Гёдель К. (1994) О расширении финитарных методов, которое еще не использовалось, В С. Феферман, изд., «Собрание сочинений, т. III ’, Oxford University Press, стр. 271–280

Griffin TG. (1989), Понятие управления как типа формул, В «POPL ’90: Материалы 17-го симпозиума ACM SIGPLAN-SIGACT по принципам языков программирования», стр. 47–58.

Guallart N (2015) Обзор теорий типов. Аксиоматес 25: 61–77

Google Scholar

Хеллман Г (1989) Математика без чисел.К модально-структурной интерпретации. Кларендон Пресс

Hinman PG. (1978) Теоретико-рекурсивные иерархии, Перспективы в логике, Издательство Кембриджского университета

Ховард У. (1970) Присвоение ординалов терминам для примитивных рекурсивных функционалов конечного типа, In R. VA Kino, J. Myhill, ed. , «Интуиционизм и теория доказательств: материалы летней конференции в Буффало, штат Нью-Йорк, 1968», Vol. 60 исследований по логике и основам математики, Северная Голландия, стр.443–458

Ховард В. (1980a) Понятие построения формул как типов, В Дж. Селдоне, Дж. Хиндли, ред., «To H.B. Карри: Очерки комбинаторной логики, лямбда-исчисления и формализма », Academic Press, стр. 479–490

Говард В. (1980b) Порядковый анализ членов конечного типа. J Symb Logic 45 (3): 493–504

Артикул Google Scholar

Kleene S (1943) Рекурсивные предикаты и кванторы. Transact Am Math Soc 53 (1): 41–73

Статья Google Scholar

Коепке П., Сейфферт Б. (2009) Порядковые машины и допустимая теория рекурсии. Ann Pure Appl Logic 160: 310–318

Статья Google Scholar

Кривино ЖЛ. (2001) «Типизированное лямбда-исчисление в классической теории множеств Цермело-Френкеля», Arch Math Logic, 40 (3): 189–205

Longley JR.(2005) Понятия вычислимости в высших типах I, В STR Cori, А. Разборов и С. Вуд, ред., «Logic Colloquium 2000», стр. 22–142

Luo Z. (1989) ECC и расширенное исчисление конструкции, In ‘Proceedings of the Fourth Annual Symposium on Logic in computer science’, стр. 385–395

Мартин-Лёф П. (1984) Интуиционистская теория типов, Исследования по теории доказательства, Библиополис

Myhill JR (1973) Некоторые свойства интуиционистской теории множеств Цермело-Френкеля, В трудах Кембриджской летней школы 1971 г. по математической логике 1, т.337 конспектов лекций по математике, стр. 206–23

Оливо П. (2008) Анализ интерпретации диалектики Гёделя с помощью линейной логики. Dialiectica 62 (2): 269–290

Статья Google Scholar

Ore CE (1992) «Расширенное исчисление конструкций (ECC) с индуктивными типами», Информационно-вычислительный том 99, выпуск 2, август 1992 г., страницы 231-264 99 (2): 231–264

Parsons C (1972) Призыв к количественной оценке замещения.J Philos 68 (8): 231–237

Статья Google Scholar

Paulin-Mohring C. (2015) Введение в исчисление индуктивных построений, In BW Paleo, D Delahaye, eds, «All about Proofs, Proofs for All», Vol. 55, College Publications

Pistone P (2018) Полиморфизм и упорная замкнутость логики второго порядка: рассказы жертв. Bull Symb Logic 24 (1): 1–52

Статья Google Scholar

Prawitz D (2006) Естественная дедукция: теоретико-доказательное исследование, впервые опубликовано, изд. 1965 г.Dover

Rathjen M (2006) Искусство порядкового анализа, В «Слушаниях Международного конгресса математиков». Европейское математическое общество 45–69

Ратьен М. (2017) «О связи теорий типов с (интуиционистскими) теориями множеств», выступление в Калифорнийском университете в Беркли 5 мая 2017 г., доступно онлайн

Ратьен М. (2018) Доказательство теория конструктивных систем: индуктивные типы и однолистность. В: Jäger G, Sieg W (eds) Feferman on Foundation », номер 13 в« Выдающемся вкладе в логику ».Springer, NewYork, pp. 385–419

Google Scholar

Roberts S (2017) Принцип сильного отражения. Версия Rev Symbc Logic 10 (4): 651–662

Статья Google Scholar

Рассел Б. (1908) Математическая логика, основанная на теории типов. Am J Math 30: 222–262

Статья Google Scholar

Скотт Д. С.(1976) Типы данных как решетки, Programming Research Group PRG-5, Computing Laboratory Оксфордского университета

Скотт Д.С. (1993) Теоретико-типовая альтернатива ISWIM CUCH, OWHY. Theor Comp Sci 121: 411–440

Статья Google Scholar

Шенфилд Дж. (1967) Математическая логика, издательство Addison-Wesley Publishing Company

Сморински К. (1980) Некоторые быстрорастущие функции. Math Intell 2 (149–154)

Тейт В. В. (1961) Вложенная рекурсия.Math Ann 143: 236–250

Статья Google Scholar

Tait WW (1965a) Функционалы, определяемые трансфинитной рекурсией. J Symb Logic 30 (2): 155–174

Артикул Google Scholar

Tait WW (1965b) Бесконечно длинные члены трансфинитного типа. В: Crossley JN, Dummett MAE (eds) Формальные системы и рекурсивные функции. Северная Голландия, Лондон, стр. 176–185

Глава Google Scholar

Tait WW (2006) Гедельская интерпретация интуиционизма.Philosophia Mathematica 14 (2): 208–228

Статья Google Scholar

Terlouw J (1982) О деревьях определения порядковых рекурсивных функционалов: уменьшение порядков рекурсии посредством повышения уровня типа. J Symb Logic 47 (2): 395–402

Артикул Google Scholar

Терлоу Дж. (1989) Een nadere bewijstheoretische analysis van GSTTs, Технический отчет, Университет Неймегена

Тьюринг А. (1937) О вычислимых числах, с приложением к проблеме Entscheidungsproblem.Proc London Math Soc Series 2 (42): 230–265

Статья Google Scholar

Тернер Р. (1990) Истина и модальность для представления знаний, Pitman Publishing

Вяэнянен Дж. (2001) Логика второго порядка и основы математики. Bull Symb Logic 7 (4): 504–520

Статья Google Scholar

ван Дален Д. (2001) Интуиционистская логика, в «Руководстве Блэквелла по философской логике».Блэквелл 224–257

фон Нейман Дж, (1967) Аксиоматизация теории множеств; Перевод J. van Heijenoort из Eine Axiomatisierung der Mengenlehre, Journal of die Reine und Angewandte Mathematik, (1925) 154: 219–240. В: van Heijenoort J (ed) From Frege to Godel: A Source Book in Mathematical Logic. Издательство Гарвардского университета, стр. 290–301

Велч П.Д., Хорстен Л. (2016) Размышляя об абсолютной бесконечности. J Philosop 113 (2): 89–111

Google Scholar

Вернер Б.(1997) Наборы в типах, типы в наборах, In M Abadi and T. Ito, eds, «TACS 1997: Теоретические аспекты компьютерного программного обеспечения», Vol. 1281 конспектов лекций по информатике, Springer, стр. 530–546

Пределы энергии в вычислениях | SpringerLink

‘) var cartStepActive = true var buybox = document.querySelector (“[data-id = id _” + отметка времени + “]”).parentNode ; []. slice.call (buybox.querySelectorAll (“. покупка-опция”)). forEach (initCollapsibles) функция initCollapsibles (подписка, индекс) { var toggle = subscription.querySelector (“. цена-опции-покупки”) subscription.classList.remove (“расширенный”) var form = subscription.querySelector (“. Purchase-option-form”) if (form && cartStepActive) { var formAction = form.getAttribute (“действие”) form.setAttribute (“действие”, formAction. replace (“/ checkout”, “/ cart”)) document.querySelector (“# сценариев электронной торговли”). addEventListener (“загрузка”, bindModal (форма, formAction, отметка времени, индекс), false) } var priceInfo = subscription.querySelector (“. price-info”) var buyOption = toggle.parentElement if (переключить && форму && priceInfo) { переключать.setAttribute (“роль”, “кнопка”) toggle.setAttribute (“tabindex”, “0”) toggle.addEventListener (“клик”, функция (событие) { var extended = toggle.getAttribute (“aria-extended”) === “true” || ложный toggle.setAttribute (“расширенный ария”,! расширенный) form.hidden = расширенный если (! расширено) { покупка вариант. classList.add («расширенный») } еще { buyOption.classList.remove («расширенный») } priceInfo.hidden = расширенный }, ложный) } } function bindModal (form, formAction, timestamp, index) { var weHasBrowserSupport = window.fetch && Array.from return function () { var Buybox = EcommScripts? EcommScripts.Ящик для покупок: null var Modal = EcommScripts? EcommScripts.Modal: null if (weHasBrowserSupport && Buybox && Modal) { var modalID = “ecomm-modal_” + отметка времени + “_” + индекс var modal = новый модальный (modalID) modal. domEl.addEventListener (“закрыть”, закрыть) function close () { форма.querySelector (“кнопка [тип = отправить]”). focus () } form.setAttribute ( “действие”, formAction.replace (“/ checkout”, “/ cart? messageOnly = 1”) ) form.addEventListener ( “Отправить”, Buybox.interceptFormSubmit ( Buybox.fetchFormAction (window.fetch), Buybox.triggerModalAfterAddToCartSuccess (модальный), console.log, ), ложный ) document. body.appendChild (modal.domEl) } } } function initKeyControls () { документ.addEventListener (“нажатие клавиши”, функция (событие) { if (document.activeElement.classList.contains (“покупка-опция-цена”) && (event.code === “Space” || event.code === “Enter”)) { if (document.activeElement) { event.preventDefault () document.activeElement.click () } } }, ложный) } function initialStateOpen () { var buyboxWidth = buybox.offsetWidth ; []. slice.call (buybox.querySelectorAll (“. покупка-опция”)). forEach (function (option, index) { var toggle = option.querySelector (“.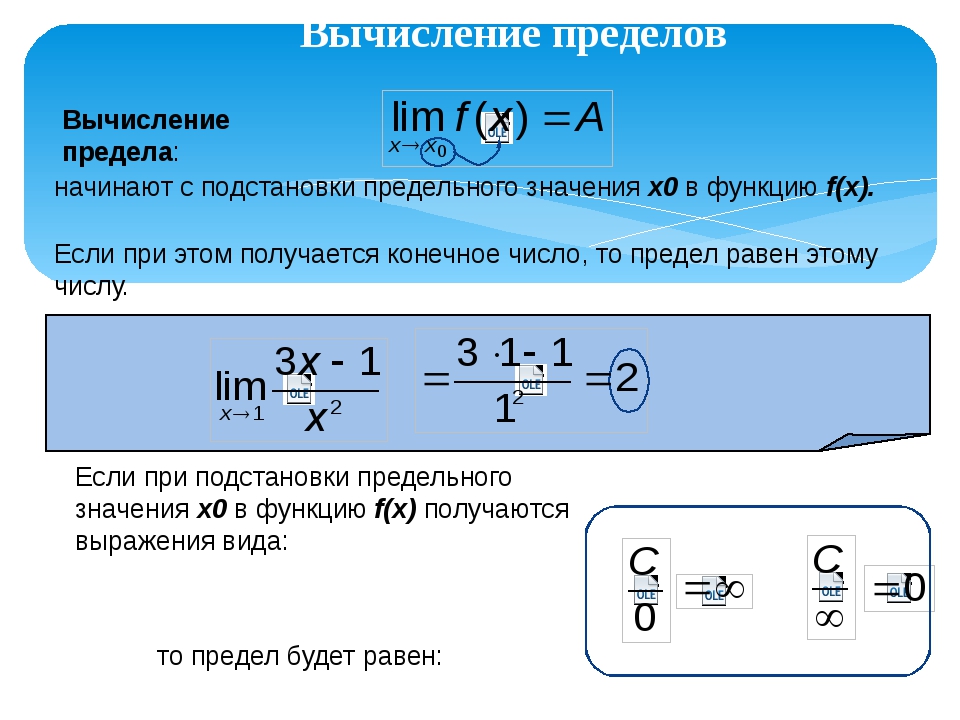 покупка-вариант-цена”) var form = option.querySelector (“. Purchase-option-form”) var priceInfo = option.querySelector (“. цена-информация”) if (buyboxWidth> 480) { toggle.click () } еще { if (index === 0) { переключать.нажмите () } еще { toggle.setAttribute (“расширенная ария”, “ложь”) form.hidden = “скрытый” priceInfo.hidden = “скрыто” } } }) } initialStateOpen () если (window.buyboxInitialised) вернуть window.buyboxInitialised = true initKeyControls () }) ()

Приложение 14: Руководство по подсчету лет службы, которые учитываются до восьмилетнего предела

Сводка руководства по академическому персоналу Раздел 133

Действует с 1 сентября 2015 г.

---

И.Расчет восьмилетнего лимита

Для лица, назначенного на учебный год (9 месяцев), восьмилетний лимит состоит из: 24 (двадцати четырех) полных кварталов; или шестнадцать (16) полных семестров; или комбинация этих двух с одним семестром, равным полутора четвертям.

Для лица, назначенного на финансовый год (11 месяцев), восьмилетний предел состоит из девяноста шести (96) месяцев работы, включая взятый отпуск.

Прекращение службы с последующим трудоустройством не влияет на подсчет услуг до прерывания.Служба в любом названии менее полного рабочего дня, будучи студентом в любом кампусе Калифорнийского университета, не засчитывается.

II. Служба в нескольких титулах имеет значение до восьмилетнего лимита

Сроки службы в нескольких титулах засчитываются в восьмилетний лимит, как указано в следующих подразделах: [1]

A. Доцент или доцент по месту жительства

Для лица с вышеупомянутым назначением, периоды службы в любом кампусе Калифорнийского университета в любой комбинации следующих названий засчитываются в восьмилетний лимит:

• Доцент
• И. о. доцента
• Приглашенный доцент
• И.о. доцента
• Приглашенный доцент
• И.о. профессора
• Приглашенный профессор
• Доцент по месту жительства
• Доцент кафедры клинической медицины (X)
• Ассистент адъюнкт-профессора более 50% времени (см. APM 280-16-c)
• Лектор – Потенциальная гарантия занятости (PSOE) на 100% времени
• Лектор – Гарантия занятости (SOE)
• Старший преподаватель (ГП)

Если иное не указано выше, назначение в любой процент времени, включая 0% (WOS), засчитывается в восьмилетний лимит, если только назначение 0% (WOS) не является также без шага.

B. Ассистент кафедры клинической медицины (X), или более 50% времени в качестве: наук о здоровье
Ассистент клинического профессора, младший адъюнкт-профессор или младший научный сотрудник

Для лица с указанным выше назначением, периоды службы в любом кампусе Калифорнийского университета в любой комбинации следующих названий засчитываются в восьмилетний лимит:

• Доцент
• И. о. доцента
• Приглашенный доцент
• И.о. доцента
• Приглашенный доцент
• И.о. профессора
• Приглашенный профессор
• Доцент по месту жительства
• Доцент кафедры клинической медицины (X)
• Ассистент клинического профессора медицинских наук, работающий более 50% времени
• Ассистент адъюнкт-профессора более 50% рабочего времени
• Помощник научного сотрудника, работающий более 50% времени
• Лектор – Потенциальная гарантия занятости (PSOE) на 100% времени
• Лектор – Гарантия занятости (SOE)
• Старший преподаватель (ГП)

Если иное не указано выше, назначение в любой процент времени, включая 0% (WOS), засчитывается в восьмилетний лимит, если только назначение 0% (WOS) не является также без шага.

C. Преподаватель (PSOE) в 100% рабочее время

Для человека с вышеупомянутым назначением периоды службы в любом кампусе Калифорнийского университета в любой комбинации следующих титулов засчитываются в восьмилетний период. Лимит:

Назначения на 100% времени:

Назначения в любой процент времени, включая 0% (WOS), кроме случаев, когда назначение 0% (WOS) также без шага:

• Доцент
• И.о. доцента
• Приглашенный доцент
• И.о. доцента
• Приглашенный доцент
• И.о. профессора
• Приглашенный профессор
• Доцент по месту жительства
• Доцент кафедры клинической медицины (X)
• Доцент клинических наук, профессор

Ассистент адъюнкт-профессора более 50% рабочего времени

III.Исключение времени из расчета лет службы:

Вице-канцлер по академическому персоналу может предоставить «Свободное время», исключив из расчета срока службы до восьмилетнего лимита: (1) некоторые отпуска, существенно не связанные с академической карьерой, как изложено в подразделе III.A ниже; и (2) определенные периоды службы по причинам, изложенным в подразделе III.B ниже. Вице-канцлер должен сообщить о таких решениях назначенному лицу в письменной форме.

1.Количество неработающего времени должно основываться на надлежащим образом задокументированном обосновании.

2. Назначенному лицу может быть предоставлено не более двух лет неработающего рабочего времени в течение восьмилетнего лимита.

3. На сроки рассмотрения (и повторного рассмотрения отказа в продлении) не повлияет исключение:

• только один квартал или один семестр от исчисления службы; или
• – период времени после 1 июля года, в котором была запланирована проверка рекламной акции.

A. Отпуска, существенно не связанные с академической карьерой

Периоды отпуска с заработной платой или без нее включаются в восьмилетний лимит, если только на основании петиции с соответствующей подтверждающей документацией проректор не определит что период отпуска должен быть исключен, поскольку деятельность, предпринимаемая в течение отпуска, по существу не связана с академической карьерой назначенного.

1. Отпуск по уходу за ребенком или отпуск по уходу за ребенком с заработной платой или без нее, предусмотренный в APM 760-25 и -27, исключается из службы в рамках восьмилетнего предела, если назначенный сотрудник не проинформирует Управление академического персонала в письменной форме не позднее, чем за один квартал. или семестр после отпуска, что не должно быть исключено.

2. Период отпуска с заработной платой или без нее, основанный на серьезном состоянии здоровья или инвалидности, предусмотренный в APM 710 и APM 715, должен быть включен в качестве службы в восьмилетний лимит, если только не на основании прошение, поданное не позднее, чем через один квартал или семестр после того, как был взят отпуск, вице-канцлер определяет, что отпуск не должен быть исключен, потому что никаких других мер, таких как сокращение преподавательских или служебных обязанностей, недостаточно.

3. В отношении всех остальных отпусков ходатайство подается во время подачи заявления на отпуск.Отпуск не может быть исключен.

B. «Нерабочее время» в течение периодов обслуживания

Запрос на исключение периодов обслуживания из расчета восьмилетнего лимита должен быть сделан, как только необходимость станет очевидной и должна быть обоснована в отношении причина и продолжительность с соответствующей документацией. Вице-канцлер может удовлетворить такой запрос на обоснованный срок до одного года по следующим причинам:

1. Деторождение и воспитание детей (см. APM 760-30)

   Уход за ребенком, который является или становится частью ближайших родственников назначенного лица, при условии, что назначенное лицо удостоверяет, что он / она является основным опекуном, ответственным за не менее 50% первичный уход за несовершеннолетним ребенком:
   до пяти лет [2]; или
   не моложе пяти лет, у которых есть медицинские потребности, инвалидность или другие особые обстоятельства, требующие значительно больше времени для ухода, чем обычно для ребенка школьного возраста, при наличии соответствующей документации от соответствующего специалиста.

   В отношении ухода за ребенком в возрасте до пяти лет проректор должен удовлетворять все такие заверенные запросы на один год вне рабочего времени при условии, что назначенное лицо предоставит Уведомление о намерении остановить часы в течение двух лет после рождения или усыновления / размещения ребенка. ребенок или в течение двух лет с момента начала приема в UCLA, в зависимости от того, что наступит позже. Сочетание отпуска по уходу за ребенком и отпуска по уходу за ребенком и «нерабочее время» не может превышать одного года; и рождение или усыновление / размещение более чем одного ребенка одновременно составляет одно событие для целей этого раздела.
   

2. Серьезное состояние здоровья, включая инвалидность

   Серьезное состояние здоровья или инвалидность, которые значительно нарушают способность выполнять основные функции приема, (1) если подтверждено соответствующими документами медицинского работника и (2) если нерабочее время является разумным приспособлением, и другого приспособления (например, сокращенного обучения и / или услуг) будет недостаточно.
   

3. Уход за ребенком, супругом, домашним партнером или родителем или их утрата

   Необходимость ухода за ребенком, супругом, домашним партнером или родителем (или, в исключительных обстоятельствах, другим близким членом семьи), которые серьезно заболели или потеряли близких в результате об их смерти, что нарушает способность выполнять основные функции приема, если это подтверждается соответствующими документами от профессионального медицинского работника.
   

4. Существенное обстоятельство, препятствующее исследованиям или творческой деятельности

   Существенное обстоятельство, не зависящее от назначенного лица, которое нарушает способность выполнять обязанности, например, стихийное бедствие или значительные задержки в предоставлении исследовательских площадей, помещений или ресурсов, необходимых для исследований, как обещано в письменное (например, письмо с предложением).

C. Назначенные лица не должны быть произвольно ущемлены при пересмотре их продвижения по службе (или компенсации) из-за того, что они решили взять отпуск по беременности и родам или по уходу за ребенком, или попытались остановить часы по причинам, перечисленным выше. Рассмотрение, отложенное из-за размещения семьи в соответствии с APM 760, должно обрабатываться процедурно так же, как и другие обзоры рекламных акций; и файл должен быть оценен без ущерба, как если бы работа была сделана в течение обычного периода службы, и это должно быть указано в письме заведующего отделом, если иное не требуется кандидатом.

D. Формы: Чтобы подать заявление на продление испытательного срока в соответствии с разделами III.A.2 и 3 и III.B.2, 3 и 4, используйте: Запрос на продление восьмилетнего испытательного срока (кроме Уход за детьми).Для уведомления APO относительно отпуска по беременности и родам или ухода за ребенком в соответствии с III.A.1 и III.B.1 (или для уведомления APO о недопустимости продления испытательного срока) используйте: Уведомление о праве на продление восьмилетнего испытательного срока. до родов или усыновления (время вне времени).

IV. Сроки подачи досье

Рассмотрение досье для продвижения по службе требуется не позднее седьмого года службы с последующим его представлением в Управление академического персонала не позднее установленных крайних сроков для назначенных на академический год и финансовый год.

A. При определении седьмого года службы для лица, назначенного на академический год (9 месяцев):

• • два (2) или три (3) квартала или один семестр службы в учебном году считаются за один год;
  • Одна (1) четверть стажа в каждом из двух академических лет считается одним годом.

Пример : Доцент X, назначенный на учебный год (9 месяцев), назначается в весеннем квартале 2016-17 гг.Эта четверть службы засчитывается в восьмилетний лимит; но 2016-17 не считаются годом работы при планировании 7-летнего обзора продвижения.

B. При определении седьмого года службы для лица, назначенного на финансовый год:

• • 6 или более месяцев работы (включая отпуск) в течение учебного года считаются за один год; и
  • менее 6 месяцев службы (включая взятые каникулы) в каждом из двух или трех академических лет, которые в сумме составляют 6 месяцев или более, считаются одним годом.

V. Ограничения при повторном приеме на работу (APM 133, Приложение A)

Если при пересмотре восьмилетнего лимита канцлер решает не продолжать назначать человека в серии, это лицо не может быть назначено ни в одном кампусе университета на какой-либо факультетский ряд или титул, перечисленные ниже, в течение пяти лет. :

• Профессор
• Руководитель педагогического образования
• И.о. профессора
• преподаватель, старший преподаватель
• Приглашенный профессор
• Преподаватель ПСОЭ
• Профессор-резидент
• преподаватель, старший преподаватель СОЭ
• Адъюнкт-профессор
• Координатор полевых работ
• Профессор клинической медицины (X)
• Руководитель полевых работ
• Клинический профессор медицинских наук
• Консультант по полевым работам
• Супервайзер по физической культуре
• Руководитель педагогического образования
• преподаватель, старший преподаватель
• Преподаватель
• преподаватель, старший преподаватель СОЭ
• Координатор полевых работ
• Руководитель полевых работ
• Консультант по полевым работам

Этот предел не препятствует назначению в качестве лектора на летней сессии или в серии «Профессор-клиницист-волонтер».

VI. Восьмилетний лимит на услуги, финансируемые из общих фондов

В дополнение к восьмилетнему лимиту, когда назначение в любой из перечисленных ниже серий поддерживается государственными фондами более 50% времени, общий период такой государственной поддержки не должен превышать восьми лет:

• Профессор-резидент
• Профессор клинической медицины (X)
• Адъюнкт-профессор
• Клинический профессор медицинских наук

---

[1] Регентский регламент 103.9 предписывает, что: «Ассистент-профессор, проработавший восемь лет в этом звании или в этом звании в сочетании с другими званиями, установленными Президентом, не может оставаться в должности после восьмого года, если не будет повышен до адъюнкт-профессора или профессора. ”

В отличие от APM 133-0, UCLA не засчитывает звания инструкторов или действующих инструкторов в рамках этого восьмилетнего лимита; и некоторые названия, перечисленные в APM 133 как подсчитываемые для восьмилетнего лимита, не используются в UCLA или больше не используются университетом.

[2] Это требование UCLA при применении APM 760-30-a.

Пересмотрено 18.01.17

Веб-страница обновлена ​​19.06.17

Крупный прогресс раскрывает пределы вычислений

Ключевое слово, конечно же, «если». Индик охотно признает, что их результат не является безусловным доказательством невозможности, которое, по его словам, является «святым Граалем теоретической информатики». «К сожалению, мы очень и очень далеки от того, чтобы доказать что-либо подобное.В результате мы делаем следующее лучшее ».

Индик также иронично признает, что он «получал несколько твитов» по ​​поводу того, что Globe преувеличивает его достижения и достижения Бачкурса. «Более точный способ сформулировать это так: [наш результат] является убедительным доказательством того, что проблема расстояния редактирования не имеет более эффективного алгоритма, чем тот, который у нас уже есть. Но люди могут по-разному интерпретировать эти свидетельства ».

Райан Уильямс определенно интерпретирует это по-разному.«Они установили замечательную связь, но у меня другая интерпретация», – сказал он. Он переворачивает проблему: «Если я хочу опровергнуть SETH, мне просто нужно быстрее решить расстояние редактирования». И даже не в такой степени, которая могла бы повлиять на то, как секвенируются геномы. Если Уильямс или кто-либо другой сможет доказать существование алгоритма дистанции редактирования, который работает даже умеренно быстрее, чем обычно, SETH уже история.

И хотя Уильямс – один из немногих экспертов, пытающихся опровергнуть SETH, это не еретическая позиция.«Я думаю, что это вполне возможно», – сказал Ааронсон. Уильямс добивается прогресса: его последнее исследование опровергает другое предположение о твердости, тесно связанное с SETH. (Он готовит работу к публикации.) Если опровержение SETH – это восхождение на Эверест, этот последний результат похож на прибытие в базовый лагерь.

Даже при том, что фальсификация SETH «могла быть результатом десятилетия», по словам Ааронсона, чтобы услышать это Уильямс, правда или ложь SETH не имеет значения. «Похоже, ценность истины не так важна для меня, пока я работаю», – сказал он.Он имеет в виду, что скальпель SETH обоюдоострый: большинство исследователей любят доказывать результаты, предполагая, что SETH верен, но Уильямс получает больше рычагов, предполагая, что это ложно. «Для меня это хорошая рабочая гипотеза», – сказал он. «Пока я считаю, что это ложь, я, кажется, могу добиться большого прогресса».

Попытки Уильямса опровергнуть SETH принесли значительные плоды. Например, в октябре он представит новый алгоритм решения проблемы «ближайших соседей».Прогресс вырос из неудачной попытки опровергнуть СЕТ. Два года назад он использовал тактику, которую он использовал, чтобы опровергнуть SETH, и применил ее к проблеме «кратчайших путей для всех пар», классической задаче оптимизации, «преподаваемой в каждой программе бакалавриата по информатике», – сказал он. Его новый алгоритм улучшил вычислительные стратегии, которые практически не изменились с 1960-х годов. А до этого другой неудачный подход привел к тому, что Уильямс получил революционное доказательство в смежной области информатики, называемой сложностью схем. Лэнс Фортноу, теоретик сложности и председатель Школы компьютерных наук Технологического института Джорджии, назвал доказательство Уильямса «лучшим достижением в области нижних оценок схем за почти четверть века».

Карта и территория

Помимо этих дополнительных преимуществ, прямая атака на SETH помогает таким исследователям, как Уильямс, добиться прогресса в одной из центральных задач теоретической информатики: составлении карты территории. Так же, как мы знаем о поверхности Луны больше, чем о глубинах наших собственных океанов, алгоритмы окружают нас повсюду, и тем не менее они, похоже, не поддаются попыткам исследователей понять их свойства.«В целом, я думаю, что мы недооцениваем силу алгоритмов и переоцениваем нашу способность их находить», – сказал Уильямс. Независимо от того, является ли SETH истинным или ложным, имеет значение возможность использовать его в качестве инструмента для отображения того, что Уильямс называет топографией вычислительной сложности.

Индик согласен. Хотя он не доказал, что расстояние редактирования невозможно решить более эффективно, он доказал, что эта теоретически решаемая проблема фундаментально связана с внутренней сложностью NP-полных задач.Работа похожа на открытие таинственного перешейка, соединяющего две суши, которые раньше считались океанами. Почему существует эта странная связь? Что это говорит нам о контурах математической береговой линии, определяющей сложные проблемы?

«P по сравнению с NP и SETH, в конечном счете, задают один и тот же вопрос, просто оценивая его по-разному», – сказал Ааронсон. «Мы хотим знать, что может быть лучше, чем слепой поиск ответов на эти очень сложные вычислительные проблемы? Есть ли более быстрый и умный путь к математической истине? Как близко мы сможем подойти? » Разница между разгадыванием загадок SETH и загадок P и NP, добавляет Ааронсон, может быть значительной по степени, но не по сути.«Каковы будут последствия открытия одной внеземной цивилизации по сравнению с тысячей?» – размышлял он. «Одно открытие более поразительное, чем другое, но оба они монументальны».

Оригинальный рассказ перепечатан с разрешения Quanta Magazine, редакционно независимого издания Фонда Саймонса, чья миссия состоит в том, чтобы улучшить понимание науки общественностью путем освещения исследований и тенденций в математике, физических науках и науках о жизни.

Вычисления, энергоэффективность и принцип Ландауэра

Вычисления, энергоэффективность и принцип Ландауэра

Габриэль Вега

5 декабря 2016 г.

Представлено как курсовая работа для Ph340, Стэнфордский университет, осень 2016 г.

Введение

Фиг.1: Здесь показана годовая энергия потребление вычислений с течением времени. Восходящие тенденции из-за прогнозируемого SIA увеличения глобальных переходов необработанных битов (которые сильно коррелируют со способностью вычислять Информация). Важно отметить, что системный уровень Включенные значения энергии на бит являются функциями не только информационные вычислительные / логические схемы, а также другие компоненты вычислительного устройства, такие как хранилище и схема интерфейса.Кривая «эталона» показывает рост потребность в энергии для системного уровня энергии на бит значения основные системы. Кривая целевой системы использует практический нижний предел уровня системы энергии на установленное значение бита такими факторами, как материалы. В предельной кривой Ландауэра используется минимальное значение энергии устройства на бит, обеспечиваемое Принцип Ландауэра. (Источник: Г. Вега, по данным SIA. [1])

Гордон Мур в 1960-х предсказал, что быть экспоненциальным ростом количества транзисторов на единицу площади кристалла.Этот повышенная плотность в значительной степени связана с полупроводниковой промышленностью. возможность изготовления транзисторов меньшего размера. Увеличение количества транзисторов привело к увеличению вычислительной мощности на размер кристалла, но имеет стоимость повышенной удельной мощности. [1] Современные компьютеры выполняют свои вычисления преимущественно в цифровой сфере с информацией передаются и управляются через перила транзисторов между низкими (нулевыми) напряжение) и высокое (положительное напряжение) состояния.Энергопотребление вычисление напрямую связано с количеством переходов между высокие и низкие состояния. [1]

Традиционные подходы, используемые для отслеживания Закон Мура и повышение энергоэффективности быстро приближаются к физическим пределы. [1] Несмотря на постоянное улучшение материалов и инженерные методы, существуют пределы того, насколько современные методы могут снизить энергопотребление. [1] Действительно, как показано на рис. 1, Ассоциация полупроводниковой промышленности (SIA) предсказала, что с современные инженерные подходы, необходимое энергопотребление для вычислений к 2040 году превысит прогнозируемые мировые поставки энергии. [1] Кроме того, по оценке SIA, текущие подходы, сосредоточенные на уменьшение размеров транзисторов станет экономически нецелесообразным к 2020 году [1]. Существует значительная потребность в повышении энергоэффективности, если вычислительные возможности будут продолжать расти по мере их увеличения. Многие считают, что закон Мура быстро приближается к своим физическим пределам, но постоянно растущий спрос на вычислительную мощность, вероятно, продолжит расти независимо.

Теоретические пределы вычислений

Многие практические ограничения вычислительной энергоэффективность связана с физическими и экономическими ограничениями и несовершенства материалов.Независимо от технологии изготовления или материалов, существует также теоретический предел минимальной энергии современные вычислительные машины могут использовать. Это дано Ландауэром. Принцип и связь между информацией и энтропией. (В обоснованность принципа Ландауэра обсуждалась, для обзора основные критические замечания и их контрапункты видят Беннета. [2])

Второй закон термодинамики

Согласно второму закону термодинамики, энтропия системы, находящейся в процессе физического процесса, никогда не уменьшается.А обратимый физический процесс – это процесс, в котором в начале и в конце процесса, нет чистой передачи тепла или работы между системой и окружающая обстановка. Другими словами, нет увеличения энтропии от процесс или его обратное действие на систему, и система может быть вернулся в исходное состояние из конечного состояния. Все остальные процессы (которые связаны с увеличением энтропии) называются необратимыми.

Если физический процесс вызывает изменение энтропии dS (dS больше или равно нулю), тогда система рассеивает тепла на количество, описанное в формуле.(1) (где T – температура в Кельвинс). Важно отметить, что физически обратимые процессы являются скорее теоретическим понятием и не встречаются в природе. В некоторых случаях, однако, можно внести изменения в физические процессы, чтобы уменьшить связанное с ними увеличение энтропии или теплопередача, которую можно представить как сделать их более обратимыми. [3]

Принцип Ландауэра

Принцип Ландауэра связывает второй закон От термодинамики к вычислениям.По принципу любой логически необратимая манипуляция информацией сопровождается увеличение энтропии в физической системе, реализующей это манипуляции. [2] Принцип Ландауэра накладывает фундаментальный предел на количество вычислений, которые могут быть вычислены на джоуль энергии. Это также иллюстрирует связь между обратимостью логических трансформации / манипуляции и термодинамическая обратимость физические системы, реализующие эти преобразования, утверждая, что «любой логически необратимая операция не может быть реализована в термодинамически обратимый способ ».[4] Важно отметить, что в то время как обратимый физический процесс неестественен, логичный преобразование (которое является абстрактным отображением входов в выходы) может быть обратимым. То есть есть логические преобразования для что обратный процесс позволяет безупречно вычислять входные данные от выходы, и никакая информация не теряется. Примеры логически необратимых манипуляции с информацией включают бинарные решения и слияние два вычислительных пути.[2] Бинарное решение, которое логически необратимое преобразование, поскольку оно включает стирание передаваемой информации в одном из входов вызывает увеличение энтропии в физическом система, реализующая это решение не менее k _B ln (2) (см. (2), где k _B – постоянная Больцмана). В свою очередь, это приводит к в теплоотдаче (dQ) в соответствии с формулой. (3) (где N – количество решения). [5]

dQ = T dS	(1)
dS & geq; k B пер (2)	(2)
dQ & geq; Nk B T ln (2)	(3)

Как отмечает Ландауэр, рассеяние энергии большей частью вычислительные процессы (в том числе выполняемые современными компьютерами) имеет «неизбежное» минимальное значение из-за того, что эти устройства «выполнить необратимые операции». [5] Этот нижний предел не может быть преодолены улучшенными материалами. Расширение теоретических пределов может требуют более фундаментальных изменений в том, как выполняются вычисления.

Обратимость и изменения в аппаратном и программном обеспечении

Может быть потенциал для улучшения энергоэффективность за счет увеличения обратимости как с логической, так и с логической точки зрения. физическая перспектива. Например, поля «Консервативная» и «Обратимые» вычисления предполагают минимизацию количества информации уничтожен.[6,7] С точки зрения оборудования такие изменения могут соответствуют сохранению низкого («0») и высокого состояний («1»). За Например, вышеупомянутые двоичные решения могут сохранять биты, которые быть уничтоженными и повторно использовать их. С точки зрения программного обеспечения такие изменения может включать включение использования энергии в критерии оптимизации и требуя логической обратимости в алгоритмах (делая их способными бежать в обоих направлениях).

Выводы

Для повышения эффективности, вероятно, потребуется комбинированная усилия и переоценка на всех уровнях вычислений от материалов до программное обеспечение.Хотя упомянутые схемные и алгоритмические изменения обеспечивают потенциальные улучшения в энергоэффективности, они сами по себе маловероятны для предотвращения предсказанной SIA ​​энергетической катастрофы от рук вычисление. Кроме того, экономика предусматривает несколько усложняющих факторы энергоэффективности, актуальные идеи в области программного обеспечения и схемотехника вряд ли преодолеет. Например, высокое состояние напряжения выше, чем казалось бы необходимого, из-за несовершенства используемые материалы и необходимость обеспечения переключения состояний выполнено правильно.Устранение таких дефектов материала в значительной степени экономически нежизнеспособен.

Спрос на вычисления, вероятно, увеличится, чтобы удовлетворить растущие вычислительные мощности. Независимо от вредного экологические последствия чрезмерного использования энергии, идея о том, что спрос казалось бы, неисчерпаемый подчеркивает важность эффективности, как в доступность энергии в не столь отдаленном будущем может оттолкнуть и ограничить расширение вычислительных возможностей. Не обесценивая важность материалы и преодоление других практических ограничений энергоэффективности, фундаментальные изменения в процессе вычислений (сохраняя ограничение в виду) может потребоваться для удовлетворения постоянно растущего спроса и ограничения энергетические затраты на вычисления.

© Габриэль Вега. Автор дает разрешение на копировать, распространять и демонстрировать эту работу в неизменном виде, с указание на автора, только в некоммерческих целях. Все остальные права, в том числе коммерческие, принадлежат автору.

Список литературы

[1] “Перезагрузка ИТ Революция: призыв к действию, Ассоциация полупроводниковой промышленности, Сентябрь 2015.

[2] С.Х. Беннетт, “Заметка о принципе Ландауэра”, Обратимые вычисления и демон Максвелла, Stud. Hist. Philos. M. P. 34 , 501 (2003).

[3] Э. Ратакришнан, Основы инженерии Термодинамика, 2-е изд. (Prentice Hall India, 2006), гл. 4.

[4] J. A. C. Ladyman et al. , г. «Связь между логической и термодинамической необратимостью», Stud. Hist. Филос. М. П. 38 , вып.1, 58 (2007).

[5] Р. Ландауэр, “Необратимость и тепло” Генерация в вычислительном процессе », IBM J. Res. Dev. 5 , № 3, 183 (1961).

[6] Т. Тоффоли, «Обратимые вычисления», в Автоматы, языки и программирование , изд. Дж. де Баккера и Дж. ван Леувен (Springer, 1980), стр. 632.

[7] Э. Фредкин и Т. Тоффоли, «Консервативная логика», в Collision-Based Computing , ed.А. Адамацкого (Springer, 2002), стр.