10.3.0. Вычисление производных.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 4.1k. Опубликовано
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x7+x5-x4+x3-x2+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:
y’=7x6+5x4-4x3+3x2-2x+1.
2. y=3x6-2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x5-2=18x5-2.
Применяем правило I, формулы 3, 5 и 6 и 1.
Применяем правило 
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4. Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Вычисление производных | Математика, которая мне нравится
Теорема. Пусть , , функции и дифференцируемы в точке . Тогда функции дифференцируемы в точке (последняя в случае ) и имеют место равенства
Доказательство.
Последнее равенство выполняется в силу непрерывности функции .
Последнее равенство выполняется в силу непрерывности функции .
Теорема о производной композиции. Пусть , множество значений содержится в . Пусть функция дифференцируема в точке , дифференцируема в точке . Тогда функция дифференцируема в точке , причем
Доказательство. По определению производной
Поэтому
При . В силу непрерывности функции в точке мы имеем также . Переходом к пределу в равенстве
и получаем требуемый результат.
Теорема о производной обратной функции 1. Пусть , обратима, — множество значений . Пусть функция дифференцируема в точке , а функция дифференцируема в точке . Тогда и .
Доказательство. .
Обозначим . Тогда
Теорема о производной обратной функции 2. Пусть , обратима, — множество значений . Пусть функция непрерывна в точке , а функция непрерывна в точке , дифференцируема в и . Тогда дифференцируема в точке и .
Доказательство.
Возьмем произвольную последовательность .
Рассмотрим
Рассмотрим последовательность . По непрерывности функции в точке
, так как . Тогда
Так как по условию, то
Следствие 1. Пусть , дифференцируема в . Тогда функция дифференцируема в и
Следствие 2. Пусть , и дифференцируемы в . Тогда функция дифференцируема в и
Тогда функция дифференцируема в и
Задачи. Приведите, если это возможно, примеры функций и , удовлетворяющих данным условиям (если это невозможно, объясните, почему):
1) и не дифференцируемы в точке , дифференцируема в ;
2) дифференцируема в точке , не дифференцируема в точке , дифференцируема в ;
3) дифференцируема в , дифференцируема в точке , не дифференцируема в ;
4) дифференцируема в , дифференцируема в , не дифференцируема в точке ;
5) дифференцируема в точке , не дифференцируема в точке , дифференцируема в точке ;
6) не дифференцируема в точке , не дифференцируема в точке , дифференцируема в точке ;
7) не дифференцируема в точке , дифференцируема в точке ;
8 ) дифференцируема в , дифференцируема в точке , не дифференцируема в ;
9) дифференцируема в , не дифференцируема в точке , не дифференцируема в ;
10) не дифференцируема в , дифференцируема в точке , дифференцируема в ;
11) дифференцируема в , не дифференцируема в точке , дифференцируема в ;
12) не дифференцируема в , не дифференцируема в точке , дифференцируема в ;
13) дифференцируема в , не дифференцируема в .
Практическая работа “Вычисление производных и дифференциалов высших порядков”
Практическое занятие №11
Тема: Вычисление производных и дифференциалов высших порядков
Цель: Формирование навыков вычисления производных и дифференциалов высших порядков
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Производная второго порядка(вторая производная) от функцииесть производная от ее первой производной:.
Производная третьего порядка(третья производная) от функцииесть производная от ее второй производной:.
Производная n – го порядка(n – япроизводная) от функцииесть производная от ее(n – 1) – ойпроизводной:.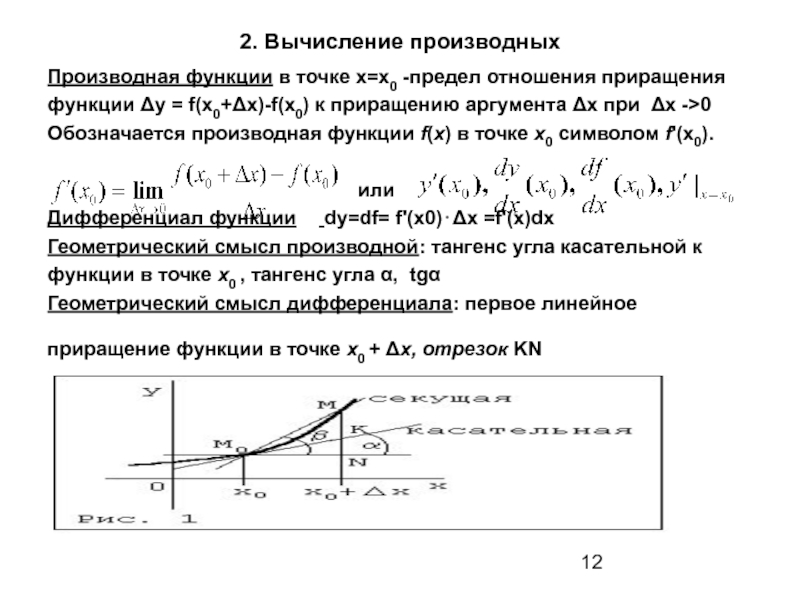
Дифференциал второго порядка(второй дифференциал) функцииесть дифференциал от ее первого дифференциала:.
Дифференциалтретьего порядка(третий дифференциал) функцииесть дифференциал от ее второго дифференциала:.
Дифференциал n – го порядка(n – ыйдифференциал) функцииесть дифференциал от ее
Примеры
Задание 1:Найти,,, …, если.
Решение:,
,
,
,,.
Задание 2:Найти дифференциалы первого, второго и третьего порядков функции.
Решение:,
,
.
Задания для самостоятельной работы
Найти производные второго порядка:
1) ; 2);
3) ; 4);
5) ; 6);
7) ; 8);
9) .
Дана функция . Найти,,.
Найти производные третьего порядка:
1) ; 2); 3).
Найти дифференциалы первого и второго порядков функции .

Найти дифференциалы первого, второго и третьего порядков функций:
1) ; 2);
3) .
Показать, что функция удовлетворяет уравнению.
Вопросы для самоконтроля:
Что называется производной второго порядка?
Что называется производной n – гопорядка?
Что называется дифференциалом функции?
Что называется дифференциалом второго порядка?
Что называется дифференциалом n – гопорядка? По какой формуле он вычисляется?
Вычисление производной в Excel | Блог Александра Воробьева
Рубрика: Справочник Excel | 3 комментария
Чем может помочь Excel при вычислении производной функции? Если функция задана уравнением, то после аналитического дифференцирования и получения формулы Excel поможет быстро рассчитать значения производной для любых интересующих пользователя значений аргумента.
Если функция получена практическими измерениями и задана табличными значениями, то Excel может оказать в этом случае более существенную помощь при выполнении численного дифференцирования и последующей обработке и анализе результатов.
На практике задача вычисления производной методом численного дифференцирования может возникнуть и в механике (при определении скорости и ускорения объекта по имеющимся замерам пути и времени) и в теплотехнике (при расчете теплопередачи во времени). Это также может быть необходимо, например, при бурении скважин для анализа плотности проходимого буром слоя грунта, при решении целого ряда баллистических задач, и т. д.
Похожая ситуация имеет место при «обратной» задаче расчета сложно нагруженных балок, когда по прогибам возникает желание найти значения действующих нагрузок.
Во второй части статьи на «живом» примере рассмотрим вычисление производной по приближенной формуле численного дифференцирования с применением выражений в конечных разностях и разберемся в вопросе – можно ли используя приближения производных конечными разностями по прогибам балки определять действующие в сечениях нагрузки?
Минимум теории.

Производная определяет скорость изменения функции, описывающей какой-либо процесс во времени или в пространстве.
Предел отношения изменения в точке функции к изменению переменной при стремлении изменения переменной к нулю называется производной непрерывной функции.
y’(x)=lim (Δy/Δx) при Δx→0
Геометрический смысл производной функции в точке – это тангенс угла наклона к оси x касательной к графику функции в этой точке.
tg (α)=Δy/Δx
Если функция дискретная (табличная), то приближенное значение ее производной в точке находят с помощью конечных разностей.
y’(x)i≈(Δy/Δx)i=(yi+1-yi-1)/(xi+1-xi-1)
Конечными разности называют потому, что они имеют конкретное, измеримое, конечное значение в отличие от величин, стремящихся к нулю или бесконечности.
В таблице ниже представлен ряд формул, которые пригодятся при численном дифференцировании табличных функций.
Центрально-разностные формулы дают, как правило, более точные результаты, но часто их нельзя применить на краях диапазонов значений. Для этих случаев пригодятся приближения левыми и правыми конечными разностями.
Вычисление производной второго порядка на примере расчета моментов в сечениях балки по известным прогибам.
Дано:
На балку длиной 8 метров с шарнирными опорами по краям изготовленную из двух спаренных стальных (Ст3) двутавров 30М опираются 7 прогонов с шагом 1 метр. К центральной части балки крепится площадка с оборудованием. Предположительно усилие от покрытия, передаваемое через прогоны на балку, во всех точках одинаково и равно F1. Подвесная площадка имеет вес 2*F2 и крепится к балке в двух точках.
Предполагается, что балка до приложения нагрузок была абсолютно прямой, а после нагружения находится в зоне упругих деформаций.
На рисунке ниже показана расчетная схема задачи и общий вид эпюр.
На следующем скриншоте представлены исходные данные.
Расчетные исходные данные:
3. Погонная масса двутавра 30М:
γ=50,2 кг/м
Сечение балки составлено из двух двутавров:
n=2
Удельный вес балки:
q=γ*n*g=50,2*2*9,81/1000=0,985 Н/мм
5. Момент инерции сечения двутавра 30М:
Ix1=95 000 000 мм4
Момент инерции составного сечения балки:
Ix=Ix1*n=95 000 000*2=190 000 000 мм4
10. Так как балка нагружена симметрично относительно своей середины, то реакции обеих опор одинаковы и равны каждая половине суммарной нагрузки:
R=(q*zmax+8*F1+2*F2)/2=(0,985*8000+8*9000+2*50000)/2=85 440 Н
В расчете учитывается собственный вес балки!
Задача:
Найти значения изгибающего момента Mxi в сечениях балки аналитически по формулам сопротивления материалов и методом численного дифференцирования расчетной линии прогибов. Сравнить и проанализировать полученные результаты.
Сравнить и проанализировать полученные результаты.
Решение:
Первое, что мы сделаем, это выполним расчет в Excel поперечных сил Qy, изгибающих моментов Mx, углов поворота Ux оси балки и прогибов Vx по классическим формулам сопромата во всех сечениях с шагом h. (Хотя, в принципе, значения сил и углов нам в дальнейшем не понадобятся.)
Результаты вычислений находятся в ячейках I5-L54. На скриншоте ниже показана половина таблицы, так как значения во второй ее части зеркальны или аналогичны представленным значениям.
Использованные в расчетах формулы можно посмотреть здесь.
Ссылка для скачивания файла с рассмотренным в статье примером: vychisleniye-proizvodnoy (xls 250,0KB).
Итак, нам известны точные значения моментов и прогибов.
Из теории мы знаем, что:
Угол поворота – это первая производная прогиба U=V’.
Момент – это вторая производная прогиба M=V’’.
Сила – это третья производная прогиба Q=V’’’.
Предположим, что столбец точных значений прогибов получен не аналитическими расчетами, а замерами на реальной балке и у нас больше нет никаких других данных. Вычислим вторые производные от точных значений прогибов, используя формулу (6) из таблицы предыдущего раздела статьи, и найдем значения моментов методом численного дифференцирования.
Mxi=Vy’’≈((Vi+1-2*Vi+Vi-1)/h2)*E*Ix
Итог расчетов мы видим в ячейках M5-M54.
Точные значения моментов, рассчитанные по аналитическим формулам сопромата с учетом веса самой балки, отличаются от найденных по приближенным формулам вычисления производных незначительно. Моменты определены весьма точно, судя по относительным погрешностям, рассчитанным в процентах в ячейках N5-N54.
ε=(Mx-Vy’’)/Mx*100%
Поставленная задача решена. Мы выполнили вычисление производной второго порядка по приближенной формуле с использованием центральных конечных разностей и получили отличный результат.
Зная точные значения прогибов можно методом численного дифференцирования с высокой точностью найти действующие в сечениях моменты и определить степень нагруженности балки!
Однако…
Увы, не стоит думать, что на практике легко получить необходимые высокоточные результаты измерений прогибов сложно нагруженных балок!
Дело в том, что измерения прогибов требуется выполнять с точностью ~1 мкм и стараться максимально уменьшать шаг замеров h, «устремляя его к нулю», хотя и это может не помочь избежать ошибок.
Зачастую уменьшение шага замеров при значительных погрешностях измерений прогибов может привести к абсурдным результатам. Следует быть очень внимательными при численном дифференцировании, чтобы избежать фатальных ошибок.
Сегодня есть приборы — лазерные интерферометры, обеспечивающие высокую скорость, стабильность и точность измерений до 1 мкм, программно отсеивающие шум, и еще много чего программно умеющие, но их цена – более 300 000$…
Давайте посмотрим, что произойдет, если мы просто округлим точные значения прогибов из нашего примера до двух знаков после запятой – то есть до сотых долей миллиметра и заново по той же формуле вычисления производной пересчитаем моменты в сечениях.
Если раньше максимальная ошибка не превышала 0,7%, то сейчас (в сечении i=4) превышает 23%, хотя и остается приемлемой в наиболее опасном сечении (ε21=1,813%).
Кроме рассмотренного численного метода вычисления производных с помощью конечных разностей можно (а часто и нужно) применить другой способ — аппроксимировать замеры степенным многочленом и найти производные аналитически, а затем сверить результаты, полученные разными путями. Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Но следует понимать, что дифференцирование аппроксимационного степенного многочлена – это тоже в конечном итоге приближенный метод, существенно зависящий от степени точности аппроксимации.
Исходные данные – результаты измерений – в большинстве случаев перед использованием в расчетах следует обрабатывать, удаляя выбивающиеся из логического ряда значения.
Вычисление производной численными методами всегда необходимо выполнять очень осторожно!
Уважаемые читатели, отзывы и комментарии к статье, размещайте в специальном блоке ниже статьи.
Чтобы получать информацию о выходе новых статей на блоге, подпишитесь на анонсы в окне, расположенном вверху страницы или сразу после статьи.
Прошу УВАЖАЮЩИХ труд автора скачать файл с примером ПОСЛЕ ПОДПИСКИ на анонсы статей.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Практическое занятие “Вычисление производных”
Практическое занятие
Тема: Нахождение производных. Применение производной к исследованию функции и построению графиков.
Цель: Освоить вычисление производных, научиться исследовать функцию с помощью производной
Средства обучения: тетради для выполнения практических занятий, презентации по теме, Интернет-ресурсы.
Содержание и порядок выполнения работы:
1. Рассмотрите теоретический материал по темам: «Правила вычисления производных», «Экстремум функции», «Выпуклость, вогнутость. Точка перегиба».
2. Рассмотрите образцы выполнения заданий.
3. Выполните тестовое задание №.1.
Выполните тестовое задание №.1.
Контрольные вопросы:
1. Дайте определение максимума (минимума) функции в точке. Что можно сказать о знаке приращения функции в достаточно малой окрестности точки максимума (минимума)?
2. Каковы необходимые условия существования экстремума функции? Каков их геометрический смысл?
3. Каково правило нахождения наибольшего и наименьшего значений функции на отрезке?
4. Дайте определение выпуклости (вогнутости) кривой на промежутке.
5. Каково правило отыскания интервалов выпуклости и вогнутости кривой?
6. Точка перегиба кривой. Как ее найти?
7. Каков алгоритм построения графика функции?
Правила вычисления производных
Производная сложной функции.
Если у=ƒ(и), и=φ(х), то у¢(х)=ƒ¢(и)·φ¢ (х).
Производная суммы.
Если у(х)=и(х)+v (х), то у¢ (х)=и¢ (х)+v¢ (х)
Производная произведения.
Если у(х)=и(х)·v(х), то у¢=и¢·v+u·v¢.
В частности, (с·и)¢=с·и¢, т. е. постоянный множитель выносится из-под знака производной. Легко убедиться, что
(u2)¢=2u·u¢, (u3)¢=3u2·u¢, … , (un)¢=n·un–1·u¢.
Производная частного.
Если , то .
Таблица производных
1. (с)¢=0
Для сложной функции: если и=и(х), то:
2. (х)¢=1
(х)¢=1
3. (хα)¢=α·хα–1, а – любое действительное число.
.
3.
4. (ах)¢=ах·ln а
4.
5. (logax)¢=
.
5.
6. (sin x)¢=cos x
6.
7. (cos x)¢= –sin x
7.
8. (tg x)¢=
8.
9. (ctg x)¢=
9.
10.
10.
11.
11.
12.
12.
13.
13.
Рассмотрите примеры
Пример 1.
у=(3–2 sin5x)4|Применяем формулы производных для иα, sin u|
y¢=4·(3–2·sin5x)3·(3–2sin5x)¢=4·(3–2·sin5x)3·(0–2·cos5x·5) = –40·(3–2·sin5x)3.
Пример 2.
.
Пример 3.
.
Пример 4.
Пример 5.
.
Экстремум функции
Исследование функции на экстремум – одно из важнейших приложений производных. Рассмотрим определение минимумов и максимумов, и способы их отыскания.
Пусть функция ƒ(х) определена и дифференцируема на некотором множестве и точка х0 – точка внутри него.
Определение. Функция ƒ(х) в точке х0 имеет максимум (минимум), если существует такая окрестность точки х0, что для всех х из этой окрестности ƒ(х) < ƒ(х0) (ƒ(х) > ƒ(х0)).
Точка х0 называется тогда точкой максимума (минимума).
Рис. 1.
1.
Показан график функции, которая имеет две точки максимума (х1 и х3) и две точки минимума (х2 и х4), причем максимальное значение может оказаться меньше минимального (ƒ(х1) < ƒ(х4)). Это подчеркивает тот факт, что мы характеризуем особенность функции только вблизи некоторой точки.
Значения функции в точках максимума и минимума называют экстремальными значениями или экстремумами. На приведенном графике видно, что точки экстремума (х1, х2, х3, х4) определяют интервалы монотонности функции, в каждом из которых производная сохраняет определенный знак. В точках экстремума, понятно, производная обращается в нуль. Сформулируем теорему о необходимом условии существования экстремума.
Теорема. Если функция ƒ(х) в точке х0 имеет экстремум, то производная функции в этой точке равна нулю, т. е. ƒ¢(х0)=0.
е. ƒ¢(х0)=0.
Заметим сразу, что условие это не является достаточным, т. е. обратное утверждение не всегда верно. Из равенства ƒ¢(х0)=0 не обязательно следует, что в точке х0 существует экстремум.
Подтверждением тому пример с функцией ƒ(х)=х3.
Найдем ƒ¢(х)=3х2. В точке х=0 ƒ¢(0)=0. Но как угодно близко к точке х=0 найдем х>0, где ƒ(х)=х3 > 0, найдем х<0, где ¦(х)=х3<0. Т. е. не существует какая-либо малая окрестность точки х=0, где для всех х значение функции в точке х=0 будет самым большим или самым малым. Поэтому точка х=0 не является точкой экстремума.
Можно рассуждать иначе. Так как производная ƒ¢(х)=3х2, то функция ƒ(х)=х3 возрастает при любых действительных х и экстремумов не имеет.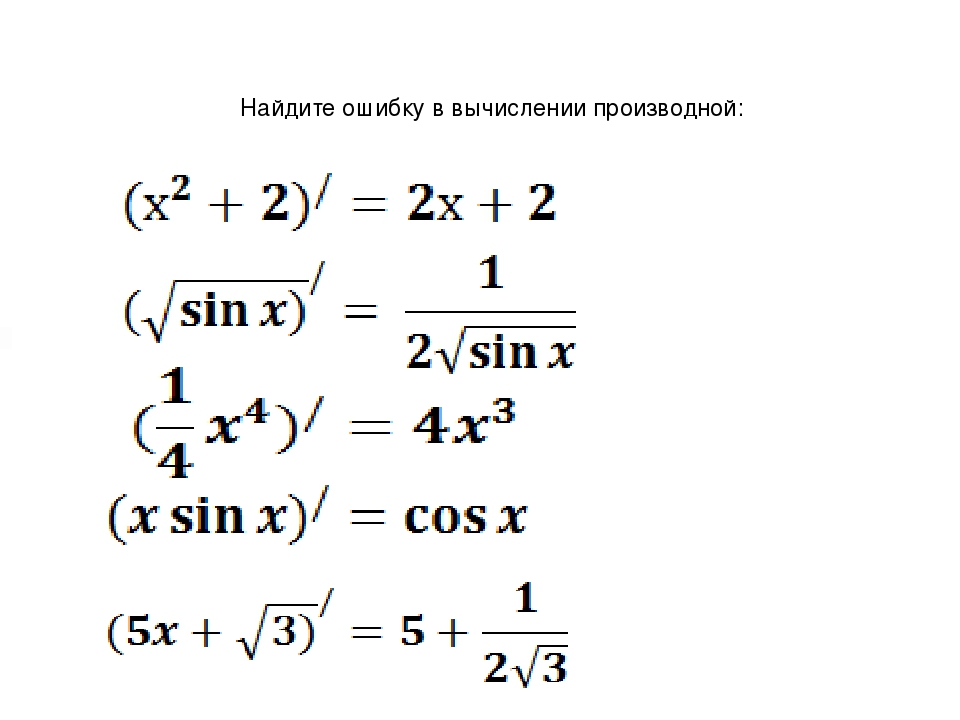
Точки, в которых выполняется необходимое условие экстремума (ƒ¢(х)=0) называются критическими.
Очевидно, что касательная к графику функции в точках, где ƒ¢(х)=0, параллельна оси абсцисс Ох.
Достаточное условие экстремума дается в следующих теоремах.
Теорема 1. Если х0 – критическая точка функции и при переходе через нее производная меняет знак, то х0 – точка экстремума, а именно, если производная меняет знак с плюса на минус – точка максимума, если – с минуса на плюс – точка минимума.
Заметим, что экстремума в точке нет, если производная не меняет знака. Правило исследования на экстремум с помощью первой производной известно из школьного курса. Достаточное условие экстремума иногда удобнее формулировать с помощью второй производной.
Пусть функция ƒ(х) дважды дифференцируема в некоторой области (т. е. ƒ(х) имеет ƒ¢(х) и ƒ¢¢(х)).
е. ƒ(х) имеет ƒ¢(х) и ƒ¢¢(х)).
Теорема 2. Если х0 – критическая точка функции ƒ(х) и ƒ¢¢(х0) > 0, то х0 – точка минимума, если ƒ¢¢(х0) < 0, то х0 – точка максимума.
С помощью второй производной определяется выпуклость или вогнутость графика функции.
Выпуклость, вогнутость. Точка перегиба.
Кривая у=ƒ(х) называется выпуклой на интервале, если все точки кривой лежат ниже любой ее касательной на этом интервале. Тогда на этом интервале
ƒ¢¢(х) < 0.
Кривая у=ƒ(х) называется вогнутой на интервале, если все точки кривой лежат выше любой ее касательной на этом интервале. Тогда на этом интервале
Тогда на этом интервале
ƒ¢¢(х) > 0
Определение. Точкой перегиба кривой называется точка, по одну сторону от которой кривая выпукла, по другую вогнута.
В точке перегиба ƒ¢¢(х)=0.
Итак, знак второй производной (как и знак самой функции и ее первой производной) свидетельствует об особенностях графика функции. Еще раз остановимся на них.
Если для всех х на интервале (а, b) ƒ(х) > 0 (ƒ(х) < 0), то график лежит выше (ниже) оси абсцисс.
Если для всех х на интервале (а, b) ƒ¢(х) > 0 (ƒ¢(х) < 0), то функция на (а, b) возрастает (убывает).
Если для всех х на интервале (а, b) ƒ¢¢(х) > 0 (ƒ¢¢(х) < 0), то график на (а, b) вогнут (выпукл).
Уравнение ƒ(х)=0 определяет «нули» функции, т. е. точки пересечения графика с осью Ох.
Уравнение ƒ¢(х)=0 определяет критические точки.
Уравнение ƒ¢¢(х)=0 определяет возможные точки перегиба.
Схема исследования функции
Для исследования функции ƒ(х) и построения графика у=ƒ(х) следует найти:
1) область определения функции и точки пересечения графика с осями координат;
2) интервалы монотонности;
3) точки экстремумов и значения функции в этих точках;
4) интервалы выпуклости и вогнутости графика;
5) точки перегиба графика;
6) построить в декартовой системе координат все полученные точки (иногда, для уточнения графика, получают дополнительные точки) и сам график.
Наименьшее и наибольшее значения функции на отрезке
При решении некоторых задач метода оптимизации важно уметь находить наименьшее или наибольшее значения функции на некотором отрезке. Эти значения функция достигает либо в критических точках, либо на концах отрезка.
Схема отыскания наименьшего и наибольшего значений функции ƒ(х) на отрезке [а, b].
1. Найти производную функции ƒ¢(х).
2. Найти критические точки из уравнения ƒ¢(х)=0.
3. Выбрать те критические точки, которые принадлежат данному отрезку [а, b] и найти значение функции ƒ(х) в каждой такой точке.
4. Вычислить значения функции ƒ(х) на концах отрезка: ƒ(а) и ƒ(b).
5. Из полученных значений функции выбрать самое большое (наибольшее) и самое малое (наименьшее).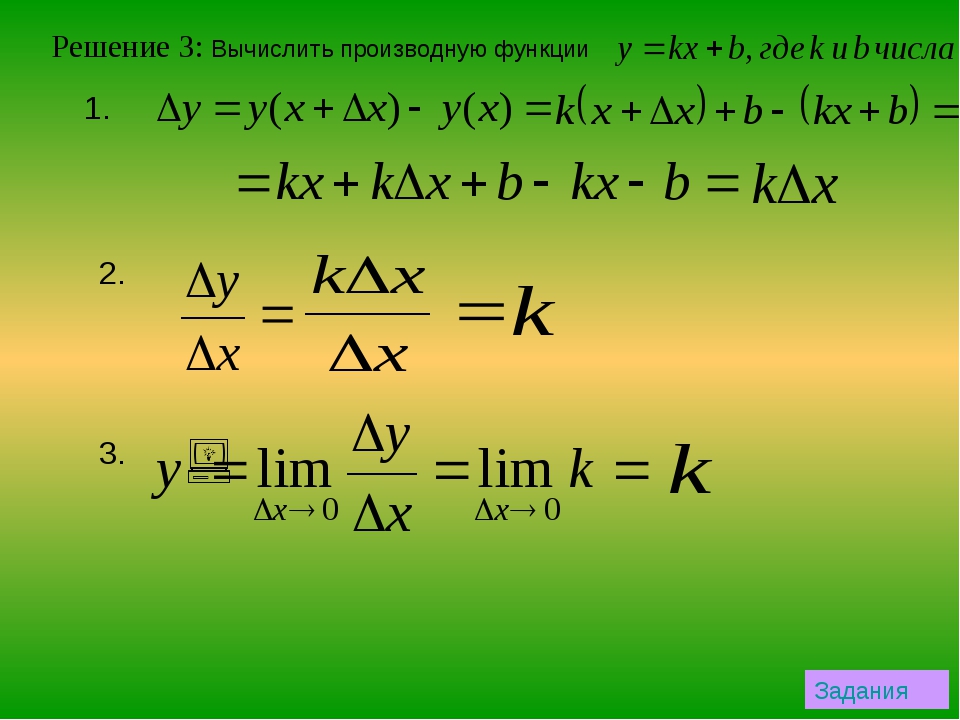
Пример 2.
Найти наибольшее и наименьшее значения функции ƒ(х)=х3–9х2+24х–10 на отрезке [0 3].
1. ƒ¢(х)=3х2–9·2х2+24.
2. ƒ¢(х)=0, 3(х2–6х+8)=0, х1=2, х2=4.
3. Точка х2=4 не принадлежит отрезку [0, 3]. Поэтому вычислим значение функции только в точке х1=2
ƒ(2)=23–9·22+24·2–10=10.
4. Значения функции на концах отрезка: ƒ(0)= –10, ƒ(3)=33–9·32+24·3–10, ƒ(3)=8.
5. Получены значения:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Наибольшее значение равно 10 и достигается в точке х=2. Наименьшее – равно –10 и достигается в точке х=0.
Пример 3.
Найти интервалы выпуклости и вогнутости и точки перегиба кривой у=х+36х2–2х3–х4.
Областью определения данной функции является множество всех действительных чисел, т. е. хЄ(–∞, +∞).
Найдем вторую производную.
у¢=1+72х–6х2–4х3.
у¢¢=72–12х–12х2= –12(х2+х–6).
Из уравнения у¢¢=0 получим абсциссу точки перегиба:
–12(х2+х–6)=0 х1= –3; х2=2.
Определим знак у¢¢ на интервалах
(–∞; –3), (–3; 2), (2, +∞).
х
(–∞, –3)
-3
(–3; 2)
2
(2; +∞)
у¢¢
–
0
+
0
–
форма кривой
выпуклая
перегиб
вогнута
перегиб
выпуклая
Найдем ординаты точек перегиба:
у(–3)=726; М1(–3; 726) – точка перегиба
у(2)=114; М2(2; 114) – точка перегиба.
На интервале (–3; 2) кривая вогнута. На интервалах (–∞; –3) и (2; +∞) – выпуклая.
Образцы выполнения заданий
Задача № 1.
Найти точки разрыва функции и построить график
Функция ƒ(х) определена для всех действительных х и непрерывна на каждом из указанных промежутков: (–∞; –1), [–1; 0], (0, +∞). Исследуем функцию ƒ(х) на непрерывность в точках х= –1 и х=0.
Для этого в каждой из этих точек найдем односторонние пределы.
Так как односторонние пределы различны, то х= –1 – точка разрыва первого рода.
Односторонние пределы равны, т. е. в точке х=0 существует предел функции и
Сравним этот предел со значением функции в точке:
Так как то в точке х=0 функция ƒ(х) непрерывна.
Построим график функции ƒ(х), учитывая, что
1) – уравнение прямой,
2) – уравнение верхней полуокружности с центром в начале координат и радиусом, равным единице, а при условии –1 £ х £ 0 уравнение определяет четверть окружности.
3) для х > 0 график задается уравнением . Точки пересечения этой кривой с осью Ох найдем из уравнения при х > 0. х=πn, где n=1, 2, 3, 4,
Рис. 2.
Задача № 2.
Составить уравнения касательных к линии в точках, где х=0 и х=4. Найти точку пересечения касательных и угол между ними. Сделать чертеж.
Уравнение касательной к линии у=ƒ(х) имеет вид
,
где у0=ƒ(х0).
В точке х=0 у(0)=ƒ(0)=5.
у¢=ƒ¢(х)=х–3 ƒ¢(0)= –3.
Уравнение касательной в точке М1(0, 5) имеет вид у–5= –3(х–0) или
у= –3х+5.
В точке х=4 у(4)=ƒ(4)=1. ƒ¢(4)=4–3=1.
Уравнение касательной в точке М2(4, 1) имеет вид у–1=х–4 или
у=х–3.
Точку пересечения касательных получим, решив систему
Точка пересечения М3(2, –1).
Угол φ между касательными найдем из формулы:
,
где k1= –3; k2=1 – угловые коэффициенты касательных.
.
Угол φ=arctg 2.
Построим данную линию – параболу с вершиной в точке, где х=3, т. к. у¢=0 при х=3. Найдем . Точка М4(3; ) – вершина параболы.
Р
ис. 3.
Задача № 3.
Исследовать функцию и построить ее график.
1. Данная функция является многочленом (можно раскрыть скобки, получим многочлен третьей степени), поэтому она определена, непрерывна и дифференцируема при любых х.
2. Найдем производную.
.
Из уравнения у¢=0 найдем критические точки: 3х·(х–2)=0, х1=0, х2=2.
Исследуем их.
х
(–∞, 0)
0
(0; 2)
2
(2; +∞)
у¢
+
0
–
0
+
у
4
0
3. Итак, функция возрастает на интервалах (–∞, 0) и (2, +∞), убывает на интервале (0; 2), имеет максимум при х=0 и минимум при х=2:
уmax=у(0)=4; уmin=у(2)=0.
4. Найдем вторую производную.
у¢¢=6·(х-1).
Кривая выпукла там, где у¢¢ < 0, т. е. 6·(х–1) < 0, х < 1.
Кривая вогнута там, где у¢¢ > 0, т. е. х > 1.
Итак, на интервале (–∞, 1) кривая выпукла; а на интервале (1, +∞) – вогнута.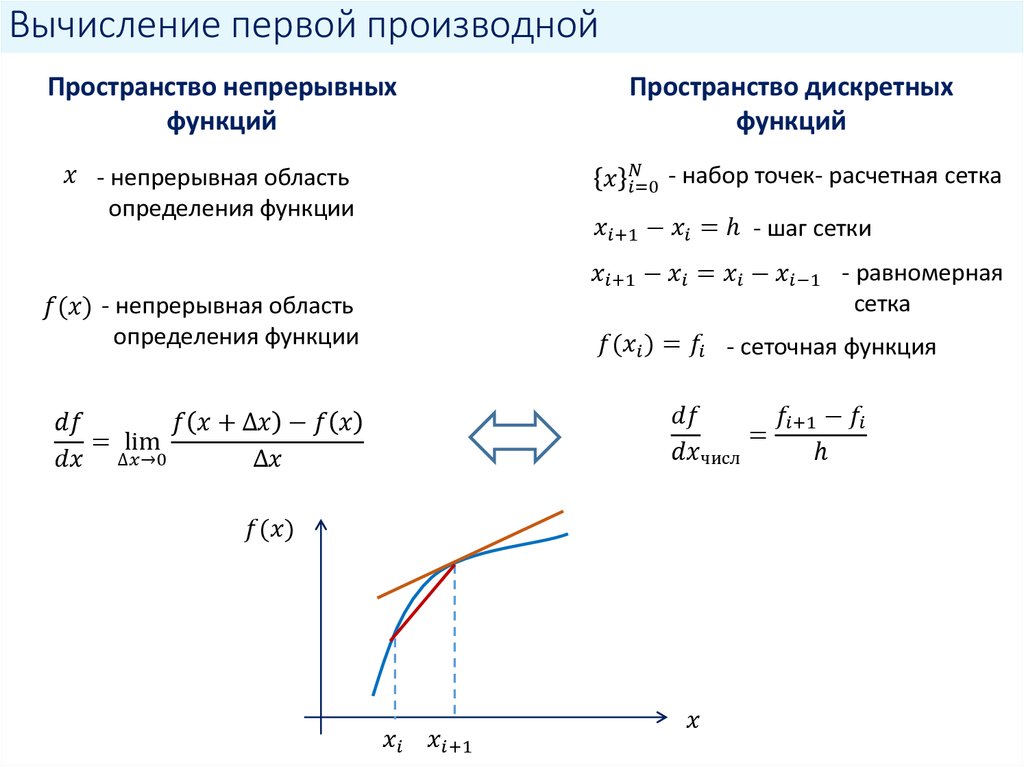
5. Точку перегиба найдем из уравнения у¢¢=0. Таким образом, х=1 – абсцисса точки перегиба, т.к. эта точка разделяет интервалы выпуклости и вогнутости кривой. Ордината точки перегиба: у(1)=2.
График функции у=(х+1)·(х–2)2 пересекает ось Ох при у=0, т. е. при х= –1 и х=2;
пересекает ось Оупри х=0, т. е. при у=4. Мы получили три точки: (–1; 0), (2; 0), (0; 4). Все полученные точки внесем в таблицу, добавив соседние с ними.
х
–2
–1
0
1
2
3
у
–16
0
3
4
2
0
4
Рис. 4 Кривая у=(х+1)(х–2)2.
Задание № 1
Вашему вниманию предлагаются задания, в которых могут быть один, два, три и большее число правильных ответов. Обвести кружочком номера всех правильных ответов
Обвести кружочком номера всех правильных ответов
1. Если то функция
1) возрастающая
2) убывающая
3) постоянная
2. Если
1) Возрастающая
2) Убывающая
3. Если , то функция
1) Возрастающая
2) Убывающая
4. Если , то функция
1) Возрастающая 3) Убывающая
2) Постоянная 4) Монотонная
5. Функция Является
1) Чётной
2) Не чётной
3) ни чётной, ни нечётной
4) Периодической
5) Не периодической
6) Тригонометрической
7) Элементарной
6. Функция Является
1) чётной
2) нечётной
3) ни чётной, ни нечётной
4) периодический
5) не периодической
6) тригонометрической
7) элементарной
7) Автор теоремы «если то функция является постоянной»
1) Роль 3) Коши 5) Декарт
2) Вейерштрасс 4) Дирихле 6) Лейбниц
8) Решение Уравнения
1) 0 3) 0 и 3 5) 2 7) 3
2) 2 и 3 4) 2 6) -5 и 1 8) 5 и 1
9) решение неравенства
1) (; 1) 3) (; 1) 5) (-;1)
2) (1; 5 ) 4) ( 2; ) 6)
10) Методом Находится сумма
1) векторов
2) прямых
3) отрезка
11) Если , то функция
1) Вогнутая 3) Выпуклая 5) Убывающая
2) Монотонная 4) Возрастающая 6) Постоянная
12) область определения функции равна
1) (;0)
2) (0; )
3) (-;)
4) (0;1)
5)
6)
7) (-1;1)
8)
9)
13) функция является
1) показательной
2) тригонометрической
3) степенной
4) логарифмической
14) если функции у=x то она является
1) чётной
2) нечётной
3) ни чётной, ни нечётной
15) функция при является
1) показательной 8) нечётной
2) Возрастающей 9) тригонометрической
3) степенной 10) постоянной
5) логарифмической 11) ни чётной, ни нечётной
6) убывающей 12) вогнутой
7) периодической 13) выпуклой
8) чётной 14) монотонной
16) область значения функции
1) (0;) 4) 7)
2) (-;+) 5) 8) (1;+ )
3) (-;0) 6) 9)
17) область определения функции
1) (0;) 4) 7)
2) (-;+) 5) 8) (1;+ )
3) (-;0) 6) 9)
18) область значения функции
1)
2)
3) (-) 5)
4) (0;) 6)
19) теорему о постоянстве функции на промежутке сформировал и доказал:
1) Роль 3) Декарт
2) Лагранж 4) Вейерштрасс
20) значение выражения при является
3.
 – 5. 7.
– 5. 7.
2. 4. – 6. 8.
21) исследование функции
Найти нули функции
Найти пересечения с осью ОХ
Найти ОДЗ
Найти точки пересечения с осью ОУ
Найти область значения функции
Найти экстремумы функции
Периодичность
Промежутки возрастания
Чётность, нечётность
Найти промежутки убывания
Построить график
Найти асимптоты
Промежутки вогнутости
Промежутки выпуклости
22) наименьшее значение функции принадлежит промежутку
(0;2)
(-2;0)
23) значение функции в точке равно
–
-1
1
3
0
27
-27
24) уравнение касательной к функции в точке имеет вид
y-3x-2=0
y-3x+2=0
y-12x+16=0
y-5x+1=0
y-3+1=0
y-9x+1=0
y-2x+4=0
y+9=0
y+1=0
y+4=0
y-9x+27=0
y-1=0
y+3x-1=0
y-27x+54=0
y-x-1=0
y-21x+45=0
y-7x+9=0
y-8x+12=0
Домашнее задание:
Исследовать функцию и построить ее график.
Список рекомендуемой литературы:
Основная:
1. Атанасян Л.С. и др. Геометрия. 10 -11: учеб. для общеобразоват. учреждений: базовый и профильный уровни М.: Просвещение, 2012г. -255 с.
2. Колмогоров А.Н. Алгебра и начала анализа – М.: Просвещение, 2014г.-383с.
3. Мордкович А.Г. Алгебра и начала анализа 10 кл. в 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) – М.: Мнемозина, 2012 г. – 424 с.
4. Смирнова И.М., Смирнов В.А. Геометрия. 10-11 кл.: учеб. для общеобразоват. учреждений М.: Мнемозина, 2013 г., 232 с.
5. Пехлецкий И.Д. Математика: учебник для студ. образоват. учреждений сред.проф. образования М.: Издательский центр «Академия», 2013 г-253с.
Дополнительная:
1.Алимов Ш.А. и др. Алгебра и начала анализа: учеб. Для 10-11 кл. общеобразоват. учрежд., М.: Просвещение, 2012г. -343с.
учрежд., М.: Просвещение, 2012г. -343с.
2. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. М.: ООО «Издательство Оникс, 2011г.- 483с
3.Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2013г.-363с.
4.Никольский С.М., Потапов М.К., Решетников Н.Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 11 кл. – М., 2013г.-453с.
Сайты в сети Интернет:
1. Онлайн библиотека [Электронный ресурс] – Режим доступа: http://www.vbbooks.ru.
2. Интернет университет информационных технологий [Электронный ресурс] Режим доступа: http: //www.intuit.ru.
3. Компьютерные электронные книги [Электронный ресурс] – Режим доступа: http://www.compebook.ru.
Критерии оценивания работы обучающихся на практическом занятии
Оценка «отлично» ставится, если обучающийся:
1) владеет полным объемом теоретического материала по теме занятия;
2) знает и понимает алгоритм нахождения точек экстремума, асимптот;
3) выполняет нахождение точек перегиба;
4) самостоятельно выполняет задание по исследованию функции и построению графика функции, используя алгоритм;
5) безошибочно находит производные функции.
Оценка «хорошо» ставится в том случае, если обучающийся:
1) владеет теоретическим материалом по теме занятия;
2) знает и понимает алгоритм нахождения точек экстремума, асимптот;
3) выполняет нахождение точек перегиба;
4) выполняет задание по исследованию функции и построению графика функции, используя алгоритм;
5) находит производные.
Оценка «удовлетворительно» ставится, если обучающийся:
1) частично владеет теоретическим материалом по теме занятия;
2) понимает алгоритм нахождения точек экстремума, асимптот;
3) выполняет задание по исследованию функции и построению графика функции, с помощью преподавателя;
4) имеет затруднения при нахождении производных.
Оценка «неудовлетворительно» ставится, если:
1) частично владеет теоретическим материалом по теме занятия;
2) путается в нахождения точек экстремума, асимптот;
3) не выполняет задание по исследованию функции и построению графика функции.
Урок 3: Вычисление производной – 100urokov.ru
План урока:
Производные некоторых элементарных функций
Основные правила дифференцирования
Производная сложной функции
Производные некоторых элементарных функций
Ранее мы для вычисления производных использовали ее определение. То есть каждый раз мы давали функции некоторое приращение ∆х, потом находили соответствующую ему величину ∆у, далее составляли отношение ∆у/∆х, после чего находили предел этого отношения при ∆х →0. Выполнение такого алгоритма довольно трудоемко. Поэтому на практике используются специальные формулы для вычисления производных.
Нам известно несколько основных функций, которые в математике чаще называют элементарными. Например, элементарными являются линейная функция, степенная, показательная, логарифмическая. Также существует несколько различных тригонометрических функций (синус, косинус, тангенс), которые тоже считаются элементарными. Попытаемся вычислить для них производные.
Попытаемся вычислить для них производные.
Начнем с линейной функции. В общем случае она выглядит так:
где k и b – некоторые постоянные числа.
Выберем произвольную точку х0 и дадим ей приращение ∆х, в результате чего мы придем в новую точку (х0 + ∆х). Вычислим значения линейной функции в этих двух точках:
Теперь мы можем найти приращение функции ∆у:
Находим отношение ∆у/∆х:
Получилось, что это отношение не зависит ни от приращения ∆х, ни от выбора исходной точки х0. Естественно, что предел этого отношения при ∆х→0 (то есть производная) также будет равен k:
Задание. Вычислите производную функции у = 4х + 9.
Обратите внимание, что в рассмотренном примере запись у′ = 4 означает функцию. Просто при любом значении х она принимает одно и то же значение, равное 4. График производной функции будет выглядеть так:
Рассмотрим два особых частных случая линейной функции. Пусть k = 1 и b = 0, тогда она примет вид у = х. Её производная тогда будет равна 1:
Пусть k = 1 и b = 0, тогда она примет вид у = х. Её производная тогда будет равна 1:
Теперь предположим, что коэффициент k = 0. Тогда функция примет вид
где С – некоторое постоянное число, то есть константа (большая буква Св таких случаях используется из-за латинского термина constanta). Производная такой функции будет равна нулю:
Задание. Найдите вторую производную функции у = 9х + 2.
Решение. Сначала вычислим первую производную:
Очень легко объяснить, почему производная константы равна нулю. Представим себе, что закон движения некоторого тела выглядит как s(t) = C, например, s(t) = 5. Это значит, что тело в любой момент времени находится в точке, находящейся в 5 метрах от какого-то начала отсчета. То есть тело находится в одной и той же точке, а это значит, что оно не двигается. Тогда его скорость равна нулю. Но производная – это и есть скорость, значит, она также равна нулю.
Далее вычислим производную для функции у = 1/х. Выберем некоторую точку х0 и дадим ей приращение ∆х. В результате имеем две точки с координатами х0 и (х0 + ∆х). Вычислим значение функции в каждой из них:
Выберем некоторую точку х0 и дадим ей приращение ∆х. В результате имеем две точки с координатами х0 и (х0 + ∆х). Вычислим значение функции в каждой из них:
Осталось найти предел данного отношения при ∆х→0. Ясно, что при этом множитель х0 + ∆х будет стремится к х0, то есть
Задание. Вычислите производные функции
Обратите внимание, что производная функции у = 1/х оказывается отрицательной при любом значении х (кроме нуля, для которого производную посчитать нельзя, так как получится деление на ноль). Это должно означать, что функция убывает в каждой своей точке, а любая касательная к ней образует с осью Ох тупой угол наклона. И это действительно так:
Мы разобрали несколько простейших примеров того, как находить формулы производных. Для этого используется понятие предела функции. Для вывода всех подобных формул требуется хорошо знать тему вычисления пределов, которая не изучается детально в школе. Поэтому мы просто дадим следующие формулы без доказательств.
Поэтому мы просто дадим следующие формулы без доказательств.
Начнем со степенной функции у = хn, где n– некоторое постоянное число. Её производная вычисляется по формуле:
Приведем примеры использования этой формулы:
Задание. Найдите производную функции у = х6 в точке х0 = 10.
Задание. Движение самолета при разгоне описывается законом движения s(t) = t3. Найдите его скорость через 5 секунд после начала разгона.
Решение. Скорость самолета в любой момент времени равна производнойs′(t). Найдем её:
Заметим, что используемая нами формула работает и в том случае, если показатель степени является отрицательным или дробным числом. Действительно, ранее мы вывели формулу
По определению отрицательной степени мы можем записать, что
Задание. Вычислите производную функции
Вычислите производную функции
Задание. Определите, в какой точке необходимо провести касательную к графику функции
чтобы она образовывала с осью Ох угол в 45°?
Решение. Тангенс угла наклона касательной равен производной. Известно, что tg 45° = 1. Значит, нам надо найти такую точку х0, в которой значение производной квадратного корня будет равно единице. Производная вычисляется по формуле:
Ответ: х0 = 0,25.
Далее изучим формулы производных для тригонометрических функций. Они выглядят так:
Рассмотрим несколько примеров использования этих формул.
Задание. Найдите производную функции у = cosx в точке х0 = π.
Решение. Мы знаем, что
Задание. Найдите угол наклона касательной, проведенной к графику у = sinx в начале координат.
Решение. Производная синуса вычисляется по формуле:
Получается, что тангенс угла наклона также равен единице. Это значит, что сам угол равен 45°. Построение показывает, что это действительно так:
Задание. Найдите производную функции у = tgx в точке х0 = π/6.
Решение. Для тангенса используется формула:
Далее рассмотрим показательную и логарифмическую функцию. Их производные рассчитываются по следующим формулам:
Обратите внимание, что в этих формулах появился натуральный логарифм, то есть логарифм, основанием которого является число е. Именно из-за наличия натурального логарифма в формулах дифференцирования он играет особо важную роль в математике и имеет отдельное обозначение. Вычислим несколько производных с помощью приведенных формул:
Напомним, что справедлива формула
Стоит обратить внимание, что функции у = ех при дифференцировании не меняется. Эта особенность функции также имеет огромное значение в математическом анализе.
Эта особенность функции также имеет огромное значение в математическом анализе.
Задание. Найдите угол наклона касательных, проведенных к графику у = ех в точке (0; 1) и к графику у = lnx в точке (1; 0).
Решение. Используем формулы производных:
Получили, что тангенс наклона касательной равен 1. Из этого следует, что угол наклона касательной равен 45°. Далее найдем производную натурального логарифма при х = 1:
Производная снова равна 1, значит, угол наклона также составит 45°, что подтверждается рисунком:
Ответ: 45°.
Задание. Вычислите производную функции у = 2х при х0 = 3.
Решение. Используем формулу
Сведем использованные нами равенства в одну таблицу производных основных функций:
Основные правила дифференцирования
До этого мы рассматривали довольно простые, то есть стандартные функции, для каждой из которых производную можно узнать из справочника или таблицы. Но что делать, если нам потребовалось продифференцировать функцию, которая состоит из нескольких основных? Например, что делать с функциями у = 5х2 + 6х – 3 или у = x•sinx?
Но что делать, если нам потребовалось продифференцировать функцию, которая состоит из нескольких основных? Например, что делать с функциями у = 5х2 + 6х – 3 или у = x•sinx?
Все более сложные функции можно получить из нескольких простых, комбинируя их. Так, функция у = х3 + х2 получается сложением функций у = х3 и у = х2, а функция у = (lnx)•(cosx) – произведением функций у = lnx и у = сosx.
Есть несколько правил, которые позволяют находить производные в таких случаях. Мы не будем их доказывать, а просто дадим их формулировки. Также будем нумеровать правила. Первое из них помогает находить производную сумму функций.
В данном случае u и v – это просто обозначение каких-то произвольных функций. Рассмотрим пример. Пусть надо найти производную функции
Правило работает и в том случае, если сумма представляет собой сумму не двух, а большего числа слагаемых:
Следующее правило позволяет выносить постоянный множитель за знак производной:
Покажем использование этого правила:
Действительно, зная эти формулы и первые два правила вычисления производных, мы можем записать, что
Задание. Вычислите значение производной функции у = 9х3 + 7х2 – 25х + 7 в точке х0 = 1.
Вычислите значение производной функции у = 9х3 + 7х2 – 25х + 7 в точке х0 = 1.
Решение. Пользуясь правилами дифференцирования, находим производную:
Несколько сложнее обстоит дело с дифференцированием функций, получающихся при перемножении простых функций. В таких случаях используется следующее правило:
Предположим, надо найти производную для функции у = х2•sinx. Её можно представить как произведение u•v, где
Примечание. В последнем случае мы в конце примера использовали формулу косинуса двойного угла:
Заметим, что иногда одно и то же задание с производной можно решить по-разному, используя или не используя правило для вычисления производной произведения функций.
Задание. Найдите производную функции у = х2•(3х + х3). Вычислите ее значение при х = 1.
Решение. Функция у представляет собой произведение более простых функций u•v, где
Задание. Продифференцируйте функцию
Продифференцируйте функцию
Решение. Здесь перед нами функция, которая представляет собой произведение сразу трех множителей. Что делать в таком случае? Надо всего лишь добавить скобки и их помощью оставить только два множителя (один их них окажется «сложным»):
Довольно сложно выглядит формула для поиска производной дроби:
Например, пусть надо найти производную функции
С помощью данного правила можно доказать некоторые равенства. Так, ранее мы уже записали (без доказательства) формулы производных тригонометрических функций:
Оказывается, формула для тангенса может быть выведена из формул для синуса и косинуса. Действительно, тангенс можно записать в виде дроби:
Задание. Найдите, в каких точках надо провести касательную к графику дробно-линейной функции
чтобы эта касательная образовала с осью Ох угол в 135°.
Решение. Угол будет равен 135° только тогда, когда значение производной будет равно (– 1) (так как tg 135° = – 1). Поэтому сначала найдем производную. В данном случае следует использовать правило 4, так как функция у явно записана как дробь:
Поэтому сначала найдем производную. В данном случае следует использовать правило 4, так как функция у явно записана как дробь:
Получили два значения х. Построив график и проведя касательные, мы убедимся, что они действительно образуют с осью Ох угол 135°:
Ответ: – 2 и 0.
Заметим, что иногда можно избавиться от необходимости использовать правило 4, если дифференцируемую функцию можно преобразовать. При этом часто помогает использование отрицательных степеней. Пусть надо продифференцировать функцию
Напрашивается решение использовать правило 4.И такой путь позволит получить правильное решение, хотя и будет несколько трудоемким. Однако можно преобразовать функцию:
У нас получилось произведение, а потому можно использовать правило 3, которое представляется более простым:
Производная сложной функции
«Сконструировать» громоздкую функцию из нескольких простых можно не только с помощью арифметических действий. Например, возьмем функции
Например, возьмем функции
В обоих случаях мы получили некоторую функцию, продифференцировать которую с помощью уже известных нам правил не получится. Функции, сконструированные таким образом, называются сложными. Есть универсальная формула, позволяющая находить производную сложной функции:
Посмотрим, как пользоваться эти правилом. Пусть надо вычислить производную функции
Она сконструирована из функции у = ex и у = sinx, причем вторая подставлена в первую. Это значит, что первую можно обозначить буквой u, а вторую – буквой v (если использовать обозначения в правиле 5):
Задание. Найдите у′, если у = sin 2x.
Решение. На этот раз в качестве исходной функции выступает
Убедиться в справедливости правила 5 можно на примере функции
Её можно продифференцировать двумя разными способами. Сначала попробуем просто избавиться от квадрата в исходной функции, используя формулу квадрата суммы:
В результате оба способа вычисления производной дали одинаковый ответ.
Задание. Найдите производную сложной функции у = (2х + 5)1000.
Решение. В данном случае мы рассматриваем комбинацию следующих функций:
Теперь мы умеем вычислять производные почти любых функций, которые можно записать с помощью элементарных функций и арифметических операций. При этом нам не надо использовать определение понятия производной и вычислять какие бы то ни было пределы. Достаточно знать производные основных функций и несколько (всего лишь 5) правил дифференцирования. Навыки дифференцирования функций пригодятся в будущем при решении практических задач, связанных с производными.
Урок 4.Вычисление производных 4.1 Вычисление производных явно заданных функций
Для вычисления производной в Maple предусмотрена процедура diff(), параметрами которой являются: а) функция, от которой берут производную, б) переменная, по которой эту
производную следует брать. Результатом выполнения процедуры является выражение,
задающее искомую производную. Кроме того, существует неактивная форма процедуры
вычисления производной – Diff (). В отличие
от активной формы (той, что начинается со строчной буквы), неактивная
используется не для непосредственного вычисления производной, а для символьной
записи самой операции.
Кроме того, существует неактивная форма процедуры
вычисления производной – Diff (). В отличие
от активной формы (той, что начинается со строчной буквы), неактивная
используется не для непосредственного вычисления производной, а для символьной
записи самой операции.
В дальнейшем выражение для производной может быть вычислено с помощью процедуры value(), если результат выполнения процедуры Diff () указать в качестве ее параметра.
Совет
Команда value() используется для вычисления значения не только
упомянутой процедурыDiff (), но и других процедур в неактивной форме.
Кроме того, для вычисления производных в Maple может использоваться оператор D. Однако в отличие от процедуры diff(), которая вычисляет производную от символьного выражения, оператор D используется для вычисления производной от оператора. Например, производную от синуса можно вычислить следующим образом.
С помощью оператора D это делается
несколько иначе.
Допустим и такой синтаксис вызова оператора D.
В последнем случае в первых скобках после оператора D указывается оператор (функция), на который действует D, а в следующих скобках – аргумент для полученного в результате оператора (в данном случае оператора D(sin)=cos).
На
заметку
С точки зрения Maple функция и оператор – практически одно и то же. Под
функцией будем, ради удобства, понимать результат действия оператора на
аргумент. Иногда, если это не приводит к недоразумениям, функцией будем также
называть и соответствующий оператор.
Далее имеет смысл остановиться более детально на решении конкретных задач.
В последнем случае в первых скобках после оператора D указывается оператор (функция), на который действует D, а в следующих скобках – аргумент для полученного в результате оператора (в данном случае оператора D(sin)=cos).
На
заметку
С точки зрения Maple функция и оператор – практически одно и то же. Под
функцией будем, ради удобства, понимать результат действия оператора на
аргумент. Иногда, если это не приводит к недоразумениям, функцией будем также
называть и соответствующий оператор.
Под
функцией будем, ради удобства, понимать результат действия оператора на
аргумент. Иногда, если это не приводит к недоразумениям, функцией будем также
называть и соответствующий оператор.
Далее имеет смысл остановиться более детально на решении конкретных задач.
Задача 4.1
Найти производную функции .y:=x->(x*sin(a)+cos(a))*(x*cos(a)-sin(a))
В первую очередь определим саму функцию, от которой следует брать производную. Сделать это можно следующим образом.
Здесь у – функция (ее название), которой в качестве значения присваивается оператор. Оператор задается так: сначала указывается аргумент (или несколько аргументов), потом отображается стрелка (›), а после стрелки задается математическое выражение, определяющее действие оператора на аргумент. После того как функция задана, ее можно дифференцировать.
Если воспользоваться оператором D, то получим несколько иной результат.
Другими словами, результат такой операции – оператор. Приведенная выше запись значит, что аргументу х в результате действия на него
оператора D(y) в
соответствие ставится выражение, которое указано после стрелки.
Приведенная выше запись значит, что аргументу х в результате действия на него
оператора D(y) в
соответствие ставится выражение, которое указано после стрелки.
Очень часто выражения, выводимые Maple в качестве результата выполнения той или иной операции, громоздки. Поэтому их приходится упрощать. В этом случае полезнапроцедураsimplify(). В качестве ее аргумента указывается выражение, которое следует упрощать. В данном случае это переменная среды %. Переменная возвращает в качестве своего значения результат выполнения последней команды, причем не обязательно в текущем рабочем листе (в рассматриваемом случае переменная возвращает вычисленное выше выражение для производной).
Но даже после упрощения выражения его вид может не
соответствовать представлениям пользователя о простоте и элегантности. На этот
случай в Maple предусмотрен ряд полезных утилит, позволяющих привести выражения
к приемлемому для пользователя виду. Среди них имеется такая процедура, как combine (). с.
с.
При дифференцировании в качестве первого аргумента процедуры diff () указывается выражение у (зависящее от х, но хочется еще раз подчеркнуть, это не функциональная зависимость) >diff(y,x);
В отличие от предыдущей задачи, зависимость выражения у от х явно не указывается (здесь как раз и проявляется то, что зависимость не является функциональной). В предыдущей задаче переменная у объявлялась как оператор, поэтому при ее вызове необходимо было указать, на какой аргумент она действует. В данном же случае у – это просто название выражения.
Однако самый незатейливый способ вычисления производной представлен ниже.
В качестве первого параметра в ней использована уже
упоминавшаяся переменная среды (%), а вторым
параметром указана опция trig. Это инструкция для вычислительного ядра
Maple использовать встроенные алгоритмы преобразования тригонометрических
выражений: в частности, произведения тригонометрических функций заменяются, где
это возможно, тригонометрическими функциями от суммы (разности) аргументов. (1/х).
(1/х).
В качестве параметра процедуры diff () можно сразу указать дифференцируемое выражение.
Поскольку очевидно, что в полученном после дифференцирования выражении имеется возможность вынести за скобки общий множитель, воспользуемся следующей командой.
Переменная среды %, указанная в качестве первого параметра процедуры collect(), определяет выражение, которое нужно преобразовать, а второй параметр указывает на то, что в выражении слагаемые следует группировать по степеням 1/х.
На
заметку
Если при вызове процедуры collect() вторым параметром указать не 1/х,
а х, результат не изменится. Причина в том, что 1/х – это х в степени -1.
Вычислительное ядро Maple достаточно эффективно работает не только с непрерывными функциями, но и с такими, которые имеют точки (или области) разрывов.
Задача 4.4
Найти производную функции
.
Определяем функцию у(х) следующим образом.
При этом целая часть числа х возвращается функцией Maple floor().
На
заметку
ВMaple есть функция trune(),
действие которой во многом аналогично действию функции floor(). Однако
функция trunc() выделяет целую часть аргумента
“в направлении О”, в то время как функция floor () выделяет ближайшее целое число, не
превышающее данное, указанное как аргумент. Для положительных чисел действия
обеих функций эквивалентны, а для отрицательных чисел результаты отличаются на
единицу.
Дальше процедура вычисления производной уже знакома.
Последнее
выражение содержит функцию floor(), у которой указано два аргумента. В этом
случае первый аргумент определяет порядок производной, второй – непосредственно
аргумент. Другими словами, floor(1,x) –
это первая производная от функции floor(x), которая во всех точках равна нулю, кроме
целочисленных значений аргумента – в этих точках производная не определена
(поскольку floor(х) в
этих точках имеет неустранимый разрыв).
Полученное выражение, при желании, можно упростить.
Чтобы представить себе, что же это за функция, построим ее график.
В качестве первого аргумента процедуры plot(), используемой для отображения двухмерных графиков, указывается выражение, график которого следует построить. В данном случае это выражение определяется значением переменной среды %. Второй аргумент является равенством, где указывается переменная, относительно которой следует строить график (левая часть равенства), а после знака равенства – диапазон ее изменения.
На
заметку
Если диапазон изменения не указать, то по умолчанию график строится на
интервале -10..10.
Следующие
параметры являются необязательными. В приведенном примере это заголовок (опция title) и шрифт
для этого заголовка (опция title-font). Значения этих опций указываются после
знака равенства: заголовок (его значение) заключается в двойные кавычки, а
шрифт – это список (в квадратных скобках через запятую указываются тип шрифта,
его стиль и размер). Подробнее об опциях процедуры plot() можно узнать из приложения в конце
книги. Там же имеется и информация о возможных значениях этих опций.
Подробнее об опциях процедуры plot() можно узнать из приложения в конце
книги. Там же имеется и информация о возможных значениях этих опций.
На
заметку
Списком в Maple называется последовательность разделенных через запятую
элементов (самого разного характера), заключенная в квадратные скобки. В списке
имеет значение порядок следования элементов – при изменении очередности
элементов по определению полагают, что список изменился. Последовательность
Maple – это группа (в обычном, не математическом значении этого слова)
выражений, разделенных запятыми. Пример последовательности: x,sin(t),5.3*6.
Пример списка: [x,sin(t),5.3*6].
Если последовательность заключить в фигурные скобки, получится множество.
От списка множество отличается тем, что не имеет значения ни порядок
следования, ни количество совпадающих элементов.
Внимание!
Некоторые параметры графиков можно изменять уже после их отображения в
области вывода непосредственно с помощью кнопок контекстной панели двухмерной
графики u команд раскрывающегося меню. Описание контекстной панели для
двухмерных и трехмерных графиков приведено в главе 1, а описание опций можно
найти в приложении.
Описание контекстной панели для
двухмерных и трехмерных графиков приведено в главе 1, а описание опций можно
найти в приложении.
Следует также иметь в виду, что внешний вид графиков, которые пользователь
увидит на экране, если введет предложенные команды, может не соответствовать
тому, что показано в книге. В этом случае желаемого результата можно добиться с
помощью уже упомянутой контекстной панели или раскрывающегося меню. Как будет
показано далее, внешний вид графиков можно задавать непосредственно с помощью
опций процедурыplot(). Однако на данном этапе это не
является первостепенной задачей.
деривативов | Безграничное исчисление
Задача о производной и касательной
Использование дифференцирования позволяет решить задачу касательной линии путем нахождения наклона [латекс] f ‘(a) [/ латекс].
Цели обучения
Определите производную как наклон касательной к точке на кривой
Основные выводы
Ключевые моменты
- Касательная линия [латекс] t [/ латекс] (или просто касательная) к плоской кривой в данной точке – это прямая линия, которая «едва касается» кривой в этой точке.

- Прямая линия называется касательной к кривой [латекс] y = f (x) [/ latex] в точке [latex] x = c [/ latex] на кривой, если линия проходит через точку [ латекс] (c, f (c)) [/ латекс] на кривой и имеет наклон [латекс] f ‘(c) [/ латекс], где [латекс] f’ [/ латекс] является производным от [латекс] f [/латекс].
- Используя производные, уравнение касательной можно сформулировать следующим образом: [латекс] y = f (a) + f {(a)} ‘(x-a) [/ latex].
Ключевые термины
- касательная : линия, касающаяся кривой в одной точке, но не пересекающая ее в этой точке
- секущая : линия, пересекающая кривую в двух или более точках
Касательная линия [латекс] t [/ латекс] (или просто касательная) к плоской кривой в данной точке – это прямая линия, которая «только касается» кривой в этой точке.Неформально это прямая, проходящая через пару бесконечно близких точек кривой. Точнее, прямая линия называется касательной к кривой [латекс] y = f (x) [/ latex] в точке [latex] x = c [/ latex] на кривой, если линия проходит через точка [латекс] (c, f (c)) [/ latex] на кривой и имеет наклон [латекс] f ‘(c) [/ latex], где f ‘ – производное от [latex] f [/ latex ].
Касательная к кривой : линия показывает касательную к кривой в точке, представленной точкой.Он почти не касается кривой и показывает наклон скорости изменения в точке.
Предположим, что кривая задана как график функции, [латекс] y = f (x) [/ latex]. Чтобы найти касательную в точке [latex] p = (a, f (a)) [/ latex], рассмотрите другую ближайшую точку [latex] q = (a + h, f (a + h)) [/ latex ] на кривой. Наклон секущей линии, проходящей через [латекс] p [/ латекс] и [латекс] q [/ латекс], равен коэффициенту разности
.[латекс] \ displaystyle {\ frac {f (a + h) – f (a)} {h}} [/ latex].
Когда точка [латекс] q [/ латекс] приближается к [латексу] p [/ латексу], что соответствует уменьшению и уменьшению [латекса] h [/ латекса], коэффициент разности должен приближаться к определенному предельному значению [латекс] k [/ latex], который представляет собой наклон касательной в точке [latex] p [/ latex]. Если [латекс] k [/ латекс] известен, уравнение касательной можно найти в форме «точка-наклон»:
[латекс] y – f (a) = k (x-a) [/ латекс]
Предположим, что граф не имеет разрыва или острого края на [латексе] p [/ латексе], и он не является ни вертикальным, ни слишком изгибающимся рядом с [латексом] p [/ латексом]. Затем существует уникальное значение [latex] k [/ latex], так что по мере приближения [latex] h [/ latex] к [latex] 0 [/ latex] коэффициент разности становится все ближе и ближе к [latex] k [ / latex], и расстояние между ними становится незначительным по сравнению с размером [latex] h [/ latex], если [latex] h [/ latex] достаточно мало. Это приводит к определению наклона касательной к графику как предела коэффициентов разности для функции [latex] f [/ latex]. Этот предел является производной функции [латекс] f [/ латекс] при [латекс] x = a [/ latex], обозначаемый [латекс] f ‘(a) [/ latex].Используя производные, уравнение касательной можно записать следующим образом:
Затем существует уникальное значение [latex] k [/ latex], так что по мере приближения [latex] h [/ latex] к [latex] 0 [/ latex] коэффициент разности становится все ближе и ближе к [latex] k [ / latex], и расстояние между ними становится незначительным по сравнению с размером [latex] h [/ latex], если [latex] h [/ latex] достаточно мало. Это приводит к определению наклона касательной к графику как предела коэффициентов разности для функции [latex] f [/ latex]. Этот предел является производной функции [латекс] f [/ латекс] при [латекс] x = a [/ latex], обозначаемый [латекс] f ‘(a) [/ latex].Используя производные, уравнение касательной можно записать следующим образом:
[латекс] y = f (a) + f {(a)} ‘(x-a) [/ латекс].
Производные финансовые инструменты и курсы изменения
Дифференциация – это способ вычисления скорости изменения одной переменной по отношению к другой.
Цели обучения
Опишите производную как изменение [латекса] y [/ латекса] по сравнению с изменением [латекса] x [/ латекса] в каждой точке графика.
Основные выводы
Ключевые моменты
- Исторически основной мотивацией для изучения дифференцирования была проблема касательной линии, задача которой для данной кривой найти наклон прямой, касательной к этой кривой в данной точке.
- Если [latex] y [/ latex] является линейной функцией [latex] x [/ latex], то [latex] m = \ frac {\ Delta y} {\ Delta x} [/ latex].
- Производная измеряет наклон графика в каждой точке.
Ключевые термины
- уклон : также называется градиентом; наклон или уклон линии описывает ее крутизну
Исторически основной мотивацией для изучения дифференцирования была проблема касательной линии, задача которой для данной кривой найти наклон прямой, касательной к этой кривой в данной точке.Слово тангенс происходит от латинского слова tangens , что означает прикосновение. Таким образом, чтобы решить проблему касательной, нам нужно найти наклон линии, которая «касается» данной кривой в данной точке, или, говоря современным языком, имеющей такой же наклон. Но что именно мы подразумеваем под «наклоном» кривой?
Но что именно мы подразумеваем под «наклоном» кривой?
В простейшем случае [latex] y [/ latex] является линейной функцией от x, что означает, что график [latex] y [/ latex], деленный на [latex] x [/ latex], представляет собой прямую линию. В этом случае [латекс] y = f (x) = m x + b [/ latex] для действительных чисел m и b, а наклон m определяется по формуле:
[латекс] \ displaystyle {m = \ frac {\ Delta y} {\ Delta x}} [/ latex]
, где символ [латекс] \ Delta [/ latex] (заглавная форма греческой буквы Delta) означает и произносится как «изменение в.”Эта формула верна, потому что:
[латекс] y + \ Delta y = f (x + \ Delta x) = m (x + \ Delta x) + b = m x + b + m \ Delta x = y + m \ Delta x [/ latex]
Отсюда следует, что [латекс] \ Delta y = m \ Delta x [/ latex].
Наклон функции : функция с наклоном, показанным для данной точки.
Это дает точное значение наклона прямой. Однако, если функция [latex] f [/ latex] не является линейной (т. Е. Ее график не является прямой линией), то изменение [latex] y [/ latex] делится на изменение [latex] x [ / latex] меняется: дифференциация – это метод нахождения точного значения для этой скорости изменения при любом заданном значении [latex] x [/ latex].Другими словами, дифференциация – это метод вычисления скорости, с которой зависимый выход [latex] y [/ latex] изменяется по отношению к изменению в независимом входе [latex] x [/ latex]. Эта скорость изменения называется производной [латекса] y [/ латекса] по отношению к [латексу] x [/ латексу]. Точнее говоря, зависимость [латекса] y [/ латекса] от [латекса] x [/ латекса] означает, что [латекс] y [/ латекс] является функцией [латекса] x [/ латекса]. Эта функциональная связь часто обозначается [латекс] y = f (x) [/ latex], где [latex] f [/ latex] обозначает функцию.Если [latex] x [/ latex] и [latex] y [/ latex] являются действительными числами, и если график [latex] y [/ latex] строится против [latex] x [/ latex], производная измеряет наклон этого графика в каждой точке.
Е. Ее график не является прямой линией), то изменение [latex] y [/ latex] делится на изменение [latex] x [ / latex] меняется: дифференциация – это метод нахождения точного значения для этой скорости изменения при любом заданном значении [latex] x [/ latex].Другими словами, дифференциация – это метод вычисления скорости, с которой зависимый выход [latex] y [/ latex] изменяется по отношению к изменению в независимом входе [latex] x [/ latex]. Эта скорость изменения называется производной [латекса] y [/ латекса] по отношению к [латексу] x [/ латексу]. Точнее говоря, зависимость [латекса] y [/ латекса] от [латекса] x [/ латекса] означает, что [латекс] y [/ латекс] является функцией [латекса] x [/ латекса]. Эта функциональная связь часто обозначается [латекс] y = f (x) [/ latex], где [latex] f [/ latex] обозначает функцию.Если [latex] x [/ latex] и [latex] y [/ latex] являются действительными числами, и если график [latex] y [/ latex] строится против [latex] x [/ latex], производная измеряет наклон этого графика в каждой точке.
Производная как функция
Если каждая точка функции имеет производную, существует функция производной, отправляющая точку [latex] a [/ latex] производной от [latex] f [/ latex] в [latex] x = a [/ latex] : [латекс] ф ‘(а) [/ латекс].
Цели обучения
Объясните, как производная действует как «функция функций»
Основные выводы
Ключевые моменты
- Производная – это оператор, область определения которого представляет собой набор всех функций, которые имеют производные в каждой точке своей области определения, а диапазон которых является набором функций.
- Функция, значение которой в [latex] x = a [/ latex] равно [latex] f ′ (a) [/ latex] всякий раз, когда [latex] f ′ (a) [/ latex] определено, а где-либо еще не определено, это также называется производной [латекс] ф [/ латекс].
- По определению производной функции [latex] D (f) (a) = f ′ (a) [/ latex], где [latex] D [/ latex] – оператор, область определения которого является набором всех функций которые имеют производные в каждой точке их области определения и диапазон которых является набором функций.
Ключевые термины
- диапазон : набор значений (точек), которые функция может получить
- домен : набор всех возможных математических объектов (точек), в которых определена данная функция
Пусть [latex] f [/ latex] будет функцией, которая имеет производную в каждой точке [latex] a [/ latex] в домене [latex] f [/ latex].Поскольку каждая точка [latex] a [/ latex] имеет производную, существует функция, которая отправляет точку [latex] a [/ latex] производной от [latex] f [/ latex] в [latex] a [/ латекс]. Эта функция записывается [latex] f ‘(x) [/ latex] и называется производной функцией или производной от [latex] f [/ latex]. Производная [латекса] f [/ латекса] собирает все производные [латекса] f [/ латекса] во всех точках домена [латекс] f [/ латекс]. Визуально производная функции [latex] f [/ latex] в [latex] x = a [/ latex] представляет наклон кривой в точке [latex] x = a [/ latex].
Производная как наклон : Показанный наклон касательной представляет значение производной кривой функции в точке [латекс] x [/ латекс].
Иногда [latex] f [/ latex] имеет производную в большинстве, но не во всех точках своей области. Функция, значение которой в [latex] a [/ latex] равно [latex] f ‘(a) [/ latex] всякий раз, когда [latex] f’ (a) [/ latex] определено, а в другом месте не определено, также называется производной. [латекс] ф [/ латекс]. Это все еще функция, но ее домен строго меньше, чем домен [latex] f [/ latex].
Прерывистая функция : В точке, где функция совершает скачок, производная функции не существует.
Используя эту идею, дифференцирование становится функцией функций: производная – это оператор, область определения которого является набором всех функций, имеющих производные в каждой точке своей области определения, а диапазон значений – набор функций. Если обозначить этот оператор как [latex] D [/ latex], то [latex] D (f) [/ latex] – это функция [latex] f ‘(x) [/ latex].Поскольку [latex] D (f) [/ latex] является функцией, ее можно оценить в точке [latex] a [/ latex]. По определению производной функции [латекс] D (f) (a) = f ‘(a) [/ latex].
Для сравнения рассмотрим функцию удвоения [латекс] f (x) = 2x [/ latex]; [latex] f [/ latex] является действительной функцией действительного числа, что означает, что он принимает числа в качестве входных и имеет числа в качестве выходных:
[латекс] 1 \ стрелка вправо 2 [/ латекс]
[латекс] 2 \ rightarrow 4 [/ латекс]
[латекс] 3 \ rightarrow 6 [/ латекс].2 [/ латекс]
[latex] D [/ latex] выводит функцию удвоения,
[латекс] x \ rightarrow 2x [/ латекс]
, который является f (x) f (x). Затем эта функция вывода может быть вычислена для получения [latex] f (1) = 2f (1) = 2 [/ latex], [latex] f (2) = 4 [/ latex] и так далее.
Правила дифференциации
Правила дифференцирования могут упростить производные, устраняя необходимость в сложных расчетах пределов.
Цели обучения
Практика использования правил дифференцирования для упрощения дифференцирования сложных выражений
Основные выводы
Ключевые моменты
- Дифференцирование с помощью полиномиального разложения может быть очень сложным и подверженным ошибкам.2} [/ латекс].
Ключевые термины
- коэффициент разности : разность функций [латекс] \ Delta F [/ latex], деленная на разность точек [латекс] \ Delta x [/ latex]: [latex] \ Delta F (x) / \ Delta x [ / латекс]
- полином : выражение, состоящее из суммы конечного числа членов, каждый член является произведением постоянного коэффициента и одной или нескольких переменных, возведенных в неотрицательную целую степень
Когда мы хотим различать сложные выражения, возможный способ дифференцировать выражение – это развернуть его и получить многочлен, а затем дифференцировать этот многочлен.Этот метод становится очень сложным и особенно подвержен ошибкам при выполнении расчетов вручную. Во многих случаях сложных расчетов пределов путем прямого применения разностного коэффициента Ньютона можно избежать, используя правила дифференцирования. Вот некоторые из самых основных правил.
Постоянное правило
Если [latex] f (x) [/ latex] является константой, то [latex] f ‘(x) = 0 [/ latex], поскольку скорость изменения константы всегда равна нулю.
Правило суммы
[латекс] (\ alpha f + \ beta g) ‘= \ alpha f’ + \ beta g ‘[/ latex]
для всех функций [latex] f [/ latex] и [latex] g [/ latex] и всех действительных чисел [latex] \ alpha [/ latex] и [latex] \ beta [/ latex].x [/ latex], как и константа 7, также использовались.
Производные тригонометрических функций
Производные тригонометрических функций можно найти с помощью стандартной формулы производной.
Цели обучения
Определение производных наиболее распространенных тригонометрических функций
Основные выводы
Ключевые моменты
- Производная синусоидальной функции является косинусоидальной функцией.
- Производная функции косинуса является отрицательной величиной функции синуса.
- Производная касательной функции – это функция секущей в квадрате.
Ключевые термины
- секущая : прямая линия, пересекающая кривую в двух или более точках
Тригонометрические функции (также называемые круговыми функциями) являются функциями угла. Они используются, чтобы связать углы треугольника с длинами сторон треугольника. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, среди многих других приложений.
Самыми известными тригонометрическими функциями являются синус, косинус и тангенс. В контексте стандартной единичной окружности с радиусом 1, где треугольник образован лучом, исходящим из начала координат и составляющим некоторый угол с осью [latex] x [/ latex], синус угла дает длину [latex] y [/ latex] -компонент (подъем) треугольника, косинус дает длину [latex] x [/ latex] -компоненты (прогон), а функция тангенса дает наклон ([латекс] y [/ latex] -компонент, разделенный на [latex] x [/ latex] -компонент).
Имея это в виду, мы можем использовать определение производной для вычисления производных различных тригонометрических функций:
[латекс] \ displaystyle {f ‘(x) = \ lim_ {h \ rightarrow 0} \ frac {f (x + h) – f (x)} {h}} [/ latex]
Например, если [латекс] f (x) = \ sin x [/ latex], то:
[латекс] \ displaystyle {f ‘(x) = \ lim_ {h \ rightarrow 0} \ frac {\ sin (x + h) – \ sin (x)} {h}} [/ latex]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h) + \ cos (h) \ cdot \ sin (x) – \ sin (x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h) + (\ cos (h) – 1) \ cdot \ sin ( x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h)} {h} + \ lim_ {h \ rightarrow 0} \ frac {(\ cos (h) – 1) \ cdot \ sin (x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ cos (x) (1) + \ sin (x) (0)} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ cos (x)} [/ латекс]
Синус и косинус : На этом изображении можно увидеть, что там, где касательная к одной кривой имеет нулевой наклон (производная этой кривой равна нулю), значение другой функции равно нулю.2 x} [/ латекс]
Правило цепочки
Цепное правило – это формула для вычисления производной композиции двух или более функций.
Цели обучения
Вычислить производную композиции функций, используя цепное правило
Основные выводы
Ключевые моменты
- Если [latex] f [/ latex] является функцией, а [latex] g [/ latex] является функцией, то цепное правило выражает производную сложной функции [latex] f \ circ g [/ latex] в термины производных [латекса] ф [/ латекса] и [латекса] г [/ латекса].
- Правило цепочки может применяться последовательно для любого количества функций, вложенных друг в друга.
- Цепное правило для [латекса] f \ circ g (x) [/ latex]: [latex] \ frac {df} {dx} = \ frac {df} {dg} \ frac {dg} {dx} [/ латекс].
Ключевые термины
- композит : функция функции
Цепное правило – это формула для вычисления производной композиции двух или более функций. То есть, если [latex] f [/ latex] является функцией, а [latex] g [/ latex] является функцией, то цепное правило выражает производную сложной функции [latex] f \ circ g [/ latex] в виде производных [латекса] ф [/ латекса] и [латекса] г [/ латекса].
Например, следуя правилу цепочки для [latex] f \ circ g (x) = f [g (x)] [/ latex], получаем:
[латекс] \ displaystyle {\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}} [/ латекс]
Метод называется «цепным правилом», потому что его можно последовательно применять ко многим функциям, вложенным друг в друга. Например, если [latex] f [/ latex] является функцией [latex] g [/ latex], которая, в свою очередь, является функцией [latex] h [/ latex], которая, в свою очередь, является функцией [latex ] x [/ latex] – то есть [латекс] f (g (h (x))) [/ latex] – затем производная от [latex] f [/ latex] по отношению к [latex] x [/ latex ] составляет:
[латекс] \ displaystyle {\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dh} \ cdot \ frac {dh} {dx}} [/ латекс]
Цепное правило имеет широкое применение в физике, химии и инженерии, а также для изучения связанных скоростей во многих других дисциплинах.2 [/ латекс]
Неявная дифференциация
Неявное дифференцирование использует цепное правило для дифференцирования неявно определенных функций.
Цели обучения
Используйте неявное дифференцирование, чтобы найти производные функций, которые не являются явно функциями [latex] x [/ latex]
Основные выводы
Ключевые моменты
- Поскольку y может быть задано как функция [latex] x [/ latex] неявно, а не явно, когда у нас есть уравнение [latex] R (x, y) = 0 [/ latex], мы можем решите это для [latex] y [/ latex], а затем дифференцируйте.
- Неявная функция – это функция, которая неявно определяется отношением между ее аргументом и его значением.
- Теорема о неявной функции утверждает, что если левая часть уравнения [латекс] R (x, y) = 0 [/ latex] дифференцируема и удовлетворяет некоторому мягкому условию на свои частные производные в некоторой точке [латекс] (a , b) [/ latex] такой, что [latex] R (a, b) = 0 [/ latex], тогда он определяет функцию [latex] y = f (x) [/ latex] на некотором интервале, содержащем [latex] а [/ латекс].
Ключевые термины
- неявный : подразумевается косвенно, без прямого выражения
Неявная функция – это функция, которая неявно определяется отношением между ее аргументом и его значением.
Если левая часть уравнения [латекс] R (x, y) = 0 [/ latex] дифференцируема и удовлетворяет некоторому мягкому условию на свои частные производные в некоторой точке [latex] (a, b) [/ latex] такой, что [latex] R (a, b) = 0 [/ latex], тогда он определяет функцию [latex] y = f (x) [/ latex] на некотором интервале, содержащем [latex] a [/ latex]. Геометрически граф, определенный как [latex] R (x, y) = 0 [/ latex], будет локально перекрываться с графиком некоторого уравнения [latex] y = f (x) [/ latex].
Для большинства неявных функций не существует формулы, определяющей их явно.2 + y = \ sin (x) [/ latex] является неявной функцией, потому что очень сложно получить формулу для [latex] y [/ latex] в терминах только [latex] x [/ latex]. Однако мы все еще можем найти производную от [latex] y [/ latex] по отношению к [latex] x [/ latex], используя неявное дифференцирование.
[латекс] \ displaystyle {2y \ cdot \ frac {dy} {dx} + \ frac {dy} {dx} = \ cos (x) = (2y + 1) \ frac {dy} {dx}} [/ латекс]
Следовательно:
[латекс] \ displaystyle {\ frac {dy} {dx} = \ frac {\ cos (x)} {2y + 1}} [/ latex]
Поскольку [латекс] y [/ latex] может быть задан как функция [latex] x [/ latex] неявно, а не явно, когда у нас есть уравнение [latex] R (x, y) = 0 [/ latex] , мы можем решить его для [latex] y [/ latex], а затем дифференцировать.Однако иногда проще дифференцировать [латекс] R (x, y) [/ латекс] относительно [латекса] x [/ латекса] и [латекса] y [/ латекса], а затем решать для [латекса] \ frac {dy} {dx} [/ латекс].
Например, учитывая выражение [латекс] y + x + 5 = 0 [/ latex], дифференциация урожайности:
[латекс] \ displaystyle {\ frac {dy} {dx} + \ frac {dx} {dx} + \ frac {d} {dx} 5 = \ frac {dy} {x} + 1 = 0} [/ латекс]. 2 [/ latex], где [latex] r [/ latex] – радиус круга.Вы можете использовать неявное дифференцирование, чтобы найти наклон касательной к окружности в точке [latex] (x, y) [/ latex]. Поскольку наклон касательной является производной в этой точке, мы находим производную неявно:
[латекс] \ displaystyle {2y \ frac {dy} {dx} + 2x \ frac {dx} {dx} = \ frac {dr} {dx} = 0} [/ латекс]
где [latex] \ frac {dr} {dx} [/ latex] равно [latex] 0 [/ latex], поскольку радиус постоянен. Затем вы можете найти формулу для [латекс] \ frac {dy} {dx} [/ latex]:
[латекс] \ displaystyle {\ frac {dy} {dx} = \ frac {-2x} {2y} = \ frac {-x} {y}} [/ latex]
, и теперь вы можете найти наклон в любой точке [latex] (x, y) [/ latex].
Путь точки на окружности : Путь точки на окружности может быть выражен только как неявная функция.
Дифференциация и скорость изменений в естественных и социальных науках
Дифференциация, по сути, вычисление скорости изменения, важна во всех количественных науках.
Цели обучения
Приведите примеры дифференциации или скорости изменений, используемых в различных академических дисциплинах.
Основные выводы
Ключевые моменты
- Дифференциация применима почти ко всем количественным дисциплинам, будь то естественные или социальные науки.
- Ученые-физики используют дифференциацию и скорость изменения для изучения того, как физическая концепция изменяется с течением времени или на расстоянии.
- Социологи используют дифференциацию и коэффициент, чтобы определить, как люди, товары и процессы меняются из-за изменения независимой переменной.
Ключевые термины
- Дифференциальная геометрия : изучение геометрии с помощью дифференциального исчисления
- импульс : (тела в движении) произведение его массы и скорости
- Валовой внутренний продукт : мера экономического производства на определенной территории с точки зрения финансового капитала за определенный период времени
Для данной функции [latex] y = f (x) [/ latex] дифференцирование – это метод вычисления скорости, с которой зависимый выход [latex] y [/ latex] изменяется по отношению к изменению в независимом входе [ латекс] х [/ латекс].Эта скорость изменения называется производной [латекса] y [/ латекса] относительно [латекса] x [/ латекса].
Скорость изменения – важное понятие во многих количественных исследованиях, и неудивительно, что дифференциация (представляющая скорость изменения) применима почти ко всем количественным дисциплинам. Например, в физике производная смещения движущегося тела по времени – это скорость тела, а производная скорости по времени – это ускорение.Второй закон движения Ньютона гласит, что производная количества движения тела равна силе, приложенной к телу. Скорость химической реакции является производной. При исследовании операций производные инструменты определяют наиболее эффективные способы транспортировки материалов и проектирования предприятий.
Производные часто используются для нахождения максимумов и минимумов функции. Уравнения, включающие производные, называются дифференциальными уравнениями и являются фундаментальными для описания природных явлений.Производные и их обобщения появляются во многих областях математики, таких как комплексный анализ, функциональный анализ, дифференциальная геометрия, теория меры и абстрактная алгебра.
Темпы изменений происходят во всех науках и во всех дисциплинах. Экономисты изучают скорость изменения валового внутреннего продукта, а социологи – скорость, с которой население голосует в определенной области. Геологи изучают скорость сдвига Земли и температурный градиент горных пород возле вулкана. Бухгалтеры изучают скорость изменения производства и поставок и то, как любое изменение может повлиять на затраты и прибыль.Городские инженеры изучают движение транспорта, чтобы спроектировать и построить более эффективные дороги и автострады.
В каждом аспекте жизни, в котором что-то меняется, дифференциация и скорость изменений являются важным аспектом в понимании мира и поиске способов его улучшить.
Связанные ставки
Проблемы связанных ставок связаны с нахождением скорости путем соотнесения этого количества с другими величинами, скорости изменения которых известны.
Цели обучения
Решение проблем, используя связанные ставки (используя количество, ставка которого известна, чтобы найти скорость, с которой изменяется связанное количество)
Основные выводы
Ключевые моменты
- Поскольку наука и инженерия часто связывают количества друг с другом, методы связанных скоростей имеют широкое применение в этих областях.
- Поскольку задачи включают несколько переменных, дифференцирование по времени или по одной из других переменных требует применения правила цепочки.
- Процесс решения проблем связанных ставок: запишите все соответствующие формулы и информацию, возьмите производную от первичного уравнения по времени, решите для желаемой переменной, вставьте известную информацию и упростите.
Ключевые термины
- переменная : величина, которая может принимать любое из набора значений
Одно из полезных применений деривативов – это помощь в вычислении соответствующих ставок.Что такое родственная ставка? В дифференциальном исчислении проблемы связанных скоростей включают нахождение скорости, с которой величина изменяется, путем соотнесения этой величины с другими величинами, скорости изменения которых известны. В большинстве случаев рассчитываемая соответствующая ставка является производной по некоторому значению. Мы вычисляем эту производную по скорости, с которой изменяется какая-то другая известная величина. Учитывая скорость, с которой что-то меняется, нас просят найти скорость, с которой изменяется значение, связанное с данной скоростью.
Скорость изменения обычно зависит от времени. Поскольку наука и техника часто связывают количества друг с другом, методы связанных скоростей имеют широкое применение в этих областях. Поскольку задачи включают несколько переменных, дифференцирование по времени или по одной из других переменных требует применения цепного правила.
Процесс решения проблем связанных ставок:
1. Запишите все соответствующие формулы и информацию.
2. Возьмем производную первичного уравнения по времени.
3. Найдите желаемую переменную.
4. Вставьте известную информацию и упростите.
См. Блок-схему решения проблем связанных ставок.
Блок-схема решения проблем, связанных с расходами : Проблемы со связанными расходами можно решать с помощью методического подхода.
Предположим, вам дана следующая ситуация.
Сферический воздушный шар наполняется воздухом. Объем изменяется со скоростью 2 кубических фута в минуту.2} V ‘} [/ латекс]
Вставьте известную информацию:
[латекс] \ displaystyle {r ‘= \ frac {1} {16 \ pi} 2 = \ frac {1} {8 \ pi}} [/ latex] фут / мин
Высшие производные
Производная уже дифференцированного выражения называется производной более высокого порядка.
Цели обучения
Вычисление высших (вторых, третьих и т. Д.) Производных функций
Основные выводы
Ключевые моменты
- Вторая производная или производная второго порядка – это производная производной функции.
- Поскольку производная функции определяется как функция, представляющая наклон исходной функции, двойная производная – это функция, представляющая наклон функции первой производной.
- Если [latex] x (t) [/ latex] представляет положение объекта в момент времени [latex] t [/ latex], то производные [latex] x [/ latex] более высокого порядка имеют физические интерпретации, например как скорость и ускорение.
Ключевые термины
- производная : мера того, как функция изменяется при изменении ее входных данных
Вторая производная или производная второго порядка – это производная производной функции.Производная функции может обозначаться как [латекс] f ‘(x) [/ latex], а ее двойная (или «вторая») производная обозначается как [латекс] f’ ‘(x) [/ latex]. Это читается как «[латекс] f [/ латекс] двойное простое число от [латекс] x [/ латекс]» или «вторая производная от [латекс] f (x) [/ латекс]. «Поскольку производная функции определяется как функция, представляющая наклон функции, двойная производная – это функция, представляющая наклон функции первой производной.
Кроме того, третья производная является производной производной производной функции, которая может быть представлена как [латекс] f ” ‘(x) [/ latex].Это читается как «[латекс] f [/ латекс] тройное простое число [латекс] x [/ латекс]» или «третья производная от [латекса] f (x) [/ латекс].»). Это может продолжаться до тех пор, пока полученная производная сама является дифференцируемой, с четвертой производной, пятой производной и так далее. Любая производная за пределами первой производной может называться производной более высокого порядка.
Если [latex] x (t) [/ latex] представляет положение объекта в момент времени [latex] t [/ latex], то производные [latex] x [/ latex] более высокого порядка имеют физические интерпретации.Вторая производная от [latex] x [/ latex] – это производная от [latex] x ‘(t) [/ latex], скорости и, по определению, ускорения объекта. Третья производная от [латекс] x [/ латекс] определяется как толчок, а четвертая производная определяется как толчок. Функция [latex] f [/ latex] не обязательно должна иметь производную – например, если она не является непрерывной. Точно так же, даже если [латекс] f [/ латекс] имеет производную, у него может не быть второй производной. См. Графическую иллюстрацию высших производных в физике.2 + 6x – 1 [/ латекс]
Вычислить производную в Excel по таблицам данных
Несколько недель назад я писал о вычислении интеграла данных в Excel. На этой неделе я хочу изменить направление и показать, как вычислить производную в Excel. Как и в случае с численным интегрированием, есть два способа выполнить это вычисление в Excel:
- Производные табличных данных на листе
- Производные функции с использованием VBA (или Visual Basic для приложений)
Для этого поста я ‘ m собираюсь сосредоточиться на вычислении производных табличных данных, а сообщение о вычислении того же самого с использованием VBA появится позже.
Это вид вычисления производной, который обычно выполняется на экспериментальных данных. Это может быть особенно полезно, когда вы не могли напрямую измерить интересующее количество, но смогли измерить его интегральную функцию.
Классическим примером, конечно же, является положение и скорость:
Скажем, например, вы провели какой-то эксперимент, в котором было трудно получить скорость напрямую. Вместо этого вы измеряли позицию в разное время: t .Вы можете импортировать данные в Excel и рассчитать скорость как производную от положения по времени.
Для выполнения этого расчета в Excel используется метод конечных разностей.
Чтобы использовать метод конечных разностей в Excel, мы вычисляем изменение «y» между двумя точками данных и делим на изменение «x» между теми же самыми точками данных:
Это называется односторонней оценкой. , потому что он учитывает только наклон данных на одной стороне интересующей точки.
Лучшей оценкой было бы вычисление среднего наклона в интересующей точке путем усреднения наклона непосредственно до и после этой точки.
Итак, если мы хотим найти наклон в y 2 (z), мы могли бы использовать этот расчет:
Давайте посмотрим, как вычислить производную в Excel на примере. Мы можем использовать данные о положении, которые были рассчитаны путем интегрирования данных о скорости в предыдущем посте, и использовать их для расчета как скорости, так и ускорения.В качестве проверки сравним рассчитанные данные ускорения с исходными данными ускорения.
Чтобы упростить задачу, я спрятал старые данные об ускорении и скорости. В конце мы посмотрим, как они сравниваются.
Сначала я вычисляю скорость, используя приведенное выше уравнение конечных разностей. Поскольку нам нужны y3 и y1, я начинаю вычисление в ячейке E5 и заполняю ее.
Затем, используя вычисленную скорость, я могу вычислить ускорение тем же методом.На этот раз расчет начинается в строке 6.
Теоретически, если мы дифференцируем данные, полученные путем интегрирования, мы должны вернуться к исходным данным. Конечно, все численные методы вносят в данные некоторую погрешность.
Но насколько велика ошибка? Давайте сравним.
В этом случае мы можем увидеть небольшие различия между исходными данными ускорения и данными, полученными путем дифференцирования. Есть также некоторые незначительные различия в двух наборах данных скорости.К счастью, ошибка численного дифференцирования не является кумулятивной, в отличие от численного интегрирования.
Таблицы данных – не идеальный способ изучить эти данные, поэтому давайте посмотрим на графики:
Трудно увидеть, потому что две линии расположены друг над другом, но для всех практических целей скорости идентичны .
Как насчет разгона?
Здесь мы видим, что в периоды неуклонно возрастающего или постоянного ускорения два набора данных очень похожи.Однако, когда в данных ускорения наблюдается разрыв (то есть время от времени 0,1, 0,45, 0,5, 0,7 и 0,75 с), ускорение, полученное дифференцированием (оранжевый), не соответствует исходным данным ускорения (синий).
Это связано с уравнением, которое мы использовали для выполнения дифференцирования. Помните, как мы получили производную в точке по , усредняя наклон по обе стороны от этой точки? Мы видим результаты здесь.
Если вы следовали инструкциям, поздравляем! Вы только что выполнили численное дифференцирование в Excel.Конечно, вычислить производную в Excel не так уж и сложно, если вы знаете, как это делать.
Вы использовали этот метод для некоторых данных? Расскажите об этом в комментариях ниже.
Как определяется цена производного инструмента?
Различные типы производных финансовых инструментов имеют разные механизмы ценообразования. Производный инструмент – это просто финансовый контракт, стоимость которого основана на каком-либо базовом активе (например, цене акции, облигации или товара). Наиболее распространенными типами производных финансовых инструментов являются фьючерсные контракты, форвардные контракты, опционы и свопы.Более экзотические производные могут быть основаны на таких факторах, как погода или выбросы углерода.
Ключевые выводы
- Производные инструменты – это финансовые контракты, используемые для различных целей, цены на которые основаны на базовых активах или ценных бумагах.
- В зависимости от типа производного инструмента его справедливая стоимость или цена будет рассчитываться по-разному.
- Фьючерсные контракты основаны на спотовой цене вместе с базовой суммой, в то время как цена опционов определяется на основе времени до истечения срока, волатильности и цены исполнения.
- Свопы устанавливаются на основе приравнивания приведенной стоимости фиксированного и переменного потоков денежных средств в течение срока действия контракта.
Основы ценообразования на фьючерсы
Фьючерсные контракты – это стандартизированные финансовые контракты, которые позволяют держателям покупать или продавать базовый актив или товар по определенной цене в будущем, которая зафиксирована сегодня. Таким образом, стоимость фьючерсного контракта зависит от цены товара при оплате наличными.
Цены фьючерсов часто будут несколько отличаться от наличной или спотовой цены базового актива.Разница между ценой товара при наличном расчете и ценой фьючерса является основой. Это очень важная концепция для управляющих портфелем и трейдеров, поскольку эта взаимосвязь между ценой наличных и фьючерсными ценами влияет на стоимость контрактов, используемых при хеджировании. Поскольку между спотовой и относительной ценой есть разрывы до истечения ближайшего контракта, основание не обязательно является точным.
В дополнение к отклонениям, возникающим из-за разрыва во времени между истечением фьючерсного контракта и спотовым товаром, качество продукции, место доставки и фактические данные также могут отличаться.Как правило, эта база используется инвесторами для оценки прибыльности доставки наличных или фактической, а также используется для поиска возможностей арбитража.
Например, рассмотрим фьючерсный контракт на кукурузу, который представляет собой 5000 бушелей кукурузы. Если кукуруза продается по цене 5 долларов за бушель, стоимость контракта составляет 25 000 долларов. Фьючерсные контракты стандартизированы и включают определенное количество и качество базового товара, поэтому ими можно торговать на централизованной бирже. Цена фьючерса изменяется относительно спотовой цены на товар на основе спроса и предложения на этот товар.
Форвардные контракты оцениваются аналогично фьючерсам, но форварды представляют собой нестандартные контракты, заключаемые между двумя контрагентами и заключаемые на внебиржевой основе с большей гибкостью условий.
Основы ценообразования на опции
Опционы также являются обычными контрактами с производными финансовыми инструментами. Опционы дают покупателю право, но не обязательство, купить или продать установленную сумму базового актива по заранее определенной цене, известной как цена исполнения, до истечения срока действия контракта.
Основная цель теории ценообразования опционов – рассчитать вероятность того, что опцион будет исполнен или окажется в деньгах (ITM) по истечении срока его действия. Цена базового актива (цена акции), цена исполнения, волатильность, процентная ставка и время до истечения срока, то есть количество дней между датой расчета и датой исполнения опциона, являются обычно используемыми переменными, которые вводятся в математические модели для получения теоретическая справедливая стоимость опциона.
Помимо цен акций и страйков компании, время, волатильность и процентные ставки также являются неотъемлемой частью точной оценки опциона.Чем дольше инвестор должен исполнять опцион, тем больше вероятность того, что он станет ITM по истечении срока его действия. Точно так же, чем более волатильным является базовый актив, тем больше вероятность того, что истечет срок его действия ITM. Более высокие процентные ставки должны привести к более высоким ценам опционов.
Самая известная модель ценообразования для опционов – это метод Блэка-Шоулза. Этот метод учитывает базовую цену акции, цену исполнения опциона, время до истечения срока действия опциона, волатильность базовой акции и безрисковую процентную ставку, чтобы определить стоимость опциона.Существуют и другие популярные модели, такие как модели ценообразования биномиального дерева и трехчленного дерева.
Основы ценообразования на свопы
Свопы – это производные инструменты, которые представляют собой соглашение между двумя сторонами об обмене сериями денежных потоков в течение определенного периода времени. Свопы предлагают большую гибкость при разработке и структурировании контрактов на основе взаимного согласия. Эта гибкость порождает множество вариантов обмена, каждый из которых служит определенной цели. Например, одна сторона может обменять фиксированный денежный поток на переменный денежный поток, который колеблется при изменении процентных ставок.Другие могут поменять денежные потоки, связанные с процентными ставками в одной стране, на денежные потоки другой страны.
Самый простой тип свопа – это простой процентный своп. В этом типе свопа стороны соглашаются обменивать процентные платежи. Например, предположим, что банк A соглашается производить платежи банку B на основе фиксированной процентной ставки, в то время как банк B соглашается производить платежи банку A на основе плавающей процентной ставки.
Стоимость свопа на дату инициирования будет равна нулю для обеих сторон.Чтобы это утверждение было верным, значения потоков денежных средств, которые стороны свопа собираются обменять, должны быть равны. Эта концепция проиллюстрирована на гипотетическом примере, в котором стоимость фиксированного участка и плавающего участка свопа будет составлять V fix и V fl соответственно. Таким образом, при посвящении:
V ж я Икс знак равно V ж л V_ {fix} = V_ {fl} Vfix = Vfl
Условные суммы не обмениваются в процентных свопах, потому что эти суммы равны и обменивать их не имеет смысла.Если предполагается, что стороны также решат обменять условную сумму в конце периода, процесс будет аналогичен обмену облигации с фиксированной ставкой на облигацию с плавающей ставкой с той же условной суммой. Следовательно, такие своп-контракты можно оценивать с помощью облигаций с фиксированной и плавающей ставкой.
Расчет производных
Чтобы иметь возможность эффективно оптимизировать конструкции и рассчитывать многие свойства требуют наличия производных. Хотя конечный для их определения можно использовать разностные методы, это неэффективно и неточно для силовых полей, поскольку числовые ошибки могут вызвать проблемы, особенно когда потенциалы не уходят точно в ноль на отсечке расстояние.Следовательно, все производные определяются аналитически. в ГУЛП. Все функциональные формы энергии имеют до аналитической секунды. доступны производные, в то время как двух-, трех- и четырехчастичные взаимодействия включать третьи производные. Кроме того, аналитические третьи производные может быть рассчитан для метода встроенного атома, но в настоящее время не для любых других потенциальных функций многих тел.
Поскольку определение производных является центральным для многих величин, дано краткое описание подхода к их расчету. здесь, в то время как более полные детали можно найти как в оригинальном Harwell Отчет [113] и последующая публикация многих эти детали [114].В конечном итоге производные инструменты двух типов: требуемые – относящиеся к атомным степеням свободы и те относительно элементарной ячейки. В GULP все производные атомных координат вычисляются в декартовой системе отсчета, а затем преобразуются к дробным производным по координатам, когда это уместно периодичность. Для элементарной ячейки взяты производные деформации, как и ранее описано.
Как декартовы производные, так и производные деформации могут быть связаны с множеством
основных величин, которые являются первыми производными по
к межатомным расстояниям, деленным на расстояние:
где в выражении для производной деформации компоненты и являются соответствующими декартовыми указаниями для данный штамм (например,грамм. подразумевает и). Подразумевается, что все количества имеют нижний индекс для обозначения что термины относятся к конкретному парному взаимодействию. Разрешите представить стенография:
Тогда вторые производные могут быть получены путем дифференцирования приведенные выше выражения еще раз и записываются как:
Точно так же третьи производные могут быть получены дальнейшим дифференцированием:
Обратите внимание, что для минимизации свободной энергии, это были третьи производные требуются только производные по двум декартовым координатам и одна деформация или три декартовых координаты.
Как в трехчастичных, так и в четырехчастичных терминах существуют производные с
относительно тригнометрической функции угла или угла
сам. Эти производные могут быть преобразованы в указанные выше формы с помощью
использование правила косинуса:
где – угол при стержневом атоме 1, лежащем между векторы и. Производные по углам поэтому получаются через выражение:
При обращении с лимитом необходимо соблюдать осторожность, поскольку или .
Расчет производных с помощью Mathematica
Расчет производных с помощью MathematicaD
Mathematica содержит функцию D , которая будет
позволяют дифференцировать данное уравнение относительно некоторых
Переменная. Фактически, D позволит вам различать
сразу весь список уравнений.
Использовать D очень просто. Первое
аргумент D – это уравнение или список уравнений, которые должны быть
дифференцированный. 2 + b x + c, {x, 2}] Вых [4] = 2 а
Интегрировать
Mathematica также содержит функцию Интегрировать это позволит вам интегрировать уравнение.(-1 + n), x] п
Out [4] = x
Список литературы
[ST94] Прикладная математикаУильям Т. Шоу и Джейсон Тигг
Аддисон-Уэсли, Менло-Парк, Калифорния (1994).
[Rob95] Инженерная математика с Mathematica
Джон С. Робертсон
Макгроу-Хилл, Нью-Йорк, штат Нью-Йорк (1995).
[GG91] Изучение математики с помощью Mathematica
Теодор В. Грей и Джерри Глинн
Аддисон-Уэсли, Менло-Парк, Калифорния (1991).
Взятие производных и дифференциация – Уроки Wyzant
Дифференцирование – это алгебраический метод нахождения производной функции в любой точке. Производная
– это концепция, лежащая в основе исчисления
. Есть два способа представить эту концепцию: геометрический путь
(как наклон кривой) и физический способ (как скорость изменения).Наклон
кривой соответствует скорости изменения при рассмотрении реальных приложений.
В любом случае наклон и мгновенная скорость изменения эквивалентны,
, и функция для нахождения обоих из них в любой точке называется производной.
Геометрическая концепция производной
Если вы когда-либо находили наклон линии на графике, это производная. Когда
мы смотрим на кривые, а не на линейные графики, становится трудно найти наклон
в каждой точке, потому что наклон
постоянно меняется.Чтобы найти наклон, можно увеличить масштаб графика
в точке и найти наклон в этой точке.
Чтобы найти уклон, можно использовать метод подъема через пробег или формулу уклона:
Чтобы получить более приближенный наклон или производную, нужно максимально приблизить два значения x
. Это утомительный процесс, если вы хотите найти наклон
для многих точек на графике.Вот где вступает в игру дифференциация. Определение производной
происходит от взятия предела
формулы наклона, когда две точки функции становятся ближе, а
– ближе друг к другу.
Например, скажем, у нас есть точка P (x, f (x)) на кривой, и мы хотим найти наклон
(или производную) в этой точке. Мы можем взять точку где-нибудь рядом с P на кривой
, скажем, Q (x + h, f (x + h)) , где h – небольшое значение. Теперь мы можем подставить эти значения
в формулу наклона:
Решение этого вопроса даст нам приблизительное значение наклона, но все равно
не даст нам точного значения.Мы хотим, чтобы h было как можно меньше, чтобы мы могли получить наклон
в точке P, поэтому мы позволяем h приближаться к 0.
Определение предела для производного инструмента
Это наклон касательной или производной в точке P. Это дает нам мгновенную скорость изменения y относительно x
.
Приведем пример. Рассмотрим функцию:
Затем мы заменяем x + h на x
.Взяв лимит, получим
Теперь упрощаем
Выносим за скобки h
Мы видим, что когда h переходит в 0, у нас остается 6x + 2.
Это линейное выражение 6x + 2 является производной функции, и мы можем найти
наклон касательной в любой точке кривой, подставив значение x
координаты.
На приведенном ниже графике исходная функция показана красным цветом, а производная – зеленым.
Обратите внимание, что, когда наклон параболы отрицательный, функция производной
ниже нуля, а когда наклон параболы положительный, функция
производной также является положительной.Когда парабола опускается и наклон меняется с отрицательного на положительный
, функция производной меняется с отрицательной на положительную. Мы можем
видеть, что при f (-1), f ‘(- 1) = -4, поэтому наклон при -1 равен -4. Точно так же при f (0) f ‘(0)
= 2, поэтому наклон при 0 равен 2.
Хотя мы видели форму производной с использованием предела, ее также можно обозначить
как dy / dx, f ‘(x) или y ’
Различные обозначения производной
d / dx означает, что мы берем производную по x.
f ‘(x) обозначает производную f (x), а y ’ обозначает производную
y.
Взятие производной от многочленов
Поиск производной для некоторых функций сложнее, чем для других, и может оказаться утомительным процессом
при использовании формулы наклона. К счастью, есть более простой способ получить
производную от
многочленов без использования пределов. Ньютон и Лейбниц открыли простой способ
найти производную более сложных функций, который требует всего нескольких шагов.Давайте рассмотрим пример
:
Первый шаг к нахождению производной – взять любой показатель в функции
и понизить его, умножив на коэффициент.
Мы опускаем 2 сверху и умножаем на 2 перед x. Затем,
, мы уменьшаем показатель степени на 1. Конечная производная этого члена равна 2 * (2) x 1 , или 4x .
Предполагается, что для второго члена показатель степени равен 1, поэтому мы уменьшаем его и умножаем
на коэффициент перед x.Затем мы уменьшаем показатель степени на 1, делая
равным 0. Окончательная производная этого члена равна 1 * (- 5) x 0 . Обратите внимание, что любое число, возведенное в степень
до 0-й степени, равно 1, поэтому наш упрощенный ответ: 1 * (- 5) * 1 или -5 .
Третий член исключен, потому что у него нет x, что означает, что это константа
. Причина этого в том, что число 3 можно записать как 3x 0 , а
, когда выпадает 0, весь член становится 0 .Теперь у нас осталась наша упрощенная производная
:
Обратите внимание, что производная линейна, а исходная функция квадратична. Производная
всегда будет на один градус меньше исходной функции. Вот общее правило
для взятия производной всех членов многочлена, где c – константа
:
Это обычно называется правилом силы (см. Доказательство правила силы).
Давайте сделаем еще один графический пример
Дифференцируемый и недифференцируемый
Теперь вы должны быть осторожны при поиске производной, потому что не каждая функция
имеет ее. Большинство функций дифференцируемы, что означает, что производная существует
в каждой точке функции. Однако некоторые функции нельзя полностью дифференцировать.
Найдем производную следующей функции при x = 0.
Предел, когда h приближается к 0 слева, отличается от того, когда h приближается к 0
справа. Это эквивалентно тому, что производная (или наклон) слева
равна -1, тогда как производная правой части равна 1. Каков наклон, где они
встречаются в начале координат?
Глядя на график, мы видим, что в начале координат нет определенного наклона
, потому что есть несколько касательных, поэтому в этой точке нет производной.
Следовательно, функция не имеет производной при x = 0, поэтому она дифференцируема
везде, кроме x = 0.
Следует отметить, что для того, чтобы функция была дифференцируемой, она должна быть непрерывной.
Поиск касательной
Ранее мы нашли наклон касательной в точке, используя предельное определение производной
. Давайте рассмотрим пример поиска касательной в заданной точке с использованием правила степени
для многочленов.
Найдите уравнение касательной к
графику f (x) = x 2 + 3x в точке (1,4).
Находим производную, используя правило степеней дифференцирования
Подставьте нашу координату x в производную, чтобы получить наклон
Теперь мы можем использовать форму наклона точки, чтобы найти уравнение касательной. (1,4) – это наша точка, а 5 – это наклон
.Физическая концепция производной
Исаак Ньютон сосредоточился на физической концепции дифференциации применительно к механике
и мгновенной скорости изменения.Что касается механики, то скорость изменения
определяется как скорость, или скорость, когда мы говорим о расстоянии за
промежуток времени. Как и в случае с геометрическим подходом, визуализируйте, что вы путешествуете на
от точки A к точке B. Мы используем формулу для наклона, чтобы найти среднюю скорость:
Теперь, если мы хотим найти мгновенную скорость, мы хотим, чтобы изменение во времени до
становилось все меньше и меньше. Мы вводим понятие предела, когда изменение времени
приближается к 0.Получаем
Обратите внимание, что это то же самое, что и геометрическое определение производной,
, но с другими переменными. Физическое определение основано на геометрическом определении
, и все правила производных применимы к обоим. Хотя вы можете найти скорость
, взяв производную, вы также можете найти ускорение, взяв
как вторую производную, то есть взяв производную от производной.
Приведем пример.
Найдите скорость и ускорение частицы с заданным положением
, равным s (t) = t 3 – 2t 2 – 4t + 5 при t = 2 , где
t измеряется в секундах и s измеряется в футах.
Скорость определяется как производная от положения.
В 2 секунды скорость составляет 0 футов в секунду.
Ускорение определяется путем взятия производной функции скорости или второй производной положения.
За 2 секунды ускорение составляет 8 футов в секунду в квадрате.
Давайте проанализируем график с физической точки зрения. Черная кривая
– это положение объекта. Обратите внимание, что когда кривая имеет горб, функция скорости
достигает 0.Представьте объект, который проходит определенное расстояние по прямой
, а затем возвращается – объект не может развернуться вокруг
, если скорость не будет равна 0. Это то же самое для ускорения
, поскольку оно относится к функции скорости. Кроме того, когда ускорение составляет
0, график функции положения выглядит как прямая линия вокруг
этой точки. Это связано с тем, что, когда ускорение равно 0, скорость объекта
остается неизменной, поэтому наклон будет постоянным.
Сводка дифференциации
Надо понимать
- Определение производной как предела, когда две точки функции становятся бесконечно близкими
- взаимосвязь между дифференцируемостью и непрерывностью
- как производные финансовые инструменты представлены графически, численно и аналитически
- , как они интерпретируются как мгновенная скорость изменения.
Таким образом, производная – это, по сути, наклон или мгновенная скорость изменения касательной линии
в любой точке кривой.Когда вы берете производную функции, вы получаете
с другой функцией, которая обеспечивает наклон исходной функции. Производная
функции должна иметь одинаковый предел слева направо, чтобы она могла быть дифференцируемой
в этой точке. Производная также может сказать нам скорость изменения одной величины
по сравнению с другой, если смотреть на ситуации в реальном мире. Если мы знаем, какое расстояние
проехал автомобиль с течением времени, производная может сказать нам, что это скорость и ускорение
в любой момент времени.
3.4 Деривативы как скорость изменения – Объем расчетов 1
Цели обучения
- Определите новое значение количества из старого значения и суммы изменения.
- Рассчитайте среднюю скорость изменения и объясните, чем она отличается от мгновенной скорости изменения.
- Применение скорости изменения смещения, скорости и ускорения объекта, движущегося по прямой линии.
- Спрогнозируйте численность населения в будущем, исходя из текущей стоимости и темпов прироста населения.
- Используйте производные инструменты для расчета предельных затрат и доходов в деловой ситуации.
В этом разделе мы рассмотрим некоторые применения производной, сосредоточив внимание на интерпретации производной как скорости изменения функции. Эти приложения включают ускорение и скорость в физике, темпы роста населения в биологии и маргинальные функции в экономике.
Помимо анализа скорости, скорости, ускорения и положения, мы можем использовать производные для анализа различных типов популяций, в том числе таких разнообразных, как колонии бактерий и города.Мы можем использовать текущую популяцию вместе со скоростью роста, чтобы оценить размер популяции в будущем. Скорость прироста населения – это скорость изменения численности населения и, следовательно, может быть представлена производной от численности населения.
Определение
Если – количество сущностей, присутствующих в популяции, то темпы прироста населения определяются равными.
Оценка населения
Население города увеличивается в три раза каждые 5 лет.Если его нынешнее население составляет 10 000 человек, какое будет его примерное население через 2 года?
Известно, что нынешнее население колонии комаров составляет 3000 человек; то есть, . Если, оцените численность популяции за 3 дня, где измеряется в днях.
В дополнение к анализу движения вдоль линии и роста населения, производные инструменты полезны при анализе изменений в стоимости, выручке и прибыли. Концепция маржинальной функции распространена в сфере бизнеса и экономики и подразумевает использование производных финансовых инструментов.Предельные затраты являются производной функции затрат. Предельный доход является производным от функции дохода. Маржинальная прибыль i является производной функции прибыли, которая основана на функции затрат и функции дохода.
Мы можем приблизительно оценить
, выбрав соответствующее значение для. Поскольку представляет объекты, разумным и малым значением для является 1. Таким образом, подставляя, мы получаем приближение.Следовательно, данное значение можно рассматривать как изменение стоимости, связанное с производством одного дополнительного элемента. Аналогичным образом аппроксимируется доход, полученный от продажи одного дополнительного объекта, и приближается прибыль, полученная от производства и продажи одного дополнительного объекта.
Применение предельного дохода
Предположим, что прибыль, полученная от продажи обедов из жареной рыбы, равна. Используйте функцию маржинальной прибыли, чтобы оценить прибыль от продажи 101-го обеда из жареной рыбы.
Ключевые понятия
- Используя, можно оценить данные и.
- Скорость изменения положения – это скорость, а скорость изменения скорости – это ускорение. Скорость – это абсолютное значение или величина скорости.
- Темпы прироста населения и текущее население могут быть использованы для прогнозирования размера будущей популяции.
- Функции предельных затрат, предельного дохода и предельной прибыли можно использовать для прогнозирования, соответственно, затрат на производство еще одного изделия, дохода, полученного от продажи еще одного изделия, и прибыли, полученной от производства и продажи еще одного изделия.
Для следующих упражнений данные функции представляют положение частицы, движущейся вдоль горизонтальной линии.
- Найдите функции скорости и ускорения.
- Определите временные интервалы, когда объект замедляется или ускоряется.
1.
2.
Решение
а.
г. Ускоряться: ; Притормаживает:
3.
5. Мяч бросается вниз со скоростью 8 футов / с с вершины здания высотой 64 фута. Через несколько секунд его высота над землей будет равна.
- Определите, сколько времени требуется мячу, чтобы коснуться земли.
- Определите скорость мяча, когда он ударяется о землю.
[показать-ответ q = ”875579 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 875579 ″] a. 5 футов / с b. 9 фут / с
7. Положение колибри, летящего по прямой линии в секундах, дано в метрах.
- Определите скорость птицы в сек.
- Определите ускорение птицы в сек.
- Определите ускорение птицы, когда скорость равна 0.
9. Функция позиции определяет положение грузового поезда в милях, где восток является положительным направлением и измеряется в часах.
- Определите направление, в котором движется поезд.
- Определить направление, в котором движется поезд.
- Определяет временные интервалы, когда поезд замедляется или набирает скорость.
10. На следующем графике показано положение объекта, движущегося по прямой линии.
- Используйте график функции положения, чтобы определить временные интервалы, когда скорость положительная, отрицательная или нулевая.
- Нарисуйте график функции скорости.
- Используйте график функции скорости, чтобы определить временные интервалы, когда ускорение является положительным, отрицательным или нулевым.
- Определите временные интервалы, когда объект ускоряется или замедляется.
11. Функция затрат в долларах компании, производящей кухонные комбайны, определяется выражением, где – количество произведенных кухонных комбайнов.
- Найдите функцию предельных затрат.
- Найдите предельные затраты на производство 12 кухонных комбайнов.
- Найдите фактическую стоимость производства тринадцатого кухонного комбайна.
Решение
а.
г.
г. 6 долларов США за товар, 0 долларов США за товар
13. [T] Прибыль получается, когда выручка превышает затраты. Предположим, что функция прибыли производителя скейтбордов имеет вид, где – количество проданных скейтбордов.
- Найдите точную прибыль от продажи тридцатого скейтборда.
- Найдите функцию предельной прибыли и используйте ее для оценки прибыли от продажи тридцатого скейтборда.
Решение
а.
г.
г. Популяция бактерий увеличивается с 0 до 10 часов; впоследствии популяция бактерий уменьшается.
г. . Скорость роста бактерий уменьшается в течение первых 10 часов. После этого популяция бактерий уменьшается с уменьшающейся скоростью.
17. Центростремительная сила объекта массы определяется выражением, где – скорость вращения, а – расстояние от центра вращения.
- Найдите скорость изменения центростремительной силы по отношению к расстоянию от центра вращения.
- Найдите скорость изменения центростремительной силы объекта массой 1000 кг, скоростью 13,89 м / с и расстоянием от центра вращения 200 метров.
Следующие вопросы касаются населения (в миллионах) Лондона по десятилетиям XIX века, которые перечислены в следующей таблице.
| Годы с 1800 | Население (млн) |
|---|---|
| 1 | 0.8795 |
| 11 | 1.040 |
| 21 | 1,264 |
| 31 | 1,516 |
| 41 | 1,661 |
| 51 | 2.000 |
| 61 | 2,634 |
| 71 | 3,272 |
| 81 | 3,911 |
| 91 | 4,422 |
18.[Т]
- С помощью калькулятора или компьютерной программы найдите наиболее подходящую линейную функцию для измерения численности населения.
- Найдите производную уравнения в (a) и объясните ее физический смысл.
- Найдите вторую производную уравнения и объясните ее физический смысл.
Решение
а.
г. . Население увеличивается.
г. . Скорость роста населения постоянна.
19.[Т]
- С помощью калькулятора или компьютерной программы найдите наиболее подходящую квадратичную кривую по данным.
- Найдите производную уравнения и объясните ее физический смысл.
- Найдите вторую производную уравнения и объясните ее физический смысл.
Для следующих упражнений рассмотрим космонавта на большой планете в другой галактике. Чтобы узнать больше о составе этой планеты, космонавт бросает электронный датчик в глубокую траншею.Датчик каждую секунду передает свое вертикальное положение относительно положения космонавта. Сводка данных датчика падения отображается в следующей таблице.
| Время после сброса (с) | Позиция (м) |
|---|---|
| 0 | 0 |
| 1 | -1 |
| 2 | -2 |
| 3 | −5 |
| 4 | −7 |
| 5 | −14 |
20.[Т]
- С помощью калькулятора или компьютерной программы найдите квадратичную кривую, которая наилучшим образом соответствует данным.
- Найдите производную функции положения и объясните ее физический смысл.
- Найдите вторую производную функции положения и объясните ее физический смысл.
Решение
а.
г. . Это скорость датчика.
г. . Это ускорение датчика; это постоянное ускорение вниз.
21.[Т]
- С помощью калькулятора или компьютерной программы найдите кубическую кривую, которая наилучшим образом соответствует данным.
- Найдите производную функции положения и объясните ее физический смысл.
- Найдите вторую производную функции положения и объясните ее физический смысл.
- Используя результат (c), объясните, почему кубическая функция не является хорошим выбором для этой задачи.
Следующие задачи относятся к уравнениям Холлинга типа I, II и III.Эти уравнения описывают экологическое событие роста популяции хищников с учетом количества добычи, доступной для потребления.
Решение
а.
г. . Когда количество добычи увеличивается, рост хищника увеличивается.
г. . Когда количество добычи чрезвычайно мало, скорость роста хищников увеличивается, но когда количество добычи превышает определенный порог, скорость роста хищников начинает уменьшаться.
г. На более низком уровне добычи жертве легче избежать обнаружения хищником, поэтому поедается меньше особей добычи, что приводит к меньшему росту хищников.
25. [T] Популяции зайца-снегоступа (в тысячах) и рыси (в сотнях), собранные за 7 лет с 1937 по 1943 год, показаны в следующей таблице. Заяц-снегоступы – основная добыча рыси.
| Численность зайца-снегоступа (тыс.) | Популяция рыси (сотни) |
|---|---|
| 20 | 10 |
| 55 | 15 |
| 65 | 55 |
| 95 | 60 |
- Постройте график точек данных и определите, какая функция типа Холлинга лучше всего соответствует данным.
- Используя значения параметров и, определите значения этих параметров, исследуя график данных.Напомним, что это измерение того, какая ценность жертвы дает половинную максимальную ценность хищника.
- Постройте результирующие функции Холлинга I, II и III поверх данных.
