Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции
Вы можете изучить и скачать доклад-презентацию на тему Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции. Презентация на заданную тему содержит 21 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас – поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Практика. Примеры решения задач по темам Вычисление предела функции Вычисление производных Исследование функции
Слайд 2
1. Предел функции
Приведены примеры решения следующих классов задач
1.1. Предел дробно-рациональной функции
1.2. Предел сложной функции
1.3. Второй замечательный предел
1.4. Первый замечательный предел
Предел функции
Приведены примеры решения следующих классов задач
1.1. Предел дробно-рациональной функции
1.2. Предел сложной функции
1.3. Второй замечательный предел
1.4. Первый замечательный предел
Слайд 3
Описание слайда:
1. Предел функции. Теоретические сведения Предел – величина А, к которой сколь угодно близко стремится некоторый процесс. В математическом анализе это – предел функции в бесконечности, предел функции в точке. Основные обозначения: Предел функции в бесконечности или – Предел функции в точке х0 : – слева, левосторонний – справа, правосторонний Условие непрерывности функции в точке
Слайд 4
Описание слайда:
1. Предел функции. Теоретические сведения.
В любом процессе значение предела, величина А, может равняться :
а)±∞ . А – бесконечно большая величина (ББВ). Процесс не ограничен
б)±0 . А – бесконечно малая величина (БМВ). Процесс ограничен
с)константе С. Процесс ограничен
Основные теоремы о пределах:
1).Функция не может иметь более одного предела
2).Предел алгебраической суммы функций равен алгебраической сумме пределов этих функций
3). Предел произведения функций равен произведению их пределов
4). Предел частного от деления двух функций равен частному их пределов, при условии, что предел делителя не равен нулю
5). Предел сложной функция f(U(x)), равен пределу f от предела U
Предел функции. Теоретические сведения.
В любом процессе значение предела, величина А, может равняться :
а)±∞ . А – бесконечно большая величина (ББВ). Процесс не ограничен
б)±0 . А – бесконечно малая величина (БМВ). Процесс ограничен
с)константе С. Процесс ограничен
Основные теоремы о пределах:
1).Функция не может иметь более одного предела
2).Предел алгебраической суммы функций равен алгебраической сумме пределов этих функций
3). Предел произведения функций равен произведению их пределов
4). Предел частного от деления двух функций равен частному их пределов, при условии, что предел делителя не равен нулю
5). Предел сложной функция f(U(x)), равен пределу f от предела U
Слайд 5
1.1. Предел дробно-рациональной функции Примеры решения:
Слайд 6
Описание слайда:
1. 1. Предел дробно-рациональной функции
Примеры решения:
1. Предел дробно-рациональной функции
Примеры решения:
Слайд 7
Описание слайда:
1.2. Предел сложной функции вычисляется по правилу . Примеры решения а) б) Решение данного класса задач основано на свойствах и графиках функции ax при ограничениях Рассматриваются два диапазона значений а:
Слайд 8
Описание слайда:
1.2. Предел сложной функции вычисляется по
правилу .
Слайд 9
Описание слайда:
1.3. Второй замечательный предел и его следствие а) Вводим новую переменную t=x-2;x=t+2
Слайд 10
Описание слайда:
1.3. Второй замечательный предел и его следствие б) в)
Слайд 11
Описание слайда:
1. 4. Первый замечательный предел и его следствие
а)
б)
Преобразуем числитель и знаменатель ;
Тогда
4. Первый замечательный предел и его следствие
а)
б)
Преобразуем числитель и знаменатель ;
Тогда
Слайд 12
Описание слайда:
2. Вычисление производных Производная функции в точке х=х0 -предел отношения приращения функции у = f(х0+х)-f(х0) к приращению аргумента х при х ->0 Обозначается производная функции f(х) в точке х0 символом f'(х0). или Дифференциал функции dy=df= f'(x0)х =f'(x)dx Геометрический смысл производной: тангенс угла касательной к функции в точке х0 , тангенс угла , tg Геометрический смысл дифференциала: первое линейное приращение функции в точке х0 + х, отрезок KN
Слайд 13
Описание слайда:
2. Таблица производных.
1. постоянная; 2.
3.
4.
6.
Правила дифференцирования
1. 2.
3. 4.
5.
Таблица производных.
1. постоянная; 2.
3.
4.
6.
Правила дифференцирования
1. 2.
3. 4.
5.
Слайд 14
Описание слайда:
2.1. Вычислить первую и вторую производную, дифференциал функции а) Решение.
Слайд 15
2.1. Вычислить первую и вторую производную, дифференциал функции
б)
Решение.
Слайд 16
Описание слайда:
2.1. Вычислить первую и вторую производную, дифференциал функции в) Решение. Обозначим: f1(x)=3x; f2(x)= cos(1-x2) Функция – сложная функция. Тогда
Слайд 17
Описание слайда:
2.1. Вычислить первую и вторую производную, дифференциал функции г) Решение. Обозначим Тогда
Слайд 18
Описание слайда:
3. Исследование функции
Решение задачи исследования функции сводится к выполнению следующих действий:
1. Определение точек разрыва, интервалов непрерывности, области определения функции (ООФ)
2. Анализ на четность, нечетность, периодичность
3. Определение (если возможно) точек пересечения функции с осями координат Х, У
4. Вычисление пределов – на границах ООФ, в точках разрыва
5. Определение точек экстремума и перегиба. Решение этой задачи связано с вычислением и последующим анализом поведения первой и второй производных функции
6. Построение графика функции
7. Определение области значений функции, ОЗФ
Анализ на четность, нечетность, периодичность
3. Определение (если возможно) точек пересечения функции с осями координат Х, У
4. Вычисление пределов – на границах ООФ, в точках разрыва
5. Определение точек экстремума и перегиба. Решение этой задачи связано с вычислением и последующим анализом поведения первой и второй производных функции
6. Построение графика функции
7. Определение области значений функции, ОЗФ
Слайд 19
Описание слайда:
3. 1. Исследование функции – примеры а) Исследуемая функция – точек разрыва нет; вертикальных асимптот нет; ООФ=(-∞;∞) – Четность: y(-1)=y(1) –функция четная – Пределы функции: На границах ООФ . Функция четная Левый и правый пределы в точках разрыва – нет Уравнение наклонной асимптоты Наклонной асимптоты нет Точки пересечения графика с осями координат
Слайд 20
Описание слайда:
а) Исследуемая функция
– Точки экстремумов и интервалы монотонности
– Точки перегиба, выпуклость, вогнутость
Результат исследования представлен в таблице 3. 1.а
1.а
Слайд 21
Описание слайда:
а) Исследуемая функция Таблица 3.1.а
Tags Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
предел функции, вычисление производных, исследование функции презентация, доклад
Практика. Примеры решения задач по темам
Вычисление предела функции
Вычисление производных
Исследование функции
1. Предел функции
Предел функции
Приведены примеры решения следующих классов задач
1.1. Предел дробно-рациональной функции
1.2. Предел сложной функции
1.3. Второй замечательный предел
1.4. Первый замечательный предел
1. Предел функции. Теоретические сведения
Предел – величина А, к которой сколь угодно близко стремится
некоторый процесс. В математическом анализе это – предел
функции в бесконечности, предел функции в точке.
Основные обозначения:
Предел функции в бесконечности
или
– Предел функции в точке х0 :
– слева, левосторонний
– справа, правосторонний
Условие непрерывности функции в точке
1. Предел функции. Теоретические сведения.
В любом процессе значение предела, величина А, может равняться :
а)±∞ . А – бесконечно большая величина (ББВ). Процесс не ограничен
Процесс не ограничен
б)±0 . А – бесконечно малая величина (БМВ). Процесс ограничен
с)константе С. Процесс ограничен
Основные теоремы о пределах:
1).Функция не может иметь более одного предела
2).Предел алгебраической суммы функций равен алгебраической сумме пределов этих функций
3). Предел произведения функций равен произведению их пределов
4). Предел частного от деления двух функций равен частному их пределов, при условии, что предел делителя не равен нулю
5). Предел сложной функция f(U(x)), равен пределу f от предела U
1.1. Предел дробно-рациональной функции
Примеры решения:
1.1. Предел дробно-рациональной функции
Примеры решения:
1.2. Предел сложной функции вычисляется по
правилу .
Примеры решения
а)
б)
Решение данного класса задач основано на свойствах и графиках
функции ax при ограничениях Рассматриваются
два диапазона значений а:
1.2. Предел сложной функции вычисляется по
правилу .
в)
г)
Решение данного класса задач основано на свойствах и
графиках функции ax при ограничениях
Рассматриваются два диапазона значений а:
1.3. Второй замечательный предел и его следствие
а)
Вводим новую переменную t=x-2;x=t+2
1.3. Второй замечательный предел и его следствие
б)
в)
1. 4. Первый замечательный предел и его следствие
4. Первый замечательный предел и его следствие
а)
б)
Преобразуем числитель и знаменатель ;
Тогда
2. Вычисление производных
Производная функции в точке х=х0 -предел отношения приращения
функции Δу = f(х0+Δх)-f(х0) к приращению аргумента Δх при Δх ->0
Обозначается производная функции f(х) в точке х0 символом f'(х0).
или
Дифференциал функции dy=df= f'(x0)⋅Δх =f'(x)dx
Геометрический смысл производной: тангенс угла касательной к
функции в точке х0 , тангенс угла α, tgα
Геометрический смысл дифференциала: первое линейное
приращение функции в точке х0 + Δх, отрезок KN
2. Таблица производных.
1. постоянная; 2.
3.
4.
6.
Правила дифференцирования
1. 2.
3. 4.
5.
2.1. Вычислить первую и вторую производную, дифференциал функции
а)
Решение.
2.1. Вычислить первую и вторую производную, дифференциал функции
б)
Решение.
2.1. Вычислить первую и вторую производную, дифференциал функции
в)
Решение. Обозначим: f1(x)=3x; f2(x)= cos(1-x2)
Функция – сложная функция. Тогда
2.1. Вычислить первую и вторую производную, дифференциал функции
г)
Решение. Обозначим Тогда
Обозначим Тогда
3. Исследование функции
Решение задачи исследования функции сводится к выполнению следующих действий:
1. Определение точек разрыва, интервалов непрерывности, области определения функции (ООФ)
2. Анализ на четность, нечетность, периодичность
3. Определение (если возможно) точек пересечения функции с осями координат Х, У
4. Вычисление пределов – на границах ООФ, в точках разрыва
5. Определение точек экстремума и перегиба. Решение этой задачи связано с вычислением и последующим анализом поведения первой и второй производных функции
6. Построение графика функции
7. Определение области значений функции, ОЗФ
3. 1. Исследование функции – примеры
а) Исследуемая функция
– точек разрыва нет; вертикальных асимптот нет; ООФ=(-∞;∞)
– Четность: y(-1)=y(1) –функция четная
– Пределы функции:
На границах ООФ . Функция четная
Функция четная
Левый и правый пределы в точках разрыва – нет
Уравнение наклонной асимптоты
Наклонной асимптоты нет
Точки пересечения графика с осями координат
а) Исследуемая функция
– Точки экстремумов и интервалы монотонности
– Точки перегиба, выпуклость, вогнутость
Результат исследования представлен в таблице 3.1.а
XII=0.33
Вогнутая/выпуклая
а) Исследуемая функция Таблица 3.1.а
Скачать презентацию
определение, как найти, примеры решений
Определение производной от функции есть обратная операция интегрированию функции. Для элементарных функций вычислить производную не составляет труда, достаточно воспользоваться таблицей производных. Если же нам необходимо найти производную от сложной функции, то дифференцирование будет уже намного сложнее, потребует большей внимательности и времени. При этом очень легко допустить описку или незначительную ошибку, которая приведет к окончательному неверному ответу. Поэтому всегда важно иметь возможность проверить своё решение. Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Нахождение производной функции (дифференцирование) это отношение приращения функции к приращению аргумента (численно производная равна тангенсу угла наклона касательной к графику функции). Если необходимо вычислить производную от функции в конкретной точке, то нужно в полученном ответе вместо аргумента x подставить его численное значение и рассчитать выражение. При решении производной онлайн вам необходимо ввести функцию в соответсвующее поле: при этом аргументом должна быть переменная x , поскольку дифференцирование идёт именно по нему. Для вычисления второй производной нужно продифференцировать полученный ответ.
При этом очень легко допустить описку или незначительную ошибку, которая приведет к окончательному неверному ответу. Поэтому всегда важно иметь возможность проверить своё решение. Это вы можете сделать с помощью данного онлайн-калькулятора, который позволяет находить производные от любых функций онлайн с подробным решением бесплатно, без регистрации на сайте. Нахождение производной функции (дифференцирование) это отношение приращения функции к приращению аргумента (численно производная равна тангенсу угла наклона касательной к графику функции). Если необходимо вычислить производную от функции в конкретной точке, то нужно в полученном ответе вместо аргумента x подставить его численное значение и рассчитать выражение. При решении производной онлайн вам необходимо ввести функцию в соответсвующее поле: при этом аргументом должна быть переменная x , поскольку дифференцирование идёт именно по нему. Для вычисления второй производной нужно продифференцировать полученный ответ.
Калькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически.
Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке.
Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует.
Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует
Как вычислить производную функции?
Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных .
Правила дифференцирования
Пусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда
Тогда
— правило дифференцирования произведения функций
— правило дифференцирования частного функций
0″> — дифференцирование функции с переменным показателем степени
— правило дифференцирования сложной функции
— правило дифференцирования степенной функции
Производная функции онлайн
Наш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
1. Производная суммы или разности Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
А проверить решение задачи на производную можно на .
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Проверить решение задачи на производную можно на калькуляторе производных онлайн .
Пример 6. Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена “шпаргалка” основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|” = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы :
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)” = – c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)” = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Вычислить и найти производную онлайн
Пример решили: 19527 раз Сегодня решили: 0 раз
Введите выражение для вычисления производной
Выражение
$$ d \over dx $$
Идет вычисление
Таблица синтаксиса
| Sin(x) | Синус (x) |
| Cos(x) | Косинус (x) |
| Tan(x) | Тангенс (x) |
| Cotan(x) | Тангенс (x) |
| Sec(x) | Секанс (x) |
| Csc(x) | Косеканс (x) |
| Arcsin(x) | Арксинус (x) |
| Arccos(x) | Арккосинус (x) |
| Arctan(x) | Арктангенс (x) |
| Arcsec(x) | Арксеканс (x) |
| Arccosec(x) | Арккосеканс (x) |
| Log(x) | Логарифм (x) по основанию e |
| Lg(x) | Логарифм (x) по основанию 10 |
| Log[a,x] | Логарифм (x) по основанию a |
| x^a | X в степени a = x^a |
| abs(x) | Модуль x = (|x|) |
| Sqrt(x) | Корень из x |
Вычисление производной
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Пусть функция f(x) определена на некотором промежутке, x – точка этого промежутка и число h ≠ 0 такое, что x + h так же принадлежит данному промежутку. Тогда предел разностного отношения
Тогда предел разностного отношения
$$ {f(x + h) – f(x) \over h } \quad $$ при $$ \quad h \rightarrow 0$$
(если этот предел существует) называется производной функции f(x) в точке x и обозначается f'(x). Таким образом,
$$ f'(x) = \lim_{h \to 0} {f(x+h) – f(x) \over h} $$
Отметим, что в формуле производной число h, где h≠0, может быть как положительным, так и отрицательным, при этом число x + h должно принадлежать промежутку на котором определена функция f(x).
Если функция f(x) имеет производную в точке x, то эта функция называется дифференциируемой в этой точке.
Если функция f(x) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Геометрический смысл производной состоит в том, что значение производной функции f(x) в точке x равно угловому коэффициенту касательной к графику функции в точке (x; f(x)). 2(3x-5))’ $$
2(3x-5))’ $$
$$ y’ = 2 \cdot ln(3x-5) \cdot (3x-5)’ $$
$$ y’ = 2 \cdot ln(3x-5) \cdot 3 $$
$$ y’ = 6 \cdot ln(3x-5)$$
Ответ:
$$ y’ = 6 \cdot ln(3x-5)$$
вычисление производной сложной функции
Вы искали вычисление производной сложной функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление производной функции сложной функции, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вычисление производной сложной функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление производной сложной функции,вычисление производной функции сложной функции,дифференцирование сложной функции,дифференцирование сложной функции примеры,дифференцирование сложных функций,дифференцирования сложной функции формулы,как брать производную сложной функции,как вычислить производную сложной функции,как найти производную сложной функции примеры,как решать производные сложные,как решать сложные производные,как решать сложные производные функции,как решать сложные функции,нахождение производных сложных функций,нахождение сложной производной,определение сложная функция,определение сложной функции,правила дифференцирования сложной функции,правило дифференцирования сложной функции,примеры дифференцирование сложной функции,примеры производная сложная,примеры производной сложной функции,примеры производные сложных функций,примеры производных сложных функций с решением,примеры решения производных сложных,примеры решения производных сложных функций,примеры решения сложных производных,примеры с решением производных сложных функций,примеры с решением сложных производных,примеры с решениями производная сложной функции,примеры сложная производная,примеры сложная функция,примеры сложной производной функции,примеры сложной функции производной,примеры сложные функции,примеры сложных производных функций с решением,примеры сложных функций,примеры сложных функций производные,примеры сложных функций производных с решением,производная корня сложной функции,производная от корня сложной функции,производная от скобки в степени,производная от сложной функции,производная от сложной функции корня,производная подкоренного выражения,производная сложная формулы,производная сложной функции корня,производная сложной функции от корня,производная сложной функции показательной,производная сложной функции примеры,производная сложной функции примеры решений,производная сложной функции примеры с решениями,производная сложной функции формулы,производная сложных функций,производная формулы сложная,производной сложной функции примеры,производные от сложных функций,производные примеры сложных функций,производные сложной функции,производные сложные примеры,производные сложных функций примеры,производные сложных функций примеры решения,производные сложных функций формулы,производные формулы сложных функций,решение сложных производных,сложная производная примеры,сложная производная формулы,сложная производная функция,сложная функция,сложная функция определение,сложная функция примеры,сложная функция примеры с решением,сложные производные,сложные производные как решать,сложные производные примеры,сложные производные примеры с решением,сложные производные формулы,сложные производные функции,сложные функции,сложные функции как решать,сложные функции примеры,сложные функции производной примеры,сложных производных примеры с решением,формула производной сложной функции,формула сложной производной,формула сложной производной функции,формула сложной функции производная,формула сложной функции производной,формулы производной сложной функции,формулы производной функции сложной,формулы производные сложных функций,формулы производных сложных,формулы производных сложных функций,формулы сложная производная,формулы сложной производной функции,формулы сложной функции производной,формулы сложных производных,формулы сложных производных функций,функции сложной производной формулы.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление производной сложной функции,вычисление производной функции сложной функции,дифференцирование сложной функции,дифференцирование сложной функции примеры,дифференцирование сложных функций,дифференцирования сложной функции формулы,как брать производную сложной функции,как вычислить производную сложной функции,как найти производную сложной функции примеры,как решать производные сложные,как решать сложные производные,как решать сложные производные функции,как решать сложные функции,нахождение производных сложных функций,нахождение сложной производной,определение сложная функция,определение сложной функции,правила дифференцирования сложной функции,правило дифференцирования сложной функции,примеры дифференцирование сложной функции,примеры производная сложная,примеры производной сложной функции,примеры производные сложных функций,примеры производных сложных функций с решением,примеры решения производных сложных,примеры решения производных сложных функций,примеры решения сложных производных,примеры с решением производных сложных функций,примеры с решением сложных производных,примеры с решениями производная сложной функции,примеры сложная производная,примеры сложная функция,примеры сложной производной функции,примеры сложной функции производной,примеры сложные функции,примеры сложных производных функций с решением,примеры сложных функций,примеры сложных функций производные,примеры сложных функций производных с решением,производная корня сложной функции,производная от корня сложной функции,производная от скобки в степени,производная от сложной функции,производная от сложной функции корня,производная подкоренного выражения,производная сложная формулы,производная сложной функции корня,производная сложной функции от корня,производная сложной функции показательной,производная сложной функции примеры,производная сложной функции примеры решений,производная сложной функции примеры с решениями,производная сложной функции формулы,производная сложных функций,производная формулы сложная,производной сложной функции примеры,производные от сложных функций,производные примеры сложных функций,производные сложной функции,производные сложные примеры,производные сложных функций примеры,производные сложных функций примеры решения,производные сложных функций формулы,производные формулы сложных функций,решение сложных производных,сложная производная примеры,сложная производная формулы,сложная производная функция,сложная функция,сложная функция определение,сложная функция примеры,сложная функция примеры с решением,сложные производные,сложные производные как решать,сложные производные примеры,сложные производные примеры с решением,сложные производные формулы,сложные производные функции,сложные функции,сложные функции как решать,сложные функции примеры,сложные функции производной примеры,сложных производных примеры с решением,формула производной сложной функции,формула сложной производной,формула сложной производной функции,формула сложной функции производная,формула сложной функции производной,формулы производной сложной функции,формулы производной функции сложной,формулы производные сложных функций,формулы производных сложных,формулы производных сложных функций,формулы сложная производная,формулы сложной производной функции,формулы сложной функции производной,формулы сложных производных,формулы сложных производных функций,функции сложной производной формулы. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление производной сложной функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, дифференцирование сложной функции).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление производной сложной функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, дифференцирование сложной функции).
Где можно решить любую задачу по математике, а так же вычисление производной сложной функции Онлайн?
Решить задачу вычисление производной сложной функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
алгоритм и примеры решений. Производная функции
Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.
Данная страница содержит список формул для нахождения производных.
Правила дифференцирования
- (k⋅ f(x))′=k⋅ f ′(x).
- (f(x)+g(x))′=f′(x)+g′(x).
- (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
- Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
- Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
- Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
- Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
- Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.

Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.
Формулы 3 и 5 докажите самостоятельно.
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x .
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3 .
Пусть y = u(x) + v(x). Для значения аргумента x +Δx имеем y (x +Δx )=u (x +Δx ) + v (x +Δx ).
Δy =y (x +Δx ) – y(x) = u(x +Δx) + v(x +Δx) – u(x) – v(x) = Δu +Δv .
Следовательно,
Доказательство формулы 4 .
Пусть y=u(x)·v(x). Тогда y (x +Δx )=u (x +Δx )·v (x +Δx ), поэтому
Δy =u (x +Δx )·v (x +Δx ) – u (x )·v (x ).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x , то они непрерывны в этой точке, а значит u (x +Δx )→u(x), v (x +Δx )→v(x) , при Δx →0.
Поэтому можем записать
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ” = u “·(v· w) + u ·(v ·w) ” = u “·v ·w + u ·(v “·w +v ·w “) = u “·v ·w + u ·v “·w + u·v ·w “.
Доказательство формулы 5 .
Пусть . Тогда
При доказательстве воспользовались тем, что v(x+ Δx) →v(x) при Δx →0.
Примеры .
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u = u (x ). Получаем функцию y , зависящую от аргумента x : y = f(u(x)).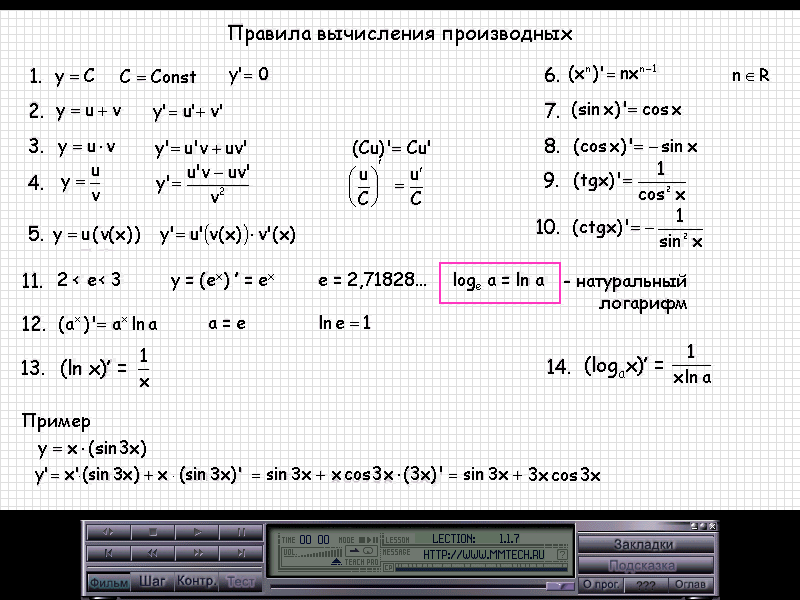 Последняя функция называется функцией от функции или сложной функцией .
Последняя функция называется функцией от функции или сложной функцией .
Областью определения функции y = f(u(x)) является либо вся область определения функции u =u (x ) либо та ее часть, в которой определяются значения u , не выходящие из области определения функции y = f(u) .
Операция “функция от функции” может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u = u (x ) имеет в некоторой точке x 0 производную и принимает в этой
точке значение u 0 = u (x 0 ), а функция y= f(u) имеет
в точке u 0 производную y ” u = f “(u 0 ), то сложная функция y = f(u(x)) в
указанной точке x 0 тоже имеет производную, которая равна y ” x = f “(u 0 )·u “(x 0 ), где вместо u должно быть подставлено выражение u = u (x ).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x .
Доказательство . При фиксированном значении х 0 будем иметь u 0 =u (x 0), у 0 =f(u 0 ). Для нового значения аргумента x 0 +Δx :
Δu = u (x 0 + Δx ) – u (x 0), Δy =f (u 0 +Δu ) – f (u 0 ).
Т.к. u – дифференцируема в точке x 0 , то u – непрерывна в этой точке. Поэтому при Δx →0 Δu →0. Аналогично при Δu →0 Δy →0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu →0)
где α→0 при Δu →0, а, следовательно, и при Δx →0.
Перепишем это равенство в виде:
Δy = y ” u Δu +α·Δu .
Полученное равенство
справедливо и при Δu =0 при произвольном
α, так как оно превращается в
тождество 0=0. При Δu =0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
При Δu =0 будем полагать α=0. Разделим все члены
полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx →0, получим y ” x = y ” u ·u ” x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от “внешней” функции f , рассматривая ее аргумент просто как переменную, и умножить на производную от “внутренней” функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y ” x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y ” x = y ” u ·u ” x . Применяя эту же теорему для u ” x получаем , т.е.
y ” x = y ” x · u ” v · v ” x = f ” u (u )·u ” v (v )·v ” x (x ).
Примеры.
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем с примера. Рассмотрим
функцию y= x 3 . Будем рассматривать равенство y = x 3 как уравнение относительно x . Это уравнение для каждого
значения у определяет единственное значение x : .
Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x 3 только в одной точке.
Поэтому мы можем рассматривать x как
функцию от y . Функция называется обратной по отношению к функции y= x 3 .
Рассмотрим
функцию y= x 3 . Будем рассматривать равенство y = x 3 как уравнение относительно x . Это уравнение для каждого
значения у определяет единственное значение x : .
Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x 3 только в одной точке.
Поэтому мы можем рассматривать x как
функцию от y . Функция называется обратной по отношению к функции y= x 3 .
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x 2 >x 1 , то f(x 2 ) > f(x 1 ).
Аналогично функция
называется убывающей , если меньшему
значению аргумента соответствует большее значение функции, т.е. еслих 2 х
1
, то f(x 2 ) > f(х 1 ).
Итак, пусть дана возрастающая или убывающая функция y= f(x) , определенная на некотором отрезке [a ; b ]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных
значения х 1
и х 2 . Пусть y 1 =f(x 1 ), y 2 =f(x 2 ). Из
определения возрастающей функции следует, что если x 1 x
2 , то у 1 у
2 . Следовательно, двум различным значениям х 1 и х 2 соответствуют два
различных значения функции у 1
и у 2 . Справедливо и обратное,
т.е. если у 1 у
2 , то из определения
возрастающей функции следует, чтоx 1 x
2 . Т.е. вновь двум различным
значениям у 1
и у 2 соответствуют два
различных значенияx 1 и x 2 . Т.о.,
между значениями x и соответствующими им значениями y устанавливается взаимно однозначное
соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области
значений функции y=f(x)) определяет единственное значение x , и можно
сказать, что x есть
некоторая функция аргумента y : x= g(у) .
Эта функция называется обратной для функции y=f(x) . Очевидно, что и функция y=f(x) является обратной для функции x=g(у) .
Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х .
Пример. Пусть дана функция y = e x . Эта функция возрастает при –∞ x x = lny . Область определения обратной функции 0 y
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a ; b ], причем f(a)=c, f(b)=d , то обратная функция определена и непрерывна на отрезке [c ; d ].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
Пример. Функция y=x 2 определена при –∞x
x
x
≤ 0 функция – убывает и обратная
для нее .
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y . Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x , а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x) , зная производную обратной функции.
Теорема. Если для функции y=f(x) существует
обратная функция x=g(y ), которая в некоторой точке у 0 имеет
производную g “(v 0 ), отличную от нуля, то в
соответствующей точке x 0 =g (x 0 ) функция y=f(x) имеет
производную f “(x 0 ), равную ,
т. е. справедлива формула.
е. справедлива формула.
Доказательство . Т.к. x=g(y) дифференцируема в точке y 0 , то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x 0 =g (y 0 ). Следовательно, при Δx →0 Δy →0.
Покажем, что .
Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy →0. Тогда Δx →0 и α(Δx)→0, т.е. .
Следовательно,
,
что и требовалось доказать.
Эту формулу можно записать в виде .
Рассмотрим применение этой теоремы на примерах.
При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :
Следует
заметить, что под знаком предела
получается выражение ,
которое не являетсянеопределенностью
ноль делить на ноль, так как в числителе
находится не бесконечно малая величина,
а именно ноль. Другими словами, приращение
постоянной функции всегда равно нулю.
Другими словами, приращение
постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения .
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для
упрощения выражения в числителе обратимся
к формуле бинома
Ньютона:
Следовательно,
Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли
к неопределенности. Для ее раскрытия
введем новую переменную ,
причем при .
Тогда .
В последнем переходе мы использовали
формулу перехода к новому основанию
логарифма.
Выполним подстановку в исходный предел:
Если
вспомнить второй
замечательный предел, то придем к
формуле производной показательной
функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем:
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов:
Осталось обратиться к первому замечательному пределу:
Таким
образом, производная функции sin
x есть cos
x .
Абсолютно
аналогично доказывается формула
производной косинуса.
Следовательно, производная функции cos x есть –sin x .
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса.
Производная обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, – это производная функции f(x) по x .
Теперь сформулируем правило нахождения производной обратной функции.
Пусть
функции y
= f(x) и x
= g(y) взаимно
обратные, определенные на
интервалах и соответственно.
Если в точке существует
конечная отличная от нуля производная
функции f(x) ,
то в точке существует
конечная производная обратной
функции g(y) ,
причем . В другой записи .
В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x – аргумент). Разрешив это уравнение относительно x , получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
. Тогда по формуле производной обратной функции получаем
Осталось провести преобразования.
Так
как областью значений арксинуса является
интервал ,
то (смотрите
раздел основные
элементарные функции, их свойства и
графики). Поэтому ,
а не
рассматриваем.
Поэтому ,
а не
рассматриваем.
Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1) .
Для
арккосинуса все делается абсолютно
аналогично:
Найдем производную арктангенса.
Для обратной функцией является .
Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть arctgx
= z ,
тогда
Следовательно,
Схожим
образом находится производная
арккотангенса:
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y = C Степенная функция y = x p (x p) ” = p · x p – 1 | Показательная функция y = a x (a x) ” = a x · ln a В частности, при a = e имеем y = e x (e x) ” = e x |
Логарифмическая функция (log a x) ” = 1 x · ln a В частности, при a = e имеем y = ln x (ln x) ” = 1 x | Тригонометрические функции (sin x) ” = cos x (cos x) ” = – sin x (t g x) ” = 1 cos 2 x (c t g x) ” = – 1 sin 2 x |
Обратные тригонометрические функции (a r c sin x) ” = 1 1 – x 2 (a r c cos x) ” = – 1 1 – x 2 (a r c t g x) ” = 1 1 + x 2 (a r c c t g x) ” = – 1 1 + x 2 | Гиперболические функции (s h x) ” = c h x (c h x) ” = s h x (t h x) ” = 1 c h 2 x (c t h x) ” = – 1 s h 2 x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1
Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x 0 = x , где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f (x) = C . Составим запись предела отношения приращения функции к приращению аргумента при ∆ x → 0:
lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C – C ∆ x = lim ∆ x → 0 0 ∆ x = 0
Обратите внимание, что под знак предела попадает выражение 0 ∆ x . Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f (x) = C равна нулю на всей области определения.
Пример 1
Даны постоянные функции:
f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = – 8 7
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а – любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый – производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби – 8 7 .
В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а – любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый – производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби – 8 7 .
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f 1 ” (x) = (3) ” = 0 , f 2 ” (x) = (a) ” = 0 , a ∈ R , f 3 ” (x) = 4 . 13 7 22 ” = 0 , f 4 ” (x) = 0 ” = 0 , f 5 ” (x) = – 8 7 ” = 0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (x p) ” = p · x p – 1 , где показатель степени p является любым действительным числом.
Доказательство 2
Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
Составим запись предела отношения приращения степенной функции к приращению аргумента:
(x p) ” = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p – x p ∆ x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x + ∆ x) p – x p = C p 0 + x p + C p 1 · x p – 1 · ∆ x + C p 2 · x p – 2 · (∆ x) 2 + . . . + + C p p – 1 · x · (∆ x) p – 1 + C p p · (∆ x) p – x p = = C p 1 · x p – 1 · ∆ x + C p 2 · x p – 2 · (∆ x) 2 + . . . + C p p – 1 · x · (∆ x) p – 1 + C p p · (∆ x) p
Таким образом:
(x p) ” = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p – x p ∆ x = = lim ∆ x → 0 (C p 1 · x p – 1 · ∆ x + C p 2 · x p – 2 · (∆ x) 2 + . . . + C p p – 1 · x · (∆ x) p – 1 + C p p · (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 · x p – 1 + C p 2 · x p – 2 · ∆ x + . . . + C p p – 1 · x · (∆ x) p – 2 + C p p · (∆ x) p – 1) = = C p 1 · x p – 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p – 1) ! · x p – 1 = p · x p – 1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3
Чтобы привести доказательство для случая, когда p – любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:
y = x p ln y = ln x p ln y = p · ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
(ln y) ” = (p · ln x) 1 y · y ” = p · 1 x ⇒ y ” = p · y x = p · x p x = p · x p – 1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x
Тогда x p
Если p есть нечетное число, тогда степенная функция определена и при x
y ” (x) = (- (- x) p) ” = – ((- x) p) ” = – p · (- x) p – 1 · (- x) ” = = p · (- x) p – 1 = p · x p – 1
Последний переход возможен в силу того, что если p – нечетное число, то p – 1 либо четное число, либо нуль (при p = 1), поэтому, при отрицательных x верно равенство (- x) p – 1 = x p – 1 .
Итак, мы доказали формулу производной степенной функции при любом действительном p .
Пример 2
Даны функции:
f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 – 1 4 , f 3 (x) = 1 x log 7 12
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:
f 1 (x) = 1 x 2 3 = x – 2 3 ⇒ f 1 ” (x) = – 2 3 · x – 2 3 – 1 = – 2 3 · x – 5 3 f 2 ” (x) = x 2 – 1 4 = 2 – 1 4 · x 2 – 1 4 – 1 = 2 – 1 4 · x 2 – 5 4 f 3 (x) = 1 x log 7 12 = x – log 7 12 ⇒ f 3 ” (x) = – log 7 12 · x – log 7 12 – 1 = – log 7 12 · x – log 7 12 – log 7 7 = – log 7 12 · x – log 7 84
Производная показательной функции
Доказательство 4
Выведем формулу производной, взяв за основу определение:
(a x) ” = lim ∆ x → 0 a x + ∆ x – a x ∆ x = lim ∆ x → 0 a x (a ∆ x – 1) ∆ x = a x · lim ∆ x → 0 a ∆ x – 1 ∆ x = 0 0
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z = a ∆ x – 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Чтобы раскрыть ее, запишем новую переменную z = a ∆ x – 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(a x) ” = a x · lim ∆ x → 0 a ∆ x – 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(a x) ” = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a
Пример 3
Даны показательные функции:
f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f 1 ” (x) = 2 3 x ” = 2 3 x · ln 2 3 = 2 3 x · (ln 2 – ln 3) f 2 ” (x) = 5 3 x ” = 5 3 x · ln 5 1 3 = 1 3 · 5 3 x · ln 5 f 3 ” (x) = 1 (e) x ” = 1 e x ” = 1 e x · ln 1 e = 1 e x · ln e – 1 = – 1 e x
Производная логарифмической функции
Доказательство 5
Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
Опираясь на определение производной, получим:
(log a x) ” = lim ∆ x → 0 log a (x + ∆ x) – log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x · log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e является верным в соответствии со вторым замечательным пределом.
Пример 4
Заданы логарифмические функции:
f 1 (x) = log ln 3 x , f 2 (x) = ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f 1 ” (x) = (log ln 3 x) ” = 1 x · ln (ln 3) ; f 2 ” (x) = (ln x) ” = 1 x · ln e = 1 x
Итак, производная натурального логарифма есть единица, деленная на x .
Производные тригонометрических функций
Доказательство 6
Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x) ” = lim ∆ x → 0 sin (x + ∆ x) – sin x ∆ x
Формула разности синусов позволит нам произвести следующие действия:
(sin x) ” = lim ∆ x → 0 sin (x + ∆ x) – sin x ∆ x = = lim ∆ x → 0 2 · sin x + ∆ x – x 2 · cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2
Наконец, используем первый замечательный предел:
sin ” x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x
Итак, производной функции sin x будет cos x .
Совершенно также докажем формулу производной косинуса:
cos ” x = lim ∆ x → 0 cos (x + ∆ x) – cos x ∆ x = = lim ∆ x → 0 – 2 · sin x + ∆ x – x 2 · sin x + ∆ x + x 2 ∆ x = = – lim ∆ x → 0 sin ∆ x 2 · sin x + ∆ x 2 ∆ x 2 = = – sin x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = – sin x
Т.е. производной функции cos x будет – sin x .
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
t g ” x = sin x cos x ” = sin ” x · cos x – sin x · cos ” x cos 2 x = = cos x · cos x – sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g ” x = cos x sin x ” = cos ” x · sin x – cos x · sin ” x sin 2 x = = – sin x · sin x – cos x · cos x sin 2 x = – sin 2 x + cos 2 x sin 2 x = – 1 sin 2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7
Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
s h ” x = e x – e – x 2 ” = 1 2 e x ” – e – x ” = = 1 2 e x – – e – x = e x + e – x 2 = c h x c h ” x = e x + e – x 2 ” = 1 2 e x ” + e – x ” = = 1 2 e x + – e – x = e x – e – x 2 = s h x t h ” x = s h x c h x ” = s h ” x · c h x – s h x · c h ” x c h 2 x = c h 2 x – s h 2 x c h 2 x = 1 c h 2 x c t h ” x = c h x s h x ” = c h ” x · s h x – c h x · s h ” x s h 2 x = s h 2 x – c h 2 x s h 2 x = – 1 s h 2 x
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Вычисление производных экспоненциальных функций
Показательная функция является одной из самых важных функций в исчислении. На этой странице мы выведем выражение для производной e x и применим его для вычисления производной других экспоненциальных функций.
Наш первый контакт с числом e и экспоненциальной функцией был на странице о непрерывных сложных процентах и числе e. На этой странице мы дали интуитивное определение числа e, а также интуитивное определение экспоненциальной функции.
Мы также вывели альтернативное выражение для экспоненциальной функции. Новым выражением экспоненциальной функции был ряд, то есть бесконечная сумма .
Вы можете спросить, определение предела намного компактнее и проще, чем эта уродливая бесконечная сумма, зачем беспокоиться?
Оказывается, самый простой способ вывести правило получения производной от e x — это использовать это представление бесконечного ряда. Почему это? Выражение ряда для e x выглядит как многочлен.
Мы можем обобщить идею полинома, допустив бесконечное число членов, как в выражении экспоненциальной функции. Бесконечный многочлен называется степенным рядом .
Отличительной чертой степенного ряда является то, что для вычисления его производной вы действуете точно так же, как и для многочлена. То есть вы берете производную почленно. Сделаем это с экспоненциальной функцией.
То есть вы берете производную почленно. Сделаем это с экспоненциальной функцией.
Производная e
xРассмотрим выражение ряда для показательной функции
Мы можем вычислить производную левой части, применяя правило для производной суммы. То есть производная суммы равна сумме производных каждого члена
Мы вычисляем производный член за членом
Мы знаем производные каждого из этих членов
Мы применяем степенное правило для вычисления производной каждого члена срок
Я добавил дополнительный термин, чтобы прояснить схему. Теперь есть некоторые числа, которые сокращаются
Мы сокращаем некоторые числа, и мы приходим к удивительному результату
Мы получили удивительный результат. Выражение для производной такое же, как и для исходной функции. То есть
Производная от e x равна e x
Производная от e x равна e x . Это одно из свойств, которое делает экспоненциальную функцию действительно важной.
Это одно из свойств, которое делает экспоненциальную функцию действительно важной.
Теперь можно на время забыть о выражении ряда для экспоненты. Он нам нужен только здесь, чтобы доказать результат выше. Теперь мы можем применить это для вычисления производной других функций, включающих экспоненту.
Пример 1: f(x) = e axВычислим производную функции
На первый взгляд может быть не очевидно, но это составная функция. Это означает, что нам нужно применить цепное правило. Внешняя функция экспоненциальная. Его производная равна самому себе. Внутренняя функция ax:
Производная внешней функции равна исходной функции
Это было просто. Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента.
Пример 2: f(x) = e x 2Рассмотрим теперь другую составную функцию
Для вычисления ее производной снова применим цепное правило. Поскольку внешняя функция экспоненциальная, ее производная равна самой себе
Поскольку внешняя функция экспоненциальная, ее производная равна самой себе
Теперь это выглядит сложнее
Здесь у нас есть произведение, поэтому мы должны использовать правило произведения. Для этого мы определяем два фактора
и применяем правило произведения
А теперь мы факторизуем e x , чтобы получить окончательный ответ.
Пример 4: f(x) = e cos(x) sin(x)Рассмотрим следующую функцию. Давайте посмотрим, что я имею в виду. Во-первых, мы применяем правило произведения
Теперь, чтобы вычислить u’, нам нужно применить цепное правило
Подключим его к правилу произведения
Пример 5: Экспонента с другим основанием, f(x)=a xТеперь давайте рассмотрим экспоненту с основанием, отличным от e.
Как вычислить производную этой функции? Мы используем прием, который регулярно используется при работе с логарифмами. Мы можем записать эту функцию как
Мы можем записать эту функцию как
Вы можете проверить, что это равенство верно, используя определение логарифма. Теперь воспользуемся свойством логарифмов, которое позволяет нам выводить показатели степени из логарифмического знака 9.0005
Теперь это экспоненциальная функция с основанием e, производную которой мы умеем вычислять.
Но используя уравнение несколькими строками выше, мы можем записать это как
Это показывает одну из причин, по которой естественным выбором в качестве основания экспоненциальной функции является число e. Для любого другого основания вы получите это ln(a), засоряющее выражение его производной.
Пример 6: f(x) = a x 2Рассмотрим
Здесь нужно применить цепное правило. Внешняя функция является экспоненциальной, поэтому мы знаем, как вычислить ее производную из предыдущего примера 9.0005
То есть. Следующим вашим шагом может быть изучение производной ln(x). Если у вас есть какие-либо сомнения или вы хотите обсудить собственную проблему, просто оставьте мне комментарий ниже.
6.2 Отличие от первых принципов | Дифференциальное исчисление
6.2 Дифференцирование из первых принципов (EMCH6)
Мы знаем, что градиент касательной к кривой с уравнением \(y = f(x)\) в точке \(x=a\) может быть определить по формуле:
\[\text{Градиент в точке} = \lim_{h\to 0}\frac{f\left(a+h\right)-f\left(a\right)}{h}\]Мы можем использовать эту формулу для определения выражения, описывающего градиент графика (или градиент касательной к графику) в любой точке графика. Это выражение (или градиент функция) называется производной.
- Производная
Производная функции \(f\left(x\right)\) записывается как \({f}’\left(x\right)\) и определяется:
\[{f}’\left(x\right)=\lim_{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\]
- Дифференциация
Процесс определения производной заданной функции.

Этот метод называется дифференциацией от первых принципов или с использованием определения.
Рабочий пример 7: Отличие от первых принципов
Вычислите производную от \(g\left(x\right)=2x-3\) из первых принципов.
Запишите формулу для нахождения производной с помощью первой принципы
\[{g}’\left(x\right)=\lim_{h\to 0}\frac{g\left(x+h\right)-g\left(x\right)}{h}\]Определить \(g\слева(x+h\справа)\)
\начать{выравнивать*} г(х) &= 2х – 3 \\ & \\ г\влево(х+ч\вправо) &= 2\влево(х+ч\вправо) – 3 \\ &= 2х + 2ч – 3 \конец{выравнивание*}Подставить в формулу и упростить
\начать{выравнивать*} {g}’\left(x\right) & = \lim_{h\to 0}\frac{2x + 2h – 3 -\left(2x – 3\right)}{h} \\ & = \lim_{h\to 0}\frac{2h}{h} \\ & = \lim_{h\to 0} 2 \\ & = 2 \end{выравнивание*}Напишите окончательный ответ
Производная \({g}’\left(x\right) = 2\).
Обозначение
Для обозначения производных используется несколько различных обозначений. Очень важно, чтобы вы научились определить эти разные способы обозначения производной и что вы последовательны в своих использование их при ответах на вопросы.
Если мы используем общепринятое обозначение \(y=f\left(x\right)\), где зависимая переменная равна \(y\) и независимой переменной является \ (x \), тогда некоторые альтернативные обозначения для производной, как следует:
\[{f}’\left(x\right)={y}’=\frac{dy}{dx}=\frac{df}{dx}=\frac{d}{dx}[f\left( х\вправо)]=Df\влево(х\вправо)={D}_{х}у\] Символы \(D\) и \(\frac{d}{dx}\) называются дифференциальными операторами, потому что они указывают на
операция дифференцирования.
\(\frac{dy}{dx}\) означает \(y\), продифференцированное по \(x\). Точно так же \(\frac{dp}{dx}\) означает \(р\), продифференцированную по \(х\).
Важно: \(\frac{dy}{dx}\) не является дробью и не означает \(dy \div дх\).
Видео: 28W2
Рабочий пример 8: Отличие от первых принципов 9{3}\) из первых принципов.
Запишите формулу для нахождения производной от первой принципы
\[{f}’\left(x\right)=\lim_{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\] 9{2} \\ &= 12\влево(\frac{1}{4} \вправо) \\ &= 3 \end{align*}- Производная \(f(x)\) в точке \(x = \text{0,5}\) равна \(\text{3}\).

- Градиент функции \(f\) в точке \(x = \text{0,5}\) равен \(\текст{3}\).
- Градиент касательной к \(f(x)\) в точке \(x = \text{0,5}\) равен \(\текст{3}\).
Рабочий пример 9: Отличие от первых принципов
Рассчитать \(\frac{dp}{dx}\) из первых принципов, если \(p\left(x\right)= – \ гидроразрыва {2} {x} \).
Запишите формулу для нахождения производной с помощью первой принципы
\[\frac{dp}{dx} =\lim_{h\to 0}\frac{p\left(x+h\right)-p\left(x\right)}{h}\]Подставить в формулу и упростить
\начать{выравнивать*} \frac{dp}{dx} & = \lim_{h\to 0}\frac{-\frac{2}{x + h} -\left(- \frac{2}{x}\right)}{h} \конец{выравнивание*}
Иногда проще написать правую часть уравнения как:
\начать{выравнивать*} \frac{dp}{dx} & = \lim_{h\to 0}\frac{1}{h} \left(\frac{-2}{x + h} + \frac{2}{x} \Правильно) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{-2x + 2(x + h)}{x(x + h)} \right) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{-2x + 2x + 2h }{x(x + h)} \right) \\ & = \lim_{h\to 0} \frac{1}{h} \left(\frac{2h }{x^{2} + xh} \right) \\ & = \lim_{h\to 0} \frac{2}{x^{2} + xh} \\ & = \фракция{2}{х^{2}} \конец{выравнивание*} 9{2}}\]
Рабочий пример 10: Отличие от первых принципов
Дифференцировать \(g\left(x\right)= \frac{1}{4}\) из первых принципов и интерпретировать
ответ.
Запишите формулу для нахождения производной от первой принципы
\[{g}’\left(x\right)=\lim_{h\to 0}\frac{g\left(x+h\right)-g\left(x\right)}{h}\]Подставить в формулу и упростить
\начать{выравнивать*} {g}’\left(x\right) & = \lim_{h\to 0}\frac{ \frac{1}{4} – \frac{1}{4}}{h} \\ & = \lim_{h\to 0}\frac{0}{h} \\ & = \lim_{h\to 0} 0 \\ & = 0 \конец{выравнивание*}Интерпретируйте ответ
Градиент \(g(x)\) равен \(\text{0}\) в любой точке графика. производная этой постоянной функции равна \(\text{0}\).
Отличие от первых принципов
Учебник Упражнение 6. {2})}{h}
\end{выравнивание*} 9{2}}{ч}\\
&=\lim_{h \to 0}\dfrac{h(-2x-h)}{h}\\
&=\lim_{h \to 0}-2x-h\\
&=-2x
\end{align*}
{2})}{h}
\end{выравнивание*} 9{2}}{ч}\\
&=\lim_{h \to 0}\dfrac{h(-2x-h)}{h}\\
&=\lim_{h \to 0}-2x-h\\
&=-2x
\end{align*}
Объясните смысл вашего ответа в (b).
Производная от \(g(x)\) равна \(g'(x) = -2x\). Градиент функции \(g\) задается выражением \(-2x\). Градиент графика зависит от значения из \(х\). 9{2} + 3ч}{ч}\\ &=\lim_{h \to 0}\dfrac{h(-4x – 2h + 3)}{h}\\ &=\lim_{ч \до 0}(-4x-2ч+3)\\ f'(x)&=-4x+3 \end{align*}
Определите производную от \(f\left(x\right)=\frac{1}{x-2}\), используя
первые принципы.
\begin{выравнивание*} f(x) & = \frac{1}{x-2}\\ f(x+h) & = \frac{1}{x+h-2}\\ f'(x)&=\lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}\\ &=\lim_{h \to 0}\dfrac{\frac{1}{x+h-2} – \frac{1}{x-2}}{h}\\ &=\lim_{ч \к 0}\dfrac{\frac{(x-2)-(x+h-2)}{(x+h-2)(x-2)}}{h}\\ &=\lim_{h \to 0}\dfrac{\frac{x-2-x-h+2}{(x+h-2)(x-2)}}{h}\\ &=\lim_{h \to 0}\left(\dfrac{-h}{(x+h-2)(x-2)}\right) \times \ гидроразрыв {1} {ч} \\ &=\lim_{h \to 0}\dfrac{-1}{(x+h-2)(x-2)}\\ f'(x)&=\frac{-1}{(x-2)^{2}} \end{выравнивание*} 9{2}}{ч}\\ &=\lim_{h \to 0}\dfrac{h(-10x-5h)}{h}\\ &=\lim_{ч \до 0}(-10x-5ч)\\ &=-10x \end{align*}
Поэтому: \начать{выравнивать*} g'(3) & = -10(3)\\ & = -30 \end{выравнивание*} 9{n}\), используя шаблон коэффициентов, заданный Треугольник Паскаля:
\[\begin{массив}{ccccccccccccc}
х \qquad & & & & & & & & 1& & &
& & \\
(x+h) \qquad& & & & & &1& &1& &
& & \\
(x+h)^2 \qquad & & & & & 1& & 2& &
1& & & \\
(x+h)^3 \qquad& & & &1& &3& &3&
&1& & \\
(x+h)^4 \qquad& & & 1& & 4& & 6& &
4& & 1& \\
. {n}\]
9{н-1}
\конец{выравнивание*}
{n}\]
9{н-1}
\конец{выравнивание*}
Это очень ценное общее правило для нахождения производной функция.
Примеры вычисления производной
By Math Original Нет комментариев
Примеры вычисления производной 9{2}}+8x$
Copyright © Math OriginalНравится:
Нравится Загрузка…
Производные – что это такое и как их решить?
Прежде чем изучать деривативы, вам нужно иметь четкое представление о пределах, наклоне и о том, как их найти.
Зачем нужны производные?
Наклон представляет собой изменение y относительно x на прямой линии . Она одинакова в каждой точке прямой. Но, конечно, это не в случае с кривая линия .
Она одинакова в каждой точке прямой. Но, конечно, это не в случае с кривая линия .
Итак, как найти наклон кривой? Он находится путем вычисления наклона секущей, проходящей через две точки кривой.
Выше приведен график функции x 2 . Мы провели секущую, чтобы найти наклон между точкой (1,1) и точкой (2,4),
Наклон равен 3. Мы нашли его с помощью калькулятора формулы наклона. Этот наклон является средним наклоном между этими точками.
Но что, если мы хотим найти наклон точки в точной точке (1,1), мгновенную скорость изменения? Как мы можем это сделать?
Здесь мы используем производные!! Давайте узнаем больше о производных и о том, как их решать.
Что такое производные?
Производные используются для определения наклона кривой в точной точке. Определение производных будет следующим:
” Производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке. ”
”
При вычислении производных мы находим дифференциал функции. Это означает, что мы находим разницу между двумя точками.
Эти точки расположены так близко друг к другу, что разница между ними почти равна нулю, а секущая линия между ними становится касательной.
Обозначения
Производные обозначаются тремя различными способами. Наиболее распространенным способом является обозначение Лабинеса.
Математик | Обозначение | ||||||
6 0,0005 | 006
| 06 | |||||
Newton | f'(x) | ||||||
Lagrange | \dot f f ˙ f, with, \dot, on top |
Как найти производные?
Надеюсь, теперь ваше замешательство по поводу деривативов и того, почему мы их используем, ясно. Перейдем к расчету производных.
Перейдем к расчету производных.
Существует два основных способа решения производных. Один является формальным, а другой – альтернативной формой. Мы изучим оба на общих примерах.
Формальное дифференцированиеЛегко вывести формулу для производных, глядя на график.
Рассмотрим синусоидальную функцию. Мы хотим вычислить наклон между двумя точками на этой кривой. Первая точка — x . Поскольку мы знаем, что y=f(x), мы можем записать точку как (x,f(x)).
Вторую точку возьмем на расстоянии х от х . Точка здесь будет (x+h,f(x+h)), где ч — произвольное значение. Это может быть любое число.
Наклон в этой точке:
Поскольку мы хотим рассчитать наклон точной точки, мы сблизим две точки так близко друг к другу, что они почти станут одной точкой, а разница между ними будет приближаться к нулю.
Для этой цели мы наложим ограничение на эту функцию. Уравнение становится таким:
Уравнение становится таким:
Это то, что мы будем называть производной или d по dx (d/dx). Теперь мы можем подставить любое значение на место х .
Таким образом, это был один из способов вычислить производную или найти наклон в точке. Перейдем ко второй и альтернативной формуле дифференцирования.
Примечание : обычно в вычислениях заменяет h . Дельта означает очень небольшое изменение. Формула наклона с :
Альтернативная формаЭто очень похоже на первую формулу. Но здесь вместо добавления расстояния к x мы возьмем совершенно другую точку (a,f(a)). Посмотрим его график:
Применяя формулу наклона, уравнение будет:
Применяя предел:
Это то же самое, что и формальный способ. Здесь вместо расстояния h мы взяли прямую точку a . Таким образом, когда x приблизится к и , расстояние будет почти нулевым. И это именно то, что мы хотим вычислить.
И это именно то, что мы хотим вычислить.
Пример
Найдите производную f(x) = x 2 .
Решение:
Шаг 1: Добавьте расстояние в x 2 . Это расстояние дельты x приблизительно равно нулю. Теперь найдем функцию для (x + ) 2 .
Шаг 2: Применение формулы наклона:
Шаг 3: Применить предельное приближение к нулю.
Следовательно, наклон при x 2 = 2x.
Какая производная от х 4 ? Найдите сами и проверьте с помощью калькулятора производных.
Правила дифференциации
Дифференциация упрощается с помощью некоторых правил. Эти правила применяются в определенных ситуациях, чтобы избежать сложных и длительных вычислений. Основные и базовые правила описаны ниже.
Постоянное правило Вероятно, это простейшее производное правило. Когда у нас нет переменной в функции, например, y=4, тогда производная равна 0.
Когда у нас нет переменной в функции, например, y=4, тогда производная равна 0.
0005
Где c — постоянное число. Это правило имеет смысл, если вы попытаетесь визуализировать его.
Поскольку x = 0, следовательно, наклона нет. А график представляет собой прямую вертикальную линию. Но давайте посмотрим на это с помощью дифференцирования.
Пример
Какова производная от f(x) = 5.
Решение:Шаг 1: Добавьте дельту x.
f(x + Δx) = 3 + Δx = 3 Δx = 0
Шаг 2: Применение формулы.
= 0/Δx
= 0
Степенное правилоСтепенное правило применяется к полиномиальным функциям. Формула:
Пример f(x 2 ), который мы решили для изучения производных, является идеальным представлением степенного правила.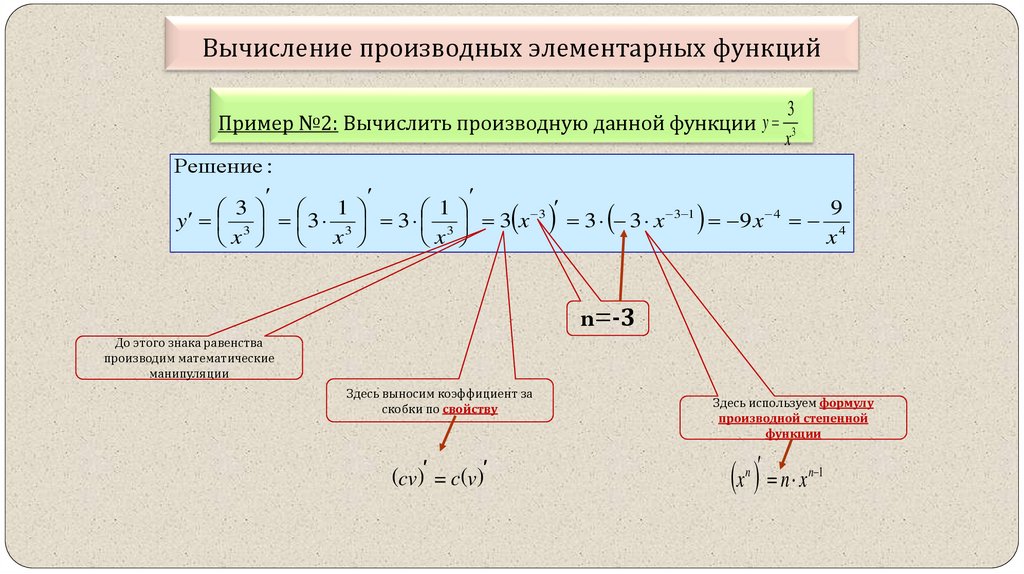 Но для большего понимания см. другой пример:
Но для большего понимания см. другой пример:
Пример:
Производная от x 6 . Решите это, используя ограничения, а также правила мощности.
Решение:
Решение с использованием ограничений.
Шаг 1: Добавьте дельту x, т.е., и расширьте уравнение.
= (x + Δx) 6
F (x + Δx) 6 = (x 6 + 6x 5 Δx +… + Δx 6 )
Шаг 2: . формула наклона.
Шаг 3: Применить ограничение.
Решение с использованием степенного правила.
Шаг 1: Запишите функцию.
f(x) = x 6
Шаг 2: Определите компоненты и примените правило степени.
As y n = ny n-1 , (мы сформировали формулу с y , чтобы избежать путаницы.)
Здесь, y = x
n = 6
6
f’(x 6 ) = (6)x 6-1 = 6x 5
Результаты обоих методов одинаковы. Это доказывает, что правило мощности верно для любых и .
Это доказывает, что правило мощности верно для любых и .
Две функции сложения или разности также подходят для правила дифференцирования. Правила, применяемые в таких ситуациях:
Для суммы:
f + g = d/dx (f) + d/dx (g)
Для разницы.
f – g = d/dx (f) – d/dx (g)
Пример:
Найдите f’(x) для 2x + 3x 2 .
Решение:
Шаг 1: Применить производную.
= d/dx ( 2x + 3x 2 )
Шаг 2: Примените правило.
= d/dx 2x + d/dx 3x 2
= 2,1x 1-1 + 3,2x 2-1
= 2 + 6x
Правило произведения Когда вычисляется производная двух функций при умножении, мы используем правило произведения. Примером такой функции будет 4x 4 (3x + 9).
Примером такой функции будет 4x 4 (3x + 9).
Формула правила произведения:
Пример:
Какова производная от 4x 4 (3x + 9)?
Решение:
Шаг 1: Применить производную.
= d/dx 4x 4 (3x + 9)
Согласно правилу произведения.
= 4x 4 d/dx (3x + 9) + (3x + 9) d/dx 4x 4
Шаг 2: Найдите d/dx (3x + 9)).
d/dx = (3x + 9)
Применить правило сумм.
= d/dx 3x + d/dx 9
= 3 + 0 … (степенное правило для 3x и постоянное правило для 9)
= 3
Шаг 3: Решить для d/dx 03 04 9000 .
Использование силового правила;
= 4.{(4)x 4-1 }
= 4,4x 3
= 16x 3
Шаг 98.
= 4х 4 .3 + (3х +9) 16x 3
= 12x 4 + 48x 4 + 144x 3
= 60x 4 + 144x 3
= x 3 (60x + 144) 998
197 = x 3 (60x + 144) 98 9018 9018 1197 = x 3 (60x + 144) = x 3 (60x + 144) . У нас есть формула произведения, но есть ли у нас формула деления? Да! И это называется частным правилом. Он в основном выводится из правила произведения для дифференциации. Частное уравнение выглядит примерно так: f(x)/g(x). Чтобы найти ее производную, ее делят на две части: f(x) * 1/g(x). Вы можете видеть, что на самом деле мы должны выполнить правило произведения. Все, что нам нужно сделать, это найти производную от 1/g(x). Следуя всем знакомому процессу применения формулы и предела, мы получим: Обратите внимание, что – это dg/dx с отрицательным знаком. Или это можно записать как: Теперь поместим это значение в формулу продукта, которую мы обсуждали выше: Принимая LCM. Это правило частных. Пример: Найдите производную от (x – 3)/(x 3 + x). Решение: Непосредственно применить правило частных. Шаг 1: Найдите производную от (x-3). = d/dx (x-3) = 1 Шаг 2: Найдите производную от (x 3 -x) = d/dx 3 0 -5 0 9000 Используя описанные выше правила; = 3х 2 – 1 Шаг 3: Используйте их в основном уравнении. После упрощения; И последнее, но не менее важное: у нас есть цепное правило. В нем говорится, что: Это для простоты. Когда функция имеет много математических операций, лучше преобразовать ее в виде двух функций, например, у нас есть функция: f(x)= (X 2 + 6) 4 Пусть g =X 2 + 6, тогда f(g) = (g) 4 где g =X 2 + 6 ИЛИ f(g(x)) = (g(x)) 2 + 6) 4 Чтобы найти его производную, сначала нужно найти разность f относительно g , а затем g'(x). Пример: Решить d/dx (X 2 + 6) 4 Решение: = g(x) 2 + 6 И f(g) = g 4 Итак, производная от f(g(x)) = d/dx f(g(x)) =f'(g(x)) .g'(х). Применение цепного правила. Шаг 1: Найдите производную g(x). d/dx = x 2 + 6 … используя правило степени для x 2 и правило констант для 6 = 2x Шаг 2: Найдите производную f(g). = d/dx г 4 = 4г 3 Шаг 3: Ввод формулы и умножение. = 4(х 2 +6) 3 . 2x = 8x.(x 2 +6) 3 Теперь у вас есть представление о решении производных. Пришло время увидеть, как выполнять неявное дифференцирование. Неявное уравнение: Уравнение, в котором переменные не могут быть разделены. Неявное дифференцирование — это простое дифференцирование, за исключением того, что оно выполняется для обеих частей уравнения. Пример: Дифференцируйте это неявное уравнение: x 2 + y 2 = z 2 Где z — константа. Решение: Шаг 1: Применить производную. d/dx (x 2 ) + d/dx(y 2 ) = d/dx(z 2 ) Шаг 2: Решение L.H.S. = d/dx (x 2 ) + d/dx(y 2 ) = 2x + 2y(d/dx) … применяя цепное правило. Шаг 3: Решите R.H.S. Производная постоянных чисел равна 0. = d/dx (z 2 ) = 0 Шаг 4: поместите значения в уравнение. 2x + 2y(d/dx) = 0 2y(d/dx) = -2x y(d/dx) = -x d/dx = -x/y Итак, при дифференцировании уравнения x 2 + y 2 = z 2 мы получили -x/y как производную. Мы используем производные, чтобы найти наклон кривой. Это процесс дифференциации. Это сложный процесс, поэтому мы используем правила дифференцирования. Один из самых быстрых автомобилей в мире, Venom F5 компании Hennessey Performance Engineering развивает максимальную скорость более \(300 миль в час\) и может изменяться от \(0\) до \ (62 мили в час\) всего за \(2,6\) секунды! 1 В этой статье вы изучите методы, которые можно использовать для расчета ускорения, которое достигает Venom F5 при приближении к своей максимальной скорости. Частное правило
Частное правило 
 После этого умножить.
После этого умножить. Неявное дифференцирование


Резюме
Производные: определение, примеры и типы
7 вычислить наклон касательной к кривой
.
Но что именно это означает?
Это означает, что вы вычисляете скорость изменения функции в точке. В частности, это может означать расчет скорости и изменения скорости во времени, как вы хотели бы сделать для Venom F5. Однако использование производных гораздо более разнообразно:
Они полезны во всех областях математики , науки и машиностроение .
Производные инструменты имеют решающее значение для бизнеса анализа .
Они необходимы для медицинских приложений.
Определение производной
Теперь, когда вы хорошо понимаете пределы, вы заложили основу для изучения исчисления!
Секущая и касательная
Чтобы по-настоящему начать изучение исчисления, вы должны вернуться к концепциям секанс и касательная прямые к кривой.
Два способа расчета наклона секущей к кривой
Вы можете рассчитать наклон секущей к кривой одним из двух способов, как показано на графиках и формулах ниже. Поскольку оба метода дают один и тот же ответ, вы можете выбрать тот метод, который проще всего вычислить.
Вы можете использовать формулу: \( m_{sec} = \frac{f(x)-f(a)}{x-a} \) для вычисления наклона секущей к кривой.
Вы можете использовать формулу: \( m_{sec} = \frac{f(a+h)-f(a)}{h} \) для вычисления наклона секущей к кривой.
Эти формулы для наклона секущей к кривой представлены в виде коэффициента разности . Их формальное определение таково:
- Пусть \(f\) будет функцией, которая определена на интервале \(I\), и пусть \(I\) содержит значение \(a\). Если \( x \) находится в \( I \) и \( x \neq a \) , то коэффициент разности : \[ Q = \frac{f(x)-f(a)}{x-a} \]
- И, частное разности с приращением \( \bf{ h } \) , которое существует, если \( h \neq 0 \), выбрано так, что \( a+h \) находится в интервале \( I \), есть: \[ Q = \frac{f(a+h)-f (a)}{h} \]
При перемещении второй точки – \( (x, f(x)) \) на верхнем графике выше и \( (a+h, f(a+h )) \) на нижнем графике выше – секущей ближе к первой точке – \( (a, f(a)) \) на обоих графиках выше – вы приблизиться к касательной линии к кривой в этой первой точке. Это приводит к тому, что вы используете пределы для определения касательной к кривой следующим образом:
Это приводит к тому, что вы используете пределы для определения касательной к кривой следующим образом:
- Пусть \(f(x)\) будет функцией, которая определена на открытом интервале, содержащем \(a\). Касательная
Более подробный обзор и примеры см. в статье о касательных линиях.
Производная функции в точке
Это использование пределов для нахождения наклона касательной к функции (или кривой) в точке приводит вас прямо к производная . По сути, термин производная — это просто специальное название для этого типа предела, а процесс нахождения (также называемый взятием) производной называется дифференцированием . Определение производной функции в точке : f'(a) \) (читается как «f-простое число a»), и при условии, что \( f(x) \) — функция, определенная на открытом интервале, который содержит \( a \), и что предел существует, определяется как: \[ f'(a) = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}. \] 9{2}-4x-4}{x-2} \]
Определение производной функции в точке : f'(a) \) (читается как «f-простое число a»), и при условии, что \( f(x) \) — функция, определенная на открытом интервале, который содержит \( a \), и что предел существует, определяется как: \[ f'(a) = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}. \] 9{2}-4x-4}{x-2} \]
- Применим определение ( здесь \( a = 2 \)).\[ f'(2) = \lim_{h \to 0} \frac{f(2+h)-f(2)}{h} \] 9{2}+8h}{h} \]
- Фактор числителя.\[ f'(2) = \lim_{h \to 0} \frac{h(3h+8)}{h} \]
- Отменить общий множитель.\[ f'(2) = \lim_{h \to 0} (3h+8) \]
- Заменить \( h = 0 \).\[ f'(2) = \lim_{ h \to 0} (3(0)+8) \]
- Оценить предел.
 \[ \bf{ f'(2) } = \bf{ 8 } \]
\[ \bf{ f'(2) } = \bf{ 8 } \]
Обратите внимание, что при использовании любого метода вы получите точно такой же ответ!
Скорости и темпы изменения
Один из наиболее распространенных способов использования производных — найти скорости и скорости изменения . Если у вас есть функция, которая представляет положение объекта во времени, называемая \( s(t) \), то его средняя скорость определяется разностным коэффициентом:
\[ v_{avg} = \frac{s(t) -с(а)}{т-а}. \]
Поскольку значения \(t\) приближаются к значению \(a\), значение \(v_{avg}\) приближается к тому, что вы называете мгновенной скоростью при \(a\). Мгновенная скорость в \(a\), обозначаемая как \(v(a)\), определяется как:
\[ v(a) = s'(a) = \lim_{t \to a} \frac{s(t)-s(a)}{t-a} .\]
Другими словами, если вы хотите найти среднюю скорость объекта во времени, вы можете сделать это, взяв производную от функции, которая представляет положение объекта во времени.
Средняя скорость по сравнению с мгновенной скоростью
Наклон секущей представляет собой среднюю скорость функции на замкнутом интервале \([a, t] \). Наклон касательной — это мгновенная скорость в точке \(а\).
Приведенный выше график поможет вам понять разницу между средней скоростью и мгновенной скоростью . На этом графике наклон секущей (зеленый) представляет собой среднюю скорость объекта за интервал времени \([a, t]\). Наклон касательной (розовый) — это мгновенная скорость объекта в момент времени \( t = a \). Положение объекта в момент времени \(t\) представлено функцией \(y = s(t)\) (синий).
Как видите, наклон касательной к функции и мгновенная скорость связаны. Вы вычисляете оба, находя производную, и оба измеряете мгновенную скорость изменения функции — скорость изменения указанной функции в определенной точке.
мгновенная скорость изменения функции \( f(x) \) при значении \(a\) является ее производной при \(a\) . Другими словами, мгновенная скорость изменения \(f(x)\) в точке \(a\) имеет значение \(f'(a)\).
Другими словами, мгновенная скорость изменения \(f(x)\) в точке \(a\) имеет значение \(f'(a)\).
Используя формулу для \(v(a)\), вы можете рассчитать мгновенную скорость объекта или использовать таблицу значений для оценки скорости движущегося объекта. Вы можете подтвердить эту оценку, используя формулу для \(v_{avg}\).
Допустим, у вас есть груз на пружине, которая колеблется вверх и вниз. Его положение в момент времени \(t\) относительно фиксированной горизонтальной линии (или датума) определяется функцией:
\[ s(t) = sin(t). \]
Используя таблицу значений, оцените \(v(0)\). Проверьте эту оценку, используя формулу для \(v(a)\).
Решение :
Вы можете оценить мгновенную скорость во времени \(t=0\), создав таблицу значений, выбрав значения \(t\), которые приближаются к \(0\), как в таблице ниже.
| \(t\) | \( \frac{sin(t)-sin(0)}{t-0} = \frac{sin(t)}{t} \) |
| \(-0,1\) | \(0,998334166\) |
| \(-0,01\) | \(0,999983333\) |
\(0. 001\) 001\) | \(0.999999833\) |
| \(0.01\) | \(0.999983333\) |
| \(0.1\) | \(0.998334166\ ) |
Из этой таблицы видно, что средняя скорость за интервалы времени, приближающиеся к \(t=0\), приближается к скорости \(1\), поэтому кажется, что \(v(0) =1\) является хорошей оценкой.
Вы можете проверить эту оценку по формуле:
\[ v(a) = s'(a) = \lim_{t \to a} \frac{s(t)-s(a)}{t-a} . \]
Используя эту формулу, вы получите:
\[ \begin{align}v(0) = s'(0) &= \lim_{t \to 0} \frac{sin(t)-sin(0) }{t-0} \\&= \lim_{t \to 0} \frac{sin(t)}{t} \\&= 1.\end{align} \]
Следовательно, \( \bf { v(0) } = \bf{ 1 } \).
Формула производной
До сих пор вы рассматривали производную функции в определенной точке. Рассматривая саму производную как функцию, вы можете найти производную функции в каждой точке ее области определения, для которой производная определена (существует предел). Ниже вы формально определяете производная функция .
Ниже вы формально определяете производная функция .
Производные функции и формула производной
Существует формула, которую можно использовать для нахождения любой производной любой функции. Он определяется как:
Пусть \(f(x)\) будет функцией. Производная этой функции по \(x\), обозначаемая через \(f'(x)\), представляет собой функцию, область определения которой состоит из значений \(x\) таких, что существует следующий предел:
\ [ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}. \]
Это называется определение производной .
Конечно, по мере изучения математического анализа вы обнаружите более эффективные способы вычисления производных функций, принимающих определенные формы. Они затронуты немного позже в этой статье, а более подробные объяснения и анализы находятся в статье о правилах дифференциации и ее подстатьях.
Использование формулы для определения производной всегда будет работать, хотя поиск производной таким способом может занять больше времени! 9{2}}{h} \]
 \[ f'(x) = \lim_{h \to 0} \frac{h(2x-2+h) }{h} \]
\[ f'(x) = \lim_{h \to 0} \frac{h(2x-2+h) }{h} \]Подробный анализ и дополнительные примеры см. в статье о производных функциях.
График производной
Поскольку функция и ее производная связаны, можно ожидать, что их графики также связаны, потому что производная дает нам скорость изменения функции. Лучше всего это видно на примере. 9{2}-2x \) и его производная \( f'(x) = 2x-2 \).
Решение :
Графики функции (синий) и ее производной (зеленый).
Когда функция (синяя) и ее производная (зеленая) изображены на одной координатной плоскости, вы можете увидеть их взаимосвязь.
- Вы можете видеть, что \( f(x) \) уменьшается для значений \( x < 1 \).
- Следовательно, при тех же значениях \(х\) \( f'(x) < 0 \).
- Вы также можете видеть, что \( f(x) \) увеличивается для значений \( x > 1 \).

- Следовательно, при тех же значениях \(х\), \( f'(x) > 0 \).
- И \(f(x)\) имеет горизонтальную касательную в точке \(x=1 \).
- Здесь \( f'(1)=0 \).
Производные и непрерывность
Теперь, когда вы построили график производной, давайте обсудим поведение этих графиков. Первое, что нужно рассмотреть, это дифференцируемость и непрерывность . Начнем с теоремы:
Теорема – Дифференцируемость влечет непрерывность
Пусть \(f(x)\) – функция, в области определения которой есть \(a\). Если \(f(x)\) дифференцируема в \(а\), то она также непрерывна в \(а\).
Обратите внимание, что эта теорема НЕ работает в обратном порядке! Из дифференцируемости следует непрерывность, но из непрерывности не следует дифференцируемость.
Доказательство теоремы: дифференцируемость влечет непрерывность.
Если \(f(x)\) дифференцируема в \(a\), то \(f'(a)\) существует и:
\[ f'(a) = \lim_{x \to a } \frac{f(x)-f(a)}{x-a}. \]
\]
Чтобы доказать это, нам нужно показать, что \(f(x)\) непрерывна в \(a\), показав, что \( \lim_{x \to a} (f(x)) = f(a )\). Итак,
\[ \begin{align}\lim_{x to a} (f(x)) &= \lim_{x \to a}(f(x)-f(a)+f(a)) \\&= \lim_{x \to a} \left( \frac{f(x)-f(a)}{x-a} \times (x-a) + f(a) \right) \\&= \left ( \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \right) \times \left( \lim_{x \to a} (x-a) \right) + \lim_ {x \to a} f(a) \\&= f'(a) \times 0 + f(a) \\&= f(a).\end{align} \]
Так как \( f( а) \) определено и \( \lim_{x \to a} (f(x)) = f(a) \), можно заключить, что \( f(x) \) непрерывна в \(a\ ).
Непрерывность не означает дифференцируемости.
Давайте посмотрим на функцию абсолютного значения:
\[ f(x) = |x|. \]
График родительской функции абсолютного значения.
Вы знаете, что эта функция везде непрерывна, но везде ли она дифференцируема? Попробуем взять производную в точке, где \( x=0 \).
\[ \begin{align}f'(0) &= \lim_{x \to 0} \frac{f(x)-f(0)}{x-0} \\&= \lim_{x \to 0} \frac{|x|-|0|}{x-0} \\&= \lim_{x \to 0} \frac{|x|}{x}. \end{align} \] 9{+}} \frac{|x|}{x} = 1. \]
\end{align} \] 9{+}} \frac{|x|}{x} = 1. \]
Другими словами, когда вы приближаетесь к пределу с левой стороны графика, предел равен \(-1\), и когда вы приближаетесь к пределу с правой стороны графика, предел равен \(+1\). Чтобы предел существовал, он должен быть непротиворечивым независимо от того, с какой стороны вы приближаетесь к пределу.
Это был только один пример, когда непрерывность не означает дифференцируемости. Краткий обзор ситуаций, когда непрерывная функция не является дифференцируемой, включает:
- Как и в случае с функцией абсолютного значения, если пределы наклона касательных к кривой слева и справа не совпадают, функция не дифференцируема.
- В случае функции абсолютного значения это привело к острому углу графика в точке \(0\). Это приводит нас к выводу, что для того, чтобы функция была дифференцируемой в точке, она должна быть «гладкой» в этой точке.
- Функция не дифференцируема ни в одной точке, где касательная к ней вертикальна.

- Функция может не быть дифференцируемой более сложными способами, например, функция, колебания которой становятся все более частыми по мере приближения к некоторому значению.
Типы производных
Поскольку сама производная является функцией, можно найти производную производной. Самый распространенный пример этого — когда речь идет о положении , скорости и ускорении :
Производная функции положения — это скорость изменения положения или скорость.
Производная функции скорости — это скорость изменения скорости или ускорение.
Когда вы берете производную от производной, новая функция называется второй производной . Вы можете продолжить этот процесс, чтобы найти третью производную , четвертую производную и т. д. Эти типы производных вместе называются производными более высокого порядка . n \), где \(n\) – натуральное число, являются строительными блоками, из которых каждый многочлен и рациональное число функции построены. Если вы хотите найти их производные, не используя определение производной, вам нужно сначала разработать формулы для дифференцирования этих функций.
n \), где \(n\) – натуральное число, являются строительными блоками, из которых каждый многочлен и рациональное число функции построены. Если вы хотите найти их производные, не используя определение производной, вам нужно сначала разработать формулы для дифференцирования этих функций.
Основные производные правила
Постоянное правило
Начнем с самой простой функции, постоянной функции: \( f(x)=c \). Правило дифференцирования постоянных функций называется постоянным правилом .
Правило констант гласит, что производная любой постоянной функции равна нулю . То есть, поскольку постоянная функция представляет собой горизонтальную линию, наклон (или скорость изменения) постоянной функции равен нулю.
Теорема – постоянное правило
Пусть \(с\) – любая константа. Если \( f(x)=c \), то производная \(f(x)\) может быть записана любым из следующих способов:
\[ f'(c)=0 \]
\ [ y'(c)=0 \]
\[ \frac{d}{dx}(c)=0 \]
Сумма, разность и постоянные множественные правила
Как и при работе с функциями, правила, помогающие находить производные функций, которые вы складываете, вычитаете или умножаете на константу.
Теорема. Правила суммы, разности и постоянного кратного числа
Пусть \(f(x)\) и \(g(x)\) – дифференцируемые функции, а \(c\) – постоянная. Тогда выполняется каждое из следующих утверждений:
Правило суммы – Производная суммы двух функций, \(f(x)\) и \(g(x)\), равна сумме производных \(f(x)\) и \(g(x)\).\[ \frac{d}{dx} (f(x)+g(x)) = \frac{d}{ dx}(f(x)) + \frac{d}{dx}(g(x)) \] или, если у вас есть\[ h(x) = f(x) + g(x), \], то \[ h'(x) = f'(x) + g'(x). \]
Правило разности . Производная разности двух функций \(f(x)\) и \(g(x)\) равна разности производных \(f(x)\) и \(g(x) \).\[ \frac{d}{dx} (f(x)-g(x)) = \frac{d}{dx}(f(x))-\frac{ d}{dx}(g(x)) \] или, если у вас есть\[ h(x) = f(x) – g(x) \],то\[ h'(x) = f'(x) – г'(х). \]
Множественное правило константы – Производная константы \(c\), умноженная на функцию, равна константе, умноженной на производную функции.
 \[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
\[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]Подробный анализ и примеры см. в статье The Power Rule.
Правило произведения
Правило произведения утверждает, что производная произведения двух функций равна: быть дифференцируемыми функциями. Тогда
\[ \frac{d}{dx}(f(x)g(x)) = \frac{d}{dx}(f(x))g(x) + f(x) \frac {d}{dx}(g(x)), \] или, если у вас есть
\[ h(x) = f(x)g(x) \]
, затем
\[ h'(x) = f'(x)g(x) + f(x)g'(x). \]
Хотя может показаться заманчивым так думать, правило произведения НЕ следует шаблону правил суммы/разности. Производная продукта НЕ ЯВЛЯЕТСЯ продуктом производных!
Подробный анализ и примеры см. в статье The Product Rule.
Правило частных
Теперь, когда вы рассмотрели производные произведения двух функций, давайте рассмотрим частные функции и разработаем правило частных.
Правило частного гласит, что производная от частного двух функций равна:
Производная функции в числителе, умноженная на функцию в знаменателе минус функция в числителе, умноженная на производную функции в в знаменателе,
Все разделить на функцию в знаменателе в квадрате.

Теорема. Правило частных
Пусть \(f(x)\) и \(g(x)\) – дифференцируемые функции. Затем 92}. \]
Хотя может показаться заманчивым так думать, правило частного НЕ следует шаблону правил суммы/разности. Производная частного НЕ ЯВЛЯЕТСЯ частным производных!
Подробный анализ и примеры см. в статье The Quotient Rule.
Комбинирование правил производных
Продолжая изучение исчисления, вы увидите, что редко можно использовать только одно правило дифференцирования для нахождения производной заданной функции. Используя изученные правила, теперь вы можете находить производные полиномиальных и рациональных функций. 9{2}-4t+70 \]
для \( 0 \leq t \leq 10 \)
, где \( t = \) число прошедших часов \(9pm \) представляет температуру вашего дома в течение ночи .
Найдите мгновенную скорость изменения температуры в полночь.
Решение :
Поскольку полночь наступает \(3\) часа после \(9pm\), вы хотите найти мгновенную скорость изменения или производную уравнения в \(t=3\).
 Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .
Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .Как найти производную функции извлечения квадратного корня?
Найдите производную функции извлечения квадратного корня \( f(x)=\sqrt{x} \).
Решение :
- Применить определение производной.\[ f'(x) = \lim_{h \to 0} \left( \frac{f(x+h)-f(x)} {h} \right) \]
- Замена \( f(x)=\sqrt{x} \).\[ f'(x) = \lim_{h \to 0} \left( \frac{\sqrt {x+h}-\sqrt{x}}{h} \right) \]
- Умножьте и разделите на \( \sqrt{x+h}+\sqrt{x} \), чтобы упростить дробь. \[ f'(x) = \lim_{h \to 0} \left( \frac{\sqrt{x+h}-\sqrt{x}}{h} \times \frac{\sqrt{x+h }+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} \right) \]
- Упростить.\[ f'(x) = \lim_{h \to 0} \left( \frac{h}{h \left( \sqrt{x+h} + \sqrt{x} \right)} \right) \]
- Сократить общий делитель \(h\).\[ f'(x) = \lim_{h \to 0} \left( \frac{1}{\sqrt{x+h }+\sqrt{x}} \right) \]
- Вычислить предел.\[ f'(x) = \frac{1}{\sqrt{x}+\sqrt{x}} \]
- Упростить .
 \[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
\[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
Теперь давайте посмотрим, как функция квадратного корня и ее производная сравниваются графически.
Постройте график функции \( f(x)=\sqrt{x} \) и ее производной \( f'(x) = \frac{1}{2\sqrt{x}}.
Решение :
График функции (синий) и ее производной (зеленый)
Когда функция (синий) и ее производная (зеленый) изображены на одной координатной плоскости, вы можете увидеть их взаимосвязь.
- Во-первых, обратите внимание, что \( f(x) \) возрастает по всей области определения. Это означает, что наклоны всех касательных линий положительны.
- Следовательно, вы ожидаете, что \( f'(x) > 0 \) для всех значений \(x\) в его области определения.
9{2}-4т+1\) (в метрах). Найдите функцию, описывающую его ускорение в момент времени \(t\). - Следовательно, \( v(t) = 6t-4 \).
Решение :
Чтобы найти функцию ускорения из функции положения, нужно взять первую и вторую производные функции положения.
 {2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]
{2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]- Вторая производная функции положения — это функция ускорения: \( s”(t) = v'(t) = a(t) \).\[ \begin{align}s”(t ) &= \lim_{h \to 0} \left( \frac{s'(t+h)-s'(t)}{h} \right) \\&= \lim_{h \to 0} \ влево( \frac{6(t+h)-4-(6t-4)}{h} \right) \\&= \lim_{h \to 0} \left( \frac{6t+6h-4- 6t+4}{h} \right) \\&= \lim_{h \to 0} \left( \frac{6h}{h} \right) \\&= \lim_{h \to 0} (6 ) \\s”(t) &= 6\end{align} \]
- 9{2}} } \).
Производные – основные выводы
- Целью производной является вычисление наклона касательной к кривой в определенной точке .
- мгновенная скорость изменения функции \( f(x) \) при значении \(a\) является ее производной при \(a\) , \( f’ (а) \) .

- Определение производной: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
- Из дифференцируемости следует непрерывность, но из непрерывности не следует дифференцируемость.
- Вы можете взять производную от производной
- Это приводит к производным высшего порядка
- Существует несколько правил производных, которые помогают нам быстрее и проще находить производные функций.
Ссылки
- https://www.hennesseyspecialvehicles.com/2021-venom-f5/
Расчет производных в PyTorch
Автор: Мухаммад Асад Икбал Хан, , 27 января 2022 г., в PyTorch Computer Vision
Последнее обновление: 11 марта 2022 г.
Производные — одно из самых фундаментальных понятий в исчислении. Они описывают, как изменения входных переменных влияют на выходные данные функции. Цель этой статьи — дать общее представление о вычислении производных в PyTorch для тех, кто плохо знаком с фреймворком. PyTorch предлагает удобный способ вычисления производных для пользовательских функций.
PyTorch предлагает удобный способ вычисления производных для пользовательских функций.
Хотя нам всегда приходится иметь дело с обратным распространением (алгоритм, который, как известно, является основой нейронной сети) в нейронных сетях, который оптимизирует параметры для минимизации ошибки для достижения более высокой точности классификации; понятия, изученные в этой статье, будут использоваться в последующих сообщениях о глубоком обучении для обработки изображений и других проблемах компьютерного зрения.
Пройдя этот урок, вы узнаете:
- Как рассчитать производные в PyTorch.
- Как использовать autograd в PyTorch для автоматического дифференцирования тензоров.
- О графе вычислений, который включает в себя разные узлы и листья, что позволяет вычислять градиенты самым простым способом (используя цепное правило).
- Как рассчитать частные производные в PyTorch.
- Как реализовать производную функций по нескольким значениям.

Начнем.
Расчет производных в PyTorch
Рисунок Джоссухи Теофиля. Некоторые права защищены.
Автоград — модуль автоматического дифференцирования в PyTorch — используется для вычисления производных и оптимизации параметров в нейронных сетях. Он предназначен в первую очередь для градиентных вычислений.
Прежде чем мы начнем, давайте загрузим некоторые необходимые библиотеки, которые мы будем использовать в этом руководстве.
импортировать matplotlib.pyplot как plt импортная горелка
импортировать matplotlib.pyplot как plt импортировать факел |
Теперь давайте воспользуемся простым тензором и установим для параметра required_grad значение true. Это позволяет нам выполнять автоматическое дифференцирование и позволяет PyTorch оценивать производные, используя заданное значение, которое в данном случае равно 3,0.
x = torch.tensor (3.0, require_grad = True) print(“создание тензора x: “, x)
y = 3 * x ** 2 print(“Результат уравнения: “, y) y.backward() print(“Производная уравнения при x = 3: “, x .град) |
Результат уравнения: tensor(27., grad_fn=
Результат уравнения: tensor(27. Производная уравнения при x = 3: tensor(18.) |
Как видите, мы получили правильное значение 18.
Расчетный графикPyTorch генерирует производные путем построения обратного графа за кулисами, а тензоры и обратные функции являются узлами графа. В графе PyTorch вычисляет производную тензора в зависимости от того, является ли он листом или нет.
PyTorch не будет оценивать производную тензора, если для его атрибута leaf установлено значение True. Мы не будем вдаваться в подробности того, как создается и используется обратный график, потому что цель здесь — дать вам общее представление о том, как PyTorch использует график для вычисления производных.
Итак, давайте проверим, как тензоры x и y выглядят внутри после их создания. Для x :
print(‘атрибут данных тензора:’,x.data)
print(‘атрибут grad тензора::’,x.grad)
print(‘атрибут grad_fn тензора::’,x. grad_fn)
print(“атрибут is_leaf тензора::”,x.is_leaf)
print(“атрибут requires_grad тензора::”,x.requires_grad)
grad_fn)
print(“атрибут is_leaf тензора::”,x.is_leaf)
print(“атрибут requires_grad тензора::”,x.requires_grad)
print(‘атрибут data тензора:’,x.data) print(‘атрибут grad тензора::’,x.grad) print(‘атрибут grad_fn тензора::’,x. grad_fn) print(“атрибут is_leaf тензора::”,x.is_leaf) print(“атрибут requires_grad тензора::”,x.requires_grad) |
атрибут данных тензора: tensor(3.) атрибут grad тензора :: tensor(18.) Атрибут grad_fn тензора :: Нет атрибут is_leaf тензора :: True атрибут required_grad тензора :: True
атрибут data тензора: tensor(3.) grad атрибут тензора:: tensor(18.) grad_fn атрибут тензора:: None is_leaf атрибут тензора:: True required_grad атрибут тензора:: True |
и для и :
print(‘атрибут данных тензора:’,y. data)
print(‘атрибут градации тензора:’,y.grad)
print(‘атрибут grad_fn тензора:’,y.grad_fn)
print(“атрибут is_leaf тензора:”,y.is_leaf)
print (“requires_grad атрибут тензора:”, y.requires_grad)
data)
print(‘атрибут градации тензора:’,y.grad)
print(‘атрибут grad_fn тензора:’,y.grad_fn)
print(“атрибут is_leaf тензора:”,y.is_leaf)
print (“requires_grad атрибут тензора:”, y.requires_grad)
print(‘атрибут данных тензора:’,y.data) print(‘атрибут grad тензора:’,y.grad) print(‘атрибут grad_fn тензора:’,y.grad_fn ) print(“атрибут is_leaf тензора:”,y.is_leaf) print(“атрибут requires_grad тензора:”,y.requires_grad) |
print(‘атрибут данных тензора:’,y.data) print(‘атрибут градации тензора:’,y.grad) print(‘атрибут grad_fn тензора:’,y.grad_fn) print(“атрибут is_leaf тензора:”,y.is_leaf) print (“requires_grad атрибут тензора:”, y.requires_grad)
print(‘атрибут данных тензора:’,y.data) print(‘атрибут grad тензора:’,y.grad) print(‘атрибут grad_fn тензора:’,y.grad_fn ) print(“атрибут is_leaf тензора:”,y. print(“атрибут requires_grad тензора:”,y.requires_grad) |
Как видите, каждому тензору присвоен определенный набор атрибутов. 92+2x+4$ и вычислить производную. Производная уравнения определяется как:
$$\frac{dy}{dx} = 12x+2$$
Оценка производной при $x = 3$,
$$\left.\frac{dy}{dx}\right\vert_{x=3} = 12\times 3+2 = 38$$
Теперь давайте посмотрим, как это делает PyTorch,
x = torch.tensor (3.0, require_grad = True) у = 6 * х ** 2 + 2 * х + 4 print(“Результат уравнения: “, y) у.назад() print(“Производная уравнения при x = 3: “, x.grad)
x = torch.tensor(3.0, required_grad = True) y = 6 * x ** 2 + 2 * x + 4 print(“Результат уравнения: “, y) y.backward () print(“Производная уравнения при x = 3 равна: “, x.grad) |
Результат уравнения: tensor(64., grad_fn= )
)
Результат уравнения: tensor(64., grad_fn= Производная уравнения при x = 3: tensor(38.) |
Производная уравнения равна 38, что верно.
Реализация частных производных функцийPyTorch также позволяет нам вычислять частные производные функций. Например, если нам нужно применить частичный вывод к следующей функции,
92+4v$$Точно так же производная по $v$ будет равна
$$\frac{\partial f}{\partial v} = 2v + 4u$$
Теперь давайте сделаем это с помощью PyTorch, где $u = 3$ и $v = 4$.
Мы создадим тензоры u , v и f и применим атрибут .backward к f для вычисления производной. Наконец, мы оценим производную, используя .grad по отношению к значениям и и против .
u = torch.tensor(3. , require_grad=True)
v = torch.tensor(4., require_grad=True) f = и**3 + v**2 + 4*и*в печатать (у)
печать (v)
печать (е) f.назад()
print(“Частная производная по u: “, u.grad)
print(“Частная производная по v: “, v.grad)
, require_grad=True)
v = torch.tensor(4., require_grad=True) f = и**3 + v**2 + 4*и*в печатать (у)
печать (v)
печать (е) f.назад()
print(“Частная производная по u: “, u.grad)
print(“Частная производная по v: “, v.grad)
1 2 3 4 5 6 7 8 9 10 11 12 | u = torch.tensor(3., require_grad=True) v = torch.tensor(4., required_grad=True)
f = u**3 + v**2 + 4*u* v
print(u) print(v) print(f)
f.backward() print(“Частная производная по u: “, ) print(“Частная производная по v: “, v.grad) |
тензор (3., required_grad = True)
тензор (4., required_grad = True)
тензор(91., grad_fn=
тензор(3. тензор(4., required_grad=True) тензор(91., grad_fn= Частная производная по u: тензор(43.) Частная производная по v: тензор(20.) |
Что делать, если у нас есть функция с несколькими значениями, и нам нужно вычислить производную по этим множественным значениям? Для этого мы воспользуемся атрибутом суммы, чтобы (1) создать скалярную функцию, а затем (2) взять производную. Вот как мы можем видеть график «функция против производной»:
# вычислить производную функции с несколькими значениями
x = torch.linspace(-20, 20, 20, require_grad = True)
У = х ** 2
у = факел.сумма (Y)
у.назад() # построение функции и производной
function_line, = plt.plot(x.detach().numpy(), Y.detach().numpy(), label = ‘Функция’)
function_line.set_color(“красный”)
производная_линия, = plt.plot(x.detach().numpy(), x.grad.detach(). numpy(), метка = ‘Производная’)
производная_линия.set_color(“зеленый”)
plt.xlabel(‘x’)
plt.legend()
plt.show()
numpy(), метка = ‘Производная’)
производная_линия.set_color(“зеленый”)
plt.xlabel(‘x’)
plt.legend()
plt.show()
1 2 3 4 5 6 7 8 10 110005 12 13 14 | # вычислить производную функции с несколькими значениями x = torch.linspace(-20, 20, 20, require_grad = True) Y = x ** 2 y = torch.sum(Y) y.назад()
# отображение функции и производной function_line, = plt.plot(x.detach().numpy(), Y.detach().numpy(), label = ‘Function’) function_line.set_color(” красный”) производная_линия, = plt.plot(x.detach().numpy(), x.grad.detach().numpy(), метка = ‘Производная’) производная_линия.set_color(“зеленый”) plt.xlabel(‘x’) plt.legend() plt.show() |
В двух сюжетах() выше, мы извлекаем значения из тензоров PyTorch, чтобы мы могли их визуализировать. Метод
Метод .detach не позволяет графу дальше отслеживать операции. Это позволяет нам легко преобразовать тензор в массив numpy.
В этом руководстве вы узнали, как реализовать производные функции для различных функций в PyTorch.
В частности, вы узнали:
- Как рассчитать производные в PyTorch.
- Как использовать autograd в PyTorch для автоматического дифференцирования тензоров.
- О графе вычислений, который включает в себя разные узлы и листья, что позволяет вычислять градиенты самым простым способом (используя цепное правило).
- Как рассчитать частные производные в PyTorch.
- Как реализовать производную функций по нескольким значениям.
О Мухаммаде Асаде Икбал Хане
Асад — писатель и практик, увлеченный ИИ и машинным обучением. Он регулярно пишет о последних разработках в области искусственного интеллекта и разработал новые алгоритмы искусственного интеллекта, помогающие создавать интеллектуальные приложения для различных организаций.


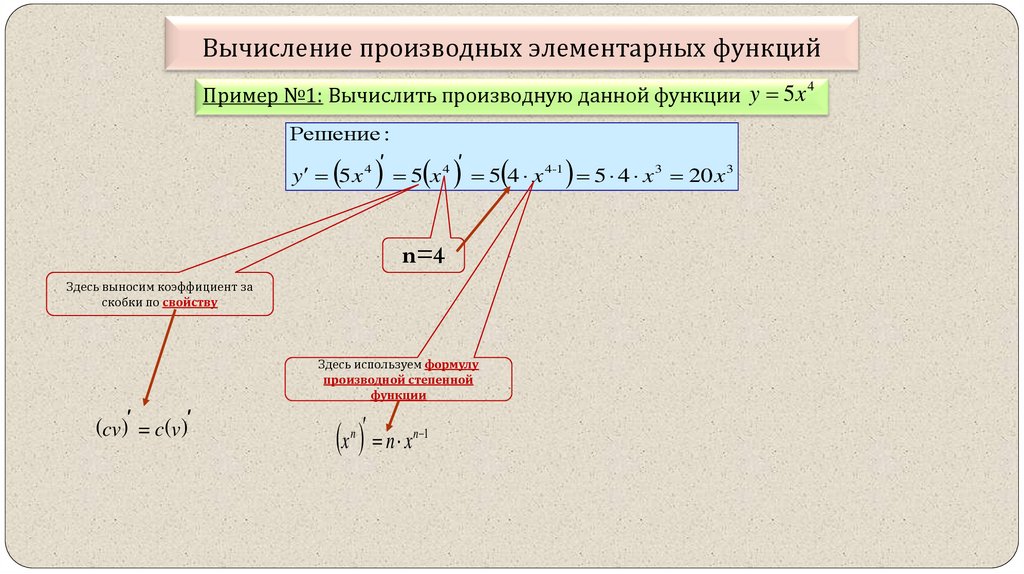

 \[ \bf{ f'(2) } = \bf{ 8 } \]
\[ \bf{ f'(2) } = \bf{ 8 } \]

 \[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
\[ \frac{d}{dx}( c \cdot f(x)) = c \cdot \frac{d}{dx}(f(x)) \] или, если у вас \[ h(x) = c \cdot f(x) \]тогда \[ h'(x) = c \cdot f'(x). \] 9{n-1} \]
 Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час .
Другими словами, вам нужно вычислить \(T'(3)\). 9{\circ} F \) в час . \[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \]
\[ \bf{ f'(x) } = \bf{ \frac{1}{2\sqrt{x}} } \] {2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]
{2}+4t-1}{h} \right) \\&= \lim_{h \to 0} \left ( \frac{h(6t+3h-4)}{h} \right) \\&= \lim_{h \to 0} (6t+3h-4) \\s'(t) &= 6t-4 \\\конец{выравнивание} \]

 , grad_fn=
, grad_fn= is_leaf)
is_leaf) , required_grad=True)
, required_grad=True)