Вычисления интегралов: Таблица интегралов

Интегрирование по частям

Пусть U(x) и V(x) – дифференцируемые функции. Тогда d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

• Решение онлайн
• Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

Также рекомендуется изучить сервис вычисление интегралов онлайн

Примеры

≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Применение метода интегрирования по частям

В связи с особенностями нахождения определенных величин, формулу интегрирования по частям очень часто используют в следующих задачах:

1. Математическое ожидание непрерывной случайной величины. Формула для нахождения математического ожидания и дисперсии непрерывной случайной величины включает в себя два сомножителя: функцию полинома от x и плотность распределения f(x).
2. Разложение в ряд Фурье. При разложении необходимо определять коэффициенты, которые находятся интегрированием от произведения функции f(x) и тригонометрической функции cos(x) или sin(x).

Типовые разложения по частям

Вид интеграла	Разложения на части
∫Pn(x)cos(ax)dx, ∫Pn(x)sin(ax)dx, ∫Pn(x)eaxdx, где Pn(x) – некоторый полином (многочлен) степени n	U(x)=Pn(x), dV(x)=cos(ax)dx
∫ln(P(x))dx	U=ln(P(x)); dV=dx
∫arcsin(ax)dx	U=arcsin(ax); dV=dx
	U=ln(x); dV=dx/x

При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=e^x, dV=xdx. Тогда dU=e^xdx, и Вряд ли интеграл ∫x2exdx можно считать проще исходного.
Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла

∫x2sin(x)dx.

Интегралы ∫eaxcos(bx)dx и ∫eaxsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.

Пример №1. Вычислить ∫xexdx.
Положим U=x, dV=e^xdx. Тогда dU=dx, V=e^x. Поэтому ∫xexdx=xex-∫exdx=xex-ex+C.

Пример №2. Вычислить ∫xcos(x)dx.
Полагаем U=x,

dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) - ∫sin(x)dx = xsin(x)+cos(x)+C

Пример №3. ∫(3x+4)cos(x)dx
Решение:

Ответ: (3x+4)sin(x)+3cos(x)+C

Методы решения неопределенных интегралов (в картинках)

Приводятся основные сведения о методах вычисления неопределенных интегралов в сжатом виде – в виде изображений. Каждая картинка снабжена заголовком и ссылкой на страницу с подробным изложением метода.

Здесь приводятся главные картинки раздела «Методы вычисления неопределенных интегралов». На этих изображениях, в кратком виде представлены главные содержания страниц раздела. На многих из них даются методы решения интегралов. Снизу от каждого изображения имеется заголовок и ссылка на страницу, к которой относится картинка. Просматривая эти картинки, можно освежить в памяти методы вычисления неопределенных интегралов.

Методы вычисления неопределенных интегралов

Представлен обзор методов вычисления неопределенных интегралов. Рассмотрены основные методы интегрирования, которые включают в себя интегрирование суммы и разности, вынесение постоянной за знак интеграла, замену переменной, интегрирование по частям. Также рассмотрены специальные методы и приемы интегрирования дробей, корней, тригонометрических и показательных функций.

Примеры решений неопределенных интегралов

Здесь представлено 48 примеров решений неопределенных интегралов.

Основные формулы и методы интегрирования

Основные формулы и методы интегрирования

Основные формулы и методы интегрирования. Правило интегрирования суммы или разности. Вынесение постоянной за знак интеграла. Метод замены переменной. Формула интегрирования по частям. Пример решения задачи.

Таблица неопределенных интегралов для студентов

Представлена таблица основных неопределенных интегралов для студентов, а также интегралы, связанные с гиперболическими функциями. Приводится таблица интегралов в дифференциальной форме и основные методы интегрирования.

Вычисление неопределенных интегралов от многочленов

Формула интеграла от многочлена в общем виде. Примеры вычисления интегралов от многочленов и степенных функций, применяя основные методы интегрирования.

Интегрирование методом замены переменной

Замена переменной в неопределенном интеграле. Формула преобразования дифференциалов. Примеры интегрирования. Примеры линейных подстановок.

Метод интегрирования неопределенного интеграла по частям

Представлен метод интегрирования неопределенного интеграла по частям. Даны примеры интегралов, вычисляющихся этим методом. Разобраны примеры решений.

Примеры решений интегралов по частям, содержащих логарифм и обратные тригонометрические функции

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых содержит логарифм, арксинус, арктангенс, а также логарифм в целой степени и логарифм от многочлена.

Примеры решений интегралов по частям, содержащих произведение многочлена на sin x, cos x или e^x

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).

Методы интегрирования рациональных функций (дробей)

Интегрирование рациональных функций (дробей)

Стандартный метод интегрирования рациональных функций: выделение целой части дроби многочленов, разложение правильной дроби на простейшие, интегрирование простейших дробей. Нестандартные методы интегрирования рациональных функций: применение степенных и дробно-линейных подстановок, интегралы с возвратными многочленами.

Деление и умножение многочленов уголком и столбиком

Приводится доказательство, что неправильную дробь, составленную из многочленов, можно представить в виде суммы многочлена и правильной дроби. Подробно разобраны примеры деления многочленов уголком и умножения столбиком.

Методы разложения многочленов на множители

Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены.

Примеры разложения многочленов на множители

Приводится 8 примеров разложения многочленов на множители. Они включают в себя примеры с решением квадратных и биквадратных уравнений, примеры с возвратными многочленами и примеры с нахождением целых корней у многочленов третьей и четвертой степени.

Методы разложения рациональных дробей на простейшие

Приведены наиболее эффективные методы разложения правильных рациональных дробей, составленных из многочленов, на простейшие. Рассмотрены характерные примеры разложения дробей.

Интегрирование простейших (элементарных) дробей

Приводится вывод формул для вычисления интегралов от простейших, элементарных, дробей четырех типов. Более сложные интегралы, от дробей четвертого типа, вычисляются с помощью формулы приведения. Рассмотрен пример интегрирования дроби четвертого типа.

Примеры интегрирования рациональных функций (дробей)

Рассмотрены примеры интегрирования рациональных функций (дробей) с подробными решениями.

Методы интегрирования иррациональных функций (корней)

Методы интегрирования иррациональных функций (корней)

Даны основные методы интегрирования иррациональных функций (корней). Они включают в себя: интегрирование дробно-линейной иррациональности, дифференциального бинома, интегралы с квадратным корнем из квадратного трехчлена. Приводятся тригонометрические подстановки и подстановки Эйлера. Рассмотрены некоторые эллиптические интегралы, выражающиеся через элементарные функции.

Интегрирование дробно-линейной иррациональности

Показано, что интегралы с дробно-линейной иррациональностью (то есть содержащие корни от дробно-линейной функции) сводятся к интегрированию рациональных функций. Разобраны примеры вычисления интегралов с корнями из дробно-линейной функции.

Интегрирование дифференциального бинома

Интегралы от дифференциального бинома сводятся к интегралам от рациональных функций в трех случаях, при определенных соотношениях между показателями степеней. Даны три подстановки, которые приводят к интегралу от рациональной функции. Даны формулы приведения, связывающие интегралы с различными значениями показателей степеней. Подробно разобран пример вычисления интеграла от дифференциального бинома.

Вычисление интегралов от многочлена дробь квадратный корень из квадратного трехчлена

Рассмотрен метод вычисления интеграла от дроби, в числителе которой находится многочлен, а в знаменателе – квадратный корень из трехчлена. Наиболее простым методом вычисления таких интегралов является метод неопределенных коэффициентов. Приведено доказательство применимости этого метода. Разобран пример вычисления такого интеграла.

Вычисление интегралов от многочлена дробь степень от двучлена квадратный корень из квадратного трехчлена

Представлен метод вычисления интегралов, в числителе дроби которых находится многочлен, а в знаменателе – произведение натуральной степени от линейной функции и квадратный корень из квадратного трехчлена. Разобраны примеры вычислений таких интегралов.

Вычисление интегралов от двучлена дробь степень от трехчлена квадратный корень из квадратного трехчлена

Приводится метод вычисления интегралов, в числителе дроби которых находится линейный двучлен, а в знаменателе – произведение квадратного трехчлена в натуральной степени на квадратный корень из трехчлена. Разобран пример вычисления такого интеграла.

Интегрирование рациональной функции от квадратного корня из квадратного трехчлена

Представлен наиболее эффективный способ интегрирования рациональной функции от квадратного корня из квадратного трехчлена. Разобран пример вычисления такого интеграла.

Вычисление интегралов тригонометрическими и гиперболическими подстановками

Рассмотрено решение интегралов от рациональной функции с квадратным корнем из квадратного двучлена с помощью тригонометрических и гиперболических подстановок. Даны формулы тригонометрических и гиперболических подстановок и примеры вычисления интегралов.

Подстановки Эйлера

Показано, что интегралы с рациональными функциями от квадратного корня из квадратичного многочлена сводятся к интегралам от рациональных функций с помощью подстановок Эйлера. Даны три подстановки Эйлера и рекомендации по их применению. Разобран пример вычисления интеграла с помощью подстановки Эйлера.

Методы интегрирования тригонометрических функций

Методы интегрирования тригонометрических функций

Представлены основные тригонометрические формулы и основные подстановки. Изложены методы интегрирования тригонометрических функций – интегрирование рациональных функций, произведение степенных функций от sin x и cos x, произведение многочлена, экспоненты и синуса или косинуса, интегрирование обратных тригонометрических функций. Затронуты нестандартные методы.

Интегрирование тригонометрических рациональных функций

Представлены методы интегрирования тригонометрических рациональных функций. Подробно рассмотрены три примера интегрирования таких функций.

Интегрирование произведения степенных функций от sin x и cos x

Показано, что интеграл от произведения степенных функций от sin x и cos x можно привести к интегралу от дифференциального бинома. При целых значениях показателей степени, такие интегралы легко вычисляются по частям или с помощью формул приведения. Дан вывод формул приведения. Приводится пример вычисления такого интеграла.

Интегрирование произведения многочлена, экспоненты и синуса или косинуса

Представлен метод вычисления интегралов, содержащих произведение многочлена, экспоненты и синуса или косинуса. Интегрирование осуществляется с применением формулы Эйлера.

Интегральный калькулятор | Лучшая онлайн-интеграция по частям Калькулятор

Знакомство с интегральным калькулятором

Наш расширенный интегральный калькулятор — это наиболее полное интегральное решение в Интернете, с помощью которого вы можете выполнять множество операций интеграции. Вам нужно ввести функцию, переменную и границы, и все готово.

Калькулятор интегрирования с шагами позволяет изучить принципы расчета интегралов, не тратя слишком много времени. Вы можете вычислить интеграл, используя интегральный калькулятор с шагами, легко онлайн.

Точно так же вы можете найти калькулятор двойного интеграла на этом сайте. Калькулятор двойного интеграла показывает вам графики, графики, шаги и визуальное представление, что помогает вам изучить расширенные концепции двойного интегрирования.

Есть много других полезных калькуляторов, которые можно использовать для получения выгоды. Точно так же вы можете определить объем тела вращения с помощью калькулятора метода шайбы и определить поперечные сечения тела вращения с помощью калькулятора метода диска.

Как решить Интеграция?

Чтобы найти определенный интеграл, вы должны сначала понять, что определенные интегралы имеют начальную и конечную точки, также известные как пределы или интервалы, представленные как (a,b) и расположенные сверху и снизу интеграла.

Мы можем обобщить интегралы на основе функций и областей, через которые выполняется интегрирование. Калькулятор интегрирования по частям с шагами помогает вычислять интегралы в цифровом виде.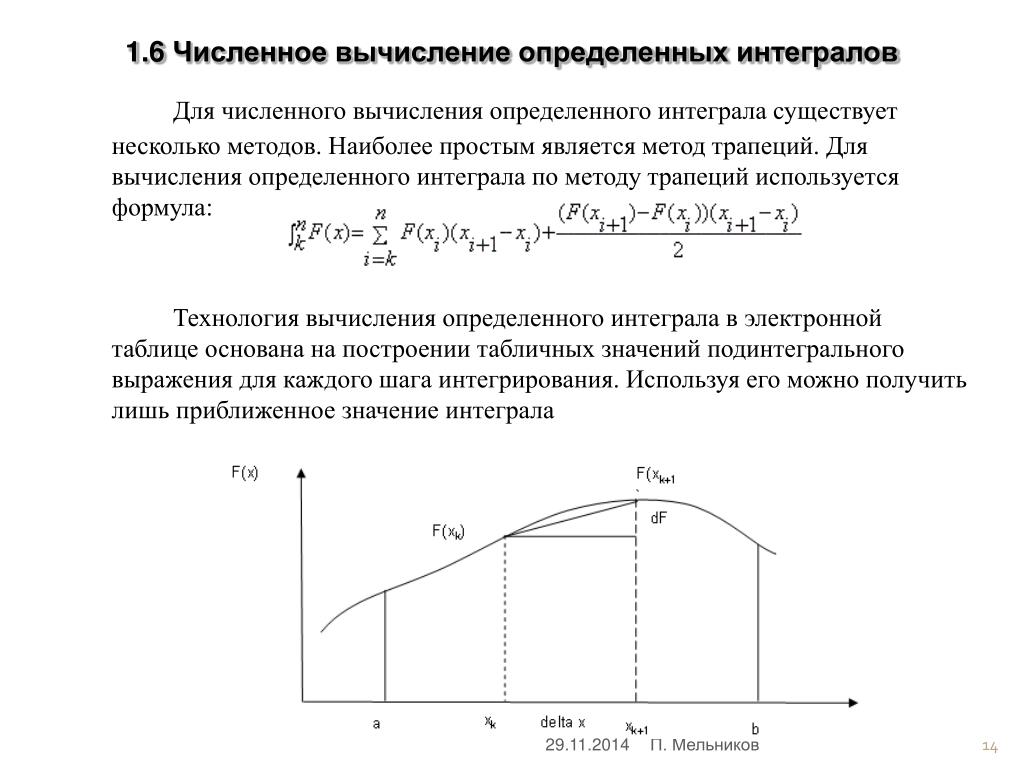

Например, линейный интеграл выражается функциями двух или более переменных с заменой интервала интегрирования кривой, соединяющей две точки на интервале. 93$$

вычисление границ: 4

-3,4

-12

С другой стороны, неопределенный интеграл отличается от определенного из-за отсутствия у первого определенных пределов.

Неопределенный интеграл, таким образом, вычисляется по формуле:

$$\int f(x)dx$$

Вышеприведенный решатель интегрирования может вычислять неопределенный интеграл и определенный интеграл, но если вы хотите вычислить только неопределенный интеграл, найдите лучший Онлайн-калькулятор неопределенного интеграла.

Связанный: Найдите этот полезный блог, чтобы узнать об определенном интеграле и неопределенном интеграле

Как вычислить неправильный интеграл?

Одна из причин, по которой определенный интеграл становится несобственным, заключается в том, что один или оба предела достигают бесконечности. Калькулятор интегрального исчисления можно использовать для вычисления неправильных интегралов.

Этот интеграл затем решается путем превращения его в проблему пределов, где c случается приближаться к бесконечности или к отрицательной бесконечности. 9c$$

$$\lim_{c\to \infty} [-\frac {1}{c}] -(-\frac{1}{1})]$$

0+1

1

Поскольку ответ на несобственный интеграл конечен, мы считаем его сходящимся.

Если вы хотите вычислить только определенные интегралы, используйте этот лучший пошаговый онлайн-калькулятор определенных интегралов.

Связанный: Используйте калькулятор метода оболочки с шагами, чтобы легко найти объем тела вращения онлайн.

Как рассчитать непрерывную интеграцию?

Основная теорема исчисления устанавливает четкую связь между интегральным и дифференциальным исчислением. Наш интегральный калькулятор с шагами способен вычислить непрерывное интегрирование.

Если f(x) непрерывна для интервала a и b при заданной переменной x и G(x) является функцией в таком смысле, что dG/dx = f(x) для всех значений x в (a,b)

Пусть f непрерывна на интервале ‘y’. Выберите точку p в y, тогда функция f(x) будет определена как:

Пусть F(x) будет следующим 9c f(t)dt$$

Для вашего удобства и углубленного изучения множественных интегралов мы предлагаем один из самых быстрых калькуляторов тройных интегралов. Этот инструмент, несомненно, поможет вам вычислить определенные и неопределенные тройные интегралы онлайн, сделав несколько кликов.

Связанный: Понимание интегрирования неполной дробью за 5 минут!

Что такое интегральный калькулятор?

В течение многих лет существовал только один способ вычислить интегралы — вычисление вручную. В наши дни у нас есть много онлайн-калькуляторов интеграции, чтобы легко рассчитать стоимость интеграции. Большинство студентов обычно имеют прочные теоретические представления об исчислении. Таким образом, вычисление интегралов или производных на самом деле не проблема, когда у нас есть такие калькуляторы, как калькулятор интегрирования или калькулятор производных.

Однако это проблема, когда дело доходит до домашних заданий, когда ученики обычно получают массу задач, требующих решения интегралов. Для получения справки, пожалуйста, прочитайте статью, в которой говорится об интеграции, ее важности и различных методах.

Было бы неразумно повторно вычислять интегралы вручную. Калькулятор определенных интегралов удобен для решения сложных задач интегрирования. Он бесплатный и простой в использовании, и вы получаете ответ почти мгновенно, так как вы можете легко найти интегральный калькулятор с пошаговыми инструкциями в Интернете.

Также используйте другие полезные математические калькуляторы, которые важны для общих процессов интеграции. Подобно калькулятору преобразования Лапласа, вы можете преобразовать интеграл данной производной функции, а калькулятор преобразования Фурье позволяет преобразовать функцию времени в частоту.

Как найти лучший калькулятор интеграции?

В Интернете доступно множество интегральных калькуляторов, например, calculated, symbolab, wolframalpha и другие.

Однако наш интегральный калькулятор объема лучше, быстрее, обладает большей функциональностью и является лучшим калькулятором интеграции с пошаговыми инструкциями, доступными в Интернете. Узнайте о преимуществах использования нашего интегрального онлайн-калькулятора.

Когда вы вводите функцию, переменную, верхнюю и нижнюю границы пределов, наш интегральный решатель вычисляет интеграл и отображает все необходимые шаги, чтобы дать пользователю лучшее понимание вычисления интегрирования.

Вы также можете рассчитать интеграцию по вертикали и интеграцию по горизонтали в области кривых с помощью нашего интегрального онлайн-калькулятора с ограничениями.

Это еще не все. Наш интегральный решатель также отображает антипроизводные вычисления для пользователей, которые могут быть заинтересованы в математической концепции и шагах, связанных с интегрированием.

Кроме того, этот калькулятор интеграции по частям поставляется с визуализацией расчета с помощью интуитивно понятных графиков.

Связанный: Как найти объем тела вращения

Как использовать интегральный калькулятор с шагами?

Пользоваться калькулятором интегрирования по частям легко и быстро.

Выполните следующие шаги:

Шаг 1: Введите функцию

Для вычисления интегралов у вас должна быть правильная функция. Вам нужно ввести свою функцию в функциональную строку калькулятора интеграции. Существует также список «пример загрузки». Вы можете щелкнуть этот список, чтобы загрузить пример уравнения для пошагового расчета интегралов.

Шаг 2. Выберите переменную

Для вычисления интегралов можно использовать три переменные. Этими переменными являются x, y и z. Роль этих трех переменных отличается друг от друга, и все они по-разному влияют на общий результат. Вы можете выбрать переменные как x, y и z из раздела переменных.

Шаг 3: Дайте значение верхней границы

Верхняя граница — это значение, которое помогает нам суммировать интеграл при его максимальном значении. Верхняя граница обозначается как U, и ее определение имеет решающее значение в процессе интегрирования. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.

Шаг 4: Введите значение нижней границы

Нижняя граница — это наименьшее значение, которое мы установили для начала интегрирования. Чтобы получить точные результаты интегрирования, наименьшее значение интервала обозначается буквой L. Чтобы получить точные результаты интегрирования. Вам необходимо ввести фактическую сумму вашего нижнего лимита в разделе нижней границы калькулятора верхней и нижней границ.

После выполнения всех вышеперечисленных шагов Нажмите кнопку “GO”.

Сразу после нажатия на кнопку заработает наш интегральный калькулятор. Калькулятор интегрирования по частям покажет вам антипроизводную, интегральные шаги, дерево разбора и график вашего результата. Все эти функции и функции делают его лучшим калькулятором линейного интеграла для вычисления интеграла сложных задач интеграции.

По мере того, как вы вводите данные, под входными данными будет отображаться визуальное уравнение, где вы можете визуализировать, как ваши входные данные будут выглядеть в уравнении.

Часто задаваемые вопросы

Как вычислять интегралы?

Есть два типа интегралов, определенные и неопределенные интегралы. Вы можете решить их оба путем интеграции. Отличие состоит в том, что в определенных интегралах нужно ставить предельные значения после интегрирования, тогда как в неопределённых интегралах предельные значения ставить не нужно. 93 (1-х) дх \;=\; \left( 3 – \frac{9}{2} \right) \;-\; \влево( -4 -2 \вправо) \;=\; \frac{21}{2} $$

Итак, площадь под данной кривой равна 21/2. Мы можем убедиться в этом, оценив интегральный калькулятор для перекрестной проверки вашего ответа.

Калькулятор интеграла — отличный ресурс для вычислений такого типа, позволяющий сэкономить ваше время.

Чему равен интеграл от 1/x?

Интеграл 1/x is,

$$ \int \frac{1}{x} dx \;=\; ln(x) + c$$

Получайте удовольствие от вычисления интегралов с интегральным онлайн-калькулятором!

Как вычислить интеграл в Excel

Интеграл — один из самых важных инструментов в математике. Его можно использовать для расчета площади, объема и многих других полезных параметров. В этом блоге мы собираемся обсудить методы вычисления интегралов в Excel.

Содержание

• Понятие интеграла
• Методы вычисления интеграла
  • Трапециевидный метод вычисления интеграла
  • Симпсоновский метод вычисления интеграла
• Итог

Понятие интеграла

В вычислительной математике есть две основные операции: интегрирование и дифференцирование. Интеграл — это обратная операция дифференцирования. Интеграция — это способ добавления кусочков, чтобы найти целое. Чаще всего его используют для вычисления площади под кривой.

Интегралы бывают двух типов: определенные и неопределенные. В неопределенном интеграле у вас должна быть формула функции F для вычисления его интеграла, которая дает F при дифференцировании. Если вы хотите вычислить интегралы с помощью Excel, забудьте о неопределенном интеграле, потому что это вопрос аналитического расчета.

Определенный интеграл относится к числовым значениям. Он используется в прикладной математике, статистике, науке и многом другом. Его можно вычислить с помощью неопределенного интеграла и численных методов.

Методы вычисления интеграла

Когда дело доходит до интегрирования, вы можете столкнуться с двумя ситуациями: у вас есть уравнение для интегрирования или соответствующие значения x и y. Как мы обсуждали ранее, Excel не может интегрироваться с использованием аналитических методов. Так что в любом случае вам придется превратить уравнение в числа.

Основываясь на вычислительной математике, мы можем вычислить интеграл двумя методами, основанными на вычислении площади геометрических фигур.

Трапециевидный метод вычисления интеграла

Этот метод предполагает, что площадь под кривой состоит из нескольких трапеций. Площадь трапеции можно рассчитать по следующей формуле:

Теперь все, что нам нужно сделать, это сложить площади этих трапеций, чтобы вычислить интеграл.

Предположим, у нас есть набор данных (x,y), связанных друг с другом с помощью F-функции.

y=F(x)

F может быть любой функцией. Чтобы вычислить интеграл этим методом, мы складываем площадь под кривой между всеми последовательными точками.

Пример : вычисление интеграла функции

Нас просят вычислить интеграл ниже:

Выполните следующие шаги:

1. Установите значение dx, которое является высотой трапеций. Назовем его «х». и установите его 0,1 в этом примере.
2. Установите значения x от 0 до 2 с шагом в желаемое значение «h».
3. Вычислите значения y, используя формулу функции.

4. Введите « = 0,1/2*(B3+B2) » в ячейку C3 и нажмите Enter. Затем щелкните маленькое поле в правом нижнем углу ячейки и перетащите его в последнюю точку (ячейка C22).
5. Теперь сложите значение площади всех трапеций, используя функцию СУММ.

Примечание: Чем ниже dx, тем точнее будет результат.

Пример : Расчет площади под кривой, когда функция недоступна.

В этом примере мы хотим вычислить площадь под кривой. Как мы обсуждали ранее, интеграция — это путь.

Здесь ∆x непостоянна. Таким образом, мы не можем установить dx; вместо этого мы используем разницу между двумя последовательными значениями x в качестве высоты трапеции. Теперь давайте вычислим интеграл, выполнив следующие действия:

1. Введите « 0,5*(B3+B2)*(A3-A2) » в ячейку C34 и нажмите Enter.
2. Нажмите на маленькое поле в правом нижнем углу ячейки и перетащите его в ячейку C, которая является ячейкой, содержащей конечную точку.
3. Вычислите сумму сумм в столбце C.

Метод Симпсона для вычисления интеграла

Метод Симпсона предполагает, что площадь под кривой образуется путем сложения нескольких парабол. Прежде чем использовать этот метод, вы должны убедиться, что у вас есть нечетное количество точек данных.

Может быть полезно упомянуть, что метод Симпсона является более точным, чем метод трапеций для вычисления интеграла.

Если функция, связывающая y с x, равна y=f(x), формула для вычисления интеграла выглядит следующим образом:

Эта формула дает площадь трех последовательных точек в виде одной параболы. Чтобы вычислить интеграл, мы должны просуммировать площади под кривой для всех парабол. Итак, результирующая формула будет:

Теперь давайте воспользуемся ею для вычисления интеграла.

Пример : Мы хотим вычислить следующий интеграл.

Выполните следующие шаги:

1. Во-первых, мы должны преобразовать функцию в числа и установить dx (или h). Если у вас есть набор данных значений x и y, проверьте, постоянна ли разница между значениями x. Если это не так, вы можете рассчитать среднее значение ∆xs как «h».

2. Мы должны установить множители для каждого значения y. Первый и последний — 1. Введите 4 в ячейку C2 и 2 в ячейку C3.