Найти пределы пользуясь правилом Лопиталя — Студопедия.Нет
а) б)
Найти первые и вторые частные производные
Провести полное исследование функции и построить их график.
Вариант 7
1) Найти косинус угла между векторами и .
2) Коллинеарны ли векторы и , построенные по векторам и ?
3) Компланарны ли векторы , и ?
4) Вычислить площадь параллелограмма, построенного на векторах и .
5) Найти расстояние от точки до плоскости, проходящей через точки .
6) Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .
Исследовать кривую второго порядка и построить ее.
Вычислить.
где , .
9) Вычислить определитель
Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя)
а) б)
в) г) д)
13) Найти производные данных функций:
14) Найти и
а) у = б)
Найти производную указанного порядка.
Найти пределы пользуясь правилом Лопиталя
а) б)
Найти первые и вторые частные производные
Провести полное исследование функции и построить их график.
Вариант 8
1) Найти косинус угла между векторами и .
2) Коллинеарны ли векторы и , построенные по векторам и ?
3) Компланарны ли векторы , и ?
4) Вычислить площадь параллелограмма, построенного на векторах и .
5) Найти расстояние от точки до плоскости, проходящей через точки .
6) Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .
Исследовать кривую второго порядка и построить ее.
Вычислить.
где , .
9) Вычислить определитель
Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя)
а) б)
в) ; г) д)
13) Найти производные данных функций:
14) Найти и
а) у = б)
Найти производную указанного порядка.
Найти пределы пользуясь правилом Лопиталя
а) б)
Найти первые и вторые частные производные
Провести полное исследование функции и построить их график.
Вариант 9
1) Найти косинус угла между векторами и .
2) Коллинеарны ли векторы и , построенные по векторам и ?
3) Компланарны ли векторы , и ?
4) Вычислить площадь параллелограмма, построенного на векторах и .
5) Найти расстояние от точки до плоскости, проходящей через точки .
6) Написать уравнение плоскости, проходящей через точку перпендикулярно вектору .
Исследовать кривую второго порядка и построить ее.
Вычислить.
где , .
9) Вычислить определитель
Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
Найти все значения корня.
Найти пределы (не пользуясь правилом Лопиталя)
а) б)
в) г) д)
13) Найти производные данных функций:
14) Найти и
а) у = х2e–x б)
Добрый день с решением ((нужно вычислить пределы функций, не пользуясь правилом Лопиталя
13.
Всего ответов: 2
Посмотреть ответы
Похожие вопросы:
Алгебра, 28.02.2019 04:20
1. разложите на множители квадратный трехчлен: 1) х2 -4х-32 ; 2) 4х2 -15x + 9 . 2. решите уравнение: 1) х4 -8×2 -9 =0; 2) (х2-7х )/(х+2)=18/(х+2) 5. расстояние между двумя пристанями, равное 72 км, моторная под.. ка проходит по течению реки на 2 ч быстрее, чем
против течения. найдите скорость течения, если собственная скорость лодки рав“,” на 15 км/ч. 4.. число 4 является корнем уравнения 3х2 + ьх + 4 = 0. найдите значение ь и второй корень уравнения. 5. при каком значении а уравнение 2х2 -8х +
а = о имеет единственный корень?
Ответов: 4
Открыть
Алгебра, 28.02.2019 11:00
.(Когда теплоходи катер плывут по течению реки, то расстояние от пристани а до пристани в тепплоход проходит в 1.5 раза быстрее катера, причем катер каждый час отстает от теплохода на 8 км.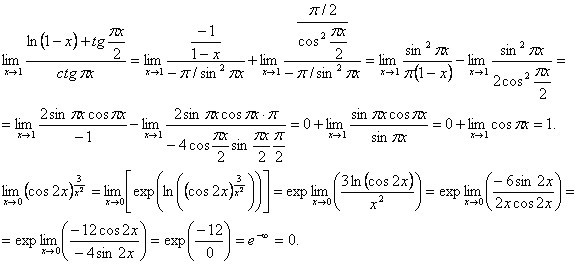 когда они плывут против течения, то
когда они плывут против течения, то
теплоход проходит путь от в до а в 2 раза быстрее катера. найти скорость течения реки и собственные скорости теплохода и катера.).
Ответов: 3
Открыть
Алгебра, 28.02.2019 12:40
Две шестеренки скреплены зубьями. большая шестеренка имеет 57 зубьев, а маленькая 38 зубьев. сколько оборотов сделает большая шестерная, когда зубья обеих шестерен займут первоночальное положение.
Ответов: 4
Открыть
Алгебра, 28.02.2019 14:00
Запишите утверждение на . языке: ..чтобы к числу прибавить разность 2-ух чисел ,можно сначала прибавить к нему уменьшаемое, а затем из полученной суммы вычесть выччетаемое.
Ответов: 2
Открыть
Алгебра, 28.02.2019 20:50
.(Велосипедист едит из одного города в другой со скоростью 10км/ч. если бы он ехал со скоростью 12 км/ч то приехал бы в конечный пункт на 4 ч раньше. какое расстояние преодолел велосипедист.).
Ответов: 2
Открыть
Алгебра, 01.03.2019 15:20
Предприниматель купил несколько подержанных автомобилей за 3500 долларов, а продал их за 5500 долларов заработав на этом 50 долларов за автомобиль. сколько автомобилей он продал?
сколько автомобилей он продал?
Ответов: 3
Открыть
Алгебра, 01.03.2019 16:00
Пасажирський поїзд проходить відстань на 10 км більше за 3 години, ніж товарний за 4.швидкість товариського поїзда на 20км/год, менше ніж швидкість пасажирського. знайти швидкість пасажирського.
Ответов: 2
Открыть
Алгебра, 01.03.2019 16:20
Вуравнении 2-4x+5y=0 выразите каждую переменную через другую
Ответов: 4
Открыть
Алгебра, 01.03.2019 18:00
Одна бригада рабочих асфальтировала 5 км 060 м шоссе, другая бригада на 2 км 280м больше. осталось покрыть асфальтом 965м шоссе. какой длины щоссе должны были асфальтировать эти бригады7
Ответов: 2
Открыть
Алгебра, 02.03.2019 03:10
Решите систему уравнений: {y-x=1 {(2y+1)(x-1)=xy+1 начало уже есть: {y=x+1 {2xy-2y+x-2=0 2(x+1)x-2(x+1)+x-2=0 а дальше как? !
Ответов: 3
Открыть
Алгебра, 02.03.2019 08:00
Обчисліть, користуючись відповідною формулою зведення: 1) cos45(градусов) 2) tg240(градусов) 3) sin 120(градусов) 4) ctg210(градусов) 5) cos150(градусов) 6)tg225(градусов) 7) sin 150(градусов) 8) ctg 240(градусов)
Ответов: 3
Открыть
Алгебра, 02. 03.2019 17:30
03.2019 17:30
Кусок стекла имеет форму квадрата. когда от него отрезали полосу шириной 20см его площадь стала равна 3500см в квадрате. найдите первоначальные размеры куска стекла.
Ответов: 4
Открыть
Вопросы по другим предметам:
Математика, 16.02.2020 22:10
Увеличь на 300 процентов число очень надо!!!…
Алгебра, 16.02.2020 22:10
В прямоугольном параллелепипеде abcda1b1c1d1 известны длины рёбер ab=6 ad=6 aa1=8 найдите синус угла между прямыми cc1 и ab1.
Желательно с рисунком!…
Другие предметы, 16.02.2020 22:10
это логический во…
Русский язык, 16.02.2020 22:10
Найдите одно односоставное и одно неполное предложение …
Геометрия, 16.02.2020 22:10
Из точки в плоскость провели две наклонные. Известно, что расстояние от этой точки до плоскости =6см. Разность проекций=12см. Найти проекции решить задачу Желательно с чертежом.…
Химия, 16.02.2020 22:09
Найдите массовую долю (%) соли в растворе полученном при смешении 200гр 10%-ного расвора соли с 300 г 20%-ного раствора той же соли.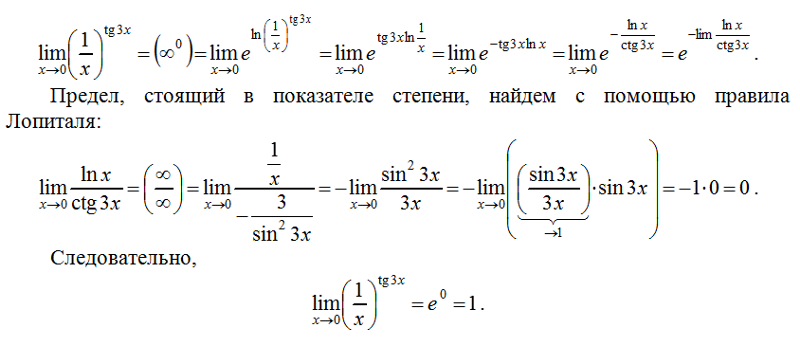 ..
..
Математика, 16.02.2020 22:09
Вычислите . Сделайте в столбик в тетради…
Химия, 16.02.2020 22:09
Химия
1) какова молекулярная масса глюкозы в атомных единицах массы?
2) масса молекулы какого вещества больше глюкозы или витамина c?
3) от чего зависит какой га…
Информатика, 16.02.2020 22:09
Задание по информатике…
Українська мова, 16.02.2020 22:09
Прочитай і спиши підкресли прізвища. Байки Леоніда Івановича Глібова, казки Івана Яковича Франка, вірші Платона Микитовича Воронька. 2.Поясни, чому слова написані з великої букви….
Другие вопросы
Предел с помощью лопиталя. Правила Лопиталя. Примеры решений. Правило Лопиталя: история и определение
Правило Лопиталя |
Правило
Лопиталя представляет
собой метод вычисления пределов,
имеющих неопределенность
типа или . Правило Лопиталя можно также применять к неопределенностям типа . Первые две неопределенности можно свести к типу или с помощью алгебраических преобразований. А неопределенности сводятся к типу с помощью соотношения Правило Лопиталя справедливо также и для односторонних пределов. |
Пример 1 |
Вычислить предел . Решение. Дифференцируя числитель и знаменатель, находим значение предела: |
Пример 2 |
Вычислить предел . Решение. Поскольку
прямая подстановка приводит к
неопределенности типа ,
применяем правило Лопиталя. |
Пример 3 |
Вычислить предел . Решение. Здесь мы имеем дело с неопределенностью типа . После простых преобразований, получаем |
Пример 4 |
Найти предел . Решение. Используя правило Лопиталя, можно записать |
Пример 5 |
Найти предел . Решение. Здесь мы встречаемся с неопределенностью типа . Обозначим . После логарифмирования получаем Соответственно, |
15. Правила Лопиталя*
Правила Лопиталя*
Швейцарский
математик Иоганн
I Бернулли (1667-1748)
после успешного окончания Базельского
университета, путешествуя по Европе, в
1690 году приезжает в Париж. В литературном
салоне философа Никола Мальбранша
(1638-1715) Иоганн знакомится с французским
математиком маркизом Гийомом Франсуа
Антуаном де Лопиталем (1661-1704). В ходе
оживленной беседы Лопиталь удивился,
как легко, “как бы играя”, юнец Бернулли
решал трудные задачи по новому исчислению.
Поэтому Лопиталь попросил прочитать
ему несколько лекций. Устные беседы
понравились Лопиталю, и он за приличный
гонорар стал получать материалы в
письменном виде. Заметим, что общеизвестное
теперь “правило Лопиталя” для раскрытия
неопределенностей также было передано
ему Иоганном. Уже в 1696 году появился
знаменитый трактат Лопиталя “Введение
в анализ бесконечно малых для понимания
кривых линий”. Вторая часть курса,
изложенного Иоганном I Бернулли, была
опубликована лишь в 1742 году и называлась
“Математические лекции о методе
интегралов и другие; написаны для
знаменитого маркиза Госпиталия; годы
1691-1692”.
Теорема (Коши). Пусть функции и непрерывны на , дифференцируемы на и . Тогда :
Доказательство. Рассмотрим функцию
Выберем так, чтобы выполнялись все условия теоремы Ролля, т.е. .
По теореме Ролля существует :
Первое правило Лопиталя
Определение. Пусть функции , непрерывны на , дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема.
Применим теорему Коши к отрезку , где . Существует :
и, значит,
Это и означает, что .
В случае, когда бесконечно, неравенство (1) заменяется на
в
зависимости от знака .
В остальном доказательство не меняется.
Второе правило Лопиталя
Определение. Пусть функции , непрерывны и дифференцируемы в , причем . Пусть . Тогда говорят, что отношение при представляет собой неопределенность вида .
Теорема. Если при указанных условиях существует
Доказательство. Пусть конечно. По выберем : в интервале выполняется неравенство
Определим функцию из условия
при . Применим к отрезку теорему Коши. Получим, что существует :
Для тех , для которых
Так как произвольно мало, то
В случае, когда , неравенство (2) заменяется на
а неравенство (4) – на неравенство
имеющим место при , достаточно близких к a в силу (3).
Аналогично рассматривается случай .
Решение пределов функции онлайн . Найти предельное значение функции либо функциональной последовательности в точке, вычислить предельное значение функции на бесконечности. определить сходимость числового ряда и многое другое можно выполнить благодаря нашему онлайн сервису – . Мы позволяем находить лимиты функций онлайн быстро и безошибочно. Вы сами вводите переменную функции и предел, к которому она стремится, анаш сервис проводит все вычисления за вас, выдавая точный и простой ответ. Причем для нахождения предела онлайн вы можете вводить как числовые ряды, так и аналитические функции, содержащие константы в буквенном выражении. В этом случае найденный предел функции будет содержать эти константы как постоянные аргументы в выражении. Нашим сервисом решаются любые сложные задачи по нахождению пределов онлайн , достаточно указать функцию и точку в которой необходимо вычислить предельное значение функции . Вычисляя пределы онлайн , можно пользоваться различными методами и правилами их решения, при этом сверяя полученный результат с решением пределов онлайн на www.сайт, что приведет с успешному выполнению задачи – вы избежите собственных ошибок и описок. Либо вы полностью можете довериться нам и использовать наш результат в своей работе, не затрачивая лишних усилий и времени на самостоятельные вычисления предела функции.
Мы позволяем находить лимиты функций онлайн быстро и безошибочно. Вы сами вводите переменную функции и предел, к которому она стремится, анаш сервис проводит все вычисления за вас, выдавая точный и простой ответ. Причем для нахождения предела онлайн вы можете вводить как числовые ряды, так и аналитические функции, содержащие константы в буквенном выражении. В этом случае найденный предел функции будет содержать эти константы как постоянные аргументы в выражении. Нашим сервисом решаются любые сложные задачи по нахождению пределов онлайн , достаточно указать функцию и точку в которой необходимо вычислить предельное значение функции . Вычисляя пределы онлайн , можно пользоваться различными методами и правилами их решения, при этом сверяя полученный результат с решением пределов онлайн на www.сайт, что приведет с успешному выполнению задачи – вы избежите собственных ошибок и описок. Либо вы полностью можете довериться нам и использовать наш результат в своей работе, не затрачивая лишних усилий и времени на самостоятельные вычисления предела функции. Мы допускаем ввод таких предельных значений, как бесконечность. Необходимо ввести общий член числовой последовательности и www.сайт вычислит значение предела онлайн на плюс или минус бесконечности.
Мы допускаем ввод таких предельных значений, как бесконечность. Необходимо ввести общий член числовой последовательности и www.сайт вычислит значение предела онлайн на плюс или минус бесконечности.
Одним из основных понятий математического анализа является лимит функции и предел последовательности в точке и на бесконечности, важно уметь правильно решать пределы . С нашим сервисом это не составит никакого труда. Производится решение пределов онлайн в течение нескольких секунд, ответ точный и полный. Изучение математического анализа начинается с предельного перехода , пределы используются практически во всех разделах высшей математики, поэтому полезно иметь под рукой сервер для решения лимитов онлайн , каковым является matematikam.ru.
Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость или .
Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость или .
Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя ». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений , Замечательные пределы . Методы решения пределов , Замечательные эквивалентности , где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.
Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.
Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.
Первое правило ЛопиталяРассмотрим функции , которые бесконечно малЫ в некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть .
Примечание : предел тоже должен существовать, в противном случае правило не применимо.
Что следует из вышесказанного?
Во-первых, необходимо уметь находить производные функций , и чем лучше – тем лучше =)
Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!
И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .
Вернёмся к Примеру 5 первой статьи о пределах , в котором был получен следующий результат:
К неопределённости 0:0 применим первое правило Лопиталя:
Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!
Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах :
На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции . После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).
Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные , следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам . Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.
Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности .
Второе правило ЛопиталяБрат-2 борется с двумя спящими восьмёрками . Аналогично:
Если существует предел отношения бесконечно больших в точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется .
При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется .
Примечание : предел должен существовать
Опять же, в различных практических примерах значение может быть разным , в том числе, бесконечным. Важно, чтобы была неопределённость .
Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить предел
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:
Таким образом, линейная функция более высокого порядка роста , чем логарифм с основанием бОльшим единицы ( и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её график является более пологим относительно того же «икса».
Пример 2
Вычислить предел
Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:
Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста , чем степенная функция с положительной степенью .
Похожие пределы встречаются в ходе полного исследования функции , а именно, при нахождении асимптот графиков . Также замечаются они и в некоторых задачах по теории вероятностей . Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.
Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел .
В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел .
Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:
Для разминки разберёмся с парой небольших воробушков:
Пример 3
Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .
Рассмотренный пример разруливается и через замечательные пределы , похожий случай разобран в конце статьи Сложные пределы .
Пример 4
Вычислить предел по правилу Лопиталя
Это пример для самостоятельного решения. Нормально пошутил =)
Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:
Пример 5
Вычислить предел, используя правило Лопиталя
Напрашивается применение замечательной эквивалентности , но путь жёстко предопределён по условию:
После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения . Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.
Пример 6
Вычислить предел, используя правило Лопиталя
Пример 7
Вычислить предел, используя правило Лопиталя
Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.
А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.
И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена .
Пример 8
Вычислить предел, используя правило Лопиталя
Поехали:
Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .
Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов . Давайте для проформы ещё один:
Пример 10
Вычислить предел функции, используя правило Лопиталя
На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:
Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость тоже не сопротивляется превращению в или :
Пример 11
Вычислить предел функции с помощью правила Лопиталя
Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций . Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.
Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:
Готово.
Исходный предел можно было попытаться свести к двум бубликам:
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.
Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».
В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен.
- Правило Лопиталя и раскрытие неопределённостей
- Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
- Раскрытие неопределённостей вида “ноль умножить на бесконечность”
- Раскрытие неопределённостей видов “ноль в степени ноль”, “бесконечность в степени ноль” и “один в степени бесконечность”
- Раскрытие неопределённостей вида “бесконечность минус бесконечность”
Правило Лопиталя и раскрытие неопределённостей
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей значительно упрощается с помощью правила Лопиталя.
Суть правила Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Вообще, под правилами Лопиталя понимаются несколько теорем, которые могут быть переданы в следующей одной формулировке.
Правило Лопиталя . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки , за исключением, может быть, самой точки , причём в этой окрестности
(1)
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
В равенстве (1) величина , к которой стремится переменная, может быть либо конечным числом, либо бесконечностью, либо минус бесконечностью.
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов “ноль делить на ноль” и “бесконечность делить на бесконечность”
Пример 1. Вычислить
x =2 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:
Пример 2. Вычислить
Вычислить
Решение. Подстановка в заданную функцию значения x
Пример 3. Вычислить
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:
Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Если предел отношения производных представляет собой неопределённость вида 0/0 или ∞/∞, то можно снова применить правило Лопиталя, т.е. перейти к пределу отношения вторых производных, и т.д.
Пример 5. Вычислить
Решение. Находим
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя . Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Правило Лопиталя: история и определение
На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли . Сформулировал его швейцарский математик Иоганн Бернулли , а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.
Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.
Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:
Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.
Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.
Кстати! Для наших читателей сейчас действует скидка 10% на
Раскрытие неопределенностей по правилу Лопиталя
В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0 . Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.
Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0 :
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0 :
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:
Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:
Теперь перейдем к примерам.
Пример 1
Найти предел по правилу Лопиталя:
Пример 2
Вычислить с использованием правила Лопиталя:
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а , то правило Лопиталя можно применять несколько раз.
Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам . Они с радостью помогут разобраться в тонкостях решения. x=lne=1
x=lne=1
в певом задании непонятен числитель
Ответ
Ответ разместил: Alrksanr
lim (при x–>0) (корень из (1+x) – корень из (1-x))/3x = {0/0} — неопределённость.
Домножим числитель и знаменатель на сопряженное выражение к числителю —
(корень из (1+x) + корень из (1-x)). Получаем
lim (x–>0) 2x/(3x* (корень из (1+x) + корень из (1-x))) = 1/3
Ответ
Ответ разместил: сема891
lim(x->0) (1 – √(1-x))/sin(3x)
Умножаем и делим на сопряженное. Я запишу отдельно.
Числитель:
(1 – √(1-x))(1 + √(1-x)) = 1 – (1-x) = x
Знаменатель:
sin(3x)(1 + √(1-x))
Теперь с Замечательного предела решаем:
lim(x->0) x/sin(3x) = 1/3
И остается
lim(x->0) 1/(1 + √(1-x)) = 1/(1 + √(1-0)) = 1/(1+√1) = 1/2.
Все вместе
1/3*1/2 = 1/6 – ЭТО ОТВЕТ
Ответ
Ответ разместил: danchik56
не знаю не знаю не знаю
+))+))+))+))+))+))+))++))+))+++))+)))+_))
Ответ
Ответ разместил: karabanovaann
Lim sin(x-1)/(x^2-1)=1/2
Ответ
Ответ разместил: Den2891
В решении использовался первый замечательный предел
lim sinx/x =1
x->0
его доказательство есть в интернете
Другие вопросы по: Математика
Путешественники по африке 3/7всего намеченного пути проехали на верблюдах, 7/12 оставшегося пути-на автомобиле, а затем на плоту спускались по реке. какую часть всего пути заняло п…
какую часть всего пути заняло п…
Опубликовано: 01.03.2019 09:10
Ответов: 1
Як ви розумієте віслів екологія мови…
Опубликовано: 02.03.2019 13:20
Ответов: 3
Скакими из перечисленных ниже веществ взаимодействует раствор h3so4: ca(oh)2,cu, sio2 ,bacl2 ….
Опубликовано: 03.03.2019 06:10
Ответов: 3
Как 0,25+1цел.35 шестидесятых (60) =…
Опубликовано: 04.03.2019 11:00
Ответов: 3
Hcl+zn- расставить коэффициенты и произвести реакцию обмена…
Опубликовано: 04.03.2019 12:10
Ответов: 2
Периметр четырехугольника abcd равен 17см, ab=5см, bc=6см, cd=ad. найди длину стороны ad….
Опубликовано: 06.03.2019 20:00
Ответов: 3
Популярные вопросы
Относительная плотность паров углеводорода по водороду равна 41. массовая доля водорода в нем равна 12,2%. выведите молекулярную формулу углеводорода….
массовая доля водорода в нем равна 12,2%. выведите молекулярную формулу углеводорода….
Опубликовано: 02.03.2019 02:40
Ответов: 2
Впарке посадили клены и дубы, при чем на каждые 4 клена приходится 1 дуб. сколько % от всех посаженных деревьев составляют клены. сколько всего посадили деревьев, если кленов 480….
Опубликовано: 02.03.2019 11:10
Ответов: 3
Деловое эссе на тему загрязнение воздуха…
Опубликовано: 03.03.2019 12:00
Ответов: 2
Составьте гомолог пентановой(валериановой) кислоты…
Опубликовано: 03.03.2019 13:40
Ответов: 1
Запишите ,как называется : 1)десятая часть сантиметра ,2)десятая часть децеметра ,3) десятая часть метра ,4)тысячная часть тонны,5)десятая часть килограмма ,6)шестидесятая часть ми…
Опубликовано: 03.03.2019 16:40
Ответов: 2
В10 одинаковых банках 16кг мёда сколько килограммов мёда в 20 таких банках?. ..
..
Опубликовано: 03.03.2019 18:10
Ответов: 2
Жизнь наша есть ( что иное как стремление к добру.( иной не умел делать того что он умел. самое большое счастье было в том что ( кто другой ,а именно он, тёма первый увидел что цве…
Опубликовано: 04.03.2019 10:10
Ответов: 2
2. что позволило первобытному человеку пережить ледниковый период?…
Опубликовано: 06.03.2019 17:10
Ответов: 2
Решите уравнение: (200+20*a): 6=60…
Опубликовано: 06.03.2019 22:10
Ответов: 3
Какова высота бетонной стены, производящей на 440кпа? (ответ по формулам и пояснение)…
Опубликовано: 07.03.2019 16:00
Ответов: 1
Больше вопросов по предмету: Математика Случайные вопросы
Найти пределы функций, не пользуясь правилом лопиталя
Ответ
Ответ разместил: gilfanovar01
ответ ответ ответ ответ ответ ответ
Ответ
Ответ разместил: Kepka229
4*(-1)+3*(1)+2(-1)+1=-2
Ответ
Ответ разместил: ученикB
Две дроби в последнем выражении в пределе дают 1 (первый замечательный предел). x=lne=1
x=lne=1
в певом задании непонятен числитель
Ответ
Ответ разместил: nyk156
Ответ
Ответ разместил: гоша206
Ответ
Ответ разместил: keril936
lim (при x–>0) (корень из (1+x) – корень из (1-x))/3x = {0/0} — неопределённость.
Домножим числитель и знаменатель на сопряженное выражение к числителю —
(корень из (1+x) + корень из (1-x)). Получаем
lim (x–>0) 2x/(3x* (корень из (1+x) + корень из (1-x))) = 1/3
Ответ
Ответ разместил: AkLeAfAr
lim(x->0) (1 – √(1-x))/sin(3x)
Умножаем и делим на сопряженное. Я запишу отдельно.
Числитель:
(1 – √(1-x))(1 + √(1-x)) = 1 – (1-x) = x
Знаменатель:
sin(3x)(1 + √(1-x))
Теперь с Замечательного предела решаем:
lim(x->0) x/sin(3x) = 1/3
И остается
lim(x->0) 1/(1 + √(1-x)) = 1/(1 + √(1-0)) = 1/(1+√1) = 1/2.
Все вместе
1/3*1/2 = 1/6 – ЭТО ОТВЕТ
Ответ
Ответ разместил: IUcenhik
не знаю не знаю не знаю
+))+))+))+))+))+))+))++))+))+++))+)))+_))
Ответ
Ответ разместил: мирахуснатдинова
Объяснение:
ответ приложен
Другие вопросы по: Математика
Найдите элемент iv группы, образующий летучее водородное соединение, в котором массовая доля элемента составляет 75 %, а в высшем оксиде массовая доля элемента равна 27,3%.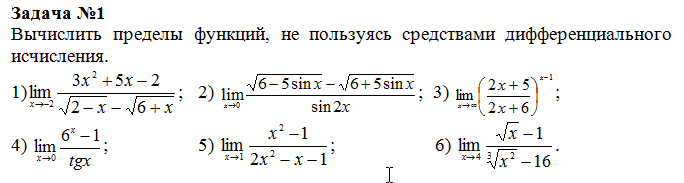 …
…
27.02.2019 04:30
Ответов: 2
Cлова, написание которых подсказывает их…
27.02.2019 17:50
Ответов: 3
Если в окружность вписан правильный треугольник площадью 9√3 и в этот треугольник вписана окружность, то площадь полученного кольца равна?…
01.03.2019 12:30
Ответов: 1
=)) в ветхом завете сказано : я убью его и отрублю голову му, и узнают все что есть бог в израиле кому пернадлежат эти слова ? протиф кого они направлены?…
01.03.2019 23:00
Ответов: 3
Определите скорость движения спутника вокруг земли по круговой орбите на высоте, равной радиусу земли, если первая космическая скорость у поверхности земли равна 8 км/с. радиус зем…
01.03.2019 23:10
Ответов: 1
За две недели дрессировок костя потратил 28 кусков сахара. это треть тех запасов сахара, которые у него были . сколько кусков сахара у кости осталось? на сколько недель дрессировки. ..
..
02.03.2019 13:50
Ответов: 1
Знаешь правильный ответ?
Найти пределы функций, не пользуясь правилом лопиталя…
Популярные вопросы
Сторони трикутника дорівнюють a, b,c. знайдіть сторони іншого трикутника, вершини якого є серединами сторін даного трикутника, якщо a=8см, b=10см, c=12см….
01.03.2019 03:50
Ответов: 1
Представить выражение в виде многочлена стандартного вида(x+y)во второй степени…
01.03.2019 09:50
Ответов: 3
Из 675г шерсти связали три одинаковых шарфа. сколько можно связать таких шарфов из 3кг шерсти?…
03.03.2019 03:40
Ответов: 1
Точки а и а1 имеют противоположные координаты. найдите эти координаты если аа1=4.8?…
03.03.2019 22:30
Ответов: 3
Найдите а1 и q прогрессии ( а n) . если а1+а4 =30. а 2+а3=10…
04.03.2019 01:20
Ответов: 2
Вчём смысл заглавия человек на часах. ..
..
04.03.2019 06:50
Ответов: 1
Решить . тракторный завод выполнил 0,8 заказа. чтобы полностью выполнить заказ, завод должен выпустить ещё 48 тракторов. сколько тракторов должен выпустить завод для выполнения зак…
07.03.2019 15:00
Ответов: 1
Передача данных через adsl- соединение заняла 2 минуты за это время был передан файл размер которого 3 750 кбайт. определите минимальную скорость (бит/c.) при которой такая передач…
08.03.2019 01:10
Ответов: 3
1. сколько штрихов на один миллиметров нанесено на дифракционную решетку, если при освещении монохроматическим светом с длиной волны 500 мкм, максимальный порядок спектра наблюдаем…
08.03.2019 04:20
Ответов: 1
Просклонять по падежам пятьсот сорок два растения…
08.03.2019 08:20
Ответов: 2
Больше вопросов по предмету: Математика Случайные вопросы
Поиск пределов и односторонних пределов
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 … 5 6 7 8 9 10 11 12 13 … 41 42 Следующая →
Исчисление 2 Помощь » Ограничения » Нахождение пределов и односторонние пределы
Возможные ответы:
Правильный ответ:
Объяснение:
Для оценки этого предела необходимо использовать правило Лопиталя. Однако, чтобы убедиться, что это правило можно использовать, вы должны сначала убедиться, что оно или форма.
Однако, чтобы убедиться, что это правило можно использовать, вы должны сначала убедиться, что оно или форма.
Это неопределенная форма, поэтому теперь мы можем использовать правило Лопиталя, взяв производную от числителя и знаменателя отдельно:
Опять же, мы приходим к неопределенной форме снова используйте правило Лопиталя:
Опять же, мы приходим к неопределенной форме , поэтому нам нужно снова использовать правило Лопиталя:
Это один из вариантов ответа.
Отчет о ошибке
Оцените следующий предел:
Возможные ответы:
Объяснение:
Чтобы оценить предел, сначала мы должны определить, правосторонний он или левосторонний; знак «плюс» «показатель степени» на 5 указывает, что он правосторонний или что мы приближаемся к значениям, немного большим, чем 5. Теперь мы используем соответствующую функцию в кусочной функции для оценки предела, функция является функцией для x значения больше или равны 5. Когда мы оцениваем предел путем замены,
Когда мы оцениваем предел путем замены,
Сообщить об ошибке
Оцените следующий предел:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы оценить предел, мы должны определить, какая часть кусочной функции соответствует числу, к которому мы приближаемся. Поскольку x приближается к положительной бесконечности, мы должны использовать функцию, соответствующую значениям x больше нуля; когда мы напрямую подставляем, мы получаем .
Отчет о ошибке
Оцените следующий предел:
Возможные ответы:
Объяснение:
Чтобы оценить предел, мы сначала должны определить, является ли предел правосторонним или левосторонним. Отрицательный знак «показатель степени» у 3 указывает на то, что мы приближаемся к 3 слева или приближаемся к числам чуть меньше 3. Следовательно, мы должны оценить предел, используя часть кусочной функции, соответствующую числам, меньшим или равным 3.
Следовательно, мы должны оценить предел, используя часть кусочной функции, соответствующую числам, меньшим или равным 3.
Когда мы пытаемся оценить предел обычными методами, мы получаем неопределенный вид . Итак, мы должны использовать правило Лопиталя для решения предела, который гласит, что
для g(a) и h(a) равны нулю.
Теперь найдем производные числителя и знаменателя и оценим предел:
Производные были найдены по следующим правилам:0005
Оцените лимит:
Возможные ответы:
Правильный ответ:
Объяснение:
В этом уравнении нет предельной ситуации (как в знаменателе), поэтому мы можем просто подставить значение, к которому x приближается, к пределу и решить:
Сообщить об ошибке
Оценить предел:
Возможные ответы:
Правильный ответ:
Объяснение:
В этом уравнении нет предельной ситуации (как в знаменателе), поэтому мы можем просто подставить значение, к которому x приближается, к пределу и решить:
Сообщить об ошибке
Оценить предел:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель. Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель будет равен нулю, когда x=0; поэтому мы пытаемся исключить знаменатель путем факторизации. Когда знаменатель больше не равен нулю, мы можем продолжить подставлять значение x в оставшееся уравнение.
Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель будет равен нулю, когда x=0; поэтому мы пытаемся исключить знаменатель путем факторизации. Когда знаменатель больше не равен нулю, мы можем продолжить подставлять значение x в оставшееся уравнение.
Сообщить об ошибке
Оценить предел:
Возможные ответы:
Правильный ответ:
4
Объяснение:
В этом уравнении нет предельной ситуации (как в знаменателе), поэтому мы можем просто подставить значение, к которому x приближается, к пределу и решить:
Сообщить об ошибке
Оценить предел:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель. Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель не будет равен нулю, когда x=0; поэтому мы продолжаем вставлять значение x во все уравнение.
Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель не будет равен нулю, когда x=0; поэтому мы продолжаем вставлять значение x во все уравнение.
Сообщить об ошибке
Оценить лимит:
Возможные ответы:
Правильный ответ:
Пояснение:
Предельной ситуацией в этом уравнении будет знаменатель. Подставьте значение, к которому x приближается, в знаменатель, чтобы увидеть, будет ли знаменатель равен 0. В этом вопросе знаменатель не будет равен нулю, когда x=1001; поэтому мы продолжаем вставлять значение x во все уравнение.
Сообщить об ошибке
← Предыдущий 1 2 … 5 6 7 8 9 10 11 12 13 … 41 42 Следующий →
Уведомление об авторских правах
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
Исчисление I Примечания, Раздел 4-5
Правило Бернулли | Что это дает нам возможность делать | Правило Лопиталя | Неопределенные продукты | Неопределенный Отличия | Проверять Концепции
название этого урока действительно должно быть:
Неопределенные формы и Правило Бернулли
Правило Лопиталя было впервые опубликовано
французский дворянин, маркиз де Л’Опиталь в первом в истории
опубликовал учебник по математическому анализу “ Analyze des infiniment petits”. pour l’intelligence des lignes courbes” в 1692 г. Но
известное правило, которое было опубликовано в этой книге, было преподнесено Лопиталю
его учитель Иоганн Бернулли в 169 г.1. Бернулли — первооткрыватель
правило. Во введении к своему учебнику Лопиталь признает
своим долгом перед Лейбницем, Якобом Бернулли и Иоганном Бернулли, но
L’Hpital считал представленные им основы своими собственными идеями.
Вот часть этого введения:
pour l’intelligence des lignes courbes” в 1692 г. Но
известное правило, которое было опубликовано в этой книге, было преподнесено Лопиталю
его учитель Иоганн Бернулли в 169 г.1. Бернулли — первооткрыватель
правило. Во введении к своему учебнику Лопиталь признает
своим долгом перед Лейбницем, Якобом Бернулли и Иоганном Бернулли, но
L’Hpital считал представленные им основы своими собственными идеями.
Вот часть этого введения:
” Я должен признаться себе очень многим обязан трудам господ Бернулли, но особенно те из настоящего профессора в Гронингене [Иоганн Бернулли] , как освободившие своими открытиями как у г-на Лейбница. их собственные я откровенно возвращаю их. Я должен здесь по справедливости
(как это сделал сам г-н Лейбниц в Journal des Scavans за август,
1694), что ученый сэр Исаак Ньютон также открыл нечто
как “Дифференциальное исчисление”, как видно из его превосходного
Принципы, впервые опубликованные в 1687 году, которые почти полностью зависят
об использовании указанного исчисления. |
Иоганн Бернулли 1667-1748, Базель Швейцария | Маркиз де L’Hpital 1661-1704, Париж Франция |
Правило Лопиталя и что это такое Дает нам возможность делать
До этого момента в нашем курсе у нас было
не удалось найти пределы всех типов выражений. Есть
несколько неопределенных
формы, которые заставили нас попытаться найти алгебраические
упрощения для. Без этих упрощений мы не могли
рассчитать эти пределы. Правило Лопиталя позволяет теперь вычислить
пределы для рациональных выражений с четырьмя различными неопределенными
формы. Вот правило Лопиталя: 9.0005
Вот правило Лопиталя: 9.0005
Когда мы рассматриваем предел: , мы можем столкнуться с несколькими различными ситуациями. Они показаны в таблице ниже:
| Состояние | Расчет лимита |
| Невозможно рассчитать . Конечно, деление на ноль невозможно. Предел может быть, а может и не быть. существует. | |
| Невозможно рассчитать . Здесь числитель и знаменатель вовлечены в войну. Если числитель выигрывает, то предел может стать положительным или отрицательным бесконечность. Если выиграет знаменатель, то предел может дойти до нуля. Мы не могу определить предел. Мы не можем сказать, существует ли предел или не существует. | |
| Невозможно рассчитать . Опять же, деление на ноль невозможно. Предел может быть, а может и не быть. существует. | |
| Это конечно может быть рассчитано и |
Правило Лопиталя
Правило Лопиталя применимо к первым двум
из вышеперечисленных ситуаций. Вот правило Лопиталя:
Вот правило Лопиталя:
Если у вас есть одна из двух прерывистых форм: или , то , если предел справа существует или равен . |
Вот несколько примеров, иллюстрирующих правило.
Пример 1
| Найти | Данная проблема. (Задача №8 в тексте) Обратите внимание, что неопределенная форма, которую мы имеем, — это форма , поэтому можно использовать правило Лопиталя. |
| Применяем правило Лопиталя, а затем мы можем оценить предел. |
Пример 2: В этом Например, мы видим, что правило Лопиталя можно применять повторно .
| Найти . | Данная проблема. (Задача №16 в тексте) Обратите внимание, что
неопределенной формой, которую мы имеем, является форма , поэтому можно использовать правило Лопиталя. |
| Здесь мы применяем правило Лопиталя и дифференцируем числитель и знаменатель отдельно. Но заметьте, что это по-прежнему ведет нас к неопределенной форме. | |
| Мы применяем правило Лопиталя во второй раз, и на этот раз, после раздельного дифференцирования числителя и знаменателя получаем придумать предел, который мы можем вычислить. Успех. |
Неопределенные продукты
Еще одна предельная проблема, которую мы можем захотеть решить. быть в состоянии рассчитать, когда и . Здесь опять идет война между нулем и бесконечностью, как они ведутся умноженные друг на друга. Мы обнаруживаем, что, проявив немного творчества, мы можем здесь также используйте правило Лопиталя. Мы можем думать о них как о: . А также так как мы видим, что у нас есть неопределенная форма и Можно использовать правило Лопиталя. Итак, «новая» неопределенная форма, Правило Лопиталя можно использовать в следующих случаях:
Пример 3 :
| Найти | Данная проблема. (Задача №22 в тексте). (Задача №22 в тексте). |
| Выполним некоторые алгебраические действия, чтобы получить предел в форму, к которой можно было бы применить L’Hopital. | |
| форма | Теперь мы делаем очень важный шаг и проверьте, находится ли этот предел в одной из неопределенных форм, которые Необходимо применять правило Лопиталя. И мы видим, что это из форма . |
| Теперь применим правило Лопиталя 3 раз. |
Неопределенный Отличия
Еще одна предельная проблема, которую мы можем захотеть решить. быть в состоянии рассчитать, когда и . Мы здесь еще одна война между двумя функциями. Используя алгебру и замены, это также может быть преобразовано в частное форма, которая дает нам одну из двух форм или .
Пример 4:
| Найти | Данная проблема. (Задача №28 в тексте). (Задача №28 в тексте). |
| Сначала мы используем некоторые тригонометрические тождества, чтобы сделать эти замены. | |
| Здесь мы используем общий знаменатель поставить выражение в 1 отношение. | |
| Форма | Теперь проверяем, находится ли он в одном из формы, к которым относится L’Hopital. |
| Теперь применим правило Лопиталя один раз, и мы успешно рассчитали лимит! |
Неопределенные формы и правило Лопиталя
Лопиталь Правило @ Platonic Realms
2.8: Использование производных для оценки пределов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5309
- Мэтью Боелкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Цели обучения
В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами:
- Как можно использовать производные, чтобы помочь нам оценить неопределенные пределы формы 0 0 ?
- Что значит сказать, что \lim_{x→∞} f (x) = L и \lim_{x→a} f (x) = ∞?
- Как производные могут помочь нам в оценке неопределенных пределов формы ∞ ∞ ?
Поскольку дифференциальное исчисление основано на определении производной, а определение производной включает предел, в определенном смысле все исчисление опирается на пределы. 2\).
2\).
Конечно, мы изучили множество различных методов оценки пределов, вытекающих из определения производной, и включили большое количество сокращенных правил, которые позволяют нам быстро и легко оценивать эти пределы. В этом разделе мы переворачиваем ситуацию с ног на голову: вместо использования пределов для оценки производных мы исследуем, как использовать производные для оценки определенных пределов. В этой теме будут объединены несколько различных идей, включая ограничения, сокращения производных, локальную линейность и аппроксимацию касательной. 92 – 1\). Найдите локальные линеаризации \(f\) и \(g\) в точке \(a = 1\) и назовите эти функции \(L_f (x)\) и \(L_g(x)\) соответственно.
 Как вы думаете, какое значение имеет \(\lim _{x→1} h(x)\)?
Как вы думаете, какое значение имеет \(\lim _{x→1} h(x)\)?Использование производных для оценки неопределенных пределов формы \(\frac{0}{0}\)
Фундаментальная идея действия предварительного просмотра \(\PageIndex{1}\) – мы можем оценить неопределенный предел формы 0 0 путем замены каждого из числителя и знаменателя их локальными линеаризациями в интересующей точке — можно обобщить таким образом, чтобы мы могли легко оценивать широкий диапазон пределов. Начнем с предположения, что у нас есть функция \(h(x)\), которую можно записать в виде \(h(x) = \frac{f (x)}{g(x)}\), где \( f\) и \(g\) дифференцируемы в точке \(x = a\) и для которых \(f (a) = g(a) = 0\). Мы заинтересованы в том, чтобы найти способ оценить неопределенный предел, заданный \(\lim_{x→a} h(x)\).
Рисунок \(\PageIndex{1}\): Слева графики f и g вблизи значения a, а также их аппроксимации касательной L_f и L_g при x = a. Справа увеличение точки a и четырех графиков.
На рисунке \(\PageIndex{1}\) мы видим наглядное представление ситуации с такими функциями \(f\) и \(g\). В частности, мы видим, что и \(f\), и \(g\) имеют х-пересечение в точке, где \(х = а\). Кроме того, поскольку каждая функция дифференцируема, каждая из них локально линейна, и мы можем найти их соответствующие аппроксимации касательной \(L_f\) и \(L_g\) в точке \(x = a\), которые также показаны на рисунке . Поскольку нас интересует предел f (x) g(x) при x → a, индивидуальное поведение \(f (x)\) и \(g(x)\) при \(x → a\) являются ключевыми для понимания. Здесь мы используем тот факт, что каждая функция и ее аппроксимация касательной становятся неразличимы при \(x → a\). Во-первых, давайте вспомним, что
\[L_f (x) = f'(a)(x – a) + f (a) и L_g(x) = g'(a)(x – a) + g(a).\]
Важное замечание, которое мы делаем, заключается в том, что при переходе к пределу, поскольку x становится сколь угодно близким к a, мы можем заменить f на L_f и заменить g на L_g, и, таким образом, мы наблюдаем, что
\[\lim_{x→a} f (x) g(x) = \lim_{x→a} L_f (x) L_g(x) = \lim_{x→a} f'(a)(x − a) + f (a) g'(a )(x − a) + g(a) . \]
\]
Далее мы помним ключевое фундаментальное предположение: что и \(f (a) = 0\), и \(g(a) = 0\), поскольку именно это делает первоначальный предел неопределенным. Подставляя эти значения вместо \(f (a)\) и \(g(a)\) в приведенном выше пределе, мы теперь имеем
\[\lim_{x→a} f (x) g(x) = \lim_{x→a} f'(a)(x − a) g'(a)(x − a) = \lim_ {x→a} f'(a) g'(a) ,\]
где последнее равенство выполняется, поскольку x приближается (но не равно) a, поэтому x−a x−a = 1. Наконец, отметим что f'(a) g'(a) постоянна относительно \(x\), и, таким образом,
\[\lim_{x→a} \dfrac{f (x)}{g(x)} = \dfrac{f'(a)}{g'(a)}.\]
Мы, конечно, неявно сделали предположение, что \(g'(a) \neq 0\), которое существенно для общий предел, имеющий значение f'(a) g'(a) . Мы резюмируем нашу работу формулировкой правила Лопиталя, которое является формальным названием показанного нами результата.
Правило Лопиталя
Пусть \(f\) и \(g\) дифференцируемы в точке \(x = a\), и предположим, что \(f (a) = g(a) = 0\) и что \(g'(a) \neq 0\). Тогда
Тогда
\[\lim_{x→a} \dfrac{f (x)}{g(x)} = \dfrac{f'(a)}{g'(a)}.\]
На практике , мы обычно работаем с несколько более общей версией правила Лопиталя, которое утверждает, что (при тех же предположениях, что и в приведенном выше правиле в рамке, и при дополнительном предположении, что g’непрерывно в точке x = a) \lim_{x→a} f (x) g(x) = \lim_{x→a} f'(x) g'(x) , если существует правый предел. 94 + 1}{ 2x} = \dfrac{6}{2} = 3. \]
Имея возможность заменить числитель и знаменатель их соответствующими производными, мы часто переходим от неопределенного предела к тому, значение которого мы можем легко определить.
Activity \(\PageIndex{2}\)
Оцените каждое из следующих ограничений. Если вы используете правило Лопиталя, укажите, где оно использовалось, и убедитесь, что его гипотезы соблюдены, прежде чем применять его.
- \(\lim_{x→0} \dfrac{ \ln(1 + x)}{x}\) 9{х-1}}\)
- \(\lim_{x→0} \dfrac{\sin(x) – x}{\cos(2x) – 1}\)
Хотя правило Лопиталя можно применять совершенно алгебраическим способом, важно помнить, что происхождение правила графическое: основная идея состоит в том, что наклоны касательных линий к f и g в точке x = a определяют значение предела f (x) g(x) при \(x → a\). Мы видим это на рисунке \(\PageIndex{2}\), который является модифицированной версией рисунка \(\PageIndex{1}\), где из сетки видно, что f'(a) = 2 и g’ (a) = −1, поэтому по правилу Лопиталя \lim_{x→a} f (x) g(x) = f'(a) g'(a) = 2 −1 = −2. Действительно, мы наблюдаем, что значение предела имеет не тот факт, что f и g обе стремятся к нулю, а скорее скорость, с которой каждая из них приближается к нулю, что определяет значение предела. Это хороший способ вспомнить, что гласит правило Лопиталя: если f (a) = g(a) = 0, предел f (x) g(x) при x → a определяется отношением наклоны f и g при x = a.
Мы видим это на рисунке \(\PageIndex{2}\), который является модифицированной версией рисунка \(\PageIndex{1}\), где из сетки видно, что f'(a) = 2 и g’ (a) = −1, поэтому по правилу Лопиталя \lim_{x→a} f (x) g(x) = f'(a) g'(a) = 2 −1 = −2. Действительно, мы наблюдаем, что значение предела имеет не тот факт, что f и g обе стремятся к нулю, а скорее скорость, с которой каждая из них приближается к нулю, что определяет значение предела. Это хороший способ вспомнить, что гласит правило Лопиталя: если f (a) = g(a) = 0, предел f (x) g(x) при x → a определяется отношением наклоны f и g при x = a.
Рисунок \(\PageIndex{2}\) : Две функции f и g, удовлетворяющие правилу Лопиталя.
Упражнение \(\PageIndex{3}\)
В этом упражнении мы графически рассуждаем по следующему рисунку, чтобы оценить пределы отношений функций, о которых известна некоторая информация.
Рисунок \(\PageIndex{3}\): Три графика, на которые есть ссылки в вопросах задания \(\PageIndex{3}\).
- Используйте левый график для определения значений f (2), f'(2), g(2) и g'(2). Затем оцените lim x→2 f (x) g(x) .
- Используйте средний график, чтобы найти p(2), p 0 (2), q(2) и q 0 (2). Затем определите значение lim x→2 p(x) q(x) .
- Используйте правый график для вычисления r(2), r 0 (2), s(2), s 0 (2). Объясните, почему вы не можете определить точное значение lim x→2 r(x) s(x) без дополнительной информации, но можете определить знак limx→2 r(x) s(x) . Кроме того, укажите, каким будет знак предела, с обоснованием. С
Пределы, включающие ∞
Понятие бесконечности, обозначаемое ∞, естественным образом возникает в исчислении, как и в большей части математики. Важно с самого начала отметить, что ∞ — это понятие, а не само число L_f. Действительно, понятие ∞ естественным образом вызывает идею пределов. Рассмотрим, например, функцию f (x) = 1 x , график которой изображен на рисунке \(\PageIndex{4}\). Заметим, что x = 0 не равно
Заметим, что x = 0 не равно
Рисунок \(\PageIndex{4}\): График f (x) = 1 x .
в области определения f , поэтому естественно задаться вопросом, что происходит при x → 0. При x → 0 + мы наблюдаем, что f (x) неограниченно возрастает. То есть мы можем сделать значение f (x) сколь угодно большим, приближая x все ближе и ближе (но не равным) к 0, сохраняя при этом x > 0. Это хороший способ подумать о том, что представляет собой бесконечность: количество стремится к бесконечности, если нет единственного числа, которому количество всегда меньше. Напомним, что когда мы пишем \lim_{x→a} f (x) = L, это означает, что мы можем сделать f (x) как можно более близким к L, взяв x достаточно близко (но не равным) к a. Таким образом, мы расширяем это обозначение и язык, чтобы включить возможность того, что либо L, либо a могут быть ∞. Например, для f (x) = 1 x мы теперь пишем lim x→0 + 1 x = ∞, что означает, что мы можем сделать 1 x сколь угодно большим, взяв x достаточно близко (но не равным) равным 0. Аналогичным образом мы естественно пишем \lim_{x→∞} 1 x = 0, поскольку мы можем сделать 1 x настолько близким к 0, насколько нам хотелось бы, взяв x достаточно большим (т. е. позволяя x увеличить без границ). В общем, мы понимаем обозначение \lim_{x→a} f (x) = ∞ как означающее, что мы можем сделать f (x) сколь угодно большим, взяв x достаточно близко (но не равным) к a, и обозначение \lim_{x→∞} f (x) = L означает, что мы можем сделать f (x) как можно ближе к L, взяв x достаточно большим. Это обозначение применимо к левым и правым пределам, плюс мы также можем использовать пределы, включающие −∞. Например, возвращаясь к рисунку \(\PageIndex{4}\) и f (x) = 1 x , мы можем сказать, что lim x→0 − 1 x = −∞ и limx→−∞ 1 x = 0. Наконец, мы пишем \lim_{x→∞} f (x) = ∞, когда мы можем сделать значение f (x) сколь угодно большим, взяв x достаточно большим. Например, \lim_{x→∞} x 2 = ∞. Обратите особое внимание на то, что пределы, включающие бесконечность, определяют вертикальные и горизонтальные асимптоты функции.
Аналогичным образом мы естественно пишем \lim_{x→∞} 1 x = 0, поскольку мы можем сделать 1 x настолько близким к 0, насколько нам хотелось бы, взяв x достаточно большим (т. е. позволяя x увеличить без границ). В общем, мы понимаем обозначение \lim_{x→a} f (x) = ∞ как означающее, что мы можем сделать f (x) сколь угодно большим, взяв x достаточно близко (но не равным) к a, и обозначение \lim_{x→∞} f (x) = L означает, что мы можем сделать f (x) как можно ближе к L, взяв x достаточно большим. Это обозначение применимо к левым и правым пределам, плюс мы также можем использовать пределы, включающие −∞. Например, возвращаясь к рисунку \(\PageIndex{4}\) и f (x) = 1 x , мы можем сказать, что lim x→0 − 1 x = −∞ и limx→−∞ 1 x = 0. Наконец, мы пишем \lim_{x→∞} f (x) = ∞, когда мы можем сделать значение f (x) сколь угодно большим, взяв x достаточно большим. Например, \lim_{x→∞} x 2 = ∞. Обратите особое внимание на то, что пределы, включающие бесконечность, определяют вертикальные и горизонтальные асимптоты функции. Если \lim_{x→a} f (x) = ∞, то x = a — вертикальная асимптота f , а если \lim_{x→∞} f (x) = L, то y = L — горизонтальная асимптота выключенный . Аналогичные утверждения можно сделать с использованием -∞, а также с левыми и правыми пределами при x → a – или x → a +.
Если \lim_{x→a} f (x) = ∞, то x = a — вертикальная асимптота f , а если \lim_{x→∞} f (x) = L, то y = L — горизонтальная асимптота выключенный . Аналогичные утверждения можно сделать с использованием -∞, а также с левыми и правыми пределами при x → a – или x → a +.
В классах предварительного исчисления обычно изучается конечное поведение некоторых семейств функций, под которым мы понимаем поведение функции при x → ∞ и при x → −∞. Здесь мы кратко рассмотрим библиотеку некоторых знакомых функций и отметим значения нескольких пределов, включающих ∞. Для естественной экспоненциальной функции e x заметим, что \lim_{x→∞} e x = ∞ и limx→−∞ e x = 0, а для родственной экспоненциальной функции затухания e −x заметим, что эти пределы обратные, с \lim_ {x→∞} e−x = 0 и limx→−∞ e−x = ∞. Обращаясь к функции натурального логарифма, мы имеем limx→0 + ln(x) = −∞ и \lim_{x→∞} ln(x) = ∞. Хотя и e x , и ln(x) неограниченно растут при x → ∞, экспоненциальная функция делает это намного быстрее, чем логарифмическая функция. Вскоре мы будем использовать ограничения для количественной оценки того, что мы подразумеваем под «быстро».
Вскоре мы будем использовать ограничения для количественной оценки того, что мы подразумеваем под «быстро».
Рисунок \(\PageIndex{5}\): Графики некоторых знакомых функций, поведение которых при x → ±∞ известно. На среднем графике f (x) = x 3 − 16x и g(x) = x 4 − 16x 2 − 8.
Для полиномиальных функций вида p(x) = an x n + an−1 x n− 1 + · · · a1 x + a0, конечное поведение зависит от знака an и от того, является ли старшая степень n четной или нечетной. Если n четно, а an положительно, то \lim_{x→∞} p(x) = ∞ и limx→−∞ p(x) = ∞, как показано на графике g на рисунке \(\PageIndex{5} \). Если вместо этого an отрицательно, то \lim_{x→∞} p(x) = −∞ и limx→−∞ p(x) = −∞. В ситуации, когда n нечетно, то либо \lim_{x→∞} p(x) = ∞, либо limx→−∞ p(x) = −∞ (что происходит, когда an положительно, как на графике f в Рисунок \(\PageIndex{5}\)), или \lim_{x→∞} p(x) = −∞ и limx→−∞ p(x) = ∞ (когда an отрицательно). Функция может не иметь предела при x → ∞. Например, рассмотрим график функции синуса справа на рисунке \(\PageIndex{5}\). Поскольку функция продолжает колебаться между −1 и 1 при x → ∞, мы говорим, что \lim_{x→∞} sin(x) не существует. Наконец, несложно проанализировать поведение любой рациональной функции при x → ∞. Рассмотрим, например, функцию q(x) = 3x 2 − 4x + 5 7x 2 + 9x → ∞\), но не существует очевидного алгебраического подхода, позволяющего найти предельное значение. К счастью, оказывается, что правило Лопиталя распространяется на случаи, связанные с бесконечностью.
Например, рассмотрим график функции синуса справа на рисунке \(\PageIndex{5}\). Поскольку функция продолжает колебаться между −1 и 1 при x → ∞, мы говорим, что \lim_{x→∞} sin(x) не существует. Наконец, несложно проанализировать поведение любой рациональной функции при x → ∞. Рассмотрим, например, функцию q(x) = 3x 2 − 4x + 5 7x 2 + 9x → ∞\), но не существует очевидного алгебраического подхода, позволяющего найти предельное значение. К счастью, оказывается, что правило Лопиталя распространяется на случаи, связанные с бесконечностью.
Правило Лопиталя (∞)
Если \(f\) и \(g\) дифференцируемы и оба стремятся к нулю или оба стремятся к ±∞ при \(x → a\) (где \(a\) может быть ∞) , тогда
\[\lim_{x→a} \dfrac{f (x)}{g(x)} = \lim_{x→a} \dfrac{f ‘(x)}{ g’ (x)} .\]
Чтобы быть технически корректными, нам нужна дополнительная гипотеза о том, что \(g'(x) \neq 0\) на открытом интервале, содержащем \(a\) или в каждой окрестности бесконечности, если \(a\) равно ∞; это почти всегда встречается на практике. 9х + х 2е х + х 2\)
9х + х 2е х + х 2\)
Когда мы рассматриваем предел отношения двух функций f (x) g(x), который приводит к неопределенной форме ∞ ∞ , по сути, мы спрашиваем, какая функция неограниченно растет быстрее. Мы говорим, что функция g доминирует над функцией f при x → ∞ при условии, что
\[\lim_{x→∞} \dfrac{ f (x)}{g(x)} = 0,\]
, тогда как \(f\) доминирует над \(g\) при условии, что \lim_{x→∞} f (x) g(x) = ∞. Наконец, если значение
\[\lim_{x→∞} \dfrac{f (x)}{g(x)}\]
конечно и не равно нулю, мы говорим, что f и g растут одновременно. оценивать. Например, из более ранней работы мы знаем, что \lim_{x→∞} x 2 e x = 0, поэтому e x доминирует над x 2 , а
\[\lim_{x→∞} 3x 2−4x+5 7x 2+9x −10 = 3 7 ,\]
, поэтому
\[f (x) = 3x 2 – 4x + 5\]
и
\[g(x) = 7x 2 + 9x – 10\]
растут с одинаковой скоростью.
Резюме
В этом разделе мы столкнулись со следующими важными идеями:
- Производные можно использовать, чтобы помочь нам оценить неопределенные пределы формы 0 0 с помощью правила Лопиталя, которое развивается путем замены функций в числителе и знаменатель с их аппроксимацией касательной. В частности, если f (a) = g(a) = 0 и f и g дифференцируемы в точке a, правило Лопиталя говорит нам, что \lim_{x→a} f (x) g(x) = \lim_{ х→а} f'(x) g'(x) .
- Когда мы пишем x → ∞, это означает, что x неограниченно возрастает. Таким образом, мы используем ∞ вместе с предельной записью, чтобы записать \lim_{x→∞} f (x) = L, что означает, что мы можем сделать f (x) как можно ближе к L, выбрав x достаточно большим, и аналогичным образом \lim_{x→a} f (x) = ∞, что означает, что мы можем сделать f (x) сколь угодно большим, выбрав x достаточно близко к a.
- Вариант правила Лопиталя также позволяет нам использовать производные, чтобы помочь нам оценить неопределенные пределы формы ∞ ∞ .
 В частности, если f и g дифференцируемы и обе 159приближаются к нулю или оба приближаются к ±∞ при x → a (где a может быть ∞), тогда \lim_{x→a} f (x) g(x) = \lim_{x→a} f'(x) г'(х) .
В частности, если f и g дифференцируемы и обе 159приближаются к нулю или оба приближаются к ±∞ при x → a (где a может быть ∞), тогда \lim_{x→a} f (x) g(x) = \lim_{x→a} f'(x) г'(х) .
Эта страница под названием 2.8: Использование деривативов для оценки пределов распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Мэтью Боелкинсом, Дэвидом Остином и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Активное исчисление
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
- Теги
- источник@https://activecalculus.
 org/single
org/single
- источник@https://activecalculus.
Вопрос Видео: Нахождение предела рациональной функции с помощью правила Лопиталя
Стенограмма видео
Нахождение предела при приближении 𝑥 к нулю единицы плюс 𝑥 все в кубе минус единица все делится на один плюс пять 𝑥 в пятой степени минус один.
Вопрос требует, чтобы мы оценили предел рациональной функции. Поскольку рациональная функция — это частное полиномов, мы можем попытаться вычислить это с помощью прямой замены. Замена 𝑥 на ноль дает нам один плюс ноль в кубе минус один, деленный на один плюс пять раз ноль в пятой степени минус один. И если мы оценим это выражение, мы увидим, что мы получаем неопределенную форму нуля, деленную на ноль. Таким образом, мы не можем оценить этот предел с помощью прямой замены. Итак, нам понадобится другой подход для оценки этого предела.
Напомним, что мы можем попытаться вычислить предел отношения двух функций, используя правило Лопиталя. Итак, напомним следующую версию правила Лопиталя. Если у нас есть две дифференцируемые функции 𝑓 и 𝑔, и производная от 𝑔 не равна нулю около некоторого значения 𝑎. Хотя производная 𝑔 как 𝑎 может быть равна нулю. И мы знаем, что предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥, и предел, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥, оба существуют и равны нулю. Тогда по этой версии правила Лопиталя предел при приближении 𝑥 к 𝑎 частного 𝑓 от 𝑥 и 𝑔 от 𝑥 равен пределу при приближении 𝑥 к 𝑎 частного от 𝑓 простого числа 𝑥 и 𝑔 простого числа 𝑥. Правило Лопиталя позволяет оценить некоторые неопределенные пределы.
Итак, напомним следующую версию правила Лопиталя. Если у нас есть две дифференцируемые функции 𝑓 и 𝑔, и производная от 𝑔 не равна нулю около некоторого значения 𝑎. Хотя производная 𝑔 как 𝑎 может быть равна нулю. И мы знаем, что предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥, и предел, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥, оба существуют и равны нулю. Тогда по этой версии правила Лопиталя предел при приближении 𝑥 к 𝑎 частного 𝑓 от 𝑥 и 𝑔 от 𝑥 равен пределу при приближении 𝑥 к 𝑎 частного от 𝑓 простого числа 𝑥 и 𝑔 простого числа 𝑥. Правило Лопиталя позволяет оценить некоторые неопределенные пределы.
Чтобы применить эту версию правила Лопиталя к пределу, данному нам в вопросе, мы сначала установим нашу функцию 𝑓 от 𝑥 как функцию в числителе нашего предела. Это один плюс 𝑥 все в кубе минус один. И мы установим 𝑔 of 𝑥 как функцию в знаменателе нашего предела. Это один плюс пять 𝑥 в пятой степени минус один.
Наконец, поскольку нам нужен предел, когда 𝑥 приближается к нулю, мы установим 𝑎 равным нулю. Теперь нам нужно проверить, что наши предпосылки для правила Лопиталя верны. Во-первых, нам нужно проверить, что обе наши функции 𝑓 и 𝑔 дифференцируемы. Мы видим, что и 𝑓 из 𝑥, и 𝑔 из 𝑥 являются полиномами. А многочлены дифференцируемы для всех действительных чисел. Итак, наша первая предпосылка для правила Лопиталя верна.
Теперь нам нужно проверить, что наши предпосылки для правила Лопиталя верны. Во-первых, нам нужно проверить, что обе наши функции 𝑓 и 𝑔 дифференцируемы. Мы видим, что и 𝑓 из 𝑥, и 𝑔 из 𝑥 являются полиномами. А многочлены дифференцируемы для всех действительных чисел. Итак, наша первая предпосылка для правила Лопиталя верна.
Далее нам нужно проверить, что 𝑔 простое число 𝑥 не равно нулю вокруг 𝑥 равно нулю. Есть несколько способов отличить 𝑔 от 𝑥. Например, мы могли бы расширить нашу скобку, а затем дифференцировать ее, используя правило степени для дифференцирования. Однако мы могли также заметить, что первый член в нашей функции от 𝑔 от 𝑥 является составной функцией. Таким образом, мы могли бы различать это, используя цепное правило.
Если мы установим некоторую функцию 𝑢 от 𝑥 равной единице плюс пять 𝑥, то мы получим, что 𝑔 от 𝑥 равно 𝑢 от 𝑥 в пятой степени минус один. Теперь мы видим, что 𝑔 является функцией 𝑢, а 𝑢 является функцией 𝑥. И мы помним, что цепное правило говорит нам, что если у нас есть две функции 𝑣 и 𝑤, где 𝑣 — функция 𝑤, а 𝑤 — функция 𝑥, то производная 𝑣 от 𝑤 по отношению к 𝑥 равна d𝑣 d𝑤, умноженному на d𝑤 d𝑥 .
Итак, применяя цепное правило к 𝑔 из 𝑥, мы получаем, что 𝑔 простое число из 𝑥 равно производной от 𝑢 в пятой степени минус единица относительно 𝑢, умноженной на d𝑢 на d𝑥. И мы могли бы оценить обе эти производные, используя правило степени для дифференцирования. Мы видим, что d𝑢 на d𝑥 равно производной от одного плюс пять 𝑥 по 𝑥. Производная постоянной единицы равна нулю. А производная от пяти 𝑥 как раз равна пяти.
И чтобы дифференцировать 𝑢 в пятой степени минус один по отношению к 𝑢, мы хотим умножить его на наш показатель степени, а затем уменьшить показатель степени на единицу. Итак, чтобы дифференцировать 𝑢 в пятой степени относительно 𝑢, мы получаем пять 𝑢 в четвертой степени. И тогда производная от отрицательной единицы по 𝑢 как раз равна нулю. Итак, мы показали, что 𝑔 простое число 𝑥 равно 25𝑢 в четвертой степени. Помните, что мы определили 𝑢 как один плюс пять 𝑥. Итак, переписав 𝑢 как один плюс пять 𝑥, мы показали, что 𝑔 простое число 𝑥 равно 25, умноженному на один плюс пять 𝑥 в четвертой степени.
Помните, мы хотим показать, что 𝑔 простое число 𝑥 не равно нулю вокруг 𝑥 равно нулю. Итак, давайте рассмотрим значения 𝑥, где 𝑔 простое число 𝑥 может быть равно нулю. Мы видим, что 𝑔 простое число 𝑥 является произведением функций. А произведение функций может быть равно нулю только в том случае, если хотя бы один из этих множителей равен нулю. И, конечно же, 25 не равно нулю. Таким образом, единственный способ, которым наша функция 𝑔 простого числа 𝑥 может быть равна нулю, — это если один плюс пять 𝑥 равен нулю. И мы можем изменить этот линейный множитель, чтобы увидеть, что 𝑥 равно отрицательной одной пятой.
Сначала мы можем быть обеспокоены тем, что не можем использовать правило Лопиталя. Однако мы можем просто выбрать интервал вокруг 𝑥, равный нулю, который не включает 𝑥, равный отрицательной одной пятой. Например, мы знаем, что 𝑔 простое число 𝑥 не может быть равно нулю на замкнутом интервале от отрицательной одной десятой до одной десятой. Итак, мы показали, что 𝑔 простое число 𝑥 не равно нулю вокруг 𝑥 равно нулю.
Далее нам нужно, чтобы предел при приближении 𝑥 к нулю 𝑓 из 𝑥 и предел при приближении 𝑥 к нулю 𝑔 из 𝑥 были равны нулю. Однако на самом деле мы показали, что это уже так. Когда мы изначально пытались оценить наш предел прямой подстановкой, мы показали, что предел при приближении 𝑥 к 𝑎 из 𝑓 из 𝑥 равен нулю, а предел при приближении 𝑥 к нулю из 𝑔 из 𝑥 равен нулю. Это всего лишь числитель и знаменатель этого предела соответственно.
Итак, мы показали, что все наши предпосылки для этой версии правила Лопиталя верны. Итак, теперь вместо вычисления предела, данного нам в вопросе, мы можем вместо этого вычислить предел, когда 𝑥 приближается к нулю 𝑓 простого числа 𝑥, деленного на 𝑔 простого числа 𝑥. Мы уже нашли выражение для 𝑔 простого числа 𝑥, поэтому давайте найдем выражение для 𝑓 простого числа 𝑥.
У нас есть это 𝑓 из 𝑥 равно единице плюс 𝑥 все в кубе минус единица. И мы могли бы различать это, используя цепное правило, как мы сделали с 𝑔 из 𝑥. Однако мы могли бы также просто расширить скобки. Мы можем расширить эти скобки либо с помощью метода FOIL, либо с помощью биномиального расширения. Мы будем использовать биномиальное разложение. Поскольку три выбирают один и три выбирают два, оба равны трем, мы получаем один в кубе плюс три раза один умножить на 𝑥 в квадрате плюс три раза один в квадрате умножить на 𝑥 плюс 𝑥 в кубе минус один, что упрощает получение 𝑥 в кубе плюс три 𝑥 в квадрате плюс три 𝑥.
Мы можем расширить эти скобки либо с помощью метода FOIL, либо с помощью биномиального расширения. Мы будем использовать биномиальное разложение. Поскольку три выбирают один и три выбирают два, оба равны трем, мы получаем один в кубе плюс три раза один умножить на 𝑥 в квадрате плюс три раза один в квадрате умножить на 𝑥 плюс 𝑥 в кубе минус один, что упрощает получение 𝑥 в кубе плюс три 𝑥 в квадрате плюс три 𝑥.
Теперь мы можем просто дифференцировать это, используя правило степени для дифференцирования. Получаем 𝑓 простое число 𝑥 равно трем 𝑥 в квадрате плюс шесть 𝑥 плюс три. Итак, теперь, когда мы нашли выражения для 𝑓 простого числа 𝑥 и 𝑔 простого числа 𝑥, мы можем переписать предел, когда 𝑥 приближается к нулю 𝑓 простого числа 𝑥, деленного на 𝑔 простого числа 𝑥, как предел, когда 𝑥 приближается к нулю из трех 𝑥 в квадрате плюс шесть 𝑥 плюс три все разделить на 25, умноженное на один плюс пять 𝑥 в четвертой степени.
И мы видим, что это предел рациональной функции. Итак, мы можем попытаться оценить это, используя прямую замену. Подстановка 𝑥 равна нулю в это частное дает нам три раза ноль в квадрате плюс шесть раз ноль плюс три, все это делится на 25 раз один плюс пять раз ноль в четвертой степени. И, наконец, мы можем вычислить это выражение, чтобы получить три, деленные на 25. Итак, мы показали, используя правило Лопиталя, что предел, когда 𝑥 приближается к нулю из единицы плюс 𝑥 все в кубе минус единица, деленная на один плюс пять 𝑥 к пятая степень минус один равно трем, деленным на 25.
Подстановка 𝑥 равна нулю в это частное дает нам три раза ноль в квадрате плюс шесть раз ноль плюс три, все это делится на 25 раз один плюс пять раз ноль в четвертой степени. И, наконец, мы можем вычислить это выражение, чтобы получить три, деленные на 25. Итак, мы показали, используя правило Лопиталя, что предел, когда 𝑥 приближается к нулю из единицы плюс 𝑥 все в кубе минус единица, деленная на один плюс пять 𝑥 к пятая степень минус один равно трем, деленным на 25.
Правило Лопиталя | Преподавание исчисления
Опубликовано Лин Макмаллин
Модуль 4 охватывает скорость изменения в задачах движения и других контекстах, связанных задачах скорости, линейной аппроксимации и правиле Лопиталя. (CED – 2019 стр. 82 – 90). На эти темы приходится около 10–15 % вопросов на экзамене AB и 6–9 % вопросов на BC.
Темы 4.1 – 4.6 Тема 4.1 Интерпретация значения производной в контексте Учащиеся изучают значение производной в ситуациях, связанных со скоростью изменения.
Тема 4.2 Линейное движение Связь между положением, скоростью, скоростью и ускорением. Эта тема может работать лучше после графических задач в Разделе 5, так как многие идеи совпадают. См. Проблемы с движением: одно и то же, другой контекст
Тема 4.3 Скорость изменения в контекстах, отличных от движения Другие приложения
Тема 4.4 Введение в связанные ставки Использование цепного правила
Тема 4.5 Решающие связанные с такими же скоростями.
Тема 4.6 Приблизительные значения функции с использованием локальной линейности и линерия . ТАНГОВАЯ ЛИНИЯ. Тема 4.7 Использование правила Лопиталя для определения границ неопределенных форм. Неопределенные формы типа и . (Могут быть включены и другие формы, но только эти две проверяются на экзаменах AP.)
Темы 4.1 и 4.3 включены в другие темы, тема 4.2 может занять несколько дней, Темы 4.4 – 4.5 сложны для многих учащихся и могут занимать 4 – 5 занятий, 4. 6 и 4.7 – два занятия каждая. Рекомендуемое время 10-11 занятий для АБ и 6-7 для ВС.
6 и 4.7 – два занятия каждая. Рекомендуемое время 10-11 занятий для АБ и 6-7 для ВС.
Сообщения на эти темы включают:
Проблемы с движением
Проблемы с движением: одно и то же, другой контекст
Speed
Примечание на скорость
Связанные ставки
Связанные проблемы с ставками I
Проблемы с таковыми ставками II
Хороший вопрос 9 – Связанные ставки
Linear ablecamition
Local Linear 1
9004 2Правило Лопиталя
Локально-линейное правило Лопиталя
Правила Лопиталя для графика
Определение неопределенного
2 Определение неопределенного0005
Вот ссылки на полный список сообщений, в которых обсуждаются десять разделов описания курса и экзамена 2019 года.
CED 2019 – Раздел 1: Пределы и непрерывность
CED 2019 – Раздел 2: Дифференциация: определение и основные свойства.
2019 CED – Раздел 3: Дифференциация: составные, неявные и обратные функции
CED 2019 – Модуль 4 Контекстное применение производной Рассмотрите возможность изучения Раздела 5 перед Разделом 4 5 перед блоком 4
2019 — CED, Раздел 6 Интеграция и накопление изменений
2019 – CED Раздел 7 Дифференциальные уравнения. Рассмотрите возможность обучения после раздела 8
2019 – CED Раздел 8. Применение интеграции. Рассмотрите возможность обучения после раздела 6, перед разделом 7.
2019 – CED. Модуль 9 Параметрические уравнения, полярные координаты и функции векторных значений
CED 2019 Модуль 10 Бесконечные последовательности и серии
05
Нравится:
Нравится Загрузка…
Опубликовано в CED 2019, Производные приложения, Ограничения, Движение | TaggedПравило Лопиталя, Правило Лопиталя, Линейное движение, локальное линейное приближение, проблемы движения, движение частиц, Связанная скорость | Оставьте ответОпубликовано Лин Макмаллин
Другое применение производной
L’Правило больницы
Местный линейный L’ -больница Демонстрация Доказательства
L’ -REGIN «Правила больницы» (2008 AB 6)
Guillaume de l’Hospital
1661 – 1704
Пересмотрено на основе сообщения от 7 ноября 2017 года
На этой неделе будет два дополнительных сообщения! Проверьте завтра некоторые предложения по «Обучению вогнутости» и в пятницу «Предвосхищение MVT».
В прошлую пятницу я внес большое обновление в пост О масштабировании. Он включает в себя предложение от читателя этого блога с диаграммой Десмос, которая рассчитает для вас баллы по шкале Кеннеди.
Нравится:
Нравится Загрузка…
Опубликовано в Производные приложения, ограничения | Метки: Правило Лопиталя | Оставьте ответОпубликовано Лин Макмаллин
Некоторые окончательные применения деривативов
L’Правило больницы
Местный линейный линейный L’ -больница Демонстрация доказательства
L’Hospital Правила график
Хороший вопрос. Вопрос AP. используется для более глубокого изучения правила Лопиталя (2008 AB 6)
Проблемы, связанные с оценкой
Проблемы со связанными ставками 1
Проблемы со связанными ставками II
Хороший вопрос 9 Бейсбол и связанные ставки
Картина точки В основном интеграция, но с привязкой к связанным ставкам.
Нравится:
Нравится Загрузка…
Опубликовано в Производные приложения, ограничения | Tagged L’Hopital’s Rule, L’Hospital’Rule, Связанная норма | Оставьте ответОпубликовано Лин Макмаллин
Когда я начал этот блог несколько лет назад, я надеялся, что мои читатели будут задавать вопросы, которые мы могли бы обсудить, или предложить идеи для дополнительных тем для написания. На самом деле этого не произошло, но я все еще очень открыт для этой идеи. (Это был НАМЕК.) С того первого года, когда у меня была вся учебная программа впереди, я стал меньше писать не потому, что не люблю писать, а потому, что у меня мало идей.
На днях я ответил на вопрос, размещенный на доске объявлений Сообщества AP по математическому анализу, об экзаменационном вопросе AB по математическому анализу. Мне пришло в голову, что этот довольно безобидный вопрос был довольно хорош. Поэтому я решил время от времени запускать серию хороших вопросов из экзаменов AP или где-либо еще, которые можно использовать для обучения помимо реальных вещей, заданных в вопросе. (Возможно, мой последний пост был в этой категории, но он был написан несколько месяцев назад.)
Обсуждая эти вопросы, я буду делать многочисленные комментарии по поводу вопроса и о том, как его развить в вашем классе. Моя идея состоит не только в том, чтобы показать, как написать хороший ответ, но и в том, чтобы использовать вопрос, чтобы глубже изучить вовлеченные концепции.
Моя идея состоит не только в том, чтобы показать, как написать хороший ответ, но и в том, чтобы использовать вопрос, чтобы глубже изучить вовлеченные концепции.
Хороший вопрос № 1: 2008 AB Экзаменационный вопрос 6.
Основа дала учащимся функцию . Студентам также сказали, что.
- Первая мысль, которая приходит в голову, почему дали производную. Причина в том, как мы увидим, что первая производная необходима для ответа на первые три части вопроса. Следовательно, студент, вычисливший неверную производную, попадет в большие неприятности (и у читателей может быть много работы по чтению неправильной работы студента). Производная вычисляется с использованием частного правила, и учащиеся должны будут продемонстрировать свое знание частного правила позже в этом вопросе; нет причин просить их сделать одно и то же дважды.
- Если вы используете это в классе, вы можете и, вероятно, должны попросить своих учеников вычислить первую производную.
 Тогда вы можете увидеть, скольким помогло бы предоставление производной .
Тогда вы можете увидеть, скольким помогло бы предоставление производной . - При обсуждении основы следует также обсудить домен, x > 0, и точку пересечения по оси x (1, 0). Другие особенности графика, такие как конечное поведение, раскрываются позже в вопросе, поэтому их можно ненадолго отложить.
Часть а попросила учащихся написать уравнение касательной в точке х = e 2 . Для этого учащиеся должны выполнить два вычисления: и . Уравнение касательной есть.
- Написание уравнения касательной является очень важным навыком и должно быть простым. Форма «точка-наклон» — это то, что нужно. Избегайте перехвата наклона.
- Касательная линия используется для аппроксимации значения функции вблизи точки касания; вы можете добавить приближенное вычисление здесь.
- Выполнив часть c, вы должны вернуться сюда и обсудить, является ли аппроксимация завышенной или заниженной, и как это определить.
 (Ответ: занижать, так как здесь график вогнутый.)
(Ответ: занижать, так как здесь график вогнутый.) - После выполнения части c вы также можете попросить их написать касательную в точке перегиба и указать, являются ли приближения вблизи точки перегиба завышенными или заниженными, и почему. (Ответ: Поскольку вогнутость здесь меняется, это зависит от того, в какую сторону от точки перегиба делается приближение. Влево — завышение, вправо — занижение.)
Часть b попросила студентов найти x -координату критической точки, определить, является ли она максимумом, минимумом или ни тем, ни другим, и «обосновать свой ответ». Чтобы заработать баллы, студенты должны были написать уравнение и решить его, получив 9 баллов.0007 х = е . Им пришлось заявить, что это максимум, потому что «меняется с положительного на отрицательное при x = e ».
Это очень стандартный вопрос экзамена AP. Чтобы расширить его в своем классе:
- Обсудите здесь, как вы узнали знак изменения производной.
 Это поможет вам разобраться в свойствах функции натурального логарифма.
Это поможет вам разобраться в свойствах функции натурального логарифма. - Обсудите, почему изменение знака говорит вам, что это максимум. (Положительная производная указывает на возрастающую функцию и т. д.)
- Выполнив часть c, вы можете вернуться сюда и попробовать второй тест производной.
- В вопросе содержится указание на критическую точку, намекая на то, что она только одна. Студенты должны научиться улавливать такие подсказки и быть осторожными, если их вычисления дают больше или меньше единицы.
- На этом этапе мы также определили, что функция возрастает на отрезке и убывает на всех остальных. Этот вопрос никогда не задается, но в классе это стоит обсудить как важные особенности графа. О том, почему это полуоткрытые интервалы смотрите здесь.
Часть c сообщила студентам, что существует ровно одна точка перегиба, и попросила найти ее координату x . Чтобы сделать это, они должны были использовать правило частного, чтобы найти это , установить это равным нулю и найти x -координата x = e 3/2 .
- Вопрос не требовал никакого обоснования для этого ответа. В классе вы должны обсудить, как будет выглядеть обоснование. Причина в том, что вторая производная здесь меняет знак. Итак, теперь вам нужно обсудить, откуда вы это знаете.
- Кроме того, теперь вы можете определить, что функция вогнута вниз на интервале и вогнута вверх на интервале . Попросите класс обосновать это.
Часть d попросила студента найти . Ответ . Хотя это кажется почти одноразовым, прибавленным к концу, потому что им нужен был еще один пункт, именно по этой причине мне нравится этот вопрос.
- Вопрос легко решается: .
- Заманчиво, но предел не может быть найден по правилу Лопиталя, потому что при подстановке вы получаете , что не является одной из форм, с которыми может работать правило Лопиталя.
- Причина, по которой мне так нравится эта часть, заключается в том, что мы уже получили достаточно информации в ходе решения задачи, чтобы найти этот предел! Функция возрастает и вогнута вниз на интервале .
 Двигаясь от максимума влево, функция пересекает ось x в точке (1, 0), продолжает двигаться на юг и становится круче. Таким образом, предел, когда вы приближаетесь к оси y справа, составляет отрицательную бесконечность. Это поведение левого конца.
Двигаясь от максимума влево, функция пересекает ось x в точке (1, 0), продолжает двигаться на юг и становится круче. Таким образом, предел, когда вы приближаетесь к оси y справа, составляет отрицательную бесконечность. Это поведение левого конца. - Как насчет поведения правого конца? (Вы спросите у своего класса.) Ну, функция положительна и убывает справа от максимума и становится вогнутой вверх после x = e 3/2 . Таким образом, он должен выровняться и приблизиться к оси x как асимптоте.
- Это ясно из примечания выше. Этот предел можно найти по правилу Лопиталя, поскольку он является неопределенным типом . Так, .
- Обратите также внимание на то, что первая производная стремится к нулю, когда x приближается к бесконечности. Это указывает на то, что график функции приближается к горизонтали по мере продвижения вправо. Вторая производная также стремится к нулю при x приближается к бесконечности, указывая на то, что график функции становится более плоским (менее вогнутым).

Этот вопрос и обсуждение в значительной степени делается аналитически (работа с уравнениями). В ходе работы мы нашли несколько важных цифр. Надеюсь, вы, студенты, обсудили это со многими добрыми словами. Чтобы завершить правило четырех, вот график.
А вот крупный план, показывающий важные особенности графика и соответствующие точки на производных.
Функция показана синим цветом, производная и максимум — красным, а вторая производная и точка перегиба — зеленым.
Наконец, эта функция и предел на бесконечности аналогичны более патологическому примеру, рассмотренному в посте от 31 октября 2012 года под названием Far Out!
Нравится:
Нравится Загрузка…
Рубрика: Хороший вопрос, Графики, Пределы | Метки: производная, Экстремальное значение, Правило Лопиталя, пределы, вторая производная | 4 ОтветыОпубликовано Лин Макмаллин
В своем последнем посте от 31 мая 2012 г. я показал, как работает правило Лопиталя. Мы рассмотрели пример
я показал, как работает правило Лопиталя. Мы рассмотрели пример
,
, который удовлетворяет требованию теоремы, называемой правилом Лопиталя, а именно функции дифференцируемы и, поскольку tan() = sin() = 0, они пересекаются на оси x в . Мы посмотрели на график, а затем увеличили его.
- Рисунок 1. y = tan(x) красным и y = sin(x) синим
- Рисунок 2. Предыдущий график увеличен.
Правило Лопиталя говорит нам, что при этих условиях предел равен пределу отношения их наклонов (или их производных, если хотите). Вы можете видеть, каково это соотношение на рисунке 2? Несмотря на то, что это не «квадратное окно», соотношение, очевидно, равно -1.
Вот еще четыре ограничения. Посмотрите, сможете ли вы найти их предложенным здесь способом. А именно, увеличьте масштаб точки пересечения функций и посмотрите, сможете ли вы найти пределы, не выполняя никаких вычислений. (Да, я знаю, что вы уже знаете первые 3, но в любом случае попробуйте эту идею. )
)
1.
2.
3. Также известный как
4.
Ответы по порядку: 1, 0, -1, -1
Нравится:
Нравится Загрузка…
Posted in Производные приложения, Производные, Графики, Ограничения | Метки: Правило Лопиталя | Оставьте ответОпубликовано Лин Макмаллин
Начну с леммы. (Мне нравится время от времени формулировать лемму хотя бы потому, что у меня есть повод объяснить, что такое лемма — простая теорема, которая используется при доказательстве основной теоремы.)
Лемма: Если две прямые пересекаются по оси x , то для любых x отношение их координат y равно отношению их наклонов.
Доказательство: две линии со склонами M 1 и M 2 , которые пересекаются ( A , 0) на x -Axis. 1 ( x – a ) и у 2 = м 2 ( x – a ). Затем
Затем
Правило L’Hôpital (Теорема): если F и G дифференцируются около x = A и F ( A ) = G ( A ) = 0, затем
, если ограничение существует.
Тот факт, что f ( a ) = g ( a ) = 0, означает, что две функции пересекаются на x – ось в точке ( a , 0). Например, функции f ( x ) = tan( x ) и g ( x ) = sin( x ) имеют это свойство при .
Рис. 1. y = tan(x) красным и y = sin(x) синим
Теперь несколько раз увеличьте масштаб с центром в .
Рисунок 2. Предыдущий график увеличен.
Ого!
Похоже на линии!!
Это свойство локальной линейности дифференцируемых функций — если вы достаточно увеличите масштаб, любая дифференцируемая функция в конечном итоге будет выглядеть линейной. Так что, возможно, применима лемма. Единственное отличие состоит в том, что наклоны «линий» являются производными, поэтому
Единственное отличие состоит в том, что наклоны «линий» являются производными, поэтому
Это не совсем доказывает правило Лопиталя, но должно дать вам и вашим ученикам хорошее представление о том, почему правило Лопиталя верно.
Тогда в нашем примере:
Но разве это не очевидно из рисунка 2?
Подумай об этом.
Подробнее об этом в следующий раз.
Нравится:
Нравится Загрузка…
Рубрика: Применение производных, Теория производных, Производные, Пределы | Метки: Правило Лопиталя, пределы | Оставьте ответБлог
для учителей и студентов математики Лин Макмаллин
Поиск
ПоискСообщения по темам
Сообщения по темамВыбрать категорию2019 CED (32)антидифференциация (8)AP экзамены по математическому анализу (111)Before Calculus (27)CAS (5)Применение производных (81)Теория производных (75)Производные (72)Дифференциальные уравнения (32) ) Хороший вопрос (10) Графики (37) Интеграция (53) Приложения для интеграции (80) Теория интеграции (47) Ограничения (43) Движение (14) MPAC (9))Параметрический (27)Полярный (17)Степенной ряд (23)Обзорный (73)Рулетки (9)Последовательности и ряды (29)Технология (19)Начало года (13)Теоремы и теория (7)Тригонометрия (1) Без категорий (55)единицы (2)Векторные (12)Письмо и чтение (24)Архивы
Архивы Выбрать месяц Сентябрь 2022 Август 2022 Июль 2022 Апрель 2022 Март 2022 Февраль 2022 Январь 2022 Ноябрь 2021 Октябрь 2021 Сентябрь 2021 Август 2021 Июль 2021 Июнь 2021 Май 2021 Апрель 2021 Март 2021 Февраль 2021 Январь 2021 Декабрь 2020 Сентябрь 2020 Ноябрь 2020 Октябрь 2020 Июнь 2020 Апрель 2020 Март 2020 Февраль 2020 Январь 2020 Декабрь 2019Ноябрь 2019 г. Октябрь 2019 г. Сентябрь 2019 г. Август 2019 г., июль 2019 г., июнь 2019 г., май 2019 г. Апрель 2019 г. Март 2019 г. Февраль 2019 г. Январь 2019 г. Декабрь 2018 г. Ноябрь 2018 г. Октябрь 2018 г. Сентябрь 2018 г. Август 2018 г., июнь 2018 г., май 2018 апрель 2018 г. Февраль 2018 г. Январь 2018 г. Декабрь 2017 г. Ноябрь 2017 г. Октябрь 2017 г. Сентябрь 2017 г. Август 2017 г., июль 2017 г., апрель 2017 г. Март 2017 г. Февраль 2017 г. Январь 2017 г., декабрь 2016 г., ноябрь 2016 г., октябрь 2016 г., сентябрь 2016 г. 2016 г., июнь 2016 года 2016 г., апрель 2016 г., март 2016 г., февраль 2016 г., январь 2016 г., декабрь 2015 г., октябрь 2015 г., сентябрь 2015 г., август 2015 г., июль 2015 г., июнь 2015 г., май 2015 апрель 2015 г. Март 2015 февраль 2015 г. Январь 2015 г. Декабрь 2014 г. 2014 г. Ноябрь 2014 г. Октябрь 2014 г. Сентябрь 2014 г. август 2014 г., июль 2014 г., июнь 2014 г., май 2014 г. Февраль 2014 г. Январь 2014 г. Ноябрь 2013 г. Сентябрь 2013 г. Август 2013 г., июль 2013 г., июнь 2013 г.
Октябрь 2019 г. Сентябрь 2019 г. Август 2019 г., июль 2019 г., июнь 2019 г., май 2019 г. Апрель 2019 г. Март 2019 г. Февраль 2019 г. Январь 2019 г. Декабрь 2018 г. Ноябрь 2018 г. Октябрь 2018 г. Сентябрь 2018 г. Август 2018 г., июнь 2018 г., май 2018 апрель 2018 г. Февраль 2018 г. Январь 2018 г. Декабрь 2017 г. Ноябрь 2017 г. Октябрь 2017 г. Сентябрь 2017 г. Август 2017 г., июль 2017 г., апрель 2017 г. Март 2017 г. Февраль 2017 г. Январь 2017 г., декабрь 2016 г., ноябрь 2016 г., октябрь 2016 г., сентябрь 2016 г. 2016 г., июнь 2016 года 2016 г., апрель 2016 г., март 2016 г., февраль 2016 г., январь 2016 г., декабрь 2015 г., октябрь 2015 г., сентябрь 2015 г., август 2015 г., июль 2015 г., июнь 2015 г., май 2015 апрель 2015 г. Март 2015 февраль 2015 г. Январь 2015 г. Декабрь 2014 г. 2014 г. Ноябрь 2014 г. Октябрь 2014 г. Сентябрь 2014 г. август 2014 г., июль 2014 г., июнь 2014 г., май 2014 г. Февраль 2014 г. Январь 2014 г. Ноябрь 2013 г. Сентябрь 2013 г. Август 2013 г., июль 2013 г., июнь 2013 г. , май 2013 г. Апрель 2013 г. Март 2013 г. Февраль 2013 г. Январь 2013 г. Декабрь 2012 г. 2012 г. 2012 г. Ок октябрь 2012 г. сентябрь 2012 г. август 2012 г. июль 2012 г.
, май 2013 г. Апрель 2013 г. Март 2013 г. Февраль 2013 г. Январь 2013 г. Декабрь 2012 г. 2012 г. 2012 г. Ок октябрь 2012 г. сентябрь 2012 г. август 2012 г. июль 2012 г.Правило Лопиталя и неопределенные формы пределов в исчислении
Теорема Лопиталя позволяет нам заменить предельную задачу другой, решение которой может быть проще. Несколько примеров представлены вместе с их решениями и подробными пояснениями.
Теорема Лопиталя
Если lim f(x) = 0 и lim g(x) = 0 и если lim [ f'(x) / g'(x) ] имеет конечное значение L или имеет форму + ∞ или – ∞, то
где lim обозначает lim x→a , lim x→a + , lim x→a – , lim x→+ ∞ или lim x→1 – ∞ 9 .
Примеры с подробными решениямиПример 1Найдите предел lim x→0 sin x / xРешение примера 1: Так как lim x→0 sin x = 0 и lim х→0 х = 0 Правило Лопиталя можно использовать для оценки вышеуказанного предела следующим образом lim x→0 sin x / x = lim x→0 [ d ( sin x ) / dx ] / [ d ( x ) / dx ] = lim x→0 cos x / 1 = 1 Пример 2Найдите предел lim x→0 ( e x – 1 ) / x Решение примера 2:Обратите внимание, что lim x→0 ( e x – 1 ) = 0 и lim х→0 х = 0 Мы можем использовать правило Лопиталя для вычисления заданного предела следующим образом: lim x→0 ( e x -1) / x = lim x→0 [d (e x -1) / dx] / [d(x) / dx] = lim x→0 e x / 1 = 1 Пример 3Найдите предел lim x→1 ( x 2 – 1 ) / (x – 1)Решение примера 3: Поскольку предел числителя lim x→1 ( x 2 – 1 ) = 0 и знаменателя lim x→1 x – 1 = 0 равны нулю, мы можем использовать правило Лопиталя для вычисления предела lim x→1 ( x 2 – 1 ) / (x – 1) = lim x→1 [ d ( x 2 – 1 ) / dx ] / [ d ( x – 1 ) / дх] = lim х→1 2 х / 1 = 2 Обратите внимание, что тот же предел может быть рассчитан с помощью первого факторинга следующим образом: lim x→1 ( x 2 – 1 ) / (x – 1) = lim x→1 ( x – 1 )(x + 1) / (x – 1) = = lim x→1 (x + 1) / 1 = 2 Пример 4Найдите предел lim x→2 ln(x – 1 ) / (x – 2)Решение примера 4: Предел числителя lim x→2 ln(x – 1) = 0 Предел знаменателя lim x→2 x – 1 = 0 Оба предела равны нулю, можно использовать правило Лопиталя lim x→2 ln(x – 1) / (x – 2) = lim x→2 [ d ( ln(x – 1) ) / дх ] / [ д ( х – 2 ) / дх ] = lim x→2 [ 1 / (x-1) ] / 1 = 1 Пример 5Найдите предел lim x→0 (1 – cos x ) / 6 x 2Решение примера 5: Предел числителя и знаменателя lim x→0 1 – cos x = 0 lim x→0 6 x 2 = 0 Можно использовать правило Лопиталя lim x→0 (1 – cos x ) / 6 x 2 = lim x→0 [ sin x ] / [ 12 x ] Новый предел также является неопределенным 0/0, и мы можем применить теорему Лопиталя во второй раз lim x→0 (1 – cos x ) / 6 x 2 = lim x→0 [ грех х ] / [ 12 х ] = lim x→0 cos x/12 = 1/12 УпражненияНайдите пределы1.  |



 Но метод г-на Лейбница
намного проще и быстрее благодаря используемым им обозначениям, а не
отметить замечательную помощь, которую он оказывает во многих случаях. ”
Но метод г-на Лейбница
намного проще и быстрее благодаря используемым им обозначениям, а не
отметить замечательную помощь, которую он оказывает во многих случаях. ” В частности, если f и g дифференцируемы и обе 159приближаются к нулю или оба приближаются к ±∞ при x → a (где a может быть ∞), тогда \lim_{x→a} f (x) g(x) = \lim_{x→a} f'(x) г'(х) .
В частности, если f и g дифференцируемы и обе 159приближаются к нулю или оба приближаются к ±∞ при x → a (где a может быть ∞), тогда \lim_{x→a} f (x) g(x) = \lim_{x→a} f'(x) г'(х) .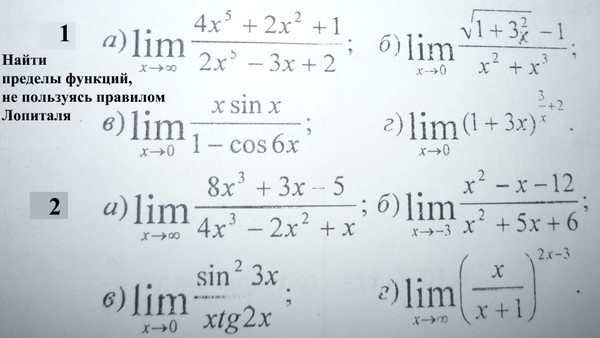 org/single
org/single