Пределы. Пошаговый калькулятор
Калькулятор находит предел функции путем различных преобразований, подстановок, первого и второго замечательных пределов, домножения на сопряженное, группировки множителей, правила Лопиталя, разложения в ряд Тейлора и свойств пределов. Вычисляет предельное значение функции в точке (слева и справа)
Введите выражение и нажмитеили кнопку
Настройки
Вычислять относительно
АвтоматическиС выбором метода решения~
автозамена
Применять правило Лопиталя Пропускать шаги с вынесением константы
Содержимое загружается
Заполните пропуски
Результат в LaTeX:
Копировать
Результат в виде выражения:
Копировать
Ввод распознает различные синонимы функций, как asin, arsin, arcsin
Знак умножения и скобки расставляются дополнительно — запись2sinx сходна2*sin(x)
Список математических функций и констант:
•ln(x) — натуральный логарифм
•sin(x) — синус
•cos(x) — косинус
•tg(x) — тангенс
•ctg(x) — котангенс
•arcsin(x) — арксинус
•arccos(x) — арккосинус
•arctg(x) — арктангенс
•arcctg(x) — арккотангенс
•sh(x) — гиперболический синус
•ch(x) — гиперболический косинус
•th(x) — гиперболический тангенс
•cth(x) — гиперболический котангенс
•sch(x) — гиперболический секанс
•csch(x) — гиперболический косеканс
•arsh(x) — обратный гиперболический синус
•arch(x) — обратный гиперболический косинус
•arth(x) — обратный гиперболический тангенс
•arcth(x) — обратный гиперболический котангенс
•sec(x) — секанс
•cosec(x) — косеканс
•arcsec(x) — арксеканс
•arccsc(x) — арккосеканс
•arsch(x) — обратный гиперболический секанс
•arcsch(x) — обратный гиперболический косеканс
•abs(x) — модуль
•sqrt(x) — корень
•exp(x) — экспонента в степени x
•pow(a,b) — \(a^b\)
•sqrt7(x) — \(\sqrt[7]{x}\)
•sqrt(n,x) — \(\sqrt[n]{x}\)
•log3(x) — \(\log_3\left(x\right)\)
•log(a,x) — \(\log_a\left(x\right)\)
•pi — \(\pi\)
alpha — \(\alpha\)
beta — \(\beta\)
•sigma — \(\sigma\)
gamma — \(\gamma\)
nu — \(\nu\)
•mu — \(\mu\)
phi — \(\phi\)
psi — \(\psi\)
•tau — \(\tau\)
eta — \(\eta\)
rho — \(\rho\)
•a123 — \(a_{123}\)
x_n — \(x_{n}\)
mu11 — \(\mu_{11}\)
Добавить страницу в закладки — CTRL+D
Возможность редактировать тексты в решении
Ссылка на это решение
75% 90% 100% 110% 125% 🔍
Вычисляю решение.
.
Оформляю..
Перевожу..
Слишком длинное выражение!
Внутренняя ошибка
Ошибка соединения
Калькулятор обновляется
Необходимо перезагрузить страницу
Ссылка скопирована!
Формула скопирована
Обновленный текст отправлен
Калькулятор пределов с шагами – онлайн и бесплатно!
Калькулятор пределов с шагами – онлайн и бесплатно!Рассчитать предел Рассчитать медиану Рассчитать интеграл Рассчитать среднее
Поделиться калькулятором пределов
Добавить в закладки
Добавьте калькулятор пределов в закладки вашего браузера
1. Для Windows или Linux – нажмите Ctrl + D .
2.
Для MacOS – нажмите Cmd + D .
3. Для iPhone (Safari) – нажмите и удерживайте , затем нажмите Добавить закладку
4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки
Как использовать?
Как пользоваться калькулятором лимита
1
Шаг 1
Введите проблему с пределами в поле ввода.
2
Шаг 2
Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.
3
Шаг 3
Во всплывающем окне выберите «Найти предел».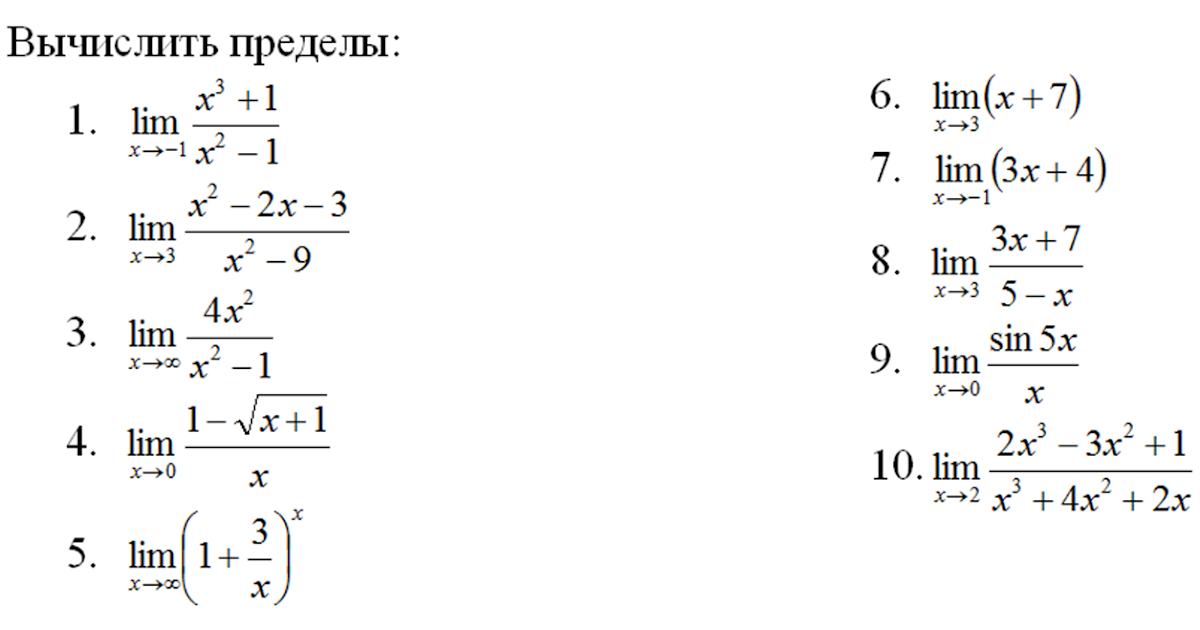
Что такое предел в математике
Предел – это математический термин, обозначающий определенное предельное число, к которому стремится бесконечная последовательность или функция. Соответственно различают предел последовательности и предел функции (в точке «на бесконечности»). Также считается, что предел может быть равен “бесконечности”.
Интуитивно понятно, что один объект склонен к другому, например, птица стремится к гнезду. Отсюда происходит интуитивное представление о желании последовательности или функции чего-либо; в рамках математического анализа это понятие желания находит свое формализацию в математических определениях предела функции и предела последовательности.
Зачем может потребоваться расчет предела
Это тот случай, когда проще объяснить термин простыми человеческими словами.
В различных науках (например, в физике) существует множество ситуаций, в которых нужно знать, что произойдет с этим явлением, процессом, эффектом, если: время стремится к бесконечности, частота стремится к определенному значению, значение X (любое другое физическое количество) стремится к нулю, бесконечности, определенному значению и т. д. Вот почему вам нужно уметь считать лимиты.
Калькулятор правил Лопиталя
Калькулятор правил Лопиталя с шагами
Калькулятор правил Лопиталя используется для нахождения пределов неопределенных функций. Этот калькулятор берет производные неопределенной функции и устанавливает предельное значение, чтобы получить числовой результат.
Как работает этот калькулятор L’hopital?
Выполните следующие шаги, чтобы найти пределы функции, используя правило Лопиталя.
- Введите функцию.
- Используйте значок клавиатуры для ввода математических клавиш.
- Введите предельное значение и выберите переменную.
- Выберите левостороннее, правостороннее или двустороннее ограничение.
- Нажмите кнопку вычислить .
- Чтобы войти в новую функцию, нажмите кнопку сброса .
- Нажмите кнопку показать еще , чтобы просмотреть результат с пошаговыми инструкциями.
Что такое правило Лопиталя?
В математическом анализе правило Лопиталя — это теорема о пределах, которая помогает нам вычислять неопределенные пределы в форме \(\frac{0}{0}\:or\:\frac{\infty }{\infty } \)
Проще говоря, правило Лопиталя помогает нам найти \(\lim _{x\to a}\left(\frac{g\left(x\right)}{h\left(x\right) }\right)\:\)
Где \(\lim _{x\to a}\:g\left(x\right)=\lim _{x\to a}\:h\left(x\ right)=0\:or\:\left(\infty \:,-\infty \right)\)
Формула правила Лопиталя
Согласно этому правилу, если существуют производные функций, то две пределы эквивалентны. Общая формула этого правила приведена ниже.
\(\lim _ {х\к а}\влево (\ гидроразрыва{г\влево(х\вправо)}}{ч\влево(х\вправо)}\вправо)=\lim _ {х\к а }\left(\frac{g’\left(x\right)}{h’\left(x\right)}\right)\)
Как использовать правило Лопиталя, чтобы найти пределы?
Ниже приведен пример решения этого правила с помощью нашего калькулятора L’hospital.