вычислить значение производной на каждом из участков графика
Вы искали вычислить значение производной на каждом из участков графика? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить значение производной функции в точке x0, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «вычислить значение производной на каждом из участков графика».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Где можно решить любую задачу по математике, а так же вычислить значение производной на каждом из участков графика Онлайн?
Решить задачу вычислить значение производной на каждом из участков графика вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.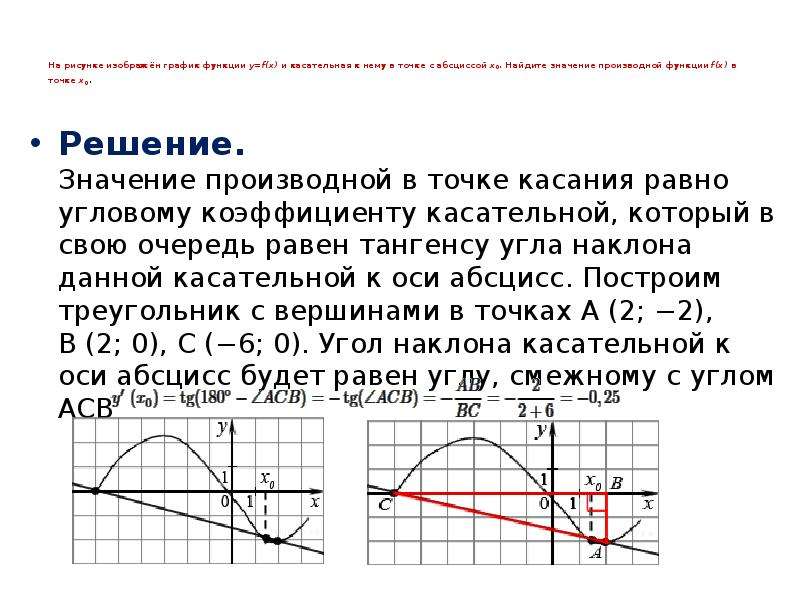
Как найти производную функции в точке x0
В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:
- Значение производной в некоторой точке x0,
- Точки максимума или минимума (точки экстремума),
- Интервалы возрастания и убывания функции (интервалы монотонности).
Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.
Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.
Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.
Вычисление значения производной. Метод двух точек
Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x0, и требуется найти значение производной в этой точке, применяется следующий алгоритм:
- Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
- Зная координаты, легко вычислить приращение аргумента Δx = x2 − x1 и приращение функции Δy = y2 − y1.
- Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.
Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x
0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x2 − x1 = −1 − (−3) = 2; Δy = y2 − y1 = 6 − 2 = 4.
Найдем значение производной: D = Δy/Δx = 4/2 = 2.
Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x2 − x1 = 3 − 0 = 3; Δy = y2
Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.
Задача.
На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x2 − x1 = 5 − 0 = 5; Δy = y2 − y1 = 2 − 2 = 0.
Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.
Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.
Вычисление точек максимума и минимума
Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:
- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x0) ≥ f(x).

- Точка x0 называется функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x
Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:
- Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
- Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x0 известно, что f’(x0) ≠ 0, то возможны лишь два варианта: f’(x0) ≥ 0 или f’(x0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
- Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума.
 Отсчет всегда ведется слева направо.
Отсчет всегда ведется слева направо.
Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.
Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:
Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.
Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:
Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].
Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:
На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.
Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.
Нахождение интервалов возрастания и убывания функции
В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≤ f(x2). Другими словами, чем больше значение аргумента, тем больше значение функции.
- Функция f(x) называется [a; b] если для любых двух точек x1 и x2 из этого отрезка верно утверждение: x1 ≤ x2 ⇒ f(x1) ≥ f(x2). Т.е. большему значению аргумента соответствует меньшее значение функции.
Сформулируем достаточные условия возрастания и убывания:
- Для того чтобы непрерывная функция f(x) возрастала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была положительна, т.
 е. f’(x) ≥ 0.
е. f’(x) ≥ 0. - Для того чтобы непрерывная функция f(x) убывала на отрезке [a; b], достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.
Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:
- Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
- Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
- Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x).
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:
Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:
Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
Вычислим их длины:
l1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l2 = 5.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−3; 3), B (5; 5), C (5; 3). Угол наклона касательной к оси абсцисс будет равен углу BAC. Поэтому
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны: В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке . Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной кграфику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственнойточке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при касательная (стандартное обозначение) касается графика функции в единственной точке .
И наша задача состоит в том, чтобы найти уравнение прямой .
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны:
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Небольшой разминочный пример для самостоятельного решения:
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции (следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Вычислить производную функции в точке .
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
Ну вот, совсем другое дело. Вычислим значение производной в точке :
В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.
Потому-что арктангенсов на студенческий век ещё хватит.
Вычислить производную функции в точке .
Это пример для самостоятельного решения.
Как найти значение производной функции F(x) в точке Хо? Как вообще это решать?
Sfash
Если формула задана, то найти производную и вместо Х подставить Х-нулевое. Посчитать
Если речь идет о б-8 ЕГЭ, график, то надо найти тангенс угла (острый или тупой) , который образует касательная с осью Х (с помощью мысленного построения прямоугольного треугольника и определения тангенса угла)
Тимур адильходжаев
Во-первых, надо определиться со знаком. Если точка х0 находится в нижней части координатной плоскости, то знак в ответе будет минус, а если выше, то +.
Во-вторых, надо знать что такое тангес в прямоугольном прямоугольнике. А это соотношение противолежащей стороны (катета) к прилежащей стороне (тоже катета) . На картине обычно есть несколько черных отметок. Из эти отметок составляешь прямоугольный треугольник и находишь тангес.
Как найти значение производной функции f x в точке x0?
Bk.Ru
В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, т.е. в Вашем случае подставить нулевой Х и вычислить полученное выражение.
Ну а ваше стремление разобраться в этом вопросе, на мой взгляд, бесспорно заслуживает +, который ставлю с чистой совестью.
Lady v
Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной (не саму производную заметьте!) в указанной точке Х0. Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. Потом составляется уравнение этой касательной в виде y=кx+b.
Потом составляется уравнение этой касательной в виде y=кx+b.
В этом уравнении коэффициент к и будет являться значением производной. остается лишь найти значение коэффициента b. Для этого находим значение у при х=о, пусть оно равно 3 – это и есть значение коэффициента b. Подставляем в исходное уравнение значения Х0 и У0 и находим к – нашу значение производной в этой точке.
Тест 1 производная правила дифференцирования вариант 1
Тест 1
Производная
Правила дифференцирования
Вариант 1
А1. Найдите производную функции .
1) 12х2 2) 12х 3) 4х2 4) 12х3
А2. Найдите производную функции .
1) -5 2) 11 3) 6 4) 6х
А3. Найдите производную функции .
Найдите производную функции .
1) 2) 3) 4)
А4. Найдите производную функции .
1) 2) 3) 4)
А5. Найдите производную функции .
1) 2) 3) 4)
А6. Вычислите значение производной функции в точке хо=2.
1) 10 2) 12 3) 8 4) 6
А7. Найдите производную функции .
1) 2) 3) 4)
А8. Вычислите значение производной
функции в точке хо=
4.
Вычислите значение производной
функции в точке хо=
4.
1) 21 2) 24 3) 0 4) 3,5
А9. Вычислите значение производной функции
в точке . 1) 2 2) 3) 4 4)
А10. Найдите производную функции .
1) 2) 3) 4)
В1. Вычислите значение производной функции в точке хо= 26.
В2. Найдите значение х, при которых производная функции равна 0.
Тест 1
Производная
Правила дифференцирования
Вариант 2
А1. Найдите производную функции .
Найдите производную функции .
1) 2) 3) 4)
А2. Найдите производную функции .
1) 7 2) 12 3) -5 4) -5х
А3. Найдите производную функции .
1) 2) 3) 4)
А4. Найдите производную функции .
1) 2) 3) 4)
А5. Найдите производную функции
.
Найдите производную функции
.
1) 2) 3) 4)
А6. Вычислите значение производной функции в точке хо=2.
1) 13 2) 3 3) 8 4) 27
А7. Найдите производную функции .
1) 2) 3) 4)
А8. Вычислите значение производной функции в точке .
1) -47 2) -49 3) 47 4) 11,5
А9. Вычислите значение производной функции
в точке . 1) 2 2) -1 3) -2 4)
А10. Найдите производную функции .
1) 2) 3) 4)
В1. Вычислите значение производной
функции в точке хо=
-7.
Вычислите значение производной
функции в точке хо=
-7.
В2. Найдите значение х, при которых производная функции равна 0.
Ответы:
Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | В1 | В2 |
1 | 1 | 3 | 4 | 2 | 3 | 2 | 3 | 1 | 1 | 4 | 2 | 4 |
2 | 2 | 3 | 3 | 1 | 4 | 1 | 2 | 2 | 3 | 3 | -9 | -4 |
Зачет по алгебре и началам анализа в 11 классе “ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ”
ЗАЧЕТЫ
ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА
В 11 КЛАССЕ
Учитель математики: Чубарь Нина
Сергеевна
Зачет по теме:
«Производная и её применение»
Теоретические вопросы:
Приращение функции и аргумента.

Определение производной.
Геометрический и физический смысл производной.
Мгновенная скорость.
Таблица производных элементарных функций.
Правила вычисления производных (производная суммы,
разности, произведения и частного).
Производная сложной функции.
Непрерывность функции. Метод интервалов.
Критические точки функции.
Стационарные точки.
Точки перегиба.
Точки экстремума функции.
Необходимое и достаточное условие существования
экстремума функции.
Наибольшее и наименьшее значение функции.
Уравнение касательной функции.
Признак возрастания и убывания функции.
Приближенные вычисления.
Исследование функции с помощью производной.
Задачи
Уровень А
–каждое задание оценивается в 3 балла
Найдите приращение функции в точке х0, если f(x)=; х0=3; Δх =0,1.

Вычислите значение производной функции f(x) = 4x7+6x4+10x при х=1.
Решите неравенство f'(x)>0, если f(x)=-6x2-15x.
Вычислите производную функции f(x)=
Найдите значение производной функции при заданном значении аргумента, если f(x)=2 tg x; x0=0.
Решите уравнение: f'(x)=0, если f(x)=-x3+4х2-9x.
Вычислите в точке х0, если f(x)=15x2-7, х0=2, Δх =0,5.
Вычислите значение производной функции f в данной точке, если
f(x)=2х ∙ cosx; x0=0.
Найдите значения х, при которых производная функции f равна нулю, если f(x)=2 x4-16х3.
Решите неравенство (3х-6)(2х+4) ≥ 0.
Найдите область определения функции f(х) = .
Точка движется прямолинейно по закону х (t) = 6t3+2t-3.
 Найдите скорость в момент времени t= 2 с.
Найдите скорость в момент времени t= 2 с.Найдите промежутки возрастания функции f(х) = 7х2-8х+3
Найдите критические точки функции f(х) = 8х3-5х2-4.
Определите, какие из них являются точками максимума, а какие – точками минимума.
Докажите, что функция f(х) = 6х5+4х не имеет критических точек.
Найдите промежутки убывания функции f(х) = 4+16х-х
Напишите уравнение касательной к графику функции f(х) = х3-6 в точке с абсциссой х0 = -1 Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку А (1;2) графика функции f(х) = х2+4х
Уровень В
–каждое задание оценивается в 4 балла
Найдите мгновенную скорость точки, движущейся по закону х (t)=t2-4, в момент времени t0=4.
Найдите f'(x), f'(-2), если f(x) = (2+)(x-2).
Решите неравенство f'(x)>0, если f(x)=sin2x.
Найдите производную данной функции f(x)=. Вычислите
2f'(-2)+3f (1).
Вычислите значение производной функции при заданном значении аргумента, если f(x)= ()∙ ctgx; x0=.
Составьте и решите уравнение: f'(x)= f(x) – 3х, если f(x)=3х+.
Найдите производную функции f(x)=(2-)∙tg2x.
Решите уравнение f'(x)=0, если f(x)=1,5sin2x-5sinx-x.
Докажите, что при всех допустимых значениях х производная функции g(x) не может принимать отрицательных значений, если: g(x)=tg.
Вычислите приближенное значение 1,005100.
На графике функции g(х) = найдите точку, в которой касательная к графику параллельна оси абсцисс.
Найдите угловой коэффициент касательной к графику функции
f(х) = (х2+2)(х3-3), в точке х0 = 2.
Найдите точки экстремума функции f(х) = (х+1)2(х+5)2.
Найдите критические точки функции f(х) = sin.
Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 6 с. Найдите угловую скорость через 40с после начала вращения.
Найдите наибольшее значение функции f(х) = (х+1)2(х+4) на данном промежутке [-5;0]
Исследуйте функцию у= 2х2+3х-5 и постройте её график.
При каких значениях n функция f(х) = непрерывна на всей числовой прямой.
Уровень C
– каждое задание оценивается в 5 баллов
Найдите корни уравнения f ‘(x)=0, принадлежащие отрезку [], если f(х) = cos (.
Найдите производную функции f(x) =, в точке х0=.
Укажите, какой формулой можно задать функцию у= f(x), если
f ‘(x)=-20 (4-5х)3.
Найдите точки, в которых f ‘(х)=0, f ‘(x)>0, если f (x)=4x+cos (4x-).
Найдите значения аргумента, удовлетворяющие условию f ‘(х)=g’ (x), если f(x)= , g (x) =.
Найдите производную функции у=tg(3x-), в точке х0=.
Дано: f(x) = csin2x+ d cosx, f ‘()= 4; f ‘()=-8. Чему равны c и d?
Вычислите скорость изменения функции у= cos () в точке х0=.
При каких значениях х выполняется равенство f ‘(х)=2, если известно, что
f (х)=2-5?
Исследуйте функцию и постройте её график: у = .
Среди всех равнобедренных треугольников с боковой стороной 5 см найдите треугольник наибольшей площади.
Исследуйте функцию у=х2 и постройте её график.
Найдите точки экстремума функции f(х) = cos 2х+2sin х .
Известно, что наименьшее значение функции f(х) = 3х2-х3 на промежутке
[-2; в] равно нулю. При каком максимальном значении выполняется это
условие?
Составьте уравнение касательной к графику функции f(х) =, если её угловой коэффициент равен к=.
Примеры решения задач по теме: «Производная»
1). Найдите приращение функции в точке х0, если f(x)=; х0=1; Δх =0,1.
Решение:
1. Находим значение х0+Δх: х0+Δх=1+0,1=1,1
2. Вычисляем значение f(x0): f(1)=
3.Вычисляем значение f(x0+Δх): f(1,1)=
4. Находим приращение функции Δf(x): Δf(x)= f(1,1)- f(1)=0,605- 0,5=0,105
Ответ: Δf(x)=0,105
2). Вычислите значение производной функции f(x) = 8x6+5x3+12x при х=1.
Решение:
1. f ‘(x) = (8x6)’ +(5x3)’ +(12x)’=8∙6х5+5∙3х2+12∙1=48х5+15х2+12
2. f ‘(1)= 48∙15+15∙12+12=75
Ответ: 75
3). Решите неравенство f ‘(x)>0, если f(x)= -10x2-17x.
Решение:
1. f ‘(x)=(-10x2)’- (17x)’= -10∙2х-17∙1= -20х-17
2. f ‘(x)>0, -20х-17>0, -20х >17, х< –
Ответ: f ‘(x)>0, при х<-.
4). Вычислите производную функции f(x)=
Решение:
f ‘(x)==
5). Найдите значение производной функции при заданном значении аргумента, если f(x)=5 tgx, x0=.
Решение:
1. f ‘(x)=( 5 tgx)’=5∙
2. f ‘()=5∙
Ответ: f ‘()=20
6). Решите уравнение: f ‘(x)=0, если f(x)=x3+х2-3x.
Решение:
1. f ‘(x)=(x3)’+(х2)’-(3x)’=∙3x2+∙2х-3∙1=2х2+х-3
2. f ‘(x)=0, 2х2+х-3=0, D= в2-4ас=12-4∙2∙ (-3)=25,
х1=
х2=
Ответ: f ‘(x)=0, при х = -1,5; 1
7). Вычислите значение производной функции в данной точке, если
f (x)=3х∙sin x, x0=0
Решение:
1. (u∙v)’=u’∙v + u∙v’
f ‘(x)=(3x)’ sin x + 3x ∙(sin x)’ = 3 ∙sin x + 3x ∙ cos x
2. f ‘(0)= 3∙ sin 0 + 3∙ 0 ∙cos 0 = 3 ∙0 + 0 ∙1 = 0
Ответ: f ‘(0)= 0
Примеры решения задач по теме «Применение производной»
1). Решите неравенство (4х-6)(5х+10) ≥ 0.
Решение:
1. Рассмотрим функцию у= (4х-8)(5х+10)
2. Найдем нули функции: у=0, (4х-8)(5х+10) = 0, 4х-8=0 или 5х+10=0
4х=8 5х=-10
+ _ +
3. “”””∙ ∙””””” х
-2 2
Ответ: (],
2). Найдите область определения функции f(х) = .
Решение:
1. Решим неравенство: 2х2+х-3≥ 0
2. Рассмотрим функцию у=2х2+х-3 и найдем ее нули:
2х2+х-3=0, D= в2-4ас=12-4∙2∙ (-3)=25,
х1=
х2=
+ – +
3. “”””∙ ∙””””” х
-1,5 1
Ответ: (],
3). Точка движется прямолинейно по закону х (t) = 5t3+30t-7 (м). Найдите скорость в момент времени t= 1 с.
Решение:
1. v(t)= х ‘(t) =(5t3+30t-7)’=5∙3t2+30∙1-0=15 t2+30
2. v(1)= 15 ∙12+30= 45 (м/с)
Ответ: v(1)= 45 м/с.
4). Найдите промежутки возрастания и убывания функции f(х) = 10х2-2х+1
Решение:
1. Область определения функции: D(f)=R
2. Найдем производную функции: f ‘(х) = (10х2-2х+1)’=10∙2х-2∙1+0=20х-2
3. Решим неравенства: а) f ‘(х)>0, б) f ‘(х)<0.
20х-2>0 20х-2<0
20х>2 20х<2
х > х <
Ответ: функция f(х) = 10х2-2х+1 возрастает при х >, убывает при х < .
5). Найдите критические точки функции f(х) = 5х3+3х2-1
Определите, какие из них являются точками максимума, а какие – точками минимума.
Решение:
1. Найдем производную данной функции: f (х) = (5х3+3х2-1)’=
=5∙3х2+3∙2х-0=15х2+6х
2. Найдем критические точки: f ‘(х)=0, 15х2+6х=0, 3х (5х+2)=0, х=0 или 5х+2=0, 5х = -2, х = -0,4
+ – +
3. “”””∙ ∙””””” х
-0,4 0
max min
Ответ: хmax= -0,4, xmin=0.
6). Напишите уравнение касательной к графику функции f(х) = 3х3+4 в точке с абсциссой х0 = 2.
Решение:
1. Найдем у0= f (х0): f(2)= 3∙23+4=28
2. Найдем f ‘(х): f ‘(х)= (3х3+4)’=3∙3х2+0=9х2
3.Найдем f ‘(х0): f ‘(2)=9∙22=36
4. Подставим полученные результаты в уравнение касательной:
у= у0 + f ‘(х0)∙ (х-х0):
у=28+36(х-2), у=28+36х-72, у=36х-44- искомое уравнение касательной.
7). Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку А (2;-3) графика функции f(х) =х3+2х.
Решение:
1. Найдем производную: f ‘(х) =(х3+2х)’=3х2+2
2. Найдем f ‘(х): f ‘(2)= 3∙22+2=14
3. tg= f ‘(2)=14
Ответ: 14
Литература.
1. Алгебра и начала математического анализа 10 класс. Учебник. Базовый и профильный уровни Никольский С.М. и др. 8-е изд. – М.: Просвещение, 2009.
2. А.П. Ершова, В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов.
3.Ю.А. Глазков, И.К. Варшавский, М.Я. Галашвили. Тесты по алгебре и началам анализа. 10 класс. Издательство «Экзамен». Москва,2010.
Задание №7. Производная. Поведение функции. Первообразная
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке
Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой в точке
При значения выражений и равны.
При этом производная функции равна угловому коэффициенту касательной, то есть .
Из второго уравнения находим или Первому уравнению удовлетворяет только .
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени получим:
.
Ответ: 3
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция возрастает.
Если , то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.
Производная функции в точках максимума и минимума функции Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке
Функция для которой является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» – в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
В какой точке значение производной набольшее
Дорогие друзья! В группу заданий связанных с производной входят задачи — в условии дан график функции, несколько точек на этом графике и стоит вопрос:
В какой точке значение производной наибольшее (наименьшее)?
Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.
Кратко повторим:
Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.
Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.
*Имеется ввиду угол между касательной и осью абсцисс.
Далее:
1. На интервалах возрастания функции производная имеет положительное значение.
2. На интервалах её убывания производная имеет отрицательное значение.
Рассмотрим следующий эскиз:
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.
В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.
Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.
При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки 3, 5 и 6 образуют с осью оХ углы лежащие в пределах от 0 до 90о, а прямые проходящие через точки 1, 2 и 4 образуют с осью оХ углы в пределах от 90о до 180о.
*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.
Теперь важный вопрос!
А как изменяется значение производной? Ведь касательная в разных точках графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.
*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:
Прямые образуют с осью оХ углы в пределах от 0 до 90о
Прямые образуют с осью оХ углы в пределах от 90о до 180о
Поэтому, если будут стоять вопросы:
— в какой из данных точек графика значение производной имеет наименьше значение?
— в какой из данных точек графика значение производной имеет наибольшее значение?
то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180о.
*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.
Значение тангенса изменяется следующим образом:
При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;
При изменении угла наклона прямой от 90о до 180о значение тангенса, а значит и производной, изменяется соответственно –∞ до 0.
Наглядно это видно по графику функции тангенса:
Говоря простым языком:
При угле наклона касательной от 0о до 90о
Чем он ближе к 0о, тем больше значение производной будет близко к нулю (с положительной стороны).
Чем угол ближе к 90о, тем больше значение производной будет увеличиваться к +∞.
При угле наклона касательной от 90о до 180о
Чем он ближе к 90о, тем больше значение производной будет уменьшаться к –∞.
Чем угол будет ближе к 180о, тем больше значение производной будет близко к нулю (с отрицательной стороны).
317543. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки –1 и 1) и две интервалам на которых функция возрастает (это точки –2 и 2).
Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим.
Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.
Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:
Видим, что тупой угол между прямой b и осью оХ находится «ближе» к 180о, поэтому его тангенс будет больше тангенса угла, образованного прямой а и осью оХ.
Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.
317544. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки –1 и 4) и две интервалам, на которых функция возрастает (это точки –2 и 1).
Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках –2 и 1 она имеет положительное значение. Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке х = 4 будет наименьшим.
Ответ: 4
Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180о.
Общие рекомендации:
1. Сначала определите знаки производной в данных точках (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).
2. Постройте касательные в этих точках.
3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.
4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.
*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без графика.
На этом всё. Успехов Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Вычислить значение производной в точке x 0 – Telegraph
Вычислить значение производной в точке x 0Скачать файл – Вычислить значение производной в точке x 0
В общем случае, что бы найти значение производной какой-либо функции по некоторой переменной в какой-либо точке, нужно продифференцировать заданную функцию по этой переменной. В вашем случае по переменной Х. В полученное выражение вместо Х поставить значение икса в той точке, для которой надо найти значение производной, то есть в Вашем случае подставить нулевой Х и вычислить полученное выражение. Такая постановка задачи на нахождение производной часто ставится для закрепления материала на геометрический смысл производной. Предлагается график некоей функции, совершенно произвольной и не заданной уравнением и требуется найти значение производной не саму производную заметьте! Для этого строится касательная к заданной функции и находится точки ее пересечения с осями координат. В этом уравнении коэффициент к и будет являться значением производной. Подставляем в исходное уравнение значения Х0 и У0 и находим к – нашу значение производной в этой точке. Если вы у нас впервые: Как найти значение производной функции f x в точке x0? Потому, что до моего ответа рейтинг этого вопроса был минус 1. Никогда бы не догадался: Видимо, поставивший минус посчитал, что такой вопрос задавать неприлично примерно как ‘сколько будет семью девять’. Ил, Вы меня удивляете Думаю Вам самому сейчас станет смешно и не понятно, как это Вы не обратили внимание на комментарий к вопросу. Ну а разве стремление к знаниям не заслуживает поощрения? Комментарий к вопросу – это ‘нет конкретно поставленного вопроса’. Но вроде не обязательно было приводить какую-нибудь конкретную функцию. Вы дали ответ в общем виде и Юля, очевидно, его поняла. А по поводу ‘Ну а разве стремление к знаниям не заслуживает поощрения? Как найти общее решение дифференциального уравнения? Как найти книжку об интегралах? Как найти в Интернете Фото по Фото? На Востоке её называют ‘точкой долголетия’. Как найти эту точку? Как найти андроид если потерял или украли? Как найти первые фотографии в инстаграме? Где и как найти свое добавленное фото на проекте ЯРОССИЯ ТВканала Россия1? Как найти все видео на компьютере, на планшете, на телефоне? Как найти блогеров для рекламы в Инстаграм Instagram? Какие жаркие районы есть на Земле? Как найти эти районы на глобусе? Задайте его нашему сообществу, у нас наверняка найдется ответ! Делитесь опытом и знаниями, зарабатывайте награды и репутацию, заводите новых интересных друзей! Задавайте интересные вопросы, давайте качественные ответы и зарабатывайте деньги. Статистика проекта за месяц. Помогите нам стать лучше. Введите контрольное число с картинки:
Решение задач по математике онлайн
Как научиться правильно жить
Настроить биос ami
Производная функции в точке
Сколько раз кормить ребенка в 5 месяцев
Эл схема rgb контроллерана atmel268
Характеристика цветка мак
Открытки с добрым днем и хорошим настроением
Бесплатная помощь с домашними заданиями
Определение беременности без теста дома
Час счастья текст
Классификация методов и приемов обучения
Задача 7 — геометрический смысл производной
Заявление на утилизацию автомобиля образец заполнения
Проверитьсебяв черных списках россии
Бочка для купания своими руками
AC Производная функции в точке
Мгновенная скорость изменения функции – это идея, которая лежит в основе исчисления. Это обобщение понятия мгновенной скорости, измеряющее, насколько быстро конкретная функция изменяется в данной точке. Если исходная функция представляет положение движущегося объекта, эта мгновенная скорость изменения и есть скорость объекта. В других контекстах мгновенная скорость изменения может измерять количество клеток, добавляемых к культуре бактерий в день, количество дополнительных галлонов бензина, потребляемых за счет увеличения скорости автомобиля на одну милю в час, или количество долларов, добавленных к выплате по ипотеке. за каждый процентный пункт увеличения процентной ставки.Мгновенную скорость изменения также можно интерпретировать геометрически на графике функции, и эта связь является фундаментальной для многих основных идей в исчислении.
Напомним, что для движущегося объекта с функцией положения \ (s \ text {,} \) его средняя скорость на временном интервале от \ (t = a \) до \ (t = a + h \) определяется как частное
\ begin {уравнение *} AV _ {[a, a + h]} = \ frac {s (a + h) -s (a)} {h} \ text {.} \ end {уравнение *}
Аналогичным образом мы даем следующее определение для произвольной функции \ (y = f (x) \ text {.} \)
Определение 1.3.1.
Для функции \ (f \ text {,} \) средняя скорость изменения \ (f \) на интервале \ ([a, a + h] \) задается значением
\ begin {уравнение *} AV _ {[a, a + h]} = \ frac {f (a + h) -f (a)} {h} \ text {.} \ end {уравнение *}
Эквивалентно, если мы хотим рассмотреть среднюю скорость изменения \ (f \) на \ ([a, b] \ text {,} \), мы вычисляем
\ begin {уравнение *} AV _ {[a, b]} = \ frac {f (b) -f (a)} {b-a} \ text {.} \ end {уравнение *}
Важно, чтобы вы понимали, как средняя скорость изменения \ (f \) на интервале связана с его графиком.
Предварительный просмотр 1.3.1.
Предположим, что \ (f \) – функция, заданная приведенным ниже графиком, а \ (a \) и \ (a + h \) – входные значения, отмеченные на оси \ (x \) -. Используйте график на рисунке 1.3.2, чтобы ответить на следующие вопросы.
Рисунок 1.3.2. График \ (y = f (x) \) для предварительного просмотра 1.3.1.Найдите и пометьте точки \ ((a, f (a)) \) и \ ((a + h, f (a + h)) \) на графике.
Постройте прямоугольный треугольник, гипотенуза которого представляет собой отрезок прямой от \ ((a, f (a)) \) до \ ((a + h, f (a + h)) \ text {.} \) Каковы длины соответствующих катетов этого треугольника?
Каков наклон линии, соединяющей точки \ ((a, f (a)) \) и \ ((a + h, f (a + h)) \ text {?} \)
Напишите содержательное предложение, объясняющее, как связаны средняя скорость изменения функции на заданном интервале и наклон соответствующей линии.
Подраздел 1.3.1 Производная функции в точке
Так же, как мы определили мгновенную скорость в терминах средней скорости, теперь мы определяем мгновенную скорость изменения функции в точке в терминах средней скорости изменения функции \ (f \) в связанных интервалах.Эта мгновенная скорость изменения \ (f \) в \ (a \) называется «производной от \ (f \) в \ (a \ text {,} \)» и обозначается \ (f ‘ (а) \ text {.} \)
Определение 1.3.3.
Пусть \ (f \) будет функцией, а \ (x = a \) значением в области определения функции. Мы определяем производную от \ (f \) относительно \ (x \), вычисленную в \ (x = a \) , обозначенную \ (f ‘(a) \ text {,} \) по формуле
.\ begin {уравнение *} f ‘(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ text {,} \ end {уравнение *}
при условии, что этот предел существует.
Вслух мы читаем символ \ (f ‘(a) \) как «\ (f \) – простое число в \ (a \)» или «производная от \ (f \), вычисленная в \ (x = a \ text {.} \) »Большая часть следующих нескольких глав будет посвящена пониманию, вычислению, применению и интерпретации производных. А пока отметим следующие важные вещи.
Сначала мы рассматриваем производную при заданном значении как наклон определенной линии.
Когда мы вычисляем мгновенную скорость изменения, мы позволяем интервалу \ ([a, a + h] \) сокращаться как \ (h \ to 0 \ text {.} \) Мы можем рассматривать одну конечную точку интервала как «скользящую по направлению» к другой. В частности, при условии, что \ (f \) имеет производную в \ ((a, f (a)) \ text {,} \), точка \ ((a + h, f (a + h)) \) будет подход \ ((a, f (a)) \) как \ (h \ to 0 \ text {.} \) Поскольку процесс принятия ограничения является динамическим, может быть полезно использовать вычислительные технологии для его визуализации. . Один из вариантов – это Java-апплет, в котором пользователь может управлять движущейся точкой. Чтобы получить полезную коллекцию примеров, рассмотрите работу Дэвида Остина из Государственного университета Гранд-Вэлли и этот особенно важный пример.Для апплетов, созданных в Geogebra 1 , см. Библиотеку Марка Рено через Университет Шиппенсбурга, этот пример особенно подходит для нашей работы в этом разделе.
Вы даже можете подумать о создании своих собственных примеров; фантастическая программа Geogebra доступна для бесплатной загрузки, ее легко изучить и использовать.На рис. 1.3.5 показана последовательность фигур с несколькими разными линиями, проходящими через точки \ ((a, f (a)) \) и \ ((a + h, f (a + h)) \ text {,} \ ), генерируемые разными значениями \ (h \ text {.} \) Эти линии (показаны на первых трех рисунках пурпурным цветом) часто называют секущими линиями кривой \ (y = f (x) \ text {.} \) Секущая линия кривой – это просто линия, проходящая через две точки на кривой. Для каждой такой линии наклон секущей линии равен \ (m = \ frac {f (a + h) – f (a)} {h} \ text {,} \), где значение \ (h \) зависит от расположения выбранной нами точки. Мы можем видеть на диаграмме, как при \ (h \ to 0 \ text {,} \) секущие линии начинают приближаться к единственной линии, проходящей через точку \ ((a, f (a)) \ text {.} \) Если предел наклона секущих линий существует, мы говорим, что результирующее значение – это наклон касательной линии к кривой. Эта касательная линия (показанная на крайнем правом рисунке зеленым цветом) к графику \ (y = f (x) \) в точке \ ((a, f (a)) \) имеет наклон \ (m = f ‘(а) \ text {.} \)
Рисунок 1.3.5. Последовательность секущих линий, приближающихся к касательной к \ (f \) в \ ((a, f (a)) \ text {.} \)Если касательная линия в \ (x = a \) существует, график of \ (f \) выглядит как прямая линия, если смотреть с близкого расстояния в \ ((a, f (a)) \ text {.} \) На рис. 1.3.6 мы объединяем четыре графика на рис. 1.3.5 в один слева и увеличиваем масштаб прямоугольника с центром в \ ((a, f (a)) \) справа. Обратите внимание на то, как касательная линия расположена относительно кривой \ (y = f (x) \) в точке \ ((a, f (a)) \) и насколько она похожа на кривую рядом с \ (x = a \ text {. } \)
Рисунок 1.3.6. Последовательность секущих линий, приближающихся к касательной к \ (f \) в \ ((a, f (a)) \ text {.} \) Справа мы увеличиваем точку \ ((a, f (a) )) \ text {.} \) Наклон касательной (выделенной зеленым цветом) к \ (f \) в точке \ ((a, f (a)) \) задается как \ (f ‘(a) \ text {.2} {h} \ text {.} \ end {уравнение *}Затем мы удаляем общий множитель \ (h \) как в числителе, так и в знаменателе и находим, что
\ begin {уравнение *} f ‘(2) = \ lim_ {h \ to 0} (-3-h) \ text {.} \ end {уравнение *}
Наконец, мы можем взять предел как \ (h \ to 0 \ text {,} \) и, таким образом, сделать вывод, что \ (f ‘(2) = -3 \ text {. 2 \) в точке \ ((2, -2) \ text {.2 \) в точке \ ((2, -2) \ text {.} \)
Следующие упражнения помогут вам изучить множество ключевых идей, связанных с производными финансовыми инструментами.
Мероприятие 1.3.2.
Рассмотрим функцию \ (f \), формула которой имеет вид \ (\ displaystyle f (x) = 3–2x \ text {.} \)
- Какой знакомый тип функции – \ (f \ text {?} \) Что вы можете сказать о наклоне \ (f \) при каждом значении \ (x \ text {?} \)
- Вычислить среднюю скорость изменения \ (f \) на интервалах \ ([1,4] \ text {,} \) \ ([3,7] \ text {,} \) и \ ([5, 5 + h] \ text {;} \) максимально упростите каждый результат.Что вы заметили в этих количествах?
- Используйте определение предела производной, чтобы вычислить точную мгновенную скорость изменения \ (f \) по отношению к \ (x \) при значении \ (a = 1 \ text {.} \), То есть вычислить \ (f ‘(1) \) с использованием определения предела. Показать свою работу. Ваш результат удивителен?
- Без дополнительных вычислений, каковы значения \ (f ‘(2) \ text {,} \) \ (f’ (\ pi) \ text {,} \) и \ (f ‘(- \ sqrt {2}) \ text {?} \) Почему?
Мероприятие 1.3.3.2 + 16t + 32 \ text {.} \) Используйте эту функцию, чтобы ответить на каждый из следующих вопросов.
Нарисуйте точный помеченный график \ (s \) по осям, представленным на рисунке 1.3.10. Вы должны уметь делать это без использования вычислительной техники.
Рисунок 1.3.10. Оси для построения \ (y = s (t) \) в упражнении 1.3.3.- Вычислите среднюю скорость изменения \ (s \) на временном интервале \ ([1,2] \ text {.} \) Включите единицы в свой ответ и напишите одно предложение, чтобы объяснить значение найденного вами значения.
- Используйте определение предела, чтобы вычислить мгновенную скорость изменения \ (s \) относительно времени, \ (t \ text {,} \) в момент \ (a = 1 \ text {.} \). Покажите свой используйте правильные обозначения, включите единицы в свой ответ и напишите одно предложение, чтобы объяснить значение найденного вами значения.
- На вашем графике в (a) нарисуйте две линии: одна, наклон которой представляет собой среднюю скорость изменения \ (s \) на \ ([1,2] \ text {,} \), другая, наклон которой представляет мгновенное скорость изменения \ (s \) в момент \ (a = 1 \ text {.{t / 5} \ text {.} \) Используйте эту функцию, чтобы ответить на следующие вопросы.
Нарисуйте точный график \ (P \) для значений от \ (t = 0 \) до \ (t = 5 \) по осям, представленным на рисунке 1.3.11. Тщательно промаркируйте шкалу на осях.
Рисунок 1.3.11. Оси для построения \ (y = P (t) \) в упражнении 1.3.4.- Вычислите среднюю скорость изменения \ (P \) между 2030 и 2050 годами. Включите единицы в свой ответ и напишите одно предложение, чтобы объяснить значение (на повседневном языке) найденного вами значения.
- Используйте определение предела, чтобы написать выражение для мгновенной скорости изменения \ (P \) относительно времени, \ (t \ text {,} \) в момент \ (a = 2 \ text {.} \ ) Объясните, почему этот предел трудно точно оценить.
- Оцените предел в (c) для мгновенной скорости изменения \ (P \) в момент \ (a = 2 \), используя несколько небольших значений \ (h \). Как только вы определили точную оценку \ (P ‘(2) \ text {,} \), включите единицы в свой ответ и напишите одно предложение (используя повседневный язык), чтобы объяснить значение найденного вами значения.
- На приведенном выше графике нарисуйте две линии: одна, наклон которой представляет собой среднюю скорость изменения \ (P \) на \ ([2,4] \ text {,} \), другая, наклон которой представляет мгновенную скорость изменения. \ (P \) в момент \ (a = 2 \ text {.} \)
- В тщательно сформулированном предложении опишите поведение \ (P ‘(a) \) при увеличении значения \ (a \). Что это отражается на поведении данной функции \ (P \ text {?} \)
Вычислить значение производной в начале координат
Вычислить значение производной в начале координат – Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 815 раз
$ \ begingroup $У меня в курсе следующий вопрос:
Пример логистической функции определяется $$ \ varphi (v) = \ frac {1} {1 + e ^ {- av}} $$ чьи предельные значения равны $ 0 $ и $ 1 $.Покажите, что производная $ \ varphi (v) $ по $ v $ определяется выражением $$ \ frac {\ mathrm {d} \ varphi} {\ mathrm {d} v} = a \ varphi (v) [1- \ varphi (v)] $$ Какова стоимость этой производной в начале координат?
Первая часть решена, но я не мог понять вторую (каково значение этой производной в начале координат?).
Кто-нибудь может мне помочь? Заранее спасибо.
BLAZE8,877913 золотых знаков3838 серебряных знаков8484 бронзовых знака
Создан 18 окт.
$ \ endgroup $ 6 $ \ begingroup $Поскольку ваша функция $$ \ varphi (v) = \ frac {1} {1 + e ^ {- av}} $$ является функцией только одной переменной (которая равна $ v $), значение производной в начале координат задается установкой $ v = 0 $ в вашем уравнении для $$ \ frac {\ mathrm {d} \ varphi } {\ mathrm {d} v} = \ frac {a} {1 + e ^ {- av}} \ left [1- \ frac {1} {1 + e ^ {- av}} \ right] = \ frac {a} {1 + e ^ {- a \ cdot 0}} \ left [1- \ frac {1} {1 + e ^ {- a \ cdot 0}} \ right] = \ frac {a} { 1 + 1} \ left [1- \ frac {1} {1 + 1} \ right] = \ frac {a} {4} $$
Создан 18 окт. 2} = \ frac {a} {4} $$
Создан 18 окт.
$ \ endgroup $ $ \ begingroup $Предельные значения – это пределы приближения функции к положительной или отрицательной бесконечности.Изобразите функцию с любым $ \ alpha $, и вы увидите результат.
Создан 18 окт.
$ \ endgroup $Не тот ответ, который вы ищете? Просмотрите другие вопросы с метками производные или задайте свой вопрос.
Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
исчисление – вычислить первую производную без функции?
Один известный мне способ требует предположения, что функция достаточно хороша, т.е.{(k)} = 0 $ для $ k \ ge n $. Однако матрично-векторное уравнение намного проще в использовании (по крайней мере, на мой взгляд).
Как оценить производную по графику
Обновлено 8 декабря 2020 г.
Ли Джонсон
Темпы изменений проявляются повсюду в науке, и особенно в физике, через такие величины, как скорость и ускорение. Производные описывают скорость изменения одной величины по отношению к другой математически, но их вычисление иногда может быть сложным, и вам может быть представлен график, а не функция в форме уравнения.Если вам представлен график кривой и вам нужно найти производную от него, вы, возможно, не сможете быть столь же точными, как с уравнением, но вы легко сможете сделать твердую оценку.
TL; DR (слишком долго; не читал)
Выберите точку на графике, в которой нужно найти значение производной.
Проведите в этой точке прямую касательную к кривой графика.
Определите наклон этой прямой, чтобы найти значение производной в выбранной вами точке на графике.
Что такое производная?
Если не считать абстрактной установки дифференцирования уравнения, вы можете немного запутаться в том, что на самом деле представляет собой производная. В алгебре производная функции – это уравнение, которое сообщает вам значение «наклона» функции в любой точке. Другими словами, он сообщает вам, насколько изменяется одно количество при небольшом изменении другого. На графике градиент или наклон линии показывают, насколько зависимая переменная (размещенная на оси y ) изменяется с независимой переменной (на оси x ).
Для прямолинейных графиков вы определяете (постоянную) скорость изменения, вычисляя наклон графика. Отношения, описываемые кривыми, не так просты, но принцип, согласно которому производная просто означает наклон (в этой конкретной точке), все еще остается в силе.
Для отношений, описываемых кривыми, производная принимает разные значения в каждой точке кривой. Чтобы оценить производную графика, вам нужно выбрать точку, в которой будет производная.Например, если у вас есть график, показывающий пройденное расстояние в зависимости от времени, на прямолинейном графике наклон будет указывать вам постоянную скорость. Для скоростей, которые меняются со временем, график будет кривой, но прямая линия, которая только касается кривой в одной точке (линия, касательная к кривой), представляет скорость изменения в этой конкретной точке.
Выберите место, где вам нужно знать производную. Используя пример зависимости пройденного расстояния от времени, выберите время, в которое вы хотите узнать скорость движения.Если вам нужно узнать скорость в нескольких разных точках, вы можете выполнить этот процесс для каждой отдельной точки. Если вы хотите узнать скорость через 15 секунд после начала движения, выберите точку на кривой через 15 секунд на оси x .
Нарисуйте линию, касательную к кривой в интересующей вас точке. Не торопитесь, потому что это самая важная и самая сложная часть процесса. Ваша оценка будет лучше, если вы проведете более точную касательную.Поднесите линейку к точке на кривой и отрегулируйте ее ориентацию так, чтобы линия, которую вы рисуете, касалась кривой только в той единственной точке, которая вас интересует.
Нарисуйте линию до тех пор, пока график позволяет . Убедитесь, что вы легко можете прочитать два значения для координат x и y , одно в начале строки, а другое в конце. Вам не обязательно рисовать длинную линию (технически подходит любая прямая линия), но более длинные линии, как правило, легче измерить наклон.
Найдите два места на вашей линии и запишите их координаты x и y . Например, представьте свою касательную линию в виде двух заметных точек на x = 1, y = 3 и x = 10, y = 30, которые вы можете назвать точкой 1. и точка 2. Использование символов x 1 и y 1 для представления координат первой точки и x 2 и y 2 для представления координат второй точки уклон м определяется как:
м = \ frac {y_2 – y_1} {x_2 – x_1}
Это показывает производную кривой в точке, где линия касается кривой.В этом примере x 1 = 1, x 2 = 10, y 1 = 3 и y 2 = 30, поэтому:
\ begin {align} m & = \ frac {30-3} {10-1} \\ \, \\ & = \ frac {27} {9} \\ \, \\ & = 9 \ end { выровнено}
В этом примере результатом будет скорость в выбранной точке. Таким образом, если ось x измеряется в секундах, а ось y – в метрах, результат будет означать, что рассматриваемое транспортное средство движется со скоростью 3 метра в секунду.Независимо от конкретной величины, которую вы рассчитываете, процесс оценки производной одинаков.
Как вычислять производные – видео и стенограмма урока
Вычислительные производные
Вы можете вспомнить нечто, называемое коэффициентом разности, из курса алгебры или предварительного исчисления. Коэффициент разности функции f ( x ) – это формула, которая дает наклон линии через любые две точки с координатами x x и x + h на функции:
( f ( x + h ) – f ( x )) / h
Это ключ к вычислению производных.Производные вычисляются путем нахождения предела коэффициента разности функции, когда h приближается к 0, как вы можете видеть ниже.
В принципе, мы можем вычислить производную f ( x ), используя определение предела производных, выполнив следующие шаги:
- Найти f ( x + h ).
- Вставьте f ( x + h ), f ( x ) и h в определение предела производной.
- Упростите коэффициент разницы.
- Возьмем предел упрощенного коэффициента разности, так как h приближается к 0.
Пример
Итак, рассмотрим нашу гоночную функцию f (x) = -7×2 + 280x. Сначала находим f ( x + h ):
f ( x + h ) = -7 ( x + h ) 2 + 280 ( x ). + h ) = -7 ( x 2 + 2 xh + h 2) + 280 x + 280 h = -7 x 2-14 xh -7 h 2 + 280 x + 280 h
Теперь мы подключаемся к определению предела, упрощаем и находим предел, как вы можете видеть здесь.
Хорошо. Теперь, когда вы это сделали, мы видим, что производная f ( x ) равна:
f ‘( x ) = -14 x + 280
Мы можем использовать эту формулу для расчета скорости победителя в любой момент гонки. Например, рассмотрим ее скорость через 10 секунд. Подставляем x = 10 в формулу производной:
f ‘( x ) = -14 (10) + 280 = 140
Мы получаем, что производная f при x = 10 составляет 140, так что за 10 секунд гонки она ехала со скоростью 140 миль в час! Вау, это так быстро!
Другой пример
Хорошо, еще один пример использования этого определения предела для вычисления производной.Рассмотрим функцию g ( x ) = 1/ x , где x ≠ 0. Чтобы найти производную, используя предельное определение производных, мы сначала находим g ( x + h ):
г ( x + h ) = 1 / ( x + h )
Теперь мы включаем g ( x + h ), g ( x ) и h в определение предела и находим предел, как вы можете видеть ниже.
Мы видим, что производная г ( x ) = 1/ x составляет г ‘( x ) = -1 / x 2.
Формулы для производных
Мы всегда можем использовать предельное определение производных для вычисления производных. Однако у нас также есть несколько хороших формул для производных различных типов общих функций. Эти формулы являются прямым результатом предельного определения функции.
Имея это под рукой, вы можете упростить задачу, поэтому не стесняйтесь просматривать таблицу ниже:
Давайте еще раз рассмотрим наш гоночный автомобиль. Из таблицы видно, что производная суммы функций – это сумма производных. Следовательно, производная нашей функции гоночного автомобиля, f ( x ) = -7 x 2 + 280 x , равна сумме производной -7 x 2 и 280 x . .
Чтобы найти эти производные, мы видим, что изображение дает формулу для производной функции вида ax n как nax ( n – 1).
Следовательно, производная от -7 x 2 равна (2) (- 7) x 2-1 = -14 x , а производная от 280 x равна (1) (280) x 0 = 280. Таким образом, производная от f ( x ) равна:
f ‘( x ) = -14 x + 280
. тот же результат, что и при использовании предельного определения производных.
Резюме урока
Производная функции, f ( x ), представляет собой скорость, с которой значение функции изменяется относительно x . Мы можем вычислять производные, используя определение предела производной, которое, как вы можете видеть здесь, выполняется путем нахождения предела разностного отношения функции, поскольку h приближается к 0:
Это определение предела можно не только использовать для вычисления производных, но мы также можем использовать его для нахождения формул для производных общих функций, которые могут значительно упростить вычисление производных в целом. 5}}}.\)
Пример 19
Найдите производную функции \ (y = {\ large \ frac {1} {x} \ normalsize} + {\ large \ frac {1} {{\ sqrt x}} \ normalsize} + {\ large \ frac { 1} {{\ sqrt [3] {x}}} \ normalsize}. \)Пример 20
Вычислить производную функции \ (y = {\ large \ frac {2} {{\ sqrt x}} \ normalsize} + 3 \ sqrt [\ large 3 \ normalsize] {x}. \)Пример 21
Найти производную функции \ (y = \ sqrt x – \ sqrt [3] {x}. \)Пример 22
Найдите производную иррациональной функции \ (y = \ sqrt {x \ sqrt x}.3}}}.} \]деривативов | Безграничное исчисление
Задача о производной и касательной
Использование дифференцирования позволяет решить задачу касательной линии путем нахождения наклона [латекс] f ‘(a) [/ латекс].
Цели обучения
Определите производную как наклон касательной к точке на кривой
Основные выводы
Ключевые моменты
- Касательная линия [латекс] t [/ латекс] (или просто касательная) к плоской кривой в данной точке – это прямая линия, которая «едва касается» кривой в этой точке.
- Прямая линия называется касательной к кривой [латекс] y = f (x) [/ latex] в точке [latex] x = c [/ latex] на кривой, если линия проходит через точку [ латекс] (c, f (c)) [/ латекс] на кривой и имеет наклон [латекс] f ‘(c) [/ латекс], где [латекс] f’ [/ латекс] является производным от [латекс] f [/латекс].
- Используя производные, уравнение касательной можно сформулировать следующим образом: [латекс] y = f (a) + f {(a)} ‘(x-a) [/ latex].
Ключевые термины
- касательная : линия, касающаяся кривой в одной точке, но не пересекающая ее в этой точке
- секущая : линия, пересекающая кривую в двух или более точках
Касательная линия [латекс] t [/ латекс] (или просто касательная) к плоской кривой в данной точке – это прямая линия, которая «только касается» кривой в этой точке.Неформально это прямая, проходящая через пару бесконечно близких точек кривой. Точнее, прямая линия называется касательной к кривой [латекс] y = f (x) [/ latex] в точке [latex] x = c [/ latex] на кривой, если линия проходит через точка [латекс] (c, f (c)) [/ latex] на кривой и имеет наклон [латекс] f ‘(c) [/ latex], где f ‘ – производная от [latex] f [/ latex ].
Касательная к кривой : линия показывает касательную к кривой в точке, представленной точкой.Он почти не касается кривой и показывает наклон скорости изменения в точке.
Предположим, что кривая задана как график функции, [латекс] y = f (x) [/ latex]. Чтобы найти касательную в точке [latex] p = (a, f (a)) [/ latex], рассмотрите другую ближайшую точку [latex] q = (a + h, f (a + h)) [/ latex ] на кривой. Наклон секущей линии, проходящей через [латекс] p [/ латекс] и [латекс] q [/ латекс], равен коэффициенту разности
.[латекс] \ displaystyle {\ frac {f (a + h) – f (a)} {h}} [/ latex].
Когда точка [латекс] q [/ латекс] приближается к [латексу] p [/ латексу], что соответствует уменьшению и уменьшению [латекса] h [/ латекса], коэффициент разности должен приближаться к определенному предельному значению [латекс] k [/ latex], который представляет собой наклон касательной в точке [latex] p [/ latex]. Если [латекс] k [/ латекс] известен, уравнение касательной можно найти в форме «точка-наклон»:
[латекс] y – f (a) = k (x-a) [/ латекс]
Предположим, что граф не имеет разрыва или острого края на [латексе] p [/ латексе], и он не вертикален и не слишком изгибается рядом с [латексом] p [/ latex].Затем существует уникальное значение [latex] k [/ latex], так что по мере приближения [latex] h [/ latex] к [latex] 0 [/ latex] коэффициент разности становится все ближе и ближе к [latex] k [ / latex], и расстояние между ними становится незначительным по сравнению с размером [latex] h [/ latex], если [latex] h [/ latex] достаточно мало. Это приводит к определению наклона касательной к графику как предела коэффициентов разности для функции [latex] f [/ latex]. Этот предел является производной функции [latex] f [/ latex] при [latex] x = a [/ latex], обозначаемой [latex] f ‘(a) [/ latex].Используя производные, уравнение касательной можно записать следующим образом:
[латекс] y = f (a) + f {(a)} ‘(x-a) [/ латекс].
Производные финансовые инструменты и курсы изменения
Дифференциация – это способ вычисления скорости изменения одной переменной по отношению к другой.
Цели обучения
Опишите производную как изменение [латекса] y [/ латекса] по сравнению с изменением [латекса] x [/ латекса] в каждой точке графика.
Основные выводы
Ключевые моменты
- Исторически основной мотивацией для изучения дифференцирования была проблема касательной линии, задача которой заключается в нахождении для данной кривой наклона прямой, касательной к этой кривой в данной точке.
- Если [латекс] y [/ latex] является линейной функцией [latex] x [/ latex], то [latex] m = \ frac {\ Delta y} {\ Delta x} [/ latex].
- Производная измеряет наклон графика в каждой точке.
Ключевые термины
- наклон : также называется градиентом; наклон или уклон линии описывает ее крутизну
Исторически основной мотивацией для изучения дифференцирования была проблема касательной линии, задача которой для данной кривой найти наклон прямой, касательной к этой кривой в данной точке.Слово тангенс происходит от латинского слова tangens , что означает прикосновение. Таким образом, чтобы решить проблему касательной, нам нужно найти наклон линии, которая «касается» данной кривой в данной точке, или, говоря современным языком, имеющей такой же наклон. Но что именно мы подразумеваем под «наклоном» кривой?
В простейшем случае [latex] y [/ latex] является линейной функцией от x, что означает, что график [latex] y [/ latex], деленный на [latex] x [/ latex], представляет собой прямую линию. В этом случае [латекс] y = f (x) = m x + b [/ latex] для действительных чисел m и b, а наклон m определяется по формуле:
[латекс] \ displaystyle {m = \ frac {\ Delta y} {\ Delta x}} [/ latex]
, где символ [латекс] \ Delta [/ latex] (заглавная форма греческой буквы Delta) означает и произносится как «изменение в.”Эта формула верна, потому что:
[латекс] y + \ Delta y = f (x + \ Delta x) = m (x + \ Delta x) + b = m x + b + m \ Delta x = y + m \ Delta x [/ latex]
Отсюда следует, что [латекс] \ Delta y = m \ Delta x [/ latex].
Наклон функции : функция с наклоном, показанным для данной точки.
Это дает точное значение наклона прямой. Однако, если функция [latex] f [/ latex] не является линейной (т. Е. Ее график не является прямой линией), то изменение [latex] y [/ latex] делится на изменение [latex] x [ / latex] варьируется: дифференциация – это метод нахождения точного значения для этой скорости изменения при любом заданном значении [латекс] x [/ латекс].Другими словами, дифференцирование – это метод вычисления скорости, с которой зависимый выход [latex] y [/ latex] изменяется по отношению к изменению в независимом входе [latex] x [/ latex]. Эта скорость изменения называется производной [латекса] y [/ латекса] по отношению к [латексу] x [/ латексу]. Точнее говоря, зависимость [латекса] y [/ латекса] от [латекса] x [/ латекса] означает, что [латекс] y [/ латекс] является функцией [латекса] x [/ латекса]. Эта функциональная связь часто обозначается [латекс] y = f (x) [/ latex], где [latex] f [/ latex] обозначает функцию.Если [latex] x [/ latex] и [latex] y [/ latex] являются действительными числами, и если график [latex] y [/ latex] строится против [latex] x [/ latex], производная измеряет наклон этого графика в каждой точке.
Производная как функция
Если каждая точка функции имеет производную, существует функция производной, отправляющая точку [latex] a [/ latex] производной от [latex] f [/ latex] в [latex] x = a [/ latex] : [латекс] ф ‘(а) [/ латекс].
Цели обучения
Объясните, как производная действует как «функция функций»
Основные выводы
Ключевые моменты
- Производная – это оператор, область определения которого представляет собой набор всех функций, имеющих производные в каждой точке своей области определения, а диапазон значений – набор функций.
- Функция, значение которой в [latex] x = a [/ latex] равно [latex] f ′ (a) [/ latex], когда [latex] f ′ (a) [/ latex] определено, а в другом месте не определено, также называется производной [латекс] ф [/ латекс].
- По определению производной функции [latex] D (f) (a) = f ′ (a) [/ latex], где [latex] D [/ latex] – оператор, область определения которого является набором всех функций которые имеют производные в каждой точке их области определения и диапазон которых является набором функций.
Ключевые термины
- диапазон : набор значений (точек), которые функция может получить
- домен : набор всех возможных математических объектов (точек), в которых определена данная функция
Пусть [latex] f [/ latex] будет функцией, которая имеет производную в каждой точке [latex] a [/ latex] в домене [latex] f [/ latex].Поскольку каждая точка [latex] a [/ latex] имеет производную, существует функция, которая отправляет точку [latex] a [/ latex] производной от [latex] f [/ latex] в [latex] a [/ латекс]. Эта функция записывается [latex] f ‘(x) [/ latex] и называется производной функцией или производной от [latex] f [/ latex]. Производная [латекса] f [/ латекса] собирает все производные [латекса] f [/ латекса] во всех точках домена [латекс] f [/ латекс]. Визуально производная функции [latex] f [/ latex] в [latex] x = a [/ latex] представляет наклон кривой в точке [latex] x = a [/ latex].
Производная как наклон : Показанный наклон касательной представляет собой значение производной кривой функции в точке [латекс] x [/ латекс].
Иногда [latex] f [/ latex] имеет производную в большинстве, но не во всех точках своей области. Функция, значение которой в [latex] a [/ latex] равно [latex] f ‘(a) [/ latex] всякий раз, когда [latex] f’ (a) [/ latex] определено, а в другом месте не определено, также называется производной. [латекс] ф [/ латекс]. Это все еще функция, но ее область строго меньше, чем область [latex] f [/ latex].
Разрывная функция : В точке, где функция совершает скачок, производная функции не существует.
Используя эту идею, дифференцирование становится функцией функций: производная – это оператор, область определения которого представляет собой набор всех функций, имеющих производные в каждой точке своей области определения, а диапазон значений – набор функций. Если обозначить этот оператор как [latex] D [/ latex], то [latex] D (f) [/ latex] – это функция [latex] f ‘(x) [/ latex].Поскольку [latex] D (f) [/ latex] является функцией, ее можно оценить в точке [latex] a [/ latex]. По определению производной функции [латекс] D (f) (a) = f ‘(a) [/ latex].
Для сравнения рассмотрим функцию удвоения [латекс] f (x) = 2x [/ latex]; [latex] f [/ latex] является действительной функцией действительного числа, что означает, что он принимает числа в качестве входных данных и имеет числа в качестве выходных:
[латекс] 1 \ стрелка вправо 2 [/ латекс]
[латекс] 2 \ rightarrow 4 [/ латекс]
[латекс] 3 \ rightarrow 6 [/ латекс].2 [/ латекс]
[latex] D [/ latex] выводит функцию удвоения,
[латекс] x \ rightarrow 2x [/ латекс]
, который является f (x) f (x). Затем эта функция вывода может быть вычислена для получения [latex] f (1) = 2f (1) = 2 [/ latex], [latex] f (2) = 4 [/ latex] и так далее.
Правила дифференциации
Правила дифференцирования могут упростить производные, устраняя необходимость в сложных расчетах пределов.
Цели обучения
Практика использования правил дифференцирования для упрощения дифференцирования сложных выражений
Основные выводы
Ключевые моменты
- Дифференцирование с помощью полиномиального разложения может быть очень сложным и подверженным ошибкам.2} [/ латекс].
Ключевые термины
- коэффициент разности : разность функций [латекс] \ Delta F [/ latex], деленная на разность точек [латекс] \ Delta x [/ latex]: [latex] \ Delta F (x) / \ Delta x [ / латекс]
- полином : выражение, состоящее из суммы конечного числа членов, каждый член является произведением постоянного коэффициента и одной или нескольких переменных, возведенных в неотрицательную целую степень
Когда мы хотим различать сложные выражения, возможный способ дифференцировать выражение – это развернуть его и получить многочлен, а затем дифференцировать этот многочлен.Этот метод становится очень сложным и особенно подвержен ошибкам при выполнении расчетов вручную. Во многих случаях сложных расчетов пределов путем прямого применения разностного коэффициента Ньютона можно избежать, используя правила дифференцирования. Вот некоторые из самых основных правил.
Постоянное правило
Если [латекс] f (x) [/ latex] является константой, то [latex] f ‘(x) = 0 [/ latex], поскольку скорость изменения константы всегда равна нулю.
Правило суммы
[латекс] (\ alpha f + \ beta g) ‘= \ alpha f’ + \ beta g ‘[/ latex]
для всех функций [latex] f [/ latex] и [latex] g [/ latex] и всех действительных чисел [latex] \ alpha [/ latex] и [latex] \ beta [/ latex].x [/ latex], как и константа 7, также использовались.
Производные тригонометрических функций
Производные тригонометрических функций можно найти с помощью стандартной формулы производной.
Цели обучения
Определение производных наиболее распространенных тригонометрических функций
Основные выводы
Ключевые моменты
- Производная синусоидальной функции является косинусоидальной функцией.
- Производная функции косинуса является отрицательной величиной функции синуса.
- Производная касательной функции – это функция секущей в квадрате.
Ключевые термины
- секущая : прямая линия, пересекающая кривую в двух или более точках
Тригонометрические функции (также называемые круговыми функциями) являются функциями угла. Они используются, чтобы связать углы треугольника с длинами сторон треугольника. Тригонометрические функции важны при изучении треугольников и моделировании периодических явлений, среди многих других приложений.
Самыми известными тригонометрическими функциями являются синус, косинус и тангенс. В контексте стандартной единичной окружности с радиусом 1, где треугольник образован лучом, исходящим из начала координат и составляющим некоторый угол с осью [латекс] x [/ латекс], синус угла дает длину [latex] y [/ latex] -компонент (подъем) треугольника, косинус дает длину [latex] x [/ latex] -компоненты (прогон), а функция тангенса дает наклон ([латекс] y [/ latex] -компонент, разделенный на [latex] x [/ latex] -компонент).
Имея это в виду, мы можем использовать определение производной для вычисления производных различных тригонометрических функций:
[латекс] \ displaystyle {f ‘(x) = \ lim_ {h \ rightarrow 0} \ frac {f (x + h) – f (x)} {h}} [/ latex]
Например, если [латекс] f (x) = \ sin x [/ latex], то:
[латекс] \ displaystyle {f ‘(x) = \ lim_ {h \ rightarrow 0} \ frac {\ sin (x + h) – \ sin (x)} {h}} [/ latex]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h) + \ cos (h) \ cdot \ sin (x) – \ sin (x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h) + (\ cos (h) – 1) \ cdot \ sin ( x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ lim_ {h \ rightarrow 0} \ frac {\ cos (x) \ cdot \ sin (h)} {h} + \ lim_ {h \ rightarrow 0} \ frac {(\ cos (h) – 1) \ cdot \ sin (x)} {h}} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ cos (x) (1) + \ sin (x) (0)} [/ латекс]
[латекс] \ displaystyle {\ quad \ quad = \ cos (x)} [/ латекс]
Синус и косинус : На этом изображении можно увидеть, что там, где касательная к одной кривой имеет нулевой наклон (производная этой кривой равна нулю), значение другой функции равно нулю.2 x} [/ латекс]
Правило цепочки
Цепное правило – это формула для вычисления производной композиции двух или более функций.
Цели обучения
Вычислить производную композиции функций, используя цепное правило
Основные выводы
Ключевые моменты
- Если [latex] f [/ latex] является функцией, а [latex] g [/ latex] является функцией, то цепное правило выражает производную сложной функции [latex] f \ circ g [/ latex] в термины производных [латекса] ф [/ латекса] и [латекса] г [/ латекса].
- Правило цепочки может применяться последовательно для любого количества функций, вложенных друг в друга.
- Цепное правило для [латекса] f \ circ g (x) [/ latex]: [latex] \ frac {df} {dx} = \ frac {df} {dg} \ frac {dg} {dx} [/ латекс].
Ключевые термины
- композит : функция от функции
Цепное правило – это формула для вычисления производной композиции двух или более функций. То есть, если [latex] f [/ latex] является функцией, а [latex] g [/ latex] является функцией, то цепное правило выражает производную сложной функции [latex] f \ circ g [/ latex] в терминах производных [латекса] ф [/ латекса] и [латекса] г [/ латекса].
Например, следуя правилу цепочки для [латекс] f \ circ g (x) = f [g (x)] [/ latex], получаем:
[латекс] \ displaystyle {\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}} [/ латекс]
Метод называется «цепным правилом», потому что его можно применять последовательно к любому количеству функций, вложенных друг в друга. Например, если [latex] f [/ latex] является функцией [latex] g [/ latex], которая, в свою очередь, является функцией [latex] h [/ latex], которая, в свою очередь, является функцией [latex ] x [/ latex] – то есть [латекс] f (g (h (x))) [/ latex] – затем производная от [latex] f [/ latex] по отношению к [latex] x [/ latex ] составляет:
[латекс] \ displaystyle {\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dh} \ cdot \ frac {dh} {dx}} [/ латекс]
Цепное правило имеет широкое применение в физике, химии и инженерии, а также для изучения связанных скоростей во многих других дисциплинах.2 [/ латекс]
Неявная дифференциация
Неявное дифференцирование использует цепное правило для дифференцирования неявно определенных функций.
Цели обучения
Используйте неявное дифференцирование, чтобы найти производные функций, которые не являются явно функциями [latex] x [/ latex]
Основные выводы
Ключевые моменты
- Поскольку y может быть задано как функция [latex] x [/ latex] неявно, а не явно, когда у нас есть уравнение [latex] R (x, y) = 0 [/ latex], мы можем решите это для [latex] y [/ latex], а затем дифференцируйте.
- Неявная функция – это функция, которая неявно определяется отношением между ее аргументом и его значением.
- Теорема неявной функции утверждает, что если левая часть уравнения [латекс] R (x, y) = 0 [/ latex] дифференцируема и удовлетворяет некоторому мягкому условию на свои частные производные в некоторой точке [латекс] (a , b) [/ latex] такой, что [latex] R (a, b) = 0 [/ latex], тогда он определяет функцию [latex] y = f (x) [/ latex] на некотором интервале, содержащем [latex] а [/ латекс].
Ключевые термины
- неявно : подразумевается косвенно, без прямого выражения
Неявная функция – это функция, которая неявно определяется отношением между ее аргументом и его значением.
Если левая часть уравнения [латекс] R (x, y) = 0 [/ latex] дифференцируема и удовлетворяет некоторому мягкому условию на свои частные производные в некоторой точке [latex] (a, b) [/ latex] такой, что [latex] R (a, b) = 0 [/ latex], тогда он определяет функцию [latex] y = f (x) [/ latex] на некотором интервале, содержащем [latex] a [/ latex]. Геометрически граф, определенный как [latex] R (x, y) = 0 [/ latex], будет локально перекрываться с графиком некоторого уравнения [latex] y = f (x) [/ latex].
Для большинства неявных функций не существует формулы, определяющей их явно.2 + y = \ sin (x) [/ latex] – неявная функция, потому что очень сложно получить формулу для [latex] y [/ latex] в терминах только [latex] x [/ latex]. Однако мы все еще можем найти производную от [latex] y [/ latex] по отношению к [latex] x [/ latex], используя неявное дифференцирование.
[латекс] \ displaystyle {2y \ cdot \ frac {dy} {dx} + \ frac {dy} {dx} = \ cos (x) = (2y + 1) \ frac {dy} {dx}} [/ латекс]
Следовательно:
[латекс] \ displaystyle {\ frac {dy} {dx} = \ frac {\ cos (x)} {2y + 1}} [/ latex]
Поскольку [латекс] y [/ latex] может быть задан как функция [latex] x [/ latex] неявно, а не явно, когда у нас есть уравнение [latex] R (x, y) = 0 [/ latex] , мы можем решить его для [latex] y [/ latex], а затем дифференцировать.Однако иногда проще дифференцировать [латекс] R (x, y) [/ латекс] относительно [латекса] x [/ латекса] и [латекса] y [/ латекса], а затем решать для [латекса] \ frac {dy} {dx} [/ латекс].
Например, учитывая выражение [латекс] y + x + 5 = 0 [/ latex], дифференциация урожайности:
[латекс] \ displaystyle {\ frac {dy} {dx} + \ frac {dx} {dx} + \ frac {d} {dx} 5 = \ frac {dy} {x} + 1 = 0} [/ латекс]. 2 [/ latex], где [latex] r [/ latex] – радиус круга.Вы можете использовать неявное дифференцирование, чтобы найти наклон касательной к окружности в точке [latex] (x, y) [/ latex]. Поскольку наклон касательной является производной в этой точке, мы находим производную неявно:
[латекс] \ displaystyle {2y \ frac {dy} {dx} + 2x \ frac {dx} {dx} = \ frac {dr} {dx} = 0} [/ латекс]
где [latex] \ frac {dr} {dx} [/ latex] равно [latex] 0 [/ latex], поскольку радиус постоянен. Затем вы можете найти формулу для [латекс] \ frac {dy} {dx} [/ latex]:
[латекс] \ displaystyle {\ frac {dy} {dx} = \ frac {-2x} {2y} = \ frac {-x} {y}} [/ latex]
, и теперь вы можете найти наклон в любой точке [latex] (x, y) [/ latex].
Путь точки на окружности : Путь точки на окружности может быть выражен только как неявная функция.
Дифференциация и скорость изменений в естественных и социальных науках
Дифференциация, по сути, вычисление скорости изменения важна во всех количественных науках.
Цели обучения
Приведите примеры дифференциации или скорости изменений, используемых в различных академических дисциплинах
Основные выводы
Ключевые моменты
- Дифференциация применима почти ко всем количественным дисциплинам, будь то естественные или социальные науки.
- Ученые-физики используют дифференциацию и скорость изменения для изучения того, как физическая концепция изменяется с течением времени или на расстоянии.
- Социологи используют дифференциацию и коэффициент, чтобы определить, как люди, товары и процессы меняются из-за изменения независимой переменной.
Ключевые термины
- дифференциальная геометрия : изучение геометрии с помощью дифференциального исчисления
- Импульс : (тела в движении) произведение его массы и скорости
- Валовой внутренний продукт : мера экономического производства на определенной территории с точки зрения финансового капитала за определенный период времени
Для данной функции [latex] y = f (x) [/ latex] дифференцирование – это метод вычисления скорости, с которой зависимый выход [latex] y [/ latex] изменяется по отношению к изменению в независимом входе [ латекс] х [/ латекс].Эта скорость изменения называется производной [латекса] y [/ латекса] относительно [латекса] x [/ латекса].
Скорость изменения – важное понятие во многих количественных исследованиях, и неудивительно, что дифференциация (представляющая скорость изменения) применима почти ко всем количественным дисциплинам. Например, в физике производная смещения движущегося тела по времени – это скорость тела, а производная скорости по времени – это ускорение.Второй закон движения Ньютона гласит, что производная количества движения тела равна силе, приложенной к телу. Скорость химической реакции является производной. При исследовании операций производные инструменты определяют наиболее эффективные способы транспортировки материалов и проектирования предприятий.
Производные часто используются для нахождения максимумов и минимумов функции. Уравнения, включающие производные, называются дифференциальными уравнениями и являются фундаментальными для описания природных явлений.Производные и их обобщения появляются во многих областях математики, таких как комплексный анализ, функциональный анализ, дифференциальная геометрия, теория меры и абстрактная алгебра.
Темпы изменений происходят во всех науках и во всех дисциплинах. Экономисты изучают скорость изменения валового внутреннего продукта, а социологи – скорость, с которой население голосует в определенной области. Геологи изучают скорость сдвига Земли и температурный градиент горных пород возле вулкана. Бухгалтеры изучают скорость изменения производства и поставок, а также то, как любое изменение может повлиять на затраты и прибыль.Городские инженеры изучают движение транспорта, чтобы спроектировать и построить более эффективные дороги и автострады.
В каждом аспекте жизни, в котором что-то меняется, дифференциация и скорость изменений являются важным аспектом в понимании мира и поиске способов его улучшить.
Связанные тарифы
Проблемы связанных ставок связаны с нахождением скорости путем соотнесения этого количества с другими величинами, скорости изменения которых известны.
Цели обучения
Решение проблем с использованием связанных ставок (с использованием количества, скорость которого, как известно, позволяет найти скорость, с которой изменяется связанное количество)
Основные выводы
Ключевые моменты
- Поскольку наука и техника часто связывают величины друг с другом, методы связанных скоростей имеют широкое применение в этих областях.
- Поскольку задачи включают несколько переменных, дифференцирование по времени или по одной из других переменных требует применения правила цепочки.
- Процесс решения проблем связанных ставок: запишите все соответствующие формулы и информацию, возьмите производную от первичного уравнения по времени, решите для желаемой переменной, вставьте известную информацию и упростите.
Ключевые термины
- переменная : величина, которая может принимать любое из набора значений
Одно из полезных применений деривативов – это помощь в вычислении соответствующих ставок.Что такое родственная ставка? В дифференциальном исчислении проблемы связанных ставок включают нахождение скорости, с которой величина изменяется, путем соотнесения этой величины с другими величинами, скорости изменения которых известны. В большинстве случаев рассчитываемая соответствующая ставка является производной по некоторому значению. Мы вычисляем эту производную по скорости, с которой изменяется какая-то другая известная величина. Учитывая скорость, с которой что-то меняется, нас просят найти скорость, с которой изменяется значение, связанное с данной скоростью.
Скорость изменения обычно зависит от времени. Поскольку наука и техника часто связывают количества друг с другом, методы связанных скоростей имеют широкое применение в этих областях. Поскольку задачи включают несколько переменных, дифференцирование по времени или по одной из других переменных требует применения цепного правила.
Процесс решения проблем связанных ставок:
1. Запишите все соответствующие формулы и информацию.
2. Возьмем производную первичного уравнения по времени.
3. Найдите желаемую переменную.
4. Вставьте известную информацию и упростите ее.
См. Блок-схему решения проблем связанных ставок.
Блок-схема решения проблем, связанных с расходами : Проблемы со связанными расходами можно решать с помощью методического подхода.
Предположим, вам дана следующая ситуация.
Сферический воздушный шар наполняется воздухом. Объем изменяется со скоростью 2 кубических фута в минуту.2} V ‘} [/ латекс]
Вставьте известную информацию:
[латекс] \ displaystyle {r ‘= \ frac {1} {16 \ pi} 2 = \ frac {1} {8 \ pi}} [/ latex] фут / мин
Высшие производные
Производная уже дифференцированного выражения называется производной более высокого порядка.
Цели обучения
Вычисление высших (вторых, третьих и т. Д.) Производных функций
Основные выводы
Ключевые моменты
- Вторая производная или производная второго порядка – это производная производной функции.
- Поскольку производная функции определяется как функция, представляющая наклон исходной функции, двойная производная – это функция, представляющая наклон функции первой производной.
- Если [latex] x (t) [/ latex] представляет положение объекта в момент времени [latex] t [/ latex], то производные [latex] x [/ latex] более высокого порядка имеют физические интерпретации, например как скорость и ускорение.
Ключевые термины
- производная : мера того, как функция изменяется при изменении ее входных данных
Вторая производная или производная второго порядка – это производная производной функции.Производная функции может обозначаться как [латекс] f ‘(x) [/ latex], а ее двойная (или «вторая») производная обозначается как [латекс] f’ ‘(x) [/ latex]. Это читается как «[латекс] f [/ латекс] двойное простое число от [латекс] x [/ латекс]» или «вторая производная от [латекс] f (x) [/ латекс]. «Поскольку производная функции определяется как функция, представляющая наклон функции, двойная производная – это функция, представляющая наклон функции первой производной.
Кроме того, третья производная является производной производной производной функции, которая может быть представлена как [латекс] f ” ‘(x) [/ latex].Это читается как «[латекс] f [/ латекс] тройное простое число [латекс] x [/ латекс]» или «третья производная от [латекса] f (x) [/ латекс].»). Это может продолжаться до тех пор, пока полученная производная сама является дифференцируемой, с четвертой производной, пятой производной и так далее. Любая производная за пределами первой производной может называться производной более высокого порядка.
Если [latex] x (t) [/ latex] представляет положение объекта в момент времени [latex] t [/ latex], то производные [latex] x [/ latex] более высокого порядка имеют физические интерпретации.Вторая производная от [latex] x [/ latex] – это производная от [latex] x ‘(t) [/ latex], скорости и, по определению, ускорения объекта. Третья производная от [латекс] x [/ латекс] определяется как толчок, а четвертая производная определяется как толчок. Функция [latex] f [/ latex] не обязательно должна иметь производную – например, если она не является непрерывной. Точно так же, даже если [латекс] f [/ латекс] имеет производную, у него может не быть второй производной. См. Графическую иллюстрацию высших производных в физике.2 + 6x – 1 [/ латекс]
- [латекс] f ” (x) = 30x + 6 [/ латекс]
- [латекс] f ” ‘(x) = 30 [/ латекс] .


 На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.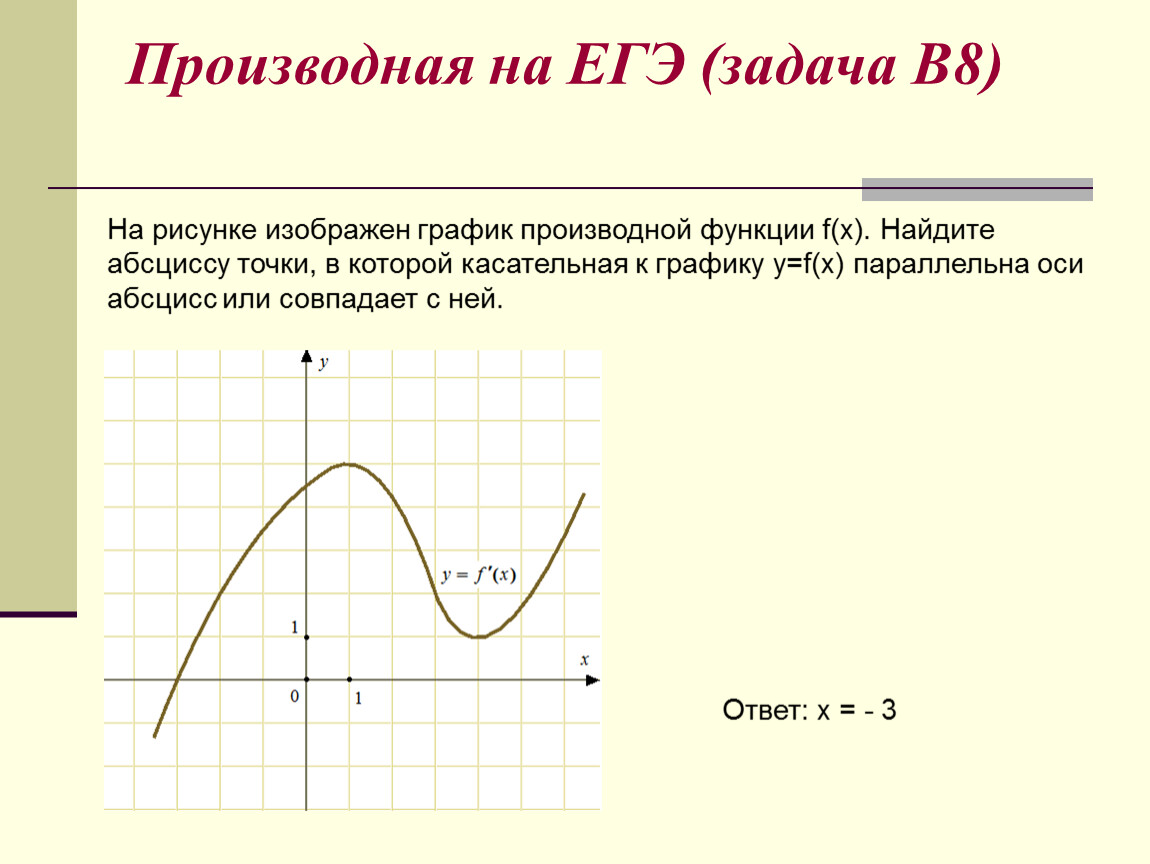
 Отсчет всегда ведется слева направо.
Отсчет всегда ведется слева направо. е. f’(x) ≥ 0.
е. f’(x) ≥ 0. В ответе укажите сумму целых чисел, входящих в эти промежутки.
В ответе укажите сумму целых чисел, входящих в эти промежутки.

 Найдите скорость в момент времени t= 2 с.
Найдите скорость в момент времени t= 2 с.