Репетитор по математике.Теория вероятности формулы и примеры решения задач
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
- Вероятность принимает значения на отрезке от 0 до 1, т.е. .
- Вероятность невозможного события равна 0, т.е. .
- Вероятность достоверного события равна 1, т.e. .
- Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е. .
Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .

Ответ получаем по формуле .
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
Ответ: 0,4
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. .
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается «шесть факториал».
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае .
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
В нашем случае .
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:
В нашем случае .
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
Ответ: 0,98.
Задача 3.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Решение:
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие «У. верно решит ровно 9 задач» входит в условие «У. верно решит больше 8 задач», но не относится к условию «У. верно решит больше 9 задач».
Однако, условие «У. верно решит больше 9 задач» содержится в условии «У. верно решит больше 8 задач». Таким образом, если мы обозначим события: «У. верно решит ровно 9 задач» — через А, «У. верно решит больше 8 задач» — через B, «У. верно решит больше 9 задач» через С. То решение будет выглядеть следующим образом:
.
Ответ: 0,06.
Задача 4.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме «Тригонометрия», либо к теме «Внешние углы». По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
Ответ: 0,35.
Задача 5.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: — лампочка горит, — лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события «лампочка перегорела», «лампочка горит», «лампочка горит»: , где вероятность события «лампочка горит» подсчитывается как вероятность события, противоположного событию «лампочка не горит», а именно: .
Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
repetitor-mathematics.ru
формулы и примеры решения задач :: SYL.ru
“Случайности не случайны”… Звучит так, словно сказал философ, но на деле изучать случайности удел великой науки математики. В математике случайностями занимается теория вероятности. Формулы и примеры заданий, а также основные определения этой науки будут представлены в статье.
Что такое теория вероятности?
Теория вероятности – это одна из математических дисциплин, которая изучает случайные события.
Чтобы было немного понятнее, приведем небольшой пример: если подкинуть вверх монету, она может упасть «орлом» или «решкой». Пока монета находится в воздухе, обе эти вероятности возможны. То есть вероятность возможных последствий соотносится 1:1. Если из колоды с 36-ю картами вытащить одну, тогда вероятность будет обозначаться как 1:36. Казалось бы, что здесь нечего исследовать и предугадывать, тем более при помощи математических формул. Тем не менее, если повторять определенное действие много раз, то можно выявить некую закономерность и на ее основе спрогнозировать исход событий в других условиях.
Если обобщить все вышесказанное, теория вероятности в классическом понимании изучает возможность возникновения одного из возможных событий в числовом значении.

Со страниц истории
Теория вероятности, формулы и примеры первых заданий появились еще в далеком Средневековье, когда впервые возникли попытки спрогнозировать исход карточных игр.
Изначально теория вероятности не имела ничего общего с математикой. Она обосновывалась эмпирическими фактами или свойствами события, которое можно было воспроизвести на практике. Первые работы в этой сфере как в математической дисциплине появились в XVII веке. Родоначальниками стали Блез Паскаль и Пьер Ферма. Длительное время они изучали азартные игры и увидели определенные закономерности, о которых и решили рассказать обществу.
Такую же методику изобрел Христиан Гюйгенс, хотя он не был знаком с результатами исследований Паскаля и Ферма. Понятие «теория вероятности», формулы и примеры, что считаются первыми в истории дисциплины, были введены именно им.
Немаловажное значение имеют и работы Якоба Бернулли, теоремы Лапласа и Пуассона. Они сделали теорию вероятности больше похожей на математическую дисциплину. Свой теперешний вид теория вероятностей, формулы и примеры основных заданий получили благодаря аксиомам Колмогорова. В результате всех изменений теория вероятности стала одним из математических разделов.
Базовые понятия теории вероятностей. События
Главным понятием этой дисциплины является “событие”. События бывают трех видов:
- Достоверные. Те, которые произойдут в любом случае (монета упадет).
- Невозможные. События, что не произойдут ни при каком раскладе (монета останется висеть в воздухе).
- Случайные. Те, что произойдут или не произойдут. На них могут повлиять разные факторы, которые предугадать очень трудно. Если говорить о монете, то случайные факторы, что могут повлиять на результат: физические характеристики монеты, ее форма, исходное положение, сила броска и т. д.

Все события в примерах обозначаются заглавными латинскими буквами, за исключением Р, которой отведена другая роль. Например:
- А = «студенты пришли на лекцию».
- Ā = «студенты не пришли на лекцию».
В практических заданиях события принято записывать словами.
Одна из важнейших характеристик событий – их равновозможность. То есть, если подбросить монету, все варианты исходного падения возможны, пока она не упала. Но также события бывают и не равновозможными. Это происходит, когда кто-то специально воздействует на исход. Например, «меченые» игральные карты или игральные кости, в которых смещен центр тяжести.
Еще события бывают совместимыми и несовместимыми. Совместимые события не исключают появления друг друга. Например:
- А = «студентка пришла на лекцию».
- В = «студент пришел на лекцию».
Эти события независимы друг от друга, и появление одного из них не влияет на появление другого. Несовместимые события определяются тем, что появление одного исключает появление другого. Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.
Действия над событиями
События можно умножать и складывать, соответственно, в дисциплине вводятся логические связки «И» и «ИЛИ».
Сумма определяется тем, что может появиться или событие А, или В, или два одновременно. В случае когда они несовместимы, последний вариант невозможен, выпадет или А, или В.
Умножение событий заключается в появлении А и В одновременно.
Теперь можно привести несколько примеров, чтобы лучше запомнились основы, теория вероятности и формулы. Примеры решения задач далее.
Задание 1: Фирма принимает участие в конкурсе на получение контрактов на три разновидности работы. Возможные события, которые могут произойти:
- А = «фирма получит первый контракт».
- А1 = «фирма не получит первый контракт».
- В = «фирма получит второй контракт».
- В1 = «фирма не получит второй контракт»
- С = «фирма получит третий контракт».
- С1 = «фирма не получит третий контракт».
С помощью действий над событиями попробуем выразить следующие ситуации:
- К = «фирма получит все контракты».
В математическом виде уравнение будет иметь следующий вид: К = АВС.
- М = «фирма не получит ни одного контракта».
М = А1В1С1.
Усложняем задание: H = «фирма получит один контракт». Поскольку не известно, какой именно контракт получит фирма (первый, второй или третий), необходимо записать весь ряд возможных событий:
Н = А1ВС1υ АВ1С1 υ А1В1С.
А1ВС1 – это ряд событий, где фирма не получает первый и третий контракт, но получает второй. Соответственным методом записаны и другие возможные события. Символ υ в дисциплине обозначает связку «ИЛИ». Если перевести приведенный пример на человеческий язык, то фирма получит или третий контракт, или второй, или первый. Подобным образом можно записывать и другие условия в дисциплине «Теория вероятности». Формулы и примеры решения задач, представленные выше, помогут сделать это самостоятельно.

Собственно, вероятность
Пожалуй, в этой математической дисциплине вероятность события – это центральное понятие. Существует 3 определения вероятности:
- классическое;
- статистическое;
- геометрическое.
Каждое имеет свое место в изучении вероятностей. Теория вероятности, формулы и примеры (9 класс) в основном используют классическое определение, которое звучит так:
- Вероятность ситуации А равняется отношению числа исходов, что благоприятствуют ее появлению, к числу всех возможных исходов.
Формула выглядит так: Р(А)=m/n.
Р обозначает вероятность события А.
А – собственно, событие. Если появляется случай, противоположный А, его можно записывать как Ā или А1.
m – количество возможных благоприятных случаев.
n – все события, которые могут произойти.
Например, А = «вытащить карту червовой масти». В стандартной колоде 36 карт, 9 из них червовой масти. Соответственно, формула решения задания будет иметь вид:
Р(А)=9/36=0,25.
В итоге вероятность того, что из колоды вытянут карту червовой масти, составит 0,25.
К высшей математике
Теперь стало немного известно, что такое теория вероятности, формулы и примеры решения заданий, которые попадаются в школьной программе. Однако теория вероятностей встречается и в высшей математике, которая преподается в вузах. Чаще всего там оперируют геометрическими и статистическими определениями теории и сложными формулами.
Очень интересна теория вероятности. Формулы и примеры (высшая математика) лучше начинать изучать с малого – со статистического (или частотного) определения вероятности.
Статистический подход не противоречит классическому, а немного расширяет его. Если в первом случае нужно было определить, с какой долей вероятности произойдет событие, то в этом методе необходимо указать, как часто оно будет происходить. Здесь вводится новое понятие «относительная частота», которую можно обозначить Wn(A). Формула ничем не отличается от классической:
Wn(A)=m/n.
Если классическая формула вычисляется для прогнозирования, то статистическая – согласно результатам эксперимента. Возьмем, к примеру, небольшое задание.
Отдел технологического контроля проверяет изделия на качество. Среди 100 изделий нашли 3 некачественных. Как найти вероятность частоты качественного товара?
А = «появление качественного товара».
Wn(A)=97/100=0,97
Таким образом, частота качественного товара составляет 0,97. Откуда взяли 97? Из 100 товаров, которые проверили, 3 оказались некачественными. От 100 отнимаем 3, получаем 97, это количество качественного товара.

Немного о комбинаторике
Еще один метод теории вероятности называют комбинаторикой. Его основной принцип состоит в том, что если определенный выбор А можно осуществить m разными способами, а выбор В – n разными способами, то выбор А и В можно осуществить путем умножения.
Например, из города А в город В ведет 5 дорог. Из города В в город С ведет 4 пути. Сколькими способами можно доехать из города А в город С?
Все просто: 5х4=20, то есть двадцатью разными способами можно добраться из точки А в точку С.
Усложним задание. Сколько существует способов раскладывания карт в пасьянсе? В колоде 36 карт – это исходная точка. Чтобы узнать количество способов, нужно от исходной точки «отнимать» по одной карте и умножать.
То есть 36х35х34х33х32…х2х1= результат не вмещается на экран калькулятора, поэтому его можно просто обозначить 36!. Знак «!» возле числа указывает на то, что весь ряд чисел перемножается между собой.
В комбинаторике присутствуют такие понятия, как перестановка, размещение и сочетание. Каждое из них имеет свою формулу.
Упорядоченный набор элементов множества называют размещением. Размещения могут быть с повторениями, то есть один элемент можно использовать несколько раз. И без повторений, когда элементы не повторяются. n – это все элементы, m – элементы, которые участвуют в размещении. Формула для размещения без повторений будет иметь вид:
Anm=n!/(n-m)!
Соединения из n элементов, которые отличаются только порядком размещения, называют перестановкой. В математике это имеет вид: Рn = n!
Сочетаниями из n элементов по m называют такие соединения, в которых важно, какие это были элементы и каково их общее количество. Формула будет иметь вид:
Anm=n!/m!(n-m)!
Формула Бернулли
В теории вероятности, так же как и в каждой дисциплине, имеются труды выдающихся в своей области исследователей, которые вывели ее на новый уровень. Один из таких трудов – формула Бернулли, что позволяет определять вероятность появления определенного события при независимых условиях. Это говорит о том, что появление А в эксперименте не зависит от появления или не появления того же события в ранее проведенных или последующих испытаниях.
Уравнение Бернулли:
Pn(m)=Cnm×pm×qn-m.
Вероятность (р) появления события (А) неизменна для каждого испытания. Вероятность того, что ситуация произойдет ровно m раз в n количестве экспериментов, будет вычисляться формулой, что представлена выше. Соответственно, возникает вопрос о том, как узнать число q.
q=1-p
Если событие А наступает р количество раз, соответственно, оно может и не наступить. Единица – это число, которым принято обозначать все исходы ситуации в дисциплине. Поэтому q – число, которое обозначает возможность ненаступления события.
Теперь вам известна формула Бернулли (теория вероятности). Примеры решения задач (первый уровень) рассмотрим далее.
Задание 2: Посетитель магазина сделает покупку с вероятностью 0,2. В магазин зашли независимым образом 6 посетителей. Какова вероятность того, что посетитель сделает покупку?
Решение: Поскольку неизвестно, сколько посетителей должны сделать покупку, один или все шесть, необходимо просчитать все возможные вероятности, пользуясь формулой Бернулли.
А = «посетитель совершит покупку».
В этом случае: р = 0,2 (как указано в задании). Соответственно, q=1-0,2 = 0,8.
n = 6 (поскольку в магазине 6 посетителей). Число m будет меняться от 0 (ни один покупатель не совершит покупку) до 6 (все посетители магазина что-то приобретут). В итоге получим решение:
P6(0)=C06×p0×q6=q6=(0,8)6=0,2621.
Ни один из покупателей не совершит покупку с вероятностью 0,2621.
Как еще используется формула Бернулли (теория вероятности)? Примеры решения задач (второй уровень) далее.
После вышеприведенного примера возникают вопросы о том, куда делись С и р. Относительно р число в степени 0 будет равно единице. Что касается С, то его можно найти формулой:
Cnm=n!/m!(n-m)!
Поскольку в первом примере m = 0, соответственно, С=1, что в принципе не влияет на результат. Используя новую формулу, попробуем узнать, какова вероятность покупки товаров двумя посетителями.
P6(2)=C62×p2×q4 = (6×5×4×3×2×1)/(2×1×4×3×2×1)×(0,2)2×(0,8)4=15×0,04×0,4096=0,246.
Не так уж и сложна теория вероятности. Формула Бернулли, примеры которой представлены выше, прямое тому доказательство.

Формула Пуассона
Уравнение Пуассона используется для вычисления маловероятных случайных ситуаций.
Основная формула:
Pn(m)=λm/m!×e(-λ).
При этом λ = n х p. Вот такая несложная формула Пуассона (теория вероятности). Примеры решения задач рассмотрим далее.
Задание 3: На заводе изготовили детали в количестве 100000 штук. Появление бракованной детали = 0,0001. Какова вероятность, что в партии будет 5 бракованных деталей?
Как видим, брак – это маловероятное событие, в связи с чем для вычисления используется формула Пуассона (теория вероятности). Примеры решения задач подобного рода ничем не отличаются от других заданий дисциплины, в приведенную формулу подставляем необходимые данные:
А = «случайно выбранная деталь будет бракованной».
р = 0,0001 (согласно условию задания).
n = 100000 (количество деталей).
m = 5 (бракованные детали). Подставляем данные в формулу и получаем:
Р100000(5) = 105/5! Х е-10 = 0,0375.
Так же как и формула Бернулли (теория вероятности), примеры решений с помощью которой написаны выше, уравнение Пуассона имеет неизвестное е. По сути его можно найти формулой:
е-λ= lim n->∞(1-λ/n)n.
Однако есть специальные таблицы, в которых находятся практически все значения е.

Теорема Муавра-Лапласа
Если в схеме Бернулли количество испытаний достаточно велико, а вероятность появления события А во всех схемах одинакова, то вероятность появления события А определенное количество раз в серии испытаний можно найти формулой Лапласа:
Рn(m)= 1/√npq x ϕ(Xm).
Xm = m-np/√npq.
Чтобы лучше запомнилась формула Лапласа (теория вероятности), примеры задач в помощь ниже.
Задание 4: Рекламный агент раздает 800 листовок. Согласно статистическим исследованиям, каждая третья листовка находит своего потребителя. Какова вероятность того, что сработает ровно 267 рекламных листовок?
n = 800;
m = 267;
p = 1/3;
q = 2/3.
Сначала найдем Xm, подставляем данные (они все указаны выше) в формулу и получим 0,025. При помощи таблиц находим число ϕ(0,025), значение которого 0,3988. Теперь можно подставлять все данные в формулу:
Р800(267) = 1/√(800 х 1/3 х 2/3) х 0,3988 = 3/40 х 0,3988 = 0,03.
Таким образом, вероятность того, что рекламная листовка сработает ровно 267 раз, составляет 0,03.

Формула Байеса
Формула Байеса (теория вероятности), примеры решения заданий с помощью которой будут приведены ниже, представляет собой уравнение, которое описывает вероятность события, опираясь на обстоятельства, которые могли быть связаны с ним. Основная формула имеет следующий вид:
Р (А|B) = Р (В|А) х Р (А) / Р (В).
А и В являются определенными событиями.
Р(А|B) – условная вероятность, то есть может произойти событие А при условии, что событие В истинно.
Р (В|А) – условная вероятность события В.
Итак, заключительная часть небольшого курса «Теория вероятности» – формула Байеса, примеры решений задач с которой ниже.
Задание 5: На склад привезли телефоны от трех компаний. При этом часть телефонов, которые изготавливаются на первом заводе, составляет 25%, на втором – 60%, на третьем – 15%. Известно также, что средний процент бракованных изделий у первой фабрики составляет 2%, у второй – 4%, и у третьей – 1%. Необходимо найти вероятность того, что случайно выбранный телефон окажется бракованным.
А = «случайно взятый телефон».
В1 – телефон, который изготовила первая фабрика. Соответственно, появятся вводные В2 и В3 (для второй и третьей фабрик).
В итоге получим:
Р (В1) = 25%/100% = 0,25; Р(В2) = 0,6; Р (В3) = 0,15 – таким образом мы нашли вероятность каждого варианта.
Теперь нужно найти условные вероятности искомого события, то есть вероятность бракованной продукции в фирмах:
Р (А/В1) = 2%/100% = 0,02;
Р(А/В2) = 0,04;
Р (А/В3) = 0,01.
Теперь подставим данные в формулу Байеса и получим:
Р (А) = 0,25 х 0,2 + 0,6 х 0,4 + 0,15 х 0,01= 0,0305.
В статье представлена теория вероятности, формулы и примеры решения задач, но это только вершина айсберга обширной дисциплины. И после всего написанного логично будет задаться вопросом о том, нужна ли теория вероятности в жизни. Простому человеку сложно ответить, лучше спросить об этом у того, кто с ее помощью не единожды срывал джек-пот.
www.syl.ru
Теория вероятностей — Википедия
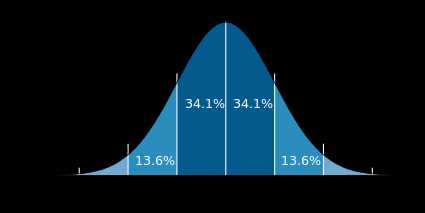 График плотности вероятности нормального распределения — одной из важнейших функций теории вероятностей
График плотности вероятности нормального распределения — одной из важнейших функций теории вероятностейТео́рия вероя́тностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Содержание
- 1 История
- 2 Основные понятия теории
- 3 См. также
- 4 Примечания
- 5 Литература
- 5.1 А
- 5.2 Б
- 5.3 В
- 5.4 Г
- 5.5 Д
- 5.6 Е
- 5.7 К
- 5.8 Л
- 5.9 М
- 5.10 Н
- 5.11 П
- 5.12 Р
- 5.13 С
- 5.14 Ф
- 5.15 Х
- 5.16 Ч
- 5.17 Ш
- 6 Ссылки
 Христиан Гюйгенс
Христиан Гюйгенс  Андрей Николаевич Колмогоров
Андрей Николаевич КолмогоровВозникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исс
ru.wikipedia.org
Высшая математика
«Теория вероятностей и математическая статистика»
Методические указания к выполнению контрольной работы для студентов заочного отделения
Варианты контрольной работы
Киров 2010
СОДЕРЖАНИЕ
Введение 4
Основные определения и теоремы 4
Вопросы для самоконтроля 8
Список рекомендуемой литературы 9
Задачи для практических занятий 9
Требования к оформлению контрольной работы 11
Разбор варианта контрольной работы 12
Варианты контрольной работы 15
Введение
Методические рекомендации предназначены для студентов заочного отделения всех специальностей Русского университета инноваций и имеют своей целью помочь студентам в освоении курса «Теория вероятностей».
Методы теории вероятностей используются при изучении массовых явлений, обработке результатов наблюдения и выявлении статистических закономерностей, в теории надежности, теории массового обслуживания. Теория вероятностей является теоретической базой статистических дисциплин, изучаемых студентами на старших курсах. Поэтому теория вероятностей занимает важное место во всем курсе высшей математики.
Между экономическими явлениями действуют многосторонние связи, и на их изменения оказывает влияние множество факторов, действующих по-разному в различные моменты времени, то есть изменения носят случайный характер. Поэтому определение общих закономерностей из наблюдаемых случайных явлений становится особенно важным. В достижении этой цели большую роль играет теория вероятностей, методы которой позволяют выделить общие закономерности, охарактеризовать процессы и явления «в среднем», «с данной степенью достоверности».
Основная трудность в изучении этого курса состоит в том, что для успешного его освоения надо научиться переводить жизненные ситуации на теоретико-вероятностный язык, пользуясь абстрактно-логическими рассуждениями. Для преодоления этих трудностей надо решить достаточно много задач.
В настоящем пособии приведены основные понятия комбинаторики и теории вероятностей, дан список задач для практических занятий, основные вопросы, которые обычно бывают включены в экзаменационные билеты, приведены решения основных типов задач, даны варианты контрольной работы и список рекомендуемой литературы.
Основные понятия комбинаторики и теории вероятностей
Решение комбинаторных задач заключается в подсчете числа тех или иных выборок из конечных множеств. Сформулируем два основных правила комбинаторики.
Правило произведения: Если объект А можно выделить из совокупности объектов т способами и после каждого такого выбора объект В можно выбрать п способами, то пара объектов (А,В) в указанном порядке может быть выбрана т • п способами.
Правило суммы: Если объект А можно выбрать из совокупности объектов т способами, а другой объект В может быть выбран п способами, то выбрать либо А, либо В можно п+т способами.
Отметим, что в первом случае мы выбираем А и В, а во втором А либо В. То есть, если нужно выбрать и тот и другой объект, то это можно сделать nm, а если выбирается только один из объектов, не важно какой, то это можно сделать n+т способами.
Наблюдаемые нами события можно подразделить на три вида.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена некоторая совокупность условий.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена некоторая совокупность условий.
Случайным называют событие, которое при осуществлении некоторой совокупности условий, может либо произойти, либо не произойти.
Под событием в теории вероятности понимают результат испытания.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Р(А) = m/n
т – число элементарных исходов, благоприятствующих А;
п – число всех возможных элементарных исходов испытания.
Заметим, что вероятность события – неотрицательное число, меньше или равное единице.
События называются равновозможными, если есть основание считать, что ни одно из них не является более возможным, чем другое.
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.
Противоположными называют два единственно возможных события, образующих полную группу.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
т W(А) =
п
т — число появлений события;
п — общее число испытаний.
Подчеркнем разницу между вероятностью и относительной частотой события. Первая величина вычисляется эмпирически, а вторая получается при эксперименте.
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А или события В или обоих этих событий.
Произведением двух событий А и В называют событие А•В, состоящее в совместном появлении (совмещении) этих событий.
Сумма двух событий соответствует событию «А или В». Произведение – событию «А и В».
Условной вероятностью РА (В) называют вероятность события
В, вычисленную в предположении, что событие А уже наступило.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, то есть
РА(В) = Р(В).
Теорема 1. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(А•В) = Р(А)•РА(В).
Теорема 2. Вероятность появления хотя бы одного из двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А + В) = Р(А) + Р(В) – Р(А • В).
Заметим, что если события несовместны, то они не могут произойти одновременно, то есть вероятность их совместного появления равна нулю. Тогда формула примет вид:
Р(А + В) = Р(А) + Р(В).
Теорема 3. Сумма вероятностей несовместных событий А1,А2,…,Ап, образующих полную группу, равна 1:
Р(А1) + Р(А2) + … + Р(Ап) = 1.
Теорема 4. Сумма вероятностей противоположных событий равна 1:
Р(А) + Р(А) =1.
Теорема 5. Вероятность появления хотя бы одного из событий А1,А2,…,Ап, независимых в совокупности, равна разности между
единицей и произведением вероятностей противоположных событий А1,А2,…,Ап :
А – вероятность появления одного из событий А1, А2,…,Ап, Р(А) = 1-Р(А1) •Р(А2)•...•Р(Ап).
Теорема 6. (Формула полной вероятности) Вероятность события А, которая может наступить лишь при условии появления одного из несовместных событий В1,В2,…,Вп, образующих полную
группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А :
Р(А) = Р(В1)• РВ1 (А) + Р(В2)• РВn (А) +… + Р(Вп)• РВп (А).
Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2 ,…,Вп, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.
Допустим, что произведено испытание в результате которого, появилось событие А. Поставим своей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами РА(В1),РА(В2),…,РА(Вп). На этот вопрос отвечают формулы Бейеса:
Р(Вi) • РВ1 (А)
РА(Вi)= ,
Р(А)
где Р(А) вычисляется по формуле полной вероятности.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной (непрерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений может быть конечным или бесконечным.
Непрерывной называют величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Законом распределения конечной дискретной величины называют таблицу, в которой занесены все возможные значения этой величины, с указанием вероятностей, с которыми эти значения могут приниматься.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
М(Х) = х1• р1+х2• р2+… + хп • рп
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания:
1. Математическое ожидание произведения двух независимыхслучайных величин равно произведению их математических ожида-ний:
М(Х•У) = М(Х)•М(У).
2. Математическое ожидание суммы двух случайных величин рав-но сумме математических ожиданий слагаемых:
М(Х + У) = М(Х) + М(У).
Способ задания дискретной случайной величины, перечнем всех ее возможных значений и их вероятностей, не является общим. Он не применим для непрерывных случайных величин. Чтобы получить более общий способ задания случайных величин вводят функции распределения.
Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т.е.
F(х) = Р(Х<х).
Иногда вместо термина «функция распределения» используют термин «интегральная функция».
Свойства функции распределения
1. Значение функции распределения принадлежит отрезку [0, 1]:
О ≤ F(х) ≤ 1.
2. Р(х) – неубывающая функция, т. е.
F(х2) ≥F(х1), если х2 > х1.
3. Вероятность того, что случайная величина примет значение, за-ключенное в интервале (а,b), равна приращению функции распределения на этом интервале:
Р(а ≤ Х ≤ b) = F(b) – F(а).
4. Если возможные значения случайной величины принадлежат ин-тервалу (а,b), то 1) F(х) = 0, при х ≤ а; 2) F(х) = 1, при х ≥ b.
studfiles.net
Учебник Теория вероятности – Самойленко, Кузнецов
Содержание
4.3.3.2.Первый центральный момент. . . . . . . . . . . . . . . . 86
4.3.3.3.Второй начальный момент. . . . . . . . . . . . . . . . . 86
4.3.3.4.Второй центральный момент . . . . . . . . . . . . . . . . 87
4.3.3.5.Связь дисперсии с начальными моментами . . . . . . . . . . 88
4.3.4.Среднее квадратичное отклонение . . . . . . . . . . . . . . . 88
4.3.5.Моменты высоких порядков . . . . . . . . . . . . . . . . . . 89
4.3.5.1.Третий центральный момент и коэффициент асимметрии. . . . 89
4.3.5.2.Четвертый центральный момент и величина эксцесс . . . . . . 90
4.4. Практикум и вопросы для самоконтроля. . . . . . . . . . . . . . . 91
5.ЧАСТНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ . . . . . . . . . . . . . . . 100
5.1.Законы распределения дискретных случайных величин . . . . . . . . 100
5.1.1.Биномиальный закон распределения . . . . . . . . . . . . . . 100
5.1.1.1.Общая характеристика биномиальной случайной величины . . . 100
5.1.1.2.Числовые характеристики биномиальной случайной величины . 101
5.1.2.Закон распределения Пуассона . . . . . . . . . . . . . . . . . 103
5.1.2.1.Простейший поток событий . . . . . . . . . . . . . . . . 103
5.1.2.2.Общая характеристика пуассоновской случайной величины. . . 104
5.1.2.3.Числовые характеристики пуассоновской случайной величины . 106
5.1.2.4.Вероятность попадания пуассоновской случайной величины на
заданный участок. . . . . . . . . . . . . . . . . . . . . 107
5.2.Законы распределения непрерывных случайных величин . . . . . . . 108
5.2.1.Равномерный закон распределения . . . . . . . . . . . . . . . 108
5.2.1.1.Общая характеристика. . . . . . . . . . . . . . . . . . . 108
5.2.1.2.Числовые характеристики . . . . . . . . . . . . . . . . . 110
5.2.1.3.Вероятность попадания случайной величины на заданный участок . . . . . . . . . . . . . . . . . . . . . . . . 111
5.2.2. Показательный закон распределения . . . . . . . . . . . . . . 112
5.2.2.1.Общая характеристика . . . . . . . . . . . . . . . . . . 112
5.2.2.2.Числовые характеристики . . . . . . . . . . . . . . . . . 113
5.2.2.3.Вероятность попадания случайной величины на заданный участок . . . . . . . . . . . . . . . . . . . . . . . . 114
5.2.3.Нормальный закон распределения . . . . . . . . . . . . . . . 115
5.2.3.1.Общая характеристика. . . . . . . . . . . . . . . . . . . 115
5.2.3.2.Числовые характеристики . . . . . . . . . . . . . . . . . 116
5.2.3.3.Вероятность попадания случайной величины на заданный участок . . . . . . . . . . . . . . . . . . . . . . . . 117
5.2.3.4. Правило трех сигм . . . . . . . . . . . . . . . . . . . . 119
5.3.Распределения, производные от нормального распределения . . . . . . 120
5.3.1.Распределение Пирсона. . . . . . . . . . . . . . . . . . . . 120
5.3.2.Распределение Стьюдента. . . . . . . . . . . . . . . . . . . 121
5.3.3. Распределение Фишера . . . . . . . . . . . . . . . . . . . . | 121 |
5.4. Практикум и вопросы для самоконтроля. . . . . . . . . . . . . . . | 122 |
6.СЛУЧАЙНЫЕ ВЕКТОРЫ И ФУНКЦИИ СЛУЧАЙНЫХ АРГУМЕНТОВ . . 128
6.1.Случайные векторы . . . . . . . . . . . . . . . . . . . . . . . 128
studfiles.net
Основы теории вероятностей.
Лекция №1
Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях.
Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания.
Выделяют три вида событий:
а) достоверные
б) невозможные
с) случайные
Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта.( например: при бросании кубика выпадет 1≤целое число≤6).
Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта. .( например: при бросании кубика выпадет число≥7, например 10).
Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта. ( например: бросили кубик один раз – выпадение числа 3 – случайное событие).
События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D,.
События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются .( например: много людей бросают кубики или один человек бросает кубик много раз).
1. Классификация случайных событий.
Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие ( например: кубику всё равно на какую грань упасть).
Совместные события – это события, которые могут произойти одновременно в результате данного опыта. ( например: бросаем 2 кубика – выпадение числа 1 и выпадение числа 3 – совместные события).
Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных.( например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).
Несколько случайных событий: образуютполную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).
Противоположные события – это равновозможные несовместные события, образующие полную группу событий. Появление события исключает появление события. ( например: орёл или решка, попадание в мишень или промах).
Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.
2 Вероятность случайного события.
Вероятность случайного события (обозначается Р(А)) –это число, которое говорит нам о степени возможности наступления события .
Существуют два определения вероятности: классическое и статистическое, каждое из них имеет свои достоинства и недостатки.
Классическое определение вероятности.
Вероятность события – это отношение числа исходов, благоприятствующих данному событию (m), к общему числу всех несовместных и равновозможных исходов данного опыта (n).
Если А – случайное событие, то
Если А – достоверное событие, то
Если А – невозможное событие, то
Пример: при бросании кубика возможно 6 исходов
Событие А: выпадет четное число. Число исходов, благоприятствующих событию А, m=3.
Достоинства: можно вычислить вероятность не производя испытания.
Недостатки: 1) не всегда известно число исходов опыта,
2) часто невозможно представить результат испытаний в виде равновозможных и несовместных событий.
Поэтому на практике часто пользуются статистическим определением вероятности.
Статистическое определение вероятности.
Пусть А – случайное событие, опыт проводился n раз, в результате опыта событие А произошло m раз, тогда m– частота наступления события А, а величина называетсяотносительной частотой события А.
Для разных n , могут заметно отличаться, но если проводим длинную серию опытов, т.е. , ток некоторому пределу.
Статистической вероятностью события А называется предел, к которому стремится его относительная частота , при неограниченном увеличении числа испытаний.
Пример: среди 1000 новорожденных 517 мальчиков. Найти относительную частоту рождения мальчиков. , тем не менее, известно, что
Так как вероятность – это число следовательно, с этими числами можно производить арифметические действия.
studfiles.net
Видео уроки по высшей математике: Теория вероятностей и статистика
Комбинаторика
Основные понятия теории вероятностей 8:44
Аксиомы теории вероятностей 8:48
Основные формулы комбинаторики 11:45
Перестановки 8:53
Перестановки с повторениями 6:41
Размещения 9:02
Сочетания 7:25
Выбор с возвращением 6:49
Задачи на комбинаторику 11:49
Вероятность событий
Несовместные события. Противоположные события 6:07
Определение вероятности 9:43
Умножение вероятностей. Условная вероятность 8:56
Независимые события. Теорема умножения для независимых событий 9:20
Задачи на сложение и умножение вероятностей 11:55
Вероятность появления хотя бы одного события 9:50
Задачи на появление хотя бы одного события 12:07
Теорема сложения вероятностей совместных событий 7:13
Задача на теорему сложения вероятностей (с шарами)-1 3:23
Задача на теорему сложения вероятностей (с шарами)-2 2:15
Примеры вычисления вероятностей 6:20
Пример. Найти вероятность выбора синих шаров 2:16
Теорема умножения вероятностей 7:59
Задача на теорему умножения (задача с шарами) 2:13
Геометрическая вероятность 5:12
Формулы Бейеса (формулы Байеса) +док-во 4:18
Полная вероятность. Формула Байеса (Бейеса). Пример 6:00
Формула Бернулли 2:57
Повторение испытаний Формула Бернулли 15:47
Локальная предельная теорема Лапласа 6:54
Интегральная теорема Лапласа 10:58
Формула Пуассона 8:33
Дискретные случайные величины
Случайная величина и закон ее распределения 3:51
Дискретная случайная величина и ее свойства. Пример 9:15
Закон распределения дискретной случайной величины 7:40
Математическое ожидание дискретной случайной и его свойства 16:11
Дисперсия дискретной случайной величины и ее свойства 16:16
Математическое ожидание и дисперсия дискретной случайной величины 4:01
Математическое ожидание и дисперсия. Теория 5:17
Закон Пуассона распределения случайной величины 2:02
Биномиальный закон распределения случайной величины 2:57
Биномиальное распределение 11:50
Геометрическое и гипергеометрическое распределения 16:26
Непрерывные случайные величины
Непрерывная случайная величина и ее свойства 6:49
Распределение непрерывной случайной величины 11:41
Функция распределения непрерывной случайной величины 11:40
Плотность распределения случайной величины 12:13
Математическое ожидание непрерывной случайной 8:17
Дисперсия непрерывной случайной величины 6:41
Задачи на непрерывные случайные величины 11:04
Равномерное распределение случайной величины 3:04
Равномерное распределение 7:51
Показательное распределение 6:28
Нормальный закон распределения. Функция Лапласа 4:22
Нормальное распределение 9:44
Найти вероятность нормально распределенной величины 3:08
Теорема Муавра-Лапласа 1:56
Теорема Муавра-Лапласа в действии 2:16
Функции случайных величин
Функция одного случайного аргумента 10:37
Функция двух случайных аргументов 9:45
Распределения хи квадрат, Стьюдента, Фишера 7:46
Закон больших чисел 8:37
Центральная предельная теорема 10:01
Распределение двух случайных величин 12:45
Зависимые и независимые случайные величины 17:10
Мода и медиана 2:16
Пример: Найти моду случайной величины 2:59
Пример: Найти медиану случайной величины 3:46
Линейная регрессия 11:44
Случайные функции 25:09
Математическая статистика
Основные понятия математической статистики 12:18
Генеральное и групповое среднее 11:02
Генеральная и выборочная дисперсия 14:55
Групповая, межгрупповая и общая дисперсия 12:39
Интервальные оценки 16:13
Проверка гипотез 13:42
Основы дисперсионного анализа 9:24
Основы корреляционного анализа 8:48
Метод Монте-Карло 12:43
Использование математической статистики в экономике 17:07
www.matem96.ru
