Высшая математика пределы для чайников подробные объяснения: Как решать пределы для чайников, примеры решений

Обратная матрица для чайников подробные примеры решений. Обратная матрица

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству

Записывают это следующим образом: или x n → a.

Неравенство (6.1) равносильно двойному неравенству

a – ε x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .

Последовательность, имеющая предел, называется сходящейся , в противном случае – расходящейся .

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .

Пусть дана функция f(x) и пусть a – предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.

Определение 2 . Постоянное число А называется

предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0

Это определение называют определением предел функции по Коши, или “на языке ε – δ “

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде

В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения

x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1 . Если существует каждый предел

(6.4)

(6.5)

(6.6)

Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.

Теорема 2.

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,

Теорема 3.

(6.11)

где e » 2.7 – основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x o , если предел

и непрерывной слева в точке x o, если предел

Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .

2. Если предел равен +∞ или -∞ или не существует, то говорят, что в

точке x o функция имеет разрыв второго рода .

Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода – в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.

Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1|

Возьмем любое ε > 0. Так как x n -1 =(n+1)/n – 1= 1/n, то для отыскания N достаточно решить неравенство 1/n1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .

Пример 3.2. Найти предел последовательности, заданной общим членом .

Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на

n . Затем, применяя теорему предел частного и предел суммы, найдем:

Пример 3.3 . . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4 . Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.

Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.

Пример 3.6 . Доказать, что предел не существует.

Решение. Пусть x 1 , x 2 ,…, x n ,… – последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞

Если x n = p n, то sin x n = sin (p n) = 0 при всех n и предел Если же
x n =2 p n+ p /2, то sin x n = sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim – от английского limit – предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача – найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция.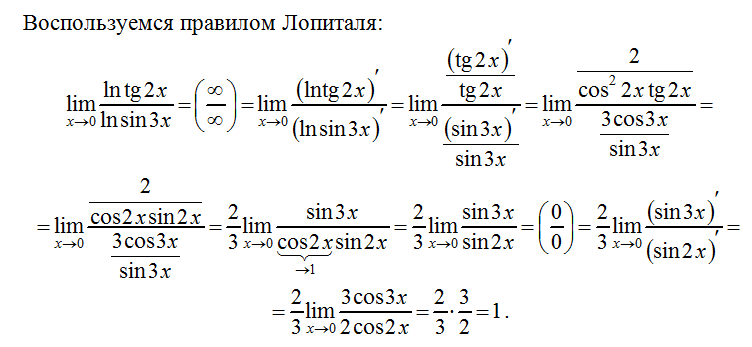 Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Понятия пределов последовательностей и функций. Когда требуется найти предел последовательности, это записывают следующим образом: lim xn=a. 2 стремится к нулю.

Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1

В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность – ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f”(x)/l”(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. (n-1)

Определение 1: матрица называется вырожденной, если её определитель равен нулю.

Определение 2: матрица называется невырожденной, если её определитель не равен нулю.

Матрица “A” называется обратной матрицей , если выполняется условие A*A-1 = A-1 *A = E (единичной матрице).

Квадратная матрица обратима только в том случае, когда она является невырожденной.

Схема вычисления обратной матрицы:

1) Вычислить определитель матрицы “A”, если ∆ A = 0, то обратной матрицы не существует.

2) Найти все алгебраические дополнения матрицы “A”.

3) Составить матрицу из алгебраических дополнений (Aij )

4) Транспонировать матрицу из алгебраических дополнений (Aij )T

5) Умножить транспонированную матрицу на число, обратное определителю данной матрицы.

6) Выполнить проверку:

На первый взгляд может показаться, что это сложно, но на самом деле всё очень просто. Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками “-” и “+”, и не терять их.

А теперь давайте вместе с Вами решим практическое задание, вычислив обратную матрицу.

Задание: найти обратную матрицу “A”, представленную на картинке ниже:

Решаем всё в точности так, как это указано в план-схеме вычисления обратной матрицы.

1. Первое, что нужно сделать, это найти определитель матрицы “A”:

Пояснение:

Мы упростили наш определитель, воспользовавшись его основными функциями. Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.

Во-вторых, мы поменяли 2 и 3 столбец определителя, и по его свойствам поменяли знак перед ним.

В-третьих, мы вынесли общий множитель (-1) второй строки, тем самым, снова поменяв знак, и он стал положительным. Также мы упростили 3 строку также, как в самом начале примера.

У нас получилась треугольный определитель, у которого элементы ниже диагонали равны нулю, и по 7 свойству он равен произведению элементов диагонали. В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.

А11 = 1*(3+1) = 4

А12 = -1*(9+2) = -11

А13 = 1*1 = 1

А21 = -1*(-6) = 6

А22 = 1*(3-0) = 3

А23 = -1*(1+4) = -5

А31 = 1*2 = 2

А32 = -1*(-1) = -1

А33 = 1+(1+6) = 7

3. Следующий шаг – составление матрицы из получившихся дополнений:

5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26:

6. Ну а теперь нам просто нужно выполнить проверку:

В ходе проверки мы получили единичную матрицу, следовательно, решение было выполнено абсолютно верно.

2 способ вычисления обратной матрицы.

1. Элементарное преобразование матриц

2. Обратная матрица через элементарный преобразователь.

Элементарное преобразование матриц включает:

1. Умножение строки на число, не равное нулю.

2. Прибавление к любой строке другой строки, умноженной на число.

3. Перемена местами строк матрицы.

4. Применяя цепочку элементарных преобразований, получаем другую матрицу.

А-1 = ?

1. (A|E) ~ (E|A-1 )

2. A-1 * A = E

Рассмотрим это на практическом примере с действительными числами.

Задание: Найти обратную матрицу.

Решение:

Выполним проверку:

Небольшое разъяснение по решению:

Сперва мы переставили 1 и 2 строку матрицы, затем умножили первую строку на (-1).

После этого умножили первую строку на (-2) и сложили со второй строкой матрицы. После чего умножили 2 строку на 1/4.

Заключительным этапом преобразований стало умножение второй строки на 2 и прибавлением с первой. В результате слева у нас получилась единичная матрица, следовательно, обратная матрица – это матрица справа.

После проверки мы убедились в правильности решения.

Как вы видите, вычисление обратной матрицы – это очень просто.

В заключении данной лекции хотелось бы также уделить немного времени свойствам такой матрицы. (2+1) = -1.

В результате вы получите матрицу дополнений, теперь транспонируйте ее. Транспонирование – это операция, симметричная относительно главной диагонали матрицы, столбцы и строки меняются местами. Таким образом, вы нашли присоединенную матрицу A*.

как решать, правила вычисления, объяснение

Примеры вычисления неопределённых интегралов

Вычисление интеграла по таблице

Интегрирование подстановкой:

Примеры вычисления интегралов

Основная формула Ньютона – Лейбница

Вычисления подстановкой

Глава 4 Дифференциальные уравнения.

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х , искомую функции у и ее производные или дифференциалы.

Символически дифференцированное уравнение записывается так:

Дифференциальное уравнение называется обыкновенным , если искомая функция зависит от одного независимого переменного.

Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

Решением (или интегралом ) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Общим решением (или общим интегралом ) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.

Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

Для решения этого уравнения нужно сначала разделить переменные:

а затем проинтегрировать обе части полученного равенства:

1. Найти общее решение уравнения

o Разделив переменные имеем

Интегрируя обе части полученного уравнения:

Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо C мы написали (1/2) lnC. Потенцируя последнее равенство получим

Это и есть общее решение данного уравнения.

Литература

В. Г. Болтянский, Что такое дифференцирование, «Популярные лекции по математике»,

Выпуск 17, Гостехиздат 1955 г., 64 стр.

В. А. Гусев, А. Г. Мордкович «Математика»

Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1

В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1.

Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. – 1990. – Т. 1.

Ильин В. А., Позняк, Э. Г. Глава 6. Неопределенный интеграл // Основы математического анализа. – 1998. – Т. 1. – (Курс высшей математики и математической физики).

Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. – 1990. – (Курс высшей математики и математической физики).

Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб.пособие-2-е изд.перераб. и доп. М.6Наука. 1989

Колягин Ю.М. Яковлев Г.Н. математика для техникумов. Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.

Щипачев В.С. Задачи по высшей математике: Учеб. Пособие для вузов. Высш. Шк. 1997г.

Богомолов Н.В практические занятия по математике: учеб. 3 – возведение в степень x + 7 – сложение x – 6 – вычитание
Другие функции: floor(x) Функция – округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция – округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция – Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Если определения из учебника слишком сложны и непонятны, прочитайте нашу статью. Мы постараемся максимально просто, “на пальцах” объяснить основные моменты такого раздела математики, как определенные интегралы. Как вычисляется интеграл, читайте в данной инструкции.

С геометрической точки зрения интеграл функции – это площадь фигуры, образуемой графиком данной функции и осью в пределах интегрирования. Запишите интеграл, проанализируйте функцию под интегралом: если подынтегральное выражение возможно упростить (сократить, вынести множитель на знак интеграла, разбить на два простых интеграла), сделайте это. Откройте таблицу интегралов, чтобы определить, производная какой функции стоит под интегралом. Ответ найден? Выпишете множитель, вынесенный за интеграл (если это имело место), запишите найденную из таблицы функцию, подставьте границы интеграла.

Для вычисления значения интеграла рассчитайте его значение в верхней границе и вычтите его значение в нижней границе. Разница – и есть искомая величина.

Чтобы проверить себя или хотя бы уяснить ход решения задачи на интегралы, удобно пользоваться онлайн-сервисом нахождения интегралов , однако прежде чем приступать к решению, ознакомьтесь с правилами ввода функций . Огромнейшее его преимущество в том, что здесь пошагово расписывается все решение задачи с интегралом.

Конечно, здесь рассмотрены лишь самые простые варианты интегралов – определенные, на самом деле разновидностей интегралов великое множество, изучаются они в курсе высшей математики, математического анализа и дифференциальных уравнений в ВУЗах для студентов технических специальностей.

>> >> >> Методы интегрирования

Определение интеграла, определенного и неопределенного, таблица интегралов, формула Ньютона-Лейбница, интегрирование по частям, примеры вычисления интегралов.

Неопределенный интеграл

Пусть u = f(x) и v = g(x) – функции, имеющие непрерывные . Тогда, по произведения,

d(uv))= udv + vdu или udv = d(uv) – vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv – ∫ vdu (8.4.)

Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv”dx к интегрированию выражения vdu=vu”dx.

Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда

∫xcosxdx = ∫x d(sin x) = x sin x – ∫sin x dx = x sin x + cosx + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например, ∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.

Определенный интеграл

Методы интегрирования , понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [ a,b] на n частей точками a= x 0 Δ x i =x i – x i-1 . Сумма вида f(ξ i)Δ x i называется интегральной суммой, а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

F(ξ i)Δx i (8.5).

Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .

Методы интегрирования имеют следующие свойства:

Последнее свойство называется теоремой о среднем значении .

Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл

∫f(x)dx = F(x) + C

и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:

F(b) – F(a). (8.6)

Геометрическая интерпретация: представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox.

Несобственные интегралы

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода – это интегралы на бесконечном промежутке, определяемые следующим образом:

(8.7)

Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится.

Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

если эти пределы существуют и конечны. Обозначение:

Примеры вычисления интегралов

Пример 3.30. Вычислить ∫dx/(x+2).

Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .

Пример 3.31 . Найти ∫ tgxdx.

Решение.∫ tgxdx = ∫sinx/cosxdx = – ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = – ln|t| + C = -ln|cosx|+C.

Пример 3.32 . Найти ∫dx/sinx

Пример 3.33. Найти .

Решение. =

.

Пример 3.34 . Найти ∫arctgxdx.

Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx – ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример 3.35 . Вычислить ∫lnxdx.

Решение. Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx – ∫x 1/x dx =
= xlnx – ∫dx + C= xlnx – x + C.

Пример 3.36 . Вычислить ∫e x sinxdx.

Решение. Применим формулу интегрирования по частям. Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= – cosx → ∫ e x sinxdx = – e x cosx + ∫ e x cosxdx. ∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx, du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx – ∫ e x sinxdx. Получили соотношение ∫e x sinxdx = – e x cosx + e x sinx – ∫ e x sinxdx, откуда 2∫e x sinx dx = – e x cosx + e x sinx + С.

Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.

Решение.Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Вычислить J = .

Решение. Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = .

Пример 3.39 . Вычислить J = .

Решение. Имеем: . Поэтому =

Как ограничения работают с функциями

Не каждая функция определена при каждом значении x. Рациональные функции, например, не определены, если знаменатель функции равен 0. Вы можете использовать предел (который, если он существует, представляет значение, к которому функция имеет тенденцию приближаться, когда независимая переменная приближается к заданному числу) посмотреть на функцию, чтобы увидеть, что она сделала бы , если бы могла.

Для этого посмотрите на поведение функции как на переменную x приближается к неопределенным значениям. Например, эта функция не определена при x = 3:

.

Вы можете посмотреть значения f ( x ) на x = 2, x = 2,9, x = 2,99, x = 2,999 и так далее. Затем можно еще раз посмотреть на значения f ( x ) с другой стороны: x = 4, x = 3,1, x = 3,01 и так далее. Все эти значения f ( x ) определены, кроме для x = 3.

Чтобы выразить ограничение в символах, вы пишете

, который читается как «предел, поскольку x приближается к c из f ( x ) составляет L. » L – это предел, который вы ищете. Чтобы предел функции существовал, левый предел и правый предел должны существовать и быть равными:

• A левый предел из ( x ) — это значение, к которому приближается f ( x ), когда x приближается к n из значений меньше c (с левой стороны графика).

• A правый предел из f ( x ) является полной противоположностью; это значение, к которому приближается f ( x ), когда x приближается к c из значений, превышающих c (с правой стороны графика).

Если и только если левый предел равен правому пределу, можно ли сказать, что функция имеет предел для этого конкретного значения c .

Математически вы должны позволить f быть функцией, а c и L — действительными числами. Затем

ровно тогда, когда

На языке реального мира эта установка означает, что если вы возьмете два карандаша, по одному в каждую руку, и начнете рисовать по графику функции в равных пропорциях, два карандаша должны сойтись в одном месте посередине, чтобы чтобы предел существовал. (На рисунке видно, что хотя функция не определена на x = 3, предел существует, поскольку x приближается к 3. )

Нахождение предела функции графически.

Для функций, которые хорошо связаны, карандаши всегда встречаются в определенном месте (другими словами, всегда будет существовать предел). Однако иногда это не так (как вы видите на рисунке, когда x приближается к –5). Популярная пошаговая функция определяется как f ( x ) = 0 для

.

и f ( x ) = 1 для x > 0. Если вы нарисуете эту функцию, вы увидите скачок единичного шага на x = 0.

Эту статью можно найти в категории :

• Предварительное исчисление,

17Исчисление – Пределы

Пределы составляют основу всех исчислений. Поэтому важно понимать и уметь пользоваться ограничениями. Эта тема немного растянет ваш разум, но если вы будете придерживаться ее, вы ее получите.

Конечные пределы, бесконечные пределы, пределы в бесконечности .

. . Объяснение терминологии

Термины «конечные пределы», «бесконечные пределы» и «пределы на бесконечности» используются по-разному в разных книгах, и у вашего инструктора может быть собственное представление о том, что они означают. На этой панели мы попытаемся разобрать случаи и объяснить различные способы использования этих терминов, а также то, как мы их используем здесь, в 17исчислении.

Когда мы говорим об ограничениях, мы имеем в виду \(\displaystyle{ \lim_{x \to c}{f(x)} = L }\). Различные термины применяются к описанию \(c\) и \(L\) и показаны в таблице ниже. Путаница заключается в терминах конечные пределы и бесконечные пределы . Они могут означать две разные вещи.

\(\displaystyle{ \lim_{x \to c}{f(x)} = L}\)
когда		термин(ы) используется
\(c\) конечен		пределы, приближающиеся к конечному значению или конечные пределы
\(c\) бесконечно \(\pm \infty\)		пределы в бесконечности или бесконечные пределы
\(L\) конечен		конечные пределы
\(L\) бесконечно \(\pm \infty\)		бесконечные пределы

Вы видите, в чем заключается путаница. Условия конечные пределы и бесконечные пределы используются для обозначения двух разных вещей, относящихся либо к \(c\), либо к \(L\). Возможно, чтобы \(c = \infty\) и \(L\) были конечными. Так это бесконечный предел или конечный предел? Это зависит от того, говорите ли вы о \(c\) или \(L\).

Как 17calculus использует эти термины
Страницы этого сайта построены на основе того, что такое \(c\), т.е. мы используем термины конечные пределы и бесконечные пределы только на основе значения \(c\) (используя первые две строки таблицы выше и игнорируя последние две). Это кажется лучшим путем, поскольку, когда нам дают задачу, мы не можем сказать, что такое \(L\), пока не закончим задачу, и, следовательно, мы не можем определить, какой у нас тип проблемы, и знать, что такое методы, которые можно использовать, пока мы не закончим с проблемой.

Важно! Убедитесь и узнайте у своего инструктора, как он использует эти термины.

Если вы хотите полную лекцию на эту тему, мы рекомендуем это видео.

Prof Leonard – Calculus 1 Lecture 1.1: An Introduction to Limits

video by Prof Leonard

Recommended Books on Amazon (affiliate links)
Полный список 17рекомендуемых книг по калькулятору
Prime Student 6-месячная пробная версия

Начало работы с лимитами

Прежде чем мы углубимся в детали работы с лимитами, давайте посмотрим эти видеоролики, чтобы получить представление о том, куда мы идем. Здесь много деталей, но на них стоит обратить внимание.

Доктор Крис Тисделл – Руководство для начинающих по ограничениям в исчислении

видео доктора Криса Тисделла

DR Chris Tisdell – Руководство для начинающих по ограничениям в исчислении – примеры

Видео DR Chris Tisdell

. Чтобы понять, почему нам нужно обсуждать обозначения, прочитайте следующую панель о том, почему обозначения важны в исчислении.

Почему обозначения важны в вычислениях

Использование правильных обозначений чрезвычайно важно в вычислениях. Если вы действительно понимаете исчисление, вы будете использовать правильные обозначения. Потратьте несколько дополнительных минут, чтобы заметить и понять нотацию всякий раз, когда вы сталкиваетесь с новой концепцией. Начните использовать правильную нотацию с самого начала.

Вы можете не думать, что это важно. Однако, если ваш нынешний (или предыдущий) учитель не требует правильных обозначений, изучите их самостоятельно. Вы можете (и, вероятно, будете) получить учителя в будущем, который потребует правильной записи, и это вызовет у вас проблемы, если вы не выучите ее сейчас. Гораздо проще выучить его правильно с первого раза, чем потом исправлять свои обозначения после того, как вы какое-то время делали это неправильно.

Правильное обозначение важно не только в классе, когда вы используете математику (или любой другой предмет, в котором используются специальные символы) в своей карьере, вам нужно будет уметь объяснять, что вы имеете в виду. Без правильных обозначений ваши идеи могут быть неправильно поняты. Это очень похоже на разговор по-английски (или на любом другом языке, который вы регулярно используете) или на его варианте, который имеет значение только для вас. Вас неправильно поймут, и это может даже повлиять на вашу способность сохранить работу.

Итак, просто решите начать использовать правильную запись прямо сейчас. Это не так сложно, и это окупится в долгосрочной перспективе.

При записи предела мы используем обозначение \(\displaystyle{ \lim_{x \rightarrow c}{~f(x)} }\). В этой нотации есть три важные части, которые должны существовать, чтобы эта нотация имела смысл.
1. Трехбуквенное сокращение «лим». Это говорит о том, что у вас есть предел.

2. Обозначение \( x \rightarrow c \). Это важно, потому что это говорит вам о двух вещах; переменная, к которой применяется предел, ‘x’, и значение, к которому он приближается, ‘c’. Отключение этого параметра при использовании предельной нотации оставляет читателю возможность угадать переменную и значение.

3. Сама функция ‘f(x)’. Без этого вы не знаете, к какой функции применяется ограничение.

Важно, чтобы у вас всегда были все три части, когда вы используете эту нотацию. Хороший учитель математики будет поощрять это, снимая баллы, если вы упустите какую-либо часть.

Примечание. В документах, написанных на машинке, в том числе в вашем учебнике, предел может быть записан как \( \lim_{x \rightarrow c}{~f(x)} \). Так написано для экономии места. Тем не менее, это не нормально писать это от руки. Вам нужно написать это как \(\displaystyle{ \lim_{x \rightarrow c}{~f(x)} }\) с \(x \to c\) непосредственно под лим .

Основная идея лимитов

Теперь, когда вы поняли обозначения, связанные с лимитами, давайте посмотрим несколько видеороликов, объясняющих основную идею лимитов и как с ними работать. Важно посмотреть первые два видео, чтобы получить полное представление.

Это первое видео является отличным вводным видео, объясняющим основную идею лимитов и то, как начать работу.

PatrickJMT – Что такое лимит? Основная идея ограничений [5 минут-6 секунд]

видео от PatrickJMT

В этом следующем видеоклипе есть отличное объяснение пределов с использованием нескольких примеров. Во-первых, несколько комментариев по порядку.
1. Во второй половине этого видео обсуждается непрерывность, особенно разрывы. Лучше всего смотреть его в контексте на странице преемственности.
2. А вообще хорошее видео. Однако в конце видео она говорит что-то неправильное. Когда она обсуждает предел на бесконечности и рассматривает три случая рациональных функций, она говорит в третьем случае, что если степень числителя больше степени знаменателя, то предел будет положительной бесконечностью. когда предел уходит в положительную бесконечность, а предел отрицательный, когда предел уходит в отрицательную бесконечность. Это не всегда так, и это намного сложнее, чем она предполагает. Нужно смотреть на знак коэффициентов и соотношение между высшими степенями. На странице с бесконечными ограничениями есть много практических задач, которые показывают, что может произойти. Кроме этого, остальная часть видео очень хороша.

Krista King Math – Пределы и непрерывность [8mins-41secs]

видео Krista King Math

Остальная часть этой страницы содержит несколько тем, связанных с ограничениями в целом. Для более глубокого изучения конкретных тем вы можете найти ссылки в меню выше. Эти отдельные страницы содержат обсуждения, видео и практические задачи. Однако, прежде чем вы приступите к этому, следующие несколько разделов содержат важную справочную информацию, необходимую для понимания других тем. Так что это поможет вам пройти через эти разделы.

Основные законы пределов

В общем, пределы подчиняются правилам алгебры, как и следовало ожидать. Однако, как и во всей высшей математике, нам нужно явно прописать правила, чтобы мы знали, что мы можем делать, а что нет. Итак, вот некоторые основные предельные законы.
Примечание. Во всех нижеприведенных случаях, когда мы утверждаем, что переменная является константой, это означает, что это действительное число, а не \(\infty\) или \(-\infty\). Однако эти правила также применяются, когда \( x \to \infty \) или \( x \to \infty \).
В этих уравнениях предполагается, что
1. \(b\), \(c\) и \(k\) являются константами
2. \(\displaystyle{ \lim_{x\to c}{~f( x)} = L }\) и \(\displaystyle{ \lim_{x\to c}{~g(x)} = M }\)
3. \(n\) — натуральное число

Постоянное правило	\(\displaystyle{ \lim_{x\to c}{ ~b } = b }\)
Правило идентификации	\(\displaystyle{ \lim_{x\to c}{~x} = c}\) 9n }\)
Операционные идентификаторы
1. Постоянное множественное правило	\(\displaystyle{ \lim_{x \to c}{[k\cdot f(x)]} = }\) \(\displaystyle{ k \cdot \lim_{x \to c}{f(x )} = kL }\)
2. Правило суммы/разности	\(\displaystyle{ \lim_{x\to c}{[f(x) \pm g(x)]} = }\) \(\displaystyle{ \lim_{x\to c}{~f(x)} \pm \lim_{x\to c}{~g(x)} = }\) \(\displaystyle{ L \pm M }\)
3. Правило умножения	\(\displaystyle{ \lim_{x\to c}{[f(x) \cdot g(x)]} = }\) \(\displaystyle{ \lim_{x\to c}{~f(x)} \cdot \lim_{x\to c}{~g(x)} = }\) \(\displaystyle{L \cdot M}\)
4. Правило разделения	\(\displaystyle{ \lim_{x\to c}{[f(x)/g(x)]} = }\) \(\displaystyle{ \frac{\lim_{x\to c}{~f(x)}}{\lim_{x\to c}{~g(x)}} = }\) \(\displaystyle{ \frac{L}{M}, ~~~ M \neq 0 }\)

В этом видео обсуждаются эти свойства и приводятся примеры, которые помогут вам понять, как их использовать.

MIP4U – Свойства пределов [7mins-29secs]

видео от MIP4U выполняются некоторые условия. Теорема: предел сложной функции Если у нас есть функции \(f(x)\) и \(g(x)\) и \(\displaystyle{\lim_{x\to c}{g(x)} = L} \) и \(\displaystyle{ \lim_{x\to c}{f(x)} = f(L)}\), то \(\displaystyle{ \lim_{x\to c}{f(g( x))} = f(L) }\) Обратите внимание, что в приведенной выше теореме мы можем написать \(\displaystyle{ \lim_{x\to c}{f(g(x))} = f \left( \lim_{x\to c}{g(x)} \right) }\), т. е. мы можем переместить предел внутрь функции \(f\). В теореме явно не указаны следующие допущения: 1. \(\displaystyle{ \lim_{x\to c}{g(x)} }\) существует – если бы предела не существовало, то мы не могли бы написать \(\displaystyle{ \lim_{x\to c}{g(x)} = L }\) 2. \(L\) находится в области определения \(f(x)\) и является конечным – если \(L\) не находится в области определения \(f(x)\) или \(L\) бесконечно, то \(f(L)\) не имеет значения Хорошо, давайте посмотрим видео, доказывающее эту теорему. Исчисление Ларсона – Доказательство – Предел сложной функции [2мин-9сек] видео Исчисление Ларсона Следующее видео содержит краткое объяснение и несколько примеров, которые помогут вам понять эту концепцию. Криста Кинг Математика – Пределы составных функций – Как их найти? [22min-5secs] video by Krista King Математика Пределы непрерывных функций Вы можете столкнуться с ограничениями функций, которые не являются полиномами, такими как натуральные логарифмы и триггерные функции. Пока функция непрерывна в своей области, вы можете перемещать ограничение внутри функции. Например, \(\displaystyle{ \lim_{x \to 1}{\ln(x)} = \ln \left[ \lim_{x \to 1}{x} \right] = \ln(1) = 0 } \). Поскольку натуральная логарифмическая функция непрерывна в своей области определения, мы можем переместить предел внутрь естественной логарифмической функции и заменить \(x\). Разница между пределом, стремящимся к ±бесконечности, и несуществующим пределом Многие люди путаются между случаем, когда предел стремится к бесконечности (или отрицательной бесконечности), и когда предел не существует. И есть веская причина для путаницы. Многие обсуждения, которые я читал, не разделяют эти два случая. Но они разные. когда предел ДЕЙСТВИТЕЛЬНО существует Когда предел достигает положительной или отрицательной бесконечности, предел ДЕЙСТВИТЕЛЬНО существует. Предел именно такой, положительная или отрицательная бесконечность. когда предел НЕ СУЩЕСТВУЕТ Существует только один случай, когда предел не существует: когда предел отличается слева от предела справа. Эта концепция требует понимания односторонних ограничений. На этой странице есть видеоролики, демонстрирующие примеры отсутствия ограничения. Для получения более подробной информации, включая графики, см. раздел замены на странице конечных пределов. И, как обычно, уточните у своего инструктора, как он определяет несуществующие ограничения. Хорошо, теперь вы готовы перейти к следующей теме, эпсилон-дельта (формальному) определению предела. лимиты 17исчисление плейлист youtube Really UNDERSTAND Исчисление Войдите, чтобы оценить эту страницу и увидеть ее текущий рейтинг. Topics You Need To Understand For This Page precalculus Related Topics and Links WikiBooks – Calculus/Formal Definition Of The Limit Вот страница, содержащая примеры (и решения), показывающие, как использовать определение предела для доказательства предела. Калифорнийский университет в Дэвисе – Примеры определения пределов. Чтобы добавить эту страницу в закладки, войдите в свою учетную запись или создайте бесплатную учетную запись. Практические проблемы с поиском У вас есть номер практической задачи, но вы не знаете, на какой странице она находится? Если это так, введите номер ниже и нажмите «страница», чтобы перейти на страницу, на которой он находится, или нажмите «практика», чтобы перейти к практической задаче. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: