Высшая математика
Занятие №1
Элементарные функции. Производная функции одной переменной.
Теоретические вопросы.
Понятие функциональной зависимости;
Основные классы элементарных функций;
а) степенная функция;
б) показательная функция;
в) логарифмическая функция;
г) тригонометрическая функция;
д) обратные тригонометрические функции.
Производная функции, ее физический и геометрический смысл. Таблица основных формул дифференцирования функций. Дифференцирование суммы, разности, произведения и частного функций.
Дифференцирование сложных функций.
Применение производных к исследованию функций. Необходимое условие возрастания и убывания дифференцируемой функции в интервале.
 Необходимое условие экстремума
дифференцируемой функции.
Необходимое условие экстремума
дифференцируемой функции.
Ю.В. Морозов «Основы высшей математики и статистики» М., 1998, стр. 4-28; 35-70;
М.С. Федорова «Методическая разработка для самостоятельной подготовки по курсу «Высшая математика, информатика» для студентов лечебного и медико-профилактического факультетов» М. 2000.
На практическом занятии выполнить задания:
1. Рассмотреть функции:
;
2. Найти производные функции и решить задачи из [2], стр. 6, №№ 2, 3, 4, 6, 8, 10, 11, 13, 14, 16, 20, 31, 32
3. Исследовать функции
Определить области возрастания, убывания, точки экстремума функций.
а) Найти производные следующих функций:
|
Задание.
Решить задачу. При ламинарном течении вязкой жидкости в трубе слои жидкости имеют различную скорость в зависимости от расстояния от оси трубы.
, где константы.
Найти выражение для градиента скорости на расстоянии от оси трубы.
б) Подготовить теоретические вопросы:
1. Понятие частного приращения функции нескольких переменных.
2. Понятие частной производной функции нескольких переменных.
Высшая математика
Занятие №2
Функция нескольких переменных. Дифференцирование функции нескольких переменных. Теоретические вопросы:
Понятие сложной функции;
Дифференцирование сложной функции;
Понятие функции нескольких переменных;
Дифференцирование функции нескольких переменных.
 Частные
производные.
Частные
производные.
Литература для подготовки:
Ю.В. Морозов «Основы высшей математики и статистики» м., 1998, стр. 52-56;
М.С. Федорова «Методическая разработка для самостоятельной подготовки по курсу «Высшая математика, информатика» для студентов лечебного и медико-профилактического факультетов».
Дифференциал функции. Производные идифференциалы высших порядков
2.2.
Дифференциал функции. Производные и дифференциалы высших порядков
Сегодня вы изучите вопросы
-
Дифференциал функции
-
Геометрический смысл дифференциала функции
-
Основные формулы дифференциалов
-
Инвариантность формы первого дифференциала
-
Производные и дифференциалы высших порядков
Изучив тему занятия, вы сможете
Основные понятия
-
дифференциал функции и его геометрический смысл
-
производные высших порядков
дифференциалы высших порядков
2. 2.1.
2.1.
Дифференциал функции
Пусть на множестве Х задана функция , которая имеет в каждой ее точке производную:
. (113)
По теореме о существовании предела переменной имеем:
, где .
Отсюда находим:
. (114)
Приращение функции в произвольной точке в равенстве (114) представлено в виде суммы двух слагаемых, каждое из которых стремится к нулю при , т.е. является б.м.в. при . Однако второе слагаемое в правой части равенства (114) является б.м.в. более высокого порядка, чем первое, в точках, где производная отлична от 0.
Действительно, .
Следовательно, первое слагаемое, линейное относительно , является главной частью приращения дифференцируемой функции . Эта часть приращения функции называется дифференциалом функции и символически обозначается через :
(115)
Найдем дифференциал независимой переменной х:
Т.к. , то:
(116)
Из равенства (115) с учетом (116) имеем:
(117)
Из формулы (117) следует, что производную по Лейбницу можно рассматривать как дробь, где — числитель, а f — знаменатель.
Следовательно, производную функции можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
В приближенных вычислениях приращение функции заменяют ее дифференциалом Как было доказано выше, второе слагаемое (114) есть б.м.в. более высокого порядка, а следовательно, разность есть б.м.в. при .
Поэтому можно положить, что:
(118)
или
Отсюда находим, что:
. (119)
Формула (119) позволяет выразить приближенно новое значение функции через старое и дифференциал этой функции.
Например, пусть требуется найти приближенное значение корня . По форме заданной величины находится функция: .
Находим . Здесь х = 8; .
По формуле (119) находим:
2.2.2.
Геометрический смысл дифференциала функции
Пусть функция дифференцируема на множестве Х; тогда на плоскости Оху график функции представляется гладкой линией L (в каждой точке этой линии имеется единственная касательная) (рис. 2.10).
2.10).
Пусть М — произвольная точка графика функции .
Построим в точке М касательную к графику функции .
Пусть т. — точка графика функции с абсциссой Сделаем дополнительные построения (см. рис. 2.10).
По рисунку 2.10, Найдем величину :
.
Т.к. , то:
. (120)
Правая часть равенства (120) есть выражение дифференциала функции .
Следовательно,
, (121)
т.е. левая часть равенства (121) есть приращение ординаты касательной. Отсюда краткое заключение.
Дифференциал функции геометрически представляет приращение ординаты касательной.
2.2.3.
Основные формулы дифференциалов
Пусть функции дифференцируемы на множестве Х. Найдем формулы дифференциалов для функций:
(последнее в точках, где ).
По определению дифференциала функции и формул дифференцирования имеем:
или .
или .
или .
В частности, если — константа или — константа, получим:
.
Найдем дифференциалы основных элементарных функций:
Из полученных равенств следует, что формулы дифференциалов аналогичны формулам для производных функции с той лишь только разницей, что вместо производных мы имеем дифференциалы .
2.2.4.
Инвариантность формы первого дифференциала
Пусть функция дифференцируема на множестве Х. Дифференциал первого порядка этой функции, как известно, равен:
(122)
Пусть , где — дифференцируемая функция на множестве Т, областью значений которой является множество Х. В этом случае переменная y является сложной функцией переменной t на множестве Т:
(123)
Найдем дифференциал сложной функции:
.
Мы видим, что форма первого дифференциала не изменилась. В этом и состоит инвариантность формы первого дифференциала.
2.2.5.
роизводные и дифференциалы высших порядков
Рассмотрим функцию Первая ее производная равна , т.е. тоже является функцией от х на множестве .
Найдем вторую ее производную:
.
Мы видим, что вторая производная также является функцией от х, которая, в свою очередь, может иметь производную, уже третьего порядка, и т.д.
Производной n-го порядка от функции называется производная от производной ()-го порядка:
.
В некоторых частных случаях иногда удается найти формулу для производной n-го порядка.
Например, пусть
Пусть требуется найти дифференциал функции :
, т.е. дифференциал функции, есть, вообще говоря, тоже функция — поэтому, в свою очередь, может иметь дифференциал (дифференциал второго порядка):
Дифференциалом n-го порядка называется дифференциал от дифференциала (n — 1)-го порядка: .
По определению,
По аналогии:
(124)
Формулу (124) легко доказать методом полной математической индукции.
Пусть формула (124) справедлива для дифференциала
-го порядка, т.е.
. (125)
Покажем, что в этих предположениях она верна и для дифференциала (k + 1)-го порядка:
Из равенства (124) следует, что , т. е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где — числитель, а — знаменатель.
е. n-ую производную, по Лейбницу, можно рассматривать как дробь, где — числитель, а — знаменатель.
Рассмотрим приложения изложенной теоремы.
Пример 1. Дана металлическая квадратная пластинка с ребром х = 100 мм. При нагревании ребро пластинки удлиняется на ∆х = 0,1 мм. Насколько увеличится при этом площадь пластинки?
Пусть S(х) — первоначальная площадь пластинки, а ∆S — приращение этой площади после нагревании.
По условию задачи .
Найдем приближенное приращение площади пластинки, заменив ее полным дифференциалом:
∆S ≈ ds = (x2)’dx = 2x ∙ dx = 2x ∙ ∆x.
По условию задачи х = 100 мм, ∆x = 0,1 мм.
Отсюда находим, что:
∆S ≈ 2 ∙ 100 мм ∙ 0,1 мм = 20 мм2.
Для оценки погрешности вычисления найдем полное приращение по формуле:
∆S = (х + ∆x)2 — х2 = 2х ∙ ∆х + ∆х2.
Следовательно, погрешность замены равна:
∆х2 = (0,1 мм)2 = 0,01 мм2.
Последнее и есть неглавная часть приращения функции , равная
Пример 2. Найти дифференциал функции y = xn.
По определению дифференциала функции имеем:
Пример 3. Найти дифференциал функции y = ax.
Имеем:
Пример 4. Найти дифференциал функции у = sinx.
Имеем:
Пример 5. Заменив приращение функции дифференциалом, найти приближенное значение arctg 1,02.
Формула применительно к данной функции перепишется так:
Отсюда находим: .
В данном случае х + ∆x = 1,02, х = 1, ∆x = 0,02.
Следовательно, .
Пример 6. Найти n-ую производную функции
Имеем: или
Отсюда можно положить, что:
.
Данное утверждение можно доказать методом полной математической индукции.
Контрольные вопросы
-
Из каких двух частей состоит полное приращение функции?
-
Чем является для функции ее линейная часть относительно приращения независимой переменной?
-
Сравните неглавную часть с главной частью.
 Ваши выводы.
Ваши выводы. -
Может ли функция иметь дифференциал в точке, если она не имеет производной в этой точке?
-
Каков геометрический смысл дифференциала функции?
-
В чем состоит инвариантность формы первого дифференциала?
Задания для самостоятельной работы
-
Найдите дифференциал функции y = x3 в точке x = 0, если по определению дифференциала.
-
Найдите дифференциал функции по формуле :
;
;
;
;
;
;
;
;
.
-
Найдите приближенное значение .
-
Найдите приближенное значение функций:
-
Найдите производные указанного порядка от заданных функций:
Дифференциация — Высшая математика
Добро пожаловать на сайт highmathematics. co.uk
co.uk
Хорошее понимание Дифференциация необходимо для успешной сдачи экзамена.
Прохождение ускоренного курса высшей математики значительно расширит ваши карьерные возможности, помогая вам поступить в колледж/университет, пройти стажировку или даже устроиться на работу. «Хороший» результат по высшей математике подготовит вас к курсу математики AH в следующем году, если вы заинтересованы. Пожалуйста, сделайте все возможное, чтобы продолжать учебу.
Для студентов, которым нужна дополнительная помощь по курсу высшей математики, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в онлайн-пакете для изучения.
Чтобы получить доступ к множеству дополнительных бесплатных ресурсов по теме , воспользуйтесь расположенной выше панелью поиска или нажмите ЗДЕСЬ, выбрав тему, которую хотите изучить.
Мы надеемся, что вы найдете этот веб-сайт полезным, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году. Ниже вы найдете:
Ниже вы найдете:
1. О дифференциации
2. Дифференциация – рабочие листы
3. Дифференциация – видео, руководства по теории и интеллект-карты
4. Основные навыки по высшей математике
5. Экзамен по высшей математике 9005 9002 Рабочие листы по темам Прошлые и практические статьи по темам
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
8. Прошлые и практические статьи по высшей математике
9. 40 вопросов и ответов по высшей математике без калькулятора
10. 200 вопросов и ответов по высшей математике
11. Практические экзаменационные работы от A до H – ответы включены
12. 264 SQA экзамен с несколькими вариантами ответов
13. Контрольные списки экзамена по высшей математике 1
5 Экзаменационные вопросы по математике по темам
15. Решения для учебников по высшей математике
16. Руководства по теории высшей математики
17. Интеллект-карты по высшей математике
18. Практические оценки по высшей математике – решения включены
Практические оценки по высшей математике – решения включены
19. Higher Maths Past Paper Video Solutions
20. Рекомендуемый учебник по высшей математике
21. Пакет онлайн-обучения, ориентированный на экзамен — для студентов, которые ищут «хороший» пропуск
Ресурсы по высшей математике
4
44 .
1. О дифференциации Чтобы узнать, как проводить дифференциацию, нажмите на ссылки “Теория дифференциации” (HSN) и “Дополнительная теория исчисления” (HSN). Также в разделах 2 и 3 ниже вы найдете видео 1 (Введение), видео 2 (Цепное правило), интеллект-карту 1 (Дифференциация) и интеллект-карту 2 (Дальнейшее исчисление) и рабочие листы по этой теме, которые помогут вашему пониманию. Настоятельно рекомендуется использовать рабочие листы 4, 5, 17 и 22 по основным навыкам, а также рабочие листы, содержащие фактические вопросы экзамена SQA.
Если вам нужна дополнительная помощь в понимании Дифференциация в Учебном пакете для онлайн-обучения вы найдете полные, простые в использовании, пошаговые решения десятков экзаменационных вопросов Higher Maths Past & Practice по всем темам. Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на онлайн-учебный пакет , посвященный экзамену , сегодня.
Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на онлайн-учебный пакет , посвященный экзамену , сегодня.
Дифференциация
Процесс дифференциации показан ниже.
- Буква n перемещается вниз перед x
- Мощность становится n – 1
- Необходимо знать, как правильно подготовиться к дифференциации
.
Правила дифференцирования и интегрирования sinax и cosax показаны ниже
- Дальнейшая тема исчисления включает дифференцирование/интегрирование sinax и cosax
- Вышеуказанные правила приведены в Списке формул экзамена по высшей математике
.- Если вас попросят дифференцировать sin³x, измените на (sinx)³ и используйте Цепное правило
- Если вас попросят дифференцировать cos³x, измените на (cosx)³ и используйте цепное правило
.
Цепное правило
.
- N идет к передней части кронштейна
- Внутри скобка остается прежней (ax + b)
- Умножить на дифференцированную первую скобку (а)
- Упростите, перенеся букву «а» на переднюю часть кронштейна
.
Пример 1
- f (x) = (3x³ – 2x² + 5)³
- f ‘(x) = 3 (3x³ – 2x² + 5)² (9x² – 4x)
Пример 2
- f (x) = sin³x = (sinx)³
- f ‘(x) = 3(sinx)²(cosx) = 3sin²xcosx
.
В приведенных выше примерах
- Питание идет вперед
- Затем мощность вычитается на 1
- Первая скобка остается прежней
- Вторая скобка первая скобка дифференцирована
.
2. Дифференциация – Рабочие листы
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.
Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.
Высшее Рабочие листы
________________________________ Рекомендуемый
________________ Рабочие листы
_________________________________________ Без ответов
________________ Примечания/комментарии
_________________________ Любезность
____________________ Теория дифференциации (HSN) Рекомендуется Теория дифференциации (HSN) Предоставлено HSN Дальнейшая теория исчисления (HSN) Рекомендуется Дальнейшая теория исчисления (HSN) Предоставлено HSN Heinemann – Дифференциация Решения для учебников Упр. 6C, 6D, 6E, 6F, 6G, 6H, 6I, 6J, 6L, 6M
, 6N, 6O, 6P, 6Q, 6R, 6S 90 Ответы 90 по ссылкам Heinemann – Дальнейшее исчисление Решения для учебников Примеры 14B, 14C, 14E, 14G, 14H, 14I, 14J, 14K Практика экзамена по основным навыкам 3 Дифференциация Без ответов Только ответы Предоставлено Mr G Rennie Практика экзамена по основным навыкам 9 Дальнейшее исчисление Без ответов Только ответы Предоставлено г-ном Г. Ренни
Ренни Основные навыки 4 Уравнение касательной к кривой Без ответов Только ответы Предоставлено г-ном Г. Ренни Основные навыки 5 Стационарные баллы Без ответов Только ответы Предоставлено г-ном Г. Ренни Основные навыки 17 Графики производных функций Без ответов Только ответы Предоставлено г-ном Г. Ренни Основные навыки 22 Дальнейшая дифференциация Без ответов Только ответы Предоставлено г-ном Г. Ренни Основные навыки 23 Дальнейшая интеграция Без ответов Только ответы Предоставлено г-ном Г. Ренни Бумага Grade Booster Paper 4 Стационарные баллы Без ответов Бумага Grade Booster Paper 6 Касательные к кривым Без ответов Grade Booster Paper 14 Оптимизация Без ответов Экзаменационный лист 1 Рекомендуемый Дифференциальный 1 (2000–2022) Без ответов 2022 Вопросы включены! Предоставлено SQA Рабочий лист экзамена 2 Дифференциация 2 (2014–2019) Без ответов Предоставлено SQA Рабочий лист экзамена 3 Дифференциация 3 (2000–2019) Без ответов Предоставлено SQA Рабочий лист экзамена 4 Дифференциация 4 (оптимизация) Без ответов Предоставлено SQA Экзаменационный лист 5 123 вопроса SQA Дифференциация 5 (Старое высшее) Без ответов Варианты ответов включены! Предоставлено SQA Рабочий лист экзамена 6 Дифференциация 6 (Старое высшее) Без ответов Предоставлено SQA Экзаменационный лист 7 Дифференциация 7 (2000–2013) Схемы выставления оценок SQA Предоставлено SQA Экзаменационный лист 8 Рекомендуемый Дальнейшее исчисление 1 (2000 – 2022) Без ответов 2022 Вопросы включены! Предоставлено SQA Рабочий лист экзамена 9 Дальнейшее исчисление 2 Без ответов Предоставлено SQA Экзаменационный лист 10 Дальнейшее исчисление 3 (старое высшее) Без ответов Несколько вариантов ответа включены! Предоставлено SQA Рабочий лист 1 Дифференциация Введение – 1 Рабочий лист 2 Дифференциация Введение – 2 Без ответов Только ответы Рабочий лист 3 Дифференциальное сопоставление Без ответов Только ответы Контрольный список экзамена 3 Дифференциация Контрольный список экзамена 5 Дополнительные расчеты
.
3. Дифференциация – видео, теоретические руководства и интеллект-карты
Спасибо авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
Видеоматериалы Larbert Maths
_______________________________________ Видео maths180.com
______________________________________ Теоретические руководства HSN
____________________________ Интеллект-карты
____________________________ Применение производных Цепное правило — возрастание/убывание Теория дифференциации (HSN) Дифференциация (HSN) Цепное правило Оптимизация — более сложные примеры Дальнейшая теория исчисления (HSN) Дифференциация (подготовка к) Замкнутые интервалы Скорость изменения и касательная к кривой Дифференциация 1 Комплексное дифференцирование Триггерные функции и правило цепочки Дифференцирование 2 Эскиз кривой Дифференциация (дальше) Производные графики Уравнения касательных Дроби и корни Функции возрастания и убывания Введение в дифференциацию Нотация Лейбница Оптимизация Стационарные точки Sin x и Cos x
.
4. Высшие математические навыки
Спасибо г-ну Г. Ренни за то, что он предоставил в свободный доступ приведенные ниже отличные ресурсы. Рабочие листы основных навыков можно использовать для общего повторения, выполнения домашних заданий, закрепления темы или подготовки к оцениванию, тестам и экзаменам. Четкие, простые в использовании, пошаговые решения для всех 33 рабочих листов основных навыков, приведенных ниже, доступны в онлайн-учебном пакете.
.
5. Экзаменационные листы по высшей математике по темам
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Рабочие листы по темам являются фантастическим учебным ресурсом, поскольку они являются реальными вопросами прошлых бумажных экзаменов. Четкие, простые в использовании, пошаговые решения для всех новых вопросов CfE по высшей математике, приведенных ниже, доступны в онлайн-пакете для изучения.
.
6. Высшая математика: прошлые и практические статьи по темам
Спасибо SQA за то, что они предоставили в свободный доступ превосходные ресурсы, указанные ниже. Вопросы и ответы разделены по темам для удобства поиска. Четкие, простые в использовании, пошаговые решения всех приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
Бумага
_____________ .
Маркировка
__________ .
круги
______ Дифференциация
& Оптимизация
____________ Exp’s
& Logs
________ Функции
и графики
_________ дальнейшие.
Интегрирование
_________ Многочлены
и квадратичные уравнения
____________ 9.
Векторы
________
Волна
Функция
_________ 2019 P1 Marking P1 Q3,16 Q1 Q14 Q10,12 Q6,11,17b Q8 Q2 Q4 Q5,7 Q13,15,17a Q9 2019 P2 Marking P2 Q15 Q7b,11 Q9,12 Q5,8 Q2,13 Q7,10 Q4 Q1 Q6b Q3 ,14 Q6a 2018 P1 Marking P1 Q4 Q6,11 Q2,11,15 Q3,14 Q10 Q7 Q1,8 Q13 Q5,9,12 2018 P2 Marking P2 Q5c,12 Q3,9 Q11 Q6 Q1 Q4,7a,10 7b,c Q5a,b Q2 Q8 2017 P1 Marking P1 Q2 Q8,15c Q12 Q1,6,15a Q3,13 Q10,15b Q4 Q9 Q7,11 Q5 Q14 2017 P2 Marking P2 Q3,10 Q4,7 Q9 Q2 Q8 Q1 Q6,11 Q5 2016 P1 Marking P1 Q4,8 Q2,9 Q14 Q6,10,12 Q5 Q15 Q3 Q1 Q13 Q7,11 2016 P2 Marking P2 Q4 Q7 Q6 Q10,11b 3b,9 Q2,3a Q1 Q8b,11a Q5 Q8a 2015 P1 Marking P1 Q11,14 Q2,7 Q6 Q4,5,13 Q12,15 Q3,8 Q9 Q10 Q1 2015 P2 Marking P2 Q5 Q8 Q2 Q7a Q4 Q3 Q1 Q7b Q6 Q9 Specimen P1 Marking P1 Q11 Q8 Q10 Q1 Q4,7 Q2,5,9 Q6,12 Q3 Образец P2 Marking P2 Q5 Q3B, 8 Q4,7 Q9 Q3A 178 Q9 Q3A 9 Q9 Q3A 18 Q9 Q3A 18 Q9 .
Exemplar P1 Marking P1 Q1 Q8,11 Q10 Q3 Q2,5 Q6 Q4,7 Q9 Образец P2 Маркировка P2 Q2 Q9,10 Q7 Q8 Q4 Q3 Q1 Q08,6 9178
.
7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
Десятки видео по высшей математике содержат качественные уроки по темам. Также включены отличные руководства по теории, интеллект-карты и рабочие листы с актуальными экзаменационными вопросами по высшей математике. Пожалуйста, нажмите на нашу новую страницу с видео и рабочими таблицами по высшей математике по темам.
.
8. Higher Maths Past & Practice Papers
Спасибо SQA за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
.
9. 40 Вопросы и ответы по высшей математике без калькулятора
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Начните с этих вопросов, чтобы укрепить свою уверенность. После того, как вы закончите, вы можете перейти к 200 вопросов экзамена по высшей математике в следующем разделе, проверяя свои ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые для понимания, пошаговые решения всех 40 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
10. 200 вопросов и ответов по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Пожалуйста, постарайтесь задать как можно больше вопросов, проверяя ответы по ходу. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
.
11. Практические экзаменационные работы от A до H – ответы включены
Спасибо SQA и Larkhall Academy за предоставление нижеприведенных превосходных ресурсов в свободном доступе. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом. Четкие, простые в использовании, пошаговые решения для практических работ от A до E доступны в онлайн-пакете для изучения.
.
12. Экзамен 264 SQA Вопросы и ответы с несколькими вариантами ответов
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Множественный выбор — это, прежде всего, вопросы уровня C, и это отличное место для начала проверки. Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее.
.
13. Контрольные списки для экзамена по высшей математике
Спасибо SQA и авторам за предоставление бесплатного доступа к приведенным ниже превосходным ресурсам. Это фантастические контрольные списки для оценки ваших знаний по высшей математике. Пожалуйста, старайтесь регулярно использовать их для повторения перед тестами, предварительными экзаменами и выпускным экзаменом.
.
14. Старые экзаменационные вопросы по высшей математике по темам
Благодарим SQA за предоставленный в свободном доступе превосходный ресурс. Рабочие листы по темам являются фантастическим дополнительным учебным ресурсом.
Тема
________ Название темы
___________________________ Ссылка
________ Примечания
___________________ Тема 1 Круги ЗДЕСЬ Ответы включены Тема 2 Дифференциация ЗДЕСЬ Ответы включены Тема 3 Экспоненты и логарифмы ЗДЕСЬ Ответы включены Тема 4 Функции ЗДЕСЬ Ответы включены Тема 5 Дальнейшее исчисление ЗДЕСЬ Ответы включены Тема 6 Графики функций ЗДЕСЬ Ответы включены Тема 7 Интеграция ЗДЕСЬ Ответы включены Тема 8 Многочлены ЗДЕСЬ Ответы включены Тема 9 Квадратика ЗДЕСЬ Ответы включены Тема 10 Рекуррентные соотношения ЗДЕСЬ Ответы включены Тема 11 Прямая линия ЗДЕСЬ Ответы включены Тема 12 Триггерные формулы сложения ЗДЕСЬ Ответы включены Тема 13 Триггерные графики и уравнения ЗДЕСЬ Ответы включены Тема 14 Векторы ЗДЕСЬ Ответы включены Тема 15 Волновая функция ЗДЕСЬ Ответы включены
.
15. Решения для учебников по высшей математике
Спасибо AHS за предоставленные решения для учебников Heinemann по высшей математике, указанные ниже. Они окажутся чрезвычайно полезными для улучшения ваших знаний по высшей математике. Обратите внимание, что может быть нечетная арифметическая ошибка.
.
16. Пособия по высшей математике
Благодарим HSN за то, что они сделали превосходные руководства по теории высшей математики бесплатными для всех. Они окажутся фантастическим ресурсом, который поможет вам закрепить ваше понимание высшей математики.
Теоретические руководства
_________________ Тема
____________________________________________ Ссылка
_______ Руководство по теории 1 Все темы Раздел 1 Теория (HSN) ЗДЕСЬ Теоретическое руководство 2 Все темы, раздел 1 — краткое руководство на одной странице (HSN) ЗДЕСЬ Руководство по теории 3 Все темы Раздел 2 Теория (HSN) ЗДЕСЬ Теоретическое руководство 4 Все темы, раздел 2 — краткое руководство на одной странице (HSN) ЗДЕСЬ Руководство по теории 5 Все темы Раздел 3 Теория (HSN) ЗДЕСЬ Теоретическое руководство 6 Все темы, раздел 3 — краткое руководство на одной странице (HSN) ЗДЕСЬ Руководство по теории 7 Все темы Разделы 1, 2 и 3 Теория (HSN) ЗДЕСЬ Руководство по теории 8 Теория кругов (HSN) ЗДЕСЬ Руководство по теории 9 Теория дифференцировки (HSN) ЗДЕСЬ Руководство по теории 10 Теория экспонент и логарифмов (HSN) ЗДЕСЬ Руководство по теории 11 Теория функций и графиков (HSN) ЗДЕСЬ Руководство по теории 12 Дальнейшая теория исчисления (HSN) ЗДЕСЬ Руководство по теории 13 Теория трансформации графиков (движение и отражение) ЗДЕСЬ Теоретическое руководство 14 Сводная таблица преобразований графиков ЗДЕСЬ Теоретическое руководство 15 Теория интеграции (HSN) ЗДЕСЬ Руководство по теории 16 Теория многочленов и квадратичных уравнений (HSN) ЗДЕСЬ Руководство по теории 17 Теория последовательностей (HSN) ЗДЕСЬ Руководство по теории 18 Теория прямых линий (HSN) ЗДЕСЬ Руководство по теории 19 Теория тригонометрии (HSN) ЗДЕСЬ Теоретическое руководство 19 Теория векторов (HSN) ЗДЕСЬ Руководство по теории 20 Теория волновых функций (HSN) ЗДЕСЬ
.
17. Интеллект-карты высшей математики
Спасибо авторам за предоставленные ниже отличные ресурсы. Они окажутся фантастическим ресурсом, помогающим вам подготовиться к оценкам, тестам и выпускному экзамену.
.
18. Оценки модулей по высшей математике – решения включены
Спасибо авторам за то, что они сделали приведенные ниже отличные ресурсы бесплатными для всех. Пожалуйста, регулярно используйте для повторения перед оценками, тестами и выпускным экзаменом.
.
19. Higher Maths Past Paper Video Solutions
Щелкните DLB Maths, чтобы просмотреть видеорешения Higher Maths Past Paper. Это отличный ресурс, который поможет вам подготовиться к оцениванию, тестам и выпускному экзамену.
.
20. Рекомендуемый учебник по высшей математике
Ниже вы найдете наш рекомендуемый учебник, который можно заказать, нажав на книгу/ссылку.
.
.
21. Учебный онлайн-пакет по высшей математике
 Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на онлайн-учебный пакет , посвященный экзамену , сегодня.
Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на онлайн-учебный пакет , посвященный экзамену , сегодня.
 Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.
Четкие, простые в использовании, пошаговые рабочие решения для всех рабочих листов, приведенных ниже, доступны в пакете онлайн-обучения.________________________________
________________
_________________________________________
________________
_________________________
____________________
, 6N, 6O, 6P, 6Q, 6R, 6S 90 Ответы 90 по ссылкам
 Ренни
Ренни
_______________________________________
______________________________________
____________________________
____________________________

5. Экзаменационные листы по высшей математике по темам

Бумага
_____________
Маркировка
__________
круги
______
& Оптимизация
____________
& Logs
________
и графики
_________
Интегрирование
_________
и квадратичные уравнения
____________ 9.
Векторы
________
Функция
_________

7. Видео по высшей математике, руководства по теории, интеллект-карты и рабочие листы
 Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.
Четкие, простые в использовании, пошаговые решения для всех представленных ниже документов CfE Higher Papers доступны в пакете онлайн-обучения.9. 40 Вопросы и ответы по высшей математике без калькулятора
 Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.
Если вы застряли, всегда обращайтесь к учителю за помощью как можно скорее. Четкие, простые в использовании, пошаговые решения всех 200 приведенных ниже вопросов доступны в пакете онлайн-обучения.11. Практические экзаменационные работы от A до H – ответы включены
12. Экзамен 264 SQA Вопросы и ответы с несколькими вариантами ответов

13. Контрольные списки для экзамена по высшей математике
________
___________________________
________
___________________

_________________
____________________________________________
_______


Благодаря пошаговым решениям экзаменационных вопросов, доступным в онлайн-учебном пакете, мы охватим все, что вам нужно знать о Дифференциация , чтобы сдать выпускной экзамен.
Для студентов, которые ищут «хороший» проход по высшей математике, вы можете рассмотреть возможность подписки на фантастические дополнительные ресурсы, ориентированные на экзамены, доступные в Online Study Pack. Подписка может стать одной из ваших лучших инвестиций.
Пожалуйста, предоставьте себе все возможности для достижения успеха, поговорите со своими родителями и подпишитесь на ориентированный на экзамен Online Study Pack сегодня.
Мы надеемся, что ресурсы на этом веб-сайте окажутся полезными, и желаем вам всего наилучшего в изучении курса высшей математики в 2023 году.
Получите учебный пакет — всего 20 фунтов стерлингов
Учителя нажмите здесь >
Не только дифференциация, но и 70 других математических понятий подробно описано
Дифференциация | Высшая математика | Maths.
 scot
scotСодержание курса
- Дифференцирование алгебраической функции, которая представляет собой или может быть упрощена до выражения в степенях \(x\)
- Дифференцирование \(k\sin\x\) и \(k\cos\x\)
- Дифференцирование составной функции с помощью цепного правила
- Определение уравнения касательной к кривой в данной точке дифференцированием
- Определение строго возрастающей или убывающей функции
- Набросок графика алгебраической функции путем определения стационарных точек и их характера, а также пересечений с осями и поведения из \(f(x)\) для больших положительных и отрицательных значений \(x\)
- Оптимизация: определение оптимального решения для данной проблемы
- Определение наибольшего и/или наименьшего значения функции на отрезке
- Решение проблем с использованием скорости изменения
- Рисование \(y=f'(x)\) по графику \(y=f(x).\)
Стандартные производные
| \(f(x)\) | \(f'(х)\) | ||||||||||||||||
| \( sin\tiny\ \normalsize ax\) \( cos\tiny\ \normalsize ax\) | \( a\tiny\ \normalsize cos\tiny\ \normalsize ax \) \( -a\tiny\ \normalsize sin\tiny\ \normalsize ax \) 93-4\sqrt{x}+\large\frac{1}{3x}\normalsize,\), где \(x\gt 0\), найдите \( \large\frac{dy}{dx}\normalsize.  4-5\) в точке, где \(x=-2\). 92-12x+1\) в интервале \(-1\leq x\leq 2\). 4-5\) в точке, где \(x=-2\). 92-12x+1\) в интервале \(-1\leq x\leq 2\).Другие важные ресурсы
Предыдущие бумажные вопросы
|

 Частные
производные.
Частные
производные.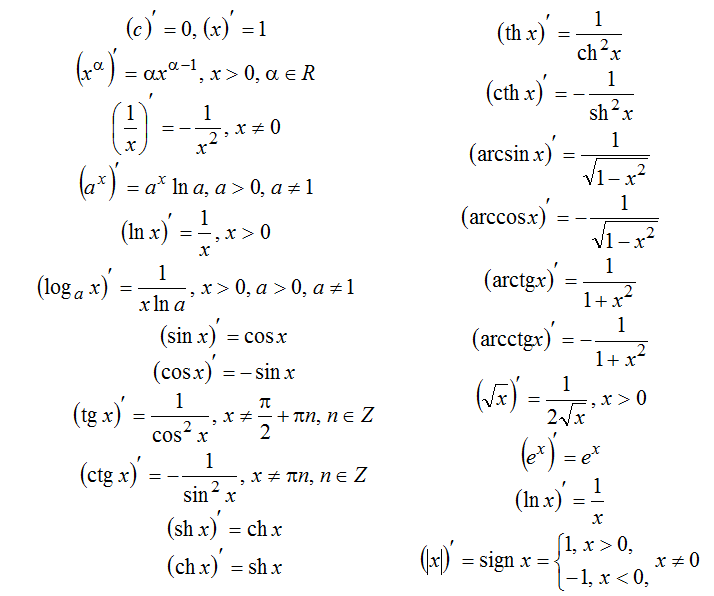 Ваши выводы.
Ваши выводы.