Тренажёр формул по физике (ЕГЭ)
Пользоваться тренажёром предельно просто. Открой нужный раздел физики в списке разделов ниже. Ты увидишь описания формул из этого раздела.
Напиши эти формулы на листочке. Затем кликни на надпись “Кликни и проверь себя” и выясни, какие из формул ты еще плохо знаешь.
Подучи и повтори всё сначала.Успехов в изучении формул по физике, да и вообще физики!
МеханикаКинематика
- Напиши формулы
- Кликни и проверь себя
Динамика
- Напиши формулы
- Кликни и проверь себя
Статика
- Напиши формулы
- Кликни и проверь себя
Гидростатика
- Напиши формулы
- Кликни и проверь себя
Законы сохранения энергии и импульса
- Напиши формулы
- Кликни и проверь себя
Механические колебания и волны
- Напиши формулы
- Кликни и проверь себя
Молекулярно-кинетическая теория
- Напиши формулы
- Кликни и проверь себя
Термодинамика
- Напиши формулы
- Кликни и проверь себя
Электростатика
- Напиши формулы
- Кликни и проверь себя
Постоянный электрический ток
- Напиши формулы
- Кликни и проверь себя
Магнитное поле
- Напиши формулы
- Кликни и проверь себя
Электромагнитные колебания и волны
- Напиши формулы
- Кликни и проверь себя
Переменный ток
- Напиши формулы
- Кликни и проверь себя
Геометрическая оптика
- Напиши формулы
- Кликни и проверь себя
Волновая оптика
- Напиши формулы
- Кликни и проверь себя
Основы специальной теории относительности
- Напиши формулы
- Кликни и проверь себя
Корпускулярно-волновой дуализм
- Напиши формулы
- Кликни и проверь себя
Физика атома и атомного ядра
- Напиши формулы
- Кликни и проверь себя
- Назад
- Вперед
Решение уравнений в математике и физике | by Math Power
Многие из вас знают, что у учеников в школе часто появляются проблемы 😞 при использовании одного учебного предмета на другом.
Например, возникают затруднения при использовании математических знаний на уроках физики 😒. И я не говорю про работу с тригонометрическими функциями, графиками, формулами сокращенного умножения и 🤯. Проблемы 😞 возникают буквально в начале курса физики в 7 классе.
Проблема — неспособность вывести формулу к задаче
Я считаю, что еще в 6 классе ученики могут освоить это на уроках математики, если сделать на этом упор, сразу после изучения отрицательных чисел . Ну и конечно обязательно стоит провести параллель с решением уравнений, ведь выведение формулы к задаче, это то же самое нахождение неизвестной в уравнении с одной переменной.
Так же для этого метода понадобится знание о том, что собой представляет противоположное и обратное число. Напомню, что обратное это число «вверх тормашками», а два числа, отличающиеся друг от друга только знаками, называют противоположными числами.
В этом методе используются две математические аксиомы, которые, надеюсь, многим знакомы:
- Для любого элемента a существует элемент, называемый ему противоположным и обозначаемый -a, для которого a+(-a)=0
- Для любого элемента a существует элемент, называемый ему обратный и обозначаемый

ИЛИ
P.S. я буду рассматривать только действия сложения и умножения, предполагая, что от них произошли действия деление и вычитание.
**Рассмотрим для начала использование этих аксиом для решения линейных уравнений.
3x+15=27
Решить уравнение, значит найти всего его корни или доказать, что их нет т.е. получить выражение вида:
x=…
Значит для достижения этого вида, нам мешают в данном уравнении числа и . «Уничтожать» не понравившиеся нам числа, мы будем обратно порядку действий т.е. с начала избавляемся от слагаемых (1 аксиома), а потом от множителей (2 аксиома).
P.S. при наличии скобок смысл остается, т.к. действия в скобках обычно производятся раньше всех, то при решении уравнения всё наоборот, 🤯 числа, заключенные в скобки будут уничтожаться последними.
Значит первым делом, мы избавимся от 15 (т.к это слагаемое). По первой аксиоме мы знаем, что 15+(-15)=0. Это и поможет нам «уничтожить» 15.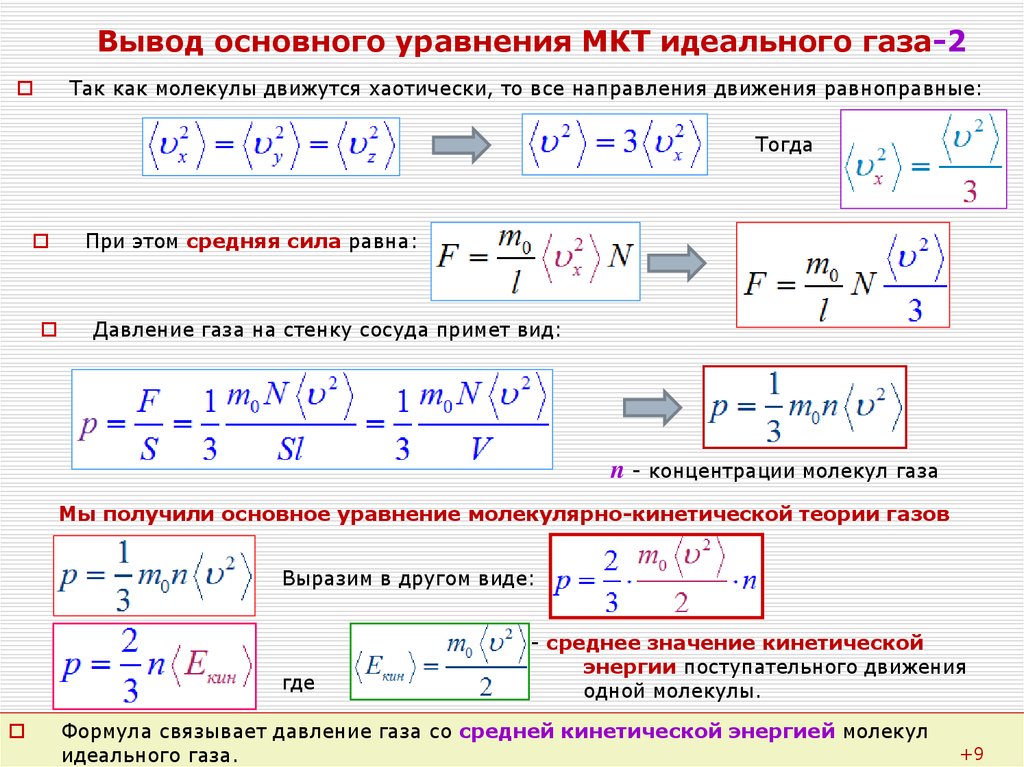
Получим:
3x+15+(-15)=27+(-15)
Не забываем все манипуляции проводить в обеих частях равенства.
3x=27+(-15)
3x=12
Эти действия очень напоминают наше любимое «перенести» через равно, но откуда это пошло? И как ученику это запомнить и понять? Нужно просто пару раз прописать решение, используя первую аксиому. Потом, без условно, это дойдет до автоматизма, но и ученик будет знать «откуда ноги ростут» 😏 у «перенести» через равно.
Далее «уничтожаем» множитель 3 по второй аксиоме мы знаем, что 3∙1/3=1. Давайте попробуем этим воспользоваться умножим обе части на 1/3.
Получим:
3∙1/3 x=12∙1/3
1∙x=(12∙1)/(1∙3)
x=4
В итоге в процессе решения уравнения ученик только прибавляет числа или выражения в обеих частях равенства или умножает на число или выражение в обеих частях. Ему не нужно думать, что на что нужно делить, что из чего нужно вычесть, нужно только понять, в каком действии участвует «уничтожаемое» число в сложении или умножении.
Рассмотрим еще один пример решения уравнений с помощью данных аксиом, в котором будут присутствовать действия деления и вычитания.
x/3–24=78
По первой аксиоме 24+(-24)=0, но у нас уже есть (-24), значит, нужно прибавить +24:
x/3–24+24=78+24
x/3=102
Теперь вспомним вторую аксиому 3∙1/3=1, но у нас уже есть 1/3, значит нужно умножить на 3:
3∙1/3 x=102∙3
x=306
Таким образом, эти аксиомы дают нам единообразный метод решения уравнений. По-моему опыту, даже самые заядлые ученики — «гуманитарии», прописывали эту святую истину несколько раз и начинали щелкать уравнения одно за другим.
Вернемся к проблеме вывода формул для задач на уроке физики 😏 и попробуем вывести -время из формулы равноускоренного движения при начальной скорости равной нулю, используя те же аксиомы:
S=(at²)/2
S=1/2∙a∙t²
Чтобы получить t=… нужно «уничтожить» два множителя a и 1/2. Мы это уже умеем по второй аксиоме:
2S=2∙1/2∙a∙t²
2S∙1/a=1/a∙a∙t²
2S/a=t²
t²=2S/a
t=√(2S/a)
Таким образом, научившись видеть эти аксиомы в числах, ученикам будет, легче перестроится на буквы и выражения.

