Вторая онлайн-консультация проекта «На все 100» была посвящена ЕГЭ по физике
ЕГЭ
18 октября 2022 ЕГЭ
1 фото
18 октября в эфир вышел второй выпуск онлайн-консультаций по подготовке к ЕГЭ «На все 100» от разработчиков экзаменационных материалов из Федерального института педагогических измерений (ФИПИ). Об этом сообщает пресс-служба Рособрнадзора.
Об особенностях выполнения экзаменационной работы и изменениях, которые ждут участников экзамена в 2023 году, рассказал член комиссии по разработке контрольных измерительных материалов (КИМ) ЕГЭ по физике Сергей Стрыгин.
Он сообщил, что существенных изменений в КИМ ЕГЭ в этом году не произошло. Так же, как и раньше, экзаменационная работа состоит из 30 заданий: 23 в первой части и 7 во второй. В этом году расширилась тематика задания 30: кроме задач на применение законов Ньютона и задач на применение законов сохранения в механике, добавлены задачи по статике.
«На экзамен отведено 3 часа 55 минут, и за это время надо успеть много: не только решить задачи, но и правильно их оформить. Я бы посоветовал основные законы и ход решения задачи набросать на черновике и после того, как вы решили задачу, сразу оформлять ее на чистовик, чтобы не терять время», – посоветовал Сергей Стрыгин.
В решении задачи необходимо сперва указать формулы, а каждую физическую формулу, которой нет в кодификаторе, нужно вывести прежде, чем использовать ее при решении. В заданиях второй части важно не забыть указать в ответе единицы измерения. Это поможет избежать наиболее распространенных ошибок. Видеозапись эфира доступна на страницах Рособрнадзора в соцсети «ВКонтакте» и других социальных сетях.
21 октября в 12:00 серию онлайн-консультаций по подготовке к ЕГЭ продолжит эфир, посвященный экзамену по русскому языку.
Новости по теме
ЕГЭ
31 октября 2022
В ЕГЭ 2023 года по биологии количество заданий увеличено с 28 до 29
Разработчики ЕГЭ рассказали о подготовке к экзамену по биологии
ЕГЭ
25 октября 2022
Экзаменационные материалы в пункты проведения ЕГЭ начнут направлять онлайн
Ранее они доставлялись на CD-дисках
ЕГЭ
25 октября 2022
ЕГЭ по информатике обсудили в эфир подкаста «На все 100»
Подкаст прошел в рамках серии онлайн-консультации Рособрнадзора от разработчиков ФИПИ
Другие новости
Национальный проект «Образование»
18 ноября 2022
По программе «Земский учитель» в сельских школах Республики Алтай приступили к работе 10 педагогов
Регионы
18 ноября 2022
В Кемерове в Театре для детей и молодежи состоялся областной семинар «Театральная пятница»
Русский язык в мире
18 ноября 2022
Открыта регистрация для зрителей на церемонию вручения Национальной премии «Патриот-2022»
|
Random converter |
Калькуляторы рычагаНажать для просмотра увеличенного изображения Калькулятор выигрыша в силе и усилия нагрузки рычагаКалькулятор определяет усилие нагрузки и выигрыш в силе для рычага любого порядка. Пример: Рассчитать выигрыш в силе и усилие нагрузки для рычага первого рода, если его плечо приложения силы равно 50 см, плечо приложения нагрузки равно 20 см и приложенное усилие равно 10 Н. Входные данные Род рычага 1 2, AE > AL 3, AEL Плечо приложения силы (входное плечо) AEсантиметр (см)метр (м)дюймфут Плечо приложения нагрузки (выходное плечо) ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Для расчета введите значения и нажмите кнопку Рассчитать. Для расчета выигрыша нужно ввести только величины плеч рычага. Если нужно рассчитать усилие нагрузки, введите приложенное усилие. Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Выигрыш в силе MA Усилие нагрузки FL Н Калькулятор положения опоры рычага I родаКалькулятор определяет положение опоры и размер плеча приложения силы рычага первого рода, в котором опора расположена между точками приложения сил. Пример: Рассчитать положение опоры рычага первого рода, если его длина равна 60 см, приложенное усилие равно 10 Н и усилие нагрузки равно 20 Н. Входные данные Общая длина рычага L=AE+ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Положение опоры (плечо нагрузки) AL м Плечо приложения силы AE м Калькулятор положения нагрузки для рычага II родаВ рычаге II рода точка опоры и точка приложения силы находятся на противоположных концах рычага. Пример: рассчитать положение нагрузки для рычага II рода, если его полная длина равна 40 см, приложенное усилие равно 10 Н и усилие нагрузки равно 20 Н. Входные данные Общая длина рычага L=AEсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Положение нагрузки (плечо нагрузки) AL м Плечо приложения силы AE=L м Калькулятор положения приложенного усилия для рычага III родаВ рычаге III рода точка опоры и нагрузка находятся на противоположных концах рычага. Пример: Рассчитать положение точки приложения нагрузки рычага III рода, если его полная длина равна 50 см, приложенное усилие равно 20 Н и усилие нагрузки равно 10 Н. Входные данные Общая длина рычага L=ALсантиметр (см)метр (м)дюймфут Приложенное усилие FEньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Усилие нагрузки FLньютон (Н)джоуль на метр (Дж/м)грамм-сила (гс)килограмм-сила (кгс)фунт-сила Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Точка приложения усилия (плечо усилия) AE м Плечо нагрузки AL=L м Определения и формулыРычаги и их типыРычаг представляет собой простейший механизм, состоящий из твердого тела, которое может вращаться вокруг неподвижной опоры. Для идеального рычага, в котором не теряется энергия и который является абсолютно жестким, отношение плеч рычага определяет отношение приложенного усилия и нагрузки. Эта взаимосвязь называется правилом рычага: Выигрыш в силе, даваемый рычагом, определяется как отношение выходной силы (нагрузки) FL к входной силе (приложенному усилию) FE: Отсюда можно определить приложенное усилие: Существует три типа рычагов, которые отличаются взаимным расположением точки опоры и плеч рычага, причем правило рычага одинаково для всех трех типов рычагов. Рычаги I рода: В этих рычагах опора находится между точками приложения сил, которые находятся на противоположных концах рычага. Примерами рычагов I рода являются качели (перекладина) и плоскогубцы. В рычагах I рода плечо нагрузки может быть больше или меньше плеча приложения силы, а выигрыш в силе может быть больше, меньше или равен единице. В рычагах I рода полная длина рычага L равна сумме длин плеча нагрузки AL и плеча усилия AE: Формулу для определения плеча нагрузки (и, соответственно, положения точки опоры) можно вывести из приведенного выше правила рычага: Рычаги II рода: В этих рычагах точка опоры и точка приложения силы расположены на противоположных концах рычага. Нагрузка приложена между опорой и усилием. Примеры рычагов II рода — тачка, щипцы для орехов и открывалка для бутылок. В рычаге второго рода плечо приложения силы всегда больше плеча приложения нагрузки и выигрыш в силе всегда больше единицы. В рычаге II рода полная длина рычага равна плечу приложения нагрузки: Плечо приложения нагрузки (или точка приложения нагрузки) рассчитывается по формуле, которая выводится из приведенного выше правила рычага: Рычаги III рода: В этих рычагах точка опоры и нагрузка расположены на противоположных концах рычага. Усилие приложено между нагрузкой и точкой опоры. Примеры рычагов III рода — метла, предплечье человека и удочка. В рычагах III рода выигрыш в силе всегда меньше единицы и плечо приложения силы всегда меньше плеча приложения нагрузки. В рычагах III рода полная длина рычага равна длине плеча приложения нагрузки: Длины плеча приложения силы (точка приложения силы) рассчитывается по формуле, выведенной из правила рычага: В экскаваторе для перемещения стрелы (рычаг III рода слева), рукояти (рычаг I рода в центре) и ковша (еще один рычаг I рода справа) используются гидравлические цилиндры Автор статьи: Анатолий Золотков Другие калькуляторы простейших механизмов:
Калькуляторы Механика |
Обычно рычаги используют для перемещения тяжелых грузов (обычно говорят об усилии нагрузки или просто грузе FL) путем приложения меньшей силы FE. Часть рычага между его концом и точкой опоры, к которой приложена нагрузка, называется плечом нагрузки AL. Вторая часть рычага, к которой приложено усилие, называется плечом приложения усилия AE. Рычаг — один из шести простейших механизмов, определенных учеными эпохи Возрождения.
+ онлайн-решатель с бесплатными шагами
Онлайн-калькулятор четвертой производной — это бесплатный инструмент, который позволяет найти производную четвертого порядка математической функции.
Инструмент принимает порядок производной и выражение функции в качестве входных данных.
вывод вычислитель выводит желаемую производную порядка заданной функции. Это мощный инструмент для студентов, математиков и исследователей, позволяющий быстро решать свои задачи.
Что такое калькулятор четвертой производной?
Калькулятор четвертой производной — это онлайн-инструмент, который вычисляет производную четвертого порядка любой сложной функции за несколько секунд.
Производная функции означает, как функция изменяется в зависимости от ее зависимой переменной. Производные более высокого порядка извлекают больше полезной информации о таких функциях, как экстремум или вогнутость.
Есть много приложений в физике, математике и искусственном интеллекте, где 9Производные 0003 более высокого порядка помогают решить проблему. Для решения многих дифференциальных уравнений требуются производные четвертого порядка.
Но если функции сложные и включают более одной переменной, трудно найти их производные.
Поэтому мы предлагаем вам этот продвинутый инструмент, известный как Калькулятор четвертой производной , чтобы легко найти решение ваших проблем.
Вы можете использовать этот удобный инструмент в своем браузере, когда вам это нужно. Это полностью бесплатный инструмент с неограниченными возможностями использования.
Как пользоваться калькулятором четвертой производной?
Чтобы использовать Калькулятор четвертой производной , , вам необходимо ввести порядок производной и математическое выражение для вашей функции. Дополнительной особенностью этого калькулятора является то, что он может вычислять производную любого порядка входной функции.
Интерфейс калькулятора прост и хорошо организован. Все поля ввода имеют метки для понимания их использования. Ниже приведены пошаговые инструкции по использованию калькулятора.
Шаг 1
Введите порядок производной в поле ‘ N ’. Для производной четвертого порядка это « n » должно быть равно 4 .
Шаг 2
Теперь поместите выражение функции в поле « F(x) ».
Шаг 3
В конце, чтобы получить решения, нажмите кнопку « Submit ». Он представит вам производную четвертого порядка данной функции.
Как работает калькулятор четвертой производной?
Калькулятор четвертой производной работает, находя производную четвертого порядка заданной функции. Значение « n » в калькуляторе показывает требуемый порядок производной.
Это значение должно быть равно четырем для вычисления производной четвертого порядка. Этот калькулятор полезен, когда есть знания о производной и ее важности в исчислении.
Что такое производная?
Производная – это скорость изменения одной величины по отношению к другой. Процедура определения производной функции называется дифференциация .
Производная функции ‘ f(x) ’ обозначается ‘ d/dx (f(x)) ’. Значение производной в исчислении можно понять, если рассмотреть кривую функции « f(x) » и взять на ней две точки.
Один из них — « (x, f(x)) », а другой — « ((x+h), f(x+h)) ». который проходит через эти две точки. Когда расстояние между двумя точками составляет примерно ноль , вторая точка соединяется с первой точкой, t, и, в конце концов, секущая линия становится касательной линией.
наклон этой касательной считается производной функции в исчислении. Он определяется математически как:
d/dx (f(x)) = наклон касательной = $ \lim_{h\to 0} \frac{f(x+h) – f(x)}{h } $
Формула выше предела используется для вычисления производной функции и называется нахождением производной с помощью первый принцип .
Производные применяются для оптимизации функций. Интервалы возрастания или убывания функции также находятся с помощью производных. Они используются для определения скорости величины путем вычисления производной смещения.
Производные высшего порядка
Производные высшего порядка, такие как четвертая производная, определяются путем нахождения последовательных производных заданной функции.
Например, когда требуется найти производную второго порядка, сначала найдите первую производную, а затем возьмите производную от первой производной. 94$.
Основные правила производных
Некоторые основные правила используются при нахождении производных. Эти правила объясняются ниже.
Степенное правило
Степенное правило гласит, что производная функции с показателем степени равна показателю, умноженному на функцию с уменьшенной на степенью .
Правило суммы и разности
Это правило определяет распределительное свойство процесса дифференцирования. Процесс может быть распределено по суммированию и вычитанию.
Правило произведения
При нахождении производной функции, являющейся произведением двух функций, правило произведения определяет производную этой функции следующим образом.
Производная равна сумме первой функции, умноженной на производной второй функции, и второй функции, умноженной на производной первой функции.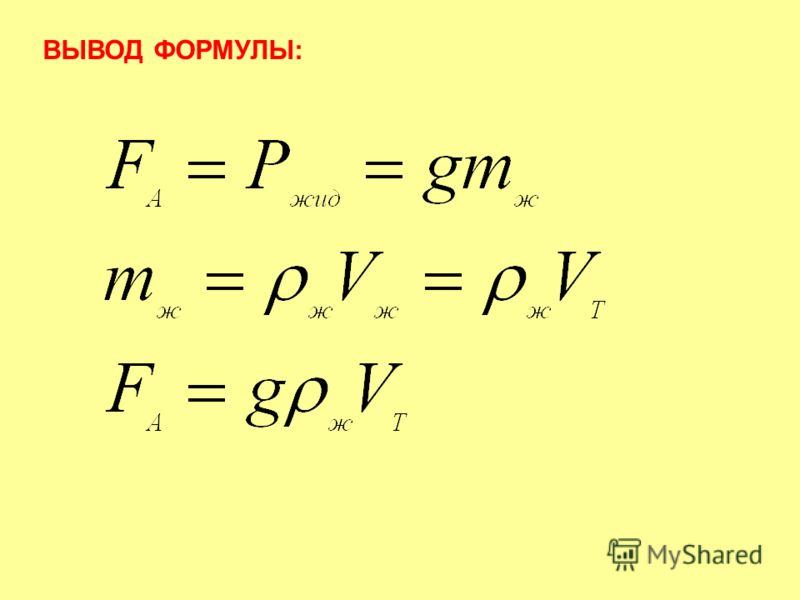
Правило константы
Производная константы равна нулю в соответствии с правилом константы производной.
Решенные примеры
Чтобы лучше понять, как работает калькулятор, давайте посмотрим на некоторые решенные примеры.
Пример 1
Студента-физика просят найти скачок для заданного вектора положения на экзамене. Для этого ему нужно вычислить производную четвертого порядка следующей функции. 9{2} – 12) sin(x)\, -\, 8x cos(x)\]
Список математических калькуляторов
Производные как dy/dx
Производные все о изменение …
… они показывают, как быстро что-то меняется (так называемая скорость изменения ) в любой момент.
В разделе «Введение в производные» (пожалуйста, прочтите сначала!)
Здесь мы делаем то же самое, но используем нотацию «dy/dx» (также называемую нотацией Лейбница ) вместо пределов.
Начнем с вызова функции “y”:
у = f(x)
1. Добавьте Δx
Когда x увеличивается на Δx, тогда y увеличивается на Δy :
у + Δу = f(х + Δх)
2. Вычесть две формулы
| От: | у + Δу = f(х + Δх) | |
| Вычесть: | у = f(x) | |
| Получить: | y + Δy − y = f(x + Δx) − f(x) | |
| Упрощение: | Δy = f(x + Δx) − f(x) |
3. Скорость изменения
Чтобы вычислить скорость (называемую скоростью изменения ), мы делим на Δx :
Δy Δx = f(x + Δx) − f(x) Δx
4. Уменьшить Δx близко к 0
Мы не можем допустить, чтобы Δx стало равным 0 (потому что это было бы делением на 0), но мы можем заставить его направиться к нулю и назвать его «dx»:
Δx dx
Вы также можете думать о “dx” как о бесконечно малом или бесконечно малом.
Точно так же Δy становится очень маленьким, и мы называем его «dy», чтобы получить:
ды дх знак равно е (х + дх) – е (х) дх
Попробуйте это на функции
Попробуем f(x) = x 2
| ды дх | = е (х + дх) – е (х) дх | ||
| = (х + дх) 2 − х 2 дх | f(x) = x | ||
| = х 2 + 2х(дх) + (дх) 2 – х 2 дх | Расширить (x+dx) 2 | ||
| = 2x(дх) + (дх) 2 дх | x 2 −x 2 =0 | ||
| = 2x + dx | Упростить дробь | ||
| = 2x | dx идет к 0 |
Таким образом, производная от x 2 равна 2x
.