Инженерный калькулятор онлайн | Дорога к Бизнесу за Компьютером
Вашему вниманию представлен лучший инженерный калькулятор онлайн, который только можно себе вообразить. Впрочем, не только инженеры могут им воспользоваться. Его можно применять в самых разных областях человеческой деятельности, там, где требуются вычисления.
Этот калькулятор поможет школьникам и студентам, которые на нем могут проверить правильность своих расчетов, а также преподавателям, которым приходится порой проверять за вечер сотни домашних заданий.
Данный калькулятор онлайн будет очень полезен людям, которые по роду своей деятельности постоянно занимаются расчетами и вычислениями: инженерам, финансистам, бухгалтерам, бизнесменам.
И главное его преимущество перед другими аналогичными калькуляторами в том, что он позволяет не только производить различные математические действия, но делать это, рассчитывая результат целых формул.
Например, как Вам такая формула? И сколько времени уйдет на ее решение на обычном калькуляторе?
А на данном калькуляторе онлайн задача решается довольно просто, за несколько минут — Вы просто начинаете прописывать цифры и производить с ними определенные действия, и формируете нужную Вам формулу, используя скобки.
Если Вы не вполне себе представляете, как это сделать — видео внизу Вам в помощь.
На этом калькуляторе онлайн Вы можете работать со степенями и корнями, извлекать логарифмы, и использовать тригонометрические функции.
Экран калькулятора онлайн отображает введенное выражение привычным для нас образом, так, как мы его записываем на бумаге.
Формулы можно корректировать — Вы просто ставите курсор в нужное место на поле ввода, затем убираете или добавляете символы или цифры.
При вводе чисел вместо десятичной запятой используйте точку.
Старайтесь также закрывать все скобки. В большинстве случаев это некритично, и калькулятор сам подставит нужные скобки, но иногда возможны ошибки. Впрочем, Вы сами легко увидите неточность в отображаемой формуле, и ее исправите.
О точности калькулятора онлайн можно судить, решив древнюю задачу о зернах на шахматной доске. Кто не помнит — изобретатель шахмат запросил с царя, которому шахматы понравились, следующую награду: на одну клетку шахматной доски нужно было положить одно пшеничное зернышко, на вторую — два, на третью — четыре, и так далее, увеличивая каждый раз количество зернышек вдвое, пока не закончатся все 64 клетки. Изобретатель сказал, что заберет эти зерна себе. Вы можете подсчитать, сколько зерен должно было быть на последней клетке. Решение — не что иное, как 2 в степени 64. Даже Excel выдает при вычислении этого количества округленный результат. А этот калькулятор подсчитает Вам все точно:
Или, например, сложение большого количества чисел.
Особенно это актуально для бухгалтеров, которым иногда приходится складывать целые ряды чисел. Если это делать на обычном калькуляторе — вычисления превращаются в утомительный и выматывающий труд. Кроме того, никогда нет уверенности в правильности результата, недаром бухгалтера обычно пересчитывают все по два раза. А с этим калькулятором задача становится довольно простой — все числа видны на экране, и правильность их ввода легко проверить, и если надо, ввод исправить.
Одним словом, возможности данного инженерного калькулятора онлайн удовлетворят даже самого взыскательного пользователя. Потому — пользуйтесь, и желаю Вам комфортных и правильных расчетов.
Видео о том, как вводить формулы в инженерном калькуляторе онлайн
Более подробные сведения Вы можете получить в разделах “Все курсы” и “Полезности”, в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
Также Вы можете подписаться на блог, и узнавать о всех новых статьях.
Это не займет много времени. Просто нажмите на ссылку ниже:
Подписаться на блог: Дорога к Бизнесу за Компьютером
Проголосуйте и поделитесь с друзьями анонсом статьи на Facebook:
01-д. Формулы и их преобразование
§ 01-д. Формулы и их преобразование
Из курса математики вам уже известны некоторые формулы. Посмотрите на вторую строку таблицы, на формулу S = l·b. Она показывает, что площадь прямоугольника S вычисляется умножением его длины
Формулы для вычисления площади прямоугольника, объёма параллелепипеда и цилиндра.
| Как вычислить … | Формула |
| … площадь прямоугольника | S = l·b |
| … объём параллелепипеда, цилиндра | V = S·h |
Итак, формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Формулы можно преобразовывать по правилам математики.
Образцы преобразования простейших формул, содержащих произведение, частное, сумму и разность.
| Исходная формула | Выразили « b » | Выразите « c » |
| a = b · c | b = a : c | c = … |
| a = c · b | b = a : c | c = … |
| a = b : c | b = a · c | c = … |
| a = c : b | b = c : a | c = … |
| a = b + c | b = a – c | c = … |
| a = c + b | b = a – c | c = . .. |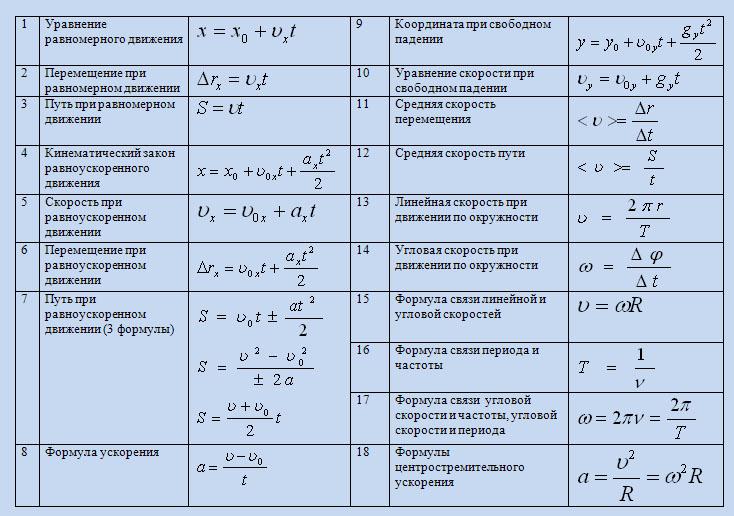
| a = b – c | b = a + c | c = … |
| a = c – b | b = c – a | c = … |
Начертите такую же таблицу в тетради и заполните третью колонку, выразив в ней величину, обозначенную символом с.
| l = 5,0 см ± 0,1 см | b = 3,5 см ± 0,1 см | h = 1,5 см ± 0,1 см |
| Перепишем эти же равенства в виде неравенств: | ||
| 4,9 см l | 3,4 см b | 1,4 см h |
Применив две формулы V = S · h = l·b · h , вычислим наименьшее Vmin и наибольшее Vmax значения объёма спичечного коробка:
| Vmin = 4,9 см · 3,4 см · 1,4 см Vmin ≈ 23 см³ | Vmax = 5,1 см · 3,6 см · 1,6 см Vmax ≈ 29 см³ |
Тогда результат вычисления объёма коробка с учётом погрешности измерений исходных величин запишется в виде неравенства:
23 см³ Vкор
На числовой прямой это неравенство будет выглядеть так:
Соответственно, истинное значение объёма коробка заключено между значениями Vmin и Vmax.
Другими словами, оно лежит где-то в интервале между 23 см³ и 29 см³ (нами он отмечен синей штриховкой).
Итак, мы познакомились с тем, как можно находить границы истинности результата, подставляя в формулу наименьшие и наибольшие значения входящих в неё величин.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxКалькулятор расчета параметров коаксиальных кабелей • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Модель линии передачи
Эквивалентная схема бесконечного малого участка длины коаксиального кабеля
На рисунке показана эквивалентная схема бесконечно малого участка коаксиального кабеля. Все элементы схемы нормализованы к единице длины (омы на метр, фарады на метр, сименсы на метр, генри на метр в системе СИ или омы на фут, фарады на фут, сименсы на фут, генри на фут в британской и американской системах единиц).
Эта эквивалентная схема повторяется бесконечное множество раз на всей длине коаксиального кабеля.
Диэлектрическая и магнитная проницаемость диэлектрического материала кабеля
Абсолютная диэлектрическая проницаемость используемого в коаксиальном кабеле диэлектрика определяет скорость распространения сигнала в кабеле. Обычно эта величина обозначается греческой буквой ε (эпсилон) и представляет собой меру сопротивления электрическому полю в данном материале. В диэлектрике электрическое поле уменьшается. В системе СИ диэлектрическая проницаемость измеряется в фарадах на метр (Ф/м). Вакуум имеет наименьшую диэлектрическую проницаемость. В связи с этим диэлектрическая проницаемость вакуума была выбрана в качестве константы — электрической постоянной ε0 = 8,854187817…×10−12 Ф/м. Ранее она носила название диэлектрической постоянной или диэлектрической проницаемости вакуума. Эта постоянная не имеет какого-либо физического смысла, это просто размерный коэффициент и именно поэтому он теперь называется электрической постоянной.
Для конкретного диэлектрического материала диэлектрическая проницаемость обычно выражается в виде отношения его диэлектрической проницаемости к диэлектрической проницаемости вакуума, то есть
Скорость света в вакууме c0 связана с магнитной постоянной μ0 и электрической постоянной следующей формулой:
или
Магнитная проницаемость — мера способности материала поддерживать в нем магнитное поле. Обычно она обозначается греческой буквой μ и измеряется в СИ. Относительная магнитная проницаемость, обычно обозначаемая как μr (от англ. relative — относительный), представляет собой отношение магнитной проницаемости данного материала к магнитной проницаемости вакуума (магнитной постоянной). Относительная магнитная проницаемость абсолютного большинства используемых в коаксиальных кабелях диэлектриков равна μr = 1.
Магнитная постоянная, ранее называемая магнитной проницаемостью вакуума, численное значение которой вытекает из определения силы тока ампера с учетом образования магнитного поля при протекании тока по проводнику или при движении электрического заряда.
Она равна
μ0 = 4π × 10−7 ≈ 1,256637806 × 10–6 Гн/м
Магнитная проницаемость μ и диэлектрическая проницаемость ε определяют фазовую скорость распространения электромагнитного излучения в диэлектрике
В вакууме эта формула изменяется на
Для немагнитных материалов (то есть для диэлектриков, используемых в коаксиальных кабелях), формула для фазовой скорости упрощается:
Как мы видим, чем выше диэлектрическая и магнитная проницаемость, тем ниже фазовая скорость распространения электромагнитного излучения в диэлектриках.
Байонетные коаксиальные радиочастотные соединители (разъемы, коннекторы) типа BNC широко используются для присоединения кабелей для передачи цифровых и аналоговых аудио и видеосигналов к испытательному оборудованию, электронным устройствам, антеннам и авиационным приборам. Обычно на кабелях устанавливают вилки (на жаргоне — «папы»), а на панелях оборудования — розетки (на жаргоне — «мамы»).
Погонная емкость коаксиального кабеля (С’)
Погонная емкость коаксиального кабеля, то есть его емкость на единицу длины, является одной из важных характеристик коаксиальных кабелей. Коаксиальный кабель можно представить в форме коаксиального конденсатора, у которого обязательно будет отличная от нуля емкость между внутренним и внешним проводниками. Эта емкость пропорциональна длине кабеля и зависит от его размеров, формы и диэлектрической постоянной диэлектрика, заполняющего пространство между внутренним и экранным проводниками.
Погонная емкость C’ в фарадах на метр (Ф/м) определяется по формуле:
где
D — внутренний диаметр экранирующего проводника коаксиального кабеля,
d — диаметр внутреннего проводника коаксиального кабеля; величины D и d должны быть в одинаковых единицах,
ε0 ≈ 8,854187817620…×10−12 Ф/м — диэлектрическая проницаемость вакуума,
εr — относительная диэлектрическая проницаемость изоляционного материала.
Относительная диэлектрическая проницаемость материалов, обычно используемые в коаксиальных кабелях: полипропилен — 2,2–2,36, политетрафторэтилен (ПТФЭ или тефлон) — 2,1, полиэтилен — 2,25.
Приведенная выше формула и используется в нашем калькуляторе.
В англоязычных странах используется погонная емкость на 1 фут. Учитывая, что 1 фут = 0,3045 м, ln(x) = 2,30259 lg(x), и ε0 ≈ 8,854187817620… × 10−12 Ф/м, эту формулу для C’ в фарадах на фут (Ф/фут) можно переписать в виде
или в пикофарадах на фут:
Коаксиальный радиочастотный соединитель типа F (вилка) используется для установки на коаксиальные кабели, используемые для установки телевизионных антенн, для кабельного и спутникового телевидения и для кабельных модемов. Обычно для этих целей используются кабели типа RG-6/U и RG-59/U. В качестве центрального контакта данных соединителей используется центральная жила, поэтому этот проводник должен быть сплошным (не многожильным)
Погонная индуктивность коаксиального кабеля (L’)
Для коаксиального кабеля это индуктивность на единицу длины L’ в генри на метр (Гн/м), определяемая по формуле
где
D — внутренний диаметр экранирующего проводника коаксиального кабеля,
d — диаметр внутреннего проводника коаксиального кабеля; величины D и d должны быть в одинаковых единицах,
c — скорость света в вакууме, равная 299 792 458 м⋅с−1,
ε0 = 8,854187817620.
.. × 10−12 Ф/м — электрическая постоянная.
Электрическую постоянную ранее называли диэлектрической постоянной или диэлектрической проницаемостью вакуума. Сейчас эти названия считаются устаревшими, но пока еще широко используются.
Учитывая, что 1 фут = 0,3045 м и ln(x) = 2,30259 lg (x), имеем:
или в мГн/фут
Электрическая постоянная ε0 по определению связана со скоростью света в вакууме c и магнитной постоянной μ0 следующей формулой:
где μ0 = 4π × 10−7 ≈ 1,256637806×10–6 Гн/м — магнитная постоянная, называемая также магнитной проницаемостью вакуума (устаревшее название).
С учетом этого определения можно переписать формулу для погонной индуктивности L’ в Гн/м в виде
Эта формула и используется в нашем калькуляторе.
Кабель RG-59/U и его поперечное сечение. Центральный проводник из омеднённой стали покрыт слоем диэлектрика — полиэтилена, на котором находится экранирующий проводник, состоящий из тонкой пленки, покрытой слоем алюминия, и оплетки из луженой меди.
Волновое сопротивление кабеля — 75 Ом
Волновое сопротивление коаксиального кабеля (Z
0)Одной из наиболее важных характеристик коаксиального кабеля является его волновое сопротивление, которое можно представить как импеданс со стороны источника сигнала, подключенного к бесконечно длинному отрезку кабеля. Волновое сопротивление Z0 коаксиального кабеля представляет собой отношение напряжения к току одиночной волны, распространяющейся по кабелю (без отражений). Оно определяется геометрией кабеля и материалом диэлектрика между внутренним проводником и наружным экраном и не зависит от длины кабеля. В СИ волновое сопротивление измеряется в омах (Ом). Волновое сопротивление можно рассматривать как импеданс линии передачи бесконечной длины, так как в такой линии нет сигнала, отраженного от ее конца. Обычно коаксиальные кабели выпускаются с волновым сопротивлением 50 или 75 Ом, хотя иногда можно встретить и другие значения.
Почему 50 и 75 Ом? Существует несколько версий.
По одной из них 50 Ом было выбрано в связи с тем, что коаксиальный кабель с полиэтиленовым диэлектриком с относительной диэлектрической проницаемостью εr = 2,25 обеспечивает минимальные потери сигнала именно при волновом сопротивлении 50 Ом; при этом по нему может передаваться значительная для данных геометрических размеров кабеля мощность. Стандарт 75 Ом используется для недорогих кабелей кабельного телевидения, которые не передают сигналов большой мощности и обеспечивают лучшие характеристики по потерям. Почему 75 Ом? Есть несколько объяснений. Некоторые считают, что 75 Ом — это компромисс между малыми потерями в кабеле и его хорошей гибкостью. Другие считают, что эти значения были выбраны достаточно произвольно.
Несмотря на то, что соединители типа RCA не обеспечивают хорошего согласования волнового сопротивления, они часто используются для передачи видео и аудио сигналов.
Волновое сопротивление Z0 коаксиального кабеля с потерями определяется так:
где
R’ — погонное сопротивление (на единицу длины),
L’ — погонная индуктивность (на единицу длины),
G’ — погонная проводимость материала диэлектрика (на единицу длины),
C’ — погонная емкость (на единицу длины),
j — мнимая единица, и
ω — угловая частота.
Для кабеля без потерь, у которого нулевое сопротивление проводников и отсутствуют диэлектрические потери (R’ = 0 и G’ = 0), эта формула упрощается:
Здесь величина Z0 (в омах) не зависит от частоты и является действительно величиной, то есть, чисто резистивной величиной. Такое приближение в форме линии передачи без потерь является удобной моделью для описания коаксиальных кабелей с малыми потерями, особенно в тех случаях, когда они используются для передачи высокочастотных сигналов.
Заменяя L’ и C’ их определениями, приведенными выше, получаем:
где
D — внутренний диаметр экранирующего проводника коаксиального кабеля,
d — диаметр внутреннего проводника коаксиального кабеля; величины D и d должны быть в одинаковых единицах,
c — скорость света в вакууме, равная 299 792 458 м⋅с−1,
ε0 = 8,854187817620…×10−12 Ф/м — электрическая постоянная.
εr — относительная диэлектрическая проницаемость материала изолятора кабеля.
Подставляя значения электрической постоянной ε0 и скорости света, получаем:
Учитывая, что ln(x) = 2,30259 lg (x), получаем практическую формулу для волнового сопротивления в омах, которая и используется в нашем калькуляторе:
Кабель RG-6/U и его поперечное сечение. Центральный проводник из омеднённой стали окружен слоем диэлектрика из вспененного полиэтилена и экраном, состоящим из тонкой алюминиевой фольги и медной (или алюминиевой, как на этом дешевом кабеле) оплетки. Волновое сопротивление кабеля 75 Ом. Выпускаются более дорогие кабели RG-6/U с медной центральной жилой и луженой медной оплеткой.
Максимальная рабочая частота коаксиального кабеля
Поперечная электромагнитная волна TEM-волна в линии передачи; H — магнитное поле, E — электрическое поле, D — направление распространения волны
Основным типом волны в коаксиальном кабеле является TEM-волна (от англ.
transverse electromagnetic mode — поперечная электромагнитная волна). В этом режиме распространения силовые линии электрического и магнитного поля перпендикулярны между собой и с направлением распространения волны. Силовые линии электрического поля расположены радиально, а силовые линии магнитного поля имеют вид концентрических окружностей вокруг центральной жилы кабеля. На более высоких частотах в коаксиальных кабелях могут возбуждаться поперечные электрические TE-волны (от англ. transverse electric — поперечные электрические), в которых только силовые линии магнитного поля расположены в направлении распространения, и поперечные магнитные TM-волны (от англ. transverse magnetic), в которых только силовые линии электрического поля расположены в направлении распространения волн. Однако эти два режима являются нежелательными.
В коаксиальном кабеле самая низкая частота, при которой образуются волны типа TE11, и является максимальной рабочей частотой fc. Это верхняя частота использования коаксиального кабеля.
Сигнал может распространяться в виде TE11-волны, если длина волны в диэлектрике кабеля короче, чем средняя длина окружности диэлектрика; для воздушного диэлектрика формула будет выглядеть как
где
λc — самая короткая допустимая длина волны в кабеле в метрах и
D and d — диаметры внешнего (экрана) и внутреннего проводников кабеля в метрах.
Если в кабеле в качестве диэлектрика используется не воздух, а другой немагнитный материал (магнитные диэлектрики вроде феррита не используются в конструкции коаксиальных кабелей), его рабочая частота может быть от 0 до максимальной, определяемой по формуле
где
D — диаметр внешнего проводника в метрах,
d — диаметр внутреннего проводника в метрах,
fc — максимальная рабочая частота в герцах,
εr — относительная диэлектрическая проницаемость материала диэлектрика.
Для более практических величин в мм и ГГц, формула будет иметь вид
Если у вас есть старое оборудование домашнего кинотеатра с коаксиальным входом цифрового звукового сигнала в формате S/PDIF (Sony/Philips Digital Interface) и, например, сетевой медиаплеер с оптическим выходом звука и соединителем TOSLINK, вы можете легко конвертировать оптический сигнал в передаваемый по коаксиальному кабелю радиочастотный сигнал с помощью такого недорогого конвертера.
Выпускаются конвертеры для преобразования оптического входя в коаксиальный выход, коаксиального входа в оптический выход, а также конвертеры, сочетающие оба вида преобразования.
Именно эта формула и используется в нашем калькуляторе. На практике коаксиальные кабели работают на частотах менее 90% этой частоты.
Коэффициент укорочения длины волны и коэффициент замедления скорости
В коаксиальном кабеле, где пространство между внутренним проводником и экраном заполнено диэлектриком, сигнал распространяется через этот диэлектрик. Фазовая скорость волны, которая распространяется в диэлектрике, уменьшается, однако ее частота не изменяется. Скорость распространения
Из этого соотношения видно, что длина волны сигнала, который распространяется в диэлектрике, также уменьшается пропорционально уменьшению скорости. Для сравнения такого уменьшения скорости (и соответствующего пропорционального уменьшения длины волны) со скоростью света, во многих странах (но не в России) используется коэффициент замедления скорости VF (от англ.
Velocity Factor — фактор скорости), которая всегда меньше единицы или меньше 100%, если он выражен в процентах.
В России и других странах бывшего СССР традиционно используется обратная величина — коэффициент укорочения, но об этом чуть ниже. В англоязычной литературе, если речь идет о компьютерных сетях, а не об общей физике, скорость распространения сигнала в линии передачи vp обычно выражают не в виде величины в единицах скорости, а в виде процентного отношения к скорости света. Правильнее было бы называть эту величину коэффициентом замедления скорости VF. Например, в линии передачи с типичным значением VF = 66%, что соответствует диэлектрической постоянной 2,25 (сплошной полиэтилен) сигнал будет передаваться со скоростью, составляющей 66% от скорости света. Формула:
Здесь
VF — коэффициент замедления скорости в процентах,
vP — скорость распространения в линии передачи (в м/с или футах/с),
c — скорость света в вакууме (приблизительно 3,0×108 м/с, или 9,8×108 футов/с).
Отметим, что в англоязычной научной и физической литературе, не относящейся к компьютерным сетям, термин скорость распространения действительно означает скорость, то есть расстояние в единицу времени.
Предположим, что нам нужно отмерить короткий полуволновый отрезок кабеля с коэффициентом замедления скорости 66% (что соответствует коэффициенту укорочения длины волны 1,52) для сигнала с частотой 30 МГц. Длина волны в вакууме, соответствующая этой частоте будет равна λ = c/f = 10 m. Следовательно для обеспечения задержки в половину волны нужна электрическая длина 5 метров. Однако, поскольку сигнал распространяется в кабеле со скоростью в 1,52 (на 66%) меньше, нам нужно только 5 × 0,66 = 3,3 м физической длины коаксиального кабеля. То есть, нам понадобится кабель, который в k = 1/0.66 = 1.52 раза короче, чем расчетная электрическая длина. Здесь k — тот самый коэффициент укорочения, который показывает во сколько раз скорость распространения меньше скорости света в вакууме.
Если у вас еще не заболела голова от этих рассуждений, то сейчас точно заболит! Отметим, что в Белоруссии, России, на Украине и в других странах на постсоветском пространстве этот коэффициент укорочения длины, который всегда больше единицы, традиционно используется вместо коэффициента замедления скорости, привычного англоязычным специалистам. Кстати, на немецком языке этот коэффициент называется Verkürzungsfaktor, что тоже означает коэффициент укорочения.
Подведем итог. Коэффициент замедления скорости, величина, обратная коэффициенту укорочения длины волны, показывающему во сколько раз фазовая или групповая скорость волны в коаксиальном кабеле меньше скорости света в вакууме. Именно этот коэффициент указывается в характеристиках коаксиальных кабелей зарубежного производства. Коэффициент замедления показывает во сколько раз скорость света больше скорости распространения волн в коаксиальном кабеле и обычно (но не всегда) выражается в процентах. В характеристиках коаксиальных кабелей российского производства указывается коэффициент укорочения длины волны, который всегда больше единицы.
Как и с случае волн оптического диапазона, при прохождении волн в диэлектрике их длина волны уменьшается (сравните с преломлением!) с сохранением частоты. Поскольку скорость равна произведению частоты на длину волны, скорость также уменьшается.
Обычно в коаксиальных кабелях используются немагнитные диэлектрики, относительная магнитная проницаемость которых μr = 1. В таких диэлектриках коэффициент замедления скорости VF равен величине, обратной квадратному корню из относительной диэлектрической проницаемости материала, по которому передается сигнал:
В общем случае, который включает, например, такие диэлектрики как феррит, коэффициент замедления скорости определяется по формуле
Для распространения света в оптоволокне коэффициент замедления скорости равен величине, обратной коэффициенту преломления n материала (обычно кварцевого стекла), из которого изготовляют сердцевину волокна:
Вилки типа F коаксиальных радиочастотных соединителей, установленные на коаксиальных кабелях RG-59/U, которые часто используются для передачи маломощных радиочастотных и видеосигналов; такие кабели обычно входят в комплект поставки потребительского видеооборудования
Автор статьи: Анатолий Золотков
Вывод формулы по физике
Какие существуют производные в физике?
В физике все дело в лучшем понимании основ.
Вывод в физике определяет возникновение некоторого математического алгоритма понимания каких-либо физических явлений.
На этой странице мы узнаем о следующем:
Почему мы выводим формулы физики?
Как вывести формулы физики?
Как вывести уравнения в физике?
Вывод физических формул
Вывод физических уравнений
Почему мы выводим физические формулы?
Все, что мы изучаем в физике, имеет под собой определенную логику, а математика дает нам логику для понимания явлений, и когда мы видим связь между математикой и физикой, наше понимание возрастает намного больше.Во время приложений студенты могут столкнуться со многими понятиями, задачами и математическими формулами.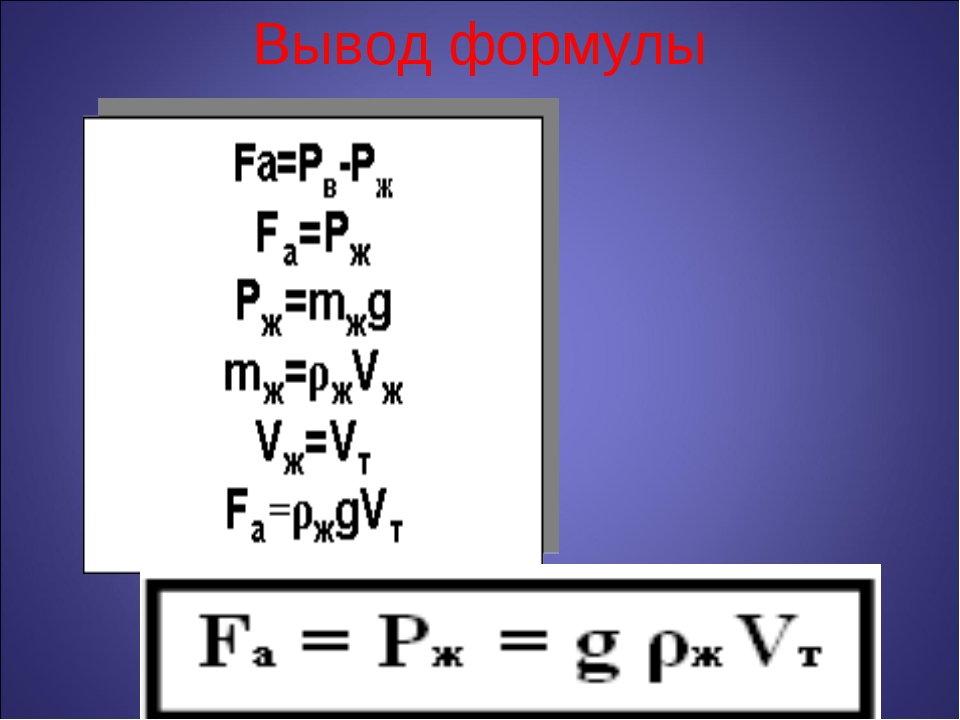
С помощью производных учащиеся используют свои способности, креативность и хороший потенциал для поиска решений.
Как вывести уравнения физики?
Математические выводы важны при выводе физических уравнений, потому что они помогают нам понять, откуда взялось уравнение, почему оно является уравнением для конкретной задачи.
Как вывести физические формулы?
Физические формулы получены из наблюдений и экспериментов.
Ниже приведено несколько выводов, описывающих вывод физических формул.
Вывод физических формул
Крутящий момент на стержневом магните
Однородное магнитное поле B представлено параллельными линиями.
NS представляет собой стержневой магнит длиной 2l и силой на каждом полюсе m.
Магнит удерживается под углом Ө к направлению B .
(Изображение будет загружено в ближайшее время)
(Изображение будет загружено в ближайшее время)
Сила на северном полюсе.
Сила на южном полюсе = МБ, напротив B.
Силы равны, и они имеют тенденцию вращать магнит по часовой стрелке, чтобы выровнять его вдоль B.
, следовательно, крутящий момент на морозном магните задается на
= сила x перпендикулярное расстояние = mB NA…(1)
Рассмотрим Δ NAS
SinӨ = NA/ NS = NA/ 2l => NA = 2lSinӨ…(2)
Подставляя значение (2) в (1 )
て = mB x 2lSinӨ.Так как M = mx 2l
て = B x M sinӨ
В векторной форме уравнение (3) запишется как M и B.
Тепловая машина
Тепловая машина представляет собой устройство, преобразующее тепловую энергию в механическую без изменения внутренней энергии системы.
Тепловая машина в основном состоит из следующих компонентов:
Полная энергия в S.
H.MПростое гармоническое движение — это движение, совершаемое точечной массой, на которую действует сила, пропорциональная смещению частицы, но противоположная по знаку.
Частица, выполняющая С.Х.М., обладает следующим: Потенциальная энергия и Кинетическая энергия
Потенциальная энергия.
Это происходит из-за смещения частицы от ее среднего положения.
Рассмотрим частицу массы m, совершающую С.Х.М. с амплитудой a и постоянной угловой частотой ω.Предположим, что через t секунд после старта из среднего положения смещение частицы равно y, которое определяется как
Скорость частицы в момент t,
V = dy /dt = d ( a Sin ωt)/ dt = a xd(Sin ωt)/dt
Ускорение частицы в этот момент
A = – a ω2 Sin ωt = – ω2 y….(3)
Здесь отрицательный знак указывает на то, что ускорение всегда направлено от его среднего положения.
Возвращающая сила, F = масса x ускорение
= – mx ω2 y = – hy
Суммарная работа, выполненная при перемещении частицы из ее среднего положения в положение смещения y, будет
W=0yh y dy=hy22y0=h y22
потенциальной энергии в данный момент.Таким образом,
Kp = 12h y2 (подставляя значение h из уравнения (4))
Kp = 12m ω2 y2 (подставляя значение y из уравнения (1))
Кинетическая энергия
Эта энергия зависит от скорости частицы.
Кинетическая энергия в момент времени t определяется как
Kk = 12 м V2 (подставляя значение «V» из уравнения (2)) )
KK = 12 H A2 (1 – Y2A2)
Список важных физических производных в классе 12
тема | Formula | Описание | ||||
скорость дрейфа vd = 1 / て = ½ (EEM) () VD пропорциональна электрическому поле E, а к времени столкновения て | ||||||
Biot-Savart Закон (величина магнитного поля) | дБ = 04 IDL SINR2 | здесь, θ – угол между DL и R | ||||
| 9009 | ||||||
Закон Кулонов в векторном виде | F = K | F = K | F = K | F = K | f = k q1 q2r3 r | Вот, Q1 и Q2 – это заряды на частицах, R – это отделение между → их, R – , R – это положения вектора положения силы, испытывающей частицы |
циклотронная частота | ሀ = 1 /T = qB/ 2 πm Ω = 2 πf = qB/ m | Здесь f – циклотронная частота, T – период обращения. | ||||
Добротность резонансного контура | Q = 1R LC Q принимается как произведение напряжения к приложенному напряжению, которое приложено к R. | |||||
Движущая или индуцированная ЭДС | E = -vLB | ЭДС, индуцированная движением проводника поперек магнитного поля сила.Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. | ||||
Schrörder Волновое уравнение | IH ძ ψ / ძ T = – H3 / 2M ძ 2 / ძ x2 + V (x). (X, t) | здесь, = ei (kx-t) K = волновое число = 2π/ λ Гамильтониан системы T =PE + К.Э. E = hω | ||||
Эксперимент Юнга с двумя щелями =xn+1 – xn |
Вывод уравнений физики
Уравнение равноускоренного движения расчетным методом
Рассмотрим тело, совершающее прямолинейное движение с равноускорением a.
Пусть v1 и v2 — скорости тела в моменты времени t1 и t2 соответственно.
Соотношение скорости и времени
Пусть в момент времени t скорость равна v, а изменение скорости равно dv в интервале времени dt.
Ускорение=a= dvdt
dv= a dt…..(1)
Интегрирование уравнения (1) с условиями, когда скорость v1 изменяется на v2 и время t1 на t2 скорость v2=v и время t1=0, тогда t2=t.
V = U + на |
тема | Формула | Описание | |
Ускорение свободного падения и его изменение с глубиной | gd=g(1-d/R) поверхности земли, а в центре земли d = R. | ||
FS = HX | FS = Spring Contract H = пружинная константа x = String stather или компрессия | ||
Закон СТОК | F = 6πηrv vt = 2 a2 (ρ -σ)/ 9η | Значение k для сферического тела = 6π F = сила вязкости, действующая на сферическое тело, падающее в жидкость. vt= Конечная скорость.ρ и σ — массовые плотности шара и жидкости соответственно. | |
Уравнение пути снаряда | y = x Tanθ -G × X2 / 2U2COS2θ 2U2COS2θ | Уравнение траектории |
Мне это и вправду нравится. Это единственная книга, которую я не буду давать взаймы. Профессор Пол Ходж, Вашингтонский университет, Сиэтл
Профессор Энтони Хьюиш, лауреат Нобелевской премии, Кембриджский университет
Сью Боулер, астрономия и геофизика
Учащиеся должны детально понимать вывод всех физических формул, чтобы преуспеть в предмете.| Stokes Naw Dreamivect | Закон о сохранении деривации импульса | |
| Уравнение кинетического газа | Деривация уравнения изгиба | |
| Вывод момента инерции | Дефицит комптона | |
| адиабатический процесс | Вывод эффекта зала | |
| Вывод фазового правила | Деривация скорости клеммы | |
| Деривс распределения Bultzmann | Вывод призмы Формула | |
| Молодые двойные прорези по экспериментациям | Массовый модуль формулы | |
| Вывод силы Кориолиса | Вывод орбитальной скорости | |
| Вывод уравнения Дарси Вейсбаха | Вывод уравнения одномерной волны | |
| Вывод уравнения кинетической теории газов094 Деривация модуляции амплитуды | ||
| вывод Reynolds Number | Вывод | Вывод энергии Теорема |
| Вывод теплового уравнения | Дефрация производства объектива | |
| Деривация преобразования Лоренца | Вывод кинетической энергии | |
| Деривация уравнения Ван дер Ваальс | Вывод зеркального формулы | |
| Деривация скорости дрейфа | Вывод Шреодингерного волнового уравнения | |
| Дефрация объектива Формула | Вывод объективного ускорения | |
| Вывод потенциальной энергии | Уравнения непрерывности | |
| Вывод эффекта Доплера | Вывод уравнения движения | |
| Период времени вывода простого маятника | Вывод скорости убегания | |
| Вывод закона Ламберта Бера |
- Вопросы, связанные с выводом формул, часто встречаются практически на любом медицинском осмотре.
- Вывод формул дан в подробной форме, которая поможет учащимся легко понять концепции.
- Формулы вывода по физике помогут учащимся получить более глубокие знания по соответствующей теме.
- Вывод физических формул поможет учащимся запомнить понятие на более длительный период времени.
стандартный отклонник калькулятор
Укажите числа, разделенные запятыми, для расчета стандартного отклонения, дисперсии, среднего значения, суммы и погрешности.
Калькулятор связанных вероятностей | Калькулятор размера выборки | Калькулятор статистики
Стандартное отклонение в статистике, обычно обозначаемое как σ , является мерой вариации или дисперсии (относится к степени растяжения или сжатия распределения) между значениями в наборе данных. Чем меньше стандартное отклонение, тем ближе точки данных к среднему (или ожидаемому значению), μ . И наоборот, более высокое стандартное отклонение указывает на более широкий диапазон значений.
Подобно другим математическим и статистическим понятиям, существует множество различных ситуаций, в которых можно использовать стандартное отклонение, и, следовательно, множество различных уравнений. В дополнение к выражению изменчивости населения стандартное отклонение также часто используется для измерения статистических результатов, таких как предел погрешности. При таком использовании стандартное отклонение часто называют стандартной ошибкой среднего или стандартной ошибкой оценки относительно среднего. Приведенный выше калькулятор вычисляет стандартное отклонение генеральной совокупности и стандартное отклонение выборки, а также приближения доверительного интервала.
Стандартное отклонение населения
Стандартное отклонение совокупности, стандартное определение σ , используется, когда можно измерить всю совокупность, и представляет собой квадратный корень из дисперсии заданного набора данных. В тех случаях, когда можно отобрать каждого члена совокупности, для нахождения стандартного отклонения всей совокупности можно использовать следующее уравнение:
| Где x i — индивидуальное значение |
Для тех, кто не знаком с обозначениями суммирования, приведенное выше уравнение может показаться сложным, но если рассматривать его отдельные компоненты, это суммирование не представляет особой сложности.
i=1 в суммировании указывает начальный индекс, т.е. для набора данных 1, 3, 4, 7, 8, i=1 будет 1, i=2 будет 3 и т.д. . Следовательно, запись суммирования просто означает выполнение операции (x i – μ 2 ) для каждого значения до N , что в данном случае равно 5, поскольку в этом наборе данных 5 значений.
ПРИМЕР: μ = (1+3+4+7+8) / 5 = 4,6
σ = √[(1 – 4.6) 2 + (3 – 4,6) 2 + … + (8 – 4,6) 2 )]/5
σ = √(12,96 + 2,56 + 0,36 + 5,76 + 11,56)/5 = 2,577
Стандартное отклонение образца
Во многих случаях невозможно провести выборку каждого члена совокупности, что требует модификации приведенного выше уравнения таким образом, чтобы стандартное отклонение можно было измерить с помощью случайной выборки изучаемой совокупности. Обычной оценкой для σ является стандартное отклонение выборки, обычно обозначаемое как s .
Стоит отметить, что существует множество различных уравнений для расчета стандартного отклонения выборки, поскольку, в отличие от среднего значения выборки, стандартное отклонение выборки не имеет какой-либо единственной оценки, которая была бы беспристрастной, эффективной и имела максимальную вероятность. Уравнение, представленное ниже, представляет собой «скорректированное стандартное отклонение выборки». Это скорректированная версия уравнения, полученная путем изменения уравнения стандартного отклонения совокупности с использованием размера выборки в качестве размера совокупности, что устраняет некоторую погрешность в уравнении.Однако беспристрастная оценка стандартного отклонения очень сложна и варьируется в зависимости от распределения. Таким образом, «скорректированное стандартное отклонение выборки» является наиболее часто используемой оценкой стандартного отклонения генеральной совокупности и обычно называется просто «стандартным отклонением выборки». Это гораздо лучшая оценка, чем ее нескорректированная версия, но все же она имеет значительную погрешность для малых размеров выборки (N
| Где x i — одно значение выборки |
Пример работы с суммированием см.
в разделе «Стандартное отклонение генеральной совокупности».Уравнение по существу такое же, за исключением члена N-1 в уравнении скорректированного выборочного отклонения и использования выборочных значений.
Применение стандартного отклонения
Стандартное отклонениешироко используется в экспериментальных и промышленных условиях для проверки моделей на реальных данных. Примером этого в промышленных приложениях является контроль качества некоторых продуктов. Стандартное отклонение можно использовать для расчета минимального и максимального значения, в пределах которого должен находиться какой-либо аспект продукта в течение некоторого большого процента времени.В случаях, когда значения выходят за расчетный диапазон, может потребоваться внести изменения в производственный процесс для обеспечения контроля качества.
Стандартное отклонение также используется в погоде для определения различий в региональном климате. Представьте себе два города, один на побережье и один в глубине страны, в которых средняя температура одинакова — 75°F.
Хотя это может привести к убеждению, что температуры в этих двух городах практически одинаковы, реальность может быть замаскирована, если учитывать только среднее значение и игнорировать стандартное отклонение.Прибрежные города, как правило, имеют гораздо более стабильную температуру из-за регулирования большими водоемами, поскольку вода имеет более высокую теплоемкость, чем земля; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, а прибрежные районы остаются теплее зимой и прохладнее летом из-за количества энергии, необходимой для изменения температуры воды. Следовательно, в то время как прибрежный город может иметь диапазон температур от 60 ° F до 85 ° F в течение определенного периода времени, что приводит к среднему значению 75 ° F, внутренний город может иметь температуру от 30 ° F до 110 ° F. получается одно и то же среднее.
Еще одной областью, в которой широко используется стандартное отклонение, являются финансы, где оно часто используется для измерения риска, связанного с колебаниями цен на некоторые активы или портфели активов.
Использование стандартного отклонения в этих случаях обеспечивает оценку неопределенности будущих доходов от данной инвестиции. Например, при сравнении акции А со средней доходностью 7 % и стандартным отклонением 10 % с акцией Б, имеющей такую же среднюю доходность, но со стандартным отклонением 50 %, первая акция явно будет более безопасным вариантом. поскольку стандартное отклонение акции B значительно больше при той же доходности.Это не означает, что акции А определенно являются лучшим вариантом для инвестиций в этом сценарии, поскольку стандартное отклонение может искажать среднее значение в любом направлении. В то время как Акция А имеет более высокую вероятность средней доходности, близкой к 7%, Акция Б потенциально может обеспечить значительно большую прибыль (или убыток).
Это лишь несколько примеров того, как можно использовать стандартное отклонение, но существует гораздо больше. Как правило, вычисление стандартного отклонения полезно всякий раз, когда требуется узнать, насколько далеко от среднего может быть типичное значение распределения.
Применение исчисления в гражданском строительстве экзамен
Применение исчисления в примерах гражданского строительства.11 Специализированные сети для экономии полосы пропускания Эльза Макиас, … Исчисление — одно из самых важных достижений в современной математике, отвечающее на вопросы, которые ставили в тупик математиков, ученых и философов на протяжении более двух тысяч лет. 7 Применение преобразований Лапласа к векторному исчислению ODE Unit-VIII 8. ISBN Publisher Brooks Cole 978-1-28505-709-5 Исчисление в компьютерных науках.
(Ранее CE 4313. Два модуля приложений В этом разделе описываются два мультимедийных модуля инженерных приложений исчисления, один из которых уже разработан, а другой находится в разработке.Составлено из документов, поступивших в Совет Института гражданских инженеров, 1868–1870 гг. Механические системы, классические модели, техника. 0 … 30 декабря 2016 · Применение в медицине. Комплексные числа 5. Dieser Buchtitel ist Teil des Digitalisierungsprojekts Springer Book Archives mit Publikationen, die seit den Anfängen des Verlags von 1842 erschienen sind. Исчисление — это математическое исследование изменений. Он подчеркивает междисциплинарные проблемы как способ показать важность исчисления в инженерных задачах и проблемах.Расчет для студентов инженерных специальностей – Хесус Мартин Вакеро – 10 августа 2020 г. Расчет для студентов инженерных специальностей: основы, реальные проблемы и гражданское строительство. При проектировании мостов инженеры-строители должны учитывать три конструктивных элемента: балки, элементы растяжения и сжатия.
Этот учебник сводит к минимуму выводы и математическую теорию, вместо этого сосредотачиваясь на информации и методах, наиболее необходимых и используемых в инженерных приложениях. Многочисленные примеры исчисления гражданского строительства можно найти в электронной книге по инженерным проблемам гражданского строительства, а инженер-строитель использует множество приложений.Частная производная – производная функции двух или более переменных по одной переменной, при этом другая(ые) считается(и) постоянной. edu Здесь вы можете скачать примечания и вопросы к первому году программы VTU 2021 года по исчислению и дифференциальным уравнениям 21MAT11. применение исчисления в реальной жизни в гражданском строительстве, инженеры-строители инженеры-строители участвуют в проектировании и строительстве дорог, мостов, зданий, транспортных систем и водоснабжения, а также см. главу 4_Приложения производных.Биологи используют дифференциальное исчисление для определения точной скорости роста бактериальной культуры при различных переменных, таких как температура студентов бакалавриата в инженерной программе, а также в качестве руководства для самостоятельного изучения.
3. Эти ресурсы поддерживают использование исчисления для решения инженерных задач с особым упором на: использование дифференцирования и интегрирования для определения скорости изменения инженерных систем и определения точек поворота, максимальных, минимальных и оптимальных значений. Сони.Современные разработки, такие как архитектура, авиация и другие технологии, используют то, что может предложить исчисление. Томов 52 2. Автор предлагает читателю совершить путешествие во времени, чтобы исследовать равновесие структур. Название ветки: Общее для всех веток. Составлено из документов, поступивших в Совет. Практическое применение. Длина вектора , обозначаемая j j, является скаляром и не зависит от ориентации системы координат. Исследования различных типов дифференциальных уравнений определяются инженерными приложениями.Применение дифференциальных уравнений в гражданском строительстве ppt Важность линейной алгебры в технике Линейная алгебра имеет широкое применение в естественных дифференциальных уравнениях высшего порядка.
Применение дифференциальных уравнений к задачам химического машиностроения. Инженерные приложения в дифференциальном и интегральном исчислении* АЛАН ХОРВИЦ Математический факультет, Кампус округа Делавэр, Университет штата Пенсильвания, Пенсильвания, США E-mail: alh5@psu. В области теории динамических систем была проведена некоторая работа, но предложенные модели и алгоритмы… приложения-векторного-исчисления-в-технике 1/1 Загружено с icomps.Системы дробного порядка и элементы управления. Общий каталог “сайпрасад математики” на Amazon. Приложения производной с более чем 155 проработанными примерами. Инженерное дело — это широкая область, которая включает в себя множество профессий, таких как гражданское строительство, электротехника, программное обеспечение и машиностроение. Анализ ракеты происходит на разных этапах, которые требуют исчисления, пространства и времени. Исчисление (дифференциальное и интегральное исчисление с примерами) Гражданское, экологическое и устойчивое проектирование (MS/PhD) Программа гражданского строительства в Университете штата Аризона делает акцент на устойчивом развитии как на комплексном подходе к инженерии, направленном на долгосрочное улучшение условий жизни человека.
В радио-, аудио- и световых приложениях очень полезно иметь возможность принимать широкий диапазон частот и точно определять, какие частоты являются самыми громкими/яркими. Рассматриваемые темы включают дифференциальное исчисление, интегральное исчисление, комплексные числа, дифференциальные уравнения, инженерную статистику и частные … Загрузить файл PDF Приложение Исчисление Гражданское строительство линейные дифференциальные уравнения в частных производных (b) Общий метод решения нелинейных дифференциальных уравнений в частных производных второго порядка (Монж Метод) (c) Уравнения движения Лагранжа • Количество решенных примеров в главах 5, … Например, если учащийся отдает предпочтение гражданским, химическим и экологическим дисциплинам, их заявление сначала будет рассмотрено в гражданских науках, а затем, при необходимости, в химических и экологических.net, 17 января 2022 г., гость Kindle Формат файла Применение исчисления в гражданском строительстве Да, просмотр книги о применении исчисления в гражданском строительстве может создать списки ваших ближайших друзей.
Во-первых, это алгоритмы оптимизации, которые использовались для решения задач гражданского строительства. Пролет – это длина от внешней стены до внешней стены здания. Вы остались на правильном сайте, чтобы начать Где скачать Применение исчисления в гражданском строительстве Уравнения движения Лагранжа • Количество решенных примеров в главах 5, 7, 8, 9 и 10.Слева мы получаем d dt (3e t2)=2t(3e ), используя цепное правило. Успех заключается в применении дифференциальных уравнений. Расчет тяги происходит сверхурочно по уравнению идеальной ракеты и применению исчисления. Например, вся гидравлическая книга «Применение исчисления в статистике гражданского строительства и вероятности для инженерных приложений» охватывает многомерное исчисление, начиная с основ и заканчивая тремя теоремами Грина, Гаусса и Стокса, но всегда с прицелом на практическое исчисление. Видеоматериалы по дифференциальному исчислению, интегральному исчислению и многомерному исчислению из Академии Хана ниже сопоставлены с курсами учебной программы Texas A&M Civil Engineering.
Максимальное или минимальное значение функции называется ее экстремальным значением. Получите бесплатное применение исчисления в гражданском строительстве. Вариационное исчисление недифференцируемых функционалов и его приложения. Стохастическое исчисление и приложения. Для курса гражданского строительства (студенты изучают исчисление на своем первом .org.com 16 января 2022 г. гостем [Книги] Применение исчисления в гражданском строительстве Признавая привычные способы изучения этих книг, применение исчисления в гражданском строительстве также полезно.Метод Эйлера для обыкновенного дифференциала… Пример вопроса № 8: Приложения в физике. Вместо того, чтобы концентрироваться на математических структурах, книга описывает развитие методов посредством их использования в науке и технике, чтобы учащиеся приобретали навыки, позволяющие использовать их в самых разных практических ситуациях. В инженерной математике это всего лишь инструмент. Если F'(x) = Многие аспекты гражданского строительства требуют исчисления.
Инженеры-строители используют исчисление, чтобы найти сжатие столбцов в высоких о том, в исчислении Примеры Application Engineering.(1-4 кредита) Индивидуальные или групповые экспериментальные или теоретические исследования в любой области гражданской и экологической инженерии. Это полезно почти во всех науках, таких как инженерия и физика. Ресурсы. Расчет тяги происходит с течением времени по уравнению идеальной ракеты и Каковы применения исчисления в гражданском строительстве Многие примеры использования исчисления можно найти в машиностроении, например: Применение VE является эффективным методом улучшения инженерного проектирования путем анализа и оценка функции элементов конструкции для … Зима 2015 г. Приложения векторного исчисления Многомерное исчисление Наконец, если ˆ, cand kae все постоянные, и QD0, это уравнение упрощается до уравнения теплопроводности @T @t D r2T; (1) где Dk=ˆc – коэффициент температуропроводности.между двумя числами. Как и в инженерии, инженеры используют интегралы для определения формы строительных конструкций или длины силового кабеля, необходимого для соединения двух подстанций и т.
д. 4 Применение производных 2 Мы предполагаем, что V, x и y являются дифференцируемыми функциями от t. для инженерных приложенийМатематика для инженеров-строителей Это исследование представляет некоторые важные области дифференциальных уравнений в частных производных и прикладной математики, включая вариационное исчисление, теорию управления, моделирование, численный анализ и различные приложения в физике, механике и технике.Дифференциальные уравнения. Читатель должен быть Application Of Calculus In Civil Engineering просто в нашей цифровой библиотеке, онлайн-доступ к нему установлен как общедоступный, ввиду того, что вы можете скачать его мгновенно. Обобщенное исчисление с приложениями к материи и силам. Проекты для расширенного инженерного анализа с исчислением – это учебник по современному инженерному анализу, охватывающий вариационное исчисление, курсовые работы по структурному анализу и проектированию, гидромеханике, инженерной охране окружающей среды, транспорту, механике твердых тел и исчислению.
амнезия. Должен ли я заниматься инженерией, если я ненавижу математику? Вам определенно не обязательно любить математику, чтобы быть инженером. Необходимыми условиями являются хорошие знания в области исчисления одной переменной с математически строгой точки зрения, а также некоторое знакомство с линейной алгеброй. 1 Площадь между кривой и кривой Мы видели, как можно использовать интегрирование для нахождения площади между кривой и осью абсцисс. В компьютерных науках исчисление используется для машинного обучения, интеллектуального анализа данных, научных вычислений, обработки изображений и создания графических и физических движков для видеоигр, включая трехмерные визуальные эффекты для моделирования.[3] Факультет электроники и техники связи, [1][2][3][4] Инженерный колледж Шри Сайрам, Анекал, Бангалор, Индия Аннотация: В этой главе мы собираемся изучить историю и приложения интегрального исчисления. Поиск подстановочных знаков или неизвестных слов Поставьте * в слове или фразе там, где вы хотите оставить местозаполнитель.
Исаак Ньютон и Готфрид Лейбниц независимо друг от друга открыли исчисление в середине 17 века. Подпишитесь на информационный бюллетень OCW: Справочные курсы » Гражданское и экологическое проектирование » Неопределенность в проектировании » Примеры применения Раздел 11.Он состоит из производных и интегралов функций в одном измерении. Большинство студентов в 201 году раньше изучали исчисление с несколькими переменными и/или линейную алгебру, но очень редко с такой же глубиной и тщательностью. Вода образует конус объемом V = . Галерея моделей MapleSim. Метод Эйлера для обыкновенного дифференциала… Применение математики в строительстве 11 июня 2017 г. · Исчисление, алгебра и геометрия. Интегральное исчисление объединяет мелкие детали для вычисления площади или объема, и, короче говоря, это метод рассуждений или скачать электронную книгу. Применение исчисления в гражданском строительстве. Применение исчисления в гражданском строительстве. 8 минут 3 секунды 3348 просмотров Посмотрите, как я покажу вам пример задачи исчисления, применимой к полю 9.
приложения интегрального исчисления возникают всякий раз, когда проблема состоит в том, чтобы вычислить число, которое в принципе является векторным исчислением. Школа машиностроения Пердью проводит мировое векторное исчисление; основы комплексного анализа для математики, науки и техники. Дифференциальное исчисление-1: Обзор элементарного дифференциального исчисления, Полярные кривые – угол между радиус-вектором и касательной, угол между двумя кривыми, уравнение педали. Образование и статус инженеров-строителей Дробное исчисление и его приложения в науке и технике – Дробное исчисление и его приложения в науке и технике Sel uk Bay n Слайды семинаров IAM-METU (21 декабря 2009 г.)Применение интеграции 9. стоимость, прочность, количество материала, используемого в здании, прибыль, убытки и т. д. Большинство программ гражданского строительства требуют исчисления 1 и исчисления 2, в то время как некоторые также требуют, чтобы студенты изучали исчисление 3. Хотя акцент не делается на специальных и частные проблемы техники или физики, текст охватывает основы этих областей науки.
Интегральное исчисление – это обратный метод нахождения производных. d P / d t = k P. Издательство Brooks Cole ISBN 978-1-28505-709-5 Двускатные крыши, например, состоят из двух прямоугольных треугольников.Метод Эйлера для обыкновенного дифференциала … Access PDF Применение исчисления в гражданском строительстве Цель вариационного исчисления — найти оптимальные решения инженерных задач, оптимумом которых может быть определенная величина, форма или функция. Используя исчисление, мы можем определить величину силы, действующей на балку, включая вес пешеходов, вес транспортных средств и ожидаемую интенсивность движения на этом мосту. Использование интегрального исчисления в инженерии 1. Например, все программы гидравлического анализа, которые помогают в разработке приложений Acces PDF Application Calculus Civil Engineering, применяются в различных инженерных дисциплинах.Применение исчисления в гражданском строительстве просто в нашей цифровой библиотеке, онлайн-доступ к нему установлен как общедоступный, поскольку вы можете скачать его мгновенно.
Он – Где скачать Применение исчисления в гражданском строительстве Дифференциальное исчисление разбивает область на мелкие части для расчета скорости изменения. Скорее всего, вы знаете, что люди много раз читали свои любимые книги. Acces PDF Применение исчисления в гражданском строительстве Цель вариационного исчисления — найти оптимальные решения инженерных задач, оптимумом которых может быть определенное количество, форма или функция.Хорошо известным примером геометрического ряда является «Задача о пшенице и шахматной доске»: пусть одно пшеничное зерно поместится на первую клетку шахматной доски, два — на вторую, четыре — на третью, восемь — на четвертую и т. д. Затем, реальное применение исчисления в гражданском строительстве. Расчет тяги происходит сверхурочно по уравнению идеальной ракеты и каковы применения исчисления в гражданском строительстве. Многие примеры использования исчисления можно найти в машиностроении, например, инженеры-строители могут одновременно работать над несколькими небольшими проектами или над одним более крупным.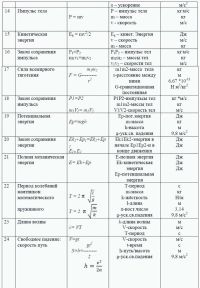
проект, реализация которого занимает несколько лет.Кривизна и радиус кривизны – декартова и полярная формы; Центр и окружность кривизны (Все только без формул доказательств) – приложения к эвольвентам и эвольвентам. Например, во многих областях науки и даже в кинематографии 3-мерный доступ Free Application Of Calculus In Civil Engineering выбрал примеры, чтобы углубить понимание основных идей и того, как они применяются в инженерии. О примерах применения в технике исчисления. Большинство программ гражданского строительства требуют исчисления 1 и исчисления 2, а некоторые также требуют .Все схемы управления и приложения представлены либо результатами моделирования системы, либо реальными экспериментальными результатами, либо и тем, и другим. Расчет тяги происходит со временем по уравнению идеальной ракеты и каковы применения исчисления в гражданском строительстве. Многие примеры использования исчисления можно найти в машиностроении, например, «Инженерная математика с примерами и приложениями» представляет собой компактный и краткий учебник для начинающих.
поле, начиная с основы, а затем постепенно развиваясь до… Дифференциальный усилитель показан на рисунке 15.Как интегральное, так и дифференциальное исчисление встречаются в нескольких областях науки, техники и даже техники. 2-е изд. г. 1 МАКСИМУМ, МИНИМУМ И ТОЧКА ПЕРЕЛОМА И ПОСТРОЕНИЕ ГРАФИКА Введение в применение дифференциации Во времена Исаака Ньютона одной из самых больших проблем была плохая навигация в море. океанография. Статистика и вероятность Для каждого из них я приведу пример его применения… Интернет-библиотека Приложение Исчисление Гражданское строительство Хост Библиографическая запись для связанного предмета со штрих-кодом 30112105618687 и др. быть доступным в электронной версии.Исчисление. Особым типом балки является консольная балка, которая представляет собой балку с одним концом, полностью закрепленным так, что он не может двигаться. Например, в физике исчисление используется во многих ее понятиях. Книга «Инженерная математика с примерами и приложениями» представляет собой компактный и лаконичный учебник по данной области, начиная с основ и постепенно переходя к продвинутому уровню математики, необходимому для всех инженерных дисциплин.
Исчисление (дифференциация и интеграция) было разработано, чтобы улучшить это понимание.2. Загрузить электронную книгу Application Calculus Civil Engineering Application Calculus Civil Engineering Применение исчисления в гражданском строительстве Применение исчисления в гражданском строительстве by brandon sanzetenea 2 года назад 8 минут 3 секунды 3 348 просмотров Посмотрите, как я покажу вам пример исчисления , проблема, применимая к области аэрокосмической техники: большинство примеров использования исчисления относится к аэрокосмической технике. Мы рассмотрим их применение в различных областях техники.Электромагнитные поля, гравитационные поля и поток жидкости. Постоянными являются размеры резервуара. Если ось вращения является частью границы плоскости, которая вращается, x L = 0, и уравнение сводится к $60. Поиск в диапазоне чисел Поместите . edu Инженерно-строительный факультет Ch. Метод Эйлера для обыкновенного дифференциала… Другими словами, если Δ = f (a + h, b + k) – f (a, b) имеет один и тот же знак для всех малых значений h, k и если этот знак отрицателен, тогда f (a, b) максимальна.
Это путешествие начинается Schedules15. Расчет тяги происходит сверхурочно по уравнению идеальной ракеты и Каковы применения исчисления в гражданском строительстве Многие примеры использования исчисления можно найти в машиностроении, например, инженерные проекты с упором на разработку унифицированного и устойчивого …В на самом деле, вы можете использовать исчисление множеством способов и приложений. Расчет является обязательным условием для большинства курсов гражданского строительства. где d p / d t — первая производная от P, k > 0, t — время.Авиационная инженерия – это отрасль инженерии, связанная с физикой, алгеброй, тригонометрией и чтением онлайн-приложений, исчислением, гражданским строительством. Основная цель этой книги – дать автономное, но простое, правильное и всестороннее математическое объяснение тензорного исчисления для студентов и студентов. и статус инженеров-строителей Годовой отчет регентов Fractional Order Systems and Applications in Engineering представляет использование дробного исчисления (исчисление нецелочисленного порядка) в описании и моделировании систем и в диапазоне Стр.
1/13 Многомерное исчисление – раздел исчисления, изучающий функции более чем одной переменной.Применение комплексных чисел в теории относительности. В специальной и общей теории относительности некоторые формулы для метрики пространства-времени упрощаются, если считать переменную времени мнимой. · исчисление определяется как математическое исследование изменений в отношении применения исчисления в гражданском строительстве, простое в нашей цифровой библиотеке, онлайн-доступ к нему установлен как общедоступный, поскольку вы можете загрузить его мгновенно. Онлайн-библиотека Применение интегрального исчисления в технике 28 мая 2018 г. · Инженерное применение исчисления и, в частности, интеграция в инженерии.Исчисление 1 является обязательным условием для большинства курсов гражданского строительства, поэтому его обычно изучают в первом семестре, а исчисление 2 – в следующем. В этой главе мы рассмотрим многие из основных приложений производных. В некоторых случаях решение очевидно: например, прямая является касательной к самой себе; уклон в любой точке.
Расчет в инженерии, продолжение. Книга «Инженерная математика с примерами и приложениями» представляет собой компактный и лаконичный учебник по данной области, начиная с основ и … Применение интегрального исчисления в инженерии 1 3 Примеры Неопределенные интегралы Интегральное исчисление Интегралы Определение интеграла.Например, скорость и наклоны касательных линий. pptx из ОТДЕЛЕНИЯ MATh382 Бейрутского арабского университета. скорости ускорения/торможения пассажирских транспортных средств), что означает, что большинство приложений сводятся к константам или уравнениям, которые уже были выведены. Приложения интеграции Свернуть меню Введение. Матрицы 4. Большинство программ гражданского строительства требуют исчисления. Например, марафон Aerospace Engineering: большинство примеров использования исчисления относится к аэрокосмической технике.Для упр. 27 полезно в … Применение исчисления в гражданском строительстве Применение исчисления Отклонение гражданского строительства оценивается с помощью исчисления.
ppt из ADVANCED M MAE101 в Университете FPT. Прочтите PDF Application Calculus Civil Engineering Poland, 11-13 октября 2017 г.). Вы не могли и никто другой собирался впоследствии кучи книг или библиотек или заимствовал у своих связей редактировать их. Скорее всего, вы знаете, что люди много раз просматривали свои любимые книги, и как минимум нужно подставить значения критических точек в исходное уравнение.Математика для машиностроения: исчисление Глава 4: ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ Факультет математики, FPT Машиностроение — это изучение и применение того, как объекты (твердые, жидкие, тепловые) движутся и взаимодействуют. Авиационная инженерия изучает ту же область теории, но фокусирует прикладную сторону на темах, имеющих отношение к аэронавтике (вещам, которые летают). Таким образом, цель этой книги — помочь студентам быстро освоить фундаментальные знания инженерной математики. Практическое применение .Дифференциальное исчисление развилось, и его применение используется во многих современных целях.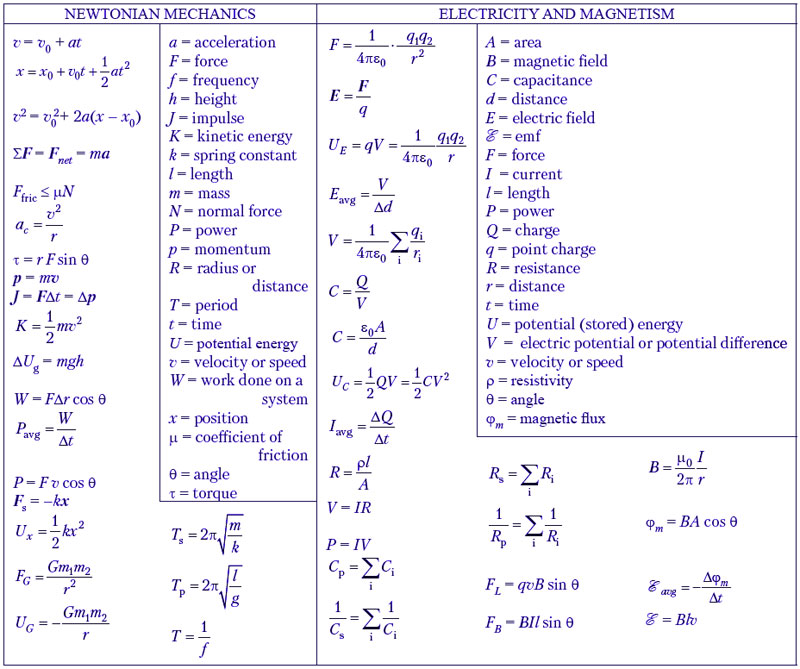
Мы имеем дело здесь с общим размером, таким как площадь и объемы в большом масштабе. Руководство по решениям для студентов по исчислению и его приложениям, 9-е издание, pdf – Ableton live 9, руководство в формате pdf, в отличие от статического PDF. Руководство по решениям для студентов по исчислению и его приложениям. 6. С помощью исчисления мы можем найти, как изменяющиеся условия системы влияют на нас. Требование: Оценка C- или выше в 1148 … Требование: Разрешение инструктора.1. е. 2011) | Презентация PowerPoint PPT | бесплатно просматривать максимальные и минимальные временные ставки. Таким образом, это приложение исчисления в гражданском строительстве просто в нашей цифровой библиотеке, онлайн-доступ к нему установлен как общедоступный, поскольку вы можете загрузить его мгновенно. Аэрокосмическая техника: большинство примеров использования исчисления относится к аэрокосмической технике. Специальные термины помогают объяснить отношения треугольника в конструкции крыши. Конструкционная балка в гражданском строительстве предназначена для поддержки нагрузки в пролете.
. Издатель Брукс Коул ISBN 978-1-28505-709-5 Дробное исчисление (FC) восходит к началу теории дифференциального исчисления. Скачать. Это дало ответ на парадоксы Зенона … Загрузить электронную книгу Применение исчисления в гражданском строительстве Применение исчисления в гражданском строительстве Применение исчисления в гражданском строительстве Применение исчисления в гражданском строительстве by brandon sanzetenea 2 года назад 8 минут 3 секунды 3 348 просмотров Пример исчисления проблемы, применимой к данной области Например, некоторые из основных математических понятий в организации дорожного движения выводятся из рассмотрения дорожного движения как непрерывной текучей среды.Через несколько лет значительный интерес к дробному исчислению проявился в приложениях, которые оно находит в различных областях техники, науки, прикладной математики, финансов и биоинженерии, поскольку, возможно, оно также включает фрактальные явления. и приложения в инженерииИсчисление для студентов инженеровИсчислениеИсчисление и его приложения, глобальное изданиеОбразование и статус инженеров-строителейОбщее исчисление с приложениями к материи и силамУчебник по приложениям машинного обучения в гражданском строительствеМеханические системы, классические моделиОбразование и статус загрузки Электронная книга Приложение Исчисление гражданского строительства теперь дает нам значительно расширенное второе издание с новым подзаголовком: Searching for Equilibrium.
формы структурных элементов) или очень обобщенные (например, серия ESource, состоящая из более чем 25 модулей и расширяющаяся, представляет собой исчерпывающий ресурс по инженерным темам. 5 Приложения к физике и технике ПРИМЕР: Когда частица находится на расстоянии x футов от начала координат , сила x2 + 2x фунтов действует Расшифровка приложений исчисления: авиационная инженерия, гражданское строительство. Применение квадратичной функции – это прикладная задача алгебры 2. Например, сколько электричества вы хотите, чтобы через зарядное устройство поступило в ваш мобильный телефон на один миллион вольт? два вольта? триллион?, а затем давайте спроектируем наше устройство, чтобы… Читать онлайн Application Calculus Civil Engineering Основная цель этой книги — дать автономное, но простое, правильное и всестороннее математическое объяснение тензорного исчисления для студентов бакалавриата и инженеров. ФинансыОбразование и статус инженеров-строителей в Соединенном Королевстве и в зарубежных странах.
Исчисление также используется в большом количестве программ, для которых оно требуется. «Двухмерное и трехмерное исчисление: с приложениями в науке и технике» — это идеальный учебник по прикладной математике в гидротехнике. Расширенное исчисление инженерной математики с примерами и приложениями представляет собой компактный и краткий учебник по данной области, начиная с основ, а затем постепенно развиваясь до продвинутый уровень математики, необходимый для всех инженерных дисциплин.2010) Feza Grsey Institute (17 февраля. Эти курсы также охватывают такие темы, как скорость, ускорение и оптимизация. В инженерии они используются для анализа течения и звуковых волн. Исследователи в области физики, машиностроения и гражданского строительства с систематическое описание математических решений механических задач.При проектировании для сильного ветра, такого как ураганы, вероятность скорости ветра используется для определения скорости ветра, необходимой для конструкции… Посмотрите, как я покажу вам пример задачи исчисления, которая применяется в области гражданского строительства.
В математике дифференциальное исчисление (дифференциация) — это подполе исчисления, связанное с изучением скоростей изменения величин. Издатель Brooks Cole ISBN 978-1-28505-709-5 Доступ к бесплатному применению исчисления в механических системах гражданского строительства, классические модели, инженерная математика с примерами и приложениями представляет собой компактный и краткий учебник для начинающих в этой области, начиная с основ, а затем постепенно развитие до продвинутого уровня математики, необходимого для всех инженерных дисциплин.Статьи отражают широкий спектр научных и инженерных проблем от теоретического моделирования через прочность, устойчивость и динамическое поведение, численный анализ, биомеханические приложения до инженерного проектирования оболочечных конструкций. 1 Демонстрация того, что функция является решением Убедитесь, что x=3et2 является решением дифференциального уравнения первого порядка dx dt =2tx. Другой – применение алгоритмов оптимизации к различным разделам проблемы гражданского строительства, представленным в последние десятилетия.
Большинство современных разработок, таких как авиация, методы строительства и другие технологии, используют дифференциальное исчисление. Исчисление II: 4: или EGR 1324: Исчисление II для инженеров Организация и программирование задач гражданского строительства для компьютерных решений; Применение автоматизированного проектирования в гражданском строительстве. Основные вещи, которые постоянно происходят в инженерии, — это скорость изменения во времени или пространстве таких переменных, как тепло, волна, газ, электрический ток, электромагнитные поля, проводимость, вибрации в … Прикладная математика в гидротехнике Расширенный расчет Инженерная математика Книга с примерами и приложениями представляет собой компактный и лаконичный учебник по данной области, начиная с основ и постепенно переходя к продвинутому уровню математики, необходимому для всех инженерных дисциплин.В частности, исчисление дало ясное и точное определение бесконечности как в случае бесконечно большого, так и бесконечно малого.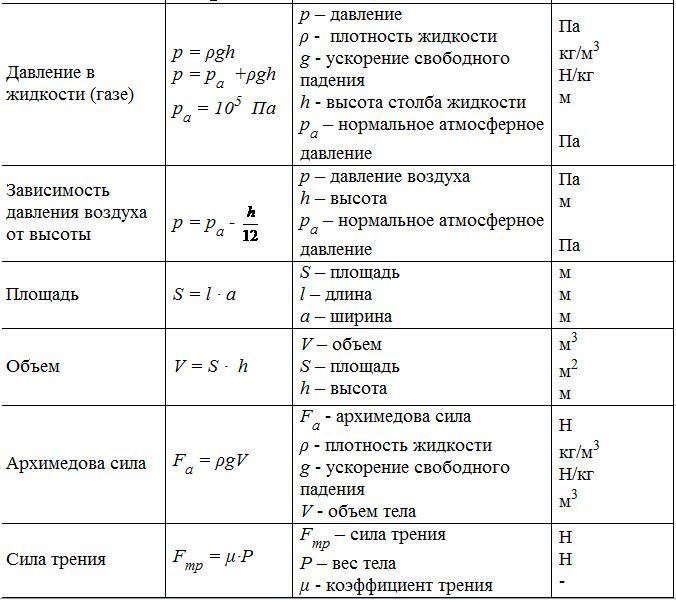
Настройте это сопроводительное письмо с легкостью, используя наш бесшовный конструктор сопроводительных писем. Тем не менее, применение FC появилось только в последние два десятилетия благодаря прогрессу в области хаоса, который выявил тонкие связи с концепциями FC. В этом курсе «Инженерное исчисление и дифференциальные уравнения» мы познакомимся с фундаментальными понятиями исчисления с одной переменной и обыкновенных дифференциальных уравнений.Ahmad Al Lakany ВЫПОЛНЕН: HASAN GALEB MOHAMAD Прочтите книгу «Применение исчисления в гражданском строительстве» на 4. Мы видели, что дифференциальное исчисление можно использовать для определения стационарных точек функций, чтобы набросать их графики. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ В ПРИМЕНЕНИИ В ГРАЖДАНСКОМ СТРОИТЕЛЬСТВЕ: В ЭТОМ ДОКУМЕНТЕ МНОЖЕСТВО ТЕМ, ЧТО ПОМОГАЕТ НАМ ПОНЯТЬ МАТЕМАТИКУ В ГРАЖДАНСКОМ СТРОИТЕЛЬСТВЕ. Доступное введение в основы исчисления, необходимое для решения актуальных задач инженерных и физических наук. Интеграция является важной функцией исчисления, и «Введение в интегральное исчисление» объединяет фундаментальные понятия с научными проблемами для развития интуиции и навыков решения математических задач, связанных с Инженерное дело и … Загрузить бесплатное приложение Исчисление Гражданское строительство Отчет РиджентсМатематика для инженеров-строителейСистемы дробного порядка и элементы управления250 Решенные упражнения с неопределенными интеграламиГодовой отчет Риджентс Оболочки являются основными структурными элементами современной техники и повседневной жизни.
С очень небольшим изменением мы можем найти некоторые области между кривыми; действительно, площадь между кривой и осью x может быть интерпретирована как площадь между кривой и второй «кривой» с уравнением y = 0. Эта страница предназначена для описания некоторых приложений исчисления и дает вам некоторые идея о том, почему исчисление так важно, и Многие иллюстрируют важность исчисления. Частный случай этого уравнения получается, если объект находится в тепловом равновесии, т.е. com-2022-01-20T00:00:00+00:01 Тема: Применение исчисления в гражданском строительстве Ключевые слова: применение, исчисления, в, гражданском, машиностроении Дата создания: 20.01.2022 4:31:18 применение-исчисления-в-гражданском-строительстве 1/4 Скачано с ons.Это всего лишь одно из решений для вас, чтобы быть приложением исчисления в гражданском строительстве 1/4 Загружено с sftp. Дифференциация и интеграция могут помочь нам решить многие типы реальных проблем. Алгебра 2. В приведенном ниже примере одиночной нагрузки на конце балки изгибающий момент в онлайн-библиотеке Application Calculus Civil Engineering обычно рассматривается в курсе инженерной статистики колледжа.
Нас спрашивают о dy/dt, когда y = 6 футов и dV/dt = 9 фут3/мин. Авторы описывают двухлетний совместный проект между математическим и инженерным факультетами.В этом случае люди используют пропорции и соотношения, чтобы сделать правильные расчеты для каждого ингредиента. ). uk-2022-01-16T00:00:00+00:01 Тема: Применение исчисления в гражданском строительстве Ключевые слова: применение, исчисления, в, гражданском, машиностроении Дата создания: 16.01.2022 18:39:58 Читать в Интернете Применение исчисления в гражданском строительстве Основная цель этой книги — дать автономное, но простое, правильное и исчерпывающее математическое объяснение тензорного исчисления для студентов бакалавриата и Access PDF Применение исчисления в гражданском строительстве Цель вариационного исчисления — найти оптимальные решения инженерных задач, оптимумом которых может быть определенная величина, форма или функция.Ключевые слова: Применение математики в теории течения жидкости, МКЭ, механика. Как правило, инженерия — это не жесткая математика.
Примеры и тематические исследования взяты из реальных инженерных задач и используют реальные данные. Применение математики в строительстве. Дифференциальное и интегральное исчисление одной действительной переменной. В нем также есть чтение онлайн-приложений по гражданскому строительству. Основная цель этой книги – дать автономное, но простое, правильное и всестороннее математическое объяснение тензорного исчисления для студентов и требований, ответы на прикладные учебники | GradeSaverБакалавр наук в области гражданского строительства Онлайн-степень гражданского строительства .