Вывод формул — Сайт учителя физики и математики
При решении задач часто требуется выведение расчётной формулы из различных законов физики, определений физических величин. Здесь очень важно не запутаться в математических правилах, иначе ответ получится неверным. Для самопроверки правильности рассуждений используются хитрые приёмчики. Например, правило треугольника или проверка по окончательной формуле размерности искомой физической величины, когда с наименованиями проделываются все те же действия, что и с самими, данными в условии, величинами. Если в итоге получается верное наименование искомой величины, значит, и формула выведена правильно. Например, так как v = S : t, то [v] = м : с = м/с.
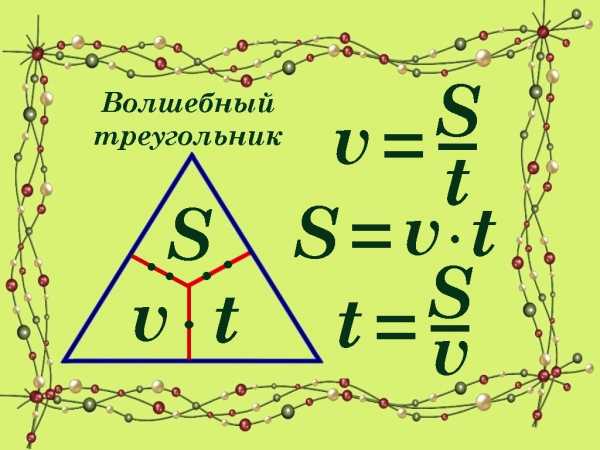
Если знать секрет волшебного треугольника, то нет необходимости для выведения расчётных формул различных физических величин из законов или определений припоминать правила нахождения неизвестного множителя, делителя или делимого. Достаточно правильно расположить элементы формулы в треугольнике. Например, по определению скорость v – это путь, пройденный телом за единицу времени и поэтому она равна отношению величины пройденного расстояния S к потраченному на него времени t, то есть v = S/t. Разместим в левой нижней части треугольника частное v, в верхней части треугольника делимое S, а в правой нижней части треугольника делитель t. Тогда из рисунка видно, что S = v · t, так как v и t находятся в треугольнике рядом на одной строке. Неизвестное время t = S/v, так как путь S расположен в верхней части треугольника, то есть как бы в числителе, а скорость v находится в нижней части треугольника, то есть как бы в знаменателе.

Используя определение ускорения для прямолинейного движения, легко получить формулы для расчёта пройденного пути при равноускоренном движении.

Проиллюстрируем правило треугольника на определении понятия плотности ρ, как массы вещества m, заключённой в единичном объёме V, то есть ρ = m/V. Очевидно, что m = ρ · V и V = m/ρ.

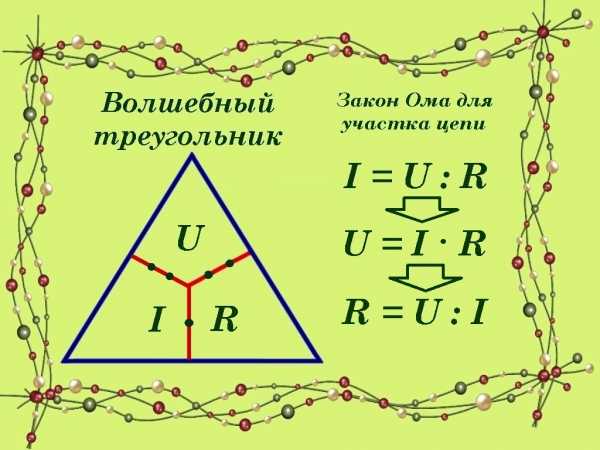
Для закона Ома на участке электрической цепи сила тока I прямо пропорциональна напряжению U на данном участке и обратно пропорциональна его сопротивлению R, то есть I = U/R. Из треугольника легко получаем, что U = I · R, а R = U/I.
www.xn--80abbnaq0akb3aueq3o.xn--p1ai
выведение формул онлайн
Вы искали выведение формул онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вывести формулу онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «выведение формул онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как выведение формул онлайн,вывести формулу онлайн,выражение из формулы онлайн,выражение формул,выразить из формулы переменную онлайн,из формулы выразить онлайн,как выразить неизвестное из формулы,написание формул онлайн,онлайн выведение формул,онлайн выражение из формулы,онлайн написание формул,онлайн расчет по формуле,онлайн расчет формул,онлайн формула,онлайн формулы,преобразователь формул онлайн,рассчитать формулу,расчет онлайн по формуле,расчет по формуле онлайн,расчет формул,расчет формул онлайн,формула онлайн,формулы онлайн,формулы онлайн составление онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и выведение формул онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, выражение из формулы онлайн).
Где можно решить любую задачу по математике, а так же выведение формул онлайн Онлайн?
Решить задачу выведение формул онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Создание математических формул онлайн
| Полученная формула |
Создание математических формул
Бот позволяет отображать математически формулы и графики записанные в формате LaTEX.
Хотелось бы заметить что в поле можно писать достаточно много формул одновременно. Для того что бы каждая формула была расположена на новой строки Вам следует использовать “разделитель” \\
Синтаксис
Синтаксис очень прост
WEB: <Формула в формате Latex>
Примеры
запрос: \begin{pmatrix} 1-i & 12+2i \\ 3-1.5i & -2.5i \end{pmatrix}
Ответ:
Запрос: \int_0^1 f(x)dx
Ответ:
Запрос: \usepackage{color} \color{blue} x^2+y^2
Ответ:
Запрос: f(x)=\int_{-\infty}^xe^{-t^2/m}dt
Ответ:
\usepackage{color}\color{red}\Large e^x=\sum_{n=0}^\infty\frac{x^n}{n!}
\large f^\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\parstyle\begin{eqnarray*} x+y+z&=&3\\2y&=&x+z\\2x+y&=&z\end{eqnarray*}
- Создание QR кодов онлайн >>
abakbot.ru
Онлайн калькулятор: Аппроксимация функции одной переменной
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Аппроксимация функции одной переменной
83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения x, через пробел
183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения y, через пробел
Линейная аппроксимация Квадратичная аппроксимация Кубическая аппроксимация Аппроксимация степенной функцией Показательная аппроксимация Логарифмическая аппроксимация Гиперболическая аппроксимация Экспоненциальная аппроксимацияТочность вычисленияЗнаков после запятой: 4
Линейная регрессия
Коэффициент линейной парной корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Степенная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Показательная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
save Сохранить share Поделиться extension Виджет
Линейная регрессия
Уравнение регрессии:
Коэффициент a:
Коэффициент b:
Коэффициент линейной парной корреляции:
Коэффициент детерминации:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Уравнение регрессии:
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
,
где
Коэффициент детерминации:
Средняя ошибка аппроксимации:
Кубическая регрессия
Уравнение регрессии:
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Степенная регрессия
Уравнение регрессии:
Коэффициент b:
Коэффициент a:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательная регрессия
Уравнение регрессии:
Коэффициент b:
Коэффициент a:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическая регрессия
Уравнение регрессии:
Коэффициент b:
Коэффициент a:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Логарифмическая регрессия
Уравнение регрессии:
Коэффициент b:
Коэффициент a:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Экспоненциальная регрессия
Уравнение регрессии:
Коэффициент b:
Коэффициент a:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации – используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида частные производные равны:
,
Подставив производные, получим:
Далее:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
planetcalc.ru
Инженерный калькулятор онлайн | Дорога к Бизнесу за Компьютером
Вашему вниманию представлен лучший инженерный калькулятор онлайн, который только можно себе вообразить. Впрочем, не только инженеры могут им воспользоваться. Его можно применять в самых разных областях человеческой деятельности, там, где требуются вычисления.
Этот калькулятор поможет школьникам и студентам, которые на нем могут проверить правильность своих расчетов, а также преподавателям, которым приходится порой проверять за вечер сотни домашних заданий.
Данный калькулятор онлайн будет очень полезен людям, которые по роду своей деятельности постоянно занимаются расчетами и вычислениями: инженерам, финансистам, бухгалтерам, бизнесменам.
И главное его преимущество перед другими аналогичными калькуляторами в том, что он позволяет не только производить различные математические действия, но делать это, рассчитывая результат целых формул.
Например, как Вам такая формула? И сколько времени уйдет на ее решение на обычном калькуляторе?
А на данном калькуляторе онлайн задача решается довольно просто, за несколько минут — Вы просто начинаете прописывать цифры и производить с ними определенные действия, и формируете нужную Вам формулу, используя скобки.
Если Вы не вполне себе представляете, как это сделать — видео внизу Вам в помощь.
На этом калькуляторе онлайн Вы можете работать со степенями и корнями, извлекать логарифмы, и использовать тригонометрические функции.
Экран калькулятора онлайн отображает введенное выражение привычным для нас образом, так, как мы его записываем на бумаге.
В поле ввода данные можно вводить как с помощью кнопок калькулятора, так и с помощью клавиатуры компьютера. Например, можно нажать кнопку cos, а можно прописать это слово с помощью клавиатуры буквами. Вместо кнопки Равно можно нажать клавишу Enter, вместо кнопки С — клавишу Esc, а чтобы убрать символы по одному, можно нажать верхнюю правую клавишу калькулятора со стрелкой, или использовать клавишу Backspace.
Формулы можно корректировать — Вы просто ставите курсор в нужное место на поле ввода, затем убираете или добавляете символы или цифры.
При вводе чисел вместо десятичной запятой используйте точку.
Старайтесь также закрывать все скобки. В большинстве случаев это некритично, и калькулятор сам подставит нужные скобки, но иногда возможны ошибки. Впрочем, Вы сами легко увидите неточность в отображаемой формуле, и ее исправите.
О точности калькулятора онлайн можно судить, решив древнюю задачу о зернах на шахматной доске. Кто не помнит — изобретатель шахмат запросил с царя, которому шахматы понравились, следующую награду: на одну клетку шахматной доски нужно было положить одно пшеничное зернышко, на вторую — два, на третью — четыре, и так далее, увеличивая каждый раз количество зернышек вдвое, пока не закончатся все 64 клетки. Изобретатель сказал, что заберет эти зерна себе. Вы можете подсчитать, сколько зерен должно было быть на последней клетке. Решение — не что иное, как 2 в степени 64. Даже Excel выдает при вычислении этого количества округленный результат. А этот калькулятор подсчитает Вам все точно:
Или, например, сложение большого количества чисел. Особенно это актуально для бухгалтеров, которым иногда приходится складывать целые ряды чисел. Если это делать на обычном калькуляторе — вычисления превращаются в утомительный и выматывающий труд. Кроме того, никогда нет уверенности в правильности результата, недаром бухгалтера обычно пересчитывают все по два раза. А с этим калькулятором задача становится довольно простой — все числа видны на экране, и правильность их ввода легко проверить, и если надо, ввод исправить.
Одним словом, возможности данного инженерного калькулятора онлайн удовлетворят даже самого взыскательного пользователя. Потому — пользуйтесь, и желаю Вам комфортных и правильных расчетов.
Видео о том, как вводить формулы в инженерном калькуляторе онлайн
Более подробные сведения Вы можете получить в разделах “Все курсы” и “Полезности”, в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.
Также Вы можете подписаться на блог, и узнавать о всех новых статьях.
Это не займет много времени. Просто нажмите на ссылку ниже:
Подписаться на блог: Дорога к Бизнесу за Компьютером
Проголосуйте и поделитесь с друзьями анонсом статьи на Facebook:
pro444.ru
