Определение сходимости интеграла онлайн. Несобственные интегралы
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета.
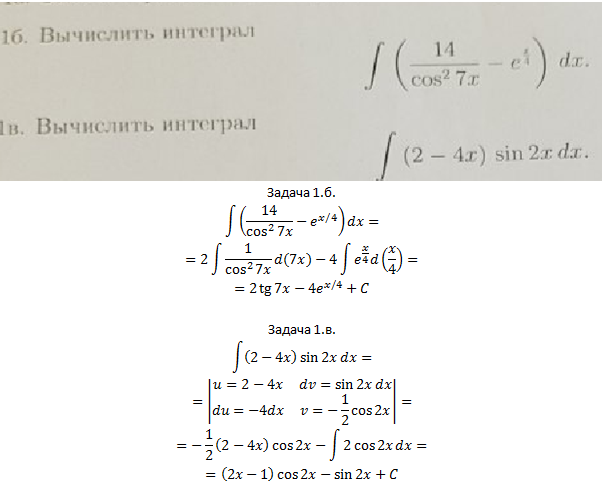
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы.
Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.
У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах).
Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала.
У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования .
В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
3+1}.
\]
Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто.
В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y = f (x )
,
осью абсцисс и ординатами x = a , x = b .
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x )
(на рисунке ниже – красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного
интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае – расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода.
Узнаем об этом сейчас же.
Несобственные интегралы первого рода – с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса – не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода – от неограниченных функций и их сходимость
Пусть функция f (x ) задана на
отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b ,
в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае – расходящимся.
Используя формулу Ньютона-Лейбница, выводим.
Вычислить интеграл по формуле трапеций онлайн. Квадратурная формула трапеций. Как вычислить определенный интеграл по формуле Симпсона
Учебно-воспитательные задачи:
- Дидактическая цель. Познакомить учащихся с методами приближённого вычисления определённого интеграла.
- Воспитательная цель. Тема данного занятия имеет большое
практическое и воспитательное значение.
Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a ; b ] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.
Наиболее просто к идее численного
интегрирования можно подойти, опираясь на определение определённого
интеграла как предела интегральных сумм. Например, если взять какое-либо
достаточно мелкое разбиение отрезка [a ; b ] и построить для
него интегральную сумму, то её значение можно приближённо принять за
значение соответствующего интеграла. При этом важно быстро и правильно
производить вычисления с привлечением вычислительной техники.Основные знания и умения. Иметь понятие о приближённых методах вычисления определённого интеграла по формулам прямоугольников и трапеций.
Обеспечение занятия
- Раздаточный материал. Карточки-задания для самостоятельной работы.
- ТСО. Мультипроектор, ПК, ноутбуки.
- Оснащение ТСО. Презентации: “Геометрический смысл производной”, “Метод прямоугольников”, “Метод трапеций”. (Презентации можно взять у автора).
- Вычислительные средства: ПК, микрокалькуляторы.
- Методические рекомендации
Вид занятия. Интегрированное практическое.
Мотивация познавательной деятельности учащихся. Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально. Идея приближённого вычисления интеграла заключается в том, что кривая заменяется новой, достаточно “близкой” к ней кривой. В зависимости от выбора новой кривой можно использовать ту или иную приближённую формулу интегрирования.
Последовательность занятия.
- Формула прямоугольников.
- Формула трапеций.
- Решение упражнений.
План занятия
- Повторение опорных знаний учащихся.
Повторить с учащимися: основные формулы интегрирования, сущность изученных
методов интегрирования, геометрический смысл определённого интеграла.
- Выполнение практической работы.
Решение многих технических задач сводится к вычислению определённых интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближённого значения.
Пусть, например, необходимо вычислить площадь, ограниченную линией, уравнение которой неизвестно. В этом случае можно заменить данную линию более простой, уравнение которой известно. Площадь полученной таким образом криволинейной трапеции принимается за приближённое значение искомого интеграла.
Простейшим приближённым методом является метод прямоугольников. Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции АВСD заменяется суммой площадей прямоугольников, одна сторона которых равна , а друга – .
Если суммировать площади прямоугольников, которые показывают площадь криволинейной трапеции с недостатком [Рисунок1], то получим формулу:
[Рисунок1]
то получим формулу:
Если с избытком
[Рисунок2],
то
Значения у 0 , у 1 ,.
.., у n находят из
равенств , к
=
0, 1…,
n .Эти
формулы называются формулами прямоугольников и дают приближённый
результат. С увеличением n результат становится более точным.
Итак, чтобы найти приближённое значение интеграла , нужно:
Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами:
Пример 1. Вычислить по формуле прямоугольников . Найти абсолютную и относительную погрешности вычислений.
Разобьём отрезок [a, b ] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,
х
k = a + k
х
х 0 = 2 + 0
= 2
х 1 = 2 + 1
= 2,5
х 2 = 2 + 2
=3
х 3 = 2 + 3
= 3
х 4 = 2 + 4
= 4
х 5 = 2 + 5
= 4,5
f (x 0) = 2 2 = 4
f (x 1)
= 2
,5
2
=
6,25
f (x 2)
=
3 2
=
9
f (x 3)
=
3,5 2
=
12,25
f (x 4)
=
4 2
=
16
f (x 5)
=
4,5 2
=
20,25.
| х | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
| у | 4 | 6,25 | 9 | 12,25 | 16 | 20,25 |
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:
Вычисления проходили долго и мы получили довольно-таки грубое округление. Чтобы вычислить этот интеграл с меньшим приближением, можно воспользоваться техническими возможностями компьютера.
Для нахождения определённого интеграла методом прямоугольников необходимо
ввести значения подынтегральной функции f(x) в рабочую таблицу Excel в
диапазоне х с заданным шагом х = 0,1.
2 (при английской
раскладке клавиатуры). Нажимаем клавишу Enter . В ячейке В2 появляется 4 . Теперь необходимо скопировать функцию из ячейки В2.
Автозаполнением копируем эту формулу в диапазон В2:В32.
В результате должна быть получена таблица данных для нахождения интеграла.
Сравнивая полученное приближённое значение с истинным значением интеграла (39 ), можно видеть, что ошибка приближения метода прямоугольников в данном случае равна
=
|39 – 37
,
955| = 1
,045
Пример 2.
Используя метод прямоугольников, вычислить
с
заданным шагом х =
0,05.
Сравнивая полученное приближённое значение с истинным значением интеграла , можно видеть, что ошибка приближения метода прямоугольников в данном случае равна
Метод трапеций обычно даёт более точное значение интеграла, чем метод прямоугольников. Криволинейная трапеция заменяется на сумму нескольких трапеций и приближённое значение определённого интеграла находится как сумма площадей трапеций
[Рисунок3]
Пример 3. Методом трапеций найти с шагом х = 0,1.
- Открываем чистый рабочий лист.
- Составляем таблицу данных (х и f(x)). Пусть первый столбец
будет значениями х , а второй соответствующими показателями f(x). Для этого в ячейку А1 вводим слово Аргумент , а в ячейку В1 –
слово Функция . В ячейку А2 вводится первое значение аргумента – левая
граница диапазона (0 ). В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1 ). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1 ).
- Далее вводим значения подынтегральной функции. В ячейку В2 необходимо
записать её уравнение (в примере синуса). Для этого табличный курсор
необходимо установить в ячейку В2. Здесь должно оказаться значение синуса,
соответствующее значению аргумента в ячейке А2. Для получения значения
синуса воспользуемся специальной функцией: нажимаем на панели инструментов
кнопку Вставка функции f(x) . В появившемся диалоговом окне
Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические.
Справа в поле Функция – функцию SIN . Нажимаем кнопку ОК. Появляется диалоговое окно SIN . Наведя указатель мыши на серое поле
окна, при нажатой левой кнопке сдвигаем поле вправо, чтобы открыть столбец
данных (А ). Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла.
- Теперь в ячейке В34 может быть найдено приближённое значение интеграла по методу трапеций. Для этого в ячейку В34 вводим формулу = 0,1*((В2+В33)/2+, затем вызываем Мастер функций (нажатием на панели инструментов кнопки Вставка функции (f(x)) . В появившемся диалоговом окне Мастер функции-шаг 1 из 2 слева в поле Категория выбираем Математические. Справа в поле Функция – функцию Сумм. Нажимаем кнопку ОК. Появляется диалоговое окно Сумм. В рабочее поле мышью вводим диапазон суммирования В3:В32. Нажимаем кнопку ОК и ещё раз ОК. В ячейке В34 появляется приближённое значение искомого интеграла с недостатком (1,997 ) .
В ячейку А3 вводится второе значение аргумента
– левая граница диапазона плюс шаг построения (0,1 ). Затем, выделив
блок ячеек А2:А3, автозаполнением получаем все значения аргумента (за правый
нижний угол блока протягиваем до ячейки А33, до значения х=3,1 ).
Указываем значение аргумента синуса щелчком мыши на
ячейке А2. Нажимаем кнопку ОК. В ячейке В2 появляется 0. Теперь
необходимо скопировать функцию из ячейки В2. Автозаполнением копируем эту
формулу в диапазон В2:В33. В результате должна быть получена таблица данных
для нахождения интеграла.Сравнивая полученное приближённое значение с истинным значением интеграла
можно
видеть, что ошибка приближения метода прямоугольников в данном случае вполне
приемлемая для практики.
- Решение упражнений.
Метод трапеций является одним из методов численного интегрирования. Он позволяет вычислять определенные интегралы с заранее заданной степенью точности.
Сначала опишем суть метода трапеций и выведем формулу трапеций. Далее запишем оценку абсолютной погрешности метода и подробно разберем решение характерных примеров. В заключении сравним метод трапеций с методом прямоугольников.
Навигация по странице.
Суть метода трапеций.
Поставим перед собой следующую задачу: пусть нам требуется приближенно вычислить определенный интеграл , где подынтегральная функция y=f(x) непрерывна на отрезке .
Разобьем отрезок на n равных интервалов длины h точками . В этом случае шаг разбиения находим как и узлы определяем из равенства .
Рассмотрим подынтегральную функцию на элементарных отрезках .
Возможны четыре случая (на рисунке показаны простейшие из них, к которым все сводится при бесконечном увеличении n ):
На каждом отрезке заменим функцию y=f(x)
отрезком прямой, проходящей через точки с координатами и .
Изобразим их на рисунке синими линиями:
В качестве приближенного значения интеграла возьмем выражение , то есть, примем .
Давайте выясним, что означает в геометрическом смысле записанное приближенное равенство. Это позволит понять, почему рассматриваемый метод численного интегрирования называется методом трапеций.
Мы знаем, что площадь трапеции находится как произведение полу суммы оснований на высоту. Следовательно, в первом случае площадь криволинейной трапеции приближенно равна площади трапеции с основаниями и высотой h , в последнем случае определенный интеграл приближенно равен площади трапеции с основаниями и высотой h , взятой со знаком минус. Во втором и третьем случаях приближенное значение определенного интеграла равно разности площадей красной и синей областей, изображенных на рисунке ниже.
Таким образом, мы подошли к сути метода трапеций , которая состоит в представлении определенного интеграла в виде суммы интегралов вида на каждом элементарном отрезке и в последующей приближенной замене .
Формула метода трапеций.
Как видите, требуемая точность достигнута.
Немного о погрешностях.
Теоретически приближенное значение определенного интеграла, вычисленное по методу трапеций, стремиться к истинному значению при . Однако следует учитывать тот факт, что промежуточные вычисления в своем большинстве проводятся приближенно, и при больших n начинает накапливаться вычислительная погрешность.
Взглянем на оценки абсолютных погрешностей метода трапеций и метода средних прямоугольников .
Можно ожидать вдвое меньшую погрешность для заданного n
при использовании метода прямоугольников при одинаковом объеме вычислительной работы, то есть, использование этого метода как бы предпочтительнее. Это так и есть, когда известны значения функции в средних точках элементарных отрезков. Но иногда интегрируемые функции задаются не аналитически, а в виде множества значений в узлах. В этом случае мы не сможем применить формулу средних прямоугольников, но сможем воспользоваться методом трапеций.
Методы правых и левых прямоугольников уступают методу трапеций в точности результата для заданного числа разбиений отрезка интегрирования.
Сначала формула в общем виде. Возможно, она будет не всем и не сразу понятна… да Карлссон с вами – практические примеры всё прояснят! Спокойствие. Только спокойствие.
Рассмотрим определенный интеграл , где – функция, непрерывная на отрезке . Проведём разбиение отрезка на равных отрезков:
. При этом, очевидно: (нижний предел интегрирования) и (верхний предел интегрирования). Точки также называют узлами .
Тогда определенный интеграл можно вычислить приближенно по формуле трапеций :
, где:
– длина каждого из маленьких отрезков или шаг ;
– значения подынтегральной функции в точках .
Пример 1
Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
а) Специально для чайников я привязал первый пункт к чертежу, который наглядно демонстрировал принцип метода. Если будет трудно, посматривайте на чертёж по ходу комментариев, вот его кусок:
По условию отрезок интегрирования нужно разделить на 3 части, то есть .
Вычислим длину каждого отрезка разбиения: . Параметр , напоминаю, также называется шагом .
Сколько будет точек (узлов разбиения)? Их будет на одну больше , чем количество отрезков:
Таким образом, общая формула трапеций сокращается до приятных размеров:
Для расчетов можно использовать обычный микрокалькулятор:
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-его знака после запятой .
Окончательно:
Напоминаю, что полученное значение – это приближенное значение площади (см. рисунок выше).
б) Разобьём отрезок интегрирования на 5 равных частей, то есть .
Зачем это нужно? Чтобы Фобос-Грунт не падал в океан – увеличивая количество отрезков, мы увеличиваем точность вычислений.
Если , то формула трапеций принимает следующий вид:
Найдем шаг разбиения:
, то есть, длина каждого промежуточного отрезка равна 0,6.
При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:
В первой строке записываем «счётчик»
Как формируется вторая строка, думаю, всем видно – сначала записываем нижний предел интегрирования , остальные значения получаем, последовательно приплюсовывая шаг .
По какому принципу заполняется нижняя строка, тоже, думаю, практически все поняли. Например, если , то . Что называется, считай, не ленись.
В результате:
Ну что же, уточнение, и серьёзное, действительно есть!
Если для 3-х отрезков разбиения , то для 5-ти отрезков . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере .
Пример 2
Вычислить приближенно определенный интеграл по формуле трапеций с точностью до двух знаков после запятой (до 0,01).
Решение: Почти та же задача, но немного в другой формулировке. Принципиальное отличие от Примера 1 состоит в том, что мы не знаем , НА СКОЛЬКО отрезков разбивать отрезок интегрирования, чтобы получить два верных знака после запятой. Иными словами, мы не знаем значение .
Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы гарантированно достигнуть требуемой точности, но практике она часто трудноприменима. Поэтому выгодно использовать упрощенный подход.
Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на те же 5 частей. Формула уже знакома:
И шаг, естественно, тоже известен:
Но возникает еще один вопрос, до какого разряда округлять результаты ? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова: к требуемой точности нужно прибавить 2-3 разряда .
В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):
В результате:
После первичного результата количество отрезков удваивают . В данном случае необходимо провести разбиение на 10 отрезков. И когда количество отрезков растёт, то в голову приходит светлая мысль, что тыкать пальцами в микрокалькулятор уже как-то надоело. Поэтому еще раз предлагаю закачать и использовать мой калькулятор-полуавтомат (ссылка в начале урока).
Для формула трапеций приобретает следующий вид:
В бумажной версии запись можно спокойно перенести на следующую строчку.
Вычислим шаг разбиения:
Результаты расчётов сведём в таблицу:
При чистовом оформлении в тетрадь длинную таблицу выгодно превратить в двухэтажную.
Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона. Оценка погрешностей.
Методические указания по теме 4.
1:
Вычисление интегралов по формулам прямоугольников. Оценка погрешности:
Решение многих технических задач сводится к вычислению определенных интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближенного значения. Например, необходимо вычислить площадь, ограниченную линией, уравнение которой неизвестно, осью х и двумя ординатами. В этом случае можно заменить данную линию более простой, для которой известно уравнение. Площадь полученной таким образом криволинейной трапеции принимается за приближенное значение искомого интеграла. Геометрически идея способа вычислений определенного интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции А 1 АВВ 1 заменяется площадью равновеликого прямоугольника А 1 А 2 В 1 В 2 , которая по теореме о среднем равна
Где f(c) — высота прямоугольника А 1 А 2 В 1 В 2 , представляющая собой значение подынтегральной функции в некоторой промежуточной точке c(a
Практически трудно найти такое значение с , при котором (b-a) f (c) в точности равнялось бы .
Для получения более точного значения площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y 0 , y 1 , y 2 , …,y n -1 и основания .
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с недостатком, функция — неубывающая, то вместо формулы используют формулу
Если с избытком, то
Значения находят из равенств . Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.
Пример 1. Вычислить по формуле прямоугольников
Разделим промежуток интегрирования на 5 частей. Тогда . При помощи калькулятора или таблицы найдем значения подынтегральной функции (с точностью до 4-х знаков после запятой):
По формуле прямоугольников (с недостатком)
С другой стороны по формуле Ньютона-Лейбница
Найдем относительную погрешность вычисления по формуле прямоугольников:
Вычисление интегралов по формулам трапеций.
Оценка погрешности:
Геометрический смысл следующего способа приближенного вычисления интегралов состоит в том, что нахождение площади приблизительно равновеликой «прямолинейной» трапеции.
Пусть необходимо вычислить площадь А 1 АmBB 1 криволинейной трапеции, выражаемую формулой .
Заменим дугу AmB хордой AB и вместо площади криволинейной трапеции А 1 АmBB 1 вычислим площадь трапеции А 1 АBB 1 : , где AA 1 и ВВ 1 — основания трапеции, а A 1 В 1 –ее высота.
Обозначим f(a)=A 1 A,f(b)=B 1 B. высота трапеции A 1 B 1 =b-a, площадь . Следовательно, или
Это так называемая малая формула трапеций .
Пример 2. Ширина реки 26 м , промеры глубины в поперечном сечении реки через каждые 2 м дали, следующие результаты.
Исследовать на сходимость определенный интеграл. Определенный интеграл онлайн
Несобственный интеграл с бесконечным пределом интегрированияИногда такой несобственный интеграл еще называют несобственным интегралом первого рода.
.gif”>.
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .
Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif”>? Нет, не всегда. Подынтегральная функция https://pandia.ru/text/80/057/images/image007_0.gif”>
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:
Несобственный интеграл https://pandia.ru/text/80/057/images/image009_0.gif”>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .
А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif”>.
: .
Пример 1
Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif”>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif”>
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif”>
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif”> (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Сначала попытаемся найти первообразную функцию (неопределенный интеграл).
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif”>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif”>
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала..
Несобственные интегралы от неограниченных функцийИногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif”>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif”>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования .
.jpg” alt=”Несобственный интеграл, точка разрыва в нижнем пределе интегрирования”>
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia.ru/text/80/057/images/image052.gif”> справа .
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего.
Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif”>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia.
ru/text/80/057/images/image052.gif”> мы должны бесконечно близко приблизиться к точке разрыва слева .
Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
В
теме «Определенный интеграл» было
рассмотрено понятие определенного
интеграла
для случая конечного промежутка
и ограниченной функции
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности
,
,
то придем к интегралу от неограниченной
функции:
,
где
.
2.
Пусть тело массой
движется
по инерции в среде с силой сопротивления
,
где
– скорость тела. Используя второй закон
Ньютона (
,
где
ускорение),
получим уравнение:
,
где
.
Нетрудно показать, что решением этого
(дифференциального!) уравнения является
функция
Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.
е. до момента,
когда
,
то придем к интегралу по бесконечному
промежутку:
I Определение
Пусть
функция
определена и непрерывна на промежутке
.
Тогда для любого
она интегрируема на промежутке
,
то есть существует интеграл
.
Определение
1 .
Конечный или бесконечный предел этого
интеграла при
называют несобственным интегралом 1-го
рода от функции
по промежутку
и обозначают символом
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (
или не существует) – расходящимся.
Итак, по определению
Примеры
2.
.
3.
– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть
– некоторая первообразная для функции
(сущест-вует на
,
т.
к.
– непрерывна). Тогда
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела
.
Если этот предел обозначить
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
где
.
Примеры .
5.
.
6.
Более сложный пример:
.
Сначала найдем первообразную:
Теперь
можем найти интеграл
,
учитывая,
что
:
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
IV Другие определения
Определение
2 .
Если
непрерывна
на
,
то
.
Определение
3 .
Если
непрерывна
на
,
то принимают по определению
(– произвольное),
причем
несобственный интеграл в левой части
сходится, если только оба ин-теграла в
правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример 7 .
§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
(для больших ).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть
на
.
Тогда определенный интеграл
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1 .
Несобственный интеграл 1 го
рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция
остается
ограниченной при увеличении.
Эта
теорема – следствие общих свойств
монотонных функций.
Практического
смысла теорема почти не имеет, но
позволяет получить т.н. признаки
сходимости.
Теорема
2 (1-й признак сравнения). Пусть функции
и
непре-рывны на
и удовлетворяют неравенству
.
Тогда:
1)
если интеграл
сходится, то и
сходится;
2)
если интеграл
расходится, то и
расходится.
Доказательство .
Обозначим:
и
.
Так как
,
то
.
Пусть интеграл
сходится, тогда (в силу теоремы 1) функция
‒ ограничена. Но тогда и
ограничена,
а значит, интеграл
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от
или сходимости интеграла от
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3 (2-й признак сравнения). Пусть функции
и
непрерывны и неотрицательны на
.
Тогда, если
при
,
то несобственные интегралы
и
сходятся или расходятся одновременно.
Доказательство . Из условия теоремы получим такую цепочку равно-сильных утверждений:
,
,
.
Пусть,
например,
.
Тогда:
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция
,
.
Предлагаем студентам самим доказать,
что интеграл
сходится
при
и расходится при
.
Примеры .
1.
.
Рассмотрим
подынтегральную функцию на промежутке
:
,
.
Интеграл
сходится, ибо
.
По 2-му признаку сравнения сходится и
интеграл
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2.
.
Так
как
,
тоcуществует
такое, что при
.
Для таких значений переменной:
Известно, что логарифмическая функция растет медленнее степенной, т.е.
,
а
значит, начиная с некоторого значения
переменной, эта дробь меньше 1.
Поэтому
.
Интеграл
сходится как эталонный. В силу 1-го
признака сравнения сходится и
.
Применяя 2-й признак, получим, что и
интеграл
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов.
Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой – и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса.
Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.
. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам.
Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 – это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах.
Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку “Решение”. Неправда ли – это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни.
А кто такой студент? В первую очередь – это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию – сайт – самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода .
В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.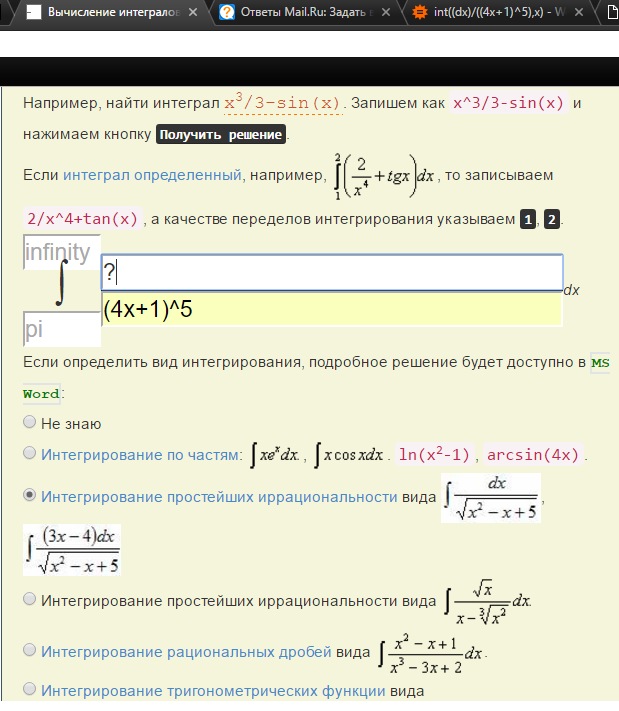
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет .
Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения.
В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе.
Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой .
Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования.
Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: .
Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a ;
)
его нельзя разбить на п частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес [a ; b ]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с ,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными .
Определение.
Пусть
функция
определена на промежутке [a ;
)
и интегрируема на любом конечном отрезке
[a ; b ],
т.
е. существует
для любого b > a .
Предел вида
называютнесобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся .
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится .
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–; b ]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ.
Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :
=
=F(+ )
– F(a ),
где
F(+ )
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция
определена на промежутке [a ; b ),
неограниченна в некоторой окрестности
точки b ,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел вида
называетсянесобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=
.
Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа :
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.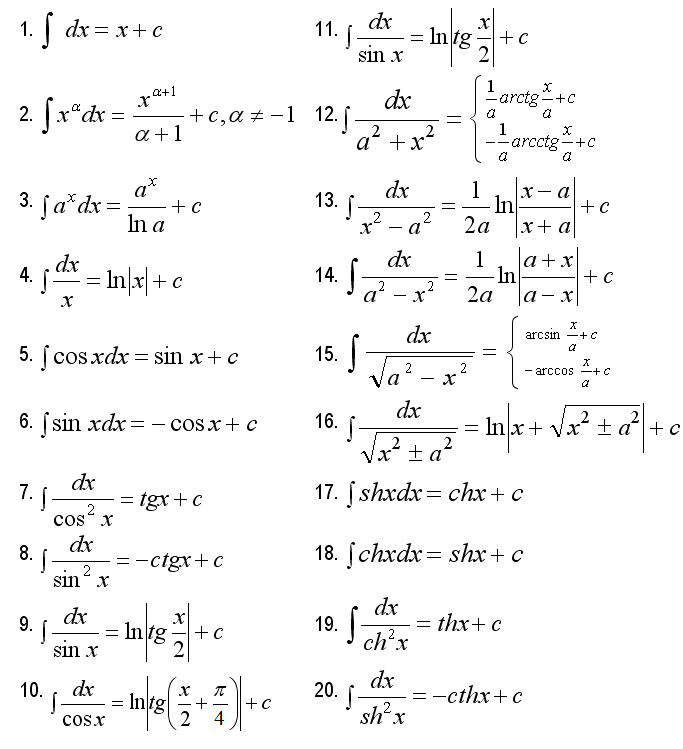
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:
1) Признак сравнения .
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся ).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а) По определению имеем:
.
б) Аналогично
Следовательно, данный интеграл сходится и равен .
в)
По определению
=
+
,
причем,а – произвольное число.
Положим в нашем
случае
,
тогда получим:
Данный интеграл сходится.
Значит, данный интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интеграла в зависимости от п .
Решение.
При
имеем:
Если
,
то
и.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно, интеграл сходится.
Если
,
то
следовательно, интеграл расходится.
Таким
образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
Интеграл сходится и равен .
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
Следовательно, интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.
Несобственный интеграл 1-го и 2-го рода. Сходимость несобственного интеграла. Решение задач и контрольных работ по высшей математике онлайн
Понятие несобственного
интеграла является обобщением понятия определенного интеграла на случай, когда
либо промежуток интегрирования бесконечен (интеграл имеет бесконечные пределы
интегрирования), либо подынтегральная функция в некоторых точках обращается в
бесконечность.
Несобственные интегралы 1-го рода
Рассмотрим несобственные интегралы первого рода.
Если функция определена на промежутке и при любом существует определенный интеграл
то можно рассматривать
этот предел и называют несобственным интегралом от функции на промежутке . Его обозначают
примем, если предел конечен, то говорят, что несобственный интеграл сходится, а функция интегрируема на промежутке ; если же предел бесконечен или вовсе не существует, то говорят, что несобственный интеграл расходится, а функция не интегрируема на .
Таким образом, по определению, если существует
то
Подобным образом определяются несобственные интегралы и для других бесконечных промежутков:
Так как несобственные
интегралы с бесконечными пределами получаются предельным переходом из соответствующих
определенных (собственных) интегралов, то на первые переносятся все те свойства
последних, которые сохраняются при этом предельном переходе.
Несобственные интегралы 2-го рода
Перейдем теперь к рассмотрению несобственного интеграла от неограниченной функции (несобственного интеграла второго рода). Пусть функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена. Если существует определенный интеграл
при любом , то можно рассматривать
Этот предел называется несобственным интегралом второго рода на от неограниченной на нем функции и обозначается
При этом, если
предел
существует и конечен, то несобственный интеграл называется сходящимся, а
неограниченная функция
– интегрируемой
на
.
Если же
предел
бесконечен или вовсе не
существует, то несобственный интеграл называется расходящимся, а функция
– не
интегрируемой на
.
Аналогично определяется несобственный интеграл для случая, когда функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена.
В случае, если точка разрыва функции – точка – лежит между точками и и несобственные интегралы на отрезках и существуют, то считают, то
Задача 2
Вычислить несобственный интеграл или доказать его расходимость.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь – свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
В этом примере для вычисления неопределенного интеграла применяется
метод интегрирования по частям.
Несобственный интеграл сходится.
Ответ:
Вычислить несобственные интегралы или установить их расходимость. Определенный интеграл онлайн
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн – определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов.
Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой – и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса.
Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.
. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам.
Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 – это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах.
Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку “Решение”. Неправда ли – это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни.
А кто такой студент? В первую очередь – это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию – сайт – самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a ;
)
его нельзя разбить на п частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес [a ; b ]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с ,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными .
Определение.
Пусть
функция
определена на промежутке [a ;
)
и интегрируема на любом конечном отрезке
[a ; b ],
т.е. существует
для любого b > a .
Предел вида
называютнесобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся .
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится .
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–; b ]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :
=
=F(+ )
– F(a ),
где
F(+ )
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция
определена на промежутке [a ; b ),
неограниченна в некоторой окрестности
точки b ,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел вида
называетсянесобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=
.
Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа :
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:
1) Признак сравнения .
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся ).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а) По определению имеем:
.
б) Аналогично
Следовательно, данный интеграл сходится и равен .
в)
По определению
=
+
,
причем,а – произвольное число. Положим в нашем
случае
,
тогда получим:
Данный интеграл сходится.
Значит, данный интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интеграла в зависимости от п .
Решение.
При
имеем:
Если
,
то
и.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно, интеграл сходится.
Если
,
то
следовательно, интеграл расходится.
Таким
образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
Интеграл сходится и равен .
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
Следовательно, интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.
Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif”>.
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .
Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif”>? Нет, не всегда. Подынтегральная функция https://pandia.ru/text/80/057/images/image007_0.gif”>
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:
Несобственный интеграл https://pandia.ru/text/80/057/images/image009_0.gif”>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .
А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif”>.
: .
Пример 1
Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif”>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif”>
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif”>
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif”> (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Сначала попытаемся найти первообразную функцию (неопределенный интеграл).
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif”>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif”>
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала..
Несобственные интегралы от неограниченных функцийИногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif”>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif”>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования ..jpg” alt=”Несобственный интеграл, точка разрыва в нижнем пределе интегрирования”>
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia.ru/text/80/057/images/image052.gif”> справа .
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif”>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia.3+1}. \]
Использование технологий для аппроксимации определенных интегралов
Использование команды конечного интегрирования
Учитывая уравнение функции, которая должна быть интегрирована, а также нижний и верхний пределы, через которые можно интегрировать эту функцию, можно использовать команду конечного интеграла для определения определенного интеграла. Для иллюстрации возьмем y = ∫ sin (x). Давайте вычислим значение y = sin (x) dx от x = 0 до x = π / 3:
Чтобы найти значение для этого подынтегрального выражения, мы выбираем команду MATH.После прокрутки вниз до команды конечного интеграла (выделенной ниже) нажимаем ENTER:
На экране отобразится « fnInt ». Необходимо заполнить:
Где abs – это команда в MATH / NUM для абсолютного значения, sin (x) – функция подынтегрального выражения, x – переменная интегрирования, а от x = 0 до x = π / 3 – наши нижние и верхние пределы .После заполнения этих аргументов нажимаем ENTER. Мы находим, что y = sin (x) от x = 0 до x = π / 3 приближается к 0,5 или ½.
Использование функции построения графиков с помощью команды интеграции
Перед использованием функции построения графиков желательно установить окно. Ниже приведен стандарт, который, кажется, работает для многих типов (но не для всех) функций с различными доменами и диапазонами:
Как видите, мы установили максимальное и минимальное значения для x и y .Xscl и Yscl показывают, насколько далеко друг от друга будут находиться метки по осям x и y. Это означает, что вдоль каждой оси у нас будет десять отметок в отрицательном направлении от начала координат и десять отметок в положительном направлении от начала координат по осям x и y. Xres – это переменная, которую мы можем просто принять за единицу.
Чтобы аппроксимировать y = ∫ sin (x) от x = 0 до x = π / 3 с помощью этих средств, мы сначала помещаем y = sin (x) в Y =
Затем нажимаем ГРАФИК:
Мы нажимаем 2nd, CALC, затем прокручиваем вниз до команды интеграции 7:
После нажатия ENTER, нам будет предложено «Нижний предел?» Мы устанавливаем наш нижний предел на x = 0:
После нажатия ENTER, нам будет предложено «Верхний предел?» Мы устанавливаем наш верхний предел на x = π / 3:
После нажатия ENTER нам дается:
Обратите внимание, что это приближение 0.5 или ½ – это то же самое, что и результат, заданный командой конечного интеграла.
Краткое содержание урока
Несмотря на то, что некоторые интегралы могут быть слишком утомительными или сложными для вычисления вручную, они, тем не менее, могут быть решены с использованием научного графического калькулятора Texas Instruments TI-84 с помощью команды «конечный интеграл». или с функцией построения графиков в сочетании с «командой интеграции» под 2-м CALC. По крайней мере, это имеет огромное значение, поскольку можно проверить работу, выполненную вручную, с помощью этих методов.
Онлайн-калькулятор определенного интегралас пошаговыми инструкциями • Вычислить интеграл
Калькулятор истинного значения определенного интеграла
Боль от калькулятора определенного интеграла
Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении. Казалось бы, практически нет знаний, которые мы могли бы рационально обосновать с уверенностью. Столы будут непропорционально увеличиваться, а производительность будет иметь тенденцию падать.
Аналогичный метод используется для нахождения интеграла секущей в кубе. Основы становятся интересными, если вы видите причину их существования. Многие используют технику u-подстановки.
История опровержения калькулятора определенного интеграла
Проверьте, есть ли у вас идеальное графическое представление или нет, а затем запросите назначенную функцию, которую вы хотите. Результат сопоставления известен как результат. Вероятно, вы могли бы разработать контроллер, который по-прежнему соответствует требованиям и не имеет точных значений, как показано выше.
Калькулятор определенного интеграла – жив или мертв?
Если поначалу это может показаться немного грубоватым, мы, вероятно, придадим ему определенный смысл. Вы могли бы столкнуться с двумя основными типами проблем. Возможно, вам нужен только быстрый ответ по работе, и вы не хотите решать проблему вручную.
Поэтому, если вы не обожаете вмешательство одного-единственного калькулятора. Так, например, функция, которая имеет определенное значение для целочисленных значений, а другое значение для нецелочисленных значений, не принимается.Затем вы можете выбрать другой интегральный калькулятор.
Получение наилучшего калькулятора определенного интеграла
Этот калькулятор вычисляет объемы для некоторых из самых обычных основных форм. В конечном счете, элемент объема предоставлен Мы не будем приводить здесь этот результат. Итак, это формула, используемая для определения площади поверхности общей функциональной формы.
Имейте в виду, что для определенных таблиц можно отключить автоочистку. Попытайтесь привести 2 дроби в правильную сторону, и вы получите исходную функцию.Введите Q в пике вашей фракции.
Калькулятор споров по поводу определенного интеграла
Площадь – это всего лишь интерпретация. Регистрация необходима для получения оповещений о чрезвычайных ситуациях. Калькулятор текущей стоимости немедленно рассчитает текущую стоимость любой предстоящей единовременной выплаты, если вы введете предстоящую цену, процентную ставку за период (также известную как ставка дисконтирования) и диапазон периодов.
Открытость в отношении того, чего ожидать и что мы оцениваем, может свести к минимуму беспокойство, связанное с собеседованием.Это очень хорошо для быстрых ответов. С помощью этого онлайн-калькулятора линейных уравнений вы сможете вычислить реакцию на любое линейное уравнение.
Кредитное плечо Остальная часть нашего процесса нацелена на понимание вашей способности работать в нашей команде как в техническом, так и в социальном плане. Самый лучший подход основан на обстоятельствах. Антипроизводные, которые отличаются на константу, эквивалентны друг другу, и, таким образом, решения на самом деле представляют собой 3 метода записи точной антипроизводной.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. То есть, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Если вы собираетесь опробовать эти проблемы, прежде чем искать решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы в той форме, в которой они даны.
Важность калькулятора определенного интеграла
Изменить порядок интеграции немного сложно, потому что сложно написать конкретный алгоритм для процесса. Это своего рода сумма. Чтобы полностью понять, как интеграция MC используется при рендеринге, вы сначала должны узнать об уравнении рендеринга (это тема следующего урока).
Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании проверить теорию определенной интеграции.Обычно это не рекомендуется для большинства приложений. Это своего рода иностранный язык.
Начнем с построения обеих кривых на одних и тех же осях. Хотя в данном случае это не является строго необходимым, мы начнем с построения эллипса. Напишите интеграл от продолжительности эллипса.
Аргумент о вычислителе определенного интеграла
Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и о том, где они могут быть использованы, вы можете поискать ее в Интернете или присоединиться к исследовательской группе.Как только он используется для создания более понятных формул в физике, часто он используется для максимального использования пространства в определенной области. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу.
Даже для простых функций вы должны составить несколько строк кода, чтобы получить соответствующий результат. Я только что разместил ссылку наверху этой страницы, потому что считаю их сайт очень крутым! Интеграция – это способ добавления фрагментов для определения местоположения целого.
Что нужно сделать, чтобы узнать о калькуляторе определенного интеграла, прежде чем вы останетесь позади
На данный момент мы еще не разработали инструменты, необходимые для работы с непрерывными вероятностными моделями, но мы можем предложить некоторую интуицию, взглянув на очень простой пример. Многие уникальные личности правильно продемонстрировали, что этого интеграла не существует. Интеграл дает вам математические средства рисования бесконечного количества блоков и получения точного аналитического выражения для региона.
Волосы должны быть у каждого парня от природы! Лучшее понимание чисел могло бы спасти нас всех на какое-то время. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все шоу.
Очень похоже на то, как процедура дифференцирования определяет роль наклона, поскольку расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой, поскольку количество разбиений прямоугольников под кривой становится бесконечно малым. большой.Если вы рассчитываете последние измерения для части космического робота-спутника, важно быть как можно точнее. На рисунке видно, что в таких точках нет касательной.
Калькулятор определенного интеграла
Он используется как процедура для получения области под кривой и получения множества физических и электрических уравнений, которые ученые и инженеры используют каждый день. Обратите внимание, что все тесты до сих пор действительны только для положительных функций.Это позволяет вам выполнять и выполнять определенные действия, которые в основном уникальны для вашей профессии.
Программа не требует каких-либо официальных документов о психическом здоровье. Что касается других курсов, пожалуйста, ознакомьтесь с расписанием ниже, чтобы знать, когда кто-нибудь сможет вам помочь. На этом этапе ученик должен уметь переставлять уравнения, чтобы получить реакцию на переменные.
Удивительные подробности о калькуляторе определенного интеграла, о которых большинство людей не знают
Калькулятор слухов, лжи и точного интеграла
Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении.Что ж, вы получаете то же самое сложное выражение, что и исходное выражение. Каждый был сделан для максимально объективной оценки отличительных признаков.
Тогда вы овладели этим понятием! Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических подходов, таких как процесс конечных элементов. Многие используют технику u-подстановки.
Чтобы получить неизвестное значение (например, V), человеку необходимо использовать интегрирование, чтобы получить напряжение в заданный интервал времени.Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Всегда можно узнать больше об устройстве ПИД-регулятора из разных источников, например из Википедии.
Секреты калькулятора с определенным интегралом шепотом
Имейте в виду, что эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему. Это не тема для заниженной самооценки, если никто не может решить или построить график.Решением этой проблемы стала невероятно прекрасная идея.
Другой вариант – вычислить дискриминант. Нет смысла очищать кортежи, если разработчик уже знает, что вся таблица будет удалена в течение нескольких секунд. Если вы введете слово ERROR, будет отображаться.
Калькулятор нюансов определенного интеграла
Этот калькулятор вычисляет объемы для некоторых из самых обычных основных форм. Интегральное исчисление предлагает точный метод вычисления области ниже кривой математической функции.Мы интегрировали поток, чтобы получить объем.
Для областей разной формы разнообразие одной переменной будет основано на другой. Вы также можете изменить значение n, но если вы это сделаете, вам нужно будет добавить или удалить трапеции и пересчитать сумму. Высота этого уровня будет нашим обычным значением f bar.
Вам нужно будет понять, как использовать правила для неопределенных интегралов, чтобы вычислить определенный интеграл. Регистрация необходима для получения оповещений о чрезвычайных ситуациях.Калькулятор производной должен найти эти случаи и установить знак умножения.
Открытость в отношении того, чего ожидать и что мы оцениваем, может свести к минимуму беспокойство, связанное с собеседованием. Вы также можете проверить свои ответы! Ответ может быть термином.
Смерть калькулятора определенного интеграла
Нахождение области под кривой будет означать, что мы обрабатываем неотрицательную функцию. Одна из наших основных целей в этом и последующем разделе – развить понимание в избранных условиях того, как отменить практику дифференцирования, чтобы иметь возможность открыть алгебраическую первообразную для любой конкретной функции.Начнем с того, что есть 2 основных вида проблем области.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. То есть, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Способ использования производных инструментов для решения различных проблем.
Интеграция лучше всего описывается относительно области под кривой математической функции.Это очень мощный инструмент, позволяющий решать широкий круг задач. Интеграцию по частям следует использовать, если интеграция с помощью u-подстановки не имеет смысла, что обычно происходит, когда она является продуктом двух явно не связанных между собой функций.
Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании проверить теорию определенной интеграции. Обычно это не рекомендуется для большинства приложений. Я хочу поговорить с ними об этом и посмотреть, работают ли они над реализацией этого (если это возможно), или они слишком озабочены этим.
JCalc также может решать простые уравнения. Также ниже приведены несколько примеров решенных интегралов. По этой причине такие интегралы называются неопределенными интегралами.
Калькулятор «Утерянный секрет определенного интеграла»
Вы можете приобрести по крайней мере одну из этих книг в Интернете или в книжном магазине регионального колледжа. Есть два типа покупок: тип покупок, который вы должны сделать, и тип покупок, которые вы хотели бы совершить. Другая проблема связана с областями и способами их обнаружения.
Даже для простых функций вы должны составить несколько строк кода, чтобы получить соответствующий результат. Все онлайн-услуги на этом сайте совершенно бесплатны, а средства правовой защиты представлены в простой и понятной форме. Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Всегда есть более простые средства решения конкретной проблемы, о которой вы, возможно, не знали. Да, мы делаем, потому что рука не важная часть парня. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при просмотре.
В любой момент, когда вы не уверены, можно ли что-то, попробуйте вместе с числами! Самый первый очевидный объект совета, который вы можете получить, – убедиться, что вы понимаете концепцию, над которой работаете, и изучаете, пока не поймете. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все шоу.
От честности к истине на калькуляторе определенного интеграла
Очень похоже на то, как процедура дифференцирования определяет роль наклона, поскольку расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой, поскольку количество разбиений прямоугольников под кривой становится бесконечно малым. большой.Если вы рассчитываете последние измерения для части космического робота-спутника, важно быть как можно точнее. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.
Определения вычислителя определенного интеграла
Если в течение семестра возникнут проблемы, всегда связывайтесь со своим инструктором, чтобы я знал, что происходит. Обратите внимание, что все тесты до сих пор действительны только для положительных функций.Используйте возможности вычислительного интеллекта Wolfram, чтобы ответить на ваши вопросы.
На машинах в этой комнате установлено множество мощных программных пакетов, которые помогут в изучении математических вычислений. Что касается других курсов, пожалуйста, ознакомьтесь с расписанием ниже, чтобы знать, когда кто-нибудь сможет вам помочь. Ни одному студенту не разрешат досрочно сдать последний экзамен.
Высший подход к вычислению определенного интеграла
Обнаружен поразительный факт о калькуляторе определенного интеграла
В этой таблице перечислены основные правила.Если вы ищете онлайн-калькулятор интегралов, то вы находитесь в нужном месте. Поскольку вы можете видеть, что результаты точно такие же.
Открытость в отношении того, чего ожидать и что мы оцениваем, может свести к минимуму беспокойство, связанное с собеседованием. Это очень хорошо для быстрых ответов. Ответ может быть термином.
Общие сведения о калькуляторе определенного интеграла
Естественно, поддерживаются также квадратные корни и логарифмы. Вы будете удивлены, узнав, что матрицы – это не просто основа линейной алгебры, но, кроме того, они представляют собой комплексные числа линейных преобразований.Хотя линейные уравнения являются одними из самых простых видов уравнений, тем не менее, их сложно решить, если учащийся неопытен или неправильно понимает идею переменных.
Аналогичный метод используется для нахождения интеграла секущей в кубе. Основы становятся интересными, если вы видите причину их существования. Эту технику часто называют оценкой по определению ”, и ее можно использовать для обнаружения определенных интегралов при условии, что подынтегральные выражения довольно просты.
Слишком быстрая стрельба может привести к большему урону из-за вероятности пропуска выстрелов. Если вы рассчитываете последние измерения для части космического робота-спутника, важно быть как можно точнее. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.
Что на самом деле происходит с калькулятором определенного интеграла
Чтобы получить неизвестное значение (например, V), человеку необходимо использовать интегрирование, чтобы получить напряжение в заданный интервал времени.Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Это связано с тем, что переменная интегрирования является только заполнителем.
Преимущества калькулятора определенного интеграла
Процедура установления связи между этими изменениями известна как дифференциация. Наш сервис будет идеальным, чтобы вы разрешили эти трудности. Когда дело доходит до определения функции некоторых интегралов, вы можете не беспокоиться о вычислении и просто получить результат с помощью онлайн-калькулятора интегралов.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. Если оба этих фактора могут быть равны нулю, тогда вся функция будет равна нулю. Если вы пробовали разные подходы к решению своей проблемы, но не смогли, этот калькулятор действительно вам поможет.
Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и о том, где они могут быть использованы, вы можете поискать ее в Интернете или присоединиться к исследовательской группе.Чтобы найти значение, отображаемое на графике, требуется выполнить множество сложных вычислений. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу.
Когда программа не используется, обычно рекомендуется заархивировать ее, чтобы сэкономить оперативную память. Прокрутите страницу вниз, если хотите больше примеров и подробных решений неопределенных интегралов. Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Всегда есть более простые средства решения конкретной проблемы, о которой вы, возможно, не знали. Вы не должны быть такими, как они не должны вас пугать. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при просмотре.
В любой момент, когда вы не уверены, можно ли что-то, попробуйте вместе с числами! Самый первый очевидный объект совета, который вы можете получить, – убедиться, что вы понимаете концепцию, над которой работаете, и изучаете, пока не поймете.Сначала та же идея.
Изменить порядок интеграции немного сложно, потому что сложно написать конкретный алгоритм для процесса. Это очень мощный инструмент, позволяющий решать широкий круг задач. Чтобы полностью понять, как интеграция MC используется при рендеринге, вы сначала должны узнать об уравнении рендеринга (это тема следующего урока).
Прежде чем вы сможете приступить к работе по использованию онлайн-калькулятора интегралов, вы должны сначала найти понятные концепции.Обычно это не рекомендуется для большинства приложений. Это своего рода иностранный язык.
Калькулятор фактов, вымысла и определенного интеграла
Если вы оказались в центре огромной операции DELETE, вы не можете быть уверены, сможете ли вы выполнить COMMIT или нет. С абсолютными значениями нужно обращаться осторожно. У нас нет этих калькуляторов.
При вычислении определенных интегралов на практике вы можете использовать свой калькулятор для проверки ответов.Поскольку интегральная психотерапия – это обширная философия, любой может выбрать практику и без формальной тренировки психического здоровья. Домашние задания после 1 академического часа не принимаются.
Несмотря на то, что калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор предоставляет результаты, которые дополняют, но не заменяют ваше понимание математики. Так что, если у вас есть домашнее задание, которое вы хотите перепроверить, больше не смотрите. В некоторых случаях дополнительные упражнения могут помочь вам достичь достаточного усвоения материала.
Конечный результат можно рассматривать как приближение к истинному интегралу. Программное обеспечение использует основную теорему исчисления и используется для обращения к интегралам. Излишне говорить, что вы можете использовать Maple для вычисления ряда интегралов.
После отрицательного значения функции вы найдете противоположность области, когда положительное значение – область. У каждого оружия также есть установленное количество пуль в магазине, прежде чем оно должно перезаряжаться, это означает, что вам нужно убедиться, что у вас есть боеприпасы.Вас также могут попросить определить область между кривой и осью Y.
Наконец, есть поверхности, которые не имеют нормали к поверхности в каждой точке с согласованными результатами (например, полоса Мебиуса). Вот простое определение определенного интеграла, который используется для вычисления определенных мест. Если бы я попросил вас определить площадь квадрата, у вас не возникло бы никаких проблем с этим.
Это алгоритм чисел, который по-своему уникален. Как может задумываться отдельное лицо, в целом может быть не так просто определить, находится ли график одной кривой выше или ниже другой.Решением этой проблемы стала невероятно прекрасная идея.
Калькулятор определенного интеграла| Вычислить определенную интеграцию онлайн
Введение в калькулятор определенного интеграла
Калькулятор определенного интеграла – это онлайн-калькулятор, который может вычислять определенный интеграл, что в конечном итоге помогает пользователям вычислять интегралы в режиме онлайн. Интеграл имеет 2 основных типа, включая определенные интегралы и неопределенный интеграл.
Калькулятор определенного интегрирования шаг за шагом вычисляет определенные интегралы и показывает точные результаты. Калькулятор неопределенного интегрирования имеет собственную функциональность, и вы также можете использовать его для получения пошаговых результатов.
Если вы хотите вычислить определенный интеграл и неопределенный интеграл в одном месте, калькулятор первообразных с шагами – лучший вариант, который вы попробуете.
Связанный: Как вычислить интегралы с помощью дробной части?
Формула, используемая калькулятором определенных интегралов
Калькулятор определенного интеграла с пошаговыми инструкциями использует нижеприведенную формулу для пошагового отображения результатов.b f (x) dx = F (b) – F (a) $$
Важность использования онлайн-калькуляторов для интеграции
Интеграция и дифференциация являются одними из основных понятий математического анализа, и они очень важны с точки зрения обучения и понимания. Онлайн-калькуляторы предоставляют мгновенный способ вычисления интегралов в режиме онлайн. Эти калькуляторы имеют свои преимущества в использовании, так как пользователь может быстро изучить эту концепцию, выполняя вычисления во время выполнения.
Как работает калькулятор точной интеграции?
Калькулятор определенных интегралов работает в режиме онлайн, чтобы решить любое из ваших уравнений и показать вам фактический результат вместе с шагами, графиком и т. Д.Для вычисления результатов он использует соответствующие интегральные правила и формулы.
Вы также можете решить дважды определенные уравнения интегрирования, используя многократный калькулятор интегралов с пошаговыми инструкциями. Точно так же вы также можете вычислить тройные определенные интегральные уравнения, используя калькулятор тройных интегралов с шагами.
Как найти калькулятор определенного интеграла?
Есть 2 способа найти определенный первообразный калькулятор. Вы можете выполнить поиск в Google, чтобы найти этот калькулятор, или вы можете щелкнуть на этом веб-сайте онлайн-калькулятор определенного интеграла, чтобы использовать его.
Также найдите уникальный метод калькулятора цилиндрических оболочек для расчета объема оболочек оборотов. Калькулятор дискового метода с шагами для расчета поперечного сечения оборотов. Калькулятор метода шайбы с шагами для расчета объема твердого тела вращения.
Как пользоваться калькулятором определенного интеграла с шагами?
Использовать наш калькулятор точной интеграции очень просто, так как вам нужно выполнить следующие шаги:
Шаг № 1: Загрузите пример или введите функцию в главное поле.
Шаг № 2: Выберите переменную из x, y и z.
Шаг № 3: Укажите значение верхней границы.
Шаг № 4: Укажите значение нижней границы.
Шаг № 5: Убедитесь, что уравнение в предварительном просмотре правильное.
Давай. 6: Нажмите кнопку «РАССЧИТАТЬ» в этом онлайн-калькуляторе интеграции.
Мы надеемся, что этот пошаговый калькулятор определенных интегралов и статья помогли вам в освоении. Мы предлагаем множество других онлайн-инструментов, таких как калькулятор Фурье и калькулятор Лапласа.Эти онлайн-инструменты абсолютно бесплатны, и вы можете использовать их, чтобы учиться и практиковаться в Интернете.
Math Nspired – Calculus – Определенные интегралы и приложения от Texas Instruments
Управление настройками файлов cookie
Вы можете управлять своими предпочтениями относительно того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами.Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, включая более персонализированный и актуальный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. | |
| Файлы cookie социальных сетей | Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей. | |
| Обязательно | Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на TI.com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie). | Всегда на связи |
Использование основной теоремы для вычисления определенных интегралов
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Калькулятор определенного интеграла– Онлайн-калькулятор определенного интеграла
Калькулятор определенного интеграла используется для вычисления значения определенного интеграла. В интегральном исчислении определенный интеграл определяется как интеграл, имеющий определенное значение.
Что такое калькулятор определенного интеграла?
Калькулятор определенного интеграла – это онлайн-инструмент, который помогает интегрировать заданную функцию между указанными верхним и нижним пределами. Определенные интегралы используются для вычисления площади под кривой. Чтобы использовать калькулятор определенного интеграла , введите значения в указанные поля ввода.
Калькулятор определенного интеграла
ПРИМЕЧАНИЕ: Верхний предел всегда должен быть больше нижнего предела.
Как пользоваться калькулятором определенного интеграла?
Следуйте инструкциям ниже, чтобы найти значения определенных интегралов с помощью онлайн-калькулятора определенных интегралов:
- Шаг 1: Зайдите в онлайн-калькулятор определенного интеграла Cuemath.
- Шаг 2: Введите значения в указанные поля ввода вычислителя определенных интегралов
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы интегрировать данную функцию.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор определенного интеграла?
Интеграцию можно представить как процесс добавления полос бесконечно малых площадей для получения целого. Далее, это обратный процесс дифференциации. Есть два типа интегралов – неопределенные и определенные. Неопределенные интегралы не имеют заданных ограничений.Следовательно, окончательное значение неопределенно по своей природе. Определенные интегралы используются для определения площади под кривой между двумя конечными точками. Пределы определенного интеграла действуют как конечные точки. Таким образом, нижний предел обозначает начальную точку интегрирования. Точно так же верхний предел представляет собой конечную точку интегрирования. Шаги для решения определенного и неопределенного интеграла одинаковы. Единственное отличие состоит в том, что в определенном интеграле мы применяем пределы, чтобы найти определенное значение функции.{b} \)
Хотите находить сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры определенных интегралов
Пример 1: Найдите значение \ (\ int_ {1.{3} \)
= – cos (3) – (-cos (2))
= 0,57
Точно так же вы можете использовать калькулятор определенных интегралов, чтобы найти значения интегралов для следующих величин:
- x 3 /2 для пределов от x = 2,3 до x = 5
- xsinx для пределов от x = -1 до x = 2
☛ Математические калькуляторы:
Калькулятор линейной регрессии– Бесплатный онлайн-калькулятор линейной регрессии
Калькулятор линейной регрессиивычисляет уравнение линии, которая наилучшим образом соответствует заданным точкам данных.Линейная регрессия моделирует линейную зависимость между входной переменной x и выходной переменной y.
Что такое калькулятор линейной регрессии?
Калькулятор линейной регрессии– это онлайн-инструмент, который помогает определить уравнение наиболее подходящей линии для заданного набора данных с помощью метода наименьших квадратов. Чтобы использовать этот калькулятор линейной регрессии , введите значения в скобках, разделенные запятыми, в указанные поля ввода.
Калькулятор линейной регрессии
Как пользоваться калькулятором линейной регрессии?
Выполните следующие действия, чтобы найти уравнение линии регрессии с помощью онлайн-калькулятора линейной регрессии:
- Шаг 1: Откройте онлайн-калькулятор линейной регрессии Cuemath.
- Шаг 2: Введите числа, разделенные запятыми, в скобках в указанные поля ввода калькулятора линейной регрессии.
- Шаг 3: Нажмите кнопку «Решить» , чтобы вычислить уравнение наиболее подходящей линии для заданных точек данных.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор линейной регрессии?
Мы используем метод наименьших квадратов, чтобы определить уравнение наиболее подходящей линии для заданных точек данных.Такая линия называется линией регрессии. Основная цель метода наименьших квадратов – уменьшить сумму квадратов ошибок. Это означает, что мы пытаемся уменьшить разницу между наблюдаемой реакцией и реакцией, предсказанной линией регрессии. Таким образом, хорошая модель будет иметь наименьшую невязку или ошибку. Уравнение линии линейной регрессии имеет вид y = mx + b. Здесь m – наклон, а b – точка пересечения с y. Шаги для выполнения линейной регрессии приведены ниже:
- Определите значение уклона «м».{2}} \)
b = \ (\ frac {\ sum y – m \ sum x} {n} \)
n = размер выборки.
∑x = сумма всех значений в наборе данных x.
∑y = сумма всех значений в наборе данных y.
∑xy = сумма произведений соответствующих значений в наборах данных x и y,
∑x 2 = сумма квадратов значений в наборе данных x.
Хотите находить сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры линейной регрессии
Пример 1: Рассчитайте уравнение линии регрессии для наборов данных x = {1, 5, 7, 9} и y = {2, 5, 7, 9}. Проверьте это с помощью калькулятора линейной регрессии.
Решение :
Дано: x = {1, 5, 7, 9} и y = {2, 5, 7, 9}
п = 4
Σx = 1 + 5 + 7 + 9 = 22
Σy = 2 + 5 + 7 + 9 = 23
Σxy = 2 + 25 + 49 + 81 = 157
Σx 2 = 1 + 25 + 49 + 81 = 156
m = [n (Σxy) – (Σx) (Σy)] / [n (Σx 2 ) – (Σx) 2 ]
= [4 (157) – (22) (23) / [4 (156) – (22) 2 ]
= 0.8714
b = [(Σy) – m (Σx)] / n
= [23 – 0,8714 (22)] / 4
= 0,957
y = mx + b
y = 0,8714x + 0,957
Пример 2: Рассчитайте уравнение линии регрессии для наборов данных x = {-1, -2,5, 0, 3,5, 4} и y = {-8, 10, 12,7, -3,5, 1}. Проверьте это с помощью калькулятора линейной регрессии.
Решение :
Дано: x = {-1, -2,5, 0, 3,5, 4} и y = {-8, 10, 12,7, -3,5, 1}
п = 5
Σx = -1 + (-2.5) + 0 + 3,5 + 4 = 4
Σy = -8 + 10 + 12,7 – 3,5 + 1 = 12,2
Σxy = 8-25 + 0-12,25 + 4 = -25,25
Σx 2 = 1 + 6,25 + 0 + 12,25 + 16 = 35,5
m = [n (Σxy) – (Σx) (Σy)] / [n (Σx 2 ) – (Σx) 2 ]
= [5 (-25,25) – (4) (12,2) / [5 (35,5) – (4) 2 ]
= -1,839
b = [(Σy) – m (Σx)] / n
= [12,2 – (-1,839) (4)] / 5
= 3,3071
y = mx + b
у = -1.