Задача коммивояжера в эксель: works.doklad.ru – Учебные материалы

Методы решения задачи коммивояжера

Дисциплина: “Программирование и основы алгоритмизации”

Тема: “Задача коммивояжора”

ВНИМАНИЕ!
Здесь приводится очень сокращённый текст курсовой работы. Если данная информация вас заинтересовала, то вы можете по указанной выше ссылке скачать бесплатно полную версию курсовой работы с исходными кодами программы, реализующей жадный алгоритм решения задачи коммивояжёра.

Методы решения задачи коммивояжера

Задача коммивояжёра, известная также как Задача о сверлильном станке или алгоритм коммивояжёра, широко применяется при разработке программного обеспечения (и не только для этого). Постановка задачи коммивояжёра и решение задачи коммивояжёра являются темой для данной курсовой работы. В курсовой работе кратко рассмотрены некоторые методы решения задачи коммивояжера и разработана программа, реализующая один из методов решения данной задачи (этот метод известен под названием Жадный алгоритм).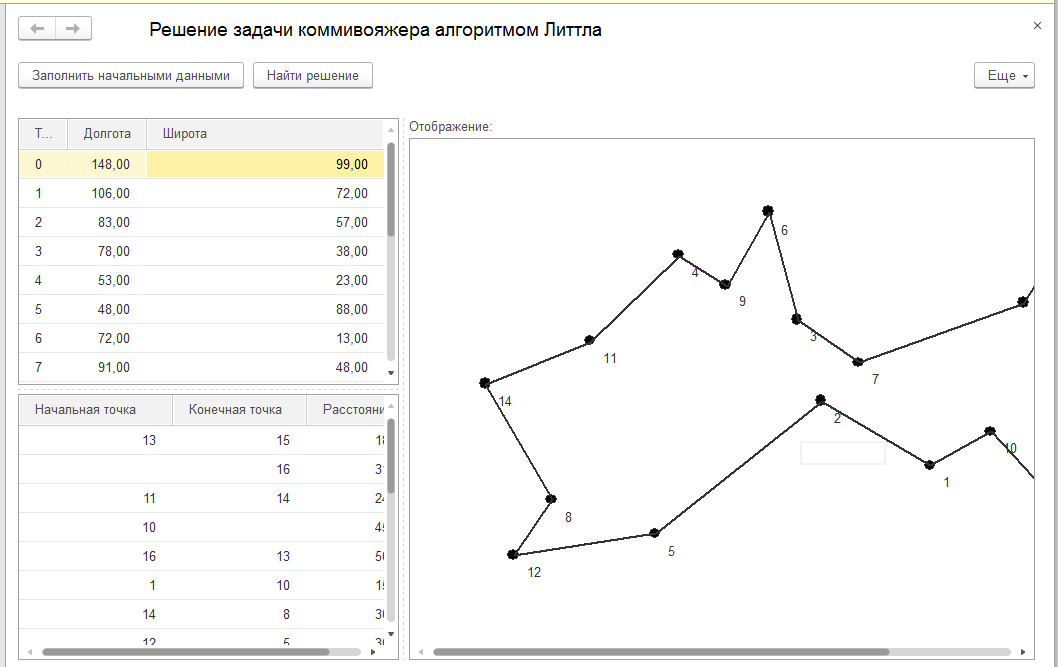

Данная курсовая работа рассматривает один из хорошо известных алгоритмов – жадный алгоритм, который будет использован при решении задачи коммивояжера. А еще мы напишем в среде разработки Delphi несложную программу, которая будет использовать этот алгоритм. Хотя среда разработки и язык программирования значения не имеют. Задачу коммивояжёра можно решить и спомощью других средств, например, Excel.

Применение задачи коммивояжера на практике подробно обсуждать не будем. Очевидно, что методы решения задачи коммивояжёра можно использовать, например, при определении оптимального маршрута автомобиля, развозящего продукты по нескольким торговым точкам.

Постановка задачи коммивояжера

Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по одному разу в неизвестном порядке города 2,3,4..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Алгоритм решения задачи коммивояжера

Жадный алгоритм

Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами.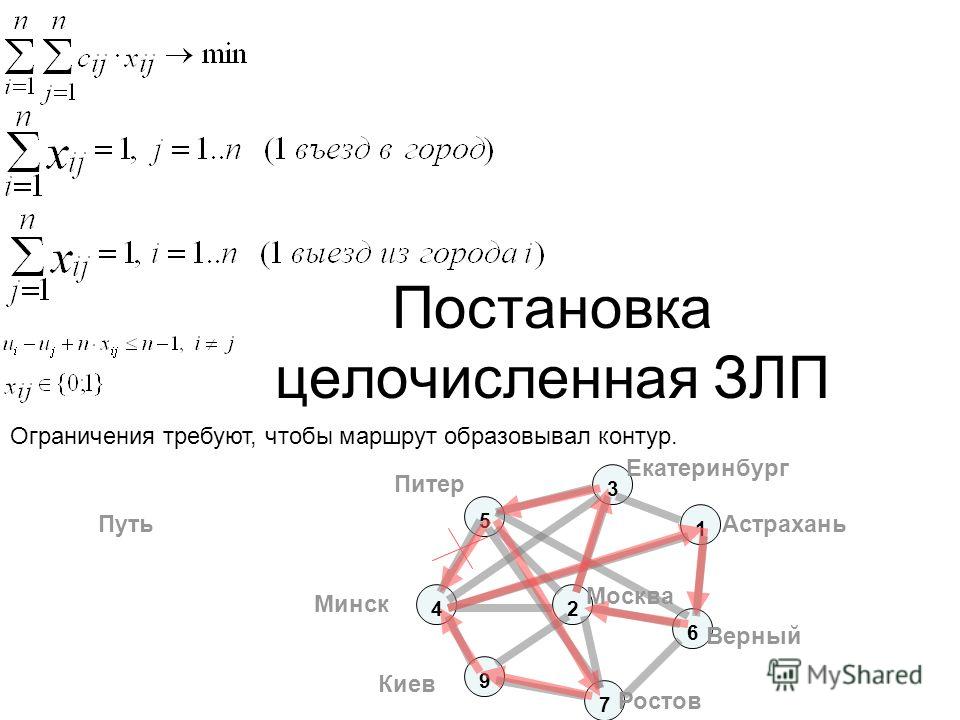 «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.

Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм «иди в ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур. Однако в некоторых ситуациях «жадный» алгоритм определяет-таки кратчайший путь.

Полный перебор

Метод полного перебора заключается в том, что выполняется перебор всех возможных комбинаций точек (пунктов назначения). Как известно из математики, число таких перестановок равно n!, где n – количество точек. Так как в задаче коммивояжера исходный пункт обычно принимается одним и тем же (первая точка), то нам достаточно перебрать оставшиеся, т.

е. количество перестановок будет равно (n–1)!. Этот алгоритм почти всегда дает точное решение задачи коммивояжера, однако продолжительность таких вычислений может занять непозволительно много времени. Известно, что при значениях n > 12, современный компьютер не смог бы решить задачу коммивояжера даже за все время существования вселенной.

Как уже упоминалось, существуют и другие алгоритмы для решения задачи коммивояжера, которые значительно точнее жадного алгоритма и значительно быстрее метода полного перебора. Однако дисциплина называется «Программирование и основы алгоритмизации», из чего следует, что на первом месте у нас все-таки программирование, а уж потом можно и с алгоритмами разбираться. Поэтому в данной курсовой работе другие алгоритмы не рассматриваются в виду относительной сложности. Да и пора бы нам уже написать какую-нибудь программу в любимой нами Delphi.

ОБЗОР СОСТОЯНИЯ ПРОБЛЕМНОЙ ОБЛАСТИ ПО ТЕМЕ: РЕШЕНИЕ ЗАДАЧИ КОММИВОЯЖЁРА

ОБЗОР СОСТОЯНИЯ ПРОБЛЕМНОЙ ОБЛАСТИ ПО ТЕМЕ: РЕШЕНИЕ ЗАДАЧИ КОММИВОЯЖЁРА

 

Введение.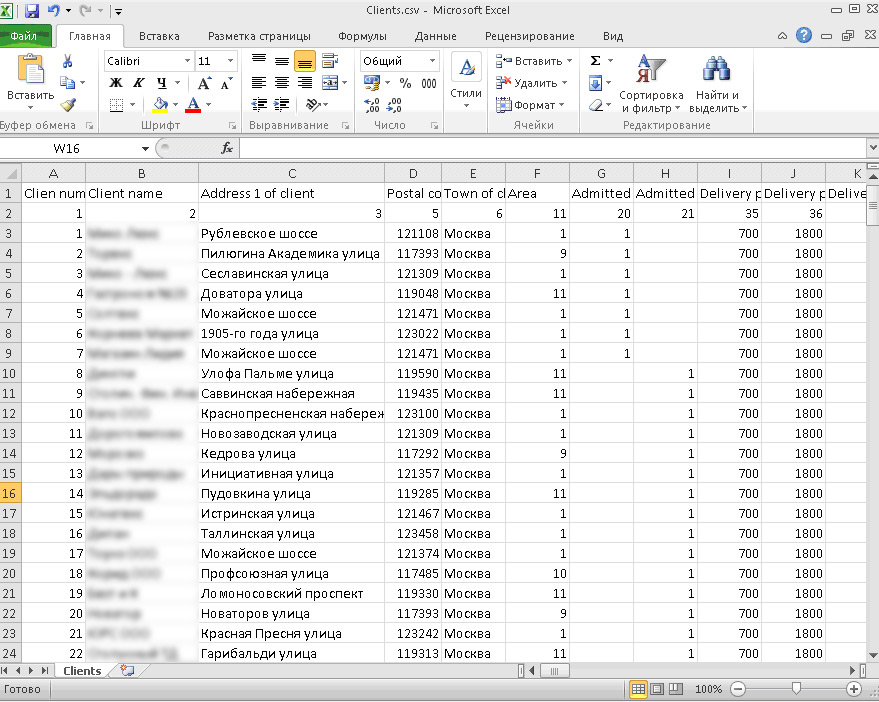

В настоящее время транспортные задачи получили широкое распространение на практике. Перевозка грузов является одной из важнейших отраслей экономики. Необходимость нахождения оптимального решения логистических задач, с минимизацией издержек на перевозку, определяется большим экономическим эффектом, поскольку явно увеличивает прибыль предприятия.

Одна из самых известных задач – задача коммивояжёра (ЗК), решением которой занимается уже не одно поколение учёных, в неформальной форме заключается в отыскании маршрута минимальной стоимости, проходящего через заданный набор городов хотя бы по одному разу с последующим возвратом в исходный город.

Большинство задач транспортной логистики являются NP – трудными (недетерминированными полиномиальными). Задачи данного класса нельзя решить с помощью детерминированной машины Тьюринга за время, растущее с ростом размерности задачи, т.е. невозможно найти решение за приемлемое время, т.к. временная сложность алгоритма для решения подобных задач представляет собой, как правило, экспоненциальную зависимость от количества входных данных. Интерес к задаче коммивояжера и актуальность разработки новых методов ее решения обуславливаются тем, что к задаче коммивояжера может быть сведена любая задача широкого спектра NP класса задач. Например, задача прокладки кабелей вычислительных сетей, задача построения изображения непрерывной линией, задача прогнозирования функций протеинов и многие другие.

1.            Постановка задачи коммивояжёра. Классическая постановка задачи коммивояжёра подразумевает использование только детерминированных переменных, а так же отношения между этими переменными – «находится на расстоянии…». В данном случае выделяются два типа объектов: города и дороги.

Все это позволяет сформулировать классическую задачу коммивояжёра в терминах теории графов:

Пусть дан  граф G=<X, D>, множество вершин  графаX = 𝑥1, 𝑥2, … , 𝑥𝑛,

|X|=n–представляет    собой   города, которые             необходимо     посетить

коммивояжёру,   а   множество   взвешенных   реберX   =   𝑑𝑑1, 𝑑𝑑, … , 𝑑𝑑𝑚𝑚, |D|=m– расстояния между городами. Требуется   найти   замкнутый   цикл, который проходит через каждую вершину графа по одному разу – гамильтонов цикл наименьшей длины.

 

Таким образом, среди всех (n-1)!/2 перестановок φ, необходимо найти минимальное значение ∑𝑛−1 𝑑𝑑𝜑𝜑(𝑖𝑖),𝜑𝜑(𝑖𝑖+1)  + 𝑑𝑑𝜑𝜑(𝑛),𝜑𝜑(1).

Хотя классическая задача коммивояжёра достаточно легко моделируется с помощью теории графов, она обладает высокой комбинаторной сложностью. Скажем, в задаче всего с 20ю городами пространство потенциальных решений при полном переборе будет равно 20!=2 432 902 008 176 640 000.

Моделирование предметной области классической задачи коммивояжёра не учитывает тот факт, что на практике мы часто сталкиваемся с неопределенностью. Например, входные данные могут быть нечеткими, либо они динамически изменяются. Таким образом, становится невозможным свести практическую задачу к классической без потери адекватности модели.[6] В условиях неопределенности возникают новые формулировки ЗК с неоднородным составом и структурой. Таким образом, формируется неклассическая задача коммивояжёра и появляется необходимость разработки принципиально отличных методов ее решения.

Методы и алгоритмы решения задачи коммивояжёра.

К фундаментальным зарубежным работам по исследованию задачи коммивояжёра относятся монографии [1], [3]. Из отечественных источников наиболее известна монография, посвященная ЗК, В.И. Мудрова, изданная еще в 1969 году. [7]

Как было отмечено выше, задача коммивояжёра относится к классу NP

–             трудных задач, и до настоящего времени не разработан ни один эффективный полиномиальный алгоритм точного решения, однако, и не доказано отсутствие его существования. Точный маршрут должен быть минимальной длины или стоимости среди всех возможных обходов. К таким алгоритмам относятся:

             Алгоритм полного перебора – прост в реализации, но подходит для решения КЗК малого размера (время решения пропорционально (n- 1)!/2 в симметричной задаче и (n-1)! в несимметричной).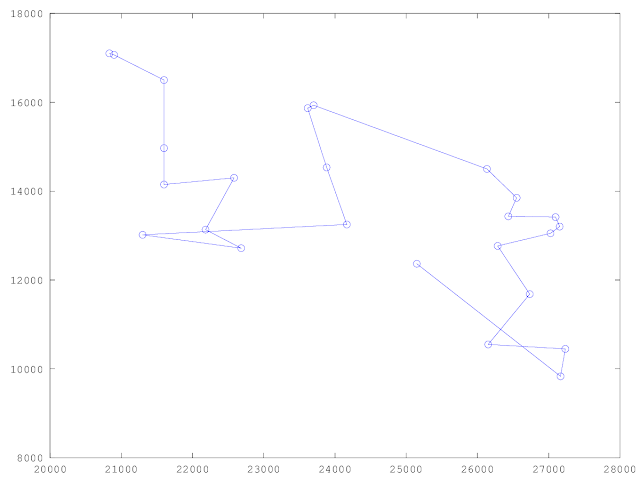

             Метод динамического               программирования      (МДМ). Вычислительная сложность алгоритма динамического программирования равна O(𝑛𝑛2 · 2𝑛−1). Достигнуто увеличение быстродействия по сравнению с предыдущим алгоритмом, однако МДМ требует высоких затрат памяти.

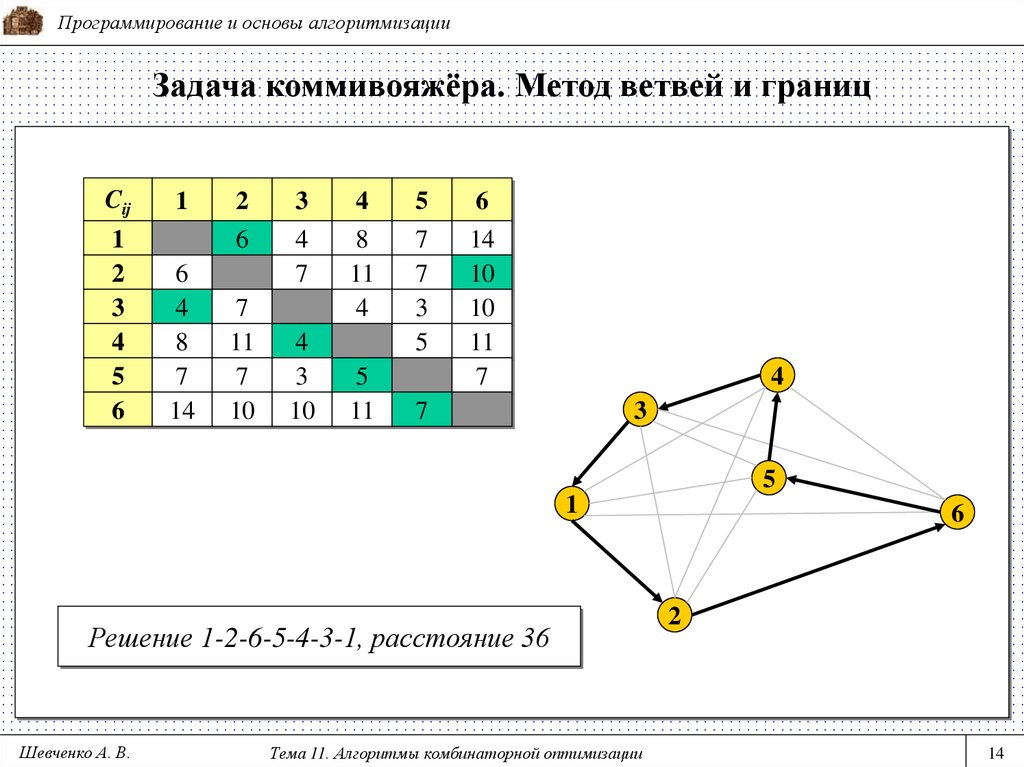
             Метод ветвей и границ – идея метода заключается в последовательном разбиении множества допустимых решений задачи коммивояжёра на непересекающиеся подмножества и на основе получаемых оценок, определять перспективные части маршрута и выстраивать, таким образом, оптимальный маршрут. Данный алгоритм обладает достаточно высокой скоростью, но вызывает затруднения на задачах высокой размерности (позволяет с помощью PC эффективно решать задачи размерностью до 100 городов).

             Матрица Татта и перманент

Очевидно, что алгоритм поиска точного маршрута требует больших вычислительных затрат и может быть использован для задач малой размерности. В связи с этим для решения задачи коммивояжёра часто

 

применяются эвристические алгоритмы, которые дают достаточно хорошее решение, но совершенно не обязательно, что оно будет лучшее – точное.

За последние 10 лет проведена большая работа в этой области. К таким методам относят: метод ближайшего соседа, метод включения ближайшего города, метод самого дешевого включения, метод кратчайшего остова, метод кратчайшего остова с паросочетанием, метод локального поиска.

Все перечисленные методы не позволяют построить оптимальный маршрут в случае многопараметричности, в условиях априорной неопределенности, с графами больших размерностей, которые были бы вместе с тем приемлемы с точки зрения затраченного времени и объема вычислений. В связи с этим относительно недавно стали активно развиваться эвристики, которые используют элементы случайности. Основанные на вероятностно-направленном переборе, эти алгоритмы позволяют строить алгоритмы случайного поиска и случайным образом осуществлять поиск эффективных решений. К ним относятся биоинспирированные алгоритмы: генетические [4], муравьиные, роевые [5].

Так же к приближенным алгоритмам относят методы, которые проводят оптимизацию на основе искусственных нейронных сетей:

В работе [6] автор сравнивает приведенные методы решения ЗК (за исключением метода с использованием матрицы Татта и перманента) и приходит к выводу, что пока не существует метода обрабатывающего множество классов отношений и переменных. Действительно, ни один метод не является релевантным сложности решения ЗК. Выводом является то, что задача разработки новых методов решения ЗК по-прежнему остается актуальной.

Заключение. Работа исследователей в отношении ЗК развивается в двух направлениях: во-первых, разрабатываются методы решения задачи коммивояжёра, которые расширяют пространство входных данных ЗК [2] (таб. 1). Разработка эффективных алгоритмов обработки данных и развитие программного обеспечения послужило основой для эволюционирования информационных технологий. Увеличение быстродействия компьютера так же позволило расширить пространство поиска ЗК.

 

Таблица 1 – Процесс расширения пространства решений ЗК

 

Второе направление в исследовании ЗК – ученые разрабатывают новые формулировки задачи коммивояжёра со снятием ограничений, введением новых типов отношений, переменных или объектов с целью синтеза приближения классической задачи коммивояжера к практической задаче и дальнейшей реализации.

Определяя вектор будущих исследований, следует отметить о необходимости проведения сравнительного анализа вышеперечисленных методов по следующим параметрам: оптимальность, стабильность работы, гибкость алгоритма и выбрать наиболее перспективные алгоритмы. А так же планируется провести их интеграцию с системой нечеткого вывода. Такие методы не только позволят использовать плохо формализованные знания экспертов, но и не потребуют нахождения аналитических взаимосвязей между компонентами, что делает их возможными для дальнейшего применения на практике.

 

Список литературы:

 

1.            Applegate D.L., Bixby R.E., Chvatal V., Cook W. J. The travelling salesman problem: a computational study. – Princeton: Princeton University Press, 2007

2.            Cook     W.J.       Milestones         in            the         Solution               of           the         TSP        instances. http://www.math.uwaterloo.ca/tsp/history/milestone.html

3.             Gutin G., A. Punnen. The travelling salesman problem and its variations // Combinatorian optimization. – Nowell: Kluwer, 2002. Vol.12

4.            Гладков Л.А., Курейчик В.М., Курейчик В.В. Генетические алгоритмы. –

Ростов-на-Дону: ООО «Ростиздат», 2004 г.

5.            Кожаров А.А., Курейчик В.М. Биоинспированные алгоритмы решение оптимизационных задач, LAPLAMBERTAcademicPublishingGmbH&Co. KG, 2011

6.            Колесников А. В., Кириков И.А., Листопад С.В., Румовская С.Б., Доманицкий А.А.. Решение сложных задач коммивояжёра методом функциональных гибридных интеллектуальных систем // под ред. А.В. Колесникова. – М: ИПИ РАН, 2011.

7.            Мудров В.И. Задача о коммивояжере. // М.: Знание, 1969. УДК 658.51.011.5

Научно-образовательный портал ТУСУР | Компьютерное моделирование управленческих решений: Учебное пособие / Семиглазов В. А. — 2017. 59 с.

Введение 5

В.1 Предисловие 5

В. 2 Пример использования надстройки Поиск решений в MS Excel 5

Глава 1. Общая характеристика задач оптимизации 14

1.1 Особенности задач оптимизации 14

1.2. Примеры типовых задач оптимизации 15

1.2.1. Задача о коробке максимального объема 15

1.2.2. Задача о пожарном ведре 15

1.2.3. Задача об оптимальной диете 16

1.2.4. Транспортная задача 16

1.2.5. Задача о минимальном пути в графе 16

1.2.6. Задача коммивояжера 17

1.2.7. Задача о рюкзаке 17

1.2.8. Задача о назначении 18

1.2.9. Задача о минимальном покрывающем дереве в графе 18

1.2.10. Задача о максимальном потоке в сети 19

1.2.11. Задача водопроводчика 19

1.3. Процесс постановки и решения задач оптимизации 20

1.4. Математическая модель задач оптимизации 20

1. 4.1. Понятие математической модели и ее основные элементы 21

1.4.2. Характеристика переменных 21

1.4.3. Характеристика ограничений 21

1.4.4. Характеристика целевой функции 22

Глава 2. Задачи линейного программирования 23

2.1. Общая характеристика задачи линейного программирования 23

2.1.1. Математическая постановка задачи линейного программирования 23

2.2. Задача о производстве красок (Оптимальный план производства) 24

2.2.1. Общая постановка задачи производственного планирования 24

2.2.2. Математическая постановка задачи о производстве красок 25

2.3. Задача об оптимальной диете (Оптимальное смешивание) 26

2.3.1. Математическая постановка задачи об оптимальной диете 26

2.3.2. Решение задачи об оптимальной диете с помощью программы MS Excel 26

2.4. Задача об изготовлении стержней (Оптимальный раскрой) 27

2. 4.1. Содержательная постановка задачи 27

2.4.2. Математическая постановка задачи об изготовлении стержней 28

2.5. Транспортная задача линейного программирования 28

2.5.1. Математическая постановка транспортной задачи 28

2.5.2. Решение транспортной задачи с помощью программы MS Excel 29

2.6. Транспортная задача целочисленного линейного программирования 29

2.6.1. Математическая постановка транспортной задачи 30

2.6.2. Решение многопродуктовой целочисленной транспортной задачи с помощью MS Excel 30

2.7. Задача о назначении 31

2.7.1. Математическая постановка задачи о назначении 31

2.7.2. Решение задачи о назначении с помощью программы MS Excel 32

2.8. Задача о рюкзаке с булевыми переменными 33

2.8.1. Математическая постановка одномерной задачи о рюкзаке с булевыми переменными 33

2. 8.2. Решение одномерной задачи о рюкзаке с булевыми переменными с помощью MS Excel 33

2.9. Задача водопроводчика 34

2.9.1. Математическая постановка задачи водопроводчика 34

Глава 3. Задачи оптимизации на графах 35

3.1. Общая характеристика задач оптимизации на графах 35

3.2. Задача о минимальном покрывающем дереве в графе 35

3.2.1. Математическая постановка задачи 35

3.2.2. Решение задач о минимальном и максимальном дереве с помощью MS Excel 36

3.2.3. Решение задачи о максимальном покрывающем дереве в графе с помощью MS Excel 36

3.3. Задача о минимальном пути в графе 37

3.3.1. Математическая постановка задачи 37

3.3.2. Решение задачи о минимальном пути в ориентированном графе с помощью MS Excel 37

3.4. Задача нахождения критического пути в ориентированном графе 38

3.4.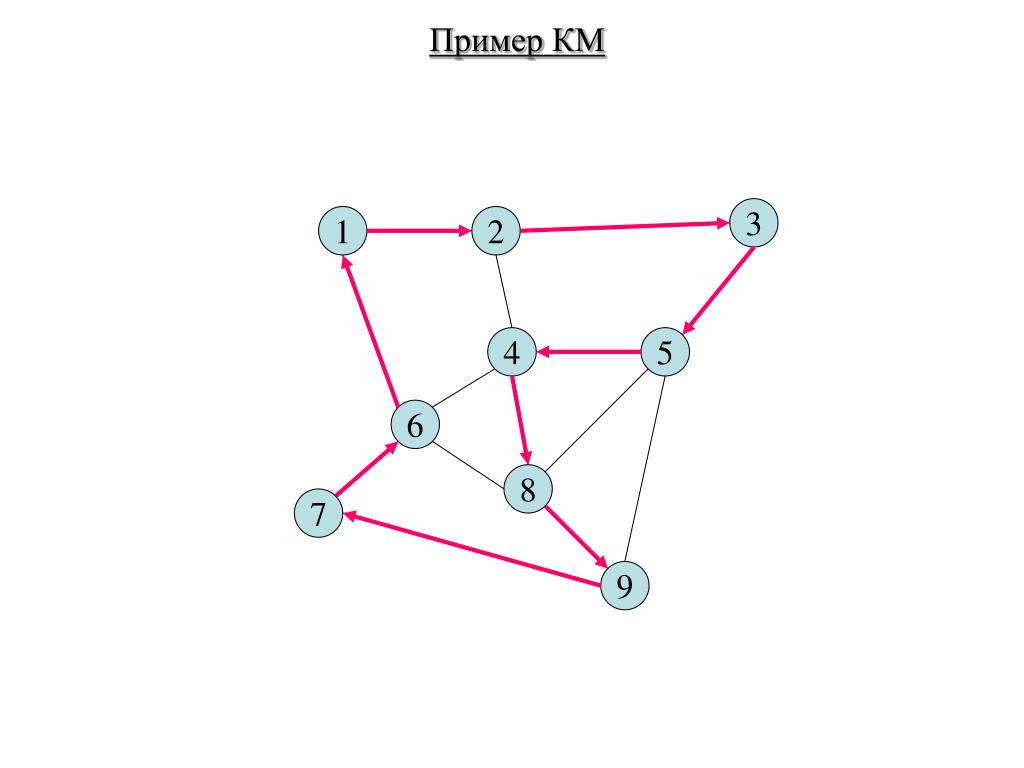 1. Содержательная постановка задачи нахождения критического пути бизнес-процесса 38

3.4.2. Математическая постановка задачи 39

3.4.3. Решение задачи нахождения критического пути в сетевом графе с помощью MS Excel 40

3.5. Задача о максимальном потоке в сети 41

3.5.1 Математическая постановка задачи 41

3.5.2. Решение задачи о максимальном потоке в сети с помощью программы MS Excel 41

Глава 4. Задачи нелинейного программирования 42

4.1. Задача о коробке максимального объема 43

4.1.1. Математическая постановка задачи о коробке максимального объема 43

4.1.2. Решение задачи о коробке максимального объема с помощью MS Excel 43

4.2. Задача о пожарном ведре 43

4.2.1. Математическая постановка задачи о пожарном ведре 43

4.2.2. Решение задачи о пожарном ведре максимального объема с помощью MS Excel 44

4. 3. Задача о строительстве универсама 44

4.3.1. Содержательная постановка задачи о строительстве универсама 45

4.3.2. Математическая постановка задачи о строительстве универсама 45

4.3.3. Решение задачи о строительстве универсама с помощью MS Excel 45

Глава 5. Задачи многокритериального программирования 46

5.1. Задачи многокритериальной оптимизации. 46

5.1.1. Математическая постановка задачи многокритериальной оптимизации 46

5.1.2. Метод уступок для решения задач многокритериальной оптимизации 48

5.1.3. Метод минимального отклонения от идеальной точки 49

5.2. Задача об оптимальной диете с двумя целевыми функциями 50

5.2.1. Математическая постановка задачи и подходы к ее решению 50

5.2.2. Решение многокритериальной задачи об оптимальной диете с помощью программы MS Excel методом уступок 51

5. 2.3. Решение двухкритериальной задачи о диете с помощью программы MS Excel методом минимального

отклонения 52

5.2.4. Решение двухкритериальной задачи о диете с помощью программы MS Excel методом аддитивной свертки 53

5.3. Задача о рюкзаке с двумя целевыми функциями 53

5.3.1. Математическая постановка двухкритериальной задачи о рюкзаке 53

5.3.2. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом уступок 54

5.3.3. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом минимального отклонения 54

5.3.4. Решение двухкритериальной задачи о рюкзаке с помощью программы MS Excel методом аддитивной свертки 55

5.4. Двухкритериальная задача о назначении 55

5.4.1. Математическая постановка двухкритериальной задачи о назначении 55

5.4.2. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом уступок 57

5. 4.3. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом минимального отклонения 57

5.4.4. Решение двухкритериальной задачи о назначении с помощью программы MS Excel методом аддитивной свертки 58

Литература 58

Решение задачи коммивояжера с помощью иммитационного моделирования

Дроздовская Виктория Игоревна¹, Дроздовский Артем Сергеевич², Алехина Алина Энодиевна^3
1Белорусский государственный университет информатики и радиоэлектроники, магистрант
²Белорусский государственный университет информатики и радиоэлектроники, магистрант
³Белорусский государственный университет информатики и радиоэлектроники, кандидат экономических наук, доцент

Drozdovskaya Viktoria Igorevna¹, Drozdovskiy Artem Sergeevich², Alehina Alina Enodievna^3
1Belarusian State University of Informatics and Radio Electronics, undergraduate
²Belarusian State University of Informatics and Radio Electronics, undergraduate
³Belarusian State University of Informatics and Radio Electronics, Candidate of Economic Sciences, Associate Professor

Библиографическая ссылка на статью:
Дроздовская В. И., Дроздовский А.С., Алехина А.Э. Решение задачи коммивояжера с помощью иммитационного моделирования // Современные научные исследования и инновации. 2016. № 10 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2016/10/72955 (дата обращения: 10.11.2021).

В настоящее время моделирование является основным методом исследований во всех областях знаний и научно обоснованным методом оценок характеристик сложных систем, в частности транспортных, используемым для принятия решений в различных сферах деятельности [1].

Имитационное моделирование — гибкий и многофункциональный подход для описания процессов складской логистики, транспортной логистики и управления цепочками поставок, применяемый на всех этапах: планирование, управление, контроль. Модель показывает взаимодействия между звеньями логистической системы, прогнозирует альтернативные варианты развития событий, помогает обнаруживать экстренные ситуации, требующие особого внимания менеджеров, создает отчетность для детального понимания поведения логистической системы. При этом моделирование может использоваться в качестве системы оперативного управления и как инструмент принятия стратегических решений [2].

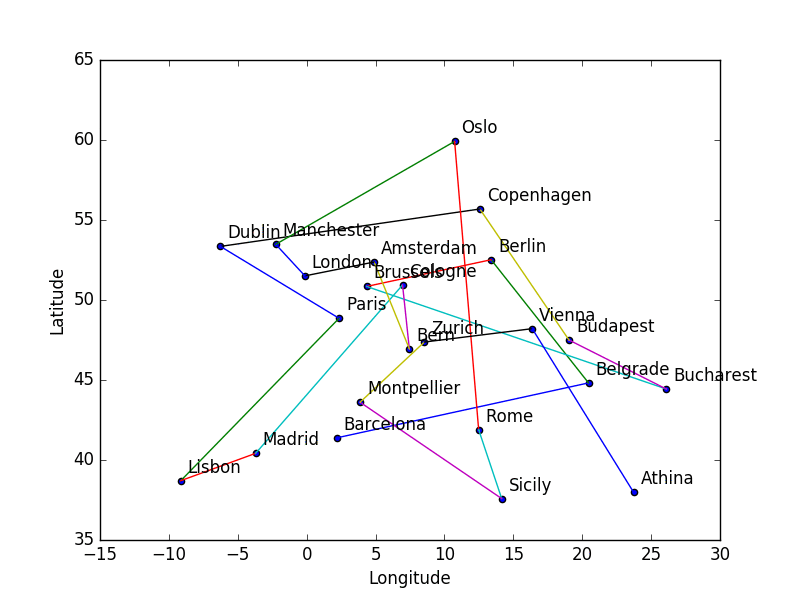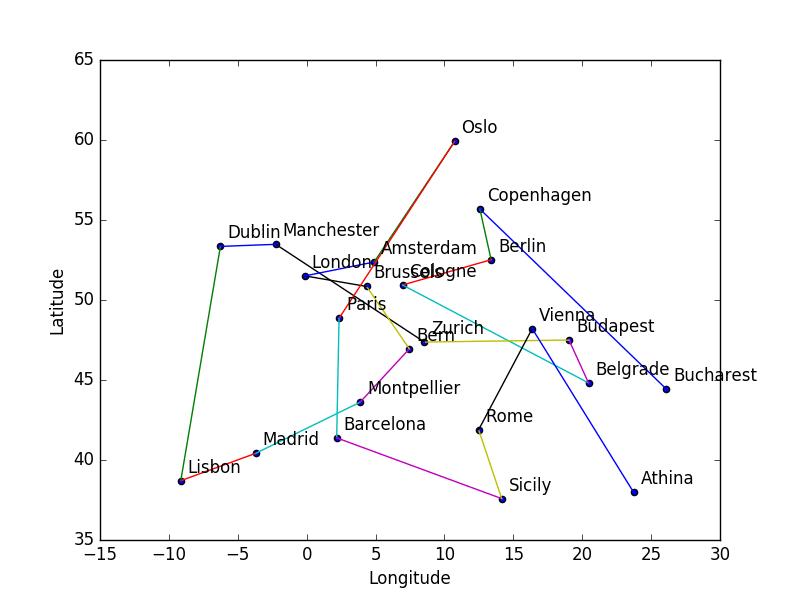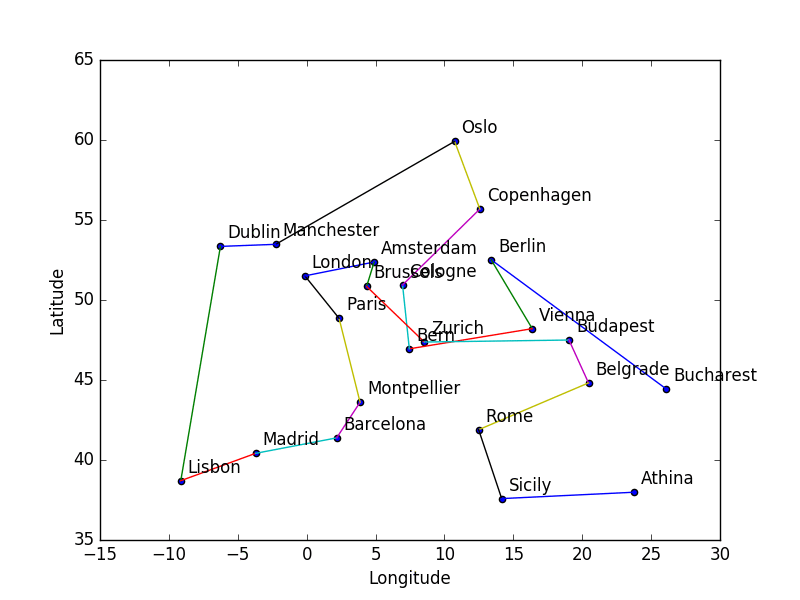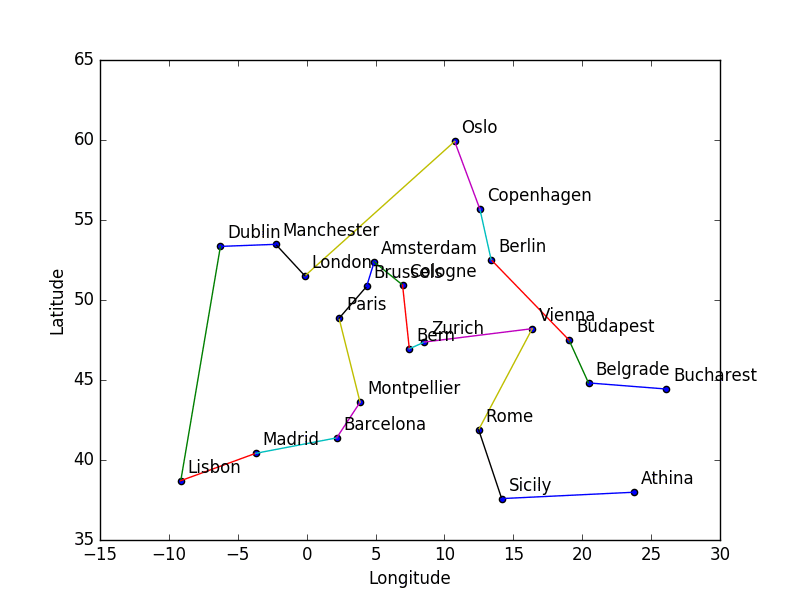
Исходными данными для задачи являются координаты месторасположения склада и магазинов-дистрибьюторов. Система имитационного моделирования AnyLogic позволят использовать импорт данных, в том числе и из Excel. Таким образом географическое местоположение склада и магазинов-дистрибьютеров целесообразно считывать из документа. Фрагмент используемого в данной работе файла Excel с данными приведены на рисунке 1.

Рисунок 1 – Исходные данные

Применение метода имитационного моделирования для решения задачи коммивояжера можно продемонстрировать на примере модели движения товаров от склада к магазинам-дистрибьюторам. Эта модель состоит из одного склада и десяти магазинов-дистрибьюторов, которые заказывают различное количество товара каждые 2-3 дня. Склад имеет в распоряжении свой парк грузовых автомобилей. Реализация заказа осуществляется следующим образом: склад получает заказ от магазина-дистрибьютора и проверяет количество товара на складе. Если заказанное количество товара имеется в наличии, склад реализует поставку к магазину-дистрибутору. Иначе заказ не выполняется, и дистрибутор ждет, пока требуемое количество товара не поступит на склад.

Модель поставки товаров основана на трех основных методологиях имитационного моделирования: системной динамике, агентном и дискретно-событийном моделировании и создана с помощью системы имитационного моделирования AnyLogic.

Данная система позволяет комбинированное использование всех трех методов. В случае имитационного моделирования транспортной сети было принято решение поместить диаграмму системной динамики и дискретно событийную диаграмму внутрь агента – объекта системы AnyLogic.

Рассмотрим агентное моделирование в рамках поставленной задачи. С точки зрения практического применения агентное моделирование можно определить, как метод имитационного моделирования, исследующий поведение децентрализованных агентов и то, как это поведение определяет поведение всей системы в целом. При разработке агентной модели, инженер вводит параметры агентов, определяет их поведение, помещает их в некую окружающую среду, устанавливает возможные связи, после чего запускает моделирование. Индивидуальное поведение каждого агента образует глобальное поведение моделируемой системы. Основным объектом системы является агент Main. Он включает в себя такие агенты, как retailers – магазины-дистрибьюторы, которых по условию 10, и warehouse – склад. Именно этот агент будет выполняемым нашей модели.
Фрагмент созданной в среде AnyLogic агентной модели представлен на рисунке 2.

Рисунок 2 – Фрагмент агентного моделирование сети

Сущности объектов склада и дистрибьюторов описаны в агентах Retailer и Warehouse соответственно. Агент Truck описывает грузовой автомобиль. Для заказа используется агент Order.

Системная динамика – это подход имитационного моделирования, своими методами и инструментами позволяющий понять структуру и динамику сложных систем.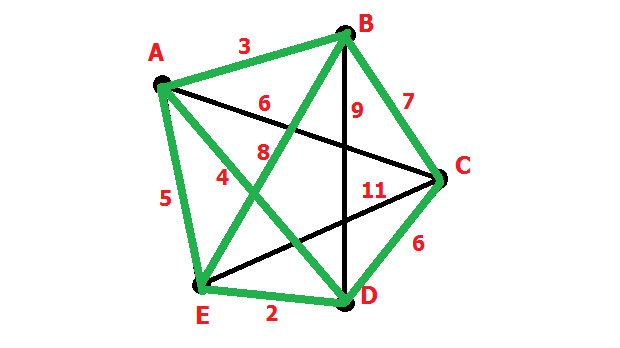 Системная динамика представлена диаграммой пополнения склада товарами. Она проиллюстрирована на рисунке 1. Параметр capacity формирует поток восполнения запасов товаров на складе productionRate. Параметр productsInStorage определяет вместимость склада. Параметр products показывает текущее количество товаров на складе. При загрузке грузовика товарами products уменьшается на величину заказа.

Рисунок 3 – Диаграмма пополнения склада товарами

Чтобы анализировать процессы, протекающие в мире, иногда удобно рассматривать их как последовательность отдельных важных моментов – событий. Подход к построению имитационных моделей, предлагающий представить реальные действия такими событиями и называется «дискретно-событийным» моделированием (discrete event modeling).

Процессное моделирование используется на среднем или низком уровне абстракции: каждый объект моделируется индивидуально, как отдельная сущность, но множество деталей «физического уровня» (геометрия, ускорения/замедления) опускается.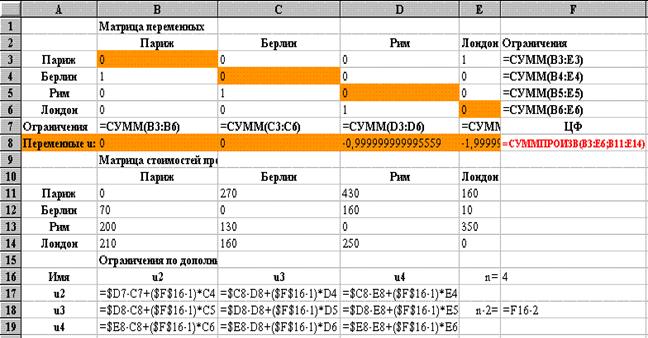 Такой подход широко используется в моделировании бизнес-процессов, производства, логистики. Данная модель является многоподходной. Дистрибуторы, грузовики и склад являются агентами, каждый из которых имеет свое поведение: диаграмма системной динамики задает пополнение склада, движение грузовиков описывает диаграмма состояний для агента Грузовик (рисунок 4).

Рисунок 4 – Диаграмма состояния грузового автомобиля

Агенты живут в пространстве ГИС. Таким образом можно либо добавлять в популяции складов и дистрибьюторов вручную, либо же, создать файл Excel с наименованиями адресов магазинов-дистрибьюторов. Встроенный поиск по ГИС карте находит места и помещает в них агентов. Грузовики движутся по существующей сети дорог, а маршруты создаются, когда автомобили начинают движение к месту назначения.

Среда выполнения позволяет выбирать время выполнения моделирования. Эксперимент можно провести с сильным ускорением, что является наиболее оптимальным для получения конечного результата к концу определенного отчетного периода. Результаты работы модели представлены на рисунке 5.

Рисунок 5 – ГИС карта с агентами модели

После выполнения модели, было получено значение кратчайшего пути доставки. Оптимальный путь составляет 67 км. А также было подсчитано общее время на доставку и время, потраченное на остановки на светофорах: 6 часов 46 минут и 35 минут, соответственно.

Для прослеживания промежуточных результатов модель можно имитировать с минимальным ускорением.

Инструмент для имитационного моделирования AnyLogic позволяет создать наглядную, понятную модель, которая обладает высоким уровнем визуализации данных.

Библиографический список

1. Akopov, A.S. Designing of integrated system-dynamics models for an oil compa-ny / A.S. Akopov // International Journal of Computer Applications in Technology – 2012. – P. 220–230..
2. AnyLogic [Электронный ресурс] / AnyLogic – Санкт-Петербург, 2016. – Режим доступа : http://www.anylogic.ru/use-of-simulation. – Дата доступа : 22. 09.2016.

---

Количество просмотров публикации: Please wait

Все статьи автора «Дроздовская Виктория Игоревна»

(PDF) Solution of optimization tasks by means of Google spreadsheets

12

Технологический аудиТ и резервы производсТва — № 6/6(26), 2015, ©  Данилевич С. Б.

МаТеМаТические МеТоды, Модели и инфорМационные

Технологии в эконоМике

УДК 65.262.1

DOI: 10.15587/2312-8372.2015.55642

РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЗАДАЧ

СРЕДСТВАМИ ТАБЛИЦ GOOGLE

В статье исследуются возможности применение бесплатных облачных сервисов таких, как

Google Drive, для создания экономико-математических инструментов с целью практического

постоянного их применения в малом и среднем бизнесе. Приведен пример создания виртуального

шаблона, позволяющего оперативно рассчитывать оптимальные маршруты между городами

Украины, выбор которых осуществляет пользователь.

Ключевые слова: облачные сервисы Google Drive, Google таблицы, дополнение Solver, задача

коммивояжера, оптимальный маршрут.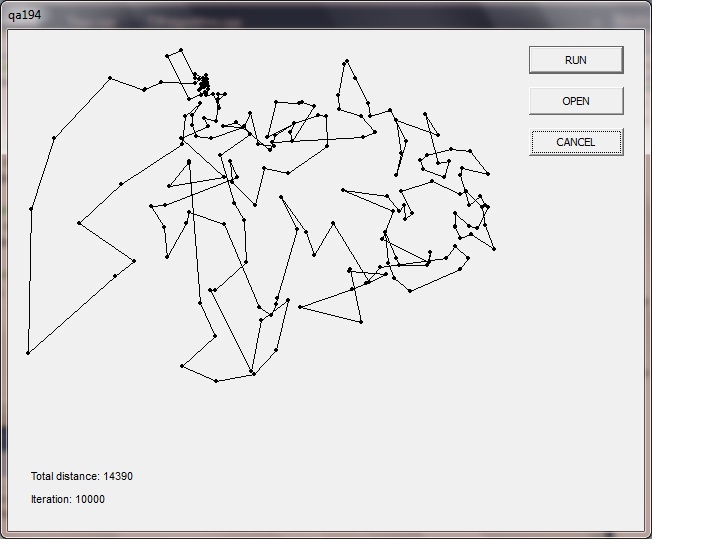

Данилевич С. Б.

1. Введение

Все больше компаний работают с программами, серви-

сами, которые полностью находятся в облаке. Они поль-

зуются преимуществами облачных технологий авто-

матизации, к которым относятся: отсутствие привязки

к конкретному аппаратному обеспечению, нет необходи-

мости установки специальных программ, проводить перио-

дическое их обновление, обеспечена квалифицированная

поддержка и др. К недостаткам можно отнести обязатель-

ное наличие Интернет, не всегда есть возможность под-

страивать предложенные сервисы под свои нужды, мень-

ше возможностей подключения внешнего оборудования.

Такая автоматизация бизнес-процессов часто позво-

ляет, в конечном счете, экономить ресурсы предприятия,

повысить конкурентоспособность.

Применение доступных, бесплатных сервисов, на-

пример, Google Drive могут помочь быстро принимать

рациональные решения представителям малого и средне-

го бизнеса. Так, Google таблицы во многом повторяют

Excel. Здесь есть арсенал встроенных функций, мож-

но подключить дополнения Solver, OpenSolver (Поиск

решения) для решения оптимизационных задач. Можно

даже записывать макросы на языке js. В таких таб-

лицах удобно анализировать результаты деятельности,

моделировать некоторые экономические процессы, до-

статочно гибко учитывать специфику данного вида

деятельности, решать задачи оптимизации бизнеса.

В частности, деятельность любой фирмы, так или иначе,

связана с транспортной логистикой, решением задачи

коммивояжера.

Конечно же пока онлайн-редакторы не могут в пол-

ной заменить настольные офисные пакеты, однако они

дают возможность совместной работы с документами,

использовать их для хранения файлов и осуществления

быстрого документооборота.

Таким образом, можно сделать вывод, что, чтобы не

привлекать дорогостоящих специалистов, представите-

лям малого и среднего бизнеса необходимо постоянно

постигать новые области знаний, учиться применять

новейшие информационные технологии, в частности,

осваивать методы имитационного моделирования, он-

лайн технологий, которые постоянно модернизируются.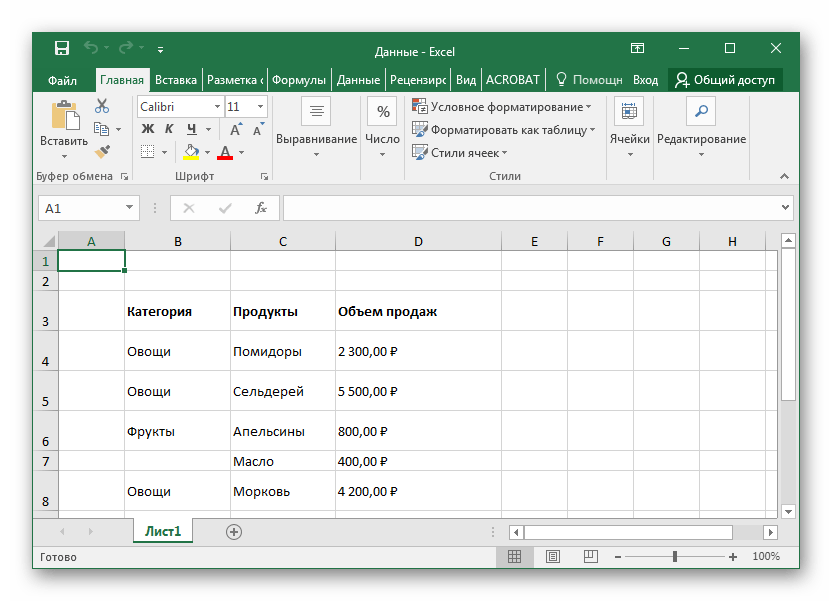

Этим обусловлена актуальность проведенных ис-

следований.

2. Анализ литературных данных

и постановка проблемы

Вопросы, связанные с имитационным компьютер-

ным моделированием широко освещаются в печати

и в INTERNET. В [1] рассмотрены сущность, функции,

принципы и методы организации компьютерного моде-

лирования в экономике. Задача коммивояжера имеет

широкое прикладное применение [2, 3]. Она являет-

ся базовой модельной задачей для многих отраслей

управленческой деятельности: в сфере маркетинга, при

обслуживании территориально распределенных объектов

вплоть до оптимизации маршрутов патрульной полиции.

Так, например, применение математических моделей

товародвижения для решения оптимизационных задач

на основе модельной задачи коммивояжера, методика

ее решения средствами MS Excel подробно рассмотрена

в [4]. Решение этой задачи совместно с другими про-

граммами описано в [5]. Эта задача является неотъем-

лемой частью более широкой задачи маршрутизации

автотранспорта (VRP — Vehicle Routing Problem) [6, 7].

В [8] проведено детальное исследование эффектив ности

существующих точных и эвристических алгоритмов ре-

шения задачи коммивояжера. В большинстве случаев

применение этих алгоритмов требует применения про-

граммирования или специальных программных решате-

лей. Тем не менее, в работе [9] показано, как используя

гибкость таблиц Excel можно довольно легко найти

решение задач, которые считались сложными.

Появление облачных сервисов открыло новые воз-

можности в профессиональной подготовке экономистов

и дальнейшего повышения квалификации [10].

3. Объект, цель и задачи исследования

Объектом исследований были бесплатные сервисы

Google Drive.

Целью исследования было исследование возмож-

ности их использования на практике для создания

базовой модели маршрутизации и создание методики

решения оптимизационных задач средствами облачных

технологий.

Для достижения поставленной цели нужно: создать

Google диск; разработать табличную модель в Google

таблице; применить дополнения Solver или OpenSolver.

Метод ветвей и границ в excel. Метод ветвей и границ

Рассмотрим задачу дискретного программирования в общем виде:

Найти -вектор неизвестных, D- конечное

множество допустимых значений этого вектора, F(x)- заданная целевая функция.

Идея метода состоит в разбиении D на непересекающиеся подмножества Di (эта процедура называется ветвлением) и вычислении верхней и нижней границ целевой функции на каждом из подмножеств. Нижнюю границу будем обозначать Н, а верхнюю Е. Соответственно Hi Eo, то это подмножество не содержит точку оптимума и может быть исключено из дальнейшего рассмотрения. Если верхняя граница Ei H заменяем Н на min Hi. Если Е=Н, то задача решена, иначе надо продолжить процедуру ветвления и вычисления верхней и нижней границ. При этом разбиению на очередном шаге могут подвергаться все или только некоторые подмножества до достижения равенства верхней и нижней границ, причём не на отдельном подмножестве, а для допустимой области в целом.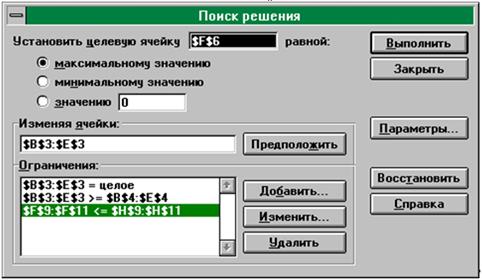

Простая идея метода ветвей и границ требует дополнительных вычислений для определения границ. Как правило, это приводит к решению вспомогательной оптимизационной задачи. Если эти дополнительные вычисления требуют большого числа операций, то эффективность метода может быть невелика.

Схему динамического программирования при движении от начальной точке к конечной (рис. 5.1) можно представлять как процедуру ветвления.

Множество всех допустимых траекторий (последовательность по-шаговых переходов) – это исходное множество D, на котором мы должны найти нижнюю и верхнюю границы, а также траекторию, на которой целевая функция достигает верхней границы и объявить рекордом соответствующее ей значение целевой функции. Построение множества состояний, получаемых после первого шага, – это первое ветвление.

Рис. 5.1.

Теперь подмножествами Di являются множества траекторий, каждая из которых проходит через соответствующую i-ую точку.

На последующих шагах после отбраковки всех путей, приводящих в любое (i-oe) состояние, кроме одного, соответствующим подмножеством является этот оставшийся путь со всеми его допустимыми продолжениями (рис. 5.1). Для каждого из таких подмножеств надо как-то найти верхнюю и нижнюю границы. Если нижняя граница превышает текущее значение рекорда, соответствующее состояние и все его продолжения отбраковываются. Если верхняя граница достигается на некоторой траектории и она меньше текущего значения рекорда, то получаем новый рекорд.

Эффективность такого подхода зависит от точности получаемых оценок, т.е. от Ei – Hi, и от затрат времени на их вычисление.

Фактически в упрощённом виде мы уже использовали этот метод при решении задачи о защите поверхности (разд. 4.6), когда отбраковывали состояния, для которых текущие затраты превышали суммарные затраты для начального приближения. В этом случае текущие затраты являются нижней границей, если считать нулевыми затраты на весь оставшийся путь, а суммарные затраты, соответствующие начальному приближению, являются рекордом. При таком подходе рекорд не обновлялся, хотя это можно было сделать построением начального приближения (верхней границы) для оставшегося пути подобно тому как это делалось для всей траектории при построении начального приближения. Получаемая без вычислений нижняя граница соответствует нулевым затратам на весь оставшийся путь и является крайне грубой оценкой, но получаемой «бесплатно», т.е. без вычислений.

Покажем как получать и использовать более точные оценки при решении рассмотренных выше и целого ряда других задач. При этом будем стремиться получать авозможно более точные границы при минимуме вычислений.

Одна из самых известных и важных задач транспортной логистики (и класса задач оптимизации в целом) – задача коммивояжера (англ. «Travelling salesman problem», TSP ). Также встречается название «задача о бродячем торговце ». Суть задачи сводится к поиску оптимального, то есть кратчайшего пути проходящего через некие пункты по одному разу. Например, задача коммивояжера может применяться для нахождения самого выгодного маршрута, позволяющего объехать определенные города со своим товаром по одному разу и вернуться в исходную точку. Мерой выгодности маршрута будет минимальное время, проведенное в пути, минимальные расходы на дорогу или, в простейшем случае, минимальная длина пути.

Кто и когда впервые начал исследовать задачу коммивояжера неизвестно, но одним из первых предложил решение подобной проблемы выдающийся математик XIX в. – Уильям Гамильтон. Здесь мы рассмотрим замкнутый вариант задачи (т.е. такой, когда в итоге мы возвращаемся в исходную точку) и ее решение методом ветвей и границ .

Общий план решения задачи коммивояжера

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующий алгоритм (последовательность действий):

1. Построение матрицы с исходными данными.
2. Нахождение минимума по строкам.
3. Редукция строк.
4. Нахождение минимума по столбцам.
5. Редукция столбцов.
6. Вычисление оценок нулевых клеток.
7. Редукция матрицы.
8. Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9.
9. Вычисление итоговой длины пути и построение маршрута.

Более подробно эти этапы решения задачи о бродячем торговце раскрыты ниже.

Подробная методика решения задачи коммивояжера

В целях лучшего понимания задачи будем оперировать не понятиями графа, его вершин и т.д., а понятиями простыми и максимально приближенными к реальности: вершины графа будут называться «города», ребра их соединяющие – «дороги».

Итак, методика решения задачи коммивояжера:

1. Построение матрицы с исходными данными

Сначала необходимо длины дорог соединяющих города представить в виде следующей таблицы:

В нашем примере у нас 4 города и в таблице указано расстояние от каждого города к 3-м другим, в зависимости от направления движения (т.к. некоторые ж/д пути могут быть с односторонним движением и т.д.).

Расстояние от города к этому же городу обозначено буквой M. Также используется знак бесконечности. Это сделано для того, чтобы данный отрезок путь был условно принят за бесконечно длинный. Тогда не будет смысла выбрать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т.п. в качестве отрезка маршрута.

2. Нахождение минимума по строкам

Находим минимальное значение в каждой строке (di ) и выписываем его в отдельный столбец.

3. Редукция строк

Производим редукцию строк – из каждого элемента в строке вычитаем соответствующее значение найденного минимума (di).

В итоге в каждой строке будет хотя бы одна нулевая клетка .

4. Нахождение минимума по столбцам

5. Редукция столбцов

Вычитаем из каждого элемента матрицы соответствующее ему dj.

В итоге в каждом столбце будет хотя бы одна нулевая клетка .

6. Вычисление оценок нулевых клеток

Для каждой нулевой клетки получившейся преобразованной матрицы находим «оценку ». Ею будет сумма минимального элемента по строке и минимального элемента по столбцу, в которых размещена данная нулевая клетка. Сама она при этом не учитывается. Найденные ранее di и dj не учитываются. Полученную оценку записываем рядом с нулем, в скобках.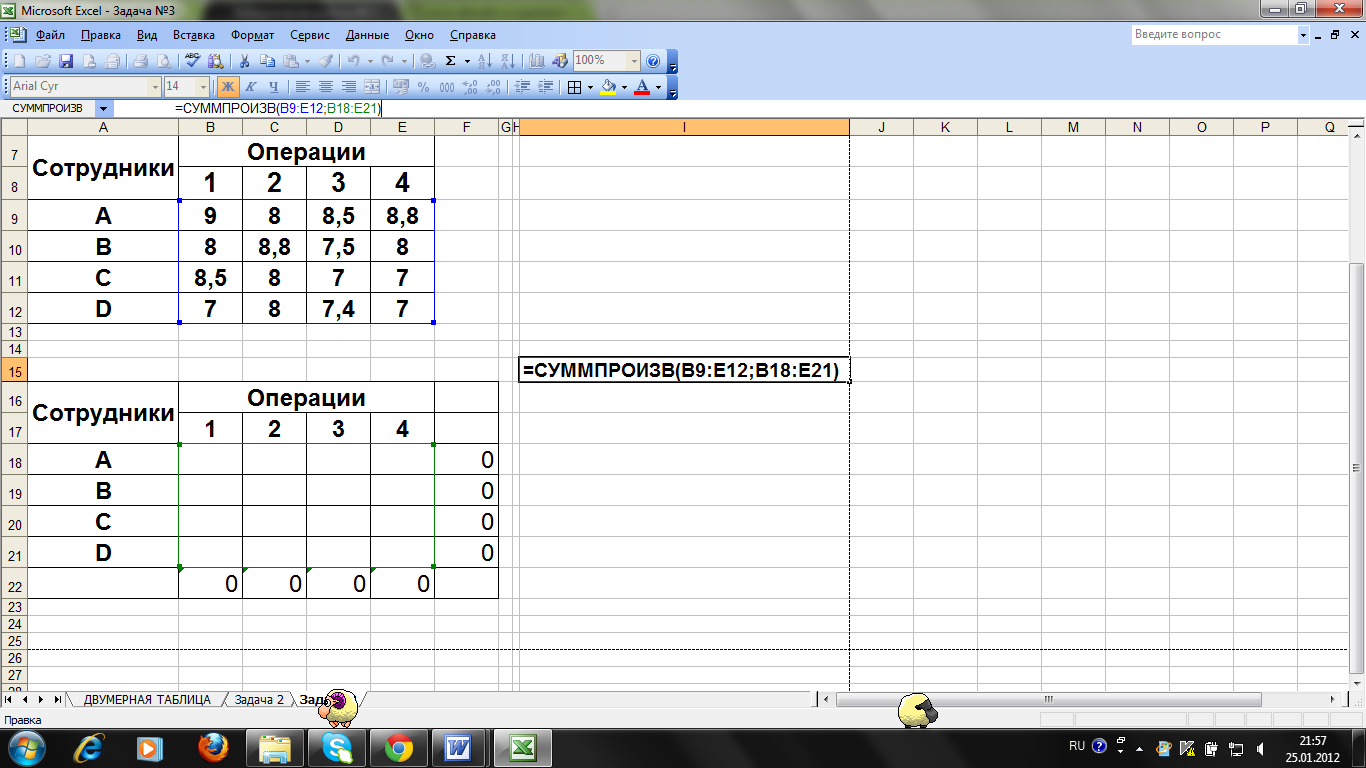

И так по всем нулевым клеткам:

7. Редукция матрицы

Выбираем нулевую клетку с наибольшей оценкой. Заменяем ее на «М ». Мы нашли один из отрезков пути. Выписываем его (от какого города к какому движемся, в нашем примере от 4-ого к 2-му).

Ту строку и тот столбец, где образовалось две «М» полностью вычеркиваем. В клетку, соответствующую обратному пути , ставим еще одну букву «М» (т.к. мы уже не будем возвращаться обратно).

8. Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9

Если мы еще не нашли все отрезки пути, то возвращаемся ко 2 -му пункту и вновь ищем минимумы по строкам и столбцам, проводим их редукцию, считаем оценки нулевых клеток и т.д.

Если все отрезки пути найдены (или найдены еще не все отрезки, но оставшаяся часть пути очевидна) – переходим к пункту 9 .

9. Вычисление итоговой длины пути и построение маршрута

Найдя все отрезки пути, остается только соединить их между собой и рассчитать общую длину пути (стоимость поездки по этому маршруту, затраченное время и т. д.). Длины дорог соединяющих города берем из самой первой таблицы с исходными данными.

В нашем примере маршрут получился следующий: 4 → 2 → 3 → 1 → 4 .

Общая длина пути: L = 30 .

Практическое применение задачи коммивояжера

Применение задачи коммивояжера на практике довольно обширно. В частности ее можно использовать для поиска кратчайшего маршрута при гастролях эстрадной группы по городам, нахождения последовательности технологических операций обеспечивающей наименьшее время выполнения всего производственного цикла и пр.

Решение задачи коммивояжера онлайн

Галяутдинов Р.Р.

© Копирование материала допустимо только при указании прямой гиперссылки на

Определения

называется непустое конечное множество, состоящее из двух подмножеств и . Первое подмножество (вершины) состоит из любого множества элементов. Второе подмножество (дуги) состоит из упорядоченных пар элементов первого подмножества . Если вершины и такие, что , то это вершины смежные.

Маршрутом в графе

называется последовательность вершин не обязательно попарно различных, где для любого смежно с . Маршрут называется цепью, если все его ребра попарно различны. Если то маршрут называется замкнутым. Замкнутая цепь называется циклом.

Постановка задачи

Коммивояжер должен объездить n городов. Для того чтобы сократить расходы, он хочет построить такой маршрут, чтобы объездить все города точно по одному разу и вернуться в исходный с минимумом затрат.

В терминах теории графов задачу можно сформулировать следующим образом. Задано n вершин и матрица {c ij }, где c ij ≥0 – длинна (или цена) дуги (i , j ),

. Под маршрутом коммивояжера z будем понимать цикл i 1 , i 2 ,…, i n , i 1 точек 1,2,…, n. Таким образом, маршрут является набором дуг. Если между городами i и j нет перехода, то в матрице ставится символ «бесконечность». Он обязательно ставится по диагонали, что означает запрет на возвращение в точку, через которую уже проходил маршрут коммивояжера , длина маршрута l (z ) равна сумме длин дуг, входящих в маршрут. Пусть Z – множество всех возможных маршрутов. Начальная вершина i 1 – фиксирована. Требуется найти маршрут z 0 ÎZ , такой, что l (z 0)= minl (z ), z ÎZ .

Решение задачи

Основная идея метода ветвей и границ состоит в том, что вначале строят нижнюю границу φ длин множества маршрутов Z. Затем множество маршрутов разбивается на два подмножества таким образом, чтобы первое подмножество

состояло из маршрутов, содержащих некоторую дугу (i, j), а другое подмножество не содержало этой дуги. Для каждого из подмножеств определяются нижние границы по тому же правилу, что и для первоначального множества маршрутов. Полученные нижние границы подмножеств и оказываются не меньше нижней границы множества всех маршрутов, т.е. φ(Z)≤ φ (), φ(Z) ≤ φ ().

Сравнивая нижние границы φ (

) и φ (), можно выделить то, подмножество маршрутов, которое с большей вероятностью содержит маршрут минимальной длины.

Затем одно из подмножеств

или по аналогичному правилу разбивается на два новых и . Для них снова отыскиваются нижние границы φ (), и φ () и т.д. Процесс ветвления продолжается до тех пор, пока не отыщется единственный маршрут. Его называют первым рекордом. Затем просматривают оборванные ветви. Если их нижние границы больше длины первого рекорда, то задача решена. Если же есть такие, для которых нижние границы меньше, чем длина первого рекорда, то подмножество с наименьшей нижней границей подвергается дальнейшему ветвлению, пока не убеждаются, что оно не содержит лучшего маршрута .

Если же такой найдется, то анализ оборванных ветвей продолжается относительно нового значения длины маршрута. Его называют вторым рекордом. Процесс решения заканчивается, когда будут проанализированы все подмножества.

Для практической реализации метода ветвей и границ применительно к задаче коммивояжера укажем прием определения нижних границ подмножеств и разбиения множества маршрутов на подмножества (ветвление).

Для того чтобы найти нижнюю границу воспользуемся следующим соображением: если к элементам любого ряда матрицы задачи коммивояжера (строке или столбцу) прибавить или вычесть из них некоторое число, то от этого оптимальность плана не изменится. Длина же любого маршрутом коммивояжера изменится на данную величину.

Вычтем из каждой строки число, равное минимальному элементу этой строки. Вычтем из каждого столбца число, равное минимальному элементу этого столбца. Полученная матрица называется приведенной по строкам и столбцам. Сумма всех вычтенных чисел называется константой приведения.

Константу приведения следует выбирать в качестве нижней границы длины маршрутов.

Разбиение множества маршрутов на подмножества

Для выделения претендентов на включение во множество дуг, по которым производится ветвление, рассмотрим в приведенной матрице все элементы, равные нулю. Найдем степени Θ ij нулевых элементов этой матрицы. Степень нулевого элемента Θ ij равна сумме минимального элемента в строке i и минимального элемента в столбце j (при выборе этих минимумов c ij – не учитывается). С наибольшей вероятностью искомому маршруту принадлежат дуги с максимальной степенью нуля.

Для получения платежной матрицы маршрутов, включающей дугу (i , j ) вычеркиваем в матрице строку i и столбец j , а чтобы не допустить образования цикла в маршруте, заменяем элемент, замыкающий текущую цепочку на бесконечность.

Множество маршрутов, не включающих дугу (i , j ) получаем путем замены элемента c ij на бесконечность.

Коммивояжер должен объездить 6городов. Для того чтобы сократить расходы, он хочет построить такой маршрут, чтобы объездить все города точно по одному разу и вернуться в исходный с минимумом затрат. Исходный город A. Затраты на перемещение между городами заданы следующей матрицей:

A	B	C	D	E	F
A	∞	26	42	15	29	25
B	7	∞	16	1	30	25
C	20	13	∞	35	5	0
D	21	16	25	∞	18	18
E	12	46	27	48	∞	5
F	23	5	5	9	5	∞

Решение задачи

Для удобства изложения везде ниже в платежной матрице заменим имена городов (A, B, …, F) номерами соответствующих строк и столбцов (1, 2, …, 6).

Найдем нижнюю границу длин множества всех маршрутов. Вычтем из каждой строки число, равное минимальному элементу этой строки, далее вычтем из каждого столбца число, равное минимальному элементу этого столбца, и таким образом приведем матрицу по строкам и столбцам. Минимумы по строкам: r 1 =15, r 2 =1, r 3 =0, r 4 =16, r 5 =5, r 6 =5.

После их вычитания по строкам получим:

1	2	3	4	5	6
1	∞	11	27	0	14	10
2	6	∞	15	0	29	24
3	20	13	∞	35	5	0
4	5	0	9	∞	2	2
5	7	41	22	43	∞	0
6	18	0	0	4	0	∞

Минимумы по столбцам: h 1 =5, h 2 =h 3 =h 4 =h 5 =h 6 .

После их вычитания по столбцам получим приведенную матрицу:

1	2	3	4	5	6
1	∞	11	27	0	14	10
2	1	∞	15	0	29	24
3	15	13	∞	35	5	0
4	0	0	9	∞	2	2
5	2	41	22	43	∞	0
6	13	0	0	4	0	∞

Найдем нижнюю границу φ (Z ) = 15+1+0+16+5+5+5 = 47.

Для выделения претендентов на включение во множество дуг, по которым производится ветвление, найдем степени Θ ij нулевых элементов этой матрицы (суммы минимумов по строке и столбцу). Θ 14 = 10 + 0,
Θ 24 = 1 + 0, Θ 36 = 5+0, Θ 41 = 0 + 1, Θ 42 = 0 + 0, Θ 56 = 2 + 0, Θ 62 = 0 + 0,
Θ 63 = 0 + 9, Θ 65 = 0 + 2. Наибольшая степень Θ 14 = 10. Ветвление проводим по дуге (1, 4).

Коммивояжер (бродячий торговец) желает посетить ряд городов и вернуться в исходный город, минимизируя суммарную длину (стоимость) переездов. Эта задача в математической форме формулируется как задача нахождения во взвешенном графе гамильтонова цикла минимальной длины и называется задачей коммивояжера.

В качестве её практического приложения можно указать следующее. Пусть имеется станок, способный выполнять несколько операций. Его перенастройка с одной операции на другую требует определенных затрат. Требуется использовать станок в циклическом режиме, минимизируя суммарные затраты на перенастройку.

В данной задаче перенастройка с одной операции на другую и обратная перенастройка могут требовать, вообще говоря, различных затрат. Поэтому и в общем случае в задаче коммивояжера рассматривается взвешенный ориентированный граф, дуги которого в прямом и обратном направлении могут иметь различные веса.

Для решения задачи коммивояжера можно попытаться использовать «жадный алгоритм», успешно примененный в задаче о минимальном остовном дереве. Упорядочим предварительно дуги по весам и будем включать дуги минимального веса, следя за тем, чтобы не возникли вершины, полустепень исхода или захода которых превышает единицу, и не появились негамильтоновы циклы. Однако, как легко убедиться, данный подход не гарантирует получение оптимального решения. В качестве простейшего контрпримера можно рассмотреть следующий граф.

Здесь каждому ребру соответствует две дуги такого же веса.

«Жадный алгоритм» прежде всего включит в цикл ребро
, как имеющее минимальный вес. Включение этого ребра, как непосредственно легко проверить, необходимо ведет к гамильтонову циклу
веса 29. Оптимальный

же гамильтонов цикл
имеет вес 12. Поэтому «жадный алгоритм» не гарантирует получения оптимального решения, хотя он может быть использован на практике в качестве полезной эвристики, во многих случаях приводящей к решениям, близким к оптимальным.

Для задачи коммивояжера не известно какого – либо эффективного алгоритма. Весьма вероятно, что такого алгоритма не существует, хотя это и не удалось до сих пор доказать. Подобные задачи не редки в дискретной математике. В случае небольшой размерности их точные решения удается получать на компьютере с помощью метода «ветвей и границ».

Под методом «ветвей и границ» понимается широкий класс методов сокращенного перебора, суть которых сводится к следующему. Множество допустимых решений А разбивается на два подмножества А 0 и А 1 , затем каждое из подмножеств также разбивается на два подмножества и т.д. Схематически это можно представить в виде дерева, начинающегося с множества всех решений и заканчивающегося его одноэлементными подмножествами, т.е. допустимыми решениями, которыми в нашем случае являются гамильтоновы циклы.

Среди допустимых решений выбирается оптимальное по функционалу качества, которым в нашем случае является длина гамильтонова цикла. Смысл метода «ветвей и границ» состоит, однако, в том, чтобы не просматривать все допустимые решения, а отсекать большинство ветвей на возможно более раннем этапе. Для этого с помощью эвристических соображений стараются сразу пойти по ветви, ведущей к решению, близкому по качеству к оптимальному. После этого большинство других ветвей отсекают с помощью границ для функционала качества, когда удается показать, что в подмножестве решений не содержится решения, лучшего по качеству, чем уже имеющееся.

Рассмотрим метод «ветвей и границ» на примере задачи коммивояжера. Пусть взвешенный орграф задан матрицей расстояний. Если некоторая дуга в графе отсутствует, то соответствующий элемент матрицы будем полагать равным ∞. Заметим, что если длины всех дуг, входящих в некоторую вершину, уменьшить на одно и то же число, то и длина оптимального гамильтонова цикла уменьшится на это же число. То же самое относится и к множеству выходящих дуг. Будем последовательно вычитать из строк и столбцов матрицы расстояний положительные числа так, чтобы элементы матрицы оставались неотрицательными. Так как длина оптимального гамильтонова цикла для графа с неотрицательной матрицей расстояний также неотрицательна, то сумма вычтенных количеств будет нижней границей для длины оптимального цикла исходного графа.

Рассмотрим пример. Пусть задан граф G с симметрической матрицей расстояний.

Значки « ∞ » на диагонали соответствуют отсутствию в графе петель – дуг, ведущих из вершины в эту же вершину. Получим, прежде всего, нижнюю границу для длины кратчайшего гамильтонового цикла. Из первой, второй, третьей и четвертой строк можно вычесть по единице, из пятой строки – два, а из пятого столбца можно вычесть ещё единицу. Это дает нижнюю границу 7, а матрица расстояний приобретает вид

Теперь выберем дугу для ветвления, т.е. разобьем множество гамильтоновых циклов на два подмножества: включающих и не включающих эту дугу. Мы рассчитываем, что данная дуга будет входить в оптимальный или близкий к оптимальному цикл. Для этого будем следовать следующему эвристическому правилу: из множества дуг нулевой длины выбирать ту, исключение которой ведет к максимальному росту нижней оценки. В нашем случае такой дугой является дуга (1,2). Запрещение этой дуги приводит к матрице

из первой строки и второго столбца которой можно вычесть по единице, что увеличивает нижнюю границу на 2 и делает её равной 9.

Включение же дуги (1,2) приводит к тому, что исключаются все остальные дуги, ведущие в вершину 2, и все остальные дуги, выходящие из вершины 1. Поэтому первую строку и второй столбец матрицы можно далее не рассматривать, и они вычеркиваются из матрицы. Кроме того, исключается дуга (2,1). Матрица принимает вид

Из её первой строки и первого столбца можно вычесть по единице, что приводит к матрице

Нижняя оценка здесь возрастает на 2 и также становится равной 9.

Нижняя оценка длины оптимального цикла остается неизменной.

Дуга (2,5) должна быть запрещена, как ведущая к появлению негамильтонова цикла, и матрица принимает вид

Нижняя оценка длины гамильтонова цикла остается, по – прежнему, равной 9.

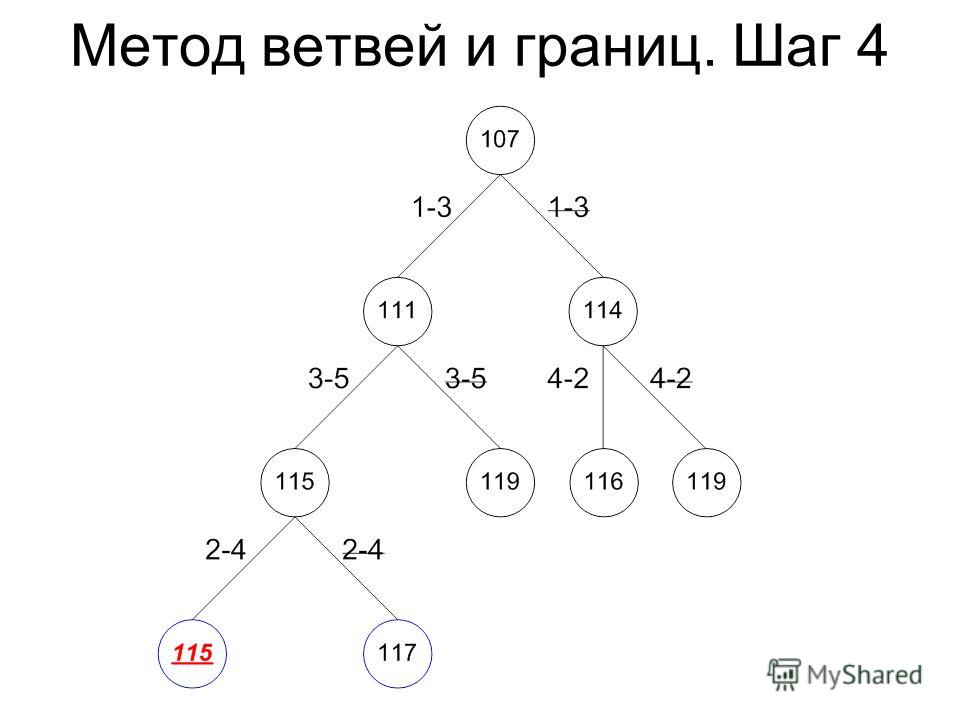
Схематически представим проведенный анализ в виде дерева, где в кружочках стоят нижние оценки длины гамильтонова цикла.

Взглянув на это дерево, непосредственно убеждаемся, что полученный гамильтонов цикл является кратчайшим, т.к. движение по любой другой ветви дерева не может привести к более короткому циклу.

Существует ли эффективный алгоритм для решения задачи коммивояжера? а) да; б) нет; в) неизвестно.

Является ли описанный метод « ветвей и границ» эффективным алгоритмом для решения задачи коммивояжера? а) да; б) нет; в) неизвестно.

Метод ветвей и границ — один из комбинаторных методов. Его суть заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.

Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.

Алгоритм решения:

Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Пусть им является план X 0 . Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи и

Если же среди компонент плана X 0 имеются дробные числа, то X 0 не удовлетворяет условию целочисленности и необходимо осуществить упорядоченный переход к новым планам, пока не будет найдено решение задачи. Покажем, как это можно сделать, предварительно отметив, что F(X 0) F(X) для всякого последующего плана X.

Предполагая, что найденный оптимальный план X 0 не удовлетворяет условию целочисленности переменных, тем самым считаем, что среди его компонент есть дробные числа. Пусть, например, переменная приняла в плане X 0 дробное значение. Тогда в оптимальном целочисленном плане ее значение будет по крайней мере либо меньше или равно ближайшему меньшему целому числу, либо больше или равно ближайшему большему целому числу. Определяя эти числа, находим симплексным методом решение двух задач линейного программирования:

Найдем решение задач линейного программирования (I) и (II). Очевидно, здесь возможен один из следующих четырех случаев:

• 1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции на нем и дают решение исходной задачи.
• 2. Одна из задач неразрешима, а другая имеет оптимальный план, среди компонент которого есть дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу, и строим две задачи, аналогичные задачам (I) и (II).
• 3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на этих планах и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и он вместе со значением целевой функции на нем дает искомое решение.

Если же значение целевой функции больше на плане, среди компонент которого есть дробные числа, то следует взять одно из таких чисел и для задачи, план которой рассматривается, необходимо построить две задачи, аналогичные (I) и (II).

4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем значение целевой функции на данных оптимальных планах и рассматриваем ту из задач, для которой значение целевой функции является наибольшим. В оптимальном плане этой задачи выбираем одну из компонент, значение которой является дробным числом, и строим две задачи, аналогичные (I) и (II).

Таким образом, описанный выше итерационный процесс может быть представлен в виде некоторого дерева, на котором исходная вершина отвечает оптимальному плану Х 0 задачи (1)-(3), а каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач (I) и (II). Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге выбирается та вершина, для которой значение функции является наибольшим. Если на некотором шаге будет получен план, имеющий целочисленные компоненты, и значение функции на нем окажется больше или равно, чем значение функции в других возможных для ветвления вершинах, то данный план является оптимальным планом исходной задачи целочисленного программирования и значение целевой функции на нем является максимальным.

Итак, процесс нахождения решения задачи целочисленного программирования (1)-(4) методом ветвей и границ включает следующие основные этапы:

• 1. Находят решение задачи линейного программирования (1)-(3).
• 2. Составляют дополнительные ограничения для одной из переменных, значение которой в оптимальном плане задачи (1)-(3) является дробным числом.
• 3. Находят решение задач (I) и (II), которые получаются из задачи (1)-(3) в результате присоединения дополнительных ограничений.
• 4. В случае необходимости составляют дополнительные ограничения для переменной, значение которой является дробным, формулируют задачи, аналогичные задачам (I) и (II), и находят их решение. Итерационный процесс продолжают до тех пор, пока не будет найдена вершина, соответствующая целочисленному плану задачи (1)-(3) и такая, что значение функции в этой вершине больше или равно значению функции в других возможных для ветвления вершинах.

Описанный выше метод ветвей и границ имеет более простую логическую схему расчетов, чем метод Гомори. Поэтому в большинстве случаев для нахождения решения конкретных задач целочисленного программирования с использованием ЭВМ применяется именно этот метод.

целочисленный программирование задача коммивояжер ранец

Задачи теории расписаний – презентация онлайн

1. Задачи теории расписаний

2. Теория расписаний

Модели теории расписаний позволяют найти:
Наиболее дешевый
порядок выполнения
работы
Наиболее быстрый порядок
выполнения работы
Задача о шлюзах
Задача о станках
Задача о коммивояжере
Через шлюз последовательно должны пройти N судов.
Известно время прохождения каждого судна – ti и ущерб от 1
часа простоя в очереди – в денежных единицах. (i- порядковый
номер судна в очереди)
Обозначения:
T1 – время шлюзования 1-ого судна
T2 – время шлюзования 2-ого судна
U2 – стоимость 1 часа простоя в ожидании своей
очереди 2-ого судна
U4 = t1+t2+t3– время простоя 4-ого судна
U4 ·(t1+t2+t3) – материальный ущерб от простоя 4-ого судна
Показатель экономической эффективности
работы шлюза связан с суммарным ущербом
от простоя судов в ожидании своей очереди
Пример:
К шлюзу одновременно подошли 4 судна, т.е.
суммарный ущерб от простоя в очереди (S):
S=U2·t1+ U3 ·(t1+t2) + U4 ·(t1+t2+t3)
N
i 1
Задача состоит в том, чтобы
T j определить такой порядок
пропуска судов через шлюз, при
j 1
котором величина S будет
минимальной.
s U i
i 2

5. Математический анализ:

Smin достигается в том случае, если судна пропускаются в
порядке убывания величины U i
Ti
Если T1= T2, U1≠U2, то пропускается вперед судно с более
дорогим простоем
Если U1=U2, T1≠T2, то пропускается вперед судно с более
быстрым шлюзованием
Критерий U
i
убывания
величины Ti
≡
Критерию
Ti
возрастания
Ui
величины

6. Решение в электронных таблицах

Задача.
Пять судов выстроились в очередь к шлюзу в порядке их
прибытия
№ судна
Время
шлюзования(
усл. время)
Ущерб от
простоя(у. е.)
1
45
2
36
3
28
4
24
5
72
5
12
7
4
3
Общий ущерб от простоя:
5
i 1
i 2
j 1
s U i T j =U2·t1+U3·(t1+t2)+U4·(t1+t2+t3)+U5· (t1+t2+t3+t4)
S=1942 усл.ден.ед.(≠min)
С помощью MS Excel найти оптимальный порядок шлюзования судов,
обеспечивающий минимальный ущерб от простоя

7. Задача о двух станках

Постановка задачи:
Имеются два обрабатывающих станка
(токарный и шлифовальный). Требуется
изготовить детали, каждая из которых сначала
обрабатывается на первом станке, а затем на
втором.
Время обработки i-й детали на j-м станке
известно и равно tij. Необходимо выбрать такой
порядок обработки(расписание работы
станков), чтобы полное время Тобщ, затраченное
на изготовление всех деталей, было
минимальным.
Расчет полного времени обработки на двух станках
Требуется изготовить 5 деталей, обрабатывая каждую
поочередно на двух станках.
№ детали
Время вытачивания
Время шлифовки
1
3
6
2
7
2
3
4
7
4
5
3
5
7
4
№
детали
Время окончания
вытачивания детали
Время окончания
шлифовки детали
Время простоя 2-го
станка
1
3
3+6=9
3
2
3+7=10
10+2=12
1
3
10+4=14
14+7=21
2
4
14+5=19
21+3=24
0
5
19+7=26
26+4=30
2
Итого:
30
8

9. Алгоритм решения задачи

Алгоритм Джонсона: расставить очередность
обработки деталей так, чтобы минимизировать время
простоя 2-го станка:
1. Среди всех времен tij выбрать минимальное
значение(если их несколько- взять любое).
2. Если это время обработки на 1-м станке, то
переместить запись в начало списка, иначе – в конец
списка.
3. Исключить эту деталь из рассмотрения и повторить
действия 1 и 2 с оставшимися деталями.
4. После m шагов будет получен оптимальный порядок
обработки деталей.
№
дет
али
1-й
станок
2-й
станок
№
дет
али
1-й
станок
2-й
станок
№
дета
ли
1-й
станок
2-й
станок
1
3
6
1
3
6
1
3
6
2
7
2
3
4
7
2
4
7
3
4
7
4
5
3
4
5
3
4
5
3
5
7
4
5
7
4
5
7
4
2
7
2
2
7
2
Шаг 1
Шаг 2
№
дета
ли
1-й
станок
2-й
станок
№
дета
ли
1-й
станок
2-й
станок
№
дета
ли
1-й
станок
2-й
станок
1
3
6
1
3
6
1
3
6
3
4
7
3
4
7
3
4
7
5
7
4
5
7
4
5
7
4
4
5
3
4
5
3
4
5
3
2
7
2
2
7
2
2
7
2
Шаг 3
Шаг 4
Шаг 5

11. Результат работы алгоритма Джонсона:

№
детал
и
Время окончания
вытачивания
детали
Время простоя
2-го станка
3
Время
окончания
шлифовки
детали
3+6=9
1
3
5
4
3+4=7
7+7=14
14+5=19
9+7=16
16+4=20
20+3=23
0
0
0
2
19+7=26
26+2=28
3
Итого:
28
6
Задание: реализовать алгоритм Джонсона в среде
программирования Паскаль (учебник, стр. 259)
3

12. Задача коммивояжера

В 1859 г. У. Гамильтон придумал игру «Кругосветное
путешествие», состоящую в отыскании такого пути, проходящего
через все вершины (города, пункты назначения) графа, чтобы
посетить каждую вершину однократно и возвратиться в
исходную. Пути, обладающие таким свойством, называются
гамильтоновыми циклами.
На плоскости (в пространстве) расположены N городов, заданы
расстояния между каждой парой городов. Требуется
найти маршрут минимальной длины с посещением каждого
города ровно один раз и с возвращением в исходную точку.
В задаче коммивояжера целевой функцией, которую надо
минимизировать, является стоимость обхода.

13. Постановка задачи коммивояжера

Задача коммивояжера была поставлена в 1934 году. Ее
сущность заключается в поиске оптимального маршрута
движения при необходимости посетить все запланированные объекты
с наименьшими финансовыми и временными издержками. Как
правило, речь идет о простом перемещении по заданным точкам, либо
с перевозкой груза небольшого формата на транспортном средстве.
Задача коммивояжера является одной из знаменитых задач
теории комбинаторики и пользуется популярностью благодаря тому,
что к ней сводится большое количество практических задач.
Среди современных практических приложений задачи можно
выделить: доставку продуктов в магазин со склада, работу почтальона
по разноске корреспонденции, мониторинг объектов (нефтяные
вышки, базовые станции сотовых операторов), изготовление отверстий
на специализированном станке.
Сотруднику компании ООО «Новые технологии» Петрову Н.И.
необходимо обновить программный продукт автоматизированного
учета в пяти организациях: А, Б, В, Г и Д. Он решил начать свой
обход с организации «А», так как она находится на первом этаже
дома, в котором проживает Петров. Сотруднику необходимо,
спланировать свой маршрут таким образом, чтобы к концу рабочего
дня обойти все организации в определенном порядке и выполнив
свою работу, вернутся домой (в пункт «А»). В каком порядке
Петрову следует обходить организации, чтобы его замкнутый тур
был кратчайшим? Расстояния между каждой парой организаций
заданы следующей квадратной матрицей (5×5):
7
5
2
9
7
3
9
1
5
3
4
8
5
6
4
7
6
3
7
7

TSP – эксперт по оптимизации

Задача коммивояжера (TSP)

Человек хочет объехать все города. Путешествие начнется с города, при этом каждый город будет посещен только один раз, и вернется в исходный город после посещения всех городов. Цель состоит в том, чтобы минимизировать расстояние / стоимость поездки.

Задача TSP очень популярна в области информатики. Впервые он был определен в 1800 году. Проблему TSP трудно решить. Это NP-сложная проблема.Это означает, что если есть n городов для путешествия, существует (n-1) факториальных возможностей для последовательности путешествий. Предполагая, что расстояние между двумя городами одинаково для обоих направлений движения, для задачи с 10 городами нужно будет попробовать 9! / 2 или 181 440 комбинаций.

Полную формулировку TSP с удалением суб-тура можно записать следующим образом:

Попробуем решить проблему 10 столиц АСЕАН. Это относительно большая проблема, но благодаря современному мощному вычислительному оборудованию и программному обеспечению мы можем решить ее даже с помощью Excel Solver.

Карта с сайта http://www.freeworldmaps.net/asia/southeastasia/physical.html

Расстояния между городами следующие.

Страна	Капитал	Аэропорт	BWN	PNH	CGK	ВТЕ	KUL	NYT	MNL	SIN	BKK	HAN
Бруней	Bandar Seri Begawan	BWN		1330	1534	1977	1487	2603	1255	1278	1833	2060
Камбоджа	Пномпень	PNH	1330		1975	757	1038	1289	1782	1138	504	1081
Индонезия	Джакарта	CGK	1534	1975		2719	1129	3083	2788	882	2297	3042
Лаос	Вьентьян	ВТЕ	1977	757	2719		1697	694	2007	1857	517	495
Малайзия	Куала-Лумпур	KUL	1487	1038	1129	1697		1970	2490	297	1221	2102
Мьянма	Нейпьидо	NYT	2603	1289	3083	694	1970		2696	2202	819	1016
Филиппины	Манила	MNL	1255	1782	2788	2007	2490	2696		2375	2188	1773
Сингапур	Сингапур	SIN	1278	1138	882	1857	297	2202	2375		1417	2218
Таиланд	Бангкок	BKK	1833	504	2297	517	1221	819	2188	1417		995
Вьетнам	Ханой	HAN	2060	1081	3042	495	2102	1016	1773	2218	995

Мы вводим эти данные в электронную таблицу Excel.Мы также настраиваем прямоугольную область в Excel, которая будет использоваться в качестве переменной решения в модели.

Требуемые рецептуры и названные диапазоны показаны ниже.

Нам нужно включить Excel Solver, прежде чем мы сможем его использовать. В Excel выберите “Файл”, затем “Вариант”. Выберите надстройки. После этого появится менеджер надстроек. Внизу экрана установите переключатель «Перейти» рядом с полем «Управление надстройками Excel». Установите флажок «Надстройка решателя», и решатель будет включен.Чтобы получить доступ к Excel Solver, перейдите в Data, и появится переключатель Solver.

Математические формулировки TSP частично находятся в ячейках электронной таблицы. Нам нужно ввести целевую ячейку, переменные решения и ограничения в диалоговое окно Excel Solver, как показано ниже.

Нажмите «Решить», чтобы получить решение, как показано ниже.

Решение, приведенное выше, может быть представлено графически следующим образом:

Формулировка учебника TSP может быть применена непосредственно для решения реальных задач.В электронной сборке TSP используется для минимизации перемещения сверлильной головки во время сверления печатной платы и времени установки компонентов с помощью машин для поверхностного монтажа. Расширенная версия модели TSP используется транспортными компаниями для определения маршрутов вывоза и доставки автомобилей.

Пожалуйста, отправьте мне электронное письмо, если вы хотите узнать больше об этом и получить модель Excel Solver TSP.

(PDF) Решение задачи коммивояжера с любыми другими ограничениями в MS Excel

423

Параметры решателя следующие.

Установите цель: $ C $ 14 (ячейка с общим пройденным расстоянием) до минимума.

Путем изменения ячеек переменных: $ B $ 10: $ B $ 13 (маршрут следования

посещения городов или магазинов).

С учетом ограничений: $ B $ 10: $ B $ 13 = Все разные

Выберите метод решения: Evolutionary

MS Excel Solver находит решение проблемы. Первоначальный маршрут движения (до использования

Инструмент Решателя использует мощность процессора компьютера для моделирования различных маршрутов

и выбирает тот, расстояние до которого минимально.Если эта задача выполняется вручную, то для четырех городов

необходимо протестировать 24 модели. Количество перестановок четырех чисел вычисляется по формуле

по следующей формуле 4! = 24.

Увеличение количества посещаемых мест увеличивает сложность задачи (до

найти лучший маршрут путешествия) в геометрической прогрессии.

4. Заключение

Задачу коммивояжера можно решить по-разному. Один из самых простых способов

– использовать инструмент Solver в MS Excel.Удовлетворены ограничения на минимальное расстояние проезда и

посещения каждого места один раз. Решение TSP дано как следствие

мест, которые можно посетить.

Увеличение количества посещаемых мест увеличивает сложность задачи (до

найти лучший маршрут путешествия) в геометрической прогрессии. Вот почему с помощью инструмента MS Excel Solver можно легко решить TSP

, не беспокоясь о количестве посещаемых магазинов.

Практическое применение предлагаемого подхода в сфере дистрибуции и

транспортной логистики.Пример, описанный в этой статье, является новаторским. Его могут использовать

других исследователей и бизнес-организаций для расширения своих программных продуктов путем адаптации

предлагаемой технологии.

Ссылки

1. Excel Solver, как целочисленные, двоичные и все разные ограничения влияют на решение. 2015

(http://www.solver.com/excel-solver-how-integer-binary-and-alldifferent-constraints-affect-

решение).

2. Цзян, К. Надежный решатель евклидовой задачи коммивояжера с надстройками MS Excel для небольших систем

.Журнал программного обеспечения, Vol. 5, No. 7, 2010, pp. 761-768

(http://ojs.academypublisher.com/index.php/jsw/article/viewFile/0507761768/1956).

3. Решатель Excel – использование всех других ограничений и эволюционного метода для выбора кратчайшего пути

, который достигает всех клиентов, 2015

(http://blog.excelmasterseries.com/2014/05/solving-traveling-salesman -проблема-with.html).

4. Расмуссен Р. ТСП в таблицах Экскурсия с гидом.Международный обзор экономического образования

(https://www.economicsnetwork.ac.uk/iree/v10n1/rasmussen.pdf).

5. Хармон М. Пошаговая оптимизация с помощью Excel Solver – Мастер статистики Excel. Excel

Master Series, США, 2012 г. (http://dl.acm.org/citation.cfm?id=2361723).

6. Freisen, D. et. al. Модель оптимизации электронных таблиц для решения задач судоку Business

Management Dynamics, Vol.2, No. 9, 2013, pp.15-22

(http: // bmdynamics.com / issue_pdf / bmd110331-% 2015-22.pdf).

Нейронная сеть для решения задач коммивояжера в Excel

Искусственный интеллект в Microsoft Excel: посмотрите, как нейронная сеть решает задачу коммивояжера

869 слов, ~ 4 минуты на чтение

Такие термины, как искусственный интеллект, машинное обучение, глубокое обучение и (искусственные) нейронные сети, в наши дни встречаются повсюду.

Если вы читаете технические новости, блоги по науке о данных или свою ленту на LinkedIn, это будет настоящим чудом, если вы не увидите хотя бы раз одно из этих выражений.

Но это всего лишь возрождение техник. Например, нейронные сети существуют уже много лет. В середине 1990-х (!) Я провел небольшое исследование и написал диссертацию об искусственных нейронных сетях. У нас даже был блог на эту тему 10 лет назад: Где резина встречается с дорогой. По какой-то причине у этой статьи не было много друзей. Мне всегда было интересно, почему. Наверное, слишком академично и недостаточно визуально.

Теперь, с недавним возрождением искусственного интеллекта и нейронных сетей, я решил сделать еще один шанс.Сегодняшний пост представляет собой обновленную, улучшенную версию нейронной сети, решающей задачи коммивояжера в Microsoft Excel.

Вы всегда хотели посмотреть, как нейронная сеть решает задачу оптимизации? Если да, то эта статья для вас. Посмотрите одно из трех видео, представленных в сообщении, или загрузите книгу Excel и поэкспериментируйте с ней на своем собственном темпе. Никаких надстроек или стороннего программного обеспечения не требуется. Все, что вам нужно сделать, это включить макросы.

Алгоритм

Нейронная сеть, представленная сегодня, точно такая же, как в исходном посте (Там, где резина встречается с дорогой).Он основан на статье Ричарда Дурбина и Дэвида Уиллшоу «Аналоговый подход к задаче коммивояжера с использованием метода эластичной сети», опубликованной в журнале Nature в 1987 году.

Не вдаваясь в математические подробности, вот основная идея этого подхода:

Многие другие алгоритмы для решения TSP начинаются с одного возможного решения и пытаются переключиться на лучшие от итерации к итерации (т. Е. С более короткой общей длиной обхода). Подход Дурбина и Уиллшоу отличается: они не начинают с реального решения.Они начинаются с эластичной сети (или адаптивного кольца), то есть круга узлов, где количество узлов кратно количеству городов в TSP. Этот круг постепенно деформируется, пока, наконец, не пройдет через все города и не описывает возможный и короткий тур.

Вы можете думать об этом кольце, как о резиновой ленте. На каждой итерации нейронная сеть случайным образом выбирает город, находит ближайший узел на кольце и тянет узел и его соседей к этому городу. Если вы визуализируете такое поведение алгоритма, это будет выглядеть так, как будто эта резинка деформируется и удлиняется до тех пор, пока не будет найдено допустимое решение.Натяжение резиновой ленты гарантирует, что перетаскивание резиновой ленты соответствует целевой функции TSP, то есть минимизации общей длины маршрута.

Обновленная версия

Как уже было сказано выше, используемый алгоритм точно такой же, как и в исходном посте. Тем не менее, я внес в книгу немало изменений, чтобы упростить работу с моделью и сделать представления более интересными:

Самым очевидным изменением является карта. Вместо того, чтобы показывать общие точки в евклидовом пространстве, сегодняшняя рабочая тетрадь решает задачи коммивояжера по городам США и предоставляет геопространственный контекст с картой США на заднем плане.

Кроме того, я упростил приборную панель:

На панели управления по-прежнему доступны только самые важные пользовательские выборы, и отображается только выборка результатов.

С учетом сказанного, я не только упростил, но и добавил несколько полезных функций:

• С помощью кнопок воспроизведения вы можете запускать, приостанавливать, возобновлять и останавливать алгоритм в любое время
• С помощью двух флажков вы можете решить, будут ли отображаться на карте все города США (т.е. не только TSP) и должны ли отображаться названия городов TSP

В правом нижнем углу панели инструментов четыре диаграммы отображают некоторые ключевые показатели алгоритма во время выполнения:

• столбчатая диаграмма показывает распределение городов, то есть как часто города выбираются случайным образом и обрабатываются во время алгоритма
• три линейных диаграммы визуализируют изменение длины адаптивного кольца, уменьшение скорости обучения и размер радиуса, т.е.е. уменьшающееся количество узлов, перемещаемых по кольцу

Теперь давайте посмотрим на это в действии:

Посмотрите примеры прямо здесь, в видео…

Вот 10 городов ТСП. Алгоритм намеренно замедляется, ожидая 200 миллисекунд после каждого шага, чтобы лучше понять, как работает нейронная сеть:

В следующем видео показано, как решается TSP для 20 городов. Нет времени ожидания, но по-прежнему обновляется экран после каждой итерации:

Наконец, 100 городов ТСП.Представления на панели управления обновляются каждые 50 ^{итераций} :

… или загрузите рабочую тетрадь и посмотрите сами

Заинтересованы не только в просмотре видео, но и в игре с моделью или даже в анализе кода? Вот так:

Загрузить TSP для решения нейронных сетей (книга Excel в архиве, 663 КБ)

Следите за обновлениями.

Глава 5 – Примеры GeneHunter в Excel> Задача коммивояжера

Пример: GHSAMPLE.XLS, рабочий лист TSP

Тип решения: пронумерованные хромосомы

Этот пример находится на вкладке TSP рабочего листа GHSAMPLE.XLS, который был установлен в подкаталог C: \ GENEHUNTER \ EXAMPLES \ EXCEL, если вы выбрали каталог по умолчанию во время установки GeneHunter. (Если вы устанавливаете весь набор программ AI Trilogy, папка GeneHunter является подпапкой C: \ AI Trilogy.)

Задача коммивояжера – хорошо известная задача, которая стала эталонным тестом для сравнения различных вычислительных методов.Ее решение вычислительно сложно, хотя проблема легко выражается. Продавец должен совершить полный закрытый тур по заданному количеству городов. Все города соединены дорогами, и каждый город можно посетить только один раз. GeneHunter решает эту проблему, минимизируя значение в ячейке D23, общую длину тура, и изменяя порядок номеров городов в ячейках B7: B21, регулируемых ячейках. Каждому городу присваивается порядковый номер от 1 до N, где N – количество городов.Названия и номера городов перечислены в диапазоне под названием «Карта» в ячейках B26: E40. Тур представлен в виде всей последовательности городских номеров.

Длина обхода вычисляется с помощью справочной таблицы, расположенной в ячейках h36: V40 в диапазоне с именем «Расстояния». В примере используется функция индекса Excel для массивов в ячейках D7: D21 для вычисления расстояния между каждой парой городов, перечисленных в столбце B. Например, расстояние между двумя номерами городов, указанными в настоящее время в ячейках B7 и B8, вычисляется с помощью следующей функции:

Индекс (расстояния, B7, B8) в ячейке D7

Расстояние между следующими двумя городами будет вычислено в ячейке D8 с помощью функции:

Индекс (расстояния, B8, B9) в ячейке D8

После вычисления расстояний между всеми парами городов (расстояние между последним городом и первым также вычисляется, чтобы замкнуть петлю), все расстояние маршрута суммируется в ячейке D23, ячейке функции пригодности, которая минимизирована.

Рисунок 5.10 Вид рабочего листа командировочного продавца

Рисунок 5.11 Рабочий лист TSP включает диапазон, называемый Карта справа, и диапазон, называемый Расстояниями, слева.

Рисунок 5.12 Вид главного диалогового окна GeneHunter для TSP

GeneHunter использует пронумерованные хромосомы и уникальные гены для решения этой проблемы.В задаче используются пронумерованные хромосомы, а не непрерывные хромосомы, потому что список городов конечен: от 1 до 15. Выбор уникальных генов гарантирует, что каждый город появится только один раз в упорядоченном списке городов для посещения. Для решения проблемы ограничений не требуется.

[PDF] Надежный инструмент для решения евклидовых проблем коммивояжера с надстройками Microsoft Excel для небольших систем

ПОКАЗЫВАЕТ 1-10 ИЗ 12 ССЫЛОК

СОРТИРОВАТЬ ПО Релевантности Статьи, на которые оказывают наибольшее влияниеНедавность

Точное решение больших асимметричных проблем коммивояжера

Результаты показывают, что алгоритм замечательно работает для некоторых классов задач, определяя оптимальное решение даже для задач с большим количеством городов, а для других классов даже небольшие проблемы препятствуют нахождению доказуемо оптимального решения.Развернуть

• Просмотреть 1 отрывок, справочная информация

Решение крупномасштабной задачи коммивояжера

Корпорация RAND в начале 1950-х годов содержала «самую выдающуюся группу математиков, работающих над оптимизацией из когда-либо созданных» [ 6]: Эрроу, Беллман, Данциг, Флад, Форд,… Развернуть

• Просмотреть 1 отрывок, справочная информация

О гамильтоновой игре (задача коммивояжера)

Аннотация: Цель данной заметки – дать метод решения задачи, связанной с задачей коммивояжера.Представляется целесообразным дать описание исходной проблемы. Один… Развернуть

• Просмотреть 1 отрывок, справочная информация

Теория спинового стекла и не только

Эта книга содержит подробное и автономное представление теории реплик спиновых стекол бесконечного диапазона. Авторы также объясняют последние теоретические разработки, уделяя особое внимание… Развернуть

• Просмотреть 1 отрывок, справочная информация

Оптимизация моделирования и программное обеспечение LINDO / LINGO

и Боб Хармель, «Алгоритм использования Excel Solver для решения задач коммивояжера»

• Оптимизационное моделирование и программное обеспечение LINDO / LINGO »
• 2005

Паттерсон и Боб Хармель,« Решение проблем коммивояжера с помощью программного обеспечения платформы Premium Solver »

• Journal of Education for Business
• 2003

An algorithm подход к решению транспортных задач линейного программирования с использованием Microsoft Solver

• Международный журнал бизнес-дисциплин,
• 2002

Задача коммивояжера | Доска сообщений MrExcel

  Функция _
SampleNoReplace _
    (_
        SampleSize As Long, _
        Нижняя граница по длине, _
        Верхняя граница по длине, _
        Необязательный IsStatic As Boolean = False _
    )
    
    Dim PopulationCollection as Collection
    Тусклая ячейка как диапазон
    Тусклый SampleArray, _
        темп до тех пор, пока _
        я до тех пор, _
        j Пока

    Если нет (IsStatic), то Excel.Application.Volatile True
    Рандомизировать
    
    Если верхняя граница <нижняя граница, то
        temp = Верхняя граница
        Верхняя граница = Нижняя граница
        Нижняя граница = температура
    Конец, если
    
    Если (SampleSize> (UpperBound - LowerBound + 1) или SampleSize <= 0), то
        SampleNoReplace = CVErr (xlErrValue)
        Функция выхода
    Конец, если
    
    Установить PopulationCollection = New Collection
    ReDim SampleArray (от 1 до SampleSize) до длины
    
    Для i = от нижней границы до верхней границы
        PopulationCollection.Добавить я
    Далее я
    
    Для i = 1 для SampleSize
        С PopulationCollection
            j = Int (Rnd * .Count) + 1
            SampleArray (i) = .Item (j)
            .Удалите j
        Конец с
    Далее я
    Установить PopulationCollection = Nothing
    
    С Excel.Application
        Если TypeName (.Caller) = "Range", то
            С .Caller
                Если .Cells.Count = 1 Тогда
                    SampleNoReplace = SampleArray
                ElseIf .Rows.Count> 1 и .Columns.Count> 1 Тогда
                    
                    Dim Rws As Long, _
                        Cols As Long, _
                        k Пока, _
                        SampleArrayResize ()
                        
                        Rws =.Rows.Count
                        Cols = .Columns.Count
                        ReDim SampleArrayResize (1 в Rws, 1 в Cols)
                        
                        Для i = 1 до Rws
                            Для j = 1 в столбцы
                                к = к + 1
                                SampleArrayResize (i, j) = SampleArray (k)
                            Следующий j
                        Далее я
                        SampleNoReplace = SampleArrayResize
                        
                ElseIf.Rows.Count> 1 Тогда
                    SampleNoReplace = Excel.Application.Transpose (SampleArray)
                Еще
                    SampleNoReplace = SampleArray
                Конец, если
            Конец с
        Конец, если
    Конец с

    Конечная функция  

Решение некоторых сетевых задач в Excel

Решение некоторых сетевых задач в Excel

Катаргин Н.В. , Финансовый университет при Правительстве Российской Федерации (Москва, Россия)

Полная статья

DOI: 10.34130 / 2070-4992-2019-1-150-159

С. 150–159.

Целью данной работы является разработка методов решения актуальных задач сетевого моделирования. По сути, предлагаются новые алгоритмы решения двух задач в Excel: выбор маршрута в дорожной сети (задача коммивояжера), размещение и подключение к потребителям электрических подстанций с обеспечением минимизации потерь в электрических сетях. Авторы умеют: «краткий план» в задаче выбора маршрута, позволяющий резко сократить количество переменных, варьируемых компьютером, нетривиальное использование сервиса Solver с использованием метода градиентного спуска для варьирования бинарных переменных, а также а также совместное изменение вещественных и двоичных переменных в задаче размещения.Решена проблема появления «островов» в задаче выбора маршрута – узлов, не связанных с основным маршрутом. Алгоритм основан на предотвращении возврата по тому же пути, за исключением особых случаев – звездных маршрутов из некоторых точек. Алгоритмы реализованы в MS Excel, для их использования не требуется программирования, а только заполнение таблиц исходными данными и несложные действия: копирование и суммирование. Выбор маршрута и размещение подстанций апробированы на сетях с 15 узлами, что достаточно для практики.Оптимальные маршруты прокладываются через реальную дорожную сеть, как без возврата в исходную точку, так и по кольцевому маршруту, как в классической задаче коммивояжера. В задаче размещения объектов также используются реальные карты (Яндекс). Проработано два варианта – с ограничением мощности подстанций и без ограничения. Этот алгоритм может быть использован для оптимизации расположения, например, баз топливно-товарных баз. При размещении объектов в узлах дорожной сети их координаты заменяются двоичными переменными с небольшими изменениями алгоритма.Результаты могут быть использованы для практической работы в области транспортной логистики и размещения новых объектов, а также для обучения студентов решению экономических задач с использованием математического моделирования и информационных технологий.

Ключевые слова: моделирование сети, маршрутизация, задача коммивояжера, размещение объектов, электрические розетки, Excel.

Список литературы

1. Дыбская В.В., Зайцев Е.И., Сергеев В.И. Логистика. Полный курс МВА: учебник.Полный курс MBA: учебник. М .: Эксмо, 2008. С. 30–39. (На русском).
2. Экономико-математическое моделирование / Под редакцией И.Н. Дрогобыцкого: учебник [Экономико-математическое моделирование / Под ред. И. Н. Дрогобыцкого: учебник]. М .: Экзамен, 2006.798 с. (На русском языке)
3. Кремер Н. Ш. и другие. Исследование операций в экономике: учебник. М .: Урайт, 2014.424 с. (На русском).
4. Рубчинский А.А. Методы и модели принятия управленческих решений. М .: Урайт, 2015. 111–113. (На русском языке)
5. Решение задачи коммивояжора рекурсивным полным перебором. Доступно на: www.habr.com/ru/post/151151/ (дата обращения: 10.09.2012)
6. Майника Э. Алгоритмы оптимизации на сетях и графах: монография.М .: Мир, 1981, с. 241–264. (На русском).
7. Беллмор М., Немхузер Г. Л., 1968. Задача коммивояжера: обзор. Исследование операций, т. 16, 3: 538–558.
8. Гарфинкель Р., Намхаузер Г. Л., 1972. Целочисленное программирование. Нью-Йорк: John Wiley, Inc., стр: 354–360.
9. Хелд М., Карп Р., 1971. Задача коммивояжера и минимальные остовные деревья, часть II. Математика. Программирование, т. 1, 1: 6–25.
10. Стехан Х. А., 1970. Теорема о симметричных задачах коммивояжера.Исследование операций, т. 18, 6: 1163–1167.
11. Галяутдинов Р. Р. Задача коммивояжора – метод ветвей и границ. (На русском). Доступно на: www.galyautdinov.ru/post/zadacha-kommivoyazhera (дата обращения: 18.11.2013)
12. Cormen, T., Leiserson, C., Rivest, R. Algoritmi. Построение и анализ. Построение и анализ. М .: МЦНМО, 2002. С. 845-846. (На русском).
13. Матай, Р., Сингх, С., Лал, М., 2010. Проблема коммивояжера: обзор приложений, формулировок и подходов к решению. В кн .: Задача коммивояжера, теория и приложения / Под ред. Д. Давендра. InTech, рp: 356.
14. Юнгер, М., Либлинг, Т., Наддеф, Д., Немхаузер, Г., Пуллейбланк, В., Райнельт, Г., Ринальди, Г., Уолси, Л., 2009. 50 лет целочисленного программирования, 1958 –2008: Ранние годы и современные исследования. Гейдельберг: Springer, стр: 785.
15. Кук, W., 2007.История ТСП. Задача коммивояжера. Дата просмотров 20.03.2019 www.math.uwaterloo.ca/tsp/history/index.htm
16. Laporte, G., 1992. Задача коммивояжера: обзор точных и приближенных алгоритмов. Европейский журнал операционных исследований, 59 (2): 231–247.
17. DAA – Задача коммивояжера. Дата просмотра 23.11.2016. www.tutorialspoint.com/design_and_analysis_of_algorithms/design_and_analysis_of_algorithms_travelling_salesman_problem.htm
18. Якобсон, Л.Применение генетического алгоритма к задаче коммивояжера, 2012 г. Дата Просмотры 20.03.2019 www.theprojectspot.com/tutorial-post/applying-a-genetic-algorithm-to-the-travelling-salesman-problem/5

Для цитирования: Катаргин Н.