Задачи метод гаусса: DSpace at Saint Petersburg State University: Invalid Identifier

Error

Sorry, the requested file could not be found

More information about this error

Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2.

The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.

4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1. 1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1. 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.

Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1. 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.

3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2. 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)

Постановка задачи

АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И КОММУНИКАЦИЙ

Кафедра

Автоматизированные системы обработки информации и управления

Курсовая робота на тему:

Астрахань – 2015

информационная часть:

СОДЕРЖАНИЕ содержание собирать в конце из заголовков

Введение

Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнениемпервой степени.

В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.

Решение систем линейных алгебраических уравнений (СЛАУ) является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности – нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.

Данная работа раскрыла вопрос решения систем уравнений, а также определила, как на практике использовать знания из курса “Алгебра и геометрия” для решения задач различного типа. Множество прикладных и чисто математических задач приводят к необходимости решения систем линейных алгебраических уравнений. Без преувеличения можно утверждать, что это одна из важнейших задач вычислительной математики. Значимость задачи породила целый ряд методов ее решения. Среди этих методов есть универсальные и специализированные. Методы отличаются друг от друга эффективностью, требованиями к объемам машинной памяти, закономерностями накопления ошибок в ходе расчетов.

Использование объектно ориентированного программирования Объектно-ориентированные программы – это не просто процедурные программы, переведенные на новый синтаксис. Они должны строится на новой философии разработки. Для них требуется новая стратегия программирования, которую часто бывает трудно освоить . Основная идея ООП: программа состоит из группы объектов, часто связанных между собой.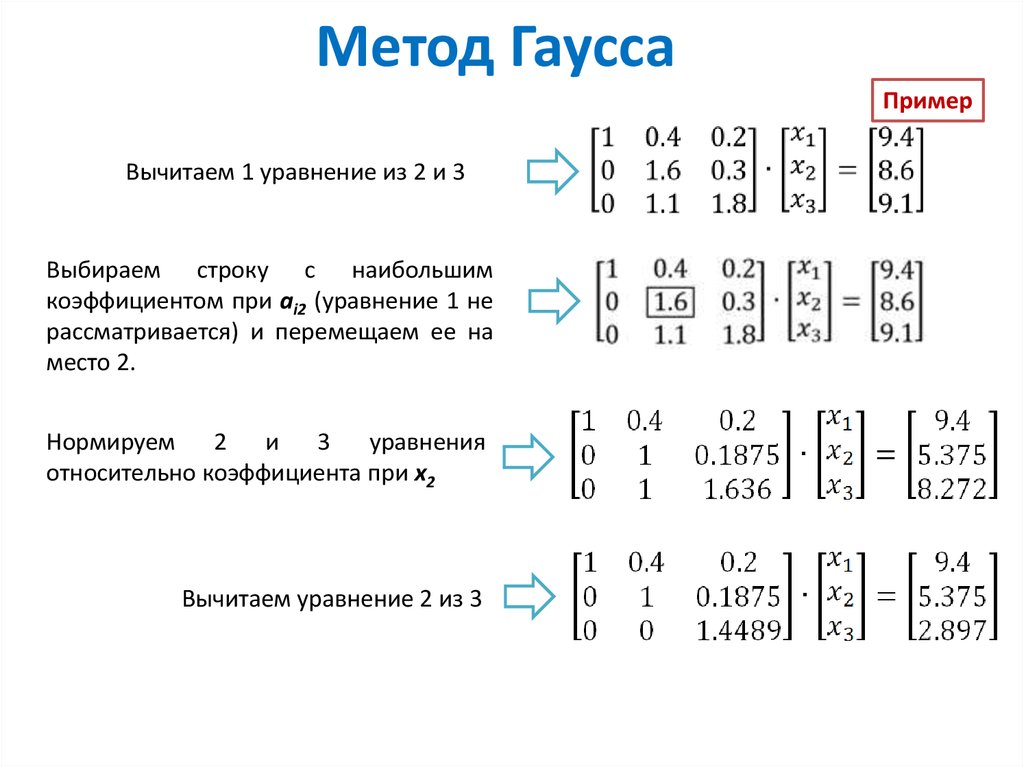 В С++ объекты описываются при помощи нового типа данных class. Класс включает в себя набор переменных (данных) и операций (методов или функций-членов), которые действуют на эти переменные. Полученными объектами можно управлять при помощи сообщений. В ООП объекты включают в себя не только данные (данные-члены), но и методы (функции-члены) воздействия на эти данные. Эти две части в сочетании образуют функциональную единицу программы. Другими словами, объекты содержат данные и методы работы с этими данными. Ниже приведены три основных преимущества объектно-ориентированных программ по сравнению с эквивалентными программами, разработанными сверху вниз. Сопровождение программы. Программы проще читать и понимать, ООП позволяет управлять сложностью программы, оставляя видимыми программисту только существенные детали. Модификация программы (добавление или исключение возможностей). Вы можете часто делать дополнения или исключения в программе, например при работе с базой данных, просто добавляя и исключая объекты. Новые объекты могут наследовать все свойства базовых объектов, необходимо только добавить или убрать отличающиеся свойства. Повторное использование. Можно сохранить грамотно разработанный объект в наборе полезных программ и затем вставить его в новую программу с небольшими изменениями или без изменений. ООП полностью принадлежит к миру С++, поскольку в С нет основного ядра- абстрактного типа данных class Поэтому переписать процедурно-ориентированную программу как объектно-ориентированную гораздо сложнее, чем просто подставить вместо одного ключевого слова другое. ООП представляет собой технику программирования, которая позволяет рассматривать основные идеи как множество объектов. Используя объекты, можно представить задачи, которые необходимо выполнить, их взаимодействие и любые заданные условия, которые должны быть соблюдены. Структура данных часто образует основы объектов; таким образом в С или С++ тип struct может образовывать элементарный объект.

Связь с объектом можно организовать при помощи сообщений. Использование сообщений похоже на вызов функций в процедурно-ориентированной программе. Когда объект получает сообщение, вступают в действие методы, содержащиеся в объекте. Методы (их иногда называют фунциями-членами) аналогичны функциям процедурно-ориентированного программирования. Тем не менее метод является частью объекта, а не чем-то отдельным, как было бы в процедурном аналоге.

С++ -язык предметно-ориентированного программирования. Язык С++ поддерживает процедурную и объектно-ориентированную парадигмы программирования.

Объектно-ориентированное программирование – это новый способ подхода к программированию. Такое программирование, взяв лучшие черты структурного программирования, дополняет его новыми идеями, которые переводят в новое качество подход к созданию программ.

Метод Гаусса при решении системы уравнений можно разделить на два этапа: прямой и обратный ход. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса.

Пусть дана система:

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Последовательно умножая первое уравнение на и складывая с i-м уравнение, исключим из всех уравнений кроме первого. Получим систему

Аналогичным образом из полученной системы исключим . Последовательно, исключая все неизвестные, получим систему треугольного вида

Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все , не равны нулю.

Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.

Метод Гаусса в математическом варианте

1. ищем сначала ненулевой элемент в первом столбце. Если все элементы первого столбца нулевые, то переходим ко второму столбцу, и так далее. Если нашли ненулевой элемент в k-й строке, то при помощи элементарного преобразования первого рода меняем местами первую и k-ю строки, добиваясь того, чтобы первый элемент первой строки был отличен от нуля;

2. используя элементарные преобразования второго рода, обнуляем все элементы первого столбца, начиная со второго элемента. Для этого от строки с номером k вычитаем первую строку, умноженную на коэффициент a_k1/a₁₁ .

3. переходим ко второму столбцу (или j-му, если все элементы первого столбца были нулевыми), и в дальнейшем рассматриваем только часть матрицы, начиная со второй строки и ниже. Снова повторяем пункты 1) и 2) до тех пор, пока не приведем матрицу к ступенчатому виду.

Программистский вариант метода Гаусса

1. индексы строк и столбцов матрицы начинаются с нуля, а не с единицы;

2. недостаточно найти просто ненулевой элемент в столбце. В программировании все действия с вещественными числами производятся приближенно, поэтому можно считать, что точного равенства вещественных чисел вообще не бывает. Некоторые компиляторы даже выдают предупреждения на каждую операцию проверки равенства вещественных чисел. Поэтому вместо проверки на равенство нулю числа a_ij следует сравнивать его абсолютную величину _ij‌ с очень маленьким числом ε (например, ε = 0.00000001). Если _ij‌ =< ε, то следует считать элемент a_ij нулевым;

3. при обнулении элементов j-го столбца, начиная со строки i + 1, мы к k-й строке, где k > i, прибавляем i-ю строку, умноженную на коэффициент

r = -a_kj/a_ij .

Такая схема работает нормально только тогда, когда коэффициент r по абсолютной величине не превосходит единицы. В противном случае, ошибки округления умножаются на большой коэффициент и, таким образом, экспоненциально растут. Математики называют это явление неустойчивостью вычислительной схемы. Если вычислительная схема неустойчива, то полученные с ее помощью результаты не имеют никакого отношения к исходной задаче. В нашем случае схема устойчива, когда коэффициент r = -a_kj/a_ij не превосходит по модулю единицы. Для этого должно выполняться неравенство Отсюда следует, что при поиске разрешающего элемента в j-м столбце необходимо найти не первый попавшийся ненулевой элемент, а максимальный по абсолютной величине. Если он по модулю не превосходит ε, то считаем, что все элементы столбца нулевые; иначе меняем местами строки, ставя его на вершину столбца, и затем обнуляем столбец элементарными преобразованиями второго рода.

Основная идея метода Гаусса- привести матрицу систему к диагональному виду, то есть все элементы главной диагонали –нули. Для приведения матрицы к такому виду, мы выбираем самую верхнюю строку матрицы, и вычитаем её из всех остальных строк, умножив её для каждой строки на некий коэффициент, так, что самый левый столбец ниже главной диагонали заполнен нулями. Вычитаемая с коэффициентом строка называется текущей строкой. Выбирая текущую строку вначале верхнюю, а потом всё ниже и ниже, мы добьёмся, что все элементы ниже главной диагонали будет равны нулю. Эту часть метода- обработка строк по текущей строке и предстоит распараллеливать.

Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a₁₁ ≠ 0, затем: 1) умножим на а₂₁ и вычтем из второго уравнения 2) умножим на а₃₁ и вычтем из третьего уравнения и т.д. Получим:

,

где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1.

d_ij = a_ij – a_i1d_1j

i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т. д.

Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы.

А* =

Таким образом, исходная система может быть представлена в виде:

,

откуда получаем:x₃ = 2;x₂ = 5;x₁= 1.

Вопросы и ответы по методу исключения Гаусса

Этот набор вопросов и ответов с множественным выбором численного анализа (MCQ) фокусируется на «Методе исключения Гаусса — 1».

1. Решите следующие уравнения методом исключения Гаусса.

 х+4y-z = -5
х+у-6z = -12
3x-y-z = 4
 

а) х = 1,64791, у = 1,14085, z = 2,08451
б) х = 1,65791, у = 1,14185, z = 2,08441
в) х = 1,64691, у = 1,14095, 86 = 1 2,
d) x = 1,64491, y = 1,15085, z = 2,09451
Просмотреть ответ

Ответ: a
Объяснение: Методом исключения Гаусса мы получаем
\(\begin{bmatrix}
1 & 4 & -1\\
1 & 1 & -6\\
3 & -1 & -1\\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix} \) = \( \begin{bmatrix}
-5\\
-12\\
4\\
\end{bmatrix} \)

По R ₂ -R ₁ и R ₃ -3R ₁
\(\begin{bmatrix}
1 & 4 & -1\\
0 & -3 & -5\\
0 & -13 & 2\\
\end{bmatrix} \) \( \begin{ bmatrix}
x\\
y\\
z\\
\end{bmatrix}\) = \( \begin{bmatrix}
-5\\
-7\\
19\\
\end{bmatrix} \)

Примечание: присоединяйтесь к бесплатным занятиям по санфаянсу в Telegram или на Youtube 4. 0000 и -1.0000\\
0 & -3.0000 & -5.0000\\
0 & 0 & 23.6667\\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix }\) = \( \begin{bmatrix}
-5\\
-7\\
49,33333\\
\end{bmatrix} \)

x+4y-z = -5
-3y-5z = – 7
23,6667z = 49,3333
Следовательно, z = 2,08451
-3y = -7+5z
Следовательно, y = -1,14085
x = -4y+z-5
Следовательно, x = 1,64791.

2. Найдите значения x, y, z в следующей системе уравнений методом исключения Гаусса.

 2x + у – 3z = -10
-2у + г = -2
г = 6
 

а) 2, 4, 6
б) 2, 7, 6
в) 3, 4, 6
г) 2, 4, 5
\(\begin{bmatrix}
2 & 1 & -3\\
0 & -2 & 1\\
0 & 0 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}\) = \( \begin{bmatrix}
-10\\
-2\\
6\\
\end{bmatrix} \)
z = 6.
-2y+z = -2
Отсюда y = 4.
2x + y – 3z = -10
Отсюда z = 6.

3. Решить данную систему уравнений методом исключения Гаусса метод.

 3x + 4y – z = -6
-2г + 10г = -8
4у – 2з = -2
 

а) (-2, -1, -1)
б) (-1, -2, -1)
в) (-1, -1, -2)
г) (-1, -1, -1)
Посмотреть ответ

Ответ: d
Объяснение: Здесь
\(\begin{bmatrix}
3 & 4 & -1\\
0 & -2 & 10\\
0 & 4 & -2\\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}\) = \( \begin{ bmatrix}
-6\\
-8\\
-2\\
\end{bmatrix} \)
Матрица почти представляет собой треугольную матрицу. Умножая строку 2 на 2 и добавляя ее к строке 3, мы получаем верхнюю треугольную матрицу с
x, y, z = (-1, -1, -1).

реклама

4. Следующая система уравнений имеет:

 x – y – z = 4
2x - 2y - 2z = 8
5х – 5у – 5з = ​​20
 

a) Единственное решение
b) Нет решения
c) Бесконечное множество решений
d) Конечные решения
Просмотреть ответ

Ответ: c
Объяснение: Умножение строки 1 на -2, затем добавление строки 1 и строки 2 1-й строки матрицы уменьшается на 0.
\(\begin{bmatrix}
0 & 0 & 0\\
2 & -2 & -2\\
5 & -5 & -5 \\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}\) = \( \begin{bmatrix}
0\\
8\\
20\\
\end{bmatrix} \)
Следовательно, решений бесконечно много.

5. Решите эту систему уравнений и прокомментируйте характер решения, используя метод исключения Гаусса.

 х + у + г = 0
-х – у + 3z = 3
-х – у – г = 2
 

a) Единственное решение
b) Нет решения
c) Бесконечное множество решений
d) Конечные решения
Просмотреть ответ

Ответ: b
Объяснение: Методом исключения Гаусса мы складываем строки 1 и строки 3, чтобы получить следующую матрицу
\(\begin{bmatrix}
1 & 1 & 1\\
-1 & -1 & 3\\
0 & 0 & 0\\
\end{bmatrix} \) \( \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}\) = \( \begin{bmatrix}
0\\
3\\
2\\
\end{bmatrix} \)

Следовательно, матрица не имеет решений, так как 0 ≠ 2.

6. Целью шагов исключения в методе исключения Гаусса является уменьшение матрицы коэффициентов до ____________
a) диагональ
b) тождество
c) нижний треугольник
d) верхнетреугольная
Просмотреть ответ

Ответ: d
Объяснение: В методе исключения Гаусса мы склонны сводить данную матрицу к верхнетреугольной матрице, чтобы найти x, y, z.

7. Деление на ноль при исключении по Гауссу системы уравнений [A] * [X]=[C] означает, что матрица коэффициентов [A] ____________
a) Обратимая
b) Несингулярная
c) Неопределяемая быть в единственном или не в единственном числе
d) Единственное число
Посмотреть ответ

Ответ: c
Объяснение: Деление на ноль в методе исключения Гаусса не связано с тем, является ли матрица вырожденной или нет.

8. В каком из следующих случаев обе части уравнения умножаются на ненулевую константу?
a) Метод исключения Гаусса
b) Несогласованная процедура Гаусса
c) Согласованная процедура Гаусса
d) Процедура замены Гаусса
View Answer

Ответ: a
нулевая постоянная. Затем матрица сводится к верхней треугольной матрице, чтобы получить значения соответствующих переменных.

9. В методе исключения Гаусса исходные уравнения преобразуются с помощью _____________
a) Операции со столбцами
b) Операции со строками
c) Математические операции
d) Операции с подмножествами
View Answer

Ответ: b
Объяснение: Операции со строками используется в методе исключения Гаусса, чтобы свести матрицу к верхней треугольной матрице и, таким образом, найти x, y, z.

10. Следующая информация касается скорости и времени транспортного средства. Он управляет квадратным уравнением v(t)=at ² +bt+c. Следовательно, найдите матрицу, которая наиболее точно представляет уравнение.

Т	с	0	14	15	20	30	35
В	м/с	0	227.04	362,78	517,35	602,97	901,67

а) \(\begin{bmatrix}
176 и 14 и 1\\
225 и 15 и 1\\
400 & 20 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}\) = \( \begin{bmatrix }
227. 04\\
362.78\\
517.35\\
\end{bmatrix} \)
b) \(\begin{bmatrix}
225 & 15 & 1\\
400 & 20 & 1\\

30 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}\) = \( \begin{bmatrix}
362,78 \\
517,35\\
602,97\\
\end{bmatrix} \)
c) \(\begin{bmatrix}
0 & 0 & 1\\
225 & 15 & 1\\
400 & 20 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}\) = \( \begin{bmatrix}
0\\
362,78\\
517,35\\
\end{bmatrix} \)
d) \(\begin{bmatrix}
400 & 20 & 1\\
900 & 30 & 1\\
1225 & 35 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}\) = \( \begin{bmatrix}
517.35\\
602.97\\
901.67\\
\end{bmatrix} \)
Просмотреть ответ

Ответ: b
Объяснение: Точки, ближайшие к t=21 сек, равны 15, 20, 30
3 V(t
0 ) = 362,78 м/с = a(15) ² +b(15)+c
V(t ₁ ) = 517,35 м/с = a(20) ² +b(20)+ c
V(t ₂ ) = 602,97 м/с = a(30) ² +b(30)+c
Следовательно,
225a+15b+c = 362,78
400a+20b+c = 517,39
+30b+c = 602,97
Что приводит нас к \(\begin{bmatrix}
225 & 15 & 1\\
400 & 20 & 1\\
900 & 30 & 1\\
\end{bmatrix} \) \( \begin{bmatrix}
a\\
b\\
c\ \
\end{bmatrix}\) = \( \begin{bmatrix}
362,78\\
517,35\\
602,97\\
\end{bmatrix} \).

11. Процесс исключения в методе исключения Гаусса также известен как _____________
a) Исключение вперед
b) Исключение назад
c) Исключение в боковом направлении
d) Исключение в поперечном направлении
Просмотреть ответ

Ответ: a
Объяснение: Процесс исключения в методе исключения Гаусса также известен как прямое исключение. В этом методе матрица сводится к верхней треугольной матрице.

12. Сокращенная форма Матричного метода исключения Гаусса также называется ____________
a) Эшелонная форма столбца
b) Эшелонная форма столбца-столбца
c) Эшелонная форма столбца-строки
d) Эшелонная форма строки
Посмотреть ответ

Ответ: d
Объяснение: Сокращенная форма матрицы в методе исключения Гаусса называется формой эшелонирования строк. Это сказано потому, что в методе исключения Гаусса учитываются только операции со строками.

Sanfoundry Global Education & Learning Series – Численные методы.

Чтобы попрактиковаться во всех областях численных методов, здесь есть полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .

Категории Численные методы MCQ

реклама

реклама

Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест

Маниш Бходжасиа, ветеран технологий с более чем 20-летним стажем работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.

Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.

7b- Практические задачи на исключение Гаусса Жордана.

Содержание

1. Практические задачи на исключение Гаусса Жордана.
   • Практические задачи для Гаусса Джордана. Первая практическая задача исключения.
   • Практические задачи на исключение Гаусса Жордана — используйте a11 в качестве точки опоры, чтобы исключить a21 и a31.
   • Используйте a22 в качестве точки опоры, чтобы исключить a32.
   • Используйте a33 в качестве точки опоры, чтобы исключить a23 и a13.
   • Используйте a22 в качестве точки опоры, чтобы исключить a12.
   • Практические задачи для второй практической задачи исключения Гаусса Жордана.
   • Используйте a22 в качестве точки опоры, чтобы исключить a32.
   • Используйте a33 в качестве точки опоры, чтобы исключить a23&a13.

Практические задачи для Гаусса Джордана – первая практическая задача исключения.

Мы введем практическую задачу исключения Гаусса-Жордана, или упрощенную форму эшелона. Практическая задача № 33 взята из книги Стюарта «Алгебра для колледжей».

Для первой практической задачи №33 на исключение Гаусса Жордана. Решите следующие системы линейных уравнений.

Вы можете щелкнуть любое изображение, чтобы увеличить его, затем нажать маленькую стрелку справа, чтобы просмотреть все остальные изображения в виде слайд-шоу.

Детали данной матрицы для практического задания №33 показаны на следующем слайде.

Практические задачи на исключение Гаусса Жордана — используйте a11 в качестве точки опоры, чтобы исключить a21 и a31.

Для данной системы линейных уравнений мы запишем эти уравнения в расширенной форме

Мы введем вертикальную черту между третьим столбцом и четвертым столбцом, чтобы показать расширенную матрицу. Следующий шаг — сделать a21 или вторую строку/первый столбец равными нулю. Убедитесь, что элемент a11 равен 1 , затем добавьте (-a21/a11)*R1 к строке2, чтобы получить нулевое значение. В этом процессе мы рассматриваем a11 как опорный элемент.

Аналогично, пусть a31 или третья строка/первый столбец равны нулю. Это делается путем добавления (-a31/a11)*R1 к строке 3, чтобы получить нулевое значение. Опять же, в этом процессе мы рассматриваем a11 как опорный элемент.

продолжить операции со строками. Убедитесь, что элемент а22 равен 1, это делается путем умножения строки 2 на (-1/2).

Используйте a22 в качестве точки опоры, чтобы исключить a32.

Используйте a22 в качестве опорной, добавив R3 к -(a23/a21)*R2. Выполните операцию со строками, чтобы получить форму редуцированного эшелона или просто верхнюю матрицу с тремя единицами по диагонали.

Обратитесь к изображению слайда, чтобы проверить необходимые операции со строками, чтобы получить сокращенную ступенчатую форму исключения Гаусса.

Используйте a33 в качестве точки опоры, чтобы исключить a23 и a13.

Наша цель — преобразовать матрицу в диагональную матрицу единиц. Мы будем использовать элемент a33, чтобы исключить a23, это делается добавлением (-a23/a33)*R3 к R2.

Точно так же мы используем элемент a33, чтобы исключить a13, это делается путем добавления (-a13/a33)*R3 к R1, чтобы получить нулевое значение. Опять же, в этом процессе мы рассматриваем a33 как опорный элемент.

Используйте a22 в качестве точки опоры, чтобы исключить a12.

Мы будем использовать элемент a22, чтобы исключить a12, это делается добавлением (-a12/a22)*R2 к R1.

Теперь мы получили требуемую матрицу диагоналей с 1 на диагоналях, пожалуйста, обратитесь к следующему слайду для наглядности.

Затем мы можем получить значения Z=1&Y=0 и X=-1. В этом методе нам не нужно делать обратные замены.

Важно проверить значения X, Y и Z в любой из трех систем уравнений, чтобы убедиться в точности решения.

Практические задачи для второй практической задачи исключения Гаусса Жордана.

1-Для второй практической задачи №38 на исключение Гаусса Жордана. Решите следующие системы линейных уравнений.

Детали данной матрицы для практического задания №38 показаны на следующем слайде.

Для данной системы линейных уравнений запишем эти уравнения в расширенной форме

Мы введем вертикальную линию между третьим столбцом и четвертым столбцом, чтобы показать расширенную матрицу. Следующий шаг — сделать a21 или вторую строку/первый столбец равными нулю. Убедитесь, что элемент a11 равен 1 . Сначала мы разделим первую строку на 10. Мы добавим (-a21/a11)*R1 к строке2, чтобы получить нулевое значение. В этом процессе мы рассматриваем a11 как опорный элемент.

Аналогично, пусть a31 или третья строка/первый столбец равны нулю. Это делается путем добавления (-a31/a11)*R1 к строке 3, чтобы получить нулевое значение. Опять же, в этом процессе мы рассматриваем a11 как опорный элемент.

Используйте a22 в качестве точки опоры, чтобы исключить a32.

Сначала разделите R2 на 5, чтобы осевая точка a22 равнялась 1; также разделите r3/5, чтобы минимизировать числа.

Используйте a22 в качестве опорной, добавив R3 к -(a23/a21)*R2. Разделите r3 на 7, чтобы a33=1.

Выполните операцию со строками, чтобы получить уменьшенную форму эшелона или просто верхнюю матрицу с тремя единицами по диагонали.

Используйте a33 в качестве точки опоры, чтобы исключить a23&a13.

Наша цель — преобразовать матрицу в диагональную матрицу единиц. Мы будем использовать элемент a33, чтобы исключить a23, это делается добавлением (-a23/a33)*R3 к R2.

Точно так же мы используем элемент a33, чтобы исключить a13; это делается путем добавления (-a13/a33)*R3 к R1, чтобы получить нулевое значение. Опять же, в этом процессе мы рассматриваем a33 как опорный элемент.

Теперь мы получили требуемую матрицу диагоналей с 1 на диагоналях, пожалуйста, обратитесь к следующему слайду для наглядности.

Затем мы можем получить значения Z=-2&Y=1 и X=+1. В этом методе нам не нужно делать обратные замены.

Важно проверить значения X, Y и Z в любой из трех систем уравнений, чтобы убедиться, что решение точное.