Задачи на метод гаусса: Решение систем линейных уравнений методом Гаусса

Метод Гаусса – примеры c решением, теоремы и формулы

Метод Гаусса – идеальный вариант для решения систем линейных алгебраических уравнений (далее СЛАУ). Благодаря методу Гаусса можно последовательно исключать неизвестные путём элементарных преобразований. Метод Гаусса – это классический метод решения СЛАУ, который и рассмотрен ниже.

Карл Фридрих Гаусс – немецкий математик, основатель одноименного метода решения СЛАУ

Карл Фридрих Гаусс – был известным великим математиком и его в своё время признали «королём математики». Хотя название «метод Гаусса» является общепринятым, Гаусс не является его автором: метод Гаусса был известен задолго до него. Первое его описание имеется в китайском трактате «Математика в девяти книгах», который составлен между II в. до н. э. и I в. н. э. и представляет собой компиляцию более ранних трудов, написанных примерно в X в. до н. э.

Метод Гаусса – последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений.

Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках (плюсы и минусы). Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Определения и обозначения

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения.

Для начала систематизируем знания о системах линейных уравнений.

Обратите внимание!

СЛАУ в зависимости от её элементов может иметь:

1. Одно решение;
2. много решений;
3. совсем не иметь решений.

В первых двух случаях СЛАУ называется совместимой, а в третьем случае – несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой.

Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений. Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:

• перемена мест уравнений системы;
• почленное умножение обеих частей на одно из уравнений на некоторое число, так, чтобы коэффициенты при первой переменной в двух уравнениях были противоположными числами;
• сложение к обеим частям одного из уравнений определённых частей другого уравнения.

Итак, когда мы знаем основные правила и обозначения, можно приступать к решению.

Теперь рассмотрим, как решаются системы методом Гаусса на простом примере:

   

где а, в, с  – заданные коэффициенты, d – заданные свободные члены, x, y, z – неизвестные. Коэффициенты и свободные члены уравнения можно называть его элементами.

Если = = = , тогда система линейных алгебраических уравнений называется однородной, в другом случае – неоднородной.

Множественные числа , , называются решением СЛАУ, если при подстановке , , в СЛАУ получим числовые тождества.

Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:

– это основная матрица СЛАУ.

– матрица столбец неизвестных переменных.

– матрица столбец свободных членов.

Если к основной матрице добавить в качестве – ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений. Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов. То есть, расширенная матрица выглядит так:

Если квадратная матрица равна нулю, она называется вырожденная, а если – матрица невырожденная.

Обратите внимание!

Если с системой уравнений:          

Произвести такие действия:

• умножать обе части любого из уравнений на произвольное и отличное от нуля число ;
• менять местами уравнения;
• к обеим частям любого из уравнений прибавить определённые части другого уравнения, которые умножаются на произвольное число ,

тогда получается эквивалентная система, у которой такое же решение или нет решений совсем.

Теперь можно перейти непосредственно к методу Гаусса.

Простейшие преобразования элементов матрицы

Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:

Из уравнения запишем расширенную матрицу:

Из данной матрицы видно, по какому принципу она записана. Вертикальную черту не обязательно ставить, но просто так удобнее решать систему.

Определение

Матрица системы – это матрица, которая составляется исключительно с коэффициентами при неизвестных. Что касается расширенной матрицы системы, так, это такая матрица, в которой кроме коэффициентов записаны ещё и свободные члены. Любую из этих матриц называют просто матрицей.

На матрице, которая написана выше рассмотрим, какие существуют элементарные преобразования:

1. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:

.

2. Если в матрице имеются (или появились) пропорциональные строки (одинаковые), тогда необходимо оставить всего лишь одну строку, а остальные убрать (удалить).

3. Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять.

4. Строку матрицы можно умножать (делить) на любое число, которое отличное от нуля.

Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу.

5. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов. Для этого возьмём изначальную нашу матрицу:

Для удобства умножаем первую строку на (-3):

Теперь ко второй строке прибавляем первую строку, которую умножали на -3. Вот что у нас получается:

В итоге получилось такое преобразование:

Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:

В матрице верхняя строка преобразовалась:

Первую строку делим на и преобразовалась нижняя строка:

И верхнюю строку поделили на то же самое число :

Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась. ВСЕГДА меняется только та строка, к которой прибавляются коэффициенты.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:

.

Обратите внимание!

Если в примере приведены десятичные дроби, метод Гаусса в этом случае также поможет решить систему линейных алгебраических уравнений. Однако, не стоит забывать, что следует избегать приближённых вычислений, так как ответ будет неверным. Лучше всего использовать десятичные дроби, а от них переходить к обыкновенным дробям.

Алгоритм решения методом Гаусса пошагово

После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:

Шаг 1. Переписываем систему в виде матрицы

Записываем матрицу:

Шаг 2. Преобразовываем матрицу: вторую строку в первом столбце приводим к нулю

Как мы привели вторую строку в первом столбце к нулю описано выше.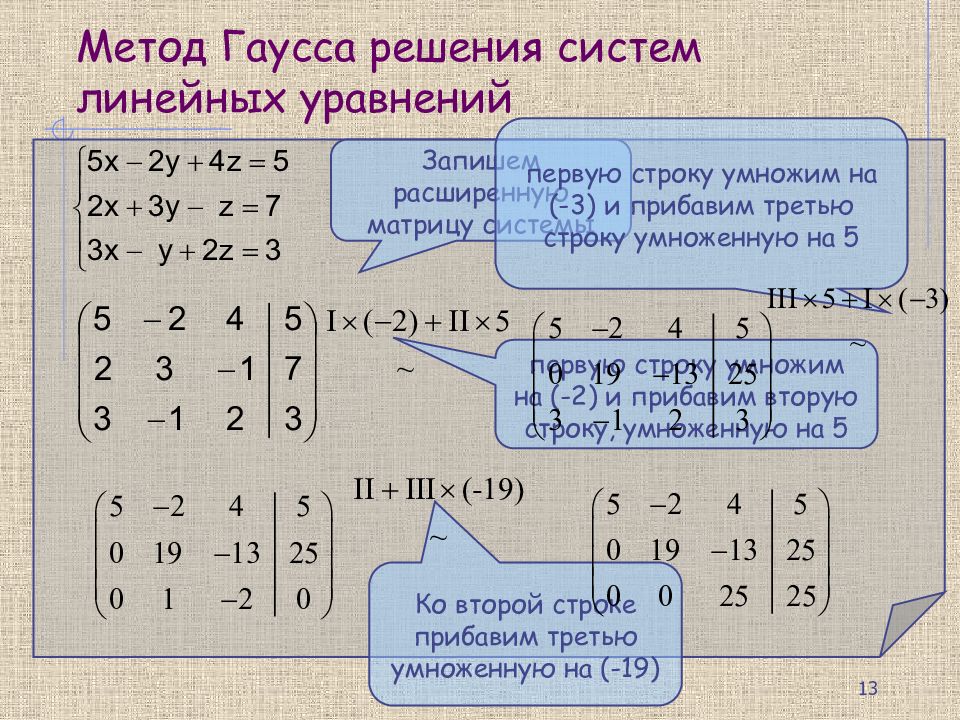

Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на .

Шаг 3. Приводим матрицу к ступенчатому виду

Теперь вторую строку можно поделить на 2 и получается:

Верхнюю строку делим на и приводим матрицу к ступенчатому виду:

Когда оформляют задание, так и отчёркивают простым карандашом для упрощения работы, а также обводят те числа, которые стоят на “ступеньках”. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид. Как правило, математики такой вид называют трапециевидным или треугольным.

Шаг 4. Записываем эквивалентную систему

После наших элементарных преобразований получилась эквивалентная система:

Шаг 5. Производим проверку (решение системы обратным путём)

Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки.:

находим : ,

,

.

После находим :

,

.

Тогда:

.

Как видим, уравнение решено правильно, так как ответы в системе совпадают.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица невырожденная, а количество в ней неизвестных равняется количеству уравнений

Как мы уже упоминали, невырожденная матрица бывает тогда, когда . Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом.

Дана система уравнений:

Для начала нужно решить первое уравнение системы относительно неизвестной переменной . Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную.

Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение.. Это нужно для того, чтобы исключить неизвестную переменную :

Из последнего, третьего уравнения мы видим, что . Из второго уравнения находим . И последнее, находим первое уравнение .

Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют – прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса.

Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:

• берём второе уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на ,
• берём третье уравнение и к его левой и правой частям прибавляем определённые части из первого уравнения, которые умножаются на .

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:

Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:

В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений. В таком случае выход есть. Нужно всего лишь уравнения переставить местами.

Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно.

В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение.

Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать (исключить) из остальных уравнений в системе. Вот и весь принцип работы с такими, на первый взгляд, сложными системами.

Решение систем линейных уравнений методом Гаусса, в которых основная матрица вырожденная, а количество в ней неизвестных не совпадает с количеством уравнений

Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:

1. На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества . В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса.

Например, вам попалась подобная система:

У нас получается такая ситуация

Как видим, второе уравнение . Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности.

Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.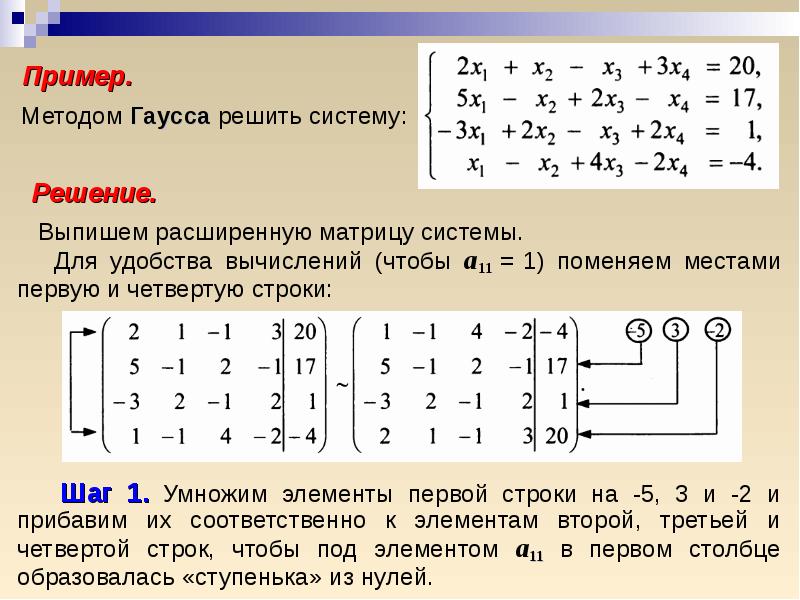

2. При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где – число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных. То есть, можно выразить по-другому. Если уравнение приняло  вид, значит система несовместна, то есть, не имеет решений. Рассмотрим на примере:

Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части (левую и правую) первого уравнения, которые соответственно, умножаются на (-1), (-2), (-3). Получается:

В третьем уравнении получилось равенство . Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений.

3. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной . Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной . Если же  уже исключались, тогда переходим к ,  и т. д.

Рассмотрим систему уравнений на таком этапе, когда уже исключилась переменная :

Такая система уравнений после преобразования выглядит так:

Вы наверное уже обратили внимание, что вместе с исключились и . Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:

Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:

Допусти, что система уравнений стала:

В этой системе нет ни одного уравнения, которое бы сводилось к . В данном случае можно было бы говорить о несовместности системы. Дальше непонятно, что же делать? Выход есть всегда. Для начала нужно выписать все неизвестные, которые стоят на первом месте в системе:

В нашем примере это , и . В левой части системы оставим только неизвестные, которые выделены зелёным квадратом а в правую перенесём известные числа, но с противоположным знаком. Посмотрите на примере, как это выглядит:

Можно придать неизвестным переменным с правой части уравнений свободные (произвольные) значения: , , , где , ,  – произвольные числа.

Теперь в правых частях уравнений нашей системы имеются числа и можно приступать к обратному ходу решения методом Гаусса.

В последнем уравнении системы получилось: , и теперь мы легко найдём решение в предпоследнем уравнении: , а из первого уравнения получаем:

= =

В итоге, получился результат, который можно и записать.

Ответ

,

,

,

,

,

.

Примеры решения методом Гаусса

Выше мы подробно расписали решение системы методом Гаусса. Чтобы закрепить материал, решим несколько примеров, в которых опять нам поможет метод Гаусса. Соответственно, начнём с самой простой системы.

Пример 1

Задача 

Решить систему линейных алгебраических уравнений методом Гаусса:

Решение

Выписываем матрицу, куда добавляем столбец свободных членов:

Прежде всего мы смотрим на элемент, который находится в матрице в левом верхнем углу (первая строка, первый столбец). Для наглядности выделим цифру зелёным квадратом. На этом месте практически всегда стоит единица:

Так как мы должны использовать подходящее элементарное преобразование строк и сделать так, чтобы элемент, который находится в матрице под выделенной цифрой превратился в . Для этого можно ко второй строке прибавить первую строку и умножить на .Однако, не сильно хочется работать с дробями, поэтому давайте постараемся этого избежать. Для этого нужно вторую строку умножить на (разрешающий элемент данного шага).

Соответственно, первая строка остаётся неизменной, а вторая поменяется:

Подбираем такое элементарное преобразование строк, чтобы во второй строке в первом столбце образовался . Для этого первую строку нужно умножить на и только после этого ко второй строке прибавить изменённую после умножения на вторую строку. Вот что получилось:

. Теперь прибавляем со второй строки первую строку . У нас получился , который записываем во вторую строку в первый столбец. Также решаем и остальные элементы матрицы. Вот что у нас получилось:

Как всегда у нас первая строка осталась без изменений, а вторая с новыми числами.

Итак, у нас получился ступенчатый вид матрицы:

Записываем новую систему уравнений:

Для проверки решаем систему обратным ходом. Для этого находим сначала :

Так как найден, находим :

.

Подставляем в изначальную нашу систему уравнений найденные и :

и .

Как видите из решения, система уравнений решена верно. Запишем ответ.

Ответ

Выше мы решали систему уравнений в двумя неизвестными, а теперь рассмотрим систему уравнений с тремя неизвестными.

Пример 2

Задача

Решить систему уравнений методом Гаусса:

Решение

Составляем матрицу, куда вписываем и свободные члены:

Что нам надо? Чтобы вместо цифры 2 появился 0. Для этого подбираем ближайшее число. Например, можно взять цифру -2 и на неё перемножить все элементы первой строки. Значит, умножаем , а потом прибавляем, при этом задействуем вторую строку: . В итоге у нас получился нуль, который записываем во вторую строку в первый столбец. Затем , и . Аналогично, и . И умножаем свободный член . Так и запишем следующую матрицу. Не забывайте, что первая строка остаётся без изменений:

Дальше необходимо проделать те же самые действия по отношению к третьей строке. То есть, первую строку нужно умножать не на (-2), а на цифру 3, так как и в третьей строке нужно коэффициенты привести у нулю. Также первую строку умножаем на 3 и прибавляем третью строку. Получается так:

Теперь нужно обнулить элемент 7, который стоит в третьей строке во втором столбце. Для этого выбираем цифру (-7) и проделываем те же действия. Однако, необходимо задействовать вторую строку. То есть, вторую строку умножаем на (-7) и прибавляем с третьей строкой. Итак, . Записываем результат в третью строку. Такие же действия проделываем и с остальными элементами. Получается новая матрица:

В результате получилась ступенчатая система уравнений:

Сначала находим : ,

.

Обратный ход:

Итак, уравнение системы решено верно.

Ответ

,

,

.

Пример 3

Система с четырьмя неизвестными более сложная, так как в ней легко запутаться. Попробуем решить такую систему уравнений.

Задача

Решите систему уравнений методом Гаусса:

Решение                                                                

В уравнении , то есть – ведущий член и пусть  ≠ 0

Из данного уравнения составим расширенную матрицу:

Теперь нужно умножить последние три строки (вторую, третью и четвёртую) на: , , . Затем прибавим полученный результат ко второй, третьей и четвёртой строкам исключаем переменную из каждой строки, начиная не с первой, а не со второй. Посмотрите, как изменилась наша новая матрица и в теперь стоит 0.

Поменяем вторую и третью строку местами и получим:

Получилось так, что = b и тогда, умножая вторую строку на (-7/4) и результат данной строки, прибавляя к четвёртой, можно исключить переменную из третьей и четвёртой строк:

Получилась такая матрица:

Также, учитывая, что  = , умножим третью строку на: 13,5/8 = 27/16, и, полученный результат прибавим к четвёртой, чтобы исключить переменную и получаем новую систему уравнений:

Теперь необходимо решить уравнение обратным ходом и найдём из последнего, четвёртого уравнения ,

из третьего: = = =

второе уравнение находим: = = = 2,

из первого уравнения: = .

Значит, решение системы такое: (1, 2, -1, -2).

Ответ

,

,

,

.

Добавим ещё несколько примеров для закрепления материла, но без такого подробного описания, как предыдущие системы уравнений.

Пример 4

Задача

Решить систему уравнений методом Гаусса:

Решение

Записываем расширенную матрицу системы:

Сначала смотрим на левое верхнее число:

Как выше уже было сказано, на этом месте должна стоять единица, но не обязательно. Производим такие действия: первую строку умножаем на -3, а потом ко второй строке прибавляем первую:

 

Производим следующие действия: первую строку умножаем на -1. Затем к третьей строки прибавляем вторую:

Теперь вторую строку умножаем на 1, а затем к третьей строке прибавляем вторую:

Получился ступенчатый вид уравнения:

Проверяем:

,

,

,

,

.

.

  Ответ

,

,

.

Заключение

Итак, вы видите, что метод Гаусса – интересный и простой способ решения систем линейных алгебраических уравнений. Путём элементарных преобразований нужно из системы исключать неизвестные переменные, чтобы систему превратить в ступенчатый вид. Данный метод удобен тем, что всегда можно проверить, правильно ли решено уравнение. Нужно просто подставить найденные неизвестные в изначальную систему уравнений.

Если элементы определителя не равняются нулю, тогда лучше обратиться к методу Крамера, а если же элементы нулевые, тогда такие системы очень удобно решать благодаря методу Гаусса.

Предлагаем ещё почитать учебники, в которых также описаны решения систем методом Гаусса.

Литература для общего развития:

Умнов А. Е. Аналитическая геометрия и линейная алгебра, изд. 3: учеб. пособие – М. МФТИ – 2011 – 259 с.

Карчевский Е. М. Лекции по линейной алгебре и аналитической геометрии, учеб. пособие – Казанский университет – 2012 – 302 с.

Метод Гаусса – теорема, примеры решений обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Метод последовательного исключения неизвестных (метод Гаусса) задачи с решением

Метод последовательного исключения неизвестных (метод Гаусса)

Решение системы линейных уравнений методом Гаусса осуществляется по следующей схеме.

1. Выбираем одно из уравнений системы, в котором коэффициент при одном из неизвестных, например, при

, отличен от нуля. Производя над уравнениями системы преобразования, которые приводят к равносильной системе, исключаем неизвестное из всех уравнений, кроме выбранного ранее. В этом заключается первый шаг метода Гаусса.

В результате первого шага может получиться такая система, о которой можно сразу сказать, что она несовместна, а следовательно, и данная система также несовместна.

Если полученная система состоит только из одного выбранного нами уравнения, то исходная система имеет одно решение или бесчисленное множество решений в зависимости от того, имеются ли свободные неизвестные. Во всех остальных случаях переходим ко второму шагу.

2. В системе, полученной в результате первого шага, выбираем одно из уравнений (отличное от выбранного в первом шаге), в котором коэффициент при другом неизвестном, например, при

, отличен от нуля. Исключаем из всех уравнений, кроме двух выбранных.

Если это нужно, аналогично производим последующие шаги.

После нескольких шагов будет иметь место один из случаев:

а) получится явно несовместная система;

б) получится треугольная система, т. е. система вида

где

, .

Система (7), а следовательно, и исходная система имеет единственное решение. Так как

, то из последнего уравнения (7) находим . В предпоследнее уравнение подставляем , получим единственное значение для , так как . Продолжая этот процесс, находим последовательно . Указанный способ нахождения неизвестных называется обратным ходом метода Гаусса;

в) получится трапециевидная система, т. е. система вида:

где

, , .

В системе (8) число неизвестных больше числа уравнений. Так как

, то из последнего уравнения этой системы единственным образом выражается через . Осуществляя обратный ход, выразим единственным образом неизвестные через . Придавая последним произвольные значения , получим бесконечно много решений системы (8), а следовательно, и данной системы.

Заметим, что при применении метода Гаусса на практике имеет смысл вместо преобразований системы производить соответствующие преобразования над строками расширенной матрицы системы, т. е. приводить расширенную матрицу системы к трапециевидной с помощью элементарных преобразований над строками.

Задача №11.

Решить методом Гаусса систему

Решение:

Расширенная матрица системы имеет вид

Прибавив ко второй строке первую, умноженную на (-2), к третьей — первую, умноженную на (-3), к четвертой — первую, умноженную на (-1), получим

Разделим третью строку на 13 и поменяем местами вторую и третью строки:

Прибавим к третьей строке вторую, умноженную на (-9), к четвертой — вторую, умноженную на (-2):

Разделив вторую строку на (-2), а третью на (-7), имеем:

Этой матрице соответствует система

Осуществляя обратный ход, находим:

Таким образом, множеством решений будет

Задача №12.

Решить методом Гаусса систему уравнений

Решение:

Расширенная матрица системы имеет вид

Поменяв местами первую и вторую строки, имеем

Прибавив ко второй строке первую, умноженную на (-2), а к третьей — первую, умноженную на (-3), получим

Прибавив к третьей строке вторую, умноженную на (-1), получим

Этой матрице соответствует система

Осуществляя обратный ход, находим:

Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Решение экономической задачи с помощью системы линейных уравнений

Аскерова Л.Н. УрГЭУ, Екатеринбург Решение экономической задачи  с помощью системы линейных уравнений Одним из методов решения систем линейных уравнений является метод Жордана­Гаусса   (метод   полного   исключения   неизвестных),   который используется   для   решения квадратных   систем   линейных   алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном   базисе   или   отыскания ранга   матрицы.   Метод   является модификацией метода   Гаусса.   Назван   в   честь К. Ф. Гаусса и   немецкого геодезиста и математика Вильгельма Йордана. Приведем   алгоритм   применения   метода   Жордана­Гаусса   на   примере решения экономической задачи: С двух заводов поставляются автомобили для двух автохозяйств, потребности   которых   соответственно   180   и   260   машин.   Первый завод   выпустил   240   машин,   а   второй   –   200   машин.   Известны затраты на перевозку машин с завода на каждое автохозяйство: Затраты на перевозку в автохозяйство, ден. ед. 1 2 1 8 10 2 12 10 Минимальные   затраты   на   перевозку   равны   4360   ден.   ед.   Найти оптимальный план перевозок машин. Решение: Составим систему линейных уравнений: Завод Запишем   СЛУ   (1)   в   табличной   форме   и   решим   методом   Жордана­Гаусса, выделяя разрешающий элемент красным цветом. 1­ую строку умножим на ­1 и прибавим к 3­й строке, также умножим на ­8 и прибавим к 5­й строке: 2­ую строку умножим на ­1 и прибавим к 3­й строке, также умножим на ­10 и прибавим к 5­й строке: 4­ую строку прибавим в 3­й, эту же строку умножим на ­1 и прибавим к 1­й строке, умножим на ­4 и прибавим к 5­й строке: Отбросим нулевую строку и разделим 5­ую строку на ­4: 4­ую строку прибавим к 1­й, эту же строку умножим на ­1 и прибавим ко 2­й и 3­й строкам: Таким образом, Х11=100; Х12=140; Х21=80; Х22=120: Ответ: оптимальный план перевозок машин предполагает перевозку из завода 1 в автохозяйство 1 100 машин и в автохозяйство 2 – 140 машин; из завода 2 в автохозяйство 1 – 80 машин и в автохозяйство 2 – 120 машин. Таким образом, составление систем линейных уравнений, в частности их решение   методом   Жордана­Гаусса,   является   эффективным   способом   при решении экономических задач определенного типа. Список использованных источников: 1. Кремер, Н.Ш. Высшая математика для экономического  бакалавриата: учебник   и   практикум   /   Н.   Ш.   Кремер,   Б.   А.   Путко,   И.   М.   Тришин, М. Н. Фридман; под ред. Н. Ш. Кремера. ­ 4­е изд., перераб. и доп. — М.:Издательство Юрайт; ИД Юрайт, 2012. ­ 909 с. 2. Лунгу   К.   Н.   Фундирование   опыта   личности   как   основа профессионально­прикладной   направленности   обучения   студента технического   вуза   //   Известия   МГТУ.   2014.   №2 (20).   URL: https://cyberleninka.ru/article/n/fundirovanie­opyta­lichnosti­kak­osnova­ professionalno­prikladnoy­napravlennosti­obucheniya­studenta­ tehnicheskogo­vuza  3. Lipschutz,   Seymour,   and   Lipson,   Mark.   «Schaum’s   Outlines:   Linear Algebra». Tata McGraw­hill edition. Delhi 2001. pp. 69­80. Научный руководитель – Кныш А.А., старший преподаватель, УрГЭУ.

Применение метода Гаусса в электротехнике Текст научной статьи по специальности «Математика»

128 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

ПРИМЕНЕНИЕ МЕТОДА ГАУССА В ЭЛЕКТРОТЕХНИКЕ

© Ерёмкин Д.С.*, Лисицын Н.С.*

Дальневосточный федеральный университет, г. Владивосток

В данной статье рассматривается тема прикладного значения метода Гаусса в электротехнике. Представлена теория, охватывающая данную тему. Проведен анализ основных вопросов. Приведены примеры, демонстрирующие практическое использование метода Гаусса при расчетах электротехнических величин.

Ключевые слова метод Гаусса, электротехника.

В современном мире математика и технические науки развиваются в тесном взаимодействии и сотрудничестве друг с другом. Сегодня трудно представить научно-техническую деятельность, где бы не использовались фундаментальные исследования в области математики. Все технические инновации, которые окружают нас в повседневной жизни, есть результат плодотворного сотрудничества техники с математикой. Взаимодействие математических и прикладных дисциплин приводит к их двустороннему обогащению. С одной стороны мы наблюдаем это в применении математического аппарата для решения технических задач. С другой стороны, инженерная практика в существенной мере определяет и стимулирует развитие самой математики. Такой симбиоз математики и технических наук уже весьма высоко зарекомендовал себя и открывает далекие перспективы в будущем.

Математика является фундаментом в инженерном деле. Инженерное дело, в ходе своего развития постоянно расширяет сферу своего приложения, и, тем самым, отвечает все более обширным и сложным техническим задачам. Также, стоит отметить, что вместе с расширением прикладной сферы инженерного дела происходит усиление его специализации. Вследствие развития науки и техники происходит расщепление основных специальностей, появляются новые, ориентированные на более узкий круг практических задач. Таким образом, инженер, являясь специалистом в узкой области, должен базировать свои знания на прочном фундаменте математических и естественных наук. Благодаря различным методам решения технических задач, математический аппарат инженера легко приспосабливается к решению задач в конкретной области.

* Кафедра Электроэнергетики и электротехники. Научный руководитель: Дмух Г.Ю., доцент кафедры Алгебры, геометрии и анализа ШЕН ДВФУ, кандидат педагогических наук.

Важнейшую роль играет умение инженера выбрать соответствующий его задаче математический аппарат и наиболее эффективно использовать его для получения требуемого результата.

В данной статье мы рассмотрим прикладное значение одного из важнейших разделов математики, а именно метода Гаусса в электротехнике. X—

ак1Х1 + ак 2 х2 + … + а кпхп = Ьк

Преобразуем систему, исключив неизвестное х во всех уравнениях системы, кроме первого. Для этого умножим обе части первого уравнения

на —— и сложим со вторым уравнением системы. Затем умножим обе час-

ти первого уравнения на

и сложим с третьим уравнением системы.

Продолжаем этот процесс, пока система не примет вид:

а11х1 + а12х2 + … + а1п Хп = Ь1

а*2х2 + … + а2п Хп = Ь2

а*2 х2 + … + а*пХп = Ьк

Затем процесс повторяется уже делением второй строки на а 22, столбец за столбцом, в итоге, матрица приводится к верхнетреугольному виду.

Второй этап решения заключается в решении ступенчатой системы, просто находя неизвестные х:

а

31

а

130 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

= й*

Хп-1 = Ьп-1 ап-1пХп

Хп-2 = Ьп-2 – ап-2пХп – ап-2п-1Хп-1

Рассмотрим на примере применение метода Гаусса в электротехнике. Для этого решим задачу по нахождению тока. Пример 1:

Схема постоянного тока содержит три замкнутых контура. Используя известный многим закон Кирхгофа для данной задачи, а именно для замкнутых контуров, получаем систему уравнений для тока в миллиамперах:

I + 212 + 313 = 20 41 – 6/2 + 8/3 =-52 -91 + 2/2 – 4/3 = 12

(1) (2) (3)

1. Вычтем из уравнения (2) уравнение (1), умножая его на 4:

0 -14/2 – 4/3 =-132

(4)

Из уравнения (3) вычтем уравнение (1), домноженное на -9:

0 + 20/2 + 23/3 = 192

2. Вычтем из уравнения (5) уравнение (4), умноженное на

0 + 0 + 17.3/3 = 4

20 -14 ‘

(5)

(6)

3. Из уравнения (6) находим /3 = = 0.2 мА, затем последовательно , -132 + 0.8

вычисляем 12 =-—-= 9.37 мА из уравнения (4), откуда находим

11 = 0,66 мА, подставляя известные нам переменные 12 и 13 в уравнение (1). – 4Д2 – 5Д3 =-15

(7)

(8) (9)

1. Вычтем из уравнения (8) уравнение (7), умножая его на 8:

0 – 39Л2 -18Я3 =-184 (10)

Из уравнения (9) вычтем уравнение (7), домноженное на 6:

0 – 34Д2-17Я3 =-165 (11)

-34

2. Вычтем из уравнения (11) уравнение (10), умноженное на -—:

0 – 0-1.308Д3 =-4.59 (12)

-4.59

3. Из уравнения (12) находим Л3 =—= 351 Ом, затем последовательно вычисляем Л2 =-— = 3.098 « 3.1 Ом из уравнения (10), откуда находим Я-[ = 2,49 Ом, подставляя известные нам переменные Я2 и Я3 в уравнение (7).

Список литературы:

1. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. -изд. 5-е. – М.: Айрис-пресс, 2005. – 279 с.

2. Сигорский В.П. Математический аппарат инженера. – изд. 2-е, стереотип. – «Техтка», 1977. – 753 с.

АНАЛИЗ СУЩЕСТВУЮЩИХ ПРОЦЕССНЫХ ПОДХОДОВ К УПРАВЛЕНИЮ ИНЦИДЕНТАМИ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ

© Костомаров В.А.*

Московский государственный университет экономики, статистики и информатики (МЭСИ), г. Москва

Рассматриваются процессные подходы, принятые в международных и национальных стандартах в области информационной безопасности и проводится сравнительный анализ представленных процессных подходов.

Ключевые слова: управление информационной безопасностью, процессный подход, менеджмент инцидентов ИБ.

* Магистрант кафедры Автоматизированных систем обработки информации и управления. Научный руководитель: Микрюков А.А. заведующий кафедрой Автоматизированных систем обработки информации и управления МЭСИ, кандидат технических наук, доцент.

Гаусса метод – Энциклопедия по экономике

Система линейных уравнений для определения коэффициентов регрессии решается методом Гаусса. Для каждого полинома заданной степени определяется остаточная дисперсия  [c.23]

При внедрении статистических методов контроля важно установить, какой закономерности подчиняется распределение контролируемых параметров изделий электронной техники (кривой нормального распределения Гаусса распределению, характеризуемому кривой Максвелла, и т. д.). Изменение величины конкретного контролируемого параметра изделия или технологического режима проявляется в изменении функ-  [c.159]

Это есть система алгебраических уравнений. Применяя метод исключения Гаусса определяем координаты вектора и0  [c.209]

Инженерные задачи Обращение квадратной матрицы методом Гаусса-Жордана , Матричные вычисления и др.  [c.107]

Вторая задача специфична для статистических связей, а первая разработана для функциональных связей и является общей. Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К. Ф. Гауссом (1777-1855). Он состоит в минимизации суммы квадратов отклонений фактически измеренных значений зависимой переменной у от ее значений, вычисленных по уравнению связи с факторным признаком (многими признаками) х.  [c.232]

Несмотря на существенную условность применения в экономическом анализе стохастических моделей, они достаточно распространены, поскольку с их помощью можно прогнозировать динамику основных показателей, разрабатывать научно обоснованные нормативы, идентифицировать наиболее значимые факторы. Многие методы, разработанные в математической статистике, базируются на понятии нормального закона распределения, введенного Карлом Гауссом. Это обусловлено следующими причинами. Во-первых, оказывается, что при экспериментах и наблюдениях многие случайные величины имеют распределения, близкие к нормальному. Во-вторых, даже если распределение некоторой случайной величины не является нормальным, то ее можно преобразовать таким образом, чтобы распределение преобразования, т.е. новой величины, было уже близким к нормальному. В-третьих, нормальное распределение мо-  [c.118]

Оценка Ь, определенная по (4.8), хотя и будет состоятельной, но не будет оптимальной в смысле теоремы Гаусса— Маркова. Для получения наиболее эффективной оценки нужно использовать другую оценку, получаемую так называемым обобщенным методом наименьших квадратов.  [c.152]

Метод Гаусса — это последовательное изменение состава опорного решения до получения оптимального варианта, не допускающего улучшения, это способ решения оптимизационной задачи, у которой оценка и ограничения являются линейными функциями. Рассмотрим алгоритм метода Гаусса на числовом примере.  [c.121]

Наиболее распространены статистические методы предупредительного контроля, основывающиеся на законе нормального распределения, характеризующегося известной кривой Гаусса.  [c.155]

Единственная переменная величина в методе фиксированных пропорций называется дельта. Эта переменная просто обеспечивает математическую формулировку метода, а также определяет, насколько агрессивно или консервативно следует вести управление. Чем меньше значение переменной, тем более агрессивным должно быть управление ресурсами. Чем больше величина переменной, тем более консервативно управление. Кривая Гаусса в Фиксированно-Пропорциональном методе не используется.  [c.89]

Модели парной регрессии. Парная линейная регрессия. Методы оценки коэффициентов регрессии. Метод наименьших квадратов (МНК). Свойства оценок МНК. Оценка статистической значимости коэффициентов регрессии. Элементы корреляционного анализа. Измерители тесноты связи (коэффициенты ковариации, корреляции и детерминации). Оценка значимости коэффициента корреляции. Дисперсионный анализ результатов регрессии. Оценка статистической значимости уравнения регрессии. Анализ ряда остатков условия Гаусса-Маркова. Нелинейные модели регрессии и их линеаризация. Выбор функции регрессии тесты Бокса-Кокса. Корреляция в случае нелинейной регрессии. Средняя ошибка аппроксимации.  [c.3]

Это формулы итерации по методу Ньютона — Гаусса. При их использовании, если степень нелинейности.Дх) высока, а стартовое значение % далеко отстоит от минимизирующего значения, то велика вероятность раскачки АХп расходимости итеративного процесса.  [c.86]

Указанная система уравнений может решаться методом Гаусса. Умножим элемент первой строки на 2/3 и, вычтя из элементов третьей строки, получим  [c.171]

Основные решаемые задачи — интерполяция и экстраполяция (собственно прогноз). Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан немецким математиком К. Гауссом в 1794—1795 гг. Могут оказаться полезными предварительные преобразования переменных. Для игроков на финансовых рынках такой подход именуется техническим анализом.  [c.137]

Решая эту систему (например, методом Гаусса), получим а0 = 18,63 а = 0,0985 а2 = 224, 6, так что модель (25.75) имеет вид  [c.565]

Для каждой трактовки степени принадлежности разработаны свои методы построения функций принадлежности. В ряде моделей мягких вычислений функции принадлежности задаются произвольно в параметрическом виде. Наиболее распространенными в приложениях теории нечетких множеств являются треугольные, трапециевидные, гауссов-ские и колоколообразные функции принадлежности. Например, треугольные функции принадлежности задаются тремя параметрами (а, Ь, с)  [c.17]

Рассматривая теорию статистических оценок с позиций применения в массовых автоматизированных производствах, можно выявить две причины, существенно ограничивающие ее применение. Во-первых, точные результаты могут быть получены по результатам контроля большого числа партий, следовательно, информация о состоянии ТП поступит со значительными задержками во времени и не может быть использована для оперативного вмешательства в ход процесса. Во-вторых, статистический анализ состояния ТП базируется на исследовании погрешностей изготовления, подчиняющихся непрерывным распределениям (законам Гаусса, Максвелла, модуля разности и т. п.), а в основу теории несмещенных оценок положены дискретные распределения. Исходя из этого, можно сделать вывод о необходимости создания таких методов оценки результатов контроля, которые позволят избежать указанных недостатков.  [c.12]

Идея информационного метода определения закона распределения заключается в следующем. Так как оценка энтропии распределена по закону Гаусса, то гипотеза о совпадении эмпирического и предполагаемого теоретического распределения принимается, если вычисленное по результатам экспериментальных данных значение Я (х) будет находиться в пределах доверительного интервала кривой нормального распределения с параметрами М[Н] и >[Я]. Нормированная по среднеквадратическому отклоне-  [c.28]

Для этой целя воспользуемся методом Гаусса г приведения системы уравнений к ступенчатому виду. Этот метод широко описан в литературе , для него существуют готовые программы для ЭВМ, поэтому останавливаться на нем не будем.  [c.41]

В примере, по методу Гаусса, вычитая 1-е уравнение из 3-го, получаем  [c.41]

В каждом варианте проверяем выполнение условий / .18/, /2.20/. Теперь ясно, для чего понадобился здесь метод Гаусса не имея условия /2.20/, пришлось бы каждое из уравнений исходной системы проверять в комбинаторном числе вариантов.  [c.42]

I. Приведение систем уравнений /2.1/ к ступенчатому виду методом Гаусса и выбор свободных переменных. Число свободных переменных – / Ш -к/. Остальные будут линейными функциями этих свободных переменных  [c.32]

Заметим, что решение по методу наименьших квадратов и оценка Гаусса-Маркова имеют одинаковые представления, что привело к нежелательному  [c.326]

Рассмотрим схему Гаусса-Маркова (у, Xf3, аффинную несмещенную оценку для /3, /3 = (Х Х) 1Х у (оценка Гаусса-Маркова), минимизируя квадратичную форму (след ковариационной матрицы оценки) при линейном ограничении (несмещенность). В 4 мы показали, что оценка Гаусса— Маркова может быть также получена минимизацией (у — Х(3) (у — Х/3) по всем /3 из R. Тот факт, что метод наименьших квадратов (который является методом аппроксимации, а не оценивания) приводит к наилучшим аффинным оценкам, является довольно неожиданным и, конечно, не тривиальным.  [c.355]

Если решать систему (8.61) методом последовательного исключения Гаусса или приведением матрицы Х Х к треугольной форме, то первый шаг состоит в делении первого уравнения на п и вычитании соответствующих кратных первого уравнения (1-й строки матрицы Х Х) из остальных уравнений (строк матрицы Х Х) таким образом, чтобы оставшиеся р элементов первого столбца матрицы Х Х обратились в нуль. Таким образом после первого шага мы получим систему уравнений вида  [c.276]

Метод Ньютона- Гаусса  [c.305]

Общая схема метода. Заметно более простым по- сравнению с предыдущим методом является метод Ньютона — Гаусса, в котором матрица tts — M71. Практика показывает, что именно для регрессионных задач его эффективность такая же, как и метода Ньютона.  [c.305]

Именно эта процедура и носит название метода Ньютона— Гаусса.  [c.306]

Для рассматриваемой экстремальной задачи метод Ньютона—Гаусса близок методу Ньютона. При линейной параметризации они совпадают. Их близость при малых вторых производных Ф1з очевидна. Имеется и более глубокая причина их близости. Действительно, при п —> оо и некоторых не слишком ограничительных предположениях в силу закона больших чисел имеем следующую сходимость (с вероятностью единица)  [c.306]

Сходимость метода Ньютона — Гаусса и его модификаций изучалась, например, в 1109,200, 2371, различные комментарии и дополнительную библиографию можно найти в [145, 146, 25, 431. Скорость сходимости в зависимости от условий,  [c.307]

При ручном способе решения эффективным может оказаться метод квадратных корней и метод последовательного исключения неизвестных (метод Гаусса), при машинном решении — метод последовательных приближений (метод Зейделя) или метод Гаусса.  [c.37]

Рассмотрим пример составления корреляционного уравнения линейного тица методом Гаусса.  [c.40]

Многочлены имеют различные степени. Степень многочлена определяется значением наибольшей степени любого из элементов. Степенью элемента является сумма показателей переменных, содержащихся в элементе. Показанное выше выражение является многочленом третьей степени, так как элемент 4 АЛ 3 имеет третью степень, и это наивысшая степень среди всех элементов многочлена. Если бы элемент был равен 4 АЛ3 ВЛ62 С, мы бы получили многочлен шестой степени, так как сумма показателей переменных (3+2+1) равна 6. Многочлен первой степени называется также линейным уравнением и графически задается прямой линией. Многочлен второй степени называется квадратным уравнением и на графике представляет собой параболу. Многочлены третьей, четвертой и пятой степени называются соответственно кубическим уравнением, уравнением четвертой степени, уравнением пятой степени и т.д. Графики многочленов третьей степени и выше довольно сложны. Многочлены могут иметь любое число элементов и любую степень, мы будем работать только с линейными уравнениями, т.е. многочленами первой степени. Решить систему линейных уравнений можно с помощью процедуры Гаусса-Жордана, или, что то же самое, метода гауссовского исключения. Чтобы использовать этот метод, мы должны сначала создать расширенную матрицу, объединив матрицу коэффициентов и столбец свободных членов. Затем следует произвести элементарные преобразования для получения единичной матрицы. С помощью элементарных преобразований мы получаем более простую, но эквивалентную первоначальной, матрицу. Элементарные преобразования производятся посредством построчных операций (мы опишем их ниже). Единичная матрица является квадратной матрицей коэффициентов, где все элементы равны нулю, кроме диагональной линии элементов, которая начинается в верхнем левом углу. Для матрицы коэффициентов шесть на шесть единичная матрица будет выглядеть следующим образом  [c.191]

Указание. Функция lsolve(A, b) возвращает вектор х решения системы Ax = b, найденного методом Гаусса с оценкой числа обусловленности. Здесь не используется явная формула решения нормальной обобщенной системы х = (АТА)” АТЬ, поскольку часто в задачах об аппроксимации эмпирических данных  [c.89]

I. Заыеним все знаки неравенства на знаки равенства в систеие /2=5/ и методой Гаусса приведем систему /2.4/, /3.5/ к системе /2.6/, /2.7/.  [c.36]

Рассмотрим итеративный метод решения задачи (4.15) вогнутого программирования, представляющий собой обобщение метода Гаусса — Зейделя покоординатного спуска. В [83] метод Гаусса — Зей-деля распространен на случай, когда на каждом шаге производится оптимизация не по отдельным переменным, а по векторам, составляющие которых — некоторые подмножества множества переменных задачи. Задача (4.15) не укладываетя в класс задач, для решения которых в [83] обосновано обобщение метода покоординатного спуска. Векторы X/j( oh ) — аргументы функции вектор-функции, определенные для разных k на различных пространствах. 218  [c.218]

Используя R/S-анализ для поддержки гипотезы фрактального рынка, я показываю модели, объясняющие полученные результаты. Часть 4 рассматривает деятельность рынка с точки зрения стохастических процессов по существу, в ней разбирается фрактальный шум. В Главе 13, на основе использования R/S-анализа, различные “цветные” шумы анализируются и сравниваются с анализом рынка. Полученные результаты удивительно похожи. Кроме того, дается значимое объяснение поведению волатильности. В Главе 14 обсуждается статистика процессов фрактального шума, которые выдвигаются в качестве альтернативы традиционному нормальному распределению (распределению Гаусса). Обсуждается влияние фрактальных распределений на модели рынка. В Главе 15 показано влияние фрактальной статистики на проблему выбора портфеля и опционное ценообразование. Рассматриваются методы адаптирования таких моделей к фрактальным распределениям.  [c.7]

В (9.14) у.ч. 0, AS — положительно полуопределенная матрица. При уя = 0 реализуется метод Ньютона—Гаусса, при y.s. ->- оо и Ая — 1 направление движения приближается к антиградиенту. Выбор f>jS. и уя в большинстве модификаций (9.14) проводится из соображений монотонного убывания  [c.307]

НОУ ИНТУИТ | Лекция | Компьютерное моделирование и решение линейных и нелинейных многомерных систем

Аннотация: Лекция рассматривает метод и алгоритм решения систем линейных уравнений методом Гаусса

При моделировании экономических задач, таких как задачи управления и планирования производства, определения оптимального размещения оборудования, оптимального плана производства, оптимального плана перевозок грузов (транспортная задача), распределения кадров и др., может быть положена гипотеза линейного представления реального мира.

Математические модели таких задач представляются линейными уравнениями. Если задача многомерна, то ее математическая модель представляется системой линейных уравнений.

Линейные математические модели также используются в нелинейных системах при условии, если эта нелинейная система условно линеаризирована.

В общем виде система линейных уравнений имеет вид:

где

a_ij – коэффициенты при неизвестных системы,

b_i – свободные члены,

x_j – неизвестные системы,

– номер строки,

– номер столбца,

n – порядок системы.

В матричной форме система линейных уравнений имеет вид:

где

Численные методы решения систем линейных уравнений (СЛУ) можно разделить на две группы:

1. точные или прямые методы,
2. приближенные методы.

Приближенные методы реализуют на ЭВМ нахождение корней с заданной точностью и являются итерационными методами.

Точные методы позволяют получить решение системы за конечное число итераций. К точным методам относятся:

• правило Крамера,
• метод Гаусса,
• метод прогонки.

Решение систем линейных уравнений методом Гаусса

Метод Гаусса является точным методом. Он позволяет получить решение системы за конечное число арифметических действий. В основе метода лежит идея последовательного исключения неизвестных. Метод состоит из двух этапов. На первом этапе (прямой ход) система при помощи последовательного исключения неизвестных приводится к треугольному виду. На втором этапе (обратный ход) из системы треугольного вида последовательно, в обратном порядке, начиная c n-го уравнения, находятся неизвестные системы.

В качестве примера возьмем систему 4 порядка.

( 9.1)

Прямой ход. На первом шаге прямого хода (к=1) находим x₁ из первого уравнения системы (9.1).

– ведущий элемент первой строки.

Если , то

( 9.2)

Обозначим:

( 9.3)

Подставляя (9.3) в (9.2), получим

( 9.4)

где

Подставляем (9.4) во 2, 3 и 4 уравнение системы (9.1), получим:

Обозначив коэффициенты при неизвестных полученной системы через , а свободные члены через перепишем полученную систему:

( 9.5)

где

Таким образом, в результате выполнения первого шага прямого хода исходная система (9.1) n-го порядка преобразована к совокупности уравнения (9.4) и системы линейных уравнений (9.5), порядок которой равен n-1.

На втором шаге прямого хода (к=2) из первого уравнения системы (9.5) находим x₂.

-ведущий элемент первой строки системы (9.5).

Если , то из первого уравнения системы (9.5) имеем:

( 9.6)

где

Подставив выражение (9.6) во второе и третье уравнения системы (9.5), получим новую систему линейных уравнений, порядок которой равен n-2.

( 9.7)

где

Таким образом, в результате выполнения второго шага прямого хода исходная система (9.1) преобразована к совокупности уравнений (9.4), (9.6) и системы линейных уравнений (9.7),порядок которой равен n-2.

Визуальное исследование гауссовских процессов

Даже если вы некоторое время читали о машинном обучении, скорее всего, вы никогда не слышали о гауссовских процессах. А если да, то репетиция основ – всегда хороший способ освежить память. В этом сообщении в блоге мы хотим дать введение в гауссовские процессы и сделать математическую интуицию, стоящую за ними, более доступной.

Гауссовские процессы – мощный инструмент в наборе инструментов машинного обучения.Они позволяют нам делать прогнозы относительно наших данных, используя предварительные знания. Наиболее очевидная область их применения – подгонка функции к данным. Это называется регрессией и используется, например, в робототехнике или прогнозировании временных рядов. Но гауссовские процессы не ограничиваются регрессией – их также можно распространить на задачи классификации и кластеризации. Для данного набора обучающих точек существует потенциально бесконечно много функций, которые соответствуют данным.Гауссовские процессы предлагают элегантное решение этой проблемы, приписывая вероятность каждой из этих функций. Среднее значение этого распределения вероятностей представляет собой наиболее вероятную характеристику данных. Кроме того, использование вероятностного подхода позволяет нам включить достоверность прогноза в результат регрессии.

Сначала мы исследуем математическую основу, на которой построены гауссовские процессы – мы приглашаем вас следовать за ними, используя интерактивные рисунки и практические примеры.Они помогают объяснить влияние отдельных компонентов и показывают гибкость гауссовских процессов. Мы надеемся, что после прочтения этой статьи вы получите визуальное представление о том, как работают гауссовские процессы и как вы можете настроить их для различных типов данных.

Многомерные гауссовские распределения

Прежде чем мы сможем исследовать гауссовские процессы, нам нужно понять математические концепции, на которых они основаны. Как следует из названия, распределение Гаусса (которое часто также называют нормальным распределением ) является основным строительным блоком гауссовских процессов.В частности, нас интересует многомерный случай этого распределения, когда каждая случайная величина распределена нормально, а их совместное распределение также является гауссовым. Многомерное гауссовское распределение определяется вектором среднего μ \ muμ и ковариационной матрицей Σ \ SigmaΣ. Вы можете увидеть интерактивный пример таких дистрибутивов на рисунке ниже. T \ right] Σ = Cov (Xi, Xj) = E [(Xi −μi) (Xj −μj) T]

Визуально распределение сосредоточено вокруг среднего, а ковариационная матрица определяет его форму.На следующем рисунке показано влияние этих параметров на двумерное распределение Гаусса. Дисперсии для каждой случайной величины находятся на диагонали ковариационной матрицы, в то время как другие значения показывают ковариацию между ними.

Гауссовские распределения широко используются для моделирования реального мира. Например, мы можем использовать их для описания ошибок измерений или явлений в предположениях центральной предельной теоремы Одно из следствий этой теоремы состоит в том, что набор независимых одинаково распределенных случайных величин с конечной дисперсией вместе распределены нормально.Хорошее введение в центральную предельную теорему дает это видео из Khan Academy. . В следующем разделе мы более подробно рассмотрим, как манипулировать распределениями Гаусса и извлекать из них полезную информацию.

Маргинализация и обусловливание

Гауссовские распределения обладают прекрасным алгебраическим свойством замкнутости при ограничении условий и маргинализации. Закрытие в условиях обусловливания и маргинализации означает, что результирующие распределения этих операций также являются гауссовскими, что делает многие проблемы в статистике и машинном обучении решаемыми.Далее мы более подробно рассмотрим обе эти операции, поскольку они являются основой гауссовских процессов.

Маргинализация и кондиционирование работают с подмножествами исходного распределения, и мы будем использовать следующие обозначения:

PX, Y = [XY] ∼N (μ, Σ) = N ([μXμY], [ΣXXΣXYΣYXΣYY]) P_ {X, Y} = \ begin {bmatrix} X \\ Y \ end {bmatrix} \ sim \ mathcal {N} (\ mu, \ Sigma) = \ mathcal {N} \ left (\ begin {bmatrix} \ mu_X \\ \ mu_Y \ end {bmatrix}, \ begin {bmatrix} \ Sigma_ {XX} \, \ Sigma_ {XY} \\ \ Sigma_ {YX} \, \ Sigma_ {YY} \ end {bmatrix} \ right) PX, Y = [XY] ∼N (μ, Σ) = N ([μX μY ], [ΣXX ΣXY ΣYX ΣYY])

Где XXX и YYY представляют собой подмножества исходных случайных величин.

Через маргинализацию мы можем извлекать частичную информацию из многомерных распределений вероятностей. В частности, учитывая нормальное распределение вероятностей P (X, Y) P (X, Y) P (X, Y) по векторам случайных величин XXX и YYY, мы можем определить их маргинальные распределения вероятностей следующим образом:

X∼N (μX, ΣXX) Y∼N (μY, ΣYY) \ begin {выровнено} X & \ sim \ mathcal {N} (\ mu_X, \ Sigma_ {XX}) \\ Y & \ sim \ mathcal {N} (\ mu_Y, \ Sigma_ {YY}) \ end {выровнен} XY ∼N (μX, ΣXX) ∼N (μY, ΣYY)

Интерпретация этого уравнения состоит в том, что каждое разбиение XXX и YYY зависит только от соответствующих ему записей в μ \ muμ и Σ \ SigmaΣ.Чтобы исключить случайную величину из гауссовского распределения, мы можем просто отбросить переменные из μ \ muμ и Σ \ SigmaΣ.

pX (x) = ∫ypX, Y (x, y) dy = ∫ypX∣Y (x∣y) pY (y) dy p_X (x) = \ int_y p_ {X, Y} (x, y) dy = \ int_y p_ {X | Y} (x | y) p_Y (y) dy pX (x) = ∫y pX, Y (x, y) dy = ∫y pX∣Y (x∣y) pY (y) dy

Это уравнение можно интерпретировать следующим образом: если нас интересует плотность вероятности X = xX = xX = x, нам необходимо рассмотреть все возможные исходы ГГГ, которые в совокупности могут привести к результату Соответствующая Википедия В статье есть хорошее описание маржинального распределения, включая несколько примеров. {- 1} \ Sigma_ {XY} \ 🙂 \\ \ end {выровнен} X∣YY∣X ∼N (μX + ΣXY ΣYY − 1 (Y − μY), ΣXX −ΣXY ΣYY − 1 ΣYX) ∼N (μY + ΣYX ΣXX − 1 ( X − μX), ΣYY −ΣYX ΣXX − 1 ΣXY)

Обратите внимание, что новое среднее значение зависит только от условной переменной, в то время как ковариационная матрица не зависит от этой переменной.

Теперь, когда мы проработали необходимые уравнения, мы подумаем о том, как визуально понять эти две операции. Хотя маргинализация и кондиционирование могут применяться к многомерным распределениям многих измерений, имеет смысл рассмотреть двумерный случай, как показано на следующем рисунке. Маргинализацию можно рассматривать как интеграцию по одному из измерений гауссова распределения, что соответствует общему определению маржинального распределения.У кондиционирования также есть хорошая геометрическая интерпретация – мы можем представить его как прорезание многомерного распределения, в результате чего получается новое гауссово распределение с меньшим количеством измерений.

Двумерное нормальное распределение в центре. Слева вы можете увидеть результат маргинализации этого распределения для Y, сродни интегрированию по оси X. Справа вы можете увидеть распределение, обусловленное заданным X, что похоже на сокращение исходного распределения.Гауссово распределение и условную переменную можно изменить, перетащив ручки.

Гауссовские процессы

Теперь, когда мы вспомнили некоторые из основных свойств многомерных гауссовских распределений, мы объединим их вместе, чтобы определить гауссовские процессы и показать, как их можно использовать для решения задач регрессии.

Сначала мы перейдем от непрерывного представления к дискретному представлению функции: Вместо того, чтобы искать неявную функцию, нас интересует прогнозирование значений функции в конкретных точках, которые мы называем контрольными точками XXX.Итак, как нам получить это функциональное представление из многомерных нормальных распределений, которые мы рассмотрели до сих пор? Стохастические процессы, такие как гауссовские процессы, по сути, представляют собой набор случайных величин. Кроме того, каждой из этих случайных величин соответствует индекс iii. Мы будем использовать этот индекс для обозначения iii-го измерения наших nnn-мерных многомерных распределений. На следующем рисунке показан пример этого для двух измерений:

Здесь мы имеем двумерное нормальное распределение.Каждому измерению xix_ixi присваивается индекс i∈ {1,2} i \ in \ {1,2 \} i∈ {1,2}. Вы можете перетащить маркеры, чтобы увидеть, как конкретный образец (слева) соответствует функциональным значениям (справа). Это представление также позволяет нам понять связь между ковариацией и результирующими значениями: лежащее в основе распределение Гаусса имеет положительную ковариацию между x1x_1x1 и x2x_2x2 – это означает, что x2x_2x2 будет увеличиваться по мере увеличения x1x_1x1 и наоборот. Вы также можете перетащить ручки на рисунке вправо и наблюдать вероятность такой конфигурации на рисунке слева.

Теперь цель гауссовских процессов состоит в том, чтобы узнать это базовое распределение из обучающих данных . Что касается тестовых данных XXX, мы обозначим обучающие данные как YYY. Как мы упоминали ранее, ключевая идея гауссовских процессов состоит в моделировании основного распределения XXX вместе с YYY как многомерного нормального распределения. Это означает, что совместное распределение вероятностей PX, YP_ {X, Y} PX, Y охватывает пространство возможных значений функции для функции, которую мы хотим предсказать.Обратите внимание, что это совместное распределение тестовых и обучающих данных имеет ∣X∣ + ∣Y∣ | X | + | Y | ∣X∣ + ∣Y∣ размеры.

Чтобы выполнить регрессию на обучающих данных, мы будем рассматривать эту проблему как Байесовский вывод . Основная идея байесовского вывода состоит в том, чтобы обновлять текущую гипотезу по мере появления новой информации. В случае гауссовских процессов эта информация является обучающими данными. Таким образом, нас интересует условная вероятность PX∣YP_ {X | Y} PX∣Y.Наконец, напомним, что гауссовские распределения замкнуты при условии, поэтому PX∣YP_ {X | Y} PX∣Y также распределяется нормально.

Теперь, когда у нас есть базовая структура гауссовских процессов, нам не хватает только одного: как нам установить это распределение и определить среднее значение μ \ muμ и ковариационную матрицу Σ \ SigmaΣ? Ковариационная матрица Σ \ SigmaΣ определяется своей ковариационной функцией kkk, которую часто также называют ядром гауссовского процесса.Об этом мы подробно поговорим в следующем разделе. Но прежде чем мы подойдем к этому, давайте поразмышляем над тем, как мы можем использовать многомерные гауссовские распределения для оценки значений функций. На следующем рисунке показан пример этого с использованием десяти контрольных точек, в которых мы хотим предсказать нашу функцию:

В гауссовских процессах мы рассматриваем каждую контрольную точку как случайную величину. Многомерное гауссовское распределение имеет то же количество измерений, что и количество случайных величин.Поскольку мы хотим предсказать значения функции при ∣X∣ = N | X | = N∣X∣ = N контрольных точек, соответствующее многомерное распределение Гаусса также NNN -размерный. Прогнозирование с использованием гауссовского процесса в конечном итоге сводится к извлечению выборок из этого распределения. Затем мы интерпретируем iii-ю компоненту результирующего вектора как значение функции, соответствующее iii-й контрольной точке.

Ядра

Напомним, что для настройки нашего распределения нам нужно определить μ \ muμ и Σ \ SigmaΣ.В гауссовских процессах часто предполагается, что μ = 0 \ mu = 0μ = 0, что упрощает необходимые уравнения для кондиционирования. Мы всегда можем предположить такое распределение, даже если μ ≠ 0 \ mu \ neq 0μ ≠ 0, и добавить μ \ muμ обратно к результирующим значениям функции после шага прогнозирования. Этот процесс также называется центрированием данных. Таким образом, настройка μ \ muμ проста – она ​​становится более интересной, если мы посмотрим на другой параметр распределения.

Умный шаг гауссовских процессов – это то, как мы устанавливаем ковариационную матрицу Σ \ SigmaΣ.п \ rightarrow \ mathbb {R}, \ quad \ Sigma = \ text {Cov} (X, X ’) = k (t, t’) k: Rn × Rn → R, Σ = Cov (X, X ′) = k (t, t ′).

Мы оцениваем эту функцию для каждой попарной комбинации контрольных точек, чтобы получить ковариационную матрицу. Этот шаг также изображен на рисунке выше. Чтобы лучше понять роль ядра, давайте подумаем о том, что описывают элементы ковариационной матрицы. Запись Σij \ Sigma_ {ij} Σij описывает, насколько сильно влияют друг на друга iii-я и jjj-я точки.Это следует из определения многомерного гауссовского распределения, в котором говорится, что Σij \ Sigma_ {ij} Σij определяет корреляцию между iii-й и jjj-й случайной величиной. Поскольку ядро ​​описывает сходство между значениями нашей функции, оно контролирует возможную форму, которую может принять подобранная функция. Обратите внимание: когда мы выбираем ядро, нам нужно убедиться, что результирующая матрица соответствует свойствам ковариационной матрицы.

Ядра широко используются в машинном обучении, например, в векторных машинах поддержки .Причина этого в том, что они допускают измерения сходства, которые выходят далеко за рамки стандартного евклидова расстояния (L2L2L2-расстояние). Многие из этих ядер концептуально встраивают входные точки в пространство более высокой размерности, в котором они затем измеряют сходство. Если ядро ​​следует теореме Мерсера, его можно использовать для определения гильбертова пространства. Более подробную информацию об этом можно найти в Википедии. На следующем рисунке показаны примеры некоторых общих ядер для гауссовских процессов. Для каждого ядра ковариационная матрица была создана из N = 25N = 25N = 25 линейно разнесенных значений в диапазоне от [−5,5] [- 5,5] [- 5,5].Каждая запись в матрице показывает ковариацию между точками в диапазоне [0,1] [0,1] [0,1].

На этом рисунке показаны различные ядра, которые можно использовать с гауссовскими процессами. У каждого ядра разные параметры, которые можно изменить, регулируя соответствующие ползунки. При захвате слайдера информация о том, как текущий параметр влияет на ядро, будет показана справа.

Ядра можно разделить на стационарных и нестационарных ядер. Стационарные ядер, например как ядро ​​RBF или периодическое ядро, являются функциями, инвариантными к переносам, а ковариация двух точек только в зависимости от их взаимного расположения. Нестационарные ядра , такие как линейное ядро, не имеют этого ограничение и зависят от абсолютного местоположения. Стационарный характер ядра RBF можно наблюдать в полосы вокруг диагонали его ковариационной матрицы (как показано на этом рисунке). Увеличение параметра длины увеличивает полосатость, так как точки, расположенные дальше друг от друга, становятся более коррелированными.Для периодического ядра у нас есть дополнительный параметр PPP, определяющий периодичность, который контролирует расстояние между каждым повторением функции. Напротив, параметр CCC линейного ядра позволяет нам изменить точку, на которой опираются все функции.

Есть еще много ядер, которые могут описывать различные классы функций, которые можно использовать для моделирования желаемой формы функции. Хороший обзор различных ядер дает Дювено.Также возможно объединение нескольких ядер – но мы вернемся к этому позже.

До распространения

Теперь мы вернемся к исходной задаче регрессии. Как мы упоминали ранее, гауссовские процессы определяют распределение вероятностей по возможным функциям. На этом рисунке выше мы показываем эту связь: каждый образец нашего многомерного нормального распределения представляет собой одну реализацию значений нашей функции. Поскольку это распределение является многомерным распределением Гаусса, распределение функций является нормальным.Напомним, что обычно мы предполагаем μ = 0 \ mu = 0μ = 0. А пока давайте рассмотрим случай, когда мы еще не наблюдали никаких обучающих данных. В контексте байесовского вывода это называется распределением предшествующего PXP_XPX.

Если мы еще не наблюдали никаких обучающих примеров, это распределение вращается вокруг μ = 0 \ mu = 0μ = 0, согласно нашему исходному предположению. Априорное распределение будет иметь ту же размерность, что и количество контрольных точек N = ∣X∣N = | X | N = ∣X∣.Мы будем использовать ядро ​​для создания ковариационной матрицы, которая имеет размерность N × NN \ умноженная на NN × N.

В предыдущем разделе мы рассмотрели примеры различных ядер. Ядро используется для определения элементов ковариационной матрицы. Следовательно, ковариационная матрица определяет, какой тип функций из пространства всех возможных функций более вероятен. Поскольку предыдущее распределение еще не содержит никакой дополнительной информации, оно идеально подходит для визуализации влияния ядра на распределение функций.На следующем рисунке показаны примеры потенциальных функций из предыдущих распределений, которые были созданы с использованием разных ядер:

Щелчок по графику приводит к непрерывным выборкам, взятым из Гауссовский процесс с использованием выбранных ядро. После каждого розыгрыша предыдущий образец уходит на второй план. Со временем можно увидеть, что функции нормально распределяются вокруг среднего µ.

Регулировка параметров позволяет контролировать форму получаемых функций.Это также влияет на достоверность прогноза. При уменьшении дисперсии σ \ sigmaσ, общего параметра для всех ядер, выборочные функции больше концентрируются вокруг среднего значения μ \ muμ. Для ядра Linear установка дисперсии σb = 0 \ sigma_b = 0σb = 0 приводит к набору функций, ограниченных для точного пересечения точки смещения ccc. Если мы установим σb = 0,2 \ sigma_b = 0,2σb = 0,2, мы сможем смоделировать неопределенность, в результате чего функции будут близки к ccc.

Заднее распределение

Итак, что произойдет, если мы увидим данные обучения? Давайте вернемся к модели байесовского вывода, в которой говорится, что мы можем включить эту дополнительную информацию в нашу модель, получив апостериорное распределение PX∣YP_ {X | Y} PX∣Y.Теперь мы подробнее рассмотрим, как это сделать для гауссовских процессов.

Сначала формируем совместное распределение PX, YP_ {X, Y} PX, Y между контрольными точками XXX и тренировочными точками YYY. Результатом является многомерное распределение Гаусса с размерностями ∣Y∣ + ∣X∣ | Y | + | X | ∣Y∣ + ∣X∣. Как вы можете видеть на рисунке ниже, мы объединяем обучающую и контрольную точки для вычисления соответствующей ковариационной матрицы.

Для следующего шага нам понадобится одна операция с гауссовыми распределениями, которую мы определили ранее.Используя , кондиционирование , мы можем найти PX∣YP_ {X | Y} PX∣Y из PX, YP_ {X, Y} PX, Y. Размеры этого нового распределения соответствуют количеству контрольных точек NNN, и распределение также нормальное. Важно отметить, что кондиционирование приводит к производным версиям среднего и стандартного отклонения: X∣Y∼N (μ ′, Σ ′) X | Y \ sim \ mathcal {N} (\ mu ‘, \ Sigma’) X∣Y∼N (μ ′, Σ ′). Более подробную информацию можно найти в соответствующем разделе об условных многомерных гауссовских распределениях. Интуиция, лежащая в основе этого шага, заключается в том, что обучающие точки ограничивают набор функций теми, которые проходят через обучающие точки.

Как упоминалось ранее, условное распределение PX∣YP_ {X | Y} PX∣Y заставляет набор функций точно проходить через каждую точку обучения. Во многих случаях это может привести к излишне сложным встроенным функциям. Кроме того, до сих пор мы считали тренировочные точки YYY идеальными измерениями. Но в реальных сценариях это нереалистичное предположение, поскольку большая часть наших данных содержит ошибки измерения или неточности.2I \ end {bmatrix} \ right) PX, Y = [XY] ∼N (0, Σ) = N ([00], [ΣXX ΣYX ΣXY ΣYY + ψ2I])

Опять же, мы можем использовать кондиционирование для получения прогнозирующего распределения PX∣YP_ {X | Y} PX∣Y. В этой формулировке ψ \ psiψ – дополнительный параметр нашей модели.

Аналогично предыдущему распределению, мы могли получить прогноз для значений нашей функции путем выборки из этого распределения. Но поскольку выборка включает случайность, полученное соответствие данным не будет детерминированным, и наш прогноз может оказаться выбросом.Чтобы сделать более осмысленный прогноз, мы можем использовать другую базовую операцию гауссовых распределений.

Путем маргинализации каждой случайной величины мы можем извлечь соответствующее среднее значение функции μi ′ \ mu’_iμi ′ и стандартное отклонение σi ′ = Σii ′ \ sigma’_i = \ Sigma ‘_ {ii} σi ′ = Σii ′ для iii-й контрольной точки. В отличие от предыдущего распределения, мы устанавливаем среднее значение μ = 0 \ mu = 0μ = 0. Но когда мы обусловливаем совместное распределение тестовых и обучающих данных, результирующее распределение, скорее всего, будет иметь ненулевое среднее μ ′ ≠ 0 \ mu ’\ neq 0μ ′ ≠ 0.Извлечение μ ′ \ mu’μ ′ и σ ′ \ sigma’σ ′ не только приводит к более значимому прогнозу, но также позволяет нам сделать заявление о достоверности прогноза.

На следующем рисунке показан пример условного распределения. Поначалу никаких тренировочных точек не наблюдалось. Соответственно, средний прогноз остается равным 000, а стандартное отклонение одинаково для каждой контрольной точки. Наведя курсор на ковариационную матрицу, вы можете увидеть влияние каждой точки на текущую контрольную точку.Пока не наблюдаются точки тренировки, влияние соседних точек ограничено локально.

Точки обучения можно активировать, щелкнув по ним, что приведет к ограниченному распределению. Это изменение отражается в записях ковариационной матрицы и приводит к корректировке среднего и стандартного отклонения прогнозируемой функции. Как и следовало ожидать, неопределенность прогноза мала в регионах, близких к обучающим данным, и растет по мере удаления от этих точек.

В матрице ограниченной ковариации мы видим, что на корреляцию соседних точек влияет данные обучения. Если прогнозируемая точка лежит на данных обучения, корреляции с другими точками нет. Следовательно, функция должна проходить прямо через него. На прогнозируемые значения, расположенные дальше, также влияют обучающие данные – пропорционально их расстоянию.

Объединение разных ядер

Как описано ранее, сила гауссовских процессов заключается в выборе функции ядра.Это свойство позволяет экспертам вводить знания предметной области в процесс и придает гауссовским процессам гибкость для отслеживания тенденций в данных обучения. Например, выбирая подходящую полосу пропускания для ядра RBF, мы можем контролировать, насколько гладкой будет результирующая функция.

Большое преимущество ядер заключается в том, что их можно комбинировать вместе, в результате чего получается более специализированное ядро. Решение, какое ядро ​​использовать, во многом зависит от предварительных знаний о данных, например.грамм. если ожидаются определенные характеристики. Примерами этого могут быть стационарный характер или глобальные тенденции и закономерности. Как было сказано в разделе о ядрах, стационарный означает, что ядро ​​инвариантно к трансляции и, следовательно, не зависит от индекса iii. Это также означает, что мы не можем моделировать глобальные тренды, используя строго стационарное ядро. Помните, что ковариационная матрица гауссовских процессов должна быть положительно полуопределенной. При выборе оптимальных комбинаций ядер разрешены все методы, сохраняющие это свойство.{\ ast} (t, t ’) = k _ {\ text {lin}} (t, t’) \ cdot k _ {\ text {per}} (t, t ’) k ∗ (t, t ′) = klin (t, t ′) ⋅kper (t, t ′)

Однако комбинации не ограничиваются приведенным выше примером, и есть больше возможностей, таких как конкатенация или композиция с функцией. Чтобы показать влияние комбинации ядер и то, как она может сохранить качественные характеристики отдельных ядер, взгляните на рисунок ниже. Если мы добавим периодическое и линейное ядра, глобальный тренд линейного ядра будет включен в объединенное ядро.В результате получается периодическая функция, которая следует линейному тренду. Если вместо этого комбинировать одни и те же ядра посредством умножения, результатом будет периодическая функция с линейно растущей амплитудой от линейного параметра ядра ccc.

Если мы возьмем образцы из комбинированного линейного и периодического ядра, мы сможем наблюдать различные сохраненные характеристики в новом образце. Сложение приводит к периодической функции с глобальным трендом, в то время как умножение увеличивает периодическую амплитуду в направлении наружу.

Зная больше о том, как комбинации ядер влияют на форму результирующего распределения, мы можем перейти к более сложному примеру. На рисунке ниже наблюдаемые данные обучения имеют восходящий тренд с периодическим отклонением. Используя только линейное ядро, мы можем имитировать нормальную линейную регрессию точек. На первый взгляд, ядро ​​RBF точно аппроксимирует точки. Но поскольку ядро ​​RBF стационарно, оно всегда будет возвращаться к μ = 0 \ mu = 0μ = 0 в регионах, более удаленных от наблюдаемых обучающих данных.Это снижает точность прогнозов, которые уходят в прошлое или будущее. Улучшенная модель может быть создана путем объединения отдельных ядер посредством добавления, которое поддерживает как периодический характер, так и глобальный восходящий тренд данных. Эту процедуру можно использовать, например, при анализе погодных данных.

Используя флажки, различные ядра могут быть объединены для создания нового гауссовского процесса. Только с помощью Комбинация ядер позволяет захватывать характеристики более сложных обучающих данных.

Как обсуждалось в разделе о GP, гауссовский процесс может моделировать неопределенные наблюдения. Это можно увидеть, выбрав только линейное ядро, поскольку оно позволяет нам выполнять линейную регрессию, даже если наблюдалось более двух точек, и не все функции должны проходить непосредственно через наблюдаемые данные обучения.

Заключение

В этой статье вы должны были получить обзор гауссовских процессов и разработать более глубокую понимание того, как они работают.Как мы видели, гауссовские процессы предлагают гибкую основу для регрессии, и существует несколько расширений, которые сделать их еще более универсальными.

Например, иногда невозможно описать ядро ​​простыми словами. Чтобы преодолеть эту проблему, изучение специализированных функций ядра из базовых данных, например, с помощью глубокого обучения, является областью постоянных исследований. Кроме того, в нескольких статьях описаны связи между байесовским выводом, гауссовскими процессами и глубоким обучением.Хотя мы в основном говорим о гауссовских процессах в контексте регрессии, они могут быть адаптированы для разные цели, например Модель -пилинг и проверка гипотез. Сравнивая различные ядра в наборе данных, эксперты в предметной области могут предоставить дополнительные знания через соответствующая комбинация и параметризация ядра.

Если мы вызвали ваш интерес, мы составили список дальнейших сообщений в блогах по теме гауссовских процессов.Кроме того, мы связали две записные книжки Python, которые дадут вам практический опыт и помогут сразу же приступить к работе.

Произошла ошибка при настройке вашего пользовательского файла cookie

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку “Назад” и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Проблемы сингулярности в модели гауссовой смеси

Этот ответ даст представление о том, что происходит, что приводит к сингулярной ковариационной матрице во время подгонки GMM к набору данных, почему это происходит, а также что мы можем сделать, чтобы этого избежать.

Поэтому лучше всего начать с повторения шагов во время подгонки модели гауссовой смеси к набору данных. {-1}} (\ boldsymbol {x_i} – \ boldsymbol {\ mu_c})) $$

$ r_ {ic} $ дает нам для каждой точки данных $ x_i $ меру: $ \ frac {Probability \ that \ x_i \ принадлежит \ to \ class \ c} {Probability \ of \ x_i \ over \ all \ classes } $ следовательно, если $ x_i $ очень близко к одному гауссовскому c, он получит высокое значение $ r_ {ic} $ для этого гауссова значения и относительно низкие значения в противном случае.K \ pi_k N (\ boldsymbol {x_i} \ | \ \ boldsymbol {\ mu_k}, \ boldsymbol {\ Sigma_k})) $$

Итак, теперь мы вывели отдельные этапы расчета, и мы должны рассмотреть, что означает сингулярность матрицы. Матрица сингулярна, если она необратима. Матрица обратима, если существует матрица $ X $ такая, что $ AX = XA = I $. Если это не указано, матрица называется особой. То есть матрица вроде:

\ begin {bmatrix} 0 & 0 \\ 0 и 0 \ end {bmatrix}

не обратима и следует в единственном числе.{-1}} $, которая является обратимой ковариационной матрицы. Поскольку сингулярная матрица необратима, это вызовет ошибку во время вычисления.
Итак, теперь, когда мы знаем, как выглядит сингулярная необратимая матрица и почему это важно для нас во время расчетов GMM, как мы могли столкнуться с этой проблемой? Прежде всего, мы получим эту ковариационную матрицу $ \ boldsymbol {0} $, указанную выше, если многомерный гауссиан попадает в одну точку во время итерации между этапами E и M. Это может произойти, если у нас есть, например, набор данных, к которому мы хотим подогнать 3 гауссиана, но который на самом деле состоит только из двух классов (кластеров), так что, грубо говоря, два из этих трех гауссианов захватывают свой собственный кластер, в то время как последний гауссиан только управляет им. поймать одну единственную точку, на которой он сидит.Как это выглядит, мы увидим ниже. Но пошагово: Предположим, у вас есть двумерный набор данных, который состоит из двух кластеров, но вы этого не знаете и хотите подогнать к нему три гауссовские модели, то есть c = 3. Вы инициализируете свои параметры на этапе E и строите гауссианы поверх ваши данные, которые выглядят что-л. вроде (возможно, вы видите два относительно разбросанных кластера слева внизу и справа вверху): После инициализации параметра вы итеративно выполняете шаги E, T. Во время этой процедуры три гауссианца как бы блуждают в поисках оптимального места.Если вы понаблюдаете за параметрами модели, то есть $ \ mu_c $ и $ \ pi_c $, вы увидите, что они сходятся, что после некоторого количества итераций они больше не изменятся, и, таким образом, соответствующий гауссиан нашел свое место в пространстве. В случае, когда у вас есть матрица сингулярностей, вы сталкиваетесь с чем-л. нравиться: Я обвел третью гауссовскую модель красным. Итак, вы видите, что этот гауссовский объект находится на одной единственной точке данных, в то время как два других требуют остальных. Здесь я должен заметить, что для того, чтобы нарисовать такую ​​фигуру, я уже использовал ковариационную регуляризацию, которая является методом предотвращения матриц сингулярностей и описывается ниже.K \ pi_k N (\ boldsymbol {x_i \ | \ \ boldsymbol {\ mu_k}, \ boldsymbol {\ Sigma_k}})} $$ вы видите, что там $ r_ {ic} $ будут иметь большие значения, если они, скорее всего, находятся в кластере c, и низкие значения в противном случае. Чтобы сделать это более очевидным, рассмотрим случай, когда у нас есть два относительно распределенных гауссиана и один очень узкий гауссиан, и мы вычисляем $ r_ {ic} $ для каждой точки данных $ x_i $, как показано на рисунке: Итак, просмотрите точки данных слева направо и представьте, что вы записываете вероятность для каждого $ x_i $ того, что он принадлежит к красному, синему и желтому гауссиану.Вы можете видеть, что для большей части $ x_i $ вероятность того, что он принадлежит к желтому гауссиану, очень мала. В приведенном выше случае, когда третий гауссиан находится на одной единственной точке данных, $ r_ {ic} $ больше нуля только для этой одной точки данных, в то время как он равен нулю для всех остальных $ x_i $. (сворачивается на эту точку данных -> Это происходит, если все другие точки с большей вероятностью являются частью гауссовского один или два, и, следовательно, это единственная точка, которая остается для гауссовской тройки -> Причина, по которой это происходит, может быть найдена во взаимодействии между сам набор данных в инициализации гауссианцев. T (\ boldsymbol {x_i} – \ boldsymbol {\ mu_c}) $$ мы видели, что все $ r_ {ic} $ равны нулю вместо одного $ x_i $ с [23.38566343 8.07067598]. Теперь формула требует, чтобы мы вычислили $ (\ boldsymbol {x_i} – \ boldsymbol {\ mu_c}) $. Если мы посмотрим на $ \ boldsymbol {\ mu_c} $ для этого третьего гауссовского языка, мы получим [23.38566343 8.07067598]. О, но подождите, это то же самое, что и $ x_i $, и это то, что Бишоп написал: «Предположим, что один из компонентов смеси модель, скажем $ j $ th компонент, имеет среднее значение $ \ boldsymbol {\ mu_j} $ точно равна одной из точек данных, так что $ \ boldsymbol {\ mu_j} = \ boldsymbol {x_n} $ для некоторого значения n “(Бишоп, 2006, стр.434). Так что же будет? Что ж, этот член будет равен нулю, и, следовательно, эта точка данных была единственным шансом для ковариационной матрицы не получить ноль (поскольку эта точка данных была единственной, где $ r_ {ic} $> 0), теперь она получает ноль и выглядит как :

\ begin {bmatrix} 0 & 0 \\ 0 и 0 \ end {bmatrix}

Следовательно, как сказано выше, это сингулярная матрица и приведет к ошибке во время вычислений многомерного гауссиана. Итак, как мы можем предотвратить такую ​​ситуацию. Итак, мы видели, что ковариационная матрица сингулярна, если это матрица $ \ boldsymbol {0} $.Следовательно, чтобы предотвратить сингулярность, мы просто должны предотвратить превращение ковариационной матрицы в матрицу $ \ boldsymbol {0} $. Это делается путем добавления очень небольшого значения (в GaussianMixture sklearn это значение установлено на 1e-6) к дигоналу ковариационной матрицы. Существуют также другие способы предотвращения сингулярности, такие как обнаружение коллапса гауссова уравнения и установка для его среднего значения и / или ковариационной матрицы нового, произвольно высокого значения (я). Эта ковариационная регуляризация также реализована в приведенном ниже коде, с помощью которого вы получаете описанные результаты.Возможно, вам придется запустить код несколько раз, чтобы получить сингулярную матрицу ковариации, поскольку, как сказано. это не должно происходить каждый раз, но также зависит от первоначальной установки гауссианцев.

  импортировать matplotlib.pyplot как plt
из стиля импорта matplotlib
style.use ('пятьдесят восемь')
из sklearn.datasets.samples_generator импортировать make_blobs
импортировать numpy как np
из scipy.stats import multivariate_normal


# 0. Создать набор данных
X, Y = make_blobs (cluster_std = 2.5, random_state = 20, n_samples = 500, центры = 3)

# Stratch dataset для получения данных эллипсоида
X = np.точка (X, np.random.RandomState (0) .randn (2,2))


класс EMM:

    def __init __ (self, X, number_of_sources, итераций):
        self.iterations = итерации
        self.number_of_sources = number_of_sources
        self.X = X
        self.mu = Нет
        self.pi = Нет
        self.cov = Нет
        self.XY = Нет



    # Определите функцию, которая будет выполняться в течение i итераций:
    def run (self):
        self.reg_cov = 1e-6 * np.identity (len (self.X [0]))
        x, y = np.meshgrid (np.sort (self.X [:, 0]), np.sort (self.X [:, 1]))
        self.XY = np.array ([x.flatten (), y.flatten ()]). T


        # 1. Установите начальные значения mu, ковариации и пи.
        self.mu = np.random.randint (min (self.X [:, 0]), max (self.X [:, 0]), size = (self.number_of_sources, len (self.X [0]) )) # Это матрица размера nxm, поскольку мы предполагаем n источников (n гауссианов), каждый из которых имеет m измерений
        self.cov = np.zeros ((self.number_of_sources, len (X [0]), len (X [0]))) # Нам нужна ковариационная матрица размером nxmxm для каждого источника, поскольку у нас есть m функций -> Мы создаем симметричные ковариационные матрицы с единицами на дигональной
        для тусклого диапазона (len (self.cov)):
            np.fill_diagonal (self.cov [dim], 5)


        self.pi = np.ones (self.number_of_sources) /self.number_of_sources # Являются "дробями"
        log_likelihoods = [] # В этом списке мы храним логарифмические вероятности для каждой итерации и строим их в конце, чтобы проверить,
                             # если мы сошлись

        # Постройте начальное состояние
        fig = plt.figure (figsize = (10,10))
        ax0 = fig.add_subplot (111)
        ax0.scatter (self.X [:, 0], self.X [:, 1])
        для m, c в zip (сам.mu, self.cov):
            c + = self.reg_cov
            multi_normal = многовариантная_нормальная (среднее = m, cov = c)
            ax0.contour (np.sort (self.X [:, 0]), np.sort (self.X [:, 1]), multi_normal.pdf (self.XY) .reshape (len (self.X), len (self.X)), colors = 'черный', альфа = 0,3)
            ax0.scatter (m [0], m [1], c = 'серый', zorder = 10, s = 100)


        mu = []
        cov = []
        R = []


        для i в диапазоне (self.iterations):

            mu.append (self.mu)
            cov.append (self.cov)


            # E Step
            r_ic = np.нули ((len (self.X), len (self.cov)))

            для m, co, p, r в zip (self.mu, self.cov, self.pi, range (len (r_ic [0]))):
                co + = self.reg_cov
                mn = многовариантное_нормальное (среднее = m, cov = co)
                r_ic [:, r] = p * mn.pdf (self.X) /np.sum ([pi_c * multivariate_normal (mean = mu_c, cov = cov_c) .pdf (X) для pi_c, mu_c, cov_c в zip (self .pi, self.mu, self.cov + self.reg_cov)], axis = 0)
            R.append (r_ic)

            # M Шаг

            # Вычислить новый вектор среднего и новые ковариационные матрицы, основываясь на вероятной принадлежности одного x_i к классам c -> r_ic
            себя.mu = []
            self.cov = []
            self.pi = []
            log_likelihood = []

            для c в диапазоне (len (r_ic [0])):
                m_c = np.sum (r_ic [:, c], ось = 0)
                mu_c = (1 / m_c) * np.sum (self.X * r_ic [:, c] .reshape (len (self.X), 1), axis = 0)
                self.mu.append (mu_c)

                # Вычислить ковариационную матрицу для каждого источника на основе нового среднего
                self.cov.append (((1 / m_c) * np.dot ((np.array (r_ic [:, c]). reshape (len (self.X), 1) * (self.X-mu_c)) .T, (сам.X-mu_c))) + self.reg_cov)
                # Вычислить pi_new, который является «долей баллов», соответственно долей вероятности, присвоенной каждому источнику
                self.pi.append (m_c / np.sum (r_ic))



            # Журнал вероятности
            log_likelihoods.append (np.log (np.sum ([k * multivariate_normal (self.mu [i], self.cov [j]). pdf (X) для k, i, j в zip (self.pi, range (len (self.mu)), range (len (self.cov)))])))



        fig2 = plt.figure (figsize = (10,10))
        ax1 = fig2.add_subplot (111)
        ax1.plot (диапазон (0, self.iterations, 1), log_likelihoods)
        # plt.show ()
        печать (mu [-1])
        печать (cov [-1])
        для r в np.array (R [-1]):
            печать (r)
        печать (X)

    def предсказывать (сам):
        # Перенесите точку на fittet gaussians
        fig3 = plt.figure (figsize = (10,10))
        ax2 = fig3.add_subplot (111)
        ax2.scatter (self.X [:, 0], self.X [:, 1])
        для m, c в zip (self.mu, self.cov):
            multi_normal = многовариантная_нормальная (среднее = m, cov = c)
            ax2.contour (np.sort (self.X [:, 0]), np.sort (self.X [:, 1]), multi_normal.pdf (self.XY) .reshape (len (self.X), len ( self.X)), colors = 'черный', альфа = 0,3)




EMM = EMM (X; 3,100)
EMM.run ()
EMM.predict ()
  

Метод исключения Гаусса | Суперпроф

Метод исключения Гаусса – еще один метод поиска решения системы. Он выполняется на расширенной матрице, и мы используем операции со строками, чтобы найти решение конкретной системы. Система должна содержать линейные уравнения, иначе метод исключения Гаусса будет пустой тратой времени и усилий.Другое название этого метода – «сокращение строк». В этом методе есть два этапа: одно – прямое исключение, а другое – обратная замена.

Оба метода разные. Многие студенты думают, что они различаются по операциям, но это неверно, они различаются по результатам. Это означает, что они дают разные результаты. Прямое исключение фокусируется на сокращении строк для перевода расширенной матрицы в эшелонированную форму. Самая большая цель прямого исключения – выяснить, есть ли у системы решения или нет? В случае, если в системе нет решения, значит, нет причин сокращать матрицу на следующем этапе.

Однако, если система выглядит многообещающей, выполняется обратная подстановка, чтобы найти результат решения. Это также последний шаг метода исключения Гаусса, и он найдет результат матрицы.

Система трех уравнений с тремя неизвестными

Метод Гаусса заключается в использовании метода исключения , так что в каждом уравнении на одно неизвестное меньше, чем в предыдущем уравнении.

1.Поместите уравнение с коэффициентом x : 1 или −1 в качестве первого уравнения. Если это невозможно с x, используйте y или z и измените порядок неизвестных:

2. Выполните метод исключения с 1-м и 2-м уравнениями для исключает член x во втором уравнении . Затем во втором уравнении поместите результат операции:

После сложения обоих уравнений:

3.Сделайте то же самое с 1-м и 3-м уравнениями с по , исключите член x :

После сложения обоих уравнений:

4. Выполните метод исключения для 2-го и 3-го уравнение:

Сложение обоих уравнений:

5. Получится другая эквивалентная система:

6. Решите систему:

Примеры

Q1

Добавление обоих уравнений:

Добавление обоих уравнений:

Q.2

Сложение обоих уравнений:

В результате сложения обоих уравнений:

2

Лучшие преподаватели по математике

Первый урок бесплатно

Задачи со словом

Q.1 Покупатель в супермаркете заплатил в общей сложности 156 долларов за 24 литра молока, 6 кг ветчины и 12 литров оливкового масла. Рассчитайте цену каждой позиции, зная, что 1 литр масла стоит в три раза дороже 1 литра молока, а 1 кг ветчины стоит столько же, сколько 4 литра масла и 4 литра молока.

молоко x

ветчина y

оливковое масло z

Размещение

:

000

000

000

000 долларов

ветчина 16 долларов

оливковое масло 3 доллара

Q.2 Видеомагазин специализируется на фильмах трех жанров: детский, вестерн и ужасы. Известно, что:

60% детских фильмов плюс 50% вестернов составляют 30% всех фильмов.

20% детских, 60% вестернов и 60% фильмов ужасов составляют половину всех фильмов в видеомагазине.

Вестернов на 100 больше, чем детских.

Найдите количество фильмов в каждом жанре.

children x

western y

horror z

Поместив уравнение 3 в оба уравнения:

Сложив оба уравнения:

000

000

дети 500 фильмов

вестерн 600 фильмов

ужасы 900 фильмов

Q.3 Стороны треугольника равны 26, 28 и 34 см. В центре каждой вершины расположены три касательные друг к другу окружности. Вычислите длину радиуса каждого круга.

Веб-сайт гауссовских процессов

Веб-сайт гауссовских процессов

Этот веб-сайт представляет собой обзор ресурсов занимается вероятностным моделированием, выводом и обучением на основе гауссовского процессы.Хотя гауссовские процессы имеют долгую историю в области статистики, они, похоже, широко использовались только в нише области. С появлением машин с ядром в сообществе машинного обучения модели, основанные на гауссовских процессах, стали обычным явлением для задач регрессия (кригинг) и классификация, а также множество более специализированных Приложения.

Гауссовские процессы для машинного обучения, Карл Эдвард Расмуссен и Крис Уильямс, MIT Press, 2006, онлайн-версия.

Статистический Интерполяция пространственных данных: некоторая теория кригинга, Майкл Л. Стейн, Springer, 1999.

Статистика для пространственных данных (пересмотренное издание), Ноэль А. К. Кресси, Wiley, 1993

сплайновые модели для Данные наблюдений, Грейс Вахба, SIAM, 1990

Байесовское исследование Кухня в отеле Вордсворт, Грасмер, Эмблсайд, озеро Округ, Великобритания, 05 – 07 сентября 2008 г.

Учебное пособие под названием “Достижения в Гауссовские процессы декабря.4-е место на выставке NIPS 2006 в Ванкувере, слайды, лекция.

Гауссовские процессы в Практический семинар в Блетчли-парке, Великобритания, 12-13 июня 2006 г.

Открытые задачи в гауссовских процессах для семинара по машинному обучению на nips * 05 в Уистлере, 10 декабря, 2005 г.

Гауссовский процесс Круглый стол в Шеффилде, 9-10 июня 2005 г.

Сеть ядер-машин сайт.

запись в Википедии по гауссовским процессам.

Веб-сайт ai-geostats для пространственная статистика и геостатистика.

Библиография гауссовского Модели процессов в веб-сайте моделирования динамических систем, поддерживаемый Юшем Коцианом.

Андреас Гейгер написал простой гауссовский процесс регрессионный Java-апплет, иллюстрирующий поведение ковариационных функций и гиперпараметры.

Матлаб Матлаб Матлаб Матлаб упаковка титул автор реализация описание млрд куб. М Машина байесовского комитета Антон Швайхофер matlab и NETLAB Расширение реализации Netlab для регрессии GP.Это позволяет масштабная регрессия на основе приближения BCM, см. также сопроводительный документ фбм Программное обеспечение для гибкого байесовского моделирования Рэдфорд М. Нил C для linux / unix Обширный и хорошо документированный пакет, реализующий методы Монте-Карло цепи Маркова для Байесовский вывод в нейронных сетях, гауссовские процессы (регрессия, двоичный и мультиклассовая классификация), модели смеси и деревья диффузии Дирихле. gp-lvm и fgp-lvm (быстрая) реализация моделей со скрытыми переменными гауссовского процесса Нил Д. Лоуренс matlab и C г / мл Код из книги Расмуссена и Вильямса: гауссовские процессы для машинного обучения. Карл Эдвард Расмуссен и Ханнес Никиш matlab и октава Набор инструментов GPML реализует приблизительные алгоритмы вывода для Гауссовские процессы, такие как распространение ожидания, Лапласа Аппроксимация и вариационный байесовский метод для широкого класса правдоподобия функции как для регрессии, так и для классификации.Поставляется с большим алгебра ковариации и функций среднего, позволяющая гибкое моделирование. Код полностью совместим с Octave 3.2.x. JMLR документ с описанием набора инструментов. c ++ – ivm Разреженные приближения на основе информационной векторной машины Нил Д. Лоуренс C ++ Программное обеспечение IVM на C ++, также включает модель шума нулевой категории для полу-контролируемого обучения. BFD Дискриминантное программное обеспечение Байеса Фишера Tonatiuh Peña Centeno Реализует гауссовский процесс интерпретация дискриминанта Кернела Фишера. гпор Гауссовские процессы для порядковой регрессии Вэй Чу C для linux / unix Программная реализация гауссовских процессов порядковой регрессии. Обеспечивает аппроксимацию Лапласа, распространение ожиданий и вариационную нижнюю границу. MCMCstuff Методы MCMC для MLP, GP и прочего Аки Вехтари matlab и C Набор функций MATLAB для байесовского вывод с помощью методов Монте-Карло цепи Маркова (MCMC).Цель этого Toolbox должен был портировать некоторые функции из fbm в Matlab для упрощения разработки для пользователей Matlab. огп Разреженные онлайн-гауссовские процессы Лехель Чато matlab и NETLAB Приблизительное онлайн-обучение в разреженных моделях гауссовских процессов для регрессии (включая несколько негауссовских функций правдоподобия) и классификации. согп Библиотека C ++ для разреженных онлайн-гауссовских процессов Дэн Гроллман C ++ Разреженная онлайн-библиотека C ++ для гауссовского процесса на основе кандидатской диссертации Лехеля Чато спгп.tgz или .zip Гауссовские процессы с разреженными псевдовходами Эд Снельсон Реализует разреженную регрессию GP, как описано в разделе «Разреженные гауссовские процессы», с использованием псевдовходов и гибких и эффективных моделей гауссовских процессов для машинного обучения. SPGP использует оптимизацию предельного правдоподобия на основе градиента для поиска подходящих базисных точек и гиперпараметров ядра в единой совместной оптимизации. тгп Деревянные гауссовские процессы Роберт Б.Грамматичность C / C ++ для R Байесовский непараметрический и нестационарная регрессия по древовидным гауссовским процессам со скачками к предельному линейная модель (LLM). Также реализованы особые случаи, включая байесовский линейный модели, линейная тележка, стационарный разделимый и изотропный гауссовский процесс регресс. Включает функции построения 1-го и 2-го графика (с более высокой размерностью возможности проецирования и срезов), а также рисование дерева, предназначенное для визуализация вывода класса tgp. См. Также Gramacy 2007 Тпрос Регрессия гауссовского процесса Дэвид Маккей и Марк Гиббс С Tpros – это программа гауссовского процесса, написанная Марком Гиббсом и Дэвидом. Маккей. GP Demo Октавная демонстрация интерполяции гауссовского процесса Дэвид Маккей октава Эта ДЕМО отлично работает с октавой 2.0 и не работает с 2.1.33. GPClass Код Matlab для классификации гауссовских процессов Дэвид Барбер и К. К. И. Уильямс Реализует аппроксимацию Лапласа, как описано в Байесовской классификации с гауссовскими процессами для бинарной и мультиклассовой классификации. VBGP Вариационная байесовская полиномиальная пробит-регрессия с гауссовскими приоритетами процесса Марк Джиролами и Саймон Роджерс Реализует вариационный аппроксимация для мультиклассовой классификации на основе гауссовского процесса как описана в статье Вариационная байесовская полиномиальная пробитная регрессия. pyGPs Гауссовские процессы регрессии и классификации Марион Нойманн Питон pyGPs – это библиотека, содержащая объектно-ориентированную реализацию Python для регрессии и классификации гауссовского процесса (GP).github gaussian-process Регрессия гауссовского процесса Ананд Патил Питон в разработке gptk Набор инструментов для гауссовского процесса Альфредо Калаитцис R Пакет gptk реализует универсальный набор инструментов для регрессии гауссовского процесса с функцией ковариации RBF. На основе реализации MATLAB, написанной Нилом Д.Лоуренс.

Другое программное обеспечение, которое может быть полезно для реализации гауссовских моделей процессов:

Ниже представлен сборник статей, относящихся к обучению в гауссовском процессе. модели. Работы отсортированы по тематике, с профессиональными работами. происходит под несколькими заголовками.

Учебники

В нескольких статьях представлены учебные материалы, подходящие для первого знакомства с обучение в гауссовских моделях процессов.Они варьируются от очень коротких [Williams 2002] до средних [MacKay 1998], [Williams 1999] к более сложным [Расмуссен и Уильямс 2006]. Все это требует лишь минимума предпосылок в виде элементарная теория вероятностей и линейная алгебра.

Регрессия

Простейшие применения гауссовских моделей процессов для (сопряженного случая) регрессия с гауссовым шумом. Смотрите приближение раздел для статей, которые имеют дело с разреженным или быстрым приближением техники.О’Хаган 1978 представляет собой раннюю ссылку от сообщества статистики для использования гауссовского процесса в качестве априорного над функции, идея, которая была представлена ​​только сообществу машинного обучения Уильямса и Расмуссена 1996.

Классификация

Точный вывод в моделях гауссовского процесса для классификации не поддается обработке. Было предложено несколько схем аппроксимации, в том числе метод Лапласа, вариационные приближения, методы среднего поля, цепь Маркова Монте-Карло и Ожидаемое распространение.См. Также приближение раздел. Мультиклассовая классификация может быть обработана явно или разложена на несколько бинарных (одна против остальных) задач. Для введения см. например Уильямс и Барбер 1998 или Кусс и Расмуссен 2005. Границы из PAC-байесовская точка зрения применена в Seeger 2002.

Ковариационные функции и свойства гауссовских процессов

Свойства гауссовских процессов контролируются (функцией среднего и) ковариационная функция. Некоторые ссылки здесь описывают ковариацию различий функции, в то время как другие дают математические характеристики, см. например.Abrahamsen 1997 за обзор. Некоторые ссылки описывать нестандартные ковариационные функции, приводящие к нестационарности и т. д.

Выбор модели

Приблизительные значения

Есть две основные причины для приближения в моделях гауссовских процессов. Либо из-за аналитической неразрешимости, например из-за нестыковок в классификации и регрессия с негауссовым шумом. Или чтобы получить вычислительную преимущество при использовании больших наборов данных за счет использования разреженного приближения.Некоторые методы решают обе проблемы одновременно. В методы аппроксимации и алгоритмы приближенного вывода весьма разнообразны, см. Quiñonero-Candela и Ramussen 2005 за объединяющую основу для разреженных приближений в Гауссовская регрессионная модель.

Ссылки статистического сообщества

Гауссовские процессы имеют долгую историю в статистическом сообществе. Они имеют особенно хорошо развита в геостатистике под названием кригинг . Статьи сгруппированы, потому что они написаны с использованием общая терминология и немного отличается от типичной машины учебные документы,

Последовательность, кривые обучения и границы

В статьях этого раздела приведены теоретические результаты по обучению. кривые , которые описывают ожидаемую производительность обобщения как функция количества учебных случаев.Последовательность решает вопрос приближается ли решение к истинному процессу генерации данных в пределе бесконечного множества обучающих примеров.

Воспроизведение гильбертовых пространств ядра

Обучение с подкреплением

Гауссовские модели процессов со скрытыми переменными (GP-LVM)

Приложения

Другие темы

Этот раздел содержит очень разнообразную коллекцию других применений вывода. в гауссовских процессах, которые не подходят ни для одной из вышеперечисленных категорий.