Примеры решения задач
Пример 1. Найти момент инерции тонкого однородного диска массой и радиусаотносительно: а) оси симметрии, перпендикулярной к плоскости диска; б) оси, совпадающей с диаметром диска.
Р е ш е н и е. а)Выберем на диске цилиндрический слой радиуса и шириной(см. рис. 3а). Так как все элементы цилиндрического слоя находятся на одном расстоянии от центра кольца, его момент инерции равен
(14)
где – масса кольца, которую можно найти, определив поверхностную плотность материала дискаи умножив ее на площадь поверхности кольцат.е.
Подставляя это значение в (14) интегрируя пов пределах от 0 до, найдем момент инерции диска относительно оси симметрии
(15)
б)
Для нахождения момента инерции диска
относительно диаметра, например оси
воспользуемся соотношением (6).
Подставляя в это выражение значение из уравнения (15), найдем момент инерции диска относительно диаметра
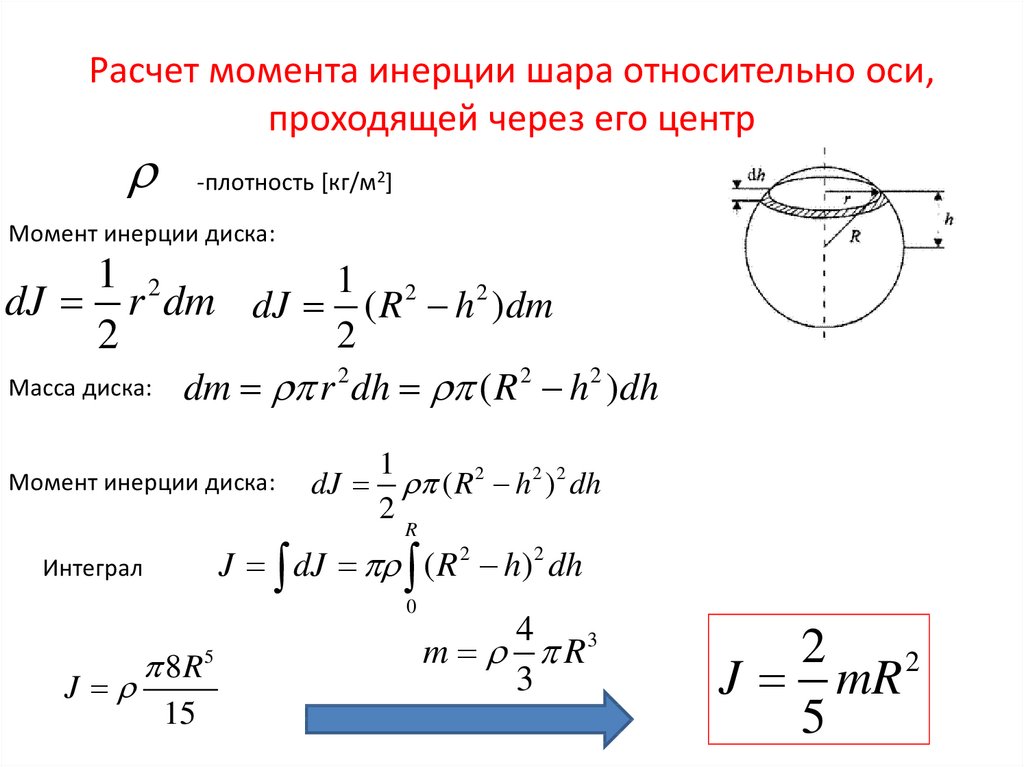
Пример 2. Найти момент инерции однородного шара массы и радиусаотносительно оси, совпадающей с центром шара.
Ре ш е н и е. Вычисление момента инерции шара прямым методом, т.е. с использованием уравнения (1) довольно трудоемкая математическая задача, поэтому для нахождения этого момента инерции воспользуемся соотношением (5). Проведем три взаимно перпендикулярные осипересекающиеся в центре шара (см. рис. 4). Очевидно, что
поэтому соотношение (5) перепишем в виде
(16)
где
– искомый момент инерции,– момент инерции шара относительно
центра шара.
Для нахождения момента инерции выберем тонкий сферический слой радиусаи толщинойцентр которого совпадает с центром шара (на рис. 4 он выделен цветом). Все элементы этого слоя находятся на одинаковом расстоянии от центра шара, поэтому его момент инерции относительно центра шара равен
. (17)
Объемная плотность шара равна , умножая ее на объем тонкого сферического слоянайдем массу сферического слоя
Подставляя это выражение в (17) и интегрируя в пределах от 0 до , найдем момент инерции шара относительно центра
С учетом этого из уравнения (16) находим искомый момент инерции шара
Пример
3. Однородный
цилиндр радиуса
раскрутили вокруг его оси до угловой
скоростии поместили затем в угол (рис.
Р е ш е н и е. Расставим силы, действующие на цилиндр. Запишем уравнение, описывающее выражение цилиндра относительно его оси
(18)
где – момент инерции цилиндра относительно этой оси. Знак “–” в левой части этого уравнения обусловлен тем, что при замедленном движении модуль углового ускоренияТак как нам необходимо найти число оборотов, которое сделает цилиндр до остановки, исключим из уравнения (18) время. Для этого умножим и разделим левую часть уравнения (18) на
где – угловая скорость вращения цилиндра в некоторый момент времени. После преобразований получим
. (19)
Прежде чем решать это уравнение, найдем выражения для сил трения. Так как центр цилиндра покоится,
Запишем
это уравнение в проекциях на оси
и(см.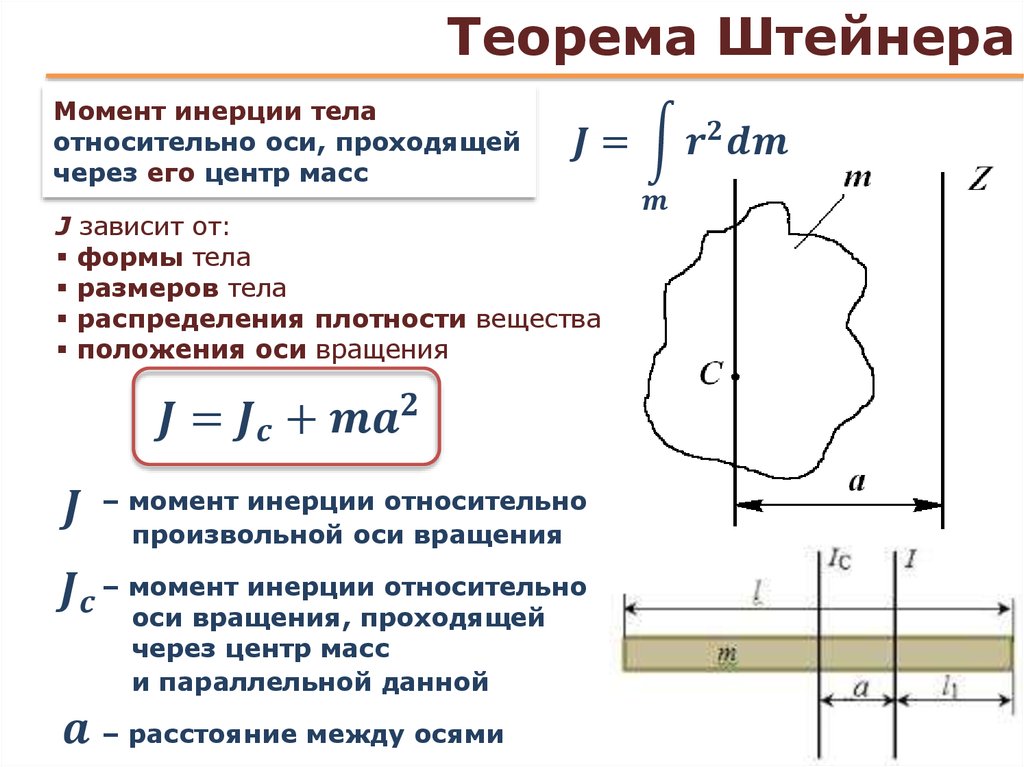
Решая эту систему уравнений, учитывая, что аполучим выражения для сил трения
Подставляя эти выражения в уравнение (19) и интегрируя левую часть этого уравнения в пределах от до 0, а правую часть в пределах от 0 до, найдем число оборотов, которое сделает цилиндр до остановки
Пример 4. Однородный шар скатывается без скольжения по наклонной плоскости, составляющей угол с горизонтом. Найти ускорениецентра шара и кинетическую энергию шара через времяпосле начала движения.
Р е ш е н и е. Решим задачу двумя способами.
а) Шар совершает
плоское движение. Свяжем подвижную
систему отсчета с центром шара. Эта
система движется поступательно
относительно наклонной плоскости, а
шар в этой системе вращается вокруг
оси, проходящей через его центр. Расставим
силы, действующие на шар в
процессе движения (см.
рис.6). Запишем
теорему о движении центра масс в проекции
на ось
(см.
рис.6)
(20)
Уравнение вращательного движения шара вокруг оси, проходящей через центр масс имеет вид
(21)
(22)
Используя формулу (13) для кинетической энергии тела, совершающего плоское движение, и учитывая, что в интересующий нас момент времени и(т.к.ипостоянные), найдем кинетическую энергию шара через времяпосле начала движения
б) Так как шар
катится без проскальзывания, точка
соприкосновения шара
с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точкуявляется мгновенной осью вращения.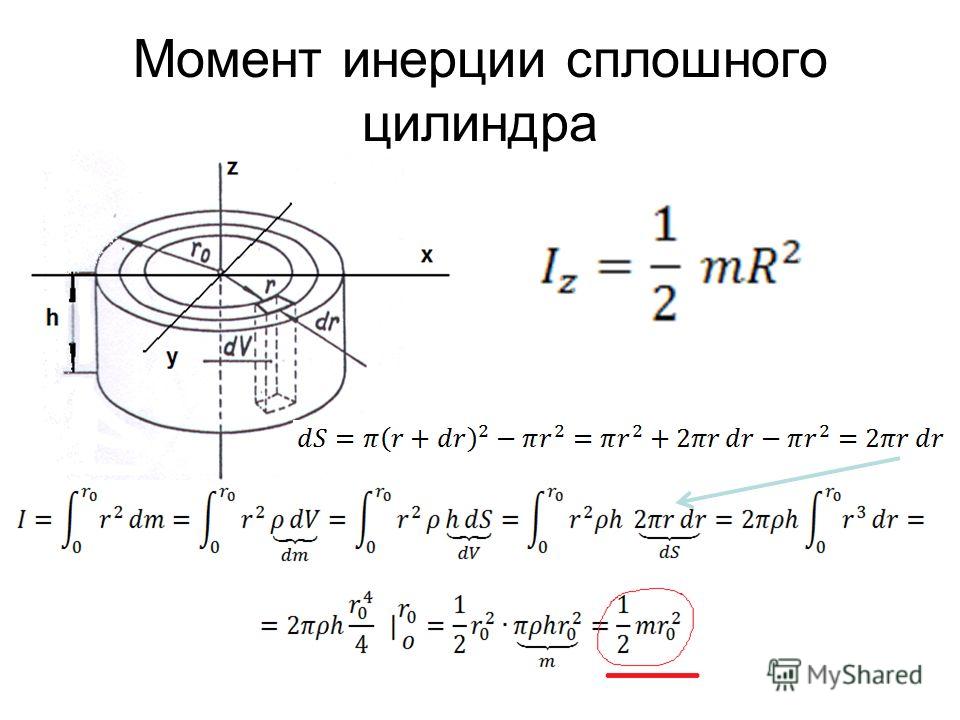
(23)
где – момент инерции шара относительно мгновенной оси вращения. Согласно теореме Штейнера момент инерцииравен
Подставляя это выражение в уравнение (23), находим ускорение центра шара и его угловое ускорение(см. уравнения (22)).
Кинетическая энергия шара, в этом случае, определяется только вращательным движением
Заметим, что при любом способе решения, кинетическую энергию шара можно найти из закона сохранения энергии (сила трения работы не совершает, т.к. эта сила – сила трения покоя). Пусть за время высота центра шара изменилась на(см. рис.6), тогда
(24)
где – расстояние, пройденное центром шара за времяПодставляя в (24) выражение дляи, находим кинетическую энергию шара
Пример
5.
Р е ш е н и е. Решим задачу двумя способами. Первое решение приведем в инерциальной системе отсчета, т.е. в системе, в которой стержень вращается. Второе решение – в неинерциальной системе отсчета, жестко связанной со стержнем.
а) Система отсчета, в которой будем решать задачу, на рис. 7 не показана. Решение задачи относительно вертикальной оси вращения не даст желаемого результата, т.к. моменты сил, действующих на стержень (сила тяжести и сила реакции в точке ), относительно этой оси равны нулю, и величина момента импульса остается постоянной.
Поэтому будем решать задачу относительно точки подвеса стержня. Напомним, что уравнение моментов относительно точки имеет вид
откуда видно, что направление изменения момента импульса совпадает по направлению с направлением момента силдействующих на стержень, поэтому в дальнейшем это уравнение будем записывать для модулейи
(25)
Момент силы реакции
в точке
равен нулю, т.
(26)
Найдем величину и направление момента импульса стержня относительно точкиДля этого выделим на стержне небольшой участок длинойи массойположение которого относительно точкизададим радиус-вектором(см. рис. 7). Обозначим величину момента импульса этого участка какТак как стержень вращается вокруг вертикальной оси, так как показано на рисунке, скоростьэтого участка будет направлена за плоскость рисунка, поэтому как следует из определения момента импульса
,
он будет направлен перпендикулярно стержню, как показано на рис. 7. Очевидно, что направления всех моментов импульса остальных участков стержня будут иметь такое же направление, поэтому результирующий момент импульса будет также перпендикулярен стержню. Учитывая, что векторы ивзаимно перпендикулярны, величинаравна
Интегрируя это уравнение
найдем величину момента импульса стержня относительно точки
Момент
импульса поворачивается вместе со
стержнем, и за время
повернется на некоторый угол,
получив приращение(см.
рис.8).
Найдем величину этого приращения
или
. (27)
Подставляя уравнение (26) и (27) в уравнением моментов (25), получим
где . Преобразуем это уравнение к виду
. (28)
Если величина
уравнение (28) имеет одно решение , и это положение устойчивое, т.е. стержень будет занимать вертикальное положение и будет вращаться вокруг собственной оси.
Если то уравнение (28) будет иметь два решение
и ,
причем можно показать, что первое решение перестает быть устойчивым, и стержень отклонится на угол, определяемый вторым решением.
б) Решим теперь
задачу в неинерциальной системе отсчета,
жестко связанной со стержнем. В этой
системе отсчета на стержень, кроме сил
взаимодействия действует центробежная
сила инерции.
Так как стержень находится
в равновесии, сумма моментов сил,
действующих на стержень, должна равняться
нулю, т.е.
где – величина момента силы тяжести,– величина момента центробежной силы инерции относительно точкиВеличина момента силы тяжести определяется уравнением (26). Для нахождения момента центробежной силы инерции воспользуемся рис. 7, считая, что стержень покоится.
На выделенный участок стержня действует центробежная сила инерции
величина момента которой, относительно точки равна
Интегрируя это выражение по всей длине стержня, получим
.
Подставляя это выражение и соотношение (26) в уравнение моментов (25), получим уравнение
,
в точности совпадающее с уравнением (28).
Надо заметить,
что решение этой задачи в неинерциальной
системе отсчета много проще, чем в
инерциальной.
Пример 6. Однородная тонкая квадратная пластинка массы может свободно вращаться вокруг неподвижной вертикальной оси, совпадающей с одной из ее сторон. В центр пластины по нормали к ней упруго ударяется шарик массылетевший со скоростьюНайти величину скорости шарикасразу после удара.
Р е ш е н и е. Система “пластина-шарик” незамкнута, так как для удержания оси пластины в неподвижном состоянии к ней необходимо приложить внешние силу. Однако надо заметить, что момент этих внешних сил относительно оси равны нулю, т.к. они приложены непосредственно к оси.
Для решения задачи воспользуемся законами сохранения энергии (удар упругий) и законом сохранения момента импульса (сумма момента внешних сил относительно оси равен нулю). Будем считать, что длина стороны пластины равна и шарик после удара будет лететь в прежнем направлении, тогда
,
где
– момент инерции пластины относительно
оси,– угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.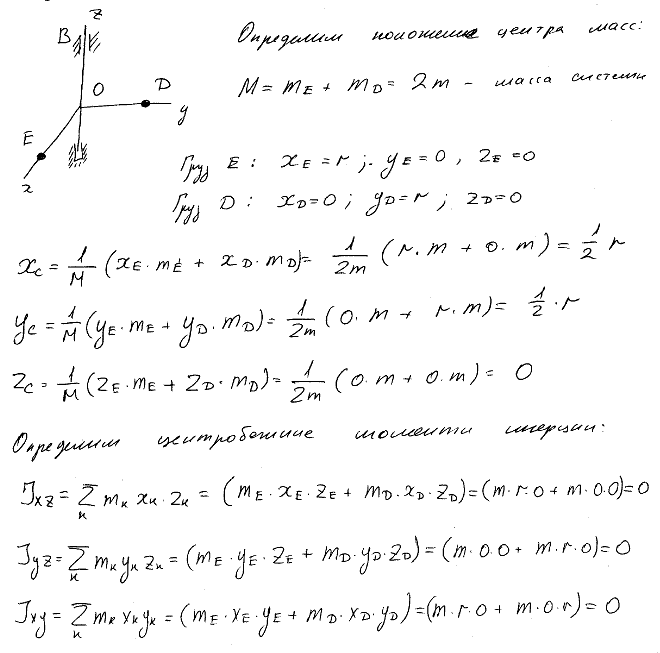
Для простоты решения этой системы перепишем ее в виде
(29)
Разделив первое уравнение не второе, получим
(30)
Решая совместно уравнения (29) и(30) и учитывая, что момент инерции пластины относительно оси, совпадающей с одной из ее сторон равен (докажите это самостоятельно), найдем скорость шарика после удара
Заметим, что если , скорость шарика после удара становится отрицательной. Это означает, что пришарик полетит в обратную сторону.
Пример
7. Однородный
диск радиуса
и массылежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концукоторой приложили постоянную горизонтальную
силуПосле начала движения диска точкапереместилась на расстояниеНайти угловую скорость диска к этому
моменту времени.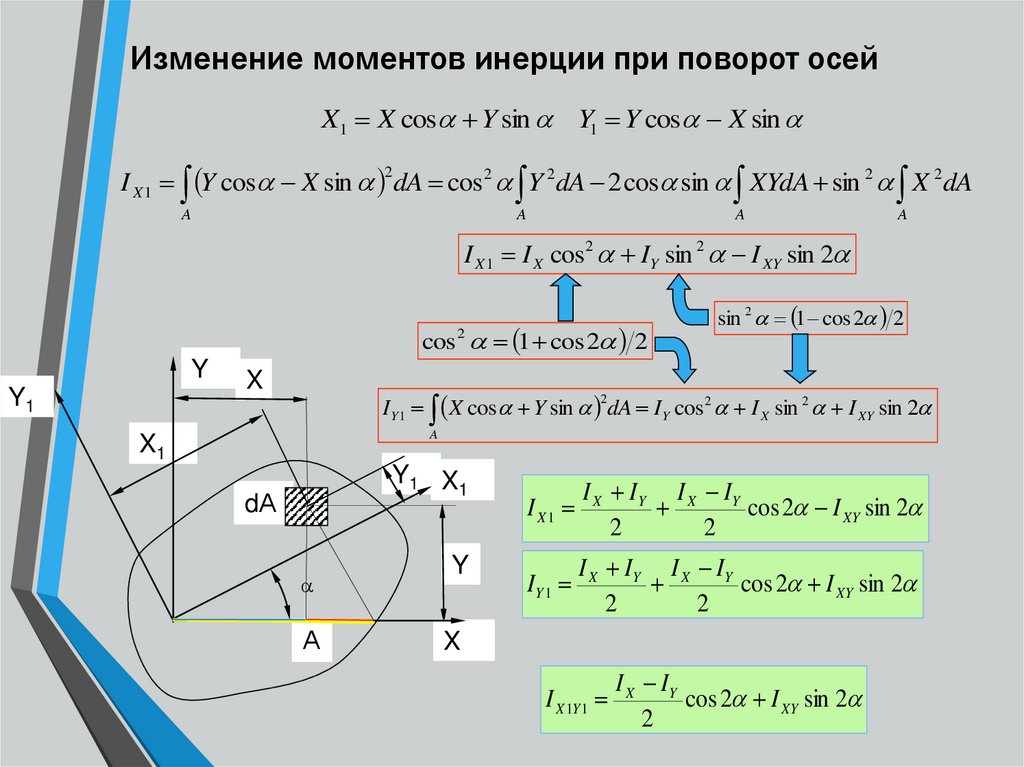
Р е ш е н и е. Под действием силы диск будет совершать плоское движение. Свяжем подвижную систему отсчета с центром масс диска. Величину ускорения центра масснайдем из второго закона Ньютона, записанного в проекции на направление движения
. (31)
В системе отсчета, связанной с центром масс, диск вращается с угловым ускорением , которое найдем из уравнения вращательного движения диска
(32)
где – момент инерции диска, относительно оси вращения.
Найдем величины скорости центра масс диска и угловой скорости его вращения к моменту времени, когда точка приложения силысовершит перемещениеТак как в начальный момент времени диск покоился, а величины ускоренийине меняются с течением времени (см. уравнения (31) и (32)), получим
Исключая из этих уравнений время найдем связь между скоростью центра масс и угловой скоростью вращения диска
(33)
Запишем теорему об изменении кинетической энергии для диска
(34)
где
– работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная силаПо определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом
. (35)
Подставляя выражения (33) и (35) в уравнение (34), найдем величину угловой скорости диска к моменту времени, когда точка приложения силы совершит перемещение
23. Механика твердого тела. Момент импульса: задачи с ответами
(Все задачи по статике и гидростатике и ответы к ним находятся в zip-архиве (615 кб), который можно скачать и открыть на своем компьютере. Попробуйте решать задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)
23.1. Легкая металлическая бочка, полностью заполненная водой, скатывается без проскальзывания с наклонной плоскости.
Как изменится ускорение бочки, если вода замерзнет? [смотрите ответ в общем файле темы]
23.2. Тонкий обруч раскрутили до угловой скорости w и вертикально поставили на горизонтальную поверхность. Какая угловая скорость будет у обруча в установившемся движении? [смотрите ответ в общем файле темы]
23.3. Чему равна кинетическая энергия тонкого обруча массой m, катящегося по горизонтальной поверхности со скоростью v? [смотрите ответ в общем файле темы]
23.4. Тонкий обруч скатывается без проскальзывания с наклонной плоскости с углом наклона α. Найти ускорение центра обруча. Каким должен быть коэффициент трения, чтобы не было проскальзывания? [смотрите ответ в общем файле темы]
23.5. Тонкий обруч радиусом R раскрутили до угловой скорости w и плашмя положили на стол. Через время t обруч остановился. Определить коэффициент трения между обручем и столом. [ μ = wR/(gt) ]
23.6. Два маленьких шарика массами m1 и m2 находятся на расстоянии l друг от друга.
Определить момент инерции системы относительно ее центра масс. [смотрите ответ в общем файле темы]
23.7. Определить момент инерции однородного стержня относительно оси, проходящей через середину стержня и составляющей угол α со стержнем. Длина стержня равна l, его масса – m. [смотрите ответ в общем файле темы]
23.8. Прямоугольник со сторонами a и b сделан из однородной проволоки. Масса единицы длины проволоки равна μ. Определить момент инерции прямоугольника относительно оси, совпадающей со стороной, длина которой равна а. [смотрите ответ в общем файле темы]
23.9. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и m2 и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы. [смотрите ответ в общем файле темы]
23.
10. Система состоит из двух, скрепленных между собой, однородных, взаимно перпендикулярных стержней массами m1 и m2 и длиной l1 и l2. Найти момент инерции системы относительно оси, проходящей через точку O и перпендикулярной плоскости системы. [смотрите ответ в общем файле темы]
23.11. Из однородного диска радиусом R вырезано круглое отверстие радиусом r. Расстояние между центрами диска и отверстия равно а, а масса фигуры — m. Определить момент инерции фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости. [указания к решению и ответ смотрите в общем файле темы]
23.12. Из однородной проволоки сделан правильный треугольник. Масса стороны треугольника равна m, его длина равна l. Определить момент инерции треугольника относительно оси: а) проходящей через центр треугольника и перпендикулярной его плоскости; б) совпадающей с одной из сторон треугольника; в) проходящей через вершину и параллельной противоположной стороне треугольника.
[смотрите ответ в общем файле темы]
23.13. Однородный шар скатывается с наклонной плоскости с углом наклона а. Найти ускорение центра шара. Каким должен быть коэффициент трения, чтобы шар не скользил? [смотрите ответ в общем файле темы]
23.14. В вагоне, движущемся с постоянной скоростью v, к потолку шарнирно подвешен стержень длиной l. На какой максимальный угол от вертикали отклонится стержень, если вагон резко остановить? [смотрите ответ в общем файле темы]
23.15. Однородный тонкий стержень длиной l поставили вертикально на горизонтальную гладкую поверхность, слегка вывели из положения равновесия и отпустили. Какую скорость будет иметь верхний конец стержня в момент удара стержня о поверхность? [ v = √(3gl) ]
23.16. Тонкий стержень AB массой m = 1 кг движется поступательно с ускорением a = 1 м/с2 под действием двух сил F1 и F2. Расстояние между точками приложения сил АС = 20 см.
Сила F2 = 5 Н. Найти длину стержня. [ 100 см ]
23.17. Неподвижный блок представляет собой однородный цилиндр массой m, подвешенный на нити к потолку. На цилиндр намотана нить, к которой подвешен груз такой же массы m. Найти силу натяжения верхней нити при свободном движении системы. Трения нет. [ T = 4mg/3 ]
23.18. На однородный диск массой m намотана нить. Свободный конец нити привязали к потолку и диск отпустили. Определить силу натяжения нити в процессе опускания диска. Считать, что нить все время вертикальна. [ T = mg/3 ]
23.19. Однородный стержень массой m подвешен горизонтально за концы на двух вертикальных нитях. Одна из нитей обрывается. Какова сила натяжения второй нити в момент обрыва? [ T = mg/4 ]
23.20. Неподвижный блок представляет собой однородный цилиндр массой m. Через блок перекинута невесомая нить, к концам которой привязаны грузы массами m1 и m2.
Определить ускорение грузов и силу натяжения нити слева и справа от блока при свободном движении системы. Проскальзывания нити и трения в блоке нет. [смотрите ответ в общем файле темы]
23.21. На однородный цилиндр массой m и радиусом R, лежащий на горизонтальной поверхности, намотана тонкая нить. За нить тянут горизонтальной силой F. При каком значении коэффициента трения цилиндр не будет проскальзывать по поверхности? [смотрите ответ в общем файле темы]
23.22. Однородный цилиндр лежит на горизонтальной поверхности. Второй такой же цилиндр катится на первый со скоростью v. Оси цилиндров параллельны. Между цилиндрами происходит абсолютно упругий удар. Определить конечные установившиеся скорости движения цилиндров. [указания к решению и ответ смотрите в общем файле темы]
23.23. Тонкостенную трубу радиусом R раскрутили вокруг оси до угловой скорости w и положили в угол между полом и стеной параллельно ребру угла. Коэффициент трения между трубой и стеной равен μ, а между трубой и полом — 2μ.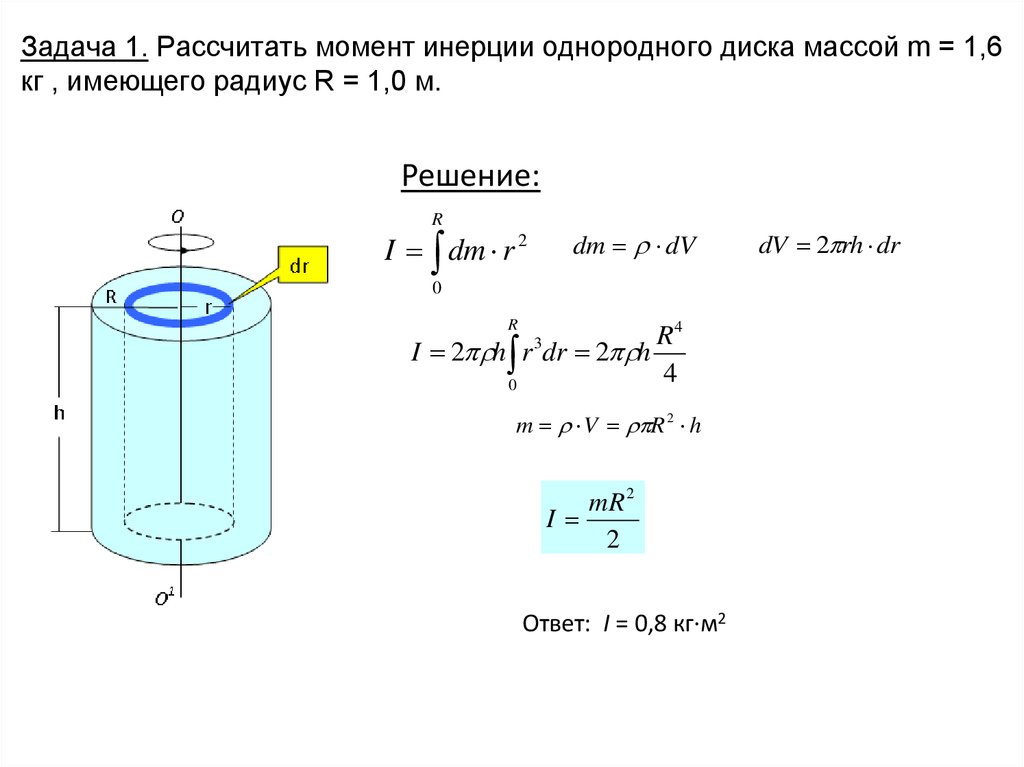
Сколько оборотов сделает труба до остановки? [смотрите ответ в общем файле темы]
23.24. Горизонтально расположенный деревянный стержень массой М и длиной l может вращаться вокруг вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массой m, летящая со скоростью v перпендикулярно стержню и оси его вращения. С какой угловой скоростью начнет вращаться стержень? [смотрите ответ в общем файле темы]
23.25. По гладкой горизонтальной поверхности по окружности движется небольшое тело, привязанное к нити. Нить продета в маленькое отверстие в поверхности. Нить начинают медленно втягивать в отверстие, уменьшая радиус окружности движения тела. Как зависит сила натяжения нити от радиуса окружности? Масса тела равна m. Считать, что при радиусе равном Ro угловая скорость движения тела была равна wo. [смотрите ответ в общем файле темы]
23.26. На массивный неподвижный блок в виде цилиндра радиусом R намотана нить, к свободному концу которой подвешен груз массой m.
В момент t = 0 систему отпускают. Написать зависимость момента импульса системы относительно оси блока от времени. Трения нет. [смотрите ответ в общем файле темы]
23.27. Стержень, расположенный горизонтально, падает без начальной скорости с высоты h и ударяется одним концом о край стола. Определить скорость центра масс стержня сразу после удара. Удар абсолютно упругий. [указания к решению и ответ смотрите в общем файле темы]
23.28. Шарик массой m влетает в спиральный лабиринт, который может свободно двигаться в пространстве, и останавливается в его центре. Начальная скорость шарика равна v, радиус лабиринта R, масса лабиринта М, его момент инерции J. Определить угловую скорость вращения лабиринта после того как шарик остановится. Размерами шарика и внешними силами пренебречь. [указания к решению и ответ смотрите в общем файле темы]
23.29. Два диска, имеющие моменты инерции J1 и J2, вращаются на одной оси с угловыми скоростями w1 и w2.
Диски прижимают друг к другу. Определить установившуюся угловую скорость вращения и количество теплоты, выделившееся при трении дисков. [смотрите ответ в общем файле темы]
23.30. Тонкий стержень длиной l и массой M стоит вертикально на гладкой горизонтальной поверхности. В его верхний конец попадает горизонтально летящая пуля массой m (m << М) и застревает в нем. При какой минимальной скорости пули стержень сразу оторвется от поверхности? [указания к решению и ответ смотрите в общем файле темы]
Далее: 30 задач по механическим колебаниям. | Вернуться к списку разделов СТАТИКИ и ГИДРОСТАТИКИ.
Момент инерции обычных форм
Теорема о параллельных осях
Пусть $I_\mathrm{cm}$ — момент инерции тела массы m относительно оси, проходящей через его центр масс C.
2. \номер
\end{выравнивание}
Момент инерции является минимальным для оси, проходящей через центр масс, т. е. $ I_\mathrm{cm} \leq I_\parallel$.
Теорема перпендикулярных осей
Пусть плоская пластинка лежит в плоскости x-y. Момент инерции пластинки относительно оси, перпендикулярной ее плоскости, определяется выражением \начать{выравнивать} I_z=I_x+I_y, \номер \end{выравнивание} где $I_x$ и $I_y$ — его моменты инерции относительно осей x и y.
Радиус вращения
Радиус вращения ($k$) тела массы $m$ вокруг оси A-A определяется как \начать{выравнивать} k=\sqrt{I/m}, \nonumber \end{выравнивание} где $I$ — момент инерции тела относительно оси А-А. 92.\номер \end{выравнивание}
Другие решенные задачи на момент инерции из IIT JEE
- Момент инерции тонкой квадратной пластины ABCD (IIT JEE 1992)
- Пусть I будет моментом инерции квадратной пластины (IIT JEE 1998)
- Тонкая проволока длиной L с одинаковой линейной плотностью массы (IIT JEE 2000)
- Одна четверть вырезана из однородного круглого диска (IIT JEE 2001)
- Твердая сфера радиуса R, расплавленная в диск (IIT JEE 2006)
- Четыре твердых сферы диаметром каждая (IIT JEE 2011)
- Пластинка изготавливается путем удаления небольшого диска диаметром 2R с диска большего размера (IIT JEE 2012)
- Плотность двух твердых сфер A и B радиуса R (IIT JEE 2015)
Похожие темы
- Кинематика твердых тел
- Момент инерции
- Угловой момент
- Угловой момент снаряда
- Крутящий момент
- Сохранение углового момента
- Фиксированная ось вращения
- Прокатка без проскальзывания колец цилиндров и сфер
- Равновесие твердых тел
- Направление силы трения на колесах велосипеда
Ссылки
- IIT JEE Physics Джитендер Сингх и Шраддхеш Чатурведи
- 300 решенных задач по механике вращения Джитендер Сингх и Шраддхеш Чатурведи
Момент инерции частиц и твердое тело – проблемы и решения
Момент инерции частицы
1.
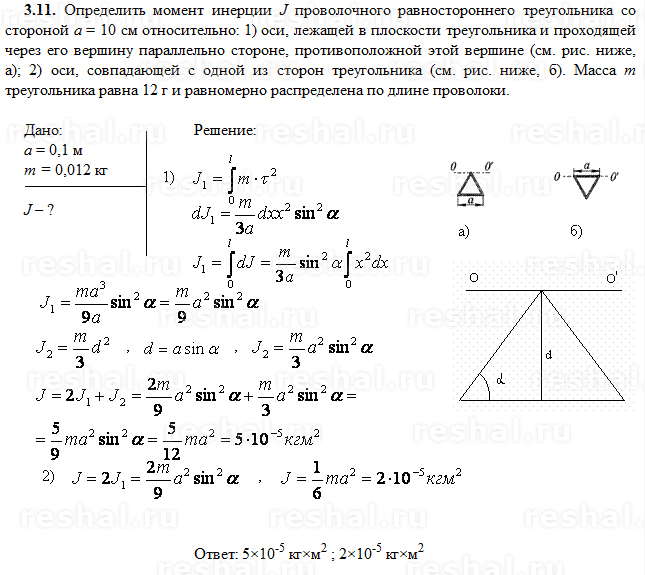Мяч массой 100 г, соединенный с одним концом шнура длиной 30 см. Чему равен момент инерции мяча относительно оси вращения АВ? Не учитывать массу шнура.
Известно:
Ось вращения на AB
Масса шара (м) = 100 грамм = 100/1000 = 0,1 кг
Расстояние между шаром и осью вращения (r) = 30 см = 0,3 м
Разыскивается: Момент инерции мяча (I)
Solution :
I = m r 2 = (0.1 kg)(0.3 m) 2
I = (0.1 kg)(0.09 m 2 )
I = 0.009 kg m 2
2. Мяч массой 100 г, m 1 , и шар массой 200 г, m 2 , соединенные стержнем длиной 60 см. Массой стержня пренебрегаем. Ось вращения расположена в центре стержня. Чему равен момент инерции шариков относительно оси вращения?
Известно:
Масса шара 1 (m 1 ) = 100 грамм = 100/1000 = 0,1 кг
Расстояние от шара 1 до оси вращения (r 1 ) = 30 см = 30/ 100 = 0,3 м
Масса мяча (м 2 ) = 200 грамм = 200/1000 = 0,2 кг
Расстояние от мяча 2 до оси вращения (r 2 ) = 30 см = 30/100 = 0,3 м
Разыскивается : момент инерции шаров
Джаваб :
I = м 1 R 1 2 + M 2 R 2 2
I = (0,1 кг) (0,3 М) 2 + (0,2 KG) (0,3 м) 2 + (0,2 KG) (0,3 м) (0,3 м) (0,3 м) (0,3 млн.
)
I = (0,1 кг)(0,09 м 2 ) + (0,2 кг)(0,09 м 2 )
I = 0,009 кг м 2 + 0,018 кг м 2 90 2
3. Мяч массой 200 г, m 1 и мяч массой 100 г, m 2, соединены стержнем длиной 60 см. Не учитывать массу стержня. Ось вращения расположена на шаре m 2 . Чему равен момент инерции шаров. Не учитывать массу стержня.
Известно:
Масса шара 1 (м 1 ) = 200 грамм = 200/1000 = 0,2 кг
Расстояние между шаром 1 и осью вращения (r 1 см = = ) 60/100 = 0,6 м
Масса шара 2 (м 2 ) = 100 г = 100/1000 = 0,1 кг
Расстояние между шаром 2 и осью вращения (r 2 ) = 0 м
Разыскивается: Момент инерции шаров
Решение:
I = M 1 R 1 2 + M 2 R 2 2
I = = = = = = = = = = = = = = = = = = = = ) + (0,2 кг)(0) 2
I = (0,2 кг)(0,36 м 2 ) + 0
I = 0,072 кг м 2
4.
Масса каждого шара равна 0,072 кг. , соединены шнуром. Длина шнура 60 см, ширина шнура 30 см. Чему равен момент инерции шариков относительно оси вращения. Не учитывать массу шнура.
Известно:
Масса мяча = м 1 = м 2 = м 3 = м 4 = 100 грамм = 100/1000 3 расстояние между осью мяча и 0,06 кг вращения (r 1 ) = 30 см = 30/100 = 0,3 м
Расстояние между шаром 2 и осью вращения (r 2 ) = 30 см = 30/100 = 0,3 м
Расстояние между шаром 3 и осью вращения (r 3 ) = 30 см = 30/100 = 0,3 м
Расстояние между шаром 4 и осью вращения (r 4 ) = 30 см = 30/100 = 0,3 м r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2
I = (0.
1 kg )(0,3 м) 2 + (0,1 кг)(0,3 м) 2 + (0,1 кг)(0,3 м) 2 + (0,1 кг)(0,3 м) 2
I = (0,1 кг)(0,09 м 2 ) + (0,1 кг)(0,09 м 2 ) + (0,1 кг)(0,09 м 2 ) + (0,1 кг)(0,09 м 2 )
I = 0,036 кг м 2
Момент инерции твердого тела
Чему равен момент инерции 2 -кг длинномерный равномерный прут длиной 2 м. Ось вращения расположена в центре стержня.
Известно:
Масса стержня (М) = 2 кг
Длина стержня (L) = 2 м
Требуется: Момент инерции
Решение:
Формула момента инерции, когда ось вращения расположена в центре длинного однородного стержня:
I = (1/12) M L 2
I = (1/12) (2 кг)(2 м) 2
I = (1/12) (2 кг)(4 м 2 )
I = (1/12)(8 кг·м 2 )
I = 8/12 кг·м 2
I = 2/3 кг·м 2
6.
Каков момент инерции однородного стержня массой 2 кг и длиной 2 м? Ось вращения расположена на одном конце стержня.
Известно:
Масса стержня (м) = 2 кг
Длина жесткого стержня (L) = 2 м
Разыскивается: Момент инерции
Решение:
момент инерции при расположении оси вращения на одном конце стержня:
I = (1/3) M L 2
I = (1/3) (2 кг)(2 м) 2
I = (1/3) (2 кг)(4 м 2 )
I = (1/ 3)(8 кг м 2 )
I = 8/3 кг м 2
7. Сплошной цилиндр массой 10 кг и радиусом 0,1 м. Ось вращения расположена в центре сплошного цилиндра, показанного на рисунке ниже. Чему равен момент инерции цилиндра?
Известно:
Масса цельного цилиндра (M) = 10 кг
Радиус цилиндра (L) = 0,1 м
Искомое: Момент инерции
Искомое: Момент инерции
Решение :
Формула момента инерции при расположении оси вращения в центре цилиндра :
6 I = ( 2) M R 2
I = (1/2) (10 кг)(0,1 м) 2
I = (1/2) (10 кг)(0,01 м 2 )
I = (1/2)(0,1 кг·м 2 )
I = 0,05 кг·м 2
8.