Задачи на уравнение и график движения по физике: система отсчета, как найти уравнение движения по графику, график скорости

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

§6. Примеры движения тела. Методы решения задач. — ЗФТШ, МФТИ

Рассмотрим некоторые характерные примеры движения тела, знание которых будет полезно при дальнейшем изучении физики.

1.Равномерное прямолинейное движение тела.

При равномерном прямолинейном движении тело совершает равные перемещения `Delta vecr`  за одинаковые промежутки времени  `Delta t`. Иными словами, скорость  `vec v` тела не зависит от времени и остаётся постоянной в процессе движения:

При этом зависимость `vec r(t)` имеет вид:

где  `vec r_0`  –  радиус-вектор тела в начальный момент времени  $$ t=0$$ . В этой связи вспомним замечание о начальных условиях,

сделанное в §4.  Вектор  $$ {\overrightarrow{r}}_{0}$$  здесь является тем начальным условием, которое позволяет однозначно определить радиус-вектор $$ \overrightarrow{r}$$ тела в любой момент времени в процессе движения.

Векторное уравнение (7) равносильно системе двух скалярных уравнений, выражающих зависимость от времени $$ t $$ координат $$ x$$ и $$ y$$ движущегося тела:

где $$ {x}_{0}$$ и $$ {y}_{0}$$ – начальные координаты тела в момент времени $$ t=0$$, а $$ {v}_{x}$$ и $$ {v}_{y}$$ -проекции вектора скорости `vecv` на координатные оси $$ Ox$$ и $$ Oy$$ соответственно.

 

Траектория равномерного прямолинейного движения тела графически представляет собой отрезок прямой линии (рис. 9), тангенс угла наклона которой к оси абсцисс равен отношению проекций скорости на оси координат: $$ \mathrm{tg}\alpha ={v}_{y}/{v}_{x}$$. Аналитическое уравнение траектории, т. е. зависимость $$ y\left(x\right)$$, легко получить, исключив параметр $$ t$$ из системы уравнений (8):

2. Неравномерное движение тела.

Для неравномерного движения характерно то, что с течением времени изменяется скорость движущегося тела, а в общем случае и его ускорение

. В качестве примера может служить движение, при котором тело проходит различные участки своего пути с разной скоростью. Такое движение принято характеризовать, прежде всего, средней путевой скоростью. Причём прилагательное «путевая» в условиях задач часто опускается.

Другим характерным примером неравномерного движения служит так называемое равнопеременное движение, которое целесообразно рассмотреть подробно, не выходя при этом за рамки школьной программы.

3. Равнопеременное движение.

Равнопеременным называется

такое неравномерное движение, при котором скорость `vec v` за любые равные промежутки   времени   `Delta t`  изменяется  на  одинаковую  величину   `Deltavecv`. В этом случае ускорение `veca` тела не зависит от времени и остаётся постоянным в процессе движения:

(при этом `vec v != “const”`, и траектория движения не обязательно прямолинейная).
При равнопеременном движении скорость $$ \overrightarrow{v}$$ тела изменяется с течением времени по закону

где `vecv_0` – скорость тела в начальный момент времени `t=0`.
В свою очередь, зависимость `vecr(t)` имеет вид:

где `vecr_0` – начальный радиус-вектор тела при `t=0`. Вновь заметим, что величины `vecv_0` и `vecr_0` представляют собой начальные условия, позволяющие в любой момент времени однозначно определить векторы `vecv` и `vecr`.

При координатном способе описания равнопеременного движения векторным уравнениям (11) и (12), равносильны следующие системы уравнений для проекций скорости и радиус-вектора тела на оси выбранной системы отсчёта. 2)/(2a_x)`.

Удобство этой формулы заключается в том, что она не содержит времени $$ t$$ в явном виде. Вместе с тем надо помнить, что формула получена в предположении о неизменности направления движения тела.

Одним из наиболее наглядных примеров равнопеременного движения является движение тела в поле тяжести Земли, которое мы имеем возможность наблюдать повседневно. Для решения задач в этом случае надо заменить в приведённых выше формулах вектор $$ \overrightarrow{a}$$ на ускорение свободного падения $$ \overrightarrow{g}$$, сообщаемое силой гравитационного притяжения всякому телу, движущемуся в поле тяжести Земли. Рассмотрим три конкретных случая такого движения.

Движение тела, брошенного вертикально.
Тело бросили с поверхности земли, сообщив ему начальную скорость $$ {\overrightarrow{v}}_{0}$$ направленную вертикально вверх. Пренебрегая сопротивлением воздуха, определите время $$ \tau $$ полёта тела до момента падения на землю; скорость тела в момент падения; максимальную высоту $$ H$$ подъёма тела над землёй; время $$ {\tau }_{1}$$ подъёма тела на максимальную высоту; путь `S`, пройденный телом за время полёта и перемещение тела.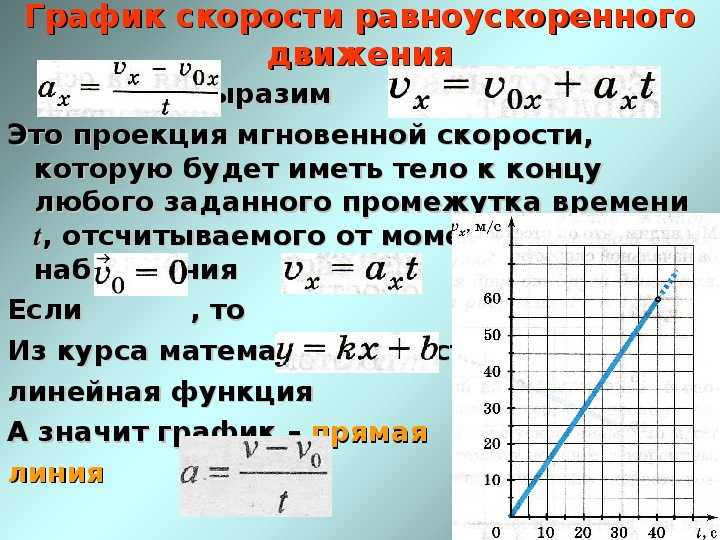

{2}+\mathrm{tg}\alpha x$$. 

График траектории тела представляетсобой участок параболы, ветви которой направлены вниз.

 

График движения – Физика тела: от движения к метаболизму

Перейти к содержимому

— полезный инструмент для визуализации и передачи информации о движении объекта. Наша цель — создать графики движения для нашего примера парашютиста, но сначала давайте убедимся, что уловили основную идею.

Мы начнем с просмотра графиков движения объекта с 2 м и 4 м/с . Объект, движущийся с постоянной скоростью, имеет нулевое значение , поэтому график зависимости ускорения от времени просто остается равным нулю:

График зависимости ускорения от времени для объекта с постоянной скоростью в нуле плоский.

Скорость постоянна, поэтому график зависимости скорости от времени останется равным 4 м/с значение:

График зависимости скорости от времени плоский (постоянный) на уровне 4 м/с .

— это скорость изменения позиции, поэтому график зависимости позиции от времени должен изменяться с постоянной скоростью, начиная с (в нашем примере 2 м ). А говорит нам скорость изменения переменной по вертикальной оси, поэтому мы можем понять наклон графика зависимости позиции от времени.

График зависимости положения от времени является линейным с наклоном, равным скорости 4 м/с , и точкой пересечения, равной начальному положению 2 м/с . График пересекает позицию на 10 метров за время 2 секунды.

Упражнения с подкреплением

Теперь давайте посмотрим на объект с расширением . Придадим нашему объекту те же 2 м , и 4 м/с , а теперь постоянное ускорение 2 м/с/с . Зависимость ускорения от времени остается постоянной на уровне 2 м/с/с :

График зависимости ускорения от времени плоский для значения ускорения, в этом примере 2 м/с/с

— это скорость изменения, поэтому ускорение — это график зависимости скорости от времени. Для нашего постоянного ускорения 2 м/с/с график скорости должен иметь постоянный наклон 2 м/с/с :

График зависимости скорости от времени является линейным с наклоном, равным значению ускорения 2 м/с/с , и точкой пересечения, равной начальному значению скорости 4 м/с .

Наконец, если изменяется с постоянной скоростью, то и график положения, представляющий скорость, также должен изменяться с постоянной скоростью. Результатом изменяющегося наклона является криволинейный график, и, в частности, кривая с постоянно меняющимся наклоном является параболической кривой или параболой .

График зависимости положения от времени объекта с постоянным ускорением представляет собой параболическую кривую. Кривизна направлена ​​вверх при положительном ускорении и вниз при отрицательном ускорении. Точка пересечения является начальной позицией, в данном примере 2 м .

Мы не обращали внимания на ситуации, потому что они относительно неинтересны. График положения постоянен при начальном значении положения, график постоянен при нуле и график также постоянен при нуле. Давайте закончим этот раздел несколькими интересными графиками — графиками объекта, который меняет направление. Например, объект, брошенный в воздух со скоростью 5 м/с , с высоты 2 м , который затем падает на землю с высоты 0 м . Пренебрегая , будет постоянным при  отрицательном  г, или -9,8 м/с/с .

График зависимости ускорения от времени для объекта плоский на уровне -9,8 м/с/с (при выборе направления вниз в качестве отрицательного).

Скорость будет положительной, но замедлится до нуля, пересечет ноль по мере того, как объект поворачивается, а затем начнет увеличиваться в отрицательном направлении.

График зависимости скорости от времени начинается с 5 м/с и линейно уменьшается, пересекая нуль примерно на 0,5 с , а затем линейно становится более отрицательным со временем и достигает – 5 м/с сразу после 1 с . Наклон составляет -9,8 м/с/с .

Положение будет увеличиваться по мере того, как объект движется вверх, а затем уменьшаться по мере того, как он падает вниз, по параболе, потому что наклон изменяется с постоянной скоростью (ускорение постоянно, поэтому скорость изменяется с постоянной скоростью, поэтому наклон положения график постоянно меняется).

График зависимости положения от времени представляет собой параболу с нисходящей кривизной, начинающуюся на отметке 2 м , с пиком около 3,3 м 9 ..

Ознакомьтесь с этой интерактивной симуляцией движущегося человека и соответствующими графиками движения:

Упражнения с подкреплением

 

Повседневный пример: предельная скорость

Давайте посмотрим на скорость нашего парашютиста, когда он находится на конечной скорости -120 миль в час , что составляет около 54 м/с . Давайте установим для этого анализа положение, в котором они достигают предельной скорости.

Ускорение равно нулю, потому что они находятся на конечной скорости:

График зависимости ускорения от времени является постоянным (плоским) при нуле.

Скорость постоянная, но отрицательная:

График зависимости скорости от времени постоянен около -52 м/с .

И позиция меняется с постоянной скоростью, становясь со временем все более отрицательной.

График зависимости положения от времени линейно убывает от нуля до -520 м после 10 с .

Ежедневный пример: полный прыжок с парашютом

Теперь давайте посмотрим на то, как наш парашютист достигает предельной скорости, начиная с начального прыжка.

Кривая зависимости ускорения от времени начинается с -9,8 м/с/с , потому что в первый момент силы сопротивления нет, поэтому дайвер на мгновение находится в свободном падении. По мере набора скорости сила сопротивления увеличивается, компенсируя большую часть веса, поэтому ускорение стремится к нулю и становится неотличимым от нуля около 15 9 .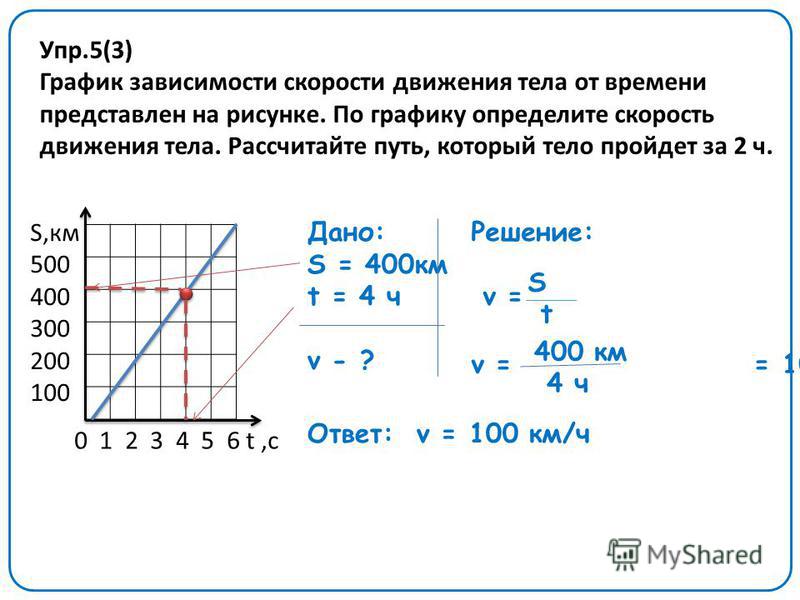 0007 с .

 

Кривая зависимости скорости от времени начинается с нуля и потому, что начальная скорость была равна нулю. Скорость остается отрицательной, потому что движение направлено вниз, но наклон не постоянный, как при свободном падении, потому что ускорение не постоянное, как при свободном падении. Это связано с тем, что сила сопротивления растет по мере увеличения скорости и в конечном итоге становится равной весу, поэтому скорость в конечном итоге начинает выравниваться и приближаться к постоянной величине 52 м/с .

 

Кривая зависимости положения от времени начинается с 3660 м и спадает к нулю с отрицательным и постепенно увеличивающимся наклоном (движение вниз и ускорение). Через 20 с парашютист приближается к точке 2750 м , и наклон становится постоянным на уровне 52 м/с , указывает на конечную скорость. Обратите внимание, что мы преобразовали нашу [pb_glossary]начальную позицию[/pb_glossary] из 12 000 футов в эквивалент 3660 м .

License

Body Physics: Motion to Metabolism by Lawrence Davis распространяется под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Графики движения: типы, уравнения и анализ

Для нефизиков карты и спидометры пригодятся при оценке изменения положения или изменения скорости объекта. Но когда вы физик, графики — особенно графики движения — очень важны для определения положения или скорости изменения скорости объекта. Как вы увидите ниже, графики движения помогают нам, студентам-физикам, лучше понять движение тела за определенный период времени.

Типы графиков движения

Существует три основных типа графиков, используемых для определения движения объекта по прямой линии : графики перемещения-времени, графики скорости-времени и графики ускорения-времени.

График зависимости смещения от времени

На рис. 1 показан график зависимости смещения от времени объекта, движущегося с постоянной скоростью . Для графика «смещение-время» смещение (обозначается d) находится на оси y, а время (обозначается t) — на оси x.

Рис. 1. График перемещение-время объекта, движущегося с постоянной скоростью. Usama Adeel — StudySmarter Originals

Из такого графика мы можем получить

• пройденное расстояние в любой момент времени,
• среднюю скорость путем вычисления наклона (градиента) графика и
• мгновенная скорость путем вычисления производной любой точки на кривой.

Чтобы рассчитать наклон p приведенного выше графика, мы используем следующее уравнение:

p=y2-y1x2-x1=∆d∆tm/s

Скорость изменения смещения – это скорость, , поэтому наклон графика смещения-времени – это скорость.

График зависимости скорости от времени

Посмотрите на график зависимости скорости от времени ниже:

Рисунок 2. График зависимости скорости от времени объекта, движущегося с постоянной скоростью. Usama Adeel – StudySmarter Originals

Для графика скорость-время скорость (v) находится на оси y, а время (t) – на оси x. Из этого графика мы можем найти

• скорость в любой момент времени,
• среднее ускорение путем вычисления наклона прямой линии,
• мгновенное ускорение путем взятия производной любой точки на кривой и
• перемещение тела путем вычисления площади под кривой (между линией и осью времени).

Чтобы вычислить наклон p приведенного выше графика, мы используем следующее уравнение:

p=y2-y1x2-x1=∆v∆tm/s2

Скорость изменения скорости есть ускорение , поэтому наклон графика скорость-время есть ускорение.

Кроме того, площадь под графиком скорость-время дает расстояние, пройденное объектом , то есть смещение.

График зависимости ускорения от времени

Для графика зависимости ускорения от времени ускорение (a) отложено по оси y, а время (t) по оси x. График ускорение-время дает нам ускорение в любой момент времени. Кроме того, 9Площадь 0007 под кривой зависимости ускорения от времени представляет изменение скорости .

Рис. 3. График зависимости ускорения от времени объекта, движущегося с равномерно возрастающим ускорением. Usama Adeel – StudySmarter Originals

Анализ графиков движения без чисел

Ниже мы рассмотрим, как рисовать графики движения для различных сценариев.

Графики движения: объект в состоянии покоя

Для объекта в состоянии покоя не будет изменения смещения, что не приведет к изменению скорости, а поскольку нет изменения скорости, изменение ускорения будет также быть нулевым.

График смещения во времени для объекта в состоянии покоя

Объект в состоянии покоя не будет двигаться. Следовательно, смещение не изменится на за интервал времени, изображенный плоской линией, параллельной оси времени.

Рис. 4. График перемещения объекта в состоянии покоя от времени. Usama Adeel — StudySmarter Originals

График зависимости скорости от времени для объекта в состоянии покоя

Скорость будет равна нулю , потому что смещение объекта не меняется. Следовательно, график для объекта без изменения его скорости во времени может быть показан прямой линией на оси времени.

Рис. 5. График зависимости скорости покоящегося объекта от времени. Usama Adeel — StudySmarter Originals

График ускорения и времени для объекта в состоянии покоя

Ускорение будет равно нулю , поскольку скорость объекта не меняется, а график ускорения и времени представляет собой плоскую линию, начинающуюся от начала координат.

Рис. 6. График ускорения объекта в состоянии покоя. Usama Adeel – StudySmarter Originals

Графики движения: объекты, движущиеся с постоянной скоростью (расстояние увеличивается со временем)

Когда объект движется с постоянной скоростью:

• Скорость изменения смещения будет равна при равномерном увеличении .
• Скорость будет представлять собой непрерывную прямую линию с положительным или отрицательным значением в зависимости от направления движения.
• Ускорение будет равно нулю , поэтому через начало координат будет проходить постоянная линия.

График смещения во времени для объекта, движущегося с постоянной скоростью

Наклон на приведенном ниже графике равен положительному , что указывает на то, что движение происходит в положительном направлении (от начала координат).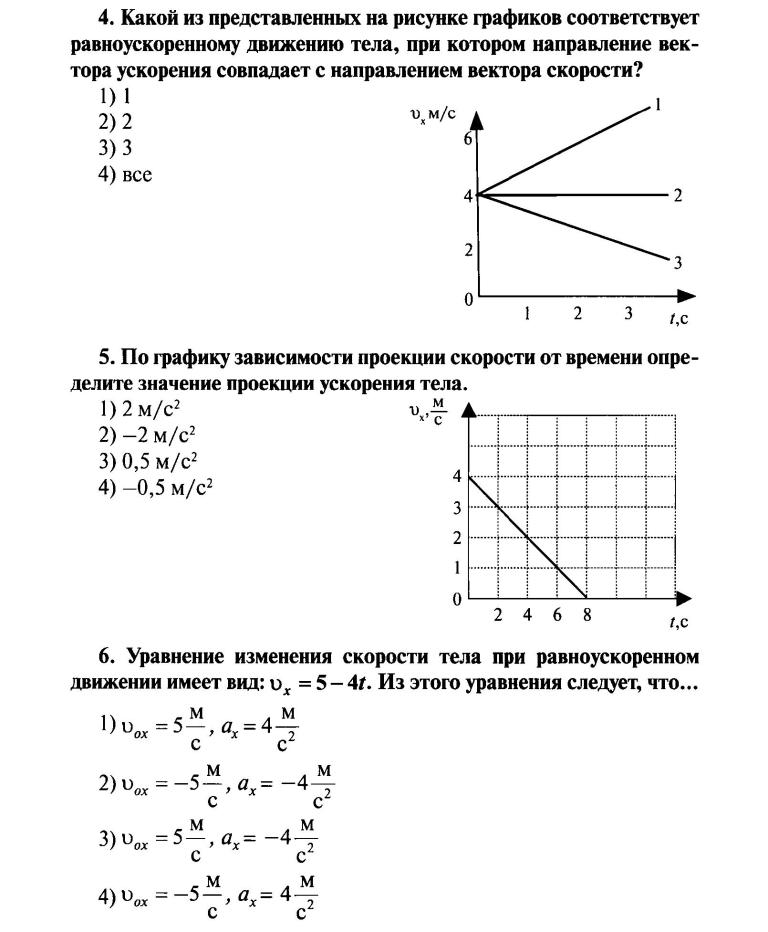 Если бы эта кривая была такой же, но с отрицательным градиентом (к началу координат), она отображала бы смещение в противоположном направлении. Кроме того, перемещение равномерно увеличивается, потому что скорость постоянна.

Рис. 7. График перемещение-время объекта, движущегося с постоянной скоростью из состояния покоя. Усама Адил – StudySmarter Originals

Вопрос: Какое направление считать положительным или отрицательным?

Ответ: Знак произвольный. Вы можете выбрать любое направление как положительное, так и отрицательное. На рис. линия в положительном направлении .

Рис. 8. График зависимости скорости объекта, движущегося с постоянной скоростью. Усама Адил – StudySmarter Originals

График зависимости ускорения от времени для объекта, движущегося с постоянной скоростью Чтобы произошло ускорение или замедление, также должно произойти изменение скорости.

Рис. 9. График зависимости ускорения объекта, движущегося с постоянной скоростью. Усама Адил – StudySmarter Originals

Графики движения: объекты, движущиеся с постоянным ускорением (расстояние увеличивается с течением времени)

Когда объект движется с постоянным ускорением:

• График перемещение-время будет представлять собой кривую с градиентом, который становится возрастающим круче .
• Скорость изменения скорости будет равномерно возрастать.
• Ускорение будет постоянным с положительным значением.

График зависимости смещения от времени для объекта, движущегося с постоянным ускорением

Ниже приведены два графика зависимости смещения от времени. Рисунок 10 соответствует постоянному ускорению , а рисунок 11 соответствует постоянному замедлению .

Рис. 10. График перемещение-время объекта, движущегося с постоянным ускорением. Usama Adeel – StudySmarter Originals

Рис. 11. График перемещение-время объекта, движущегося с постоянным замедлением. Усама Адил – StudySmarter Originals

Если вы возьмете касательные в разных точках обеих вышеприведенных кривых, вы увидите, что наклон графика смещения-времени на рисунке 10 становится все круче и круче. Это указывает на то, что скорость увеличивается . На рисунке 11 градиент постепенно уменьшается , что указывает на то, что скорость уменьшается .

Рис. 12. График перемещение-время объекта, движущегося с постоянным ускорением. Наклон становится круче, что указывает на постоянное ускорение. Усама Адил – StudySmarter Originals

Рис. 13. График перемещение-время объекта, движущегося с постоянным ускорением. Склон становится более пологим, что указывает на постоянное замедление. Usama Adeel – StudySmarter Originals

График зависимости скорости от времени для объекта, движущегося с постоянным ускорением

График скорости от времени для объекта с постоянным ускорением будет представлять собой равномерно возрастающую линию, как показано на рисунке ниже.

Рис. 14. График зависимости скорости объекта от времени, движущегося с постоянным ускорением. Усама Адил – StudySmarter Originals

График зависимости ускорения от времени для объекта, движущегося с постоянным ускорением

Поскольку ускорение не меняется во времени и является постоянным, график зависимости ускорения от времени может быть представлен прямой линией.

Рис. 15. График ускорение-время объекта, движущегося с постоянным ускорением. Usame Adeel – StudySmarter Originals

Графики движения: Объект движется с постоянным замедлением (расстояние увеличивается со временем)

Когда объект движется с постоянным замедлением:

• График смещение-время будет представлять собой кривую с градиентом, который становится все более и более горизонтальным.
• Скорость изменения скорости будет равномерно уменьшаться .
• Ускорение будет постоянным , но с отрицательным значением.

График смещения во времени для объекта, движущегося с постоянным замедлением

Поскольку тело замедляется, кривая приближается к постоянному (неизменному) значению .

Рис. 16. График перемещение-время объекта, движущегося с постоянным замедлением. StudySmarter Originals – Usama Adeel

График зависимости скорости от времени для объекта, движущегося с постоянным замедлением

График зависимости скорости от времени при постоянном замедлении будет представлять собой однородную линию, постоянно уменьшающуюся от некоторого значения.

Рис. 17. График зависимости скорости объекта, движущегося с постоянным замедлением. Усама Адил – StudySmarter Originals

График ускорение-время для объекта, движущегося с постоянным замедлением

Постоянная линия с отрицательным ускорением показывает, что объект замедляется с постоянным значением.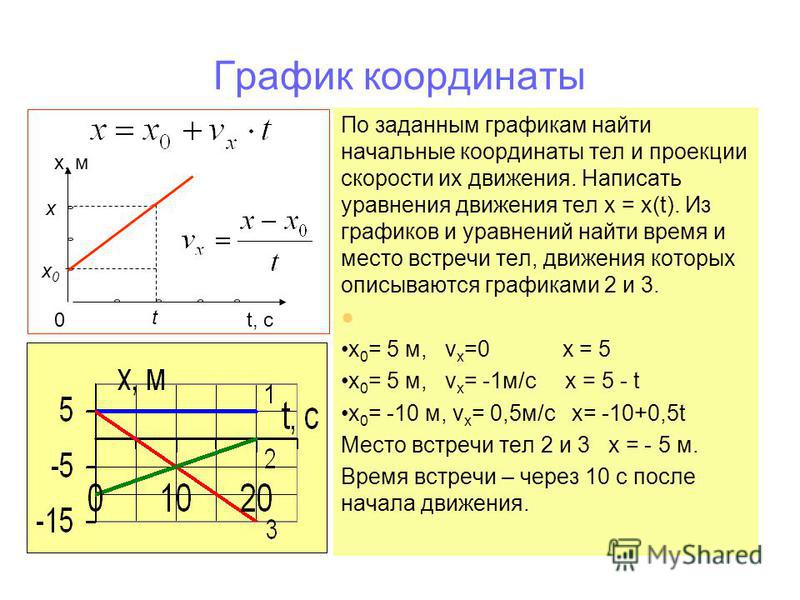

Рис. 18. График ускорение-время объекта, движущегося с постоянным замедлением. Usama Adeel – StudySmarter Originals

Графики движения: подбрасывание объекта прямо вверх с возвратом объекта к бросающему

В этом сценарии объект, скажем, мяч, подбрасывается вверх таким образом, что он попадает в руку через некоторое время. Сопротивлением воздуха можно пренебречь, и единственные силы, действующие на мяч, исходят от бросающего (чтобы подбросить мяч вверх) и гравитационного притяжения мяча до тех пор, пока он не приземлится в руке бросающего. Направление вверх считается положительным.

График смещения-времени для предмета, брошенного вертикально вверх

График смещения-времени для предмета, брошенного вертикально вверх и затем приземлившегося в руке метателя, показан ниже.

Рис. 19. График перемещения объекта, подброшенного в воздух и пойманного на той же высоте, от времени. Usama Adeel — StudySmarter Originals

Как только мяч подброшен в воздух, его смещение увеличивается, потому что мы приняли направление вверх как положительное. Когда он достигнет вершины, градиент графика смещения-времени на короткое время станет равным нулю, что указывает на то, что мяч меняет свое направление и с этого момента будет двигаться вниз. Поэтому график будет двигаться вниз, пока шарик не достигнет исходного положения.

Но почему график представляет собой кривую, а не прямую линию? Ускорение из-за силы тяжести постоянно, со значением 9,81 м/с ² . Таким образом, с момента броска мяча и до того, как он будет пойман, замедление за счет силы тяжести и ускорение за счет свободного падения будут постоянными и отличными от нуля.

График зависимости скорости от времени для объекта, брошенного вертикально вверх

График зависимости скорости от времени для объекта, брошенного вертикально вверх и приземлившегося в руке метателя, показан ниже.

Рис. 20. График зависимости скорости тела, подброшенного в воздух и пойманного на одной высоте. Usama Adeel – StudySmarter Originals

Мяч брошен вверх с некоторой начальной скоростью u. Когда мяч достигает вершины, его скорость равномерно уменьшается, пока не достигнет нуля, где мяч на короткое время покоится. После этого мяч движется вниз с равномерно возрастающей скоростью.

Поскольку пройденное расстояние вверх и вниз будет одинаковым из-за пренебрежимо малого сопротивления воздуха, начальная скорость будет равна конечной скорости -u. Итак, 9В этом случае площадь 0007 обоих регионов A и B будет равна .

Почему наклон графика становится отрицательным, а не положительным после того, как u достигает нуля? Поскольку направление вверх принимается за положительное, как только направление мяча изменится вверху, движение будет направлено вниз в отрицательном направлении с постоянным ускорением свободного падения.

График времени ускорения для предмета, брошенного вертикально вверх

График времени ускорения для предмета, брошенного вертикально вверх и затем приземлившегося в руке метателя, показан ниже.

Рис. 21. График зависимости ускорения объекта, подброшенного в воздух и пойманного на одной высоте. Usama Adeel – StudySmarter Originals

Ускорение является постоянным -9,81 м/с ² на протяжении всего смещения , поскольку график зависимости скорости от времени равномерно уменьшается.

После того, как мяч подброшен в воздух, сила тяжести действует в направлении, противоположном движению вверх. Поскольку движение вверх считается положительным, сила тяжести будет отрицательной. Как только мяч достигает своей вершины, мяч меняет направление. Следовательно, гравитационная сила по-прежнему будет отрицательной.

Графики движения – ключевые выводы

• Существует три основных типа графиков, касающихся линейного движения: график смещения-времени, график скорости-времени и график ускорения-времени

• Из графика смещения-времени графика, вы можете рассчитать среднюю скорость и мгновенную скорость, рассчитав наклон графика.