Главная
Задачи по физике оформление: Ошибка 403 — доступ запрещён

Задачи по физике оформление: Ошибка 403 — доступ запрещён

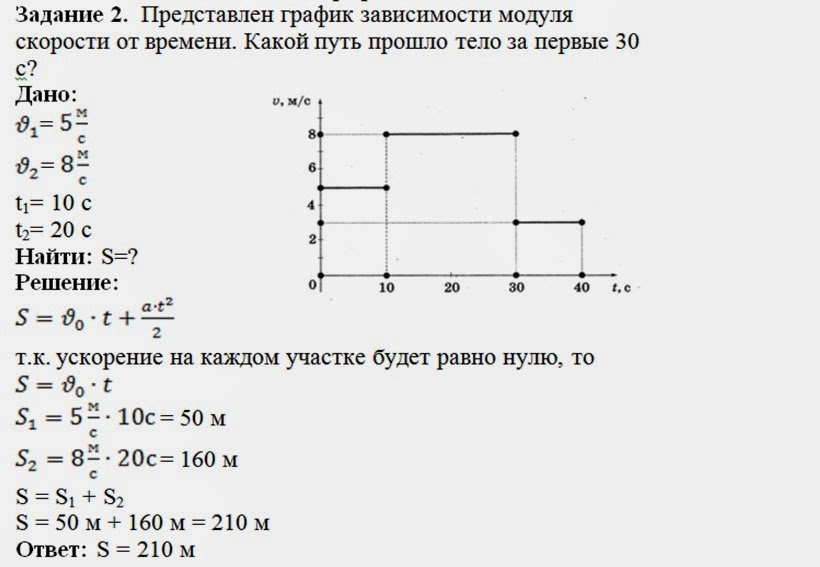
Пример оформления задач по физике

При решении задач по физике важно получить правильный ответ? Конечно. Однако нельзя забывать о требованиях, касающихся оформления. Правильный ответ при неверной записи условия, решения не гарантирует получение хорошей оценки. Чтобы добиться наиболее оптимального результата, нужно научиться оформлять задачи согласно существующим нормам. Для этого обязательно соблюдать следующий алгоритм.

СОДЕРЖАНИЕ

1. Внимательно прочитайте условие

Согласно статистике большая часть обучающихся допускает ошибки еще на этапе чтения условия задачи. Происходит это из-за невнимательности, нежелания вдуматься в текст. Такая халатность, даже при умении решать задачи по физике, нередко приводит к неверным результатам. Именно поэтому учителя-практики советуют ответственнее относиться к ознакомлению с условием задачи. Если соблюсти такое требование, то досадных ошибок можно избежать. В противном случае работа будет напрасной, результат – отрицательным.

2. Запись краткого условия

Запись условия задачи под заголовком «Дано» производится в левом столбике тетрадного листа. Это поле обозначается прямой линией. Для обозначения текстовой информации используются общепризнанные обозначения (к примеру, масса обозначается латинской буквой m, скорость – v). Рядом с буквенным обозначением указывается число, которое прозвучало в задании. Следует быть внимательным, так как нередко числа в условии нет, оно подразумевается. Например, читаем: «При кипении воды жидкость …. » (мы знаем, при какой температуре происходит), а записываем в «Дано» t + 100 °С.

Когда все данные, которые содержатся в условии, записаны, не спешите подводить черту в левой колонке. Нередко в процессе решения приходится дописывать какие-то еще дополнительные цифры и обозначения. Наличие свободного места в этой части задачи – не ошибка.

Важно! Числовые данные необходимо указывать вместе с единицами измерения. Если она должна быть представлена в виде дроби, ее именно так и нужно записывать. Это обязательно! При несоблюдении данного правила преподаватели снижают оценку, даже если задача решена правильно.

В «Дано» также обязательно следует указать, что именно нужно найти в итоге. Для этого используются не слова, а буквенные обозначения искомого. Если этого не сделать, ошибка неизбежна. Пренебрежение правилами приведет к снижению оценки.

3. Перевод единиц измерения в СИ

Рядом с колонкой «Дано» находится еще одна, не менее важная. Ее размер почти такой же. Называется она «СИ».

В задании могут прозвучать различные цифры и данные, которые необходимо перевести в общепринятую международную систему единиц физических величин. Даже если ничего переводить в систему СИ не нужно, колонка с этим названием должна быть записана.

4. Чертежи

Вполне возможно, что при решении задачи по физике понадобится чертеж. Это могут быть оси координат, вектора скорости, перемещения и прочее. В ряде случаев без них справиться с заданием не получится.

Запомните! Чертеж, даже если он выполняется «для себя», должен быть аккуратным, правильным.

5. Запись решения.

Чтобы произвести все необходимые расчеты и найти искомые данные, можно воспользоваться двумя способами записи решения задачи:

— по действиям;

— вывести окончательную формулу и произвести окончательный расчет (учащимися 7-9 классами – по желанию, в 10-11 – обязательно).

Задача должна быть решена, поэтому выбор способа записи в этой части не столь важен.

Важно! Не можете решить задачу по физике, но понимаете примерно, что должно получиться в итоге? Попробуйте «распутать» ее с конца. Придется подумать, что нужно для того, чтобы рассчитать искомую величину.

6. Запись и проверка ответа

Одна из распространенных ошибок учеников и студентов – слишком короткая запись ответа. Формулировать ее нужно целой фразой, не забывая о правильности записи физической величины с полученным числовым значением.

Правильное оформление задачи по физике, все-таки, не самое главное. Нужно уметь ее решать. Что делать, если правильно оформлены колонки «Дано» и «СИ», а с решением проблемы? Справиться с проблемой можно 2 способами: воспользоваться решебником, услугами учителя-физика или сторонней профессиональной помощью.

Однако в решебнике ответа к необходимой задаче можно и не найти, к тому же, гарантировать правильность записанного никто не будет. Обратиться за разъяснением к учителю физики, который сам же и задал ее решить? Это неудобно, по меньшей мере.

Поэтому наша компания предлагает свою помощь в решении и оформлении задач по физике. Услуга не ограничивается получением правильного ответа и записи условия. Специалист разъяснит ход решения, благодаря чему с однотипной задачей в следующий раз можно будет справиться самостоятельно.

Правила решения физических задач

Эта страница посвящена изложению основных правил, которым нужно следовать при оформлении решения большинства физических задач. Конечно, кто-то может сказать, что все это – азбучные истины. Что ж, тогда можно сразу перейти к задачам, щелкнув по нужному разделу меню. Я же ориентируюсь на тех, “кто в танке”.

В физике принято условие задачи представлять в виде краткой записи, где перечисляются основные данные, приведенные в полном условии и указывается, что надо найти. Если в полном условии даются только буквенные обозначения величин, то в краткой записи перечисляются эти буквы. Если, кроме того, даются еще и числовые значения, то указываются и они. Бывает и так, что какой-то параметр задан не буквой, а о нем просто говорится словами, например, “за 2 часа тело прошло восемь километров”. В этом случае надо самому выбрать буквенное обозначение параметра. Так, время можно обозначить как t, T, путь – как S, L, d. Вообще, можно, конечно, использовать любую букву любого алфавита, но, все-таки, следует стараться следовать установившимся традициям в буквенных обозначениях тех или иных величин. Что касается записи числовой меры, то здесь надо быть внимательным. Дело в том, что одна и та же физическая величина может быть в полном условии представлена разными числовыми мерами. Так, например, время в одном месте условия может быть представлено годами, в другом месте минутами, а в третьем – секундами. Необходимо вначале выполнить перевод этих разных единиц измерения в какую-то одну единственную, которая и будет применяться при числовых подсчетах. И этот перевод обычно делается, когда записывается краткое условие задачи. Например, в одном месте задачи говорится о двух годах, а в другом – о пяти сутках. Вы же решили, что будете использовать измерение времени в часах. Тогда в кратком условии пишете:
t1 = 2 года = 2·365 сут = 2·365·24 ч = 17520 ч. Аналогично и с другими величинами. Только имейте в виду, что, если, например, Вы решили в качестве измерения расстояний использовать метры, а для измерения времени – секунды, то размерность производных единиц оказывается жестко определенной Вашим выбором. Так, скорость Вы обязаны измерять в м/с, а ускорение – в м/с2. И, если в том же полном условии, например, скорость задана в км/ч, то ее обязательно надо перевести в м/с. Допустим, сказано, что v = 72 км/ч. Тогда Вы в кратком условии пишете:
v = 72 км/ч = 72·1000/3600 м/с = 20 м/с, то есть Вы километры перевели в метры, умножив 72 на 1000 (напомню, что в одном километре 1000 метров), а вместо часа в знаменателе поставили 3600 с (в часе, как известно, 3600 секунд). Промежуточные вычисления можно не приводить (Вы их выполняете отдельно, где-нибудь в черновике), а сразу записать:
t1 = 2 года = 17520 ч, v = 72 км/ч = 20 м/с.

Важно! Выбор единиц измерения диктуется не только соображением удобства. Так, гораздо удобнее измерять время обращения планет вокруг Солнца в годах, а не, скажем, в секундах. Диаметр планеты – в километрах, а не в миллиметрах, а длину спичечного коробка – в сантиметрах, а не в метрах. Часто при выборе единиц имерения при решении задач исходят именно из соображения удобства (и я, при показе решений задач, буду иногда так поступать). Здесь, правда, есть одно но. Дело в том, что во всем мире принята единая система, которая диктует выбор единиц измерения. Это – всем известная система СИ (Система Интернациональная). Так вот, в соответствии с принятыми Международными нормами, Вы обязаны использавать не любые единицы измерения, а только те, которые предписаны этой системой. В частности, например, длину следует измерять в метрах, время – в секундах, массу – в килограммах. Про удобство забудьте. Как быть? А быть так: если хотите, чтобы к Вам никто и никогда не придрался, пользуйтесь СИ! Вы всегда сможете аргументировать свой выбор тем, что Вы – законопослушный гражданин и вовсе не собираетесь нарушать Международные соглашения, хотя и глубоко страдаете оттого, что, например, поганую бациллу птичьего гриппа вынуждены измерять в метрах, а не в микронах. Такой, заведомо беспроигрышный подход, оправдан с разных точек зрения. Представьте, что Вы сдаете вступительный экзамен в институт. Перед экзаменатором – проблема, кому отдать предпочтение: и Вы, и Ваш конкурент проявили одинаковые знания из области физики, одинаково нестандартно подходите к анализу сложных физических ситуаций и т. д. И Вы, и Ваш конкурент правильно решили предложенные задачи. Но Вы дали ответ в км/ч, а конкурент – в м/с, то есть в системе СИ. Экзаменатор предпочтет конкурента и всегда аргументирует свой выбор. Так что бдите!

Часто спрашивают, надо ли делать рисунок к задаче? Смотря, какая задача. Бывает, что он и не нужен. А нередко без рисунка и решение выполнить трудно. Общий подход такой: рисунок не помешает никогда. Только не отягощайте его несущественными для данной задачи деталями, и, конечно, делайте его аккуратно, неряшливый рисунок может оказать медвежью услугу.

Из своего опыта преподавания знаю, что многие учащиеся почему-то сразу “бросаются” на числовые значения физических величин, данных в условии задачи. Забудьте на время о числах! Поверьте, для преподавателя или экзаменатора не так важно, проползла черепаха за отведенное время 10 метров или 50 сантиметров. Для него важна логика решения задачи, Ваше умение применять нужные для этого законы, корректное использование математических методов. Поэтому – совет: выполните задачу в общем виде, получите окончательную расчетную формулу, то есть формулу, куда входят величины, данные в условии задачи, а уж потом подставляйте числа и анализируйте полученный результат. Иногда такой анализ может принести пользу. Например, при определении расстояния, пройденного той же черепахой за 10 минут, получилось значение, равное 100 км. Согласитесь, что какая-то странная черепаха получилась. Хорошо, если ошиблись в арифметике, а вдруг сам подход к решению неверен? В любом случае, надо все проверять.

Играет роль и то, насколько аккуратно оформлено решение: если бардак в тетради, то нередко то же самое и в голове. Вообще, решение задачи – это Ваше творчество. Проявите его так, чтобы все убедились в качестве Ваших знаний.

И еще вот на что следует обратить внимание. Очень часто авторы учебников и задачников и, конечно, учащиеся отождествляют искомый параметр с параметром вообще. Попытаюсь на примере объяснить, о чем идет речь. Допустим для решения задачи Вы используете кинематическое уравнение движения: r = vt. Если v = const, то, согласно этому уравнению, радиус-вектор точки линейно зависит от времени, какой бы момент мы ни рассматривали. Время течет, радиус-вектор меняется, но характер зависимости остается прежним. Говорят, что t – это текущее время, а r – это текущий радиус-вектор. Если же мы интересуемся конкретным радиус-вектором в конкретное время, то как нам обозначить эти конкретные значения? Видимо, обозначения r и t для этого уже не подойдут, поскольку так мы обозначили текущие значения. Следовательно, надо выбрать какие-то другие обозначения. Какие? Да какие угодно, например, можно использовать те же буквы, но с индексом (верхним или нижним, буквенным или числовым – неважно). Так, один конкретный момент времени можно обозначить как t1. В этот момент радиус-вектор будет иметь значение r1. В другой момент времени t2 радиус-вектор будет r2 и так далее. Не хотите использовать индекс? Тогда обозначьте конкретные величины другими буквами, не такими, как текущие значения. Надеюсь, теперь Вам понятно, что фраза “Найти значение r радиус-вектора и значение t времени, когда тело достигло максимальной точки подъема” не является корректной. Ведь речь идет о конкретной точке, в которой тело будет находиться в конкретный момент времени и, следовательно, будет иметь конкретный радиус-вектор. Поэтому эти конкретные значения надо обозначить иначе, чем текущие (поставить индексы). Может, кто-то скажет, что мелочи все это. Да, отождествление обозначений текущих и конкретных параметров ошибкой назвать трудно, криминалом это не является. Просто – это признак дурного тона. Это все-равно, как появиться в приличном обществе в грязной обуви и мятом костюме. Тебе ничего не скажут, но мнение о тебе составят, и будет оно ни каким-нибудь неопределенным (текущим), а весьма конкретным. Очень советую с самаго начала приучать себя к аккуратности в обозначениях величин. Физика – не тот предмет, куда можно входить в грязной обуви.

В заключение приведу порядок решения задаx по пунктам. В этих пунктах Вы встретите правила, касающиеся векторных величин. Выше я об этом ничего не говорил, поскольку знаю, что это Вы поймете только после того, как решите (или изучите предлагаемые на этом сайте решения) хотя бы десятка задач. Тем не менее, я включил указанные пункты. После того, как приобретете опыт, вернитесь к ним. Тогда Вы окончательно поймете, что к чему. Итак,

Порядок решения задач

  1. Сделать краткую запись условия задачи, где отразить все встречающиеся в задаче данные и соотношения между ними. Буквенное обозначение данных (если оно не приведено в условии задачи) выбирать в соответствии с принятыми в физике символами. Приведенные в задаче числовые значения физических величин перевести в систему СИ. В краткой записи условия также отразить искомые величины. Принято после буквенных символов этих величин (или искомого соотношения между ними) ставить знак вопроса.
  2. Желательно сделать рисунок в соответствии с условием задачи. Обычно это оказывает большую помощь в решении. Рисунок не должен быть мелким. Выполнять его надо аккуратно, не загромождая ненужными или несущественными деталями.
  3. Если в задаче фигурируют векторные величины, необходимо выбрать систему отсчета. В качестве системы координат часто выбирают прямоугольную систему. При этом, если векторные величины, встречающиеся в задаче, действуют вдоль прямой, то пользуются одной координатной осью (любой), расположенной вдоль этой прямой. Если векторы расположены в плоскости, пользуются двумя осями, если в пространстве – тремя.
  4. Выбор направления осей и начала координат произволен. Однако его стараются сделать таким, чтобы решение получилось проще, но это приходит с опытом, накопленным при решении задач.
  5. Сделать математические записи соотношений, куда входят векторные величины. Эти соотношения должны соответствовать физическим процессам, анализу которых и посвящена данная задача.
  6. Спроектировать указанные соотношения на выбранные координатные оси.
  7. Вновь записать полученные в проекциях соотношения, но уже для конкретных физических параметров (например, для конкретного времени, скорости и т. д.).
  8. Полученные выражения будут такими же, как предыдущие (п. 5), только обозначениям конкретных параметров либо придать другие буквенные символы, либо, если принято решение оставить символы прежними, сопроводить их, например, каким-либо индексом (верхним или нижним).
  9. Пользуясь методами векторной алгебры, найти те проекции векторных величин, для определения которых достаточно данных, приведенных в условии задачи. При этом проекции векторов окажутся выраженными через их модули, которые либо приведены в условии задачи, либо их нужно найти.
  10. Используя полученные соотношения и привлекая в случае необходимости другие скалярные соотношения между данными условия задачи, находят неизвестные величины. Правильность полученного математического выражения для искомой величины целесообразно проверить по соответствию размерности, полученной из формулы, той размерности, которая принята для этой величины.
  11. В последнюю очередь (если того требует условие задачи) в конечную формулу подставляют числовые значения.
  12. Полученные числовые значения искомых величин желательно проанализировать с точки зрения их реальности. Если, например, масса комара окажется равной нескольким тоннам, а скорость автомобиля окажется близкой к скорости света, то вначале следует проверить правильность числовых расчетов и уже потом – весь ход решения задачи.

    Пожалуйста, не забудьте поделиться о прочитанном со своими друзьями в соц. сетях (см. кнопки ниже).

     

    Задания по физике для старших классов, основанные на больших идеях

    Когда учителя проводят соревнования в классе, они часто разрабатывают разовые соревнования, в которых учащиеся должны увидеть, кто построит самую высокую башню или кто правильно ответит на большинство вопросов на игровом шоу. В таких ситуациях обычно побеждают самые талантливые ученики, что может усилить их самовосприятие и подавить вовлеченность. Самые способные ученики получают всевозможные награды (внутренние и внешние) и, как правило, возвращаются и снова стараются в следующий раз. Студенты, которые не преуспевают в этих соревнованиях, часто плохо справляются, плохо себя чувствуют и думают, что они неспособны.

    Чтобы сохранить преимущества конкуренции и побудить всех учащихся продолжать стараться изо всех сил, я разработал задачи, основанные на больших идеях на уроках физики в старшей школе. Они основаны на концепции «редизайна», которая происходит в середине многонедельных соревнований.

    Вот рекомендации, которые я использую для создания веселых, инклюзивных, полезных и глубокомысленных конкурсов:

    • Заранее предоставьте учащимся ускоренный курс, чтобы получить базовый уровень знаний.
    • Установите параметры таким образом, чтобы был спектр успеха.
    • Установите первый крайний срок для первоначального тестирования.
    • Позвольте детям изменить дизайн и улучшить его.
    • Распределите рабочие дни на несколько недель, устраивая дни с более традиционным контентом между ними, чтобы дети могли думать о других идеях и не уставать.

    Соревнования за большие идеи

    Задание: В этом году по физике я организовал шестинедельный конкурс, в котором я предложил учащимся увидеть, какая группа сможет собрать робота Lego EV3, который проедет 15 метров меньше всего. количество времени. Это было завершено в начале года, когда физика занималась силами и движением. Дети использовали Lego Mindstorms в нескольких предыдущих лабораториях, поэтому они были немного знакомы с роботами и программным обеспечением.

    Вначале ученики пробовали многое. Некоторые бывшие в употреблении шестерни; некоторые сосредоточились на том, чтобы сделать их похожими на автомобиль. Многие обнаружили, что даже заставить роботов двигаться прямо было довольно сложно. Они построили роботов слишком высокими, поэтому они упали. Студенты продолжали двигаться вперед и собирать данные.

    Пока они построили робота, который прошел 15 метров и продолжал попытки, они получали полный балл, поэтому оценка не была мотиватором. Однако группы были заинтересованы в том, чтобы продолжать вводить новшества, чтобы сократить время, необходимое их роботу для перемещения. Мы работали по пятницам и всякий раз, когда они заканчивали обычные занятия в классе.

    Пауза: Примерно через три недели мы сделали паузу и повесили на стену номера, чтобы студенты могли их увидеть. Каждая группа могла видеть свое место в турнирной таблице по сравнению с другими группами. Тогда они могли видеть, что делают другие, и вносить изменения.

    Изучение того, что сработало: Все учащиеся посмотрели на группы с самыми быстрыми роботами, чтобы узнать, что у них хорошо получается. Они начали замечать, какие физические свойства имеют значение: редуктор, качественная конструкция и низкий центр масс имели огромное значение, в то время как аэродинамика, казалось, не имела никакого значения. На веб-сайте класса я разместил видеоролики о конструкции зубчатых передач и шасси, и класс понял, что лучшие группы сосредоточены на этом элементе конструкции. В рабочее время я ходил по группам и разговаривал с ними. Группы, которые боролись, получили небольшой дополнительный толчок. Я призвал детей поговорить с другими группами о том, что сработало.

    Редизайн: Процесс редизайна превращает это соревнование в практику равенства, повышая уровень мышления и понимания для всех. После промежуточной проверки учащиеся провели оставшееся время в классе, совершенствуя свой собственный дизайн. Это требует дополнительного времени, но студенты, чьи роботы были немного медленнее, имели возможность повторить, а группы с быстрыми роботами также могли попробовать что-то новое для улучшения.

    Важность этапа редизайна невозможно переоценить. На этом этапе происходит так много критического мышления, решения проблем, упорства и веселья. Поскольку группы также соревнуются друг с другом, чтобы сократить свое время, лучшие группы продолжают работать над улучшениями.

    Насколько эффективен этап редизайна?

    После нашего испытания роботов я хотел узнать, насколько учащиеся смогли применить на практике то, что они узнали на этапе перепроектирования. На этот раз я предложил студентам сконструировать сани, которые могли бы тянуть наибольший вес. Мы изучали работу и энергию, и соревнование по тяге саней требовало от студентов включения идей трения, силы, расстояния и простых механизмов.

    Разные группы использовали разные подходы, в том числе шкивы, шестерни, добавление большего количества колес, добавление массы для увеличения трения в машине и т. д. Опять же, на полпути мы сделали паузу, чтобы посмотреть, где все находятся, поучиться друг у друга и заняться переделкой. . Удивительно, но между первоначальным испытанием и фазой редизайна три группы с самыми низкими показателями смогли улучшить показатели в среднем на 866 процентов. Верхняя группа также внесла новшества, увеличив вес на 42 процента. Почти каждая группа показала значительное улучшение.

    Хотя эти соревнования требуют времени и могут вызвать разочарование учащихся, если что-то пойдет не так, я думаю, они того стоят. Наука — это гораздо больше, чем рабочие листы и задачи: благодаря этим конкурсам студенты не только узнают больше о содержании курса путем проб и ошибок в течение нескольких недель, но также учатся справляться с разочарованием и повторять идеи.

    Ученикам нравятся эти соревнования — они, как правило, сосредотачиваются на том, чтобы побить свой лучший результат, а не на том, кто побьет их. Когда я разговариваю со студентами позже в этом году или в следующем году, они обычно сосредотачиваются на этой части.

    Три научно-исследовательских подхода к планированию физической деятельности

    NASA/ADS

    Три научно-обоснованных подхода к планированию занятий по физике

    • Баят Баруни, Амин
      • ;
    • Фон Корф, Джошуа
      • ;
    • Томс, Брайан Д.
      • ;
    • Топдемир, Зейнеп
      • ;
    • Чини, Жаклин Дж.
    Аннотация

    В курсах физики в колледжах обычно используются различные виды деятельности, включая лабораторные работы, учебные пособия и учебные программы в студии. Преподаватели должны выбирать между использованием исследовательских мероприятий, разработкой собственных мероприятий или модификацией существующих мероприятий. Выбор инструкторов зависит от их собственных целей и целей деятельности, из которой они выбирают. Чтобы помочь им в разработке или модификации деятельности для их ситуации, мы изучаем исследовательскую деятельность, чтобы определить их цели и особенности деятельности, связанные с этими целями. Поскольку в большинстве занятий учащимся предлагается выполнять задания, чтобы помочь им в обучении, шестьдесят шесть заданий из одиннадцати различных учебных программ, основанных на исследованиях, были закодированы для действий учащихся.

    Схема кодирования, содержащая сорок девять кодов в десяти категориях, была разработана на основе набора заданий, интервью с некоторыми дизайнерами заданий и рекомендаций лабораторного отчета Американской ассоциации учителей физики за 2014 год. Результаты были изучены с использованием кластерного анализа k-средних, выявившего три кластера дизайна. Мы обозначили эти кластеры как «Мышление как ученые», «Концепции обучения», «Создание моделей». Эти три кластера отражают различные цели проектирования. В кластере «Думай как ученый» действия делают акцент на планировании экспериментов учащимися, обсуждении, анализе ошибок, проверке разумности, подтверждении заявлений и создании предположений или упрощений. Кластер концепций обучения фокусируется на прогнозировании результатов и экспериментальных наблюдениях. Кластер Building Models делает упор на обсуждение и ответы на вопросы по физике или математике, которые не используют собранные данные. Эта работа связывает общие черты, проявляющиеся в физической деятельности, с целями и стратегиями проектировщиков.
    Таким образом, это может предоставить инструкторам более простой способ создания действий, которые достигают желаемых результатов.


    Публикация:

    Электронные распечатки arXiv

    Дата публикации:
    Сентябрь 2020
    DOI:
    10.48550/архив.2009.04020
    архив:
    архив: 2009.04020
    Биб-код:
    2020arXiv200904020B

    Оставить комментарий