Задания к уроку по теме “Блоки” | Методическая разработка по физике (7 класс) по теме:
Урок 55:
Применение закона равновесия рычага к блоку.
Внимательно прочитайте § 59 учебника и выполните в тетради следующие задания:
- Опишите, что представляет собой блок.
- Выпишите из учебника определения неподвижного и подвижного блока. Сделайте в тетради соответствующие рисунки (рис.164 – неподвижный блок; рис.166 – подвижный блок).
- Внимательно изучив § 59, становится понятным, что любой блок схематически можно представить как рычаг. Внимательно изучите «превращение» неподвижного блока в рычаг, рассмотренное ниже и аналогично осуществите «превращение» подвижного блока в рычаг. Затем, используя условие равновесия рычага (применив его к блоку), сделайте вывод о выигрыше в силе, которую дает подвижный и неподвижный блоки.
А
О
В
А
А
О
А
В
l2
А
А
l1
Здесь l1 = AO – плечо силы F1;
l2 = ОВ – плечо силы F2.
Но АО = ОВ, значит l1 = l2, то есть неподвижный блок – равноплечный рычаг.
Запишем условие равновесия рычага:
; но l1 = l2, значит
или F1 = F2.
ВЫВОД: Неподвижный блок выигрыша в силе не дает. Он лишь позволяет менять направление действия силы.
- Ответьте на вопросы:
Для каких целей применяют неподвижный блок?
Как легче подниматься вверх: лезть по веревке или подниматься при помощи неподвижного блока?
- Внимательно разберите пример решения задачи:
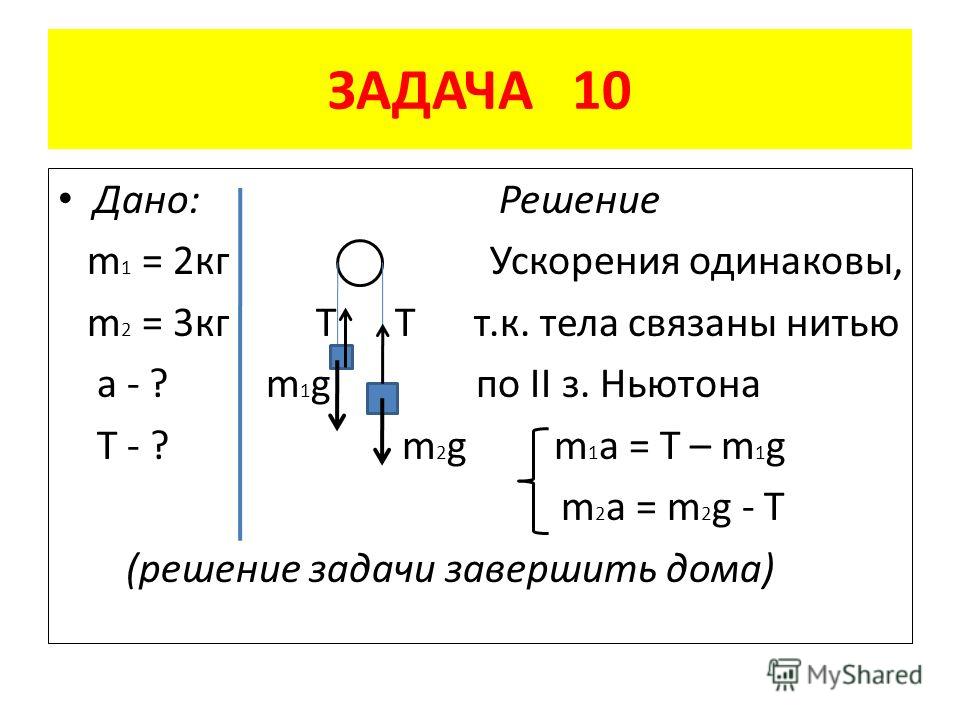
Задача: Груз какого веса можно поднять с помощью подвижного блока, если тянуть веревку с силой 150Н.
Дано: Си: Решение:
F = 40Н 1) Т.к. блок подвижный, то он может давать выигрыш в силе в 2 раза. Это означает,
P = ? что с помощью данного блока можно поднять груз в 2 раза большего веса, чем сила, приложенная к веревке.
P = F·2 = 40Н·2 = 80Н
Ответ: P = 80 Н.
- По образцу решите задачу: С какой силой надо тянуть веревку, чтобы поднять кирпич весом 50Н с помощью подвижного блока? А с помощью неподвижного?
Проверьте себя (Ответ: 25Н)
- Внимательно разберите пример решения задачи:
Задача: С помощью подвижного блока подняли груз на высоту 10 м, прилагая силу 120 Н. Какая работа была совершена при этом?
Дано: Си: Решение:
F = 120Н 1) А = F·s = Fтяж груза·h
h = 10м 2) Учитывая, что блок подвижный, вспомним, что он дает выигрыш в силе в 2 раза.
A = ? Это значит, что прикладывая силу F = 120 Н к подвижному блоку, мы сможем поднять груз в 2 раза большего веса, т.е. Fтяж груза = 2·F = 2 · 120Н = 240Н
3) А = Fтяж груза·h = 240Н·10м = 2400 Дж
Ответ: А = 2400 Дж.
- По образцу решите задачу: Вычислите работу, совершаемую при подъеме ведра с песком весом 200Н на высоту 5 м с помощью подвижного блока?
Проверьте себя (Ответ: 1000Дж)
- Придумайте задачу на изучаемую тему и решите ее.

- Домашнее задание:
§ 59, задачи 762,768 (из сборника задач Лукашика), письменно.
Решебник к сборнику задач по физике для 7-9 классов Лукашик В.И. Иванова Е.ВIV. РАБОТА И МОЩНОСТЬ. ПРОСТЫЕ МЕХАНИЗМЫ. ЭНЕРГИЯ. 29(30). Блоки
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
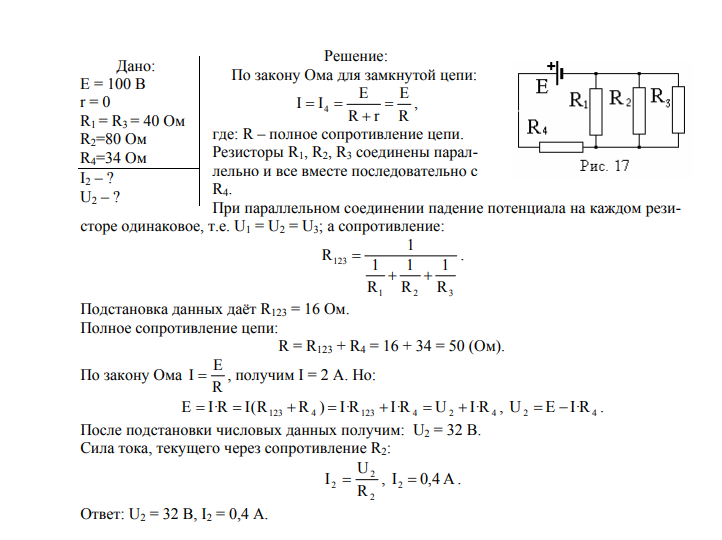
- 757. Отвечая у доски по теме «Неподвижные блоки», ученик сделал рисунок (рис. 215), где нужно было показать, что с помощью веревки и блока уравновешены два груза. Какую ошибку он допустил в рисунке?
- 758. Объясните, зачем пользуются неподвижным блоком, ведь выигрыша в силе он не дает. Где его удобно использовать?
- 759. Каковы должны быть показания динамометров в положениях А и В (рис. 216)? (Груз не движется.)
- 760. Через неподвижный блок перекинута цепь (рис. 217). В каком случае динамометр будет показывать меньшую силу при равномерном подъеме груза? Почему?
- 761.
 В какой из систем неподвижных блоков (рис. 218) надо приложить большую силу для подъема одного и того же груза, если трение в каждом из блоков одинаковое?
В какой из систем неподвижных блоков (рис. 218) надо приложить большую силу для подъема одного и того же груза, если трение в каждом из блоков одинаковое? - 762°. На рисунке 219 динамометр А показывает силу 20 Н. Что должен показать динамометр Б?
- 763. Как легче подниматься вверх: лезть по веревке или поднимать себя при помощи блока (рис. 220)?
- 764°. Будет ли система, состоящая из рычага и блока (рис. 221), находиться в равновесии?
- 765°. Для подъема одного и того же груза используют две системы блоков (рис. 222, 1, 2). Равные ли силы надо приложить в точках А, если трение в каждом блоке одинаково, а вес подвижного блока много меньше веса груза? Ответ объясните.
- 766°. Определите показание динамометра (рис. 223), если вес каждого шарика равен 10 Н. Рычаг находится в равновесии. (Весом блока пренебречь.)
- 767. На рисунке 224 показано одно из чудес древних египетских жрецов. Как только на жертвеннике загорался огонь, двери храма раскрывались.
 Объясните, на чем основано это чудо. (В жертвеннике воздух. Жертвенник при помощи трубы соединен с кожаным мешком.)
Объясните, на чем основано это чудо. (В жертвеннике воздух. Жертвенник при помощи трубы соединен с кожаным мешком.) - 768. Какой наибольший груз может приподнять мальчик, масса которого равна 42 кг, пользуясь одним подвижным и одним неподвижным блоком (рис. 225)?
- 769*. При помощи неподвижного блока поднимают из воды гранитную плиту объемом 0,03 м3. Какую силу прилагают рабочие, когда плита находится в воде; над поверхностью воды? (Трение не учитывать.)
- 770°. Вес подвижного блока равен 1,2 Н. Его груз весит 6 Н (рис. 226). Чему будет равно показание динамометра при равномерном подъеме груза? (Трение не учитывать.)
- 771. Груз какой массы можно поднять с помощью подвижного блока, вес которого 20 Н, прилагая к свободному концу веревки усилие 210 Н, если не учитывать трение?
- 772*. Груз какого веса надо прикрепить к свободному концу троса, чтобы система блоков (рис. 227) находилась в равновесии? (Трением и весом блоков пренебречь.)
- 773.
 Какую силу надо приложить к свободному концу троса А, чтобы трос, перекинутый через неподвижный блок, был натянут с силой 4000 Н (рис. 228)?
Какую силу надо приложить к свободному концу троса А, чтобы трос, перекинутый через неподвижный блок, был натянут с силой 4000 Н (рис. 228)? - 774*. На концах невесомой нерастяжимой нити, перекинутой через легкий неподвижный блок, подвешены два груза, массы которых равны 100 и 200 г. В начальный момент времени грузы покоятся на высоте 2 м от пола. Пренебрегая трением, определите ускорение грузов
- 775*. Гиря массой 500 г соединена с другой гирей массой m2 легкой нерастяжимой нитью, перекинутой через невесомый блок. Чему должна быть равна масса второй гири, чтобы первая гиря двигалась вверх с ускорением 2,4 м/с2; первая гиря двигалась бы вниз с тем
- 776*. Две гири А и B массами по 1 кг соединены легкой нерастяжимой нитью, перекинутой через блок (рис. 229). Найдите ускорение, с которым движутся гири; силу натяжения нити. (Трением можно пренебречь.)
- 777*. На наклонной плоскости с углом 30° при основании лежит брусок массой 1 кг (рис. 230). Гиря такой же массы присоединена к бруску с помощью невесомой нерастяжимой нити, перекинутой через легкий блок.
 Определите ускорение, с которым движутся оба тела,
Определите ускорение, с которым движутся оба тела, - 778*. Два тела соединены невесомой нерастяжимой нитью, перекинутой через легкий блок (рис. 229). Масса тела Б равна 2 кг. Коэффициент трения тела Б о горизонтальную поверхность равен 0,1. Какой массой обладает тело А, если оба тела движутся равномерно?
- 779*. К пружинным весам (рис. 231) подвешен блок. Через блок перекинут нерастяжимый шнур, к концам которого привязаны грузы массами 1 и 2 кг. Какой вес будут регистрировать пружинные весы во время движения грузов? (Весом блока и шнура пренебречь.)
- 780*. При помощи подвижного блока поднимают груз на высоту 4 м, прилагая силу 100 Н. Вес блока равен 20 Н, а вес груза 165 Н. Какую дополнительную работу надо совершить, чтобы с помощью указанного блока поднять груз на высоту 4 м?
- 781*. На опоре стоит рабочий и с помощью блока равномерно поднимает груз, вес которого равен 480 Н (рис. 232). Вычислите давление, производимое рабочим на опору, если его вес 720 Н, а площадь ступней составляет 320 см2.

- 782*. Поднимая при помощи подвижного блока ведро с песком весом 200 Н на высоту 5 м, производят работу 1020 Дж. Какой процент составляет энергия, которая была затрачена непроизводительно?
- 783. Какую силу надо приложить к тросу А (рис. 233), чтобы трос В был натянут с силой 1 кН?
- 784. С какой силой натянут трос А, если вес груза равен 100 Н (рис. 234)?
Поиск по сайту
Двойная проблема: задачи двух тел
До сих пор наше исследование ограничивалось анализом отдельных объектов, движущихся под действием законов Ньютона. Но что произойдет, если есть два объекта, так или иначе соединенных друг с другом? Например, эвакуатор может буксировать автомобиль по шоссе. Как проводится такой анализ? Как определяется ускорение эвакуатора и автомобиля? А как насчет силы, действующей между эвакуатором и автомобилем? В этой части Урока 3 мы попытаемся проанализировать такие ситуации. Мы обнаружим, что анализ ведется таким же общим образом, как и при наличии одного объекта — с помощью диаграмм свободного тела и законов Ньютона.
Основной подход
Ситуации с участием двух объектов часто называют ситуациями двух тел. Появляясь как задачи физики, задачи двух тел характеризуются набором двух неизвестных величин. Чаще всего (хотя и не всегда) двумя неизвестными являются ускорение двух объектов и сила, передаваемая между двумя объектами. К двум проблемам с телом обычно можно подойти, используя один из двух основных подходов. Один из подходов включает в себя сочетание системного анализа и анализа отдельных органов. В системном анализе два объекта рассматриваются как один объект, движущийся (или ускоряющийся) вместе как единое целое. Масса системы есть сумма масс двух отдельных объектов. Если задействовано ускорение, ускорение системы такое же, как и у отдельных объектов. Системный анализ обычно выполняется для определения ускорения системы. Системный анализ сочетается с анализом отдельных объектов. При индивидуальном объектном анализе любой из двух объектов выделяется и рассматривается как отдельный, независимый объект.
Двойное сочетание системного анализа и анализа отдельных объектов является одним из двух подходов, которые обычно используются для анализа задач двух тел. Второй подход предполагает использование двух отдельных анализов отдельных объектов. При таком подходе диаграммы свободного тела строятся независимо для каждого объекта, а второй закон Ньютона используется для связи отдельных значений силы с массой и ускорением. Анализ каждого отдельного объекта генерирует уравнение с неизвестным. В результате получается система двух уравнений с двумя неизвестными. Система уравнений решается для определения неизвестных величин.
В качестве первого примера двух подходов к решению задач двух тел рассмотрим следующий пример задачи.
Пример задачи 1:
Коробка массой 5,0 кг и коробка массой 10,0 кг касаются друг друга. Горизонтальная сила 45,0 Н приложена к ящику массой 5,0 кг, чтобы ускорить движение обоих ящиков по полу. Силами трения пренебречь и определить ускорение ящиков и силу, действующую между ящиками.
Первый подход к этой проблеме предполагает двойное сочетание системного анализа и анализа отдельных объектов. Как уже упоминалось, системный анализ используется для определения ускорения, а анализ отдельных объектов используется для определения сил, действующих между объектами. В системном анализе два объекта рассматриваются как один объект. Разделительная линия, разделяющая объекты, игнорируется. Масса системы из двух предметов 15,0 кг. Диаграмма свободного тела для системы показана справа. На систему действуют три силы: сила тяжести (Земля тянет вниз массу 15,0 кг), нормальная сила (пол давит на систему, чтобы выдержать ее вес) и приложенная сила (рука притягивается).
Теперь, когда ускорение определено, можно выполнить анализ отдельного объекта для любого объекта, чтобы определить силу, действующую между ними. Неважно, какой объект выбран; результат будет одинаковым в любом случае. Здесь анализ отдельного объекта проводится на объекте массой 10,0 кг (только потому, что на него действует на одну силу меньше). Диаграмма свободного тела для объекта весом 10,0 кг показана справа. На него действуют только три силы – сила тяжести на 10,0 кг, опорная сила (от пола толкает вверх) и правая контактная сила (F контакт ). Поскольку объект массой 5,0 кг ускоряется вправо, он будет толкать вправо объект массой 10,0 кг; это называется контактной силой (или нормальной силой, или приложенной силой, или…). Вертикальные силы уравновешивают друг друга, так как нет вертикального ускорения. Единственной неуравновешенной силой на объекте массой 10,0 кг является Fконтакт. Эта сила является результирующей силой и равна m•a, где m равно 10,0 кг (поскольку данный анализ относится к объекту массой 10,0 кг), а a уже определено равным 3,0 м/с 2 . Чистая сила равна 30,0 Н. Эта результирующая сила представляет собой силу объекта массой 5,0 кг, толкающего объект массой 10,0 кг вправо; его величина равна 30,0 Н.
Здесь анализ отдельного объекта проводится на объекте массой 10,0 кг (только потому, что на него действует на одну силу меньше). Диаграмма свободного тела для объекта весом 10,0 кг показана справа. На него действуют только три силы – сила тяжести на 10,0 кг, опорная сила (от пола толкает вверх) и правая контактная сила (F контакт ). Поскольку объект массой 5,0 кг ускоряется вправо, он будет толкать вправо объект массой 10,0 кг; это называется контактной силой (или нормальной силой, или приложенной силой, или…). Вертикальные силы уравновешивают друг друга, так как нет вертикального ускорения. Единственной неуравновешенной силой на объекте массой 10,0 кг является Fконтакт. Эта сила является результирующей силой и равна m•a, где m равно 10,0 кг (поскольку данный анализ относится к объекту массой 10,0 кг), а a уже определено равным 3,0 м/с 2 . Чистая сила равна 30,0 Н. Эта результирующая сила представляет собой силу объекта массой 5,0 кг, толкающего объект массой 10,0 кг вправо; его величина равна 30,0 Н. Таким образом, ответы на два неизвестных для этой задачи равны 3,0 м/с 2 и 30,0 Н.
Таким образом, ответы на два неизвестных для этой задачи равны 3,0 м/с 2 и 30,0 Н.
. Теперь рассмотрим решение этой же задачи, используя второй подход — использование анализ двух отдельных объектов. В процессе этого второго подхода мы проигнорируем тот факт, что знаем, каковы ответы, и предположим, что решаем проблему впервые. В этом подходе выполняются два отдельных анализа диаграммы свободного тела. На приведенных ниже диаграммах показаны диаграммы свободного тела для двух объектов.
Обратите внимание, что сзади на объект весом 5,0 кг действуют четыре силы. Две вертикальные силы — F грав и F норма — являются очевидными силами. Приложенная сила 45,0 Н (F , приложение ) является результатом нажатия рукой на задний объект, как описано в постановке задачи и показано на диаграмме. Контактная сила, направленная влево на объект массой 5,0 кг, — это сила объекта массой 10,0 кг, толкающего влево объект массой 5,0 кг. Когда делается попытка толкнуть задний объект (объект массой 5,0 кг) вперед, передний объект (объект массой 10,0 кг) отталкивает его назад. Эта сила равна и противоположна давлению заднего объекта на передний объект. Эта сила обозначается просто как F свяжитесь с для обеих диаграмм свободного тела. На диаграмме свободного тела для объекта массой 10,0 кг действуют только три силы. Еще раз, две вертикальные силы – F грав и F норма – являются очевидными силами. Горизонтальная сила — это просто объект массой 5,0 кг, толкающий вперед объект массой 10,0 кг. Приложенная сила 45,0 Н не действует на этот 10,0-килограммовый объект; оно воздействует на объект массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела.
Когда делается попытка толкнуть задний объект (объект массой 5,0 кг) вперед, передний объект (объект массой 10,0 кг) отталкивает его назад. Эта сила равна и противоположна давлению заднего объекта на передний объект. Эта сила обозначается просто как F свяжитесь с для обеих диаграмм свободного тела. На диаграмме свободного тела для объекта массой 10,0 кг действуют только три силы. Еще раз, две вертикальные силы – F грав и F норма – являются очевидными силами. Горизонтальная сила — это просто объект массой 5,0 кг, толкающий вперед объект массой 10,0 кг. Приложенная сила 45,0 Н не действует на этот 10,0-килограммовый объект; оно воздействует на объект массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела.
Теперь цель этого подхода состоит в том, чтобы сгенерировать систему из двух уравнений, способных решить для двух неизвестных значений. Использование F net = m•a с диаграммой свободного тела для объекта массой 5,0 кг даст следующее уравнение 1: диаграмма свободного тела для объекта массой 10,0 кг даст приведенное ниже уравнение 2:
F контакт = 10,0•a
(Обратите внимание, что единицы измерения были исключены из уравнений 1 и 2, чтобы очистить уравнения up . ) Если выражение 10.0•a подставить в уравнение 1 для F связаться с , то уравнение 1 сводится к одному уравнению с одним неизвестным. Уравнение принимает вид
) Если выражение 10.0•a подставить в уравнение 1 для F связаться с , то уравнение 1 сводится к одному уравнению с одним неизвестным. Уравнение принимает вид
45,0 – 10,0•a = 5,0•a
Пара шагов алгебры приводит к значению ускорения 3,0 м/с 2 . Это значение a можно подставить обратно в уравнение 2, чтобы определить силу контакта:
F контакт = 10,0•a = 10,0 •3,0
F contact = 30.0 N
Как видно, использование второго подхода для решения задачи двух тел дает те же два ответа для двух неизвестных. Теперь мы попробуем те же два подхода к очень похожей задаче, включающей силу трения.
Пример задачи 2:
Коробка массой 5,0 кг и коробка массой 10,0 кг касаются друг друга. Горизонтальная сила 45,0 Н приложена к ящику массой 5,0 кг, чтобы ускорить движение обоих ящиков по полу. Коэффициент кинетического трения равен 0,200. Определить ускорение и контактную силу.
Наше первое решение этой проблемы будет включать двойную комбинацию системного анализа и анализа отдельных объектов. Как вы, вероятно, заметили, пример задачи 2 похож на пример задачи 1 за исключением того, что поверхность не лишена трения в примере задачи 2. Таким образом, при проведении системного анализа во втором примере необходимо учитывать трение в 15-килограммовой системе. . Таким образом, диаграмма свободного тела для системы теперь включает четыре силы — те же три, что и в примере задачи 1, плюс сила трения, направленная влево. Сила трения в системе может быть рассчитана как μ•F норма , где F норма — нормальная сила, действующая на систему. Норма F системы равна силе тяжести, действующей на систему массой 15,0 кг; это значение равно 147 Н. Таким образом,
F трения = μ•F норма = (0,200)•(147 Н) = 29,4 Н
Вертикальные силы уравновешивают друг друга — в соответствии с тем фактом, что нет ускорение. Горизонтальные силы не уравновешивают друг друга. Чистую силу можно определить как векторную сумму F приложение и F трение . То есть F net = 45,0 Н, справа + 29,4 Н, слева; они добавляют к 15,6 Н, правильно. Теперь ускорение можно рассчитать, используя второй закон Ньютона.
Горизонтальные силы не уравновешивают друг друга. Чистую силу можно определить как векторную сумму F приложение и F трение . То есть F net = 45,0 Н, справа + 29,4 Н, слева; они добавляют к 15,6 Н, правильно. Теперь ускорение можно рассчитать, используя второй закон Ньютона.
a = F нетто / м = (15,6 Н/15,0 кг) = 1,04 м/с 2
объект, чтобы определить силу, действующую между ними. Опять же, не имеет значения, какой объект выбран; результат будет одинаковым в любом случае. Объект массой 10,0 кг выбран для анализа отдельного объекта, поскольку на него действует на одну силу меньше; это облегчает решение. На тело массой 10,0 кг действуют четыре силы. Две вертикальные силы очевидны – сила тяжести (98,0 Н) и нормальной силы (равной силе тяжести). Горизонтальные силы — это сила трения слева и сила объекта массой 5,0 кг, толкающего объект массой 10,0 кг вперед; это обозначено как F , контакт на диаграмме свободного тела. Чистая сила — векторная сумма всех сил — всегда может быть найдена путем сложения сил в направлении ускорения и вычитания сил в противоположном направлении. Этот F net равен контакту F – F фрикцион . Применение второго закона Ньютона к этому объекту дает уравнение:
Чистая сила — векторная сумма всех сил — всегда может быть найдена путем сложения сил в направлении ускорения и вычитания сил в противоположном направлении. Этот F net равен контакту F – F фрикцион . Применение второго закона Ньютона к этому объекту дает уравнение:
F контакт – F трение = (10,0 кг)•(1,04 м/с 2 )
Сила трения на этом 10,0-килограммовом объекте не равна то же, что и сила трения в системе (поскольку система была на тяжелее ). Значение F frict можно рассчитать как мк•F норма , где F норма — нормальная сила, испытываемая объектом массой 10,0 кг. F норма массы 10,0 кг равно силе тяжести, действующей на объект массой 10,0 кг; это значение равно 98,0 Н. Итак,
F трение = мк•F норма = (0,200)•(98,0 Н) = 19,6 Н
Итак, теперь значение 19,6 Н можно подставить в приведенное выше уравнение и F контакт можно рассчитать:
F контакт – 19,6 Н = (10,0 кг)•(1,04 м/с 2 )
F контакт = (10,0 кг)•(1,04 м/с 2 ) + 19,6 Н
Ф контакт = 30,0 Н
Таким образом, использование двойной комбинации системного анализа и анализа отдельных тел позволяет определить две неизвестные величины – 1,04 м/с 2 для ускорения и 30,0 Н для F контакта . Теперь мы увидим, как два анализа отдельных объектов могут быть объединены для создания системы двух уравнений, способной найти решение для двух неизвестных. Еще раз начнем анализ с предположения, что мы решаем задачу впервые и не знаем ни ускорения, ни контактной силы. Диаграммы свободного тела для отдельных объектов показаны ниже.
Теперь мы увидим, как два анализа отдельных объектов могут быть объединены для создания системы двух уравнений, способной найти решение для двух неизвестных. Еще раз начнем анализ с предположения, что мы решаем задачу впервые и не знаем ни ускорения, ни контактной силы. Диаграммы свободного тела для отдельных объектов показаны ниже.
Теперь на 5-килограммовый объект сзади действует пять сил. Две вертикальные силы — F грав и F норма — являются очевидными силами. Приложенная сила 45,0 Н (F , приложение ) является результатом нажатия рукой на задний объект. Контактная сила, направленная влево на объект массой 5,0 кг, — это сила объекта массой 10,0 кг, толкающего влево объект массой 5,0 кг. Его величина равна контактной силе, действующей на передний объект массой 10,0 кг со стороны заднего объекта массой 5,0 кг. Эта сила обозначается просто как F свяжитесь с для обеих диаграмм свободного тела. Наконец, сила трения, направленная влево, является результатом трения о пол, по которому движется объект массой 5,0 кг. На диаграмме свободного тела для объекта весом 10,0 кг теперь действуют четыре силы. Две вертикальные силы – F грав и F норма – очевидны. Контактная сила, направленная вправо (F , контакт ) — это просто объект массой 5,0 кг, толкающий вперед объект массой 10,0 кг. А направленная влево сила трения является результатом трения о пол. Опять же, на этот 10,0-килограммовый объект не действует приложенная сила 45,0 Н; оно воздействует на объект массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела. Сила трения для каждого объекта может быть определена как μ•Fnorm, где F норма — нормальная сила, испытываемая отдельными объектами. На каждый объект действует нормальная сила, равная его весу (поскольку вертикальные силы должны уравновешиваться). Таким образом, силы трения для объекта массой 5,0 кг (вес 49,0 Н) и объекта массой 10,0 кг (вес 98,0 Н) составляют 0,200•49,0 Н и 0,200•98,0 Н соответственно.
На диаграмме свободного тела для объекта весом 10,0 кг теперь действуют четыре силы. Две вертикальные силы – F грав и F норма – очевидны. Контактная сила, направленная вправо (F , контакт ) — это просто объект массой 5,0 кг, толкающий вперед объект массой 10,0 кг. А направленная влево сила трения является результатом трения о пол. Опять же, на этот 10,0-килограммовый объект не действует приложенная сила 45,0 Н; оно воздействует на объект массой 5,0 кг и уже было рассмотрено на предыдущей диаграмме свободного тела. Сила трения для каждого объекта может быть определена как μ•Fnorm, где F норма — нормальная сила, испытываемая отдельными объектами. На каждый объект действует нормальная сила, равная его весу (поскольку вертикальные силы должны уравновешиваться). Таким образом, силы трения для объекта массой 5,0 кг (вес 49,0 Н) и объекта массой 10,0 кг (вес 98,0 Н) составляют 0,200•49,0 Н и 0,200•98,0 Н соответственно.
Используя эти значения F frict и второй закон Ньютона, можно написать систему двух уравнений, которую можно решить для двух неизвестных значений. Использование сети F = m•a с диаграммой свободного тела для объекта массой 5,0 кг даст уравнение 3 ниже: Диаграмма свободного тела для объекта массой 10,0 кг даст приведенное ниже уравнение 4:
Использование сети F = m•a с диаграммой свободного тела для объекта массой 5,0 кг даст уравнение 3 ниже: Диаграмма свободного тела для объекта массой 10,0 кг даст приведенное ниже уравнение 4:
F контакт – 19,6 = 10,0•a
уравнения up .) Из уравнения 4, F контакт = 10.0•a + 19.6. Подставив это выражение для контакта F в уравнение 3 и выполнив соответствующие алгебраические операции, мы получим значение ускорения:
45,0 – (10,0•a + 19,6) – 9,8 = 5,0•a
45,0 – 19,6 – 9,8 = 15,0•а
15,6 = 15,0•а
a = (15,6/15,0)= 1,04 м/с 2
Это значение ускорения можно подставить обратно в выражение для контакта F , чтобы определить контактное усилие:
F контакт = 10,0•a + 190,6 = 10,0•(1,04) + 19,6
F контакт = 30,0 N
Опять же мы обнаруживаем, что второй подход с использованием анализа двух отдельных объектов дает один и тот же набор ответов для двух неизвестных. Последний пример задачи будет включать вертикальное движение. Подходы останутся прежними.
Последний пример задачи будет включать вертикальное движение. Подходы останутся прежними.
Пример задачи 3:
Мужчина входит в лифт с двумя ящиками, один над другим. Верхний ящик имеет массу 6,0 кг, а нижний ящик имеет массу 8,0 кг. Мужчина устанавливает две коробки на метрической шкале, сидя на полу. При ускорении вверх из состояния покоя мужчина наблюдает, что весы показывают значение 166 Н; это сила, действующая вверх на нижнюю коробку. Определить ускорение лифта (и ящиков) и силы, действующие между ящиками.
Оба подхода будут использоваться для решения этой проблемы. Первый подход предполагает двойное сочетание системного анализа и анализа отдельных объектов. Для системного анализа два ящика считаются единой системой массой 14,0 кг. На эту систему действуют две силы — сила тяжести и нормальная сила. Диаграмма свободного тела показана справа. Сила тяжести рассчитывается обычным способом, используя 14,0 кг в качестве массы.
F грав = м•г = 14,0 кг • 9,8 Н/кг = 137,2 Н
Поскольку существует вертикальное ускорение, вертикальные силы не будут уравновешены; значение F grav не равно значению нормы F . Нормальная сила указана в условии задачи. Эта нормальная сила в 166 Н представляет собой восходящую силу, действующую на нижний ящик; он действует как сила на систему, поскольку нижний ящик является частью системы. Чистая сила представляет собой векторную сумму этих двух сил. Так
F net = 166 Н, вверх + 137,2 Н, вниз = 28,8 Н, вверх
Ускорение можно рассчитать по второму закону Ньютона: м/с 2 = ~2,1 м/с 2
Теперь, когда системный анализ был использован для определения ускорения, можно выполнить анализ отдельного объекта на любой коробке, чтобы определить силу, действующую между их. Как и в предыдущих задачах, не имеет значения, какой ящик выбран; результат будет одинаковым в любом случае.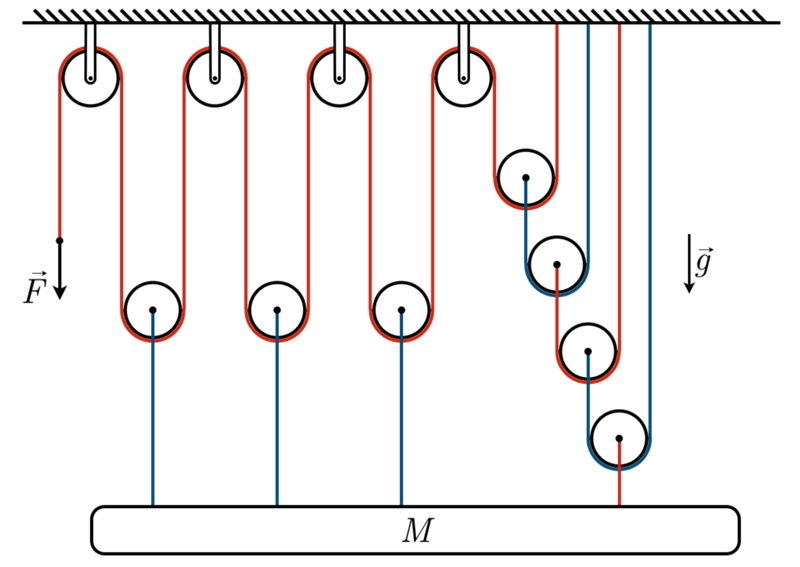 Верхний ящик используется в этом анализе, так как он сталкивается с одной силой меньше. Диаграмма свободного тела показана справа. Сила тяжести на верхнем ящике равна m•g, где m = 6,0 кг. Сила тяжести равна 58,8 Н. Сила, направленная вверх, неизвестна, но ее можно рассчитать, если F net = m•a уравнение применяется к диаграмме свободного тела. Поскольку ускорение направлено вверх, сторона уравнения Fnet будет равна силе в направлении ускорения (F контакт ) за вычетом противодействующей силы (F грав ). Итак,
Верхний ящик используется в этом анализе, так как он сталкивается с одной силой меньше. Диаграмма свободного тела показана справа. Сила тяжести на верхнем ящике равна m•g, где m = 6,0 кг. Сила тяжести равна 58,8 Н. Сила, направленная вверх, неизвестна, но ее можно рассчитать, если F net = m•a уравнение применяется к диаграмме свободного тела. Поскольку ускорение направлено вверх, сторона уравнения Fnet будет равна силе в направлении ускорения (F контакт ) за вычетом противодействующей силы (F грав ). Итак,
F контакт – 58,8 N = (6,0 кг)•(2,0571 м/с2)
(Обратите внимание, что здесь используется неокругленное значение ускорения; при определении окончательного ответа произойдет округление.) Решение для F контакт дает 71,14 Н. Эту цифру можно округлить до двух значащих цифр — 71 Н. Таким образом, двойное сочетание системного анализа и анализа отдельных тел приводит к ускорению 2,1 м/с 2 и контактной силе 71 Н.
Теперь для решения той же проблемы будет использоваться второй подход к решению проблемы. В этом решении анализ двух отдельных объектов будет объединен для создания системы двух уравнений, способных найти решение для двух неизвестных. Мы начнем этот анализ, предположив, что решаем задачу впервые и не знаем ни ускорения, ни контактной силы. Диаграммы свободного тела для отдельных объектов показаны ниже.
Обратите внимание, что значения F grav для двух блоков включены в диаграмму. Они были рассчитаны с использованием F grav = m•g, где m=6,0 кг для верхнего ящика и m=8,0 кг для нижнего ящика. Контактная сила (F , контакт ) на верхнем ящике направлена вверх, поскольку нижний ящик толкает его вверх, когда система из двух объектов ускоряется вверх. Контактное усилие (контакт F ) на нижней коробке направлено вниз, поскольку верхняя коробка давит вниз на нижнюю коробку, когда происходит ускорение. Эти две контактные силы равны друг другу, поскольку они возникают в результате взаимного взаимодействия между двумя ящиками. Третьей силой на нижний ящик является сила весов, толкающих его вверх с силой 166 Н; это значение было указано в условии задачи.
Эти две контактные силы равны друг другу, поскольку они возникают в результате взаимного взаимодействия между двумя ящиками. Третьей силой на нижний ящик является сила весов, толкающих его вверх с силой 166 Н; это значение было указано в условии задачи.
Применение второго закона Ньютона к этим двум диаграммам свободного тела приводит к уравнению 5 (для коробки массой 6,0 кг) и уравнению 6 (для коробки массой 8,0 кг).
F контакт – 58,8 = 6,0 • a
166 – F контакт – 78,4 = 8,0 • a
Теперь, когда разработана система из двух уравнений, для решения уравнения два можно использовать алгебру неизвестные. Уравнение 5 можно использовать для записи выражения для контактной силы (контакт F ) через ускорение (а).
F , контакт = 6,0 • a + 58,8
Это выражение для F , контакт можно затем подставить в уравнение 6. Тогда уравнение 6 примет вид
166 – (6,0 • a + 58,8) – 78,4 = 8,0 • a
Следующие алгебраические шаги выполняются над приведенным выше уравнением для определения ускорения.
166 – 6,0 • а – 58,8 – 78,4 = 8,0 • а
166 – 58,8 – 78,4 = 8,0 • а + 6,0 • а
28,8 = 14,0 а
а = 2,0571 м/с 2 = ~2,1 м/с 2
Теперь значение ускорения (a) можно подставить обратно в выражение для F , контакт (F , контакт = 6,0 • a + 58,8), чтобы найти F , контакт . Контактное усилие составляет 71,14 Н (~71 Н).
Следует отметить, что второй подход к этой задаче дает те же числовые ответы, что и первый подход. Студентам предлагается использовать тот подход, который им наиболее удобен.
Для дополнительной практики рассмотрите следующие задачи двух тел. А укороченная версия решения предоставлена для каждой задачи. К теме задач двух тел мы вернемся в следующей главе, когда будем рассматривать ситуации, связанные со шкивами и объектами, движущимися в разных направлениях.
1. Грузовик везет легковой автомобиль по пересеченной местности. Масса грузовика 4,00×10 3 кг, масса легкового автомобиля 1,60×10 3 кг. Если движущая сила, возникающая при повороте колес грузовика, равна 2,50×10 4 Н, затем определить ускорение автомобиля (или грузовика) и силу, с которой грузовик тянет автомобиль. Предположим, что силы сопротивления воздуха пренебрежимо малы.
Грузовик везет легковой автомобиль по пересеченной местности. Масса грузовика 4,00×10 3 кг, масса легкового автомобиля 1,60×10 3 кг. Если движущая сила, возникающая при повороте колес грузовика, равна 2,50×10 4 Н, затем определить ускорение автомобиля (или грузовика) и силу, с которой грузовик тянет автомобиль. Предположим, что силы сопротивления воздуха пренебрежимо малы.
2. Ящик массой 7,00 кг прикреплен веревкой 1 к ящику массой 3,00 кг. веревка 1. Коэффициент трения между землей и ящиками 0,120.
3. Два больших бревна тянут через поле трактором. Цепочка соединяет бревна друг с другом; переднее бревно соединяется с трактором отдельной цепью. Масса лобового бревна 180 кг. Масса заднего бревна 220 кг. Коэффициент трения между бревнами и полем составляет примерно 0,45. Натяжение цепи, соединяющей трактор с передним бревном, равно 1850 Н. Определить ускорение бревна и натяжение цепи, соединяющей два бревна.
4. Два ящика скреплены прочной проволокой и прикреплены к потолку лифта второй проволокой (см. схему). Масса топбокса 14,2 кг; масса нижнего ящика 10,4 кг. Лифт поднимается вверх со скоростью 2,84 м/с 2 . (Предположим, что проволока относительно безмассовая .)
(a) Найдите натяжение верхней проволоки (точки соединения A и B).
(b) Найдите натяжение нижнего провода (точки соединения C и D).
Перейти к следующему уроку:
2 и 3 вертикально сложенных ящика примеры физики с трением уравнения и силы в системе? Вам просто нужно справиться с этим шаг за шагом.
Пожалуйста, подумайте о том, чтобы сделать мне пожертвование, используя Paypal: https://paypal.me/BAIZEGAMING
Подумайте о том, чтобы купить нам кофе за наши усилия –
BTC – 33iDpHvwwcMyxhrv83rL75TXpmgBd72Xv
Пример: Давайте рассмотрим приведенную выше диаграмму, на которой показаны два сложенных друг на друга ящика или груза. Масса 1 равна 15 кг, масса 2 равна 5 кг. Под массой 1 находится пол со статическим и кинетическим коэффициентами трения 0,3 и 0,2 соответственно. Коэффициенты статического и кинетического трения между боксами 1 и 2 равны 0,4 и 0,32 соответственно.
Масса 1 равна 15 кг, масса 2 равна 5 кг. Под массой 1 находится пол со статическим и кинетическим коэффициентами трения 0,3 и 0,2 соответственно. Коэффициенты статического и кинетического трения между боксами 1 и 2 равны 0,4 и 0,32 соответственно.
Вопрос: Какую максимальную силу можно приложить к массе 1, прежде чем две массы начнут двигаться вместе?
Когда они собираются двигаться вместе, вы можете рассматривать их как единый объект. Используйте коэффициент статического трения между ящиком 1 и полом, не путайте всю информацию, которую вам дали!
Для силы трения:
\[{F_F} = {\mu _S}{F_N}\]
Нормальная сила нижнего ящика равна весу всех ящиков.
\[{F_F} = (0,3)(15 + 5)(9,81)\]
\[{F_F} = 58,86Н\]
И помните, что m*a = сумма всех сил
\[ ma = {F_{применяется}} – {F_F}\]
Теперь «только начать движение» означает, что ускорение равно 0.
\[{F_{применяется}} = {F_F}\]
\[ {F_{applied}} = 58,86 Н\]
Таким образом, максимальная сила, которую вы можете приложить, прежде чем система начнет двигаться, составляет примерно 58,86 Н.
Вопрос: Какую максимальную силу вы можете приложить к нижнему блоку без того, чтобы верхняя коробка начала соскальзывать с нижнего блока? (Иногда они сформулируют это так: «Сколько силы вам нужно, чтобы начать выталкивать нижний блок», это просто один и тот же тип вопроса, научитесь распознавать, как они могут формулировать вопросы по-разному!)
Хитрость заключается в том, что для того, чтобы верхний ящик не начал скользить, ускорение верхнего ящика должно быть равно ускорению нижнего ящика.
Вы можете сделать вертикальный баланс сил на втором ящике, помните, что в сумме он равен 0, потому что верхний ящик не «слетит» с нижнего ящика:
\[{F_N} – {m_2}g = m{a_y } = 0\]
\[{F_N} = {m_2}g\]
\[{F_N} = (5)(9.81)\]
\[{F_N} = 49,05N\]
сила на верхней коробке может быть равна силе трения на верхней части без проскальзывания. Используйте коэффициент статического трения между боксами 1 и 2 прямо сейчас!
\[{F_F} = {\mu _S}{F_N}\]
\[{F_F} = (0,4)(49,05N)\]\[{F_F} = 19,62N\]
\ [{m_2}a = {F_F} = 19,62\]
\[a = \frac{{19,62}}{5}\]
\[a = 3,92\]
Таким образом, верхний ящик может иметь максимум ускорение 3,92 м/с2, которое также будет ускорением для нижнего ящика, чтобы выполнялось условие «отсутствия проскальзывания». Теперь составим уравнения для нижнего ящика:
Теперь составим уравнения для нижнего ящика:
Есть еще одна хитрость при расчете силового баланса нижнего ящика! У вас есть трение от пола, но также есть трение между ящиками 1 и 2, действующее на ящик 1!
Представьте, что вы сдвинули коробку 1 вправо.
Хорошо, у него будет регулярная кинетическая сила трения слева, которая противоположна направлению движения.
Если ящик 1 толкнуть вправо, ящик 2 сверху сдвинется влево, в направлении, противоположном направлению ящика 1.
Но это означает, что сила трения ящика 2 будет направлена вправо.
Теперь, когда есть трение между двумя ящиками, член силы трения появится в обоих ящиках в противоположных направлениях! Таким образом, если в ящике 2 сила трения справа, то в ящике 1 сила трения слева. Это статическая сила, потому что она действует до того, как ящик 2 начнет скользить или двигаться.
Для баланса вертикальной силы на ящике 1 (обратите внимание, теперь используйте кинетическое трение между ящиком 1 и полом и используйте статическое трение для трения между ящиком 1 и ящиком 2):
\[{F_N} – ({ m_1} + {m_2})g = 0\]
\[{F_N} = (15 + 5)g = 0\]
\[{F_{F,этаж}} = (0,2)(15 + 5 )(9. 81)\]
81)\]
\[{F_{F,floor}} = 39,24N\]
Трение между ящиками имеет ту же величину, что и в верхнем ящике:
\[{F_{F , между ящиками}} = 19,62 Н\]
Теперь просуммируйте все горизонтальные силы для нижнего блока, помните, что ускорение соответствует верхнему блоку для отсутствия проскальзывания:
\[{F_{приложено}} – {F_{F,floor}} – {F_{ F, между ящиками}} = {m_1}a\]
\[{F_{приложено}} = (15)(3,92) + 39,24 + 19,62\]
Вы получаете 117,67 Н. Это максимальное количество силы, которую вы может применяться к нижнему блоку, не вызывая проскальзывания верхнего блока.
Вопрос: Теперь к нижнему ящику приложена сила 150 Н. Каково ускорение каждого ящика?
Теперь 150 > 117, поэтому верхний ящик начнет скользить, и у каждого ящика будет свое собственное ускорение. Теперь вы будете использовать кинетический коэффициент трения для верхней коробки.
Для верхнего ящика:
\[{F_{F,между ящиками}} = {\mu _k}{F_{N,top}} = {\mu _k}{m_2}g\]
\[{ F_{F, между ящиками}} = (0,32)(5)(9,81)\]
\[{F_{F, между ящиками}} = 15,70\]
\[15,70 = {m_2}{a_2}\]
\[{a_2} = \frac{{15,70}}{5} = 3,14\]
Сила трения между полом и нижним ящиком такая же, как и раньше:
\[{F_{F,floor}} = (0,2)(15 + 5)(9,81)\]
\[{F_{F,floor}} = 39,24 Н\]
Произвести горизонтальный баланс сил на нижнем ящике:
\[{F_{приложенный}} – {F_{F,этаж}} – {F_{F,между ящиками}} = {m_1}{a_1}\]
\[150 – 39,24 – 15,70 = (15){a_1}\]
Получаем a1 = 6,33 м/с2, а ранее мы нашли a2 равным 3,14 м/с2, что является ускорением нижнего и верхнего ящиков соответственно.
Вопрос: Верхний ящик имеет незначительную длину, а нижний ящик имеет длину 8 м. Через какое время верхняя коробка упадет с нижней? 92} = 8\]
Решение, примерно t = 2,24 секунды. По истечении этого времени верхний блок не может угнаться за нижним блоком и падает с нижнего блока.
3 сложенных друг на друга ящика Пример задачи
Пример: Теперь рассмотрим систему из трех вертикально сложенных ящиков на диаграмме ниже:
Рассмотрим ящики 1, 2 и 3, сложенные, как показано выше, массы равны 9 кг, 6 кг и 3 кг соответственно. Коэффициенты статического трения составляют 0,3 между полом и ящиком 1, 0,2 между ящиками 1 и 2 и 0,25 между ящиками 2 и 3.
Вопрос : Каковы ускорения ящиков, когда к ящику 2 приложена сила 10 Н?
\[{F_F} = {\mu _S}{F_N}\]
\[{F_F} = (0,2)(3 + 6)(9,81)\]\[{F_F} = 17,66N\ ]
А также добавьте силу трения от верхней коробки, (0,25)(3)(9,81)
Вы увидите, что эти статические силы трения превышают 10 Н приложенной силы.
Поскольку сила трения превышает приложенную силу, коробки будут двигаться вместе с одинаковым ускорением, поэтому вы приложите 10 Н ко всем массам сразу. Таким образом, вы можете рассматривать это как движение всех трех вместе. 92}\) .
Вопрос : Каковы ускорения ящиков, когда к ящику 2 приложена сила 30 Н?
Теперь эта приложенная сила превышает силу трения, удерживающую ящик 2.
Вы можете найти чистое ускорение второго ящика, используя результирующую силу. Но помните, что верхний блок также будет иметь силу трения, которая применяется к блоку 2. Теперь каждый блок будет иметь разное значение ускорения, будьте осторожны!
\[{F_F} = (0,25)(3)(9,81)\]
\[{F_F} = 7,36 Н\] 92}\).
Итак, обратите внимание, что силы трения 17,66 Н и 7,36 Н действуют на блок 2? Каждый из них действует на блок 3 и блок 1 соответственно.
Это третий закон Ньютона для трения, трение будет иметь равные и противоположные направления между поверхностями. В этом случае интерфейсы — это поверхности между блоками.
В этом случае интерфейсы — это поверхности между блоками.
Других горизонтальных сил для ящика 3 нет.
Для ящика 3, верхний ящик:
\[{a_3} = \frac{{7.36}}{3} = 2.45\]
Для ящика 1, нижний ящик:
\[{F_F} = (0,3)(3 + 6 + 9)(9,81)\]
\[{F_F} = 52,97 Н\]
Сила трения от блок 2, который идет к блоку 1, составляет всего 17,66 Н и ниже значения, указанного выше. Итак, блок 1 не движется и имеет ускорение, равное 0. Если бы нижний блок не имел трения, он тоже ускорялся бы.
Просто помните, что в подобных задачах член силы трения всегда будет парным в противоположном направлении на границе между блоками. Исключением является блок на полу, у которого будет собственное трение без пары, потому что пол ничего не делает. Но если у вас есть блок поверх этого блока, его трение будет сопряжено с блоком под ним.
Предположим, что правый положительный, а левый отрицательный. Скажем, у вас есть 2 блока, сложенных друг на друга — вы толкаете нижний блок вправо, и этот блок будет иметь трение влево, ну, а верхний блок будет иметь собственное трение вправо, которое также переносится вниз к нижнему блоку.


 В какой из систем неподвижных блоков (рис. 218) надо приложить большую силу для подъема одного и того же груза, если трение в каждом из блоков одинаковое?
В какой из систем неподвижных блоков (рис. 218) надо приложить большую силу для подъема одного и того же груза, если трение в каждом из блоков одинаковое?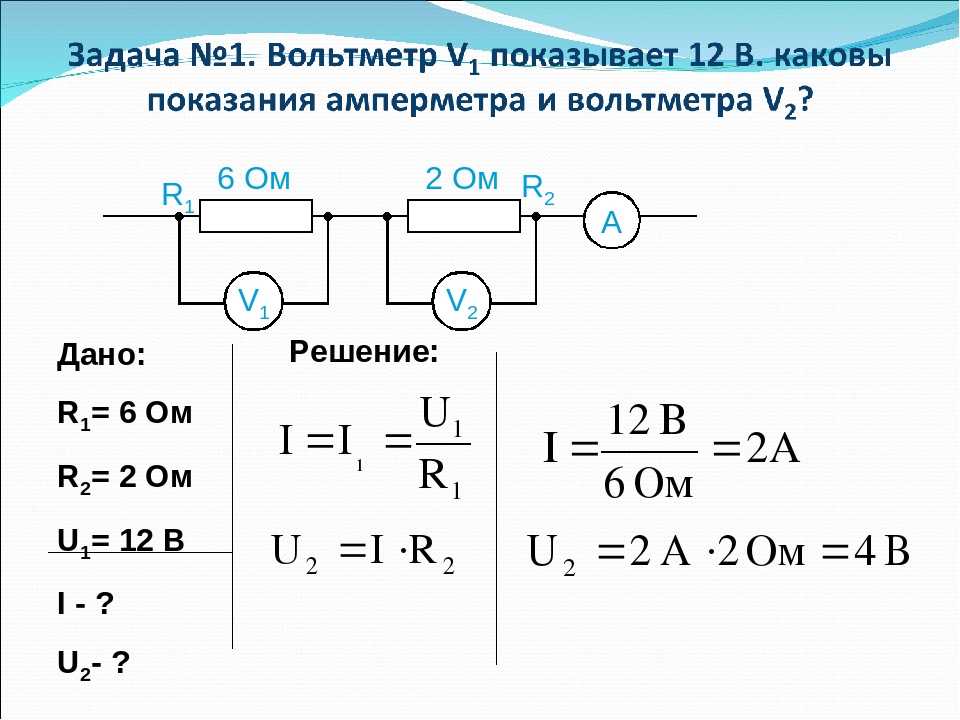 Объясните, на чем основано это чудо. (В жертвеннике воздух. Жертвенник при помощи трубы соединен с кожаным мешком.)
Объясните, на чем основано это чудо. (В жертвеннике воздух. Жертвенник при помощи трубы соединен с кожаным мешком.) Какую силу надо приложить к свободному концу троса А, чтобы трос, перекинутый через неподвижный блок, был натянут с силой 4000 Н (рис. 228)?
Какую силу надо приложить к свободному концу троса А, чтобы трос, перекинутый через неподвижный блок, был натянут с силой 4000 Н (рис. 228)? Определите ускорение, с которым движутся оба тела,
Определите ускорение, с которым движутся оба тела,