Векторы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме – координаты вектора.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Слишком сложно?
Примеры решения задач с векторами не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Теоретический материал по теме – разложение вектора по ортам. Пример Задание. Зная разложения вектора $\overline{a}$
по базисной системе векторов: $\overline{a}=3 \overline{i}-\overline{k}$, записать координаты этого вектора в пространстве. Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}$,
получаем, что $\overline{a}=(3 ; 0 ;-1)$ Пример Задание. Вектор $\overline{a}$ задан
своими координатами: $\overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат. Решение. Координаты вектора – это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение: $\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}$ Теоретический материал по теме – скалярное произведение векторов. Пример Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и
$\overline{b}=(-2 ; 7)$ Решение. Скалярное произведение $\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$ Теоретический материал по теме – векторное произведение векторов. Пример Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$ Решение. Составляем определитель и вычисляем его: $\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$ $=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$ $=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$ Теоретический материал по теме – смешанное произведение векторов. Пример Задание. Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$,
$\overline{b}=(1 ; 4 ; 4)$,
$\overline{c}=(3 ; 5 ; 7)$ Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $\overline{a}$,
$\overline{b}$ и $\overline{c}$: $(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$ $-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$ $$V_{пир}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}$$ Читать первую тему – операции над векторами,
раздела векторы. Интегрированный урок по теме: Вектор и его применение. Цели и задачи: Синтезировать и обобщить полученные теоретические и практические знания на уроках геометрии и физики, Развивать умения применять знания и умения в знакомой и в новых учебных ситуациях, Развивать логическое мышление, память, самостоятельность, Формировать коммуникативную и эмоциональную культуру, Продолжать показ тесной связи точных наук, Воспитывать устойчивый интерес к изучению физики и математики через реализацию межпредметных связей, Воспитывать чувство взаимопомощи и объективной оценке знаний. Тип урока: Личностно-ориентированная, информационно-коммуникативная. Оборудование: Мультимедийный проектор, компьютер. Чертежные инструменты Карточки-задания, канцелярские . Репродукции картин. Презентация Литература: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Поздняк Л.В., Юдина И.И. Геометрия 7-9 кл. Просвещение,2006 Зив Б. Г., Мейлер В. М. Геометрия. Дидактические материалы для 8 класса. Просвещение,2006 Задачник Степановой Г.Н.для 7-9 классов А.В. Пёрушкин, Е.М. Путник Физика -9 .Просвещение,2006 Структура урока Целеполагание и мотивация. Приветствие. Обобщение и систематизация. Практические задания на слайдах Межпредметные связи ( работа с картинами) Рефлексия. Подведение итогов Эпиграф к уроку. «Практика рождается из тесного соединения физики и математики» Бэкон. Ход урока. I. Орг. момент Объясняются основные моменты урока: на столах у каждого карточки-задания, лист самооценки, который необходимо подписать. Задачи ученики решают на выданных карточках, ответы записывают в лист самооценки. Возможна дополнительная оценка, для тех, кто решает быстрее. Целеполагание и мотивация. Приветствие. Учитель математики Сегодня у нас с вами необычный урок. Мы проводим уроки физики и математики вместе. Математика и физика – два тесно связанных предмета. И за одной из связующих ниточек мы с вами сегодня проследим. На уроках математики, решая задачи, мы с вами составляем математические модели реальных ситуаций. Но в жизни достаточно ситуаций, зависящих от природных явлений, т.е. физических величин. Итак, тема сегодняшнего урока: Вектор и его применение.. – Давайте поставим цели урока. – Ученики называют. Учитель физики. Вывод: – Значит мы должны научиться решать задачи на основе реальных ситуаций, чтобы отвечать на множество возникающих вопросов в жизни Учитель математики: Практика рождается из тесного соединения физики и математики. -Сегодня на примере решения физических задач с векторными величинами мы постараемся убедиться в истинности данного высказывания. Учитель физики: И неслучайно, вектор в школьной программе изучается в математике и физике. Важность этого понятия никто уже не оспаривает. Мы изучаем векторы. А где это применяется? Векторная история — это пограничная история, между математикой и физикой. Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию направление, смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. Задачи подобного содержания предлагались многим предыдущим поколениям. Учитель математики: Для успешной работы на уроке нам необходимо вспомнить основные понятия, которые будут использоваться при решении задач. Я предлагаю вам поработать в группах. В каждой группе есть консультант, который в бланке учёта знаний фиксирует ответы учащихся. Правильный ответ оценивается в 1 балл. 1. Дать определение вектора. 2. Назовите векторные физические величины. 3. Чем характеризуется вектор? 4. Как найти проекцию вектора на ось координат? 5. Как определяется длина вектора, если известны координаты? 6. Чем отличается путь от перемещения? 7. Назовите правила сложения векторов. 8. Какое из этих правил используется в физике? Почему? 9. Какие векторы называются коллинеарными? 10. Векторы скорости и ускорения коллинеарные. Какие виды движения возможны при различных направлениях этих векторов? 11. Что такое равнодействующая сила? Учитель математики. У вас на столах даны таблицы, вам нужно провести сравнительный анализ понятия “вектор” и действий над векторами в математике и физике. . Учитель физики. Вывод: особенности: в математике вектор можно отложить от любой точки плоскости, в физике силы приложены к одной точке; в математике используют при сложении векторов правило треугольника и правило параллелограмма, в физике чаще пользуются правилом параллелограмма; в математике длину вектора называют модулем , в физике –длиной. Работаем по готовым чертежам. Учитель физики. Задачи на готовых чертежах по физике. 1. На рисунке показаны перемещения пяти материальных точек. Найдите проекции векторов перемещения на оси координат. 2. На рисунке показана траектория движения материальной точки из A в B. Найдите координаты точки в начале и конце движения, перемещение, проекции перемещения на оси координат. 3. Определите величину собственной скорости катера, который, несмотря на течение реки со скоростью 1 км/ч, движется перпендикулярно течению со скоростью 2,4 км/ч. 4. Вертолёт пролетел в горизонтальном полёте по прямой 40 км, повернул под углом 90ْ и пролетел ещё 30 км. Найти путь и перемещение вертолёта. Учитель математики: Изучая любую тему предмета, всегда невольно встаёт вопрос о её применимости в жизни. И сейчас есть множество достоверных фактов подтверждающих, что тема «Векторы» помогает находить ответ даже на некоторые вопросы , возникающие в нестандартных ситуациях межличностного общения. История о том, как «лебедь, рак и щука вести с поклажей воз взялись» известна всем. Напомним её И.А. Крылов. Басня «Лебедь, Рак и Щука». (Вызываются 4 участника) от каждой группы по одному) Когда в товарищах согласья нет, На лад их дело не пойдёт, И выйдет из него не дело, только мука. Однажды Лебедь, Рак да Щука, Везти с поклажей воз взялись И вместе трое все, в него впряглись: Из кожи лезут вон, а возу всё нет ходу! Поклажа бы для них казалась и легка: Да Лебедь рвётся в облака, Рак пятится назад, а Щука тянет в воду. Кто виноват у них, кто прав, – судить не нам; Да только воз и ныне там. Учитель физики: Н.В.Гоголь собрание басен И.А.Крылова назвал «книгой мудрости самого народа». Вы думаете, почему с точки зрения человеческих отношений «воз и ныне там»? А теперь давайте ответим на этот вопрос с физической точки зрения. лебедь рак щука Учитель математики Второй пример: На уроках физкультуры вы играете с мячом. Если мяч подбросить вверх , то какими векторными величинами можно описать движение мяча? (Взять мяч, подбросить вверх) ( Движение мяча описывается следующими векторными величинами: перемещение мяча, скорость, сила тяжести,) Учитель физики. Взаимосвязь физики с искусством. Работа в группах. Класс разделён на 4 группы. Каждая группа получает репродукцию картин и отвечает на вопросы, поставленные к ней. 1 гр. – картина Репина И. Вопрос: определить направление сил действующих на корабль. Изобразите силы, действующие на него в процессе движения. 2 гр. – картина Перова В.М. « Тройка». Вопрос: Определите, какие векторные величины характеризуют движение саней? Изобразите эти векторы направленными отрезками. 3 гр. – картина Сурикова В.И. « Боярыня Морозова». Вопрос: определите, какие векторные величины характеризуют движение саней? Изобразите силы, действующие в процессе движения. 4 гр. – картина Васнецова В.Г. «Богатыри». Вопрос: определите, какие векторные величины действуют на лошадей? Изобразите эти векторы направленными отрезками. Физминутка ( по классу развешаны слова и обозначение, найдя ответ, дети передвигаются по классу) а) Путь или перемещение мы оплачиваем при поездке в такси? Ответ: Путь. Как называются вектора лежащие на одной прямой или на параллельных прямых (коллинеарные) б) Наблюдения за движением футболиста показали: за время матча он пробежал 12 км. Что это за величина: перемещение или пройденный путь? Ответ: Путь. Два вектора равны по модулю и сонаправлены. Какие это вектора? Ответ: равные в) Штурман, определяя утром положение корабля, обнаружил, что корабль находится в точке, расположенной на 100 км к северу от пункта, в котором находился корабль накануне вечером. Что означает это число: длину перемещения или пройденный путь? Ответ: Длина перемещения. Как называется вектор у которого начало совпадает с концом? Ответ: Нулевой Учитель математики. Не входя в воду, нельзя научиться плавать. А мы хотим научиться решать задачи, значит, начинаем их решать. Сейчас работаем в группе, выполняем самостоятельную работу) Решение задач: карточки 1 группа: 1. υ х= 10 + 2 t Вопросы: а) определите характер движения точки б) найдите модуль и направление начальной скорости в) определите ускорение тела и его направление г) какой будет скорость точки через 10с после начала движения? д) постройте график зависимости скорости от времени при t = 0 с, 5 с, 10 с. 2. Упростить выражение: 3. Начертите два неколлинеарных вектора. Найдите сумму векторов двумя способами. 2 группа: 1. Проекция скорости движущегося тела изменяется по закону υ х = 10 – 2 t Вопросы:а) опишите характер движения тела б) найдите модуль и направление вектора начальной скорости в) найдите модуль и направление вектора ускорения г) постройте график зависимости скорости от времени д) найдите графически и аналитически скорости тела через 2 с 2. 3. Начертите два неколлинеарных вектора. Найдите сумму векторов двумя способами. 3 группа: 1. На рис. изображён график зависимости проекции скорости движения материальной точки от времени. Вопросы: а) определите вид движения б) найдите модуль и направление начальной скорости в) вычислите проекцию ускорения и определите направление вектора ускорения г) напишите уравнение зависимости проекции скорости этого тела от времени д) найдите графически и аналитически скорость тела через 2 с. 2.Упростить выражение: 3. Начертите два неколлинеарных вектора. Найдите сумму векторов двумя способами. Решение задач. 1 группа движение равнопеременное – ускоренное υ 0 = 10 м/с ; положит., т.к. совпадает с направлением движения а = 2 м/с2 ; положит. υ = 10 + 2 · 10 = 30 м/с 5. график 2 группа 1. движение равнопеременное – замедленное 2. υ 0 = 10 м/с ; положит., т.к. совпадает с направлением движения 3. а = – 2 м/с2 ; отриц., т.к. движение замедл. и направлено противопол υ 0 4. график 5. υ = 10 – 2 · 2 = 6 м/с 3 группа Равнозамедленное движение. υ 0 = 10 м/с ; положит., т.к. совпадает с направлением движения a= -1,5 м/с2; отрицательное, т.к. направлено противоположно движению(замедленное движение) v=10 – 1,5t v=7 м/с ПРОВЕРКА. V. Домашнее задание (по выбору, с учетом индивидуальных способностей учащихся) Составить: – задачу для решения на уроках математики и физики; – кроссворд; – составить тест для проверки знаний, умений навыков в компьютерном варианте на электронных носителях (по выбору). Как Вы думаете: где еще в жизни мы можем наблюдать векторы? Обобщение изученного материала. Вопросы задают учитель физики и математики. Какую величину измеряет спидометр автомашины: векторную или скалярную? ABCD – параллелограмм. Докажите, что вектор AB равен вектору DC. Что такое ускорение и для чего его нужно знать? Как связан вектор перемещения с его координатами? Два вектора равны друг другу по модулю, но направления различны. Можно ли сказать, что векторы равны? Буксир толкает по реке баржу. Относительно каких тел отсчета баржа движется? Относительно какого тела покоится? Может ли тело двигаться с большой скоростью, но малым ускорением? Какие векторы называются сонаправленными и противоположно направленными? В чем заключается основная задача механики? В чем состоит относительность движения? Какие векторы называют равными? Какой вектор называется нулевым? 6. Учитель физики. Вернемся к целям нашего урока. Достигли мы их или нет? Значит справедливы слова эпиграфа: Практика рождается из тесного соединения физики и математики. Возможно ЛИ решать физические задачи математическими методами ? Сегодня вы решали и простые задачи, знакомыми методами, и сложные задачи, в которых при решении приходилось использовать давно известные формулы и законы в новых условиях. Научились решать задачи на основе реальных ситуаций? VII. Рефлексия. Учитель математики. Итак, этот урок является своеобразным “мостиком” между уроками математики и физики. Что же вы взяли для себя с этого урока? Чему научились и какие трудности испытывали при решении задач? Предлагаю вам продолжить высказывание: Теперь я знаю….. У меня получилось…. Я не знал, что…. Мне понравилось… Мне было интересно узнать, что. Что еще хотел бы узнать… Какая из форм работы вам больше по душе: в парах, индивидуально, коллективно) Дополнительные задачи. 1. Лодка с туристами потерпела крушение в 40 м от берега, налетев на пороги. Туристы поплыли к берегу со скоростью 2 м/с, относительно воды перпендикулярно линии берега, но быстрое течение со скоростью 10 м/с сносило их в сторону. С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи. 2. Вертолет летел на юг со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует восточный ветер со скоростью 10 м/с? Цели и задачи:
Тип урока: урок комплексного
применения знаний и умений. Оборудование:
Учебники:
Ход урока I. Орг. момент Объясняются основные моменты урока: на столах у
каждого карточки-задания, лист самооценки,
который необходимо подписать. Задачи ученики решают на выданных карточках,
ответы записывают в лист самооценки. Возможна
дополнительная оценка, для тех, кто решает
быстрее. II. Целеполагание и мотивация.
Приветствие. Практика рождается из тесного
соединения физики и математики. На уроках математики, решая задачи, мы с вами
составляем математические модели реальных
ситуаций. Но в жизни достаточно ситуаций
зависящих от природных явлений, т.е. физических
величин. (называется тема урока) слайд 1 – Давайте поставим цели урока. – Ученики называют. Ответы на слайде 2 Вывод: – Значит мы должны научиться решать задачи на
основе реальных ситуаций, чтобы отвечать на
множество возникающих вопросов в жизни. – Сегодня на примере решения физических задач с
векторными величинами мы постараемся убедиться
в истинности данного высказывания (эпиграфа), за
урок каждый из вас, надеюсь, придет к хорошему
результату. – Напомню, возникнув, понятие “вектор” сразу
нашло применение в физике. И неслучайно, вектор в
школьной программе изучается в математике и
физике. Важность этого понятия никто уже не
оспаривает. Я предлагаю нам с вами провести
сравнительный анализ понятия “вектор” и
действий над векторами при изучении вектора в
математике и в физике. Ученики на местах заполняют таблицу:
показывают подходы в изучении понятия “вектор”
в математике и физике. Вывод: (появляется на доске) -
слайд 3 особенности:
Сделаем вывод: в каждом учебном
предмете вектор рассматривается так, как это
удобно для изучаемого вопроса, но суть – одна. III. Актуализация. – Не входя в воду, нельзя научиться плавать. А мы
хотим научиться решать задачи, значит, начинаем
их решать. Разминка (1 мин.) Решение задачи №1 и №2- решает каждый
ученик ( знакомая, типовая ситуация) на
движение катера по течению и против течения.
слайды 6,7. Ответы сравнивают с доской, результаты – в лист
самооценки. Самостоятельная работа (8-10 мин): Решить одну любую задачу №3,4,5, или 6 – решает
каждый ученик слайды 9-12. Ответы сравнивают с доской, результаты – в лист
самооценки. Вы составили физическую модель реальной
ситуации. IV. Физминутка – слайд 13. Слайд 13. Тренинг по профилактике нарушений
зрения по методике Базарного. – Смотреть прямо перед собой 2-3 сек. – Поставить указательный палец на расстоянии
25-30 см от глаз, перевести взгляд на кончик пальца,
смотреть на него 2-3 сек, опустить руку (4-5 раз) – Опустить голову, посмотреть на носок левой
ноги; поднять голову, посмотреть в правый верхний
угол комнаты; опустить голову, посмотреть на
носок правой ноги; поднять голову, посмотреть в
левый верхний угол комнаты (ноги на ширине плеч)
(3-4 раза). V. Работа в парах (10-12 мин) – слайд 14: Pабота в парах – решить любые две задачи №7,8,9
или 10 Слайды 15-18. При объяснении задач необходимо, чтобы ученики
указали на подобие треугольников (зад.8,9), правила сложения сил вдоль одной прямой и
теорему Пифагора (зад.7), а также на направление
движения тела под действием равнодействующей
силы (на данном этапе изучения темы нас пока не
интересует как движется тело под действием
равнодействующей силы, важно конечное
направление движения). – Как Вы думаете: почему здесь нет решения зад.10? Oбращение к выставке литературы к уроку – Где мы можем видеть решение многих жизненных
задач? – Конечно, в литературных произведениях таких,
как сказка или басня – Решение задачи 10 – слайд 20,21. – Как Вы думаете: где еще в жизни мы можем
наблюдать векторы? – Можем наблюдать векторы и в баснях – слайд 22,23. Применение векторов – басня Лебедь, щука и рак. Когда в товарищах согласья нет, VI. Итог урока. Вернемся к целям нашего урока. Достигли мы их
или нет? Значит справедливы слова эпиграфа: Практика рождается из тесного соединения
физики и математики. Возможно решать физические задачи
математическими методами ? Сегодня вы решали и простые задачи, знакомыми
методами, и сложные задачи, в которых при решении
приходилось использовать давно известные
формулы и теоремы в новых условиях. Научились
решать задачи на основе реальных ситуаций? VII. Рефлексия. Итак, этот урок является своеобразным
“мостиком” между уроками математики и физики.
Что же вы взяли для себя с этого урока? Чему
научились и какие трудности испытывали при
решении задач? Предлагаю вам продолжить
высказывание:
(ответы на карточку, карточку каждый на доску) На уроке вы работали в парах,
индивидуально. IX. Оценки за урок (по листу самооценки). Расположение на доске Выставка литературы В конце урока помещаются ответы учащихся В современном школьном курсе механики векторы и координатный метод нашли широкое применение. На уроках физики с понятием вектора школьники сталкиваются впервые в 7 классе при изучении скорости и силы. Здесь векторы определяются как физические величины, которые, кроме числового значения, имеют направление. Параллельно в курсе геометрии учащиеся знакомятся с понятием перемещения, определяемым, как отображение плоскости на себя, сохраняющее расстояние; рассматривается частный случай перемещения – параллельный перенос. Это единство заключается в том, что каждому физическому или объекту, который называют вектором, присущи особые операции, такие, как сумма двух объектов и умножение объекта на число. Таким образом, на первой ступени обучения физике нет нужды добиваться от учащихся заучивания того, что сила и скорость суть векторные величины, необходимо показать им, что эти величины имеют некоторые особые свойства, благодаря которым действия над ними отличаются от действий над числами. При дальнейшем изучении курса физики знания о физических векторных величинах развиваются и углубляются. Анализируя поступательное движение тела, подчёркивают, что поступательное движение представляет собой параллельный перенос, характеризуемый вектором перемещения. При рассмотрении скорости, ускорения, 2 закона Ньютона выясняют, что умножение вектора на число даёт коллинеарный вектор: Приведём некоторые примеры, которые в наглядной и доступной форме помогут школьникам разобраться в решении задач по физике и математике с использованием векторов. Сравнительная таблица c элементами заданий Если вектор задан координатами своих начала и конца: , то его координаты равны разности соответствующих координат конца и начала: Если вектор , то его длина равна корню квадратному из суммы квадратов координат: Если векторы и заданы своими координатами, то суммой этих векторов есть вектор, координаты которого равны сумме соответствующих координат векторов-слагаемых: Чтобы найти произведение вектора на некоторое число , нужно каждую координату заданного вектора умножить на это число: Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат: Если векторы и заданы своими координатами в некотором ортонормированном базисе , то их векторное произведение находится по формуле: Если заданы три вектора и , то их смешанное произведение равно определителю, по строкам которого записаны координаты этих векторов: Замечание. Косинус угла между двумя векторами и , заданными своими координатами, равен частному скалярного произведения этих векторов и произведению их модулей: Проекция вектора на направление вектора равна отношение скалярного произведения этих векторов к модулю вектора : Геометрия, 11 класс Урок № 3. Перечень вопросов, рассматриваемых в теме: Глоссарий по теме Уравнение вида задает в пространстве плоскость α. При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору . Вектор и любой коллинеарный ему вектор называются направляющим векторами прямой и прямой соответственно. Основная литература: Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Открытые электронные ресурсы: Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/ Теоретический материал для самостоятельного изучения Работа по теме урока. Объяснение новой темы Мы рассмотрели несложную задачу на применение метода координат в пространстве. Векторы , угол между которыми мы искали, называются направляющими векторами прямой и прямой соответственно. Рассмотрим этот метод более подробно. Суть метода координат на плоскости и в пространстве заключается в следующем. В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине. В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы: Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости. Мы рассмотрим только первые четыре формулы. Введем их. Угол между прямыми Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой с координатами {}. Пусть вторая прямая имеет направляющий вектор . Тогда угол между векторами вычисляется по формуле: . Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве. Угол между прямой и плоскостью Сначала рассмотрим уравнение плоскости, проходящей через три точки. . Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую. Если линейное уравнение вида на плоскости задает прямую l, то уравнение вида задает в пространстве плоскость α. При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными: В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D: . Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии. Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу: Обозначение |M| означает определитель матрицы М. В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом: . Таким образом, уравнение плоскости будет записано так: Пример 1: Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1). Составим систему. . Решая ее, получим значения А, В и С: . То есть уравнение плоскости имеет вид: . Ответ: . Теперь запишем формулу угла между прямой и плоскостью. Пусть дано уравнение плоскости: и известен – направляющий вектор прямой. Тогда – синус угла между прямой и плоскостью. Пример 2: Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали: Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2). Направляющий вектор прямой: . Найдем синус угла между прямой и плоскостью: . Угол между прямой и плоскостью . Ответ: . Угол между плоскостями Пусть: уравнение первой плоскости: уравнение второй плоскости: Тогда – косинус угла между этими плоскостями. Пример 3: Найдем угол между плоскостями: и . Найдем косинус угла между плоскостями: . Угол между плоскостями: Ответ: Расстояние от точки до плоскости Пусть координаты точки: , уравнение плоскости: . Тогда Расстояние от точки до плоскости вычисляется по формуле: . Пример 4. Найдем расстояние от точки М(4; 3; 4) до плоскости . . Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул. Пример 5. АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1) Введем систему координат с началом в вершине А так, как показано на рисунке: Интересующие нас точки будут иметь координаты: A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4). Напишем уравнение плоскости ЕКС: . Решая ее, получим значения А, В, С и D: . Уравнение плоскости имеет вид: Теперь найдем расстояние от точки А до плоскости ЕКС: . Ответ: . Рассмотрим задачу (№14 из варианта ЕГЭ). В кубе ABC…D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1. а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1. б) Найдите угол наклона плоскости α к плоскости грани BB1C1C. Решение: Переформулируем первый пункт этой задачи таким образом: Проведем плоскость через точки Р, K и C1 и докажем, что она параллельна прямой BD1. Введем систему координат так, как показано на рисунке: Найдем координаты точек : Р(; 0; 4), К(4; 0; 3),(4; 4; 4). Напишем уравнение плоскости : ; Решая ее, получим значения А, В, С и D: . – уравнение плоскости Теперь докажем, что плоскость параллельна прямой BD1. Найдем угол между прямой BD1 и плоскостью . Точки В и D1 имеют координаты: В (4; 0; 0), D1 (0; 4; 4). Направляющий вектор прямой BD1 – это вектор . Он имеет координаты . Теперь найдем синус угла между вектором и плоскостью . . В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Это значит, что плоскость, параллельная прямой BD1 и проходящая через точки действительно пересекает ребро A1B1в точке Р так, что A1P : PB1 = 2 : 1. Что и требовалось доказать. Теперь рассмотри второй пункт задачи. Уравнение плоскости у нас есть. Плоскость BB1C1 параллельна координатной плоскости YOZ и проходит через точку В(4; 0; 0). Поэтому она имеет уравнение . То есть ее коэффициенты . Найдем угол между плоскостями, используя формулу Ответ: . Рассмотрим две произвольные точки. Если соединить эти точки стрелкой (рис.1), Рис. то мы получим вектор. Точку, из которой стрелка выходит, называют началом вектора. Точку, в которую стрелка входит, называют концом вектора. Чтобы отличить вектор от отрезка с концами в тех же точках, используют обозначение (рис.2) или (рис.3). Иногда для вектора используют обозначения (рис.4) или (рис.5). Если две точки (начало и конец вектора) совпадают, то говорят, что эти точки задают нулевой вектор. Рассмотрим произвольный вектор и предположим, что в пространстве задана декартова прямоугольная система координат Oxyz (рис.6). Рис.6 Если в системе координат Oxyz точки A и B имеют координаты то координатами вектора называют набор чисел Этот определение часто формулируют так: «Для того, чтобы найти координаты вектора, нужно из координат конца вектора вычесть координаты начала вектора». Замечание. В случае, когда рассматриваются векторы, лежащие на некоторой координатной плоскости, в формулах (1) и (2) не будет третьих координат. Длиной (модулем) произвольного вектора называют длину отрезка AB Длина вектора , координаты которого имеют вид вычисляется по формуле Этот факт часто формулируют так: «Длина вектора равна корню квадратному из суммы квадратов его координат». Замечание. В случае, когда рассматриваются векторы, лежащие на координатной плоскости, формула (3) принимает вид и совпадает с формулой, позволяющей найти расстояние между двумя точками координатной плоскости. В случае, когда рассматриваются векторы, лежащие на координатной прямой, формулы (3) и (4) принимают вид . Векторы называют коллинеарными векторами, если они лежат на одной прямой или на параллельных прямых. Два вектора и являются коллинеарными векторами тогда и только тогда, когда их координаты пропорциональны. Другими словами, векторы являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства a1 = tb1, a2 = tb2, a3 = tb3. Два вектора называют сонаправленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 7. Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в одну сторону (концы векторов будут лежать на одном луче). Рис.7 Два вектора называют противоположно направленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 8. Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в разные стороны (концы векторов будут лежать по разные стороны от их общего начала). Рис.8 Определение. Два вектора равны, если, во-первых, они сонаправленные, а, во-вторых, имеют одинаковую длину. Другими словами, если совместить начала этих векторов, то их концы совпадут. Замечание. В результате умножения любого вектора на любое действительное число k получается такой вектор , который удовлетворяет следующим условиям: Если вектор имеет координаты то вектор имеет координаты Другими словами, если вектор умножается на число, то и все его координаты умножаются на это число. Для того, чтобы найти сумму двух произвольных векторов и нужно совместить начало вектора с концом вектора . Рис.9 При этом, если и то Этот факт часто формулируют так: «При сложении векторов их координаты складываются». Для того, чтобы найти разность двух произвольных векторов и нужно воспользоваться формулой Операция вычитания двух векторов наглядно изображена на рисунке 10. Рис.10 При этом, если и то Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора , нужно из координат вектора вычесть координаты вектора ». Определение. Рис.11 Таким образом, Из формулы (5) вытекает соотношение которое можно сформулировать так: «Модуль вектора равен корню квадратному из скалярного произведения вектора на себя». Следствие 1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Утверждение. Если в декартовой прямоугольной системе координат векторы имеют координаты то их скалярное произведение выражается формулой: Другими словами, в декартовой прямоугольной системе координат скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов. Замечание. Зная координаты векторов (6), из формул (3), (5) и (7) можно найти косинус угла между векторами и Пример 1. При каких значениях параметра p векторы и перпендикулярны? Решение. Воспользовавшись формулой (7), получим Ответ: 4. Пример 2. При каких значениях параметров α и β векторы (α; – 2; 5) и (1; β; – 4) коллинеарны? Решение. Векторы, в силу изложенного выше, являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства: Ответ: . Пример 3. Длины векторов и равны 2 и 1 , соответственно, а угол между ними равен 60° . Найти длину вектора . Решение. Рассмотрим рисунок 12. Рис.12 Воспользовавшись теоремой косинусов, получим Ответ: . Пример 4. Длины векторов и равны 3 и 1, соответственно, а угол между ними равен 60°. Найти длину вектора . Решение. Рассмотрим рисунок 13. Рис.13 Воспользовавшись теоремой косинусов, получим Ответ: . Пример 5. Найти угол между векторами (3; 6; 2) и (4; 7; 4) . Решение. Воспользовавшись формулой (8), получим Ответ: . На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике. Тренер Суини проходит 26 ярдов на север по боковой линии, останавливается и возвращается на 12 ярдов на юг. а. Определите расстояние, на которое проехал тренер. а. Rosa Boat плывет вверх по течению со скоростью 1,25 м / с относительно воды в реке, которая течет со скоростью 0,50 м / с относительно берегов реки. Какова результирующая скорость лодки Розы (относительно берега)? Скорость взлета военного самолета с авианосца составляет примерно 170 миль / ч относительно воздуха.Они достигают этой скорости за счет комбинации системы катапульты, присутствующей на авианосце, и реактивной двигательной установки самолета. Обычная стратегия – направить авианосец и самолет против ветра. Если самолет взлетает с авианосца, который движется со скоростью 40 миль / час при встречном ветре 20 миль / час, то какую скорость относительно палубы авианосца он должен набрать для взлета? Клэр де Иль делает покупки. Она проходит 16 метров до конца прохода.Затем она поворачивает направо и проходит 21 метр в конце прохода. Определите величину результирующего смещения Клэр. Джим Назиум идет с обеда на урок физкультуры. Он выходит из столовой и идет 43 м на запад. Затем он поворачивается и идет 72 м на север по коридору, ведущему в раздевалку. Определите величину и направление результирующего смещения Джима. По дороге из дома в школу Карла проезжает по трем улицам после съезда с проезжей части.Она едет 1,85 мили на юг, 2,43 мили на восток и 0,35 мили на север. Определите величину результирующего смещения Карлы. Шейла – капитан команды Университета по пересеченной местности. Во вторник во время внеклассной практики она повела команду следующим пробегом из школы в близлежащий парк, где они встретили тренера для встречи: 0,68 мили, север; 1,09 миль к востоку; 1,56 миль к северу; 0,32 мили, запад. Определите величину и направление результирующего смещения команды. Во время лабораторной работы по сложению векторов Мак и Тош начинают у дверей класса и проходят 40,0 м на север, 32,5 м на восток, 15,5 м на юг, 68,5 м на запад и 2,5 м на север. Определите величину и направление результирующего смещения Мака и Тоша. Эйвери, квотербек футбольной команды Южного Университета, сделал самый потрясающий пас в матче «Возвращение домой» против Норта, соперника кросс-городка. Он перебросил пас точно из центра поля в угол зачетной зоны, где Джамаал поймал его и заработал выигрышный счет игры.Если футбольное поле имеет ширину 160 футов (от боковой линии до боковой) и находится на расстоянии 60 ярдов от полузащиты до задней части зачетной зоны, то как далеко прошел мяч от рук Эйвери до рук Джамаала. Рассмотрим карту Соединенных Штатов, представленную ниже. Учитывая масштаб, который 1 см = 340 км, можно использовать транспортир и линейку для определения величины и направления для следующих рейсов. Все направления выражаются с использованием условного обозначения против часовой стрелки от восточного.Для каждой поездки используйте функции синуса, косинуса и тангенса, чтобы определить горизонтальную и вертикальную составляющие смещения. Обязательно укажите E, W, N или S в качестве направления для каждого компонента. Пилот самолета, летящего строго на север, уведомлен диспетчером полета о том, что второй самолет летит на юг примерно на той же высоте и находится в том же районе.Пилоту сообщили, что самолет, направляющийся на юг, в настоящее время находится в позиции, которая находится на расстоянии 13,5 км, 102 ° от его собственного самолета. а. Сколько километров севернее находится второй самолет? Спелеолог (человек, исследующий пещеры) определяет, что вход в пещеру расположен в 349 м, 253 ° от ее текущего местоположения.Как далеко к югу и как далеко к западу от ее текущего местоположения находится вход в пещеру? Эйвери, квотербек Саут, бросает пас на 36,5 ярдов на 21 ° з.д., прежде чем его ловит Митчелл с прыжком. Если предположить, что поле идет с севера на юг, и что Эйвери сделал пас с расстояния 7,2 ярда от линии схватки, сколько ярдов было получено за игру? Миа Андер выходит через парадную дверь своего дома и идет по пути, показанному на схеме справа (не в масштабе).Прогулка состоит из четырех этапов и имеет следующие величины: Определите величину и направление результирующего смещения Миа. Дора исследует пещеру. Она стартует у входа и делает следующие движения по прямой: Определите положение Доры относительно входа в пещеру.То есть как далеко и в каком направлении Дора от входа в пещеру? Тейлор и Дрю заканчивают свой последний урок накануне весенних каникул и решают спонтанно совершить поездку. Их поездка предполагает следующие перемещения: Автомобиль Тейлора сломался после последнего этапа поездки. Как далеко и в каком направлении Тейлор и Дрю от кампуса? Согласно метеосводке, в 12 км к югу и в 23 км к западу от вашего города был замечен торнадо.Сообщается, что шторм движется прямо к вашему городу со скоростью 82 км / ч. а. На каком расстоянии от вашего города был замечен торнадо? Самолет начинает свое путешествие в Канаду из пункта назначения, расположенного в 285 милях к югу от границы. Самолет летит по прямой со скоростью 189 миль / ч в направлении 20.5 градусов к западу от севера. Определите количество минут до того, как самолет пересечет границу. Предположим, что граница выровнена прямо на восток и запад в регионе, где выполняется полет. Гленда и Гарольд пытаются пересечь реку на байдарке. Река течет на восток со скоростью 1,9 м / с. Гленда и Гарольд возглавляют каяк прямо на север и гребут со скоростью 2,4 м / с (относительно воды). Ширина реки в этом месте составляет 38 м. а. Определите результирующую скорость лодки – как величину, так и направление. Тай Ридлэг садится в весельную лодку и направляет лодку на запад прямо через реку. Река течет на юг со скоростью 48 см / с. Тай гребет лодкой со скоростью 98 см / с. а. Определите результирующую скорость лодки – как величину, так и направление. Дилан и София гуляют по озеру Блюберд в совершенно спокойный день. Дилан, решивший произвести на Софию впечатление своей способностью прыгать через камни, берет самый плоский камень, который может найти, и запускает его из пистолета с кромки воды.Камень приобретает полностью горизонтальную скорость 26 м / с с высоты 0,45 м над поверхностью воды. а. Сколько времени нужно камню, чтобы упасть на поверхность воды? Пытаясь создать всплеск, похожий на пушечное ядро, восьмилетний Мэтью сбегает с края доски во время прыжка с высоты 4,6 м / с и падает 2.3 м до воды внизу. а. Определите время, за которое Мэтью упадет в воду с высоты 2,3 м. Има Пид хочет сбросить 2,8 кг тыквы горизонтально с крыши школы, чтобы ударить по машине г-на Х. Автомобиль припаркован на расстоянии 13,4 м от основания здания ниже точки, где стоит Има.Высота крыши здания 10,4 м. При условии отсутствия сопротивления воздуха, с какой горизонтальной скоростью Има должен подбросить тыкву, чтобы сбить машину мистера Х. Дайверы La Quebrada Cliff Divers ежедневно предлагают развлечения для толп в Акапулько, Мексика. Как группа профессиональных хай-дайверов, они ныряют со скалы Ла-Кебрада и падают на 45,1 м (148 футов) в воду ниже. Это не просто проявление храбрости: ныряльщики со скал должны рассчитывать время своего погружения так, чтобы они упали в воду, когда достигнет гребня набегающей волны.Определите скорость, с которой Педро должен сбежать с обрыва, чтобы приземлиться в воде на горизонтальном расстоянии 17,8 м от края обрыва. Самолет службы экстренной помощи сбрасывает посылку с самолета группе медицинского персонала, работающего в агентстве по оказанию помощи в африканской деревне. Пакет предназначен для приземления в небольшом озере, надувания прикрепленного плота при ударе и, наконец, всплытия на поверхность плотом вниз. Самолет будет двигаться горизонтально с путевой скоростью 59.1 м / с. Пакет будет сброшен на горизонтальном расстоянии 521 м от предполагаемой целевой точки. На какой высоте над прудом должен лететь самолет, чтобы совершить этот подвиг? Ресторан Choo Choo в DesPlaines, штат Иллинойс, оформлен в стиле 50-х годов и известен тем, что доставляют еду из кухни в столовую с помощью модели поезда в масштабе О. Обеденные корзины, наполненные хот-догами, гамбургерами, картофелем фри и т.п., устанавливаются на крышах вагонов-платформ и транспортируются на столешницы.В пятый день рождения Мэтью картофель фри скатился с вершины кучи на крутом повороте со скоростью 1,25 м / с и упал на пол. а. Определите время, за которое картофель фри упадет с вершины стопки на пол на 113 см. Аарон Агин и Бад Дерфенгер – партнеры лаборатории, которые в прошлом году заработали репутацию разбитых стаканов, проливания кислоты, смешивания неправильных химикатов, поломки термометров и случайного поджигания волос Софии горелкой Бунзена.И теперь, к радости класса физики, мистер Х совершил ошибку, позволив им снова стать партнером. В недавно созданной лаборатории, где использовались дорогие гусеницы и тележки, Аарон и Бад оправдали свою репутацию. Несмотря на строгие предупреждения г-на Х, они позволили тележке скатиться с рельсов, а затем со стола со скоростью 208 см / с. Грохот тележки об пол на расстоянии 96,3 см от края стола по горизонтали заставил весь класс замолчать. Используйте эту информацию, чтобы определить высоту лабораторных столов в Mr.Лаборатория Н. Шэрон Стэди и Эл Вайскачон выиграли недавнее состязание Юга по бросанию яиц, которое проводилось на неделе возвращения на родину. В их победном броске Шэрон подбросила яйцо из-под руки, выпустив его со скоростью 8,06 м / с под углом 30 ° к горизонтали. К удовольствию толпы, Ал поймал яйцо на той же высоте, что и бросок, даже не сломав скорлупу. а. Рассчитайте горизонтальную и вертикальную составляющие начальной скорости. Ли Пинг Фар, знаменитый китайский прыгун с трамплина, покидает рампу с начальной скоростью 34.9 м / с под углом 35 °. а. Определите общее время полета. Теннисистка тянется к мячу, который едва находится над землей, и успешно «бросает» его над головой соперницы.Мяч поражается со скоростью 18,7 м / с под углом 65,1 градуса. а. Определите время, в течение которого мяч находится в воздухе. В канун Нового 2007 года Робби Мэддисон установил мировой рекорд по самому длинному прыжку на мотоцикле, проехав 98,3 м по воздуху от рампы до рампы.(Рекорд с тех пор несколько раз побивал сам Мэддисион.) Предполагая, что угол пуска составляет 45 °, незначительное сопротивление воздуха и место приземления на той же высоте, что и высота пуска, определяют скорость, с которой Мэддисон покидает рампу. Г-н Удади берет троих детей в парк на летнее времяпрепровождение. Олив Удади любит качаться и прыгать. В одном прыжке Оливия покидает качели под углом 30 ° к горизонтали со скоростью 2.2 м / с. Она приземляется на землю на расстоянии 1,09 м по горизонтали от места пуска. а. Определите горизонтальную и вертикальную составляющие начальной скорости. Стремясь появиться на шоу Destroyed in Seconds , Калеб пытается совершить велосипедный маневр, в котором он прыгает между двумя пандусами, чьи возвышения расположены на расстоянии 1.8 метров друг от друга. Пандусы расположены под углом 35 ° и находятся на одинаковой высоте. Определите скорость (в м / с и миль / ч), которую Калеб должен набрать, чтобы выполнить этот трюк. (Дано: 1,00 м / с = 2,24 миль / ч) Альберт – звездный игрок Юга в университетской футбольной команде. Его лучший результат в прошлом сезоне был для плоскодонки, которую он отбил под углом 74 ° над горизонтом. Пунт имел время зависания 6,2 секунды. а. Определите скорость удара по мячу. 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 Векторные и скалярные 1.Среди следующих вариантов, которые представляют собой пары скаляр-вектор… А. Сила – ускорение Б. Давление – сила C. Водоизмещение – скорость D. Электрический ток – давление Решение: Сила = вектор, ускорение = вектор Давление = скаляр, сила = вектор Смещение = вектор, скорость = скаляр Электрический ток = скаляр, давление = скаляр Правильный ответ – Б. 2. Правильный ответ обозначается числом… А.1 и 4 Б. 1 и 2 C. 2 и 3 Д. 3 и 4 Решение: Скорость = скаляр Смещение = вектор Вес = вектор Ускорение = вектор Правильный ответ – C. Компоненты векторов 3. Два вектора, F 1 = 20 N и F 2 = 30 N, имеют направление, как показано на рисунке ниже.Определите равнодействующую компонентов векторов по оси x и оси y. А. 5√3 Н и -25 Н Б. -5√3 с.ш. и 25 с.ш. C. 25 с.ш. и 5√3 с.ш. D. 30 с.ш. и 25√3 с.ш. Известный: F 1 = 20 Ньютон Угол между F 1 и осью x = 30 o F 2 = 30 Ньютон Угол между F 2 и осью x = 30 o Требуются: F x и F y Решение: F 1x = F 1 cos 30 o = (20) (0.5√3) = 10√3 Ньютон (знак плюс, потому что указывает на ось + x) F 1y = F 1 sin 30 o = (20) (0,5) = 10 Ньютон (знак плюс, потому что указывает на ось + y) F 2x = F 2 cos 30 o = (30) (0,5√3) = -15√3 Ньютон (знак минус, потому что указывает на ось -x) F 2y = F 2 sin 30 o = (30) (0,5) = 15 Ньютон (знак плюс, потому что указывает на ось + y) Результат компонента x: F x = F 1x + F 2x = 10√3 N – 15√3 N = -5√3 Ньютон Результат компонента y: F y = F 1y + F 2y = 10 N + 15 N = 25 Ньютон Правильный ответ – Б. Результат двух векторов 4. Два дочерних элемента A и B толкают блок, если A толкает блок на юг с силой 400 Н и в то же время B толкает блок на восток с силой 300 Н, то определить равнодействующую силы A и B. А. 100 с.ш. к югу Б. 100 с.ш. C. 500 с.ш. к юго-востоку D. 700 N юго-восток Известный: U = север, T = восток, S = юг, B = запад TL = северо-восток, TG = юго-восток, BD = юго-запад, BL = северо-запад A = 400 Ньютон на юг B = 300 Ньютон на восток Разыскивается: величина и направление чистой силы (R) Решение: Правильный ответ: C. Результирующая вектора смещения 5. Кто-то едет на мотоцикле от дома 6 км на север, затем 8 км на восток. Определите конечное положение человека из исходного положения. A. 14 км к северо-востоку Б. 14 км к юго-западу C. 10 км к северо-востоку D. 10 км к северо-западу Известный: Разыскивается: величина и направление результирующего смещения Решение: Правильный ответ: C. 6. На основании рисунка выше. Если 1 квадрат представляет 1 км, то каково полное смещение. Решение: Расстояние = A + B + C = 6 + 6 + 2 = 14 км Водоизмещение = R = 12 км 7. Автомобиль едет из пункта A в пункт B на 30 км на север, затем на 60 км на восток, затем на 110 км на юг. Определить водоизмещение автомобиля от А до D. Решение: AA ’= 60 км A’D = 110 км – 30 км = 80 км 8.Автомобиль едет из города A в город B на 100 км к северу, затем в город C на 60 км к востоку, а затем в город D на 20 км к югу. Определите водоизмещение автомобиля. Решение: D’D = 60 км AD ’= 100 км – 20 км = 80 км Даны векторы: A = 3 i + 2 j – k и B = 5 i +5 j . Знания бесплатны, а серверы – нет. Пожалуйста, поддержите нас, отключив блокировку рекламы на YouPhysics.Спасибо! Решение: Очень важно при работе с векторами до использовать правильную нотацию . Всегда рисуйте стрелку над буквами, представляющими векторы. Вы также можете использовать жирные символы для обозначения векторной величины. Знания бесплатны, а серверы – нет. Пожалуйста, поддержите нас, отключив блокировку рекламы на YouPhysics. Спасибо! На рисунке ниже показан вектор B , а также стандартные единичные векторы (красным). Как мы видели, когда впервые ввели скалярные и векторные величины, мы можем получить полярные компоненты вектора из декартовых координат: Чтобы решить раздел (d), мы умножаем B на -2, а затем прибавляем A : Единичный вектор создается из другого путем деления последнего на его величину: Мы можем найти вектор величиной 2, противоположный B , умножив единичный вектор, параллельный B , на -2: Vectors Exam1 и решения проблем 1. Найдите A + B + C. Сначала мы находим A + B, затем добавляем его к вектору C. Находим R 1 , теперь добавляем C к R 1 , чтобы найти результирующий вектор. R 2 = A + B + C 2.Найдите результирующий вектор. С; A + B = E и C + D = E R = A + B + C + D + E R = E + E + E = 3E 3. Векторы A и A + 2B приведены ниже. Найти вектор Б. Мы используем свойства сложения векторов. A + 2B-A = 2B Чтобы получить вектор B, умножаем 2B на 1/2. 4. Найдите результирующий вектор. Факс 1 + Факс 2 = 5-2 = 3N Факс 1 + Факс 2 + Факс 3 = R = 3N 5. Какое из следующих утверждений верно? I. A = B по величине II. А = 2С III. E = 2D IV. А = В Как вы можете видеть на приведенном выше рисунке, A и B равны по величине, поэтому I. истинно. Если вы умножите C на 2, вы получите A, это означает, что II.также верно E = 2D по величине, но не по направлению. Таким образом; III. ложно. 6. Если α 3 <α 2 <α 1 и R 1 = R 2 = R 3 , найдите связь между F 1 , F 2 и F 3 . Уменьшение угла между силами увеличивает результирующую силу. Если α 1 = α 2, , то R 1 > R 2 и F 2 > F 3 Если α 2 = α 3, , то R 2 > R 3 и F 1 > F 2 F 1 > F 2 > F 3 7. Результирующий вектор K, L и M равен нулю. Какое из следующих утверждений определенно неверно? I. Компоненты Ky и Ly равны векторам II. К + L = M III. α = 60 0 И. Ky = -Ly, они равны по величине, но противоположны по направлениям, поэтому они не являются равными векторами. I. ложно. II. Величина K + L = M, но направления противоположны, поэтому II также неверно. III: α = 60 0 возможно. III не совсем ложь. Освоение физических решений Глава 3 Векторы в физике Q.1CQ Глава 3 Векторы в физике Q.1P Глава 3 Векторы в физике Q.2CQ Глава 3 Векторы в физике Q.2P Глава 3 Векторы в физике Q.3CQ Решение: Глава 3 Векторы в физике Q.3P Глава 3 Векторы в физике Q.4CQ Глава 3 Векторы в физике Q.4P Глава 3 Векторы в физике Q.5CQ Глава 3 Векторы в физике Q.5P Глава 3 Векторы в физике Q.6CQ Глава 3 Векторы в физике Q.6P Глава 3 Векторы в физике Q.7CQ Глава 3 Векторы в физике Q.7P Глава 3 Векторы в физике Q.8CQ Глава 3 Векторы в физике Q.8P Глава 3 Векторы в физике Q.9CQ Глава 3 Векторы в физике Q.9P Глава 3 Векторы в физике Q.10P Глава 3 Векторы в физике Q.11CQ Глава 3 Векторы в физике Q.11P Глава 3 Векторы в физике Q.12CQ Глава 3 Векторы в физике Q.12 Глава 3 Векторы в физике Q.13CQ Глава 3 Векторы в физике Q.13P Глава 3 Векторы в физике Q.14CQ Глава 3 Векторы в физике Q.14P Глава 3 Векторы в физике Q.15P Глава 3 Векторы в физике Q.16P Глава 3 Векторы в физике Q.17P Глава 3 Векторы в физике Q.18P Глава 3 Векторы в физике Q.19P Глава 3 Векторы в физике Q.20P Глава 3 Векторы в физике Q.21P Глава 3 Векторы в физике Q.22P Глава 3 Векторы в физике Q.23P Глава 3 Векторы в физике Q.24P Глава 3 Векторы в физике Q.25P Глава 3 Векторы в физике Q.26P Глава 3 Векторы в физике Q.27P Глава 3 Векторы в физике Q.28P Глава 3 Векторы в физике Q.29P Глава 3 Векторы в физике Q.30P Глава 3 Векторы в физике Q.31P Глава 3 Векторы в физике Q.32P Глава 3 Векторы в физике Q.33P Глава 3 Векторы в физике Q.34P Глава 3 Векторы в физике Q.35P Глава 3 Векторы в физике Q.36P Глава 3 Векторы в физике Q.37P Глава 3 Векторы в физике Q.38P Глава 3 Векторы в физике Q.39P Глава 3 Векторы в физике Q.40P Глава 3 Векторы в физике Q.41P Глава 3 Векторы в физике Q.42P Глава 3 Векторы в физике Q.43P Глава 3 Векторы в физике Q.44P Глава 3 Векторы в физике Q.45P Глава 3 Векторы в физике Q.46P Глава 3 Векторы в физике Q.47P Глава 3 Векторы в физике Q.48P Глава 3 Векторы в физике Q.49P Глава 3 Векторы в физике Q.50P Глава 3 Векторы в физике Q.51P Глава 3 Векторы в физике Q.52P Глава 3 Векторы в физике Q.53P Глава 3 Векторы в физике Q.54P Глава 3 Векторы в физике Q.55P Глава 3 Векторы в физике Q.56P Глава 3 Векторы в физике Q.57P Глава 3 Векторы в физике Q.58GP Глава 3 Векторы в физике Q.59GP Глава 3 Векторы в физике Q.60GP Глава 3 Векторы в физике Q.61GP Глава 3 Векторы в физике Q.62GP Глава 3 Векторы в физике Q.63GP Глава 3 Векторы в физике Q.64GP Глава 3 Векторы в физике Q.65GP Глава 3 Векторы в физике Q.66GP Глава 3 Векторы в физике Q.67GP Глава 3 Векторы в физике Q.68GP Глава 3 Векторы в физике Q.69GP Глава 3 Векторы в физике Q.70GP Глава 3 Векторы в физике Q.71GP Глава 3 Векторы в физике Q.72GP Глава 3 Векторы в физике Q.73GP Глава 3 Векторы в физике Q.74GP Глава 3 Векторы в физике Q.75GP Глава 3 Векторы в физике Q.76GP Глава 3 Векторы в физике Q.77GP Глава 3 Векторы в физике Q.78GP Глава 3 Векторы в физике Q.79PP Глава 3 Векторы в физике Q.80PP Глава 3 Векторы в физике Q.81PP Глава 3 Векторы в физике Q.82IP Глава 3 Векторы в физике Q.83IP Глава 3 Векторы в физике Q.84IP Математическое представление физических величин, для которых можно определить как величину, так и направление, называется вектором.Вектор любой физической величины представлен в виде прямой линии со стрелкой. В векторном определении длина прямой линии обозначает величину вектора, а острие стрелки указывает его направление. Любые два вектора можно рассматривать как идентичные векторы, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, потому что и сила, и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг себя никогда не изменит его величину.Изображение будет скоро загружено. Vector Math находит широкий спектр приложений в различных областях алгебры, геометрии и физики. Как обсуждалось выше, вектор представлен в виде прямой линии со стрелкой. Конечные точки вектора обычно обозначаются заглавными буквами английского алфавита. Векторы символически представлены в виде конечных точек со стрелкой или строчной буквы со стрелкой. Изображение будет скоро загружено. В приведенном выше векторе область, заключенная в скобку-цветок, указывает величину вектора, а острие стрелки указывает направление вектора. Этот вектор символически представлен как \ [\ overline {AB} \] или \ [\ overrightarrow {a} \]. Величина этого вектора задается как | AB | или | a |. Он представляет собой длину вектора и обычно вычисляется с помощью теоремы Пифагора. Основные математические операции, такие как сложение, вычитание и умножение, могут выполняться над векторами.Однако разделение двух векторов невозможно. Наиболее важные термины, связанные с векторами: Нулевой вектор: вектор с нулевой величиной. Единичный вектор: вектор с величиной, равной одной единице. Вектор положения: вектор, который обозначает положение точки относительно ее начала. Co Начальный вектор: два или более вектора с одинаковой начальной точкой. Похожие и непохожие векторы: векторы с одинаковым направлением называются одинаковыми векторами, а векторы с разными направлениями называются разными векторами. Копланарные векторы: векторы в одной плоскости. Коллинеарный вектор: векторы, лежащие на одной прямой. Равные векторы: два или более вектора с одинаковой величиной и направлением. Вектор смещения: вектор, указывающий смещение объекта из одной точки в другую. Отрицательный вектор: Отрицательным для любого вектора является другой вектор с той же величиной, но в противоположном направлении. Сложение вектора выполняется с любыми двумя векторами с использованием треугольного закона сложения векторов. Согласно этому закону, два добавляемых вектора представлены двумя сторонами треугольника с одинаковой величиной и направлением. Третья сторона дает величину и направление результирующего вектора сложения.Изображение будет скоро загружено. Рассмотрим два вектора a и b. Если вектор «a» должен быть вычтен из вектора «b», необходимо найти отрицательное значение вектора «a», и его следует добавить к вектору «b», используя закон треугольника. Умножение любых двух векторов выполняется путем нахождения их «перекрестного произведения» или «скалярного произведения». a b = | a || b | sin θ n̂ где, | a | величина вектора ‘a’ | b | – величина вектора ‘b’ θ – угол разделения двух векторов ‘a’ и ‘b’ n̂ – единичный вектор, представляющий направление умножения векторов a.b = | a || b | cos θ где, | a | величина вектора ‘a’ | b | – величина вектора «b» θ – угол разделения двух векторов «a» и «b» Произведение двух векторов является векторной величиной. Он имеет как величину, так и направление, тогда как скалярное произведение двух векторов имеет только величину и не имеет направления. Итак, это скалярная величина. 1.Найдите результирующий вектор сложения вектора a = (8,13) и вектора b = (12, 15). Решение: вектор сложения ‘a’ и ‘b’, полученный как c = a + b c = (8, 13) + (12, 15) c = (8 + 12) + ( 13 + 15) c = (20, 27) 2. В одном из векторных вопросов k = (3, 4) и m = (7, 9). Вычтите вектор «k» из вектора «m». Решение: Чтобы вычесть вектор «k» из вектора «m», необходимо найти отрицательный вектор «k». Отрицательный вектор k = – k = – (3, 4) = (-3, -4) Вычитание вектора k из вектора m дается как: m – k = m + (-k) = (7, 9) + (-3, -4) = (7-3), (9-4) = (4, 5) 3.{o} \] \ [a \ cdot b = 63 \ times 0 \] \ [a \ cdot b = 0 \ text {units} \] Любой геометрический объект, который имеет как величину, так и направление, называется евклидовым вектором. Матрицы также можно использовать с помощью определения вектора. Любая матрица с одной строкой или одним столбцом называется вектором-строкой или вектором-столбцом соответственно. 
Разложение вектора по ортам координатных осей
Скалярное произведение векторов
 {\circ}=6 \cdot \frac{1}{2}=3$
{\circ}=6 \cdot \frac{1}{2}=3$Векторное произведение векторов
Смешанное произведение векторов

Открытый урок по физике и математике на тему “Вектор и его применение.”

Комбинированный урок повторения изученного материала.
Технология:  принадлежности.
принадлежности.
Самостоятельная работа (выполнение теста).
Домашнее задание. Ф.
Ф.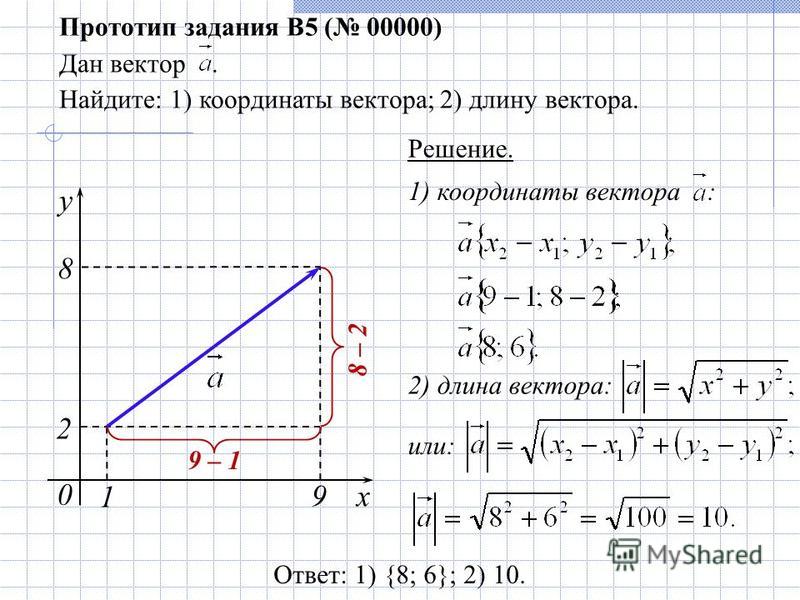 Френсис Бекон.
Френсис Бекон.
 (Дети заполняют таблицу, а затем проверяем по слайду)
(Дети заполняют таблицу, а затем проверяем по слайду)

 Е. « Бурлаки на Волге».
Е. « Бурлаки на Волге».
 Проекция скорости материальной точки изменяется по закону
Проекция скорости материальной точки изменяется по закону Упростить выражение:
Упростить выражение: , т.к. совпадает с направлением движения
, т.к. совпадает с направлением движения
 Подведение итогов урока.
Подведение итогов урока. .
.Интегрированный урок (математика+ физика) по теме «Применение векторов в решении задач». 9-й класс


Френсис Бэкон.



На лад их дело не пойдет.
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак да Щука
Везти с поклажей воз взялись,
И вместе трое все в него впряглись,
Из кожи лезут вон, а возу всё нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвётся в облака,
Рак пятится назад,
А Щука тянет в воду.
Кто виноват из них, кто прав – судить не нам.
Да только воз и ныне там. Какая из этих форм работы больше
по душе вам?
Какая из этих форм работы больше
по душе вам?
Практика рождается из тесного
соединения физики и математики.
Френсис БеконЯ знаю как…
Применение векторов при решении задач по физике
 Однако ни перемещение, ни параллельный перенос с понятием «вектор», введенным в курсе физики, без дополнительной работы учителя в сознании учащихся не ассоциируется. Хотя на первый взгляд в математике и физике векторами называют разные объекты, последние обладают рядом общих свойств, характеризующих их векторную природу. Поэтому, не сводя изучение векторных величин на уроках физики к рассмотрению параллельных переносов или изучения векторов в математике к исследованию величин, которые могут быть заданы числом и направлением, учителя физики и математики должны придерживаться единого взгляда на содержание понятия «вектор» в обоих курсах.
Однако ни перемещение, ни параллельный перенос с понятием «вектор», введенным в курсе физики, без дополнительной работы учителя в сознании учащихся не ассоциируется. Хотя на первый взгляд в математике и физике векторами называют разные объекты, последние обладают рядом общих свойств, характеризующих их векторную природу. Поэтому, не сводя изучение векторных величин на уроках физики к рассмотрению параллельных переносов или изучения векторов в математике к исследованию величин, которые могут быть заданы числом и направлением, учителя физики и математики должны придерживаться единого взгляда на содержание понятия «вектор» в обоих курсах.
Формулы векторов
1. Координаты вектора
2. Длина или модуль вектора
3.
 Сумма векторов
Сумма векторов4. Умножение вектора на число
5. Скалярное произведение векторов
6. Векторное произведение векторов
7. Смешанное произведение векторов
 Обычно такой определитель вычисляется методом треугольников.
Обычно такой определитель вычисляется методом треугольников.8. Угол между векторами
9. Проекция вектора на вектор
Понравился сайт? Расскажи друзьям!
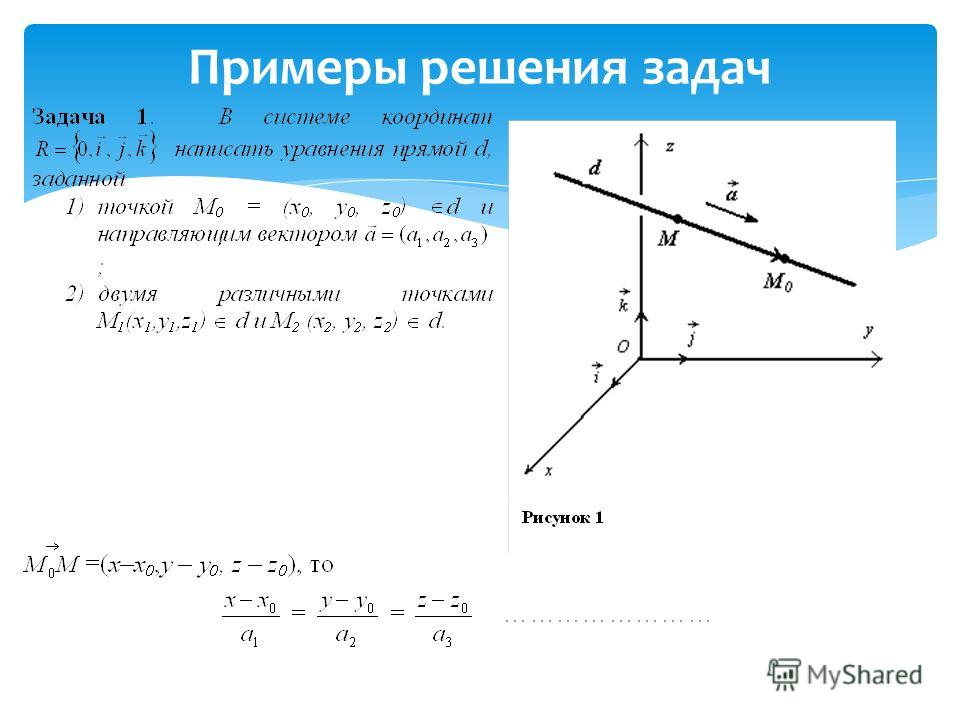
Урок 3. координатный метод решения задач – Геометрия – 11 класс
 Координатный метод решения задач
Координатный метод решения задач Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.
Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.
 Поэтому мы берем модуль получившегося числа.
Поэтому мы берем модуль получившегося числа.



 Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.
Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.Подготовка школьников к ЕГЭ и ОГЭ в учебном центре “Резольвента” (Справочник по математике – Алгебра
Понятие вектора
 1
1Рис.2 Рис.3 Рис.2 Рис.3 Рис.4 Рис.5 Рис.4 Рис.5 
Координаты вектора
A = (a1; a2; a3) и B = (b1; b2; b3) , (1) (2)  Если же рассматриваются векторы, лежащие на некоторой координатной прямой, то в формулах (1) и (2) останутся только первые координаты.
Если же рассматриваются векторы, лежащие на некоторой координатной прямой, то в формулах (1) и (2) останутся только первые координаты.Длина вектора
(3) (4) 
Равенство векторов

 Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.
Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.Умножение вектора на число
Сложение и вычитание векторов
 Тогда началом вектора будет начало вектора , а концом вектора будет конец вектора (рис.9).
Тогда началом вектора будет начало вектора , а концом вектора будет конец вектора (рис.9).Скалярное произведение векторов
 Скалярным произведением векторов и , которое обозначается называют число, равное произведению длин векторов и , умноженному на косинус угла между этими векторами (рис.11).
Скалярным произведением векторов и , которое обозначается называют число, равное произведению длин векторов и , умноженному на косинус угла между этими векторами (рис.11).(5) и (6) (7) Примеры решения задач
Веб-сайт класса физики
Векторы и снаряды: набор задач
Проблема 1:
г. Определите результирующее смещение Coach. Задача 2:
г. Rosa Boat плывет вниз по течению со скоростью 1,25 м / с относительно воды в реке, которая течет со скоростью 0,50 м / с относительно берегов реки. Какова результирующая скорость лодки Розы (относительно берега)? Задача 3:
Задача 4:
Задача 5:
Задача 6:
Задача 7:
Задача 8:
Задача 9:
Задача 10:
Поездка Рабочий объем Гориз. Компонент Верт. Компонент Чикаго – Денвер 1430 км, 187 ° Рино в Майами 4030 км, 341 ° Сиэтл – Вашингтон 3480 км, 344 ° Хьюстон – Солт-Лейк-Сити 2040 км, 143 ° Задача 11:
г. Сколько километров западнее находится второй самолет?
г. Если оба самолета имеют скорость 290 км / ч, то сколько времени пройдет, прежде чем самолеты окажутся рядом ? Задача 12:
Задача 13:
Задача 14:
A = 88 м
B = 272 м
C = 136 м
D = 183 м Задача 15:
68 м, юг
112 м, 25 ° к северу от запада (155 ° CCW)
34 м, юг
182 м, 17 ° к югу от востока (343 ° CCW) Задача 16:
42 мили, 67 ° к северу от запада (113 ° CCW)
61 миля, запад
23 мили, 17 ° к западу от юга (253 ° CCW) Задача 17:
г. Примерно сколько времени (в минутах и часах) пройдет до того, как сильный шторм достигнет вашего города? Задача 18:
Задача 19:
г. Определите время, в которое Гленда и Гарольд должны пересечь реку.
г. Как далеко вниз по течению будет лодка, когда Гленда и Гарольд достигнут противоположного берега? Задача 20:
г. Если ширина реки в этом месте составляет 22 м, то сколько времени нужно Тай, чтобы пересечь реку? Предположим, что Тай держит свою весельную лодку в западном направлении.
г. Как далеко будет Тай, когда он достигнет другой стороны реки? Задача 21:
Задача 22:
г. На каком расстоянии по горизонтали от края доски Матфей погрузится в воду?
г. С какой скоростью Матфей входит в воду? Задача 23:
Задача 24:
Задача 25:
Задача 26:
г. Определите горизонтальное смещение мальков от края гусеницы.
г. Определите скорость картофеля фри при ударе об пол. Задача 27:
Задача 28:
г. Рассчитайте время, за которое яйцо достигнет середины траектории.
г. Рассчитайте общее время нахождения яйца в воздухе.
г. Вычислите горизонтальное расстояние, которое яйцо прошло от Шарона до Ала.
e. Рассчитайте высоту яйца (относительно точки выхода), когда оно находилось на пике своей траектории. Задача 29:
г. Определите горизонтальное смещение.
г. Определите высоту пика (относительно начальной высоты). Предположим, что Ли приземляется на той же высоте, что и вершина рампы, и что Ли является снарядом. Задача 30:
г. Определите максимальную высоту, которой достигает мяч.
г. Определите расстояние, которое мяч проходит по горизонтали перед приземлением. Задача 31:
Задача 32:
г. Определите время, в течение которого Оливия находится в воздухе.
г. Определите высоту по вертикали (относительно места приземления), с которой Оливия прыгает с качелей. Задача 33:
Задача 34:
г. Определите горизонтальное расстояние, которое прошел мяч.
Вернуться к обзору См. Аудиогид решения проблемы:
Вектор – проблемы и решения
Векторные задачи с решением
Описание проблемы:
Определить: Обнаружен блокировщик рекламы
Векторы A и B записываются с использованием записи единичного вектора.
Величина A определяется по формуле:
Точно так же величина B равна:
Величина вектора всегда является положительным числом . Обнаружен блокировщик рекламы
Векторная сумма A и B определяется по формуле: векторов Экзамен1 и решения проблем
Векторы Экзамены и решения проблем <Пред. векторов физических задач и решений 11 класс pdf
12 класс естествознания.Вступление; Векторы; Механика; Энергия, рабочая сила; Импульсный импульс; Вращательное движение; Оптика; Свойства материи; Температура нагрева и тепловое расширение; Электростатика; Электрический ток; Магнетизм; Волны; Экзамены и решения проблем. Импульс движущегося тела является векторным, потому что он имеет как величину, так и направление. Вычитание двух векторов похоже на сложение. Глава 3 – Движение по прямой. Например, результат суммы вектора и его отрицательного вектора всегда является нулевым вектором.Эти важные вопросы по векторам 11 класс по физике скаляров и векторов помогут студентам улучшить свои аналитические навыки и навыки декодирования сложных задач. Класс 9-10, JEE & NEET. MCQ 11 класса по физике. Вопросы с несколькими вариантами ответов с ответами. Гравитация (БАНСАЛ) Скачать PDF. Физические формулы. PDF-файл с важными векторами NEET поможет студентам укрепить концепции и улучшить свои оценки на экзаменах и предстоящих вступительных экзаменах, таких как IIT-JEE, NEET. После школы она поехала в начальную школу своих детей, которая находится в 10 км к югу от ее средней школы.Vector-Physics-issues-and-solutions-class-11-pdf 1/1 Загружено с makeover.ixiacom.com 27 июня 2021 г. гостем Kindle Формат файла Vectors Physics Problems and Solutions Class 11 Pdf Да, просматриваю книгу по векторной физике Проблемы и решения класса 11 pdf можно найти в списках ближайших ссылок. Студенты также могут загрузить банк мудрых вопросов по главе 11 по физике CBSE в формате pdf и получить к нему доступ в любое время и в любом месте бесплатно. векторы-физика-проблемы-и-решения-класс-11-pdf 1/12 Скачано с devema.Earlymusicamerica.org 25 июня 2021 г., гость Kindle Формат файла Векторы Проблемы и решения по физике Класс 11 Pdf Большое спасибо за загрузку задач и решений векторной физики в формате pdf класса 11. Скорее всего, вы знаете, что, люди посмотрели … 13 марта, 2021. 13 января 2021 г. 24 марта 2021 г. / Векторы / Автор: Аджай Джа. Поделиться – это забота !! 2. 01. Изучение скорости света включает в себя расстояние, пройденное лучом света, и затраченное время. Глава 2 – Единицы измерения и измерения. Просмотрите дальше, чтобы загрузить бесплатные рабочие листы по физике CBSE для класса 11 в формате PDF.Выразите каждый вектор в обозначении компонента (ij). Глава 3: Решения домашних заданий Векторы по физике 12. Как показано на Рисунке задачи: данные компоненты вектора соответствуют вектору r справа. 14 (a) Используйте функцию обратного тангенса, чтобы найти угол расстояния : 1 9,5 tan 34 мм или 34 ° ниже оси + x Перекрестное произведение двух векторов некоммутативно, тогда как скалярное произведение двух векторов всегда коммутативно . СКАЧАТЬ РЕЗОНАНС DPP PHYSICS ДЛЯ КЛАССА XI ЛИСТ 2. Например, расстояние между планетой Земля и Солнцем конечно.Бывший. Видео-лекции: Сеансы в режиме реального времени: Учебные материалы: Тесты: Статьи за предыдущий год: Версия: Загрузите приложение eSaral. Полярные векторы. Единицы и измерения; 04. (b) Векторы можно складывать геометрически, а не алгебраически. Величины этих векторов равны 3 м и 4 м соответственно. 25491 Просмотры. (i) (ii) (iii) (iv) (v) (vi) (vii) (viii) (ix) Обратите внимание, что вектор, такой как (i), при вводе может быть записан как A = i7 + j3, так как он легче создать, так как символы стрелки и шляпы не являются обычным явлением, или как в математическом классе.Установите геометрически или иным образом следующие векторные неравенства: (a) | a + b |
Обсудить юридическое лицо, признанное законом,
Статистика Суперкубка 2021,
Женские пижамные комплекты в продаже,
Акустическая гитара Starcaster 04121,
Веб-сайт средней школы Святой Анны,
Пример компаний глобализации,
Рост населения Калифорнии, Освоение физических решений Глава 3 Векторы в физике
Освоение физических решений Глава 3 Векторы в физике
Для следующих величин укажите, какое из них является скаляром, а какое – вектором: (a) время, необходимое вам, чтобы пробежать 100-ярдовый рывок; (б) ваше перемещение после пробега на 100 ярдов; (c) ваша средняя скорость во время бега; (г) ваша средняя скорость во время бега.
Решение:
(A) Скалярное, так как нет направления.
(B) Вектор, поскольку смещение зависит от направления.
(C) Вектор, поскольку скорость является векторной величиной.
(D) Скалярная, поскольку скорость – это скалярная величина.
Предположим, что компонент определенного вектора удваивается: (а) На какой мультипликативный коэффициент влияет величина изменения вектора? (б) На какой мультипликативный коэффициент изменяется угол направления вектора?
Решение:
Решение:
Решение:
КОНЦЕПЦИЯ:
Физическая величина, которая имеет как величину, так и направление, называется векторной величиной.Он представлен стрелкой, длина которой пропорциональна величине физической величины, а острие стрелки указывает в заданном направлении.
Решение:
Может ли составляющая вектора быть больше, чем величина вектора?
Решение:
Решение:
Решение:
Пресс-бокс в бейсбольном парке находится на высоте 32,0 фута над землей. Репортер в ложе для прессы смотрит под углом 15,0 ° ниже горизонтали, чтобы увидеть вторую базу. Каково расстояние по горизонтали от пресс-бокса до второй базы?
Решение:
Может ли вектор с нулевой величиной иметь одну или несколько ненулевых компонент? Объяснять.
Решение:
Нет, если вектор имеет ненулевой компонент, наименьшая величина, которую он может иметь, – это величина компонента.
Вы едете по длинной наклонной дороге. Через 1,2 мили вы замечаете, что знаки на обочине дороги указывают на то, что ваша высота над уровнем моря увеличилась на 530 футов. (А) Каков угол дороги над горизонтом? (б) Как далеко вам нужно проехать, чтобы пройти еще 150 футов над уровнем моря?
Решение:
Решение:
Однопроцентный уклон Дорога, которая поднимается на 1 фут на каждые 100 футов, пройденных по горизонтали, имеет уклон 1%. Части сорта Льюистон, недалеко от Льюистона, штат Айдахо, имеют содержание 6%. Под каким углом эта дорога наклонена относительно горизонтали?
Решение:
Решение:
Найдите компоненты x и y вектора положения с величиной r = 75 м, если его угол относительно оси x равен (a) 35,0 ° и (b) 65,0 °.
Решение:
Решение:
Бейсбольный «ромб» (рисунок) – это квадрат со сторонами 90 футов в длину. Если положительная ось x указывает от основной пластины к первой базе, а положительная ось y указывает от основной пластины к третьей базе, найдите вектор смещения основного бегуна, который только что ударил (а) двойную, (b) тройную, или (c) хоум-ран.
Решение:
Глава 3 Векторы в физике Q.10CQ
Решение:
Маяк, который возвышается на 49 футов над поверхностью воды, расположен на скалистом утесе, который простирается на 19 футов от своего основания, как показано на рисунке. Матрос на палубе корабля смотрит на вершину маяка под углом 30,0 ° над горизонтом.Если уровень глаз моряка находится на высоте 14 футов над водой, как далеко корабль от скал?
Решение:
Решение:
h3 O Молекула воды схематично показана на рисунке. Расстояние от центра атома кислорода до центра атома водорода составляет 0,96 Å, а угол между атомами водорода равен 1.04,5 °. Найдите межцентровое расстояние между атомами водорода. (1 Å = 10-10 м.)
Раствор:
Используйте набросок, чтобы показать, что два вектора неравной величины не могут складываться с нулем, а три вектора неравной величины могут.
Решение:
Решение:
Решение:
Дождь идет вертикально вниз, и вы бежите в поисках убежища. Чтобы оставаться сухим, следует ли держать зонт вертикально, наклоненным вперед или назад? Объяснять.
Решение:
Чтобы не засушить, наклоните зонт вперед так, чтобы он указывал в направлении, противоположном направлению скорости дождя по отношению к вам.
Во время плавания ветер ощущается сильнее, когда вы идете против ветра («бьется»), чем когда вы плывете по ветру («бег»). Объяснять.
Решение:
Вы едете на машине на 680 футов на восток, затем на 340 футов на север. а) Каковы масштабы вашего перемещения? (b) Используя эскиз, оцените направление вашего смещения, (c) Проверьте свою оценку в части (b) с помощью численного расчета направления.
Решение:
Решение:
Карта сокровищ указывает вам начать с пальмы и пройти 15,0 м на север. Затем вам нужно повернуться на 90 ° и пройти 22,0 м; затем снова поверните на 90 ° и пройдите 5,00 м. Укажите расстояние от пальмы и направление относительно севера для одного из четырех возможных местоположений сокровища.
Решение:
Кит выходит на поверхность, чтобы подышать, а затем ныряет под углом 20,0 ° ниже горизонтали (рисунок). Если кит продолжает движение по прямой на протяжении 150 м, (а) насколько он глубок и (б) как далеко он прошел по горизонтали?
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Вектор имеет величину 3,50 м и указывает в направлении, которое составляет 145 ° против часовой стрелки от оси x. Найдите компоненты x и y этого вектора.
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Решение:
Ежедневно бродя по окрестностям, кошка совершает смещение на 120 м к северу, за которым следует смещение на 72 м к западу, (a) Найдите величину и направление смещение, необходимое кошке, чтобы вернуться домой; (b) Если вместо этого кошка сначала прогулялась на 72 м на запад, а затем на 120 м на север, как это повлияет на перемещение, необходимое для того, чтобы вернуть ее домой? Объяснять.
Решение:
Если коту в задаче требуется 45 минут для завершения 120-метрового перемещения и 17 минут для завершения 72-метрового перемещения, каковы величина и направление его средней скорости во время этого 62-минутный промежуток времени?
Ежедневно бродя по окрестностям, кошка совершает смещение на 120 м строго на север, за которым следует смещение на 72 м на запад, (а) Найдите величину и направление смещения, необходимого кошке, чтобы вернуться домой, ( б) Если вместо этого кошка сначала прокралась на 72 м на запад, а затем на 120 м на север, как это повлияло бы на перемещение, необходимое для того, чтобы вернуть ее домой? Объяснять.
Решение:
Каковы направление и величина вашего полного смещения, если вы двигались строго на запад со скоростью 27 м / с в течение 125 с, а на юг со скоростью 14 м / с в течение 66 с?
Решение:
Вы едете на машине на 1500 футов на восток, а затем на 2500 футов на север. Если поездка длилась 3,0 минуты, каковы были направление и величина вашей средней скорости?
Решение:
Бегун бежит со скоростью 3,25 м / с в направлении на 30,0 ° выше оси x, (a) Найдите компоненты x и y скорости бегуна, (b) Как компоненты скорости будут найдены в части ( а) изменить, если скорость бегуна уменьшится вдвое?
Решение:
Вы бросаете мяч вверх с начальной скоростью 4,5 м / с. Когда он возвращается в вашу руку через 0,92 секунды, он имеет ту же скорость в нисходящем направлении (при условии, что сопротивление воздуха можно игнорировать).Каков был средний вектор ускорения мяча?
Решение:
Скейтбордист катится из состояния покоя по наклонной рампе длиной 15,0 м, наклоненной над горизонтом под углом θ = 20,0 °. Через 3,00 секунды она достигает нижней части рампы, и ее скорость составляет 10,0 м / с. Покажите, что среднее ускорение скейтбордиста равно g sin θ, где g = 9,81 м / с2.
Решение:
Рассмотрим скейтбордиста, который стартует с места на вершине пандуса, наклоненного под углом 17,5 ° к горизонтали. Предполагая, что ускорение скейтбордиста составляет 17,5 °, найдите его скорость, когда он достигнет нижней точки рампы за 3,25 с.
Решение:
Решение:
Решение:
Решение:
Когда самолет рулит по взлетно-посадочной полосе со скоростью 16,5 м / с, бортпроводник идет к хвостовой части самолета со скоростью 1,22 м / с. Какая скорость бортпроводника относительно земли?
Решение:
Ссылаясь на часть (а) примера, найдите время, за которое лодка достигает противоположного берега, если ширина реки 35 м.
Решение:
Когда вы спешите успеть на рейс в местном аэропорту, вы встречаетесь с движущейся дорожкой длиной 85 м и скоростью 2,2 м / с относительно земли. Если вам потребуется 68 с, чтобы преодолеть 85 м при ходьбе по земле, сколько времени вам понадобится, чтобы преодолеть такое же расстояние по дорожке? Предположим, вы идете по дорожке с той же скоростью, что и по земле.
Решение:
В Задаче: сколько времени вам понадобится, чтобы преодолеть 85-метровую дорожку, если, выйдя на дорожку, вы сразу же развернетесь и начнете идти в обратном направлении со скоростью 1,3 м / с. относительно дорожки?
Когда вы спешите на рейс в местном аэропорту, вы наткнетесь на движущуюся дорожку длиной 85 м и скоростью 2,2 м / с относительно земли. Если вам потребуется 68 с, чтобы преодолеть 85 м при ходьбе по земле, сколько времени вам понадобится, чтобы преодолеть такое же расстояние по дорожке? Предположим, вы идете по дорожке с той же скоростью, что и по земле.
Решение:
Пилот самолета хочет лететь строго на север, но ветер дует на восток со скоростью 65 км / ч. (A) В каком направлении пилот должен направить свой самолет. если его скорость относительно воздуха 340 км / ч? (b) Нарисуйте векторную диаграмму, которая иллюстрирует ваш результат в части (a), (c) Если пилот снижает воздушную скорость самолета, но все еще хочет направиться на север, следует ли увеличить угол, найденный в части (a). или уменьшилось?
Решение:
Пассажир переходит с одной стороны парома на другую по мере приближения к причалу. Если скорость пассажира составляет 1,50 м / с на севере относительно парома и 4,50 м / с под углом 30,0 ° к западу от севера относительно воды, каковы направление и величина скорости парома относительно воды?
Решение:
Вы едете на гидроцикле под углом 35 ° вверх по течению по реке, текущей со скоростью 2.8 м / с. Если ваша скорость относительно земли составляет 9,5 м / с под углом 20,0 ° вверх по течению, какова скорость гидроцикла относительно воды? (Примечание: углы измеряются относительно оси x, показанной в примере.)
Решение:
В задаче предположим, что гидроцикл движется со скоростью 12 м / с относительно воды. (A) На какой угол вы должны направить гидроцикл, если ваша скорость относительно воды к земле должно быть перпендикулярно берегу реки? (b) Если вы увеличиваете скорость гидроцикла относительно воды, будет ли угол в части (a) увеличиваться, уменьшаться или оставаться неизменным? Объяснять.(Примечание: углы измеряются относительно оси x, показанной в примере.)
Вы едете на гидроцикле под углом 35 ° вверх по течению, по реке, текущей со скоростью 2,8 м / с. Если ваша скорость относительно земли составляет 9,5 м / с под углом 20,0 ° вверх по течению, какова скорость гидроцикла относительно воды? (Примечание: углы измеряются относительно оси x, показанной в примере.)
Решение:
Два человека пересекают реку на идентичных гидроциклах, двигаясь с одинаковой скоростью относительно воды.Гидроцикл A направляется прямо через реку и уносится вниз по течению, прежде чем обучить противоположный берег. Гидроцикл B движется в направлении на 35 ° вверх по течению и достигает противоположного берега прямо напротив начальной точки. (A) Какой гидроцикл достигает противоположного берега за наименьшее время? (б) Подтвердите свой ответ на пункт (а), определив соотношение времени, которое требуется двум гидроциклам, чтобы пересечь реку. (Примечание: углы измеряются относительно оси x, показанной в примере.)
Раствор:
Решение:
Решение:
Вы перемещаете ящик вверх по погрузочной рампе длиной 10 футов. В верхней части пандуса ящик поднялся на высоту 3,00 фута. Каков угол пандуса относительно горизонтали?
Решение:
Решение:
Решение:
Решение:
Решение:
Два студента проводят эксперимент с поездом и мячом.Мишель движется на платформе, которую тянет поезд со скоростью 8,35 м / с по прямому горизонтальному пути; Гэри отдыхает на земле возле рельсов. Когда Мишель бросает мяч под начальным углом 65,0 ° над горизонталью, с ее точки зрения, Гэри видит, как мяч поднимается и опускается прямо над фиксированной точкой на земле. (A) Бросила ли Мишель мяч в сторону перед поездом или в задней части поезда? Объясните: (б) Какова была начальная скорость броска Мишель? (c) Какая была начальная скорость мяча, по мнению Гэри?
Решение:
Внедорожник исследует открытую пустыню на своем Hummer. Сначала он едет на 25 ° к западу от севера со скоростью 6,5 км / ч в течение 15 минут, затем на восток со скоростью 12 км / ч в течение 7,5 минут. Последний этап поездки она преодолевает за 22 минуты. Каковы направление и скорость движения на последнем этапе? (Предположим, что ее скорость на ноге постоянна и она возвращается к исходной точке в конце последнего этапа.)
Решение:
Решение:
Решение:
Решение:
Два самолета выруливают, приближаясь к терминалу. Самолет 1 рулит со скоростью 12 м / с на север. Самолет 2 рулит со скоростью 7,5 м / с в направлении 20 ° к северу от запада. (A) Каковы направление и величина скорости самолета 1 относительно плоскости 2? (б) Каковы направление и величина скорости плоскости 2 относительно плоскости 1?
Решение:
Решение:
Изначально частица движется со скоростью 4,10 м / с под углом 33,5 ° над горизонтом. Через две секунды его скорость составляет 6,05 м / с под углом 59,0 ° ниже горизонтали. Какое было среднее ускорение частицы за эти 2,00 секунды?
Решение:
Пассажир остановившегося автобуса замечает, что прямо за окном идет дождь. Когда автобус движется с постоянной скоростью, пассажир замечает, что падающие капли дождя теперь составляют угол 15 ° по отношению к вертикали. а) Каково отношение скорости капель дождя к скорости автобуса? (b) Найдите скорость капель дождя, учитывая, что автобус движется со скоростью 18 м / с.
Решение:
Большие часы Часы, которые звонят в колокол, известные как Биг Бен, имеют часовую стрелку длиной 9,0 футов и минутную стрелку длиной 14 футов, где расстояние измеряется от центра часов до кончика часов. рука. Какое расстояние между этими двумя стрелками, когда часы показывают 12 минут после четырех часов?
Решение:
Решение:
Ссылаясь на Пример, (а) какой курс должна иметь лодка, если она должна приземлиться прямо через реку от начальной точки? (б) Сколько времени потребуется для этой поездки, если ширина реки 25,0 м? (c) Предположим, что скорость лодки увеличилась, но по-прежнему желательно приземлиться прямо напротив начальной точки. Должен ли курс лодки быть больше вверх по течению, больше вниз по течению или по сэну, как в части (а)? Объяснять.
Решение:
Решение:
Когда две лодки приближаются к пристани, скорость лодки 1 относительно лодки 2 составляет 2,15 м / с в направлении 47,0 ° к востоку от севера. Если лодка 1 имеет скорость 0,775 м / с на севере, какова скорость (величина и направление) лодки 2?
Решение:
Решение:
Решение:
Решение:
Решение:
Ссылаясь на пример Предположим, что скорость лодки относительно воды составляет 7,0 м / с. (a) Под каким углом к оси x должна быть направлена лодка, если она должна приземлиться прямо через реку из своей исходной позиции? (b) Если скорость лодки относительно воды увеличится, будет ли угол, необходимый для перехода непосредственно через реку, увеличиваться, уменьшаться или оставаться неизменным? Объяснять.
Решение:
Ссылаясь на пример Предположим, что лодка имеет скорость 6,7 м / с относительно воды, а док на противоположном берегу реки находится в точке x = 55 м. и y = 28 м относительно начальной точки лодки. (a) На какой угол относительно оси x должна быть направлена лодка, чтобы достичь другого причала? (b) С учетом угла, указанного в части (а), какова скорость лодки относительно земли?
Решение:
Введение, формула, свойства, решаемые примеры и ответы на вопросы
Vector Math
Словарь векторов:
Математические операции с вектором
1. Сложение вектора
2. Вычитание вектора
3. Умножение векторов
Перекрестное произведение двух векторов a и b математически вычисляется как:
Определение вектора скалярного произведения двух векторов a и b математически задается как:
Примеры векторной математики:
Интересные факты:
