Задачи С1 ЕГЭ по физике
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Решение задач С1 ЕГЭ по физике
Критерии оценкивыполнения задания С1
Приведено полное правильное решение, включающее следующие элементы:
верно указаны физические явления и законы и дан верный ответ;
приведены рассуждения, приводящие к правильному ответу. 3 балла.
Представлено правильное решение и получен верный ответ, но
указаны не все физические явления или законы, необходимые для полного
правильного ответа;
ИЛИ не представлены рассуждения, приводящие к ответу.

Правильно указаны физические явления или законы, но
в рассуждениях содержится ошибка, которая привела к неверному ответу
ИЛИ содержится только правильное указание на физические явления или
законы
ИЛИ представлен только правильный ответ. 1 балл.
Все случаи решения, которые не соответствуют вышеуказанным
критериям. 0 баллов.
Задание С1 (демо)
На рисунке приведена электрическая цепь,
состоящая из гальванического элемента,
реостата, трансформатора, амперметра и
вольтметра. В начальный момент времени
ползунок реостата установлен посередине
и неподвижен. Опираясь на законы
электродинамики, объясните, как будут
перемещения ползунка реостата влево.
ЭДС самоиндукции пренебречь по
сравнению с ε.
1. Во время перемещения движка реостата
показания амперметра будут плавно
увеличиваться, а вольтметр будет
регистрировать напряжение на концах
вторичной обмотки.
 Примечание: Для
Примечание: Дляполного ответа не требуется объяснения
показаний приборов в крайнем левом
положении. (Когда движок придет в крайнее
левое положение и движение его прекратится,
амперметр будет показывать постоянную силу
тока в цепи, а напряжение, измеряемое
2. При перемещении ползунка влево сопротивление цепи
уменьшается, а сила тока увеличивается в соответствии с законом
Ома для полной цепи I=
цепи.
ε/(R+r), где R – сопротивление внешней
3. Изменение тока, текущего в первичной обмотке реостата
вызывает изменение индукции магнитного поля, создаваемого
этой обмоткой. Это приводит к изменению магнитного потока
через вторичную обмотку трансформатора.
4. В соответствии с законом индукции Фарадея возникает ЭДС
индукции εинд =-ΔΦ/Δt во вторичной обмотке, а
следовательно, напряжение U на ее концах, регистрируемое
вольтметром.
Задание С1 (2009)
Между двумя металлическими близко
укреплёнными на изолирующих
подставках, подвесили на шёлковой
нити лёгкую металлическую
незаряженную гильзу.
 Когда пластины
Когда пластиныподсоединили к клеммам
высоковольтного выпрямителя, подав
на них заряды разных знаков, гильза
пришла в движение. Опишите
движение гильзы и объясните его.
+
–
Под действием эл. поля пластин
изменится распределение электронов в
гильзе и произойдёт её электризация:
левая сторона будет иметь отрицательный
заряд, а правая сторона – положительный.
уменьшается с ростом расстояния
между ними. Поэтому притяжение к
пластинам ближних к ним сторон гильзы
будет больше отталкивания
противоположных сторон гильзы, и
гильза будет двигаться к ближайшей
пластине, пока не коснётся её.
В момент касания пластины гильза
приобретёт заряд того же знака, какой
имеется у пластины, оттолкнётся от неё и
будет двигаться к противоположной
пластине. Коснувшись её, гильза
поменяет знак заряда, вернётся к первой
пластине, и такое движение будет
периодически повторяться.

Задание С1 (2009)
Задание С1 (2009)
пластинах большой площади
располагаются заряды, указанные на
рисунке. Какой заряд находится на
правой плоскости третьей пластины?
1
2
3
q
2q
-3q
Суммарное электрическое поле внутри пластины
должно быть равно нулю, иначе в ней будет течь ток.
Значит, поле зарядов, расположенных левее этого
массива, должно компенсироваться полем зарядов,
расположенных справа от него.
Поэтому, во-первых, суммарный заряд всех трех
пластин должен быть распределён так, что
суммарный «левый» заряд равен (по величине и по
знаку) суммарному «правому» заряду.
Во-вторых, суммарный заряд всех трёх пластин
равен нулю:
q+2q-3q=0.
пластины (как и справа от него) должен
располагаться суммарный нулевой заряд. Это
достигается в том случае, когда на правой
поверхности третьей пластины находится 0.
Задание С1
Задание С1
Задание С1 (2010)
Задание С1
Задание С1
Задание С1
English Русский Правила
Задачи С1 ЕГЭ по физике презентация, доклад
Решение задач С1
ЕГЭ по физике
Критерии оценки выполнения задания С1
Приведено полное правильное решение, включающее следующие элементы:
приведены рассуждения, приводящие к правильному ответу. 3 балла.
Представлено правильное решение и получен верный ответ, но
указаны не все физические явления или законы, необходимые для полного правильного ответа;
ИЛИ не представлены рассуждения, приводящие к ответу. 2 балла.
Правильно указаны физические явления или законы, но
в рассуждениях содержится ошибка, которая привела к неверному ответу
ИЛИ содержится только правильное указание на физические явления или законы
ИЛИ представлен только правильный ответ.
Все случаи решения, которые не соответствуют вышеуказанным критериям. 0 баллов.
Задание С1 (демо)
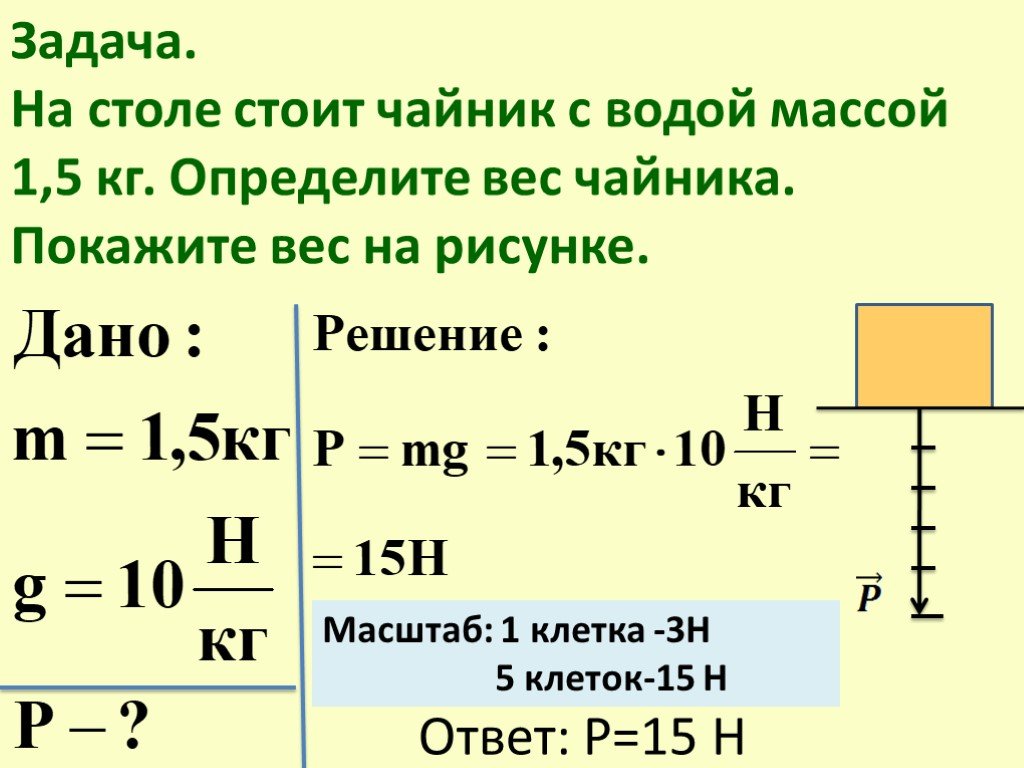
На рисунке приведена электрическая цепь, состоящая из гальванического элемента, реостата, трансформатора, амперметра и вольтметра. В начальный момент времени ползунок реостата установлен посередине и неподвижен. Опираясь на законы электродинамики, объясните, как будут изменяться показания приборов в процессе перемещения ползунка реостата влево.
ЭДС самоиндукции пренебречь по сравнению с ε.
1. Во время перемещения движка реостата показания амперметра будут плавно увеличиваться, а вольтметр будет регистрировать напряжение на концах вторичной обмотки. Примечание: Для
левое положение и движение его прекратится, амперметр будет показывать постоянную силу тока в цепи, а напряжение, измеряемое вольтметром, окажется равным нулю.
 )
)2. При перемещении ползунка влево сопротивление цепи
уменьшается, а сила тока увеличивается в соответствии с законом Ома для полной цепи I=ε/(R+r), где R – сопротивление внешней цепи.
3. Изменение тока, текущего в первичной обмотке реостата вызывает изменение индукции магнитного поля, создаваемого этой обмоткой. Это приводит к изменению магнитного потока через вторичную обмотку трансформатора.
4. В соответствии с законом индукции Фарадея возникает ЭДС индукции εинд =-ΔΦ/Δt во вторичной обмотке, а следовательно, напряжение U на ее концах, регистрируемое вольтметром.
Задание С1 (2009)
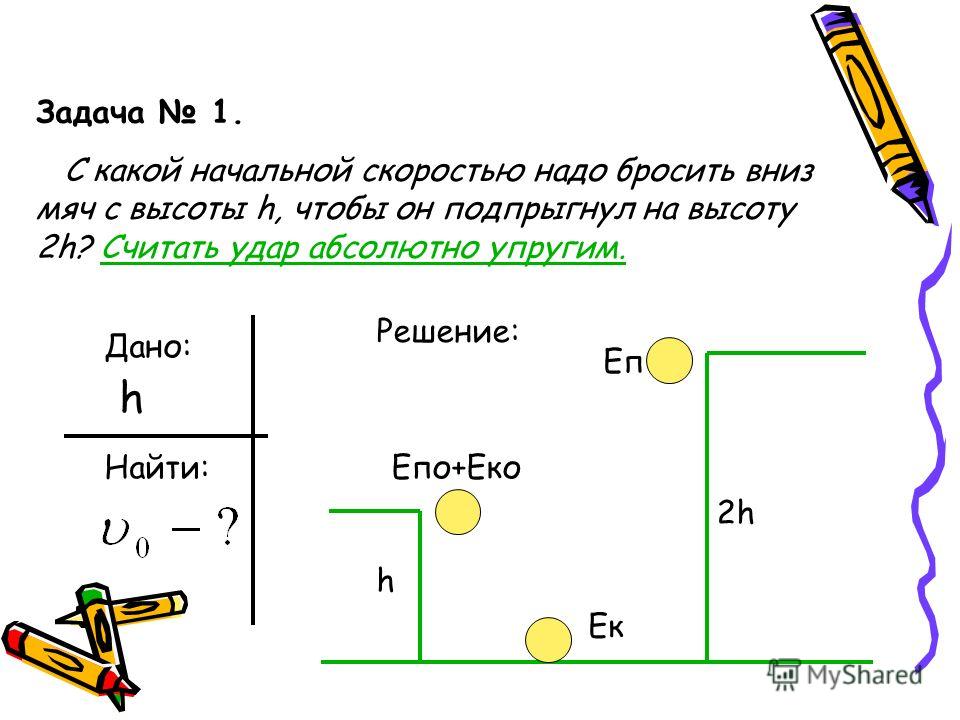
Между двумя металлическими близко расположенными пластинами, укреплёнными на изолирующих подставках, подвесили на шёлковой нити лёгкую металлическую незаряженную гильзу. Когда пластины подсоединили к клеммам высоковольтного выпрямителя, подав на них заряды разных знаков, гильза пришла в движение.
Под действием эл. поля пластин изменится распределение электронов в гильзе и произойдёт её электризация: левая сторона будет иметь отрицательный заряд, а правая сторона – положительный.
Сила взаимодействия заряженных тел уменьшается с ростом расстояния между ними. Поэтому притяжение к пластинам ближних к ним сторон гильзы будет больше отталкивания противоположных сторон гильзы, и гильза будет двигаться к ближайшей пластине, пока не коснётся её.
В момент касания пластины гильза приобретёт заряд того же знака, какой имеется у пластины, оттолкнётся от неё и будет двигаться к противоположной пластине. Коснувшись её, гильза поменяет знак заряда, вернётся к первой пластине, и такое движение будет периодически повторяться.
+
–
Задание С1 (2009)
Задание С1 (2009)
На трёх параллельных металлических пластинах большой площади располагаются заряды, указанные на рисунке.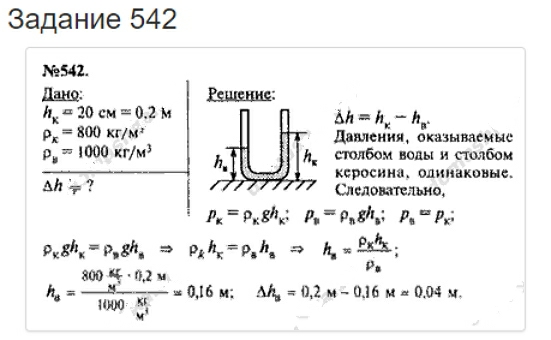 Какой заряд находится на правой плоскости третьей пластины?
Какой заряд находится на правой плоскости третьей пластины?
1
2
3
q
2q
-3q
Суммарное электрическое поле внутри пластины должно быть равно нулю, иначе в ней будет течь ток. Значит, поле зарядов, расположенных левее этого массива, должно компенсироваться полем зарядов, расположенных справа от него.
Поэтому, во-первых, суммарный заряд всех трех пластин должен быть распределён так, что суммарный «левый» заряд равен (по величине и по знаку) суммарному «правому» заряду.
Во-вторых, суммарный заряд всех трёх пластин равен нулю:
q+2q-3q=0.
Значит, слева от проводящего массива третьей пластины (как и справа от него) должен располагаться суммарный нулевой заряд. Это достигается в том случае, когда на правой поверхности третьей пластины находится 0.
Задание С1
Задание С1
Задание С1 (2010)
Задание С1
Задание С1
Задание С1
Скачать презентацию
Практические задачи: решения для конденсаторов — physics-prep.
 com
comПрактические задачи: решения для конденсаторов
1. (легко) Определите количество заряда, накопленного на одной из пластин конденсатора (4×10 -6 Ф) при подключении через аккумулятор на 12 вольт.
C = Q/V
4×10 -6 = Q/12
Q = 48×10 -6 C
2. (просто) площадь пластин, если емкость равна точно 1 Ф.
C = ε O A/D
1 = (8,85×10 -12 ) A/(2,0×10 -3 )
A = 2,3×10 8 M 2
3. (Умеренный) Рассчитайте напряжение батареи, подключенной к плоскому конденсатору с площадью пластин 2,0 см 2 и расстоянием между пластинами 2 мм, если заряд, накопленный на пластинах, составляет 4,0 пКл.
Площадь = 2,0 см 2 (1 м/100 см) 2 = 2,0×10 -4 м 2
C = ε o A/d
С = (8,85×10 -12 )(2,0×10 -4 )/(2,0×10 -3 )
C = 8,85×10 -13
C = Q/V
9 0905 8,805 4.
 0x10 -12 /V
0x10 -12 /V V = 4,5 вольта
4. (легко) Плоский конденсатор состоит из металлических пластин, каждая площадью 0,2 м 2 . Емкость 7,9 нФ. Определить расстояние между пластинами.
C = ε o A/d
7,9×10 -9 = 8,85×10 -12 (0,2)/d
d = 2,2×10 -4 m = 0,22 мм
5. (легко) Конденсатор (параллельная пластина) заряжается от батареи постоянного напряжения. Как только конденсатор достигает максимального заряда, батарея вынимается из цепи. Опишите любые изменения, которые могут произойти в количествах, перечисленных здесь, если пластины будут сдвинуты ближе друг к другу.
а. Заряд (Заряд, нанесенный на пластины, не меняется при извлечении батареи, поэтому заряд и плотность заряда остаются такими же, когда пластины сближаются.)
б. Емкость (Поскольку емкость C = ε o А/д, а площадь не меняется, любое уменьшение расстояния между пластинами (d) приведет к увеличению емкости. )
)
c. Напряжение (Поскольку C = Q/V, а заряд не меняется, увеличение емкости означает уменьшение напряжения.)
d. E-поле (Поскольку ΔV = -Ed, E-поле останется прежним, так как напряжение и расстояние уменьшатся пропорционально.)
6. (умеренная) Микросхемы памяти с произвольным доступом используются в компьютерах для хранения двоичной информации в форме «единиц» и «нулей». Один из распространенных способов сохранить единицу — это зарядить очень маленький конденсатор. Разумеется, тот же конденсатор без заряда представляет собой «ноль». Микросхема памяти содержит миллионы таких конденсаторов, каждый из которых соединен с транзистором (действующим как переключатель), образуя «ячейку памяти». Типичный конденсатор в ячейке памяти может иметь емкость 3×10 -14 F. Если напряжение на конденсаторе, показывающее «единицу», равно 0,5 В, определите количество электронов, которые должны двигаться по конденсатору, чтобы зарядить его.
C = Q/V
3×10 -14 = Q/(0,5)
Q = 1,5×10 -14 C
#electrons = общий заряд/заряд на электрон
#electrons = 1,5×10 -14 14 x10 -19
#electrons = 93750 электронов
7. (легко) C 1 = 10 Ф и C 2 = 5 Ф. Определить эффективную емкость C 1 и C 2 соединены последовательно и параллельно.
(легко) C 1 = 10 Ф и C 2 = 5 Ф. Определить эффективную емкость C 1 и C 2 соединены последовательно и параллельно.
Последовательно:
1/C = 1/C 1 + 1/C 2
1/C = 1/10 + 1/5
C = 3,3 F
Параллельно:
C = C 1 + C 2
C = 10 + 5 = 15 F
8. (умеренная) Если два конденсатора в вопросе № 7 были подключены к 50-вольтовой батарее, определите напряжение на конденсаторах для каждого типа подключения.
Для последовательного соединения:
Заряд каждого конденсатора равен заряду эффективной емкости.
C = Q/V
3.3 = Q/50
Q = 165 C
Для конденсатора 10 Ф:
10 = 165/В
В = 17 В
Для конденсатора 5 Ф:
5 = 165/В
В = 33 вольта
Для параллельного соединения:
Напряжение одинаковое (50 В) на каждом конденсаторе.
9. (умеренная) Оцените схему, показанную ниже, чтобы определить эффективную емкость, а затем заряд и напряжение на каждом конденсаторе.
Эквивалентная емкость 4 мкФ. Напряжение на эквивалентном конденсаторе равно 20 вольт.
Это напряжение также присутствует на обоих конденсаторах емкостью 2 мкФ, которые были созданы последовательными комбинациями в каждой ветви.
Найдите заряд каждого конденсатора емкостью 2 мкФ:
C = Q/V
2 мкФ = Q/20
Q = 40 мкКл
Конденсаторы емкостью 4 мкФ в каждой ветви имеют такой же заряд, что и конденсаторы емкостью 2 мкФ. Используйте это, чтобы найти напряжение на каждом:
C = Q/V
4 мкФ = 40 мкКл/В
V = 10 вольт
Таким образом, каждый из исходных конденсаторов емкостью 4 мкФ имеет заряд 40 мкКл и напряжение 10 вольт.
10. (умеренная) Оцените схему, показанную ниже, чтобы определить эффективную емкость, а затем заряд и напряжение на каждом конденсаторе.
Эффективная емкость 6 мкФ при напряжении 100 В.
Напряжение на конденсаторах 4 мкФ и 2 мкФ также равно 100 В
Заряд конденсатора 4 мкФ:
C = Q/V
4 мкФ = Q/100
Q = 400 мкКл
Заряд конденсатора емкостью 2 мкФ:
C = Q/В
2 мкФ = Q/100
Q = 200 мкКл
Все три конденсатора емкостью 6 мкФ также имеют заряд 200 мкФ.
Найдите напряжение для конденсаторов емкостью 6 мкФ:
C = Q/В
6 мкФ = 200 мкКл/В
В = 33,3 В
напряжение на каждом конденсаторе.
Эквивалентная емкость 6 мкФ. Напряжение на эквивалентной емкости составляет 40 В, как и напряжение на конденсаторах емкостью 3 мкФ, и такое же, как на конденсаторах емкостью 1 мкФ и 2 мкФ.
Найдите заряд конденсатора емкостью 1 мкФ:
C = Q/V
1 мкФ = Q/40
Q = 40 мкКл
Найдите заряд конденсатора 2 мкФ:
C = Q/В
2 мкФ = Q/40
Q = 80 мкКл
Найдите заряд конденсатора 3 мкФ:
C = Q/V
3 мкФ = Q/40
Q = 120 мкКл
Это одинаковый заряд на каждом из конденсаторов емкостью 6 мкФ.
Найдите напряжение на каждом из конденсаторов емкостью 6 мкФ:
C = Q/В
6 мкФ = 120 мкКл/В
В = 20 В
0205
К концу этого раздела вы сможете:
- Объясните, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
- Вычислите разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определите чистую емкость сети конденсаторов
Несколько конденсаторов можно соединить вместе для использования в различных приложениях. Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как 9.0215 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как 9.0215 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.
Серия Комбинация конденсаторов
На рис. 8.11 показано последовательное соединение трех конденсаторов, расположенных в ряд внутри цепи. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 8.1. При подключении этой последовательной комбинации к аккумулятору с напряжением V каждый из конденсаторов приобретает одинаковый заряд Q . Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q. Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентная емкость ) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы последовательного соединения имеют одинаковый заряд .
Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q. Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая эквивалентная емкость ) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы последовательного соединения имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с пластины первого конденсатора (обозначаем -Q-Q), он должен быть помещен на пластину второго конденсатора (обозначаем +Q), +Q) и так далее.
Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с пластины первого конденсатора (обозначаем -Q-Q), он должен быть помещен на пластину второго конденсатора (обозначаем +Q), +Q) и так далее.
Рисунок 8.11 а) Три конденсатора соединены последовательно. Величина заряда на каждой пластине равна Å . (b) Цепь конденсаторов в (а) эквивалентна одному конденсатору, который имеет меньшую емкость, чем любая из отдельных емкостей в (а), а заряд на его обкладках равен . .
Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны соответственно V1=Q/C1V1=Q/C1, V2=Q/C2V2=Q/C2 и V3=Q/C3V3=Q/C3. Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:
В=В1+В2+В3.В=В1+В2+В3.
Потенциал В измеряется на эквивалентном конденсаторе, удерживающем заряд Q и имеющем эквивалентную емкость CSCS. Вводя выражения для V1V1, V2V2 и V3V3, получаем
Вводя выражения для V1V1, V2V2 и V3V3, получаем
QCS=QC1+QC2+QC3.QCS=QC1+QC2+QC3.
Отменяя заряд Q , получаем выражение, содержащее эквивалентную емкость CSCS трех последовательно соединенных конденсаторов:
1CS=1C1+1C2+1C3.1CS=1C1+1C2+1C3.
Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.
Комбинация серий
Для последовательно соединенных конденсаторов обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:
1CS=1C1+1C2+1C3+⋯.1CS=1C1+1C2+1C3+⋯.
8,7
Пример 8.4
Эквивалентная емкость последовательной сети
Найдите общую емкость трех последовательно соединенных конденсаторов, если их отдельные емкости равны 1000 мкФ, 1000 мкФ, 5000 мкФ, 5000 мкФ и 8000 мкФ, 8000 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.7 с тремя членами.
Раствор
Мы вводим данные емкости в уравнение 8.7:
1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкF1CS=1,325 мкФ.1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкФ1CS=1,325 мкФ.
Теперь инвертируем этот результат и получаем CS=мкФ1,325=0,755мкФ.CS=мкФ1,325=0,755мкФ.
Значение
Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.
Параллельная комбинация конденсаторов
Параллельная комбинация трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рис. 8.12 (а). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих обкладках . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
8.12 (а). Поскольку конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих обкладках . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:
Q=Q1+Q2+Q3.Q=Q1+Q2+Q3.
В левой части этого уравнения мы используем соотношение Q=CPVQ=CPV, которое верно для всей сети. В правой части уравнения мы используем соотношения Q1=C1V, Q2=C2V, Q1=C1V, Q2=C2V и Q3=C3VQ3=C3V для трех конденсаторов в сети. Таким образом, мы получаем
CPV=C1V+C2V+C3V.CPV=C1V+C2V+C3V.
Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:
СР=С1+С2+С3. СР=С1+С2+С3.
Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.
Параллельная комбинация
Для конденсаторов, соединенных параллельно, эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,
CP=C1+C2+C3+⋯.CP=C1+C2+C3+⋯.
8,8
Рисунок 8.12 а) Три конденсатора соединены параллельно. Каждый конденсатор подключен непосредственно к аккумулятору. б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.
Пример 8,5
Эквивалентная емкость параллельной сети
Найдите общую емкость для трех конденсаторов, соединенных параллельно, учитывая, что их отдельные емкости составляют 1,0 мкФ, 5,0 мкФ и 8,0 мкФ, 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.
Стратегия
Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8. 8 с тремя членами.
8 с тремя членами.
Раствор
Ввод данных емкостей в уравнение 8.8 дает
CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ. CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ.
Значение
Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.
Сети конденсаторов обычно представляют собой некоторую комбинацию последовательных и параллельных соединений, как показано на рис. 8.13. Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.
Рисунок
8.13
а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. (б) C1C1 и C2C2 соединены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно C3.C3. Таким образом, эквивалентная емкость всей сети представляет собой сумму CSCS и C3.C3.
(б) C1C1 и C2C2 соединены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно C3.C3. Таким образом, эквивалентная емкость всей сети представляет собой сумму CSCS и C3.C3.
Пример 8,6
Эквивалентная емкость сети
Найдите общую емкость комбинации конденсаторов, показанной на рис. 8.13. Предположим, что емкости известны с точностью до трех знаков после запятой (C1=1,000 мкФ, C2=5,000 мкФ, (C1=1,000 мкФ, C2=5,000 мкФ, C3=8,000 мкФ).C3=8,000 мкФ). Округлите ответ до трех знаков после запятой.
Стратегия
Сначала мы определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы C1C1 и C2C2 включены последовательно. Их комбинация, обозначенная CS,CS, параллельна C3.C3.
Решение
Поскольку C1 и C2, C1 и C2 включены последовательно, их эквивалентная емкость CSCS получается с помощью уравнения 8. 7:
7:
1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.
Емкость CSCS подключена параллельно с третьей емкостью C3C3, поэтому мы используем уравнение 8.8, чтобы найти эквивалентную емкость C всей сети:
C=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ. =CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.
Пример 8,7
Сеть конденсаторов
Определите чистую емкость C комбинации конденсаторов, показанной на рис. 8.14, когда емкости равны C1=12,0 мкФ, C2=2,0 мкФ, C1=12,0 мкФ, C2=2,0 мкФ и C3=4,0 мкФ3=4,0 мкФ. Когда на комбинации сохраняется разность потенциалов 12,0 В, найти заряд и напряжение на каждом конденсаторе.
Рисунок 8.14 а) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.
Стратегия
Сначала мы вычисляем чистую емкость C23C23 параллельного соединения C2C2 и C3C3. Тогда C – это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.
Тогда C – это чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.
Раствор
Эквивалентная емкость для C2C2 и C3C3 равна
C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.
Вся комбинация из трех конденсаторов эквивалентна двум конденсаторам, включенным последовательно,
1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.
Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 8.14(b). Поскольку конденсаторы соединены последовательно, они имеют одинаковый заряд Q1=Q23Q1=Q23. Кроме того, конденсаторы имеют общую разность потенциалов 12,0 В, поэтому Q112,0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.
Теперь разность потенциалов на конденсаторе 1 равна
V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В.